TNF and IL-10 are major factors in modulation of the phagocytic cell environment in lung and lymph node in tuberculosis: a next generation two compartmental model

Abstract

Tuberculosis (TB) is one of the earliest recorded human diseases and still one of the deadliest worldwide. Its causative agent is the bacteria Mycobacterium tuberculosis (Mtb). Cytokine-mediated macrophage activation is a necessary step in control of bacterial growth, and early immunologic events in lymph node and lung are crucial to the outcome of infection, although the factors that influence these environments and the immune response are poorly understood.

Our goal is to build the next-generation two-compartmental model of the immune response to provide a gateway to more spatial and mechanistic investigations of Mycobacterium tuberculosis infection in the LN and lung. Crucial immune factors emerge that affect macrophage populations and inflammation, namely TNF-dependent recruitment and apoptosis, and IL-10 levels. Surprisingly, bacterial load plays a less important role than TNF in increasing the population of infected macrophages and inflammation.

Using a mathematical model, it is possible to distinguish the effects of pro-inflammatory (TNF) and anti-inflammatory (IL-10) cytokines on the spectrum of phagocyte populations (macrophages and dendritic cells) in the lung and lymph node. Our results suggest that TNF is a major mediator of recruitment of phagocytes to the lungs. In contrast, IL-10 is a factor in balancing the dominant macrophage phenotype in LN and lung.

1. Introduction

Tuberculosis (TB) is one of the earliest recorded human diseases and still one of the deadliest worldwide (WHO, 2009). Its causative agent, Mycobacterium tuberculosis (Mtb), primarily enters the lungs and initiates infection there. Phagocytic cells (macrophages and dendritic cells) are central to innate and adaptive immune responses to M. tuberculosis infection. Bacilli are inhaled into the lungs, taken up by dendritic cells and transported to a thoracic lymph node (LN) for priming of immune responses. Within the lung, resident and recruited macrophages engulf bacteria, and lymphocytes and more macrophages are recruited to form a granuloma. A granuloma is the environment in tissue that is the site of infection and functions to control bacteria and limit pathology in the lung. It is a collection of cells and bacteria that forms typically in a spheroid shape. This is defined as an inflammatory process, as the bacterium and host cell interactions lead to production of cytokines and other effector molecules. However, too much inflammation can lead to excessive pathology and a poor disease outcome for the host (Flynn, 2006). Cytokine-mediated macrophage activation is a necessary step in the control of bacterial growth (Flynn and Chan, 2001). In most cases, the host controls bacterial replication and dissemination, and maintains an asymptomatic infection (termed latent tuberculosis). A small percentage of humans do not control the infection and develop active tuberculosis, either as primary disease or reactivation of a latent infection.

Murine models of tuberculosis have been extensively used to identify important contributors to the immune response to this pathogen. In the mouse, it was demonstrated that the LN is the first site of expression of effector function for T cells, followed by spleen and lung (Chackerian et al., 2002). CD4+ T cells are recognized as the primary mediators of anti-tuberculosis immunity (Mogues et al., 2001; Orme, 1987), although CD8+ T cells also appear to have a role in resistance (Brookes et al., 2003; Lazarevic and Flynn, 2002). T cell priming (CD4+ and CD8+ T cells) that occurs in lymph nodes (LNs) is key to successful development of protective adaptive immunity and host resistance to Mtb infection (Orme, 1987). Once primed, T cells circulate to the lung to participate in the local immune response there. Early immunologic events in LN and lung are thought to be crucial to the outcome of infection but factors that influence these environments are poorly understood.

We previously developed a series of mathematical models that qualitatively and quantitatively characterize the cellular and cytokine network during infection in lung (Marino et al., 2007; Sud et al., 2006; Wigginton and Kirschner, 2001), and in lung and LN (Marino and Kirschner, 2004; Marino et al., 2004). In this work our goal is to develop the next-generation two-compartmental model to investigate more mechanistic details involved in the immune response during Mycobacterium tuberculosis infection. By focusing on cytokines important for the interplay between phagocyte populations and inflammation, we seek to indentify the control mechanisms for immune control in the lung and LN environments in tuberculosis.

We use a novel fitting scheme to match our updated model to experimental data (on bacterial and cell type numbers) from M. tuberculosis-infected mice generated herein. The mouse model was used for this study due to the availability of reagents and ability to obtain samples from lung and LN at multiple time points.

Model fitting was performed by a generalized non-linear least squares implementation (NLLS, see (Marino and Voit, 2006) for details). Sensitivity analyses were performed to determine key mechanisms affecting cellular processes during infection using an approach we have refined (Marino et al., 2008). Our results identified crucial immune factors that affect macrophage populations, namely TNF-dependent recruitment and apoptosis, and IL-10 levels. Surprisingly, TNF plays a more important role than bacterial load in increasing the population of infected macrophages and, together with IL-10, balancing the dominant macrophage phenotype in the LN and lung.

2. Materials and Methods

2.1. Experimental data

Data were collected from C57BL/6 mice infected with M. tuberculosis (H37Rv or Erdman strains) by exposure to aerosolized bacteria in an aerosolization unit (Intox, New Mexico) for 30 minutes. The dose of bacteria for different groups of mice was modulated by the concentration of M. tuberculosis in the nebulizer chamber (8.6e5/ml and 8.7e6/ml), resulting in a range of doses between 3–185 cfu/lung inocula doses. At time points 1, 8, 14, 21, 28, 43 and 99 days post-infection, a total of 80 mice were sacrificed (12 mice per each time point, except for day 1 where only 8 mice were sacrificed). Bacterial loads were measured, by plating serial dilutions of lung and LN homogenates on 7H10 agar and colonies were counted after incubation of plates at 37°C/5% CO₂ for 21 days. Day 1 is used to determine the inoculum dose in the lung (bacterial load at day 1 in the lymph node is 0, as well as all the activated T cells). Bacterial load data are shown in Figure S1 of Supporting Information online.

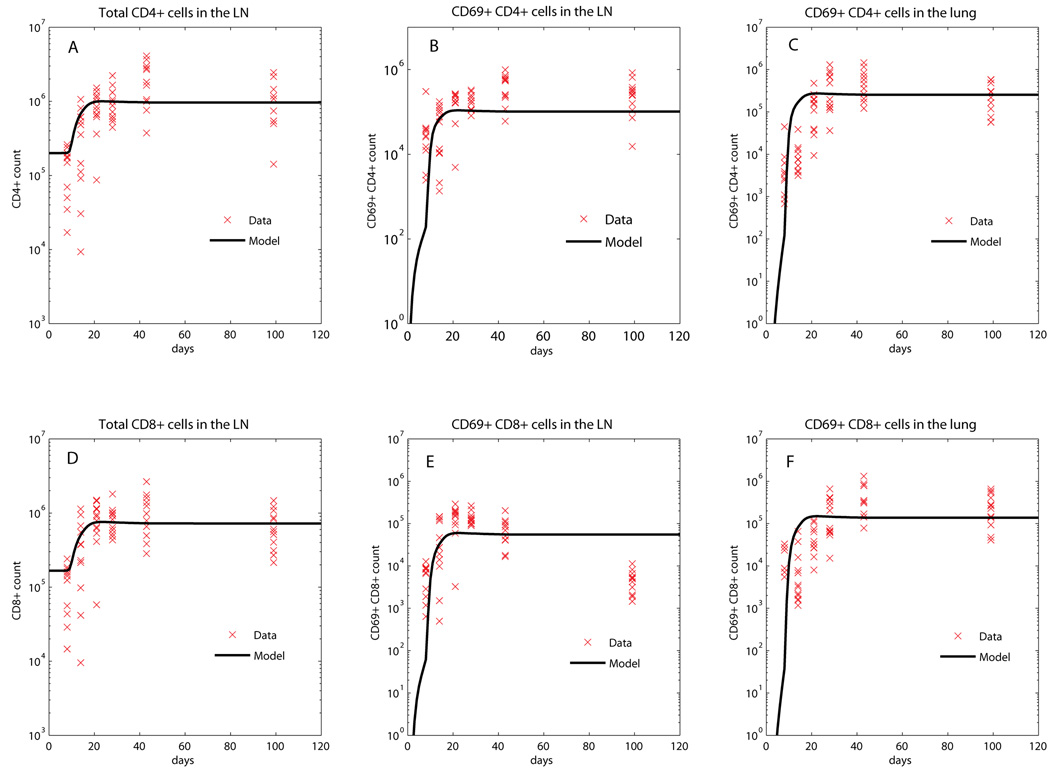
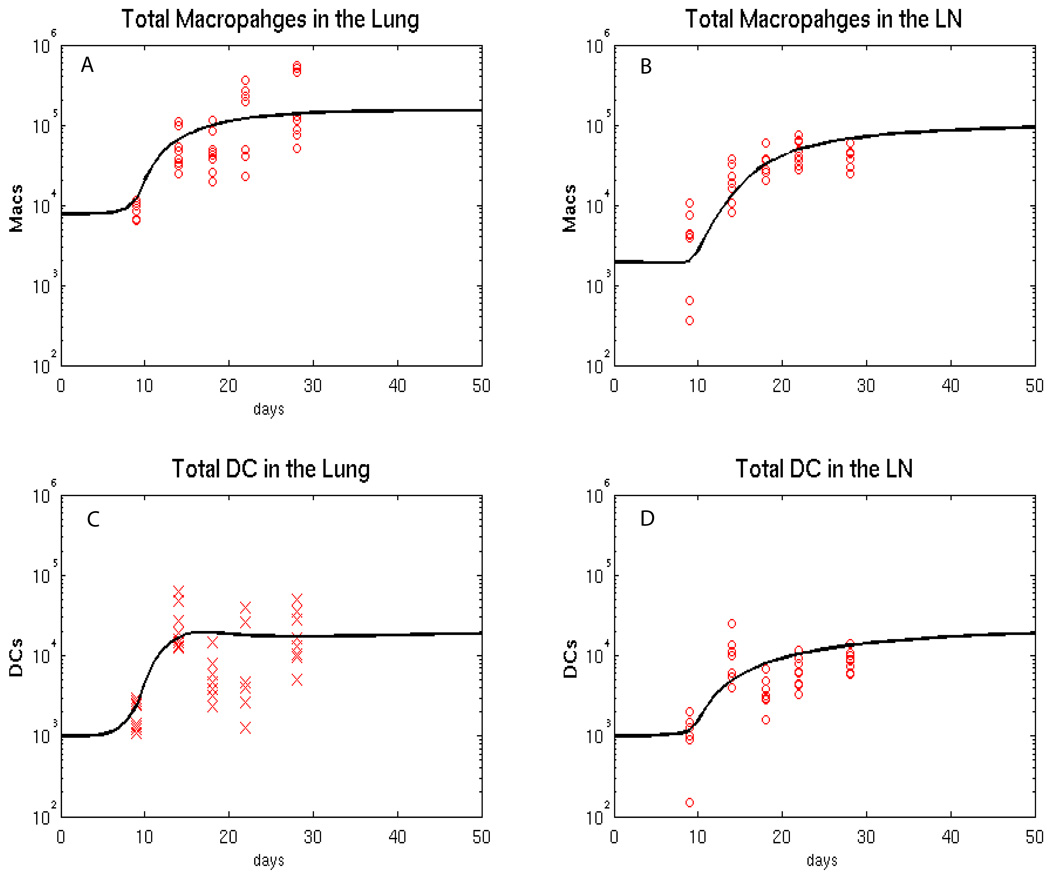
Total live cells in lungs and LNs were counted by trypan blue exclusion from single cell homogenate suspensions. Macrophage and dendritic cell data were obtained in a second experiment, where mice were sacrificed at day 9, 14, 18, 22, 28, (8 mice per time point). Additional data were collected in separate experiments for initial estimates for baseline (uninfected) values of macrophage, dendritic cell, and naïve CD4+ and CD8+ T cells before infection (day 0 of the experiments, Table S3). Flow cytometry was used to identify cell types in lungs and LN. Monocyte and lymphocyte gates, based on forward and side scatter, were used to identify populations, and specific markers to identify each type of cell. Anti-CD4 Alexa fluor 700 (BD, clone RM4–5) and anti-CD8 pacific blue (BD, clone 53–67) cell surface markers were used to identify T cells, while anti-CD69 FITC (BD, clone H1.2F3) was used as an early activation marker for T cells. Anti-GR-1 APCCy7 (BD, clone RB6–8C5), anti-CD11b PerCP (BD, clone Mac-1a) and anti-CD11c PECy7 (BD, clone HL3) were used to identify macrophages (CD11c−/CD11b+/GR-1-) and dendritic cells (GR-1-/CD11c+/CD11b+ or GR-1-/CD11c+/CD11b−). Figure 3 and Figure 4 show lymphocyte and macrophage/dendritic cell data, respectively.

Figure 3.

Fitting of the model (CD4+ and CD8+ T cell populations) to the data. The black curves represent the best fit of our mathematical model to the data, while all the data are shown by red x. Panel A: total number of CD4+ T cells in the LN (Naïve CD4 [N₄]+ Precursor Th1 $\text{Th}1[{\widehat{\mathrm{T}}}_1^{\text{LN}}]+\text{Th}1[{\mathrm{T}}_1^{\text{LN}}]$). Panel B: number of CD69+/CD4+ T cells in the LN ($(\text{Precursor}\text{Th}1[{\widehat{\mathrm{T}}}_1^{\text{LN}}]+\text{Th}1[{\mathrm{T}}_1^{\text{LN}}])$. Panel C: number of CD69+/CD4+T cells in the Lung (Precursor Th1 [T̂₁] +Th1 [ T₁ ]). Panel D: total number of CD8+T cells in the LN (Naïve CD8 [N₈]+Precursor effector CD8 $[{\mathrm{T}}_{80}^{\text{LN}}]+\text{IFN}-\mathrm{\gamma }$ producing CD8 $[{\mathrm{T}}_8^{\text{LN}}]+\text{CTL}[{\mathrm{T}}_{\mathrm{C}}^{\text{LN}}]$). Panel E: number of CD69+/CD8+ T cells in the LN (Precursor effector CD8 $[{\mathrm{T}}_{80}^{\text{LN}}]+\text{IFN}-\mathrm{\gamma }$ producing CD8 $[{\mathrm{T}}_8^{\text{LN}}]+\text{CTL}[{\mathrm{T}}_{\mathrm{C}}^{\text{LN}}]$. Panel F: number of CD69+/CD8+ T cells in the Lung (Precursor effector CD8 [ T₈₀ ]+IFN-γ producing CD8 [ T₈ ]+CTL [ T_C ]).

Figure 4.

Fitting of the model (macrophage and dendritic cell populations) to the data. The black curves represent the best fit of our mathematical model to the data, while all the data are shown by red x. We equally split CD11b+c+ and CD11b+c- cell data between Macs and DCs. We tried other alternative Mac/DC proportions (data not shown) where we first assigned 30% of CD11b+c+ to DC and 70% of CD11b+c+ to macrophages and then viceversa. The major impact is on DC data and the fitting was adjusted to match the new data. The major parameter changes were on DC recruitment parameters (lower rc₃ and rc₄, to match the lower DC data) and higher priming parameters (k₁₄ and k₁₇, to increase the resulting lower levels of primed T cells in the LN). Panel A: estimated total number of macrophages in the Lung. Panel B: estimated total number of macrophages in the LN. Panel C: estimated total number of DCs in the lung. Panel D: estimated total number of DCs in the LN.

2.2. Two compartmental mathematical model

We previously developed different mathematical models exploring cell trafficking between the lung and LN (Marino and Kirschner, 2004; Marino et al., 2004) and the role of TNF and CD8+ T cells in the lung (Marino et al., 2007; Sud et al., 2006) in M. tuberculosis infection. We now merge these two models to develop our next-generation model to consistently replicate data derived herein. The updated two-compartmental model has 32 equations with 210 parameters. Bacteria are not modeled explicitly; since we have precise data available on the dynamics of bacteria populations in this system, we use the time courses of bacteria as input functions for the model in the lung (CFUlung) and LN (CFUln) Section 2.13 and Figure S1 show the details of how the CFU functions are generated and used. The remaining equations in the system of non-linear ODE model comprise macrophage (resting, infected, classical and alternatively activated), dendritic cell (immature and mature) and lymphocyte populations in both lung and LN. Naïve CD4+ and CD8+ T cells are primed in the LN and migrate to the lung as both precursor or effector T helper cells and precursor or effector cytotoxic T lymphocytes (CTLs). These cells elicit their effector functions at the site of infection (lung) after becoming fully differentiated. Cytokines (TNF, IFN-γ, IL10 and IL12) are also explicitly modeled, both in lung and LN. Table I describes the variables in the model. A diagram describing the dynamics of macrophage populations in the lung is presented in Figure 1. The non-linear ordinary differential equation system is shown in Supporting Information online, as well as diagrams of the remaining cell dynamics.

Table 1.

list of all the variables represented in the 32 equations ODE system. Measure units are number of cells or bacteria in the whole organ (lung or lymph node) and pg/ml for cytokine concentrations.

Variable (# of equations)	Lung (18)	Lymph Node (20)
	Resting [M0], classically activated	Resting $[M_0^{LN}]$, classically activated
Macrophages (8)	[MA], alternatively activated [M2] infected [MI]	$[M_A^{LN}]$, alternatively activated $[M_2^{LN}]$, infected $[M_I^{LN}]$
Dendritic Cells (4)	Immature [IDC], Mature [MDCL]	Immature [IDCLN], Mature [MDC]
Lymphocytes (12)	Precursor Th1 [T̂1, Th1 [T1] Precursor effector CD8 [T80], IFN-γ producing CD8 [T8], CTL [TC]	Naïve CD4 [N4], Naïve CD8 [N8] Precursor Th1 $[{\widehat{T}}_1^{LN}],\text{Th}1[T_1^{LN}]$, Precursor effector CD8 $[T_{80}^{LN}]$, IFN-γ producing CD8 $[T_8^{LN}],\text{CTL}[T_C^{LN}]$
Cytokines (8)	TNF [Fα], IFN-γ [Iγ], IL 12 [I12], IL 10 [I10]	$\text{TNF}[F_{\alpha }^{LN}],\text{INF}-\mathrm{\gamma }[I_{\gamma }^{LN}],$ $\text{IL}12[I_{12}^{LN}],\text{IL}10[I_{10}^{LN}]$

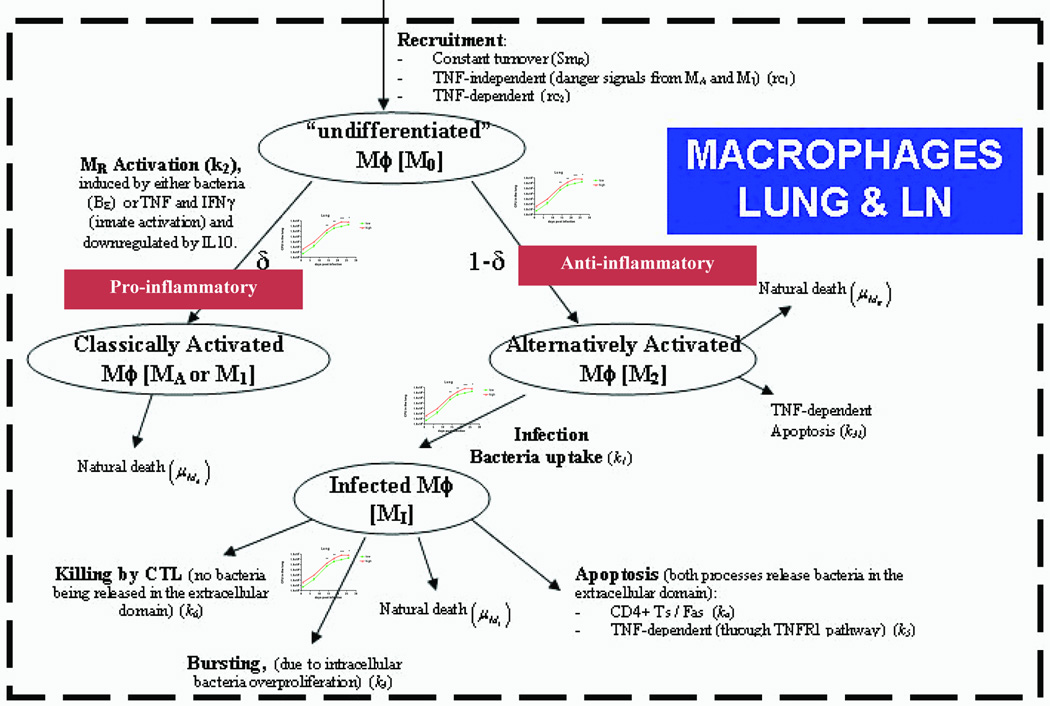
Figure 1.

Diagram of macrophage dynamics in the lung and lymph node that are represented in the model. The parameters in parenthesis represent how each mechanism is described in the model equations. CFU input/forcing functions are represented by the graphs (see Figure S1 for details on these graphs) on the branches describing M₀ differentiation to CAM (or as referred in the literature as M₁), AAM infection, and M_I bursting.

2.3. Macrophage dynamics: macrophage polarization functional

Similarly to a recent study (Day et al., 2009), we describe four different macrophage subpopulations, both in lung (equations (1)–(4)) and LN (equations (5)–(8)): uncommitted/resting/resident (M₀), infected (M_I), classically (M_A), and alternatively activated (M₂). Both sets of equations represent identical macrophage subpopulations, with identical terms and different parameter labels and values (where necessary). The pool of uncommitted/resting/resident macrophages (M₀) is referred to as resident macrophages. A diagram of macrophage dynamics is shown in Figure 1.

Equation (1) describes the dynamics of resident macrophages (M₀) in lung. A pool resides in the blood (as monocytes) and is constantly recruited to the lung. Monocyte differentiation produces a constant net turnover of resident macrophages, where the constant S_M0 is a function of M₀ death rate (µ_M0), alternative macrophage activation rate (k₇) and of the initial condition for M₀ (M₀(0)), namely S_M0 =(k₇+µ_M0)M₀(0) (similar functional forms are given for the constants S_M0a, s_IDC , S_IDCLN , S_N4 and S_N8. Recruitment is influenced by either inflammation, captured as a function of M_I and M_A (rc₁ term) or Tumor Necrosis Factor-TNFα (F_α, rc₂ term) (Algood et al., 2004; Hehlgans and Pfeffer, 2005).

We define the term d in the lung (see equation (1), equation (3), equation (4))

$$\mathrm{\delta }=(\left(\frac{{\mathrm{I}}_{\mathrm{\gamma }}}{{\mathrm{I}}_{\mathrm{\gamma }}+{\text{hs}}_2}\right)\left(\frac{\text{CFUlung}+{\mathrm{f}}_1{\mathrm{F}}_{\mathrm{\alpha }}}{\text{CFUlung}+{\mathrm{f}}_1{\mathrm{F}}_{\mathrm{\alpha }}+{\text{hs}}_3}\right)\left(1-\frac{{\mathrm{I}}_{10}}{{\mathrm{I}}_{10}+{\text{hs}}_{{\mathrm{I}}_{10}}}\right))$$

and the term δ_LN in LN (see equation (5), equation (7) and equation (8))

$${\delta }_{\text{LN}}=\left(\frac{{\mathrm{I}}_{\mathrm{\gamma }}^{\text{LN}}}{{\mathrm{I}}_{\mathrm{\gamma }}^{\text{LN}}+{\text{hs}}_{2\mathrm{a}}}\right)\left(\frac{\text{CFU}\text{ln}+{\mathrm{f}}_1{\mathrm{F}}_{\mathrm{\alpha }}^{\text{LN}}}{\text{CFU}\text{ln}+{\mathrm{f}}_1{\mathrm{F}}_{\mathrm{\alpha }}^{\text{LN}}+{\text{hs}}_{3\mathrm{a}}}\right)\left(1-\frac{{\mathrm{I}}_{10}^{\text{LN}}}{{\mathrm{I}}_{10}^{\text{LN}}+{\text{hs}}_{{\mathrm{I}}_{10}^{\text{LN}}}}\right)$$

to capture the effect of both cytokine environment and bacterial load on resident macrophage activation (Martinez et al., 2008). We refer to δ and δ_LN as macrophage polarization functionals or MPFs since they drive macrophage activation.

These MPF terms are defined as a function of three different cytokines (IFN-γ [I_γ], TNF [F_α] and IL-10 [I₁₀]) and live bacteria (CFUlung and CFUln). This follows since, upon infection (i.e., live bacteria), one of the first cytokines to be produced by mast cells, endothelial cells, macrophages and lymphoid cells is TNF (Korbel et al., 2008; Lin et al., 2007). TNF is crucial in recruitment of inflammatory cells. It initiates and sustains chemotactic action by virtue of stimulating chemokine production (CCL-2, 3, 4, 5, 8 and CXCL-9, 10, 11, (Algood et al., 2004)) and induction of adhesion molecules (such ICAM-1) on the vascular endothelium (Roach et al., 2002). Another key cytokine for triggering inflammation is IFN-γ. IFN-γ is predominantly secreted by innate cells (mainly natural killer cells, s_g terms in equation (26) and equation (30) in the Supporting Information online) right after infection and upon signaling by interleukin 12 (IL-12) and by T cells upon instruction by interleukin 12 (IL-12) and IL-18 (Korbel et al., 2008) and . In fact, a second wave of IFN-γ production occurs when adaptive immune cells are generated (α₅, α₆, α₈ and α₉, terms, see equation (26) and equation (30) in the Supporting Information online)) and is sustained throughout infection. The role of IL-10 is mainly anti-inflammatory. IL-10 down-regulates macrophage activation, inhibiting IFN-γ inducible genes, reactive oxygen and nitrogen intermediates (reviewed in (Moore et al., 2001)).

The main assumption of the model is that without infection (no live bacteria, i.e. CFUlung=CFUln=0), there is essentially no cytokine production, therefore no inflammation occurs and the MPFs are zero (i.e., δ = δ_LN = 0 ). As soon as infection occurs (CFUlung>0, CFUln>0), cytokine environment is altered, as well as the numbers and phenotypes of cells present at the site of infection (lung) and in LN. In the model, infection translates into δ > 0 and δ_LN > 0.

2.4. Classical versus alternatively activated macrophages

Depending on bacterial load (CFUlung and CFUln) and cytokine profile, resident macrophages (M₀) can differentiate either into a type 1 phenotype (classically activated macrophages, CAM, labeled as M_A in equation (3)), or a type 2 phenotype (alternatively activated macrophages, AAM, labeled as M₂ in equation (4)).

As described in Martinez, et al. (2008) AAMs can be divided in three subtypes: M_2a, M_2b, and M_2c. The phenotype of an alveolar macrophage (in the lung in a non-infectious case) seems to be closest to the M_2a type macrophage, rather than an M_2b type that produces much higher levels of IL-10. However, the pool of undifferentiated macrophages (M₀) is constantly replenish with infiltrating macrophages upon infection. While without infection the AAM (M₂) equations represent the M_2a phenotype, upon infection all the M2 phenotypes are collectively modeled in the AAM equations. In fact, in the absense of infection the default M₀ activation is biased towards an alternatively activated phenotype or M_2a (AAM, k₇ term, see equation (4)) (Martinez et al., 2008). Alveolar macrophage (M_2a) only produces IL-10 (and TNF) when infected with Mtb (Engele et al., 2002). Comparable data are shown by Giacomini et al (Giacomini et al., 2001) and Hickman et al (Hickman et al., 2002). Similar assumptions guided the modeling of macrophage phenotypes in the lymph node environment.

The main difference between classically and activated macrophage phenotypes in the model is that AAM becomes immediately infected (M_I, see equation (2)) when a bacterium is phagocytized (k₁ term), while CAM (M_A) immediately kills any bacteria that are phagocytized and thus cannot become infected (Day et al., 2009). We also assume that M_I cannot be activated in the classical way (through IFN-γ) but that AAM can be activated to become a M_A (k₂₁ term, see (Martinez et al., 2008)).

2.5. Switching Time

Based on a recent study (Day et al., 2009), the concept of switching time is defined as the time needed to switch from an AAM-dominated to a CAM-dominated lung environment on M. tuberculosis infection. The biological relevance of increasing switching times is that a delay in CAM presence in lung may be responsible for M. tuberculosis gaining an initial “foothold” (Day et al., 2009). One of the goals of our sensitivity analysis is to investigate which mechanisms affect switching time, both in lung and in LN.

2.6. Macrophage infection and killing

Once infected, macrophages (equation (2)) can either die naturally (µ_MI, burst, get killed by apoptosis or by cytotoxic mechanisms. Bursting (k₃) is caused by intracellular bacteria proliferation and is represented by a Hill term (n=2). M_I killing is due to the concentration of type 1 lymphocytes – T₁ (through Fas-FasL-induced apoptosis, k₄ term) (Vignali et al., 2008), soluble TNF (through TNFR1 apoptosis pathway, k₅ term) (Hehlgans and Pfeffer, 2005) and CTLs - T_C (through granzyme and perforin, k₆ term) (Flynn and Chan, 2001)). See Supporting Information online for details on equations describing lymphocyte and cytokine dynamics. The TNF-dependent apoptosis mechanism also affects M_A and M₂ (same rate, k₅ term). Equation (5)–Equation (8) are similar to equation (1)–Equation (4): they describe macrophage dynamics in LN (see Supporting Information online for equations). Macrophage dynamics in LN are an exact replica of those in lung (different rates and rate constants are only allowed for model fitting and uncertainty and sensitivity analysis).

2.7. Dendritic Cell Dynamics

A diagram (Figure S2) of dendritic cell dynamics in both compartments and the equations are presented in Supporting Information online. We model two types of dendritic cell populations in each compartment: immature dendritic cells (IDCs) and mature dendritic cells (MDCs). Recruitment and uptake/maturation mechanisms are present in both compartments. Upon bacterial uptake, DCs mature and migrate to the LN to prime naïve lymphocytes. We assume that DCs die in the LN and never migrate out.

2.8. Lymphocytes Dynamics

Diagrams (Figure S3, Figure S4 and Figure S5) and equations of lymphocytes dynamics in both compartments are shown in Supporting Information online. Naïve CD4+ and naïve CD8+ T cells are only present in LN, where they are naturally recruited and primed by MDCs. Precursor effector cells (T0 and T80) proliferate (clonal expansion) and migrate out of the LN into the blood to reach the site of infection. IL-10 acts as a down-regulatory mechanism for T cell expansion, in both compartments. T cell differentiation is mainly via MDCs but we also include a mechanism by which both infected and activated macrophages can act as antigen presenting cells and induce T cell differentiation (both in lung and LN). TNF-induced apoptosis is a shared regulatory mechanism for effector T cells in both compartments.

2.9. Cytokine production dynamics

Cytokines are produced by a large variety of cells involved both in innate and adaptive immunity (Lucey et al., 1996). We modeled four cytokines (TNF, IFN-γ, IL-12 and IL-10) in both compartments with identical mechanisms. Table S1 (Supporting Information online) lists cytokine production by cell types. TNF is mainly secreted by macrophages (activated and infected) and mature DC. The presence of bacteria (CFUlung) enhances TNF production by CAM (M_A), while IL-10 inhibits it. IFN-γ is mainly secreted by lymphocytes in close interaction with CAM and DCs (Barnes et al., 1993; Tsukaguchi et al., 1999). Additional sources of IFN-γ (e.g., natural killer cells - NKs) are present only if both bacteria and IL-12 are present (s_g term). IL-12 is mainly produced by mature DC (Giacomini et al., 2001) and CAM (Chensue et al., 1995; Fulton et al., 1996): IFN-γ increases IL-12 secretion, while IL-10 inhibits it (Fulton et al., 1998). Infected AAMs are the main producers of IL-10 (Giacomini et al., 2001; Hickman et al., 2002; Martinez et al., 2008).

2.10. Novel Model fitting approach

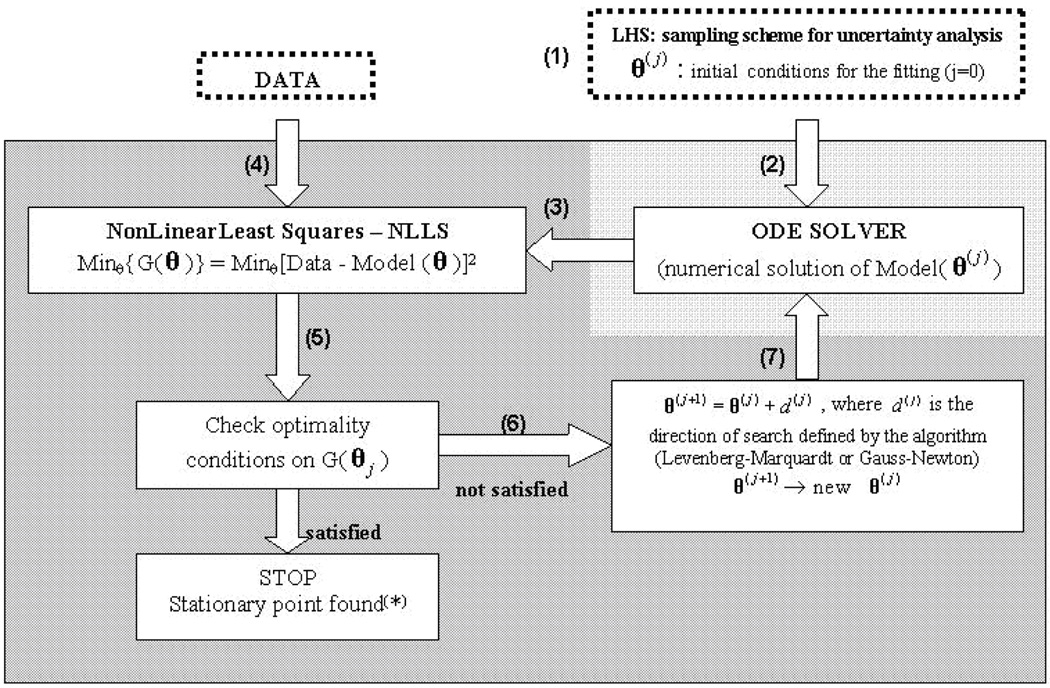
Our goals are to first recapitulate the mouse data with the model (model fitting) and second, to use the model to determine the key mechanisms that affect specific cellular processes, including recruitment, activation, infection and trafficking (using uncertainty and sensitivity analysis). To accomplish these goals we use tools from nonlinear programming, statistics and probability. Model fitting and parameter estimation of independent parameters of the mathematical model described in equations (1)–(32) are performed by implementing and solving a Non-Linear-Least-Squares (NLLS) problem (see Figure 2 for a schematic diagram of the main steps of the algorithm). Due to the large size of the system, it is necessary to initialize the algorithm with an adequate initial guess (vector θ⁽⁰⁾) for the set of parameters we want to estimate (vector θ). We accomplish this task by using techniques from uncertainty analysis (see Uncertainty and Sensitivity Analysis section).

Figure 2.

Schematic diagram of the model fitting module. minimization algorithm, numerical method. (*)Technically a stationary point is found (that could be either a local or global minimum, as well as a saddle point)

The parameter space was extensively sampled (5000 samples, Table S2 in Supporting Information online for the ranges used, LHS1 ranges column) by Latin Hypercube Sampling (LHS) and all trajectories that were outliers to the experimental data (LHS experiment 1, LHS1) were qualitatively rejected. Then, we visually selected one of the remaining trajectories (i.e., the one that most closely fit the data). The corresponding set of parameter values were used as a starting point for the NLLS fitting algorithm (i.e. θ⁽⁰⁾, see step (1) in Figure 2). We did not use any quantitative criteria to select the trajectories that most closely fit the data (e.g., Sum of Squared Errors - SSE). The purpose of this preliminary step (LHS1) was to select a qualitatively adequate initial condition for the fitting and ensure that we start the optimization close enough to a local optimum.

Since we seek to indentify the key mechanisms for immune control in lung and LN environments during M. tuberculosis infection, we focused our analysis only on parameters related directly to recruitment, infection/uptake, activation, killing, apoptosis, priming and trafficking. We fit only 130 of the 210 parameters of the model: 80 parameters (primarily related to cytokine production rates and half-life parameters) have been set to reasonable values (based on published models and the results of LHS1). Since the model is specified as an ordinary differential equation (ODE) system, a numerical solver generates temporal dynamics for each variable at each iteration of the optimization algorithm for each parameter choice (vector θ^(j), see step (2)). The numerical predictions (step (3)) for the time span under analysis are then compared to the data (step (4)). If optimality conditions are met (step (5)), the algorithm stops. Otherwise, new parameter choices are selected (i.e., θ^(j+1), see step (6)) and passed again to the numerical solver (step (7)). Model fitting has been performed by superimposing reasonable box constraints on parameter values such as maximum and minimum rates and half saturation constants. See Marino et al (2006) for details on the fitting algorithm implementation. Matlab© (Copyright 1984–2009 The MathWorks, Inc. Version 7.9.0.529 (R2009b) 32-bit 3, August 12, 2009, www.mathworks.com) platform and its numerical methods (ode15s function) were used to numerically solve the system of 32 non-linear ordinary differential equations, as well as to perform model fitting (lsqcurvefit function in the Optimization toolbox).

2.11. Model validation: virtual deletion and depletion

To validate the mathematical model, we recapitulate experimental approaches and known data, for example, TNF gene knockouts and TNF neutralization studies. These can be simulated with our mathematical model as virtual deletion and depletion simulations, respectively, as previously described (Marino et al., 2007). Virtual deletions remove an element from the system at day zero while virtual depletions mimic experimental conditions where an element can be depleted or neutralized via antibody treatment at any time during the infection. We use the time course of infected macrophages as a proxy for infection progression (since bacterial time courses are used as input/forcing functions and are fixed).

2.12. Uncertainty and Sensitivity Analysis to reveal key factors that control immune dynamics

There are variances in many of the parameter values of the mathematical model due to extensive variability in the data, which often are incomplete. Such variances require a systematic evaluation of the uncertainty in the system in order to assess effects of uncertainties in our parameter estimation on model outcomes. The purpose of uncertainty analysis is to quantify the degree of confidence in the existing experimental data and parameter estimates. We use Latin Hypercube Sampling (LHS) to extensively and efficiently explore the parameter space. LHS is the most efficient sample-based approach among the more general class of Monte Carlo methods (see (Marino et al., 2008) for a review).

LHS allows an un-biased estimate of the average model output, with the advantage that it requires fewer samples than simple random sampling to achieve the same accuracy (Mckay et al., 1979). It is a so-called stratified sampling without replacement technique, where the random parameter distributions are divided into N equal probability intervals, which are then sampled. N represents the sample size.

Sensitivity analysis (SA) is a method for quantifying uncertainty in any type of complex model. The objective of SA is to identify critical inputs (parameters and initial conditions) of a model and to quantify how input uncertainty affects model outcome(s). We use a generalized correlation coefficient, namely partial rank correlation coefficient (PRCC) as sensitivity analysis index. PRCC is the most efficient and reliable among the sample-based indexes (Saltelli and Marivoet, 1990) and it provides a robust sensitivity measure for nonlinear but monotonic relationships between inputs and outputs, as long as little to no correlation exists between the inputs (see (Marino et al., 2008) for details). Matlab scripts to perform US analysis are available online at http://malthus.micro.med.umich.edu/lab/usanalysis.html (Marino et al., 2008).

We performed two LHS experiments. The purpose of the first (LHS1) was to select an adequate initial condition for the NLLS algorithm. LHS1 explores large ranges (several logs) for all parameters. The set of outputs generated is filtered and only the trajectories close enough to the data are retained. We then select one trajectory (that qualitatively recapitulated the data) and the corresponding set of parameter values as the initial condition for the optimization algorithm in the model fitting module. The second LHS experiment (LHS2) was performed after an adequate fit to the data was obtained. LHS2 experiment comprises 2500 samples where the parameter estimates resulting from the model fitting step are used as averages of uniform probability density function distributions (Table S2, column Baseline (best fit)). They are multiplied by 1e⁻² and 1e² to get minimum and maximum for each interval of variation for the sampling of LHS2. Our sensitivity analysis is based on the outputs generated by the LHS2 experiment.

When performing sensitivity analyses it is necessary to identify the output(s) that will be correlated with parameter dynamics. Outputs such as cell numbers, recruitment, differentiation, and activation of cells for the sensitivity analysis performed here were chosen to indentify key mechanisms for immune control in the lung and LN environments following infection. Specifically, we correlate changes in parameters with numbers of infected and activated macrophages, mature and immature DCs, switching time (the time needed to switch from an AAM dominant to a CAM dominant lung environment after infection) and macrophage polarization functional.

2.13. Novel use of Data on Bacterial levels as a forcing function

One main assumption throughout the model building process is that data on bacterial counts (see Figure S1 in the Supporting Information online) are used as external input/forcing functions for the ODE model. Median trajectories as CFU in lung (CFUlung) and LN (CFUln) were used for the model fitting and parameter estimation. In order to use the CFU time course data as input/forcing functions for the two-compartmental ODE model, a stepwise linear interpolation is implemented for each time step that is selected by the numerical solver. The ODE solver uses a variable step size algorithm to obtain the numerical solutions and the stepwise linear interpolation is necessary to generate continuous set of data for the CFU time courses.

To account for the effects of bacterial numbers in our uncertainty and sensitivity analysis, we captured the effect of bacterial load over time with a parameter linked to what we labeled virtual CFU trajectories, generated as follows. For each time point, the min and max experimental data values are selected and used as extremes of a uniform probability distribution. We defined 7 ranges for the lung data (one per each day on which CFU data have been collected in lung, i.e. day 1, 8, 14, 21, 28, 43 and 99) and 6 ranges for LN data (one per each day on which CFU data have been collected in LN, i.e. day 8, 14, 21, 28, 43 and 99). We then apply LHS to generate N samples for each range in both compartments. Each set of N values is then sorted and labeled sequentially, from 1 to N. Virtual CFU trajectories are generated by connecting each sample by stepwise linear interpolation and we only connect the data points with the same label (see Figure S6, Panel A). For example, the virtual trajectory k (k<N) connects over time all the samples labeled with k. The only constraint superimposed was that virtual trajectories 1 and N connect the actual minimum and maximum points (taken from the data and not from the samples), respectively (see Figure S6, Panel B). The independence condition required by LHS is then fulfilled by randomly shuffling the sequence 1, 2, …., N. This sequence is then used as our CFU parameter for sensitivity analysis. If either bacterial levels in lung (CFUlung) or LN (CFUln) show a significant PRCC with respect to the output under study, then we speculate with confidence that different bacterial dynamics have an impact on that particular output.

3. Results

3.1. Model fitting and parameter estimation

Figure 3 and Figure 4 show the NLLS algorithm best fit on the experimental data for T cell, macrophage and dendritic cell populations in lung and LN generated herein. For cell types where we do not have experimental data, we predict the dynamics of these populations (e.g. infected versus activated macrophages, or mature versus immature dendritic cells) in lung and LN (Figure 5 and Figure 6). We discuss in detail the best fit results and parameter estimate values in the Comparing parameter estimates section of Supporting Information online.

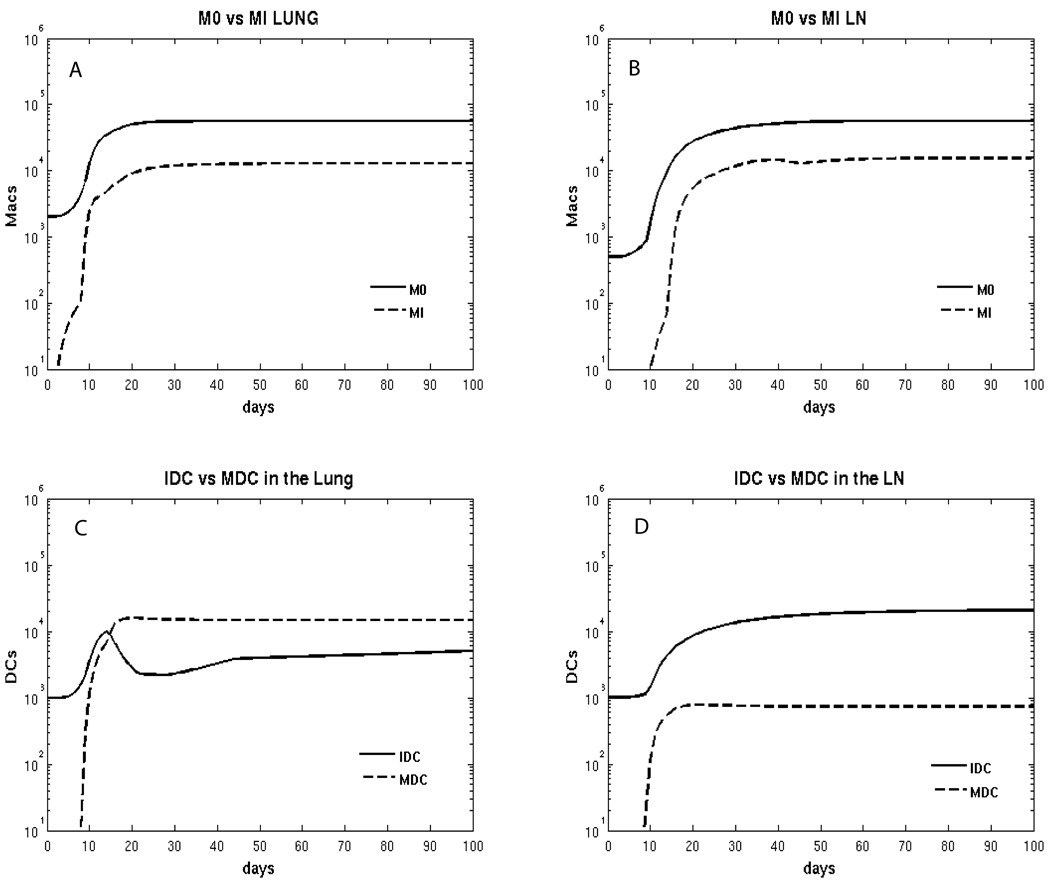
Figure 5.

Model predictions for macrophage and dendritic cell subpopulations. Panel A: total number of resident (M₀) and infected (M_I) macrophages in the Lung. Panel B: total number of resident (M₀) and infected (M_I) macrophages in the LN. Panel C: total number of immature and mature DCs in the lung. Panel D: total number of immature and mature DCs in the LN.

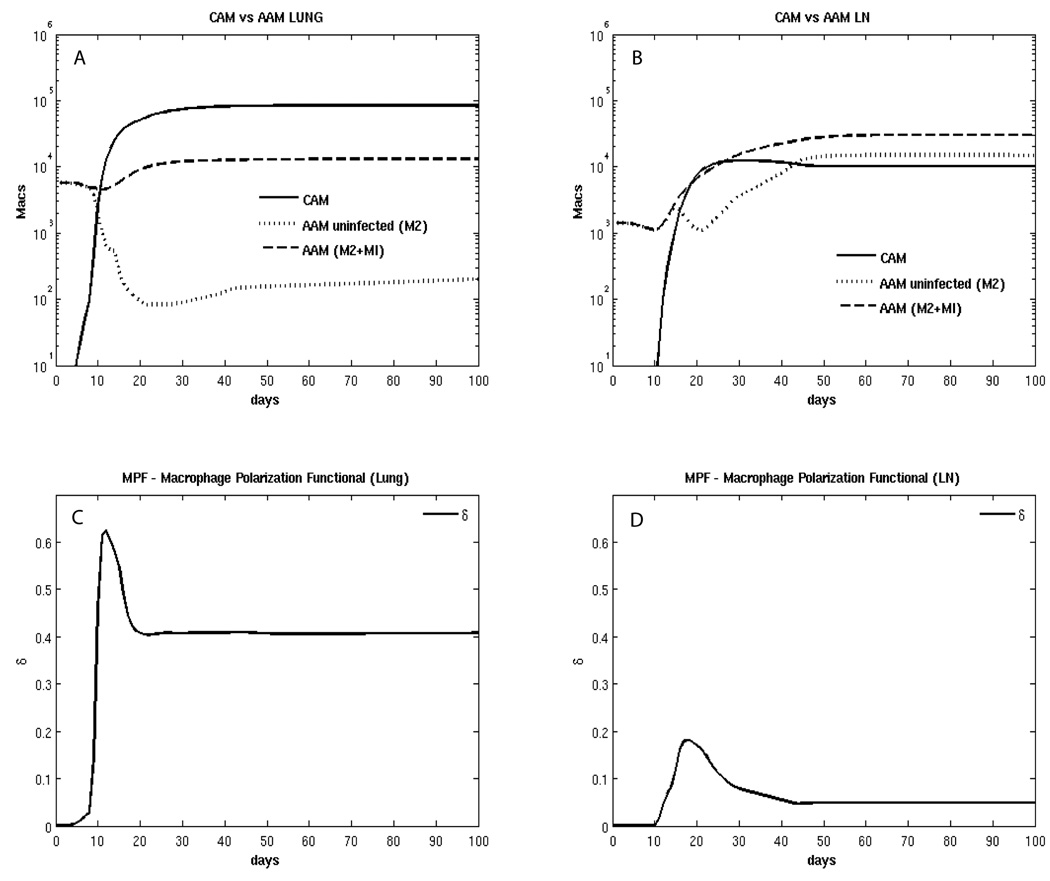
Figure 6.

Model predictions for macrophage and dendritic cell subpopulations. Panel A: total number of classically activated (CAM) and alternatively activated (AAM) macrophages in the Lung. AAM are divided between uninfected (M2) and total (M2 + MI). Panel B: total number of classically activated (CAM) and alternatively activated (AAM) macrophages in the LN. AAM are divided between uninfected (M2) and total (M2 + MI). Panel C: dynamics of δ, defined as Macrophage polarization functional (MPF) in the lung. Panel D: dynamics of δ_LN, MPF in the LN.

3.2. T-cell fitting

In all cases, we adequately replicated the experimental data, with the exception of the late decline of CD8+CD69+ T cells observed in LN (Figure 3E). This decline is not mirrored in the CD4+CD69+ T cell data in LN (Figure 3B). The reasons for this decline remain unclear. Possibilities include a reduction in antigen availability threshold for CD8+ T cell activation, or unresponsiveness of CD8+ T cells to priming in infected LN after a period of infection. It is also possible that CD69 is not a reliable activation marker, especially for later in infection when other factors, such as cytokines, might affect expression of CD69. Specific reagents for tracking primed T cells (e.g. MHC Class I and II multimers) are necessary to accurately assess M. tuberculosis-specific primed and effector T cells. Fitting of CD69+CD8+ T cells in the LN was not improved when parameters directly affecting naïve T cell recruitment, T cell proliferation and/or differentiation in the LN were varied, even by several orders of magnitude (data not shown). In addition, no decline was observed in effector CD8+ T cell data in the lung (Figure 3F), suggesting that mechanisms other than CD8+ T migration from the LN affect effector CD8+ T cell numbers in lung.

3.3. Macrophage fitting and prediction

Figure 4 shows the fitting results for total macrophage (A, B) and dendritic cell (C, D) populations in lung and LN compartments. Both cell types increase 2-fold during infection.

Our model predicts that resting (Figure 5A, B) and activated (Figure 6A, B) macrophages comprise the large majority of the macrophage populations in lung and LN. In agreement with the literature (Cooper, 2009), our prediction indicates that infected macrophages represent approximately 1–10% of the total macrophage population (Figure 5A, B). The model demonstrates that there is an initial increase in AAM, followed by a large increase in CAM (at day 10 post infection) in lung (Figure 6A). However, in LN, there is a much smaller increase in CAM, and at later time points, the AAM and CAM populations are equal in the LN (Figure 6B).

This difference is likely due to corresponding macrophage polarization scenarios (or MPF, see Figure 6C, D), with 2–4 fold higher CAM polarization occurring in lung. Less MPF corresponds in the model to fewer classically activated macrophages, which may contribute to impaired control of infection. There are also higher bacterial numbers in lung at all time points, compared to LN (see Figure S1), affecting macrophage polarization.

In the “best fit” scenario shown in Figure 6, we predict a faster switching time when comparing to the results of Day et al (Day et al., 2009). Our switching time is within 10 to 13 days in the lung (versus 50 days predicted by Day et al., see Figure 2A in (Day et al., 2009)), and 17 to 22 days in the LN (not predicted by Day et al). Our uncertainty and sensitivity analysis experiments (LHS2, see Sections 3.6–3.8 and Table S4) resulted in values for switching time up to 60, 70 and 106 days in the lung and 27–30 days in the LN (data not shown). However, the fitting in those cases was not good. One possible explanation is that we modeled murine infection data, while Day et al predicted human TB infection

3.4. Dendritic cell fitting and predictions

Comparing lung and LN compartments, the scenario predicted for the dendritic cell subsets shows completely different profiles. By as early as 2 weeks post infection, mature DCs represent the majority of DCs in the lung (Figure 5C), while in LN they are more than 1 log lower than the immature phenotype (Figure 5D), probably due to the difference in the amount of M. tuberculosis bacilli in each compartment available for interaction with DCs. The first mature DCs appear in LN 10–15 days post infection, likely as a result of trafficking of infected DC from the lung; this is in line with published experimental findings (Chackerian et al., 2002; Reiley et al., 2008; Wolf et al., 2008), and may account for the relatively slow initiation of the adaptive T cell response to this pathogen.

3.5. Model validation: virtual depletions

We focused our model validation on virtual depletions of three cytokines represented in the model: TNF, IFN-γ and IL-10. Since CFU data are available to day 99 during infection, we start the depletions at day 100.

Experimental data demonstrate a key role for both TNF (Flynn et al., 1995) and IFN-γ (Flynn et al., 1993) in mounting and/or maintaining a protective response to M. tuberculosis (mice and humans), while data on IL-10 depletion are not conclusive. Some data point to necessary roles for IL-10 in infection control (Denis and Ghadirian, 1993; Murray et al., 1997; Turner et al., 2002), while others suggest IL-10 plays no part in the dynamics (Erb et al., 1998; North, 1998).

Our virtual TNF depletion experiment confirms the key role of TNF demonstrated in the literature (Ehlers, 2003; Flynn et al., 1995): infected macrophage populations (in lung and LN) increase after TNF is depleted from both compartments (data not shown), recapitulating that TNF depletion is detrimental for the host. Similar dynamics are confirmed in virtual IFN-γ depletion (data not shown). Virtual IL-10 depletion suggests a key regulatory role for IL-10 in MDC maturation and trafficking to the LN (MDCs in LN significantly increase after IL-10 depletion, data not shown), as well as in controlling classical macrophage activation and macrophage polarization, especially in the lung (the MPF term δ reaches its maximum after IL-10 depletion).

3.6. TNF effects on phagocyte populations and macrophage polarization

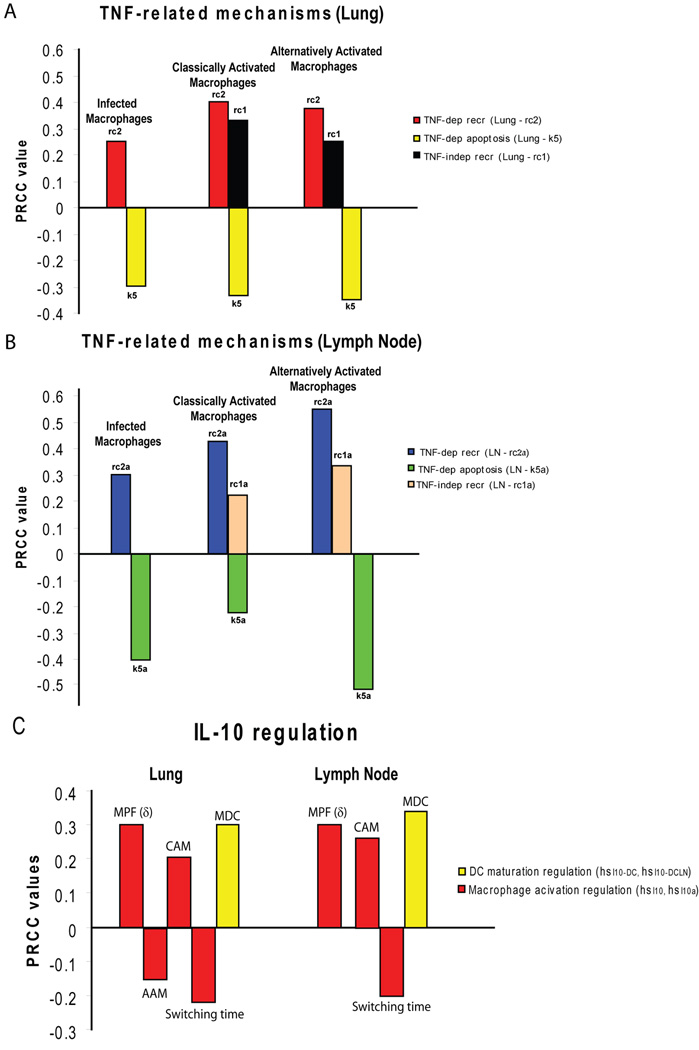
From our sensitivity analysis results, TNF emerges as a major factor in determining macrophage and dendritic cell phenotypes and numbers (Figure 7A, B, Table S4). TNF-dependent, but not TNF-independent recruitment of resting macrophages (rc₂, rc_2a) significantly increased the number of infected and activated macrophages (both CAM and AAM), in lung and LN. This is likely due to an increase in the potential pool of new resident macrophages for infection and activation. TNF-dependent recruitment of immature DCs to the lung (rc₄) also has a positive impact on the number of mature DCs in the same compartment (Table S4). TNF-independent recruitment of resting macrophages (rc₁ and rc_1a) appears only to positively affect the AAM population in lung and LN (Figure 7A, B). TNF-dependent apoptosis mechanisms of infected macrophages (k₅, k_5a) are generally the strongest negative regulator of all macrophage populations, both in lung and LN (Figure 7A, B).

Figure 7.

Sensitivity analysis results for the LHS2 experiment. The correlation index is Partial Rank Correlation Coefficient (PRCC) and it is shown on the y-axes- only significant results are shown. In this context, a positive impact of a particular mechanism on a specific output (positive PRCC) means that if that mechanism is increased/enhanced, the output will likely increase, or vice versa. On the other hand, a negative impact (negative PRCC) is when an increase in a specific mechanism results in a decrease in the output, and vice versa. There is a strict criteria for significance (p<1e-3) and only PRCC>±0.15 are shown. Panel A: TNF-related mechanisms affecting macrophage numbers (infected, CAM and AAM) in the lung at day 100 post infection. Panel B: TNF-related mechanisms affecting macrophage numbers (infected, CAM and AAM) in LN at day 100 post infection. Panel C: IL-10-related mechanisms affecting MPF (δ), activated macrophage (CAM and AAM) and mature DC numbers, as well as switching time, in each compartment (lung and lymph node).

3.7. Effects of macrophage and DC infection rates on phagocyte populations and macrophage polarization

Higher macrophage infection rates in the lung and LN (k₁ and k_1a) obviously increase the number of infected macrophages, but they also increase MPF in the lung early in infection (Table S4). Higher overall macrophage infection rates reduce the number of AAM in both compartments, likely due to the pro-inflammatory cytokine production by macrophages in response to infection. The mature DC population is positively affected by higher uptake/infection rates (k₁₂ and k_12a) in both compartments (Table S4): higher uptake rate by DC in the lung has a strong effect only very early during infection, where more MDC are generated in the lung and, as a consequence, more MDC can migrate to the LN. Bacterial dynamics have a modest positive effect on macrophage infection in the lung and on DC maturation in both compartments (Table S4).

3.8. IL-10 effects on phagocyte populations

The effect of IL-10 on total numbers of CAM and MDC is represented by the term $\left[1-\left(\frac{{\mathrm{I}}_{10}}{{\mathrm{I}}_{10}+{\text{hs}}_{{\mathrm{I}}_{10}}}\right)\right]$ in the MPF terms δ (equation (1), equation (3) and equation (4)) and δ_LN (equation (5), equation (7) and equation (8)). The sensitivity analysis predicts that hs_I10 is strongly positively correlated with numbers of these cells (Figure 7C). This follows since mathematically this term simplifies to $\left[\frac{{\text{hs}}_{{\mathrm{I}}_{10}}}{{\text{hs}}_{{\mathrm{I}}_{10}}+{\mathrm{I}}_{10}}\right]$ which gets smaller as IL-10 levels get larger and as hs_I10 gets much larger compared to IL-10. IL-10 regulation (hs_I10 and hs_I10a) is consistently important for balancing CAM and AAM in the lung, as well as dendritic cell maturation (hs_I10-DC and hs_I10-DCLN) and MPF (Figure 7C): more IL-10 results in a decrease in CAM and MDC, and an increase in AAM, in lung and LN. This has the effect of dampening MPF in the lung. This result agrees with a published study where IL-10 may limit DC maturation and migration upon bacterial uptake (Demangel et al., 2002). Switching time (AAM to CAM environment) is negatively affected by higher IL-10 saturation thresholds: more IL-10 is needed to skew the macrophage population to an AAM phenotype.

Not surprisingly, the switching time and the numbers of CAM and AAM in both the lung and the lymph node are dependent on their respective activation rates (CAM: k₂ and k_2a; AAM: k₇ and k_7a). The activation rates for AAM have a significantly positive effect on the total number of infected macrophages, since AAM cannot eliminate bacilli efficiently (Table S4).

4. Discussion

Mycobacterium tuberculosis (Mtb), the causative agent of tuberculosis (TB), is an extraordinarily successful pathogen that primarily infects the lungs. In most cases, the human host can control bacteria replication and dissemination, and maintain an asymptomatic infection (termed latent tuberculosis). A small percentage of humans do not control the infection and develop active tuberculosis, either as primary disease or reactivation of a latent infection (due to factors such as HIV infection and aging). Why and how individuals experience different outcomes is still poorly understood. Experimental studies have uncovered several immune factors that influence host control of infection and maintenance of latency. Because these studies are complex, expensive, and sometimes not possible in vivo, we take a computational approach and developed a detailed, two compartmental (i.e., lung and lymph node) mathematical model to investigate some of the mechanisms involved in the complex immunobiology of tuberculosis. The mathematical model reflects the complexity of the disease as well as the need for experimentalists to generate data for as many mechanistic details as possible to allow useful and specific predictions. Model calibration and validation is ultimately based on experimental data.

The outcome of M. tuberculosis infection is believed to be dependent on a balance of pro-and anti-inflammatory factors in the infected tissues. In this work, we focused on the effects of pro-inflammatory (TNF) and anti-inflammatory (IL-10) cytokines on the spectrum of phagocyte populations in lung and LN. Our results demonstrate that TNF is a major mediator of recruitment of phagocytes (macrophages and dendritic cells) to the lungs, but it does not differentially affect CAM and AAM numbers. In contrast, IL-10 appears to be a factor in balancing which macrophage environment is dominant in the lung and LN: AAM (anti-inflammatory) or CAM (pro-inflammatory). The outcome of infection and the severity of the disease may well be dependent on the balance of macrophage types in the lungs (Day et al., 2009), as this likely contributes to pathology. This suggests that biasing the macrophage population to an AAM phenotype, perhaps due to co-infection with other pathogens or the presence of underlying lung disease such as asthma, could be detrimental to control of tuberculosis. In other words, pushing the lung to an even more TH2 setting will increase the AAM population and shift the balance (or make the shift to CAM harder). In contrast, biasing to a CAM environment could increase inflammation and resulting damage and pathology. A balance must be reached that facilitates reduction in bacterial numbers yet preserves lung tissue. Bacterial numbers in lung had a surprisingly modest effect on macrophage dynamics, positively affecting the numbers of infected macrophages (M_I) and MDC, as well as MPF. In contrast, our previous studies using an agent-based model approach demonstrated a major role for bacterial numbers in size of the granuloma (Ray et al., 2009), which one could interpret loosely as inflammation. This highlights the importance of using different mathematical approaches to explore a specific biological question to uncover the effects of different processes that are present in the system (Gammack et al., 2005). Further work to reconcile these findings is ongoing.

In this work we developed a complex, two compartmental (i.e., lung and LN), non-linear ODE system (32 equations, 210 parameters) to consistently replicate data from a murine model. We used data on bacterial numbers over time to drive temporal immuno-dynamics of cells and cytokines in lung and LN during M. tuberculosis infection. By combining nonlinear programming, statistics, and probability techniques, we described a sophisticated methodology to adequately address model fitting and extensive uncertainty and sensitivity analysis of a large and complex nonlinear system of ODEs. This model can now be exploited in future work to incorporate data with variable and evolving bacterial dynamics to explore the effects on all processes in the system.

Model fitting was implemented as a generalized non linear least squares (NLLS) algorithm, using stepwise linear interpolations of the median trajectories for the CFU data as input functions. Uncertainty and sensitivity analysis was performed by combining Latin Hypercube Sampling (LHS) and Partial Rank Correlation Coefficients (PRCCs) to predict key mechanisms affecting cellular processes during infection within and between LN and lung. For the first time, to our knowledge, we describe a method to incorporate a function (CFU over time) as a parameter for the US analysis. We accomplished this by projecting the variability of the CFU data over time into a set of nested stepwise linear interpolators and sequentially labeling these curves based on the order of the samples for each time point.

Our model represents the first step in integrating multi-organ experimental data in a quantitative setting. By focusing on the cytokines important for the interplay between phagocyte populations and inflammation, we have identified roles for TNF and IL-10 in control of the lung environment in tuberculosis. This model can be further exploited to investigate key questions about lymphocyte dynamics and effects on control of infection and pathology, and trafficking of cells between LN and lungs. Additional data will be necessary for these investigations, which are crucial to our understanding of the dynamics of tuberculosis.