Individual versus systemic risk and the Regulator's Dilemma

Abstract

The global financial crisis of 2007–2009 exposed critical weaknesses in the financial system. Many proposals for financial reform address the need for systemic regulation—that is, regulation focused on the soundness of the whole financial system and not just that of individual institutions. In this paper, we study one particular problem faced by a systemic regulator: the tension between the distribution of assets that individual banks would like to hold and the distribution across banks that best supports system stability if greater weight is given to avoiding multiple bank failures. By diversifying its risks, a bank lowers its own probability of failure. However, if many banks diversify their risks in similar ways, then the probability of multiple failures can increase. As more banks fail simultaneously, the economic disruption tends to increase disproportionately. We show that, in model systems, the expected systemic cost of multiple failures can be largely explained by two global parameters of risk exposure and diversity, which can be assessed in terms of the risk exposures of individual actors. This observation hints at the possibility of regulatory intervention to promote systemic stability by incentivizing a more diverse diversification among banks. Such intervention offers the prospect of an additional lever in the armory of regulators, potentially allowing some combination of improved system stability and reduced need for additional capital.

The recent financial crises have led to worldwide efforts to analyze and reform banking regulation. Although debate continues as to the causes of the crises, a number of potentially relevant factors have been identified. Financial regulation was unable to keep pace with financial innovation (1, 2), was fragmented in its nature (2), and did not address important conflicts of interest (1, 3–7). More generally, an issue raised by the crises is that of individual vs. systemic risk: regulation was focused on the health of individual firms rather than the stability of the financial system as a whole (1, 2, 4, 8–10). In this paper, we investigate a particular issue that, although not necessarily at the heart of the recent crises, is of great relevance given the newly found interest in systemic regulation. Specifically, we explore the relationship between the risks taken by individual banks and the systemic risk of essentially simultaneous failure of multiple banks.

In this context, we use a deliberately oversimplified toy model to illuminate the tensions between what is best for individual banks and what is best for the system as a whole. Any bank can generally lower its probability of failure by diversifying its risks. However, when many banks diversify in similar ways, they are more likely to fail jointly. This joint failure creates a problem given the tendency for systemic costs of failure to grow disproportionately with the number of banks that fail. The financial system can tolerate isolated failures, but when many banks fail at one time, the economy struggles to absorb the impact, with serious consequences (11–13). Thus, the regulator faces a dilemma: should she allow banks to maximize individual stability, or should she require some specified degree of differentiation for the sake of greater system stability? In banking, as in many other settings, choices that may be optimal for the individual actors may be costly for the system as a whole (14), creating excessive systemic fragility.

Our work complements an existing theoretical literature on externalities (or spillovers) across financial institutions that impact systemic risk (15–32). Much of this literature has focused on exploring liability-side interconnections and how, although these facilitate risk-sharing, they can also create the conditions for contagion and fragility. For instance, some researchers have shown the potential for bankruptcy cascades to take hold, destabilizing the system by creating a contagion of failure (20, 26). When one firm fails, this failure has an adverse impact on those firms to whom it is connected in the network, potentially rendering some of these susceptible to failure. Most obviously affected are those firms to whom the failed institution owes money, but also, the firm's suppliers and even those companies that depend on it for supplies can be put in vulnerable positions. Another insightful strand of research has emphasized the potential for other forms of interdependence to undermine systemic stability, irrespective of financial interconnections: fire sales of assets by distressed institutions can lead to liquidity crises (28). In a very recent approach, the financial crisis is understood as a banking panic in the “sale and repurchase agreement” (repo) market (33). Other recent studies have drawn insights from areas such as ecology, epidemiology, and engineering (34–39).

The present paper builds on the early work by Shaffer (22) and Acharya (23) to explore the systemic costs that attend asset-side herding behavior. Other recent contributions in this direction have considered situations where assets seem uncorrelated in normal times but can suddenly become correlated as a result of margin requirements (refs. 29 and 32 have comprehensive reviews of relevant contributions). In the current work, we use the simplest possible model to investigate other systemic and regulatory implications of asset-side herding, thereby knowingly side-stepping these and many other potential features of real world financial networks. We do not claim that asset-side externalities were at the center of the recent crisis or were more important than other contributory factors. Also, we do not take any position on the extent to which the asset price fluctuations that we consider are because of external economic conditions altering the fair value of certain assets, fire sale effects temporarily depressing the value of assets, price bubbles leading to banks overpaying for assets whose prices subsequently collapse when the bubble bursts, general loss of confidence because of uncertainty, global economic imbalances, or other factors. Rather, we study asset-side herding, because it can have very important and not fully explored implications. Possible extensions of our work are discussed in SI Text.

We present a framework for understanding the tradeoffs between individual and systemic risk, quantifying the potential costs of herding and benefits of diverse diversification. We then show how systemic risk can be largely captured by two directly observable features of a set of bank allocations: the average distance between the banks in the allocation space and the balance of the allocations (i.e., distance from the average allocation to the individually optimal allocation). We hope that our work may offer insight to policy makers by providing a set of tools for exploring this particular facet of systemic risk.

Model

Consider a highly stylized world, with N banks and M assets. An asset here can be considered as something in which a bank can invest and that can inflict losses or gains proportional to the level of investment. At time t = 0, each bank chooses how to allocate its investments across the asset classes. At some later time, t = 1, the change in value of each asset is drawn randomly from some distribution. All assets are assumed to be independent and identically distributed. A bank has then failed if its total losses exceed a given threshold. We recognize that many other factors may cause bank failures, including fire sale effects, interconnections between banks, liquidity issues, and general loss of confidence, but these issues are not the focus of the present work.

For illustrative simplicity, we will take the asset price fluctuations to be drawn from a student t distribution with 1.5 degrees of freedom, a long-tailed distribution often used in financial models (40, 41). The distribution is additionally specified by a probability p that a bank will fail if all its investments are in a single asset class. As we will show, our main findings seem remarkably robust to changes in the detailed assumptions used, including the choice of distribution and the probability p.

We define X_ij as the allocation of bank i to asset j. We also define V_j as the loss in value between time t = 0 and t = 1 of asset j (with negative losses representing profits) drawn from a student t distribution as described above. The total loss incurred by bank i at time t = 1 is, thus, 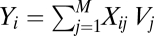. Bank i is then said to have failed if Y_i > γ_i (that is, if its total losses exceed a given threshold γ_i set by its capital buffer). Additional model details are in SI Text.

Results

We now examine the outcomes of this system. Fig. 1A illustrates how the probability of individual bank failure depends on the allocation between two asset classes when p = 10%. The individually optimal allocation for any given bank, in the sense of minimizing risk for expected return, is to distribute equal amounts into each asset class. We call this individually optimal allocation O*, and we call the associated probability of individual failure p*. When all banks are at the individual optimum, we call the configuration uniform diversification, because all banks adopt a common diversification strategy. Uniform diversification, thus, represents a state of the banks maximally herding together in the sense of adopting the same set of exposures. Readers familiar with the standard finance literature will recognize these allocations as those allocations selected under modern portfolio theory (42).

Fig. 1.

Probability of bank failure with two banks and two asset classes, A1 and A2. A fundamental tension exists between individual and system risk. Shown are the results of simulations in which the initial value of each asset is one; the loss incurred by each asset after some time t is sampled from a student t distribution with 1.5 degrees of freedom with mean = 0 and a 10% chance of being great than 1; and both banks have capital buffers such that a total loss greater than 1 causes failure. Shown is the average fraction of failures over 10⁶ loss samplings. Each bank's individual probability of failure is minimized by investing equally in A1 and A2 (i.e., diversifying uniformly) (A). Uniform diversification, however, does not minimize systemic risk. Instead, the probability of joint failure is minimized by having one bank invest entirely in A1, whereas the other invests entirely in A2 (B). We next consider the cost function c = k^s, where k is the number of failed banks, and with s moving from (C) a linear system cost of bank failure (s = 1) to (D and E) a system cost that is progressively convex (s = 1.3 in D; s = 2 in E). The lowest cost configurations are marked by a gray sphere.

Fig. 1B illustrates the probability of total system failure in this system of two banks, p_SF (i.e., the probability that both banks fail simultaneously). Unlike individual failure, we find that the probability of joint failure is not minimized by uniform diversification. Instead, a reduction in the probability of joint failure can be achieved by moving the banks away from each other in the space of assets. Indeed, the minimal probability of joint failure is achieved by having each bank invest solely in its own unique asset, which we will call full specialization. Thus, we observe a tension between what is best for an individual bank and what is safest for the system as a whole. The regulator faces a dilemma: should she allow institutions to maximize their individual stability or regulate to safeguard stability of the system as a whole?

To explore this dilemma, we introduce a stylized systemic cost function c = k^s, where k is the number of banks that fail and s ≥ 1 is a parameter describing the degree to which systemic costs escalate nonlinearly as the number of failed banks increases. When many banks fail simultaneously, private markets struggle to absorb the impact. Instead, society incurs real losses, and the economy's long-term potential may be affected (13). Our particular choice of cost function is, of course, an illustrative simplification, but as we show below, our results are robust to considering alternative nonlinear cost functions, and our model is easily extendable to consider any particular cost function of interest.

Fig. 1 C–E shows the expected systemic cost of failure C for two banks and two asset classes using various values of s. For a linear cost function (s = 1), expected cost is minimized under uniform diversification. In this special case, individual and systemic incentives are aligned. However, when we consider more realistic cases where the cost function is convex (so that the marginal systemic cost of bank failure is increasing), the configuration that minimizes C is no longer uniform diversification but rather, a configuration with diverse diversification. As s increases, an increasingly larger departure from uniform diversification is required to minimize C.

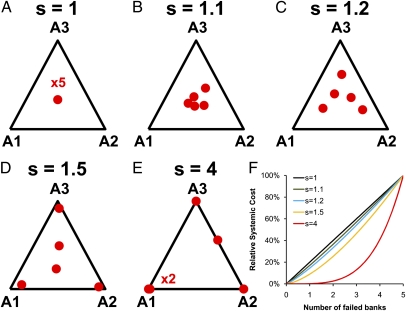
In Fig. 2, we illustrate a more general case of five banks investing in three assets, randomly sampling 10⁵ asset allocations. For varying degrees of nonlinearity s, we show the configuration with the lowest expected cost C. When the cost function is linear, the lowest cost configuration is again uniform diversification O*, where each bank allocates one-third of its investments to each asset. As we increase s, we find that pushing the banks away from uniform diversification to diverse diversification reduces C.

Fig. 2.

Lowest expected cost configurations for different levels of cost function nonlinearity s. (A–E) We consider five banks investing in three assets, with losses drawn from a student t distribution with 1.5 degrees of freedom having a mean = 0 and a 10% chance of being great than the banks' failure threshold of 1. Shown is the lowest expected cost allocation of 10⁵ randomly selected allocations over 10⁶ loss samplings. As s increases, the lowest expected cost configuration moves farther from uniform diversification. The cost function for various values of s is shown in F.

To further explore the relationship between the positioning of banks in asset space and the expected systemic cost, we define D as the average distance between the asset allocations of each pair of banks, scaled so that the distance between banks exposed to nonoverlapping sets of assets is one. We also define a second parameter G to describe how unbalanced the allocations are on average, which is defined as the distance between the average allocation across banks and the individually optimum allocation O*. SI Text has more detailed specifications of D and G. Note that, if all banks adopt the individually optimum allocation, both D and G are zero. Thus, in this case, all banks either survive or fail together, and the system behaves as if there were only a single representative bank. This finding is true regardless of assumptions about how the asset values fluctuate, but of course, it may not extend to more complex models with features such as stochastic heterogeneity across banks.

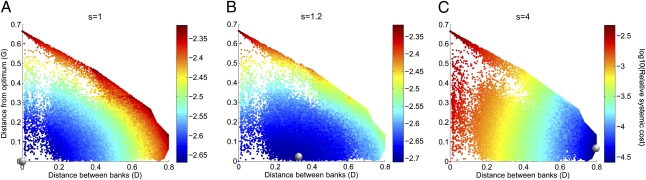
In Fig. 3, we show expected cost C as a function of D and G across 10⁵ random allocations of five banks on three assets. As we have already seen in Fig. 2, in the special case of s = 1, expected cost is minimized by uniform diversification at D = G = 0; thus, expected cost is increasing in both distance D and imbalance G. At larger values of s, expected cost remains consistently increasing in imbalance G, but the relationship between cost and distance D changes. At s = 1.2, cost is large for distances that are either too small or too large. The relationship between distance and cost is clearly nonlinear, and cost is lowest at an intermediate value of D. As s increases to s = 4, cost is now lowest when distance is large, and thus, cost is decreasing in D. Providing additional evidence for the ability of D and G to characterize systemic cost, regression analysis finds that D, D², and G together explain over 90% of the variation in log(C).

Fig. 3.

The systemic risk presented by a given set of allocations is largely characterized by two distinct factors: (i) the distance between the banks’ allocations D and (ii) the imbalance of the average allocation G, defined as the distance between the average allocation and the individually optimal allocation. Shown is the expected cost C associated with 10⁵ randomly chosen allocations as described in Fig. 2. When the cost function is linear (s = 1), the configuration that minimizes system cost has the banks herding in selecting the portfolio that minimizes individual risk of failure, 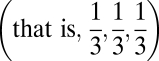(A). As the cost function becomes more nonlinear (s = 1.2), the cost-minimizing distance between the banks becomes larger. Here, the configurations that minimize system cost are associated with having banks at an intermediate distance from each other, while still having low imbalance G (B). With stronger nonlinearity (s = 4), the cost-minimizing configuration puts banks as far apart from each other as possible in asset space—large D (although still keeping the average location as close as possible to the individual optimum, i.e., small G) (C). Regressing log(C) against D, D², and G explains 97% of the variation in cost at s = 1, 90% of the variation in cost at s = 1.2, and 99% of the variation in cost at s = 4.

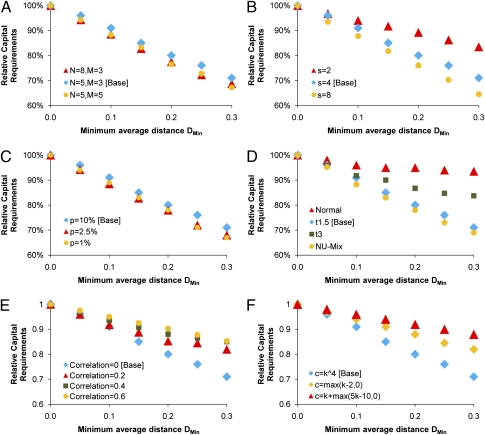
All of this information suggests that it may be possible in principle, and it could provide a useful guide in practice, to regulate expected systemic cost. For a given level of capital, regulators might set a lower bound on distance D and an upper bound on imbalance G. As shown in Fig. 4, fixing G = 0 and requiring D to exceed some value of D_Min results in a substantial reduction in the capital buffer needed to ensure that the worst-case expected cost remains below a given level. We particularly consider the worst-case expected cost to take into account potential strategic behavior on the part of the banks. This most pessimistic case shows that, even if the banks are colluding to purposely maximize the probability of systemic failure, regulating D and G creates substantial benefit for the system. Fig. 4 also illustrates the robustness of our results to model details. We observe similar results when varying model parameter values, including the number of banks and assets (Fig. 4A), the nonlinearity of the cost function (provided that s is not too low) (Fig. 4B), and the value of p (Fig. 4C). We also observe similar results when varying the distribution of the asset prices (provided that the tails of the distribution are heavy enough) (Fig. 4D) and when considering assets with a substantial degree of correlation (Fig. 4E and SI Text). Furthermore, Fig. 4F shows that our results continue to hold when considering alternate cost functions in which (i) the system can absorb the first i bank failures without incurring any cost, with systematic cost then increasing linearly for subsequent failure (i = 2 in our simulations), and (ii) each of the first i failures causes a systemic cost C₁, whereas each additional failure above i causes a larger systemic cost C₂ (i = 2, C₁ = 5, and C₂ = 30 in our simulations; SI Text has discussion of the various cost functions). This robustness is extremely important, because many of these features are difficult to determine precisely in reality. Because our results do not depend on the details of these assumptions, the importance of diverse diversification may extend beyond the simple model that we consider here.

Fig. 4.

Imposing a minimum on the distance D can appreciably reduce the capital needed to ensure a given maximum expected cost in our model. For a given set of parameters M, N, and p and a given asset price distribution, we calculate the expected systemic cost C when all banks act to minimize their individual risk (uniform diversification with G = 0 and D = 0). We then impose a minimum average distance D_Min, while keeping G = 0. Forcing the banks apart from each other lowers the expected cost for a given level of capital. Thus, for each value of D_Min, we find the level of capital for which the worst case (highest expected cost) of 10⁶ random allocations still gives an equivalent expected cost (within 2%) to that incurred under uniform diversification. Simulation results were also verified using nonlinear optimization. Shown in blue is the result for a base case of five banks, three asset classes, s = 4, and the asset prices each generated independently from a student t distribution with 1.5 degrees of freedom having p = 10% probability of failure for a bank invested only in one asset. We see that, as D_Min increases, banks need to hold less capital in reserve to ensure the same level of system stability. We then show that this result is qualitatively robust to varying the model parameters M and N (A), the nonlinearity of the cost function s (B), the type of distribution (student t with 1.5 degrees of freedom, student t with 3 degrees of freedom, normal distribution, or a mix with the loss having a 5% probability of being from a uniform distribution in the range 0–10 and a 95% probability of being from a normal distribution; D), the degree of correlation between the asset price fluctuations (E), and the choice of cost function, where k is the number of failed banks (F). The alternative cost functions are discussed in greater detail in SI Text. In all of the above cases, the loss distributions on a single asset have a mean = 0 and a p = 10% chance of being greater than the failure threshold of 1. Our results are also robust to changing this failure probability p (C).

Regulatory changes under discussion are estimated to require banks to increase their Core Tier One capital substantially in the major developed economies (43). In this context, the potential ability of diverse diversification to reduce capital buffers is of great economic significance. Estimates suggest that, for each 1% reduction that does not compromise system stability, sums in excess of $10 billion would be released for other productive purposes, with the economic benefits likely to be substantial (43, 44).

Discussion

There is a growing appreciation that prudent financial regulation must consider not only how a bank's activities affect its individual chances of failure but also how these individual-level choices impact the system at large. The analysis presented in this paper highlights a particular aspect of the problem that a systemic regulator will face: when the marginal social cost of bank failures is increasing in the numbers of banks that fail, systemic risk may be reduced by diverse diversification. This nonlinearity of the systemic cost is a natural assumption. The societal costs of dealing with bank failures grow disproportionately with the numbers that fail. Hence, the regulator may wish to give banks incentives to adopt differentiated strategies of diversification.

These results also have implications beyond the financial system. For example, the tension between individually optimal herding and systemically optimal diversification is a powerful theme in ecological systems (45, 46). Natural selection pressures organisms in a given species to adapt (in the same way) to their shared environment. However, maintenance of diversity is essential for protecting the species as a whole from extinction in the face of fluctuating environments and emergent threats such as new parasite species. Herding is also an issue for human societies in domains other than banking. In the context of innovation, for example, people often herd around popular ideas and fads, creating systemic costs by making it difficult for new ideas to be appreciated (47).

In our model, the expected systemic cost of bank failures is largely explained by two global parameters of risk exposure and diversity. Both these parameters can be derived by the regulator without the need for complicated calculations of systemic risk, and they can be decomposed into their contributions from individual actors. We also show that a given level of expected systemic cost can be achieved with a more efficient use of capital if the regulator is able to encourage a suitable level of diversity between banks in the system. Thus, this framework presents a potentially useful tool for systemic regulation; our analysis points to the possibility of regulation that combines knowledge of system aggregates and individual bank positions to identify and induce the desired degree of diverse diversification. The practical design of this aspect of regulatory strategy can only emerge from a fuller program of research.

In the meantime, it is our hope that the insights developed in this paper can weigh on the deliberations that are gathering pace surrounding the reform of financial regulation. Active discussion is under way regarding the design of capital surcharges based on an individual bank's contribution to systemic risk (4, 10, 48). Meanwhile, it is increasingly recognized that financial reporting must improve significantly to support the function of the systemic regulator, and discussion has turned to the practical details of data gathering and analysis (1, 4, 8–10). The basic notion that common diversification strategies can increase systemic risk is not entirely absent from current policy thinking (7), and it predates the recent crisis (49); however, it has received relatively little attention in the literature. A priority for future research is to convert theoretical insights into practical approaches for regulators.