Link between statistical equilibrium fidelity and forecasting skill for complex systems with model error

Abstract

Understanding and improving the predictive skill of imperfect models for complex systems in their response to external forcing is a crucial issue in diverse applications such as for example climate change science. Equilibrium statistical fidelity of the imperfect model on suitable coarse-grained variables is a necessary but not sufficient condition for this predictive skill, and elementary examples are given here demonstrating this. Here, with equilibrium statistical fidelity of the imperfect model, a direct link is developed between the predictive fidelity of specific test problems in the training phase where the perfect natural system is observed and the predictive skill for the forced response of the imperfect model by combining appropriate concepts from information theory with other concepts based on the fluctuation dissipation theorem. Here a suite of mathematically tractable models with nontrivial eddy diffusivity, variance, and intermittent non-Gaussian statistics mimicking crucial features of atmospheric tracers together with stochastically forced standard eddy diffusivity approximation with model error are utilized to illustrate this link.

Predicting the long-range behavior of complex systems in nature in diverse disciplines ranging from climate change science (1, 2) to materials (3) and neuroscience (4) is an issue of central importance in contemporary engineering and science. Accurate predictions are hampered by the fact that the true dynamics of the system in nature are actually unknown due to inadequate scientific understanding or inadequate spatiotemporal resolution in the imperfect computer models used for these predictions; in other words, there are significant model errors compared to the true signal from nature. Recently, information theory has been utilized in different ways to systematically improve model fidelity and sensitivity (5, 6), to quantify the role of coarse-grained initial states in long-range forecasting (7, 8), and to make an empirical link between model fidelity and forecasting skill (9, 10). Imperfect models for complex systems are constrained by their capability to reproduce certain statistics in a training phase where the natural system has been observed; for example, this training phase in climate science is roughly the 60-y dataset of extensive observations of the Earth’s climate system. For long-range forecasting, it is natural to guarantee statistical equilibrium fidelity for an imperfect model, and a framework using information theory is a natural way to achieve this in an unbiased fashion (5–8, 10). First, equilibrium statistical fidelity for an imperfect model depends on the choice of coarse-grained variables utilized (5, 6); second, equilibrium model fidelity is a necessary but not sufficient condition to guarantee long-range forecasting skill (8). For example, ref. 11, Sect. 2.6, extensively discusses three very different strongly mixing chaotic dynamical models with 40 variables and with the same Gaussian equilibrium measure, the TBH, K-Z, and IL96 models, so that all three models have the same climate equilibrium fidelity but have completely different forecasting skill; simple examples with one- and two-dimensional stochastic systems are presented in ref. 5 where there is perfect equilibrium fidelity but there is an intrinsic barrier to capturing the correct sensitivity with the imperfect models; several empirical examples in climate science where simply improving climate fidelity did not result in improved forecasting skill are noted in ref. 10. On the other hand, there are notable examples where improving equilibrium fidelity results in improved model sensitivity (5) or intermediate range forecasting skill (10). The central issue addressed here is the following one: Is there a systematic way to improve long-range forecasting skill of imperfect models satisfying equilibrium fidelity? Is there a systematic set of statistical prediction tests in the training phase beyond equilibrium fidelity that guarantees improved long-range forecasting skill for an imperfect model?

The main goal of the present paper is to provide such a direct link by utilizing fluctuation dissipation theorems (FDTs) for complex dynamical systems (11–13) together with the framework of empirical information theory for improving imperfect models developed recently (5, 6). After a summary of relevant formulas of empirical information theory, the main link utilizing FDT is developed. This is followed afterward by demonstration of this approach on a suite of mathematical test models, which despite their simplicity and mathematical tractability, nevertheless, mimic crucial statistical features of complex systems such as Earth’s climate.

Improving Models Through Empirical Information Theory

The natural way (14, 15) to measure the lack of information in one probability density, 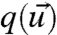, compared with the true probability density, 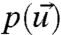, is through the relative entropy, 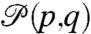, given by

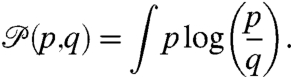[1]

Consider the least biased probability measure 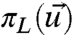consistent with L empirical measurements, 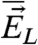, of the perfect model (14, 16, 17); for example, these measurements could correspond to the mean and covariance of a coarse-grained subset of variables in which case 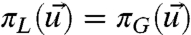is a Gaussian distribution (18). The first issue to contend with is the fact that 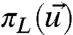is not the actual perfect model density but only reflects the best unbiased estimate of the perfect model given the L measurements, 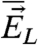. 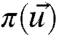Let denote the probability density of the perfect model, which is not actually known. Nevertheless, 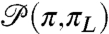precisely quantifies the intrinsic error in using the L measurements of the perfect model, 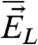. Consider an imperfect model with its associated probability density, 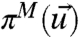; then the intrinsic model error in the climate statistics is given by 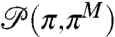. Consider a class of imperfect models, 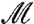, the best imperfect model for the coarse-grained variable is the 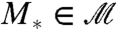so that the perfect model has the smallest additional information beyond the imperfect model distribution 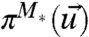; i.e.,

[2]

The following general principle (6, 11) facilitates the practical calculation of Eq. 2:

[3]

In Eq. 3, S(π) = -∫π log π is the absolute entropy (11, 14, 16, 17) of the probability measure π. The entropy difference, in Eq. 3 precisely measures the intrinsic error from the L measurements of the perfect system. The most practical setup for applying the framework of empirical information theory developed above arises when both the perfect system measurements and the model measurements involve only the mean and covariance of the variables 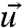so that π_L is Gaussian with climate mean 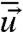and covariance R, whereas π^M is Gaussian with model mean 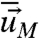and covariance R_M (14, 19). Next, the framework developed in ref. 5 of systematic general principles for improving model fidelity as well as model sensitivity is briefly summarized. Assume that the perfect system or the model system or both are perturbed in a fashion so that 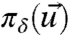, the unknown perfect distribution, 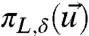, the measured distribution, and 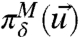, the model distribution, all vary smoothly with the parameter δ; i.e.,

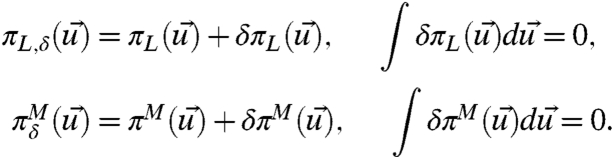[4]

Rigorous theorems guarantee this smooth dependence under minimal hypothesis for stochastic dynamical systems (20). By assuming the parameter δ is small enough and doing leading order Taylor expansion, the following general result emerges:

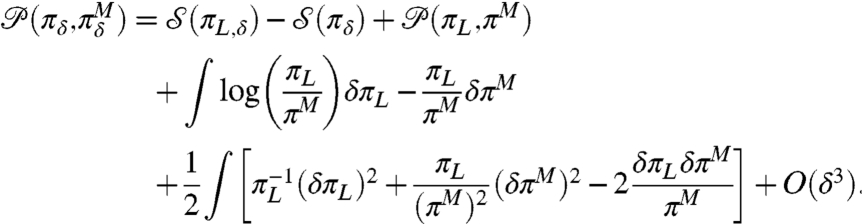[5]

Statistical equilibrium fidelity (5, 6, 10) consistent with the L measurements of a coarse-grained variable 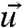for an imperfect model arises when

[6]

The interest here regards dynamically perturbed probability distributions for both nature, 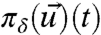, and the imperfect model, 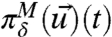, and the crucial question of whether the coarse-grained statistical behavior of the dynamics of the imperfect model, 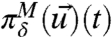, accurately predicts the coarse-grained statistics of the perfect dynamics, 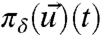. Recall from the introduction (5, 10, 11) that there are many explicit examples of imperfect models satisfying Eq. 6 where there is no prediction skill in the imperfect model. Under Gaussian assumptions with diagonal covariance matrices and perfect model fidelity, the formula in Eq. 5 becomes (5)

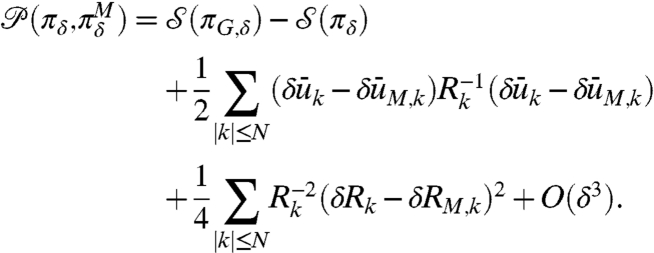[7]

The first (second) summation in Eq. 7 is the signal (dispersion) contribution to the model error.

FDT as a Link Between Fidelity and Forecast Skill

Assume the perfect model is a dynamical system with noise

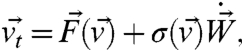[8]

for 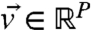, where σ is a P × K noise matrix and 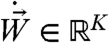is a K-dimensional white noise. The associated Fokker–Planck equation for the probability density 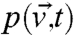is

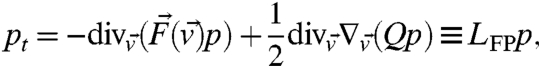[9]

where Q = σσ^T. The ideal equilibrium state associated with Eq. 8 is the probability density 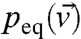that satisfies L_FPp_eq = 0, and the equilibrium statistics of some functional 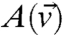are determined by

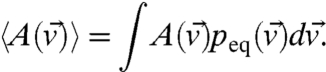[10]

Next, perturb the system in Eq. 8 by the change 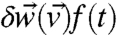; that is, consider the perturbed equation

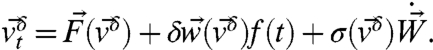[11]

Calculate perturbed statistics by utilizing the Fokker–Planck equation associated with Eq. 11 with initial data given by the unperturbed statistical equilibrium. Then, FDT (11) states that if δ is small enough, the leading order correction to the statistics in Eq. 10 becomes

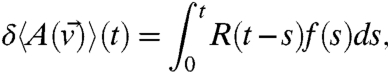[12]

where R(t) is the linear response operator that is calculated through correlation functions in the unperturbed climate

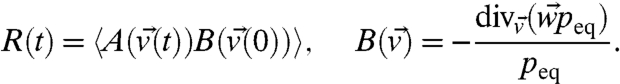[13]

The noise in Eq. 8 is not needed for FDT to be valid but, in this form, the equilibrium measure needs to be smooth. Such a rigorous FDT response is known to be valid for a wide range of dynamical systems under minimal hypothesis (20). Although the Markov assumption in Eq. 8 is very reasonable for the dynamics of the perfect model representing the natural system provided the dimension P is large enough, the practical use of Eqs. 8–13 is hampered by the fact that the dynamics in Eq. 8, the equilibrium measure in Eq. 10, and even the dimension of the phase space P for the perfect dynamics are unknown. Nevertheless, crucially one is interested in the long-range forecasting skill of the response in Eq. 11 to the change in external forcing; here δf(t) might be an impulsive constant change or a gradual change such as a ramp function (see Eq. 28 below). Furthermore, as for example in climate change science, one is interested not only in the actual response of the natural system but also in the response when anthropogenic effects of human activity are included so that δf(t) assumes a variety of different forms and magnitudes in various scenarios. However, what is only actually known about the natural system are measurements, 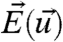, for 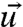, a coarse-grained collection of variables in a subspace during a training phase interval of time. The imperfect models are assumed to be given by a known dynamical system

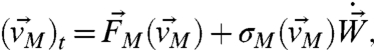[14]

which has similar structure to Eq. 8 but the phase space for the imperfect model, 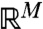, is often completely different from that of the natural system with usually M ≪ P, but the natural system in Eq. 8 and the imperfect model share the common variables, 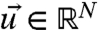; a simple example illustrating this is discussed in ref. 5, equations 15–21. Now, perturb both the perfect model (Eq. 8) and the imperfect model (Eq. 14) by 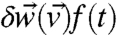to generate the perfect probability density, 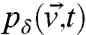, and the imperfect probability density, 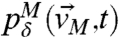exactly through Eq. 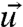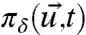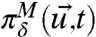13; on the common coarse-grained variables , let , denote the corresponding marginal probability densities. As in Eq. 2, we are interested in the best imperfect models that minimize 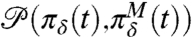for a given prediction horizon t and perturbed forcing scenario, 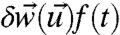. In general, using the coarse-grained functionals, 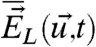(one should keep in mind the mean and covariance of 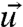to define 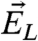) and applying Eq. 3 yields

[15]

with

[16]

The corresponding perturbed values of the functionals 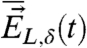and 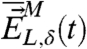are defined through Eq. 16 by

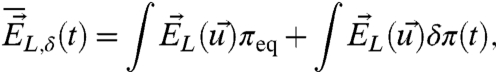[17a]

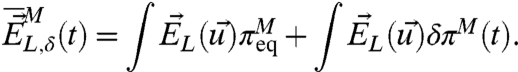[17b]

At this stage in the discussion, only exact formulas for the perfect and imperfect predictions have been utilized in the above framework to characterize the predictive skill of the imperfect model.

A potentially practical quantitative link between climate fidelity and forecast skill is defined through the fluctuation dissipation formulas in Eqs. 11–13. First, by assuming the validity of FDT and that the perturbation strength, δf(t), is sufficiently small, from Eq. 12,

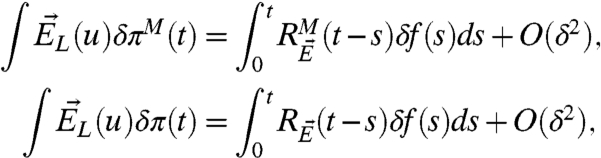[18]

where 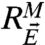, 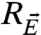are the corresponding response operators for the imperfect and perfect models defined through the correlation functions from Eq. 13 in the unperturbed systems. Now, with statistical equilibrium fidelity from Eq. 6 satisfied by the imperfect model, by definition the leading term in Eq. 17a exactly equals the leading term in Eq. 17b so that at δ = 0, 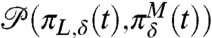vanishes identically and the perturbation formulas in Eqs. 7 and 13 can be applied directly with the approximation in Eq. 18 from FDT. For example, if u is a scalar variable like the global temperature in climate science with 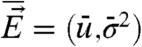, the mean 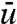, and the variance 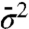, then Eqs. 16 and 18 yield

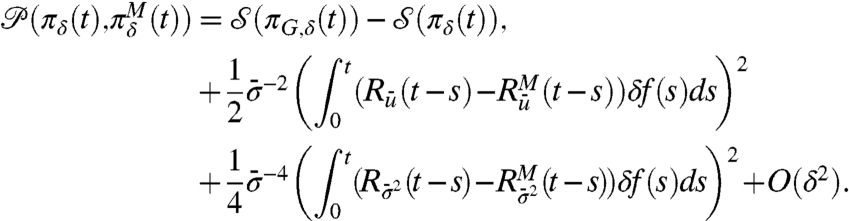[19]

In Eq. 19, σ² is the statistical equilibrium variance of both the perfect and imperfect models that coincide with equilibrium fidelity; also 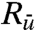, 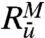and 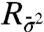, 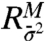are, respectively, the mean and variance linear response operators. In the more general setting, where the mean and covariance of vectors are measured, the more general formulas in Eqs. 7 and 12 are readily used (see the second example in the present paper). The formula in Eq. 19 and its generalizations illustrates that the skill of an imperfect model in predicting forced changes for the statistical equilibrium with general external forcing is directly linked with the skill in estimating the linear response operators for the mean and variance in a suitably weighted fashion as dictated by information theory.

The advantage of utilizing this FDT approximation is that the predictive skill of the imperfect model response operator 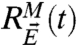to external forcing can be evaluated through specific experiments in the training period where the fidelity with observed data of the perfect model can be monitored. To illustrate this, perturb the initial data for the perfect and imperfect model systems in the direction δu in a statistical fashion so that one generates statistical solutions of the unperturbed perfect and imperfect models with perturbed initial data,

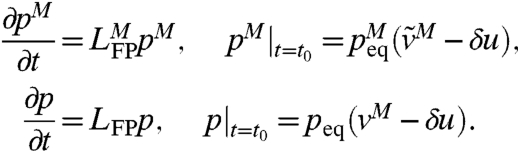[20]

Consider the marginal distribution in 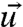of p^M and p and set 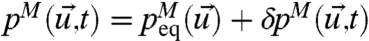, 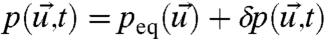; because we are utilizing linear response theory as in Eqs. 12 and 13, it is a general mathematical fact (12, 21) that for δ small enough, the linear response operators can be calculated from Eq. 20:

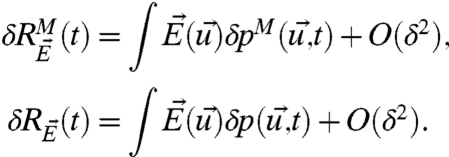[21]

Thus, model errors in the training period for a given imperfect model can be assessed with the tools of information theory (6, 11, 14) such as Eqs. 2–7 above by utilizing superensembles for the specific kicked ensemble perturbations for p^M given in Eq. 20; furthermore, in this training period, 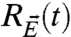does not need to be calculated explicitly but only the statistical fidelity of 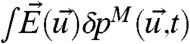with the actual observed data in nature. These points are illustrated in the example at the end of this paper.

General Comments on the Link

We proposed the general approach through FDT here to establish a link with firm mathematical underpinning for improving the long-range forecasting of imperfect models with changes in external forcing by evaluating the skill of related superensemble experiments defined in Eqs. 20 and 21 in the training phase using information theory; formally, this link is valid only for sufficiently small perturbations with δ ≪ 1, and equilibrium fidelity was utilized at the onset to control leading order errors. However, we proposed this link as a useful empirical guideline in general so it is important to understand the strengths and weaknesses of the above approach. First, note that the evaluation of the forced response operators in Eq. 19 requires skill for the mean-square averaged response operators 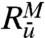, 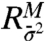whereas skill in the training phase is, on the surface, more demanding because pointwise evaluation of 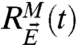is made; thus depending on the nature of the forcing, only less stringent suitable time averages of Eq. 21 are needed in evaluating the skill metric in Eq. 19. Second, there is a growing literature in developing theory (11, 21–24) and algorithms for FDT (25–35). In fact, the earliest applications that tested the original suggestion of Leith (28) utilized the kicked perturbations in Eq. 20 without model error to evaluate the response operator (25, 26), and these algorithms have been improved recently (33, 35); their main limitation is that they can diverge at finite times when there are positive Lyapunov exponents (26, 33, 35). Alternative algorithms utilize the quasi-Gaussian approximation (11) in the formulas in Eq. 13; these algorithms have been demonstrated to have high skill in both mean and variance response in the midlatitude upper troposphere to tropical forcing (30, 31) as well as for a variety of other large dimensional turbulent dynamical systems that are strongly mixing (11, 32, 34). There are recent blended response algorithms that combine the attractive features of both approaches and give very high skill for both the mean and variance response for the L-96 model (32, 36) as well as suitable large dimensional models of the atmosphere (34) and ocean (27) in a variety of weakly and strongly chaotic regimes. Note that the information metric in Eq. 19 requires objective model improvement of both the mean and variance response to actually improve skill. Finally, there are linear regression models (37) that try to calculate the mean and variance response directly from data; these linear regression models can have very good skill in the mean response but necessarily have no skill (21) in the variance response required in Eq. 19; they necessarily have an intrinsic barrier (5, 6) in model error response when the perfect model has a large variance response. In fact, one can regard all of the above approximations as defining various systems with model error in calculating the ideal response of a perfect model (11); this is a useful exercise for understanding the information theoretic framework on model error and response proposed here.

An Instructive Elementary Example

Consider the system given by the two linear stochastic equations

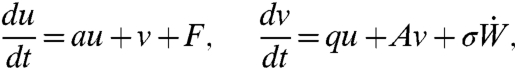[22]

where 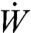is white noise; the system of equations in Eq. 22 has smooth Gaussian statistically steady state provided that

[23]

Regard u alone as a coarse-grained variable of interest and the perfect model as defined by stochastic solutions for Eq. 22 with a specific choice of a, q, A, F, σ satisfying 23; here the imperfect models satisfy the same requirements as in Eq. 22 and 23 but with imperfect coefficients a_M, q_M, A_M, F_M, σ_M. For linear stochastic systems like that in Eq. 22 and 23, the framework of linear response theory developed in Eqs. 8–13 above is exact without approximations; thus, it is possible to classify in elementary fashion all the imperfect models that have equilibrium fidelity and then characterize all imperfect models with the same linear response operator defined from Eqs. 12 and 13 for the change in external forcing with F in Eq. 22 replaced by F + δf(t). First, simple calculations establish that there is a three parameter family of imperfect models with the same equilibrium statistics for u determined by the two equations

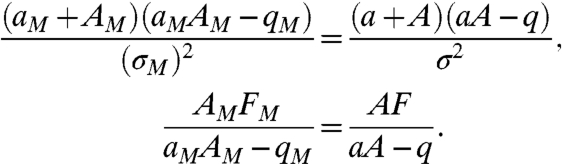[24]

It is also easy to calculate that the imperfect models with the same mean response to a change in constant external forcing, where δf(t) is proportional to a Heaviside function, necessarily satisfy the additional constraint

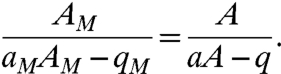[25]

The variance response (21) to any change in external forcing is identically zero for any linear stochastic model, 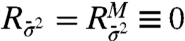for all of the stochastic models satisfying Eq. 22 and 23, and the model error information response metric from Eq. 19 has only signal contribution from 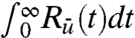. Furthermore, the two parameter family of imperfect models satisfying Eqs. 24 and 25 can have significant model error yet, they have perfect information content for the crucial forced response as required, whereas other models with perfect fidelity in Eq. 24 can have a significant model error in the response.

Improving Response in a Complex Test Model

The previous examples were elementary because they involved only linear stochastic equations, yet they revealed subtle behavior for improving models and their sensitivity. Here, we utilize the instructive models introduced and analyzed by the authors (6, 38, 39) with nontrivial eddy diffusivity, variance spectrum, and intermittent non-Gaussian statistics like tracers in the atmosphere (40) as the perfect models to provide a highly nontrivial demonstration of improving the response of imperfect models through information theory.

The perfect model has a zonal (east–west) mean jet, U(t), a family of planetary and synoptic scale waves with north–south velocity v(x,t) with x, a spatially periodic variable representing a fixed midlatitude circle in the east–west direction, and tracer gas T(x,t) with a north–south environmental mean gradient α, molecular diffusivity κ, and damping d_T. The dynamical equations for these variables are

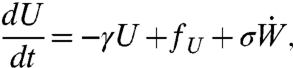[26a]

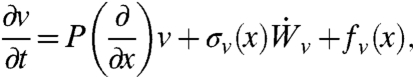[26b]

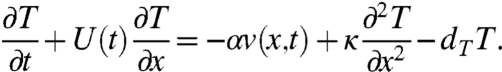[26c]

The functions f_U, f_v(x) are known constant in time functions, whereas 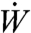, 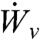represent random white noise fluctuations in forcing. The equation in Eq. 26b for the turbulent planetary waves is solved by Fourier series with independent scalar complex variable versions of the equation in Eq. 26a for each different wave number k (6); in Fourier space the operator 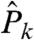has the form 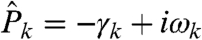with frequency 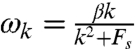corresponding to the dispersion relation of baroclinic Rossby waves and dissipation γ_k = ν(k² + F_s) where β is the north–south gradient of rotation, F_s is the stratification, and ν is a damping coefficient; the white noise forcing for Eq. 26b is chosen to vary with each spatial wave number k to generate an equipartition energy spectrum for planetary scale wave numbers 1 ≤ |k| ≤ 10 and a |k|^-5/3 turbulent cascade spectrum for 11 ≤ |k| ≤ 52. The zonal jet 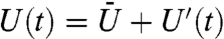, where 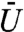is the climatological constant mean with γ, and σ chosen so that this jet is strongly eastward, whereas the random fluctuations, U^′(t), have a standard deviation consistent with such eastward dynamical behavior. Here, the imperfect models are Gaussian with the same dynamics for the zonal jet and Rossby waves from Eqs. 26a and 26b, but the tracer equation is given by

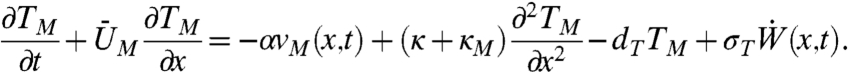[27]

In Eq. 27, κ_M is an eddy diffusivity coefficient, often utilized for parameterization of unresolved turbulence in climate science (40, 41), whereas 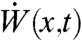denotes space–time white noise forcing with variance parameter σ_T. In the rapid decorrelation limit of Eq. 26a, the exact eddy diffusivity for the tracer, 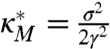, is valid (6, 39) and here 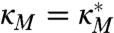. The standard parameterizations in climate science are deterministic and, in ref. 5, we utilized the models in Eq. 27 with σ_T ≡ 0 as typical deterministic imperfect models to improve by stochastic forcing for σ_T ≠ 0 using information theory. In fact, the optimal stochastic forcing to minimize the lack of information in Eq. 2 for the climatology gave essentially perfect climate fidelity for the large-scale wave number k = 1.

Next, we study the sensitivity of the perfect model in Eqs. 26 to the perturbations of external forcing. The model in Eqs. 26 has constant in time statistical steady state with the mean and covariance computable analytically as shown in ref. 38. Consider a ramp perturbation of the external forcing for U(t):

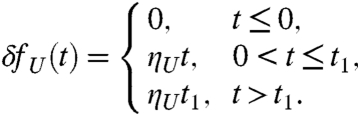[28]

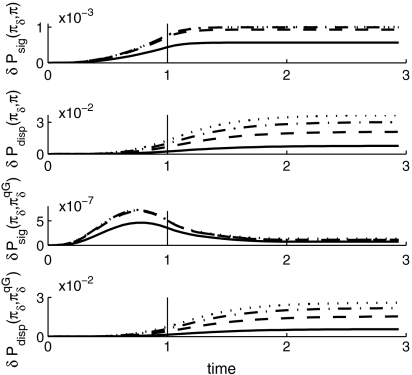
where t₁ is the time during which δf_U(t) grows linearly in time at the rate η_U and after which δf_U(t) is held fixed. This kind of external forcing perturbation mimics, for example, the scenario when at the first stage of climate change the forcing of the cross-sweep increases and at the second stage, the external forcing is fixed at a larger value and is not changing in time anymore. First, we focus on the impact of this external perturbation on the statistics of the tracer. The exact reponse of the system in Eq. 26 to the external perturbation, δf_U(t), can be computed analytically as shown in ref. 38. We use the following parameters in our experiments: γ_U = 2/3, σ_U = 2, f_U = 4, β = 8.91, F_s = 16, ν = 0.1, d_T = 0.1, κ = 0.001, α = 2, and the perturbation δf_U(t) from Eq. 28 with η_U = 0.05 and t₁ = 1, which corresponds to a 5% perturbation at the end of the first time unit and for the remaining two time units, so that the whole system was monitored during three time units as the perturbation was applied. As a result of such perturbation, the mean of the cross-sweep, U, grows and reaches a perturbed steady-state value, while the mean and the variance of the tracer, T_k, decrease in absolute value and also reach steady-state values. On the other hand, the variance of the cross-sweep as well as the mean and variance of the waves, v_k, stay unchanged due to the uncorrelated and Gaussian structure of the velocity field. Next, we quantify the sensitivity of the model in Eq. 26 by measuring additional information due to the perturbation, δf_U(t), via Eq. 7 with 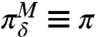, the equilibrium unperturbed steady state. In the first two panels in Fig. 1, we show the signal and dispersion parts of the additional information for the spatial coarse grainings up to k = 1, 3, 6, and 10 Fourier modes. The perturbation δf_U(t) causes a much more significant response in the variance than in the mean because, as shown in Fig. 1, the signal is always at least one order of magnitude smaller than the dispersion. Moreover, as the number of Fourier modes in the coarse graining increases to k = 3 and more, the signal part saturates; i.e., including more than three modes in the coarse graining does not provide additional information in the signal part. On the other hand, the dispersion part grows significantly as the coarse graining increases. By comparing the first two panels of Fig. 1, we conclude that the mean of the tracer takes less time to adjust to a perturbed steady state than the variance. This delayed response to external perturbations can have potentially important practical implications.

Fig. 1.

(Upper Two) Signal and dispersion parts of 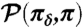from Eq. 7 measuring the sensitivity of the tracer model Eq. 26 to the ramp-type perturbation, δf_U(t). (Lower Two) Signal and dispersion parts of 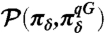from Eq. 7 measuring model error due to the use of quasi-Gaussian FDT from Eqs. 10 and 11 for predicting climate response to the same ramp-type perturbation. The vertical line shows when the perturbation, δf_U(t), stopped changing at the rate 5% per unit time and became constant leading to a new climate. The solid line corresponds to the coarse graining with only 1 mode; dashed line, 3 modes; the dash-dotted line, 6 modes; and the dotted line, 10 modes.

Next, we study how well the FDT-based algorithms can predict the true response of the model in Eqs. 26 to the same ramp perturbation, δf_U(t), from Eq. 28. Using Eqs. 12 and 13, we compute the mean and variance response operators to the perturbation of the forcing. Note that p_eq from Eq. 13 is strongly non-Gaussian with fat exponential tails (38, 39), and we approximate it with a Gaussian distribution with the same mean and covariance. On the other hand, the two-point correlator from Eq. 13 is computed numerically over the true non-Gaussian equilibrium measure. This procedure leads to the quasi-Gaussian FDT (qG-FDT) (23). In the last two panels in Fig. 1, we demonstrate the error in using qG-FDT for predicting the response to the ramp perturbation, δf_U(t), from Eq. 28. We quantify the error using Eq. 7 with 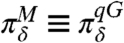, the qG-FDT response. We note that the signal part of the information is very small for all coarse grainings, which reflects the fact that the mean response is predicted well using qG-FDT. On the other hand, the dispersion part is almost as large as it was in the sensitivity study above. This shows that the variance response is not predicted accurately. Indeed, we checked that the qG-FDT variance response is significantly smaller than the true variance response, although qG-FDT predicts the sign and the shape of the variance response correctly.

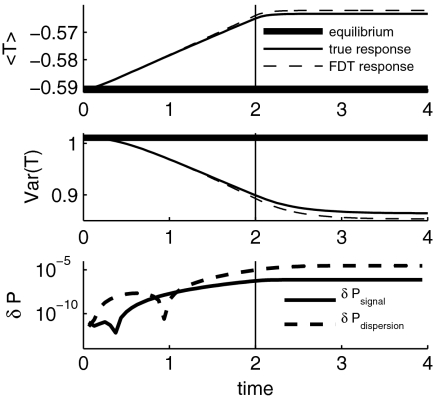
To avoid errors due to the quasi-Gaussian approximation, one can utilize the kicked response strategy advocated above in Eqs. 20 and 21 and compute the exact FDT response. We compute the response operator by kicking the system at time t = 0 by δU = 0.1 from its equilibrium value 〈U〉 = 6 and monitoring the decay of the perturbed system back to equilibrium. The coupling of the tracer to the cross-sweep in Eq. 26 naturally forces the tracer out of the equilibrium until it relaxes back to equilibrium. We use the exact analytical formulas from ref. 38 to compute the mean and variance of the tracer for given kicked initial conditions. However, these formulas use an assumption that the statistics of the system including the tracer are Gaussian at the initial time t = 0, which is not the case for the tracer in equilibrium as the authors showed in refs. 38 and 39. To circumvent the systematic errors that the Gaussian assumption brings, we subtract the statistics computed using the unperturbed Gaussian initial conditions from the statistics computed with the kicked Gaussian initial conditions. Note that even if we use the unperturbed equilibrium initial conditions, the system will deviate from equilibrium due to the imposed Gaussian initial conditions and only after some relaxation time, the statistics will approach equilibrium again. This is exactly the effect that we want to eliminate when computing the kicked response. In Fig. 2, we demonstrate the high skill of the kicked FDT algorithm in predicting both the mean and the variance response to the ramp perturbation. Here, the perturbation δf_U(t) is growing for two time units at the rate of 2% per time unit and then stays fixed for another two time units at the level of 4%. We note that for the first two time units, the FDT and exact responses are practically indistinguishable and then they deviate slightly. We also note that the lack of information measured via Eq. 7 with 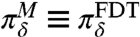is very small and although the dispersion part is a little larger than the signal part, both mean and variance responses are predicted with an extremely high accuracy, which makes the kicked FDT a very plausible approach to make climate change predictions in realistic models. However, one should be careful in computing the kicked response for the systems with positive Lyapunov exponents (26, 33, 35).

Fig. 2.

High skill of FDT in predicting the response to the ramp-type perturbations, δf_U(t). (Upper) The unperturbed equilibrium and perturbed mean tracer as functions of time as well as the FDT prediction obtained using the kicked perturbation experiment; (Middle) the same as Upper but for the variance of the tracer; (Lower) the signal and dispersion parts of 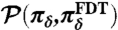from Eq. 7. The vertical line shows when the perturbation, δf_U(t), stopped changing at the level 2% per unit time and became constant leading to a new climate.

Finally, we comment on using the imperfect model with eddy diffusivity and optimal noise in Eq. 27 for predicting climate change in the true model from Eq. 26. Following ref. 5, we find the optimal noise σ_T for an eddy diffusivity 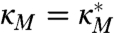by minimizing information theoretic metric 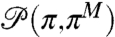in equilibrium, i.e., by tuning the imperfect model to have the perfect climate. In ref. 5, the authors have shown that the same optimal noise provides a significant improvement in the predictive skill for the impulsive external perturbation in the information theoretic sense. We note that the imperfect model has only moderate skill in predicting the climate response to the ramp perturbation because of its limited skill in predicting the true variance response with very good skill in predicting the true mean response as noted earlier.

Concluding Discussion

Equilibrium statistical fidelity on suitable coarse-grained variables is a necessary but not sufficient condition for predictive skill for imperfect models in long-range forecasting with changes in external forcing (5, 7, 8, 10); an elementary example is presented above (see Eq. 22), which demonstrates this in the present context. In many applications to complex systems with model error, it is crucially important to provide guidelines to improve the predictive skill of imperfect models for their response to changes in external forcing. Here, a direct link has been developed between fidelity of specific test problems in the training phase and predictive skill for the forced response by systematically combining appropriate concepts of information theory with those based on the fluctuation dissipation theorem. The strengths and weaknesses of the approach were summarized. Here, a suite of mathematically tractable models with nontrivial eddy diffusivity, variance, and intermittent non-Gaussian statistics (5, 6, 38, 39) mimicking crucial features of atmospheric tracers (40) were utilized together with stochastically forced eddy diffusivity approximations with model error to demonstrate this link. The high skill of the systematic strategy on this unambiguous nontrivial test model is encouraging for future developments.