Anion currents in yeast K⁺ transporters (TRK) characterize a structural homologue of ligand-gated ion channels

Abstract

Patch clamp studies of the potassium-transport proteins TRK1,2 in Saccharomyces cerevisiae have revealed large chloride efflux currents: at clamp voltages negative to -100 mV, and intracellular chloride concentrations >10 mM (J. Membr. Biol. 198:177, 2004). Stationary-state current-voltage analysis led to an in-series two-barrier model for chloride activation: the lower barrier (α) being 10–13 kcal/mol located ∼30% into the membrane from the cytoplasmic surface; and the higher one (β) being 12–16 kcal/mol located at the outer surface. Measurements carried out with lyotrophic anions and osmoprotective solutes have now demonstrated the following new properties: (1) selectivity for highly permeant anions changes with extracellular pH; at pH_o=5.5: I⁻≈Br⁻>Cl⁻>SCN⁻>NO₃⁻, and at pH_o 7.5: I⁻≈Br⁻>SCN⁻>NO₃⁻>Cl⁻. (2) NO₂⁻ acts like “superchoride”, possibly enhancing the channel's intrinsic permeability to Cl⁻. (3) SCN⁻ and NO₃⁻ block chloride permeability. (4) The order of selectivity for several slightly permeant anions (at pH_o=5.5 only) is formate > gluconate > acetate ≫ phosphate⁻¹. (5) All anion conductances are modulated (choked) by osmoprotective solutes. (6) The data and descriptive two-barrier model evoke a hypothetical structure (Biophys. J. 77:789, 1999) consisting of an intramembrane homotetramer of fungal TRK molecules, arrayed radially around a central cluster of four single helices (TM7) from each monomer. (7) That tetrameric cluster would resemble the hydrophobic core of (pentameric) ligand-gated ion channels, and would suggest voltage-modulated hydrophobic gating to underlie anion permeation.

Introduction

Uncoupled, channel-like, ion fluxes through certain ion-coupled substrate transporters began to be recognized about 20 years ago [84], and subsequently were widely observed in amine transporters and excitatory amino acid transporters of vertebrate neural tissues [27, 54, 70], as well as in a variety of invertebrates (reviewed in Ref. [76]). Some such movements were shown to be triggered by application of the principal substrate, but found to occur in non-stoichiometric quantities (transport-associated currents); others arose under special conditions in the absence of substrate (constitutive leakage currents). In different transporters, these uncoupled fluxes comprise mainly chloride ions or sodium ions, which augment the normal transport fluxes.

A discovery of patently outsized currents in the yeast Saccharomyces cerevisiae [9], associated with the potassium-uptake proteins Trk1p and Trk2p, led to a demonstration of uncoupled chloride fluxes through these transporters, as well [50]. That finding proved particularly interesting because TRK proteins are sequence similar to microbial potassium channels [24, 44], and have been shown to fold like K⁺ channels [23, 33, 48, 59, 84, 91]. That is, each single molecule of yeast Trk1p or Trk2p is folded into an internal tetramer with four pairs of transmembrane (TM) helices bracketing four recurrent strands to form a selectivity filter for K⁺. In Fig. 1a, these K⁺ filters are depicted as magenta clusters. The most distal pair of TM helices in each molecule, designated M1_D and M2_D (colored bars in Fig. 1a), is far better conserved among fungal species than are the other three pairs [61], and was postulated to coordinate a supertetramer of TRK monomers [23]. The axial pore of this structure would be lined by four copies of M1_D, and could provide a pathway for chloride currents [68].

Fig. 1.

Models for TRK structure and for chloride conduction. a Tetramer co-organized by proximation of M1_D helices in four separate TRK monomers: cylinder and wire diagrams in green, gray, blue, and red (counterclockwise) depict the backbone structures as originally proposed by Durell and Guy [23]. Cylinders represent TM helices M1_D (near center) and M2_D, while the other TM helices: M1_A−M2_A, M1_B−M2_B, M1_C−M2_C progress ccw within each monomer. Magenta figures represent the four selectivity sequences comprising the K⁺ pathway, central to each monomer: a QTGLO, b DLGYS, c SAGFT, and d TVGLS, for Trk1p in Schizosaccharomyces pombe. Central blue ball indicates the proposed pathway for chloride transit through the supertetramer [68]. Coordinate map provided by Dr. HR Guy. Drawing via PyMOL (DeLano Scientific, & Schrödinger LLC, Portland, OR, USA). b Diagram of two energy barriers to chloride transit, in series through the membrane dielectric. Parameters to be fitted, under stationary-state conditions, are a₁, b₂, A=exp(E_α/RT), and B=exp(E_β/RT)

The steady-state voltage-dependence of these outsized TRK currents resembles that of the mammalian glutamate transporter EAAT5 [1, 88] expressed in Xenopus oocytes. However, the implied Cl⁻ flux through the yeast TRK proteins swamps those proteins' normal K⁺ transport function and is certainly not initiated by K⁺ transport [50]. The findings on Saccharomyces have proven consistent with the observation that KCl in conventional penetrating microelectrodes (1−3 M) strongly depolarizes the membranes of yeast-like spherocytes of Neurospora, a normally large-celled mycelial organism [10]. Given expected yeast membrane voltages near −200 mV, the underlying chloride permeability via TRK proteins probably serves to keep cytosolic Cl⁻ below ∼1 mM, even with extracellular concentrations >1 M. However, the actual functional reason for conspicuous cross-species sequence conservation in the M1_D and M2_D helices remains to be determined (see “Discussion” section).

In principle, chloride could be transported by mechanisms other than conventional ion channels or carriers since it behaves both as a weak chaotropic ion—capable of disrupting protein structure [17, 86]—and as a lipid-soluble ion [64, 85] which might diffuse through the hydrophobic regions in membrane proteins. Indeed, chaotropic anions are known to inhibit P-type transport ATPases [34, 49, 67, 83], to bias the Na⁺, K⁺ ATPase toward its E₁P conformation [49, 80], and to modulate nerve and muscle behavior by means of altered membrane surface potential [20, 37, 40]. At least part of their lipophilicity is thought to lie in an ability to combine with protons and to diffuse through phospholipids as neutral molecules (viz., HCl, HNO₃, HSCN, etc. [31, 64, 85]). Such action could dissipate transmembrane pH gradients, uncouple proton-coupled ion transport reactions, and induce pseudo-anion currents associated with membrane depolarization.

In the present case, however, such essentially physical-chemical transfer processes can be largely discounted [50], because (a) deletion of both of the yeast TRK proteins eliminates more than 90% of the chloride-dependent currents; (b) the current–voltage relationship in the presence of chloride is strongly rectifying, with exponential (Eyring) kinetics, rather than Nernst–Planck kinetics; and (c) elevated intracellular chloride evokes inward currents— implying net chloride efflux; whereas elevated extracellular chloride evokes no corresponding outward currents.

The present experiments were undertaken to determine the selectivity of the TRK-Cl⁻ pathway, particularly with regard to other halide and chaotropic ions; and to determine the extent of validity of the two-barrier kinetic model previously developed for Cl^- currents. The resultant data demonstrate that other halides permeate even better than chloride itself; that more chaotropic ions can supplant/block halide ions; and that osmoprotective solutes can choke the currents due either to halide ions (Cl⁻) or to strongly chaotropic ions (SCN⁻). All of these findings are compatible with anion conduction through a central (fifth) pore in the K⁺ transport proteins, which would be formed by spontaneous membrane assembly of TRK tetramers [23], and which bears a strong structural resemblance to the well-known ligand-gated anion channels.

Methods

Strains

Four strains of S. cerevisiae were used in these experiments: our principle “wild-type” strain EBC202; its parents BS202/203; the derived double knockout strain for genes TRK1 and TRK2: EBK202; and a separate “wild-type,” K837. The latter strain was provided by Dr. Kyle Cunningham (Department of Biology, Johns Hopkins University, Baltimore); and BS202/203, by Dr. Albert Smith (Yale Department of Molecular, Cellular, and Developmental Biology; now of the Icelandic University, Reykjavik). The two EB strains were constructed in this laboratory by Dr. Esther Bashi using standard yeast genetics techniques [47]. All of these strains are equipped with an array of useful markers, and their full genotypes are given at the bottom of this paragraph. The TRK1 and TRK2 genes, deleted from EBK202, encode the two proteins which mediate active transport of potassium in Saccharomyces, and—under special conditions—channel the conspicuous anion effluxes described in detail below [50, 68]. The PMR1 gene, deleted from K837 and from the EB strains, encodes a Golgi-resident calcium pump, whose deletion results in useful enlargement of both intact cells and spheroplasts of yeast, so that cells ∼8 μm in diameter can routinely be selected for patch clamping. Detailed genotypes are as follows.

• K837: Mata ade2-1 can1-100 his3-11,15 leu2-3,112 trp1-1 ura3-1 pmr1∷HIS3 URA3∷PMC1-lacZ (pKC217 plasmid, integrated; W303 background);

• BS202/203: Mata/Matα ade2-1 can1-100 his3-11,15 leu2-3,112 trp1-1 ura3-1 lys2-ΔNhel (W303 background);

• EBC202: Mata ade2-1 can1-100 his3-11,15 leu2-3,112 trp1-1 ura3-1 lys2-ΔNhel pmr1Δ∷TRP1;

• EBK202: Mata ade2-1 can1-100 his3-11,15 leu2-3,112 trp1-1 ura3-1 lys2-ΔNhel pmr1Δ∷TRP1 TRK1Δ∷TRP1 TRK2Δ∷TRP1.

Growth media, spheroplasting

Cells were normally grown in shaking liquid YPD-Ca medium (1% yeast extract, 2% bactopeptone, 2% glucose, plus 10 mM CaCl₂), at 30°C, to a final OD₆₀₀ of 0.8–1.2; the added calcium was required for normal growth of pmr 1 Δ strains. Also, for the trk1Δ and trk1Δ −trk2Δ strains, 90 mM KCl was added to YPD-Ca. In experiments with molar concentrations of intracellular osmoprotective solutes (Figs. 5 and 8), 1 M glycerol was added to growth medium and was also added to the extracellular media for protoplasting and recording. Glycerol, at concentrations up to 1 M, has no readily observable deleterious effect on yeast, other than slight retardation of growth (doubling times of 1.9–2.1 h, instead of the normal 1.75 h, at 30°C), and has been found useful as a chemical chaperone [26, 91].

Fig. 5.

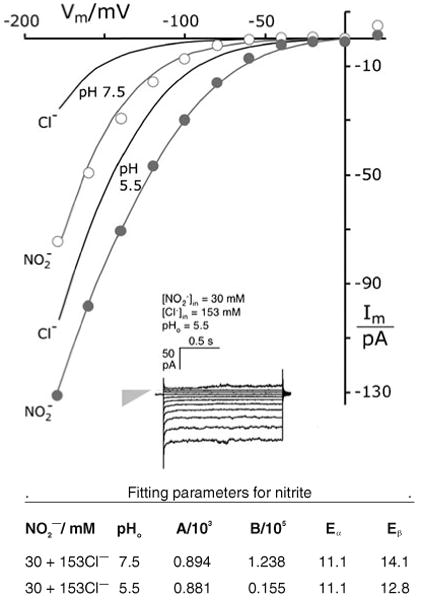
Nitrite ions augment chloride currents through the TRK proteins. Gray plots, curves. Currents measured with 30 mM NO₂⁻ replacing equivalent KCl in buffer G-Cl. Equation 1 fitted with ϕ set at unity and a₁=0.279; other parameters tabulated below. Black curves Fitted reference current-voltage curves, taken from Fig. 4, for pure chloride. Methods as in Figs. 2 and 3; strain EBC202. Inset Sample current traces in the presence of 30 mM NO₂⁻. Gray triangle designates null current (point) and leak conductance (height, 410 pS)

Fig. 8.

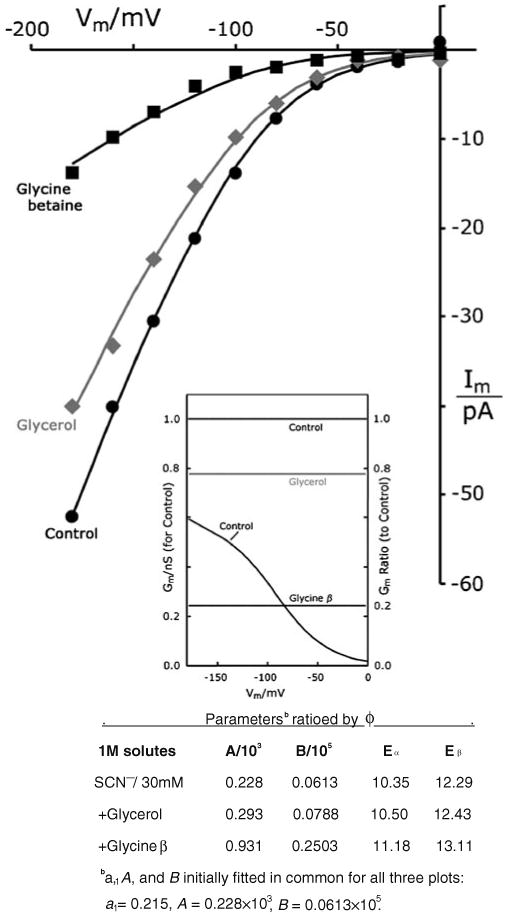
Osmoprotective solutes choke currents of chaotropic ions. I–V plots with buffer G-SCN supplemented by molar concentrations of glycerol or glycine betaine (pH_o 5.5 only). All three plots fit by Eq. 1, with all parameters found in common except f, which optimized at 0.777 for glycerol, and at 0.245 for glycine betaine. Methods as in Figs. 6 and 7. Control data were obtained similarly to those for 30 mM SCN^- in chloride (pH 5.5), from Fig. 7. Strain EBC202. Fitted and ratioed parameter values are tabulated below. Inset Conductance– voltage curve corresponding to the control I–V curve (SCN^-) and scaled on the left ordinate; plus conductance ratios (divided by control), scaled on the right ordinate. Horizontal lines lie at the original fit values of ϕ. [Concentration terms in the numerator of Eq. 1 were chosen rather arbitrarily; intracellular = 30 mM, on the literal assumption that Cl⁻ currents were blocked; and extracellular = 3 mM, to minimize calculated offset currents (see METHODS)]

Cells were spheroplasted as previously described [7, 68]. Briefly, late exponential phase cultures were spun down, washed in 50 mM KH₂PO₄ at pH 7.2, preincubated 0.5 h in the same buffer supplemented with 0.2% β-mercaptoethanol (β-ME; buffer A), centrifuged, then resuspended in buffer A plus 1.2 M sorbitol (buffer B) containing 0.6 units of zymolyase 20 T (Cat. 3320921, ICN Biomedicals, Inc., Irvine, CA, USA), and incubated under slow nutation (45 min, 30°C). Resulting spheroplasts were spun down and resuspended in stabilizing buffer (buffer C: 220 mM KCl, 10 mM CaCl₂, 5 mM MgCl₂, 5 mM MES brought to pH 7.2 with Tris base, +0.2% glucose), where they could be maintained for several hours (23°C) before use. For recording, ∼2 μl of suspension was pipetted directly onto the chamber bottom, and cells were allowed to settle (and attach lightly to the chamber bottom) for about 10 min before the chamber was flushed with sealing solution (buffer D).

Recording buffers were simple modifications of those already described for patch clamp studies of Saccharomyces [7, 68]. Buffer D (sealing solution, extracellular) and buffer 5.5 contained 150 mM KCl, 10 mM CaCl₂, 5 mM MgCl₂, 1 mM MES titrated to pH 7.5 (buffer D), or to pH 5.5, with Tris base; and buffer G-Cl (whole cell pipette buffer), contained 175 mM KCl, 1 mM EGTA, 0.15 mM CaCl₂ (free Ca⁺⁺=100 nM), 4 mM MgCl₂, and 4 mM ATP, titrated to pH 7.0 with KOH. Other salts, used to replace all (175 mM) or part (30 mM) of the KCl in buffer G-Cl included potassium salts of bromide, iodide, nitrite, nitrate, thiocyanate, and gluconate. Buffer G-30 (used in Fig. 2) replaced 153 mM KCl with equivalent K-gluconate, to give total intracellular chloride concentration ([Cl⁻]_i)=30 mM. All KCl replacement buffers contained 8.3 mM residual Cl⁻ from the magnesium and calcium salts. For testing intracellular osmoprotective solutes—molar glucose, glycerol, sorbitol, trehalose, and glycine betaine—molar glycerol was maintained in all extracellular solutions, as noted above.

Fig. 2.

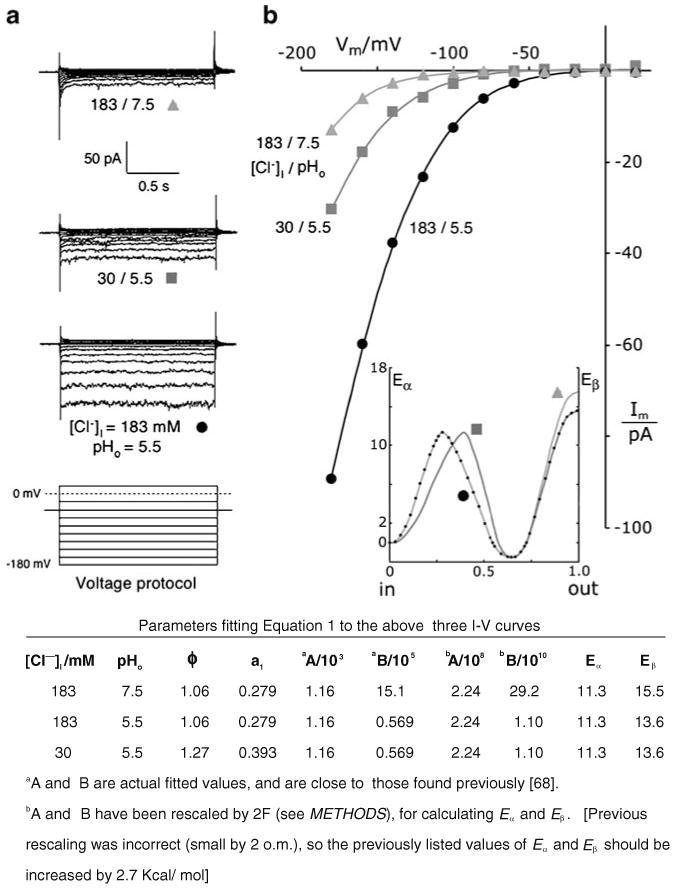
TRK-mediated, voltage-driven anion effluxes (inward currents) depend strongly on [Cl⁻]_i and pH_o. a Typical patch clamp traces from a cluster of experiments on wild-type Saccharomyces spheroplasts using a standard voltage-clamp protocol (bottom stack). Reference (holding) voltage at −40 mV; from there, 1.5-s clamp pulses were imposed to +100 mV, +80…0 mV, −20…−160, and −180 mV. Actual data were truncated positive to +20 mV. Measured currents are shown for one cell with standard intracellular chloride (183 mM), at two different extracellular pH values 7.5, 5.5, and for a second cell at pH 5.5, with lowered intracellular chloride 30 mM. As previously observed [68], all current traces settled to stable values in < 200 ms. Extracellular solutions: buffer D (pH 7.5) and buffer 5.5; intracellular solutions: buffer G-Cl and G-30 (see “Methods” section, recording buffers). Data all from strain EBC202. b Current-voltage plots corresponding to the record sets in a obtained by averaging currents sampled between 0.75 and 1.35 s along each trace, then correcting for leakage (see “Methods” section). Smoothed curves through the plotted points were calculated via Eq. 1, which had been fitted simultaneously to all three plots, with a₁ forced to its previously determined values [68] and with the number of common parameters maximized. The full set of fitted values is shown in the table below. Inset idealized drawing to illustrate behavior of the two postulated energy barriers controlling chloride permeation. The height of barrier β would decrease with falling pH_o; and a₁, the peak position of barrier α, would shift deeper into the membrane with falling [Cl⁻]_i. b₂, the fractional distance from the peak of barrier β to the outer surface of the membrane dielectric, was fixed at zero

Patch recording

Borosilicate pipettes, prepared as previously described [7], were connected to an EPC9 amplifier [68], which was managed by “Pulse” software (HEKA Elektronik, Lambrecht, Germany) on a PowerMacG4 computer (Apple Computer Inc., Cupertino, CA, USA). Yeast membrane currents were measured in the “whole-cell” recording mode, using a staircase of 1.5 or 2.5-s voltage pulses (from a holding voltage of −40 mV) to +100 mV, +80…−180, −200 mV, in 20 mV decrements. Steady-state current-voltage curves (I–V curves) were generated by averaging the values sampled between 50% and 90% of each trace and plotting the averages against the clamped voltage for each pulse. Data were usually collected between +100 and −180 mV, but the actual data displays were truncated at +20 mV, since positive (outward) currents were unrelated to the TRK proteins [7, 50]. Resulting I–V curves were corrected for current leakage by subtracting an ohmic line corresponding to the minimal slope near the origin [50]. Small residual scatter was observed in the apparent short-circuit currents due to the very low slope conductance near-zero voltage, but this could be minimized by adding an error term (I_e) to the descriptive transport model fit to each I–V plot (see Eq. 1 below). The common sealing adjuvant, potassium fluoride, was tested (at mM concentrations) in pipette solutions for a few experiments, but had no effect on leakage currents; higher concentrations were avoided because of likely interference with chloride permeability. Data were routinely collected at 2 kHz and filtered at 250 Hz.

The model

Previous quantitative analysis of TRK-chloride currents showed that most of the steady-state data can be described equally well by either of two models. The first and more familiar of the two is a conventional voltage-gated channel whose characteristic gating voltage is strongly pH-sensitive: shifting ∼37 mV positive per pH unit, from −270 mVat pH 7.5 to −160 mVat pH 4.5.

The other model, illustrated in Fig. 1b, postulates that anions transiting the TRK proteins must cross two activation–energy barriers, twice acquiring excess energy in a manner similar to ordinary chemical reactions [12, 38, 46, 52, 53]. This two-barrier model has proven the more cogent, for two main reasons: first, occasional yeast spheroplasts which tolerate very large clamping voltages (−220 to −300 mV) all display exponentially increasing conductances at the extreme voltages (Fig. 13 in Ref. 68). This feature is predicted by the two-barrier model, whereas a limiting (ohmic) conductance is predicted by the gated-channel model.

Second, transit through two barriers accords qualitatively with the association of four TRK molecules, described in Fig. 1a, as originally proposed by Durell and Guy [23]. The resulting central pore would be lined by four copies of the sequence 1075-LRKQLSFDLWFLFLGLFIICIC-1096 (M1_D, in Saccharomyces Trk1p). The side chains of Trp1084s and Phe1091s would point directly into the channel and form tight rings, viz., energy barriers against the passage of chloride ions. Furthermore, Arg1076 and Lys1077 would lie in a wide vestibule at the inner end of the central pore, where their eight positive charges should act as an electrostatic sieve for anions.

A simple mathematical formulation of the two-barrier model expresses voltage-driven transit of single chloride ions, under stationary-state conditions, as Equation 1:

$$I_m=\varphi z_{c}F\frac{C{l}_i\text{exp}(z_{c}F{a}_1{V}_m/RT)-C{l}_o\text{exp}(-z_{c}F(1-a_1)V_m/RT)}{A+B\text{exp}(-z_{c}F(1-a_1-b_2)V_m/RT)}+I_e,$$ (1)

where, I_m is the measured current, and I_e represents scattered error in the short-circuit current for each I–V curve. Cl_i and Cl_o are the intracellular (pipette) and extracellular concentrations of chloride ions, with their valence z_c=−1; z_cF converts chemical flux to current, and FV_m/RT is the “reduced” (dimensionless) membrane voltage. a₁ represents the fractional distance of the first barrier (α) from the inner face of the membrane dielectric, b₂ represents the fractional distance of the second barrier (β) from the outer face of the membrane dielectric, A=exp(E_α/RT) is the reciprocal of the Boltzmann expression relating reaction velocity to activation energy (E_α) at barrier α, and B=exp(E_β/RT) is the corresponding term for barrier β. The membrane's electric field is assumed to be constant, under steady-state conditions, so that the voltage offsets at barriers α and β are specified by the products a₁V_m and b₂V_m, respectively.

These equations contain four intrinsic parameters determining the detailed shapes of current–voltage curves under different experimental conditions: a₁, b₂, A, and B. However, only three of these actually vary; in trial optimizations, b₂ usually assumes its minimal value (zero) and has therefore been fixed at zero, for all of the analysis described below (see Fig. 5 in Rivetta et al. [68] and Fig. 1b, here). Finally, ϕ is an experimental scaling factor used mainly to rationalize data from spheroplasts of different size. It cannot be determined independently of A and B, and must be fixed (usually=1.0) for at least one plot in each I–V dataset. Additional details are given at the end of this section, and in the legend to Fig. 1.

[Caveat: a perhaps unconventional feature of this model is the required variation a₁ of barrier α, upon large changes in subtrate ion concentration or upon the addition of neutral osmoprotective solutes (see, e.g., Figs. 2 and 6). That requirement could be suppressed by introducing a third activation barrier, with its own position and amplitude: viz., two more parameters. But since the environment of biological membranes: including pH, ionic strength, electric field, boundary solutes, etc., can affect detailed membrane structure, the usual preference for modeling with fixed-position barriers seems arbitrary. For the present measurements and description, it is also unnecessary.]

Fig. 6.

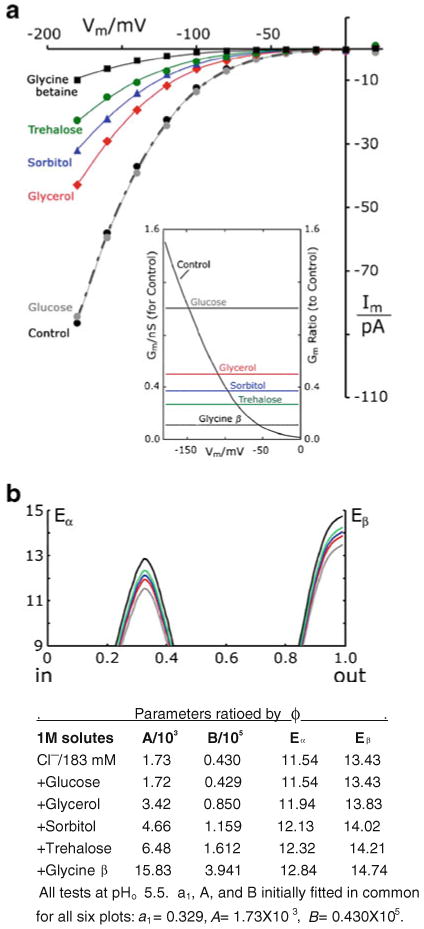
Osmoprotective solutes choke halide currents through TRK. a I–V plots with buffer G-Cl supplemented by molar concentrations of five different neutral solutes (pH_o 5.5 only). All six plots fit by Eq. 1, with all parameters found in common, except for the scaling factor (ϕ). ϕ optimized at 1.004, 0.506, 0.371, 0.267, and 0.109, respectively, for glucose, glycerol, sorbitol, trehalose, and glycine betaine. Average I–V data for at least three separate trials with each solute. SEMs at −180 mV were six to seven for glucose, glycerol, and sorbitol; three for trehalose; and one for glycine betaine. All cells except controls were grown, protoplasted, and measured in 1 M glycerol. Controls were grown and protoplasted in the usual manner, without glycerol (see “Methods” section). Other methods as in Figs. 2 and 3. Strain EBC202. Inset conductance-voltage curve corresponding to the control I–V curve and scaled on the left ordinate; plus conductance ratios (divided by control), scaled on the right ordinate for the five solutes. Horizontal lines at the original fit-values of ϕ. b Idealized drawings of the energy–barrier curves which result from dividing the peak parameters, a and b, by fitted value of ϕ for each solute. Display truncated below 9 Kcal/mol

Equation 1 extrapolates along an exponential asymptote at large negative membrane voltages [68], and— because b₂=0—along a horizontal asymptote at large positive voltages (Equation 2):

$$\underset{V_m\to -\infty }{\text{lim}}{I}_m=\varphi \left[\frac{z_{c}FC{l}_i}{A}\right]\text{exp}(z_{c}F{a}_1{V}_m/RT),\underset{V_m\to +\infty }{lim}{\text{I}}_m=\varphi \left[\frac{-z_{c}FC{l}_o}{B}\right]\cdot$$ (2a, b)

In order to reconcile units on the right-hand side of Eqs. 1 and 2a, b with the units of current, it is convenient to assign units of permeability (cm/s) to the scaling factor ϕ. Then, because the data: measured currents, membrane voltage, Cl⁻ concentration, and cell size are in pA/cell, mV, mM, and (μm² surface, respectively, the practical (fitted) values of A and B must be rescaled by the factor 1.93×10⁵. This is numerically equal to 2F, where 2 represents the standard yeast spheroplast surface area of 200 (μm². Actual curve fitting has been carried out via a variant of the Marquardt algorithm [58], augmented with a parameter-coincidence matrix to accommodate multiple simultaneous plots.

Results

Confirming the chloride conductance

Previous experiments [68] showed that chloride currents through the yeast TRK proteins could be quantitatively described via the two-barrier model, allowing only a single parameter to vary, either with changes of [Cl^-]_i or with extracellular pH (pH_o). The present repeat of those experiments has reinforced the general observation, and has demonstrated numerical stability of the actual parameters, as illustrated by Fig. 2. The current traces in Fig. 2a were obtained from two different spheroplasts: one patch perfused with 183 mM Cl⁻(buffer G-Cl), and the other with [Cl^-]_i lowered to 30 mM by potassium gluconate replacement of KCl. Two values of pH_o were tested on the first spheroplast: 7.5 (buffer D) and 5.5 (buffer 5.5). The “inward” or negative currents, plotted downward, were clearly diminished by lowering [Cl^-]_i and by raising pH_o. The latter effect mimicked an 80 mV negative offset of the I–V plot, with no obvious change of shape; this observation essentially coincides with an offset of 37 mV per pH unit reported previously [68].

Fits of Eq. 1 to the resulting I–V plots (Fig. 2b) were carried out with a₁ set identically to the previously determined values at the two Cl⁻ concentrations, and allowing only parameter B (height of barrier β) to vary between the two pH_o values (documented in Fig. 2 legend). The purported barrier shapes and positions are diagramed in inset of Fig. 2b, to show that lowering pH_o from 7.5 to 5.5 lowered the (β barrier by 1.9 Kcal/mol, and that reducing [Cl^-]_i from 183 to 30 mM moved the α peak deeper into the membrane dielectric (0.279→0.393). As noted by a caveat in “Methods” section, displacement of the α peak by changes of [Cl^-]_i could be suppressed by adding a third activation barrier (having two more parameters), but with little effect on the quality of fit. Thus, the two-barrier model describes these TRK-mediated chloride currents both efficiently and consistently with previous findings.

The same two intracellular ion concentrations, and extracellular pH values, were used as standard test points for further experiments.

Bromide, iodide

Currents of Br⁻ and I⁻ were assessed by replacing KCl in buffer G-Cl with either 175 mM KBr or 175 mM KI (buffers G-Br and G-I). Resulting patch clamp traces (Fig. 3) showed significantly larger currents than with chloride, at both pH_o values tested and for both halides. Furthermore, the relative spacings of traces, per 20-mV step, differed for Br⁻ and I⁻ from that for Cl⁻; and quantitative analysis of this feature identified enlarged leakage currents relative to those for Cl⁻. Leakage–current amplitudes and conductances are indicated in Fig. 3 by the gray triangles, which also point to the null currents in each stack of traces. Finally, traces at the most negative voltages (−160, −180 mV) bore occasional bursts of noise with the character of conventional gated ion channels. Control measurements on yeast spheroplasts deleted of the TRK genes (trk1Δ−trk2Δ; Fig. 3b) also revealed enlarged non-TRK-related currents in bromide or iodide, relative to chloride.

Fig. 3.

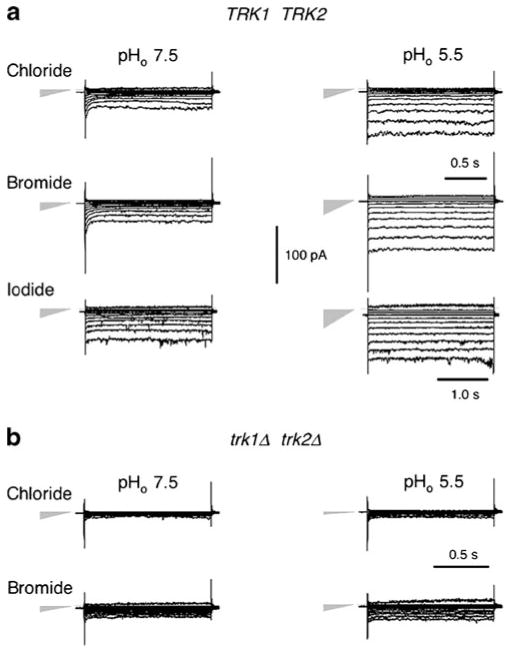
Raw data traces showing the effects of different halide ions (intracellular) on inward currents through yeast plasma membranes. a Wild-type cells, strain EBC202. b trk1Δ-trk2Δ cells, strain EBK202. Gray triangles on the left designate both the null-current level (point) and the relative leak conductance (height) for each stack. For reference, leak conductance with iodide at pH 5.5 was 290 pS. Note occasional channel-like “switched” noise at the higher voltages, especially with iodide. “Methods” section as for Fig. 2a. Extracellular solutions: buffer D or buffer 5.5; intracellular (pipette) solutions: buffer G-Cl; G-Br, or G-I: 175 mM KBr or 175 mM KBr replacing equivalent KCl from buffer G-Cl

Figure 4 demonstrates the leakage-corrected I–V plots for Br^- (red diamonds) and I⁻ (green squares) to be nearly identical with each other at both pH_o values, but to be distinct from those for Cl⁻ (black disks). Equation 1 could easily be fitted to these six datasets, when the intracellular mixture of 8 mM residual chloride plus 175 mM bromide or iodide was treated as if it represents a single ionic species at 183 mM (necessitated by the fact that Eq. 1 does not explicitly include terms for different ion species). All significant differences among the I–V plots could be generated by small shifts of activation energy at barrier β (outer face of the membrane; Fig. 4 legend). Clearly, there is no qualitative distinction among the voltage dependences of chloride, bromide, or iodide currents through the yeast TRK proteins. This peculiar anionic pathway, which was previously shown to be non-saturating for Cl⁻ [68], is therefore a generalized halide channel, being about equally permeable to I⁻ and Br⁻, and somewhat less permeable to Cl⁻ in the range of experimentally accessible voltages.

Fig. 4.

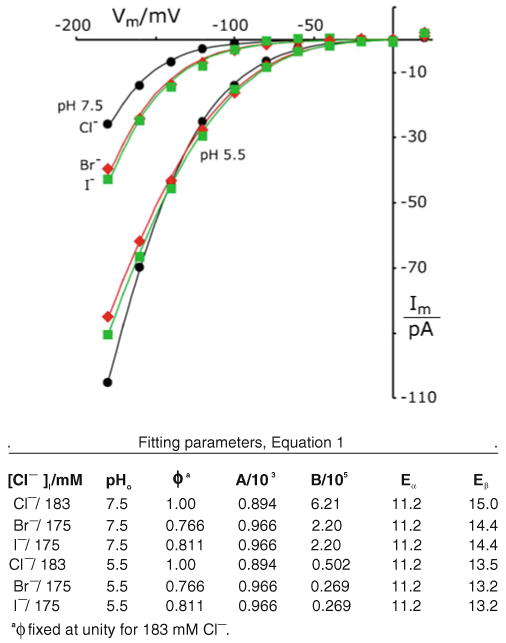
The TRK inwardly rectifying pathway is permeable to all three common halides. Plots represent averaged I–V data from all halide records generated as in Fig. 3, for wild-type spheroplasts. Smooth curves calculated with a₁=0.279 as previously determined for 183 mM Cl⁻ (Fig. 2), and the other parameters fitted simultaneously for all six plots (see Table below). Methods as in Figs. 2 and 3. Yeast strains EBC202 and K837. [To reduce clutter, scatter bars have been omitted from the plots, but SEMs at −180 mV varied in the range 4– 10 pA, and tapered to less than 1.5 pA at −100 mV, i.e., to within the height of the plot symbols]

Nitrite ions augment the chloride currents

Apart from very strongly chaotropic ions (see below), most other anions tested carried very much smaller currents through the TRK proteins than did chloride—typically less than 10%—when fully replacing KCl in the intracellular solution; also, they failed to block chloride currents when added at lower concentrations (∼40 mM [50]). Tested ions included polyaspartate, divalent anions such as sulfate, selenate, and glutarate, and a variety of monovalents: azide, acetate, chloroacetate, isethionate, bromate, bicarbonate, and dihy-drogenphosphate. Formate and MES (zwitterionic) were minor exceptions—supplanting 15–20% of the chloride currents. However, nitrite proved a major exception: 30 mM nitrite, replacing equivalent KCl in the patch– pipette solution (buffer G-NO₂), dramatically augmented the total TRK-mediated currents, as shown in Fig. 5.

How the recorded currents actually partition between chloride and nitrite was not determined, but measured current amplitudes roughly correspond to expectation for pure chloride concentrations of 500 mM at pH 7.5 and 250 mM at pH 5.5 [68]. Detailed analysis of the I–V plots via Eq. 1 yielded parameters fully consistent with the halide measurements in Fig. 4: in particular, the same position and value of barrier α sufficed for nitrite as for all the halides (a₁=0.279, E_α=11.2 Kcal/mol). Only lowering of barrier β by less than 1 kcal/mol was required by the 30 mM NO₂⁻, an effect which could most simply be related to increased permeability of the 153 mM Cl⁻ still present.

Osmoprotectants modulate halide currents

The suggestion that nitrite ions might enhance chloride permeation through TRK proteins prompted systematic testing of reagents expected to have an opposite effect via membrane stabilization. Most familiar of these so-called kosmotropic agents are trehalose, glycine betaine, and glycerol [13, 19, 26, 60], to which we added also glucose and sorbitol, as controls for pure osmotic effects. Preliminary experiments, in which KCl in buffer G-Cl was partially replaced by sorbitol, had yielded unexpectedly small TRK-dependent currents [50], and molar glycerol had been shown to serve as a chemical chaperone [26, 91] without hampering growth. Data from a full experiment with molar solutes are shown in Fig. 6a.

Resulting I–V plots all had sensibly the same shape, without any offset along the voltage axis, and all could be described by the same parameter set allowing only the scaling factor ϕ to vary from curve-to-curve. Perhaps as a consequence of growth conditioning in glycerol, the α peak appeared slightly higher and deeper in the membrane (E_α= 11.2→11.5 Kcal/mol; a₁=0.279→0.329) than for pure chloride experiments (cf. Fig. 5 legend with Fig. 3 legend); but E_β was in the normal range. For the whole family of I–V plots, conductances declined exponentially toward zero voltage, and the conductance ratios (G_m/G_control) were flat lines at the fitted values of ϕ, as shown in inset of Fig. 6a.

Apart from impossible changes of cell size, at least two distinct physical processes could simply scale down the TRK-dependent Cl⁻ currents: (1) different osmoprotectants blocking different fractions of the TRK-dependent chloride pathways, each in all-or-nothing fashion; or (2) osmoprotectants reacting with all TRK molecules in the yeast membrane, in a manner to elevate E_α and E_β by the same fractional amount (different fraction for each compound). This interpretation is represented in Fig. 6b and fits naturally into the general concept of the two-barrier model.

Inhibitory effects of strong chaotropic ions

Very chaotropic anions seem to destabilize Saccharomyces spheroplasts, but we were able to complete about two dozen current–voltage scans with 30–175 mM thiocyanate or nitrate. Current records for 30 mM thiocyanate displayed the usual spread due to large leakage currents (Fig. 7a, inset). After correction for this effect, SCN⁻ actually reduced the total TRK-mediated current at pH_o 5.5 and did so in manner to suggest that chloride conductance was blocked —despite the predominance of 153 mM Cl⁻ in the pipette solution. Furthermore, identical inward currents were observed with 30 mM SCN⁻, whether the major anion was Cl⁻ itself (diamonds) or was the barely conducted reference anion, gluconate (open circles at 145 mM, +8.3 mM Cl⁻ from other salts in buffer G-Cl). Finally, transport appeared chemically saturated at 30 mM, showing no significant increase of plotted currents at 175 mM (triangles). [For reference, voltage-driven currents with chloride only (Fig. 7, control) not only did not saturate as a function of concentration, even out to 590 mM [68], but depended more steeply on membrane voltage—prominently so at pH 5.5.] These comparisons became more complicated at pH 7.5 (Fig. 7b), but again with no distinction between chloride itself and gluconate. And for 175 mM SCN⁻, currents were actually reduced, relatively to those for 30 mM SCN⁻.

Fig. 7.

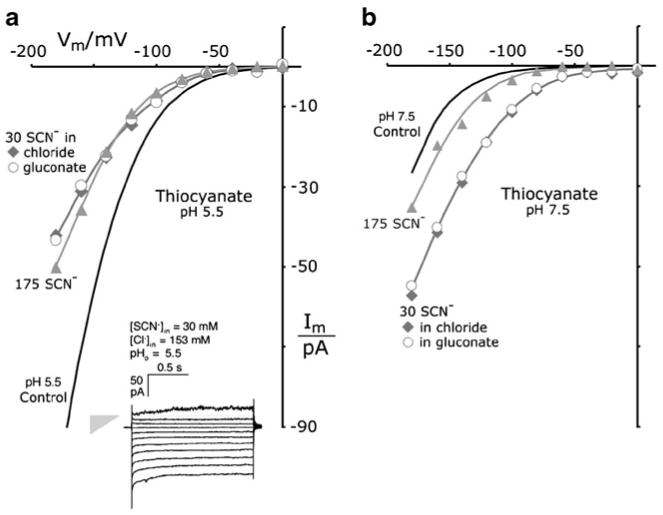
Thiocyanate supplants chloride currents through the TRK proteins. a Measurements at pH_o 5.5. b Measurements at pH_o 7.5. I–V plots for averaged data with 175 mM SCN⁻ (gray triangles) and with 30 mM SCN⁻ (gray diamonds, open circles). Gluconate buffer (intracellular) contained 30 mM KSCN+145 K-gluconate, replacing the 175 mM KCl of buffer G-Cl. Six experiments carried out with SCN⁻+Cl⁻, two with SCN⁻+gluconate. Smooth curves for thiocyanate are all drawn “by eye.” Controls (black curves) are the fitted chloride curves from Fig. 4. Inset Sample current traces in the presence of 30 mM SCN⁻. Gray triangle designates null current (point) and leak conductance (height=448 pS). Methods as in Figs. 2 and 3. Strain EBC 202

I–V plots in the presence of 30 mM nitrate ions differed quantitatively from those with 30 mM SCN⁻, in being superposable for pH_o 5.5 and 7.5 and lying roughly halfway between the two control plots for Cl⁻ ions (data not shown). Although the general meaning of this result is unclear, decreased current relative to Cl⁻ alone, at pH 5.5, implies that NO₃⁻ ions—like SCN⁻ ions—also block chloride transport.

Equation 1 has not been fitted to the I–V plots for nitrate and thiocyanate because of difficulty in specifying concentrations, with more than one permeant species. It is nevertheless clear that these very chaotropic ions react quite differently with the TRK protein than halide ions do; most importantly, SCN⁻ and NO₃⁻ ions block chloride currents. Easily demonstrated saturation in the latter effect implies a non-competitive mode of inhibition.

Osmoprotectants also choke thiocyanate currents

The results above imply that very chaotropic non-halide ions restructure the anion pathway through TRK proteins, likely by binding tightly within the channel. The question naturally arises, therefore, of whether or how osmoprotective solutes might affect conduction of the chaotropic ions. Tests were carried out with 1 M glycerol or 1 M glycine betaine included in the patch pipette, along with 30 mM thiocyanate. The mechanical stability of yeast spheroplasts was improved by both agents, and the SCN⁻ -related currents (Fig. 8) were reduced, though not as effectively as Cl⁻ currents had been (Fig. 6, above). Currents remaining in 1 M glycerol were 0.78×control, and in 1 M glycine betaine were 0.25 × control. The ratioed conductance lines in Fig. 8 inset show these two fractions clearly. Again, only small barrier elevations, E_α and E_β, were required.

Computing ionic selectivity

Since the I–V relationship defined by Eq. 1 is strongly non-linear, conductance (dI_m/dV_m) and conventional permeability become convoluted measures of ionic selectivity. Therefore, practical comparison of the channel's selectivity for different ions requires another measure, one applicable over the testable range of membrane voltages. The I–V plots themselves—in Figs. 3, 4, 5, and 7—suggest that chord conductances (G_m) at −180 mV, if corrected for ion concentrations and cell size, would reasonably mirror average ionic permeabilities between 0 and −180 mV. The appropriate calculations are summarized in Table 1.

Table 1. Comparative ionic permeabilities via chord conductances at −180 mV.

Test Ion	Conc. (mM)	Figure no.	pHo	Size (ϕ)	Im pA	Gm pS	aP/107 cm s−1
Cl−	183	4	7.5	1.0	26.7	148	1.13
Br−	175b	4	7.5	0.77	41.6	231	2.29
I−	175	4	7.5	0.81	44.1	245	2.30
SCN−	175c	7	7.5	1.0	35.2	196	1.49
NO3−	175	–	7.5	1.0	45.8	254	1.94
SCN−	30b	7	7.5	1.0	55.6	309	13.6
NO3−	30	–	7.5	1.0	39.7	220	9.72
NO2−	30d	5	7.5	1.0	52.6	416	12.9
Cl−	183	4	5.5	1.0	105.0	583	4.45
Br−	175b	4	5.5	0.77	85.6	476	4.70
I−	175	4	5.5	0.81	90.7	504	4.74
SCN−	175c	7	5.5	1.0	49.9	277	2.11
NO3−	175	–	5.5	1.0	45.8	254	1.94
Formate	175	–	5.5	1.0	15.9	88.4	0.671
Gluconate	175	–	5.5	1.0	8.3	46.2	0.351
Acetate	175	–	5.5	1.0	4.6	25.5	0.194
H2PO4−	170e	–	5.5	1.0	1.2	6.9	0.054
Cl−	30b	2	5.5	1.27	30.3	168	5.83
SCN−	30	7	5.5	1.0	42.7	237	10.5
NO3−	30	–	5.5	1.0	39.7	220	9.72
NO2−	30d	5	5.5	1.0	60.2	730	14.7

^aFormally, G_m] ₋₁₈₀=−I_m]₋₁₈₀/0.18, and the relevant permeability (e.g., for Cl⁻) is P_Cl=(RT/2F²)×(G_m]₋₁₈₀)/[Cl⁻]_i, where the factor 2 represents the standard surface area, 2×10⁻⁶ cm². P_Cl is normalized (÷ ϕ) for cell surface areas (see values in figure legends)

^bAll buffer solutions contained 8.3 mM residual Cl⁻, which was included in the total concentration used to calculate permeabilities, except for SCN⁻ and NO₃⁻. See legend to Fig. 4

^cFor thiocyanate and nitrate, only their actual concentrations (175 and 30 mM) were used, assuming simultaneous blockade of chloride. See esp. legend to Fig. 7

^dCalculations done as if NO₂⁻ currents added to Cl⁻ currents appropriate for 153 mM. This would be the superchloride behavior suggested in the text description of Fig. 5

^eCorrected from 175 mM, due to second dissociation at pK_a=7.2

With salts at high concentration, the highest permeabilities obtained for iodide, decreasing in the order I⁻ ≈Br⁻ >NO₃⁻ > SCN⁻ >Cl⁻ at pH 7.5; and in the order I⁻ ≈Br⁻ >Cl⁻ >SCN⁻ > NO₃⁻ at pH_o 5.5. Decrease over the range is about twofold, and the increase of permeability from pH 7.5 to 5.5 is also approximately twofold. At the low concentration (30 mM), there are no data for bromide and iodide, but the other calculated permeabilities decline from nitrite, in the order NO₂⁻ ≈SCN⁻ >NO₃⁻ at pH 7.5; and in the order NO₂⁻ > SCN⁻ ≈NO₃⁻ >Cl⁻ at pH 5.5. Again, decrease over the range is approximately twofold, but without a significant effect of pH_o. These are not large differences in permeability, and bespeak a rather non-selective anion pathway through the TRK proteins. However, currents and calculated permeabilities were much smaller for a wide range of other anions tested at pH 5.5 [50] and ordered in Table 1; Cl⁻≫formate>gluconate>acetate≫ phosphate⁻¹.

The relatively large permeabilities calculated for 30 mM salts, compared with 175 mM salts (10–15×10⁻⁷ cm/s, cf. 2–5×10⁻⁷ cm/s), result from strong non-linearity between measured currents and concentrations, for both SCN⁻ (Fig. 7) and NO₃⁻.

Discussion

General features

The purpose of this investigation has been to complete a quantitative, stationary-state description of the surprising phenomenon of anion conduction through the TRK potassium transport proteins of S. cerevisiae [50, 68]. Stationary-state measurements have been enforced by the yeast, since all practicable conditions for whole-cell patch clamping have produced “always on” TRK-Cl⁻ currents, or at least, on- and off-switching faster than the patch clamp amplifier.

Given the operational necessity of stationary-state analysis, the two-barrier model of Eq. 1 provides a simple, but quantitative description of the TRK-mediated anion currents, which can be shown to apply equally well to either protein, TRK1 or TRK2, and to their mixture in wild-type cells (Cl⁻ experiments [50]). A remarkable additional fact is that the measured stationary-state I–V relationship for yeast TRK proteins strongly resembles the whole-cell I–V relationships for a wide variety of plant cells, viz., with conspicuous inward rectification at large negative membrane voltages [6, 18, 21, 30, 87].

Most surprising about the two-barrier formulation for TRK-mediated currents is the range of data which it can accommodate with almost all parameters held in common for different test conditions. Indeed, of the four parameters intrinsic to Eq. 1, the two positional parameters proved very stable: b₂ being close to zero and completely insensitive to our experimental manipulations; and a₁ responding only to large changes of permeant-ion concentration (intracellular; see esp. Fig. 2). The latter fact suggests that changes of ionic strength, in the cytoplasm (pipette solution), should contort the intracellular end of the channel.

Parameter B, representing the height of the outer barrier (β), has proven by far the most important parameter in the model. Modest changes in its value alone can accommodate all I–V differences related to changes of pH_o, regardless of which permeant ions are involved (Figs. 2, 4, 5, 7); and as well, differences of selectivity between Cl⁻ and Br⁻ or I⁻ (Fig. 4), or between chloride and its admixture with nitrite (Fig. 5). The observed practical significance of B owes both to its mathematical role as a determinant of shape in the midrange of I–V data (viz., −100 mV to −180 mV), and to the greater height of that barrier, relative to barrier α (E_β>E_α by 2–4 Kcal/mol). The calculated sensitivity of B to changes of pH_o is intuitively reasonable since barrier β would reside at the interface with extracellular solution; but adjustment of B in response to changes of the intracellular ionic species is more difficult to rationalize, and presumably must involve a cascade of structural adjustments, as different ions transit the channel.

Selectivity and structural homology

There are two dominant functional characteristics of TRK-mediated anion currents through the Saccharomyces plasma membrane, as demonstrated in Figs. 2, 4, 5, and 7 and Table 1. (1) Low selectivity among halide and non-halide chaotropic ions, but strong discrimination against all other anions which have been tested. (2) Very strong inward rectification: conduction is activated by large negative voltages and represents large anion effluxes, but is essentially blocked at positive membrane voltages. Another important characteristic is (3) insensitivity to conventional anion channel blockers such as disulfonic stilbenes [50].

The apparent order of selectivity, at the high salt concentration (175 mM) varies somewhat with pH_o: I⁻≈ Br⁻>NO₃⁻>SCN⁻>Cl⁻, at pH 7.5; and I⁻≈Br⁻>Cl⁻> SCN⁻>NO₃⁻, at pH_o 5.5; but the permeability change over the whole range is only approximately twofold, as is the change from pH 5.5 to 7.5. [Similar relationships hold at the low salt concentration (30 mM), even though the calculated permeabilities are several fold higher due to non-linearity of the I–V curves.] Thus, the TRK pathway for anions is essentially non-selective with respect to halides and chaotropic ions, even though it clearly discriminates against other small anions, viz., Cl⁻≫formate>gluconate>acetate≫phosphate⁻¹. This sort of selectivity is unknown among ClC class channels and Cl⁻ -conducting ABC proteins [16, 55, 81], but resembles that in glycine-receptors (GlyR) and related ligand-gated anion channels [12, 25, 56].

A very broad sequence search failed to identify any structures homologous to the fungal TRK-M1_D helices, among bona fide chloride channels, transporters, or pumps. This negative information, plus the characteristic selectivity, noted above, of the TRK–anion pathway prompted us to review sequences and structures in ligand-gated ion channels (LGICs). The central pore of LGICs comprises a barrel stave array of five transmembrane helices (designated M2 or α2), one from each monomer within an assembled pentameric protein. And the M1_D helix of yeast TRK proteins bears remarkable similarity to those LGIC barrel staves. Figure 9a compares two yeast M1_D sequences (+flanks) with M2 sequences from two anion-selective LGICs (GlyR, GABA_AR) and two cation-selective LGICs (nAchR, ELIC). Figure 9b compares the opposition of two pore-lining helices in the Durell and Guy model for SpTrk1 with two pore-lining helices from the recent crystal structure for ELIC (pentameric [11, 35]).

Fig. 9.

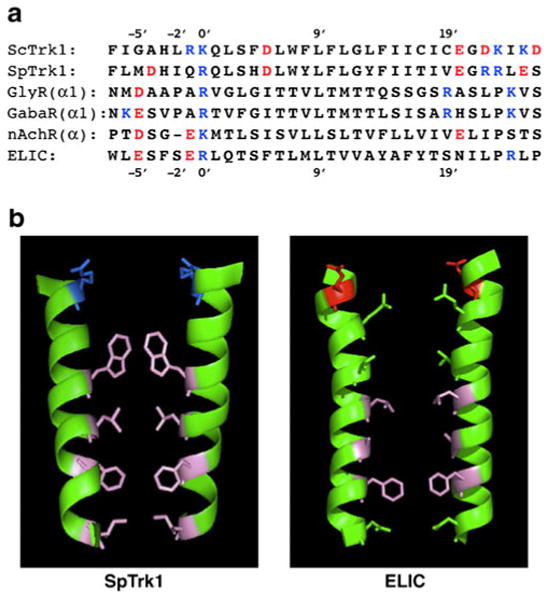
Comparison of yeast transmembrane segments M1_D and pore-lining segments (M2, α2) of four ligand-gated ion channels (LGICs). a Primary sequences, in order top to bottom: S. cerevisiae; Schizosaccharomyces pombe, human glycine receptor α1 subunit, GABA_A receptor α subunit (highly conserved sequence, identical in many species: human, mouse, rat, chicken, zebrafish, etc.); nicotinic acetylcholine receptor α subunit (also highly conserved: human, etc.); Erwinia chrysanthemi, recently crystallized bacterial homologue of nAchR [11, 36]. Customary numbering convention for LGICs, with 0′ lying at the internal face of the membrane and 20′ at the external face. b Ribbon models of paired transmembrane segments for SpTrk1 (left panel; the sequence directly modeled by Durell and Guy [23]) and for ELIC, spanning from −1′ at the inner surface of the membrane to 20′ at the outer surface. Stick figures depict only those side chains pointing into the channel. Blue basic amino acids, red acidic amino acids, pink hydrophobic amino acids, green uncharged polar amino acids. [The guanidinium side-chain on arginine at 0′ in ELIC projects away from the pore, and therefore is not shown. Bona fide LGIC channels are pentameric; the postulated structure for TRK-Cl⁻ channels is tetrameric.] Drawing via PyMOL (DeLano Scientific, & Schrödinger LLC, Portland, OR, USA)

Charge selectivity (anion versus cation) of LGIC channels can be controlled by the residue at position −1′. When that residue is uncharged, like alanine in wild-type GlyR or GABA_AR, the channel is anion selective; when it is negative, like glutamate in nAchR, ELIC, or certain mutants of GlyR, the channel is cation selective [63]. It seems likely that charge selectivity in the yeast structure would follow a similar rule. We are currently testing this hypothesis in ScTrk1 having glutamate substituted for arginine and lysine at positions −1′ and 0′, and also for the obstructing tryptophane and phenylalanine residues at positions 7′ and 14′ (mutants constructed by Dr. Jost Ludwig, University of South Bohemia, Czech Republic).

Both pores in Fig. 9b are depicted in presumed closed states, which would be enforced by hydrophobic exclusion of water, and therefore exclusion of hydrated ions. For LGICs, elaborate machinery has evolved in the surrounding protein to control gating; and there is much discussion of how that might work, focusing on Arg/Lys-0′ and adjacent residues, on the center of the membrane adjacent to Leu-9′, and on changes in tilt of the M2 helices [11, 36, 62, 65, 82]. For the yeast TRK-Cl⁻ conductance, no organic ligands, TRK segments, or β subunits are presently known to effect gating. The only secure gating factor is strong membrane hyperpolarization, as modulated by extracellular pH: at pH_o 4.5, the apparent gating voltage is near −160 mV; and at pH_o 7.5, near −270 mV (Fig. 2 above; see also [68]). High-voltage gating, sometimes called punch through [29, 92], is qualitatively consistent with the predominance of bulky, hydrophobic side chains within the pore, as depicted in Fig. 9b (left panel). Indeed, that structure should be an excellent experimental model for hydrophobic gating [5, 3, 45, 90], wherein rapid conductance transitions and sharp thresholds are expected [4, 42].

Protein stabilization

Hydrophobic gating may also provide a plausible physical mechanism for osmoprotective agents to scale down Cl⁻ and SCN⁻ currents through the TRK proteins (Figs. 6, 8). Channels poised at the threshold for hydrophobic closure could be triggered by increasing the osmotic (diffusion) gradient between the channel interior and neutral but hydrophilic solutes in the surround. Thus, the number of channels conducting at any one voltage or time—not the intrinsic barrier amplitudes (see text for Fig. 6)—would be modulated by osmoprotective solutes.

Alternatively, suppression of TRK-chloride currents by organic osmolytes can be viewed as a specific case of such osmolytes' well-known ability to stabilize protein structures. In other kinds of experiments from the literature, polyalcohols and sugars—including the above-tested agents—have been shown to protect proteins from disruption by heat, salt, and freezing [2, 13, 43, 66, 71]. And some, especially glycerol and glycine betaine, have been widely adopted in evolution as “compatible” solutes, displacing cytoplasmic salt in salt-tolerant microorganisms and plants [51, 89], while trehalose has turned up acutely in most organisms which can survive complete dedhydration [41, 79].

In the specific case of the putative TRK oligomer, all four effective osmolytes could stabilize TRK either (1) in a monomeric state where the facultative chloride channel does not exist, or (2) in a water-excluded oligomer, viz., hydrophobically gated shut. Discrimination between these two possibilities should be revealed by elevating temperature. In the first case, the temperature coefficient of the effects in Figs. 6 and 8 should be unequivocally positive (suppression of currents with rising temperature), whereas in the second case an interval of negative temperature coefficient would be expected (enhancement of currents with rising temperature). Experiments into the influence of temperature on TRK-chloride currents are being undertaken. More generally, thermal denaturation may be a very useful way to characterize the underlying process of protein stabilization by kosmotropic agents.

[One trivial suggestion can easily be dismissed: these osmolyte effects upon TRK-Cl currents do not depend on altered ionic properties of the cytoplasmic (pipette) solutions. This was shown by a simple comparison of the observed current scaling (Figs. 6, 8) with effects of molar osmolytes on measured solution conductances and on actual salt concentrations, as affected by the partial volumes of osmolytes (A. Rivetta & C. L. Slayman, unpublished expts.). In particular, 1 M glucose and 1 M sorbitol both depressed buffer G-Cl conductance by ∼35%; but glucose had no effect on the TRK-Cl currents, while sorbitol reduced those currents by ∼63%. And, 1 M glucose and 1 M glycine betaine have the same concentrating effect on the KCl-to-water ratio (viz., the same partial molar volumes, ca. 100 ml/Mol), but only glycine betaine diminished the TRK-Cl currents, and that by ∼89%.]

End notes

A major handicap to hard mechanistic analysis of this fungal TRK-anion channel is the lack of independent evidence for oligomerization within the membrane to form a pore that is not committed to K⁺ transport. While a tetramer is easiest to imagine, trimers and pentamers might also serve, or perhaps even a dimer. The latter has, in fact, been demonstrated in a crystal structure for the bacterial homologue VpTrkH (inVibrio parahemolyticus; 3.5Å resolution, M. Zhou, personal communication [14]). That structure confirms a K⁺ channel-like arrangement for the two potassium pathways [23] and shows the bacterial protein to be dimerized in the crystal at a complicated hydrophobic interface involving M1_D and M2_C. Thus, oligomerization of TRK-type proteins does occur. However, outside the actual K⁺ pathway, VpTrkH and the fungal TRK proteins share no sequence conservation; and even within the M1_D helix itself, overlapping leucine (L/I) heptads found in the fungal proteins are not copied in the bacterial protein. Thus, identical oligomerization of TRK monomers in Saccharomyces compared with Vibrio seems unlikely.

Apart from the fact itself—of anion conduction through a K⁺-transport protein—two particular features of the stationary-state data will demand detailed mechanisms: the anomalous interactions of chloride with thiocyanate (Fig. 7), nitrate, or nitrite (Fig. 5); and the very strong inward rectification, which allows essentially zero outward current (Cl⁻ influx) via the TRK-Cl⁻ pathway. Anomalous (non-linear or paradoxical) permeabilities, frequently observed when two ionic species traverse the same transport pathway, have classically been attributed to interactions within multi-ion, single-file channels [39]. But other schemes also work, including charged wide-channel models [28], allosteric models, and simple enzyme kinetic models [22, 32]. The phenomenon of very strong rectification has also been frequently observed in stationary-state I–V measurements of ligand-gated ion channels, esp., during whole-cell recording [8, 69, 78]. As a feature of yeast TRK-Cl⁻ currents, therefore, strong rectification provides a further argument in support of TRK oligomerization.

Another important yet unanswered question is the actual biological function of the TRK-anion pathway, viz., the reason for especial sequence conservation in helices M1_D and M2_D, across fungal species [24, 61]. The short answer is that we do not know. But a significant possibility is that it provides the normal escape route for metablic anions to balance charges during net proton ejection by the plasma-membrane proton pump ([72, 75]). In Neurospora crassa, for example, net proton extrusion rises approximately tenfold as pH_o is raised over the range 5–9, with a high pH value >20, and a low value <2 mMol/kg cell water/min [74]. The high value corresponds to pump currents required to sustain membrane voltage; and it is roughly balanced by release of carboxylic acid anions, whereas charge balance at low pH is maintained predominantly by proton reentry coupled to nutrient uptake. The major carboxylic anions released under normal laboratory conditions for Saccharomyces are lactate, malate, and succinate [73]; and for Neurospora are malate, α-ketoglutarate, glutamate, fumarate, citrate, and succinate (C.L. Slayman & P. Kaminski, unpublished data; lactate not measured). Although none of these anions has been tested in the yeast TRK system, formate, acetate, and several inorganic divalent ions proved to be poor substitutes for Cl⁻ [50]. Those trials were carried out at pH_o=5.5, however; and because release of carboxylate anions rises steeply with pH_o, the intriguing possibility exists that TRK permeability to metabolic divalent ions might actually increase with rising pH_o. [Carboxylic-acid transporters, per se, have been only sparingly studied in fungi, and almost always in regard to uptake of those anions as alternative carbon sources [15, 57, 77]. There has been little interest in efflux, outside of industrial processing.]