Muscle synergies as a predictive framework for the EMG patterns of new hand postures

Abstract

Synchronous muscle synergies have been suggested as a framework for dimensionality reduction in muscle coordination. Many studies have shown that synergies form a descriptive framework for a wide variety of tasks. We examined if a muscle synergy framework could accurately predict the EMG patterns associated with untrained static hand postures, in essence, if they formed a predictive framework. Hand and forearm muscle activities were recorded while subjects statically mimed 33 postures of the American Sign Language alphabet. Synergies were extracted from a subset of training postures using non-negative matrix factorization and used to predict the EMG patterns of the remaining postures. Across the subject population, as few as 11 postures could form an eight-dimensional synergy framework that allowed for at least 90% prediction of the EMG patterns of all 33 postures, including trial-to-trial variations. Synergies were quite robust despite using different postures in the training set, and also despite using a varied number of postures. Estimated synergies were categorized into those which were subject-specific and those which were general to the population. Population synergies were sparser than the subject-specific synergies, typically being dominated by a single muscle. Subject-specific synergies were more balanced in the coactivation of multiple muscles. We suggest as a result that global muscle coordination may be a combination of higher order control of robust subject-specific muscle synergies and lower order control of individuated muscles, and that this control paradigm may be useful in the control of EMG-based technologies, such as artificial limbs and functional electrical stimulation systems.

1. Introduction

The motor system's coordination of the many degrees of freedom (DOFs) associated with performing a task has been termed an ill-posed problem because of the biomechanical and neuromuscular redundancies in the anatomical structure (Bernstein 1967). It has been suggested that the central nervous system (CNS) coordinates musculature to build complex motor patterns based upon dimensionally reduced sets of fundamental control modules. These control modules, when combined sequentially or in parallel, produce a wide range of observable patterns of movement (Mussa-Ivaldi and Solla 2004). This concept has been formally articulated in the neuromotor synergy hypothesis, which states that `… low-level, neurally based patterns significantly constrain intentional actions' (Lee 1984). Indeed, this idea is not new and has been postulated since the turn of the 20th century (Bernstein 1967, 1971, Sherrington 1906)—only the nomenclature and proposed physiological manifestations of these patterns have changed. Most recent is the idea of fundamental muscle coordination patterns, termed muscle synergies (Bernstein 1971, Tresch et al 1999). These researchers defined a muscle synergy to be a set of muscles whose relative activation levels are neurally predetermined. A single muscle can simultaneously belong to multiple synergy sets, and it is the weighted combinations (i.e. activation levels) of these synergy sets that determine global muscle activation patterns. Muscle synergies are an attractive idea because empirical evidence suggests that muscle patterns are potentially encoded in the distributed activities of neurons in the M1 motor cortex (Holdefer and Miller 2002, Kakei et al 1999). Furthermore, muscle synergies have been shown to form the basis of complex muscle coordination patterns involved in activities such as kicking, swimming, jumping of frogs (Bizzi et al 2002, Cheung and Tresch 2005, d'Avella and Bizzi 2005, d'Avella et al 2003, Saltiel et al 2001, Tresch et al 1999, 2002), postural standing and muscle responses to postural perturbations (Ting and Macpherson 2005, Torres-Oviedo et al 2006) and human arm movements (d'Avella et al 2006, Soechting and Lacquaniti 1989).

Regarding hand control, several studies have presented evidence that the coordination of intrinsic joint positions associated with a wide variety of hand postures could be described by a dimensionally reduced kinematic synergy framework. Studies in typing (Soechting and Flanders 1997), hand shaping for tool use (Santello et al 1998), dynamic posture formation (Mason et al 2001, 2004) and miming of the American Sign Language (ASL) alphabet (Jerde et al 2003) have reported that the high-dimensional kinematics of the hand can be described by a lower dimensional set of basis postures, which are combined to produce the more complex joint positions. Recent studies have been focused on examining similar synergistic-based dimensionality reduction paradigms with regard to the EMG activities associated with hand postures (Breteler et al 2007, Ishida et al 2007, Weiss and Flanders 2004, Overduin et al 2008). One study of note aimed to describe the hand postures associated with the ASL alphabet and with grasping of everyday objects with a low-dimensional set of muscle synergies, and to align these muscle synergies with kinematic synergies of the hand (Weiss and Flanders 2004). The investigators reported that the six-dimensional EMG patterns associated with the hand postures for grasping everyday objects could be described at a rate of 80–90% by a three- or four-dimensional set of muscle synergies. A similar study from the same laboratory expanded the synergy framework from that of static synergies to that of time-varying synergies to explore the timing of muscle activations during finger spelling (Breteler et al 2007). These time-varying synergies, initially explored in the locomotion of frogs (d'Avella et al 2003), are essentially pre-stereotyped patterns of EMG bursts in a given muscle group. This study reported that four time-varying synergies, reduced from essentially a six-muscle set, could account for 80% of the temporal EMG patterns observed during hand coordination during finger spelling.

One shortcoming of many of the studies reported in the muscle synergy literature is that though a basis set of synergies is found to describe the observed data sets, there is little compelling evidence to suggest that the extracted muscle synergies have real physiological significance and hence could be used as more than a description of the observed data. These studies show that muscle synergies form a descriptive framework for the EMG patterns observed during a set of tasks, but they do not explore if these synergies can form a predictive framework for a brand new set of tasks. Demonstrating a predictive framework is a more powerful assertion, and would more strongly suggest that muscle synergies are a reasonable governing paradigm of neural control by the central nervous system. The investigation of whether or not muscle synergies form a predictive framework for a wide variety of hand postures would suggest that the synergies are robust and general, rather than specific to the investigated tasks. Robustness and generality have been articulated by other investigators as a necessary testable hypothesis for validation of the muscle synergy concept (Lee 1984). Therefore, the aim of this work was to investigate if muscle synergies form a robust lower dimensional framework for the prediction of the EMG patterns of new untrained static hand postures. It was hypothesized that a reduced set of muscle synergies describing a small set of static hand postures could predict the EMG patterns from a wide variety of new static hand postures with comparable accuracy. Consequently, the number of synergies necessary to adequately predict the EMG patterns of new hand postures would not exponentially grow with an increase in the size of the predicted set. Within this hypothesis, the following questions were specifically examined.

• How many synergies are needed to completely describe this lower dimensional predictive framework, and how robust are these synergies between postures and persons?

• How many hand postures are needed to define the muscle synergy set of this framework?

• What is the predictive power of the established framework?

2. Materials and methods

Seven research subjects (age 29.1 ± 11.0 years), all of which were self-described right-hand dominant, participated in this study. No subject had known history of any neuromuscular disorders. All subjects gave informed consent to the procedures as approved by the Northwestern University Office for the Protection of Research Subjects (NUOPRS) Institutional Review Board. The subjects are referred to by their subject ID number (SID_1–7).

2.1. Electromyography

EMG activities were recorded from three intrinsic muscle/anatomical muscle groups and eight extrinsic muscles of the hand during the experimental tasks. Intramuscular EMG signals were recorded from flexor digitorum profundus (FDP), flexor digitorum superficialis (FDS), extensor digitorum communis (EDC), extensor digiti minimi (EDM), extensor indicis propius (EIP), extensor pollicis longus (EPL), abductor pollicis longus (APL), flexor pollicis longus (FPL) and first dorsal interroseous (FDI). Bipolar percutaneous electrodes were inserted mid-muscle belly using Basmajian's single needle technique (Basmajian and Stecko 1962), and in accordance with the standard anatomy and electromyography text (Perotto and Delagi 2005). Intramuscular electrodes were 0.0055 inch diameter (0.14 mm) stainless-steel wire, and Teflon coated with exposed tips for recording (<3 mm bipolar electrode spacing). Electrode placements were verified by observing the kinematic responses to low current electrical stimulation (performed percutaneously using the fine-wire electrodes). The small intra-electrode distance aided in minimizing recording of cross-talk from adjacent muscles. This was verified prior to data collection by visual inspection of the EMG patterns associated with the appropriate voluntary joint movements. For the multi-compartment muscles FDS, FDP and EDC, deliberate attempts were made to record primarily from the fourth compartment (controlling ring-finger movement). Successful placement in the fourth compartment was verified by electrical stimulation in all subjects, although rare residual stimulation effects were observed in the third (middle finger) or the fifth (pinky finger) compartment in a few subjects. Several studies have shown that there is significantly less functional independence between the middle, ring and pinky fingers, versus high functional independence of the index finger (Schieber 1991, Schieber and Poliakov 1998). Given this accepted result and that the majority of the hand postures used in the experimental protocol required the middle, ring and pinky fingers to work in concert, the recorded EMG signals were adequate representations of the appropriate muscle activity of the desired hand grasps. Surface EMGs were recorded using standard bipolar Ag/AgCl electrodes (2.0 cm differential spacing) from the thenar eminence (TE) intrinsic muscle group (consisting of opponens pollicis, abductor pollicis brevis and flexor pollicis brevis) and the hypothenar eminence (HTE) intrinsic muscle group (consisting of opponens digiti minimi, abductor digiti minimi and flexor digiti minimi). Placement of the surface electrodes was performed by instructing the subject to oppose the pinky finger and thumb, and then palpating for the area of largest muscle bulge. Electrical stimulation was not used with the sEMG electrodes. sEMG electrodes were additionally taped or wrapped with Coban Self-Adherent Wrap (3M Technologies, St Paul, MN) to ensure consistent contact and location throughout the experiment.

All EMG data were recorded using a Noraxon (Phoenix, AZ) Telemyo 2400R System™. The sixteen-channel system includes a wireless transmitter–receiver system with an adjustable internal gain up to 2000 (transmitter: 2, receiver: 1000), a bandwidth of 20–1000 Hz and an internal sampling rate of 3000 Hz. The analog signals from the receiver were then fed through a 12 bit A/D board, and digitally sampled at 3000 Hz. The data were recorded and visualized using an in-house custom built virtual instrument interface in National Instruments (Austin, TX) LabVIEW Developer's Environment version 7.2. Raw EMG was saved in a standard ASCII file for further processing.

2.2. Tasks and data collection

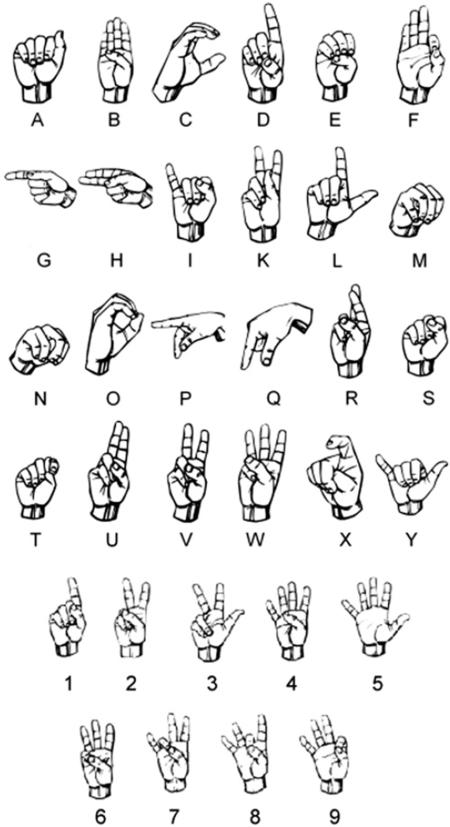
Subjects were seated upright in a comfortable chair with their dominant arms and wrists supported. Wrist movement was not restricted. Subjects were instructed to shape their dominant hands into each of 33 static letters and numbers of the American Sign Language (ASL) posture set (figure 1). Many of the hand postures included in the ASL set are very similar to hand postures for grasping objects. For example, the letter `C' is very similar to the power/cylindrical hand posture used to grasp large objects, and the number `9' is very similar to a pinch/tip hand posture used to grasp minute objects between the thumb and the index finger. Thus, the ASL posture set provides a sufficient spanning of the hand postures for grasping and digit individuation. Dynamic letters `J' and `Z' were omitted from the finger-spelling task, along with the number `0', which was visually the same as the letter `O'. During the electromyography phase of the study (prior to data collection), subjects familiarized themselves with the hand positions of the ASL set so that they would be consistent in performing the hand postures during the data collection phase. The published literature has suggested that this learning phase gives ample time for subjects to learn to produce consistent hand postures congruent with that of fluent ASL spellers (Jerde et al 2003, Weiss and Flanders 2004).

Figure 1.

Subjects shaped their hand into each of 33 static letters and numbers of the American Sign Language (ASL) alphabet. `J' and `Z' were omitted from the study. `0' was omitted because it was visually the same as the letter `O'.

Initiated by an audio cue, subjects were shown on a computer screen the letter and hand position to replicate. The subjects had 8 s to create and hold the specified hand posture in a static position. They typically took 1–2 s to create the posture, and then statically held it for the remaining 6–7 s. At the end of the 8 s period, the visual aid was cleared and an audio cue instructed the subjects to return to the rest position. The next letter was presented after a 2 s rest period. This rest period served to washout any potential effects the previous hand posture may have on the motor strategy used to produce the next hand posture. The subjects were instructed to only apply as much force necessary to maintain the hand in the given posture, and specifically were instructed to not co-contract their muscles beyond this required level. Hence, the hand position and force level of posture were self-selected by each subject. The investigator monitored the subjects' performances for consistency of hand positions. Subjects had little to no trouble producing the intended hand postures. Minor errors in digit positioning were not corrected by the investigator during trials, and all trials were used in the offline analysis. While hand kinematics were not quantitatively measured during the finger-spelling task, post hoc analysis of the associated EMG patterns revealed that the postures were repeatable and distinct from one another (see figure 5). The presentation order of the ASL set was completely randomized so as to remove any effects that order could have on the muscle coordination patterns used to produce the hand postures. Each subject completed seven trials of miming the full ASL set, with a 5 min break given between each trial to minimize the possibility of fatigue. EMG activities were recorded from the 11 aforementioned muscles during the entire phase of ASL miming. Time, ASL letter and EMG voltages were saved to an ASCII file for later processing.

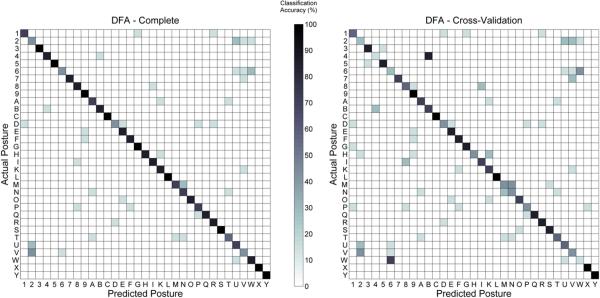
Figure 5.

The representative discrimination matrices of subject SID₄ show that the EMG patterns for the 33 mimed ASL letters were distinct and repeatable across several trials. Perfect discrimination would be represented by a solid black diagonal surrounded by all white boxes. The discrimination levels for both the complete (left—81% discrimination) and cross-validation (right—64% discrimination) data sets are significantly greater than chance (1/33). Similar observations were made for all subjects (see table 1).

2.3. Data pre-processing

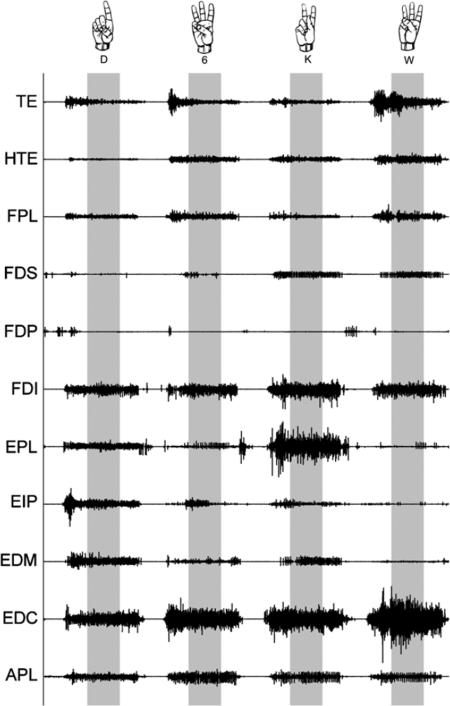
All EMG signals were filtered using a sixth-order Butterworth bandpass with (low, high) cutoff frequencies of (30, 600) Hz, and a second-order Butterworth notch filter with (low, high) cutoff frequencies of (59.5, 60.5) Hz, respectively. To only capture the static phases of the mimed ASL postures, the portions of EMGs from t = 2.5 s to t = 5 s per posture were used for the remaining analyses (figure 2). The root-mean-square (RMS) values of the resulting signals were computed over this range of static miming. These values were normalized relative to the resting and maximum activities of the respective muscles observed during maximal voluntary contraction (MVC) tests, such that all resultant muscle activities ranged between 0 and 1. Normalization is standard practice and serves to give an estimate of the relative contribution of each muscle to a given response (Tresch et al 1999). Each miming of posture was represented as an 11-dimensional vector in normalized muscle space, with each dimension corresponding to one of the recorded muscles. Hence each full trial of a set of mimed postures was represented as a data matrix {V_i | i = 1, …,7} of dimensions 11 × 33 (muscles × number of postures). The full data matrix V = {V_i} of recorded activity for each subject was thus of dimensions 11 × 231.

Figure 2.

Intramuscular EMGs were recorded from FDP, FDS, EDC, EDM, EIP, EPL, APL, FPL and FDI. Surface EMGs were recorded from TE (consisting of the intrinsic thumb muscles APB, FPB and OPP) and HTE (consisting of the intrinsic pinky finger muscles ADM, FDM and ODM). Needle electrode placements were verified using low current electrical stimulation. Subjects formed and held the instructed postures for 8 s, but only the steady state portion from t = 2.5 s to t = 5 s was analyzed (highlighted in gray).

A discriminant function analysis (DFA) (Santello et al 1998, Santello and Soechting 1998) was performed to quantify how distinct the EMG patterns associated with each posture were from one another, and also how repeatable they were between trials. This analysis represents the data in multidimensional muscle space and finds linear discriminant functions that serve to maximize the ratio of the intergroup to intra-group variances, for the purposes of maximally separating the data. In this work, discriminant analysis was implemented in two stages: first using all data points, and then second using a leave-one-out cross-validation method. It is this second implementation that tests the validity of the discriminant functions by assessing how well a new trial of a given posture can be classified. Reported for each subject are the classification accuracies using stage 1 (complete implementation) and stage 2 (cross-validation implementation) analyses.

2.4. Muscle synergy extraction algorithm

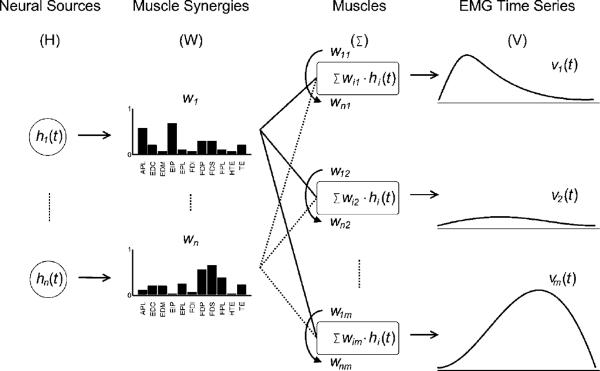
The generalized feed-forward muscle synergy model (MSM) that has been proposed for muscle coordination in the current motor control literature, and is referred to in this paper, is illustrated in figure 3. A single synergy represents the fixed spatially correlated activations of a group of muscles. Each synergy vector of muscle correlations $\{{\overrightarrow{w}}_i\mid i=1,\dots ,n\}$ is activated by a corresponding time-varying neural input h_i (t). The total activation of a given muscle j is the sum of its representations in each synergy (i.e. w_ij) weighted by the respective input (h_i(t)), as given by

$$\begin{array}{c}\hfill v_j\left(t\right)=\sum _{i=1}^n{w}_{\mathit{ij}}\cdot h_i\left(t\right)\{v,w,h\}\ge 0\hfill \\ \hfill \forall \{i=1,\dots ,n,j=1,\dots ,m\}.\hfill \end{array}$$ (1)

The full model is written in matrix form as

$$\begin{array}{c}\hfill {\mathbf{V}}_{m\times o}={\mathbf{W}}_{m\times n}\times {\mathbf{H}}_{n\times o}\hfill \\ \hfill {\mathbf{V}}_{m\times o}=\left[\begin{array}{c}\hfill {\stackrel{\rightharpoonup }{v}}_1\left(t\right)\hfill \\ \hfill {\stackrel{\rightharpoonup }{v}}_2\left(t\right)\hfill \\ \hfill ⋮\hfill \\ \hfill {\stackrel{\rightharpoonup }{v}}_m\left(t\right)\hfill \end{array}\right],\hfill \\ \hfill {\mathbf{W}}_{m\times n}=\left[\begin{array}{cccc}\hfill w_{11}\hfill & \hfill w_{21}\hfill & \hfill \cdots \hfill & \hfill w_{n1}\hfill \\ \hfill w_{12}\hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill w_{n2}\hfill \\ \hfill \dots \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill w_{1m}\hfill & \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill w_{\mathit{nm}}\hfill \end{array}\right]\hfill \\ \hfill \text{and}{\mathbf{H}}_{n\times o}=\left[\begin{array}{c}\hfill {\stackrel{\rightharpoonup }{h}}_1\left(t\right)\hfill \\ \hfill {\stackrel{\rightharpoonup }{h}}_2\left(t\right)\hfill \\ \hfill ⋮\hfill \\ \hfill {\stackrel{\rightharpoonup }{h}}_n\left(t\right)\hfill \end{array}\right],\hfill \\ \hfill \hfill \end{array}$$ (2)

where V is the m × o (m muscles, o observations) recorded EMG data matrix, W is the m × n (n synergies, m > n) column-wise matrix of synergies and H is the n × o matrix of time-varying neural inputs. V is given, and W and H are to be determined. Equation (1) is the time-dependent version of the synergy model, but it was used in the current work in the form of equation (3). The average EMG patterns of o discrete observations are predicted rather than the temporal pattern of a single observation:

$$\begin{array}{c}\hfill v_j\left[r\right]=\sum _{i=1}^n{w}_{\mathit{ij}}\cdot h_i\left[r\right]\{v,w,h\}\ge 0\hfill \\ \hfill \forall \{i=1,\dots ,n,j=1,\dots ,m,r=1,\dots ,o\}.\hfill \end{array}$$ (3)

Figure 3.

Neural input sources (H) send command signals which act as multipliers to each muscle synergy (W). The results are then summed to produce the observed EMG activities of each muscle (V). V is given, and W and H are determined by non-negative matrix factorization (NMF).

Several algorithms exist for determining W and H, including principal components analysis (PCA) and independent components analysis (ICA). In this work, nonnegative matrix factorization (NMF) was chosen because it has been reported to outperform PCA, and perform as well as ICA, in determining known synergies underlying a data set in the presence of noise (Tresch et al 2006). Furthermore, it does not restrict the discerned synergies to be orthogonal or statistically independent, as do PCA and ICA respectively (Hyvarinen et al 2001, Hyvarinen and Oja 2000). Finally, given that muscle activations (and inhibitions) are positive valued voltages, the synergy components discerned by NMF likely have more physiological relevance due to the restriction of non-negativity (Lee and Seung 1999). The NMF algorithm has been fully described elsewhere (Lee and Seung 1999, 2001). Briefly, the random initialized estimation matrices W_est and H_est are iteratively updated using multiplicative rules given by

$$\begin{array}{c}\hfill W_{n+1}=W_n\ast \frac{V\times H_n^T}{W_n\times H_n\times H_n^T}\hfill \\ \hfill H_{n+1}=H_n\ast \frac{W_n^T\times V}{W_n^T\times W_n\times H_n}\hfill \\ \hfill W_{n+1}\left(a\right)=\frac{W_{n+1}\left(a\right)}{\text{norm}\left(W_{n+1}\left(a\right)\right)}\forall \text{columns}‘a’,\hfill \end{array}$$ (4)

where `*' is the element-wise multiplication, `/' is the element-wise matrix division and `×' is the standard matrix multiplication.

The goodness-of-fit metric of the estimated matrices is the amount of variance explained (VE) of V by V_est, where V_est = W_est × H_est. Updating continues until the change in variance explained in k = 20 consecutive iterations is less than a tolerance ε = 1 × 10⁻⁵.

2.5. Synergy analysis of EMG data

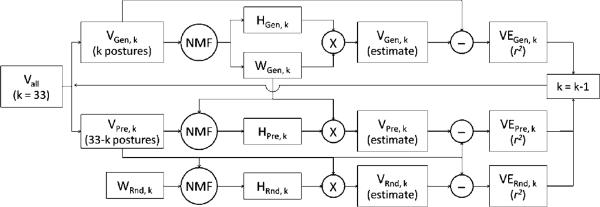
Figure 4 shows a block diagram of the synergy extraction analysis. Non-negative matrix factorization was used to determine a dimensionally reduced set of n basis vectors (i.e. muscle synergies) that could adequately characterize the full 33-letter, seven-trial EMG data matrix V. The set of 33 letters was divided into a generative set (V_Gen,k) of size k letters for estimating and validating the synergies, and a predicted set (V_Pre,k) of size 33-k new letters for assessing the predictive power of the estimated synergies. Synergies were estimated from the EMG patterns of the generative set of postures, resulting in W_Gen,k (the muscle synergies underlying V_Gen,k) and H_Gen,k (the time-varying inputs of W_Gen,k with respect to V_Gen,k), and a corresponding variance explained of VE_Gen,k. W_Gen,k was then used to predict the EMG patterns of the set of new letters (V_Pre,k). Specifically, NMF was applied to V_Pre,k, with only H_Pre,k (time-varying inputs with respect to V_Pre,k) updated according to the NMF rules, while W_Gen,k was held constant. V_Pre,k was then compared to the estimated EMG data matrix given by W_Gen,k × H_Pre,k, resulting in a variance explained (r²) value VE_Pre,k that was the measure of the predictive power of the synergy framework defined by W_Gen,k. For a baseline comparison, we used two methods to assess how much of the predictive power (r²) of W_Gen,k with respect to V_Pre,k could be attributed to simple data fitting or random chance. First, synergy sets were extracted and validated, as described above, from artificial structureless data created by independently and randomly shuffling the samples of each muscle in the experimental data (Cheung et al 2005, d'Avella and Bizzi 2005, d'Avella et al 2006), resulting in an explained variance VE_Art,k. Second, V_Pre,k was estimated using an exponentially distributed random and non-updated synergy set W_Rnd,k, resulting in corresponding temporal neural inputs H_Rnd,k and an explained variance VE_Rnd,k (d'Avella et al 2003). The random synergies were drawn from an exponential distribution because this probability density function provides a level of sparseness that is comparable to what has been reported and is commonly accepted for physiological signals (Bell and Sejnowski 1997, Olshausen and Field 1996, Vinje and Gallant 2000).

Figure 4.

Muscle synergies were extracted from the EMG patterns of the ASL hand postures using non-negative matrix factorization (NMF) analysis. The full data set (V_all) was split into a generative set of k hand postures (V_Gen,k) for the extraction of synergies, and a predicted set of 33-k new hand postures (V_Pre,k) for assessing the predictive power of the synergy framework. Synergies (W_Gen,k) and the associated neural inputs (H_Gen,k) were estimated from the generative set of postures, and an r² quantified the validity of the estimates. The unmodified estimated synergies (W_Gen,k) were then used to predict the EMG patterns of the new set of hand postures, and the resultant neural input matrix (H_Pre,k)and r² were calculated. Finally, an unmodified random set of synergies (W_Rnd,k) was used to predict the new set of postures, and the resultant neural input matrix (H_Rnd,k) and r² were calculated. Synergy analysis was performed for k = 33 down to k = 1 posture.

This estimation of synergies and the prediction of new EMG patterns were performed for generative sets of size k 33 … 1 posture(s). Given k postures, there were $\left(\begin{array}{c}\hfill 33\hfill \\ \hfill k\hfill \end{array}\right)$ different generative sets to choose from, and ${\sum }_{k=1}^{33}\left(\begin{array}{c}\hfill 33\hfill \\ \hfill k\hfill \end{array}\right)\approx 8.59\times {10}^9$ total generative sets. Given the non-trivial computational time necessary to processNMFon both the generative and predicted EMG sets, it was unfeasible to run all sets. Hence out of all possible combinations of generative sets for a given k postures, 20 were randomly selected as representative sets. Of these 20, the set which explained the most variance of the corresponding 33-k predicted postures was chosen as the optimal set for a given size k. Reported for each optimal set of size k are the number of synergies n necessary to define the predictive synergy framework, the variance explained of the generative and predicted EMG posture sets by this framework and the variance explained of the predicted EMG posture sets by the set of random synergies. The minimum number of synergies n_min and the minimum number of generative postures k_min necessary to form an adequate predictive framework for all 33 of the ASL postures are also reported. n_min was determined as that corresponding to k_min which could explain greater than 90% of the variance in the predicted EMG posture set.

With experimental data, the correct number of synergies is unknown. Hence, the synergy analysis described was performed with the estimated number of synergies n allowed to range from 1 to 13, resulting in a curve that related the variance explained (VE) of V by V_est to n. The correct number of synergies was defined to be the knee of this curve, which was the point at which estimating additional synergies did not significantly explain more of the data variance (Tresch et al 2006). Specifically, this was determined to be the smallest n such that a linear fit of the VE versus n curve, from n to 13, had a residual mean square error (MSE) less than 5 × 10⁻⁵. This MSE method and the chosen threshold are well in line with what has been used in the accepted literature (Cheung et al 2005). Reported for each subject are the final number of estimated synergies n and the corresponding variance explained by the synergy set.

Given all generative posture sets of size k, 20 of the $\left(\begin{array}{c}\hfill 33\hfill \\ \hfill k\hfill \end{array}\right)$ were chosen for analysis. Hence the choice of postures could influence the structure of the estimated synergies. Furthermore, changing k could potentially alter the structure of the estimated synergies. To assess the effect of using different generative sets on synergy estimation, the estimated synergy sets were aligned using a best-matching algorithm. The degree of matching between any two synergies was quantified using the normalized dot product (NDP), given by

$${\text{NDP}}_{\mathit{AB}}=\frac{\stackrel{\rightharpoonup }{A}•\stackrel{\rightharpoonup }{B}}{\mid \stackrel{\rightharpoonup }{A}\mid \cdot \mid \stackrel{\rightharpoonup }{B}\mid }.$$ (5)

Synergies were linked using a best-match algorithm in which the NDP was calculated for all synergy pairs between two sets of estimates. The pair with the highest NDP was deemed a match, and the process repeated until all synergies were linked that were matched above random chance.

Finally, the robustness of synergies across the subject population was examined. Each subject's predictive synergy framework could be composed of exclusively subject-specific synergies. Alternatively, there could be one synergy framework with a high predictive power for the investigated population. Still, each subject's predictive framework could be composed of both population- and subject-specific synergies. To assess this, the best-match algorithm and NDP values were used to align synergies across the subject population. Reported for all subjects are the population- and subject-specific synergies.

3. Results

3.1. Discrimination and repeatability of EMG patterns

Discriminant function analysis (DFA) revealed that the EMG patterns associated with the 33 mimed ASL letters and numbers were distinct from one another and repeatable across several trials. The population averaged discrimination percentages for the complete and cross-validation data sets were 81.8 ± 3.6% and 64.7 ± 5.3%, respectively. Discrimination matrices (actual postures versus predicted postures) for a representative subject are reported in figure 5, and the discrimination percentages for all subjects are reported in table 1. Discrimination was greater than chance (1/33), and many of the incorrect classifications were between posturally and visually similar letters, such as between the letters `M' and `N', between the number `2' and the letters `U' and `V', and between the number `6' and the letter `W'. These discrimination rates are higher than what has been previously reported for EMG-based discrimination of ASL hand postures (Weiss and Flanders 2004), despite the current study's classification of a larger number of postures.

Table 1.

Discrimination rates for all subjects.

SID	Complete (%)	Cross-validation (%)
1	84.4	61.5
2	87.4	75.3
3	81.8	62.8
4	81.0	66.2
5	76.2	59.7
6	82.7	66.2
7	79.2	61.5

3.2. Predictive power of muscle synergies of hand postures

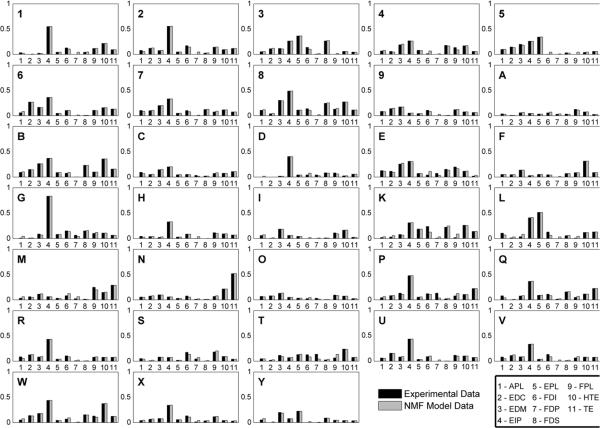
Muscle synergies were extracted from the various ASL posture generative sets and used to predict EMG patterns of the new hand postures. The number of extracted synergies for each generative set was determined empirically based on finding the knee of the respective VE versus n curve. An example is shown in figure 6 for k = 13. For this subject, the set of EMG patterns associated with miming the 13 selected ASL letters could be described by 8 estimated synergies, a reduction from the original 11-dimensional muscle set. This set of eight synergies accounted for on average (mean ± SD) 98.1 ± 0.5% of the variance in the 91 EMG patterns (13 postures × 7 trials) of the generative posture set (i.e. V_Gen,13) and 92.0 ± 5.0% of the variance in the 140 EMG patterns (20 postures ± 7 trials) of the predicted posture set (i.e. V_Pre,13). For comparison, eight random synergies only accounted for 42.7 ± 16.5% of the variance in V_Pre,13, and eight synergies accounted for 71.8 ± 2.9% of the variance in the randomly shuffled data set (V_Art,13). Hence the predictive power of the estimated synergies was significantly greater than that of using randomly constructed synergies (p ≤ 0.001) or random data (p ≤ 0.001), suggesting that the estimated synergies contained significant and relevant information on the structure of EMG coordination patterns of the predicted hand postures. The ability of the estimated synergies to faithfully predict the EMG patterns of both sets of hand postures is illustrated in figure 7. Similar predictive abilities of the estimated synergy sets were observed for all subjects and all posture combinations.

Figure 6.

Synergies were estimated (`●' curve) using a generative ASL posture set of size k = 13. The EMG patterns of 20 new ASL postures were predicted using both the estimated synergies (`◯' curve) and randomly generated synergies (`Δ' curve). The knee was determined based upon the `●' curves, and is highlighted in gray. The fact that the variance curve of the predicted data using the estimated synergies is significantly higher than that using random synergies (`Δ' curve) or reshuffled data (`□'curve), and is comparable to the variance curve of the original postures, suggests that the estimated synergies contained significant and relevant information about the predicted hand postures more so than would be expected by chance.

Figure 7.

Estimates of the EMG patterns (gray bars) based upon the synergies and sources deduced from the muscle synergy model were able to faithfully recreate the experimentally observed EMG patterns of the entire ASL static hand posture set (black bars). Data are shown for the same subject as in figure 6.

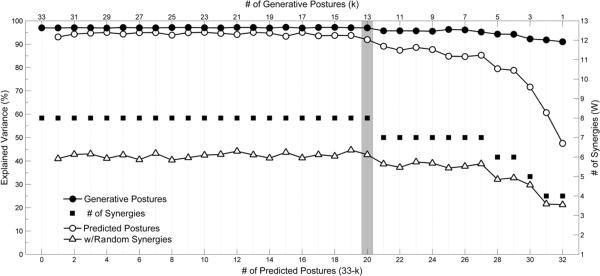
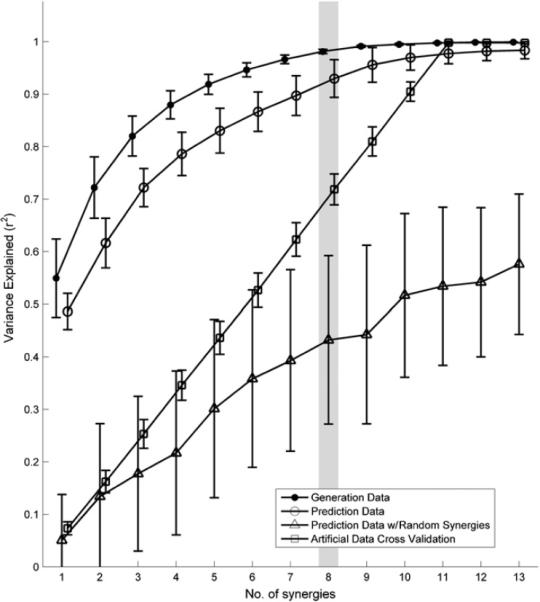
For each subject, the minimum number of postures k_min necessary to define a synergy framework that would generalize to all 33 postures was determined by plotting the variance explained of each generative set V_Gen,k versus the number of postures in the set (i.e. VE versus k). Data for a representative subject are shown in figure 8. The number of estimated synergies n_min necessary to span the EMG space of k_min postures (i.e. the knee of each VE versus k curve) is also shown, as well as the corresponding variance explained by the random set of synergies. The average k_min and n_min for all subjects was 11 postures and 8 synergies, respectively.

Figure 8.

Each line curve represents a separate phase of the predictive NMF analysis performed on one characteristic subject. The line curves illustrate the variance of the EMG data sets of the generative (`●' curve,left y-axis, top x-axis) and predicted (`◯' and `Δ'curves, left y-axis, bottom x-axis) ASL posture sets explained by the estimated synergies, and the corresponding number of estimated synergies (`∎' plot, right y-axis, top x-axis). The plots are aligned such that the n synergies used to estimate k generative postures were the same used to predict 33-k predicted postures. Above a knee, the predictive power of the estimated synergies did not significantly increase. This knee k_min (designated by the column highlighted in gray) was chosen such that the estimated synergies had a predictive power of at least 90%. k_min for this subject was 13 generative postures, corresponding to n_min of 8 synergies. For comparison, the predictive power of n_min = 8 random synergies was approximately 40%.

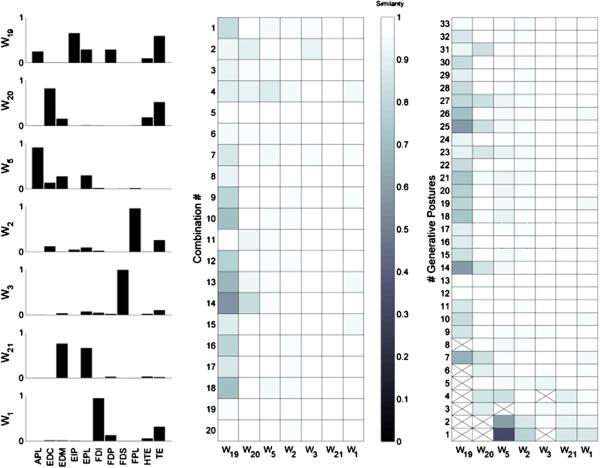
The robustness of the synergies found at the knee (k_min) of the plot shown in figure 8 was examined for each subject both across posture combinations involving the same number of generative postures, and across combinations involving varying numbers of generative postures. Figure 9 shows the robustness of one subject's estimated synergies across the 20 different randomly selected generative posture sets. Robustness was quantified by the normalized dot product (NDP). The figure shows for a single subject that the majority of extracted synergies were consistent despite the many different combinations of postures used to generate them. Similar observations of robustness were made in all other subjects. The average NDP for all estimated synergies across the investigated population was 0.91 ± 0.10, compared to an expected NDP value of 0.14 ± 0.11 for randomly generated synergies. The effect of the number of predictor postures k on the robustness of the estimated synergies was also quantified using the NDP. The synergies estimated at the knees (gray shade) of the plots similar to figure 8 were compared to the synergies estimated at all other points k. Figure 9 (right column) shows for one subject the robustness of the estimated synergies, relative to increasing the number of postures used to define the predictive framework. Again, the estimated synergies proved highly robust to increasing the number of postures used to generate the synergies of the predictive framework. Adding additional postures did not change the structure of existing synergies. Rather the same synergy structures were maintained, or new synergies were added to the framework. All subjects showed similarly high levels of synergy robustness.

Figure 9.

The estimated synergies for one subject (bar plots, left column), and their robustness (similarity matrices, middle and right column). Synergies are numbered to match those in figure 10. Robustness (i.e. similarity) was assessed across the 20 different randomly selected combinations of generative postures (middle column), and quantified using the normalized dot product (NDP), which ranged from 0 (no similarity black) to 1 (perfect similarity, white). All robustness values were significantly greater than expected by random chance (0.14 ± 0.11). Synergy robustness was also assessed relative to changing the number of generative postures k (right column). Increasing k did not largely alter the structure of the existing synergies. A cross means that the synergy did not match another synergy in that compared set above random chance.

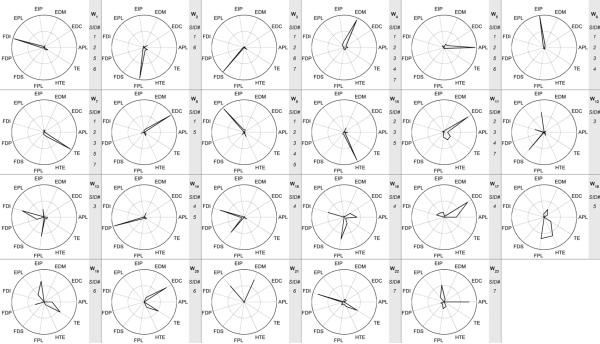
Finally, the similarity of the synergy structures across the subject population was examined. The estimated synergies for each subject were aligned using the described best-match algorithm, based upon the NDP, to determine if subjects exhibited the same predictive synergy framework, if each subject had a separate synergy framework or some combination thereof. The threshold for similarity was two standard deviations above the similarity of randomly exponentially distributed synergies. The aligned synergies are shown in figure 10. Many synergies (W₁, W₃, W₄, W₅, W₆, W₇, W₉ and W₁₁) were general enough to exist across the majority of the subject population, while others only showed up in individual subjects. Examining the structure of these synergies shows that the general population synergies were sparser than the subject-specific synergies, and were usually dominated by one muscle, with some subject-dependent minor residual activity from peripheral muscles. Synergy W₁ primarily governed the activity of FDI, synergy W₃ primarily governed the activity of FDS, synergy W₄ primarily governed the activity of EDM and to a lesser extent EIP, synergy W₅ primarily governed the activity of APL, synergy W₆ primarily governed the activity of EIP, synergy W₇ primarily governed the activity of the intrinsic TE group and to a lesser extent the intrinsic HTE group, synergy W₉ primarily governed the activity of EPL and synergy W₁₁ primarily governed the activity of EDC balanced with the activities of TE and HTE intrinsic groups. While these population-wide synergies were not exhibited by all subjects, some of the observed subject-specific synergies were slight variants of these population synergies. The structures of the population-wide synergies are summarized in table 2. It should be noted that several individuals did exhibit subject-specific synergies that represented balanced activation of two or more muscles, such as W₁₂ and W₁₃ of SID₃.

Figure 10.

The estimated synergies (using the mean square error method) defining the predictive framework for all subjects are represented as radial plots in each of the 23 boxes, where each muscle's representation to the synergy is given by the distance from the center. The synergies were aligned to determine which synergies were shared across the population versus which were subject specific. The gray box to the right of each plot shows the synergy number and the SIDs of which subjects shared that synergy. Many synergies, such as W₁, W₃, W₄, W₅, W₆, W₇, W₉ and W₁₁ were exhibited across the predictive frameworks of several subjects, while others such as W₁₅–W₂₃ were subject specific.

Table 2.

Composition of synergies general to the investigated population.

Synergy	Subjects	Primary muscle components
W 1	4	FDI
W 3	4	FDS
W 4	5	EDM (and EIP to a lesser extent)
W 5	4	APL
W 6	4	EIP
W 7	5	TE (and HTE to a lesser extent)
W 9	5	EPL
W 11	4	EDC (and TE and HTE to a lesser extent)

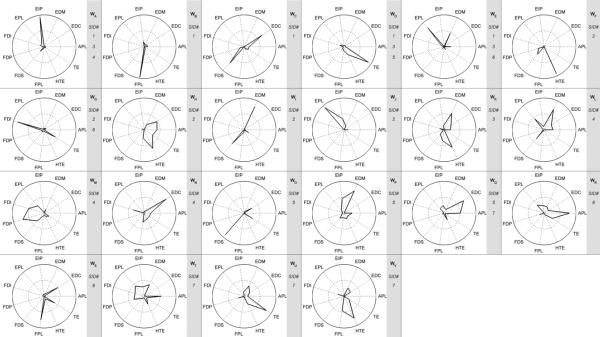
From figure 10, it appears that many of the estimated synergies that were common to multiple subjects were dominated by a single muscle. This is likely due to a high mean square error threshold value of the linear fit of the VE versus n curves. By lowering this threshold, the number of estimated synergies is reduced, and the synergies are less sparse. Shown in figure 11 are the estimated synergy sets for all subjects if a hard threshold of 85% had been used on the VE versus n curves, rather than the MSE method. The average number of synergies estimated per subject using the hard threshold of 85% is 4.3 ± 0.5. Overall the estimated synergies are less sparse than those shown in figure 10, but there are also fewer synergies that are shared among several subjects. The synergies also show a different structure than that estimated by the MSE method. For example, for subject SID₆, synergy W₂₀ (figure 10), which is dominated by contributions from EDC and TE, has been altered to W_S (figure 11), which includes a significant contribution from FPL. This is of note because synergy W₂ (figure 10), which reappears as synergy W_B (figure 11), is no longer shared by subject SID₆. By reducing the number of synergies estimated through the use of a hard threshold of 85%, the activity of FPL that is independent from that of EDC and TE is not captured in subject SID₆. Similarly, in subject SID₄, the distinct coactivation synergy W₁₅ (figure 10)of FDI and FDS is not separated from the activities of other muscles, as shown by synergy W_M (figure 11).

Figure 11.

Estimated synergies for all subjects using a hard threshold of 85% explained variance on the VE versus n curves, rather than the mean square error method (MSE). The synergies have been named W_A–W_V to distinguish from synergies W₁–W₂₃ in figure 10. Estimated synergies are less sparse than those shown in figure 10. However, there are fewer shared synergies among the subject population using the hard threshold of 85% than by using the MSE method.

4. Discussion

This work has investigated the power of a muscle synergy framework in predicting the EMG patterns of new static hand postures. Few studies have examined the concept of muscle synergies as a dimensionality reduction paradigm for the production of a wide variety of hand postures. One investigation in particular showed that a six-dimensional coordinate muscle space could be reduced to a three- to four-dimensional coordinate muscle synergy framework, while describing 80–90% of the variance observed in the EMG data associated with grasping and ASL spelling (Weiss and Flanders 2004). The efficacy of this framework in predicting new hand postures, which speaks to their robustness and generality, is a testable and necessary hypothesis given the accepted definition of muscle synergies (Lee 1984). However, this was not explored in their work. The study in effect established that muscle synergies can form a descriptive framework for a wide variety of known hand postures. The results of the current work described in this paper demonstrate that muscle synergies are robust and generalizable enough to predict the EMG patterns of new hand postures.

4.1. Predictive power of muscle synergies

The nature of muscle synergies, as the concept has been presented in the literature, is that they serve to reduce the dimensionality of muscle coordination. Hence the muscle coordination patterns associated with a wide variety of intentional tasks could be solely composed of these motor primitives. On one extreme, the neuromotor system could use a small set of shared synergies to construct all possible intentional tasks (i.e. voluntary movements). On the other extreme, every possible intentional task could have its own governing set of specific synergies for muscle coordination. Given this second extreme, however, the dimensionality of control would exponentially increase with the addition of new tasks, contradicting one of the main advantages of the synergy concept. Hence, it seems more likely that, should synergies be a viable means of coordination, a small set of synergies would be able to account both for existing and new tasks. Several studies have suggested that voluntarily movements are made of both task-specific and task-independent (shared) synergies that are possibly encoded in the spinal cord, and some of which are independent of sensory inputs (Cheung et al 2005, d'Avella and Bizzi 2005, Saltiel et al 2001). Therefore, predictive power is a necessary property of muscle synergies. It must be noted that the prediction of EMG patterns in the strictest sense is not experimentally achievable since there is presently no way to record the physiological inputs (i.e. the coefficients H) to muscle synergies. However, the ability of synergies estimated from one set of movements to generalize to the EMG patterns of a new set of movements without training suggests that the synergies contain in their structures real physiological information about the nature of the coordination of the movements.

The results of this study show that the 90% predictive power of new static hand tasks could be achieved with an average of as few as 11 static hand postures and 8 muscle synergies. 80% predictive power required on average 7 muscle synergies, reduced from 11 original dimensions. This compares to the Weiss study that required four muscle synergies (reduced from six original dimensions) for 80% descriptive power. Of interest is that for all subjects, the predictive power of the muscle synergy framework reached an asymptote past the critical number of postures. The addition of new postures to the generative set did not increase the overall predictive power of the framework. This, along with the fact that the predictive power with respect to the new hand tasks was comparable to that of the original hand tasks, suggests that each static hand task does not require its own set of synergies. Rather, a limited set can account for these new postures. Furthermore, as shown in figure 8, the number of synergies did not significantly increase past this critical number. Hence, the extracted synergies were not posture specific, but rather contained information pertinent to the construction of the EMG activity of these new hand postures. Had this not been true, the predictive power of the extracted synergies would have been on par with those of random synergies. This observation of task independence is in agreement with that of other researchers, who have shown that task-independent muscle synergies can be elicited from stimulating various sites within the frog spinal cord (Saltiel et al 2001).

4.2. Structure of muscle synergies

The synergies extracted from the mimed hand postures show that, within any given subject, a muscle can belong simultaneously to multiple synergies. This is consistent with the muscle synergy model, and what has been observed in other muscle coordination studies of standing, locomotion and grasping (Ting and Macpherson 2005, Weiss and Flanders 2004, d'Avella et al 2003, Tresch et al 1999). Of interest is that the majority of synergies that were found to be shared amongst the subject population were very sparse in nature. Each of the non-subject-specific synergies (8 out of 23) seemed to primarily control the activity of an individual muscle. It seems thus that these synergies (actually not synergies but individuated muscles) may form a basic low-level paradigm of individuated muscle control that is common to the general population. Higher level paradigms of control involving synergies that coactivate multiple muscles may then be more subject specific, depending on the neuromuscular architecture of each individual. This possible hierarchy of control is in congruence with what has been proposed based upon cortical mapping studies, namely that there may be a level of somatotopic individuated control of the degrees of freedom of the hand superimposed over the distributed activation of neurons that coordinate multiple DOFs (Schieber 1999). What is clear is that both types (individuated control versus synergy-based control) exist and are utilized within an individual subject for predicting the EMG patterns of a wide variety of hand postures. This may explain why other studies have reported what seems to be flexibility in the synergistic activities of two or more muscles (Maier and Hepp-Reymond 1995b, Macpherson 1991). Depending on the task, low-level individuated control may be more pronounced than high-level coordinated synergy control, and vice versa.

It should be noted that the estimated synergies are static in nature and have no temporal component to their structures. Rather, it is the synergy weights that vary in time, giving rise to the observed temporal activation patterns. In other words, the synergies are what the current literature refers to as `synchronous synergies', rather than `time-varying synergies' (Breteler et al 2007, d'Avella and Bizzi 2005, d'Avella et al 2003). The argument of whether synergies are synchronous or time varying is unresolved, and one could possibly even think of synchronous synergies as a subset of time-varying synergies. In the current work, we chose to explore synergies as explicitly synchronous structures because the inherent dilemma in a time-varying synergy structure paradigm is that the problem of neural control is arguably not simplified over simply controlling the temporal activations of individual muscles. Also, many investigations have shown that a synchronous synergy structure is sufficient for estimating muscle reflex patterns and voluntary movements (Cheung et al 2005, Ting and Macpherson 2005, Torres-Oviedo et al 2006, d'Avella and Bizzi 2005). Though other studies have suggested that there is an increase in the descriptive explained variance by using time-varying synergy structures over synchronous structures (Breteler et al 2007, d'Avella and Bizzi 2005), it is unclear whether the gain in explained variance outweighs the increase in computational complexity. It would be informative in future work to explore if time-varying synergies also form a sufficient and robust predictive framework for voluntary movement.

4.3. Robustness of muscle synergies

By using varying combinations of the possible $\left(\begin{array}{c}\hfill 33\hfill \\ \hfill k\hfill \end{array}\right)$ sets of k predictor postures to estimate the predictive synergy framework, the different synergy sets could have been estimated. The majority of estimated synergies were remarkably stable despite different postures being included in the predictor set. This suggests that the estimated synergies were not highly dependent on which postures are used to estimate them, giving more credence to their task independence. There were two subjects, however, who each seemed to exhibit a single unstable synergy, in that the appearances of the synergies were dependent on which postures were included in the predictor set. This suggests that there are some synergies that were posture dependent, whereas the majority of synergies were shared by a large number of the hand postures. The estimated synergies also showed robustness to the addition of postures to the predictor set. Adding new postures to the predictor set could have maintained the current synergy framework, augmented the current synergy framework by simply adding new synergies (increasing the dimensionality) or entirely altered the structure of some of the synergies in the current framework. The fact that the synergy framework of subjects was not significantly altered in structure with the addition of new postures further suggests that they are task independent, and not highly labile in the presence of new task demands.

4.4. What is the `correct' number of synergies?

One unresolved issue in dimensionality reduction problems is determining the appropriate number of underlying uncorrelated dimensions. A wide variety of methods have been employed in the literature, including that used in this investigation (mean square error of a linear fit), and thresholding at an arbitrarily decided value. The methodology of deciding the `correct' number of synergies has the potential of affecting the structures of the estimated synergies and hence the results of these investigations. Take for example the subject whose explained variance curve is shown in figure 6. Using the linear fit method as described in this paper, eight synergies were found to define the reduced dimensional space. However, using thresholds of 90% and 80%, as has been reported in other investigations, the dimensionality of the synergy space becomes 5D and 3D, respectively. Reducing the dimension of the space likely alters the structures of the estimated synergies. While some retain their structure, other synergies disappear or become less sparse with a decrease in the cutoff threshold. Thus, by decreasing the threshold, the synergy sets resemble groups of muscle activation more than individuated muscle control. As shown in figure 11, these synergies are thus specific to each subject and do not generalize well across the multiple subjects. There is no real justification for choosing an arbitrary cutoff of 80% or even 90%. It seems that the linear fit approach is a more systematic method of deciding the number of synergies because it determines the point at which more synergies do not significantly add to the explained variance. Thus, even though the synergies estimated using this method are more sparse and resemble control of individuated muscles, this is arguably a better representation of the control scheme implemented by the motor system.

4.5. Muscle synergies as a possible paradigm of control

Given a small and robust set of muscle synergies, how might they be used within a control paradigm for neural prosthetic devices? One could imagine a scenario in which the time-varying weighting matrix H is used as an input command signal to drive a set of single degree-of-freedom (DOF) kinematic outputs, or multi-DOF postural kinematic synergies or eigenpostures (Mason et al 2001, Santello et al 1998) in a multi-articulated hand prosthesis. It is well known that users do not activate muscles or joints, particularly during hand coordination, in complete isolation of one another due to common motor drive and biomechanical constraints (Winges and Santello 2004, Schieber and Santello 2004, Hager-Ross and Schieber 2000). Thus taking advantage of what are potentially the natural groupings of muscles into synergies may be advantageous for natural control of neural prostheses. To be used in such a control scheme, users would need to volitionally modulate the weights of these synergies. It is unclear whether users can voluntarily modulate these input weights on command, though preliminary work in our laboratory suggests that users can do so in a virtual environment given visual feedback (Ajiboye 2007). Knowledge of muscle synergies may also be advantageous in applications of functional electrical stimulation (FES) for hand control. The Freehand® is an implantable FES system for restoring hand grasping and release to individuals who have sustained cervical spinal cord injuries resulting in quadriplegia (Kilgore et al 1989). By stimulating synergistic groups of muscles (Kilgore and Peckham 1993), lateral and palmar grasping hand function is produced. Knowledge of the underlying groupings of muscles into synergies may aid in expanding the repertoire of postures the hand could achieve.

5. Conclusion

Muscle synergies have been proposed as a means of control of the motor system to coordinate the many neuromuscular degrees of freedom. While many studies have shown that muscle synergies can form a descriptive framework for a large number of tasks, this study has shown that, using a small number of hand postures, synergies can form a predictive framework for a wide variety of hand postures. Furthermore, the synergy structures are robust to the addition of new hand postures. The sparseness of some of the synergies common to the subject population suggests that the neuromotor system may use a dualistic approach for control, rather than exclusively synergies or individual muscles, depending on the task requirements.

Muscle synergies as a basis of control have potential for use in many myoelectric applications, such as EMG pattern recognition for prosthetics, functional electrical stimulation for movement restoration and other EMG-based technologies because these simple building blocks of muscle coordination could be used to produce more complex muscle coordination patterns and hence more complex movements. This investigation has shown that the EMG patterns of new complex hand postures can be accurately produced from a small finite set of static robust muscle synergies. Future work stemming from this investigation includes demonstrating that individuals can accurately control these synergies in a virtual task with visual feedback, and finally in a real-time EMG-based technology.