Abstract
Background
The transmission of infectious disease amongst the human population is a complex process which requires advanced, often individual-based, models to capture the space-time details observed in reality.
Methods
An Individual Space-Time Activity-based Model (ISTAM) was applied to simulate the effectiveness of non-pharmaceutical control measures including: (1) refraining from social activities, (2) school closure and (3) household quarantine, for a hypothetical influenza outbreak in an urban area.
Results
Amongst the set of control measures tested, refraining from social activities with various compliance levels was relatively ineffective. Household quarantine was very effective, especially for the peak number of cases and total number of cases, with large differences between compliance levels. Household quarantine resulted in a decrease in the peak number of cases from more than 300 to around 158 for a 100% compliance level, a decrease of about 48.7%. The delay in the outbreak peak was about 3 to 17 days. The total number of cases decreased to a range of 3635-5403, that is, 63.7%-94.7% of the baseline value.
When coupling control measures, household quarantine together with school closure was the most effective strategy. The resulting space-time distribution of infection in different classes of activity bundles (AB) suggests that the epidemic outbreak is strengthened amongst children and then spread to adults. By sensitivity analysis, this study demonstrated that earlier implementation of control measures leads to greater efficacy. Also, for infectious diseases with larger basic reproduction number, the effectiveness of non-pharmaceutical measures was shown to be limited.
Conclusions
Simulated results showed that household quarantine was the most effective control measure, while school closure and household quarantine implemented together achieved the greatest benefit. Agent-based models should be applied in the future to evaluate the efficacy of control measures for a range of disease outbreaks in a range of settings given sufficient information about the given case and knowledge about the transmission processes at a fine scale.
Background
Since the beginning of the new millennium, epidemics of severe acute respiratory syndrome (SARS), avian influenza (bird flu) and H1N1 influenza (swine flu) have emerged repeatedly amongst the human population raising public concerns, particularly over future risk of disease, and underlying the need for increased understanding of transmission processes and the efficacy of alternative methods of control [1-9]. The transmission of an infectious disease amongst the human population is a complex process involving the time lines of infectious diseases, infection probability, contacts between individuals, demographic dynamics that determine the contact pattern and the occasional imported infection. At both the micro (for a single infection) and macro levels (the infection network) there exist a plethora of factors, objects and processes that combine to create complex scenarios, and this complexity varies from setting to setting.
Although several studies [10-12] have investigated the infection process directly by infecting healthy volunteers with the influenza virus in an experimental setting, for ethical reasons and because of the complexity involved, scientific experiments generally do not provide a feasible solution for the study of infectious disease transmission and the testing of control measures in a real world setting. This is especially true across whole communities or cities. It is, therefore, difficult to gain enough insight into the interplay of the various factors to predict the development of epidemics and formulate appropriate mitigation strategies. In these circumstances, modelling and simulation are potentially the most powerful tools available to increase understanding of infectious disease transmission processes and disease outbreaks. Importantly, modelling and simulation provide an important foundation for testing possible control measures [13].
It is difficult to build a satisfactory model of the transmission of infectious diseases due to deficiencies in both theory and data [14]. On the one hand, human knowledge of the infectious disease transmission process is limited at both the micro and macro levels. At the micro level, the exact process of a single infection for most types of infectious disease is unclear, even today [15]. At the macro level, disease diffusion amongst the human population is a complex process, as many factors, both social and physical, can contribute with different magnitudes to disease outcomes. On the other hand, it is difficult to obtain all the data required for model building, validation and simulation, especially for bottom-up approaches that require knowledge at the micro level.
In this paper, we argue that agent-based models (ABM) provide a powerful means to increase our understanding of infectious disease transmission. ABMs are computational models for simulating the actions and interactions of autonomous individuals within a heterogeneous population. ABMs are bottom-up models. That is, the macro-level behaviour of the whole system is generated by the simulation of the behaviour of agents at the micro-level. ABMs, formulated in different disciplines such as computer science [16], geography [17-20], epidemiology [21-25], and other interdisciplinary fields [26-28], can be applied to simulate the outbreak of infectious diseases and bio-terror attacks, and to explore the efficacy of control measures. The most important advantages of ABMs are that they can consider the heterogeneity of both individuals and environment, and also the stochastic essence of infectious disease transmission. ABMs can express explicitly the differences between individuals in terms of the attributes that influence the process of disease transmission such as physical, social, economic and environmental characteristics. For example, age, gender, occupation and lifestyle variables all contribute to the subsequent disease experience of an individual and the probability of infecting other individuals [29]. The interaction between individuals, which is one of the key components determining infectious disease transmission, can be expressed explicitly in the model. Using ABMs, the heterogeneity of the time lines of infectious diseases, infection probability, demographic dynamics that determine the contact pattern, and the occasional imported infection, can all be considered.
Influenza, an illness caused by ribonucleic acid (RNA) viruses that infect the respiratory tract, is transmitted mainly through the air by coughs or sneezes. Due to the high mutation rate of the virus, protection from any vaccine normally lasts only one year. In February 2007, the Centers for Disease Control and Prevention (CDC) in the United States issued the Community Strategy for Pandemic Influenza Mitigation [30] which is based upon an early, targeted, layered application of multiple partially effective non-pharmaceutical measures. Coupled with specific uses of antiviral influenza medications, these strategies aim to reduce transmission of pandemic influenza and mitigate the disease. Briefly, the main four interventions are: (1) isolation of influenza cases; (2) voluntary home quarantine of members of households with influenza; (3) school closure, which includes the dismissal of students from school (also including colleges, universities and childcare facilities) and school-based activities; (4) social distancing measures to reduce contact in the community and workplace. It also recommended that the intervention duration should be up to 12 weeks.
Amongst the four control interventions, the first two are straightforward and widely accepted by both the public and decision-making agents. The last two are controversial due to the high social and economic costs from closing schools and public places for certain periods, as well as the social and economic impacts of people refraining from their normal activities. Although non-pharmaceutical control measures are believed to be vital in curtailing the spread of disease, the quality of the evidence on which to base non-pharmaceutical pandemic planning decisions is poor [31]. Further, some research conclusions are contradictory. Take school closure as an example: although the importance of school pupils in the transmission of infectious diseases is acknowledged by most research [25,32-37], the effectiveness of school closure is not. As reviewed by the World Health Organization Writing Group [38] and Aledort et al. [31], although the majority of studies suggest the effectiveness of school closure, some previous studies showed that more cases developed after a school holiday, while schools that were kept open had a protective effect.
According to the Community Strategy for Pandemic Influenza Mitigation [30], the three major goals of mitigating a community-wide epidemic are: (1) delay the exponential growth in incident cases; (2) reduce the epidemic peak, and (3) reduce the total number of incident cases.
In this study, three properties of an epidemic outbreak were used to evaluate the effectiveness of a set of control measures. These were: (1) the total number of cases, (2) the number of cases at the peak and (3) the day number when the outbreak peaks.
This paper presents an analysis in which control measures are tested for a hypothetical influenza outbreak in Eemnes, a small city in the Netherlands, generated from the simulation of individuals' movements around the city and consequent interactions using a published ABM: Individual Space-Time Activity-based Model (ISTAM) [39,40]. ISTAM was applied to simulate an influenza outbreak for the same city in an earlier study, and the analysis included the spatial distribution of infection within the city, infection distribution at different types of locations and network analysis. This paper focuses on testing the CDC's suggested control measure strategies. This research provides new information which may be beneficial to the design of a control strategy for epidemic outbreaks, especially for some controversial intervention options such as school closure. Since the novel ABM framework, upon which the paper builds, was published previously by the authors, the basic structure and parameters of the model can be obtained from [32] and only a brief summary is given here. For the sake of brevity and clarity, the focus is on the efficacy of three of the CDC control measures.
The paper is organised as follows. The next section outlines the research methods. Then the simulation results and analysis are presented, followed by a section that discusses the merits and limitations of our approach. The last section draws conclusions regarding the application of ISTAM and remaining research issues.
Methods
ISTAM is a bottom-up ABM in which the transmission network is built on the simulated physical contacts between individuals at a fine space-time scale [39,40]. At this scale, human social behaviour, the environment's physical conditions and the transmission mode of the specific infectious disease are considered. Activity bundle (AB) is a key concept in ISTAM. An AB is a semantic space where contact probability varies as a function of the dynamics of humans inside the bundle. The simulation is at two levels: people's movements between ABs and contact between individuals within ABs.
It is accepted that the possibility of infection for susceptible individuals increases with proximity to infectious individuals [41-43]. In addition, there exist social rules for how close humans can approach each other. Hall [44] identified four distances: intimate distance, personal distance, social distance and public distance. The values of the above distances vary between populations from different cultures, ages, genders etc. This knowledge provides a basis for within-AB simulation. For example, the model should focus on the changing distances between individuals and, specifically, when the distances are small enough for infection. The contacts between individuals are driven by social purposes or constrained by physical conditions or both, while infection per se is a physical process. Some contacts are indispensable for undertaking some activities. For example, an individual who goes shopping will generally make contact with the salesperson when checking out. Some contacts, although not purposeful, occur due to the restriction of the environment. For example, on a crowded bus, passengers must sit or stand in proximity. The first type of contact is voluntary and is determined by the individuals. The second type of contact is involuntary and is not wholly determined by the individuals.
The spatial distribution pattern of individuals can be observed in most types of AB. One example is provided by a restaurant: people sit in clusters which reflect the existence of different groups. Another example is provided by individuals visiting a library: people may try to find an empty table and sit as far as possible from each other [45]. In some ABs, such as in a lecture room, individuals are assumed to remain static during the simulation time unit. In other ABs, movements must be considered. At fine spatial scales, individuals' movement patterns may be strongly confined by the physical condition of the current AB and the status of other individuals. Three properties of humans' space-time dynamics within ABs that have been observed in reality are considered when modelling individuals within ISTAM: (1) individuals' static spatial distribution patterns, (2) individuals' movement patterns and (3) minimum distances between individuals. For more details about within-AB simulation using ISTAM, see [39].
ISTAM was previously applied to simulate hypothetical influenza outbreaks within the campus of the University of Southampton [40] and the city of Eemnes in the Netherlands [39]. The latter case provided an example of the simulation of the individual-based transmission of infectious disease at the whole city level. For the latter case, the first requirement was to build the population and the spatial structure of the city of Eemnes. The social and spatial structures of the city were built based on surveyed data of individuals' daily activities, synthesized data of households and land use data from previous research [46]. Properties such as family structure, number of cars and income level were assigned to every household and properties such as age and gender, and activity patterns, were assigned to every individual. Among the whole population of 8382 people, 3.2% were 4 years old or younger, 3.5% were between 5 and 9, 6.4% were between 10 and 17, 71.3% were between 17 and 64, and 15.6% were 65 years or older.
During the simulation, individuals' daily activities were generated from a distribution of observed activity patterns and then individuals' movements between ABs and the interaction of individuals within ABs were simulated. During these interactions, infection was possible conditional upon contact between individuals. For the latter case, parameters such as the contact frequency and contact intimacy which determine how often individuals come into contact and the probability for a contact to bring about infection in the model were calibrated by studies which indicated the average number of daily contacts for a person and the basic reproductive number for influenza R0 (the average number of secondary cases caused by each case of an infectious disease), respectively. In ISTAM, the latent period for influenza was assumed to be 1 to 3 days, the incubation period was one day longer than the latent period and the infectious period was 3 to 6 days [47-49]. The proximity and duration required for infection were assumed to be 1.5 m and 10 minutes, respectively.
A baseline simulation of a hypothetical disease outbreak in the city of Eemnes based on ISTAM was presented previously [39]. This paper extends the baseline model by testing three CDC control measures for a hypothetical influenza outbreak in Eemnes using ISTAM. These were:
(1) refrain from social activities (A): the probability of an individual to visit certain places such as social, leisure and sports facilities was decreased to a certain level;
(2) school closure (S): the probability of a pupil to visit school was decreased to 0;
(3) household quarantine (H): a certain proportion of individuals was required to stay at home at all times.
Because in reality, compliance to a control measure may be less than 100%, especially for the cessation of social activities and household quarantine, a series of compliance levels (25%, 50%, 75% and 100%) were tested for both A and H. Two or three control measures can work together denoted by the abbreviations AS, AH, SH and SHA, with a default 50% compliance level for both A and H and 100% compliance level for S. The scenario with no control measures (denoted by N) was also tested for comparison purposes.
An alert value (a threshold number of infection cases) was used to denote how quickly the control measure was implemented. At the beginning of each day, if the number of infection cases is greater than the alert value, the control measure will be implemented. This meant that there was a small delay of less than one whole day duration between exceeding the alert threshold and intervention. All control measures were assigned an alert value of 20 cases except N. Additionally, for control measure SH, a series of alert values (20, 50, 100, 200, 500 and 1000) and a series of rates of transmission (with R0 of 1.24, 1.79, 2.42, and 2.60) were explored. For each of the above scenarios, 300 simulations were run.
Results
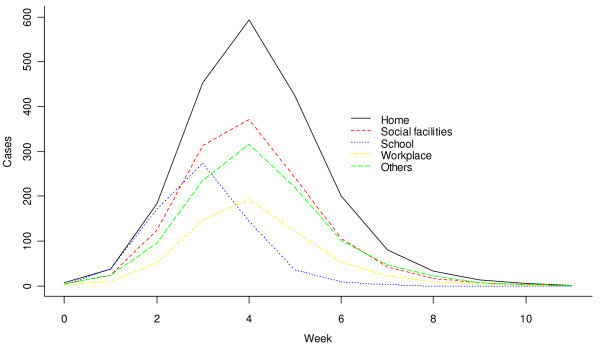
Firstly, baseline simulations (N) were analyzed. Five individuals were selected randomly to be the index cases (the initial patients with influenza) and R0 was calibrated to be 1.79 [48]. Figure 1 shows the number of new cases from different ABs over time (in weeks). The three basic properties can be found in Table 1: on average, it took 31 days for the number of new infection cases to reach the peak, that is, 308 cases per day. The total number of cases during the outbreak was 5703.
Figure 1.
Number of new cases from different ABs plotted against time (aggregated to units of a week) for the scenario N, estimated over 300 simulations.
Table 1.
Total number of cases, peak number of cases and peak day under different control measures
| Scenario ID |
Compliance level |
Probability of outbreak (%) |
Total cases |
Compared with N (%) |
95% CI | Peak cases |
Compared with N (%) |
95% CI | Peak day |
Compared with N (%) |
95% CI |
|---|---|---|---|---|---|---|---|---|---|---|---|
| N | > 99 | 5703 | 5539-5872 | 308 | 274-345 | 31 | 22-44 | ||||
| 25% | 99 | 5709 | 100.1 | 5522-5913 | 309 | 100.3 | 280-354 | 30 | 96.8 | 23-39 | |
| A | 50% | 100 | 5706 | 100.1 | 5537-5879 | 307 | 99.7 | 272-344 | 31 | 100.0 | 23-44 |
| 75% | 100 | 5701 | 100.0 | 5481-5921 | 307 | 99.7 | 264-346 | 31 | 100.0 | 23-44 | |
| 100% | 98% | 5695 | 99.9 | 5533-5890 | 308 | 100.0 | 271-349 | 32 | 103.2 | 23-51 | |
| S | 100% | 100 | 5461 | 95.8 | 5233-5666 | 219 | 71.1 | 187-256 | 39 | 125.8 | 30-51 |
| 25% | 100 | 5403 | 94.7 | 5138-5583 | 277 | 89.9 | 244-307 | 34 | 109.7 | 23-51 | |
| H | 50% | 93 | 4992 | 87.5 | 4758-5215 | 244 | 79.2 | 215-278 | 35 | 112.9 | 23-51 |
| 75% | 94 | 4428 | 77.6 | 4199-4704 | 204 | 66.2 | 178-243 | 41 | 132.3 | 23-65 | |
| 100% | 68 | 3635 | 63.7 | 3376-3843 | 158 | 51.3 | 131-192 | 46 | 148.4 | 29-84 | |
| AS | 50%, 100% | > 99 | 5449 | 95.5 | 5240-5648 | 222 | 72.1 | 192-253 | 39 | 125.8 | 30-51 |
| AH | 50%, 50% | 97 | 5000 | 87.7 | 4754-5244 | 243 | 78.9 | 209-276 | 35 | 112.9 | 23-51 |
| HS | 50%, 100% | 97 | 4494 | 78.8 | 4219-4781 | 134 | 43.5 | 107-160 | 48 | 154.8 | 36-71 |
| AHS | 50%, 50%, 100% | 97 | 4453 | 78.1 | 4008-4753 | 135 | 43.8 | 104-162 | 51 | 164.5 | 36-79 |
Alert value is 20 for all scenarios except N.
Table 2 shows the distribution of infection across different classes of AB. The four main infection sources were household (36%), social place (22.2%), workplace (10.9%) and school (11.9%). The peak day (i.e., day of the outbreak peak) of new infections was the fourth week for most types of AB (Figure 1), although, notably, was the third week for schools. Most infections at schools occurred from pupil to pupil. This implied that the epidemic outbreak was strengthened amongst children and then spread to adults. The control measure specific to schools may, therefore, be important, especially during the early stages of an outbreak.
Table 2.
The proportion of infections between different types of AB using different control measures
| N | 95% CI | % | S | 95% CI | % | H | 95% CI | % | HS | 95% CI | % | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Home | 2049 | 1931-2137 | 36.0 | 2284 | 2197-2367 | 42.1 | 2129 | 2012-2246 | 42.7 | 2197 | 2043-2347 | 49.3 |
| Work | 618 | 570-660 | 10.9 | 630 | 580-678 | 11.6 | 478 | 430-524 | 9.6 | 469 | 422-529 | 10.5 |
| Shops, post offices and banks | 429 | 387-472 | 7.5 | 454 | 413-487 | 8.4 | 312 | 268-347 | 6.3 | 315 | 269-362 | 7.1 |
| Healthcare facilities | 493 | 458-538 | 8.7 | 536 | 481-580 | 9.9 | 359 | 325-404 | 7.2 | 385 | 345-432 | 8.6 |
| Sports and cultural facilities | 171 | 141-206 | 3.0 | 194 | 157-232 | 3.6 | 130 | 106-157 | 2.6 | 154 | 113-194 | 3.4 |
| Social facilities | 1253 | 1181-1339 | 22.0 | 1312 | 1224-1416 | 24.2 | 936 | 855-1016 | 18.8 | 926 | 856-1002 | 20.8 |
| School | 677 | 653-706 | 11.9 | 20 | 9-43 | 0.4 | 637 | 606-663 | 12.8 | 16 | 7-34 | 0.3 |
Alert value is 20 for all scenarios except N; compliance level is 50% for H.
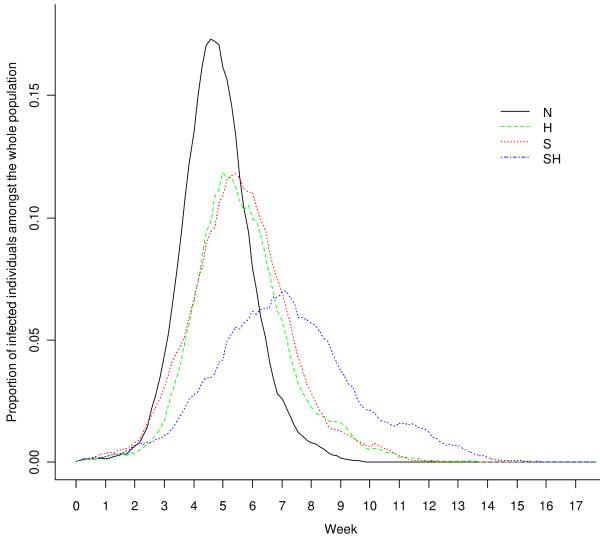
For different control measures, the three properties of the outbreak under each scenario are given in Table 1. The proportion of infected individuals was plotted against time in Figure 2 for scenarios N, S, H and SH (for each scenario, the result of a "typical" simulation run is shown in which the three properties of the outbreak were similar to the average values for the 300 simulation runs). The implications from Table 1 and Figure 2 are:
Figure 2.
Proportion of infected individuals amongst the whole population plotted against time (aggregated to units of a day) for the scenarios N, S, H and SH, estimated by a selected typical simulation.
(1) Amongst each single control measure, A was relatively ineffective. The values of all three properties for A were similar to those under the baseline scenario N, with almost no variation with compliance level.
(2) H was a very effective control measure, especially in limiting the peak number of cases and total number of cases, with large differences between compliance levels. The decrease in the peak number of cases for H was from more than 300 to around 158 for a 100% compliance level, a decrease of about 48.7%. The delay in the peak day was about 3 to 17 days. Moreover, the total number of cases decreased to a range of 3635 - 5403, that is, 63.7% - 94.7% of the baseline value.
(3) The effectiveness of S was less than that of H: the peak number of cases decreased to about 71.1% and the peak day was delayed by about 8 days. The effectiveness of S in reducing the total number of cases was small, a reduction of about 4.2%.
(4) For multiple control measures, since A had almost no effect, it is not surprising to see that AH was similar to H, AS was similar to S and AHS was similar to HS. HS (and AHS) were the most effective control strategies: the peak number of cases decreased by 56% to 57%, the total number of cases decreased by 21% to 22% and the peak day was delayed by 17 to 20 days.
Table 2 lists the distribution of infections between different types of AB amongst S, H and HS (A is excluded due to its ineffectiveness). Compared with N, S reduced the infection in schools to a very low level, but infection within other ABs also increased in absolute number, compensating for the gain. Compared with N, H reduced the total infection, and the effectiveness varied amongst different types of AB. Thus, the transmission environments (ABs) most resistant to control were home and school, with decreases of 33% and 41%, respectively, while for all other ABs the total number of cases decreased by 63 - 69%. HS was the most effective control measure for all types of AB, with the lowest infection rates for any AB type.
Table 3 shows the three properties of the outbreak controlled by HS (with a 50% compliance level for household quarantine), with alert values increasing from 20 to 1000. Clearly, the higher the alert value, the larger the total number of cases and peak number of cases, and the earlier the peak day. With a lower alert value, that is, intervening earlier, control measures were more effective.
Table 3.
Total number of cases, peak number of cases and peak day under HS control with various alert values
| Alert value (infection cases) |
Probability of outbreak (%) |
Total cases |
Compared with 20 (%) |
95% CI | Peak cases |
Compared with 20 (%) |
95% CI | Peak day | Compared with 20 (%) |
95% CI |
|---|---|---|---|---|---|---|---|---|---|---|
| 20 | 97 | 4494 | 4219-4781 | 134 | 107-160 | 48 | 36-71 | |||
| 50 | 98 | 4503 | 100.2 | 4209-4832 | 142 | 106.0 | 119-174 | 38 | 79.2 | 23-51 |
| 100 | 98 | 4520 | 100.6 | 4152-4869 | 152 | 113.4 | 110-191 | 37 | 77.1 | 24-51 |
| 200 | 99 | 4586 | 102.0 | 4239-4839 | 173 | 129.1 | 139-208 | 31 | 64.6 | 23-44 |
| 500 | 97 | 4743 | 105.5 | 4454-5083 | 210 | 156.7 | 168-261 | 29 | 60.4 | 20-37 |
| 1000 | 97 | 4954 | 110.2 | 4752-5163 | 272 | 203.0 | 237-316 | 29 | 60.4 | 22-43 |
Compliance level is 50% for H, 100% for S.
Table 4 shows the three properties of the outbreak controlled by HS (with a 50% compliance level for household quarantine) for four values of R0 (1.24, 1.79, 2.42, and 2.60). By comparing the set of outcomes under control measure HS with the corresponding N scenario (for the same R0) (Table 4), it can be seen that the control measure HS was more effective for smaller R0 values. Because the smaller the R0, the lower the probability of an outbreak, the greater the relative decrease in total number of cases and peak number of cases, and the greater the relative delay in the peak day.
Table 4.
Total number of cases, peak number of cases and peak day with or without HS control for four values of R0
|
R0 value |
With HS? |
Probability of outbreak (%) |
Total cases |
Compared with N (%) |
95% CI | Peak cases |
Compared with N (%) |
95% CI | Peak day |
Compared with N (%) |
95% CI |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.236 | No | 80 | 3958 | 3575-4298 | 149 | 122-174 | 40 | 23-67 | |||
| Yes | 41 | 2449 | 61.9% | 895-2989 | 44 | 29.5% | 17-51 | 94 | 235.0% | 48-197 | |
| 1.79 | No | > 99 | 5703 | 5539-5872 | 308 | 274-345 | 31 | 22-44 | |||
| Yes | 97 | 4494 | 78.8% | 4219-4781 | 134 | 43.5% | 107-160 | 48 | 154.8% | 36-71 | |
| 2.419 | No | 100 | 6955 | 6860-7066 | 503 | 460-561 | 25 | 22-30 | |||
| Yes | 100 | 6299 | 90.6% | 6142-6434 | 335 | 66.6% | 293-380 | 34 | 128.0% | 29-43 | |
| 2.596 | No | 100 | 7522 | 7435-7585 | 658 | 607-720 | 22 | 19-26 | |||
| Yes | 99 | 7154 | 95.1% | 7063-7259 | 495 | 75.2% | 461-539 | 28 | 127.3% | 23-32 | |
Discussion
From the ISTAM model, school closure resulted in about a 4.2% reduction in the total number of cases and a 28.9% reduction in the peak number of cases. These reductions were rather low compared with some empirical studies [36,37] which suggest approximately a 15% reduction in the total number of cases and a 40% reduction in the peak number of cases. As Table 2 shows, with school closure, infection in schools was reduced to a very low level, but infection within other ABs increased in absolute number. The explanation is that school closure alone can move pupils' daily activities from school to home, and infection risk at home and other ABs may actually increase. This is consistent with other studies [31,32,50-53]. Milne et al. [51] argued in a comparison study that differences in effectiveness can arise from differences in assumptions about the timing and duration of school closure. It would be interesting to implement such finer level differences within the ISTAM model in future. Another explanation is that the current model does not consider the age dependence of susceptibility and infectiousness. For example, children may be more susceptible and infectious than adults [54,55]. This should be explored in the future.
This research highlighted the importance of combining control measures. As shown in Table 1, school closure alone was not particularly effective, but when combined with home quarantine, it reduced the total number of cases more than the sum of these two control measures alone. It should be noted that although the three control measures are applicable to different levels of aggregation (refraining from social activity is applicable to individuals, household quarantine is applicable to all members within households and school closure is applicable to all students), they are not independent of each other. For example, individuals under household quarantine automatically refrain from social activities, and students under household quarantine do not go to school. The overlap between control measures may explain the enhancing effect of combining measures. The combination of non-pharmaceutical measures with pharmaceutical measures needs to be investigated in the future, particularly as for infectious diseases with large R0, the effectiveness of non-pharmaceutical measures was shown to be limited.
ISTAM is a novel model for simulating the transmission of infectious disease. The two-level structure (separating between-AB and within-AB activities) makes ISTAM flexible such that it can be applied to novel circumstances. The concept of AB plays a key role: both the building of individual activity patterns and simulation within ABs depends on how well the ABs are defined and classified. The merits of simulation by ISTAM are: (1) ISTAM is straightforward and provides a process-based representation of the real world, (2) using ISTAM, it is easy to account for important factors, neglect less important factors and include random factors in the model and (3) ISTAM facilitates the modelling of human actions (both active and reactive) and the interaction between humans at fine scales. ISTAM, if fed with activity pattern data, can simulate effectively individuals' movements at between-AB and within-AB levels. Providing data sources are sufficient, the model can be extended readily to larger study areas although the effort involved in data collection and model implementation is likely to be substantial and time-consuming.
Despite the above advantages of ISTAM, the utility of the results presented here in terms of control measures depends on the ability of the ISTAM model to represent real-world processes such as human behaviour and movement patterns, both between and within ABs (generally buildings), the spatial structure of the set of ABs themselves, particularly at within-AB level, transmission probability as a function of the space-time separation between individuals, and the natural history of the targeted disease such as the time lines describing the evolution of infection and disease within the host (e.g., latent, infectious, incubation and symptomatic periods). For example, it is assumed that one requirement for transmission is a susceptible person within a certain distance of an infectious person. In fact, for most airborne infectious diseases, airborne disease agents may stay suspended in the air or survive on some surfaces such as door handles for an extended period of time. This suggests co-location may not be a strict requirement for infection. Applying an extended definition of effective contact will be a challenge for future research. Another problem arises due to limited validation. It was not possible to validate the model directly due to the lack of historical data on the impact of non-pharmaceutical control measures on disease outbreaks in Eemnes. Nevertheless, several strategies were implemented to validate the model indirectly [39], with satisfactory results.
The emergent space-time pattern of disease in a given region depends on the parameters of both the disease transmission model and the spatial and social network structures in place in the environment in which transmission takes place. In particular, it is expected that changes in the parameters of the (simulation) model will lead to observable changes in the space-time pattern of disease. Simulation models provide an important means for evaluating the sensitivity of emergent patterns and their space-time character to changes in model parameters. Thus, while the results of ABMs such as ISTAM depend on model parameterization, sensitivity analysis can be used to investigate the range of parameter values that leads to similar evidence for decision-making, providing reassurance to decision-makers.
If the association between elements of environmental and social structures and disease outcomes can be quantified then it should be possible to map the vulnerability of entire settlements to specific diseases. It is well-known that the behaviour characteristics of individuals can be modified to reduce the likelihood of disease transmission. However, the effects of spatial structural elements such as boarding school versus day school education for children and settlement structure (e.g., out-of-town supermarkets versus local shops) are less well studied. Again, such knowledge would be useful in terms of planning containment strategies and such knowledge can only be provided by simulation models such as ISTAM.
Conclusions
ISTAM was used to quantify the efficacy of three of the social control measures recommended by the CDC. Such quantification, while carrying uncertainty due to model structure and parameterization, is not possible by other means such as in vivo, real life, epidemiological or biological experiments. Sensitivity analysis was used to explore the outcome of the simulation for a range of parameter values (compliance level, alert value, R0). For the simulated influenza outbreak in the city of Eemnes, the Netherlands, household quarantine was the most effective control measure in terms of the three indices including total number of cases, peak number of cases and peak day used to assess efficacy. Refraining from social activities was the least effective control measure. School closure alone was of limited efficacy, unless combined with other control measures such as household quarantine. When school closure was used singly, a proportion of infections were displaced to other settings. This conclusion has important implications and is consistent with other research [31,32,52,53].
ABMs should be applied in future to evaluate the efficacy of control measures for a range of disease outbreaks in a range of settings, conditional upon the availability of sufficient information about the scenario (e.g., demographics, the built environment and humans' daily activities) and knowledge about the transmission processes at a fine scale (specifically, the relationship between transmission and the space-time dynamics of individuals).
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
All three authors contributed to the study design. YY implemented the model, analysed the results and drafted the paper. PMA took a key part in paper writing. DE provided the data sources and contributed to data preparation. All authors critically reviewed and revised versions of the manuscript.
Pre-publication history
The pre-publication history for this paper can be accessed here:
Contributor Information
Yong Yang, Email: yongyang@umich.edu.
Peter M Atkinson, Email: pma@soton.ac.uk.
Dick Ettema, Email: ettema@geo.uu.nl.
Acknowledgements
The authors are grateful to the Worldwide Universities Network (WUN) for funding a research visit of YY to the University of Utrecht during which the ISTAM model was fitted to the city of Eemnes.
References
- Bauch CT, Lloyd-Smith JO, Coffee MP, Galvani AP. Dynamically Modeling SARS and Other Newly Emerging Respiratory Illnesses. Epidemiology. 2005;16:791–801. doi: 10.1097/01.ede.0000181633.80269.4c. [DOI] [PubMed] [Google Scholar]
- Ginsberg J, Mohebbi MH, Patel RS, Brammer L, Smolinski MS, Brilliant L. Detecting influenza epidemics using search engine query data. Nature. 2009;457(7232):1012–1014. doi: 10.1038/nature07634. [DOI] [PubMed] [Google Scholar]
- Cohen J, Enserink M. As Swine Flu Circles Globe, Scientists Grapple With Basic Questions. Science. 2009;324(5927):572–573. doi: 10.1126/science.324_572. [DOI] [PubMed] [Google Scholar]
- Fraser C, Donnelly CA, Cauchemez S, Hanage WP, van Kerkhove MD, Hollingsworth TD, Griffin J, Baggaley RF, Jenkins HE, Lyons EJ, Jombart T, Hinsley WR, Grassly NC, Balloux F, Ghani AC, Ferguson NM, Rambaut A, Pybus OG, Lopez-Gatell H, Alpuche-Aranda CM, Chapela IB, Zavala EP, Guevara DME, Checchi F, Garcia E, Hugonnet S, Roth C. The WHO Rapid Pandemic Assessment Collaboration. Pandemic Potential of a Strain of Influenza A (H1N1): Early Findings. Science. 2009;324(5934):1557–1561. doi: 10.1126/science.1176062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Medlock J, Galvani AP. Optimizing Influenza Vaccine Distribution. Science. 2009;325(5948):1705–1708. doi: 10.1126/science.1175570. [DOI] [PubMed] [Google Scholar]
- van Rijswoud E. Flu: weighing up conflicting expert information. Nature. 2009;460(7255):571. doi: 10.1038/460571b. [DOI] [PubMed] [Google Scholar]
- Yang Y, Sugimoto JD, Halloran ME, Basta NE, Chao DL, Matrajt L, Potter G, Kenah E, Longini IM Jr. The Transmissibility and Control of Pandemic Influenza A (H1N1) Virus. Science. 2009;326(5953):729–733. doi: 10.1126/science.1177373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riley S, Fraser C, Donnelly CA, Ghani AC, Abu-Raddad LJ, Hedley AJ, Leung GM, Ho L-M, Lam T-H, Thach TQ, Chau P, Chan K-P, Lo S-V, Leung P-Y, Tsang T, Ho W, Lee K-H, Lau EMC, Ferguson NM, Anderson RM. Transmission Dynamics of the Etiological Agent of SARS in Hong Kong: Impact of Public Health Interventions. Science. 2003;300(20):1961–1966. doi: 10.1126/science.1086478. [DOI] [PubMed] [Google Scholar]
- Ferguson NM, Fraser C, Donnelly CA, Ghani AC, Anderson RM. Public Health Risk from the Avian H5N1 Influenza Epidemic. Science. 2004;304(5673):968–969. doi: 10.1126/science.1096898. [DOI] [PubMed] [Google Scholar]
- Carrat F, Vergu E, Ferguson NM, Lemaitre M, Cauchemez S, Leach S, Valleron A-J. Time Lines of Infection and Disease in Human Influenza: A Review of Volunteer Challenge Studies. American Journal of Epidemiology. 2008;167(7):775–785. doi: 10.1093/aje/kwm375. [DOI] [PubMed] [Google Scholar]
- Lau LLH, Cowling BJ, Fang VJ, Chan K-H, Lau EHY, Lipsitch M, Cheng CKY, Houck PM, Uyeki TM, Peiris JSM, Leung GM. Viral Shedding and Clinical Illness in Naturally Acquired Influenza Virus Infections. Journal of Infectious Diseases. 2010;201(10):1509–1516. doi: 10.1086/652241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suess T, Buchholz U, Dupke S, Grunow R, Mad Heiden, Heider A, Biere B, Schweiger B, Haas W, Krause G. Shedding and Transmission of Novel Influenza Virus A/H1N1 Infection in Households - Germany, 2009. American Journal of Epidemiology. 2010;171(11):1157–1164. doi: 10.1093/aje/kwq071. [DOI] [PubMed] [Google Scholar]
- Hethcote HW. The Mathematics of Infectious Diseases. Society for Industrial and Applied Mathematics Review. 2000;42:599–653. [Google Scholar]
- Koopman JS. Infection transmission science and models. Journal of infectious disease. 2005;58:S3–S8. [PubMed] [Google Scholar]
- Koopman JS. Modeling Infection Transmission. Annual Review of Public Health. 2004;25:303–326. doi: 10.1146/annurev.publhealth.25.102802.124353. [DOI] [PubMed] [Google Scholar]
- Carley K, Fridsma D, Casman E, Yahja A, Altman N, Chen L, Kaminsky B, Nave D. BioWar: Scalable Agent-based Model of Bioattacks. IEEE Transactions on Systems, Man and Cybernetics. 2004;36:252–265. [Google Scholar]
- Bian L. A conceptual framework for an individual-based spatially explicit epidemiological model. Environment and Planning B: Planning and Design. 2004;31:381–395. doi: 10.1068/b2833. [DOI] [Google Scholar]
- Bian L, Liebner D. In: GIS, Spatial Analysis and Modelling. Maguire D, Batty M, Goodchild M, editor. USA: ESRI Press; 2005. Simulating Spatially Explicit Networks for Dispersion of Infectious Diseases; pp. 245–264. [Google Scholar]
- Dibble C, Feldman PG. The GeoGraph 3D Computational Laboratory: Network and Terrain Landscapes for RePast. Journal of Artificial Societies and Social Simulation. 2004;7(1) [Google Scholar]
- Perez L, Dragicevic S. An agent-based approach for modeling dynamics of contagious disease spread. International Journal of Health Geographics. 2009;8(1):50. doi: 10.1186/1476-072X-8-50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halloran ME, Longini IM, Nizam A, Yang Y. Containing bioterrorist smallpox. Science. 2002;298:1428–1432. doi: 10.1126/science.1074674. [DOI] [PubMed] [Google Scholar]
- Riley S, Ferguson NM. Smallpox transmission and control: Spatial dynamics in Great Britain. Proceedings of the National Academy of Sciences. 2006;103(33):12637–12642. doi: 10.1073/pnas.0510873103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Longini IM, Nizam A, Xu S, Ungchusak K, Hanshaoworakul W, Cummings DAT, Halloran ME. Containing pandemic influenza at the source. Science. 2005;309:1083–1087. doi: 10.1126/science.1115717. [DOI] [PubMed] [Google Scholar]
- Ferguson NM, Cummings DAT, Cauchemez S, Fraser C, Riley S, Meeyai A, Iamsirithaworn S, Burke DS. Strategies for containing an emerging influenza pandemic in Southeast Asia. Nature. 2005;437(8):209–214. doi: 10.1038/nature04017. [DOI] [PubMed] [Google Scholar]
- Ferguson NM, Cummings DAT, Fraser C, Cajka JC, Cooley PC, Burke DS. Strategies for mitigating an influenza pandemic. Nature. 2006;442:448–452. doi: 10.1038/nature04795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Epstein JM, Cummings DAT, Chakravarty S, Singa RM, Burke DS. Toward a Containment Strategy for Smallpox Bioterror: An Individual-Based Computational Approach. Center on Social and Economic Dynamics, Johns Hopkins University; 2002. [Google Scholar]
- Epstein JM. Controlling Pandemic Flu: The Value of International Air Travel Restrictions. PloS ONE. 2007. [DOI] [PMC free article] [PubMed]
- Eubank S, Guclu H, Anil Kumar V, Marathe M, Srinivasan A, Toroczkai Z, Wang N. Modelling disease outbreaks in realistic urban social networks. Nature. 2004;429:180–184. doi: 10.1038/nature02541. [DOI] [PubMed] [Google Scholar]
- Elliott P, Wakefield JC, Best NG, Briggs DJ. In: Spatial epidemiology: methods and applications. Elliott P, Wakefield JC, Best NG, Briggs DJ, editor. Oxford, UK: Oxford University Press; 2000. Spatial Epidemiology: methods and applications. [Google Scholar]
- Interim Pre-Pandemic Planning Guidance: Community Strategy for Pandemic Influenza Mitigation in the United States, Early, Targeted, Layered Use of Nonpharmaceutical Interventions. http://www.pandemicflu.gov/professional/community/community_mitigation.pdf
- Aledort JE, Lurie N, Wasserman J, Bozzette SA. Non-pharmaceutical public health interventions for pandemic influenza: an evaluation of the evidence base. BMC Public Health. 2007;7(208) doi: 10.1186/1471-2458-7-208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hatchett RJ, Mecher CE, Lipsitch M. Public health interventions and epidemic intensity during the 1918 influenza pandemic. Proceedings of the National Academy of Sciences. 2007;104(18):7582–7587. doi: 10.1073/pnas.0610941104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markel H, Lipman HB, Navarro JA, Sloan A, Michalsen JR, Stern AM, Cetron MS. Nonpharmaceutical interventions implemented by US cities during the 1918-1919 influenza pandemic. JAMA. 2007;298(6):644–654. doi: 10.1001/jama.298.6.644. [DOI] [PubMed] [Google Scholar]
- Yasuda H, Yoshizawa N, Kimura M, Shigematsu M, Matsumoto M, Kawachi S, Oshima M, Yamamoto K, Suzuki K. Preparedness for the Spread of Influenza: Prohibition of Traffic, School Closure, and Vaccination of Children in the Commuter Towns of Tokyo. Journal of Urban Health. 2008;85(4):619–635. doi: 10.1007/s11524-008-9264-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawaguchi R, Miyazono M, Noda T, Takayama Y, Sasai Y, Iso H. Influenza (H1N1) 2009 outbreak and school closure, Osaka Prefecture, Japan. Emerging Infectious Diseases. 2009;15(10):1685. doi: 10.3201/eid1510.091029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cauchemez S, Valleron A-J, Boelle P-Y, Flahault A, Ferguson NM. Estimating the impact of school closure on influenza transmission from Sentinel data. Nature. 2008;452(7188):750–754. doi: 10.1038/nature06732. [DOI] [PubMed] [Google Scholar]
- Cauchemez S, Ferguson NM, Wachtel C, Tegnell A, Saour G, Duncan B, Nicoll A. Closure of schools during an influenza pandemic. The Lancet Infectious Diseases. 2009;9(8):473–481. doi: 10.1016/S1473-3099(09)70176-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Group WHOW. Nonpharmaceutical Interventions for Pandemic Influenza, National and Community Measures. Emerging Infectious Diseases. 2006;12(1):88–94. doi: 10.3201/eid1201.051371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Y, Atkinson PM, Ettema D. Simulation of Infectious Disease Transmission within a City: the Application of ISTAM to Eemnes by Role-based AB Simulation. Journal of the Royal Society Interface. 2008;5:759–772. doi: 10.1098/rsif.2007.1218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Y, Atkinson PM. Individual space-time activity-based model: a model for simulation of airborne infectious disease transmission by activity bundle simulation. Environment and Planning B: Planning and Design. 2008;35(1):80–99. doi: 10.1068/b32162. [DOI] [Google Scholar]
- Oppong JR, Mikler AR, Moonan P, Weis S. Innovative Internet Community Systems. Heidelberg: Springer Berlin; 2006. From Medical Geography to Computational Epidemiology - Dynamics of Tuberculosis Transmission in Enclosed Spaces; pp. 189–197. [Google Scholar]
- Hutton MD, Stead WW, Cauthen GM, Bloch AB, Ewing WM. Nosocomial transmission of tuberculosis associated with a draining abscess. Journal of Infectious Disease. 1990;161:286–295. doi: 10.1093/infdis/161.2.286. [DOI] [PubMed] [Google Scholar]
- Noakes CJ, Beggs CB, Sleigh PA, Kerr KG. Modelling the transmission of airborne infections in enclosed spaces. Epidemiology and Infection. 2006. pp. 1–10. [DOI] [PMC free article] [PubMed]
- Hall ET. The Hidden Dimension. New York, USA: Doubleday; 1966. [Google Scholar]
- Given LM, Leckie GJ. "Sweeping" the library: Mapping the social activity space of the public library. Library and Information Science Research. 2003;25:365–385. doi: 10.1016/S0740-8188(03)00049-5. [DOI] [Google Scholar]
- Ettema D, Jong KD, Timmermans H, Bakema A. In: Land use modeling. Koomen E, Bakema A, Stillwell J, editor. Scholten H: Springer; 2006. PUMA: Multi-agent modelling of urban systems; pp. 237–258. [Google Scholar]
- Elveback LR, Fox JP, Ackerman E. Stochastic stimulation models for two immunization problems. SIMS Conference on Epidemiology: 1975. 1975. pp. 90–103.
- Longini IM, Halloran ME, Nizam A, Yang Y. Containing pandemic influenza with antiviral agents. American Journal of Epidemiology. 2004;159:623–633. doi: 10.1093/aje/kwh092. [DOI] [PubMed] [Google Scholar]
- Longini I, Nizam A, Xu S, Ungchusak K, Hanshaoworakul W, Cummings D, Halloran M. Containing pandemic influenza at the source. Science. 2005;309:1083–1087. doi: 10.1126/science.1115717. [DOI] [PubMed] [Google Scholar]
- Glass RJ, Glass LM, Beyeler WE, Min HJ. Targeted social distancing design for pandemic influenza. Emerging Infectious Diseases. 2006;12(11):1671–1681. doi: 10.3201/eid1211.060255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milne GJ, Kelso JK, Kelly HA, Huband ST, McVernon J. A Small Community Model for the Transmission of Infectious Diseases: Comparison of School Closure as an Intervention in Individual-Based Models of an Influenza Pandemic. PloS ONE. 2008;3(12):e4005. doi: 10.1371/journal.pone.0004005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koonin LM, Cetron MS. School Closure to Reduce Influenza Transmission. Emerging Infectious Diseases. 2009;15(1):137–138. doi: 10.3201/eid1501.081289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Germann TC, Kadau K, Longini IM, Macken CA. Mitigation strategies for pandemic influenza in the United States. Proceedings of the National Academy of Sciences. 2006;103(15):5935–5940. doi: 10.1073/pnas.0601266103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishiura H, Oshitani H. Household Transmission of Influenza (H1N1-2009) in Japan: Age-specificity and Reduction of Household Transmission Risk by Zanamivir Treatment. The Journal of International Medical Research. 2011;39:619–628. doi: 10.1177/147323001103900231. [DOI] [PubMed] [Google Scholar]
- van Boven M, Donker T, van der Lubben M, van Gageldonk-Lafeber RB, te Beest DE, Koopmans M, Meijer A, Timen A, Swaan C, Dalhuijsen A, Hahne S, van den Hoek A, Teunis P, van der Sande MAB, Wallinga J. Transmission of Novel Influenza A(H1N1) in Households with Post-Exposure Antiviral Prophylaxis. PloS ONE. 2010;5(7):e11442. doi: 10.1371/journal.pone.0011442. [DOI] [PMC free article] [PubMed] [Google Scholar]