Abstract
Chemical exchange saturation transfer (CEST) provides a new imaging contrast mechanism sensitive to labile proton exchange. Pulsed-CEST imaging is better suited to the hardware constraints on clinical imaging systems compared with traditional continuous wave (CW)-CEST imaging methods. However, designing optimum pulsed-CEST imaging sequences entails complicated and time consuming numerical integrations. In this work, a simplified and computationally efficient technique is provided to optimize the pulsed-CEST imaging sequence. An analysis was performed of the optimal average irradiation power and the optimal irradiation flip angle (FA) as a function of the acquisition parameters and sample properties in both a two-pool model and a three-pool model of endogenous amine exchange. Key simulated and experimental results based on a creatine/agar tissue phantom include: 1) that the average irradiation power is a more meaningful sequence metric than is the average irradiation field amplitude, 2) that the optimal average powers for CW and pulsed-CEST imaging are approximately equal to each other for a relevant range of solute frequency offsets, exchange rates, and concentrations, 3) that an irradiation FA of 180° is optimal or near optimal, independent of the other acquisition parameters and the sample properties, and 4) that higher duty cycles yield higher CEST contrast.
Keywords: MRI, chemical exchange magnetization transfer (CEST), pulsed-CEST
Introduction
Chemical exchange saturation transfer (CEST) has recently been proposed as a new cellular and molecular imaging method. In CEST, exchangeable solute protons are saturated and the transfer of these protons to water is subsequently detected, which provides a mechanism for indirect detection of dilute labile protons that usually are undetectable by conventional MRI (1-3). CEST exchanging sites include endogeneous amines (4, 5) (e.g. amide proton transfer or APT) and hydroxyls (6) (e.g., glycogen CEST or glycoCEST), as well as labile sites on exogeneous paramagnetic agents (7-11) (paraCEST). Applications include imaging of tumors (4), ischemic acidosis (5), skeletal muscle and liver (6), mobile proteins and peptides (12), pH effects (9, 13) metabolite concentration (7), enzymatic activity (14), temperature (15), and drug delivery (16). However, the CEST contrast is usually very low, and quantitative measurements (calculated from the CEST contrast) are limited by the low SNR, thus making CEST signal optimization of central importance.
Two approaches to saturate labile protons have been used for CEST imaging: continuous-wave (CW), e.g. (17), and pulsed irradiation, e.g. (18, 19). In the CW technique, a long (on the order of seconds) off-resonance rectangular RF irradiation pulse precedes multi-echo acquisitions. Optimization is straightforward in the CW-CEST case because 1) there is an analytic solution that facilitates simple and rapid calculation, and 2) there is only one acquisition parameter (Bcw = rf field amplitude) that needs to be optimized. However, major drawbacks of this approach are its high specific absorption rate (SAR) and long acquisition time. Furthermore, most commercial MR scanners can not generate such long irradiations. The pulsed-CEST imaging technique addresses the SAR and hardware issues by using an irradiation scheme of repetitive short RF pulses. However, in this case, there is no analytical solution to the modified Bloch equations because of the presence of shaped RF pulses with time-varying amplitudes, and there are three independent acquisition parameters (e.g., rf amplitude, pulse width, and duty cycle) that need to be optimized. Therefore, the design of the pulsed-CEST imaging sequence requires non-trivial numerical integrations.
In this study, we provide a simple technique to optimize the pulsed-CEST imaging sequence by using the analytical solution for the CW-CEST signal and thus avoiding more complex numerical integration, and by an advantageous choice of the three independent acquisition parameters We first address the parameter choice by examining whether the average irradiation power, which is defined to be the mean square irradiation field, B2avg power (defined by Eq. [1]), or the mean irradiation field, Bavg field (defined by Eq. [3]), is a more meaningful sequence metric. We also examine the optimal Bavg power dependence (or lack there of) on the irradiation flip angle (FA) and duty cycle of the pulse sequence, and the frequency offset, exchange rate, and concentration of the CEST agents, using both a two-pool model (water and solute pool) and a three-pool model (water, solute, and macromolecular pool). Irradiation FA and duty cycle effects on the pulsed-CEST contrast are also included in forming an optimized protocol. Finally, we also analyze the relative role of saturation and rotation in pulsed-CEST imaging and the detrimental effects of pulsed methods on the spectrum resolution (or width of the signal dips).
Methods
Phantom Preparation
Creatine plus agar samples served as tissue phantoms, with the agar providing a short T2 macromolecular proton pool. A 3% agarose solution (w/w) was heated to boiling. Creatine was then added to the agar solution to reach a concentration of 50 mM. The solution was transferred into two tubes. The pH of the solution in the two tubes was titrated to 6.0, and 6.4 at 46°C, and the samples were left at room temperature to solidify before acquisition. All chemicals were purchased from Sigma-Aldrich (St. Louis, MO, USA).
MRI and Experiment
All images were acquired on a 9.4 T Varian small animal scanner at roughly 17°C. The phantom was positioned coaxially within a 38 mm ID volume coil. The main magnetic field (B0) was shimmed and the RF field (B1) was calibrated before experiments. T1 images were acquired using an inversion recovery fast spin-echo (IR-FSE) sequence.
The CW-CEST imaging utilized a 7.5 s irradiation pulse (long compared to the measured T1 of 2.8 s to ensure a steady-state condition) followed by single-shot spin-echo echo planner imaging (EPI) readout and a recovery time of 5 s. Images had a field of view (FOV) of 30 mm × 30 mm, matrix size of 64 × 64, bandwidth (BW) of 250 kHz, echo time (TE) of 50 ms, number of averages (NA) of 4, and slice thickness of 2 mm.
For pulsed-CEST imaging, the CW irradiation pulse was replaced by a series of Gaussian RF irradiation pulses (18). After each pulse, a crusher gradient (with alternating sign) was applied to spoil residual transverse magnetizations. Each irradiation pulse had a duration ti, flip angle θ (when applied on-resonance), and inter-pulse delay td. 400 pre-pulses were performed before an EPI acquisition to ensure the system reached steady state. For example, a pulsed-CEST sequence with a Bavg power of 1μT, irradiation FA of 180°, and duty cycle of 50%, has a ti of 10.8 ms, a PTR (pulse train time of repetition) of 21.7 ms, and a total irradiation time of 400*PTR = 8.68 s. All images had the same acquisition geometry, NA, and acquisition parameters as in CW-CEST imaging.
To determine the creatine/agar phantom sample parameters, a CW-CEST Z-spectrum was acquired with offsets from -1600 Hz to 1600 Hz (- 4 ppm to + 4 ppm at 9.4 T) with an interval of 50 Hz (0.125 ppm at 9.4 T). Data processing was conducted in MATLAB (Mathworks, Natick, MA, USA).
The CW-CEST contrast in steady state is a function of the applied irradiation field Bcw. Since Bcw has no time dependence, it is equal to both the average field and the square root of the average of the square of the field, i.e. power. The pulsed-CEST contrast is a function of the irradiation pulse shape (Gaussian, in our case), irradiation FA (θ), irradiation pulse duration (ti), and the delay between successive irradiation pulses (td). Alternatively, the pulse sequence can be described by the pulse shape, Bavg power or Bavg field, θ, and duty cycle (dc). The first three columns of table 1 list the range of sequence parameters in three sets of experiments on the creatine/agar gel. PTR, which is ti+td, was varied to satisfy θ, duty cycle, and Bavg power or Bavg field choices by using Eq [2] or Eq [4] and ranges from 10.5 ms to 148.1 ms and from 11.4 to 143.5 ms for the first and second pulsed experiment sets, respectively. An irradiation offset of 750 Hz was used to match the metabolite offset at 9.4 T.
Table 1.
Parameter ranges for CW and pulsed CEST experiments and simulations.
| CW exper. | pulsed exper. 1 | pulsed exper. 2 | CW sim. | pulsed sim. 1 | pulsed sim. 2 | |
|---|---|---|---|---|---|---|
| Bavg power (μT) | 0.1 – 2.0 | 0.4 – 1.2 | 0.1 – 2.0 | 0.1 – 2.0 | ||
| Bavg field (μT) | 0.1 – 0.8 | 0.1 – 2.0 | ||||
| θ (°) | 140 - 220 | 140 - 220 | 100 - 1100 | 100 - 1100 | ||
| dc (%) | 10 - 90 | 10 - 90 | 10 – 90 | 10 – 90 |
For pulsed- CEST imaging, Bavg power and Bavg field can be calculated by using the following equations (20)
| (1) |
| (2) |
| (3) |
| (4) |
where Bavg power and Bavg field are the field strengths of a continuous wave irradiation with the same average power or field, respectively, as the pulsed-CEST. γ is the gyro-magnetic ratio of the proton (with units rad / (s·T)). p1 is the ratio of the average amplitude to the maximum amplitude of the irradiation pulse and p2 is the ratio of the average of the square of the amplitude to the square of the maximum amplitude of the irradiation pulse. For the Varian standard version Gaussian pulse used in our experiments, p1 = 0.416 and p2 = 0.295.
The CEST difference is defined as the difference between the signals when applying positive (S(+)) and negative (S(-)) offset irradiations (see Eq. [5]), where (-) represents the offset of the exchanging metabolite and (+) is the offset on the symmetrically opposite side of the water peak. CEST contrast is the CEST difference normalized by the non-irradiated control case (S0) (see Eq. [6]).
| (5) |
| (6) |
Numerical Simulation and Data Processing
The Z-spectrum obtained from the CW-CEST experiment was numerically fitted to a three-pool model, in which only exchange between water and solute, and exchange between water and macromolecule was considered. The longitudinal relaxation time for bulk water was separately determined by an inversion recovery experiment to be 2.8 s. Longitudinal relaxation times for solute protons and semisolid macromolecules were set for fitting purposes to be 1 s (18); The transverse relaxation time for the semisolid macromolecules was set to be 15 μs and a Gaussian lineshape was assumed, matching (18), which uses a similar phantom. The simulated solute proton frequency offset from water is 750 Hz. There are then six independent variables left to be determined: the transverse relaxation rates for bulk water (T2w) and solute protons (T2s), the concentration for solute proton (fs) and semisolid macromolecules (fm) relative to water, the magnetization transfer (MT) exchange rate from macromolecules to water (kmw), and the chemical exchange rate from solute to water (ksw). These sample parameters are determined by a least squares fit to the Z-spectrum by integrating the coupled Bloch equations, as discussed below. The fitted parameters were then utilized for simulations of the CEST signal to optimize contrast and to examine the effects of varying sequence and sample parameters.
The CEST signal was simulated for a wider range of acquisition parameters than those in the experiments, which are given in the last three columns of table 1. PTR was varied to satisfy the Bavg power, θ, and duty cycle choices, and varied between 4.5 ms and 3 s. All parameter ranges were simulated concurrently, covering a three-dimensional parameter space.
For each set of acquisition parameters, the CEST signal was simulated for a variety of sample parameters. We varied the solute frequency offset (500, 750, 1250, 2000, 3000 Hz), exchange rate (50, 85, 100, 150, 200, 250, 500, 1000 Hz), and concentration relative to water (0.001, 0.0013, 0.002, 0.003, 0.004, 0.005). The experimentally determined values of the creatine/agar sample are given in bold. Each parameter was varied individually, with all other sample parameters remaining at the experimentally determined creatine/agar values. At exchange rates of 500 and 1000 Hz, only a limited range of θ values was examined, since an optimum θ value at high exchange rate is not well defined, as will be discussed in the Results section. All simulations were performed with both the full three-pool model, and, to analyze the CEST effect without MT, with a two-pool model, in which the concentration of the macromolecular pool was set to zero. Additional simulations of the effects of solid pool asymmetry and RF pulse bandwidth were performed as described in the Discussion section.
The three-pool model contains seven coupled Bloch equations and can be written as , where A is a 7 × 7 matrix. The water and solute pools each has three coupled equations representing their x, y, and z components. The macromolecular pool has a single coupled equation representing the z component, with an additional term for saturation effects (21). A Gaussian absorption lineshape (which has been found appropriate for agar (22)) was used for the macromolecular pool in all simulations of the phantom, and a super-Lorentzian absorption lineshape (which best fits biological tissue (23-26)) was used to simulate in vivo amide imaging. While the differential equation must be integrated for pulsed-CEST, the steady state CW-CEST signal was simply calculated by setting one side of the differential equations to zero, giving M = −A−1M0. All numerical calculations of the pulsed-CEST signal integrated the differential equations through the pulse sequence using the ordinary differential equation (ODE) solver in MATLAB. The simulation stopped when the difference in magnetization differed by less than 0.01% from that of the previous repetition. Spoiling was modeled by nulling the transverse components of the magnetization before and after the irradiation pulse.
The primary use of these simulations will be to optimize the CEST contrast, as given by Eq. [6]. However, asymmetry of the macromolecular MT effects around the water resonance complicates in vivo CEST contrast, but is not present in our creatine/agar phantom. This effect can be described by a first order approximation (23):
| (7) |
where CESTcontrastsym is the normalized CEST difference assuming the macromolecular MT effect is symmetric. MTR′asym is the difference between the conventional magnetization transfer (MTR) values at the positive offset and the corresponding negative offset assuming there is no CEST effect. Δm is the frequency offset between the macromolecule pool and the water pool. To attain specifically CEST based signal difference, CESTcontrastsym should be maximized, and MTR′asym should be minimized. Therefore, CESTcontrastsym−|MTR′asym(Δm)| is the optimization target. As the center of the MT Z-spectrum shifts upfield from the water signal, MTR′asym is negative (23). Therefore, the proposed optimization target in this case is actually the CESTcontrast, as defined by Eq. [6]. To test the proposed optimization method when there is macromolecular asymmetry, simulations were performed for amide imaging at 4.7 T (frequency offset from water is 3.5 ppm) by using the three-pool model with Δm = 2.34 ppm (23). Other parameters used are T1w= 3 s, T2w= 2 s, T1s= 0.77 s, T2s= 33 ms, T1m= 1 s, T2m= 15 μs, fs= 0.0013, fm= 0.0210, kmw= 48 Hz, and ksw= 28 Hz (5, 17).
Results
A Z-spectrum acquired with CW-CEST imaging on the creatine/agar sample at 9.4 T was fit to the three-pool exchange model, giving parameter fits of T2w= 45 ms, T2s= 13 ms, fs= 0.0013, fm= 0.0210, kmw= 48 Hz, and ksw= 85 Hz.
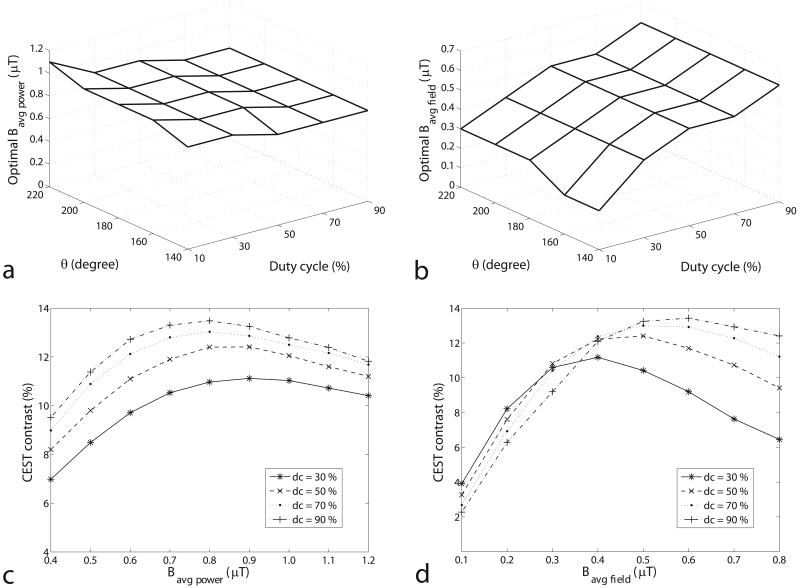
Figures 1a and 1b show the Bavg field and Bavg power that optimize CEST contrast as a function of θ and duty cycle in the experimental pulsed-CEST results. While the optimal Bavg power in figure 1a is roughly independent of the other acquisition parameters (varying in a range from 0.8 to 1.1 μT, or 30% of the average value), the optimal Bavg field in figure 1b is highly dependent on the other acquisition parameters (varying in a range from 0.2 to 0.6 μT, or 100% of the average value). Figures 1c and 1d illustrate the underlying CEST contrast dependencies on Bavg power and Bavg field, respectively. The curves for different duty cycles in figure 1c, but not in figure 1d, have similar maximum positions and are approximately proportional to each other. Therefore, specifying Bavg power (but not Bavg field) can ensure optimum or near optimum conditions. Thus, Bavg power is a more meaningful sequence metric than is Bavg field.
FIG. 1.
The experimental Bavg power (a) and Bavg field (b) that optimize the pulsed CEST contrast as a function of θ and duty cycle in the creatine/agar sample. Note that the optimal Bavg power is relatively independent of θ and duty cycle, while the optimal Bavg field is not. PTR is varied in order to find the optimal Bavg power and Bavg field at each θ and duty cycle. Similar results are found (but not shown) at pH = 6.0 at 9.4 T and pH = 6.4 at 4.7 T and in simulations of this creatine/agar sample and pseudo-phantoms with different frequency offsets (500 Hz to 3000 Hz), exchange rates (50 Hz to 250 Hz), and solute concentrations (0.001 to 0.005). The near independence of the optimal Bavg power on the other acquisition parameters makes Bavg power a more meaningful sequence metric than Bavg field. Figures (c) and (d) plot the CEST contrast as a function of Bavg power and Bavg field, respectively, at θ = 180°. Note the similar dependence on Bavg power at all duty cycles.
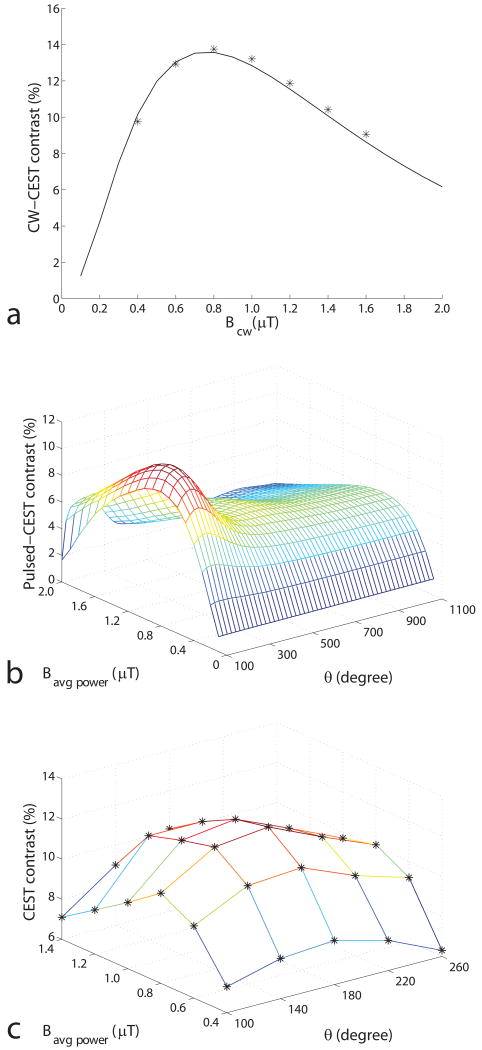
Figure 2a shows the simulated and experimental CW-CEST contrast of the creatine/agar sample as a function of irradiation field strength Bcw. The optimal Bcw is approximately 0.8 μT. Figure 2b and 2c shows the simulated and experimental pulsed-CEST contrast as a function of Bavg power and θ. The optimal Bavg power and θ are 0.9 μT and 180°, respectively. The corresponding PTR and ti are 24.0 and 12.0 ms, respectively.
FIG. 2.
a) Simulated and experimental CW-CEST contrast as a function of Bcw. b) Simulated and c) experimental pulsed-CEST contrast as a function of Bavg power and θ at 9.4 T with a duty cycle of 50%. Stars in a) and c) represent the experimental results. (Simulation results calculated using other duty cycles, and for pseudo-samples with varied solute frequency offset, exchange rate, and concentration give similar results, but are not shown here.) The CEST contrast was simulated using a three-pool model. PTR is varied, while duty cycle is maintained at 50%, according to Eq (2). Note in (b) that the optimal Bavg power is independent of θ, and the optimal θ is independent of Bavg power. Optimal Bavg power is largely dictated by direct and macromolecular MT saturation effects, while optimal θ is dictated by solute rotation effects, (additional damped oscillations can be observed at θ ≈ 540°,) as will be discussed in figure 6.
Figure 2b and 1a also illustrates the advantage of describing the pulsed-CEST sequence with Bavg power, θ, and dc (instead of Bavg field, θ, and dc or ti, θ, and dc or any other 3 parameter combinations.) The optimal Bavg power is roughly independent of θ and dc. The optimal θ is roughly independent of Bavg power and dc. That is, Bavg power, θ, and dc are in some sense orthogonal coordinates. Therefore, the three parameters can be optimized independently using relatively simple and fast computational approaches.
An alternative (and intuitive) approach would be to have the irradiation pulse duration (ti) be an independent variable (instead of being a function of Bavg power, θ, and duty cycle). However, this choice leads to non-orthogonal independent variables that cannot be optimized independently. Furthermore, choosing long ti values that avoid direct saturation (an intuitive choice) leads to non-optimum contrast. For example, when a maximum dc of 50% is assumed, the optimized simulated contrast using a 2-pool model is 13.0% (with direct saturation of 13.2% S0 as indicated by the reference scan) when using ti = 12.0 ms, Bavg power = 0.9 μT, and θ = 180°. Increasing ti to 133.8 ms by increasing θ are 2000° (and not changing Bavg power) gives a CEST contrast of 6.4% and direct saturation of 13.4%. Increasing ti to 27.1 ms by decreasing Bavg power to 0.4 μT (and not changing θ) gives a CEST contrast of 8.2% and direct saturation of 2.9%. That is, increasing ti above the value dictated by the optimum Bavg power and θ may lessen direct saturation, but at the cost of CEST contrast.
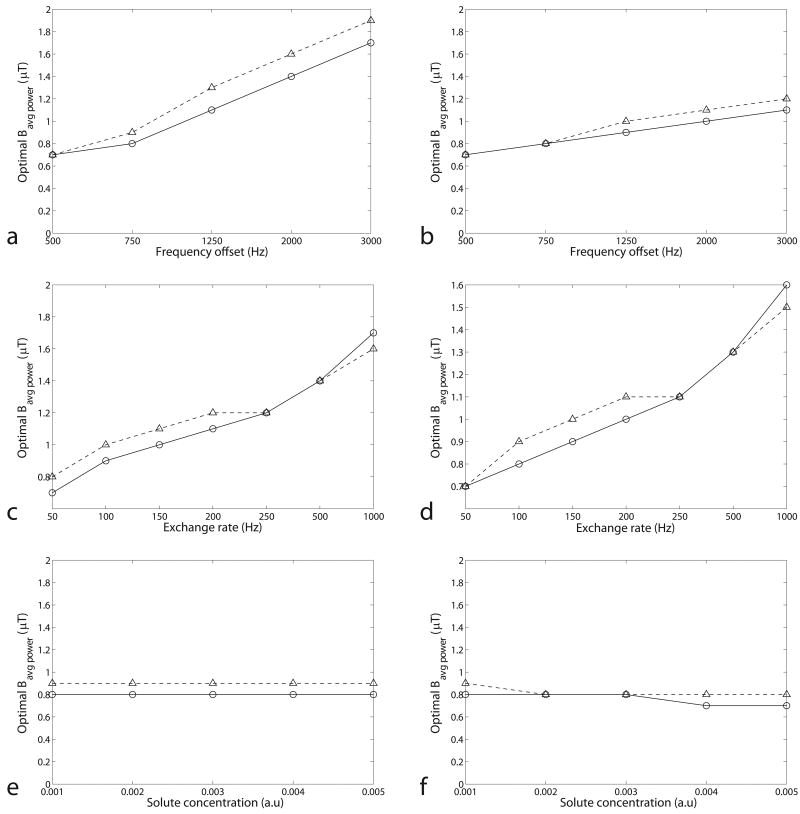
Figure 3 plots simulated optimal Bavg power as a function of frequency offset, exchange rate, and solute concentration in the two-pool and three-pool model. Note that the optimal Bavg power trend increases with frequency offset and exchange rate, but is independent of the solute concentration. In addition, the optimal Bavg power in CW-, and pulsed-CEST imaging are similar in all cases (though the less power efficient pulsed saturation method requires slightly greater power to reach optimal conditions). Therefore, the optimal Bavg power can be acquired by the relatively simple calculation of the optimal Bcw in CW-CEST imaging. Note that CW and pulsed CEST do not, in general, have the same signal dependence on power, but they do have similar optimum power values.
FIG. 3.
Simulated optimal Bavg power at dc = 50% as a function of frequency offset (a), exchange rate (c), and solute concentration (e) in the two-pool model, and frequency offset (b), exchange rate (d), and solute concentration (f) in the three-pool model. Circle and triangle represent CW and pulsed-CEST, respectively. (Remember that in CW-CEST, Bcw = Bavg power.) Note the similar dependence of the optimal Bavg power in CW and pulsed-CEST on the sample parameters. The non-specified sample parameters are from the fitting results of a CW-CEST experiment on a creatine/agar phantom. These results are based on simulations with a Bavg power spacing of 0.1 μT, resulting in discrete jumps.
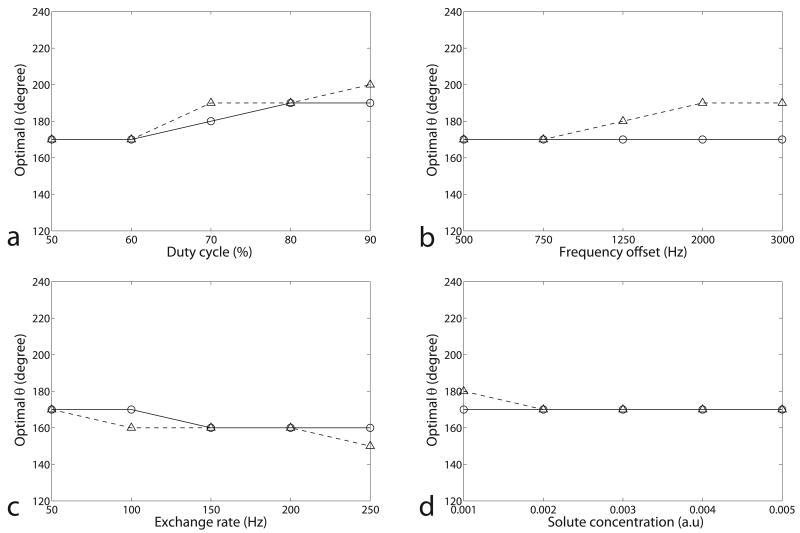
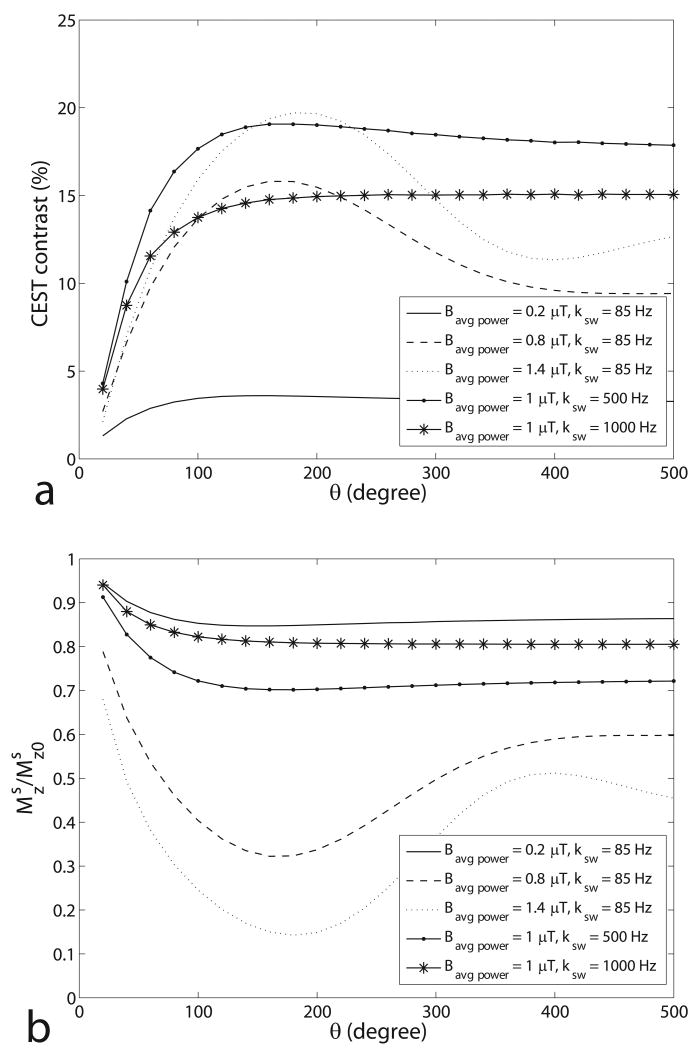
Figure 4 shows the simulated optimal θ for pulsed-CEST imaging as a function of duty cycle, frequency offset, exchange rate, and solute concentration in the two-pool and three-pool model. It can be concluded that the optimal θ is roughly independent of the acquisition parameters and samples (varying in a short range from 150° to 200°). However, for samples with higher exchange rates or relatively low Bavg power, an optimal θ does not exist, which will be discussed in figure 6. Fortunately, it was found from figure 6 that the contrast at 180° is close to the maximum contrast, thus making θ = 180° an optimum or near-optimum choice in all of our simulations.
FIG. 4.
Simulated optimal θ as a function of duty cycle (a), frequency offset (b), exchange rate (c), and solute concentration (d) in the two-pool (triangle) and three-pool model (circle). The non-specified sample parameters are from the fitting results of a CW-CEST experiment on a creatine/agar phantom. Calculations were performed for a range of θ (140° – 220°) with a step of 10°, resulting in discrete jumps. For (b), (c), and (d), dc = 50%. Note that the optimal θ, which is around 180°, is roughly independent of the duty cycle, frequency offset, exchange rate, and concentration.
FIG. 6.
Simulated pulsed-CEST contrast (a) and normalized average z-magnetization of solute protons in a PTR (b) as a function of θ using a two-pool model. is the average z-magnetization of solute protons in a PTR, and is the equilibrium magnetization of solute pool. For these simulations, the weak irradiation pulse approximation was used, ignoring spill over effect on the free water protons. Note the oscillating nature of the signal dependence on θ, which is present in all our simulations with γBavg power ≥ ksw, but not at lower powers (solid line) or higher exchange rates (solid-star line), as expected.
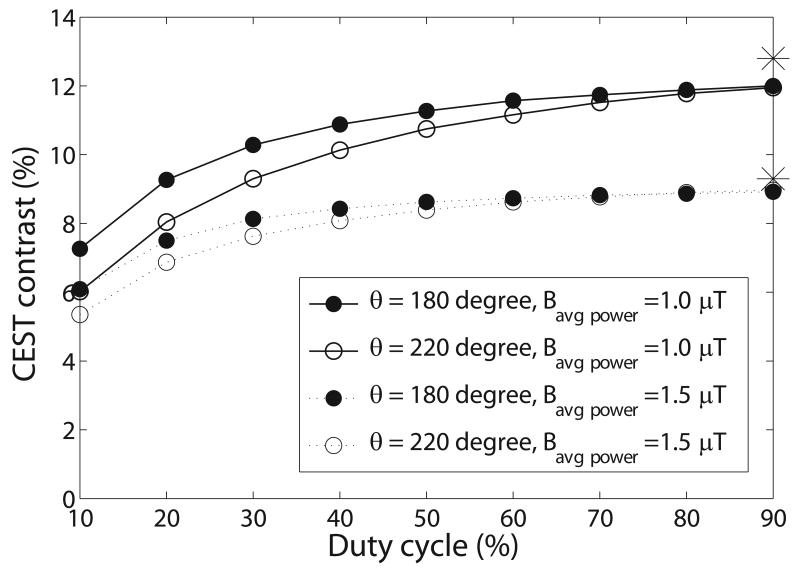
Figure 5 shows the simulated pulsed-CEST contrast as a function of duty cycle. The contrast increases with duty cycle, but is close to the maximum value at a duty cycle of 50%. Although a higher duty cycle yields higher CEST contrast, duty cycle may be limited due to inherent amplifier constraints on duty cycle or pulsewidth (with the ti_limit leading to ), or due to required spoiling times (with the td_limit leading to . However, if the only limitation is the SAR limit, which is a function of Bavg power, then CW-CEST will give superior contrast compared to pulsed-CEST.
FIG. 5.
Simulated pulsed-CEST contrast as a function of duty cycle using a three-pool model. Each line was calculated using the same Bavg power and θ. The two asterisks on the far right represents the contrast in CW-CEST imaging with a Bcw of 1 μT and 1.5 μT, which deviate from the extrapolations to 100% duty cycle using the same Bavg power due to the effect of the Gaussian pulse shape. Note that the CEST contrast at a duty cycle of 50% is close to the maximum CEST contrast in each line. The parameters used are from the fitting results of the creatine/agar sample. Simulations of pseudo-phantoms with different frequency offsets (500 Hz to 3000 Hz), exchange rates (50 Hz to 1000 Hz), and solute concentrations (0.001 to 0.005) also give the same conclusion.
The rough independence of the optimal Bavg power on θ and dc acquisition parameters and the rough independence of the optimal θ on Bavg power and dc and the sample properties (offset, exchange rate, and concentration) can be exploited to optimize the pulsed-CEST imaging sequence. First, by identifying the optimal Bavg power by measuring or calculating the optimal Bcw of CW-CEST imaging; Second, by setting θ equal to 180°; Third, by choosing a duty cycle as high as possible, and then calculating the PTR according Eq. (2).
For example, for the creatine/agar sample at 9.4 T, the optimal Bcw was found to be 0.8 μT using the M = −A−1M0 CW signal equation. Using a duty cycle of 50%, PTR and ti can be calculated to be 27.0 ms and 13.5 ms, respectively. The maximum CEST contrast by using the proposed guidelines is then 11.49% (vs 11.54% when numerically integrating for all Bavg power and θ possibilities to optimize the CEST contrast within the same duty cycle constraints). This demonstrates that our proposed technique is an effective way to design pulsed-CEST imaging sequences for amine exchange. If, on the other hand, the exchange rate is increased outside the amine regime to, say, 2000 Hz, the optimal Bcw is 1.8 μT. Following the design guidelines by setting θ to 180° (with PTR and ti calculated to be 12.0 ms and 6.0 ms) gives a simulated contrast of 7.37% (vs 7.72% when optimizing via numerical integration of all Bavg power and θ possibilities). The primary cause of the contrast difference in this fast exchange example is the θ value, which is 2000° in the latter case.
In vivo imaging may be complicated by macromolecular MT asymmetry, affecting the CEST contrast. Simulation results for amide proton transfer (APT) imaging on a 4.7 T scanner (not shown) indicate that the optimal Bcw of 0.3 μT is close to the optimal Bavg power of 0.4 μT in pulsed-CEST imaging (when using a simulation resolution of 0.1 μT); the optimal θ is near 180° at all powers and duty cycles (corresponding to a ti value of 36.1 ms at optimum Bavg power and 50% duty cycle); and the CEST contrast increases with the duty cycle. That is, our proposed optimization technique is still applicable when the solid pool is asymmetric.
Discussion
In this paper, we give the simulated CEST contrast as a function of Bavg power and θ. Figures 2a and 2b show that for both CW- and pulsed-CEST, there is a single optimal Bavg power (or Bcw). Below this value, solute saturation and rotation is too slow (relative to exchange). Above this value, the water pool is saturated by direct irradiation and indirect solid-pool MT effects, both of which decrease CEST contrast. In contrast to these saturation effects, the CEST contrast dependence on θ is dominated by solute rotation effects. Figure 6 shows the simulated pulsed-CEST contrast and average z-magnetization of solute protons over a PTR as a function of θ. To isolate the effects of solute proton rotation, a two-pool model was used that avoids macromolecular pool effects. Likewise, spill over effects were ignored by assuming weak irradiation pulses that have no direct effect on the free water protons. The simulations in figure 6 were performed at constant irradiation power by varying PTR with θ. Figure 6b shows that at medium and high powers (Bavg power = 0.8 μT and 1.4 μT), the z-magnetization of the solute protons (averaged over the PTR) oscillates very roughly like cos(θ). This oscillation induces a corresponding effect in the CEST contrast, as seen in figure 6a. Since no direct water effects were included in these simulations, this CEST contrast oscillation is due entirely to spin exchange with the solute. Note that at lower power (Bavg power = 0.2 μT) or higher exchange rate as in glycoCEST (ksw ≈ 1000 Hz), this rotation effect disappears.
While the simulations have focused on endogenous amine exchange with direct relevance to APT, aspects are relevant to glycoCEST and paraCEST. The significantly faster exchange rates and smaller frequency offsets in glycoCEST compared to APT eliminates the solute rotation effect that makes θ = 180° optimum. Nonetheless, simulations (not shown) indicate that θ = 180° and Bavg power = Bcw, optimum is still a near optimum choice. For paraCEST agents, there is a large range of possible offsets and exchange rates, but optimum simulated Bcw > 10 μT are not uncommon. Issues of SAR compliance, amplifier limits, and, for pulsed-CEST, extremely high pulse bandwidths, motivate the typical use of lower Bavg power and higher θ values than the guidelines for amine CEST presented in this manuscript.
We have thus far only addressed issues of CEST contrast. An additional issue is the width of the CEST dip, as this affects the CEST spectrum resolution and the ability to isolate CEST effects originating from a single exchanging site. CW-CEST imaging utilizes a long irradiation pulse before acquisition, which results in a very narrow band off-resonance excitation that saturates the labile protons. However, pulsed-CEST uses multiple short duration high intensity RF irradiation pulses that may cause a wider bandwidth off-resonance excitation. Simulations (not shown) indicate that the FWHM (full width at half maximum) of the CEST dip at Bavg power of 0.6 μT, 1.0 μT, 1.4 μT, (with corresponding ti of 18.1 ms, 10.8 ms, 7.7 ms) and Bcw of 1 μT are 0.37 ppm, 0.55 ppm, 0.76 ppm, and 0.37 ppm, respectively, at 9.4 T. It was found that the pulsed-CEST dip widens as Bavg power increases (and the ti decreases). The relative importance of contrast and resolution in a given system should dictate the applied Bavg power.
In the current work, we have ignored issues that complicate peak selection for in vivo imaging, such as exchangeable protons on multiple side groups, MT solid pool asymmetry, and errors in determining the water resonance. Such issues may complicate image interpretation even when applying optimum or near-optimum acquisitions. For example, previous studies, e.g. (5), that have applied a θ of 180° (in line with our proposed guidelines but given without explanation) have measured CEST peaks at unexpected frequency offsets.
In contrast to our results, Sun et al. (18) have found that it is the optimal average irradiation magnetic field amplitude (Bavg field) in pulsed-CEST that equals the optimal field amplitude (Bcw) in CW-CEST. (Although their manuscript refers to the “average power,” their Eq. [1] matches our average field definition in Eq. [3].) Our experimental results in figure 1b indicate that the optimal Bavg field depends on the duty cycle. Sun et al.'s choice of 50% duty cycle happens to match the CW case, but this equivalence is not true in general for Bavg field, though it is roughly true for Bavg power. Figures 1c and 1d illustrate this differing CEST contrast dependence on duty cycle. (Note also, for comparison purposes, that Sun et al.'s plots use the average field during the pulse (private communication), which at 50% duty cycle, differ by a factor of two from calculations such as ours based on the average field during a PTR.)
Conclusion
In this study, we find that the optimal Bavg power for pulsed CEST is roughly independent of θ and duty cycle, and is similar to the optimal Bcw for CW CEST. We also find that the optimal θ is near 180°, independent of acquisition parameters and sample properties such as frequency offset, exchange rate, and solute concentrations. Optimizing the choice of Bavg power and θ using these guidelines is a computationally efficient technique for designing pulsed-CEST imaging sequences.
Acknowledgments
We thank Thedore Towse, Adrienne Dula, Bruce M. Damon, and Seth A Smith for helpful discussions, and NIH grant EB001452 and Vanderbilt Bridge Grant (Gochberg) for funding.
References
- 1.Ward KM, Aletras AH, Balaban RS. A new class of contrast agents for MRI based on proton chemical exchange dependent saturation transfer (CEST) J Magn Reson. 2000;143:79–87. doi: 10.1006/jmre.1999.1956. [DOI] [PubMed] [Google Scholar]
- 2.Snoussi K, Bulte JWM, Gueron M, van Zijl PC. Sensitive CEST agents based on nucleic acid imino proton exchange: detection of poly(rU) and of a dendrimer-poly(rU) model for nucleic acid delivery and pharmacology. Magn Reson Med. 2003;49:998–1005. doi: 10.1002/mrm.10463. [DOI] [PubMed] [Google Scholar]
- 3.Querol M, Bogdanov A., Jr Amplification strategies in MR imaging: activation and accumulation of sensing contrast agents (SCAs) J Magn Reson Imaging. 2006;24:971–982. doi: 10.1002/jmri.20724. [DOI] [PubMed] [Google Scholar]
- 4.Jones CK, Schlosser MJ, van Zijl PC, Pomper MG, Golay X, Zhou J. Amide proton transfer imaging of human brain tumors at 3T. Magn Reson Med. 2006;56:585–592. doi: 10.1002/mrm.20989. [DOI] [PubMed] [Google Scholar]
- 5.Zhou J, Payen JF, Wilson DA, Traystman RJ, van Zijl PC. Using the amide proton signals of intracellular proteins and peptides to detect pH effects in MRI. Nat Med. 2003;9:1085–1090. doi: 10.1038/nm907. [DOI] [PubMed] [Google Scholar]
- 6.van Zijl PC, Jones CK, Ren J, Malloy CR, Sherry AD. MRI detection of glycogen in vivo by using chemical exchange saturation transfer imaging (glycoCEST) Proc Natl Acad Sci U S A. 2007;104:4359–4364. doi: 10.1073/pnas.0700281104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Aime S, Delli Castelli D, Fedeli F, Terreno E. A paramagnetic MRI CEST agent responsive to lactate concentration. J Am Chem Soc. 2002;124:9364–9365. doi: 10.1021/ja0264044. [DOI] [PubMed] [Google Scholar]
- 8.Zhang S, Merritt M, Woessner D, Lenkinski R, Sherry AD. PARACEST agents: modulating MRI contrast via water proton exchange. Acc Chem Res. 2003;36:783–790. doi: 10.1021/ar020228m. [DOI] [PubMed] [Google Scholar]
- 9.Aime S, Barge A, Delli Castelli D, Fedeli F, Mortillaro A, Nielsen FU, Terreno E. Paramagnetic lanthanide(III) complexes as pH-sensitive chemical exchange saturation transfer (CEST) contrast agents for MRI applications. Magn Reson Med. 2002;47:639–648. doi: 10.1002/mrm.10106. [DOI] [PubMed] [Google Scholar]
- 10.Zhang S, Trokowski R, Sherry AD. A paramagnetic CEST agent for imaging glucose by MRI. J Am Chem Soc. 2003;125:15288–15289. doi: 10.1021/ja038345f. [DOI] [PubMed] [Google Scholar]
- 11.Woessner DE, Zhang S, Merritt ME, Sherry AD. Numerical solution of the Bloch equations provides insights into the optimum design of PARACEST agents for MRI. Magn Reson Med. 2005;53:790–799. doi: 10.1002/mrm.20408. [DOI] [PubMed] [Google Scholar]
- 12.Zhou J, Van Zijl PC. Chemical exchange saturation transfer imaging and spectroscopy. Progr NMR Spectrosc. 2006;48:109–136. [Google Scholar]
- 13.Aime S, Delli Castelli D, Terreno E. Novel pH-reporter MRI contrast agents. Angew Chem Int Ed Engl. 2002;41:4334–4336. doi: 10.1002/1521-3773(20021115)41:22<4334::AID-ANIE4334>3.0.CO;2-1. [DOI] [PubMed] [Google Scholar]
- 14.Yoo B, Pagel MD. A PARACEST MRI contrast agent to detect enzyme activity. J Am Chem Soc. 2006;128:14032–14033. doi: 10.1021/ja063874f. [DOI] [PubMed] [Google Scholar]
- 15.Zhang S, Malloy CR, Sherry AD. MRI Thermometry based on PARACEST agents. J Am Chem Soc. 2005;127:17572–17573. doi: 10.1021/ja053799t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Khemtong C, Kessinger CW, Gao J. Polymeric nanomedicine for cancer MR imaging and drug delivery. Chem Commun. 2009;24:3497–3510. doi: 10.1039/b821865j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sun PZ, Van Zijl PC, Zhou J. Optimization of irradiation power in chemical exchange dependent saturation transfer experiments. J Magn Reson. 2005;175:193–200. doi: 10.1016/j.jmr.2005.04.005. [DOI] [PubMed] [Google Scholar]
- 18.Sun PZ, Benner T, Kumar A, Sorensen AG. Investigation of optimizing and translating pH-sensitive pulsed-chemical exchange saturation transfer (CEST) imaging to a 3T clinical scanner. Magn Reson Med. 2008;60:834–841. doi: 10.1002/mrm.21714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Liu G, Ali MM, Yoo B, Griswold MA, Tkach JA, Pagel MD. PARACEST MRI with improved temporal resolution. Magn Reson Med. 2009;61:399–408. doi: 10.1002/mrm.21863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ramani A, Dalton C, Miller DH, Tofts PS, Barker GJ. Precise estimate of fundamental in-vivo MT parameters in human brain in clinically feasible times. Magn Reson Imaging. 2002;20:721–731. doi: 10.1016/s0730-725x(02)00598-2. [DOI] [PubMed] [Google Scholar]
- 21.Sled JG, Pike GB. Quantitative interpretation of magnetization transfer in spoiled gradient echo MRI sequences. J Magn Reson. 2000;145:24–36. doi: 10.1006/jmre.2000.2059. [DOI] [PubMed] [Google Scholar]
- 22.Henkelman RM, Huang X, Xiang QS, Stanisz GJ, Swanson SD, Bronskill MJ. Quantitative interpretation of magnetization transfer. Magn Reson Med. 1993;29:759–766. doi: 10.1002/mrm.1910290607. [DOI] [PubMed] [Google Scholar]
- 23.Hua J, Jones Ck, Blakeley J, Smith SA, van Zijl PC, Zhou J. Quantitative Description of the asymmetry in magnetization transfer effects around the water resonance in the human brain. Magn Reson Med. 2007;58:786–793. doi: 10.1002/mrm.21387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Tozer D, Ramani A, Barker GJ, Davies GR, Miller DH, Tofts PS. Quantitative magnetization transfer mapping of bound protons in multiple sclerosis. Magn Reson Med. 2003;50:83–91. doi: 10.1002/mrm.10514. [DOI] [PubMed] [Google Scholar]
- 25.Morrison C, Henkelman RM. A model for magnetization transfer in tissues. Magn Reson Med. 1995;33:475–482. doi: 10.1002/mrm.1910330404. [DOI] [PubMed] [Google Scholar]
- 26.Morrison C, Stanisz G, Henkelman RM. Modeling magnetization transfer for biological-like systems using a semi-solid pool with a super-Lorentzian lineshape and dipolar reservoir. J Magn Reson B. 1995;108:103–113. doi: 10.1006/jmrb.1995.1111. [DOI] [PubMed] [Google Scholar]