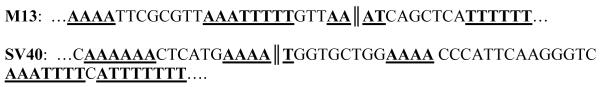Effect of magnesium ions and temperature on the sequence-dependent curvature of DNA restriction fragments

Abstract

Transient electric birefringence has been used to quantitate the curvature of two DNA restriction fragments, a 199-base pair fragment taken from the origin of replication of the M13 bacteriophage and a 207-base pair fragment taken from the VP1 gene in the SV40 minichromosome. Stable curvature in the SV40 and M13 restriction fragments is due a series of closely spaced A-tracts, runs of 4 to 6 contiguous adenine residues located within 40 or 60 base pair “curvature modules” near the center of each fragment. The M13 and SV40 restriction fragments exhibit bends of ~45° in solutions containing monovalent cations and ~58° in solutions containing Mg²⁺ ions. The curvature is not localized at a single site but is distributed over the various A-tracts in the curvature modules. Thermal denaturation studies indicate that the curvature in the M13 and SV40 restriction fragments remains constant up to 30°C in solutions containing monovalent cations, and up to 40°C in solutions containing Mg²⁺ ions, before beginning to decrease slowly with increasing temperature. Hence, stable curvature in these DNA restriction fragments exists at the biologically important temperature of 37°C.

1. Introduction

Double-stranded DNA molecules in the native B-conformation are usually described as wormlike coils with a persistence length of ~50 nm [1, 2]. However, certain DNA molecules contain sequences that impart stable curvature to the helix backbone. Such curved DNA molecules are often identified because they migrate anomalously slowly in polyacrylamide gels [3]. Many efforts have been made over the years to identify the sequences responsible for the curvature and to assess the magnitudes of the bend angles, using a variety of experimental techniques. These studies have shown that stable curvature of the DNA helix axis is most often observed when multiple A-tracts, runs of 4 to 6 contiguous adenine (A) or thymine (T) residues occur in phase with the 10 base pair (bp) helix repeat [3-5]. Mixed A/T sequences not interrupted by a T-A step also function as A-tracts [3, 4, 6, 7].

NMR studies using residual dipolar couplings have shown that the A-tract bend angle varies from 9° to 23°, depending on the number of adenine residues in the A-tract [7-9]. Topological studies of plasmids containing phased A₆-tracts have indicated that the bend angle is 20° ± 2° per A-tract [10, 11]. Two studies of the rate of cyclization of oligomers containing phased A-tracts have indicated that the bend angle per A-tract is 15° [12] or 17° – 21° [13]. Atomic force microscopy (AFM) measurements have suggested that the average bend angle per A-tract is 13° [14]. The variable results lead to the conclusion that the apparent A-tract bend angle depends on A-tract length, sequence context and the method used to measure curvature.

Electro-optic methods have also been used to measure A-tract-induced DNA bending. In transient electric birefringence (TEB) or dichroism (TED) experiments, the DNA molecules are oriented by a pulsed electric field. The decay of the birefringence (or dichroism) after the electric field is removed is a sensitive measure of DNA length because the rotational relaxation times characterizing the decay are approximately proportional to the third power of DNA length [15]. Measuring the relaxation times as a function of ionic strength allows a distinction to be made between stable curvature and anisotropic flexibility [16-18]. If the ratio of the relaxation times (τ-ratio) of a putatively bent DNA molecule and a normal fragment containing the same number of base pairs is independent of ionic strength, the target DNA is stably curved; if the τ-ratios vary significantly with ionic strength, the target DNA is anisotropically flexible. The τ-ratios can also be used to estimate the bend angle if the location of the bend is known [18-20]. Global fitting of the τ-ratios of a series of overlapping DNA fragments allows both the bend angle and its sequence position to be determined independently [21-23].

Early TEB and TED studies of ~240 base pair (bp) fragments taken from trypanosome kinetoplast DNA found that the average bend angle was 52° [16] or 84° [24]. Since each kinetoplast fragment contained four centrally located A-tracts, the average bend angle per A-tract was 13° or 18°, respectively. More recently, TEB has been used to characterize the curvature in two other DNA restriction fragments [22, 23, 25]. One is a 207-bp fragment taken from the origin of replication of the bacteriophage M13, which has been engineered into a plasmid called Litmus 28; the second is a 199-bp fragment taken from the gene for VP1, the major capsid protein in the simian virus 40 (SV40) minichromosome. Both restriction fragments migrate anomalously slowly in polyacrylamide gels [22, 23]. TEB measurements [22] have shown that the M13 and SV40 fragments are stably curved, with bend angles of 44° ± 2° [25] and 46° ± 2° [23], respectively, in solutions containing monovalent cations. The sequence surrounding each of the bend centers contains a series of closely spaced A-tracts in a “curvature module” of 40 or 60 base pairs, located near the center of each fragment. Replacing the curvature modules by sequences of equal length but without A-tracts eliminates the curvature, indicating that the A-tracts in the curvature modules are necessary and sufficient to cause stable bending of the helix axis [23, 25]. The magnitude of the M13 bend angle and its sequence location have been confirmed by atomic force microscopy [26], verifying the accuracy of the bend angles determined by TEB.

We have now measured the curvature of the M13 and SV40 restriction fragments in solutions containing Mg²⁺ ions and compared the bend angles with those observed in solutions containing only monovalent cations. The dependence of the bend angles on temperature has also been measured. We find that Mg²⁺ ions increase the A-tract-induced bend angles by ~30%. The bend angles are independent of temperature from 4°C to 30°C in solutions containing monovalent cations and from 4° to 40°C in solutions containing Mg²⁺ ions. The bend angles then decrease slowly with increasing temperature as the DNA conformation gradually becomes more like that of normal B-form DNA.

2. Materials and methods

2.1. DNA samples

The 207-bp M13 fragment, 199-bp SV40 fragment, and overlapping fragments of similar sizes were isolated by restriction enzyme digestion of Litmus 28 (New England Biolabs) and the SV40 genome (Invitrogen Life Technologies), respectively, using standard methods [27]. Normal DNA fragments of various sizes were isolated by restriction enzyme digestion of plasmids pUC19, pBR322 and Litmus 28 [2]. The specific methods used to prepare the relatively large quantities DNA needed for the TEB studies have been described previously [2, 17, 22, 23]. Briefly, after restriction enzyme digestion, the desired fragments were isolated by agarose gel electrophoresis, subcloned into the polylinker of plasmid pUC19, and amplified by the polymerase chain reaction (PCR). After restriction enzyme digestion, the desired fragments were separated by electrophoresis in overloaded agarose gels, excised from the gel, and the agarose dissolved with a chaotropic salt (QIAquick gel extraction kit, Qiagen). Finally, the DNA fragments were concentrated and desalted by adsorption on small DEAE columns, eluted into the desired buffer and stored at −20°C until needed. A 217-bp fragment, consisting of the 207-bp M13 fragment plus 5 linker base pairs on each end, was also studied. Since the results were identical for the 207-bp and 217-bp fragments, they are not distinguished in the following text. Sequence variants of the M13 and SV40 fragments containing variable numbers of A-tracts in the curvature modules were prepared by site-directed mutagenesis, as described previously [23]. The DNA samples were dissolved in three different buffers, called buffers B, C and F. Each buffer contained 1 mM Tris-Cl, pH 8.0. In addition, buffer B contained 0.1 mM EDTA, buffer C contained 0.01 mM EDTA, and buffer F contained 0.1 mM Mg²⁺.

2.2. TEB measurements

The apparatus and procedures used to carry out the TEB measurements have been described previously [2, 17, 26]. Briefly, the apparatus includes a helium-neon laser, polarizer, quarter wave plate, analyzer typically rotated −3° from the crossed position, and a photodiode-based optical amplifier with zero suppression circuit [17]. The time constant of the detector was ~0.23 μs. Square wave pulses were generated by a Model 605P Cober high power pulse amplifier used in the single shot mode. The Kerr cell was a shortened 1-cm path length quartz spectrophotometer cell chosen for its negligible strain birefringence. The parallel plate platinum electrodes had a 1.5-mm separation and were mounted on a Teflon support of standard design [28]. The stray light constant of the optical system, with the DNA solution and electrodes in the cell, was ≤1 × 10⁻⁵. The cell was thermostated at 20° unless otherwise indicated.

The field-free decay of the birefringence was analyzed using a nonlinear least squares fitting program adapted from Bevington [29]. The decay curves of fragments ≤250 bp in size could be fitted with a single relaxation time; larger fragments required two relaxation times to fit the data, as described previously [30]. The relaxation times obtained for each fragment under each set of experimental conditions, using 15 single-shot pulses, were averaged to give the mean relaxation times, τ, used for further analysis. Control experiments showed that the mean relaxation times were reproducible within ±1.5% on the same day, and within ±3% on different days, even when using different, independently prepared DNA stock solutions. Other control experiments showed that the mean relaxation times were independent of the duration of the applied pulse from 3 – 30 μs, independent of the electric field from 1.0 – 9.0 kV/cm, and independent of DNA concentration from 5 – 25 μg/mL. Therefore, most experiments were carried out using an electric field strength of 5 kV/cm (where the amplitude of the birefringence is in the Kerr region), a pulse duration of 8 μs and a DNA concentration of 14 μg/mL. Under such conditions, the DNA molecules are not perturbed by the electric field.

The relaxation times observed for curved and normal DNA fragments containing the same number of base pairs were used to calculate τ-ratios, τ_R, defined as τ_curved/τ_normal. The values of τ_curved were measured for each of the curved fragments in each of the buffers used in this study. The values of τ_normal were taken from previously measured [2] fitting functions describing the power law dependence of the terminal relaxation times of electrophoretically normal DNA fragments of various sizes on the number of base pairs in the fragment [2, 17]. This procedure ensures that the relaxation times of the curved fragments are compared with the relaxation times of “average” normal fragments containing the same number of base pairs, measured under the same experimental conditions. The estimated accuracy of the τ-ratios is ±2%.

If the bend in a stably curved DNA molecule is centrally located, the τ-ratios can be used [18] to determine the apparent bend angle, θ, from equation (1):

$$\theta =1.462{\cos }^{-1}\left({\tau }_R\right)+0.005{\left[{\sin }^{-1}(1-{\tau }_R)\right]}^{2.3}.$$ (1)

If the position of the bend is not known, both the bend angle and its sequence position can be determined by the method of overlapping fragments [22]. Birefringence relaxation times are measured for a series of DNA molecules containing the putative bend at different positions in the sequence. The τ-ratios are then compared with theoretical curves derived for once-broken rods with bends of different magnitudes located at different distances from the fragment ends [20, 22]. The calculations are repeated iteratively with different assumptions about the magnitude or location of the bend, until the τ-ratios lead to a consistent set of bend angles and positions in the overlapping fragments [22, 23, 25]. The calculation assumes only that the fragments have similar flexibilities, which is necessarily true for highly overlapped fragments containing approximately the same number of base pairs. The calculation also assumes that the bend in a particular sequence is independent of the distance of that sequence from the end of the fragment.

2.3. Temperature studies

The optical densities of the 201-bp M13 fragment, the 199-bp SV40 fragment and normal controls of similar size were measured as a function of temperature using a Gilford Response II spectrophotometer with 0.3 cm³ quartz microcuvettes. The heating rate was 0.1°C/min. Melting temperatures (T_m) were determined from maxima in plots of d(OD)₂₆₀/dT as a function of temperature. TEB measurements of the same samples were also made as a function of temperature. The birefringence cell was allowed to equilibrate for at least five minutes at each temperature before measuring the relaxation times. To check the accuracy of the temperature in the thermostated birefringence cell, the relaxation times observed at representative temperatures, τ_obs, were converted to 20°C using equation (2):

$${\tau }_{20}=\left(\frac{{\eta }_{20}{T}_{\mathit{obs}}}{{\eta }_{\mathit{obs}}293}\right){\tau }_{\mathit{obs}}.$$ (2)

where η is the viscosity of water at the indicated temperature. The calculated relaxation times agreed with the values measured at 20°C within ±3%.

3. Results and discussion

3.1. Stable curvature of the M13 and SV40 restriction fragments

TEB relaxation times were measured in buffers B and C for the 207-bp M13 fragment, the 199-bp SV40 fragment and a 335-bp restriction fragment taken from the SV40 terminus of transcription. All three restriction fragments migrated anomalously slowly in polyacrylamide gels [23], suggesting that they might be stably bent or curved. As shown in Table 1, the τ-ratios observed for the 199-bp SV40 fragment and the 207-bp M13 fragment were reasonably independent of cation concentration, indicating that their helix backbones are stably curved. By contrast, the τ-ratios of the 335-bp SV40 fragment varied significantly with cation concentration, suggesting that this fragment is anisotropically flexible, not stably curved.

Table 1.

Comparison of τ-ratios in solutions with different Na⁺ ion concentrations

	τ-ratio1
Buffer cations	207-bp M13	199-bp SV40	335-bp SV40
0.5 mM Tris+ + 0.02 mM Na+	0.87	0.87	0.87
0.5 mM Tris+ + 0.2 mM Na+	0.91	0.84	0.99

¹Estimated uncertainty of the τ-ratios is ±0.02

3.2. Birefringence relaxation times observed in solutions with and without Mg²⁺ ions

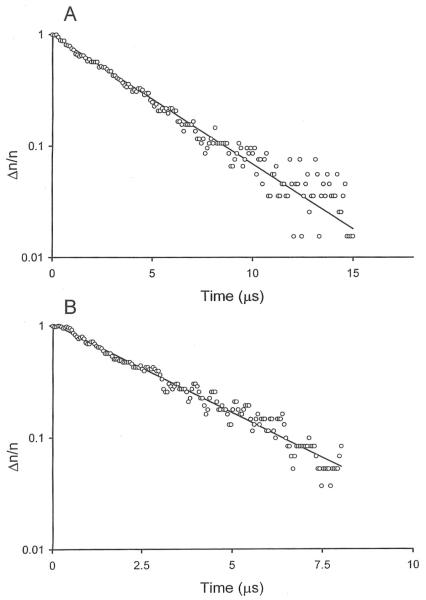
The decay of the birefringence of the 199-bp SV40 fragment in buffers B and F (without and with Mg²⁺ ions, respectively) is illustrated in Figure 1. Monoexponential decay curves were observed in both buffers, as expected for DNA fragments of this size [30]. However, the relaxation times observed in solutions containing Mg²⁺ ions were significantly faster than observed in solutions containing monovalent cations. Similar results were observed for the 207-bp M13 fragment (data not shown).

Figure 1.

Semilogarithmic plots of the dependence of the fractional decay of the birefringence, Δn/n, of the 199-bp SV40 fragment on the time elapsed after removal of the electric field, in μs. A, Decay observed in buffer B, without Mg²⁺ ions, τ = 3.74 μs; B, decay observed in buffer F, containing 0.1 mM Mg²⁺ ions, τ = 2.83 μs.

3.3. Analysis of curvature in the M13 and SV40 restriction fragments

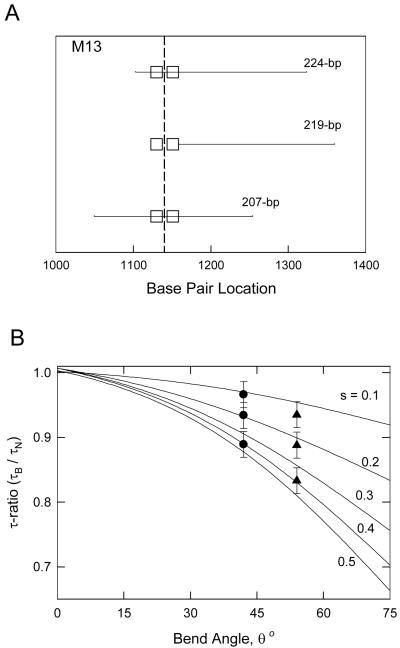
To determine the magnitude of the bend angle in the 207-bp M13 restriction fragment and the location of the bend in the sequence, three overlapping restriction fragments containing 207-, 219- and 224-bp were analyzed. The relationship between the overlapping fragments is indicated schematically in Figure 2A. For ease of reference, the two longest A-tracts in each sequence are indicated by square boxes. Since the three overlapping fragments contained approximately the same number of base pairs, differences in their flexibilities were minimal.

Figure 2.

Overlapping M13 restriction fragments. A, Schematic diagram of the sequences of the overlapping 224-, 219- and 207-bp fragments. The square boxes represent A-tracts in each fragment containing 6 or more contiguous A or T residues. The apparent bend center is indicated by a vertical dashed line. B, Theoretical curves (solid lines) relating τ-ratios to bend angles and the relative distance, s, of the bend from the end of the fragment. (●), Average τ-ratios of the 224-, 219- and 207-bp M13 fragments (from top to bottom) in buffers B and C (without Mg²⁺ ions); (▲), τ-ratios of the same fragments in buffer F, with Mg²⁺ ions.

The τ-ratios obtained for the overlapping M13 restriction fragments are compared with theoretical equations [20] relating the bend angle, θ, to the fractional distance of the bend from one end of the fragment, s. The closed circles represent the average τ-ratios observed for the three fragments in buffers B and C (without Mg²⁺ ions), while the closed triangles represent the τ-ratios observed in buffer F (with Mg²⁺ ions). Only one set of θ and s values gives a constant bend angle at a single sequence location for the three fragments. The analysis indicates that the average bend angle observed in solutions containing monovalent cations is 44° ± 2°, centered at about 1153 ± 2 bp in the Litmus 28 sequence. In buffer F, containing Mg²⁺ ions, the apparent bend angle increases to 56° ± 2°, while the location of the bend center remains essentially constant.

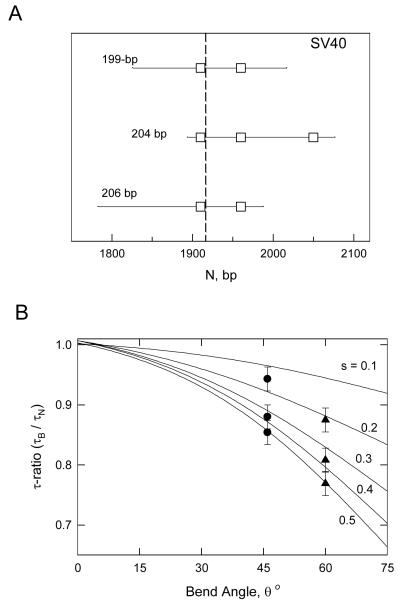
Three overlapping SV40 restriction fragments containing 199-, 204- and 206-bp were analyzed by the same method. The relationship between the overlapping SV40 restriction fragments is indicated schematically in Figure 3A, where the square boxes correspond to A- or T-tracts containing six or more residues. The average τ-ratios observed in buffers B and C (without Mg²⁺ ions) are shown as the solid circles in Figure 3B; the τ-ratios observed in buffer F (with Mg²⁺ ions) are indicated by the solid triangles. A global fit of the τ-ratios with the theoretical curves indicates that the SV40 fragments contain a bend of 46° ± 2°, centered at about 1922 ± 2 bp in the SV40 sequence, in solutions containing monovalent cations. The apparent bend angle increases to 60° ± 2° in solutions containing Mg²⁺ ions. As observed with the M13 fragments, the location of the apparent bend center in the SV40 fragments is independent of whether or not the buffer contains Mg²⁺ ions.

Figure 3.

Overlapping SV40 restriction fragments. A, Schematic diagram of the sequences of the 199-, 204- and 206-bp fragments. The square boxes represent A-tracts in each fragment containing 6 or more A or T residues. The apparent bend center is indicated by a vertical dashed line. B, Theoretical curves (solid lines) relating τ-ratios to bend angles and the relative distance, s, of the bend from the end of the fragment. (●), Average τ-ratios of the 204-, 206- and 199-bp fragments (from top to bottom) in buffers B and C, without Mg²⁺ ions; (▲), τ-ratios of the same fragments in buffer F, with Mg²⁺ ions.

The ~30% increase in the bend angles observed for the M13 and SV40 restriction fragments in solutions containing Mg²⁺ ions is similar to, but somewhat smaller than, the 50% increase in the NMR shape functions (related to the translational diffusion coefficients) observed for small DNA oligomers containing one or two phased A-tracts [31]. However, the present observations were made in solutions containing 0.1 mM Mg²⁺, while the NMR studies were carried out in solutions containing 20mM Mg²⁺. The NMR shape functions suggest that the bend angle increases with increasing [Mg²⁺].

3.4. Curvature modules in the M13 and SV40 restriction fragments

The 40 bp sequence surrounding the apparent bend center in the M13 fragment and the 60-bp sequence surrounding the apparent bend center in the SV40 fragment contain multiple, relatively closely spaced A-tracts, as shown in Scheme 1. These two sequence motifs are called “curvature modules” for brevity, because replacing them with random-sequence DNA eliminates the curvature of the original fragments [22, 23, 25].

Scheme 1.

Top: Litmus 28 sequence from 1128 to 1167 bp, containing the M13 origin of replication. Bottom: SV40 sequence from 1904 to 1964 bp. A- and T-tracts in each sequence containing four or more A or T residues without an intervening TA step are indicated by bold type and underlining. The locations of the apparent bend centers are indicated by double vertical lines.

3.5. Contribution of individual A-tracts in the curvature modules to the overall bend

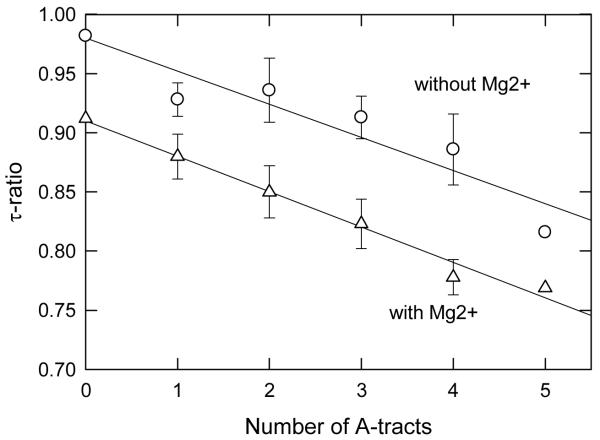
The contribution of the individual A-tracts in the curvature modules to the overall bend was studied in detail for the SV40 fragment by replacing the A-tracts, singly and together, with other sequences. The τ-ratios observed in buffers B and F are plotted in Figure 4 as a function of the number of A-tracts in the curvature module. For clarity, the τ-ratios observed for sequence mutants containing the same number of A-tracts have been averaged; the error bars represent the standard deviation of the individual τ-ratios from the average. The results indicate that the τ-ratios observed in buffers with and without Mg²⁺ ions, and hence the bend angles, decrease linearly as the number of A-tracts in the curvature module decreases. Therefore, the bend is distributed over the entire curvature module and is not localized to a single kink site. Similar results are observed with the M13 curvature module [32].

Figure 4.

Dependence of the τ-ratios observed for SV40 sequence variants containing different numbers of A-tracts in the curvature module on the number of A-tracts. The error bars represent the average τ-ratios observed for sequence variants containing the same number of A-tracts. (○), τ-ratios observed in buffers B and C, without Mg²⁺ ions; and (△), τ-ratios observed in buffer F, with Mg²⁺ ions. The lines were drawn by linear regression (r² = 0.88 for buffers B and C; r² = 0.98 for buffer F).

The relatively large error bars in Figure 4 reflect the fact that the A-tracts in the curvature module contain different numbers of residues and, in addition, are not spaced exactly 10 base pairs apart, in phase with the helix repeat. As a result, different A-tracts contribute differently to the overall bend, depending on the proximity and phasing of the other A-tracts. In particular, the A₄-tract in the center of the SV40 curvature module contributes relatively little to the overall curvature, because it is nearly out-of-phase with the other A-tracts [33]. Hence, this curvature module effectively contains five A-tracts. The average bend angle per A-tract is thus ~9° in solutions containing monovalent cations (46° ÷ 5) and ~12° per A-tract in solutions containing Mg²⁺ ions (60° ÷ 5). Since the M13 curvature module contains four A-tracts, the average bend per A-tract is ~11° in solutions containing monovalent cations (44° ÷ 4) and ~14° in solutions containing Mg²⁺ ions (56° ÷ 4). These values are somewhat smaller than bend angles of 9° to 21°observed per A-tract in synthetic DNA oligomers containing phased A-tracts[7-13], most likely because of the variable phasing of the A-tracts in the M13 and SV40 curvature modules.

3.6. Temperature dependence of curvature with and without Mg²⁺ ions in the solution

The thermal melting temperatures observed by UV absorption for the 207-bp M13 fragment, the 199-bp SV40 fragment and normal controls containing 198- and 208-bp are summarized in Table 2. The melting temperatures of all fragments in buffers B and C (without Mg²⁺ ions) are significantly lower than observed in buffer F (with Mg²⁺ ions), as expected [34]. In addition, the curved fragments melted in a single thermal transition, while the normal fragments usually exhibited two transitions. The two transitions can be attributed to the fact that the left (5’) half of each normal fragment has a significantly different percentage of A+T residues than the right (3’) half, as shown in the last three columns of Table 2. It is well known that DNA melting temperatures decrease with increasing A+T content [34]. By contrast, the curved M13 and SV40 fragments have a relatively uniform percentage of A+T residues across the whole molecule, so they melt in a single thermal transition.

Table 2.

Melting temperatures of curved and normal DNAs in different buffers

DNA	Buffer B	Buffer C	Buffer F	A+T Ratio, %
				Left	Right	Average
Normal 198-bp	53.8, 55.21	58.4, 60.01	84.7, 86.51	34	52	42
Curved 199-bp	47.8	47.5	80.4	62	54	58
Normal 208-bp	53.8, 55.21	54.6	84.2, 86.11	53	38	44
Curved 207-bp	45.7	46.4	77.7	71	61	66

¹Two thermal transitions were observed.

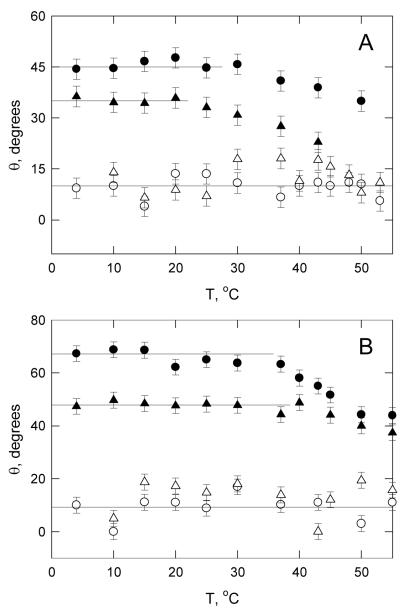
The temperature dependence of the curvature of the M13 and SV40 fragments was determined by measuring the τ-ratios from 4° to 55°C in buffers B and F. For comparison, similar measurements were carried out with the normal 198- and 208-bp fragments. The bend angles were calculated from equation (1), for simplicity. The results are illustrated in Figure 5. The normal 198- and 208-bp fragments exhibited approximately constant bend angles averaging 11° ± 4° in buffer B and 12° ± 5° in buffer F, within the range expected theoretically [35, 36] and observed experimentally [37, 38] for random-sequence wormlike-coil DNA molecules. The constancy of the bend angles of the normal fragments with increasing temperature indicates that the flexibility of DNA is approximately independent of temperature over the indicated range.

Figure 5.

Dependence of the apparent bend angles observed for curved and normal DNAs on temperature. A, buffer B, without Mg²⁺ ions; and B, buffer F, with Mg²⁺ ions. The DNAs are: (○), normal 198-bp fragment; (△), normal 209-bp fragment; (●), curved 199-bp SV40 fragment; (▲), curved 207-bp M13 fragment. The horizontal lines are drawn to guide the eye.

Different results were observed for the M13 and SV40 fragments. The apparent bend angles were constant from 4°C to ~30°C in buffer B (with monovalent cations) and constant to ~40°C in buffer F (with Mg²⁺ ions). At higher temperatures, the apparent bend angles decreased slowly with increasing temperature. Since previous studies have shown that the relaxation times of normal DNA restriction fragments are independent of temperature until the temperature of strand separation is reached [32], the results suggest that the curvature of the M13 and SV40 fragments decreases gradually above a threshold temperature that depends on the type of cation in the solution. Previous studies with DNA oligomers containing phased A-tracts have indicated that A-tract-induced curvature decreases continually with increasing temperature, becoming zero at 37° to 40°C [10, 31, 39, 40]. If this were true for all DNA molecules containing phased A-tracts, A-tract-induced DNA curvature would be irrelevant for biological function. However, the birefringence results obtained here indicate that the M13 and SV40 fragments retain about half their original curvature at 37°C in solutions containing monovalent cations and retain all their curvature at 40°C in solutions containing Mg²⁺ ions. Hence, it seems likely that the close juxtaposition of the A-tracts in the M13 and SV40 curvature modules and/or the variable spacing of the A-tracts leads to greater stabilization of the curvature of the helix backbone.

4. Concluding remarks

The results described here have shown that the M13 and SV40 restriction fragments are stably curved in solution. The bend angles of the two fragments are nearly equal, and increase from ~45° in solutions containing monovalent cations to ~60° in solutions containing Mg²⁺ ions. The bends are delocalized and spread out over 40 to 60 base pair curvature modules containing multiple closely spaced A-tracts. The [Mg²⁺] concentration used in the present studies, 0.1 mM, is close to the basal cytosolic free Mg²⁺ level [41, 42]. Hence, the 60° bend angles observed for the M13 and SV40 fragments in buffer F may be typical of the bends associated with clustered A-tracts in DNA under physiological conditions. The M13 and SV40 fragments remain significantly curved at the biologically important temperature of 37°C, especially when the solution contains Mg²⁺ ions, suggesting that A-tract-induced DNA curvature may contribute importantly to biological function.

The studies described here have also shown that normal, non-A-tract-containing DNA fragments are flexible and exhibit an average bend of ~10°, similar to the values predicted theoretically [35, 36] and observed experimentally using other methods [37, 38]. The average bend angle in the normal fragments is independent of temperature from 4° to 55°C, suggesting that DNA flexibility is relatively constant over this temperature range. Interestingly, this result agrees with early measurements of the persistence length of sonicated bacteriophage DNA, which showed that the persistence length decreased only by ~10% when the temperature was increased from 5° to 49°C [43].