The contribution of entropy, enthalpy, and hydrophobic desolvation to cooperativity in repeat-protein folding

Summary

Cooperativity is a defining feature of protein folding, but its thermodynamic and structural origins are not completely understood. By constructing consensus ankyrin repeat protein arrays that have nearly identical sequences, we quantify cooperativity by resolving stability into intrinsic and interfacial components. Heteronuclear NMR and CD spectroscopy show that these constructs adopt ankyrin repeat structures. Applying a one-dimensional Ising model to a series of constructs chosen to maximize information content in unfolding transitions, we quantify stabilities of the terminal capping repeats, and resolve the effects of denaturant into intrinsic and interfacial components. Reversible thermal denaturation resolves interfacial and intrinsic free energies into enthalpic, entropic, and heat capacity terms. Intrinsic folding is entropically disfavored, whereas interfacial interaction is entropically favored and attends a decrease in heat capacity. These results suggest that helix formation and backbone ordering occurs upon intrinsic folding, whereas hydrophobic desolvation occurs upon interfacial interaction, contributing to cooperativity.

Introduction

Cooperativity is a hallmark of protein folding, involving energetic coupling of elements that are distant in sequence and structure. Despite a long-standing appreciation of the significance of cooperativity in protein folding (Lumry and Biltonen, 1966), experimental studies of cooperativity are typically restricted to a “yes” (the transition is all-or-none) or “no” (the transition has populated intermediates) description. Equilibrium unfolding transitions, induced most often by chemical denaturants or temperature increase are tested for 1) a single, sigmoidal transition that can be fitted with a two-state model, 2) coincidence of transitions measured by different probes, and 3) sensitivity coefficients (m-values for chemical denaturation; ΔC_p and ΔH values for thermal denaturation) that match empirical relations (Myers et al., 1995; Robertson and Murphy, 1997). In favorable cases, van’t Hoff (two-state model-dependent) enthalpies can be compared to calorimetric enthalpies. These approaches have shown all-or-none cooperativity to be common in folding of both globular proteins and in many elongated proteins. However, the underlying structural and thermodynamic mechanisms of cooperativity (i.e., quantitative coupling energies and entropies) have remained elusive.

Substantial insight into the cooperativity of the folding transition has come from a marriage of statistical thermodynamics and simplified structural models and energy functions. Lattice models with native-centric energy functions (Go, 1983; Taketomi et al., 1975) show some features of cooperative folding, suggesting a mismatch between entropy and enthalpy decreases may contribute to a free energy barrier separating the native and denatured states, a suggestion supported using off-lattice models (Oliveberg and Wolynes, 2005; Onuchic et al., 2000; Thirumalai and Hyeon, 2005; Weinkam et al., 2005). These simplified models suggest plausible sources of cooperativity, but cannot quantitatively resolve cooperativity into its energetic and structural components.

Quantitative dissection of protein folding cooperativity requires statistical thermodynamic models that can be used to analyze data directly. Nearest-neighbor, or “Ising” models (Ising, 1925; Poland and Scheraga, 1970) have been a staple for analyzing cooperativity in simple linear systems, including the helix-coil transition (Doig, 2002; Poland and Scheraga, 1970; Zimm, 1960), and magnetization in arrays of spins systems (Ising, 1925; Onsager, 1944). These models represent structure with repeating units, and give conformational energy as a sum of intrinsic stabilities of the units and coupling energies between neighboring units. The magnitude of the interfacial coupling energy, along with the instability of individual units, determines the extent of cooperativity of the system as a whole. Although there has been interest in applying these models to globular proteins (Munoz, 2001), the heterogeneity of globular proteins precludes representation in terms of structural units and their intrinsic and interactions energies.

In the last decade, proteins with regular, repetitive structure have become increasingly popular for studies of protein folding (Kloss et al., 2008) and for application of Ising models (Aksel and Barrick, 2009; Kajander et al., 2005; Mello and Barrick, 2004; Wetzel et al., 2008). Analysis of folding energies of a series of overlapping ankyrin repeat constructs (33 residues each) from the Drosophila Notch receptor indicate that cooperativity results from stabilizing nearest-neighbor interactions that offset intrinsically unstable repeats, although sequence variation among repeats prevents analysis at the single-repeat level.

Recently, several groups have built and analyzed repeat proteins with greatly reduced sequence variation, thereby enabling more exact thermodynamic models of folding (Kajander et al., 2005; Mosavi et al., 2002; Wetzel et al., 2008). Here we use a series ankyrin constructs that have nearly identical repeats to give a complete description of folding thermodynamics. The structure of a three-repeat construct matches the target ankyrin fold. Guanidine hydrochloride (GdnHCl) and thermal denaturation of this series are resolved into intrinsic and interfacial energies, providing a quantitative representation of folding cooperativity. Intrinsic and interfacial energies are further resolved into enthalpic and entropic components, as well as GdnHCl sensitivity and heat capacity terms. Both chain entropy decrease and hydrophobic desolvation play a major role in folding cooperativity, which is enhanced by GdnHCl.

Results

Sequence design

Several laboratories have shown that identical consensus ankyrin repeat proteins (CARPs) require modification of the terminal repeats for high solubility. Pluckthun and coworkers built soluble, folded CARPs using N- and C-terminal caps from GABP-β, a naturally occurring ankyrin repeat protein, (18 and 17 sequence differences between N- and C-terminal caps and internal repeats; (Wetzel et al., 2008)). We obtained soluble CARPs by embedding a different consensus sequence within the ankyrin domain of the Drosophila Notch receptor (Tripp and Barrick, 2007). Here, we sought to maintain solubility of this consensus sequence using single-repeat “caps” that closely match the consensus sequence. This capping strategy resembles that of Peng and coworkers (Mosavi and Peng, 2003), which targeted nonpolar residues on the solvent exposed face of the terminal repeats. We substituted four nonpolar residues each on the N- and C-terminal repeats with charged or polar residues (Table 1).

Table 1.

Ankyrin consensus sequence and variants used in this study.

1

6

11

16

21

26

31

•

•

•

•

•

•

•

Secondary structurea

e

e

e

e

e

e

H

H

H

H

H

H

H

e

e

e

H

H

H

H

H

H

H

H

H

e

e

e

e

e

e

e

e

N-terminal cap (N)

S

K

D

G

N

T

P

L

H

N

A

A

K

N

G

H

A

E

E

V

K

K

L

L

S

K

G

A

D

V

N

A

R

Consensus repeat (R)

S

K

D

G

N

T

P

L

H

L

A

A

K

N

G

H

A

E

I

V

K

L

L

L

A

K

G

A

D

V

N

A

R

Consensus trp-substituted repeat (W)

S

K

D

G

W

T

P

L

H

L

A

A

K

N

G

H

A

E

I

V

K

L

L

L

A

K

G

A

D

V

N

A

R

C-terminal cap (C)

S

K

D

G

N

T

P

E

H

L

A

K

K

N

G

H

H

E

I

V

K

L

L

D

A

K

G

A

D

V

N

A

R

•

•

•

•

•

•

•

1

6

10

16

21

26

31

Sequence substitutions to capping repeats (N and C) and to introduce a tryptophan at position five (N5W) are shown in bold.

^aThe secondary structure, as determined by TALOS+ (Shen et al., 2009) for the central repeat (R) of NRC, is shown along with the numbering scheme used here (H, helix; e, extended). See Figure S5 for cloning procedures

To further minimize sequence differences, we characterized constructs with a single capping repeat, either at the N- or C-terminus. These constructs are essential for resolving stability differences between capping and internal repeats (Aksel and Barrick, 2009). Feasibility of this single-cap approach was suggested from studies of singly capped consensus TPR arrays (Main et al., 2003) and by studies of Notch-consensus fusions (Tripp and Barrick, 2007). To monitor unfolding using fluorescence, we replaced an asn at position 5 with a trp (Table 1, repeat W). In the hidden Markov model on which the ankyrin consensus sequence is based (Finn et al., 2008), this is the most common position for trp.

Solution structure of consensus ankyrin repeat proteins

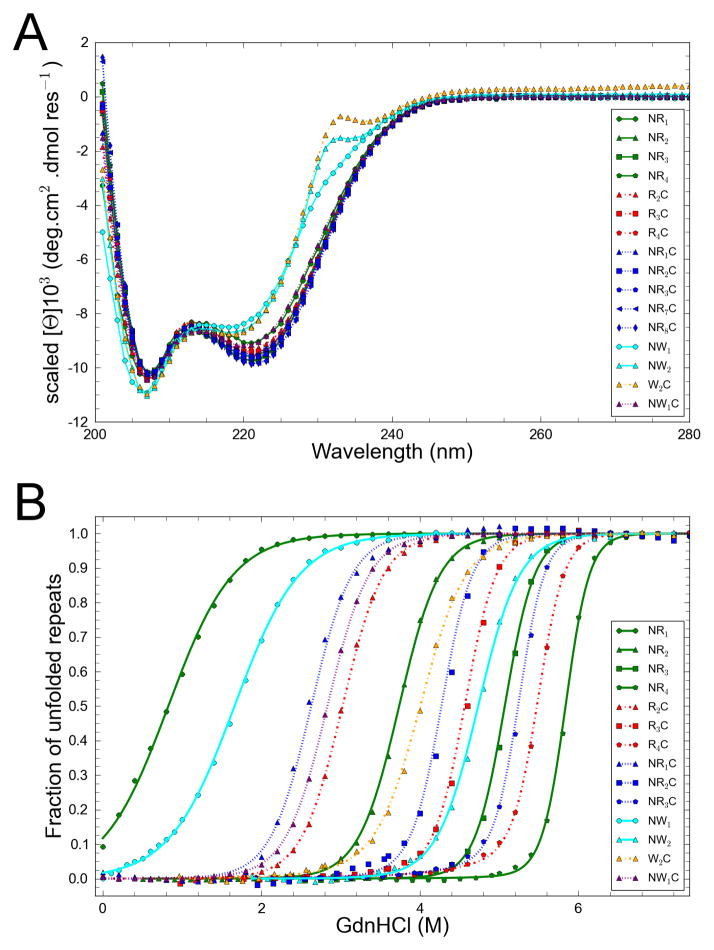
CARPs containing capping repeats at either the N-terminus, the C-terminus expressed to high levels in E. coli, as did doubly capped constructs. Although CARPs partitioned largely to the cell pellet, they could be solublized, purified, and highly concentrated. All constructs have α-helical secondary structure, as judged by far-UV CD spectroscopy (Figure 1A). For constructs lacking trp at consensus position 5, we find only minor differences in molar residue ellipticity from construct to construct. These differences are no larger than prep-to-prep variation, and are likely to result from uncertainties in concentration determination, rather than differences in structure. To compare shapes of CD spectra of different constructs, we scaled spectra from 206–222 nm (Figure 1A). For constructs lacking trp substitutions, spectral shapes are nearly identical, indicating a similar secondary structure content. Constructs with trp at position five show a positive CD feature around 230 nm, likely a result of exciton coupling of the trp side chains. Velocity sedimentation studies indicate that constructs containing N-caps are monomeric to concentrations above 100 μM (Figure S1). For R₄C, we find a weak tendency towards self-association, although at concentrations used here for unfolding studies, only monomeric protein would be populated.

Figure 1. Far UV CD spectra and GdmHCl unfolding transitions of consensus ankyrin repeat proteins.

To compare shape (A), spectra are scaled to the same average intensity as NR₂ from 206–222 nm. Spectra have similar shapes, except for constructs with trp substitution at position 5. (B) GdnHCl titration of CARPs. Constructs are as indicated in the legend. Lines result from global fits of an Ising model the transitions shown here and to two replicate transitions for each construct (not shown). Curves are normalized after fitting by subtracting the fitted baselines. Transitions are independent of concentration over the range studied here (see text and Figure S1). Conditions: 150 mM NaCl, 25 mM Tris-HCl pH 8.0, 20°C.

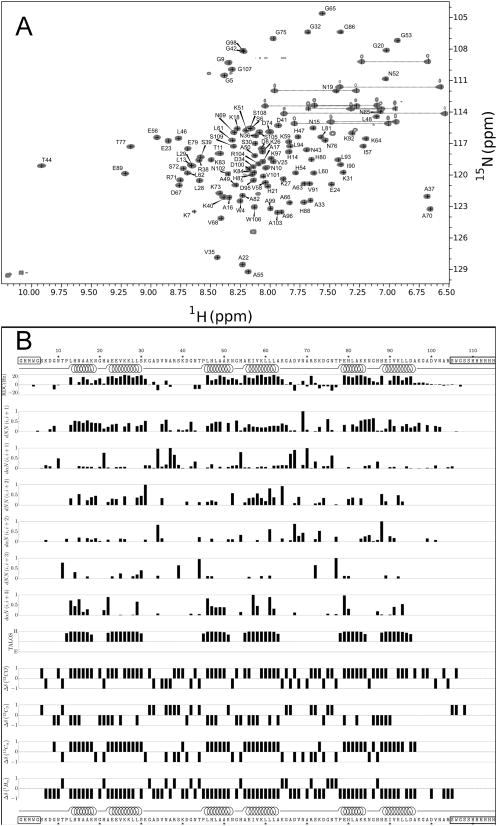
To probe whether these constructs adopt an ankyrin fold, we used NMR to determine the structure of NRC. Although the three repeats have high sequence similarity, the ¹H-¹⁵N-HSQC spectrum of NRC shows high dispersion. 126 cross-peaks can be detected, and almost all are baseline resolved (Figure 2A). This is close to the 135 potential cross-peaks expected from primary sequence (113 non-prolyl backbone NH’s, two trp side chain NH’s, 10 asn side chain NH₂’s).

Figure 2. NMR data for a three-repeat consensus ankyrin protein.

(A) ¹⁵N-¹H HSQC spectrum of uniformly ¹⁵N-labelled NRC at 800 MHz (pH 6.5, 25°C). For examples of strip plots used for assignment, see Figure S2. (B) Amide ¹H-¹⁵N residual dipolar couplings, short- and medium-range NOEs (normalized to the maximum NOE value of each type), predicted secondary structure from TALOS+ (Shen et al., 2009), and chemical shift deviation from random coil-values, calculated using CSI v2.0 (Wishart and Sykes, 1994). Boxed regions of sequence correspond to unstructured regions (horizontal line, Figure 3C). Residues that are helical in the NMR structure, as determined using STRIDE (Heinig and Frishman, 2004), are indicated by spirals.

Using standard 3D NMR methods (Figure S2), we assigned backbone and side-chain ¹⁵N, ¹³C, and ¹H resonances, and measured ¹H-¹H NOE intensities. We could assign 104 backbone NH resonances, including all NH’s in the ankyrin repeats. Consistent with known ankyrin repeat structures, we find two stretches with measurable H(N),H(N)(i,i+1) and Hα,HN(i,i+3) NOEs, positive ¹³C_α and ¹³CO chemical shift deviation, and negative ¹H_α chemical shift deviation in each repeat (Figure 2B). Inputting chemical shifts into TALOS+ (Shen et al., 2009), two helices are predicted in the same position of each repeat, matching helix locations in known ankyrin repeat proteins.

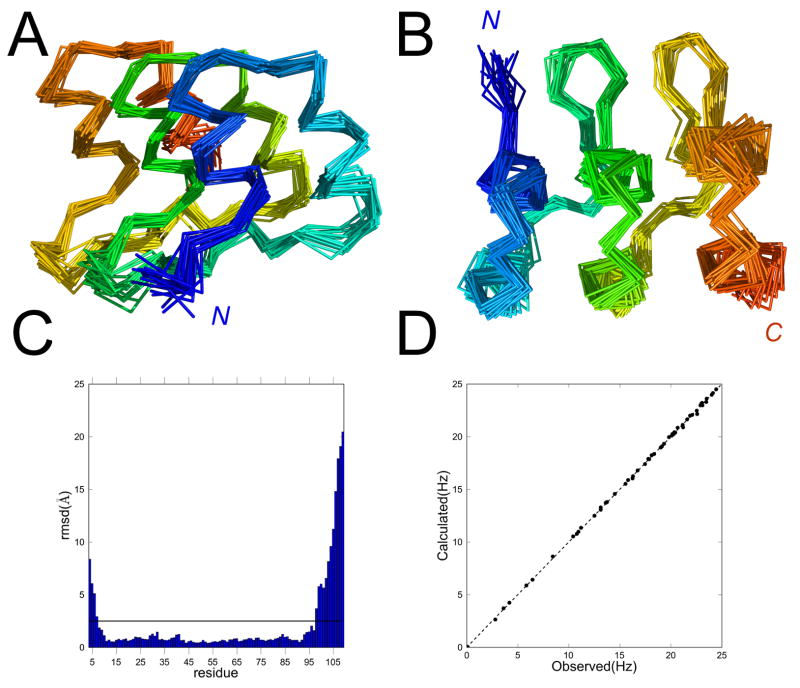
To determine the structure and relative orientations of the ankyrin repeats of NRC, we generated and refined 20 structural models using short- and long-range ¹H-¹H NOEs (Table 2). To help define relative orientations of the helices with respect to the molecular axis, we included residual dipolar couplings (RDCs) from a partly aligned NRC sample at a late stage of structural refinement. Resulting structures superpose well over the helical regions of the three repeats, with an average backbone RMSD of 1.0 Å (Table 2, Figure 3; pdb ID 2L6B). Residues on the N- and C-termini with significantly higher RMSD are not part of the consensus ankyrin sequence, but correspond to cloning sites and the his₆-tag, respectively (Figure 2B). Measured RDC values, which vary significantly throughout the sequence (but show regular periodicity among repeats; Figure 2B), are consistent with the resulting structures (Figure 3D). The solution structure of NRC is very similar to other ankyrin repeat proteins (Figure 3A, B). As designed, the substitutions in the N- and C-terminal caps are solvent exposed, and point away from the central repeat (Figure 3D). Thus, these substitutions are not expected to perturb interaction with neighboring repeats.

Table 2.

NRC NMR solution structure statistics

RMSD statistics		NOE distance constraints
Number of residues	86 (12–97)a	Total	1354
Backbone (Ǻ)	1.00±0.26	Intraresidual (i,i)	327
Heavy atom (Ǻ)	1.92±0.24	Sequential (i,i+1)	358
15N-1H RDC		Short-range (i,i+2)	127
Number of constraints	53	Medium-range (i,i+3)	175
DP = 14.06	| =0.545	Long-range (i,i+j; j ≥ i + 4 )	367

NMR structure calculation is performed using CYANA via the UNIO interface as described in Supplementary Material. The structure statistics are obtained from the ensemble of 20 models generated at the end of 7 successive CYANA runs. N- and C-terminal residues with a low density of NOEs are excluded from RMSD calculations. RDC data were used at a late stage of refinement for further optimization of the models using XPLOR-NIH (Supplementary Material). Axiality (D_P) and rhombicity (|) are calculated from RDC data and the refined structure by XPLOR-NIH.

^aResidue range used for RMSD calculations.

Figure 3. Solution structure of NRC.

(A) Cα-traces of 20 models superposed using backbone atoms from residue 12 to 97. (B) Representative ribbon structure, showing substitution sites in N- and C-terminal caps, and position 5 (asn->trp) of the internal (R) repeat in stick representation. The model shown is the closest (in Cartesian space) to the ensemble average. The middle and right views are from the N- and C-termini respectively. (C) Backbone RMSD of the twenty structures in the ensemble. The horizontal line shows the deviation (2.5 Ǻ) selected as a cutoff for structural superposition (panels A, B) and analysis (Table 2). (D) Calculated RDC values (averaged from the final structural models) agree well with measured RDC values. Structures are rendered using PyMOL (DeLano, 2003).

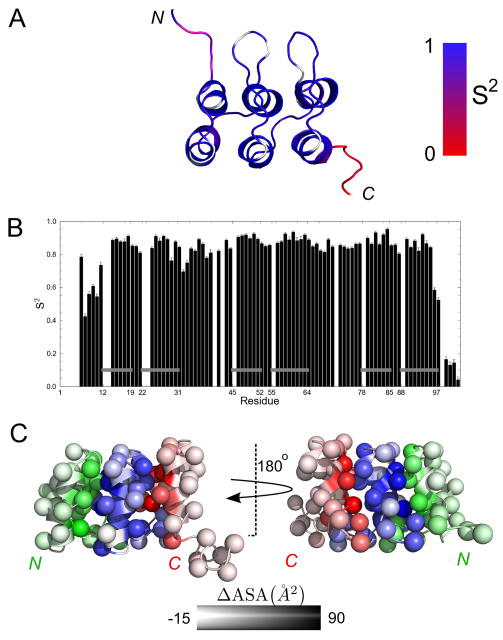
To assess dynamic flexibility, we measured R₁ and R₂ values for backbone ¹⁵N nuclei, and quantified ¹⁵N-¹H NOE intensities. Data were analyzed using ModelFree, and local (residue by residue) motional models were selected based on comparison of χ² values, assuming an F-distribution (Mandel et al., 1995). We find uniformly low dynamic motion (high order parameter, S²) extending from the start of the first helix of the N-cap through the last helix of the C-cap (Figure 4). This includes the two extended recognition loops that connect adjacent repeats (N to R and R to C). The observation that these loops are well-ordered in an unbound state (and in a construct defined only by consensus information) suggests that this important recognition element can be rigid on the ps-ns time scale, as was observed in p19^INK4d (five repeats; (Renner et al., 1998)). The increased motion seen in the binding loops of IκBα (six repeats; (Cervantes et al., 2009)) may reflect the greater overall dynamics seen in the unbound state of that particular protein. Not surprisingly, the terminal regions of NRC, which show higher backbone RMSD values, show significantly lower S² values, i.e., significantly higher conformational dynamics on the psec-nsec timescale.

Figure 4. Backbone dynamics of NRC.

(A) Residues in a representative ribbon structure (Figure 3) are coded according to an order parameter S² (see text and Table S1). White regions correspond to prolyl residues or to residues that could not be assigned to any local model by the modelfree approach (Mandel et al., 1995). (B) S² values as a function of sequence. Gray horizontal bars correspond to α-helices. (C) Apolar surface area burial upon formation of interfaces between repeats. For clarity, side chains are represented by spheres centered at C_®. N-cap, R and C-cap repeats are colored by green, blue and red respectively. Degree of burial is depicted by color intensity. Burial of interfacial surface area is calculated by subtracting the solvent accessible surface area of the NRC NMR structures from N-cap, R, and C-cap fragments (excised from NRC). Values represent the average from all 20 structures in our ensemble.

Guanidine hydrochloride induced unfolding transitions of consensus ankyrin repeat proteins

To measure CARP stability, the effects of the N- and C-terminal capping substitution, and to resolve stability into intrinsic and nearest-neighbor interaction energies using an Ising model, we monitored GdnHCl-induced unfolding using CD spectroscopy. We have measured unfolding curves on four different series of CARPS of different lengths. One series includes only N-terminal caps (NR to NR₄; two to five repeats, respectively), a second includes only C-terminal caps (R₂C to R₄C, three to five repeats), and a third includes both N- and C-terminal caps (NRC to NR₃C, three to five repeats). In addition, a fourth series includes one or more trp-substituted consensus repeats with different capping configurations (NW, NW₂, W₂C, NWC). For R₄C, which shows weak self-association by AUC, unfolding transitions are independent of concentration from 0.6 to 12 μM (Figure S1).

Several general trends emerge from the GdnHCl unfolding transitions (Figure 1B). 1) All constructs unfold with a single sigmoidal transition. 2) Within each series, stability increases with repeat number, as seen by increases in the GdnHCl unfolding midpoint. 3) The steepness of the transition increases with increasing repeat number. 4) Comparing constructs of the same length but different end repeats shows capping repeats to contribute less to stability than internal consensus repeats. 5) Of the two caps, the C-terminal caps are least stabilizing, as was seen by (Yu et al., 2006). 6) Trp substitution at position five is stabilizing; this unexpected stability enhancement permits a full unfolding transition to be observed for a two-repeat construct (NW), which strongly constrains the fitted values of intrinsic versus interfacial denaturant dependence in the Ising analysis (see below).

Ising analysis of GdnHCl induced unfolding transitions

To determine the intrinsic and nearest-neighbor interaction free energies, we globally fitted an Ising model to the CARP unfolding transitions in Figure 1B (solid lines). The fitted model includes independent intrinsic folding energy parameters for the N-cap, C-cap, internal consensus repeats, and trp-substituted (W) consensus repeats (ΔG_N, ΔG_C, ΔG_R, ΔG_W). Since substitutions to the N- and C-caps point away from neighboring (R) repeats (Figure 3B), we use a single interfacial energy for interaction of N, R, and C repeats (ΔG_i,i+1; for algebraic reasons, changes in cap stability cannot be resolved into intrinsic vs. interfacial terms, see Equations S2–S3). However, we expect that substitution of trp at position five may alter contacts with adjacent repeats. Thus, we included separate interfacial energies for W repeats (Table 3).

Table 3.

Parameters obtained from GdnHCl titration data at pH 8, 20°C.

ΔGN	ΔGR	ΔGW	ΔGC	mi
6.13±0.17	5.24±0.17	3.40±0.12	7.75±0.19	0.58±0.03
ΔGR-R	ΔGW-W	ΔGN-W	ΔGW-C	mi,i+1
−12.54±0.27	−11.77±0.20	−11.89±0.23	−11.81±0.24	0.27±0.05

Free energies and m-values are in kcal mol⁻¹ and kcal mol⁻¹ M⁻¹ respectively. Confidence intervals (at the 95 percent level) are obtained by bootstrap analysis (1,000 iterations), assuming parameter uncertainties to be normally distributed. The intrinsic free energy is represented as ΔG_X, where X indicates the type of repeat (N, R, W, C; see Figure 1 legend). The free energy of the interface between the repeats X-Y is represented as ΔG_X-Y. Denaturant effects are modeled with a single intrinsic m-value (m_i), and a single interfacial m-value (m_i,i+1), regardless of the repeat sequence (N,R,W,C).

We model the GdnHCl dependence of stability with two independent terms affecting intrinsic (m_i) and interfacial stability (m_i,i+1). We assume m_i and m_i,i+1 to be independent of repeat identity (N, R, W, C). In our initial fitting studies of constructs that contained only combinations of repeats N, R, and C (i.e., no W repeats), we found m_i and m_i,i+1 to have a strong inverse correlation, and thus were poorly resolved in the fit. This is because the number of repeats is directly correlated with the number of interfaces, although the two values are offset (i.e., repeats=interfaces+1). Including W repeats (and the NW construct, with only one interface for two repeats) decreases the correlation between m_i and m_i,i+1. The fitted free energies of N, R, and C repeats change very little when W repeats are excluded from the fit (not shown), indicating that this additional level of parameterization does not compromise fitted free energy values.

The Ising model can be well-fitted to the GdnHCl unfolding transitions with 10 globally shared thermodynamic parameters (Table 3) fitted to fourteen well-resolved curves from different constructs (in triplicate), in addition to local baseline parameters for each construct. Uncertainties in fitted parameters were estimated by bootstrap analysis of residuals at the 95% confidence level (Aksel and Barrick, 2009). Uncertainties in fitted free energies are typically quite low (0.1 to 0.3 kcal/mol, less than 3% of the total parameter value). Uncertainties in fitted m-values are somewhat larger (5 and 18% of the total parameter value for m_i and m_i,i+1, respectively), but are still low enough to provide insight into the origin of the GdnHCl dependence.

The fitted free energies for intrinsic folding and interfacial interaction are consistent with a high level of global cooperativity observed in the unfolding transitions. The interfacial interactions are all very stabilizing, ranging from −11.5 to −12.5 kcal/mol per interface, in the absence of denaturant and at 20 °C, pH 8.0. This strong favorable interaction is offset by an unfavorable intrinsic folding energy, ranging from +3.5 to +7.5 kcal/mol per repeat. This partitioning of free energies rarifies partly folded states: single folded repeats are strongly disfavored, but when one or more repeats are folded, the folding and subsequent interfacial interaction of nearest-neighbor repeats (with favorable free energy +5.5 −12 = −6.5 kcal/mol) drives the reaction towards the fully folded state.

As described above, variation in repeat identities allow us to quantify differences in stability between N- and C-terminal capping repeats, and between R and W repeats. Modeled as intrinsic stability differences, the C-terminal capping repeat has the lowest stability of all the repeats, with an intrinsic folding free energy 2.5 kcal/mol higher than the consensus R repeat (Table 3). The N-terminal capping repeat has an intrinsic folding free energy in between the C and R repeats. In contrast, the W repeat is more stabilizing than the consensus R repeat by ~1.8 kcal/mol, although interfaces between W repeats are modestly less stabilizing than those between R repeats (0.6 to 0.8 kcal/mol).

Taking advantage of the constraint provided by W-containing constructs, we find the denaturant sensitivity of intrinsic folding to be twice that of interfacial interaction (Table 3). This observation is consistent with burial of polar backbone surface area in intrinsic folding, which would be expected if the α-helices became ordered in this step. The nonzero interfacial m-value may result from a solublizing effect of GdnHCl on the interfaces, but also likely result from the fact that not all thirty-three residues of each terminal repeat are folded (Figure 3). Adding a new repeat to the N- or C-terminus of a folded cluster of repeats would promote folding of the last few residues at the old end of the cluster; the denaturant sensitivity of this coupled folding would show up in the nearest-neighbor term (m_i,i+1).

Thermal unfolding of consensus ankyrin repeat proteins

With the goal of resolving the free energies of intrinsic folding and interfacial interaction into enthalpy, entropy, and heat capacity changes, we sought conditions in which we could measure complete, reversible thermal unfolding transitions. Although thermal transitions were neither complete nor fully reversible at pH 8.0, we found that we could obtain full reversibility at pH 5, and by adding low concentrations of GdnHCl (<1.2 M), we could obtain complete unfolding transitions (Figure S3).

Because of the variable amounts of GdnHCl at pH 5.0, Ising analysis of CARP thermal unfolding required both thermal unfolding parameters (ΔH, ΔS, and ΔC_p; parameters of primary interest here) and GdmHCl sensitivities, both for interfacial and intrinsic interactions. In addition, cross-terms are needed to describe the effect of GdnHCl on thermal denaturation. We modeled this coupling as a linear dependence of free energy, entropy, and heat capacity on GdnHCl (Nicholson and Scholtz, 1996). A linear urea dependence for heat capacity of unfolding of the Notch ankyrin domain has been observed (Zweifel and Barrick, 2002). To better determine the effects of GdnHCl on thermal unfolding parameters, we supplemented the pH 5.0 thermal transitions (Figure 5A) with GdnHCl unfolding transitions at different temperatures (Figure 5B). Both the thermal- and GdnHCl-induced unfolding transitions were fitted globally (64 curves total) with an Ising model (Figure 5; Table 4). To further constrain the cross-terms, we fixed the relative GdnHCl sensitivities of intrinsic folding and interfacial interaction to the value found at pH 8.0, 20°C (m_i,i+1/m_i=0.5), and also at extreme values ranging from an entirely intrinsic to a largely interfacial GdnHCl effect. We find slightly better fits when the GdnHCl effect is intrinsic, but for the most part, the data are well-fitted for all ratios explored.

Figure 5. Temperature dependence of consensus ankyrin repeat unfolding.

(A) Thermal denaturation of CARPs in varying amounts of guanidine hydrochloride (see legend). (B) GdnHCl titrations at different temperatures. Lines result from global fits, with m_i,i+1/m_i=0.5. For each construct (legend) there are eight GdnHCl titrations performed at 5, 10, 15, 20, 25, 30, 35 and 40°C (increasing color from 5 to 40°C). (C) Three dimensional representation of the temperature and GdnHCl dependence of CARP folding. Curves in (A) and (B) and surfaces in (C) result global Ising analysis as a function of temperature and GdnHCl, with m_i,i+1/m_i=0.5. Surfaces in (C) are, from left to right, NR₂, NR₂C, R₃C, NR₃, NR₃C, R₄C, NR₄. Conditions: 150mM NaCl, 25 mM NaOAc, pH 5.0. To compare reversibility and structure at pH 8.0 and 5.0, see Figure S3.

Table 4.

Parameters from temperature dependence studies of consensus ankyrins at pH 5, 20°C.

	mi,i+1/mi=0	mi,i+1/mi=0.5a	mi,i+1/mi=1	mi,i+1/mi=10	SASA based energiesb
					Desolvation	Conformational
ΔGN	6.86±0.06	7.33±0.06	7.59±0.06	8.35±0.07	8.4±0.1
ΔGR	6.02±0.05	6.50±0.05	6.76±0.06	7.52±0.07	10.9±0.1
ΔGC	8.52±0.06	9.00±0.07	9.27±0.07	10.05±0.11	10.7±0.1
ΔGi,i+1	−10.66±0.11	−11.28±0.10	−11.64±0.11	−12.65±0.12	−12.1±0.1
ΔSi	−41.6±4.9	−41.0±5.2	−40.2±5.4	−38.8±5.9	54±0.6	−121±0.3
ΔSi,i+1	56.0±7.1	55.1±7.4	53.9±7.7	51.9±8.4	125±0.6	−67±0.3
ΔCp;i	−51±71	23±73	60±82	191±95	−113±5.6
ΔCp;i,i+1	−330±102	−420±104	−470±117	−640±135	−379±5.6
mi	1.01±0.01	0.73±0.01	0.57±0.00	0.12±0.00	NA
$m_i^S$	2.1±0.5	1.6±0.3	1.3±0.3	0.3±0.1	NA
$m_i^C$	−50±8	−38±6	−30±5	−6±1	NA
I2	8.11×10−5	8.75×10−5	9.31×10−5	11.70×10−5	NA

Free energies are in kcal•mol⁻¹; entropies and heat capacities are in cal•mol⁻¹•K⁻¹; m-values are in kcal•mol⁻¹•M⁻¹; $m_i^S$ and $m_i^C$ are in cal•mol⁻¹•M⁻¹•K. In each column, the m_i,i+1/m_i ratio has been fixed to the indicated value to better constrain the fit. Confidence intervals are the results of 5,000 iterations of bootstrap analysis as described in Table 4. For population plots based on fitted parameters, see Figure S4.

For all m_i,i+1/m_i ratios explored, we find the entropy/enthalpy decomposition of the intrinsic folding energy to be opposite to that of the interfacial interaction energy (Table 4). Folding of individual repeats is enthalpically unfavorable but entropically favorable, with entropy making the larger contribution, resulting in an unfavorable intrinsic folding free energy. In contrast, the interfacial interaction is enthalpically unfavorable at 20°C, but it is highly stabilized entropically. The heat capacity decrement (ΔC_p, which is negative for protein folding) is partitioned entirely into the interfacial interaction: within the bootstrap error, intrinsic folding of a single repeat has no heat capacity change (Table 4).

Discussion

The motivations of the present study are to better understand cooperativity in protein folding. We measure local and long-range coupling free energy, and decompose each term into enthalpy, entropy, heat capacity, and denaturant sensitivity. These parameters, provide insight into bonding (ΔH), configurational restriction (ΔS), hydrophobic solvation (ΔC_p, along with ΔH and ΔS compensation (Prabhu and Sharp, 2005)), and burial of surface area (m-value).

Owing to their linear, repetitive architecture, the stability of repeat proteins and their high folding cooperativity can be described using a one-dimensional nearest-neighbor Ising model (Kajander et al., 2005; Mello and Barrick, 2004; Wetzel et al., 2008). In contrast to the simple systems traditionally analyzed with the Ising formalism, repeat proteins comprise all of the structural elements found in globular proteins, including hydrogen bonded secondary structure (helix, turn, and sheet, depending on the type of repeat), burial and packing of nonpolar side chains, and charge interactions among surface groups (Kloss et al., 2008), and thus have direct relevance to non-repeat (globular) proteins. In contrast to natural sequence-variable repeat proteins, synthetic repeat proteins with identical repeats can be represented with a limited set of parameters, decreasing the number of unknowns that must be extracted from experimental data. For a “homopolymer” with identical repeats, just two sets of parameters are needed (ΔG_i and ΔG_i,i+1, along with associated denaturant and thermal parameters). Because a repeat protein array of n repeats has n−1 interfaces, ΔG_i and ΔG_i,i+1 can be resolved by comparing the stabilities of a small number of constructs of different length (in principal, as few as two). However, the need to substitute polar residues on the termini to provide solubility introduces additional parameters, and thus, additional unknowns. Experimental resolution of these additional unknowns is facilitated by inclusion of constructs that lack one or the other capping repeat. This can be seen by representing constructs of different lengths as a system of linear equations (Equation S1; (Aksel and Barrick, 2009)).

Free energies of intrinsic folding, interfacial interaction, and global cooperativity

Comparing the free energies of intrinsic folding and interfacial interaction provides a unique means to quantify cooperativity in protein folding. High cooperativity should result both favorable interfacial interactions and unfavorable intrinsic folding. We find both of these conditions to be met: at pH 8.0 and 5.0, interfacial interaction free energies to be stabilizing by 11–12.5 kcal/mol, whereas intrinsic folding free energies are +4 to +8 kcal/mol, depending on pH and repeat identity.

One way to represent these two components of cooperativity as a difference, or “mismatch”. The energy mismatch here (intrinsic minus interfacial) is around 15–17 kcal per mol per repeat, which are reasonably close the mismatch determined by Pluckthun et al. for an array of capped consensus ankyrin repeats (17.5 to 13.7 kcal/mol; (Wetzel et al., 2008)). This mismatch is consistent with the high level of cooperativity observed experimentally. This mismatch is significantly larger than that observed in an experimental study of consensus TPR unfolding (Kajander et al., 2005). Like ankyrin repeats, TPR repeats have two antiparallel helices, although the sequence, helix lengths, turn structures, and interhelical geometries differ considerably. On a single-helix level, the intrinsic/interfacial energy mismatch is only 6.8 kcal/mol (+2.3 and −4.5 kcal/mol for intrinsic folding and interfacial interaction, respectively (Kajander et al., 2005).

Effects of sequence and pH variation on intrinsic and interfacial stability

Both at pH 8 and pH 5, ΔG_R<ΔG_N<ΔG_C, spanning a range of 2.5 kcal/mol (Tables 3, 4). Thus, our cap substitution decreases stability. Although we cannot analytically resolve these capping effects into intrinsic versus interfacial terms (equations S2–S3), we can resolve the intrinsic versus interfacial effects of trp substitution at position five. The stabilization seen by W repeats results from a decrease in intrinsic folding free energy by ~1.8 kcal/mol per repeat, which is modestly offset by a slight increase in interfacial interaction energy (0.7 kcal/mol; Table 3).

The decrease in stability seen as the pH is lowered from 8 to 5 results primarily from an increase in the interfacial interaction energy (+1.9 kcal/mol; Tables 3, 4). There is a smaller, uniform increase in the intrinsic folding free energy (0.73, 0.78, and 0.77 kcal/mol for the N, R, and C repeats). Since the effect of pH in this range is likely to be linked to histidine ionization (two per N, R repeat; three in the C repeat), we expect the charged form of one or both histidines to weaken interactions between repeats, perhaps through electrostatic repulsion among these basic repeats (predicted pI of 9.52 for R).

Resolution of cooperativity into entropy, enthalpy, and heat capacity terms

The observation that intrinsic folding is entropically unfavorable (Table 4) suggests a loss of backbone configurational degrees of freedom. Along with a compensating favorable enthalpy change (Table 4), a significant unfavorable GdnHCl term (Table 3) suggests formation of native α-helical structure in the intrinsic folding step. Thermodynamic studies of monomeric α-helices have shown helix formation to be enthalpically favorable, entropically unfavorable (Scholtz et al., 1991), and destabilized by GdnHCl (Smith and Scholtz, 1996).

The observation that interfacial interaction is entropically favorable but enthalpically unfavorable at low temperature (20°C) suggests a decrease in solvation of nonpolar groups. Hydrophobic desolvation at low temperature is favored by a large entropy increase that is partly offset by an enthalpy increase (Baldwin, 1986; Privalov and Gill, 1988). A hallmark of the hydrophobic effect is a large decrease in heat capacity upon desolvation. The observation that the ΔC_p decrease seen for CARP folding is partitioned entirely into interfacial interaction suggests that hydrophobic groups are desolvated in this second step. The NMR structure of NRC shows substantial burial of nonpolar surface area between adjacent repeats (Figure 4C).

The interfacial interaction parameter provides long-rage coupling and is critical for cooperative folding. The experimentally observed partitioning of hydrophobic desolvation into the interfacial interaction step indicates that hydrophobicity makes an important contribution to cooperativity in protein folding. However, we expect the interface formation to involve close packing, in addition to hydrophobic desolvation. Like nonpolar desolvation, interfacial packing is likely to involve long-range contacts distributed over many residues, consistent with cooperativity. In molten globule states of proteins, in which nonpolar surfaces are desolvated in the absence of rigid packing interactions, folding cooperativity is decreased. Simulation suggests that both hydrophobic desolvation and packing may contribute to cooperativity in folding (Kaya and Chan, 2003; Liu and Chan, 2005).

Using the NMR structure of NRC as a template, we generated structural model for longer constructs, and used these models to estimate solvent-accessible surface-area (SASA) based ΔH, ΔS, and ΔC_p values for unfolding (Hilser et al., 2006). Assuming linear additivity of intrinsic and interfacial terms, we resolved these energy terms into intrinsic and interfacial components (Table 4). The resulting SASA based terms agree surprisingly well with experimental values. Most notably, intrinsic folding is entropically unfavorable, due in large part to conformational entropy decrease, whereas interfacial interaction is entropically driven, due largely favorable desolvation. Also consistent with our findings, the heat capacity decrement is largely interfacial (Table 4).

Free energy landscapes with entropic and enthalpic resolution

Using the fitted energy terms from Ising analysis (Table 3), folding free energy landscapes can be depicted in quantitative detail (Mello and Barrick, 2004; Tripp and Barrick, 2008; Wetzel et al., 2008). The free energy landscape for NR₃C is shown in Figure 6A. Because the N- and C-terminal caps are less stable than the internal consensus repeats, partly folded conformations involving the central repeats have lower energy than conformations with structured termini, imparting a slightly concave shape from left to right. As with other repeat proteins analyzed in this way (Kloss et al., 2008; Mello and Barrick, 2004), favorable interfacial interactions tip the landscape towards the native state, once folding advances from a high energy point involving a single folded repeat.

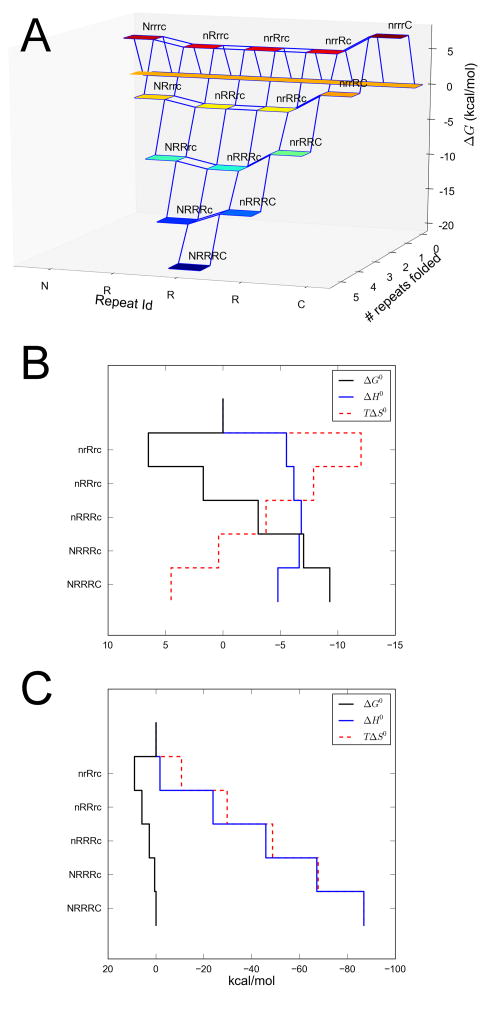
Figure 6. Folding free energy landscape of NR₃C.

(A) Colored squares correspond to partially folded microstates. Folded and unfolded repeats are indicated using upper and lower case, respectively (e.g., nrRRC has the N-cap and first R repeat unfolded, the last three repeats folded). Energies are calculated at 20°C in the absence of GdnHCl. (B, C) Free energy, entropy, and enthalpy versus extent of folding (vertical). At low temperature (20 °C; panel B), structuring the first repeat is unfavorable because it is entropically costly. When subsequent repeats are added, the array becomes stabilized, largely as a result of a favorable energy increase from interfacial pairing, but also because of a modest enthalpy decrease. At high temperature (T_m=84°C; panel C), enthalpy and entropy compensate one another. This compensation is imperfect, such that the first repeats to fold are entropically destabilized more than they are enthalpically stabilized, rarifying partly folded states.

Decomposition of the intrinsic and interfacial terms into entropy, enthalpy, and heat capacity provides a more fundamental description of the progress of folding (Figure 6B, C). At 20°C, the folding enthalpy decreases (becomes more negative, relative to the unfolded state) as folding progresses (Figure 6B). This enthalpy decrease is substantial in the first step (folding a single repeat) but is smaller in subsequent steps of folding (folding paired with interaction with a structured neighbor). Overall, the reaction is enthalpy driven, but this drive comes largely from the first step (at 20°C, the last steps are enthalpically opposed as a result of cap substitutions). With the exception of the first step, where entropy strongly opposes folding, entropy increases with each folding/interface formation step. Thus, although there is an early entropy bottleneck at low temperature, folding is driven by entropy increase (Figure 6B) from solvent displacement from the interface.

Because of the large heat capacity decrease upon folding, this picture changes at higher temperatures. At 84°C, the T_m for NR₃C (Figure 6C), entropy and enthalpy compensate one another. In the first step in folding, a destabilizing entropy decrease exceeds a stabilizing enthalpy decrease. As before, folding of a single repeat is disfavored. In subsequent steps, the enthalpy decrease is greater (more stabilizing) than the entropy decrease, decreasing the overall free energy. This higher temperature picture is equivalent to analysis of funneled models for folding at T_f, and as predicted, imperfect enthalpy-entropy compensation gives rise to a cooperative two-state folding as a result of an entropy barrier (Go, 1983; Oliveberg and Wolynes, 2005; Onuchic et al., 2000; Taketomi et al., 1975; Thirumalai and Hyeon, 2005).

Although the current study is, to our knowledge, the first experimental decomposition of intrinsica and interfacial ΔH, ΔS, and ΔC_p values for repeat protein folding, a simulation using a Go model of consensus TPR unfolding has been analyzed using an Ising-type framework (Ferreiro et al., 2008). Like the present study at high temperature, this simulation suggested intrinsic folding to be entropically opposed but enthalpically favored, although the lack of solvent in the simulation precludes detailed comparison. The interfacial interaction energy was only modeled to involve an enthalpic component (Ferreiro et al., 2008); whether the large interfacial entropy change identified here is specific to ankyrin versus TPR repeats, or simply reflects the lack of solvent in the simulations, remains to be seen.

The effect of denaturant on cooperativity

Although the free energy mismatch described above is consistent with high cooperativity in the absence of denaturant, GdnHCl could diminish cooperativity if its effect was interfacial. In contrast, we find the fitted m_i-value is to be twice the m_i,i+1-value (Table 3), suggesting a further enhancement of cooperativity by GdnHCl in the transition region. GdnHCl preferentially destabilizes isolated folded repeats and, to a lesser extent, small clusters of folded repeats, which have higher repeat/interface ratios than fully folded CARPs.

To further explore the extent of cooperativity through the GdnHCl unfolding transition, we used fitted Ising parameters to calculate the populations of partly folded states as a function of GdnHCl concentration (Figure S4). Although similar plots have been made for denaturant-induced unfolding of other repeat protein arrays (Mello and Barrick, 2004; Wetzel et al., 2008), the analysis here is based on an experimentally determined partitioning of the denaturant dependence into intrinsic and interfacial stability. We find that for short constructs (three to five repeats), fully folded and unfolded conformations dominate, with populations of partly folded states remaining below 20 percent (Figure S4). However, for longer constructs, partly folded states populate significantly through the transition, and are dominated by species with one or both caps unfolded (in particular, the C-terminal cap; Figure S4). These partly folded states are formed, in part, as a result of the higher intrinsic instability of the capping repeats (Table 3), as is seen in the highly destabilized C-terminal cap of Pluckthun et al. (Yu et al., 2006).

Because of this end-fraying, the unfolding transitions of longer constructs are predicted to show a broad pre-transition around 5–6 M GdmHCl, followed by a sharp transition at higher GdmHCl. To test this prediction, we made consensus ankyrin repeat proteins containing 9 and 10 repeats (NR₇C and NR₈C) and monitored unfolding by GdnHCl titration. These longer constructs unfold extremely slowly, making equilibration difficult. By equilibrating samples for two days (Experimental Procedures), we were able to obtain unfolding curves quite close to equilibrium (Figure S4). As predicted from the Ising model, these curves show a pre-transition from 5–6 M, followed by a sharp transition of greater amplitude. The minor differences (~0.2 M) between the midpoints of the major predicted and observed transitions may result from small errors in the fitted parameters, although we suspect incomplete equilibration to be a more likely contributor.

Although the methods used here to quantify the local and long-range interactions cannot be directly applied to globular proteins, the parameters determined here provide insight into globular protein stability. Partly folded structures of globular proteins that retain a subset of local interactions (e.g., secondary structures) will lose a disproportionate number of long-range interactions, even more than for the CARP substructures described here. Given the strong stabilizing long-range interactions found here, this would disproportionately destabilize partly folded structures. Native-state hydrogen exchange (NSHX) on globular proteins identifies such a stability gap between the native and partly unfolded states (intercepts in Figure 5 of (Englander et al., 2002)). This gap is critical for the observation, based on NSHX studies, that unfolding is highly cooperative through the GdnHCl transition despite a manifold of partly folded states with lower free energy than the denatured state (Englander et al., 2002).

Experimental Procedures

Cloning, expression and purification

CARP arrays were cloned as described in supplemental material (Figure S5). CARPS were expressed in BL21(DE3), and were purified as described in supplemental material.

Circular dichroism spectroscopy

All CD measurements were done using AVIV Model 400 CD spectrometer (Aviv Associates, Lakewood, NJ). Far UV CD spectra were collected using a 1 mm pathlength quartz cuvette; protein concentrations ranged from 20 to 60 μM depending on construct size. At least three wavelength scans with 1 nm step-size and 5 second averaging time were combined.

GdnHCl induced unfolding transitions at pH 8.0

GdnHCl induced unfolding titrations were obtained using a Hamilton 500 titrator (Reno, NV), and were monitored by CD at 222 nm. Protein concentration ranged from 2 to 6 μM. Measurements were made in a silanized 1 cm quartz cuvette. Signal was averaged for 30 seconds at each step. To ensure full equilibration, a delay of several times the relaxation time (or a minimum of 180 seconds to ensure mixing) was introduced between GdnHCl injection and data acquisition. For NR₇C and NR₈C, relaxation times were too long for automated titration. Instead, individual samples–were equilibrated at 20°C for two days prior to measurement.

To determine ΔG_i, ΔG_i,i+1, m_i, and m_i,i+1, unfolding transitions of CARPS of different length and sequence composition were fitted globally to a heteropolymer Ising model using Isingbul, an in-house program for nearest neighbor analysis of protein denaturation data (Aksel and Barrick, in preparation). Confidence intervals were determined at the 95% level by bootstrapping the residuals (see Aksel and Barrick, 2009).

Thermal and GdnHCl induced unfolding transitions at pH 5.0

Simple thermal denaturation experiments were performed in 1°C steps. For combined thermal/GdnHCl denaturation experiments, a single automated GdnHCl titration was generated in which the temperature was scanned (5°C increments) at each GdnHCl step. Equilibration times were decreased to minimize diffusion from the titrator tubing. Thermal melts were jointly fitted with GdnHCl melts at different temperatures using Isingbul, with a model that assumes that ΔG, ΔS, and ΔC_p vary linearly with GdnHCl (see Supplementary Material).

NMR spectroscpy

¹⁵N- and ¹⁵N,¹³C-labeled NRC was expressed and purified as described above, using M9 minimal media supplemented with ¹⁵NH₄Cl and ¹³C-labeled glucose (Cambridge Isotope Laboratories; Andover, MA). Unless otherwise noted, NMR samples contained 2 mM NRC, 25 mM NaCl, 25 mM Na₂HPO₄, 5% D₂O, pH 6.5. This pH maximized the number of well-resolved peaks in the ¹H,¹⁵N-HSQC spectrum, presumably by decreasing exchange-broadening of labile amide protons. For ¹³C-edited 3D NOESY-HSQC experiments, ¹⁵N,¹³C labeled NRC was lyophilized and re-dissolved in buffered D₂O (Cambridge Isotope Laboratories) at least three times to remove exchangeable amide protons. For residual dipolar coupling (RDC) experiments, 0.5 mM NRC was aligned using a liquid crystalline medium containing 5 percent (by weight, relative to H₂O/D₂O) C12E6, with 1-hexanol (Sigma-Aldrich; St. Lous, MO) at a mole ratio (to C12E6) of r=0.64 (Ruckertt and Otting, 2000).

Double- and triple-resonance spectra used to make resonance assignments are listed in Supplementary Material along with assignment methods, RDC measurement, structure determination, and ¹⁵N-backbone dynamics. Assignments have been deposited in the BMRB (accession number 17306). Structural coordinates have been deposited in the PDB (accession number 2L6B).

^aThe m_i,i+1/m_i ratio obtained from GdnHCl titration experiments at pH 8.0, 20°C.

^bSASA-based ΔH, ΔS_conf, ΔS_solv, and ΔC_p values were calculated from solvent accessible surface areas using parameters described in (Hilser et al., 2006), using the NRC NMR structure determined here to calculate native-state SASA values for models of NR_x, NR_yC and R_yC (x=1 to 4, y=2 to 4). Intrinsic and interfacial values were obtained by least-squares fitting, assuming additivity (Aksel & Barrick, 2009). Uncertainties are least-squares estimates.