A quantitative review of the ubiquitous relapse curve

Abstract

The primary goal of this study is to ascertain whether relapse to drug dependence, in terms of continuous abstinence assessment, exhibits a typical pattern that can be characterized by a common quantitative function. If the relapse curve is indeed ubiquitous, then some underlying mechanism must be operating to shape the curve that transcends variables such as drug class, population or treatment type. Survival analyses are performed on 20 alcohol and tobacco-treatment studies using the proportions of individuals remaining abstinent following a period of initial abstinence. Several parametric models of relapse are compared and the results demonstrate that a log-logistic distribution is the most accurate reflection of the available data and the basic shape of the relapse curve is uniform. In the vast majority of reports examined, the rate of relapse decelerates after initial abstinence has been achieved, and therefore the amount of accumulated time abstinent may be the transcending variable that operates to shape the relapse curve.

1. Introduction

Relapse following a period of abstinence is a cardinal feature of drug dependence. Consequently, relapse prevention is one of the most central issues in the treatment field. One important question is whether a ubiquitous process characterizes relapse, or whether relapse is functionally dependent upon specific variables such as treatment methodologies and substances of abuse. A study published over 30 years ago demonstrated that nicotine, heroin, and alcohol produced highly similar rates of relapse over a one-year period (Hunt, Barnett, & Branch, 1971). Across these three drugs, the relapse curve (or the proportion of individuals remaining abstinent following treatment termination) conformed to a single distinct pattern: the majority of patients relapsed early post-treatment, and thereafter relapse rate decelerated dramatically. This reversed J-shaped function observed with relapse indicates that relapse may have ubiquitous dynamics. Based on this finding, the primary goal of this study is to quantitatively characterize the J-shaped function and determine whether the shape of the relapse curve is truly pervasive among treatment outcomes.

If the reversed J-shaped function is common among treatment outcomes, then this might suggest that there is a unifying mechanism acting to slow the rate of relapse after a certain point in time following treatment. Higgins, Badger, & Budney (2000) demonstrated that the odds of achieving long-term abstinence increase in an orderly fashion relative to the duration of within-treatment abstinence. Given these data, one might conclude that practicing abstinence aids long-term resistance to relapse. Indeed, many patients report that remaining abstinent gets easier with each passing day (Brownell, Marlatt, Lichtenstein, & Wilson, 1986), and this phenomenon may account for the deceleration of relapse rate with time.

Relapse prevention (Marlatt & Gordon, 1985) is predicated on the notion that yielding to temptation is a continual threat, and that long-term abstinence depends on the ability of the patient to develop an awareness of potential triggers and the skills to manage the urge to use substances. Prolonged abstinence strengthens self-efficacy, which in turn leads to long-term success; therefore, the relapse prevention model also supports the assertion that resistance to relapse is determined by a patient’s history of uninterrupted abstinence. Furthermore, Zhu and Pierce (1995) constructed an intervention that emphasizes early post-treatment contact to promote long intervals of continuous abstinence and improve long-term treatment success. Therefore, an examination of the shape of the relapse curve across extant treatment studies may yield further evidence to support the assertions made by Higgins et al. (2000), Marlatt and Gordon (1985), and Zhu and Pierce (1995). If the duration of uninterrupted abstinence is a significant variable moderating long-term abstinence, then the rate of post-treatment relapse must decelerate in all outcomes, regardless of the nature of the treatment.

To examine whether uninterrupted abstinence promotes long-term abstinence, the present analysis compares the applicability of four parametric models for survival data to available post-treatment relapse data (20 studies, published between 1968 and 2003). The survival function for each study is given by the proportions of individuals exhibiting continuous abstinence in days since treatment initiation. If the rate of post-treatment relapse remains constant over time, then abstinence attrition should occur in equal proportions across time intervals. Therefore, a model that assumes a constant hazard rate would be appropriate. If, however, abstinence begets abstinence (Higgins et al. 2000) then the model will have a decreasing hazard rate.

The most commonly used models in analyzing time-to-event data are the exponential, Weibull, log-normal, and log-logistic distributions. These models are frequently chosen by researchers because they offer insight to the hazard rate (Moeschberger, 1997). The one-parameter exponential distribution survival function is given by

$$S(x)=exp[-\lambda x],\lambda >0,x>0,$$

and the exponential distribution is characterized as having a constant hazard function, or h(x) = λ. This property is generally referred to as the “lack of memory” property or “old as good as new” model (Moeschberger, 1997). This lack of memory model would describe a proportionate change in abstinence attrition over time until all individuals have relapsed. Alternatively, the Weibull distribution survival function is given by:

$$S(x)=exp[-\lambda x^{\alpha }],\lambda >0,\alpha >0,x>0.$$

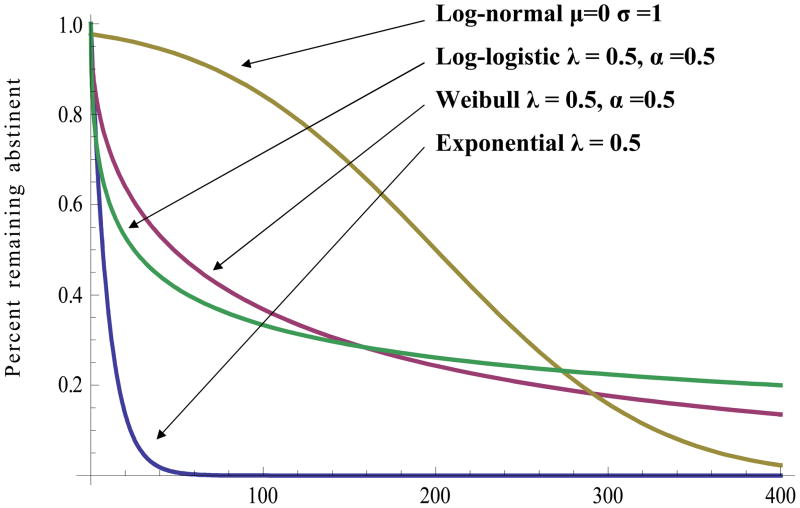
Note that the one-parameter exponential distribution is a special case of the two-parameter Weibull distribution, with α = 1. The parameter λ is commonly referred to as the scale parameter and α is the shape parameter. The Weibull distribution allows for an increasing (α > 1), decreasing (α < 1), or constant (α = 1) hazard function h(x) = λαx^α−1 (Moeschberger, 1997). Figure 1 illustrates the functional differences of each of the distributions for comparison.

Figure 1.

A visual comparison of the predictions of the four different parametric survival models.

A third possibility exists that the hazard of relapse in indeed nonlinear, but nonlinear in a manner that can only be described by a model in which the hazard is not monotonically decreasing. The normal and log-normal distributions survival functions are defined by the parameters μ and σ (the mean and standard deviation), and the cumulative distribution function Φ(z) of the standard normal. The survival function of the log-normal distribution is given by

$$S(x)=1-\mathrm{\Phi }\left(\frac{lnx-\mu }{\sigma }\right),-\infty <x<\infty .$$

The log-normal distribution is characterized by hazard function that is hump-shaped; its value at t=0 is zero, and then increases to a maximum, and then decreases to zero as x approaches infinity (Moeschberger, 1997). This model would describe an increase in the abstinence attrition for some initial time period and then the risk of relapse would eventually decrease until reaching an asymptote of zero (i.e. after a long period of time, there is essentially no chance of relapse).

The log-logistic is similar to the log-normal distribution in that the hazard function is also hump-shaped. The log-logistic distribution is described by

$$S(x)=\frac{1}{1+\lambda x^{\alpha }},\lambda >0,\alpha >0,x>0,$$

with the hazard function $h(x)=\frac{\alpha \lambda x^{\alpha -1}}{1+\lambda x^{\alpha }}$ where $\alpha =\frac{1}{\sigma }$ and λ = e^−μ/σ. If α = 1/σ ≤ 1 then the hazard rate strictly decreases to zero over time. If α = 1/σ > 1 then hazard rate increases initially to a maximum at time ${\left[\frac{(\alpha -1)}{\lambda }\right]}^{1/\alpha }$ and then decreases to zero as time approaches infinity (Moeschberger, 1997.). There is a closed formula for determining the maximum hazard in the log-logistic model and its parsimony is a major advantage over the log-normal model.

The log-logistic, log-normal and Weibull distributions are similar in that they all predict an infinitely decreasing hazard (α < 1) after some point, but the log-logistic and log-normal distribution can also account for a peak in the rate of hazard when the Weibull cannot. If the hazard rate is infinitely decreasing, then uninterrupted abstinence (or abstinence practice) may be a critical determinant of long-term abstinence.

2. Methodology and Results

2.1 Data analysis

Parametric survival analysis was performed on extant post-treatment relapse studies of substance dependence using four models (described above). Those studies that were included in the current analysis (a) assessed continuous abstinence, either by survival analysis or line-plot, at a minimum of five time points within a one-year period, and (b) assessed treatment variables or moderating variables on post-treatment substance-dependence relapse (See Table 1 for a list of studies), and (c) demonstrated 100% abstinence at time zero for all populations included within each study. Reports were discovered using the National Library of Medicine’s Entrez PubMed, and a search was created using the keywords: continuous abstinence, treatment, substance or drug, and dependence. The keywords were utilized independently and in each combination, and the results of the search were limited to (using the Pubmed “limits” feature): humans, adult +19 years, clinical trials, randomized-controlled trial, and reports written in English. Studies that reported only point-prevalence data were excluded from the analysis because point-prevalence data violate the monotonically decreasing assumption of survival analysis.

Table 1.

Comparison of three different models using the Anderson-Darling statistic. Shaded cases: the lowest of three values for the Anderson-Darling statistic. Maximum Likelihood Estimate (MLE’s) parameters of the log-logistic distribution are also included in the table. “Maximum hazard” is represented in terms of days from time point zero. “DEC” indicates that the hazard function is continually decreasing with the maximum risk-of-relapse at time point zero.

Study	n’s	Anderson-Darling Statistic			MLE’s for log-logistic model			Drug	Synopsis	Criteria for inclusion
		Log-logistic	Log-normal	Weibull	Location (P)	Scale (V)	Max Hazard (i)
Allsop et al. 1997								ALCOHOL	Relapse prevention was compared to no-additional treatment and discussion-group control conditions with a population of men	Survival analyzed for one year
No additional Tx/control group	18	2.373	2.363	2.474	3.598	0.81	11.323
Discussion/control group	20	2.208	2.197	2.248	4.304	0.706	39.805
Relapse prevention group	19	11.791	11.824	11.803	5.065	1.103	DEC
Dorus et al. 1989								ALCOHOL	Lithium carbonate was used to treat alcoholism in depressed and non-depressed men; either major depression or dysthymia	Survival analyzed for one year
Placebo/depressed	89	49.9	49.903	49.924	5.152	1.127	10.834
Placebo/nondepressed	139	18.38	18.457	18.402	4.862	0.934	DEC
Lithium/depressed	82	20.195	20.233	20.229	3.711	1.926	DEC
Lithium/non-depress	89	16.201	16.278	16.211	4.635	1.056	DEC
Fuller et al. 1986								ALCOHOL	Disulfiram compared to control in treatment of alcoholic men	Survival analyzed for one year
No disulfiram/control	199	12.736	12.738	12.739	3.73	1.621	DEC
250 mg disulfiram	202	13.851	13.903	13.863	4.078	1.635	DEC
1 mg disulfiram/control	204	21.591	21.614	21.6	4.233	1.957	DEC
George et al. 1992								ALCOHOL	Homovanillic acid (DA metabolite) correlated with treatment success at one year	Survival analyzed for one year
LDOPA + carbidopa	12	5.252	5.254	5.267	3.455	2.096	DEC
Placebo w/counsel	11	5.871	5.885	5.877	4.734	0.838	28.774
5-HT + carbidopa	8	10.888	10.873	10.897	4.694	1.59	DEC
Gonzales et al. 2002								TOBACCO	Men and women treated with bupropion open label, then moved to double blind; results report the double-blind phase of testing	Continous abstinence reported at weeks 8, 12, 24, 36 and 52.
Placebo males	98	11.098	11.093	11.102	4.175	2.156	DEC
Bupropion males	112	15.498	15.5	15.5	4.96	2	DEC
Buproprion females	118	16.997	17.001	16.999	5.25	1.699	DEC
Placebo females	104	11.566	11.57	11.568	4.54	1.996	DEC
Greenfield et al. 2000								ALCOHOL	Self-efficacy scores used to differentiate risk-of-relapse among a population	Survival analyzed for one year
High SCQ	98	104.527	104.516	104.61	5.064	1.194	DEC
Low SCQ	98	0.691	0.963	0.633	3.277	0.725	13.13
Hays et al. 2001								TOBACCO	Bupropion open-label treatment followed by double-blind phase; results report the double-blind phase of testing	Survival analyzed for two years
Bupropion	214	27.358	27.349	27.391	5.218	1.695	DEC
Placebo	215	18.209	18.2	18.242	4.409	1.982	DEC
Jorenby et al. 2003								TOBACCO	Bupropion open-label treatment followed by double-blind phase; results report the double-blind phase of testing	Continuous abstinence assessed for 9 weeks of psychotherapy and then at weeks 10, 12, 26 and 52 of follow-up
Bupropion	244	10.042	10.047	10.05	0.459	4.084	DEC
Bupropion + nicotine patch	245	18.07	18.071	18.089	1.2	4.217	DEC
Nicotine patch only	244	8.11	8.12	8.153	−1.051	3.272	DEC
Placebo	160	7.051	7.059	7.076	−2.415	2.443	6.108
Kesoe & Salaspuro, 1990							DEC	ALCOHOL	Hazelden-type treatment compared to treatmeant-as-usual; controlled-drinking and total-abstinence outcomes were reported.	Survival analyzed for one year; only abstinence groups included in analysis
Traditional+Hazelden/AA	63	4.33	4.326	4.306	3.15	0.833	DEC
Traditional/no AA	54	3.88	3.882	3.907	2.86	1.508	DEC
Lowman et al. 1996							DEC	ALCOHOL	Review of a multisite trial of relapse prevention	Survival analyzed for one year
Inpatient	442	24.31	24.327	24.307	5.008	1.089	DEC
Outpatient	121	6.562	6.571	6.619	3.601	1.326	DEC
Project MATCH 1997								ALCOHOL	Participants were matched to either 12-step treatment, Motivational Enhancement or Cognitive-Behavioral Skilll sTherapy	Survival analyzed for one year
Aftercare	952	11.616	11.617	11.618	4.644	1.763	DEC
Outpatient	774	5.188	5.186	5.193	2.796	1.997	8.778
Pokorny et al. 1968								ALCOHOL	90-day treatment program results monitored over a one-year period	Continuous abstinence assessed at regular intervals for one year
Inpatient	113	9.646	9.657	9.661	4.352	1.454	DEC
Sass et al. 1996								ALCOHOL	Patients received double-blinded acamprosate or placebo and then were followed during a non-medication interval	Survival analyzed for 96 weeks
Acamprosate	136	31.435	31.431	31.436	5.387	1.594	DEC
Placebo	136	12.026	12.025	12.024	4.567	1.249	DEC
Schmidt et al. 2002								ALCOHOL	Double-blind lisuride or placebo for 6 months, and 6 month follow-up	Survival analyzed for one year
Lisuride	57	2.605	2 607	2.624	3.94	0.881	68.933
Placebo	63	13.716	13.685	13.72	4.844	1.005	28.557
Schneider et al. 1996								TOBACCO	All inhalers available for 6 months with follow-up for an additional 6 months	Survival analyzed for one year
Nicotine inhaler	112	4.29	4.261	4.352	2.306	1.727	DEC
Placebo inhaler	111	2.555	2.53	2.817	1.803	1.024	DEC
Stevens & Hollis, 1989								TOBACCO	Two-weeks of intensive psychotherapy intervention followed by monthly patient follow-up	Self-reported survival analyzed for one year
Social-support	184	3.41	3.281	3.181	4.44	0.587	DEC
Skills-training	205	7.095	7.059	7.042	4.567	0.816	DEC
No treatment/control	198	2.956	3.122	3.011	4.645	4.329	DEC
Zelman et al. 1992								TOBACCO	Skills training and social support used in combination with two nicotine exposure therapies, continuous abstinence correlated to craving severity	Survival analyzed for one year
High craving + rapid smoking	59	5.393	5 385	5.553	3.522	1.013	DEC
High craving + nicotine gum	59	35.914	35.901	35.931	5.481	1.726	DEC
Low craving + rapid smoking	50	55.552	55.549	55.553	7.054	1.976	DEC
Low craving + nicotine gum	50	21.327	21.3	21.356	4.548	1.465	DEC
Zhu et al. 2000								TOBACCO	Assitance programs (self-help, counseling, and nicotine replacement) were selected by patients	Survival analyzed for one year
No assistance/control	841	2.394	2.381	2.411	2.365	1.634	DEC
Smoking-cessation assistance	1143	7.459	7.414	7.483	3.401	1.443	DEC
Zhu et al. 2002								TOBACCO	Patients had the opportunity to receive counseling, and these groups were compared to a forced telephone intervention	Survival analyzed for one year
Initiative/counseling	1046	25.319	25.329	25.338	4.409	1.971	DEC
Multiple telephone intervention	1973	2.061	2.086	2.077	2.242	1.916	DEC
No intiative or counseling	1309	7 882	7.875	7.905	1.861	2.893	DEC
Zhu et al. 1996								TOBACCO	Patients were randomized into three groups and followed for one year to evaluate the effectiveness of a telephone counseling program	Survival analyzed for one year
Self-help	841	1.781	1.799	1.788	1.355	1.85	DEC
Telephone counseling, single	1143	1.87	1.89	1.881	1.809	1.945	DEC
Telephone counseling, multiple	1046	2.451	2.99	2.221	1.799	1.899	DEC

The results of the literature search produced 71 studies in total that reported continuous abstinence, but only 20 (~30%) of these followed patient outcome for one year or longer with a minimum of five assessment points within the first year. The vast majority of studies were excluded because they did not follow patient outcome for one year or longer (39 out of 71). The five-timepoint criterion was established to compare equitably those studies which provided graphical survival data to those studies which reported only percent-continuous abstinent data at various time intervals. The central question that was addressed with the current analysis was whether long-term abstinence is related to uninterrupted abstinence, or whether the hazard of relapse changes as a function of time-abstinent. Many of the clinical trials discovered in the literature search included an assessment of continuous abstinence for only 12 weeks; therefore, these studies could not be included because they provided no data on long-term abstinence, defined here as continuous assessment at one year or longer. Patient outcomes of greater than one year would have been more ideal for the purposes of the present analysis, but continuous abstinence assessment at intervals greater than one year are a rarity for practical reasons. Unfortunately, in terms of the utilization of continuous-abstinence assessment, treatment research with opioid and/or cocaine-dependent populations follow patient outcomes for a shorter duration of time (e.g. 12 weeks) than those studying alcohol or tobacco dependence. For those investigations that followed survival for one year or longer, all but two (Stephens, Roffman & Simpson, 1994; and Winters et al. 2002) involved either nicotine or alcohol-dependent populations. Worth mentioning is that Stephens et al. (1994) evaluated survival outcomes for marijuana dependence for over a year, but 100% abstinence was not achieved at the beginning of the investigational period, so these data are not included in the present analysis. Winters et al. (2002) evaluated the efficacy of behavioral couples therapy for heterosexual couples in which the female was diagnosed with a substance-use disorder (non-specified), not substance dependence.

Each study included more than one treatment group and the 20 studies produced 53 different relapse curves. On the occasion that only graphical data were available, such as the case with survival analysis, digiMatic software (1995, FEB Software) was utilized to approximate percent-abstinent data points. Relapse was defined as post-abstinence drug use, either a single use of the drug or a return to one’s pre-treatment level of drug use; both definitions are prevalent in the literature and pertain to the termination of continuous abstinence (Donovan, 1996; Miller, 1996).

Data were analyzed using the survival distribution analysis package in Minitab 15 (2006, Minitab, Inc.). Since the studies provided summary tables using time intervals to relapse, the actual time to relapse for each participant is unknown. Furthermore, relapse after one year was generally not provided in the studies. Thus, the data are interval-censored and right-censored.

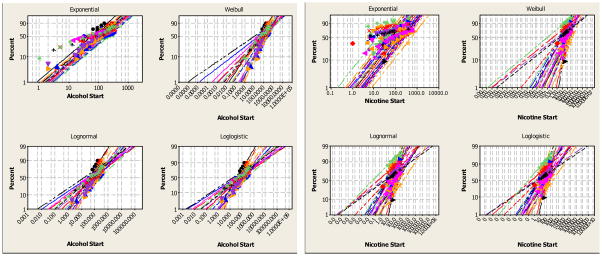
The probability plot is a graphical technique for assessing whether or not a data set follows a given distribution (Chambers, Cleveland, Kleiner, & Tukey, 1983). Percentiles of the data from each study were plotted against the percentiles of the theoretical distribution (ordinate and abscissa, respectively, see Fig. 2). The probability plot should fall in a straight line if the distribution fits the model reasonably well; deviations from the line plot would indicate that the data deviate from the assumed model. Probability plots were generated to compare all four models (see Fig. 2). The graphical data suggest that the exponential model fails in comparison because the probability plots for the exponential fall away from a straight line, and therefore, the constant hazard rate inherent in the exponential model is not an accurate depiction of the available data.

Figure 2.

Probability plots for studies that involved either alcohol (left) or nicotine (right) relapse.

Further analysis was conducted to distinguish between the Weibull, the log-normal distributions, and the log-logistic distributions to assess whether the hazard rate begins to decelerate at the very beginning of abstinence (as described by the Weibull model) or whether a peak risk or relapse exists somewhere after time point zero (as described by the log-logistic and log-normal models). Maximum likelihood estimation (MLE) was the methodology used to determine the parameters for the four models. The MLE was used to determine how accurately the parameters in each function reflected the true distributions based on the available data and the MLE is typically used when dealing with data sets that contain a relatively large number of censored data (Reliasoft, 2003). The Anderson-Darling statistic (D’Agostino & Stephens, 1986) was then utilized to test the goodness-of-fit of the MLE parameters (see table 1).

Minitab utilizes the weighted-squared distance between the fitted line of the probability plot and the nonparametric step function to conduct the Anderson-Darling test. According to the manufacturer, the Anderson-Darling statistic in Minitab is weighted more heavily in the tails of the distribution, thereby allowing for a more refined comparison of the models. Compared to the log-normal or Weibull distribution, the log-logistic was associated with a smaller or equivalent Anderson-Darling statistic in 28 out of a total of 53 cases (see table 1). Furthermore, the Anderson-Darling statistics differed significantly between the two best-fitting models and the Weibull distribution (Wilcoxon signed-ranks test, Z(53) = 5.11 and 3.511, p’s < .05 for the log-logistic and log-normal comparisons to the Weibull, respectively). The Anderson-Darling statistics for the log-logistic and log-normal models did not differ significantly (Z(53) = 0.619, p > .05). Although it was not possible to distinguish statistically between the fit of the log-normal and log-logistic distributions, given that the log-logistic involved a more solvable, closed-formula, the principle of parsimony recommends that the log-logistic was the more appropriate model.

A comparison of the Anderson-Darling statistics among the treatment groups within each study indicated that larger values were associated with better treatment outcomes (e.g. see the Anderson-Darling statistics for Greenfield et al. 2000, table 1). This result may seem somewhat paradoxical because lower Anderson-Darling statistics were associated with a better fit of the model. The apparent paradox can be explained because each model assumes a horizontal asymptote at zero (because each model is a distribution function). However, since the data were censored at the end of one year, the Anderson-Darling statistic was required to reconcile the difference between the fitted model and the tail behavior of a survival function in which the tail was greater than zero. If a treatment group was successful in remaining abstinent at the end of one year, the tail associated with that treatment group would be further from the asymptote of zero assumed by the model. Therefore, higher Anderson-Darling statistics (for any model distribution) were indicative of better treatment outcomes.

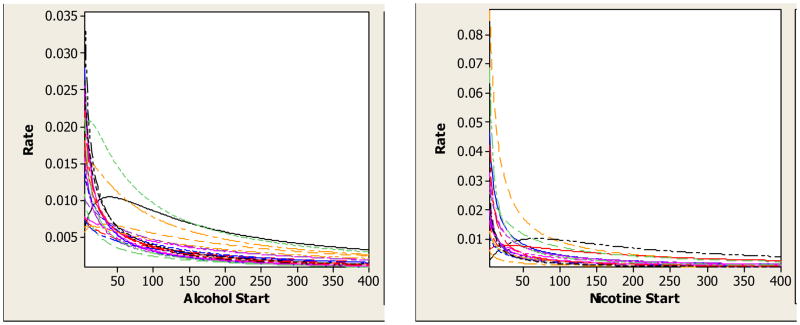
The log-logistic distribution provides the opportunity to evaluate relative changes in the risk of relapse by allowing for the identification of a point of maximum hazard. Table 1 lists the study groups and the point (day) of maximum hazard associated with each study group. The vast majority of study groups are associated with a rapidly decelerating hazard function (indicated by DEC) and after day 100, the risk of relapse is essentially zero (Fig. 3). Only 9 groups, out of a total of 53, were associated with a maximum hazard at some time point between day one in the abstinence period and day 70. The log-logistic model also demonstrates that some individuals, even a very small proportion, remain abstinent in a finite time period and the hazard rate (Fig. 3) indeed reaches an asymptotic level at zero before day 365.

Figure 3.

The hazard functions for the log-logistic distribution for alcohol (left) and nicotine (right) studies.

3. Discussion

In the majority of cases assessed, parametric survival analysis in which four models (exponential, Weibull, log-normal and log-logistic) were compared demonstrates that the risk of relapse decelerates with time and that the log-logistic distribution is the most appropriate model for the available data. The results also suggest that the shape of the relapse curve is relatively invariant across 20 different studies. Although many factors may contribute to relapse of drug use, the uniformity of the shape of the relapse curve suggests that these factors produce quantitative variation in an otherwise invariant process (see Fig. 4). The present analysis provides support for the proposition that relapse to drug dependence exhibits a typical pattern across a constellation of variables.

Figure 4.

Analysis of continuous abstinence from all 20 studies. On the occasion that only graphical data were available, digiMatic software (1995, FEB Software) was utilized to approximate percent-abstinent data points.

For only a handful of studies included in the present analysis, the maximum risk of relapse was not immediately decelerating; the maximum risk of relapse was noted to occur prior to reaching 70 days of continuous abstinence and decelerated thereafter. However, the majority of studies demonstrated a decelerating risk of relapse after a period of initial abstinence (time point zero), and the hazard of relapse declines to nearly zero after 100 days, see Fig. 3. Therefore, one might conclude that 100 days of uninterrupted abstinence represents an important treatment milestone and any patient who has managed to achieve this milestone likely also possesses the ability to remain abstinent for one year or longer. The results presented here can support such a conclusion only to the extent that the probability of relapse decelerates for all of the data analyzed after the 100-day mark. The log-logistic distribution can be utilized by a researcher or treatment practitioner to make predictions about the long-term success of a given treatment after 100 days, and continuous abstinence at one-year seems to be a good predictor of continuous abstinence at up to four years (Daughton et al. 1999).

The shape of the log-logistic distribution may bear some resemblance to curves that represent the extinction of learned behavior. Continuous abstinence can be viewed as the extinction of self-administration behavior and relapse viewed as reacquisition (e.g. Redish et al. 2007). However, given the evidence that extinction is not unlearning but rather the learning of a new association (Bouton, 2004), one can speculate that abstinence is a context-dependent learned behavior that retroactively interferes with drug self-administration during the initial treatment period. Relapse to substance abuse may represent an incomplete transfer of the new learned behavior (abstinence) across environments. The very nature of the continuous abstinence curve can be taken to support the assumption that, at least for some individuals, the transfer of abstinence behavior from the treatment period to the post-treatment interval is less subject to context-dependent renewal of drug self-administration. The present analysis and interpretation would also suggest that renewal of drug self-administration (relapse) is less likely to occur over time. At present, however, experimental evidence does not yet exist to support this conclusion and the authors would be overextending the current findings to suggest specific behavioral mechanisms underlying an individual’s resistance to relapse. Furthermore, point-prevalence analysis (rather than continuous abstinence) would be a more appropriate analogy to extinction given that point-prevalence and extinction curves are not monotonically decreasing functions.

The current analysis and results are limited to alcohol and tobacco-dependence treatment research. The primary purpose of the present analysis was to evaluate long-term treatment success in the context of uninterrupted abstinence; therefore, the analysis excluded those investigations of continuous abstinence for less than one year. Treatment studies evaluating cocaine and heroin dependence tend to follow patients for 12 weeks or less, so generalization of the present results to illicit drugs is impossible. A future, separate analysis of the first 12 weeks of treatment is warranted to determine whether relapse to illicit drugs also follows the log-logistic distribution.

The major finding of the parametric survival analyses is that the hazard of relapse declines as a function of time; all but a few studies demonstrate an ever-decreasing hazard rate and these results may lead one to conclude that abstinence begets abstinence. Time abstinent may interact with other variables such as treatment type to bolster relapse resistance, and the present findings might lead one to conclude that uninterrupted abstinence should continue to be a primary goal for treatment providers. The results from the parametric comparison provide some support for the concept that practicing abstinence results in better treatment outcomes, and in fact, this may be the mechanism responsible for the shape of the ubiquitous relapse curve.