Skip to main content
PMC home page
Proceedings of the Royal Society B: Biological Sciences logoLink to Proceedings of the Royal Society B: Biological Sciences
. 2011 Feb 23;278(1720):2915–2923. doi: 10.1098/rspb.2010.2614

Emergence, spread, persistence and fade-out of sylvatic plague in Kazakhstan

Lise Heier 1, Geir O Storvik 1,2, Stephen A Davis 3, Hildegunn Viljugrein 1,4, Vladimir S Ageyev 5, Evgeniya Klassovskaya 6, Nils Chr Stenseth 1,*
PMCID: PMC3151704  PMID: 21345866

Abstract

Predicting the dynamics of zoonoses in wildlife is important not only for prevention of transmission to humans, but also for improving the general understanding of epidemiological processes. A large dataset on sylvatic plague in the Pre-Balkhash area of Kazakhstan (collected for surveillance purposes) provides a rare opportunity for detailed statistical modelling of an infectious disease. Previous work using these data has revealed a host abundance threshold for epizootics, and climatic influences on plague prevalence. Here, we present a model describing the local space–time dynamics of the disease at a spatial scale of 20 × 20 km2 and a biannual temporal scale, distinguishing between invasion and persistence events. We used a Bayesian imputation method to account for uncertainties resulting from poor data in explanatory variables and response variables. Spatial autocorrelation in the data was accounted for in imputations and analyses through random effects. The results show (i) a clear effect of spatial transmission, (ii) a high probability of persistence compared with invasion, and (iii) a stronger influence of rodent abundance on invasion than on persistence. In particular, there was a substantial probability of persistence also at low host abundance.

Keywords: Yersinia pestis, great gerbil, space–time dynamics, Bayesian imputation, spatial correlation

1. Introduction

Plague, caused by the bacterium Yersinia pestis, is known for its impact on human history through a series of pandemics: the Justinian plague in the sixth century, the Black Death starting around 1350 and the Third Pandemic in the nineteenth century [1]. The primary reservoir of the bacterium is populations of wild rodents in Central Asia, where the bacterium evolved some 1500–20 000 years ago [2]. Today, a few thousand cases of human plague are reported each year from countries in Asia, Africa and the Americas, and most of these are believed to be linked to local wildlife reservoirs of plague [3–5]. In many countries, early treatment with antibiotics can be problematic, and in these places plague remains a serious threat to public health [6,7].

A better understanding of the dynamics of sylvatic1 plague would improve the predictions of new outbreaks, making early warning and treatment possible. The dataset from the Pre-Balkhash plague system in Kazakhstan (electronic supplementary material, figure S1), where the main host and vectors of plague are the great gerbils (Rhombomys opimus) and their fleas (Xenopsylla spp.) [8,9], has been monitored since 1949 in order to prevent transmission of the disease to humans. The high spatial resolution and the long study period of the resulting dataset make the types of analyses we do here, possible.

Previous studies based on the Pre-Balkhash dataset include Davis et al. [10,11], who studied predictive gerbil abundance thresholds for plague, and Stenseth et al. [12] and Samia et al. [13], who studied climatic influences on plague occurrence. All these studies (but the second) concentrated on data from up to four selected areas of 40 × 40 km2 where plague monitoring had been most regular. At the scale of 20 × 20 km2, Kausrud et al. [14] studied great gerbil dynamics, and at an even finer scale, 10 × 10 km2, Frigessi et al. [15] developed a model of the great gerbil–flea dynamics. At the scale of the whole focus, Kausrud et al. [16] reconstructed past plague outbreaks based on climatic indices.

In the stochastic model presented here, we distinguish between plague invasion and persistence at the scale of 20 × 20 km2, and take into account the presence of plague in neighbouring areas. A Bayesian imputation technique was used in order to handle poor data in the response and explanatory variables. Our resulting model describes the local space–time dynamics of sylvatic plague, and is an improvement on the threshold model by Davis et al. [10], which was fitted to annual time-series data from just two of the 40 × 40 km2 areas from which data were collected. The importance of separating the phases of invasion and persistence when modelling abundance thresholds for infectious diseases was emphasized by Lloyd-Smith et al. [17], partly in response to Davis et al. [10], who presented a model with a single abundance threshold for both processes. Here, we study whether differences between invasion and persistence are detectable in the Pre-Balkhash dataset, and relate them to known and plausible mechanisms.

When a disease appears in an area with apparently no endemic cycle going on inside it or in the vicinity of it, the invasion may be called an emergence (or re-emergence if it has been there before). Human plague is infamous for its ability to re-emerge after long periods of (seeming) absence [18,19], and the Pre-Balkhash dataset suggests that the same phenomenon happens in wildlife, although in this case at a smaller temporal scale. The mechanism(s) for re-emergence of plague is unknown, although many hypotheses exist [20], including survival of bacteria in the soil [21] or fleas [22], phases with less virulent bacteria in the hosts [22,23] and long-distance transportation by birds or carnivores from areas with ongoing epizootics [24,25]. Recent studies of the plague system in Colorado, USA, indicate a low, but non-zero prevalence of plague in inter-epizootic periods [26,27], supporting the hypothesis that plague circulates among favourable microfoci [28].

Spatial transmission of plague is suggested when the risk of having plague in an area is greater when nearby areas are infected. Spread of plague has been studied by several authors: Stapp et al. [29], Girard et al. [25] and Snäll et al. [30] focused on plague outbreaks among prairie dogs in the USA; Davis et al. [31] showed in a simulation model that stochastic spread from colony to colony will naturally lead to the existence of an abundance threshold for invasion of plague; and Salkeld et al. [32] found a similar percolation threshold for an alternate host to be an important driver for plague outbreaks in prairie dogs. Here, we investigate how the extent of plague in neighbouring areas, as well as past host abundance, influences the probability of plague invasion. Possible explanations for emergence and spread are discussed.

2. Material and methods

(a). The Pre-Balkhash plague ecosystem

Our study area was the Pre-Balkhash plague focus in Kazakhstan, a semi-desert covering 32 000 km2 southwest of Lake Balkhash (electronic supplementary material, figure S1). The main host of plague in this area is the great gerbil, R. opimus [8,33], and the main vectors are fleas of the genus Xenopsylla [8,9]. The great gerbil is a facultatively social rodent, living in family groups of 3–14 individuals inhabiting and defending discrete, permanent burrow systems [34,35]. They can have up to three litters during one season, and those born in spring can have their first litter the following autumn [34]. The abundance of great gerbils fluctuates greatly from year to year, and with it the proportion of occupied burrow systems. Plague epizootics are observed at irregular intervals, each epizootic lasting for 2–5 years, separated by periods of 2–8 years [10]. Although many great gerbils die from plague, many others are relatively resistant to the disease [36], and the abundance of great gerbils can remain high during outbreaks [10], contrasting the devastating effect that plague has on prairie dog colonies in the USA [36].

Plague outbreaks in the Pre-Balkhash area are typically preceded by a build-up of great gerbil abundance. That is, the average abundance over 2 years is observed to exceed a threshold before an epizootic occurs [10]. Climatic conditions influence the plague system further: Stenseth et al. [12] found that high temperatures in spring and high precipitation in summer each leads to increased plague prevalence once the host abundance is above the threshold.

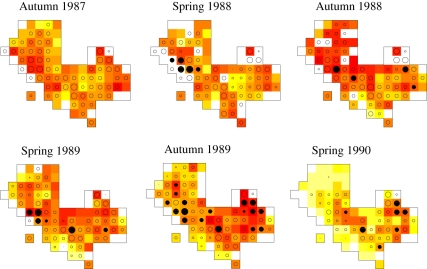
The epizootic during 1988–1995 may serve as an illustration of a typical outbreak: after a period of low gerbil abundance, it started to increase in autumn 1986 in areas close to the Iliy and Karatal rivers (electronic supplementary material, figure S1). In spring 1988, an outbreak started in the western part of the area (figure 1), and the following autumn, additional emergences were observed in the eastern part. In spring 1989, the active sites had moved (but note that plague may have been present also where it was not observed; while observed presences are certain, observed absences are not). In the autumn, the outbreak had spread to a larger area. In spring 1990, the gerbil abundance dropped in the western parts, and from then on, plague was hardly observed in these areas, but persisted in the eastern area throughout the rest of the study period (not shown in the figure). This example illustrates how the location and extent of outbreaks change as they progress. This observation motivated our study of the space–time dynamics of plague.

Figure 1.

Figure 1.

Open in a new tab

Example of a plague epizootic in the Pre-Balkhash area (see electronic supplementary material, figure S1, for reference to map). Open circles, no great gerbils found positive for plague; filled circles, at least one great gerbil found positive. Circle size indicates the number of individuals tested. Colour indicates great gerbil abundance, from yellow (low) to red (high).

(b). The dataset

The data were collected every spring and autumn from 1949 to 1995 at a number of sites within the focus, and include abundance estimates of great gerbils and fleas, as well as results of testing great gerbils and other small mammals and their fleas for plague (electronic supplementary material). We did not include data on flea abundance or plague presence in fleas in our analyses, both because the sampling process was partly unknown, and because inclusion of fleas would require imputation of missing data at an extra level, implying an even more complex analysis. Hence, we based our models on data from great gerbils only.

The focus is divided into ca 90 so-called primary squares, areas of 20 × 20 km2. Abundance measures were mostly at this scale, the observation point being located in the middle of the square. The primary squares are in turn divided into four 10 × 10 km2 sector areas. The results from plague testing of trapped rodents and fleas are recorded at the sector scale.

In any particular season, zoologists would visit only a fraction of the many sectors in the focus. Because of many missing values at the sector level, we aggregated records from up to four sectors to form estimates at the primary square level, on which we based our analyses. Because the observation process was designed for plague surveillance and not for statistical analysis, the method of sector selection is complex and partly unknown. We chose to ignore this, treating the data as though the selection of sectors was random.

(c). Defining invasion, persistence and ‘plague in nearby areas’

We define an invasion event to be the appearance of plague in a square where it was absent the season before. Likewise, a persistence event may be defined as the continuation of plague presence in a square from one season to the next. Our modelling approach will be based on using the presence/absence of plague as a response variable. Thus, we used in our model the possibility of invasion or persistence, using the previous season's absence or presence of plague, respectively, as an explanatory variable (electronic supplementary material, figure S2).

The true presence/absence of plague is only partly reflected by the data, since the records are based on relatively small numbers of gerbils tested. Thus, no positive tests may sometimes be recorded even if plague was present. For this reason, we do not use the observations directly as response and explanatory variables; instead, variables describing the true state of the system are treated as hidden. Our analyses are performed on multiple simulations (imputations) of the real presence and absence of plague (§2e).

The extent of plague in nearby areas the previous season was defined as the weighted average of the binary variables corresponding to the presence/absence of plague in the eight neighbouring squares (electronic supplementary material, figure S2). In this second explanatory variable, the corner squares were given weight = 0.4 compared with the adjacent squares, based on preliminary analyses using the Akaike information criterion (AIC) (electronic supplementary material). Other formulae for the extent of nearby infection were also tested (e.g. just presence/absence of plague in neighbouring squares). The results showed that the specific form in which the presence of plague in neighbouring squares was defined was not very important.

An emergence event may be defined as an invasion event where plague was absent from neighbouring squares the previous season. An illustration of invasion and persistence is given in the electronic supplementary material, as well as an overview of the raw data where these definitions have been applied.

(d). Great gerbil abundance

For a specific season, great gerbil abundance was defined as the proportion of burrow systems that were occupied by family groups of great gerbils. It was estimated every spring and autumn by walking a field transect that included either 15 or 30 burrow systems. Davis et al. [10] used a temporal mean of abundance as a predictor for plague, formed by values up to 2 years before the plague observations. Here too, past gerbil abundance was defined as a temporal mean, but over a slightly different time period. We included the season when plague testing was performed, and went only 1.5 years back in time. This set of four seasons was chosen on the basis of preliminary analyses of the raw dataset, where abundance measures based on different sets of seasons were ranked by the use of the AIC. As an alternative, estimates of the great gerbil density were also tested as a covariate. This alternative showed less explanatory power, partly because the density estimates were inherently more uncertain, and has not been considered further.

(e). Analyses

We modelled the probability that plague was present in a square i at time t, yi,t, as a logistic function of the following explanatory variables: yi,t−1, presence/absence of plague in the square the previous season; 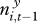Inline graphic, extent of plague in nearby areas the previous season as explained above; gi,t, past gerbil abundance in square i; st, season (spring/autumn). The software R [37] was used for all data manipulation and analyses.

Limited sample sizes and missing observations presented challenges to the analyses. Standard GLM-type models do not account for uncertainty in explanatory variables, and only data points with complete records can be included. In order to effectively use the available data, imputation methods were applied. Only space–time points (i,t) that became complete after imputation were included in the final analysis.

Firstly, while records with one or more positive tests imply that plague was present, records with only negative tests may be due to an insufficient number of tests performed, giving uncertainty about presence of plague. This was accounted for in the analyses by the use of a Bayesian imputation technique [38]: instead of analysing the recorded presence/absence data directly, we made multiple simulations (imputations) of the true presence/absence of plague, based on observations, number of gerbils tested and a priori probabilities of plague presence. The spatial correlation structure seen in the plague records was incorporated in the imputations through spatially correlated random effects (see the electronic supplementary material for details). In cases where no tests were performed, data were not imputed, as this might introduce additional noise in the models.

Secondly, the extent of plague in neighbouring squares (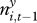Inline graphic) was often unknown because of missing values, as plague data were not imputed where no gerbils had been tested. We introduced a pragmatic criterion that at least five neighbouring squares, of which at least two adjacent squares, must be sampled if the extent of plague was to be calculated. This was a compromise between having good information about each data point, and having enough data in the analyses.

Thirdly, there were missing observations of great gerbil abundance. These values were imputed as well, again based on a model taking spatial correlation into account (electronic supplementary material). In this case, we averaged over a large number of imputations, as the strong spatial correlation in the abundance data [14] made this part of the uncertainty less important than the uncertainty in the plague data. Where abundance records were missing from a larger area, some of the imputed values were not included in the further analysis owing to their high level of uncertainty.

For each of 50 imputed datasets, we performed a logistic regression with spatial correlation using generalized linear mixed model (GLMM) analyses [39]. A model with no interaction effects can be formulated as

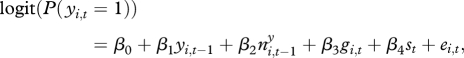(e). 2.1

where ei,t are zero-mean spatially correlated random effects modelling the spatial correlation in the response variable. The random effects are assumed to be Gaussian distributed with an exponential correlation structure including a nugget effect. Alternative models including interactions between the explanatory variables were considered as well. Generalized additive mixed models were also tried, but did not give significant nonlinear effects, and hence the models were reduced to the GLMM.

Estimation of parameters and standard errors was performed for each imputed dataset independently by the glmmPQL routine contained in the MASS library [40]. The results were combined through the routine MIcombine within the mitools package [41] to give estimates, confidence intervals and p-values for testing whether coefficients were significantly different from zero [38].

Model selection was performed by backward selection from a full model, i.e. with all interaction terms included. No AIC value was available, firstly because spatial correlation was included in the analyses, secondly because the results from the imputed datasets must be combined. Hence, we used a selection criterion based on the significance values of the covariates and interaction terms in the model, with an acceptance level of 0.05. The resulting model is reported in §3a.

The testing of interaction terms asks whether the influence of one explanatory variable depends on the value of another, e.g. whether gerbil abundance has a different effect on persistence than on invasion. A non-significant result will show that we cannot prove that there is such a difference. This could mean that they are more or less equal, but it could also result from scarcity of data. Because of the latter possibility, it may be interesting to ask an alternative question: whether the effect of one variable is different from zero for all categories of the other. Through specific parametrizations of the model, we consider the question: Is there a significant effect of gerbil abundance on persistence as well as on invasion? Similarly, the effect of plague in neighbouring squares is tested for persistence versus invasion, spring versus autumn, etc. Results of these tests are reported in §3b.

Evaluation of the model was performed by a receiver operating characteristic (ROC) analysis [42] for the final model in §3b. This was done by calculating true and false positive rates for each of the 50 imputations separately, using the model estimates corresponding to each imputation. The results were combined by calculation of the mean and standard error at each threshold value. The resulting ROC graph is presented in §3c.

3. Results

(a). Basic model

After model selection, the model included all main effects except season, and no interaction effects.

(a).

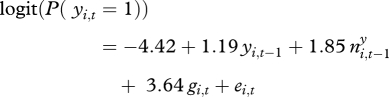It showed that the probability of plague presence increased with plague presence the previous season (yi,t−1 = 1), with the extent of plague in neighbouring squares the previous season (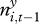Inline graphic) and with past great gerbil abundance (gi,t) (table 1 and electronic supplementary material, figure S5). The probability of invasion (yi,t−1 = 0) was close to 0 at low gerbil abundances, and increased to 0.2–0.5 at high abundances, depending on the extent of plague in neighbouring squares. For persistence (yi,t−1 = 1), the probability increased from 0.1–0.3 at low abundances to 0.4–0.8 at high abundances. No interaction terms were found to be significant, meaning, for example, that the influence of plague in neighbouring squares was not found to differ between invasion and persistence.

Table 1.

Estimated parameters in the basic model. Betas are defined in model (2.1).

parameter estimate s.e. p-value
β0: constant term −4.42 0.46 <1.00 × 10−13
β1: presence of plague previous season 1.19 0.27 1.67 × 10−5
β2: extent of plague in neighbouring squares previous season 1.85 0.53 5.16 × 10−4
β3: past great gerbil abundance 3.64 0.76 2.06 × 10−6
Open in a new tab

(b). Reparametrized models

The reparametrized model for testing whether the effect of plague in neighbouring squares was significant for persistence as well as invasion was as follows (notation simplified w.r.t. spatial correlation):

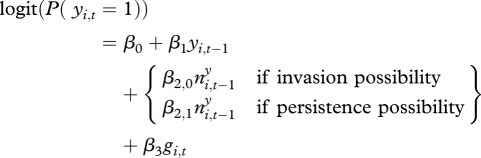(b). 3.1

All parameters were found to be statistically significant, and the estimates of β2,0 and β2,1 for 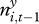Inline graphic for invasion versus persistence, respectively, were relatively similar (electronic supplementary material, table S2a). Hence, the effect of plague in neighbouring squares was found to be important in both invasion and persistence events, and of similar magnitude.

The reparametrized model for testing the effect of gerbil abundance for persistence versus invasion was as follows:

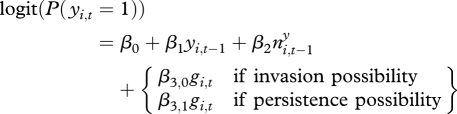(b). 3.2

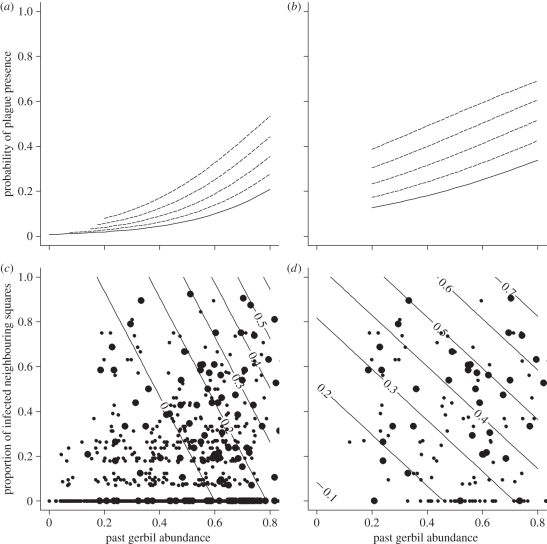
Here, the influence of gerbil abundance was found to be highly significant for invasion (β3,0), but non-significant for persistence (β3,1). The estimate of the latter was about half the estimate of the former (electronic supplementary material, table S2b and figure 2). This result shows that gerbil abundance is important in invasion events, but that we cannot make such a conclusion for persistence events. Seen together with the result from the basic model, the effect of gerbil abundance on persistence events is unknown, having a range of possible values including 0 and the combined estimate β3 from the basic model, and a point estimate approximately halfway between the two.

Figure 2.

Figure 2.

Open in a new tab

Reparametrized model including one non-significant parameter estimate: influence of gerbil abundance on plague persistence. This parameter cannot be shown to be different from neither zero nor the joint value for invasion and persistence. (a,b) Probability of plague presence (ordinate), given past great gerbil abundance (abscissa) and extent of plague in neighbouring squares. Solid lines correspond to 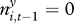Inline graphic; dashed lines correspond to 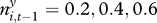Inline graphic and 0.8, in increasing distance to the abscissa. (c,d) Corresponding contour plots showing probability of plague presence, including data from a randomly selected imputation. Large points denote imputed presence of plague, small points denote imputed absence of plague.

Analogous models were tested with respect to season, as well as combinations of season and plague presence previous season. The general result showed that parameter estimates and significance levels were similar for spring and autumn, confirming the main result that seasonal effects could not be shown. The exception was that the effect of spread seemed clear for invasion in autumn but not in spring, and for persistence in spring but not in autumn (electronic supplementary material, table S2c–d).

(c). Model evaluation by receiver operating characteristic analysis

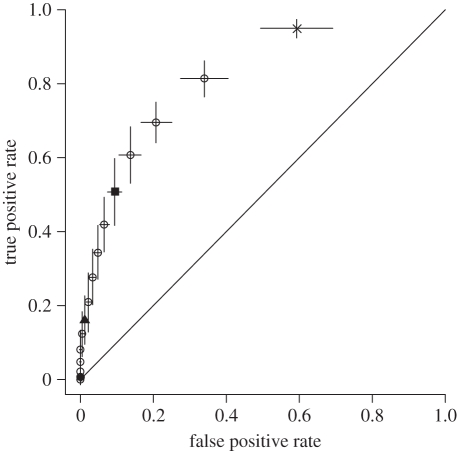
ROC analysis was performed on the final model in §3b. The results are presented in figure 3, showing the good fit of the model to the imputed data.

Figure 3.

Figure 3.

Open in a new tab

ROC curve for the final model reported in §3b (figure 2). Each point on the curve corresponds to a threshold defining whether plague absence or presence should be predicted, based on the estimated probability. Mean ± 2 s.e. are shown for the false positive rate and true positive rate for each threshold value, based on the 50 imputations. The diagonal line shows the performance of a model with no predictive power. Threshold values: cross symbol, 0.05; filled square, 0.25; filled triangle, 0.5; filled circle, 0.75.

4. Discussion

In this study, we present a statistical model seeking to describe the complex and ever-changing spatial distribution of plague in the Pre-Balkhash region. We found invasion of plague to be highly dependent on past great gerbil abundance, as was also found by Davis et al. [10]. This agrees with percolation models for the spatial spread of infectious diseases [31]. Persistence of plague was found to be highly probable at the biannual scale, reflecting the inherent resistance of great gerbils to the disease, and their high reproductive rate. That persistence frequently occurred despite low abundances suggests that the threshold identified by Davis et al. [10] is less reliable for predicting persistence than invasion, at least at the temporal and spatial scales used in this paper. Presence of plague in neighbouring areas was found to increase the risk of both invasion and persistence; for invasion, this suggests spread from one area to another; for persistence, the interpretation seems less clear.

No differences between seasons were found. Still, differences are likely to exist, because of, for example, different behaviour of great gerbils in summer and winter, and seasonal variation in flea dynamics [43,44]. Climatic variation from year to year might explain the lack of statistical significance of season. Stenseth et al. [12] found, for a different model formulation, climatic and seasonal effects in their plague threshold model; however, additional analyses including the same variables in our model showed no effects. Likewise, more differences between invasion and persistence could be expected, as well as interaction between gerbil abundance and plague in neighbouring areas. More regular sampling, generally larger samples for plague testing, and greater accuracy in gerbil and flea abundance would probably give more details on the plague dynamics in this area.

Plague is a vector-borne disease, and flea abundance is likely to be an important determinant of plague transmission rates [44–46]. The flea data in the Pre-Balkhash dataset make it in principle possible to include fleas in a more complete dynamic model [47–49]. However, because the sampling process is partly unknown and more complicated than for the gerbil data, inclusion of flea data would demand more sophisticated modelling and inference methods than discussed in this paper. The data suggest, though, that flea abundance may explain part of the observed lag between gerbil abundance increase and plague outbreaks (currently being the subject of further work within our research group). Further, plague in fleas is a possible factor facilitating persistence [22]. In the Pre-Balkhash dataset, however, plague was not found in fleas in inter-epizootic periods, except immediately before or after an outbreak (electronic supplementary material). A closer study of this would require additional fieldwork with subsequent use of modern molecular techniques.

(a). Invasion versus persistence

The probability of an invasion event was found to be generally lower than that of a persistence event. Persistence, in contrast to invasion, does not depend on arrival or activation of bacteria from a reservoir. It does, however, depend on a continued influx of new susceptibles, or on a large number of individuals surviving the disease. Great gerbils are relatively resistant to plague, and can have three litters in each season. Further, their aggregated spatial structure may lead to metapopulation dynamics, which enhances persistence of predators and diseases [32,50].

Great gerbil abundance had a strong effect on invasion, while its influence on persistence was less clear: for invasion, the slope (at logit scale) was 4.31 with a p-value of 4.03 × 10−5, while for persistence, the estimate was 2.10 with a p-value of 0.087 (electronic supplementary material, table S2b). One explanation may be that the length of the fade-out process depends on the rate of host population decrease, another that an important predictor has been ignored. This may be the flea abundance, or the influx of susceptible gerbils through births and immigration, which may be measured for example by the change in abundance or density. Attempts were made to include the latter covariate; however, no significant results were obtained (see electronic supplementary material for a list of covariates tested).

Comparing our results with the threshold model by Davis et al. [10], our findings reflect theirs for invasion events, but diverge in persistence events. Both models found very low invasion probabilities at low gerbil abundances (the lack of a sharp threshold in our results may be due to our choice of method and spatial scale). Like invasion, persistence may be expected to show threshold behaviour. However, a persistence threshold may not be easily observed in the data, for reasons given above. Moreover, the time lags used in the gerbil abundance estimates may be important. Davis et al. [10], working with a lag of 2 years, found that a threshold corresponding to an abundance of 0.33 worked well for persistence as well as invasion. With a 1.5 year lag, on the other hand, we found a substantial probability (0.1–0.5) of plague persistence also below this threshold. A preliminary analysis of persistence over the whole year, which gives a longer lag between abundance estimate and plague sampling, showed that the persistence probability at low abundances indeed drops to low levels.

(b). Emergence

We found that emergence at the scale of 20 × 20 km2 was observable as a distinct event; in the raw dataset as well, there were clear examples of this. In agreement with previous analyses [11], the emergence probability depended on past great gerbil abundance. The abundance threshold found in Davis et al. [11] corresponds to 0.4 in our analyses, below which we found the probability to be smaller than 0.05.

Although our analysis cannot confirm or rule out any of the proposed explanations for emergence, there may be indirect support to the hypothesis that the migratory bird Oenanthe isabellina and its fleas play a role in importing the disease to an area and spreading it fast [24,51]. Seen in the data are two cases of spatial clusters of emergence events in spring, at times when no plague was found anywhere else in the focus. O. isabellina nests in gerbil burrows, and in order to find a suitable nesting place, flies from burrow to burrow, possibly transporting infected fleas.

(c). Spatial transmission

For invasion, we found a significant effect of spread over summer. A plausible explanation is dispersal by the host: although great gerbils are mostly stationary, staying close to and defending their burrow systems, they also undertake shorter or longer travels. Shorter travels are up to 400 m away [52] and include those to so-called outskirt colonies, which are small, non-defended burrow systems where the gerbils can hide if a danger appears while they collect food. These outskirt colonies can be shared by several gerbil families and are believed by zoologists in Kazakhstan to be important for transmission of infected fleas from one gerbil colony to another. Longer travels include dispersal, happening in the summer mostly by young males, which travel up to 5 km to join a new family group [52,53]. This, with the observation that the number of sick animals peaks during summer [54], may explain the summer spread of plague.

For persistence, we also found an effect of plague in neighbouring areas, at least between autumn and next spring. This result raises the question why spread should be important for maintenance of plague in one area—one might think that the already ongoing epizootic would be sufficient to fuel its continuation. The mechanism for spread is also unclear: during the winter months, great gerbils are relatively inactive, although they do show movement in late autumn and early spring, when they move into or out of winter-dwelling burrows. Alternatively, the effect of plague in neighbouring squares could be due to spatial correlation not captured by the analyses, meaning that the general prevalence is high, which facilitates persistence to the next season.

5. Conclusion

The categorization of plague data into invasion and persistence showed that these event types depended differently on host abundance, as anticipated by Lloyd-Smith et al. [17]. Our results confirm that the distinction may be important in analysis of zoonosis data. Further, presence of plague in neighbouring areas was found to be important for both invasion and persistence. A plausible mechanism for spread is transport from colony to colony by great gerbils and their fleas, but birds and larger mammals may also contribute. Regardless of the mechanism, it is of great practical interest that the distribution of plague in the current season can help predict the distribution of plague in the next, along with information on the abundance of the rodent host. This is a valuable scientific basis for improving plague surveillance in Kazakhstan, where predictive models stand to relieve the financial pressures brought about by labour-intensive surveillance programmes.

Acknowledgements

The analysis reported in this paper was funded through the Centre for Ecological and Evolutionary Synthesis at the University of Oslo. We thank Ole Chr. Lingjærde for inspiration and ideas in the early phase of this project, Mike Begon for comments on the manuscript and Kyrre Kausrud for fruitful discussions. We are also grateful to the hundreds of zoologists in Kazakhstan who collected the data. Finally, we wish to thank two anonymous reviewers for their valuable comments and suggestions.

Endnotes

1

Referring to wildlife, in contrast to domestic animals or humans.

References

  • 1.Drancourt M., Raoult D. 2002. Molecular insights into the history of plague. Microbes Infect. 4, 105–109 10.1016/S1286-4579(01)01515-5 (doi:10.1016/S1286-4579(01)01515-5) [DOI] [PubMed] [Google Scholar]
  • 2.Achtman M., Zurth K., Morelli C., Torrea G., Guiyoule A., Carniel E. 1999. Yersinia pestis, the cause of plague, is a recently emerged clone of Yersinia pseudotuberculosis. Proc. Natl Acad. Sci. USA 96, 14 043–14 048 10.1073/pnas.96.24.14043 (doi:10.1073/pnas.96.24.14043) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Stenseth N. C., Atshabar B. B., Begon M., Belmain S. R., Bertherat E., Carniel E., Gage K. L., Leirs H., Rahalison L. 2008. Plague: past, present, and future. PLoS Med. 5, 9–13 10.1371/journal.pmed.0050003 (doi:10.1371/journal.pmed.0050003) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Tikhomirov E. (ed.) 1999. Epidemiology and distribution of plague. Geneva, Switzerland: World Health Organization [Google Scholar]
  • 5.WHO 2006. International meeting on preventing and controlling plague: the old calamity still has a future. Wkly Epidemiol. Rec. 81, 278–284 [PubMed] [Google Scholar]
  • 6.Kilonzo B. S., Mvena Z. S. K., Machangu R. S., Mbise T. J. 1997. Preliminary observations on factors responsible for long persistence and continued outbreaks of plague in Lushoto district, Tanzania. Acta Tropica 68, 215–227 10.1016/S0001-706X(97)00096-X (doi:10.1016/S0001-706X(97)00096-X) [DOI] [PubMed] [Google Scholar]
  • 7.Chanteau S., Ratsitorahina M., Rahalison L., Rasoamanana B., Chan F., Boisier P., Rabeson D., Roux J. 2000. Current epidemiology of human plague in Madagascar. Microbes Infect. 2, 25–31 10.1016/S1286-4579(00)00289-6 (doi:10.1016/S1286-4579(00)00289-6) [DOI] [PubMed] [Google Scholar]
  • 8.Pollitzer R. 1966. Plague and plague control in the Soviet Union: a review. New York, NY: Fordham University [Google Scholar]
  • 9.Serzhan O. S., Ageyev V. 2000. Geographical distribution and host complexes of plague-infected fleas in relation to some problems of paleogenesis of plague enzootics. Quarantine Zoonotic Dis. Kazakhstan 2, 183–192 [Google Scholar]
  • 10.Davis S., Begon M., De Bruyn L., Ageyev V. S., Klassovskiy N. L., Pole S. B., Viljugrein H., Stenseth N. C., Leirs H. 2004. Predictive thresholds for plague in Kazakhstan. Science 304, 736–738 10.1126/science.1095854 (doi:10.1126/science.1095854) [DOI] [PubMed] [Google Scholar]
  • 11.Davis S., Leirs H., Viljugrein H., Stenseth N. C., De Bruyn L., Klassovskiy N., Ageyev V., Begon M. 2007. Empirical assessment of a threshold model for sylvatic plague. J. R. Soc. Interface 4, 649–657 10.1098/rsif.2006.0208 (doi:10.1098/rsif.2006.0208) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Stenseth N. C., et al. 2006. Plague dynamics are driven by climate variation. Proc. Natl Acad. Sci. USA 103, 13 110–13 115 10.1073/pnas.0602447103 (doi:10.1073/pnas.0602447103) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Samia N. I., Chan K. S., Stenseth N. C. 2007. A generalized threshold mixed model for analyzing nonnormal nonlinear time series, with application to plague in Kazakhstan. Biometrika 94, 101–118 10.1093/biomet/asm006 (doi:10.1093/biomet/asm006) [DOI] [Google Scholar]
  • 14.Kausrud K. L., Viljugrein H., Frigessi A., Begon M., Davis S., Leirs H., Dubyanskiy V., Stenseth N. C. 2007. Climatically driven synchrony of gerbil populations allows large-scale plague outbreaks. Proc. R. Soc. B 274, 1963–1969 10.1098/rspb.2007.0568 (doi:10.1098/rspb.2007.0568) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Frigessi A., Holden M., Marshall C., Viljugrein H., Stenseth N. C., Holden L., Ageyev V., Klassovskiy N. L. 2005. Bayesian population dynamics of interacting species: great gerbils and fleas in Kazakhstan. Biometrics 61, 230–238 10.1111/j.0006-341X.2005.030536.x (doi:10.1111/j.0006-341X.2005.030536.x) [DOI] [PubMed] [Google Scholar]
  • 16.Kausrud K. L., et al. 2010. Modeling the epidemiological history of plague in Central Asia: palaeoclimatic forcing on a disease system over the past millennium. BMC Biol. 8, 112. 10.1186/1741-7007-8-112 (doi:10.1186/1741-7007-8-112) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Lloyd-Smith J. O., Cross P. C., Briggs C. J., Daugherty M., Getz W. M., Latto J., Sanchez M. S., Smith A. B., Swei A. 2005. Should we expect population thresholds for wildlife disease? Trends Ecol. Evol. 20, 511–519 10.1016/j.tree.2005.07.004 (doi:10.1016/j.tree.2005.07.004) [DOI] [PubMed] [Google Scholar]
  • 18.Bertherat E., et al. 2007. Plague reappearance in Algeria after 50 years, 2003. Emerg. Infect. Dis. 13, 1459–1462 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Batra H. V., Tuteja U., Agarwal G. S. 1996. Isolation and identification of Yersinia pestis responsible for the recent plague outbreaks in India. Curr. Sci. 71, 787–791 [Google Scholar]
  • 20.Eisen R. J., Gage K. L. 2009. Adaptive strategies of Yersinia pestis to persist during inter-epizootic and epizootic periods. Vet. Res. 40, 01. 10.1051/vetres2008039 (doi:10.1051/vetres2008039) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Drancourt M., Houhamdi L., Raoult D. 2006. Yersinia pestis as a telluric, human ectoparasite-borne organism. Lancet Infect. Dis. 6, 234–241 10.1016/S1473-3099(06)70438-8 (doi:10.1016/S1473-3099(06)70438-8) [DOI] [PubMed] [Google Scholar]
  • 22.Wimsatt J., Biggins D. E. 2009. A review of plague persistence with special emphasis on fleas. J. Vector Borne Dis. 46, 85–99 [PubMed] [Google Scholar]
  • 23.Khrustselevskiy V. P., Khrustselevskaya N. M. 1968. On the role of plague strains with different virulence and their role in the natural focality of this disease. Materialy V nauch konf protivochum uchrezd Sred Azii i Kazakhstana, pp. 76–79 Alma-Ata, Khazkstan: Central Asian Plague Control Institute [Google Scholar]
  • 24.Burdelov A. S., Kasenova A. K. 2001. Contacts of Isabelline wheatear and its specific fleas with plague causative agent. Karantin i zoonoz infektsii v Kazakhstane 4, 17–19 [Google Scholar]
  • 25.Girard J. M., Wagner D. M., Vogler A. J., Keys C., Allender C. J., Drickamer L. C., Keim P. 2004. Differential plague-transmission dynamics determine Yersinia pestis population genetic structure on local, regional, and global scales. Proc. Natl Acad. Sci. USA 101, 8408–8413 10.1073/pnas.0401561101 (doi:10.1073/pnas.0401561101) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Biggins D. E., Godbey J. L., Gage K. L., Carter L. G., Montenieri J. A. 2010. Vector control improves survival of three species of prairie dogs (cynomys) in areas considered enzootic for plague. Vector Borne Zoonotic Dis. 10, 17–26 10.1089/vbz.2009.0049 (doi:10.1089/vbz.2009.0049) [DOI] [PubMed] [Google Scholar]
  • 27.Matchett M. R., Biggins D. E., Carlson V., Powell B., Rocke T. 2010. Enzootic plague reduces black-footed ferret (Mustela nigripes) survival in Montana. Vector Borne Zoonotic Dis. 10, 27–35 10.1089/vbz.2009.0053 (doi:10.1089/vbz.2009.0053) [DOI] [PubMed] [Google Scholar]
  • 28.Fedorov V. N. 1944. On mechanism of plague microbe preservation in non-epizootic years. Vestnik microb, epidem i parazitol, pp. 27–39 (Collection of articles devoted to the 25th anniversary of Microbe Institute). Saratov, Russia: State Research Institute of Microbiology and Epidemiology of the South-East of the USSR (Microbe) [Google Scholar]
  • 29.Stapp P., Antolin M. F., Ball M. 2004. Patterns of extinction in prairie dog metapopulations: plague outbreaks follow El Nino events. Front. Ecol. Environ. 2, 235–240 [Google Scholar]
  • 30.Snäll T., O'Hara R. B., Ray C., Collinge S. K. 2008. Climate-driven spatial dynamics of plague among prairie dog colonies. Am. Nat. 171, 238–248 10.1086/525051 (doi:10.1086/525051) [DOI] [PubMed] [Google Scholar]
  • 31.Davis S., Trapman P., Leirs H., Begon M., Heesterbeek J. A. P. 2008. The abundance threshold for plague as a critical percolation phenomenon. Nature 454, 634–637 10.1038/nature07053 (doi:10.1038/nature07053) [DOI] [PubMed] [Google Scholar]
  • 32.Salkeld D. J., Salathe M., Stapp P., Jones J. H. 2010. Plague outbreaks in prairie dog populations explained by percolation thresholds of alternate host abundance. Proc. Natl Acad. Sci. USA 107, 14 247–14 250 10.1073/pnas.1002826107 (doi:10.1073/pnas.1002826107) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Gratz N. 1999. Rodent reservoirs and flea vectors of natural foci of plague. Plague manual: epidemiology, distribution, surveillance and control, pp. 63–96 Geneva, Switzerland: World Health Organization [Google Scholar]
  • 34.Naumov N. P., Lobachev V. S. 1975. Ecology of the desert rodents of the U.S.S.R. (jerboas and gerbils): great gerbil. In Rodents in desert environments (eds Prakash I., Ghosh P. K.), pp. 549–598 The Hague, The Netherlands: Dr W. Junk Publishers [Google Scholar]
  • 35.Randall J. A., Rogovin K., Parker P. G., Eimes J. A. 2005. Flexible social structure of a desert rodent, Rhombomys opimus: philopatry, kinship, and ecological constraints. Behav. Ecol. 16, 961–973 10.1093/beheco/ari078 (doi:10.1093/beheco/ari078) [DOI] [Google Scholar]
  • 36.Gage K. L., Kosoy M. Y. 2005. Natural history of plague: perspectives from more than a century of research. Annu. Rev. Entomol. 50, 505–528 10.1146/annurev.ento.50.071803.130337 (doi:10.1146/annurev.ento.50.071803.130337) [DOI] [PubMed] [Google Scholar]
  • 37.R Development Core Team 2009. R: a language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing [Google Scholar]
  • 38.Rubin D. B. 2004. Multiple imputation for nonresponse in surveys. New York, NY: John Wiley & Sons, Inc [Google Scholar]
  • 39.Breslow N. E., Clayton D. G. 1993. Approximate inference in generalized linear mixed models. J. Am. Stat. Assoc. 88, 9–25 10.2307/2290687 (doi:10.2307/2290687) [DOI] [Google Scholar]
  • 40.Venables W. N., Ripley B. D. 2002. Modern applied statistics with S, 4th edn. New York, NY: Springer [Google Scholar]
  • 41.Lumley T. 2010. mitools: tools for multiple imputation of missing data. R package version 2.0. See http://www.R-project.org
  • 42.Fawcett T. 2006. An introduction to ROC analysis. Pattern Recogn. Lett. 27, 861–874 10.1016/j.patrec.2005.0.010 (doi:10.1016/j.patrec.2005.0.010) [DOI] [Google Scholar]
  • 43.Wilder A. P., Eisen R. J., Bearden S. W., Montenieri J. A., Tripp D. W., Brinkerhoff R. J., Gage K. L., Antolin M. F. 2008. Transmission efficiency of two flea species (Oropsylla tuberculata cynomuris and Oropsylla hirsuta) involved in plague epizootics among prairie dogs. Ecohealth 5, 205–212 10.1007/s10393-008-0165-1 (doi:10.1007/s10393-008-0165-1) [DOI] [PubMed] [Google Scholar]
  • 44.Tripp D. W., Gage K. L., Montenieri J. A., Antolin M. F. 2009. Flea abundance on black-tailed prairie dogs (Cynomys ludovicianus) increases during plague epizootics. Vector Borne Zoonotic Dis. 9, 313–321 10.1089/vbz.2008.0194 (doi:10.1089/vbz.2008.0194) [DOI] [PubMed] [Google Scholar]
  • 45.Eisen R. J., Bearden S. W., Wilder A. P., Montenieri J. A., Antolin M. F., Gage K. L. 2006. Early-phase transmission of Yersinia pestis by unblocked fleas as a mechanism explaining rapidly spreading plague epizootics. Proc. Natl Acad. Sci. USA 103, 15 380–15 385 10.1073/pnas.0606831103 (doi:10.1073/pnas.0606831103) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 46.Wilder A. P., Eisen R. J., Bearden S. W., Montenieri J. A., Gage K. L., Antolin M. F. 2008. Oropsylla hirsuta (Siphonaptera: Ceratophyllidae) can support plague epizootics in black-tailed prairie dogs (Cynomys ludovicianus) by early-phase transmission of Yersinia pestis. Vector Borne Zoonotic Dis. 8, 359–367 10.1089/vbz.2007.0181 (doi:10.1089/vbz.2007.0181) [DOI] [PubMed] [Google Scholar]
  • 47.Webb C. T., Brooks C. P., Gage K. L., Antolin M. F. 2006. Classic flea-borne transmission does not drive plague epizootics in prairie dogs. Proc. Natl Acad. Sci. USA 103, 6236–6241 10.1073/pnas.0510090103 (doi:10.1073/pnas.0510090103) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 48.Foley P., Foley J. 2010. Modeling susceptible infective recovered dynamics and plague persistence in California rodent-flea communities. Vector Borne Zoonotic Dis. 10, 59–67 10.1089/vbz.2009.0048 (doi:10.1089/vbz.2009.0048) [DOI] [PubMed] [Google Scholar]
  • 49.Samia N. I., Kausrud K. L., Heesterbeek J. A. P., Ageyev V. S., Begon M., Chan K. S., Stenseth N. C. In press The dynamics of the plague-wildlife-human system in Central Asia is controlled by two epidemiological thresholds. Proc. Natl Acad. Sci. USA. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 50.Hanski I. 1999. Metapopulation ecology. New York, NY: Oxford University Press [Google Scholar]
  • 51.Kalabukhov N. I. 1969. Lasting interruptions in epizootic activity of natural plague foci and their possible causes. Zoology Zh. 43, 165–178 [Google Scholar]
  • 52.Rotschild V. E. 1978. Spatial structure of plague natural focus and methods of its study. Moscow, Russia: Publishing house of Moscow University [Google Scholar]
  • 53.Randall J. A., Rogovin K. A. 2002. Variation in and meaning of alarm calls in a social desert rodent Rhombomys opimus. Ethology 108, 513–527 10.1046/j.1439-0310.2002.00797.x (doi:10.1046/j.1439-0310.2002.00797.x) [DOI] [Google Scholar]
  • 54.Begon M., Klassovskiy N., Ageyev V., Suleimenov B., Atshabar B., Bennett M. 2006. Epizootiologic parameters for plague in Kazakhstan. Emerg. Infect. Dis. 12, 268–273 [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Proceedings of the Royal Society B: Biological Sciences are provided here courtesy of The Royal Society

RESOURCES