Disentangling the effect of genes, the environment and chance on sex ratio variation in a wild bird population

Abstract

Sex ratio theory proposes that the equal sex ratio typically observed in birds and mammals is the result of natural selection. However, in species with chromosomal sex determination, the same 1 : 1 sex ratio is expected under random Mendelian segregation. Here, we present an analysis of 14 years of sex ratio data for a population of song sparrows (Melospiza melodia) on Mandarte Island, at the nestling stage and at independence from parental care. We test for the presence of variance in sex ratio over and above the binomial variance expected under Mendelian segregation, and thereby quantify the potential for selection to shape sex ratio. Furthermore, if sex ratio variation is to be shaped by selection, we expect some of this extra-binomial variation to have a genetic basis. Despite ample statistical power, we find no evidence for the existence of either genetic or environmentally induced variation in sex ratio, in the nest or at independence. Instead, the sex ratio variation observed matches that expected under random Mendelian segregation. Using one of the best datasets of its kind, we conclude that female song sparrows do not, and perhaps cannot, adjust the sex of their offspring. We discuss the implications of this finding and make suggestions for future research.

1. Introduction

Fisher's principle of equal investment states that, all else (including the cost of producing male and female offspring) being equal, natural selection favours the production of an equal number of sons and daughters, resulting in an evolutionarily stable strategy of 1 : 1 sex ratio [1]. Although this principle is often considered the null model for sex ratio evolution, testing its predictions in birds and mammals has proved challenging [2].

The fact that most bird and mammal populations, for which the costs of producing a son or a daughter are often similar, show primary sex ratios close to equality (e.g. [3]) appears to support Fisher's principle. This is unsurprising, however, given that it was this ubiquity of unbiased sex ratios that Fisher aimed to explain [2]. Furthermore, although Fisher's principle of equal investment predicts primary sex ratio to be biased towards the cheaper sex in those populations in which males and females differ in costs, it is in such cases where one sex may benefit more from increased investment in terms of fitness, violating a major assumption underlying Fisher's principle of equal investment [4]. To complicate matters further, these differences in the fitness returns of sons and daughters may be dependent on environmental factors, such as maternal condition or paternal attractiveness [4,5]. Hence, it is extremely difficult to formulate accurate predictions for the population mean primary sex ratio, especially in natural vertebrate populations [2,4]. However, such predictions are essential if we want to be able to conclude anything from patterns in population- or species-level mean sex ratio data.

Adaptive explanations for population mean sex ratios typically being close to equality are further hampered by the fact that in species with chromosomal sex determination (XY in most mammals and some insects, and ZW in, among others, birds) exactly the same 1 : 1 primary sex ratio is expected via the random segregation of the two sex chromosomes in the heterogametic sex (males in mammals and females in birds). This raises the question of whether the equal sex ratios so commonly observed in vertebrate populations solely reflect Mendelian segregation (i.e. chance), or whether parents also possess some means of overcoming the constraints imposed by chromosomal sex determination, generating variation in sex ratio that can be shaped by selection. Distinguishing between these two possibilities is a key requirement for any empirical study of adaptive sex ratio theory.

One step towards testing whether observed sex ratios reflect Mendelian segregation versus adaptive sex ratio variation is to quantify the variation in sex ratio within a population (rather than simply estimating the mean sex ratio). If sex ratios are shaped by Mendelian sampling alone (our null model), the expected variance in sex ratio (the proportion of offspring that is male) at the population level is equal to p(1 − p)/n, where p is the probability of producing a male offspring and n is the brood or litter size. Any factor that introduces variation in p, irrespective of whether it is genetic or environmental, will cause the within-population variance in sex ratio to deviate from this expectation [6]. This will be so even if the mean population sex ratio does not deviate from 0.5. Hence, a comparison of the observed variance in sex ratio to that expected under Mendelian sampling can provide valuable information on the existence of individual variation in p, and hence the opportunity for selection to shape sex ratio variation. However, most studies have focussed on estimating the mean sex ratio and largely ignored its variance. Indeed, evidence of extra-binomial variance (i.e. overdispersion) in sex ratio is typically treated as a statistical nuisance, rather than as a parameter of biological interest (as pointed out in [6]).

As sex ratio theory views sex ratio as an adaptive trait that is at least partly under genetic control, we would expect the extra-binomial variance in sex ratio to have an additive genetic component [4,7,8]. However, while virtually all life history, morphological and behavioural traits have been found to be heritable to some degree, also in natural populations (e.g. [9]), evidence that sex ratio is heritable in species with heterogametic sex determination is scarce and inconclusive. In Drosphila melanogaster, for example, additive genetic variance for sex ratio was effectively zero, and its narrow sense heritability was estimated to have an upper bound of a mere 0.3 per cent [7]. In Drosphila mediopunctata, on the other hand, sex ratio was found to have a statistically significant heritability of 41 per cent [10]. Furthermore, despite a major economic interest in biasing sex ratios through artificial selection in livestock, studies that provide evidence for the existence of a heritable component to sex ratio variation in poultry and cattle are outnumbered by studies that do not [11]. For example, in one of the largest studies of its kind, the heritability of litter sex ratio in Iberian pigs was estimated to be less than 0.01 per cent [12].

Despite several well-known examples of adaptive primary sex ratio adjustment in birds (e.g. [13–16], but see [17]), the mechanism that allows females (the heterogametic sex) to control the sex of their offspring at conception remains elusive [18–20]. However, while most studies are limited to measuring sex ratios at conception or hatching, Fisher's equal investment principle posits that it is the investment until independence from parental care that is shaped by selection. Thus, provided that parents can distinguish male from female offspring, this opens the possibility of altering offspring sex ratio after birth [4]. Although this may be costly in many species, in altricial birds, where most parental investment takes place after birth, these costs may be relatively small. Any estimate of sex ratio variation should thus ideally cover the full period across which parental investment occurs, rather than focus on primary sex ratio variation alone.

Few studies have explicitly tested for the presence of variation in sex ratio over and above the sampling variation introduced by Mendelian segregation in a natural population, and to our knowledge, no study has tested whether this extra-binomial variance has a heritable (additive genetic) component. Doing this requires detailed sex ratio data for numerous related individuals, ideally not only at birth, but also at the time when offspring become independent from parental care.

Here we analyse 14 years of sex ratio data from a pedigreed population of songs sparrows (Melospiza melodia) on Mandarte Island, both soon after hatching and at independence from parental care. Brood parasitism by brown-headed cowbirds (Molothrus ater), food availability and paternal song complexity have been reported to influence sex ratio at the time of fledging or independence from parental care in other song sparrow populations [21,22]. Furthermore, in song sparrows on Mandarte, variation in male reproductive success is greater than in female reproductive success, extra-pair paternity is relatively high [23], and males are slightly larger than females [24], each of which may be associated with skews in offspring sex ratio. Hence, if females have some form of control over the sex ratio of their brood, adaptive sex ratio manipulation, and hence individual variation in p, could reasonably be expected in this system. Additionally, owing to the small size and the isolated nature of the population, and the absence of any inbreeding avoidance, both the mean and the variance in inbreeding are relatively high [25], and inbreeding may introduce additional (adaptive or non-adaptive) variation in sex ratio [26].

The inherently non-Gaussian distribution of sex ratio causes major statistical complications in estimating components of genetic and non-genetic variance and hence heritability. Hence, we use a generalized linear animal model to explicitly separate variance in sex ratio into variance owing to both genetic and non-genetic effects, as well as binomial sampling. This allows us to quantify the amount of individual variation in sex ratio, and the degree to which this variation is heritable, thereby testing a central tenet of adaptive sex ratio theory.

2. Material and methods

(a). Study population and dataset

A resident population of song sparrows (M. melodia) inhabiting Mandarte Island (ca 6 hectares) near the south-eastern coast of Vancouver Island, Canada, has been monitored intensively since 1975 [25]. All song sparrows hatched on Mandarte, as well as all adult immigrants (1.1 yr⁻¹ on average), are colour-ringed and can be identified individually. All breeding attempts are being closely monitored, and all social parents (those incubating clutches and provisioning chicks) are identified. Circa 24 days post-hatching, when offspring begin foraging independently, territories are searched for offspring that have survived until independence from parental care.

During 1993–2006, blood samples were collected from virtually all chicks that survived to ca 6 days post-hatch [23]. In 2004, nestlings were individually marked and a blood sample was taken when they were 1 day old to estimate the mortality rate between hatching and day 6. In that year, this mortality was negligible (less than 2%). Brood sizes varied between one and four, with a mean brood size (±standard deviation) of 2.73 (±0.97). We determined the sex of 1850 nestlings from a total of 699 broods using standard and well-established molecular protocols [27]. Polymerase chain reaction amplification of the CHD1 gene was performed with the primer pair P2 and P8. A subset of the samples was amplified with the primer pair P2 and P17. The sex of 42 nestlings from 36 clutches could not be determined, because of technical problems or because no blood sample was available. In addition, as we know which offspring reach independence from parental care [25], we have data on the sex ratio at independence from parental care of all 606 broods in which at least one offspring survived (mean brood size at independence: 2.05 ± 0.86 offspring).

Before 1993, we used observations of parental behaviour to assign offspring to parents. From 1993 onwards, blood samples from the complete adult population allowed us to assign offspring to their genetic parents with high statistical confidence [23]. These analyses showed that 28 per cent of offspring were sired by an extra-pair male, while all mothers were correctly assigned by behaviour [23]. Based on this, we reconstructed the pedigree for the complete population, going back to the beginning of the study in 1975 [21,22]. Paternity assignment for individuals hatched before 1993 will contain errors due to extra-pair paternity. While these errors may bias heritability estimates downwards, omitting the social pedigree for 1975–1992 reduces statistical power (also see [28]). Here, we present results based on the complete pedigree (1975–2006), noting that analyses based only on the genetic pedigree from 1993 onwards give very similar results and lead to identical conclusions.

Non-informative animals, i.e. animals without sex ratio data that were not responsible for a pedigree link between two individuals with sex ratio data, were removed from the pedigree using the prunePed function in the R package MCMCglmm [29,30]. This pruned pedigree contained 746 individuals, 113 of which had unknown parents. Individual pedigrees went back 7.99 generations on average, and 22 at most. Fifty-eight per cent of the pairwise coefficients of relatedness were non-zero, and 27 per cent was greater than or equal to 0.125. The mean relatedness was 0.081 (excluding coefficients of relatedness equal to zero). In total, the pedigree contained 566 links between full sibs, and 358 and 393 links between maternal and paternal half sibs, respectively. Finally, 43 per cent of the individuals had a non-zero coefficient of inbreeding (0.066 on average). Summary statistics were calculated with the help of the R package Pedantics [31].

(b). Generalized linear mixed model analyses

Our dataset allowed us to estimate the variance in offspring sex ratio, both at ca 6 days post-hatching and at independence from parental care, and to test how much of the observed variation in sex ratio was accounted for by additive genetic variance as opposed to environmental/non-additive genetic and sampling variance.

Variance components were estimated by fitting a generalized animal model. An animal model is a specific type of mixed model that explicitly takes into account the resemblance among all relatives. It models an individual's phenotype as a function of a number of fixed and random effects, including a random additive genetic ‘animal’ effect. The variance–covariance structure of the latter is proportional to the pairwise coefficients of relatedness among all individuals in the pedigree. Thereby an animal model allows us to fully exploit all pedigree data, and to simultaneously account for a number of potentially confounding environmental effects [32–34]. Fitting an animal model, or any mixed model for that matter, with non-Gaussian traits using (restricted) maximum-likelihood techniques is challenging. Hence, we used Bayesian Markov chain Monte Carlo (MCMC) techniques implemented in the R package MCMCglmm [30,35].

The probability of having a male offspring (p) was modelled as a trait of the mother, fitting a random additive genetic (animal) effect, as well as random effects of brood and individual (i.e. maternal) identity. The ‘animal’ effect estimates the variance in p that can be attributed to additive genetic variance (V_A) among females. The ‘individual’ effect accounts for variation in p among females for any reasons other than additive genetic effects, for example, owing to environmental experiences/conditions that are preserved across repeated records from the same female. Thereby it accounts for the non-independence of multiple broods laid by a single female. Although the variance accounted for by ‘individual’ over and above the additive genetic variance V_A is referred to as the permanent environment variance (V_PE), at least some of the non-additive genetic variance will be incorporated in this term. Finally, the ‘brood’ effect accounts for any environmental and part of the non-additive genetic variation in p that may exist among broods (V_brood). We did not include any fixed effects in addition to our fixed intercept, the latter providing an estimate of the mean (logit transformed) probability of producing a male.

Models were run with priors for the random brood (V_brood), permanent environment (V_PE) and additive genetic (V_A) variances set to 1, and a degree of belief (ν) of 1. As we only have a single observation per trial (i.e. each offspring's sex is realized only once), the residual variance V_R cannot be estimated in binary models [36,37]. V_R was therefore fixed at a value of 10, which in our case was found to optimize mixing of the chains (i.e. minimized autocorrelations among subsequent iterations). Estimates were insensitive to the choice of the priors (prior variances ranging from 0.01 to 100). Parameter expansion was used to avoid poor mixing if variance component estimates were close to zero. All models were run for 1 000 000 iterations, preceded by a burn-in of 50 000 iterations. Estimates of every 100th iteration were stored to reduce the autocorrelation among subsequent iterations (autocorrelations were weaker than 0.05 for all variance components). This resulted in an effective sample size of 8000–10 000 for all random effects. This provides us with the posterior probability density functions for the intercept and all variance components, and thereby with the most probable size of each variance component, as well as its 95% credible interval (CI). The latter provides a measure of the precision of the estimate. If the estimate is not statistically different from zero, the upper limit of the CI provides an estimate of the smallest variance we would have been able to detect. Note that, as the lower limit of the variance components is bound to zero, their CIs can be extremely close to, but they cannot overlap zero.

The absolute sizes of the variance components depend on the value chosen for the residual variance. This makes it difficult to interpret them directly, or to compare them with estimates from other studies which assume a different residual variance. Although here we could rescale the variance components by the assumed residual variance, we were primarily interested in whether any variance components were significantly greater than zero, and in the proportion of the variance accounted for by additive genetic variance (i.e. the heritability). The heritability of sex ratio on the underlying (logit-linear) liability scale, i.e. the proportion of the variance in logit(p) that has an additive genetic basis, was calculated as

where π²/3 is the distribution-specific variance for the logistic distribution [37]. Because all variance components are affected similarly by the value at which V_R is fixed, the heritability is independent of the value at which V_R is fixed.

Although the availability of pedigree data makes it possible to explicitly test whether any individual variation in p has a genetic basis, the generalized mixed model framework employed here can provide important insights into the nature of sex ratio even in the absence of pedigree data. For example, whenever one has sex ratio data for multiple broods or litters per female, the variance explained by ‘individual’ provides us with an estimate of its repeatability, and thereby of the upper limit of its heritability (but see [38]). Thus, although high-quality pedigree data are available for only few populations, it is possible to obtain a standardized measure of the amount of among-individual variation in sex ratio in any population and species for which longitudinal data on individually marked individuals is available.

(c). Simulations

Because variances can take only positive values in the mixed model described above, these models cannot detect any underdispersion in sex ratio. Thus, to supplement these analyses, and to visualize the similarities and differences between the observed distribution of sex ratio and that expected under Mendelian sampling, we also performed a series of simulations (following [6]). Note that these simulations only require data on the number of male and female offspring in a nest or litter, and hence they allow for the quantification of the degree of overdispersion in any population for which individual sex ratio data are available.

We generated 100 000 new datasets, and for each simulated dataset, we then used the observed distribution of brood sizes (or strictly speaking of the number of sexed offspring per brood) and generated for each brood a random number of males, assuming a constant probability of producing a male (p) equal to the observed population mean sex ratio. Thereby we take into account the variation in sex ratio introduced by variation in brood size, which is crucial in species like the song sparrow that have relatively small broods. From these simulated datasets, we calculated the mean expected frequency of each sex ratio and its 95% CI. This provides us with the expected distribution of sex ratios under the null model of random Mendelian segregation, against which to compare the observed sex ratio distribution. The degree to which the observed variance exceeds the expected variance provides a measure of the degree of overdispersion, and thus of the variance in p. Although here we present only analyses combining all brood sizes, analysing all brood sizes separately (excluding brood sizes of one) leads to identical conclusions.

R scripts for both the MCMCglmm analyses and the simulations are available as electronic supplementary material.

3. Results

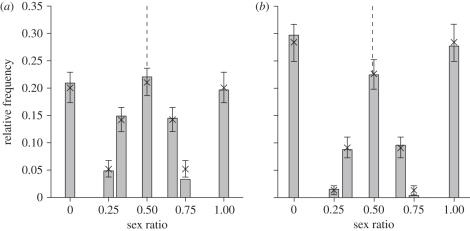
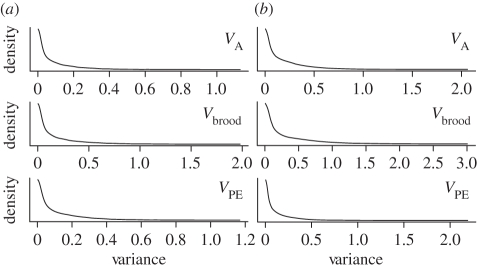
Across all years, the mean sex ratio across all offspring, and hence the average probability of a female producing a male offspring (p), was very close to 0.5 (day 6: p = 0.499, 95% CI: 0.459–0.530; independence: p = 0.491, 95% CI: 0.459–0.530). The variance in sex ratio observed was 0.115 at day 6, and 0.150 at independence (figure 1). Despite this substantial observed variation in sex ratio among broods, there was no evidence for variation in p. Specifically, estimates of V_A, V_brood and V_PE all converged towards zero (figure 2). Consequently, the heritability of sex ratio was estimated to be 6.03 × 10⁻⁵ at day 6, with a 95% CI ranging from 0 to 2.4 per cent, and 1.78 × 10⁻⁴ at independence (95% CI: 0–4.2%).

Figure 1.

(a) Observed variation in sex ratio at day 6 (grey bars) and (b) at independence from parental care (grey bars), and the simulated sex ratio distribution expected under random Mendelian segregation and equal probability of producing a male or a female (mean, indicated with crosses and its 95% CI). The sex ratio is expressed as the proportion of males in a brood. The dashed lines indicate the mean observed sex ratio.

Figure 2.

The posterior probability density functions for, from top to bottom, the additive genetic variance (V_A), the brood variance (V_brood) and the permanent environmental variance (V_PE) in the probability of having a male offspring (a) at day 6 and (b) at independence from parental care.

The absence of any extra-binomial variance in sex ratio was confirmed by simulations, which show a very close fit between the observed variance in sex ratio and that expected under random Mendelian segregation (random expectation for day 6: 0.115; independence: 0.148; figure 1). The 95% CI of the ratio between the observed and the expected (i.e. simulated) variance ranged from 0.941 to 1.063 (mean: 1.000) at day 6, and from 0.962 to 1.065 at independence (mean: 1.011). The observed sex ratio variance was greater than the expected variance in 48 (at day 6) and 66 per cent (at independence) of the simulations.

4. Discussion

Variation in the probability of producing a son or a daughter among individuals or broods, which provides the basis for adaptive sex ratio theory, creates extra-binomial variance in sex ratio. We observed considerable variation in brood sex ratio, both at the nestling stage and at independence from parental care (figure 2). However, despite ample statistical power (as illustrated by the narrow CIs on our heritability estimates), owing to our large amount of sex ratio data, a comprehensive pedigree and the application of state-of-the-art analytical tools that are designed to use these data to their full potential, we find no evidence for extra-binomial variation in sex ratio, with both genetic and environmental effects explaining less than a few per cent of the variation. Thus, although it has been argued that randomness is not a reasonable null hypothesis when it comes to sex ratio, and that statistical tests of sex ratio variation should focus on trying to distinguish adaptive from non-adaptive variation [19], here we show that variation in sex ratio observed in the song sparrow population on Mandarte Island over this 14 year period can completely be attributed to random Mendelian segregation and variation in brood size alone.

There are a number of potential explanations for the absence of extra-binomial variance in sex ratio in general, and of genetic variation in particular [39]. First, selection on sex ratio may be absent or very weak in this population. This may be because the fitness costs and benefits of producing sons and daughters are equal in song sparrows living on Mandarte. However, as pointed out in §1, results from previous studies on this and other song sparrow populations make this unlikely [21–24]. Alternatively, there may be so many opposing selective forces acting on sex ratio that net selection is weak [39]. However, although sex ratio being selectively neutral may explain the fact that the mean sex ratio is close to equality, it does not explain the absence of environmentally induced variation, which has been argued to be common [19]. Similarly, traits more distantly associated with fitness are typically found to have relatively high levels of additive genetic variation (e.g. [40–42]).

Alternatively, there may be strong selection favouring equal sex ratios, for example, because the benefits of sex ratio manipulation are off-set by the costs of sex ratio control [43], or by selection against parental control from the perspective of the gametes [19,44]. As a consequence of such strong selection, all genetic variation underlying sex ratio variation that was once present may have been eroded [45]. In fact, the mechanism of chromosomal sex determination itself can be viewed as the outcome of such strong selection [39]. Furthermore, sex ratio theory does not make any assumptions about whether additive genetic variation for sex ratio is present in contemporary populations [18]. However, although traits under strong selection, such as fitness traits, typically have low heritabilities, they do generally still show genetic variation [40–42]. Furthermore, if selection was indeed strongly favouring a 1 : 1 sex ratio, we might expect the evolution of a mechanism that reduces the random variation around the optimal 1 : 1 sex ratio, at least in very small populations [46]. Except for the unlikely case in which the effects of such a variance-reducing mechanism (resulting in variance in p within broods) would exactly balance any variance in p among broods, we would expect this to result in sub-binomial variance in sex ratio, or underdispersion [6]. However, our simulations show no evidence for such a phenomenon.

Finally, our results are compatible with the view that female song sparrows are unable to exercise control over the sex of their offspring. Why song sparrows living on Mandarte Island would be different in this respect from other passerine species [13–16], which have been reported to be able to escape from the constraints imposed by random sex chromosome segregation, remains an open question. Explaining such fundamental differences among species or populations is a major challenge [2,20]. For example, in the absence of strong selection favouring adaptive sex ratio manipulation, a costly sex ratio-biasing mechanism may have disappeared from the population. Alternatively, such a mechanism may have never evolved in the first place. A first step towards answering these questions would be to estimate the relative roles of genes, the environment and chance in a wide range of other species.

The animal model analyses allow us to estimate the importance of additive genetic effects in shaping sex ratio variation (i.e. V_A). However, we cannot a priori rule out a role for non-additive genetic effects, for example owing to dominance. While testing for dominance variance directly is far from trivial, we can indirectly test for the existence of directional dominance by testing for inbreeding depression in sex ratio. However, although significant effects of inbreeding have been found within this population for a number of traits (e.g. [47,48]), and one would expect to find an effect of inbreeding on sex ratio in at least some populations and species [26], the absence of any extra-binomial variation implies that there is no room for non-additive genetic effects shaping variation in sex ratio. Similarly, the lack of extra-binomial variation suggests that, in contrast to a nearby mainland song sparrow population [21], there is no effect of brown-headed cowbird parasitism on sex ratio. Indeed, the sex ratio of local recruits to the Mandarte population is unrelated to parasitism after 36 years of study (unpublished data; correlation between level of parasitism and mean sex ratio of recruits: r = −0.01, n = 36, p = 0.95), and no consistent effect of parasitism on nestling survival or mass has been detected [49,50]. This lends support to the assumption of equal offspring sex ratios in spatial models of the impact of parasitism on host demography, which predict population trends that closely match long-term censuses for replicate study populations and the study region as a whole [51].

One might argue that one does not so much expect genetic variation in sex ratio per se, but rather in how females adjust the sex ratio of their brood in response to factors like food availability, their condition or mate attractiveness [5,18,20]. In other words, for differential sex ratio manipulation to evolve, we require plasticity in sex ratio to be heritable, rather than the mean sex ratio. However, any genetic variation in plasticity (i.e. the slope of the reaction norm) is likely to generate variation in sex ratio (which we did not find). Furthermore, if sex ratio was a function of some (unmeasured) heritable male characteristic (e.g. attractiveness), we would expect a significant effect of a female's mate on the sex ratio of her brood. However, treating sex ratio as a trait of the male, rather than as a trait of the female, provided identical results with our dataset (results not presented). Although the statistical framework that would allow us to estimate the heritability of sex ratio plasticity is in place [52], in the absence of any extra-binomial variance in sex ratio we are unable to explore this possibility with our dataset. However, other species with good evidence for adaptive sex ratio adjustment would offer an excellent opportunity to quantify the genetic basis of sex ratio plasticity.

Using one of the best datasets of its kind, we conclude that female song sparrows do not adjust the sex of their offspring. We cannot unequivocally determine whether this is because they cannot adjust their sex ratio, or because they do not need to, but for now the former would appear to be the most parsimonious explanation. More generally, we emphasize the importance of testing for extra-binomial variation or overdispersion, or in other words, whether there is any variation in sex ratio that needs explaining. Given that this is relatively straightforward using the methods outlined here, doing this across a wide range of populations and species can provide us with an unbiased estimate of the relative magnitude of extra-binomial sex ratio variation, irrespective of a priori reasons to expect adaptive sex ratio manipulation. Such an analysis could identify the potential for adaptive sex ratio manipulation across a wide range of taxa.