Connectivity dominates larval replenishment in a coastal reef fish metapopulation

Abstract

Direct estimates of larval retention and connectivity are essential to understand the structure and dynamics of marine metapopulations, and optimize the size and spacing of reserves within networks of marine-protected areas (MPAs). For coral reef fishes, while there are some empirical estimates of self-recruitment at isolated populations, exchange among sub-populations has been rarely quantified. Here, we used microsatellite DNA markers and a likelihood-based parentage analysis to assess the relative magnitude of self-recruitment and exchange among eight geographically distinct sub-populations of the panda clownfish Amphiprion polymnus along 30 km of coastline near Port Moresby, Papua New Guinea. In addition, we used an assignment/exclusion test to identify immigrants arriving from genetically distinct sources. Overall, 82 per cent of the juveniles were immigrants while 18 per cent were progeny of parents genotyped in our focal metapopulation. Of the immigrants, only 6 per cent were likely to be genetically distinct from the focal metapopulation, suggesting most of the connectivity is among sub-populations from a rather homogeneous genetic pool. Of the 18 per cent that were progeny of known adults, two-thirds dispersed among the eight sub-populations and only one-third settled back into natal sub-populations. Comparison of our data with previous studies suggested that variation in dispersal distances is likely to be influenced by the geographical setting and spacing of sub-populations.

1. Introduction

In marine ecosystems, the extent to which discrete populations are linked by dispersal (either larvae, juveniles or adults) is termed connectivity [1]. Connectivity can have different meanings and implications depending on the scale considered and how it is measured. From an evolutionary perspective, connectivity can be defined as the degree to which gene flow affects evolutionary processes within populations (genetic connectivity) [2]. From an ecological perspective, demographically connected populations are those in which population growth rates are affected by dispersal [3]. Demographic connectivity has been acknowledged as a vital parameter for understanding the dynamics of populations and how they respond to natural and/or human disturbances [4–8]. Most populations of marine organisms are likely to function as metapopulations where numerous sub-populations are connected to varying degrees by larval dispersal [9–11]. Estimates of the magnitude of retention within and connectivity among sub-populations at ecological timescales are essential to understand natural metapopulation dynamics (e.g. [12–14]) and model human impacts on marine ecosystems [15]. In addition, the efficacy of management strategies, such as no-take marine reserve networks, depends on how individual reserve populations function and how they are connected to the metapopulation at larger scale [16,17]. How individual reserves function depends on the degree to which they are self-sustaining, are connected to zones open to fishing and are connected to other reserves in the network [11,17,18]. These functions cannot be confirmed without quantifying patterns of retention within and connectivity among populations. While the nature of demographic connectivity among marine populations is beginning to be described [16,19], the factors that shape its variation remain poorly understood.

The metapopulation concept is particularly applicable to coral reef organisms with pelagic larvae, as adult populations are usually restricted to discrete patches of reef habitat [10,17]. Recent empirical studies have revealed that local replenishment of coral reef fishes is significantly higher than previously envisaged [20–24]. However, in all these studies, a significant proportion of the newly settled juveniles originated from locations beyond the spatial extent of focal populations. Coupled biophysical models have suggested that ecologically relevant larval dispersal in reef fishes occurs over scales of 10–100 km in the Caribbean Sea [25,26] and along the Great Barrier Reef [27]. These modelling studies have also predicted that levels of self-recruitment may be highly variable among reefs. Testing these model predictions requires estimates of retention within and connectivity among sub-populations on a larger scale than has previously been available.

Empirical studies of demographic connectivity have suggested that variation in dispersal distance among species is more likely to be influenced by geographical isolation and spacing of reefs than individual species characteristics [17]. Modelling studies have provided some support for this idea, with lower simulated self-recruitment of reef fish species along an extensive system of barrier reefs [27] than on more isolated oceanic reefs in the Caribbean [26]. However, field data on population connectivity remain insufficient to test the accuracy of these simulated dispersal outcomes. The empirical studies conducted to date, using otolith chemistry [24], mass marking of larvae [21,22,28] and DNA parentage analysis [22,23], have primarily been limited to estimating levels of self-recruitment within populations. While one study has documented dispersal from a small island to distant reefs [23], we have no direct quantitative estimates of connectivity in situations where sub-populations are distributed among several sites with suitable habitats.

The aim of this study was to apply parentage analysis and assignment tests based on hyper-variable microsatellite DNA markers to investigate self-recruitment and demographic connectivity among sub-populations using as a model the panda anemonefish (Amphiprion polymnus) in Bootless Bay, Papua New Guinea. The approach was based on the identification of offspring produced by genotyped parents. Natal origins of recently settled recruits can then be determined providing the location of the parents is known or can be assumed at the time of conception. Parentage analysis based on microsatellite markers has been validated in two species of anemonefishes, A. polymnus [22] and Amphiprion percula [23], by comparing the results with those obtained by simultaneous use of chemical tagging techniques on the same individuals. These data represent the first direct estimates of self-recruitment and connectivity among geographically isolated sub-populations of a coral reef fish.

2. Methods

(a). Study species and location

The panda clownfish (A. polymnus) is a southeast Asian endemic that lives in close association with discrete aggregations of two species of anemone (Stichodactyla hadonni and Heteractis crispa) occurring in sandy habitats associated with coral reefs [29]. Each anemone is usually occupied by one breeding pair and up to eight smaller non-breeders and juveniles. The female (the largest individual) lays demersal eggs on the upper surface of shells or dead coral next to the anemone. Embryos develop over a period of 6–7 days before hatching [29] and post-larvae settle into anemones after a pelagic larval phase lasting 9–12 days [30].

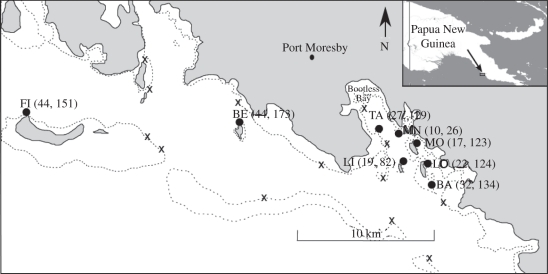
The study location encompassed Bootless Bay and an area of coast adjacent to Port Moresby, Papua New Guinea. This area supported a metapopulation of eight spatially discrete sub-populations (termed sites to avoid confusion with other sub-population definitions; figure 1). Distances among sites varied from 1 to 30 km. With the exception of Fishermen Island (FI) anemones within each site were confined to an approximately 1 ha patch of shallow sand and seagrass. At each site (except for FI), an exhaustive search for all anemones colonized by A. polymnus was performed prior to tissue collections. The sub-population of FI was spread over a larger area and we estimated that nearly 50 per cent of this sub-population was sampled. In total, 215 anemones hosting A. polymnus were found among the eight sites (figure 1).

Figure 1.

Map showing the eight sites of anemone aggregations hosting A. polymnus in the Bootless Bay area (black filled circles). Crosses indicate locations with potential suitable habitat that were explored but no anemones hosting A. polymnus were found. The number of anemones and sampled A. polymnus at each site are indicated in brackets. Inset: location of Bootless Bay in Papua New Guinea. Site abbreviations are as follows: Manubada Island (BE), Lion Island (LI), Taurama (TA), Motupore North Patch reef (MN), Motupore Island (MO), Loloata Island (LO), Loloata South Bank (BA) and Fishermen Island (FI). Broken lines represent the limit of shallow reefs.

(b). Sampling and genotyping

A total of 942 individuals were sampled among the eight sites between January and April 2008. Each fish was captured by SCUBA using hand nets, measured (total length TL), fin clipped underwater in situ, and then released back into the same anemone. Fish that were too small to be fin clipped (less than 30 mm) were collected. In addition, all juveniles settling on each anemone over the sampling period were captured using hand nets. Finally, at the end of the experiment 15–30 fertilized eggs were collected (randomly within the clutch) from five egg clutches, each from a different anemone. All samples were preserved in 95 per cent ethanol and returned to the laboratory for subsequent genotyping. For all analyses, fish were divided into three categories according to their size. The first category ‘breeders’ consisted of the female and male (the two biggest individuals) of each anemone. The remaining fish were then divided into two arbitrary categories: ‘non-breeders’ (greater than 50 mm) and ‘juveniles’ (less than 50 mm).

Details of the 18 microsatellite loci and genotyping procedure are described in Quenouille et al. [31] and Beldade et al. [32]. After DNA extraction, three multiplex polymerase chain reactions (PCRs) were performed per individual, using fluorescently labelled primers to process 18 microsatellite loci containing a mixture of dimer and tetramer repeats. PCR products were processed on a Beckman Coulter sequencer CEQ 8000 Genetic Analysis System and the resulting electropherograms were scored manually. Uncertainties were reconciled by re-amplification and comparison. Alleles were scored as PCR product size in base pairs. Allelic frequency and expected heterozygosity under Hardy–Weinberg equilibrium were calculated for each locus in Genalex v. 6 [33]. Tests for Hardy–Weinberg and linkage disequilibrium were conducted using Genepop v. 3.4. [34] and significance levels were adjusted with sequential Bonferroni corrections for multiple tests with p < 0.05. All 18 loci satisfied Hardy–Weinberg and linkage disequilibrium assumptions.

(c). Population structure

We estimated genetic variability within and among sites and between resident breeders, non-breeders and juveniles using F and R statistics via analysis of molecular variance (AMOVA) in Arlequin v 3.11 [35]. Tests for statistical significance for all estimates were based on 10⁴ random permutations, and significance levels were adjusted with a sequential Bonferroni correction for multiple tests.

(d). Parentage analysis

Parentage analysis was performed using Famoz [36]. The algorithm in this package calculates the log of the odds ratio (LOD) scores for parent–offspring relationships and constructs statistical tests for parentage assignment. Tests are based on simulations that generate offspring from genotyped parents (H₀: the most probable parent is the true parent) or from allele frequencies in the population (H₁: the most probable parent is not the true parent). For each analysis, allelic frequencies were estimated from the 942 genotyped individuals and these estimations were assumed to match the true allele frequencies in the population. Then, simulations of sets of 10⁴ juveniles were carried out under the two possible hypotheses (H₀ and H₁ above) and subsequent statistical tests were constructed to decide whether a given parent would be selected as the true parent or true parent pair. The distribution of the simulated LOD scores under the two hypotheses was plotted and the intersection between these distributions was designated as the threshold decision value (individuals with LOD scores above the threshold value were accepted as true parents). Famoz also allows for the introduction of an error rate in the LOD score calculation that takes into account the genotyping errors and null alleles [37]. Introduction of this error, even if it underestimates the real error rate, can reduce type I and II errors related to the parentage tests [37,38]. We evaluated four different error rates and chose the best compromise between introduced error and type I and II statistical errors. An error rate of 10⁻³ yielded the lowest statistical type I and II errors (0.10% ± 0.04 and 4.2% ± 0.4, respectively) and was used for all further parentage analyses. Tests evaluations were done using the software option ‘parentage test simulation’. We performed 30 test simulations for each introduced error rate to estimate mean type I and II statistical errors.

All loci showed Mendelian segregation after comparing 36 successfully genotyped eggs of five different clutches (from each sampled egg clutch, eight eggs were randomly sub-sampled and screened for 18 loci) with the respective genotyped parents. None of the 942 screened individuals shared the same diploid genotype. Anemonefish are considered monogamous with only the two biggest fish (breeders) been reproductively active in the fish colony [29]. However, we used our dataset to test whether some non-breeder fish were contributing to offspring production in this population. In this preliminary test, all parentage assignments consisted of breeders. None of the sub-adults (non-breeders) was associated with a breeder of the same anemone as the most probable parent pair of any of the juveniles in the sample. However, a few non-breeders were assigned as single parents to juveniles. Given the nature of these assignments, we considered them to be more probable full sib or half sib rather than parent/offspring relationships. The presence of full sib or half sib relationships can lead to false positive parent–offspring assignments and significantly bias parentage analysis [39,40]. Therefore to eliminate this source of error a second and final parentage analysis was performed using only breeders as potential parents.

(e). Assignment test

We used Geneclass2 [41] to assign or exclude juveniles from the Bootless Bay population (AMOVA analysis revealed no significant genetic differences between sites, therefore all sites were considered as one single genetic pool, see §3 for details). This approach does not assume that the true candidate population has been sampled and can be advantageous in situations where it is not possible to sample all potential populations [42]. Genotypes of all breeders and non-breeders (n = 451) were used as the reference population. The likelihood that a new recruit came from the Bootless Bay population was computed with the partially Bayesian criterion of Rannala and Mountain [43]. Then, this likelihood ratio was compared with a distribution of 10⁴ genotypes simulated ratios from the reference population with a Monte Carlo algorithm [44]. A new recruit was determined to have originated from a different population when the probability of exclusion from Bootless Bay was greater than 95 per cent (p < 0.05).

3. Results

(a). Population genetic structure

There was no significant genetic differentiation among the eight sub-populations. Both global F_ST and R_ST were low (F_ST = 0.0011, R_ST = 0.0021) and not significantly different from zero (p-values 0.11 and 0.08, respectively). Pairwise F_ST values among all samples were low (<0.0106) and only one out of 120 pairwise comparisons was significantly greater than 0 after Bonferroni corrections (electronic supplementary material, table S1a). Similarly, pairwise R_ST values among all samples were low (less than 0.0219) and none were significantly greater than 0 after Bonferroni corrections (electronic supplementary material, table S1b). We concluded that the eight sites were one single genetic pool for all following analyses.

(b). Evaluation of parentage assignment

Parentage analysis assigned 100 juveniles, from a total of 491 that were genotyped to a sampled parent or parent pair from one of the eight sites. Almost half (45%) of these recruits were assigned independently to both the male and female in the same anemone, while the remaining recruits (55%) were assigned to a single parent. We excluded from further analysis all juveniles assigned to only one parent that presented two or more confirmed mismatches between their genotypes and that of the assigned parent (11 juveniles). The remaining 89 recruits were accepted as being true offspring of the parents to which they were assigned. No juveniles were assigned to two parents from different anemones. Overall, missing values accounted for 1.5 per cent of the genetic data and were distributed among all loci (there were no particular loci with consistent missing data).

(c). Self-recruitment and connectivity

Local recruitment (n = 89) accounted for 18.2 per cent of total recruitment (n = 491) to the focal population (table 1 and figure 2). Of these local recruits, 35 (7.1%) individuals settled into anemones at the same site as their parents (self-recruits) while 54 (11.1%) settled in a site other than their natal anemone site (local connectivity). At the site level, self-recruitment averaged 7.5 per cent across all sites, but with variability among sites, ranging from 0 per cent at Lion Island (LI) site to 27 per cent (16 of 59 individuals) at Taurama (TA). The number of juveniles that settled in a given site but came from a different site than that of their natal anemone (local connectivity) averaged 12.3 per cent and varied among sites from 5.7 per cent (4 of 70 individuals) in site Loloata South Bank (BA) to 20 per cent (2 of 10 individuals) in site Motupore North Patch reef (MN; table 1 and figure 2).

Table 1.

Amphiprion polymnus connectivity matrix among eight sub-populations in and nearby Bootless Bay, calculated by identifying the natal origins of juveniles using parentage analysis. Numbers in brackets on the source sites names correspond to the number of breeders that were sampled at each site. The numbers on brackets on the sink sites correspond to the number of juveniles sampled at each site. LD indicates the number of juveniles sampled at each site that had an exclusion probability greater than 0.95 to belong to the genetic pool of Bootless bay and classified as long-distance immigrants. In the last two columns, %SR corresponds to the percentage of self-recruitment and %LC to the percentage of local connectivity.

		source site								LD	%SR	%LC
		BA (57)	LO (37)	MO (29)	TA (48)	LI (31)	MN (13)	BE (57)	FI (62)
sink site	BA (70)	4	—	1	1	—	1	1	—	10	5.7	5.7
	LO (69)	3	3	2	1	1	2	1	1	2	4.3	15.9
	MO (70)	1	3	1	3	2	2	—	1	1	1.4	17.1
	TA (59)	—	—	1	16	1	1	—	1	3	27.1	6.8
	LI (42)	1	1	—	3	—	—	1	1	3	0	16.7
	MN (10)	1	—	—	—	—	1	1	—	—	10.0	20.0
	BE (102)	3	1	1	1	1	1	7	1	8	6.8	8.8
	FI (68)	—	—	2	2	—	—	1	3	4	4.4	7.3
	total (490)	13	8	8	27	5	8	12	8
	average										7.5	12.3

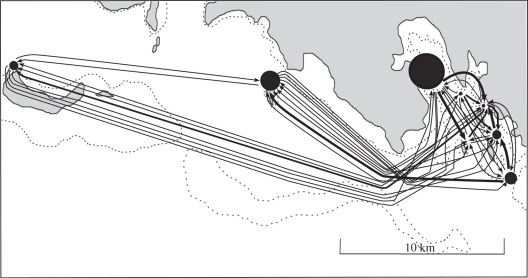
Figure 2.

Zoomed map of the Bootless Bay area showing inferred individual dispersal trajectories (arrows) of A. polymnus juveniles between anemone patches based on parentage analysis. Self-recruitment is represented by black circles. Thickness of arrows and diameter of circles are proportional to the number of juveniles with similar trajectories. For more details about individual trajectories see table 1.

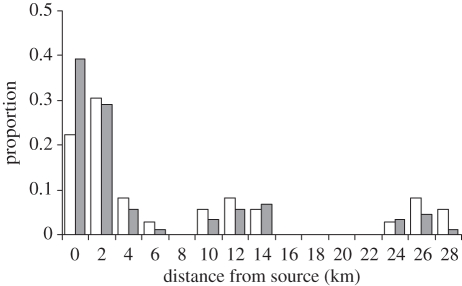
We examined larval dispersal as a function of linear distance among sites for those individuals identified by DNA parentage analysis as being offspring of breeders from the focal metapopulation (figure 3). Linear distances among sites were grouped in classes (classes' sizes of 2 km each), with self-recruitment considered a separate class. Approximately 68 per cent of locally spawned recruits (approx. 12.4% of all juveniles) settled within 3 km of their natal site and 75 per cent of these recruits (approx. 13.5% of all juveniles) settled within 7 km of their natal site. The last 25 per cent of the juveniles identified by the parentage analysis (4.7% of all juveniles) dispersed between 7 and 28 km away from their site of origin. The multi-modal dispersal distribution of juveniles differed significantly from the frequency of linear distances among the eight sites (figure 3; χ² = 20.04, d.f. = 9, p < 0.05). We found that higher numbers of larvae recruited back to their natal sites with concomitantly lower numbers of larvae dispersing longer distances than predicted based on the distributions of distances among sites.

Figure 3.

Distribution of the frequency of distances among sites (unfilled bars) and frequency of newly settled juveniles (filled bars) according to the estimated dispersal distance obtained from parentage analysis. Labels on the x-axis correspond to the mean value of the distance classes. Note that the zero (0) distance class represents juveniles that settled in the same site as their parents (self-recruits).

Assignment tests revealed that 31 of 491 juveniles had a probability less than 0.05 of being from the same genetic pool as the focal metapopulation. These individuals probably came from one or more genetically distinct populations and accounted for 6.3 per cent of total recruitment. Altogether, parentage analysis and assignment tests accounted for 24.5 per cent of sampled juveniles. The remaining recruits approximately 75 per cent were sourced from a similar gene pool to that of the focal metapopulation but we can infer little more about the origin and dispersal distances of these individuals.

4. Discussion

This study provides the first direct estimates of self-recruitment and demographic connectivity among multiple sub-populations in a coastal coral reef metapopulation. Our results indicated that larval retention within the metapopulation was dominated by local exchange among sites, rather than self-recruitment at the site level. At the other extreme, a small number of individuals came from one or more genetically distinct populations, presumably well beyond the geographical boundaries of our study. The majority of the recruits were genetically indistinguishable from the focal metapopulation, but did not match any of the breeders that we genotyped. Because the sampling within the focal metapopulation was fairly complete, we hypothesize that most of these juveniles represent dispersal from other non-sampled sites along the adjacent coastline.

Compared with our previous study in this location [45], by doubling the number of microsatellite markers used, we reduced the statistical errors linked to likelihood-based parentage assignments to less than 5 per cent (both type I and II errors based on simulated data). In addition, we were able to increase substantially the spatial scale and provide for the first time direct estimates of larval exchange among sub-populations spaced up to approximately 28 km from each other. At this geographical scale, levels of self-recruitment were highly variable among sites, but sites with higher numbers of breeders tended to have more self-recruits than sites with fewer breeders (table 1). The exception was site TA, which had by far the highest level of self-recruitment despite not representing the largest breeding population. Site TA was located in a relatively protected location close to the head of the bay, while all the other sites with larger breeding populations were outside the bay (Manubada Island (BE) and FI) or in more exposed locations (BA). Interestingly, in terms of proportions, the site with the second highest self-recruitment rate was MN, a site with a small breeding population also sheltered within the head of the bay. Larvae spawned at these sheltered sites (TA and MN) would therefore likely be less susceptible to advection by alongshore current flows than larvae from more exposed locations outside Bootless Bay. In addition, the proportion of larvae locally spawned that recruited to their natal sites was over-represented compared with the proportion expected based on the distribution of distances among sites. However, almost half of these self-recruiters were from site TA, indicating that shorter dispersal distances may be a feature of the most protected sites in coastal embayments. Overall, the frequency distribution of known dispersal trajectories appears to be largely explained by the geographical spacing, location and size of the sub-populations. Certainly, the different modes in this distribution coincide with the frequency of spacing between sites.

The high variation in levels of self-recruitment among sites, and the relationship between self-recruitment and population size is consistent with the model of James et al. [27] for the Great Barrier Reef whereby large reefs contributed more than smaller ones to the local larval pool. Our mean estimate of self-recruitment per site (7.5%) is similar to mean simulated values among 321 relatively continuous reefs along the Great Barrier Reef. In their simulations, James et al. estimated that virtual larvae returning to their natal reef comprised less than 10 per cent of the settling cohort for most of the reefs. While local retention of larvae may be an advantage in environments were habitat is limited or separated by great distances [17], this advantage may not be extended to situations where habitats are more continuously distributed as in Bootless Bay. Particular sites, with high replenishment rates, such as TA site in this study, could play a crucial role in sustaining the stock in the entire metapopulation [12,46].

The coastal geographical setting may be critical in explaining the low self-recruitment pattern of our focal clownfish metapopulation. In the present study, levels of self-recruitment at both ‘site’ (ranged from 0 to 27%, average 7.5%) and ‘metapopulation’ level (18%) were relatively low compared with published values for A. polymnus and other clownfish species (A. percula) at more isolated locations in Kimbe Bay (Papua New Guinea) [20,22,23]. These values also correspond to the lowest empirical estimate of self-recruitment measured so far among coral reef fishes (reviewed in [17]). However, our estimate of self-recruitment at the metapopulation level for 2008 (18%) is close to that of our previous estimate of 25 per cent obtained at a smaller spatial scale in Bootless Bay (excluding MN, BE and FI) sampled in 2005–2006 [45], suggesting that these results are not atypical of this region and that the geographical settings do have an important role in determining the observed dispersal pattern.

In contrast to low self-recruitment estimates in Bootless Bay for A. polymnus, Almany et al. [20] reported consistent high self-recruitment rates in Kimbe Island for two species with contrasting life-history characteristics (A. percula: benthic eggs and approx. 11 days of pelagic larval duration (PLD) and Chaetodon vagabundus: pelagic eggs and approx. 38 days of PLD). Both Amphiprion species have similar life-history characteristics and differences between studies in Bootless Bay and Kimbe Island suggest that, at ecological timescales, dispersal kernels may be more influenced by the relative isolation or geographical setting of the focal populations than species-specific life-history characteristics [47]. Still, this trend clearly needs to be tested in more species and locations before any conclusion can be made. Besides, other studies based on geochemical signatures in otoliths suggest that this is not a general rule. Patterson et al. [48] showed that Pomacentrus coelestis on Lizard Island exhibited 75 per cent self-recruitment even though it has many other reefs relatively close by, while Patterson & Swearer [49] showed that Coris picta exhibited 26–65% self-recruitment on isolated Lord Howe Island. However, until all existing methods to estimate self-recruitment are cross-validated, comparisons among them should be made cautiously [17].

Parental analysis suggested that most sites received a higher proportion of recruitment from larvae spawned at different sites within the metapopulation than from self-recruitment. This high connectivity among sites was probably underestimated, in particular that between the inside and outside of Bootless Bay, as it was not possible for us to exhaustively search all potential areas outside of the Bay. This lack of sampling presumably explains a significant proportion of the approximately 300 juveniles that settled in our study area and were left unassigned either by parentage analysis or assignment tests. It seems that a much larger sampling effort along the coast line will be necessary to find the origin of those juveniles.

Assignment tests detected that a non-negligible percentage (6.3%) of the juveniles sampled in this location were genetically distinct from the focal metapopulation. We hypothesize that these recruits were long-distance immigrants, but unfortunately, even if this was confirmed, we could not estimate how far these juveniles had travelled. This would require much more extensive sampling of genetic signatures at greater distances to the east and west of Bootless Bay. If indeed these genetically distinct recruits are long-distance immigrants, they may play an important role in buffering extinction risk in this metapopulation [50]. However, the fact that these individuals apparently belonged to a different genetic pool suggests that either we have fortuitously captured a very rare dispersal event, or that the juveniles that we collected would not have successfully reproduced if we had not captured them. This is because a constant exchange of this magnitude with successful reproduction of these individuals should lead to homogenization of these genetic pools [2]. The question that remains is how variable this contribution is over time and whether or not these individuals are capable of successfully integrating into their new population.

In conclusion, given the relatively low-observed self-recruitment rates, a high proportion of connectivity among sites, and the relatively high proportion of long-distance dispersal, it appears that connectivity and not self-recruitment dominates larval replenishment in this focal clownfish metapopulation. We found that 18 per cent of juveniles in Bootless Bay settled between 0 and 28 km from their place of origin while over 80 per cent were likely to have dispersed from populations beyond our studied sites. These results have significant implications for the design of MPA network in this area as they indicate that a single MPA inside Bootless Bay may not be sufficient to maintain the metapopulation if unprotected sources were to collapse. In addition, while there is consistent evidence that life-history characteristics of individual species can play an important role in terms of dispersal at evolutionary (genetic) timescales [51–54], the suggestion that the spatial distribution of suitable habitats may have more impact on levels of demographic connectivity than life-history characteristics of individual species clearly deserves more attention in future studies. If this happens to be true, it will have encouraging implications for the use of MPAs to offer protection to coral reef fish assemblages [55]. Testing this hypothesis at more locations, and on more species, remains a top priority for conservation biologists working in coral reef ecosystems.