Abstract
It is well known that competition among kin alters the rate and often the direction of evolution in subdivided populations. Yet much remains unclear about the ecological and demographic causes of kin competition, or what role life cycle plays in promoting or ameliorating its effects. Using the multilevel Price equation, I derive a general equation for evolution in structured populations under an arbitrary intensity of kin competition. This equation partitions the effects of selection and demography, and recovers numerous previous models as special cases. I quantify the degree of kin competition, α, which explicitly depends on life cycle. I show how life cycle and demographic assumptions can be incorporated into kin selection models via α, revealing life cycles that are more or less permissive of altruism. As an example, I give closed-form results for Hamilton’s rule in a three-stage life cycle. Although results are sensitive to life cycle in general, I identify three demographic conditions that give life cycle invariant results. Under the infinite island model, α is a function of the scale of density regulation and dispersal rate, effectively disentangling these two phenomena. Population viscosity per se does not impede kin selection.
Keywords: Altruism, density dependence, dispersal, hard selection, kin selection, population viscosity, Price equation, scale of competition, soft selection, subdivided populations
The efficacy of kin selection depends in large part on the extent to which individuals associate with relatives (Hamilton 1963, 1964). Hamilton (1963, 1964) showed that a trait deleterious to individual fitness but beneficial to others (e.g., cooperation or altruism) can increase in frequency as long as br − c > 0, where b is the benefit to recipients of an act, c is the cost to the actor, and r is the degree of relatedness between actor and recipients. Hamilton (1964) suggested that population viscosity—low dispersal rate from natal groups—is one mechanism that will generate high relatedness. However, when there is competition for limiting resources at a local scale, the same kin-structure that causes cooperation to be preferentially directed toward relatives also causes competition to occur disproportionately among relatives (Grafen 1984; Wade 1985; Kelly 1992, 1994a; Taylor 1992; Wilson et al. 1992; Queller 1994). Thus, the benefits of kin-cooperation can potentially be negated by kin-competition.
The cooperation-negating threat of kin competition has heightened the sense that true altruism in nature poses a serious conceptual dilemma. In particular, a number of models have shown that increased kinship is exactly balanced by increased kin competition, making it impossible for true altruism to evolve (Charlesworth 1979; Taylor 1992;Wilson et al. 1992; Gardner and West 2006). Yet true altruism does exist in nature, creating a potential contradiction between theory and observation. One solution to this problem is to modify basic model assumptions, allowing for overlapping generations (Taylor and Irwin 2000), “empty sites” that relax local competition (Mitteldorf and Wilson 2000; Alizon and Taylor 2008; Lion and Gandon 2009), or propagule dispersal (Gardner and West 2006; Lehmann et al. 2006). This would seem to constrain altruism to species exhibiting these unique properties. However, a number of other models find no such constraints, but require a crucial assumption that the factors causing competition are independent from those determining relatedness. For instance, Kelly (1992, 1994a) demonstrated that when the scales of density regulation, dispersal, and cooperation are allowed to vary independently, no such balancing of relatedness and kin competition occurs. Similarly, Grafen (1984) and Queller (1994) allowed relatedness of social partners and competitors to vary independently, also eliminating the exact balancing of these effects. Still other models (Boyd 1982; Frank 1998) introduce a parameter that modulates between local and global density regulation, so that kin competition can simply be turned “off” while other model parameters are unaffected.
The use of different approaches and assumptions among these models has prevented a rigorous conceptual unification of results, obscuring the biological causes of kin competition and the routes to its amelioration. In particular, it is not clear why so-called “closed” models (Charlesworth 1979; Taylor 1992; Wilson et al. 1992; Gardner and West 2006) find that true altruism is impossible, while “open” models (Boyd 1982; Grafen 1984; Kelly 1992; Queller 1992; Kelly 1994a; Frank 1998) do not. Open models, which contain free parameters that are assumed to be independent of other model parameters (Gardner and West 2006), have been criticized on the grounds that the same forces determining kin competition are those determining relatedness, so that the ability of open models to solve the viscosity dilemma is largely illusory, with the effect vanishing when transformed into closed models (Gardner and West 2006). Indeed, a large body of empirical and theoretical work has been motivated by the premise that relatedness and the scale of competition are inexorably intertwined, or as stated by Kummerli et al. 2009b, “relatedness and the scale of competition … will not usually be independent” (emphasis added).
The contradictory conclusions of open and closed models require resolution, which is one of the aims of the present article. Two additional limitations of existing models (both open and closed) is that (1) they only account for a single round of density regulation (although see Gardner and West 2006), and (2) that results apply only under specific demographic and life cycle assumptions. The generality of conclusions and relationships among models remain unclear. It would be especially useful if any particular density regulation or life cycle assumption could be encapsulated by a single, tunable parameter (Frank 1998; Gardner and West 2006). This would provide a tool that clarifies the connections between existing models, greatly simplifies modeling, and allows for the determination of how specific life cycles and demographic conditions influence the evolution of altruism.
To investigate the role of demography and life cycle in shaping the response to kin selection, I define a parameter, α, that measures the intensity of kin competition. The degree of “kin competition” as defined here is the correct demographic concept for accurately and completely predicting evolutionary change for any life cycle, whereas some definitions of “soft selection” or “scale of competition” are often inadequate in this respect (see below). I show that the intensity of kin competition is a function of the scale of density regulation, dispersal rate, and life cycle. These results provide a single, tunable parameter that disentangles the ecological and demographic causes of kin competition and reveals the role of life cycle in determining the interaction between density regulation and dispersal.
Furthermore, I show that the multilevel Price equation (Price 1972; Hamilton 1975; Wade 1985) includes both selection and demography, and then derive a version that cleanly partitions these effects. The result is a general description of selection in a subdivided population with an arbitrary degree of kin competition. This equation is of considerable theoretical and empirical utility. I then demonstrate that a number of previous models (e.g., Boyd 1982; Grafen 1984; Wade 1985; Taylor 1992; Kelly 1994a; Queller 1994; Frank 1998; and Gardner and West 2006) are special cases of this single equation. To demonstrate the power and utility of the model, I give closed-form results for Hamilton’s rule for a three-stage life cycle. I find three demographic conditions that produce life cycle invariant quantitative results, and show that altruism is most favored in life cycles in which competition occurs late in life. In addition, I find that population viscosity per se does not impede kin selection.
THE SEMANTICS OF SOFT SELECTION
The evolutionary consequences of genotype-independent competition have been investigated theoretically and empirically by reference to the terms “hard/soft selection” in classical population genetics and, more recently, “the scale of competition” in the social evolution literature. Both of these conceptual frame-works have suffered from a lack of consistency in usage. Hard-and soft-selection are terms introduced by Wallace (1968, 1975) for the purpose of exposing the ecological conditions that impinge on genetic load calculations. According to Wallace (1975), soft selection is both density- and frequency-dependent, whereas hard selection is neither. Soft selection eliminates the correlation between the size of a population and its genetic composition, with important implications for the expression of the genetic load (Wallace 1968, 1975). This definition is closely allied with that of Wade (1985, pers. comm.), Goodnight et al. (1992), and Whitlock (2002), who also define hard/soft selection in terms of the genetic correlation with group productivity. Christiansen (1975) was the first to apply the terms hard and soft selection to a metapopulation context, where he defined soft selection as local density regulation before dispersal, and hard selection as the case in which there is no density regulation before dispersal. Dempster (1955), in an attempt to reveal the assumptions leading to Levene’s (1953) condition for a protected polymorphism in a subdivided population, distinguished between constant zygote number and constant adult number assumptions. Although Dempster (1955) did not use the terms hard and soft selection, his dichotomy was later couched in these terms, with constant zygote number corresponding with hard selection, and constant adult number with soft selection.
The difference between these definitions can be highlighted with an example. Take the model of Taylor (1992) who investigated selection in a group-structured population composed of inelastic patches. According to Taylor’s assumptions, there is no density regulation before dispersal, there is a constant proportion of adults per group at the time of reproduction, and the expression of group productivity depends on the dispersal rate. Therefore, this is a hard selection model sensu Christiansen (1975), a soft-selection model sensu Dempster (1955), and a hybrid model sensu Wade (1985), Goodnight et al (1992) and Whitlock (2002).
There is also inconsistency in the usage of the term “scale of competition.” Frank (1998) defined it as, “the spatial scale of density dependent competition,” which aligns precisely with the connotation of the term. However, this term is often used to mean competition among individuals that originate locally, rather than competition that occurs locally. For example, Gardner and West (2006) find that the “scale of competition” is a function of dispersal. Although dispersal may affect the genetic composition of a density-regulated neighborhood, it nonetheless does not affect the size (spatial scale) of this neighborhood (Kelly 1992, 1994a). Thus, the definitions of the scale of competition technically differ between Frank (1998) and Gardner and West (2006). Throughout this article, I will be explicit about the sense in which I use each of these terms. I then show the quantitative relationships between disparate definitions using the generalized degree of kin competition parameter, α.
Apart from semantics, there has been general disagreement in the literature about the relationship between soft selection and group selection (reviewed in Okasha 2006). Using the Price approach, Wade (1985) found that soft-selection eliminates group selection. On the other hand, Goodnight et al. (1992) employed the method of contextual analysis (Heisler and Damuth 1987) and concluded that soft-selection is actually a form of group selection. The Price approach partitions the total selection differential into among- and within-group components, so that group selection occurs when there is heritable variation in fitness among groups (Wade 1985). As soft-selection eliminates the variation in fitness among groups, the Price approach concludes that soft-selection eliminates group selection. Contextual analysis differs from this in that the selection differential is partitioned into context-dependent (i.e., social) and context-independent components using partial linear regression (Heisler and Damuth 1987; Goodnight et al. 1992). Under soft-selection, the fitness of a phenotype depends on its context. For example, individuals with intermediate phenotype may have high fitness in a group of low phenotype individuals, but low fitness in a group of high phenotype individuals. Thus, contextual analysis finds that soft-selection constitutes a form of group selection (Goodnight et al. 1992), contrary to the conclusion of the Price approach. Below, I demonstrate that the Price approach, when the population is subdivided into regulation groups, also reveals that soft-selection includes a group-component of selection, independently supporting the conclusion of Goodnight et al. (1992).
Results
LIFE CYCLE
I consider a generalized life cycle. Let L be the number of life cycle stages that an individual undergoes. Selection and/or density regulation can occur at any life stage, and stages are separated by dispersal of individuals among groups. If there are multiple bouts of selection or density regulation within a single stage, the quantitative consequences of these events are aggregated into a single value. Diagrammatically, we have: Life Stage 1 → Dispersal 1 → Life Stage 2 → Dispersal 2 …→ Life Stage k → Dispersal k→…→Life Stage L→Reproduction. The individuals remaining in group i at the end of life stage L are the founders of group i in the following generation.
THE MULTILEVEL PRICE EQUATION WITH KIN COMPETITION
Consider a population subdivided into M local groups, where “groups” are defined as discrete units wherein social interactions occur at random with respect to genotype (there is no kin recognition). “Group” is used as a generic term, and can mean habitat patch, deme, trait group, family, etc. Individuals undergo an arbitrarily complex life cycle composed of dispersal, selection, and density regulation in no particular order, and generations are discrete and nonoverlapping.
Let there be some trait of interest, z. The change in the mean value of this trait in the population over a single generation, Δz̄, is given by the multilevel Price equation (Price 1972; Hamilton 1975; Wade 1980, 1985). Assuming unbiased transmission of trait-values between parents and offspring (i.e., no meiotic drive, etc.), this can be written,
| (1) |
where zi is the mean phenotype of individuals in group i, zij is the phenotype of individual j in group i, gi and wij are relative among-and within-group fitness, respectively, E[X] is the expected value (i.e., the mean) of X, and cov(X, Y) is the covariance between X and Y. The first term in equation (1) accounts for evolutionary change due to differential productivity of groups, whereas the second term accounts for evolutionary change due to selection among individuals within groups (Price 1972; Hamilton 1975; Wade 1985; Frank 1998; Michod 1999; Rice 2004).
Among-group relative fitness, gi, is defined as the relative contribution of group i to the total population in the next generation. This counts all individuals from group i, whether they are still in group i at the end of the life cycle (individuals are reindexed at the beginning of each generation). By definition, gi = ∑Wij/∑∑Wij, where ∑Wij is the total number of individuals contributed by group i to the next generation, and ∑∑Wij is the total number of individuals contributed by the global population to the next generation. Group fitness, gi, can be affected by both selection and demography (Fig. 1). Typically, the Price equation only accounts for selection, where the relative contribution of a group to the total population after selection is, wi = ∑Wij(s)/∑∑Wij(s). The superscript “(s)” denotes that the population is censused after selection. But demography also affects fitness by setting boundaries on the number of individuals produced by each group (Fig. 1). This acts to decouple selection and group productivity, such that ∑Wij is not necessarily equal to ∑Wij(s). On the other hand, genotype-independent local density regulation does not affect within-group relative fitness (because demography-induced mortality is genotype-independent by assumption), even though it affects absolute within-group fitness (Fig. 1). This means that demography only affects relative among-group fitness, gi, not relative within-group fitness, wij (see also Crow and Kimura 1970 Chapter 1). Thus, the correct fitness to use in the Price equation is gi, which accounts for both selection and demography, and not wi, which only accounts for selection.
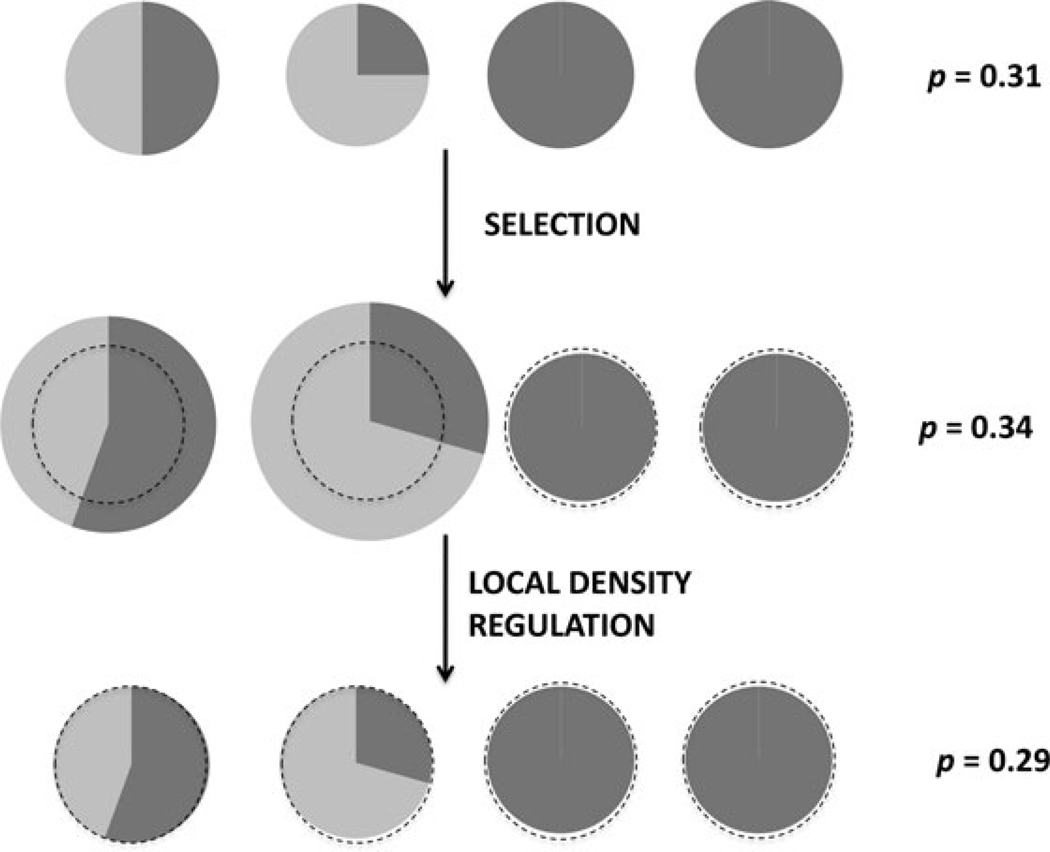
Figure 1.
A representation of a population undergoing social selection followed by strict local density regulation. Altruists are designated in light gray, and allele frequency change was computed with b = 0.8 and c = 0.2 (these large selection coefficients are for the sake of illustration). Selection reduces the frequency of altruists within groups, but altruistic groups are more productive. The net result is an increase in the frequency of altruists in the global population. Local density regulation, however, eliminates differential group productivity, but maintains the postselection within-group frequency of altruists. Thus, density regulation reduces the frequency of altruists. This demonstrates that despite the fact that density regulation is genotype-independent within the density-regulated neighborhood, density regulation affects altruistic groups more than nonaltruistic groups, and so is genotype dependent at the group level.
Following Whitlock (2002), we can write a group fitness function that simultaneously accounts for selection and demography
| (2) |
Whitlock (2002) defined a linear operator, b, as the degree of hard selection. In the present notation, Whitlock’s b is replaced by (1 − α). Thus, α is the degree of soft selection sensu Whitlock (and Wallace (1968), Wade (1985) and Goodnight et al. (1992)). The use of (1 − α) rather than b is for the sake of comparison with other kin selection models (e.g., Frank 1998; Gardner and West 2006). When α = 1 (strict soft selection), gi = 1, which means that all groups contribute equally to the next generation. When α = 0 (strict hard selection), gi = wi, meaning that groups contribute to the next generation in proportion to their fitness. To avoid confusion with other definitions of soft selection, I will refer to α as the “degree of kin competition,” although α is equivalent to some definitions of soft-selection and local competition (see Discussion).
Substituting equation (2) into equation (1) we find,
| (3) |
This simple modification of the Price equation completely accounts for the effects of kin competition on evolution in structured populations. The additional term, −αcov(wi, zi), accounts for demographic selection. The decoupling of group fitness and genotype by density regulation noted above is demonstrated in equation (3) by the fact that the covariance of wi with zi shrinks to zero with increasing kin competition. When α = 1 and α = 0, we retrieve Wade’s (1985) results for the hierarchical Price equation under soft and hard selection, respectively.
To understand how a “genotype-independent” process can affect the response to selection, it must be pointed out that “genotype-independent” local regulation is genotype-dependent at the group level. This is because groups composed of high fitness genotypes suffer a greater reduction in absolute and relative fitness than a group composed of low fitness individuals (Fig. 1). This creates a nonzero covariance between genotype and group fitness that allows density-regulation to contribute to an evolutionary response.
Because we have made no assumptions about life cycle, dispersal, or density regulation, both α and equation (3) are general with respect to these processes. In addition, because of the generality of the Price equation, equation (3) can be used to model the effects of kin competition using population genetic, quantitative genetic, or ESS approaches (Rice 2004).
HAMILTON’S RULE WITH KIN COMPETITION
Most kin selection studies of kin competition provide their central result as a modified form of Hamilton’s rule. Therefore, to compare equation (3) to these results, it is necessary to begin by deriving Hamilton’s rule. In Appendix A, I provide a derivation of Hamilton’s rule from equation (3) by first deriving a recursion for allele frequency change under Hamilton’s linear fitness function, and then solving for the conditions for allele frequency increase (Δp > 0). For both haploids and diploids, the conditions for increase in allele frequency under these assumptions is
| (4) |
Equation (4) was first derived by Boyd (1982), who employed a very different approach (eq. 4 is retrieved from eq. 19 in Boyd (1982) by setting r̄ = r in his equation, which corresponds to indiscriminant sociality, as assumed here). Boyd defined a parameter h (in place of α in the present model) as a linear measure of the intensity of density regulation. Frank (1998), using his direct fitness approach, derived Hamilton’s rule with kin-competition as: r[b − a(b − c)] − c > 0. Rearrangement shows that Frank’s result and equation (4) are equivalent, with α replaced by a in his notation. Frank defined a as the spatial scale of density regulation (Frank 1998). Both Boyd and Frank explicitly model only the effects of density regulation. However, I show below that α measures more than just density regulation, and that the only case in which α is exclusively determined by density regulation is when (1) density regulation occurs at only a single life stage, and (2) when this is the same life stage in which selection acts. Thus, Boyd and Frank’s results are special cases of the more general solution of equation (4), which in turn is a special case of equation (3).
THE DEGREE OF KIN COMPETITION
To understand the factors that control the degree of kin competition, and to connect disparate models, I derive a value of α in terms of independent causal parameters. To begin, note that the average change in relative group density due to selection is proportional to the among-group selection gradient, βwi, zi. To maintain a constant global population density, an increase in the relative size of a group by a factor βwi, zi must be matched by an equivalent decrease in relative density within the density-regulated neighborhood. Only a fraction, r, of those receiving the benefit of cooperation (i.e., increased group density) are related, whereas a fraction, rd,k, of those experiencing the decrement in fitness (i.e., reduction in group density) due to density regulation are related. Here, rd,k is the relatedness of altruists in a density regulated area at life stage k, which is equivalent to Grafen’s (1984) rxe. From equation (A2) (see Appendix A), this leads to a version of Hamilton’s inequality that reads, r (βwi, zi − βwij, zij) + βwij, zij − rd,k βwi, zi > 0. Rearranging we find
| (5) |
Equation (5) is a multilevel selection formulation of Hamilton’s rule with kin competition. Under the additive linear model (Appendix A) this retrieves Grafen’s (1984) result. Unlike Grafen’s (1984) result, equation (5) applies for arbitrary fitness functions, when there is dominance or inbreeding, and when traits are continuous characters. Goodnight (pers. comm.) has obtained a similar result using contextual analysis.
Using Grafen’s (1985) formulation of relatedness and following Queller (1994), we can write r = ∑(py − p)/∑(px − p) and rd,k = ∑(pd − p)/∑(px − p), where p is the mean frequency of the altruism allele in the total population; py is the frequency in recipients of altruism; px is the frequency in donors of altruism; and pd is the frequency of altruist alleles in a density-regulated area. From this we have, (r − rd,k) = ∑(py − pd)/∑(px − p). It is possible to define a scaling parameter that makes pd equal p with no kin competition, and equal py with strict kin competition. This parameter is equivalent to the degree of kin competition parameter, αk. Thus, we can write, pd = py − (1 − αk)(py − p). Substituting and rearranging gives
Solving for αk we find
| (6) |
This is an intuitive and empirically tractable measure of the degree of kin competition. Substituting equation (6) into equation (4) and rearranging retrieves the same form of Hamilton’s rule as that found by Grafen (1984) and Queller (1994). As equation (6) only applies for a single life stage, this assumption is implicit in both Grafen’s and Queller’s derivations.
THE STRENGTH OF DEMOGRAPHIC SELECTION
Density-regulation contributes an additional level of population substructuring: the density-regulated neighborhood (Fig. 2), which I will sometimes call the “regulation group” (Kelly 1994a). By analogy to Wright’s F-statistics, we can define a set of identity coefficients with respect to the regulation group: fdt = Vd/p(1 − p), and fsd = Vr/pr(1 − pr), where p is the mean allele frequency in the population, pr is the mean allele frequency among social groups within a regulation group, Vd is the variance among regulation groups, and Vr is the variance among social groups within a regulation group (Fig. 2). All measures are taken within a single life stage, although I omit the subscript “k” on identity coefficients, variances, and allele frequencies in this section to make the notation easier to read. By definition, rd,k = Vd/Vt, where Vt is the total genic variance. In haploids, rd,k = fdt. Substituting equation (11) and the variance definition of rd,k into the partial regression form of equation (3) (see eq. A1), we find that
| (7) |
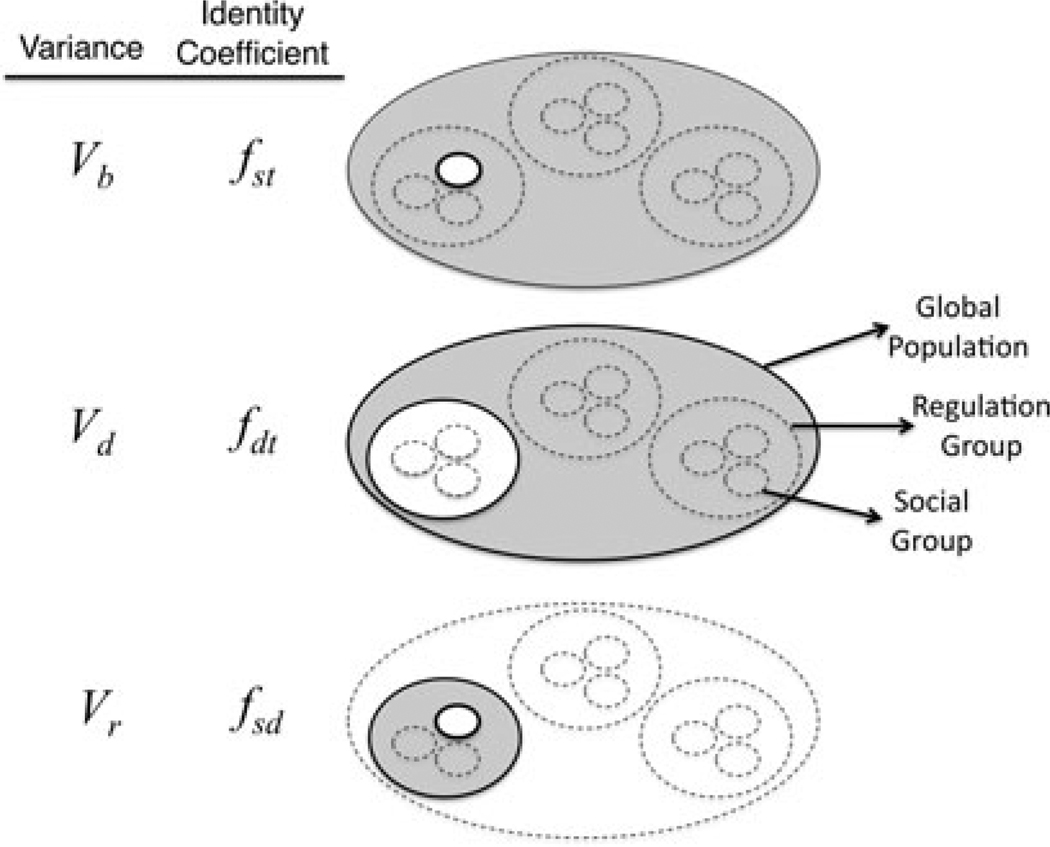
Figure 2.
The hierarchical partitioning of a structured population. The largest oval represents the global population, which is then structured into regulation groups (intermediate ovals) and social groups (smallest ovals). Variance components and identity coefficients can be defined with respect to hierarchical groups. Vb is the variance among social groups with respect to the global population; Vd is the variance among regulation groups with respect to the global population; and Vr is variance among social groups within a single regulation group.
Equation (7) was implicit in the analysis of Kelly (1994a). The second term on the right-hand side of equation (7) is the strength of demographic selection, which is always opposite in sign to the group selection component (the first term on the right-hand side) with a magnitude proportional to Vd, the variance among density-regulated neighborhoods. This term demonstrates that there is always an implicit third level of selection in group-structured populations, that among regulation groups (Fig. 2). With global density regulation, Vd = 0, while with local density regulation, Vd = Vb. Thus, the Price partitioning, like contextual analysis (Goodnight et al. 1992), also finds that soft-selection contains a group-selection component.
It follows immediately from definitions that Vr = Vb − Vd (also see Fig. 2). Substituting into equation (7) gives
| (8) |
Kelly (1994a) first derived equation (8) via a very different route, demonstrating that kin competition is accounted for by measuring among-group variance with respect to the density-regulated neighborhood. The derivation provided here shows that this is equivalent to modifying relatedness with respect competitors, as Queller (1994) did. These results are not general, however, because they only account for the effects of density regulation in a single life stage. Equation (3) generalizes this result to any life cycle, and, like equation (7), has the advantage that it makes explicit all three levels of selection.
DENSITY DEPENDENCE, DISPERSAL, LIFE CYCLE, AND KIN COMPETITION
A value for α in terms of explicit model parameters can be obtained by applying the appropriate identity coefficients to equation (6). With the assumption of island model population structure (Wright 1931), this obtains a relationship between dispersal and the scale of density regulation. The following results are presented for asexual haploids for simplicity, but extensions are readily made to any genetic system. I make the standard assumption of weak selection, which ensures that genotypic distributions are approximately independent of selection, and that group size is approximately invariant among groups and between generations. Equation (6) applies more generally and requires none of these assumptions.
Assuming infinite island population structure and weak selection, the following result can be derived for relatedness at life stage k in a haploid population with L life stages and with groups of effective size N (Appendix B),
| (9) |
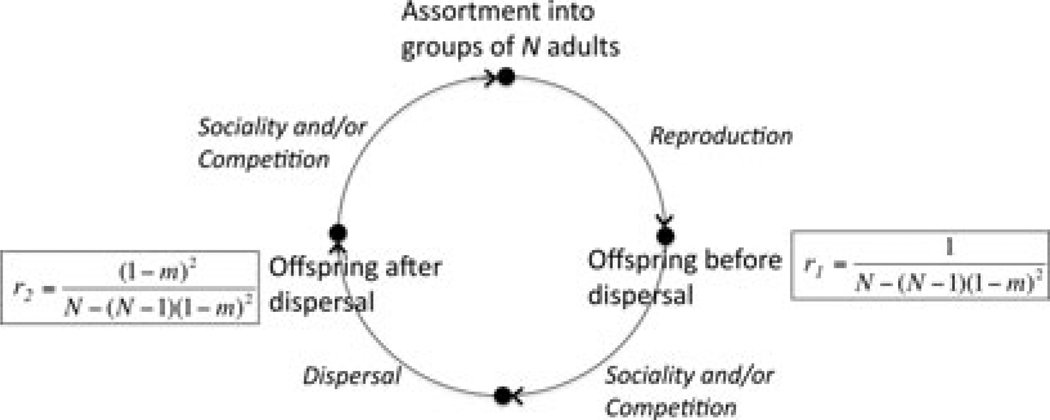
where mj and mi are the effective rates of dispersal among groups at the end of life stage j and i, respectively, and where m0 = 0 by definition. Throughout, the subscript “e” (e.g., Ne and me) will be dropped from N and m to simplify the notation. Figure 3 diagrams a life cycle with L = 2 and presents r1 and r2 for this case.
Figure 3.
A life-cycle diagram for a structured population with discrete, nonoverlapping generations. Groups are founded by N adults who reproduce to form the next generation. Social interactions and competition among offspring can occur either before or after offspring disperse away from their natal group. The relatedness (shown in boxes) of offspring in a social group depends on the stage in the life cycle when it is measured.
Define dk as the “scale of density regulation” at life stage k. In a group structured population, the spatial scale of density regulation will be determined by the number of social groups in a density-regulated neighborhood, Md, so that dk = 1/Md (Fig. 4). If all competitors in a density-regulated neighborhood belong to the same social group, the Md = 1, giving dk = 1 (“local density regulation”). With “global density regulation,” dk = 0. The value of dk is assumed to be genotype independent, so that it is determined by factors extrinsic to the population, such as resource availability, limited space for nesting/pupation/breeding sites, density-dependent predation, etc. (Wallace 1975; Roughgarden 1979).
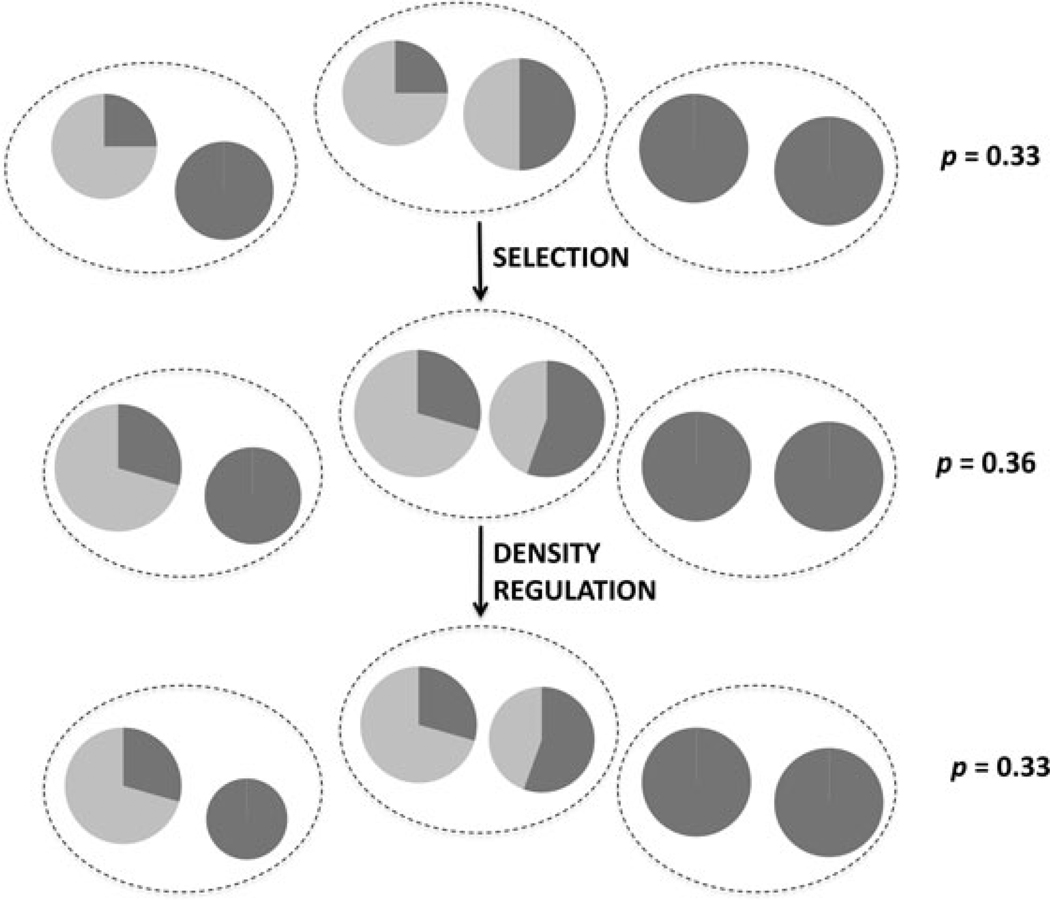
Figure 4.
Individuals compete in a density-regulated neighborhood wherein the total number of individuals is kept at a constant value, K. In this case, each regulation group is composed of two social groups. The fitness effects in the figure are b = 0.8 and c = 0.2, and altruists are designated in light gray. After selection, K individuals are chosen at random to form the next generation such that each neighborhood contributes the same proportion of individuals. After density regulation, groups retain their same post-selection relative sizes within each neighborhood, but their absolute size is constrained by K. Altruism evolution is impeded by the inability of altruist-rich regulation groups to contribute more than altruist-poor neighborhoods to the next generation, although this constraint is weakened by larger spatial scales of regulation. For comparison, final frequency of altruists in the figure would be p = 0.31 under strict local density regulation.
Within a density-regulated neighborhood, a proportion, dk, of individuals has a relatedness of rk (the within social-group relatedness at life stage k), whereas the remaining fraction, (1 − dk), has a relatedness of ro. It can be shown that ro ~ 0 in the island model. First, the separation of time scales assumed in calculations of identity coefficients (Rousset 2004 and references therein) is preserved within the regulation group under the island model because the regulation group is composed of a random sample of social groups from the population. Thus, we are justified in treating only those alleles that originate from a focal group in that generation as having alleles ibd (identical by descent). If density regulation occurs before dispersal, then ro = 0 (individuals outside the social group cannot share alleles ibd from the parental generation). If density regulation occurs after dispersal, then some competitors from outside the social group may be related. Under the island model, all Nm dispersers are evenly distributed about the population with a density of Nm/NT, of which, a fraction r shares alleles ibd with the focal individual. So, ro = rNm/NT, which is negligible because NT is very large relative to N. Thus, the relatedness in a density-regulated neighborhood at life stage k is
| (10) |
Equation (10) will not necessarily hold for other population structures, such as stepping stone dispersal, because competitors outside of the group may be a nonrandom sample of the total population when d < 1 and the assumption of separation of time scales between neighboring groups may break down.
Combining equations (6) and (10) gives
| (11) |
Further substituting equation (9) into equation (11) gives
| (12) |
where mj is the effective dispersal rate at the end of life stage j, and where m0 = 0 by definition. In most models, selection occurs in the first life stage, so that we have α1 = d1. By definition, this is the degree of soft selection sensu Christiansen (1975).
Equation (12) demonstrates the relationship between kin competition, density regulation, and dispersal. In particular, it shows that density regulation, the ultimate cause of kin competition, is independent of dispersal. With global density regulation (dk ~ 0), kin competition is not influenced by dispersal. Alternatively, with high dispersal, m ~ 1, kin competition is not influenced by density regulation. Thus, both nonlocal density regulation (dk < 1) and dispersal (m > 0) provide escapes from kin competition. Thus, viscosity per se does not increase kin competition.
GENERALIZING THE DEGREE OF KIN COMPETITION PARAMETER
So far, the analysis has only considered the degree of kin competition at individual life stages, αk. To adequately describe evolution, we need to know the degree of kin competition over the entire life cycle, α. The derivation of α is simple: Because density regulation at one life stage can only act on the residual product of density regulation from the previous stage, the total degree of kin competition over a single generation equals
| (13) |
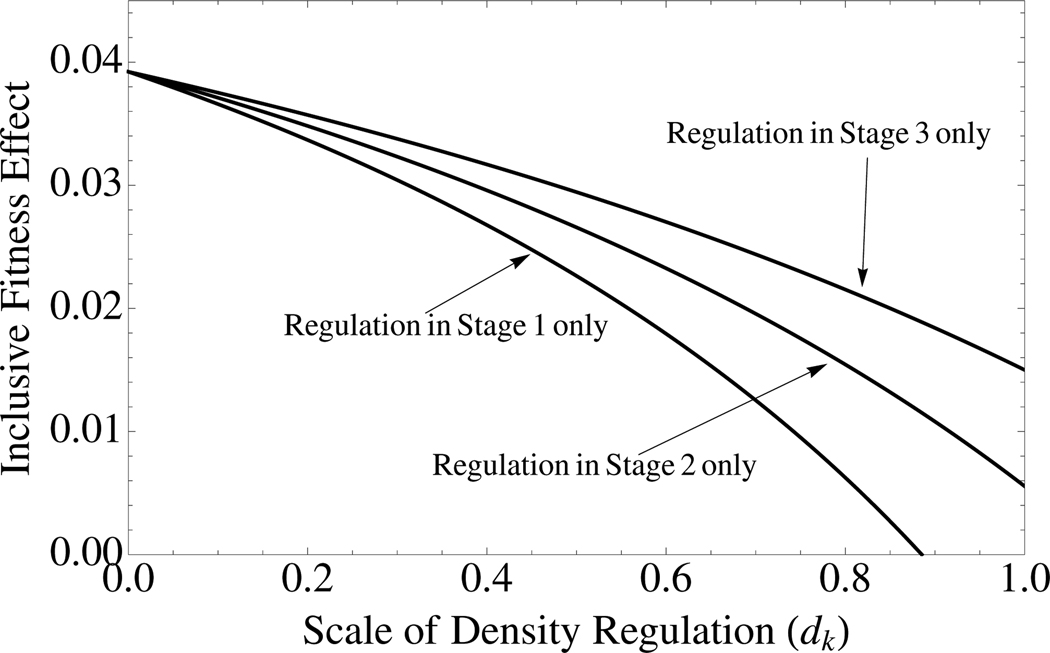
where α0 = 0 by definition. These results apply to arbitrarily complex life cycles. One implication of equation (13) is that kin competition in early life has a more drastic effect on total kin competition than kin competition at later life stages (Fig. 5 and the next section). By substituting equation (13) into equation (4), we can retrieve results for Hamilton’s rule for arbitrary life cycles and patterns of density regulation.
Figure 5.
Density regulation during early life stages has a larger effect on kin competition than density regulation in later stages. The curves are given by equation (14) with parameter values are b = 0.1, c = 0.01, N = 4, and m = 0.1. For the bottom curve, d1 = dk, d2 = 0, d3 = 0; for the middle curve d1 = 0, d2 = dk, and d3 = 0; and for the top curve d1 = 0, d2 = 0, and d3 = dk.
Gardner and West (2006) modeled altruism evolution in a population composed of inelastic groups, with a single dispersal stage and an arbitrary degree of density-regulation before dispersal. They equated their resulting version of Hamilton’s rule with Frank’s (1998) result to solve for Frank’s scale of competition parameter, a. They found that a = s + (1 − s)(1 − m)2, where s is the degree of soft selection sensu Christiansen (1975). From equation (13) with L = 2, it is found that α = d1 + (1 − d1)d2(1 − m1)2. Noting that α1 = d1 = s in their notation, and that they assumed d2 = 1, we immediately retrieve their result as a special case of equation (13). Applying this value of α to equation (4), we retrieve their result for Hamilton’s rule with kin competition as a special case.
Taylor (1992) assumed a two-stage life cycle (L = 2) with no density regulation before dispersal (d1 = 0), but strict density regulation after dispersal (d2 = 1). Substituting into equation (13) gives α = (1 − m)2. Substituting this value into equation (4) retrieves Taylor’s result, b/N − c > 0, which shows that increased relatedness is exactly balanced by increased kin competition due to their mutual dependence on dispersal rate. Equation (13) quantifies why this relationship exists. Importantly, either assuming elastic populations (d2 = 0), or a life cycle in which competition and cooperation both occurred before dispersal, leads to α = d1 and the conclusion that dispersal (population viscosity) has no effect on the intensity of kin competition. The assumptions of inelastic populations and competition after dispersal creates the exclusive dependence of kin competition on dispersal, leading to the conclusion that viscosity is an impediment to the evolution of altruism (Taylor 1992; Wilson et al. 1992; Gardner and West 2006). Indeed, in a subsequent paper, Gardner and West state that, “relatedness and the scale of competition…will not usually be independent” (Kummerli et al. 2009a). Equations (12) and (13) suggest that this conclusion is reliant on the dual assumptions of population inelasticity and the life cycle considered.
CLOSED-FORM SOLUTIONS FOR HAMILTON’S RULE IN A THREE-STAGE LIFE CYCLE
Here, I give closed-form results for Hamilton’s rule with L = 3 (Table 1 and eq. 14 below). A life cycle with three stages is a plausible natural scenario. Consider a holometablous insect species: social interactions occur among larvae, as is commonly observed (Costa 2006), who also may compete for limited resources before dispersal; after larval dispersal, individuals compete for limited pupation sites; finally, emerging adults disperse and then compete among other adults for limited nesting or breeding sites before reproduction. This life cycle involves three rounds of density regulation and two rounds of dispersal. Combining equations (4), (9), (12), and (13), setting L = 3, and assuming haploidy and whole-group altruism (see Appendix A), we obtain Hamilton’s rule under the island model for three life stages
| (14) |
Table 1.
Closed-form results for Hamilton’s rule with three life stages. d1, d2, and d3 are the scales of density regulation for life stages one, two, and three, respectively. α is the degree of kin competition. For clarity, both dispersal rates are set equal, m1=m2=m, and selection is assumed to occur in the first life stage. The rows are organized from most permissive to the spread of altruism at the top, to most restrictive at the bottom. When d1=1, the values of d2 and d3 are irrelevant. Fitness effects are scaled for “whole-group” altruism (see Appendix A).
| d1 | d2 | d3 | α | Hamilton’s rule | |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | ||
| 0 | 0 | 1 | (1−m)4 | ||
| 0 | 1 | 0 | (1−m)2 | ||
| 0 | 1 | 1 | (1−m)2+(1−m)4−(1−m)6 | ||
| 1 | n/a | n/a | 1 | −c>0 |
Equation (14) is difficult to interpret, so a series of special cases are given in Table 1. One insight easily obtained from equation (14) is that strict density regulation in the first life stage, d1 = 1, completely eliminates the benefit term, whereas this is not true for strict density regulation at later life stages.
LIFE CYCLE INVARIANT RESULTS
A number of generalities are demonstrated by the cases in Table 1. It can be proven by induction that there are three demographic conditions that give the same quantitative result for life cycles of any length L: (1) With global density regulation at all life stages (dk = 0 for all k ≤ L), we recover the standard form of Hamilton’s rule, unattenuated by kin competition: br − c > 0 (Table 1, first row). Unlike the next two cases, this result is not strictly invariant because r will always depend on L (eq. 9). (2) With the assumption of strict density regulation at the final life stage and global regulation in all previous stages (dL = 1 and dk = 0 for all k < L), a commonly assumed life cycle (Taylor 1992; Gardner and West 2006), the benefits of altruism are exactly balanced by demographic counterselection, so that evolution is entirely independent of dispersal. The result in this case will always be: b/N − c > 0 (Row 2 in Table 1; Taylor 1992). (3) With strict density regulation in the first life stage (d1 = 1), only the within-group component of selection remains, giving, −c > 0. Density regulation in subsequent life stages does not affect evolution.
In addition to these three life-cycle invariant results, another general property is that density regulation early in life is more restrictive to the spread of altruism than regulation in later life (Table 1, Fig. 5).
Discussion
Competition among kin impedes the evolution of cooperation by eliminating the correlation between genotype and relative group productivity. The ultimate cause of reduced variance in group productivity is density-dependent regulation at a local scale. Life cycle and the spatial scale of density regulation jointly determine the relatedness of individuals within a regulation group at the time of density regulation. Because individuals are less related after dispersal than before, kin competition is reduced in later life stages. When density regulation is global at all life stages there is no kin competition.
The degree of kin competition at life stage k is quantified exactly by the ratio of the genetic variance among regulation groups to the variance among social groups, αk = Vd/Vb. Assuming weak selection, this is equivalent to, αk = rd,k/r (eq. 6), which can be estimated from neutral markers (Queller and Goodnight 1989; Lynch and Ritland 1999) if the regulation group can be accurately identified. This result is robust to variations in population structure, including extinction/recolonization (Wade and McCauley 1988; J. D. Van Dyken, unpubl. ms.), age-structured populations, and populations with nonrandom composition of regulation groups, such as in truly viscous populations in which dispersal range is limited (Kimura and Weis 1964) or where multiple broods are laid by a single female in neighboring patches or on a single host plant.
Under the infinite island model, rd,k = dkrk and we find that the degree of kin competition at life stage k is αk = dk ∏ (1 − mi)2 (eq. 12). This shows that density regulation, the ultimate cause of kin competition, and viscosity are independent in the island model. Kin competition is determined by the interaction between the intensity (or spatial scale) of density regulation, dispersal, and life cycle. The general expression for α (eq. 13) provides a simple means of introducing any arbitrary life cycle or demographic assumption into kin selection models to readily compare the effects of these assumptions on model outcomes.
Previously, kin competition has been accounted for by measuring relatedness with respect to competitors (Queller 1994), measuring variance among social groups with respect to the density-regulated neighborhood (Kelly 1994a), or by discounting the benefits of cooperation by the decrement in fitness experienced by kin (Grafen 1984; Frank 1998). The multilevel Price partitioning of equation (3) cleanly separates the effects of kin competition from both variance (relatedness) and group benefit, demonstrating that kin competition neither strictly affects relatedness nor group benefit. Rather, the Price partitioning reveals the existence of a demographic counterselection term, −αcov(wi, zi) = βwi, zi Vd, which quantifies the response to density-dependent selection. Demographic selection is always opposite in sign to group selection, with a strength proportional to the degree of kin competition multiplied by variance among social groups, or, equivalently, the variance among regulation groups (αVb = Vd). This demonstrates that kin competition is an independent causal component of the total evolutionary response.
The Price equation intrinsically incorporates population elasticity, making it a simple alternative to more complicated models of elasticity (van Baalan and Rand 1998; Mittledorf and Wilson 2000; Alizon and Taylor 2008; Lion and Gandon 2009), although there are numerous reasons to prefer these other methods, including the fact that they make models spatially explicit (Wade et al. 2010). Although the result αk = rd,k/r is also robust to elasticity, the result αk = dk(1 − mk)2 requires the assumption of weak selection so that identity coefficients developed under neutrality could be used, and that changes in group size would be small enough that island model assumptions hold to a first approximation. An explicit accounting of the effect of group elasticity on identity coefficients will need to be conducted to test the robustness of this approximate result to large fluctuations in group size.
Previous work has applied models of kin competition to explain a number of disparate phenomena, including genetic conflict (Hurst 1991; Wade and Beemen 1994; Gardner and West 2004), parasite virulence (Lively 2009), communal foraging (Kelly 1994b), harming behavior (Gardner and West 2004; Gardner et al. 2004), sex-limited dispersal (Gardner 2010), worker policing in eusocial hymenoptera (Gardner and West 2004), and the benefits of propagule mode dispersal for the evolution of altruism (Gardner and West 2006; Lehmann et al. 2006). Although none of these phenomena are explicitly considered here, applying the present approach to these problems is the subject of ongoing work.
KIN SELECTION, SOFT SELECTION, MULTILEVEL SELECTION
Using the method of contextual analysis, Goodnight et al. (1992) found that soft selection, despite eliminating the among-group component of selection (Wade 1985), actually constitutes a form of group selection itself. The Price partitioning of equation (3) independently justifies this view, showing that soft selection occurs when the strength of demographic selection acting among regulation groups is equal in magnitude, and opposite in sign, to selection among social groups. In addition, from equations (4) and (A4) it can be seen that high relatedness is not sufficient to generate a response to kin selection. This is because the intensity of kin competition controls the magnitude of group selection, which is required for kin selection to act. When strict kin competition turns off group selection, cooperation cannot evolve, regardless of the degree of relatedness, providing independent support for the theoretical result of Bijma and Wade (2008), who found that kin selection requires both relatedness and group selection.
It is possible to quantify the disparate definitions of “soft selection” and “local competition” in terms of the kin competition parameter α. The degree of soft selection sensu Wade (1985) and Whitlock (2002) and the scale of competition sensu Gardner and West (2006) are both equivalent to the total degree of kin competition, α. The degree of soft selection sensu Christiansen (1975) is the scale of density dependence in the first life stage, which happens to equal the degree of kin competition in the first life stage, α1 = d1. Strict soft selection sensu Dempster (1955) occurs when either α = 1, d1 = 1, or dL = 1, where dL is density regulation at the final life stage. In all three cases, the number of adults will remain constant between generations. Because Boyd (1982) and Frank (1998) did not specify a life-cycle, the scale of competition sensu Boyd (1982) and Frank (1998) is equal to dk, the scale of density regulation at any given life stage. These definitions are all equivalent under strict local density regulation in the first life stage (α1 = d1 = 1), but are not equivalent otherwise.
Importantly, only α accurately predicts evolutionary dynamics under all life cycles. Although the terms “hard” and “soft selection” were used by Christiansen (1975) to dichotomize the conditions favoring a protected polymorphism in a subdivided population, these conditions do not dichotomize cleanly under his definition. With some models (e.g., Christiansen 1975; Taylor 1992) the predictions of soft and hard selection become equivalent when dispersal probability equals zero or one. This compromises the utility of this conceptual dichotomy as a general principle. Likewise, Dempster (1955)’s definition fails because constant adult number does not always guarantee strict kin competition, specifically in cases in which there is dispersal before reproduction. On the other hand, the degree of kin competition achieves a clean dichotomy that is general under all model assumptions. This makes “kin competition” the most cromulent concept in terms of accurately depicting evolutionary dynamics.
WHICH TRAITS WILL BE AFFECTED BY KIN COMPETITION?
For a trait to experience kin competition, density-regulation must occur locally and be independent of the trait itself. A number of factors regulate density, including finite space, limited resources, predation, herbivory, parasitism, and weather (Roughgarden 1979). There are numerous social traits that interact with these factors (Gardner and West 2006 give the example of alarm-calling, for instance), generating a correlation between local density and genotype that prohibits strict kin competition on these traits. For example, predation-induced mortality can be reduced by alarm calling, aggregation, group defense, parental care, or nest building (Seyfarth et al. 1980; Dangerfield et al. 1998; Queller and Strassman 1998); parasites can be reduced by social grooming (Hart 1992); nest building or collective thermoregulation can prevent mortality due to extreme temperatures (Kronenberg and Heller 1982; Arnold 1988). Social traits involved in niche construction (Odling-Smee et al. 1996) should likewise promote elasticity and thus ameliorate kin competition. Resource limitation is a common source of density regulation that can potentially impose kin competition (Kelly 1994b). Resource limitation will fail to cause kin competition when there are genotypes that differ in the consumption or production of public goods. Public goods games hold a special place in the theory of social evolution. Consumption of public goods is described by the tragedy of the commons (TOCs) (Hardin 1968; Frank 1992, 1998, 2010), which is a public goods game in which overconsumption of a shared resource reduces local carrying capacity, whereas prudent resource use by “cooperators” increases local carrying capacity. This scenario will occur whenever there are diminishing returns of resource consumption on fitness, or a trade-off between growth rate and yield (Pfeiffer et al. 2001; Novak et al. 2006). In a TOC scenario, where regulation is imposed only by resource limitation, local density will necessarily correlate with genotype, prohibiting strict kin competition.
Furthermore, kin competition via resource limitation will be diminished when public goods production by “cooperators” leads to increased local carrying capacity (Platt and Bever 2009). Public goods production can increase carrying capacity by making available previously inaccessible resources, such as with iron-scavenging siderophores (Buckling et al. 2007) or manufactured metabolites (Platt and Bever 2009) in bacteria, or as with agriculture in ants, termites, ambrosia beetles, and humans (Mueller et al. 2005); or by fostering cross-feeding whereby metabolic byproducts are used in alternative metabolic pathways that increase local yield (Pfeiffer and Bonhoeffer 2004). In these cases, the very nature of sociality is inexorably tied to the ability to increase local density in the face of limited resources, thus mitigating kin competition.
On the other hand, Brockhurst et al. (2008) showed that public goods production may decrease under nutrient stress. This provides an interesting route by which kin competition can act: nutrient availability may limit the expression of sociality, rather than directly regulate local density, thus prohibiting the expression of differential group productivity. Another potential complexity of kin competition is that genotype independence may exist in a species until a novel genotype (or environment) arises that promotes group elasticity. This means that the degree of kin competition is often a transient, evolvable character.
Where should we look for kin competition? In general, kin competition will be most intense on traits that do not directly interact with factors regulating local density. In a population under regulation by multiple factors, a trait that overcomes one factor may be impeded by another, such as when group defense against predation increases resource pressure. In this case, group defense may not experience kin competition via predation, but it may via resource limitation. Inversely, gains in local yield by prudent resource consumption (i.e., the TOC) may be offset by increased local predation or parasite pressure, for example, preventing the evolution of cooperative self-restraint. Interactions between density-regulating factors may be an important ecological constraint on social evolution.
Additionally, there may be segments of the population that do not contribute to group productivity, restricting kin competition to traits expressed by these individuals. For example, sex-limited dispersal can eliminate the correlation between group productivity and many traits of the nondispersing sex. This has been observed in male fig wasps (West et al. 2001; see also Gardner 2010 for an explicit model). In fig wasps, individuals mate locally within a fruit followed by dispersal of a single sex, typically females (Hamilton 1967). Because males do not contribute to group productivity (Colwell 1981; Wilson and Colwell 1981), group selection is blind to the social traits of males, unless these traits correlate with low fertility or reduce the number of the dispersing sex (females). West et al. (2001) found that there was no correlation between relatedness (i.e., the strength of group selection) and male–male aggression in fig wasps. The absence of group selection on male aggression indicates, by definition, the action of kin competition.
Finally, dispersal itself is trait subject to kin selection. Most models of dispersal evolution assume inelastic populations, with selection before dispersal and strict local density regulation after dispersal (Hamilton and May 1977; Frank 1986, 1998; Gandon and Michalakis 2001), although see Parvinen et al. 2003. The present results show that the evolution of dispersal rates will be quite different under different life cycle or ecological assumptions. When density regulation is global at all stages, there will be no selection for increased dispersal by social evolution. Likewise, there will never be social selection for increased dispersal if social interactions occur at the same life cycle stage as density regulation.
EXPERIMENTAL DATA
Experiments using the siderophore-producing bacterium Pseudomonas auerugenosa have shown that kin competition can control the correlation between genotype and differential group productivity (Griffin et al. 2004; Kummerli et al. 2009a). Siderophore-production aids in iron uptake necessary for growth, and is individually costly but group beneficial. Experiments on these bacteria modulated the intensity of local competition to determine the effect of selection for cooperative genotypes in mixed culture. Although couched in terms of inclusive fitness, the design of Griffen et al.’s (2004) and Kummerli et al.’s (2009a) experiments are nearly identical to the classic group selection experiments of Wade (1976, 1977, 1982). The local competition treatment is analogous to the nongroup selection controls of Wade, while the global competition treatment mirrors Wade’s group selection protocol. As predicted, when group selection is turned off, cooperation cannot evolve. These experiments, along with the present theoretical analysis, support the theoretical conclusion of Bijma and Wade (2008) that kin selection requires both relatedness and group selection.
Two recent experiments, one with Pseudomonas auregonasa (Kummerli et al. 2009b) and the other with the colocin (toxin) producing bacteria Escherichia coli (Le Gac and Doebli 2010) indicate that viscosity and local competition are distinct. Unlike Griffin et al. (2004) and Kummerli et al. (2009a), these experiments create the viscous and nonviscous environments (by varying the density of agar media) that subsequently generate selection. This is arguably more realistic than using experimenter-imposed selection. In both cases, cooperation evolved under highly viscous media, demonstrating empirically that viscosity per se does not impede kin selection.
Clearly, estimates of the strength of kin competition in nature are needed. Kelly (1997) applied a regression-based approach to quantify the degree of soft selection in a natural plant metapopulation. Future studies could apply equations (6) and (13) to estimate the intensity of kin competition in natural populations, although this method will be limited by the ability to accurately identify the density-regulated neighborhood. Until empirical measures are conducted on a wider range of species, the prevalence and efficacy of kin competition in nature remains in question.
ACKNOWLEDGMENTS
I thank C. Lively and M. J. Wade for helpful discussions and comments on a number of very early drafts. I also thank A. Gardner, C. Goodnight, and J. K. Kelly for their careful reading of this manuscript and for their many helpful comments. This work was supported by an NSF IGERT Fellowship, and NIH Grant 5R01GM084238-02 to M. J. Wade.
Appendix A
DERIVATION OF HAMILTON’S RULE FROM THE MULTILEVEL PRICE EQUATION
Equation (3) can be used to derive Hamilton’s rule by using the standard n-ploid population genetic model with Hamilton’s linear fitness function. Let there be a diploid population with alleles A and a segregating at a single biallelic locus controlling altruism. Homozygous AA individuals are altruists, whereas aa homozygotes are nonaltruists who nonetheless receive the benefit of altruism from social partners. Heterozygous Aa individuals behave altruistically with probability h, the degree of dominance of the altruistic allele. Assume that social interactions are indiscriminant, such that they occur within the group at random with respect to genotype. Define pij as the frequency of allele A in individual j in group i which takes on the values (0, ½, 1). Then pi is the mean frequency of allele A in group i, and p is the mean frequency of A in the global population. Expressing the altruistic trait decreases the fitness of the altruist j by an amount cj, but increases the fitness of a recipient k by an average amount bk. Assuming that Hardy–Weinberg proportions obtain, on average, within groups (Falconer and Mackay 1996), the mean and genotypic fitnesses in group i are, respectively,
| (A1a) |
| (A1b) |
| (A1c) |
| (A1d) |
where Nalt,i = Ni(pi2 + 2pi(1 − pi)h) is the number of altruists in group i (Wilson 1975; Wade 1978, 1979, 1980). Note that in this form, individual altruists do not receive the benefits of their own altruism (this corresponds to ‘others-only’ altruism [Pepper 2000]). When altruism feedback onto the altruist (“whole-group” altruism [Pepper 2000]), each benefit term in equation (A1b–d) is simply replaced by bkNalt,i.
Rewriting equation (3) in its regression coefficient form (Wade 1985) and assuming additivity (h = ½), gives,
| (A2) |
where βwi, pi and βwij, pij are the partial regression coefficients of group and individual allele frequency on group and individual fitness, respectively (Wade 1985; Frank 1998; Rice 2004). Vb is the variance in allele frequency among all groups, and Vw is the average within-group variance in individual allele frequency (i.e., Vw = E[varw(pij)]. Values for these variance components are given for neutral alleles by Wright (1951, 1965). The among-group partial regression coefficient, βwi, pi, can be found by taking the derivative of equation (A1a) with respect to pi. The within-group partial regression coefficient βwij, pij is the “average excess” divided by (1 − p) (Falconer and Mackay 1996), which is equal to the difference in the marginal within-group fitness of each allele (Rice 2004). This can be written as, βwij, pij = (WA,i* − Wa,i*), where WA,i* = piWAA,i + (1 − pi)WAa,i and Wa,i* = (1 − pi)Waa,i + piWAa,i are the marginal fitness of the A and a alleles, respectively, within group i.
Invoking a change of variables allows us to describe both “others-only” and “whole-group” altruism by the same equations. For others-only altruism, we define b = bk(Ni − 1) as the total benefit dispensed by an altruist, and −c = −cj − bk as the net cost incurred by an altruist. With whole-group altruism, b = bkNi and −c = −cj. In both cases, using the fitness model above (eq. A1), with no dominance or inbreeding (as assumed by Hamilton [1963, 1964]) we find that, βwi, pi = (b − c), and βwij, pij = −c. Applying this to equation (A2) gives
| (A3) |
Equation (A3) applies even for loci under strong selection. Making the standard assumption of weak selection, the variance in allele frequency among- and within-groups is Vb = pqfst and Vw = pq(1 − fst)/2, respectively (Wright 1951; Wright 1965), where fst is Wright’s measure of population subdivision. Substituting into equation (A3) gives
| (A4) |
The quantity in square brackets is the inclusive fitness effect for the current model, which determines the direction of evolution. Setting equation (A4) equal to zero and noting that r = Vb/(Vb + Vw) = 2fst/(1 + fst) is the kin selection coefficient of relatedness (Hamilton 1975; Michod and Hamilton 1980; Frank 1992, 1998; Queller 1992), after some algebra we obtain equation (4) in the main text.
Appendix B
RELATEDNESS AT LIFE STAGE K
Assuming neutrality, a recursion can be obtained for relatedness based on the probability of identity by descent. For simplicity, assume haploidy, where r = fst. Let N be the number of individuals founding a group. Relatedness of individuals within a group before dispersal, rBD, is given by the probability that two genes chosen at random from within the group descended from the same gene copy in the previous generation (1/N) plus the probability that the two genes descended from different gene copies in the previous generation (1 − 1/N) times the probability that these two gene copies were related in the previous generation (rt−1) and that neither dispersed ((1 − m)2)
| (B1) |
At equilibrium, rt = rt−1 = r. Substituting into equation (B1) and solving gives
| (B2) |
Alternatively, relatedness can be measured after dispersal. In this case, relatedness is given by the probability that two alleles chosen at random are identical by descent from the previous generation and that neither copy migrated in that generation. The recursion and equilibrium relatedness in this case ar,
| (B3) |
| (B4) |
This reasoning can be extending to allow multiple bouts of dispersal, leading to equation (9) in the main text.
LITERATURE CITED
- Alizon S, Taylor P. Empty sites can promote altruistic behavior. Evolution. 2008;62:1335–1344. doi: 10.1111/j.1558-5646.2008.00369.x. [DOI] [PubMed] [Google Scholar]
- Arnold W. Social thermoregulation during hibernation in alpine marmots (Marmota marmota) J. Comp. Physiol. B. 1988;158:151–156. doi: 10.1007/BF01075828. [DOI] [PubMed] [Google Scholar]
- Bijma P, Wade MJ. The joint effects of kin, multilevel selection and indirect genetic effects on response to genetic selection. J. Evol. Biol. 2008;21:1175–1188. doi: 10.1111/j.1420-9101.2008.01550.x. [DOI] [PubMed] [Google Scholar]
- Boyd R. Density-dependent mortality and the evolution of social interactions. Animal Behavior. 1982;30:972–982. [Google Scholar]
- Brockhurst MA, Buckling A, Racey D, Gardner A. Resource supply and the evolution of public-goods cooperation in bacteria. BMC Biology. 2008;6:20. doi: 10.1186/1741-7007-6-20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckling A, Harrison F, Vos M, Brockhurst MA, Gardner A, West SA, Griffin A. Siderophore-mediated cooperation and virulence in Pseudomonas aeruginosa. FEMS Microbiol. Ecol. 2007;62:135–141. doi: 10.1111/j.1574-6941.2007.00388.x. [DOI] [PubMed] [Google Scholar]
- Charlesworth B. Note on the Evolution of Altruism in Structured Demes. Am. Nat. 1979;113:601–605. [Google Scholar]
- Christiansen FB. Hard and soft selection in a subdivided population. Am. Nat. 1975;109:11–16. [Google Scholar]
- Colwell RK. Group selection is implicated in the evolution of female-biased sex ratios. Nature. 1981;290:401–404. [Google Scholar]
- Costa JT. The Other Insect Societies. Cambridge, MA: Harvard University Press; 2006. [Google Scholar]
- Crow JF, Kimura M. An introduction to population genetics theory. New York: Harper & Row; 1970. [Google Scholar]
- Dangerfield JM, Mccarthy TS, Ellery WN. The mound-building termite Macrotermes michaelseni as an ecosystem engineer. J. Trop. Ecol. 1998;14:507–520. [Google Scholar]
- Dempster ER. Maintenance of genetic heterogeneity cold spring harbor symposia on quantitative. Biology. 1955;20:25–32. doi: 10.1101/sqb.1955.020.01.005. [DOI] [PubMed] [Google Scholar]
- Falconer DS, Mackay TFC. Introduction to quantitative genetics. Essex, England: Prentice Hall; 1996. [Google Scholar]
- Frank SA. Dispersal polymorphisms in subdivided populations. J. Theor. Biol. 1986;122:303–309. doi: 10.1016/s0022-5193(86)80122-9. [DOI] [PubMed] [Google Scholar]
- Frank SA. A kin selection model for the evolution of virulence. Proc. Biol. Sci. 1992;250:195–197. doi: 10.1098/rspb.1992.0149. [DOI] [PubMed] [Google Scholar]
- Frank SA. Foundations of social evolution. Princeton, NJ: Princeton Univ. Press; 1998. [Google Scholar]
- Frank SA. Demography and the tragedy of the commons. J. Evol. Biol. 2010;23:32–39. doi: 10.1111/j.1420-9101.2009.01893.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gandon S, Michalakis Y. Multiple causes of the evolution of dispersal. In: Clobert J, Danchin E, Dhondt AA, Nichols JD, editors. Dispersal. New York: Oxford Univ. Press; 2001. pp. 155–167. [Google Scholar]
- Gardner A. Sex-biased dispersal of adults mediates the evolution of altruism among juveniles. J. Theor. Biol. 2010;262:339–345. doi: 10.1016/j.jtbi.2009.09.028. [DOI] [PubMed] [Google Scholar]
- Gardner A, West SA. Spite and the scale of competition. J. Evol. Biol. 2004;17:1195–1203. doi: 10.1111/j.1420-9101.2004.00775.x. [DOI] [PubMed] [Google Scholar]
- Gardner A, West SA. Demography, altruism, and the benefits of budding. J. Evol. Biol. 2006;19:1707–1716. doi: 10.1111/j.1420-9101.2006.01104.x. [DOI] [PubMed] [Google Scholar]
- Gardner A, West SA, Buckling A. Bacteriocins, spite and virulence. P. R. Soc. Lond B. 2004;271:1529–1535. doi: 10.1098/rspb.2004.2756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodnight CJ, Schwartz JM, Stevens L. Contextual analysis of models of group selection, soft selection, hard selection, and the evolution of altruism. Am. Nat. 1992;140:743–761. [Google Scholar]
- Grafen A. Natural selection, kin selection, and group selection. In: Krebs JR, Davies NB, editors. Behavioral ecology. Oxford: Blackwell Scientific Publications; 1984. pp. 62–84. [Google Scholar]
- Grafen A. A geometric view of relatedness. Oxford Surv. Evol. Biol. 1985;2:28–89. [Google Scholar]
- Griffin AS, West SA, Buckling A. Cooperation and competition in pathogenic bacteria. Nature. 2004;430:1024–1027. doi: 10.1038/nature02744. [DOI] [PubMed] [Google Scholar]
- Hamilton WD. The evolution of altruistic behavior. Am. Nat. 1963;97:354–356. [Google Scholar]
- Hamilton WD. The genetical evolution of social behaviour. I. J. Theor. Biol. 1964;7:1–16. doi: 10.1016/0022-5193(64)90038-4. [DOI] [PubMed] [Google Scholar]
- Hamilton WD. Extraordinary sex ratios. Science. 1967;156:477–488. doi: 10.1126/science.156.3774.477. [DOI] [PubMed] [Google Scholar]
- Hamilton WD. Innate social aptitudes of man: an approach from evolutionary genetics. In: Fox R, editor. Biosocial antrhopology. London: Malaby Press; 1975. pp. 133–153. [Google Scholar]
- Hamilton WD, May RM. Dispersal in stable habitats. Nature. 1977;269:578–581. [Google Scholar]
- Hardin G. The tragedy of the commons. Science. 1968;162:1243–1248. [PubMed] [Google Scholar]
- Hart BL. Behavioral adaptations to parasites: an ethological approach. J. Parasitol. 1992;78:256–265. [PubMed] [Google Scholar]
- Heisler IL, Damuth J. A method for analyzing selection in hierarchically structured populations. Am. Nat. 1987;130:582–602. [Google Scholar]
- Hurst LD. The incidences and evolution of cytoplasmic male killers. Proc. R. Soc. Lond. B. 1991;244:91–99. [Google Scholar]
- Kelly JK. Restricted migration and the evolution of altruism. Evolution. 1992;46:1492–1495. doi: 10.1111/j.1558-5646.1992.tb01139.x. [DOI] [PubMed] [Google Scholar]
- Kelly JK. The effect of scale dependent processes on kin selection: mating and density regulation. Theor. Popul. Biol. 1994a;46:32–57. doi: 10.1006/tpbi.1994.1018. [DOI] [PubMed] [Google Scholar]
- Kelly JK. A model for the evolution of communal foraging in hierarchically structured populations. Behav. Ecol. Sociobiol. 1994b;35:205–212. [Google Scholar]
- Kelly JK. Fitness variation across a subdivided population of the annual plant impatiens capensis. Evolution. 1997;51:1100–1111. doi: 10.1111/j.1558-5646.1997.tb03957.x. [DOI] [PubMed] [Google Scholar]
- Kimura M, Weiss GH. Stepping stone model of population structure + decrease of genetic correlation with distance. Genetics. 1964;49:561–576. doi: 10.1093/genetics/49.4.561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kronenberg F, Heller HC. Colonial thermoregulation in honey bees (Apis mellifera) J. Comp. Physiol. B. 1982;148:65–76. [Google Scholar]
- Kummerli R, Gardner A, West SA, Griffin AS. Limited dispersal, budding dispersal, and cooperation: an experimental study. Evolution. 2009a;63:939–949. doi: 10.1111/j.1558-5646.2008.00548.x. [DOI] [PubMed] [Google Scholar]
- Kummerli R, Griffin AS, West SA, Buckling A, Harrison F. Viscous medium promotes cooperation in the pathogenic bacterium Pseudomonas aeruginosa. Proc. Biol. Sci. 2009b;276:3531–3538. doi: 10.1098/rspb.2009.0861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Gac M, Deobli M. Environmental viscosity does not affect the evolution of cooperation during experimental evolution of colicigenic bacteria. Evolution. 2010;64:522–533. doi: 10.1111/j.1558-5646.2009.00814.x. [DOI] [PubMed] [Google Scholar]
- Lehmann L, Perrin N, Rousset FO, Day T. Population demography and the evolution of helping behaviors. Evolution. 2006;60:1137–1151. [PubMed] [Google Scholar]
- Levene H. Genetic equilibrium when more than one ecological niche is available. Am. Nat. 1953;87:331. [Google Scholar]
- Lion S, Gandon S. Habitat saturation and the spatial evolutionary ecology of altruism. J. Evol. Biol. 2009;22:1487–1502. doi: 10.1111/j.1420-9101.2009.01769.x. [DOI] [PubMed] [Google Scholar]
- Lively CM. Local host competition in the evolution of virulence. J. Evol. Biol. 2009;22:1268–1274. doi: 10.1111/j.1420-9101.2009.01743.x. [DOI] [PubMed] [Google Scholar]
- Lynch M, Ritland K. Estimation of pairwise relatedness with molecular markers. Genetics. 1999;152:1753–1766. doi: 10.1093/genetics/152.4.1753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michod RE. Darwinian dynamics: evolutionary transitions in fitness and individuality. Princeton, NJ: Princeton Univ. Press; 1999. [Google Scholar]
- Michod RE, Hamilton WD. Coefficients of relatedness in sociobiology. Nature. 1980;288:694–697. [Google Scholar]
- Mitteldorf J, Wilson DS. Population viscosity and the evolution of altruism. J. Theor. Biol. 2000;204:481–496. doi: 10.1006/jtbi.2000.2007. [DOI] [PubMed] [Google Scholar]
- Mueller UG, Gerardo NM, Aanen DK, Six DL, Schultz TR. The evolution of agriculture in insects. Ann. Rev. Ecol. Evol. Syst. 2005;36:563–595. [Google Scholar]
- Novak M, Pfeiffer T, Lenski RE, Sauer U, Bonhoeffer S. Experimental tests for an evolutionary trade-off between growth rate and yield in E-coli. Am. Nat. 2006;168:242–251. doi: 10.1086/506527. [DOI] [PubMed] [Google Scholar]
- Odling-Smee FJ, Laland KN, Feldman MW. Niche construction. Am. Nat. 1996;147:641–648. [Google Scholar]
- Okasha S. Evolution and the levels of selection. New York: Oxford Univ. Press; 2006. [Google Scholar]
- Parvinen K, Dieckmann U, Gyllenberg M, Metz JAJ. Evolution of dispersal in metapopulations with local density dependence and demographic stochasticity. J. Evol. Biol. 2003;16:143–153. doi: 10.1046/j.1420-9101.2003.00478.x. [DOI] [PubMed] [Google Scholar]
- Pepper JW. Relatedness in trait group models of social evolution. J. Theor. Biol. 2000;206:355–368. doi: 10.1006/jtbi.2000.2132. [DOI] [PubMed] [Google Scholar]
- Pfeiffer T, Bonhoeffer S. Evolution of cross-feeding in microbial populations. Am. Nat. 2004;163:E126–E135. doi: 10.1086/383593. [DOI] [PubMed] [Google Scholar]
- Pfeiffer T, Schuster S, Bonhoeffer S. Cooperation and competition in the evolution of ATP-producing pathways (vol 292, pg 504, 2001) Science. 2001;293:1436–1436. doi: 10.1126/science.1058079. [DOI] [PubMed] [Google Scholar]
- Platt TG, Bever JD. Kin competition and the evolution of cooperation. Trends Ecol. Evol. 2009;24:370–377. doi: 10.1016/j.tree.2009.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price GR. Extension of covariance selection mathematics. Ann. Hum. Genet. 1972;35:485–490. doi: 10.1111/j.1469-1809.1957.tb01874.x. [DOI] [PubMed] [Google Scholar]
- Queller DC. Quantitative genetics, inclusive fitness, and group selection. Am. Nat. 1992;139:540–558. [Google Scholar]
- Queller DC. Genetic relatedness in viscous populations. Evol. Ecol. 1994;8:70–73. [Google Scholar]
- Queller DC, Goodnight KF. Estimating relatedness using genetic-markers. Evolution. 1989;43:258–275. doi: 10.1111/j.1558-5646.1989.tb04226.x. [DOI] [PubMed] [Google Scholar]
- Queller DC, Strassmann JE. Kin selection and social insects. BioScience. 1998;48:165–175. [Google Scholar]
- Rice SH. Evolutionary theory: mathematical and conceptual foundations. Sunderland, MA: Sinauer; 2004. [Google Scholar]
- Roughgarden J. Theory of population genetics and evolutionary ecology: An introduction. Upper Saddle River, NJ: Prentice Hall; 1979. [Google Scholar]
- Rousset F. Genetic structure and selection in subdivided populations. Princeton, NJ: Princeton Univ. Press; 2004. [Google Scholar]
- Rousset F. Separation of time scales, fixation probabilities and convergence to evolutionarily stable states under isolation by distance (vol 69, pg 165, 2006) Theor. Popul. Biol. 2006;69:165–179. doi: 10.1016/j.tpb.2005.08.008. [DOI] [PubMed] [Google Scholar]
- Seyfarth RM, Cheney DL, Marler P. Monkey responses to three different alarm calls: evidence of predator classification and semantic communication. Science. 1980;210:801–803. doi: 10.1126/science.7433999. [DOI] [PubMed] [Google Scholar]
- Taylor P. Altruism in viscous populations—an inclusive fitness model. Evol. Ecol. 1992;6:352–356. [Google Scholar]
- Taylor PD, Irwin AJ. Overlapping generations can promote altruistic behavior. Evolution. 2000;54:1135–1141. doi: 10.1111/j.0014-3820.2000.tb00549.x. [DOI] [PubMed] [Google Scholar]
- van Baalen M, Rand DA. The unit of selection in viscous populations and the evolution of altruism. J. Theor. Biol. 1998;193:631–648. doi: 10.1006/jtbi.1998.0730. [DOI] [PubMed] [Google Scholar]
- Wade MJ. Group selections among laboratory populations of Tribolium. Proc. Natl. Acad. Sci. USA. 1976;73:4604–4607. doi: 10.1073/pnas.73.12.4604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wade MJ. An experimental study of group selection. Evolution. 1977;31:134–153. doi: 10.1111/j.1558-5646.1977.tb00991.x. [DOI] [PubMed] [Google Scholar]
- Wade MJ. Kin selection: a classical approach and a general solution. Proc.Natl. Acad. Sci. USA. 1978;75:6154–6158. doi: 10.1073/pnas.75.12.6154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wade MJ. The evolution of social interactions by family selection. Am. Nat. 1979;113:399–417. [Google Scholar]
- Wade MJ. Kin selection: its components. Science. 1980;210:665–667. doi: 10.1126/science.210.4470.665. [DOI] [PubMed] [Google Scholar]
- Wade MJ. Group selection: migration and the differentiation of small populations. Evolution. 1982;36:949–961. doi: 10.1111/j.1558-5646.1982.tb05465.x. [DOI] [PubMed] [Google Scholar]
- Wade MJ. Soft selection, hard selection, kin selection, and group selection. Am. Nat. 1985;125:61–73. [Google Scholar]
- Wade MJ, Beeman RW. The population dynamics of maternal-effect selfish genes. Genetics. 1994;138:1309–1314. doi: 10.1093/genetics/138.4.1309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wade MJ, McCauley DE. Extinction and recolonization: their effects on the genetic differentiation of local populations. Evolution. 1988;42:995–1005. doi: 10.1111/j.1558-5646.1988.tb02518.x. [DOI] [PubMed] [Google Scholar]
- Wade MJ, Wilson DS, Goodnight C, Taylor D, Bar-Yam Y, de Aguiar MA, Stacey B, Werfel J, Hoelzer GA, Brodie ED, 3rd, et al. Multilevel and kin selection in a connected world. Nature. 2010;463:E8–E9. doi: 10.1038/nature08809. discussion E9–E10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallace B. Polymorphism, population size, and genetic load. In: Lewontin RC, editor. Population biology and evolution. Syracuse, NY: Syracuse University Press; 1968. pp. 87–108. [Google Scholar]
- Wallace B. Hard and soft selection revisited. Evolution. 1975;29:465–473. doi: 10.1111/j.1558-5646.1975.tb00836.x. [DOI] [PubMed] [Google Scholar]
- West SA, Murray MG, Machado CA, Griffin AS, Herre EA. Testing Hamilton’s rule with competition between relatives. Nature. 2001;409:510–513. doi: 10.1038/35054057. [DOI] [PubMed] [Google Scholar]
- Whitlock MC. Selection, load and inbreeding depression in a large metapopulation. Genetics. 2002;160:1191–1202. doi: 10.1093/genetics/160.3.1191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson DS. A theory of group selection. Proc. Natl. Acad. Sci. USA. 1975;72:143–146. doi: 10.1073/pnas.72.1.143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson DS, Colwell RK. Evolution of sex ratio in structured demes. Evolution. 1981;35:882–897. doi: 10.1111/j.1558-5646.1981.tb04952.x. [DOI] [PubMed] [Google Scholar]
- Wilson DS, Pollock G, Dugatkin L. Can altruism evolve in purely viscous populations? Evol. Ecol. 1992;6:331–341. [Google Scholar]
- Wright S. Evolution in Mendelian populations. Genetics. 1931;16:97–159. doi: 10.1093/genetics/16.2.97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S. The genetical structure of populations. Ann. Eugen. 1951;15:323–354. doi: 10.1111/j.1469-1809.1949.tb02451.x. [DOI] [PubMed] [Google Scholar]
- Wright S. The interpretation of population structure by F-statistics with special regard to systems of mating. Evolution. 1965;19:395–420. [Google Scholar]