Effects of Simplifying Choice Tasks on Estimates of Taste Heterogeneity in Stated-Choice Surveys

Abstract

Researchers usually employ orthogonal arrays or D-optimal designs with little or no attribute overlap in stated-choice surveys. The challenge is to balance statistical efficiency and respondent burden to minimize the overall error in the survey responses. This study examined whether simplifying the choice task, by using a design with more overlap, provides advantages over standard minimum-overlap methods. We administered two designs for eliciting HIV test preferences to split samples. Surveys were undertaken at four HIV testing locations in San Francisco, California. Personal characteristics had different effects on willingness to pay for the two treatments, and gains in statistical efficiency in the minimal-overlap version more than compensated for possible imprecision from increased measurement error.

Introduction

The stated-choice (SC) question format is one of several stated-preference approaches that use hypothetical scenarios, described by multiple attributes, to elicit individuals’ preferences for goods and services. SC surveys, known also as discrete-choice experiments or choice-format conjoint analysis, have been extensively used in health economics to understand the preferences of patients, physicians or care-givers (Mark & Swait, 2003; Ryan et al., 2001; Diener, O’Brien, & Gafni, 1998; Johnson, Desvousges, Ruby, Stieb, & Civita, 1998) after its intensive use in marketing research and in environmental economics (Green & Rao, 1971; Louviere & Hensher, 1983; Bennett & Adamowicz, 2001; Olsen & Smith, 2001; Holmes &Adamowicz, 2003). SC surveys have been adapted to measure the willingness to pay for health care services (Wordswort, Ryan, Skatun, & Waugh, 2006; Johnson, Banzhaf, & Desvousges, 2000), or to calculate tradeoffs among different attributes, such as benefit-risk tradeoffs (Ratcliffe, Buxton, McGarry, Sheldon, & Chancellor, 2004; Johnson et al., 2007).

Devising SC survey instruments that are both effective and efficient in eliciting preference data requires decisions at many stages of survey development. In some cases there is little empirical basis to guide such decisions. Researchers’ decisions about various aspects of study design can influence the way subjects answer the preference-elicitation questions. Such decisions may include features of the experimental design. Combinations of attribute levels that appear in the sets of scenarios that define the preference-elicitation tasks constitute an experimental design with defined statistical properties (Louviere, Hensher, & Swait, 2000). One of the features of a statistically optimal experimental design is minimal overlap. Overlap occurs in a particular choice set when levels of one or more attributes do not vary between comparison scenarios. For example, the cost-attribute level could be $50 for both alternatives A and B in the same choice set. To obtain the most statistically efficient preference estimates and maximize tradeoff information, SC surveys typically use an orthogonal design with minimum attribute overlap.

As noted by Swait and Adamowicz (1996), SC surveys often are designed to provide desirable statistical characteristics that will be useful in the model estimation stage. In addition to consideration of minimal overlap, important characteristics include attribute orthogonality, level balance, and utility balance (Huber & Zwerina, 1996). More recent contributions to the experimental-design literature, however, indicate that utility balance is not necessarily a desirable design property (Kanninen, 2002). Researchers often informally weigh measurement-error concerns against statistical efficiency. Zwerina and colleagues (1996) showed that, from a statistical perspective, smaller set sizes (i.e., fewer simultaneous attribute comparisons) reduce statistical efficiency. However, Zwerina’s conclusion assumes that the respondents’ individual error levels do not change. A respondent’s individual-specific error during a particular task may decrease if the task is simplified. Reduction in this individual-specific error can therefore lower or even reverse the efficiency gained by considering more attribute comparisons. Because of this potential difficulty, there may be a tradeoff between statistical efficiency and measurement error (Maddala, Phillips, & Johnson, 2003; Viney, Savage, & Louviere 2005).

Previous SC studies have shown that task complexity leads to preference instability as the experiment progresses (Johnson, Desvousges, Ruby, Stieb, & Civita, 1998; Johnson, Banzhaf, & Desvousges, 2000; Saelensminde, 2002; Arentze, Borgers, Delmistro, & Timmermans, 2003). DeShazo and Fermo (2002) found that choice complexity significantly affects welfare estimates. Arentze and colleagues (2003) also found that task complexity has significant effects on data quality. A recent study showed that missing information (excluding relevant attributes) increased choice consistency (Islam, Louviere, & Burke, 2007). These findings suggest that the difficulty of SC surveys may impair the validity and reliability of the results.

Overlap also may reduce respondent fatigue, which could arise from answering a large number of choice questions, or from increasing complexity (Swait & Adamowicz, 2001). Several studies investigated whether repeated choice tasks lead to fatigue (Bradley & Daly, 1994; DeShazo & Fermo, 2002; Maddala, Phillips, & Johnson, 2003; Arentze, Borgers, Delmistro, & Timmermans, 2003). Arentze and colleagues (2003) and Hensher and colleagues (2001) found no significant effect of fatigue over a number of choice sets. To our knowledge, only one study has investigated whether the degree of overlap affects any of these findings (Maddala, Phillips, & Johnson, 2003).

Marketing research has investigated how sensitive decision strategies are to context effects (Payne, 1982; Johnson & Meyer, 1984). A common concern about context effects involves the relational properties of choice alternatives, that is, how the evaluation of a given alternative depends on the other options in the choice set (Simonson & Tversky, 1992). For example, Chernev (2004) suggests that decision strategies depend on the dispersion of attribute values within each of the alternatives. Another possible cognitive effect may be to shift the focus of subjects’ attention among attributes. Overlap may affect the choice probability for the alternative with the better value of the most important attribute when attributes differed in importance (Johnson & Meyer 1984; Payne 1976; Payne, Bettman, & Johnson 1993), or overlap may shift attention away from the deficiencies of the alternative with the dominant attribute (Tversky, Sattath, & Slovic, 1988). Chernev (1997) found that when attributes vary in importance, overlap enhanced the likelihood of choosing the alternative with the better level of the most important attribute. However, when attributes have similar importance, overlap displayed a trend in the opposite direction, leading to an equalization of choice probabilities.

The practical usefulness of SC data depends on its validity and reliability. Using constructed stimuli to elicit preference measures raises questions about hypothetical bias and whether the resulting preference measures are robust to variations in the stimuli. Researcher decisions about survey construction, particularly experimental design, may affect subject responses to the questions. The purpose of this current study is to evaluate whether the net effect of simplifying the choice task – by using a design with more attribute-level overlap – increases or decreases the precision and size of taste-heterogeneity estimates. We administered two versions of the survey instrument. The first survey was the standard, minimal-overlap instrument in which nearly all attributes levels varied between scenarios. The other survey, the increased-overlap survey, presented two attributes with the same levels in each choice, thereby allowing subjects to compare fewer attributes when making decisions.

Increased overlap reduces the number of attribute levels that change in a given choice task and thus may improve the precision of subjects’ evaluation of the marginal rates of substitution for the attributes that do vary. On the other hand, we obtain fewer total tradeoff evaluations, which reduces the statistical power of the design for a given sample size. This study aims to provide researchers with evidence on these potential quality/quantity tradeoffs from an experiment where the frequency of overlaps is experimentally controlled. In this paper, we extended Maddala and colleagues’ (2003) study, which used a random-effects probit model, by exploring the consequences of overlap for estimating taste heterogeneity using mixed-logit/hierarchical-Bayes (MLHB) modeling. We can quantify the pattern of taste heterogeneity for each preference-parameter estimate. Thus this study evaluates precision specifically in terms of how much information is obtained about taste heterogeneity from preference data obtained from simpler choice tasks compared to more difficult choice tasks.

METHODS

Empirical Study

This experiment was part of an SC study that examined preferences for HIV testing methods (see Phillips, Maddala, & Johnson (2002) for details). We identified six key features of an HIV test based on a literature review, the advice of clinical experts, and focus-group studies (Table 1). The study was approved by the Internal Review Board of University of California-San Francisco.

Table 1.

Attributes and Levels Used in the Survey

Attributes	Levels
Location	Doctor’s office, public clinic, home
Price	$0, $10, $50, $100
Sample Collection	Draw blood, swab mouth, urine sample, prick finger
Timeliness/Accuracy	Results in 1–2 wks. almost always accurate, immediate results almost always accurate, immediate results less accurate
Privacy	Only you know- not linked, phone-not linked, in person-not linked, phone-linked, in person-linked
Counseling	Talk to a counselor, read brochure then talk to counselor

We first developed an orthogonal, balanced "flat" main-effects fractional-factorial design in 40 rows (Zwerina, Huber, & Kuhfeld, 1996). We then used an algorithm programmed in GAUSS (2004) to search randomly drawn designs for the maximum D-efficiency (Huber & Zwerina, 1996). This algorithm finds an efficient paired-scenario choice design based on the OMED flat design that minimizes the average variance around the preference parameters. Developing choice sets for the increased-overlap instrument did not affect level balance since the same candidate set was used. Increased overlap, however, does affect orthogonality and effectively reduces the number of contrasts evaluated, leading to reduced statistical efficiency.

We constructed two designs in which we varied the degree of attribute overlap within choice sets. In the minimal-overlap instrument, the overlap between attributes levels within choice sets was an average minimum of 0.25. This means that the overlap within a choice set was 0 for most questions, but in some instances, one attribute level within a choice set was overlapped. In the increased-overlap instrument, two attributes had the same level (overlapped) within choice sets for every choice set in the instrument. We considered an overlap greater than two attributes within a choice set but it severely reduced efficiency. We determined, therefore, that a two-attribute overlap between scenarios within a choice set would be preferable, hypothesizing that we could recover the slight loss in efficiency with more consistent and less “noisy” subject responses.

We placed scenarios for the minimum-overlap instrument into choice sets based on maximizing the D-efficiency score, which is the inverse of the average variance around the parameter estimates (D-efficiency = 6.52 for the minimum-overlap design, and D-efficiency = 3.75 for the increased-overlap design). We measured this score by defining a group of choice sets given anticipated β, that minimized the “size” of the covariance matrix (Zwerina, Huber, & Kuhfeld, 1996). In contrast, developing the questions for the increased-overlap instrument involved a more complex method. First, we chose a candidate set of scenarios as those with the highest D-efficiency score. From the candidate set, we randomly picked two attributes as targets for the overlap in scenarios. Scenarios that matched on those two attributes were then selected from the full factorial design. We repeated this several times and then selected the set of questions with the highest D-efficiency score.

Each respondent was presented with a series of 11 discrete-choice questions, and was asked to choose one of two scenarios in each question. Surveys were fielded at four publicly funded HIV-testing locations in San Francisco, California between November, 1999 and February, 2000. In these locations. 380 HIV testers were approached, and 365 agreed to complete the survey (96% response rate). The final sample size was 353 after 11 respondents with missing data and one respondent who chose either test A in all his/her choice questions were excluded. The sample was composed of 179 subjects who completed the minimum-overlap survey and 174 subjects who completed the increased-overlap survey. We conducted chi-square analyses on the distribution of gender, ethnicity, and sexual orientation, and on the average income and education level, and found no significant differences between the respondents in the two samples.

Estimation of Heterogeneous Preferences

MLHB models are an extension of random-parameter or mixed-logit models. They have several advantages over conventional conditional-logit and mixed-logit models (Hole 2008; Revelt & Train, 1998). A number of applications have investigated preference heterogeneity represented by random-parameter distributions (Bhat, 1998; 2000; Greene, Hensher, & Rose, 2006; Huber & Train, 2001; Rose & Black, 2006; Train & Sonnier, 2004). This procedure has been incorporated into recent versions of widely available software packages such as LIMDEP (2005) and GAUSS (2004). For this implementation, we adapted GAUSS code developed by Train (2003). Advantages of this approach include the following:

• Accounting for within-sample correlations (panel effects): SC surveys present repeated tasks for each respondent. The choice respondents make in one task is not independent of the choice they make on the other tasks. MLHB accounts for repeated observations for each respondent.

• Accounting for unobserved taste heterogeneity: Most models do not account for heterogeneity in tastes and assume that the effect of an attribute is the same for all respondents with any observable characteristics incorporated in estimation. However, respondents’ preferences may vary as a result of unobserved factors. Such unobserved taste heterogeneity biases population estimates (Train, 2003).

• Estimation of both population-level and individual-level partworth parameters for every attribute level: Individual-level parameter estimates facilitate additional analysis that is impossible with population parameters alone.

Although all parameter estimates are determined simultaneously in practice, MLHB can be thought of as a two-step estimation problem. First, estimate mixed-logit population parameters that allow each parameter to be a random variable indicating the distribution of tastes among respondents. These population parameters then serve as priors in a Bayesian update using information obtained from each respondent’s pattern of choices. Under quite general conditions, the mean of the Bayesian posterior of a parameter can be interpreted as a classical estimator (Train, 2003). Huber and Train (2001) compared MLHB and classical methods for estimating individual preferences, and obtained virtually equivalent conditional partworth estimates.

Respondents’ choices indicate alternatives that lead to higher levels of satisfaction (Greene, 1993). Therefore, we can specify an individual i’s utility for a commodity profile described by question j as

$${\text{U}}_{\text{ijr}}={\text{V}}_{\text{i}}({\text{X}}_{\text{ijr}},{\text{p}}_{\text{ijr}},{\text{Z}}_{\text{i}};{\beta }_{\text{i}},{\delta }_{\text{i}})+{\text{e}}_{\text{ij}}(\text{j}=1,\dots ,10),$$ (1)

where U_ijr is individual i’s utility for commodity profile described by question j, choice r (A,B); V_i is the nonstochastic part of the utility function; X_ijr is a vector of attribute levels (except for price) in question j for choice r; p_ijr is a scalar representing the price level attribute in question j for choice r; Z_i is a vector of personal characteristics; β_i is a vector of attribute parameters; δ_i is the price parameter and e_ij is the error term. Further, β_i can be decomposed to $\left(\frac{{\eta }_i}{\mu }\right)$, where η_i is an individual-specific parameter and μ is the scale parameter inversely related to variance. The utility difference of the attribute profile for question j for individual i is defined as:

$$\mathrm{\Delta }{U}_{ij}=V_{\mathit{ijA}}-V_{\mathit{ijB}}+{\epsilon }_{ij}=\left[\sum _{\text{m}=1}^{17}{\beta }_{\text{mAj}}+\delta {\text{p}}_{\text{Aj}}\right]-\left[\sum _{\text{m}=1}^{17}{\beta }_{\text{mBj}}+\delta {\text{p}}_{\text{Bj}}\right]+{\epsilon }_{\text{ij}}$$ (2)

where m denotes the coefficients on all attribute levels, other than price.

The dependent variable is the response choice, while the independent or explanatory variables represent the difference in levels for each attribute. Personal characteristics and experimental treatment are not included in the model because they do not vary between choice sets for a given individual. Because we estimate preferences by modeling differences in utility, varying the level of overlap reduces efficiency by lowering the number of attribute comparisons in the increased-overlap instrument.

Categorical attributes are effects coded. Using effects coding, one can compute an effect size for each attribute level; the parameter estimate for the base (omitted) category cannot be recovered from dummy-coded attributes. The parameter value for the base category is equal to the negative sum of the parameter values for all other categories of that variable and thus effects-coded parameter estimates sum to zero. In contrast, dummy coding perfectly confounds the base level of an attribute with the overall or grand mean. Consequently, it is impossible to disentangle the utility for the base levels with the grand mean (Hensher, Rose, & Greene, 2005). Combining a continuous variable such as price adds no new complications of interpretation as long as one is aware that zero corresponds to the mean effect for categorical attributes. Thus, the utility of the mean profile is zero plus the price coefficient times the mean price.

Hypotheses

Previous studies have shown that different elicitation methods may produce distinct results because of differences in the respondents’ ability to respond consistently to the task and because of how they make choices (Huber, 1997). Therefore, we examined whether the differences in choice complexity resulted in different patterns of estimated taste heterogeneity. Specifically, we evaluate:

• Whether taste heterogeneity indicated by the means and variances of individual-level partworth distributions is significantly different between the two survey versions;

• Whether there are significant differences in estimated taste heterogeneity in the relative importance of attributes in the two survey versions;

• Whether overlap difference affects taste heterogeneity indicated by the influence of covariates on predicted individual willingness to pay (WTP).

• Whether taste heterogeneity indicated by the choice-probability distributions for alternative, realistic HIV tests vary between the two survey versions.

RESULTS

The MLHB estimates of partworth distribution means and standard deviations are presented in Table 2. MLHB provides a coefficient estimate for each respondent. The estimates in Table 2 are the means of the distributions of individual-level parameter estimates and the mean standard deviations for the same distributions.

Table 2.

MLHB Estimates: Parameter Distribution Means and Standard Deviations (Standard Errors in Parentheses)

Variable	All Respondents		Increased Overlap		Minimal Overlap
	Coefficient (Std. err.)	St. Dev. (Std. Err)	Coefficient (Std. err.)	St. Dev. (Std. Err)	Coefficient (Std. err.)	St. Dev. (Std. Err)
Testing Location
public clinic	0.425 (0.079)	0.939 (0.106)	0.392 (0.144)	1.012 (0.159)	0.582 (0.109)	1.044 (0.145)
doctor’s office	−0.353 (0.078)	0.697 (0.096)	−0.253 (0.171)	0.731 (0.161)	−0.386 (0.075)	0.762 (0.135)
home	−0.072 (0.060)	0.679 (0.098)	−0.140 (0.124)	0.716 (0.132)	−0.196 (0.086)	0.803 (0.141)
Sample Collection Method
draw blood	−0.462 (0.095)	1.161 (0.152)	−0.473 (0.179)	1.176 (0.177)	−0.341 (0.134)	1.449 (0.154)
swab	0.366 (0.089)	0.607 (0.095)	0.289 (0.184)	0.605 (0.158)	0.467 (0.164)	0.618 (0.144)
urine	0.309 (0.095)	0.780 (0.200)	0.332 (0.244)	0.690 (0.178)	0.160 (0.130)	1.164 (0.166)
prick finger	−0.213 (0.112)	0.597 (0.123)	−0.147 (0.155)	0.713 (0.171)	−0.285 (0.134)	0.600 (0.134)
Timeliness/Accuracy
1–2 weeks	−0.264 (0.072)	1.172 (0.136)	−0.459 (0.112)	1.232 (0.140)	−0.070 (0.097)	1.192 (0.161)
immediate less accurate	−0.650 (0.092)	0.927 (0.123)	−0.710 (0.135)	0.968 (0.144)	−0.694 (0.114)	0.962 (0.153)
immediate more accurate	0.914 (0.089)	0.786 (0.117)	1.169 (0.156)	0.791 (0.163)	0.764 (0.120)	0.776 (0.146)
Privacy
only you know	0.836 (0.132)	0.654 (0.142)	1.041 (0.226)	0.845 (0.269)	0.772 (0.176)	0.582 (0.146)
by person, not linked	0.714 (0.113)	1.503 (0.163)	0.599 (0.181)	1.901 (0.245)	0.931 (0.147)	1.324 (0.146)
by phone, not linked	0.348 (0.120)	0.662 (0.132)	0.694 (0.194)	0.717 (0.188)	0.156 (0.135)	0.682 (0.130)
by person, linked	−0.750 (0.155)	0.723 (0.129)	−1.042 (0.281)	0.708 (0.187)	−0.648 (0.155)	0.794 (0.149)
by phone, linked	−1.147 (0.131)	1.020 (0.135)	−1.292 (0.165)	1.434 (0.215)	−1.211 (0.184)	0.651 (0.178)
Availability of counseling
in-person counseling	−0.278 (0.098)	0.793 (0.169)	−0.444 (0.166)	0.944 (0.181)	−0.123 (0.141)	0.746 (0.144)
brochure	0.278 (0.098)	0.793 (0.169)	0.444 (0.166)	0.944 (0.181)	0.123 (0.141)	0.746 (0.144)
Test price
price	−0.050 (0.006)	0.079 (0.031)	−0.049 (0.011)	0.061 (0.043)	−0.057 (0.012)	0.111 (0.081)
# of observations	3865		1914		1951
# of respondents	354		175		179

F-test results indicate that the minimum-overlap mean estimates have significantly smaller standard errors in all but two cases, while the minimum-overlap standard-deviation estimates have significantly smaller standard errors in half of the cases at the 5% level. This result suggests possible increases in measurement error are more than offset by improvements in statistical power in the minimum-overlap design.

We observed several significant differences in partworth distribution parameters between versions. Swait and Louviere (1993) suggest that scale parameter may cause differences in the coefficient estimates when comparing two different sets of data. We thus eliminated any potential effect of scale differences between models by dividing all parameters by the price coefficients in each model. Table 3 contains t-tests and chi-squared tests for differences in means and variances for these individual-level, rescaled partworth distributions. Twenty-four of thirty-six tests are statistically significant and two more are marginally insignificant at the 5% level. The Testing Location and Timeliness/Accuracy attributes have the fewest significant differences.

Table 3.

P-values for Tests of Difference of Parameter Distributions

Attribute	Mean	Variance
Testing Location
public clinic	0.0013	<0.0001
doctor’s office	0.0026	0.1221
home	0.2094	0.1019
Sample Collection Method
draw blood	0.1056	<0.0001
swab	<0.0001	0.2123
urine	0.0026	<0.0001
prick finger	<0.0001	0.1976
Timeliness/Accuracy
1–2 weeks	<0.0001	0.7651
immediate less accurate	0.8103	0.3787
immediate more accurate	<0.0001	0.6355
Privacy
only you know	<0.0001	<0.0001
by person, not linked	0.0025	<0.0001
by phone, not linked	<0.0001	0.0259
by person, linked	<0.0001	<0.0001
by phone, linked	0.2685	<0.0001
Availability of counseling
in-person counseling	<0.0001	<0.0001
brochure	<0.0001	<0.0001
Test price
price	0.1834	<0.0001

Wald test results indicate that there are a number of significant differences between levels for the same attribute. Furthermore, these differences vary by the survey instrument. According to these results, the Counseling attribute is significantly different than the Reading Brochure attribute in the increased-overlap version (P<0.001), whereas it is not in the minimum-overlap version (P = 0.217). On the other hand, “wait 1–2 weeks” versus “more accurate,” “only you know” versus “phone-not linked,” “person-not linked” versus “phone-not linked,” and “phone-linked” versus “person-linked” are significantly different in the minimum-overlap model (P<0.001). For these hypotheses, the Wald test fails to reject the increased-overlap model. These results indicate that minimum-overlap model discriminates among attribute levels better than the increased-overlap model, and subjects’ estimated preferences for levels within the same attribute may be influenced by the statistical efficiency of the experimental design. These results may be explained by the fact that subjects pay more attention to the levels when the levels vary between the alternatives.

Taste Heterogeneity in Relative Importance Measures

Differences between the best and worst levels of each attribute indicate the relative importance of attributes. Because MLHB estimates produce a separate set of parameter estimates for each respondent, we are able to calculate the relative importance of each attribute at the individual level. Taste heterogeneity implies that attribute importance order may vary across individuals. As discussed previously, individual-level estimates are respondent-level Bayesian updates of population parameters using information provided in each respondent’s pattern of choices. Designs with less overlap provide more statistical information from a set of observed choices because respondents reveal tradeoffs in more dimensions of the design space. Thus resulting preference estimates will be more sensitive to variations in individual tastes. Thus we should be able to characterize differences in taste dispersions among attributes more accurately.

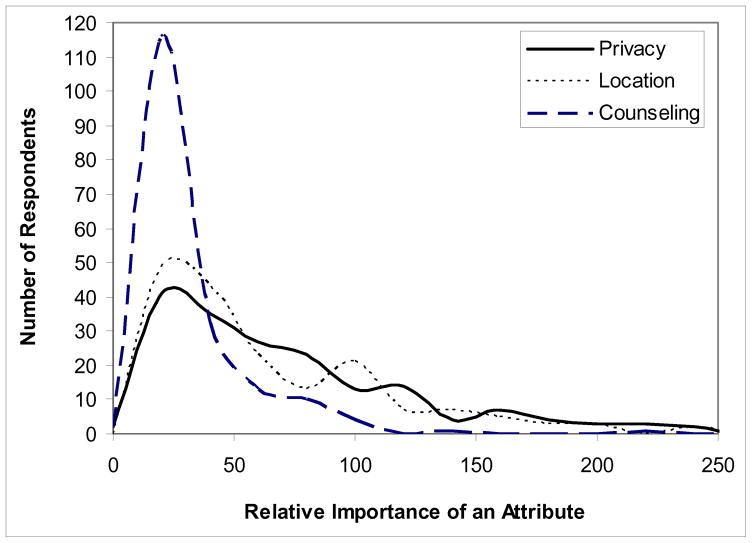
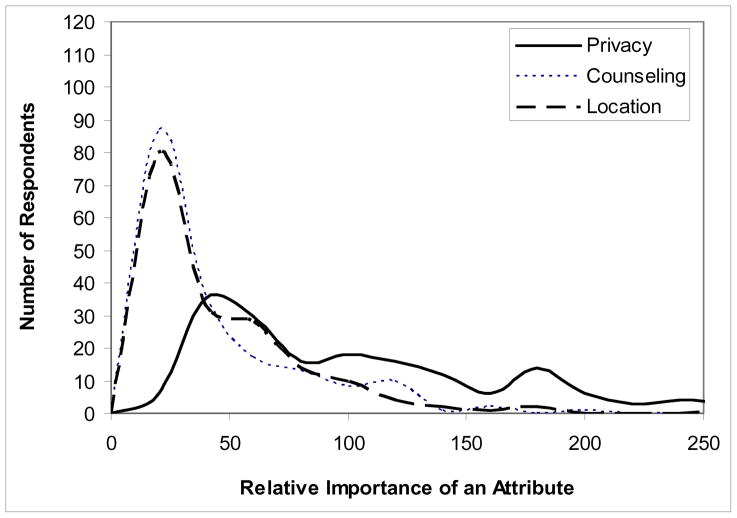
Figures 1 and 2 are plots of the taste distributions of the relative importance scores for the attributes ranked first, third, and fifth for each overlap version. Both versions rank Privacy as most important and the distributions of that attribute are similar for both versions. The variance in both cases is relatively large, indicating considerable taste heterogeneity among subjects. The minimum-overlap version ranks Testing Location and Counseling in the third and fifth positions, while the increased-overlap version reverses the order of these two attributes. Moreover, comparison of the distributions of the lower-ranked attributes indicates that the minimum-overlap distributions discriminate more strongly among taste distributions. There is relatively little heterogeneity in the least-important attribute; heterogeneity for the third most important attribute falls between the other two. In contrast, the increased-overlap distributions are quite similar, suggesting that overlap reduces the design’s ability to capture heterogeneity in preferences across subjects. These results suggest that the minimum-overlap version is more effective in identifying taste differences.

Figure 1.

Distribution of difference between best and worst levels: minimum-overlap version.

Figure 2.

Distribution of difference between best and worst levels: Increased-overlap version.

We also investigated how the number of overlaps affects perceived attribute importance. It would be interesting to analyze how overlaps for individual attribute levels affected individual parameter estimates. Unfortunately, our data do not support an analysis of how overlaps for each attribute level affected the importance of other attributes and attribute levels because the number of overlaps is not systematically distributed over attribute levels. Instead, we regressed the number of overlaps in the two most important attributes (Privacy and Timeliness/Accuracy) on the relative importance of the other non-price attributes (Testing Location, Sample Collection Method, and Availability of Counseling). Table 4 compares the importance ranks based on the minimum-overlap, increased-overlap, and the predicted ranks implied by the regression estimates, setting overlap equal to zero, as well as the regression estimates. The effect of the number of important-attribute overlaps on the Location and the Collection Method attribute is negative, but positive for Counseling. These results suggest that shifting subjects’ attention from the more important attributes to the less important attributes increases the marginal importance of Counseling but decreases the marginal importance of Location and the Collection Method.

Table 4.

Relative Importance of Attributes: Experimental Treatments and Predictions Based on Overlap Regression Estimates

Model	Relative Importance Rank			Regression Estimates
	Minimum Overlap	Increased Overlap	Regression Prediction for Zero Overlap	Coefficient	Std. Err.	P>t
Testing Location	3	5	4
Constant				0.1543	0.0063	0.000
Number of overlaps in more important attributes				−0.0038	0.0017	0.022
Sample Collection Method	4	4	3
Constant				0.1734	0.0063	0.000
Number of overlaps in more important attributes				−0.0033	0.0017	0.050
Availability of Counseling	5	3	5
Constant				0.0855	0.0054	0.000
Number of overlaps in more important attributes				0.0028	0.0014	0.046

The predicted ranks of the Location, Method, and Counseling attributes are 4, 3, and 5, respectively, compared to 3, 4, and 5 for the minimum-overlap model. However, the difference in the Location and Method constant terms is numerically small, although statistically significant. In the increased-overlap model, Location became the least important attribute, whereas Counseling became the third most important attribute. The increased-overlap ordering is a clear reversal of the relative importance of the Location and Counseling attributes.

Taste Heterogeneity in Willingness to Pay

Stated-choice surveys frequently elicit WTP estimates for individual attribute levels and combinations of levels that are of commercial or policy interest. In our case, the reliability of WTP estimates is relevant for assessing public investments in HIV testing programs. We compared WTP estimates (Holmes &Adamowicz, 2003) from both minimal-overlap and increased-overlap designs. We obtained WTP estimates for the difference between the best HIV test and worst HIV test (defined by the largest and smallest level coefficient for each attribute) for each respondent using the individual-level MLHB parameter estimates. We regressed the log of individual WTP on age, income, and qualitative covariates using the following specification:

$$\text{Log}(\text{WTP})={\beta }_{\text{constant}}+{\beta }_{\text{age}}·log(\text{Age})+{\beta }_{\text{male}}+{\beta }_{\text{nonwhite}}+{\beta }_{\text{income}}·\text{Income}+{\beta }_{\text{college}}+{\beta }_{\text{taken}\text{test}\text{before}}+{\beta }_{\text{homosexual}}$$ (3)

Table 5 indicates that regressing individual WTP estimates on covariates for the two survey versions yields important differences. None of the statistically significant covariates are significant for both survey versions and three covariates have opposite signs. We expected income to be a significant determinant of WTP, but income is significant only for the minimum-overlap version. Being nonwhite and homosexual are also significant for this version, but not for the increased-overlap version. Moreover, the F statistic indicates poor overall statistical significance for the increased-overlap version (P = 0.313).

Table 5.

WTP Regression Models

Variable	Increased Overlap	Minimal Overlap
Constant	4.140 ***	5.108 ***
Log Age	0.417	0.060
Male	−0.103	−0.216
Nonwhite	−0.164	0.560 ***
Income	0.033	0.379 **
College	−0.278 **	0.073
Tested Previously	−0.277	−0.430 *
Homosexual	0.017	−0.268
N	163	171
F value	1.19	3.69
Pr > F	0.313	0.001
Adjusted R2	0.008	0.01

^***Significant at the 1% confidence level.

^**Significant at the 5% confidence level.

^*Significant at the 10% confidence level.

Taste Heterogeneity in Choice Probabilities

An important public-health question is how the differences in estimated taste heterogeneity between the two versions affect likely uptake for realistic test alternatives. We calculated the choice probabilities for each subject for 3 different HIV tests. The first is a test at a public clinic, which assumes a blood draw, accurate results in one to two weeks, in-person linked results, in-person counseling, and no cost. The second is a test at a doctor’s office, which has the same features as a public clinic test but costs $50. The third is a home test, which assumes a finger prick, instant results, no one other than you will know the results, brochure counseling, and $10 cost.

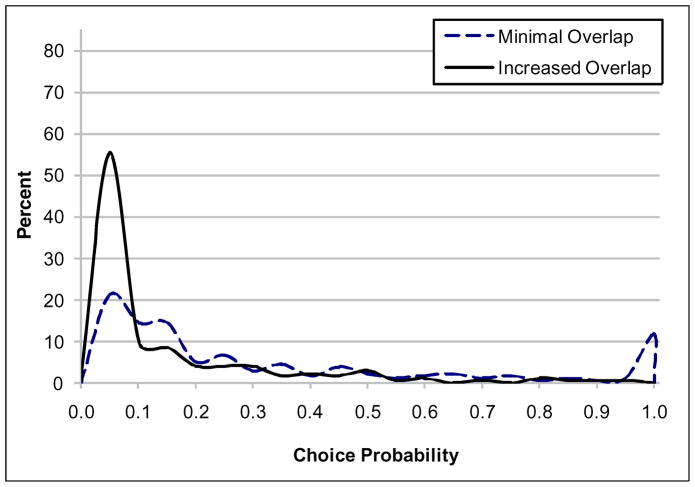
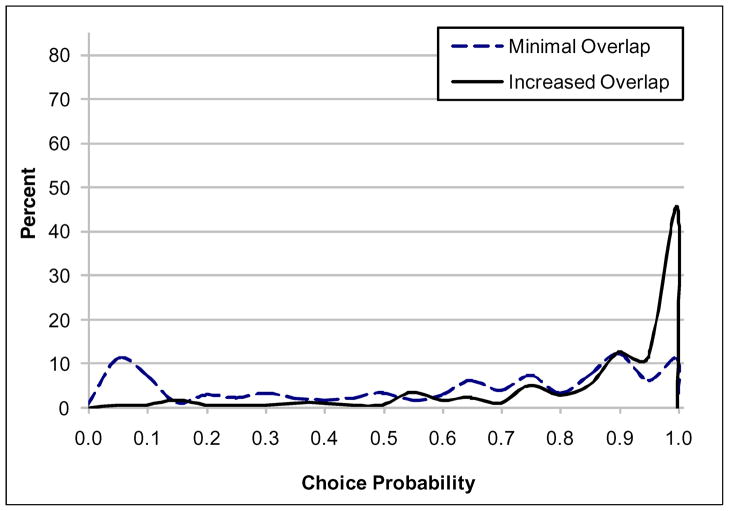
Table 6 compares the predicted choice-probability means, medians, and standard deviations and Figures 3, 4, and 5 compare the corresponding distributions for increased-overlap and minimal-overlap versions, respectively. The mean choice probabilities are significantly different between the two survey versions (p<0.01), for all three tests. The mean and median predicted choice probability is highest for the home test for both survey versions. However, the mean home-test choice probability is 0.84 for the increased-overlap version and only 0.57 for the minimal-overlap version, while the mean, while the mean choice probability for the public-clinic test is 0.03 for the increased-overlap version compared to 0.12 for the minimal-overlap version. Equally important, the standard deviations for all three tests are larger for the minimal-overlap version, confirming greater estimated taste heterogeneity than for the increased-overlap version.

Table 6.

Predicted Individual Choice Probabilities

Test	Increased Overlap	Minimal Overlap
Public Clinic
Mean	0.032	0.124
Median	0.005	0.054
Standard Deviation	0.080	0.172
Doctor’s Office
Mean	0.125	0.308
Median	0.040	0.150
Standard Deviation	0.188	0.325
Home
Mean	0.843	0.568
Median	0.930	0.672
Standard Deviation	0.217	0.339

Figure 3.

Distribution of predicted choice probabilities for a public clinic test

Figure 4.

Distribution of predicted choice probabilities for a doctor’s office test

Figure 5.

Distribution of predicted choice probabilities for a home test

The single-peaked choice-probability distributions have similar shape for the public-clinic test in Figure 3, with the same modes at about 0.05. However, about 94% of the predicted choice probabilities for the increased-overlap version are less than or equal to 0.10, while the minimal-overlap version predicts far less preference agreement with only about 57% of the subjects having predicted choice probabilities less than or equal to 0.10.

Choice-probability distributions for the other two tests indicate similarly strong differences in the ability of the two versions to identify differences in taste heterogeneity. The minimal-overlap distribution for the doctor’s-office test actually is bimodal, with 23 of 179 subjects (13%) strongly preferring that test to the other two tests (choice probability greater than or equal to 0.90). The increased-overlap estimates identify only one subject that strongly prefers the doctor’s-office test. Similarly, there are 34 of 179 (19%) minimal-overlap subjects with a preference for the home test that is strongly divergent from that of the majority (choice probability less than or equal to 0.10). Only 2 increased-overlap subjects (1%) are identified as having that preference.

DISCUSSION

This study examined whether simplifying the choice task in SC designs, by using a design with more overlap of attribute levels, provides advantages over standard minimum-overlap methods. We hypothesized that the increased-overlap design would reduce measurement error, but could affect statistical efficiency. In this study, we extended Maddala and colleagues’ study (2003) by using MLHB models to estimate individual-level preference parameters to account for taste heterogeneity. We reported tests of several hypotheses regarding possible differences in estimates from these two experimental designs. Test results confirm that preference distributions are significantly different in several respects.

The MLHB means and variances of partworth, relative importance, WTP, and choice-probability distributions are clearly different. The minimum-overlap estimates appear to be much more sensitive to variations in taste heterogeneity relative to the increased-overlap estimates. The minimum-overlap regression model also explains predicted WTP better. Fewer covariates are significant in the increased-overlap regression model. In particular, insignificant income means that the model fails a theoretical validity test. We failed to find evidence that increasing overlap to reduce measurement error compensates for statistical inefficiencies of the increased-overlap experimental design for HIV testing. However, we found evidence that the number of overlaps in the most important two attributes shifted respondents’ attention to the other attributes and influenced the perceived relative importance of less-important attributes. These results suggest that overlap influences the way subjects evaluate competitive features and our ability to detect systematic differences in tastes among subjects.

Finally, we found that the minimum-overlap estimates were much more sensitive to taste heterogeneity as indicated by variations in predicted choice probabilities for three realistic HIV tests. Based on the results from the increased-overlap model, policy makers could conclude that there is very little interest in HIV tests in public clinics or doctor’s offices. However, MLHB estimates of minimal-overlap preferences indicate that about 38% of subjects had a probability greater than 0.5 of choosing one of those tests and a significant proportion of subjects had a very strong preference for the doctor’s-office test. These preferences were not detected in the increased-overlap estimates.

These results are of interest to researchers who use SC surveys. This experiment suggests, at least under some circumstances, that survey designers may reach different quantitative and qualitative conclusions about the distribution of tastes by using a survey designed to reduce measurement error.

An important limitation of our study is that the number of overlaps in each attribute level is not similar. Some of the attributes have more overlapped levels than others. It is therefore difficult to quantify how sensitive the importance of a particular attribute is to the number of overlaps in various other attribute levels. Second, we created a main-effects experimental design. The results might have been different if we created a design that allow for interactions. Third, only one of the attributes was a numerical attribute. Although some categorical attribute levels were naturally ordered, we had no expectation about the ordering of levels for other qualitative attributes. It is possible that the type of the attributes may have affected the results of the study. We recommend a systematic experiment on the effect of overlap for future research. An experiment may systematically investigate how the number of overlap in each attribute and attribute level affects the estimates. This type of a study may also help explain whether the estimates are sensitive to which attributes and attribute levels are overlapped. Finally, we forced respondents to choose between two alternatives. Future research may investigate how the number of alternatives or an opt-out alternative influences the overlap effect.