Abstract
The multiple inert gas elimination technique (MIGET) provides a method for estimating alveolar gas exchange efficiency. Six soluble inert gases are infused into a peripheral vein. Measurements of these gases in breath, arterial blood, and venous blood are interpreted using a mathematical model of alveolar gas exchange (MIGET model) that neglects airway gas exchange. A mathematical model describing airway and alveolar gas exchange predicts that two of these gases, ether and acetone, exchange primarily within the airways. To determine the effect of airway gas exchange on the MIGET, we selected two additional gases, toluene and m-dichlorobenzene, that have the same blood solubility as ether and acetone and minimize airway gas exchange via their low water solubility. The airway-alveolar gas exchange model simulated the exchange of toluene, m-dichlorobenzene, and the six MIGET gases under multiple conditions of alveolar ventilation-to-perfusion, V̇A/Q̇, heterogeneity. We increased the importance of airway gas exchange by changing bronchial blood flow, Q̇br. From these simulations, we calculated the excretion and retention of the eight inert gases and divided the results into two groups: 1) the standard MIGET gases which included acetone and ether and 2) the modified MIGET gases which included toluene and m-dichlorobenzene. The MIGET mathematical model predicted distributions of ventilation and perfusion for each grouping of gases and multiple perturbations of V̇A/Q̇ and Q̇br. Using the modified MIGET gases, MIGET predicted a smaller dead space fraction, greater mean V̇A, greater log(SDVA), and more closely matched the imposed V̇A distribution than that using the standard MIGET gases. Perfusion distributions were relatively unaffected.
Keywords: Mathematical model, bronchial circulation, alveolar heterogeneity, ventilation, perfusion
INTRODUCTION
The multiple inert gas elimination technique (MIGET) is a tool that has significantly advanced our understanding of pulmonary gas exchange. Experimentally, six soluble inert gases are infused into a peripheral vein and measured in the exhaled breath, the arterial blood, and venous blood. The MIGET mathematical model 51 analyzes these measurements by dividing the lung into 50 gas exchange units, each characterized by a single ventilation-perfusion ratio, and generating distributions of ventilation, V̇A, and perfusion, Q̇, as a function of these 50 gas exchange units. Ventilation distributed to high V̇A/Q̇ units represents dead space and perfusion to low V̇A/Q̇ units represents shunt. Further analysis of these distributions can quantify gas exchange efficiency during conditions such as chronic obstructive pulmonary disease 48, exercise 16, and asthma 49.
The MIGET is dependent on three major assumptions: 1) steady-state mass flux; 2) negligible diffusion barrier in the alveolus; and 3) negligible interaction of inert gases with the airways. The validity of the first two assumptions was assessed under a range of conditions within the context of gas exchange during partial-liquid ventilation 46. The third assumption has been debated but its validity has not been settled. The argument in favor of the assumption is based in alveolar gas exchange theory; the V̇A/Q̇ of the airway (ratio of airway ventilation to bronchial blood flow) is greater than 100 and therefore qualifies as dead space. The arguments contesting this assumption are more diffuse but integrate both experimental and theoretical results. In some experimental studies, the excretion of acetone in relation to ether does not follow the MIGET predicted trend 9,12,55 and dead space as predicted by inert gases decreases as the blood solubility increases 20,41. Additionally, theoretical studies showed that acetone exchanges predominately within the airways during tidal breathing and these predictions were used to explain inert gas data from humans and dogs 1,56. Because neither argument has been proven conclusively, an experimental investigation was performed to directly assess this assumption. That study used a novel aortic pouch preparation to alter bronchial blood flow (a major factor in airway gas exchange) and demonstrated that changes in bronchial blood flow affected the excretion of highly blood-soluble gases (e.g., ether and acetone) more than low blood-soluble gases (e.g., SF6 and ether) 38. But this study could not conclusively resolve the effect of airway gas exchange on MIGET. Still, the question remains unsettled.
In recent years, the number of studies using the MIGET has decreased as other non-invasive scanning techniques, offering enhanced spatial resolution, have taken its place and institutional review boards have increased restrictions on invasive techniques. However, it is possible that a MIGET renaissance could occur through the use of endogenous gases coupled with highly sensitive, parts-per-billion (ppb) measuring devices. Many endogenous gases have been identified as potential biomarkers (e.g., methane, ethane, pentane, isoprene, etc) and have been measured at ppb concentrations in the exhaled breath 7,31,33 and new techniques are being developed to rapidly measure and resolve these gases at ppb levels 10,32,47,52. Currently, the motivation for measuring these gases in the exhaled breath is to diagnose metabolic disturbances, cancer, heart disease, and other diseases. However, it is possible that a set of six to ten endogenous blood soluble gases could be judiciously selected to replace the standard six infused MIGET gases. Endogenous gases would eliminate the invasive infusion of exogenous gases, but arterial and venous blood samples would still be necessary. The selection of these gases will be critical to ensure that they satisfy all MIGET assumptions. We expect that the findings of this study will guide that task.
In this study we use a mathematical model of airway and alveolar gas exchange 1 to investigate the effects of airway gas exchange on the MIGET and answer two questions: 1) Does airway gas exchange affect the MIGET; and 2) Under what conditions does airway gas exchange most affect MIGET? To resolve these questions, we change two factors influencing airway gas exchange. We replace the two soluble gases that are the most susceptible to interaction with the airways, acetone and ether, with gases that are more inert with respect to the airways (i.e., low water solubility). Additionally, we change bronchial blood flow, a significant factor in airway gas exchange, within the mathematical model. From this theoretical study, an experimental investigation could be carried out to confirm or deny our predictions.
METHODS
Summary of Approach
Alveolar exchange of inert gas depends, predominately, on three physiological factors: ventilation rate, perfusion rate, and blood solubility of the inert gas. However, airway gas exchange depends on three different factors: 1) water and blood solubility of the gas; 2) delivery of gas to the airway tissue via perfusion of bronchial circulation; and 3) diffusion of gas from the bronchial circulation through the tissue and into the airway lumen. Because the physiological mechanisms of gas exchange are different between airways and alveoli 3, we exploit two mechanisms unique to airway gas exchange to explore its impact on MIGET: the solubility characteristics of the gases (mechanism 1) and the rate of bronchial blood flow (mechanism 2).
Blood and water solubility
We know that blood solubility, as measured by the blood to air partition coefficient - λb, is a primary factor in determining where a gas exchanges in the lung. Gases with λb<1 and λb>100 exchange completely in the alveoli and airways, respectively, while gases between these two ranges exchange in both the airways and alveoli 1. The water solubility of gas, as measured by the water to air partition coefficient -λw, is as important as blood solubility because the mucus, which lines the airway wall and is in intimate contact with the respired air, is assumed to have solubility characteristics like water. Generally a distinction between water and blood solubility is not made because the two measures are similar for most gases 30. However, some gases like methyl ethyl ketone (MEK) and m-dichlorobenzene (m-DCB) have similar blood solubilities (λb(MEK)=202 and λb(m-DCB)=201) but disparate water solubilities (λw(MEK)=254 and λw(m-DCB)=5.5) 36,37. Based on their blood solubilities alone, these gases should exchange completely in the airways. However, a theoretical study has shown that the majority of gas exchange for MEK occurs in the airways while that for m-DCB occurs in the alveoli 45. For m-DCB, the reduced mucus solubility relative to the blood solubility hinders gas exchange with the upper airways and shifts gas exchange into the alveoli.
In a similar manner, ether and acetone, the most blood-soluble of the MIGET gases, are predicted to exchange in the airways based on their solubilities in water and blood 1. Therefore, to examine the impact of airway gas exchange (via these two gases) on the MIGET predictions, we replaced ether and acetone in the MIGET analysis with two gases of similar blood solubility but decreased water solubility (toluene for ether and m-DCB for acetone) and, thereby, theoretically minimized the influence of airway gas exchange on MIGET. A comparison of the MIGET predictions using ether and acetone versus the two replacement gases provided a straightforward means for evaluating the effect of airway gas exchange on the MIGET predictions.
Bronchial blood flow rate
The rate of bronchial blood flow, Q̇br, can influence the amount of airway gas exchange for a wide spectrum of gases. Experimentally, increases in bronchial blood flow in excised and whole animal preparations 38,43 produce increases in soluble gas elimination. Theoretical calculations 1,5,19 align with these experimental findings. In this study, we alter bronchial blood flow rate within our mathematical model from zero (Q̇br = 0.01 ml/s) to five-times the normal value (Q̇br = 5 ml/s). Changes in bronchial blood flow directly change the contribution of airway gas exchange to total pulmonary gas exchange. We compare the MIGET predictions resulting from different levels of bronchial blood flow to examine the effect of the bronchial circulation and airway gas exchange on the MIGET.
A previously published mathematical model of airway and alveolar gas exchange 1 was modified to include two discrete alveolar compartments. The model simulated the exchange of eight soluble gases (six MIGET and two replacement gases) for a range of alveolar ventilation-perfusion heterogeneity and bronchial blood flow conditions. The model outputs from each gas were appropriately grouped and analyzed using the MIGET mathematical model 51. MIGET predictions for each condition and inert gas combination were compared and contrasted to MIGET predictions from other conditions and inert gas combinations.
Lung Model
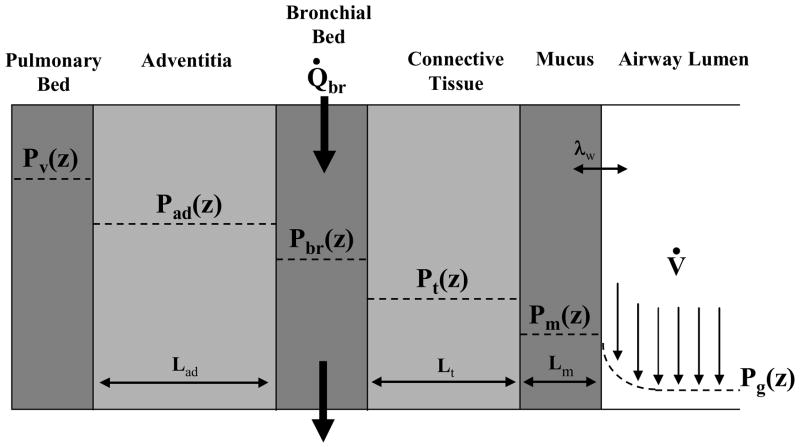
A detailed description of the model has been published previously 1. Only the essential features will be described here. The airway tree has a symmetric bifurcating structure through 18 Weibel generations. The respiratory bronchioles and alveoli are lumped together into a single alveolar unit. The dimensions for the upper and lower respiratory tract are taken from Hanna 21 and Weibel 53, respectively. Axially, the airway tree is divided into 480 control volumes. Radially, the airways are divided into six layers (Figure 1): 1) the airway lumen, 2) a thin mucous layer, 3) connective tissue layer (epithelium and mucosal tissue), 4) the bronchial circulation, 5) the adventitial layer, and 6) the pulmonary circulation. Functionally, the upper respiratory tract and cartilaginous airways (generations < 10) only have the first four layers. Within a control volume, the surface area for exchange between radial layers is assumed to be equal for all layers except for the bronchial capillary bed. The capillary bed has less area for exchange because it is interspersed throughout the wall and does not form a continuous layer around the airway. In the alveolar unit, the concentration of soluble gas is allowed to vary with time and depends on the pulmonary blood flow, ventilation, blood solubility, and concentration of soluble gas in the incoming blood and air as described by a mass balance on the alveolar compartment.
Fig. 1.
Model control volume. The source of soluble gas for this diagram is the blood (pulmonary venous and bronchial arterial). Blood enters the bronchial bed compartment with a partial pressure, Pa. Soluble gas is transported by secretion and diffusion across a series of annular layers before entering the passing airstream. The ratio of gas solubility between the mucus and air layers is specified by a water-air partition coefficient, λw. The thickness of the mucus (Lm), connective tissue (Lt), and adventitial layer (Lad) are calculated from data in the literature.
Within each airway layer, concentration and temperature values are bulk averages for the entire layer. The air in the lumen is considered a mixture of dry air, water vapor and a single soluble gas. Mass and energy are transported between control volumes by bulk convection and axial diffusion through the lumen. Radial transport between the gas phase and mucous layer is described with heat and mass transfer coefficients that are determined from empirical correlations 8,25. Near the air-mucus interface, local vapor-liquid equilibrium is described by Raoult’s law for water and a water-air partition coefficient, λw, for each soluble gas. The mucous layer is assumed to have the properties of water and can change thickness depending on local hydration. A minimum mucous layer thickness is maintained by filtration of water from the bronchial circulation through the connective tissue layer and into the mucous layer. Transport of water and dissolved soluble gas between these three layers occurs via filtration and diffusion (Fick’s law). The connective tissue layer and the adventitial tissue layer are treated as a binary mixture of dilute soluble gas and water. The diffusivity of a soluble gas through the connective and adventitial tissue is assumed to be 33% of its diffusivity in water 17. For a soluble gas, the tissue solubility is assumed to be equal to blood solubility. The dimensions of the connective tissue, bronchial circulation and adventitial tissue compartments (i.e., radial thickness, surface area and cross-sectional area) are calculated by scaling measurements made in sheep 2 to those of a human 1. The bronchial circulation is modeled as an axial series of annular sheets of blood interposed between the connective and adventitial tissue layers. Blood enters the control volume at body temperature and a systemic concentration of soluble gas, exchanges energy and mass via filtration and diffusion with the surrounding tissue and leaves the control volume at a venous temperature and soluble gas concentration. Adjacent to the adventitial tissue layer, the pulmonary capillary bed is assumed to be at body temperature and the concentration of soluble gas is assumed to be the average (calculated after each half breath) of the soluble gas concentration entering and leaving the alveolar unit via the pulmonary circulation. The concentration of soluble gas in the venous blood entering the pulmonary circulation is specified. The systemic concentration of soluble gas is calculated by solving the equation describing mass accumulation in the alveolar compartment.
We chose a functional residual capacity of 2650 ml and the vital capacity from the Weibel lung model, 5000 ml. The dimensions of the airway wall compartments were calculated using data and a method outlined previously 1. The lengths and diameters of the intraparenchymal airways were scaled to ensure the ratio of the airway volume to the vital capacity was constant and to represent the lung at functional residual capacity.
Mass and energy balances around each control volume produce three partial- and nine ordinary-differential equations in time and space. The equations are solved simultaneously for the following twelve dependent variables: the mole fraction of soluble gas in the air, mucous, connective tissue, bronchial bed, and adventitial tissue layers; the temperature of the air, mucous, connective tissue, bronchial bed, and adventitial tissue layers; the mole fraction of water in the air; and the mucous thickness. The twelve differential equations are solved numerically using previously published boundary conditions 1. The spatial dimensions are solved by upwind finite difference while the time derivatives are handled using LSODE, an integrating software package developed by Hindmarsh 22. The mass balance around the alveolar compartment is integrated separately from the airway control volumes using LSODE. On inhalation, outputs from the airway model are inputs to the alveolar model and vice versa for exhalation.
Inclusion of alveolar heterogeneity
Originally, the model described a single path from the mouth to the alveoli. To investigate the impact of airway gas exchange on measurements of alveolar gas exchange heterogeneity, a second airway path, geometrically identical to the first, was added at a prescribed generation number, ns, to account for ventilation heterogeneity. Ventilation heterogeneity for all airway generations greater than ns was introduced with a single change at generation ns. Airflow leaving generation ns was split asymmetrically between the daughters. Daughter A received the majority of airflow with the remainder of the airflow entering daughter B. Airflow leaving all other generations (n≠ns) in both paths was split evenly between daughters. Thus at a given airway generation where n>ns, airways descending from Daughter A were ventilated at larger rates than those airways descending from Daughter B. Essentially, this asymmetry in ventilation produced two paths (A and B) beginning at generation ns and ending with two unique alveoli. Path A (from daughter A) received the majority of the ventilation and terminated into an alveolar unit that was ventilated at a larger rate than the alveolar unit at the terminus of path B. While ns=9 was chosen for this study, greater (lesser) ns values would cause a smaller (larger) affect of airway gas exchange on MIGET. Specifying the fraction of pulmonary blood flow to each alveolus set the ventilation-perfusion ratios for alveolus A and B.
Computer Simulations
Before a tidal breath is simulated for each soluble gas, the model first must reach breath-to-breath steady-state conditions. The temperature, water concentrations, and soluble gas concentrations within the mathematical model were brought to steady-state conditions by simulating tidal breathing at functional residual capacity. A respiratory rate of 12 br/min, a sinusoidal flow waveform, and a tidal volume of 500 ml were used. The inspired air temperature and relative humidity was set at 23 °C and 50 %, respectively. Steady-state conditions were reached when the end-exhaled temperature and soluble gas concentration changed by less than 0.1% between breaths. Then, the model simulated a single tidal breath for each soluble gas.
Tidal breathing conditions
The excretion of the six MIGET gases, SF6, ethane, cyclopropane, halothane, ether, and acetone, and the two additional highly blood-soluble gases, toluene and m-dichlorobenzene (m-DCB), were simulated during tidal breathing. The blood-air and water-air partition coefficients for each gas are listed in Table 1. For each gas, the model simulated twelve conditions where each condition partitioned ventilation and pulmonary blood flow differently between the two paths and two alveoli as listed in Table 2. Each condition was repeated four times to study the effect of bronchial blood flows: 0.01, 1, 3, and 5 ml/s. Forty-eight simulations (12 V̇A/Q̇ conditions x 4 Q̇br) were performed for each soluble gas under breath-to-breath steady-state conditions.
Table 1.
Literature values for blood-air and water-air partition coefficients of the six MIGET gases and two additional gases (bold) at 37 °C. Both the standard MIGET gases and modified MIGET gases include the first four gases listed.
Table 2.
The fraction (F) of ventilation (V), and pulmonary perfusion (Qp) distributed to path A and alveoli A are enumerated by condition on the left while the V̇A/Q̇ for alveoli A and B listed on the right. Bronchial blood flow was split evenly between both paths for all conditions.
| Condition | FV | FQp | (V̇A/Q̇)A | (V̇A/Q̇)B |
|---|---|---|---|---|
| 1 | 1/2 | 1/2 | 1 | 1/1 |
| 2 | 5/9 | 4/9 | 5/4 | 4/5 |
| 3 | 3/5 | 2/5 | 3/2 | 2/3 |
| 4 | 2/3 | 1/3 | 2 | 1/2 |
| 5 | 5/7 | 2/7 | 5/2 | 2/5 |
| 6 | 3/4 | 1/4 | 3 | 1/3 |
| 7 | 4/5 | 1/5 | 4 | 1/4 |
| 8 | 5/6 | 1/6 | 5 | 1/5 |
| 9 | 6/7 | 1/7 | 6 | 1/6 |
| 10 | 7/8 | 1/8 | 7 | 1/7 |
| 11 | 8/9 | 1/9 | 8 | 1/8 |
| 12 | 9/10 | 1/10 | 9 | 1/9 |
Ventilation and perfusion distributions
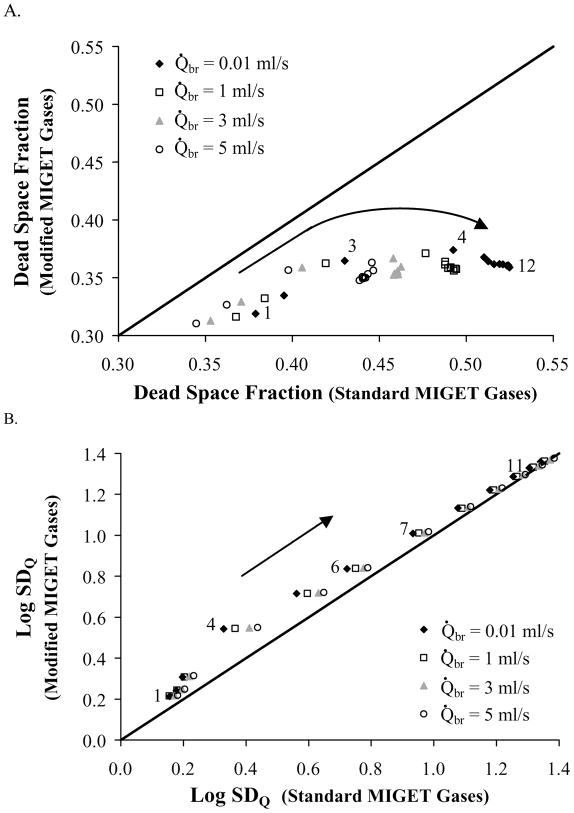
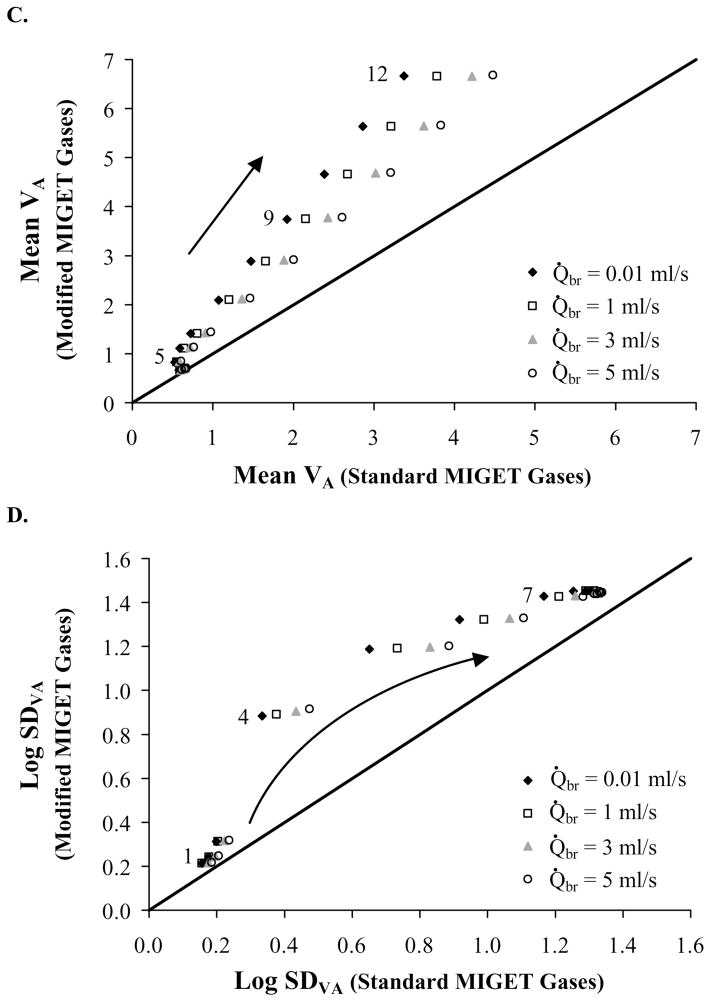
For each of the 48 simulations, an excretion, E=PE/Pv where PE and Pv are the mixed exhaled and mixed venous partial pressure, and a retention, R=Pa/Pv where Pa is the mixed arterial partial pressure, were calculated for each of the eight gases. The MIGET algorithm requires six gases of different blood solubility to predict distributions of ventilation and perfusion. The eight gases were divided into two groups: 1) standard MIGET gases - SF6, ethane, cyclopropane, halothane, ether, and acetone; and 2) modified MIGET gases - SF6, ethane, cyclopropane, halothane, toluene, and m-dichlorobenzene. Excretions and retentions from each group of six gases for a given condition (V̇A/Q̇ and Q̇br) were analyzed using the MIGET model 51 to recover distributions of alveolar ventilation and pulmonary perfusion as a function of V̇A/Q̇. Within the MIGET algorithm, the relative weighting among gases of differing blood solubilities was unchanged for all simulations. Because they are commonly used to estimate alveolar gas exchange efficiency 34,55, the first two moments of both distributions, dead space fraction, and two dispersion indices (DISPR-E and (a-A)D-AREA) were the MIGET outputs examined here.
RESULTS
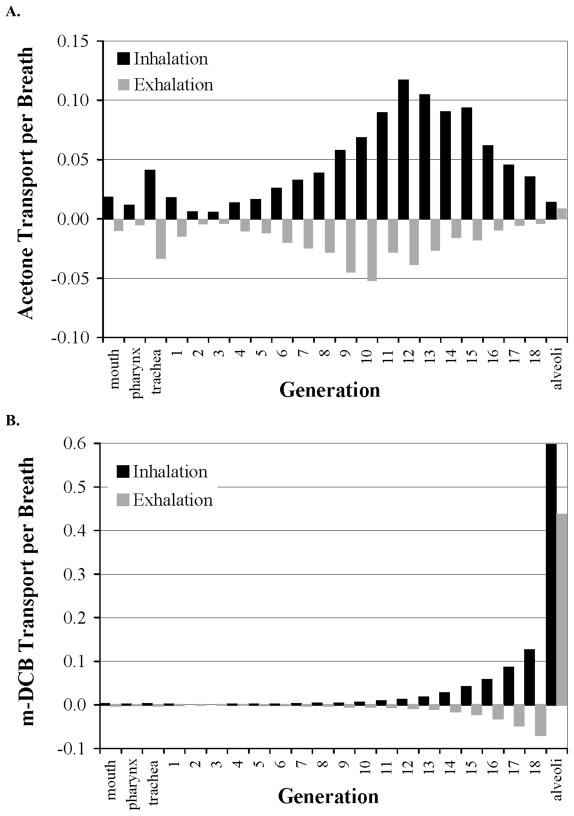
The solution of the mathematical model yields axial profiles of partial pressure within the airway lumen and airway wall layers for any desired time during inspiration and expiration. From these axial profiles of soluble gas partial pressure, the flow of soluble gas (mol/s) from the airway wall to the airway lumen for a given axial position (e.g. the trachea) and time interval can be calculated. For a given portion of the airway tree such as an airway generation, these flows of soluble gas can be summed together over all time points throughout an inspiration and/or expiration. Figure 2A and 2B display the axial distribution of soluble gas flows for acetone and m-DCB, respectively, over a single inspiration and exhalation under homogeneous ventilation and perfusion (Condition 1 from Table 2). Acetone exchange between the airspace and mucus occurs throughout many airway generations with maximum flow (i.e., exchange) occuring at generation 12 that is similar in magnitude to flows in all other generations. In contrast, m-DCB exchanges predominately in the alveoli. The exchange of m-DCB summed over inspiration and exhalation is an order of magnitude larger in the alveoli than in any other airway generation. A similar shift in the axial distribution of gas flows was seen for toluene relative to ether. These shifts in location of gas exchange are a consequence of the disparity between λw for these particular gases that have similar λb (Table 1).
Fig. 2.
The axial distribution of acetone (panel A) and m-dichlorobenzene, m-DCB, (panel B). Gas flows between the airstream and mucus during inspiration (black columns) and exhalation (gray columns) for a tidal breath performed under matched ventilation and perfusion (condition 1). Positive (negative) flows denote transport into the airstream (mucus) from the mucus (airstream). m-DCB has a similar blood solubility but 20-fold smaller water solubility than acetone and is the reason that m-DCB exchanges predominately in the alveoli while acetone exchanges almost completely in the airways. Each flow has been normalized by the total inspiratory soluble gas flow.
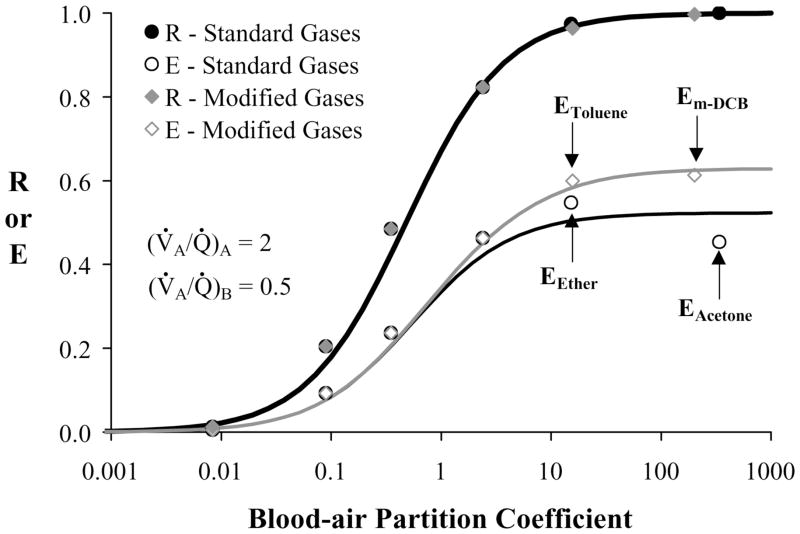
Retention and excretion values for the standard and modified MIGET gases, exchanging under condition 4 ((V̇A/Q̇)A = 2 and (V̇A/Q̇)B =0.5), and Q̇br= 1 ml/s, are shown in Figure 3. While no difference exists between the retention values of the two sets of gases, the excretion values for ether and acetone are less than their replacements, toluene and m-DCB. The former gases have reduced values because of airway gas exchange. During inhalation, the airstream absorbs these gases from the airway mucus, and during exhalation, soluble gas in the airstream deposits on the airway wall to replenish gas lost on inhalation. Because of their low λw, toluene and m-DCB exchange only minimally in the airways, minimally exhibit this absorption-desorption behavior with the airway wall, and as a result have relatively large excretion values as predicted by the Farhi kernal 14. The predicted excretion for acetone, EAcetone, is less than the excretion for ether, EEther, for the conditions presented in Figure 3 because acetone exchanges completely in the airways while the exchange of ether is split evenly between the airways and alveoli 1. EAcetone is insensitive to changes in V̇A/Q̇ (ΔE/Δ(V̇A/Q̇)A = 0.001), depends predominately on Q̇br (ΔE/ΔQ̇br = 0.017), and varies between 0.41 and 0.51 for the range studied. EEther is primarily affected by V̇A/Q̇ (ΔE/Δ( V̇A/Q̇)A = −0.011), is minimally affected by Q̇br (ΔE/ΔQ̇br = 0.005), and found to vary from 0.57 to 0.47 over the conditions studied. In contrast, Em-DCB is unaffected by V̇A/Q̇ or Q̇br (ΔE/Δ(V̇A/Q̇)A = −0.001 and ΔE/ΔQ̇br = 0.002), and changes only 1% among all conditions studied. EToluene depends strongly on V̇A/Q̇(ΔE/Δ(V̇A/Q̇)A = −0.026), is unaffected by Q̇br (ΔE/ΔQ̇br = 0.002), and varies between 0.62 and 0.42 in this study.
Fig. 3.
Retention (solid symbols) and excretion (open symbols) values for the standard (circles) and modified (diamonds) MIGET gases for condition 4 (Table 1) and Q̇br = 1 ml/s are shown with MIGET predicted retention (thick) and excretion (thin) curves. For both sets of gases, the MIGET predicted retention curves are the same but the predicted excretion curve for the modified gases (gray line) asymptotes to a greater value because toluene and m-DCB have greater excretions than ether and acetone, respectively.
The excretions and retentions predicted by the airway-alveolar gas exchange model for both the standard MIGET gases and the modified MIGET gases were analyzed using the MIGET model 51. For all conditions studied, the MIGET algorithm predicted the excretion and retention data of the modified gases better (e.g., an average improvement of 48% for condition 1 and 20% for condition 10 as calculated by a sum of squared errors) than that of the standard gases. Comparing the two sets of gases, the MIGET predicted retention curves were the same, but the excretion curves diverged for λ b>5. The divergence in the MIGET predictions was caused by the differences in the excretion values of the highly soluble gases (Fig. 3).
The MIGET predicted ventilation and perfusion distributions for both sets of gases were compared to the imposed distributions and to each other. For the high V̇A/Q̇ mode (V̇A/Q̇ > 1) of the ventilation or perfusion distribution, the V̇A/Q̇ unit receiving the largest portion of ventilation or perfusion, as predicted by MIGET, was determined and listed in Table 3 with the imposed (V̇A/Q̇)A for each condition where Q̇br = 1 ml/s. For the ventilation distribution, MIGET predicted a larger (V̇A/Q̇)A for the modified gases than the standard gases at each condition. The MIGET predictions were closer to the imposed (V̇A/Q̇)A when using the modified gases as measured by a sum of squared error. Likewise for the perfusion distribution, MIGET predictions for (V̇A/Q̇)A were larger when using the modified gases as compared to the standard gases and were closer to the imposed (V̇A/Q̇)A when using the modified gases. For the low V̇A/Q̇ mode (V̇A/Q̇ < 1), the MIGET predicted V̇A/Q̇ unit receiving the largest amount of ventilation or perfusion were equivalent for both sets of gases for most of the 12 conditions where Q̇br = 1 ml/s and differed by one V̇A/Q̇ unit when the prediction differed. For this low mode, MIGET always under predicted the imposed V̇A/Q̇ but better predicted the low mode V̇A/Q̇ when using the modified MIGET gases.
Table 3.
Comparison of the imposed (V̇A/Q̇)A and the MIGET predicted V̇A/Q̇ unit from the high mode (V̇A/Q̇ > 1) that had the greatest amount of ventilation or perfusion. MIGET predictions using data from the standard and modified MIGET gases for all 12 conditions where Qbr = 1 ml/s were analyzed. MIGET better predicts the imposed model distributions when using data from the modified as compared to the standard MIGET gases.
| High V̇A/Q̇ unit with the greatest ventilation | High V̇A/Q̇ unit with the greatest perfusion | ||||
|---|---|---|---|---|---|
| Condition | Imposed (V̇A/Q̇)A | Standard MIGET gases | Modified MIGET gases | Standard MIGET gases | Modified MIGET gases |
| 1 | 1 | --- | --- | --- | --- |
| 2 | 1.2 | --- | --- | --- | --- |
| 3 | 1.6 | --- | --- | --- | --- |
| 4 | 2 | --- | 3.94 | --- | 2.14 |
| 5 | 2.5 | 1.76 | 3.94 | --- | 2.63 |
| 6 | 3 | 2.15 | 3.94 | 1.76 | 2.63 |
| 7 | 4 | 2.63 | 4.82 | 2.15 | 3.22 |
| 8 | 5 | 3.22 | 4.82 | 2.63 | 3.94 |
| 9 | 6 | 3.94 | 5.90 | 3.22 | 3.94 |
| 10 | 7 | 4.82 | 7.23 | 3.94 | 4.82 |
| 11 | 8 | 4.82 | 8.84 | 4.82 | 4.82 |
| 12 | 9 | 5.90 | 8.84 | 4.82 | 5.90 |
--- indicates no high V̇A/Q̇ present
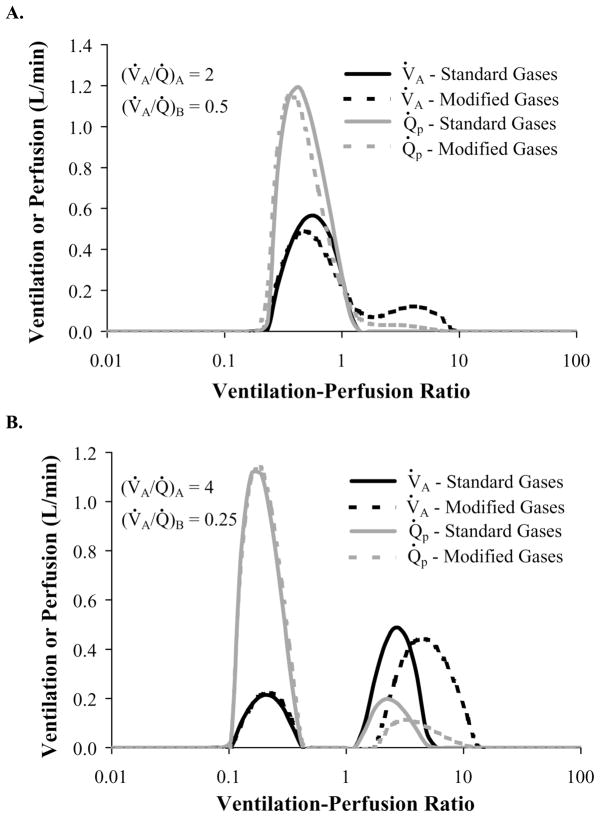
A graphical depiction of the MIGET predicted ventilation and perfusion distribution is shown in Figure 4 for conditions 4 (panel a) and 7 (panel b) and Q̇br = 1 ml/s. For condition 4, V̇A and Q̇ distributions are unimodal for the standard MIGET gases but bimodal for the modified MIGET gases. For the modified MIGET gases, the second mode seen at high V̇A/Q̇ values represents the alveolar compartment, (V̇A/Q̇)A = 2, modeled by the airway-alveolar gas exchange model. When compared to the unimodal perfusion distribution for the standard MIGET gases, the distribution for the modified MIGET gases has a smaller (height and width) low V̇A/Q̇ mode and a high V̇A/Q̇ not seen with the standard gases. Thus, the MIGET algorithm interpreted the differences in the excretion and retention data between the two sets of gases as a shift in blood flow from the low V̇A/Q̇ unit to a high V̇A/Q̇ unit. A comparison of the ventilation distributions showed that the modified MIGET gases have a high V̇A/Q̇ mode which is not present in the ventilation distribution of the standard MIGET gases. In order to predict a high V̇A/Q̇ mode for the modified MIGET gases, the MIGET algorithm reduced the predicted amount of dead-space ventilation between the two sets of gases (Fig. 5a) by 22 %. For condition 7 (Fig. 4b), the V̇A and Q̇ distributions are bimodal for both sets of gases. While the low V̇A/Q̇ mode for each distribution is the same for both sets of gases, the high V̇A/Q̇ mode for both V̇A and Q̇ distributions are shifted to the right, broader, and shorter for the modified MIGET gases as compared to the corresponding distributions using the standard MIGET gases. Additionally, the high V̇A/Q̇ mode of the ventilation distribution for the modified gases was enhance by a 27% reduction in predicted dead space ventilation for the modified gases as compared to the standard gases. Typically, the mean and standard deviation of each distribution are reported as summary statistics. Using the modified MIGET gases, the mean and log standard deviation for both the V̇A and Q̇ distributions are greater than those statistics using the standard MIGET gases. These changes are greater for the V̇A distribution than for the Q̇ distribution because most of the mass of the V̇A distribution resides in the high V̇A/Q̇ mode, which is more sensitive to changes in the highly soluble inert gases.
Fig. 4.
MIGET predicted ventilation (black) and perfusion (gray) distributions for the modified gases (dashed) are broader than and shifted to the right of the standard gases (solid). These differences increase (more for ventilation than perfusion) as V̇A/Q̇ heterogeneity increases from condition 4 (panel A) to 7 (panel B) with Q̇br = 1 ml/s.
Fig. 5.
V̇A and Q̇ distribution statistics for the modified MIGET gases versus those for the standard MIGET gases. MIGET predicts a smaller dead space fraction (panel A) using the modified gases given the same Q̇br (different symbols) and V̇A/Q̇ condition (numerically labeled per Table 2). Dead space fraction calculated using the standard MIGET gases is sensitive to changes in Q̇br. Data labels correspond to conditions (Table 2) and arrows point towards increasing V̇A/Q̇ heterogeneity. Log SDQ (panel B) is independent of the set of MIGET gases except for conditions of intermediate V̇A/Q̇ heterogeneity. The mean V̇A/Q̇ of the ventilation distribution (panel C) is greater for the modified gases than the standard gases and is sensitive to Q̇br when using the standard gases. Log SDV (panel D) is substantially greater for the modified gases, particularly for conditions of intermediate V̇A/Q̇ heterogeneity, and sensitive to Q̇br when using the standard gases.
The MIGET algorithm analyzed the retention and excretion values generated by the airway-alveolar gas exchange model for each combined V̇A/Q̇ and Q̇br condition. This analysis yielded ventilation and perfusion distributions versus V̇A/Q̇ which were subsequently distilled into summary statistics such as dead space fraction and log standard deviation of the perfusion distribution (log SDQ). We plotted some of these distribution statistics for the modified MIGET gases against those for the standard MIGET gases (Fig. 5A–D). MIGET predicted a smaller dead space fraction (Fig. 5A) using the modified gases given the same Q̇br (different symbols) and V̇A/Q̇ condition (numerically labeled per Table 2). This smaller MIGET calculated dead space for the modified MIGET gases is because toluene and m-DCB have little airway interaction which leads to greater excrections and, thus, reduces the “dead space effect” present with the standard MIGET gases (dead space fraction =1-E). Dead space fraction is more sensitive to changes in Q̇br when calculated using the standard MIGET gases than when calculated using the modified MIGET gases. In Figure 5, data labels indicate V̇A/Q̇ conditions (Table 2) and arrows point towards increasing V̇A/Q̇ heterogeneity. The mean V̇A/Q̇ of the perfusion distribution (not shown) is relatively unaffected by MIGET gas selection or bronchial blood flow. A small increase (~5%) in the mean V̇A/Q̇ of the perfusion distribution is predicted for (V̇A/Q̇)A < 2 conditions when the standard gases are replaced by the modified gases. Log SDQ (Fig. 5B) is independent of the set of MIGET gases except for intermediate V̇A/Q̇ heterogeneity. When using the standard MIGET gases, log SDQ calculated from these intermediate V̇A/Q̇ conditions are affected by changes in bronchial blood flow. The mean V̇A/Q̇ of the ventilation distribution (Fig. 5C) is greater for the modified gases than the standard gases and is sensitive to Q̇br when using the standard gases. Figure 5D shows that the log standard deviation of the ventilation distribution (log SDV) is substantially greater for the modified gases, particularly at intermediate V̇A/Q̇ conditions, and sensitive to Q̇br when using the standard gases.
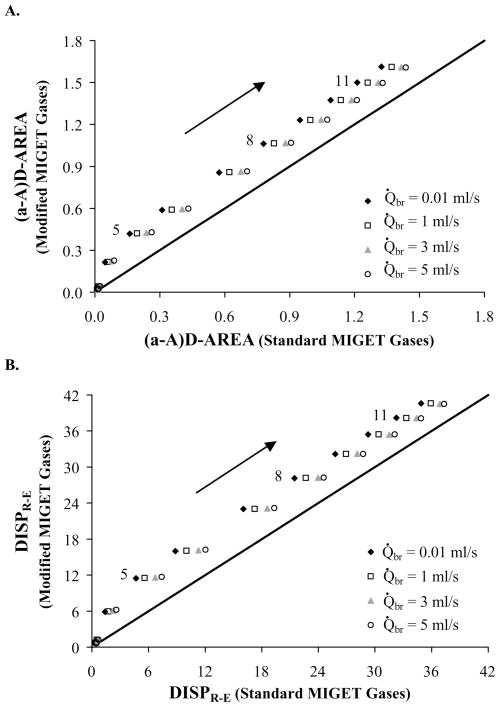
In addition to the distribution statistics, investigators have described additional statistics that are derived directly from the retention and excretion data rather than the calculated ventilation and perfusion distributions. One measure, (a-A)D-AREA, quantifies the area under the curve of the arterial-alveolar partial pressure difference versus the solubility of each gas 24. An increase in the area under this (a-A)D curve indicates an increase in V̇A/Q̇ heterogeneity. Another measure, the dispersion (DISPR-E), calculates the root mean square value of the retention minus excretion values over the six gases and can be conceptualized as an average arterial-alveolar difference for the inert gases 16. While both (a-A)D-AREA and DISPR-E can be further defined to describe only the retention or excretion data, we only present the broad index here because the finer indices follow the same general trend. Figure 6A and 6B show that (a-A)D-AREA and DISPR-E for the modified MIGET gases are greater than those values calculated using the standard MIGET gases. These results indicate that the modified MIGET gases recover a larger measure of V̇A/Q̇ heterogeneity that that calculated using the standard MIGET gases.
Fig 6.
Statistics calculated from the retention and excretion data. MIGET using modified MIGET gases predicts a greater area under the curve of arterial-alveolar difference, (a-A)D-AREA, (panel A) and a greater dispersion between measured retentions and excretions, DISPR-E, (panel B). The modified MIGET gases recover a larger measure of V̇A/Q̇ heterogeneity. Data labels correspond to conditions (Table 2) and arrows point towards increasing V̇A/Q̇ heterogeneity.
DISCUSSION
When the MIGET was developed and appropriate tracer gases were selected, the idea of airway gas exchange was novel and only a few studies had described or examined this phenomenon 6,11. The notion that both blood and water solubility affected the location of gas exchange was not recognized. Research in the 1980s and 1990s, using human experiments and mathematical models, demonstrated that highly blood-soluble gases like acetone, ethanol, and acetic acid exchanged in the airways 18,39,40,44,56. Some studies investigating the washin-washout of gases indicated that water solubility was important 26,40. However, the cumulative effects of both blood solubility and water solubility on gas exchange efficiency were not addressed until Twedt 45. Twedt examined the differential effects of blood and water solubility on pulmonary gas exchange and these insights provided the basis for this study.
Using our current understanding of pulmonary gas exchange, MIGET gases can be selected that have physical characteristics which fulfill the MIGET criteria and minimize airway gas exchange. From our recent investigations, gases that are highly soluble in both blood and water (λw=λb>100 like acetone) exchange primarily in the airways (Fig 2A). The mechanism of this exchange has been described for elimination of soluble gases from the body 1,3,4,18,23. Fresh inhaled air absorbs inert gas from the airway mucus, depletes the concentration of soluble gas in the mucous layer, and becomes fully saturated with highly soluble gas before reaching the alveoli. Because of the small bronchial blood flow and significant tissue barrier between this circulation and mucous layer, the airway wall and mucus are not replenished with soluble gas before exhalation begins. On exhalation, respired air encounters a lower concentration of soluble gas in the mucus. Therefore, a large driving force for the deposition of soluble gas onto the mucus promotes the recovery of soluble gas by the mucous layer, decreases the soluble gas concentration in the air, delays the appearance of soluble gas in the exhaled breath as captured by an expirogram 4,18, and reduces the mixed-expired gas concentration. This mechanism can be used to explain why gases that are both highly soluble in blood and water are affected by bronchial blood flow as seen in Figure 5 for the standard MIGET gases. For these gases, increases in bronchial blood flow help to replenish the mucous layer with soluble gas which in turn decreases the air-mucous gradient for deposition of soluble gas during exhalation and leads to a greater concentration of soluble gas in the exhaled breath.
To eliminate the influence of airway gas exchange on MIGET, we chose to replace acetone with m-dichlorobenzene (Table 1), a gas with a high blood solubility (λb>100) but low water solubility (λw≪λb). Because the mucous layer has water-like solubility characteristics, this layer is much less permeable to this low water soluble gas, the mucous layer acts as a barrier to the exchange of m-dichlorobenzene between the airway lumen and bronchial circulation, and airway gas exchange is hindered. As a result, gas exchange is shifted, almost completely, to the alveoli (Fig 2B). Although ether is less soluble in blood and water than acetone (Table 1), we replaced it with toluene because our mathematical model predicted that ether exchanges almost 50% in the airways 1. Toluene was chosen because its low water solubility inhibited its exchange with the airways, but its blood solubility, which is similar to ether, enabled it to satisfy the MIGET requirements.
Shunt was not included in these simulations because airway gas exchange was not expected to affect the MIGET predictions of shunt. In support of this assumption, our results showed that the mean of the perfusion distribution was relatively unaffected by MIGET gas selection and log SDQ was only slightly affected (Fig. 5B). However, airway gas exchange did affect the ventilation distribution. MIGET partitions total ventilation into two specific categories: dead space ventilation and ventilation participating in alveolar gas exchange. To determine dead space ventilation, the MIGET model is fit to the “data” from the excretion simulations (Fig. 3, thin black and gray lines). The fitting algorithm places larger weights on the excretions of halothane and ether than it does on the excretion of acetone and produces a best-fit excretion curve (Fig. 3) by, in a gross sense, varying the partition of ventilation between dead space and alveolar gas exchange. The best-fit excretion curve provides a graphical means for calculating dead space fraction. The fraction of dead space ventilation can be calculated from Figure 3 as simply the difference between the maximum excretion, 1, and the excretion of a highly blood-soluble gas, λb=1000 24. Thus, the fraction of dead space ventilation is proportional to 1-E(λb=1000) where E(λb=1000) is the excretion value of a hypothetical gas (λb=1000) calculated from the MIGET generated best-fit curve of the excretion data. Because the absorption-desorption mechanism of airway gas exchange effectively decreases the excretion of ether and acetone which in turn decreases the MIGET predicted E(λb=1000), a comparison between the standard MIGET gases (which include ether and acetone) and the modified MIGET gases (which exclude gases that exchange in the airways) reveals these changes in the partitioning of alveolar and deadspace ventilation. Compared to the standard MIGET gases, MIGET using the modified MIGET gases predicts a smaller dead space fraction (Fig. 5A) and a larger mean and log SDVA of the ventilation distribution (Fig 5C and 5D).
Additionally, MIGET predictions using the standard gases are affected by increases in bronchial blood flow whereas MIGET predictions using the modified gases are quite unaffected by Q̇br. The relative effect of airway gas exchange on the standard MIGET gases, via ether and acetone, can be seen through the effect of bronchial blood flow on the predicted dead space fractions (Fig 5A) and ventilation distributions (Fig 5C and 5D). Increases in bronchial blood flow replenish, more quickly, the airway wall with soluble gas during the breathing cycle and, therefore, reduce the gradient for desorption during exhalation. Thus, the excretion of ether and acetone is increased and MIGET predictions are altered by: 1) reducing the predicted dead space fraction; and 2) increasing the amount of ventilation participating in gas exchange as observed via statistical increases in mean V̇A and log SDVA.
A comparison of log SDVA predicted from the modified gases to that predicted from the standard gases (Fig. 5D) reveals a non-linear offset for conditions 4 through 6. This nonlinearity corresponds to the ability of MIGET to resolve the bimodal distributions (Fig. 4). Using modified gases, the ventilation and perfusion distributions are resolved into two modes for all conditions 4 and greater ((V̇A/Q̇)A ≥ 2), but using the standard gases, these distributions are separated into two modes for only conditions 6 and greater ((V̇A/Q̇)A ≥ 3). For conditions 4 to 6, the log SDVA reflects a bimodal distribution for the modified gases and a unimodal distribution for the standard gases (Fig. 4), explaining this non-linear relationship. Similar logic can be used to explain the mild non-linear relationship observed for log SDQ (Fig 5B). It is important to note that the recovered distributions, not simply the summary statistics, should be examined when testing this theory with animal experiments. The recovered ventilation distribution using the modified MIGET gases should be broader and may have two modes as compared to the thinner, unimodal distribution predicted with the standard MIGET gases.
It is important to determine which set of gases provides the best estimated ventilation and perfusion distributions as compared to the imposed distributions. A good representative condition is shown in Fig. 4B. For the low mode (V̇A/Q̇ =0.25), both sets of gases provide a good representation of the imposed ventilation and perfusion distribution. However, for the high mode (V̇A/Q̇ =4), the modified gases provided a better estimate of the ventilation and perfusion distribution with the peak of each distribution at a V̇A/Q̇ of 4.82 and 3.22, respectively. Using the standard gases, these peaks occur at V̇A/Q̇ of 2.63 and 2.15, respectively. The modified gases always described the high mode better than the standard gases. In addition, mean and log SD estimated from the MIGET in our conditions 1–6 were within the range of experimental measurements in humans 15,35,49,55.
The main limitations of the airway-alveolar gas exchange model have been discussed previously and include, the diffusing capacity of the airways, the airway wall dimensions, airway transfer coefficients, and bronchial circulation model 1,4. In addition to these limitations, the model does not account for anatomic heterogeneity that could have a secondary impact on gas exchange heterogeneity. The model has a symmetrically bifurcating structure with uniform airway diameters and lengths across each airway generation. This structure results in a series of geometrically uniform path lengths to each alveoli and uniform radial airway structure across an airway generation. Additionally, the model does not account for sequential emptying (i.e., temporal gas exchange heterogeneity) which may impact the magnitude of airway gas exchange during exhalation. While these limitations could affect the results presented here, their effects should be minor relative to the primary factors driving gas exchange heterogeneity (ventilation and perfusion heterogeneity in both the airways and the alveoli), which were captured by the pulmonary gas exchange model.
We hypothesized that two of the standard MIGET gases, ether and acetone, interacted with the airways and this interaction affected MIGET predictions of alveolar gas exchange. To reduce the impact of airway gas exchange, we substituted toluene and m-dichlorobenzene for ether and acetone, respectively, because toluene and m-dichlorobenzene have low water solubilities (i.e., they have minimal interaction with the airways) and have similar blood solubilities to those of the replaced gases. However, toluene and m-dichlorobenzene are not special in their blood solubility characteristics and other gases could have fulfilled those criteria of low water solubility and high blood solubility. In place of ether, we could have chosen tetrachloroethylene (λb=12.3, λw=0.72), ethylbenzene (λb=28.2, λw=1.78), or any isomer of xylene (λb~35, λw~2) 30. However, we found only two adequate replacements for acetone: m-dichlorobenzene or o-dichlorobenzene (λb=423, λw=9.00) 30. While the exact choice of gases is unimportant for this theoretical study, experimentally replicating this study may require use of a different replacement gas because of multiple factors: detection limitations of the gas chromatograph; in vivo interactions between the set of inert gases; gas interaction during sample analysis; rate of metabolism; or toxicity.
In addition to measurement of exhaled gases for the MIGET technique, measurement of the exhaled breath is becoming more commonplace. An increase in social and medical awareness has promoted breath tests for assessing legal compliance (e.g., alcohol breath test), detecting the amount of exposure to environmental and occupational toxicants (e.g., toluene, ozone), and measuring endogenous markers of systemic and pulmonary disease (e.g., isoprene, acetone, nitric oxide) 27,29. The increase in the prevalence of breath tests has been enabled by the relative non-invasive nature of the test and the advent of parts-per-billion sensitive and fast responding measurement devices such as the SIFT mass spectrometer 42. As a result, the design of appropriate breath tests will be required for each gas of interest and testing scenario. In addition to the traditional factors such as endpoint, gas properties, subject characteristics, and homogeneity of ventilation and perfusion, the effects of blood and water solubility, as described in this manuscript, should be given the same weight as the more traditional factors.
In summary, we have used a mathematical model describing airway and alveolar gas exchange to explore the effects of airway gas exchange on the MIGET predictions of alveolar gas exchange efficiency. For this study, an airway-alveolar gas exchange model calculated the excretions and retentions of the six MIGET gases and two additional gases, toluene and m-dichlorobenzene, under varying levels of alveolar ventilation-perfusion heterogeneity and bronchial blood flows. These two additional gases had similar blood solubility as ether and acetone, respectively, but much lower water solubility, which minimized their airway exchange. The MIGET mathematical model analyzed the excretion and retention data from two groupings of these eight gases and more accurately predicted the excretion and retention data from the modified MIGET gases. The results from the standard MIGET gases, which included ether and acetone, were compared to those from the modified MIGET gases, which included toluene and m-dichlorobenzene. Only the standard gases were affected by bronchial blood flow, a significant factor in airway gas exchange. In addition, the following differences were observed.
Relative excretions
The excretions of toluene and m-DCB were larger than ether and acetone, respectively, and the difference between Em-DCB and EAcetone was greater than that between EToluene and EEther (Fig. 3). The modified MIGET gases have relatively larger excretions because the concentration of these species is unaffected during the transport from the alveoli to the mouth whereas the concentration of ether and acetone decreases during delivery to the mouth via desorption in the airways.
Ventilation distribution
The ventilation distributions recovered by MIGET using the modified gases as compared to the standard gases more closely resembled the imposed distribution, were broader (larger log SDVA, Fig. 5D), were bimodal instead of unimodal with the second mode representing units with V̇A/Q̇ >1 (Fig. 4), and had a greater mean of the ventilation distribution (Fig. 5C).
Dead space
The inert gas dead space was smaller when using the modified gases as compared to the standard gases because MIGET calculated dead space is proportional to 1-Emax where Emax is the excretion for a gas with λb~1000 predicted from the best-fit of the MIGET model through the experimental excretions. Emax predicted using the modified MIGET gases is greater than that using the standard MIGET gases.
Arterial-Alveolar inert gas difference
Statistics that summarize the arterial-alveolar difference for the inert gases such as (a-A)D-AREA and DISPR-E were larger for the modified gases as compared to the standard gases (Fig. 6). This trend held for subtypes of these statistics that only examine the excretion or retention data. The modified MIGET gases recover a larger measure of V̇A/Q̇ heterogeneity than that calculated using the standard MIGET gases.
Acknowledgments
This work was supported, in part, by the National Institute for Biomedical Imaging and Bioengineering Grants T32 EB001650 and BE 001973, the National Heart, Lung, and Blood Institute Grants HL 64368 and HL073598, and the National Science Foundation Grant 04-607/NIH.
References
- 1.Anderson JC, Babb AL, Hlastala MP. Modeling soluble gas exchange in the airways and alveoli. Ann Biomed Eng. 2003;31:1402–1422. doi: 10.1114/1.1630600. [DOI] [PubMed] [Google Scholar]
- 2.Anderson JC, Bernard SL, Luchtel DL, Babb AL, Hlastala MP. Axial and radial distribution of the bronchial vasculature in sheep. Respir Physiol Neurobiol. 2002;132:329–339. doi: 10.1016/s1569-9048(02)00078-2. [DOI] [PubMed] [Google Scholar]
- 3.Anderson JC, Hlastala MP. Breath tests and airway gas exchange. Pulm Pharmacol Ther. 2007;20:112–117. doi: 10.1016/j.pupt.2005.12.002. [DOI] [PubMed] [Google Scholar]
- 4.Anderson JC, Lamm WJE, Hlastala MP. Measuring airway exchange of endogenous acetone using a single exhalation breathing maneuver. J Appl Physiol. 2006;100:880–889. doi: 10.1152/japplphysiol.00868.2005. [DOI] [PubMed] [Google Scholar]
- 5.Bui TD, Dabdub D, George SC. Modeling bronchial circulation with application to soluble gas exchange: description and sensitivity analysis. J Appl Physiol. 1998;84:2070–2088. doi: 10.1152/jappl.1998.84.6.2070. [DOI] [PubMed] [Google Scholar]
- 6.Cander L, Forster RE. Determination of pulmonary parenchymal tissue volume and pulmonary capillary blood flow in man. J Appl Physiol. 1959;14:541–551. [Google Scholar]
- 7.Cao WQ, Duan YX. Breath analysis: Potential for clinical diagnosis and exposure assessment. Clin Chem. 2006;52:800–811. doi: 10.1373/clinchem.2005.063545. [DOI] [PubMed] [Google Scholar]
- 8.Chilton TH, Colburn AP. Mass transfer (absorption) coefficients: prediction from data on heat transfer and fluid friction. Ind Eng Chem. 1934;26:1183–1187. [Google Scholar]
- 9.Corte P, I, Young H. Ventilation-perfusion relationships in symptomatic asthma. Response to oxygen and clemastine. Chest. 1985;88:167–175. doi: 10.1378/chest.88.2.167. [DOI] [PubMed] [Google Scholar]
- 10.Diskin AM, Spanel P, Smith D. Time variation of ammonia, acetone, isoprene and ethanol in breath: a quantitative SIFT-MS study over 30 days. Physiol Meas. 2003;24:107–119. doi: 10.1088/0967-3334/24/1/308. [DOI] [PubMed] [Google Scholar]
- 11.DuBois AB, Rogers RM. Respiratory factors determining the tissue concentrations of inhaled toxic substances. Respir Physiol. 1968;5:34–52. doi: 10.1016/0034-5687(68)90075-3. [DOI] [PubMed] [Google Scholar]
- 12.Dueck R, Young I, Clausen J, Wagner PD. Altered distribution of pulmonary ventilation and blood flow following induction of inhalation anesthesia. Anesthesiology. 1980;52:113–125. [PubMed] [Google Scholar]
- 13.Eger EI, 2nd, Larson CP., Jr Anaesthetic Solubility in Blood and Tissues: Values and Significance. Br J Anaesth. 1964;36:140–144. doi: 10.1093/bja/36.3.140. [DOI] [PubMed] [Google Scholar]
- 14.Farhi LE. Elimination of inert gas by the lung. Respir Physiol. 1967;3:1–11. doi: 10.1016/0034-5687(67)90018-7. [DOI] [PubMed] [Google Scholar]
- 15.Freyschuss U, Hedlin G, Hedenstierna G. Ventilation-perfusion relationships during exercise-induced asthma in children. Am Rev Respir Dis. 1984;130:888–894. doi: 10.1164/arrd.1984.130.5.888. [DOI] [PubMed] [Google Scholar]
- 16.Gale GE, Torre-Bueno JR, Moon RE, Saltzman HA, Wagner PD. Ventilation-perfusion inequality in normal humans during exercise at sea level and simulated altitude. J Appl Physiol. 1985;58:978–988. doi: 10.1152/jappl.1985.58.3.978. [DOI] [PubMed] [Google Scholar]
- 17.George SC, Babb AL, Deffebach ME, Hlastala MP. Diffusion of nonelectrolytes in the canine trachea: effect of tight junction. J Appl Physiol. 1996;80:1687–1695. doi: 10.1152/jappl.1996.80.5.1687. [DOI] [PubMed] [Google Scholar]
- 18.George SC, Babb AL, Hlastala MP. Dynamics of soluble gas exchange in the airways. III. Single-exhalation breathing maneuver. J Appl Physiol. 1993;75:2439–2449. doi: 10.1152/jappl.1993.75.6.2439. [DOI] [PubMed] [Google Scholar]
- 19.George SC, Souders JE, Babb AL, Hlastala MP. Modeling steady-state inert gas exchange in the canine trachea. J Appl Physiol. 1995;79:929–940. doi: 10.1152/jappl.1995.79.3.929. [DOI] [PubMed] [Google Scholar]
- 20.Guenard H, Manier G, Castaing Y, Varene N. Series dead space for inert gases in healthy subjects. Pflugers Arch. 1985;403:384–387. doi: 10.1007/BF00589250. [DOI] [PubMed] [Google Scholar]
- 21.Hanna LM, Scherer PW. Regional control of local airway heat and water vapor losses. J Appl Physiol. 1986;61:624–632. doi: 10.1152/jappl.1986.61.2.624. [DOI] [PubMed] [Google Scholar]
- 22.Hindmarsh A. LSODE (computer software) Livermore, CA: Laurence Livermore Laboratory; 1981. [Google Scholar]
- 23.Hlastala MP, Anderson JC. The impact of breathing pattern and lung size on the alcohol breath test. Ann Biomed Eng. 2007;35:264–272. doi: 10.1007/s10439-006-9216-3. [DOI] [PubMed] [Google Scholar]
- 24.Hlastala MP, Robertson HT. Inert gas elimination characteristics of the normal and abnormal lung. J Appl Physiol. 1978;44:258–266. doi: 10.1152/jappl.1978.44.2.258. [DOI] [PubMed] [Google Scholar]
- 25.Ingenito EP. PhD. Cambridge, MA: Massachusetts Institute of Technology; 1984. Respiratory fluid mechanics and heat transfer. [Google Scholar]
- 26.Johanson G. Modeling of respiratory exchange of polar-solvents. Ann Occup Hyg. 1991;35:323–339. doi: 10.1093/annhyg/35.3.323. [DOI] [PubMed] [Google Scholar]
- 27.Kupari M, Lommi J, Ventila M, Karjalainen U. Breath acetone in congestive heart failure. Am J Cardiol. 1995;76:1076–1078. doi: 10.1016/s0002-9149(99)80304-x. [DOI] [PubMed] [Google Scholar]
- 28.Lowe HJ, Hagler K. Determination of volatile organic anaesthetics in blood, gases, tissues and lipids: Partition coefficients. In: Porter R, editor. Gas Chromatography in Biology and Medicine. London: Churchill; 1969. pp. 86–103. [Google Scholar]
- 29.Mendis S, Sobotka PA, Euler DE. Expired hydrocarbons in patients with acute myocardial infarction. Free Radic Res. 1995;23:117–122. doi: 10.3109/10715769509064026. [DOI] [PubMed] [Google Scholar]
- 30.Meulenberg CJ, Vijverberg HP. Empirical relations predicting human and rat tissue:air partition coefficients of volatile organic compounds. Toxicol Appl Pharmacol. 2000;165:206–216. doi: 10.1006/taap.2000.8929. [DOI] [PubMed] [Google Scholar]
- 31.Miekisch W, Schubert JK, Noeldge-Schomburg GF. Diagnostic potential of breath analysis--focus on volatile organic compounds. Clin Chim Acta. 2004;347:25–39. doi: 10.1016/j.cccn.2004.04.023. [DOI] [PubMed] [Google Scholar]
- 32.Moser B, Bodrogi F, Eibl G, Lechner M, Rieder J, Lirk P. Mass spectrometric profile of exhaled breath--field study by PTR-MS. Respir Physiol Neurobiol. 2005;145:295–300. doi: 10.1016/j.resp.2004.02.002. [DOI] [PubMed] [Google Scholar]
- 33.Phillips M, Cataneo RN, Cummin AR, Gagliardi AJ, Gleeson K, Greenberg J, Maxfield RA, Rom WN. Detection of lung cancer with volatile markers in the breath. Chest. 2003;123:2115–2123. doi: 10.1378/chest.123.6.2115. [DOI] [PubMed] [Google Scholar]
- 34.Roca J, Wagner PD. Contribution of multiple inert gas elimination technique to pulmonary medicine. 1. Principles and information content of the multiple inert gas elimination technique. Thorax. 1994;49:815–824. doi: 10.1136/thx.49.8.815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Rodriguez-Roisin R, Ferrer A, Navajas D, Agusti AG, Wagner PD, Roca J. Ventilation-perfusion mismatch after methacholine challenge in patients with mild bronchial asthma. Am Rev Respir Dis. 1991;144:88–94. doi: 10.1164/ajrccm/144.1.88. [DOI] [PubMed] [Google Scholar]
- 36.Sato A, Nakajima T. Partition-coefficients of some aromatic-hydrocarbons and ketones in water, blood and oil. Br J Ind Med. 1979;36:231–234. doi: 10.1136/oem.36.3.231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Sato A, Nakajima T. A structure-activity relationship of some chlorinated hydrocarbons. Arch Environ Health. 1979;34:69–75. doi: 10.1080/00039896.1979.10667371. [DOI] [PubMed] [Google Scholar]
- 38.Schimmel C, Bernard SL, Anderson JC, Polissar NL, Lakshminarayan S, Hlastala MP. Soluble gas exchange in the pulmonary airways of sheep. J Appl Physiol. 2004;97:1702–1708. doi: 10.1152/japplphysiol.01272.2003. [DOI] [PubMed] [Google Scholar]
- 39.Schrikker AC, de Vries WR, Zwart A, Luijendijk SC. The excretion of highly soluble gases by the lung in man. Pflugers Archiv - European Journal of Physiology. 1989;415:214–219. doi: 10.1007/BF00370595. [DOI] [PubMed] [Google Scholar]
- 40.Schrikker AC, de Vries WR, Zwart A, Luijendijk SC. Uptake of highly soluble gases in the epithelium of the conducting airways. Pflugers Archiv - European Journal of Physiology. 1985;405:389–394. doi: 10.1007/BF00595693. [DOI] [PubMed] [Google Scholar]
- 41.Schrikker AC, Wesenhagen H, Luijendijk SC. Intrapulmonary gas mixing and dead space in artificially ventilated dogs. Pflugers Arch. 1995;430:862–870. doi: 10.1007/BF00386187. [DOI] [PubMed] [Google Scholar]
- 42.Smith D, Spanel P, Davies S. Trace gases in breath of healthy volunteers when fasting and after a protein-calorie meal: a preliminary study. J Appl Physiol. 1999;87:1584–1588. doi: 10.1152/jappl.1999.87.5.1584. [DOI] [PubMed] [Google Scholar]
- 43.Souders JE, George SC, Polissar NL, Swenson ER, Hlastala MP. Tracheal gas exchange: perfusion-related differences in inert gas elimination. J Appl Physiol. 1995;79:918–928. doi: 10.1152/jappl.1995.79.3.918. [DOI] [PubMed] [Google Scholar]
- 44.Tsu ME, Babb AL, Ralph DD, Hlastala MP. Dynamics of heat, water, and soluble gas exchange in the human airways: 1. A model study. Ann Biomed Eng. 1988;16:547–571. doi: 10.1007/BF02368015. [DOI] [PubMed] [Google Scholar]
- 45.Twedt MM. MS. Seattle, WA: University of Washington; 1996. An analysis of the effects of axial dispersion and tissue solubility on gas exchange in the upper airways. [Google Scholar]
- 46.vanLöbensels EM, Anderson JC, Hildebrandt J, Hlastala MP. Modeling diffusion limitation of gas exchange in lungs containing perfluorocarbon. J Appl Physiol. 1999;86:273–284. doi: 10.1152/jappl.1999.86.1.273. [DOI] [PubMed] [Google Scholar]
- 47.von Basum G, Dahnke H, Halmer D, Hering P, Murtz M. Online recording of ethane traces in human breath via infrared laser spectroscopy. J Appl Physiol. 2003;95:2583–2590. doi: 10.1152/japplphysiol.00542.2003. [DOI] [PubMed] [Google Scholar]
- 48.Wagner PD, Dantzker DR, Dueck R, Clausen JL, West JB. Ventilation-perfusion inequality in chronic obstructive pulmonary disease. J Clin Invest. 1977;59:203–216. doi: 10.1172/JCI108630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Wagner PD, Hedenstierna G, Bylin G. Ventilation-perfusion inequality in chronic asthma. Am Rev Respir Dis. 1987;136:605–612. doi: 10.1164/ajrccm/136.3.605. [DOI] [PubMed] [Google Scholar]
- 50.Wagner PD, Naumann PF, Laravuso RB. Simultaneous measurement of eight foreign gases in blood by gas chromatography. J Appl Physiol. 1974;36:600–605. doi: 10.1152/jappl.1974.36.5.600. [DOI] [PubMed] [Google Scholar]
- 51.Wagner PD, Saltzman HA, West JB. Measurement of continuous distributions of ventilation-perfusion ratios: theory. J Appl Physiol. 1974;36:588–599. doi: 10.1152/jappl.1974.36.5.588. [DOI] [PubMed] [Google Scholar]
- 52.Wang CJ, Scherrer ST, Hossain D. Measurements of cavity ringdown spectroscopy of acetone in the ultraviolet and near-infrared spectral regions: Potential for development of a breath analyzer. Appl Spectrosc. 2004;58:784–791. doi: 10.1366/0003702041389193. [DOI] [PubMed] [Google Scholar]
- 53.Weibel ER. Morphometry of the human lung. New York: Academic Press; 1963. [Google Scholar]
- 54.Wilhelm E, Battino R, Wilcock RJ. Low-pressure solubility of gases in liquid water. Chem Rev. 1977;77:219–262. [Google Scholar]
- 55.Young IH, Corte P, Schoeffel RE. Pattern and time course of ventilation-perfusion inequality in exercise-induced asthma. Am Rev Respir Dis. 1982;125:304–311. doi: 10.1164/arrd.1982.125.3.304. [DOI] [PubMed] [Google Scholar]
- 56.Zwart A, Luijendijk SC, de Vries WR. Excretion-retention data of steady state gas exchange in tidal breathing. I. Dependency on the blood-gas partition coefficient. Pflugers Arch. 1986;407:204–210. doi: 10.1007/BF00580677. [DOI] [PubMed] [Google Scholar]