Diffusion based Abnormality Markers of Pathology: Towards Learned Diagnostic Prediction of ASD

Abstract

This paper presents a paradigm for generating a quantifiable marker of pathology that supports diagnosis and provides a potential biomarker of neuropsychiatric disorders, such as autism spectrum disorder (ASD). This is achieved by creating high-dimensional nonlinear pattern classifiers using Support Vector Machines (SVM), that learn the underlying pattern of pathology using numerous atlas-based regional features extracted from Diffusion Tensor Imaging (DTI) data. These classifiers, in addition to providing insight into the group separation between patients and controls, are applicable on a single subject basis and have the potential to aid in diagnosis by assigning a probabilistic abnormality score to each subject that quantifies the degree of pathology and can be used in combination with other clinical scores to aid in diagnostic decision. They also produce a ranking of regions that contribute most to the group classification and separation, thereby providing a neurobiological insight into the pathology. As an illustrative application of the general framework for creating diffusion based abnormality classifiers we create classifiers for a dataset consisting of 45 children with autism spectrum disorder (ASD) (mean age 10.5 ± 2.5 yrs) as compared to 30 typically developing (TD) controls ( mean age 10.3 ± 2.5 yrs). Based on the abnormality scores, a distinction between the ASD population and TD controls was achieved with 80% leave one out (LOO) cross-validation accuracy with high significance of p < 0.001, ~84% specificity and ~74% sensitivity. Regions that contributed to this abnormality score involved fractional anisotropy (FA) differences mainly in right occipital regions as well as in left superior longitudinal fasciculus, external and internal capsule while mean diffusivity (MD) discriminates were observed primarily in right occipital gyrus and right temporal white matter.

1. Introduction

Methods for population-based statistics have been developed with the aim of elucidating group differences as well as probing certain regions of the brain based on one or more hypotheses. The majority of the studies use methods like voxel-based morphometry (VBM) (Ashburner and Friston 2000; Ashburner and Friston 2001; Good, Scahill et al. 2002; Ridgway, Henley et al. 2008) that study the whole brain in the absence of a hypothesis, or investigate spatial hypothesis driven region of interest (ROI)-based studies (Kubicki, Westin et al. 2002; Alexander, Lee et al. 2007). Such studies have been commonly carried out on structural MRI (sMRI) as well as on diffusion tensor MRI (DTI). Although voxel-based (VBM) statistics has been established as a conventional technique in neuroimaging, it can be significantly biased toward group differences that are highly localized in space and therefore may not be suitable for analysis of non-focal diseases like psychiatric disorders (Davatzikos 2004). VBM methods do not however lend themselves to the statistical identification of spatially-distributed patterns of voxel differences (where the changes in individual voxels or voxel clusters may be sub-threshold and escape identification). In contrast, region of interest (ROI-based analyses performed on certain preselected ROI’s require a priori knowledge of the affected regions, specific to pathology (for example, specific fiber tracts affected in schizophrenia). These methods have a lower exploratory power (since only few ROI’s are used) and it is difficult to combine the effect of several separate ROIs (perhaps representing a functional network) that change differently during the course of pathologic progression. Thus, these traditional techniques (VBM or ROI based) only identify local statistical group differences and may not be sensitive to combinations of spatially discrete changes needed for effective group discrimination nor are they capable of providing a measure of the degree of pathology on a single subject basis, or a ranking of regions that contribute to this measure.

This has led to the need for methods that can learn subtle brain pattern differences and provide a quantifiable score that serves as a patho-physiological diagnostic marker and also reflects the extent of pathology. This is expected to aid in the study of neuro-developmental disorders such as ASD, the diagnosis of which is exclusively based on clinical assessment measures, where the addition of an abnormality score created from imaging modalities will augment diagnostic decision, especially in the setting of ambiguity. Furthermore, by identifying key anatomic substrates (features) that provide such diagnostic utility, by their contribution to such an abnormality score, we gain potential neurobiological insight into the basis of the disorder. Towards these goals, our paper presents a methodology for creating ROI-based pattern classifiers that provide a sensitive and specific diagnostic and prognostic biomarker in the form of an abnormality score. These scores computed from the classifier can in principle be used as an additional clinical evaluation, thereby aiding in the diagnostic decision.

High dimensional pattern classification methods like support vector machines (SVMs) can be used to capture multivariate relationships among various anatomical regions for more effective characterization of group differences as well as for quantifying the degree of pathological abnormality associated with each subject. These methods provide better group separability than traditional linear methods such as principal components analysis (PCA) when patient and control groups cannot be easily separated (see Figure 1). Several pattern classification methods have been adopted in the neuro-imaging community essentially to enhance group separation between patients and healthy controls. These studies have been carried out mainly in structural MR imaging (Yushkevich, Joshi et al. 2003; Lao, Shen et al. 2004; Fan, Shen et al. 2007; Pohl and Sabuncu 2009), functional MR imaging (Cox and Savoy 2003; LaConte, Strother et al. 2005; Mourao-Miranda, Bokde et al. 2005; De Martino, Gentile et al. 2007) and a few using diffusion tensor MR imaging (Caan, Vermeer et al. 2006; Wang and Verma 2008; Lange, Dubray et al. 2010). These studies can be distinguished based on the different steps of pattern classification adopted, namely: feature extraction, feature selection, classifier training and classifier testing or cross-validation. Typically used methods for feature extraction involve using direct features like structural volumes and shapes (Golland, Grimson et al. 2005; Pohl and Sabuncu 2009), principal component analysis (PCA) (Mourao-Miranda, Bokde et al. 2005; Narr, Bilder et al. 2005; Caan, Vermeer et al. 2006), automated segmentation(Fan, Shen et al. 2007), wavelet decomposition (Lao, Shen et al. 2004) and Bayes error estimation (Wang and Verma 2008). High dimensionality of the feature space and limited number of subjects pose a significant challenge in classification (Golland, Grimson et al. 2005). To solve this problem, feature selection is performed in order to produce a small number of effective features for efficient classification and to increase the generalizability of the classifier. Feature selection methods that are commonly used for structural and functional neuro-imaging data involve filtering methods (e.g. ranking based on Pearson’s correlation coefficient) (Fan, Shen et al. 2007) and/or wrapper techniques (e.g. recursive feature elimination (RFE)) (De Martino, Gentile et al. 2007; Fan, Shen et al. 2007). Classifiers are then trained on the selected features either using linear classifiers like linear discriminant analysis (LDA) (Caan, Vermeer et al. 2006) or non-linear classifiers like k-nearest neighbors (kNN) (Wang and Verma 2008), quadratic discriminant analysis (QDA) (Lange, Dubray et al. 2010) and support vector machines (SVM) (Cox and Savoy 2003; LaConte, Strother et al. 2005; Mourao-Miranda, Bokde et al. 2005; Ecker, Rocha-Rego et al. 2010). Prior to their application to a new test subject, it is important that the classifier be cross-validated, for which leave-one-out is a widely adopted technique. These cross-validated classifiers can then be applied to a new subject. The majority of the previous classification work was implemented on structural or fMRI images, although there were few studies that dealt with DTI-based classification. Caan et al. (2006) used fractional anisotropy (FA) and linear anisotropy images as their features, followed by dimensionality reduction using PCA and trained the data using linear discriminant analysis (LDA)(Caan, Vermeer et al. 2006). This classifier was thus limited to linear models and could not capture complex non-linear relationships. Quadratic classifiers were employed by Lange et al. (Lange, Dubray et al. 2010) to create Autism specific classifiers using DTI based features computed in two regions in the brain. Similarly, Adluru et al. trained SVM classifiers on chosen fiber tracts shape features (Adluru 2009). Although such methods give reasonable classification accuracy, they are hypothesized to certain brain regions making it difficult to understand brain region interactions. In addition, the components cannot provide a physiological insight into the regions that contribute to the group separability. Wang et al. trained a k-NN classifier trained on full brain volume FA and geometry maps (Wang and Verma 2008). Although a non-linear classifier was employed, it was over the full brain and the output was complicated for clinical interpretation.

Figure 1.

An example depicting the basic idea behind non-linear SVM. The samples are mapped into a high dimensional feature space where a separating hyperplane is constructed. Here the x-axis can be considered as FA and y-axis as MD to be specific to diffusion.

In this paper, we describe a new classification methodology based on DTI features of anisotropy and diffusivity (Moseley, Cohen et al. 1990; Pierpaoli, Jezzard et al. 1996) computed from atlas-based regions of interest (ROI). Our classifiers can be used to assign an abnormality score to each subject relative to the abnormality patterns learned from the population. This score can then be used to complement clinical scores, thereby aiding in diagnosis and potentially enhanced disease characterization. The regions elucidated by the classifier provide a neurobiological insight into the pathology and the ranking of features can be used for hypothesis generation for studies based on the regions implicated. A primary example of a non-focal brain disorder is Autism Spectrum Disorder (ASD). Studies have indicated widespread brain abnormalities that include gray matter, white matter volume differences and atrophy in frontal, parietal and limbic regions (Brambilla, Hardan et al. 2003; Waiter, Williams et al. 2004; Hazlett, Poe et al. 2005; McAlonan, Cheung et al. 2005; Stigler, McDonald et al. 2010) mainly based on structural MRI. Recently, studies using Diffusion Tensor Imaging (DTI) have indicated white matter (WM) abnormalities (Verhoeven, De Cock et al. 2010) in ASD. VBM studies using DTI have reported lower white matter integrity mainly in the corpus callosum, internal and external capsule, temporal white matter, superior and inferior longitudinal fasciculus (Barnea-Goraly, Kwon et al. 2004; Alexander, Lee et al. 2007; Keller, Kana et al. 2007; Lee, Bigler et al. 2007; Verhoeven, De Cock et al. 2010). ROI based studies have hypothesized abnormalities in the arcuate fasciculus (Fletcher, Whitaker et al. 2010), superior temporal gyrus and temporal stem (Lee, Bigler et al. 2007) in ASD. We apply our proposed method to create classifiers for a population of children with ASD and typically developing (TD) controls, in order to demonstrate the applicability of the classifier as well as the use of the measures and ranked regions produced by the classifier in quantifying symptom severity. The ROI’s over the entire brain are used as features, as opposed to hypothesis based classifiers introduced in Lange et al. (Lange, Dubray et al. 2010). Despite the high heterogeneity of the ASD population, and a relatively low sample size, we have obtained classifiers with good cross-validation accuracy which produces scores that demonstrate their ability to quantify symptom severity based on correlations with clinical severity scores.

2. Methods

2.1. Datasets and Preprocessing

The evaluable dataset consisted of 45 subjects with ASD (42 males and 3 females) and 30 typically developing (TD) (14 males and 16 females), age and non-verbal IQ-matched controls. See table 1 for detailed population demographics. The patient dataset was heterogeneous (as is representative of the clinical population) as 13 subjects of the 45 ASD subjects were diagnosed with language impairment while the other 32 subjects showed language function in the normal range (Clinical Evaluation of Language Fundamentals-edition 4 (CELF-4) core language index > 85) (Semel 2003). The DWI images for all ASD and TD subjects were acquired on Siemens 3T Verio™ scanner using a 32 channel head coil. Diffusion tensor imaging was performed using a single shot spin-echo, echo-planar sequence with the following parameters: TR/TE=16900/70 ms, b-value of 1000 s/mm² and 30 gradient directions as well as a single b=0 s/mm² image. Eighty 2 mm contiguous axial slices of 128 × 128 matrix (FOV 256mm) yielded 2mm isotropic data. The total scan time was 6.2 minutes. Qualitative analysis (QA) of the images was performed manually and the ones with poor quality were removed. The dataset in this study of 75 subjects was created after passing QA. Eddy current and motion correction was not performed, but scans with head movement were removed in the QA.

Table 1.

Population demographics, cognitive test scores and abnormality scores computed by the classifier

	TD Controls	ASD patients	T-statistic	Group- comparison
Number of subjects	30 (14M, 16F)	45 (13 LI+, 32 LI−) (42M, 3F)	-	-
Age	10.3±2.5	10.5±2.5	0.35	0.73
SRS$	44.2±7.4	78.2±10.5	16.1	<0.001
SCQ#	3.5±2.7	19.3±4.9	17.7	<0.001
CELF-4@	108.1±11.3	92.7±16.9	−4.7	<0.001
CELF-4 (LI−)	”	100.8±10.7	−2.6	<0.012
CELF-4(LI+)	”	72.8±12.2	−8.8	<0.001
Abnormality score*	0.22±0.52	−0.46±0.39	−5.9	<0.001

^$Social responsiveness scale (SRS) SRS score is a standard socio-psychological biomarker indicating social impairments. It was only measured for 44/45 ASD and 29/30 TD.

^#Social Communications Questionnaire (SCQ) evaluates social functioning and communication skills based on a questionnaire.

^@Clinical Evaluation of Language Fundamentals-edition 4 (CELF-4) score is a marker of language impairment in ASD. Therefore it is highly significant in TD vs. LI+ and less so in TD vs LI−.

^*The abnormality score is computed from the proposed classification technique using the LOO validation.

After the data was acquired, the diffusion tensor images were reconstructed from the DWI data using multivariate linear fitting (Pierpaoli and Basser 1996). Spatial normalization of all the tensor images was then carried out via a high dimensional elastic registration known as DROID (Ingalhalikar, Yang et al. 2010). The deformable registration utilized the full tensor information by integrating intensity and orientation into a hierarchical matching framework. Following the spatial normalization, the mean FA (a measure of diffusion directional anisotropy) and MD (a measure of net, or average, diffusivity) for each of the 176 ROI’s were derived for each subject. Each ROI feature value was then normalized to between 0 and 1 for all the subjects based on the population.

2.2 Procedure

We now describe, in detail, the creation of region-based diffusion classifiers using Support Vector Machines (SVMs). A non-linear SVM is amongst the most powerful pattern classification algorithms, as it can obtain maximal generalization when predicting the classification of previously unseen data compared to other nonlinear classifiers (Vapnik 1998). By using a kernel function, it maps the original features of the labeled subjects into higher dimensional space where it computes a hyperplane such that the distance of the samples from this hyperplane is maximized, thereby optimally separating the population. Having found such a hyperplane, the SVM can then predict the classification of an unlabeled subject by mapping it into the feature space and checking on which side of the separating plane the example lies. Figure 1 illustrates the idea behind SVM based pattern classification.

We propose the creation of two-class classifiers which delineate patients from controls. Our method of creating ROI-based SVM classifiers using DTI-based information involves 4 steps: a. Feature extraction b. Feature ranking and selection c. Classifier training and d. Cross-validation. We now describe each of the steps in detail.

2.2.1. Feature Extraction

The method begins with spatial normalization of all the tensor images (45 ASD and 30 TD) to a standard atlas known as “EVE” (Huang, Hua et al. 2005; Mori, Wakana et al. 2005; Mori, Oishi et al. 2008), consisting of 176 anatomical ROI’s as shown in figure 2. (More information on this atlas can be found at http://cmrm.med.jhmi.edu/cmrm/atlas/human_data/). In the earlier studies that involved classification (Caan, Vermeer et al. 2006; Wang and Verma 2008), voxels of the whole brain were used as features. This is challenging for training classifiers as the sample size is relatively small (≈50 to few hundred) while the voxel-wise data dimensionality is very high (≈10⁶). As a result of the inter-individual structural variability, using fewer features computed from predefined regions of interest may lower the dimensionality while maintaining the spatial context, thereby producing more robust features (Fan, Shen et al. 2007). An advantage of using predefined structural ROI’s rather than spatial clusters (Lao, Shen et al. 2004; Fan, Shen et al. 2007) is that they can be combined with other discrete measurements (for e.g. MEG values, fMRI signal) taken from the anatomical ROI’s. They also tend towards more well-defined neurobiological interpretation, based on functional anatomic organization. Additionally, the ROI’s can be used together for a full brain analysis or the approach can be transformed to a hypothesis driven analysis by using only a hypothesis-driven subset of ROI’s. Thus we used the ROIs in the Eve atlas described above (representative slices can be seen in Fig. 2). However our framework is generalizable to different atlases in which ROIs are informed by different segmentations (Liu, Young et al. 2006; Hasan, Halphen et al. 2007; Liu, Li et al. 2007; Hasan and Frye 2011).

Figure 2.

Figure showing sample (a) FA and (b) MD maps computed from DTI image. (c) ROI map of the EVE template showing 176 structures. These regions are implemented as the basis for the features used to construct the pattern classifier. Details about the Eve template can be found at (Mori, Oishi et al. 2008).

In ASD, investigators have observed that the diffusion differences are substantially described by fractional anisotropy (FA) and mean diffusivity (MD) maps in the autistic patients relative to the controls (Alexander, Lee et al. 2007). FA and MD are features that can be computed from diffusion data that provide different characterizations of brain tissue. Representative slices from FA and MD maps of a subject are shown in figure 2. We computed the FA and MD maps from spatially normalized tensor images for each subject and then averaged over each ROI. Thus, each subject was associated with a feature vector (eq. 1) that involved ‘n’ ROI’s (n = 176, in our case). Eq. 1 describes the feature vector where each component is an average of the scalar values in that particular ROI.

$$f_s=({\mathit{ROI}}_1^{\mathit{FA}},{\mathit{ROI}}_2^{\mathit{FA}},\dots ..,{\mathit{ROI}}_n^{\mathit{FA}},{\mathit{ROI}}_1^{\mathit{MD}},{\mathit{ROI}}_2^{\mathit{MD}},\dots .,{\mathit{ROI}}_n^{\mathit{MD}})$$ (1)

It may be noted that while we have only used the FA and MD values computed from the diffusion data, the features are generalizable and can include addition diffusion measures such as radial and axial diffusivity, as well as volumetric features for each of the ROIs. This will augment the values for each of the ROIs, but the rest of the procedure will remain the same. Increasing the feature types also of course increases the dimensionality of the problem, exposing the limited sample size.

2.2.2 Feature Ranking and Selection

This step provides us with regions that most contribute to the patient-control classification and provide an insight into the physiology, as to which regions are important. Mathematically, identifying the most characteristic features is critical for minimizing the classification error. This can be achieved by ranking and selection of the relevant features and eliminating all the redundant features. In machine learning, feature ranking and selection is mainly divided into two categories. The first one is called as a wrapper technique which involves the predictor function (in our case SVM classifier) and has a direct goal of minimizing the classification error by providing different subsets of features. The other category includes filtering the features using a performance evaluation metric computed directly from the data and do not include a direct feedback from the classifier (Guyon 2006). Filtering removes the features which have little chance to be useful in the classification.

To find a compact discriminatory subset of features we chose a filtering method known as the signal-to-noise (s2n) ratio coefficient filter (Golub, Slonim et al. 1999). This method ranks features with the ratio of the absolute difference of the class means over the average class standard deviation and is known to work efficiently for heterogeneous datasets. For a feature vector x_i and class labels Y, the signal to noise ratio is given by equation 2. In this equation, μ(y+) and μ(y−) are the mean values while σ²(y+) and σ²(y−) are the variance for class y+ and y− respectively. This criterion is similar to the Fisher criterion, the T test criterion, and the Pearson correlation coefficient that are widely used (Guyon et al., 2006).

$$s2n(x_i,Y)=\frac{\mu (y+)-\mu (y-)}{{\sigma }^2(y+)+{\sigma }^2(y-)}$$ (2)

Based on these s2n coefficients, the features are ranked. To find the optimal number of features ‘n’ to be used in the classifier, the method suggested by Guyon et al. was implemented (Guyon 2006). This method is explained in detail in section 2.2.4.

2.2.3. Classifier training

The input to the classifier consists of feature matrix X and a vector Y of class labels consisting of 1 and −1 values defining the two classes (1 indicating TD and −1 indicating ASD in our case). The classifier uses a non-linear mapping Ф: R_d → H which maps the feature space R_d to a higher dimensional space H. The dataset (x_i, y_i), i = 1, 2….l for l samples, is transformed to (Ф(x_i), y_i). The SVM then solves the following problem:

$${\mathit{min}}_{\omega ,\beta ,\xi }\frac{1}{2}{\omega }^T\omega +C{\sum }_{i=1}^l{\xi }_i$$ (3)

subject to constraints,

$$\begin{array}{cc}\hfill y_i({\omega }^T& \Phi \left(x_i\right)+b)\ge 1-{\xi }_i\hfill \\ \hfill & {\xi }_i\ge 0,i=1,\dots l\hfill \end{array}$$

In equation 3, ω is the vector of coefficients, C defines the margin, b is a constant and ξ_i measures the degree of misclassification.

We implement a non-linear classifier using the Gaussian radial basis function (RBF) as a kernel function (Ф(x_i)^TФ(x_j)) that is defined by equation 4 where x_i and x_j are two feature vectors and γ controls the size of the Gaussian kernel.

$$K(x_i,x_j)=\exp \left(-\frac{{\Vert x_i-x_j\Vert }^2}{2y^2}\right)$$ (4)

Based on the distance from the hyperplane, the classifier computes a probabilistic score between 1 and −1 for each test subject. When the probabilistic score is ≥ 0, the subject is classified as class 1 (controls), otherwise as class −1 (patients). The probabilistic classifier score, therefore, represents the level of abnormality in the subject.

2.2.4. Cross-validation

The standard way for validating the classifier model is by implementing the leave-one-out (LOO), also known as jack-knife, cross validation method. In this validation, one sample is chosen for testing, while other samples are used for feature selection and training classifiers using the methods described in section 2.2.3. The classifier is then evaluated based on the classification result of the test subject. By repeatedly leaving each subject out as a test subject, obtaining its abnormality score, and averaging over all the left-out subjects we obtain the average classification rate.

The entire procedure can be understood via the schematic shown in figure 3. After the feature ranking step that determines the best number of features ‘n’ that shall be used in the final classifier model, the cross validation error for each feature subset is taken into consideration. For each training subset (in our case, when one subject was left out as test in each iteration), all the features were ranked and the cross validation error was computed sequentially by adding one feature at a time. The error was then averaged for the feature set of same size and the number of features ‘n’ was the one that provided the smallest average error. Details can be found in (Guyon 2006).

Figure 3.

Flow chart summarizing the entire DTI based classification procedure.

To further show the performance of our method the receiver operating characteristic (ROC) curves were plotted for the LOO classifiers that yielded the reported classification result. The ROC is a plot of sensitivity vs. (1-specificity) of the classifier when the discrimination threshold is varied. At each step, the true positives (TP), false positives (FP), true negatives s (TN) and false negatives (FN) are computed. From these, the sensitivity is computed as TP/(TP+FN) while specificity is computed as TN/(TN+FP). The sensitivity vs. (1-specificity) of the classifier is plotted by varying the discrimination threshold. ROC curves depict the effectiveness of the classifier model and are also utilized for computing the optimum kernel size.

3. Results

3.1 Classification Results

For our dataset, in each LOO iteration, feature selection was performed using the signal to noise ratio filter described in section 2.2.2. The number of features n was computed by method described in section 2.2.4. The optimal number of selected features n for this dataset was 18 out of 352.

A Gaussian function was implemented as a kernel and a suitable kernel size was determined after testing different σ values ranging from 0.01 to 1. Based on ROC curves plotted for LOO validation, the kernel size was picked. The choice of sigma was also validated using Fisher discrimination introduced in Wang et al. (Wang, Xu et al. 2003). It was found that the ROC curves were steep enough for kernel range of 0.05-0.15 for our dataset. Although choosing sigma is specific to the dataset, it does not need to be repeated for each new additional subject. The C value (from equation 3), which is the trade off parameter between training error and SVM margin, was tested for values 1-2000 using the ROC curves with a fixed sigma and it was observed that values close to 100 were a better choice for our classification (based on the ROC sensitivity-specificity tradeoff).

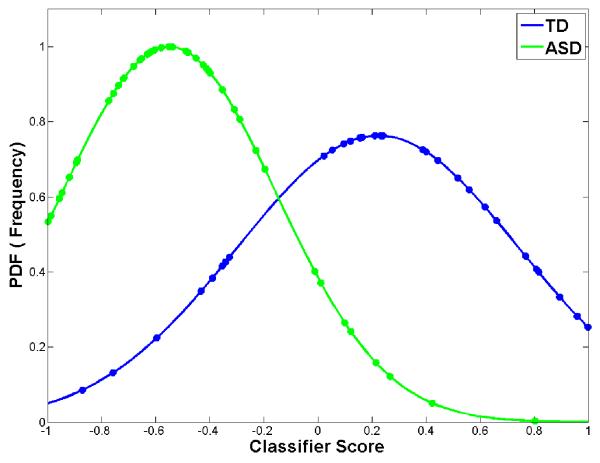
Figure 4 shows the classification results. In figure 4(a) the abnormality scores are plotted against the number of subjects from the LOO cross validation while in figure 4(b) a normal probability density function (PDF) which represents the likelihood of each abnormality score is plotted against the abnormality score. The average LOO accuracy was 80% (15/75 subjects misclassified). When the patient scores from LOO classification were split into language impaired and non-language impaired groups and then plotted (4(c)) it was observed that patients without language impairment were located in between the TD and language impaired ASD, suggesting a quantitative interpretation of the abnormality score in terms of language impairment severity.

Figure 4.

Fig. displaying the LOO classification performance (80% average accuracy). (a) Abnormality score plotted against number of subjects when LOO cross validation is performed. The line shows the separability between populations (b) PDF of the LOO score plotted. This delineates the separation between two groups. (c) When the abnormality scores are divided into 3 groups (TD, ASD LI− and ASD LI+) the non-language impaired lie between the TD and LI+. The EMD for LI+ and TD was 0.86, while for LI+ and LI− it was 0.18 (d) ROC curve for the LOO classification with AUC of 0.81.

It is important to note that the positive classifier (> 0) score indicates the subject to be classified as a control while the negative score represents the classification as a patient. In figure 4(b) the y-axis indicates the probability density function (PDF) values of the classifier scores plotted against the scores where the peak for each curve represents the mean abnormality score. The controls and patient scores were very well separated with a highly significant p-value (< 0.001). The Earth Mover’s distance (Rubner, Tomasi et al. 1998) provides a measure of the overlap of two PDFs, zero when they overlap completely. The EMD of the ASD and TD PDFs shown in Fig. 4(b) is 0.71 suggesting good separation.

For further validation the ROC curves were plotted as shown in figure 4(d). For the LOO classification, the area under the curve (AUC) was 0.81. The classification was robust with a specificity of 84% and a sensitivity of 74%.

Besides computing the abnormality score, it is important to know which areas of the brain significantly contributed towards the classification. The selected features can be considered as discriminating features that contributed the most towards separating the two groups. Figure 5 displays a representative slice of the selected 18 ROI’s that were obtained after feature ranking and selection over the entire dataset, overlaid on the template image.

Figure 5.

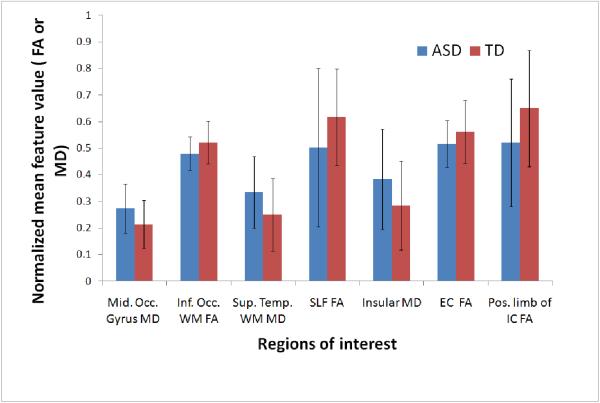
Output of feature selection and ranking: (a) Top ranked ROI’s mapped on template image. These ROI’s contributed largely towards classification based on s2n ranking (see table 2). The means and standard deviations of some of these ROI’s (shown by yellow arrows) are plotted in (b). The scatter plot for top features (Middle occipital gyrus MD vs Inferior occipital WM FA) is shown in (c) It can be noted that using only 2 top features cannot discriminate the populations. Plot (d) for other 2 ranked features (superior occipital gyrus (MD) and Insular right (MD) suggest the same. Therefore in (e) we have plotted the top 2 PCA components (after performing PCA on top 18 features) which show the discriminative power of all the 18 features together.

The regions that contributed most to the classification in terms of their FA measures were: right internal and external capsule, the left superior longitudinal fasciculus and inferior occipital white matter and in terms of their MD measure were: occipital gyrus, superior temporal white matter, insular cortex and areas around the left caudate (5). Figure 5 displays the areas of significance. Table 2 summarizes these top regions of interest that discriminate the two groups optimally.

Table 2.

Top ranked features from the feature selection

Rank	DTI measure	Region of Interest
1	MD	Middle Occipital Gyrus left
2	FA	Inferior Occipital white matter right
3	MD	Superior Temporal white matter right
4	FA	Fornix (Column and Body) left
5	FA	Superior Longitudinal Fasciculus left
6	MD	Superior Occipital Gyrus right
7	MD	Insular right
8	FA	Inferior Occipital Gyrus right
9	MD	Middle Temporal White matter right
10	FA	External Capsule right
11	MD	Retrolenticular part of Internal Capsule right
12	FA	Caudate Nucleus Left
13	MD	Inferior temporal White matter right
14	FA	Hippocampus left
15	FA	Posterior Corona Radiata left
16	MD	Caudate Nucleus Left
17	FA	Cuneus left
18	FA	Posterior Limb of Internal capsule right

The bar chart in figure 5(b) shows mean and standard deviation of the two groups for a few features (ranked frequently in the top 18). Figure 5(c and d) display scatter plots for a few features. In figure 5(c) the graph is plotted between 2 top ranked features (middle occipital gyrus(MD) and inferior occipital WM (FA)) while the plot in figure 5(d) is between two other top ranked features (superior occipital gyrus (MD) and insular (MD)). Figure 5(e) is the projection of all the 18 features into the principal component (PCA) space. The x-axis is the first PCA component while the y-axis is the second PCA component.

3.3. Relationship with clinical scores

The severity of ASD can be assessed with scores from measures such as the Social Responsiveness Scale (SRS) and the Social Communication Questionnaire (SCQ) values (Rutter 1994; Constantino and Todd 2005). The SRS score is a standard socio-psychological marker indicating social impairments and usually lies in the range of 70-120 for ASD population while it is lower (≈<70) for TD controls. SCQ is another behavioral marker that evaluates social functioning and communication skills based on a questionnaire and is known to be high in the ASD population (≈ 10-32) in comparison with the TD controls (≈ below 10).

A hypothesis testing was performed between the abnormality scores of the ASD and TD subjects and the result was compared against the results from a similar t-test carried out on these clinical assessment scores. Table 1 contains the summary of the statistical analyses showing the mean, standard deviation and the p-values. Figure 6(a) and (b) display the plots between the abnormality score of the correctly classified TD and ASD samples from LOO testing and the SRS and SCQ values respectively. In both the cases, the decrease in the abnormality score showed relatively higher SRS and SCQ scores in the ASD patients. The correlation coefficient r was −0.15 with SRS and −0.12 against SCQ in ASD’s. Although these correlations are weak, they are merely used to depict that the abnormality scores can be used in conjunction with a clinical score of choice for the population under study.

Figure 6.

Linear regression between abnormality score of TD’s and ASD’s from the LOO validation against (a) SRS score and (b) SCQ score. Mis-classified subjects were not considered in this regression analysis. For the correctly classified subjects, the correlation coefficient ‘r’ for was −0.152 and −0.12 for SRS and SCQ respectively for the ASD patients. While for TD subjects it was −0.177 and −0.205 for SRS and SCQ respectively. The linear fit indicates that the abnormality score reduces (towards −1) as the clinical scores increase in patients.

4. Discussion

This paper presents a method for creating diffusion-based classifiers for a clinical population that provides an abnormality score for each subject, based on the learned patterns of changes induced by pathology. In addition, the classifier elucidates regional changes that most contribute to this group difference, thereby, by inference, identifying regions that are most implicated in the pathology. The technique employs high-dimensional non-linear SVM pattern classifiers, using atlas based ROI’s extracted from the DTI data. The classification procedure consisted of computing diffusion based features like FA and MD features in each ROI, followed by feature selection, classifier training and testing. The method described is general and applicable to alternate diffusion and structural features, and to any clinical population.

We applied this new method to a population of ASD subjects and TD controls, to serve as an exploratory sample to demonstrate feasibility and applicability. The probabilistic abnormality score was computed for each test subject and was plotted against the PDF or the frequency of the score. An average LOO classification of 80% was achieved using the top features chosen by the signal to noise filter at each iteration. From 4(a and b), it can be observed that majority of the controls and patients were correctly classified and the peaks of the PDF curves (Fig. 4b) were well separated from each other based on the EMD value of 0.71 (0 being complete overlap). The mean abnormality score for patients was −0.46±0.39 while for controls it was 0.22±0.5 (where 1 is a perfect control and −1 is a perfect patient and the abnormality score is a continuous numeric value between −1 and 1). Fig. 4(c) shows PDFs fitted to the three groups (TD, LI+, LI−) separately, with the distance being 0.18 between LI+ and LI− , while it was 0.86 between LI+ and TD indicating a closeness between the populations with pathology. The classifiers were therefore able to learn the underlying variability in the population as a result of the pathology of autism. Based on the learned patterns of pathology, a test subject could be assigned a numeric value that yields a measure of the likelihood of pathology based on the population. This measure gives an insight into disease progression and symptom severity.

The ROC curve displayed in figure 4(d) provided another measure of classification performance. Based on this curve, the two crucial parameters of the classifier, the sigma and C values (described in section 2.3) were chosen such that the classifier displayed a superior sensitivity-specificity tradeoff. The large area under the ROC curve (0.81) also signifies good performance statistic for the classifier assuming no knowledge of the true ratio of the misclassification costs.

In ASD, there is pathological evidence of structural anomalies implicating white matter abnormalities (Casanova, Buxhoeveden et al. 2002; Maas, Mukherjee et al. 2004; Casanova, El-Baz et al. 2009). Furthermore, there is strong indication suggesting cognitive impairment and neurological deficits that can be related to changes in axon myelination and impairment in white matter connectivity(Verhoeven, De Cock et al. 2010). Previous investigations involving voxelwise or ROI based methods in ASD have reported widespread reductions in FA in the white matter of children with autism relative to typically developing controls (Barnea-Goraly, Kwon et al. 2004; Alexander, Lee et al. 2007; Keller, Kana et al. 2007; Mengotti, D’Agostini et al. 2011). Recently, DTI based classification using the QDA method (Lange, Dubray et al. 2010) demonstrated high classification accuracy based on diffusion tensor features selected a priori from only two brain regions. Although this approach clearly demonstrates the utility of DTI in distinguishing ASD from TD and introduces the value of multivariate pattern classifiers, reliance on a priori selected ROI’s precludes determination of ranked region-wise contributions (neural substrates of a disease) to classifier accuracy and also limits consideration of region-wise interactions. In our full brain ROI based method, the top features chosen by the signal to noise filter, are the most discriminating features that were selected after training the entire dataset and have maximum contribution towards group differences between TD and ASD subjects. The top 18 features were mapped on the template ROI in figure 5(a). Table 2 lists the areas of interest and the respective DTI feature (FA or MD in our case) that was involved. The chart in figure 5(b) shows the mean and standard deviations for the two groups for a few features. Even though the directions of these effects in the barcharts is consistent with the literature (elevated MD and reduced FA in ASD), it is clear that the magnitude of the group difference may be small compared with the intersubject variation for any single feature (or region). Thus the small effects and large error bars would likely preclude identification of these by using traditional VBM methods (as they are sub-threshold of significance). However, the classifier is able to combine multiple “weak” trends and build a composite function exploiting these multiple small effects to yield overall effective discrimination of pathology. Figures 5 (c, d) shows that the pairwise separability of the features underline the fact that just any two features are not sufficient to distinguish the population. This is further emphasized by Fig 5(e), where the 2 PCA components computed from the top ranked features, are able to differentiate the groups better. The 2 PCA components present a visualization of the 18 dimensional space of top-ranked features, showing that feature combinations increase discrimination.

The discriminating regions with MD features mainly included the occipital gyri, inferior temporal gyrus and inferior temporal white matter regions, which have been identified in studies mainly using structural MRI (Verhoeven, De Cock et al. 2010). The regions where FA measures could discriminate between the two classes included internal and external capsule that were previously shown by Keller et al. (Keller, Kana et al. 2007). FA measure was also identified in superior longitudinal fasciculus (SLF) which is known to be affected in language impaired population (Fletcher, Whitaker et al. 2010). Other areas of interest included temporal white matter, corona radiata, hippocampus and caudate nucleus. Even though these anatomic substrates do not appear to be directly associated with core behavior of the autism phenotype, it is a strength of this method as it can help new hypothesis by identifying indirect networks. As shown in Hazlett et al. (Hazlett, Poe et al. 2005) structural changes are widespread in autism, making our results consistent with literature.

Since there is no gold standard for evaluation of the abnormality score, we compared the classifier performance against the SRS and SCQ scores in ASD. As can be seen in table 1, last row, there was a significant difference between ASD and TD groups based on the abnormality score (as well as the clinical scores). As a result the abnormality score given by the classifier can be considered as a quantification of the pathology that may be used in addition to the clinical scores which only delineate socio-psychological behavior. Figure 6(a) and (b) display the abnormality scores of the correctly classified ASD subjects plotted against the SRS and SCQ scores. Although the linear fit is non-significant, the negative slope indicates the expected trend. Finally it was observed that only a few of the misclassified subjects followed the linear trend.

Classifying populations in a spectrum disorder like ASD is challenging since neuropathology is complex and highly heterogeneous across the patient population. Also the sample size, compared to the dimensionality of the features may not be large enough for training the classifier, thus limiting the validation to LOO method. Moreover, with such small sample size it is difficult to represent the entire disease spectrum, thus limiting the generality of conclusions regarding the pathology of ASD. Also, in future it is necessary to perform more validations on a larger sample size with more detailed clinical characterization before employing the abnormality score as a biomarker.

Nevertheless, the experimental results indicated that our technique can achieve high classification rate in ASD study (as a result of feature selection and a non-linear SVM construction). Based on the abnormality score of the test subject, our method can quantify the likelihood of pathology. The classifier does not need to be retrained for the same population after cross-validation and the method can delineate the regions that contribute maximally to the classification. Furthermore, the use of regional features offers multifold advantages: (a) The whole brain ROI’s can be implemented in the case when there is no prior knowledge about the disorder, and if there is an existing hypothesis, only certain ROI’s can be utilized. (b) The top ranked ROI’s can be further analyzed and compared with other cognitive scores. For example, in our case, the FA values from SLF can be correlated against the scores from language tasks (c) The use of structural ROI’s simplifies the clinical interpretation of pathology induced changes. This provides a unique insight into patho-physiology of disease.

The main purpose of this paper was to present the emerging methodology along with an application to a disease population that demonstrates its feasibility and applicability. The major contribution of this method lies in quantifying the abnormality of a single subject based on patho-physiological changes that occur in neurological and psychiatric disorders which other standard methods cannot. It can be applied to various studies involving disease progression, treatment effects, etc. It can also be implemented to test the phenotypic manifestations in non-focal psychiatric diseases like schizophrenia (Ingalhalikar, Kanterakis et al. 2010). Furthermore, the framework of our technique is versatile enough to use any atlas as well as hypothesis-based features that are suitable in that particular analysis. As the proposed framework is general, and will gain from the addition of alternate diffusion measures as well as volumetric measures from structural data. We propose to extend the diffusion features by using other diffusion scalars and gradient measures (Savadjiev, Kindlmann et al. 2010) as well as use the whole log-Euclidean form of the tensor as our feature. Moreover, we plan on creating multi-modal classifiers by incorporating volumetric information from the structural images together with DTI information.

In conclusion, we have provided a novel paradigm for creating region-based diffusion classifiers that can be created from any patient-control population by learning the patterns of disease. The classifiers assign an abnormality score to each subject that can be combined with clinical scores to aid in diagnosis, and the scores can be used to study group separation. The classifiers also produce a set of ranked regions that provide physiological insight into the patterns of pathology in the brain, and are a source of hypothesis generation for future studies.

Research Highlights.

• Diffusion based pattern classifier that creates a quantifiable marker of pathology

• Framework includes feature ranking and selection and cross-validation

• Supports diagnosis and gives a potential biomarker of neuropsychiatric disorders

• Produces ranking of atlas-based regions providing physiological insight

• Abnormality scores can be correlated with population specific clinical scores

• Applied to an example population of autism with a high classification accuracy