Abstract
Previously we showed that the cellular protein P58IPK contributes to viral protein synthesis by decreasing the activity of the anti-viral protein, PKR. Here, we constructed a mathematical model to examine the P58IPK pathway and investigated temporal behavior of this biological system. We find that influenza virus infection results in the rapid activation of P58IPK which delays and reduces maximal PKR and eIF2α phosphorylation, leading to increased viral protein levels. We confirmed that the model could accurately predict viral and host protein levels at extended time points by testing it against experimental data. Sensitivity analysis of relative reaction rates describing P58IPK activity and the downstream proteins through which it functions helped identify processes that may be the most beneficial targets to thwart virus replication. Together, our study demonstrates how computational modeling can guide experimental design to further understand a specific metabolic signaling pathway during viral infection in a mammalian system.
Keywords: P58IPK and Dnajc3, mathematical model, sensitivity analysis, influenza virus, vaccinia virus
INTRODUCTION
Every year influenza virus infects millions of people worldwide. While the vast majority of infections do not result in death, highly virulent influenza strains can evolve into global pandemics that dramatically increase incidence of mortality. Recent emergence of influenza viruses resistant to ribavirin and oseltamvir (Regoes and Bonhoeffer, 2006) further demonstrates the need for better therapeutics against influenza virus infection. Mathematical models of influenza virus infection can illustrate how cellular factors affect virulence, which in turn can identify new therapeutic targets to modulate the impact of the virus.
During infection, influenza virus abrogates cellular mRNA translation and facilitates viral mRNA translation (Garfinkel and Katze, 1992). The host cell utilizes multiple mechanisms to prevent translation of viral transcripts, such as the interferon-induced activation of PKR. PKR is a dsRNA-activated protein kinase that phosphorylates the alpha subunit of eukaryotic translation initiation factor 2 (eIF2α), thereby inhibiting protein synthesis (Dever, 2002). To evade this inhibition response, influenza virus has the capacity to limit PKR activation by activating the host cell protein P58IPK, a cellular inhibitor of PKR (Lee et al., 1992). P58IPK’s ability to regulate and prevent the phoshorylation of eIF2α activity signifies that P58IPK is a critical component of cellular and viral mRNA translation.
Recently we demonstrated that influenza virus mRNA translation becomes less efficient in the absence of P58IPK, using mutant mouse embryonic fibroblasts (MEFs) lacking P58IPK (Goodman et al., 2007). These measurements suggested that increased PKR activation and eIF2α phosphorylation decreased the mRNA translation efficiency. Here we create a mathematical model to probe potential interactions among these proteins, extending our previous experimental work and enhancing our understanding of dynamic behavior among proteins in this viral replication pathway. We used previous experimental data to construct our model, both in structure and in specific parameter values. We performed additional experiments to confirm the structure of the model and test its predictions. Furthermore, we were able to use the model to simulate conditions not readily tested in the laboratory, such as inhibition of the PKR-specific effects due to P58IPK. Because P58IPK also becomes activated during ER stress (Liu and Kaufman, 2003), this mathematical model provides a useful structure for incorporating other P58IPK-activating stimuli, merging the dynamic responses of viral infection with the unfolded protein response or other pathways through which P58IPK functions. Similarly, the model also provides a platform for testing other PKR inhibitors to study how PKR kinetics respond to a variety of infection systems, making this model a relevant tool for cell biologists and virologists alike.
RESULTS
Model development
This study focuses on the role of P58IPK during virus infection, exploring the mechanisms through which P58IPK regulates eIF2α phosphorylation. The initial model structure was based on a simplified conceptual model presented by Goodman, et al. that included two eIF2α kinases, PKR and PERK (Goodman et al., 2007). Subsequently we removed the PERK kinase, as it is not activated by influenza virus infection (Goodman et al., 2007)(Goodman and Katze, unpublished data), nor does our model include an ER stress stimulus to activate the PERK kinase. We arrived at the current model structure (Fig. 1), described by five ordinary differential equations (ODEs), where t is time:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
Figure 1. Schematic of model.
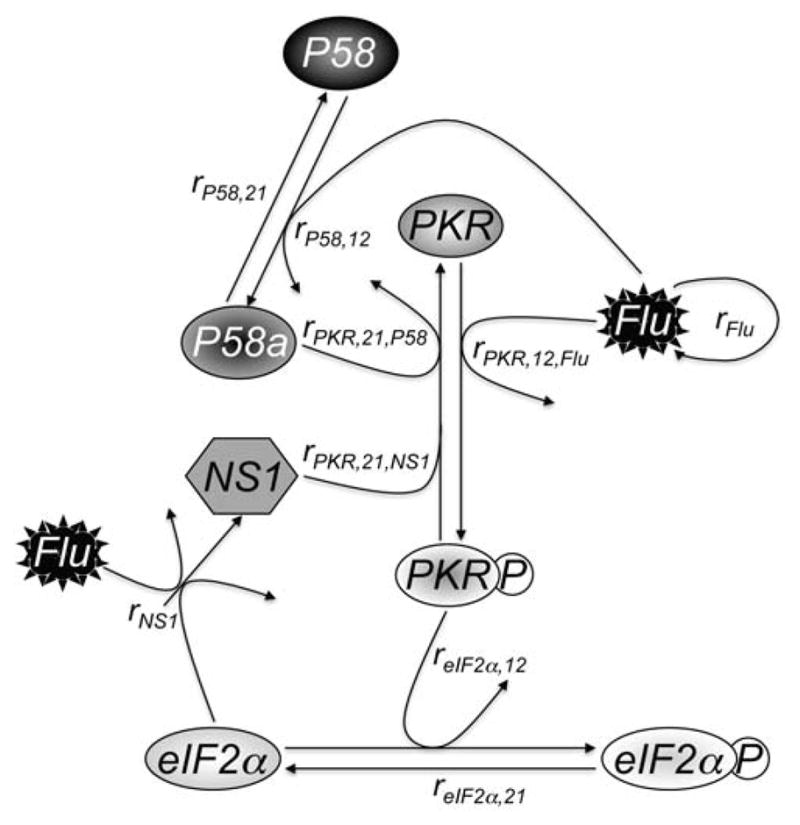
Flu, which grows logistically as described in Eq. 4, infects a cell and activates PKR at a rate of rPKR,12,Flu and activates P58 at a rate of rP58,12. Active P58 (P58a) inhibits active PKR (PKRP) at a rate of rPKR,21,P58, while NS1, which is synthesized in the presence of Flu and unphosphorylated eIF2α at a rate of rNS1, inhibits PKRP at a rate of rPKR,21,NS1. P58a is deactivated at an intrinsic rate of rP58,21. PKRP phosphorylates eIF2α at a rate of reIF2α,12, while dephosphorylation of eIF2αP occurs at a rate of reIF2α,21. Equations and more detail are given in the text.
In the model P58a represents activated P58IPK protein; PKRP phosphorylated, activated PKR protein; eIF2αP phosphorylated, inactive eIF2α protein; Flu the overall level of infection within the host cell; and NS1 influenza NS1 protein. In the model we have represented key enzymatic reactions and cellular processes of the P58IPK pathway relevant to influenza infection. First influenza virus activates P58IPK (Eq. 1) (Lee et al., 1992). Secondly influenza virus also activates PKR(Eq. 2), leading to PKR phosphorylation (Dey et al., 2005), while active P58IPK (P58a) and NS1 increase PKR deactivation (Lu et al., 1995). Phosphorylated PKR is not deactivated by the enzymatic reaction phosphorylating eIF2α (Eq. 3) (Dey et al., 2005). The level of influenza virus increases logistically, with carrying capacity, K (Eq. 4). NS1 is synthesized in the presence of eIF2α and influenza virus, but is consumed in the PKR deactivation reaction, as NS1 binds dsRNA, which is synthesized as an intermediate of viral genome replication and is the substrate which normally activates PKR (Dey et al., 2005). We assume no natural degradation of proteins over the timecourse of the model. The model presented here assumes that the total concentration of any host protein is constant, with the sum of the active and inactive states equaling the total (e.g., P58_total = P58a(t) + P58(t)). We then derived parameter values (Table 1) for the model as described in the Methods section. Briefly parameter values were derived either from known values in the experimental literature or from optimizing the fit of the model to a set of previously observed early time-point time courses (Goodman et al., 2007). These viral infections were performed in two cell lines, wild-type (P58IPK+/+) and P58IPK−/− mouse embryonic fibroblasts (MEFs), with observations made at 6–9 h post-infection. We used these experimental data as a training set, reserving other, newly obtained experimental data as a test set (described below). After fitting the model to the training set, model output agreed well with experimental data points for phosphorylated PKR, phosphorylated eIF2α, and NS1. Overall correlation coefficients (Pearson) between output and experimental data were 0.95 and 0.91 for experiments performed in the presence (P58IPK+/+) and absence (P58IPK−/−) of P58IPK, respectively (Fig. 2). As a negative control, we simulated the absence of influenza infection (Flu(0)=0), and the model displayed the expected behavior, with no activation of any of the cellular proteins and no change in influenza virus levels (data not shown).
TABLE 1.
Model Parameters and Initial Conditions
| Symbol | Meaning | Value (reference) |
|---|---|---|
| rPKR,12,Flu | Rate of influenza virus-mediated PKR phosphorylation | 0.1263 PFU−1·h−1 |
| rPKR,21,P58 | Rate of P58IPK-mediated PKR inhibition | 0.3 nM−1·h−1 (Lee et al., 1994b) |
| rPKR,21,NS1 | Rate of NS1-mediated PKR inhibition | 0.025 nM−1·h−1 (Lu et al., 1995) |
| rP58,12 | Rate of influenza virus-mediated P58IPK activation | 0.0879 PFU−1·h−1 |
| rP58,21 | Rate of P58IPK deactivation | 0.052 h−1 |
| reIF2α,12 | Rate of PKR-mediated eIF2α phosphorylation | 0.0793 nM−1·h−1 |
| reIF2α,21 | Rate of eIF2α dephosphorylation | 0.0243 h−1 |
| rFlu | Rate of influenza virus growth | 0.075 h−1 (Borland and Mahy, 1968) |
| rNS1 | Rate of NS1 growth | 0.05 PFU−1·h−1 (Lamb et al., 2001) |
| K | Cell’s carrying capacity of influenza virions | 100 PFU (Goodman et al., 2010) |
| PKR_total | Initial concentration of all PKR species | 2 nM |
| PKRP(0) | Initial concentration of phosphorylated PKR | 0 nM |
| P58_total | Initial concentration of all P58IPK species (wild-type) | 10 nM |
| P58a(0) | Initial concentration of active P58IPK (wild-type) | 0 nM |
| eIF2α_total | Initial concentration of all eIF2α species | 2 nM |
| eIF2αP(0) | Initial concentration of phosphorylated eIF2α | 0 nM |
| Flu(0) | Initial dose of influenza virus | 5 PFU |
| NS1(0) | Initial concentration of influenza NS1 protein | 0 nM |
Highlighted parameters were determined by the Nelder-Mead optimization algorithm described in the Methods section.
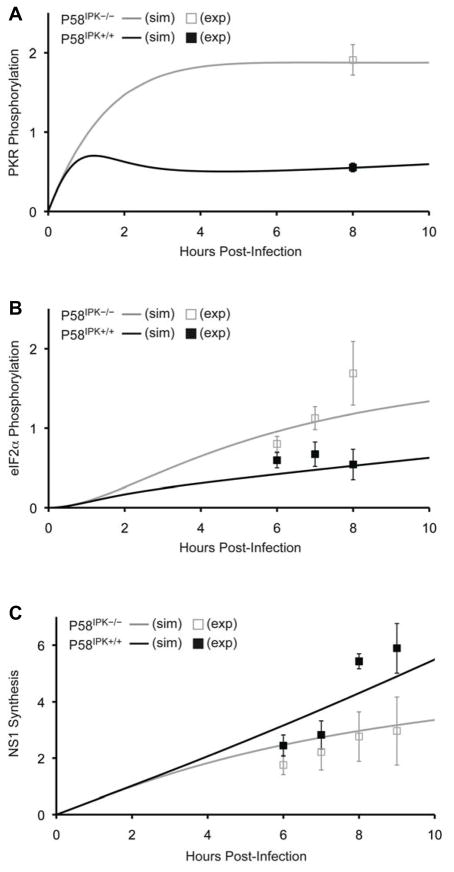
Figure 2. Dynamics of PKR and eIF2α phosphorylation in the presence and absence of P58IPK during influenza virus infection.
Model results simulate (sim) the predicted timecourses for PKR phosphorylation (A), eIF2α phosphorylation (B), and NS1 synthesis (C) over the first 10 h post-infection, in the presence (black lines) or absence of P58IPK (grey lines). The data are normalized and represented as arbitrary units. Experimental (exp) data (replotted from Figs. 2 and 3 (Goodman et al., 2007), Copyright © American Society for Microbiology, Journal of Virology, Vol. 81, p. 2221–2230, 2007) are shown at discrete timepoints with black or grey boxes.
Simulations predict faster activation of PKR and eIF2α phosphorylation with decreased NS1 synthesis in the absence of P58IPK
Model predictions for PKR and eIF2α phosphorylation follow measured biological trends in the absence and presence of P58IPK at 6–9 h post-infection (Fig. 2). The model output also provides an indication of what happens within influenza virus-infected cells at shorter time scales, up to 10 h post-infection. In the model, PKR becomes increasingly phosphorylated in the absence of P58IPK up to 4 h post-infection (Fig. 2A), at which point it reaches stable, maximal activation. In contrast, in the presence of P58IPK, PKR phosphorylation increases until 1 h p.i, then decays briefly due to increased P58IPK activation and slowly increases thereafter. EIF2α phosphorylation (Fig. 2B) lags PKR phosphorylation, with eIF2α phosphorylation developing more slowly in the presence of P58IPK. EIF2α phosphorylation inhibits initiation of translation (Dever, 2002), leading to an inverse correlation between levels of eIF2α phosphorylation and viral protein synthesis. Simulation results confirm this correlation, following measured biological trends for NS1 synthesis in the presence and absence of P58IPK (Fig. 2C).
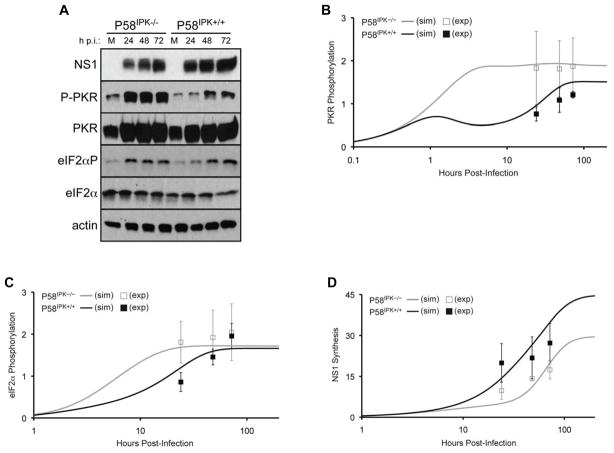
Preliminary model predictions showed intriguing behavior at longer time points, prompting us to perform influenza virus infections in P58IPK−/− and P58IPK+/+ MEFs to examine longer timepoints post-infection. With these data, we could generate a test set of biological data for comparison with predicted behavior from the simulations. As a result, we infected P58IPK−/− and P58IPK+/+ MEFs with influenza virus for 24, 48, and 72 h and subsequently determined levels of NS1, PKR phosphorylation, and eIF2α phosphorylation (Fig. 3A). Quantification of the results from three independent experiments constituted our test set of data. Correlation coefficients among the test set of biological data and simulation results were 0.96 and 0.95 in the presence and absence of P58IPK, respectively (Fig. 3B–D).
Figure 3. Dynamics of PKR and eFI2α phosphorylation and NS1 synthesis for long-sustained times post-infection.
P58IPK−/− and P58IPK+/+ MEFs were mock-infected (M) or infected with the WSN strain of influenza virus at 1 PFU/cell for 24, 48, or 72 h. The levels of influenza virus NS1, phosphorylated PKR and eIF2α, total PKR and eIF2α, and actin were determined by immunoblot analysis (A). Densitometry analysis (mean pixel value multiplied by total pixels) of three independent experiments was performed to determine the relative levels of NS1, phosphorylated PKR, and phosphorylated eIF2α. A ratio of the phosphorylated protein band and total protein band was normalized to that of the genotype-matched mock-infected sample. NS1 was normalized to actin. 200 h simulation (sim) results are shown for PKR phosphorylation (B), eIF2α phosphorylation (C), and influenza virus NS1 synthesis (D), in the presence (black line) or absence of P58IPK (grey line). The data are normalized and represented as arbitrary units. Densitometry data derived from the experimental (exp) results is shown at discrete timepoints with black or grey boxes with standard deviations.
After testing the model on the experimental data at 24–72 h post-infection, we then used the model to make predictions of and gain insight into the longer-term behavior of the biological system. We calculated the steady-state solution of the model analytically, and upon substituting the optimized parameter set, we derived the steady-state values and time to reach steady-state (Table 2). Other solutions in which parameter values reached zero were disregarded, as this was not observed experimentally. Longer-term simulations showed that PKR phosphorylation occurs more slowly in the presence of P58IPK, reaching steady-state at 56 h (Fig. 3B). In addition, steady-state PKR phosphorylation is ~25% less in the presence of P58IPK than in its absence. In the presence of P58IPK, PKR phosphorylation reaches steady-state 10 h before eIF2α phosphorylation (Fig. 3C). In the absence of P58IPK, however, the kinetics of eIF2α phosphorylation lag PKR phosphorylation. Steady-state values for eIF2α phosphorylation show a minimal difference between the two genotypes, suggesting that other eIF2α kinases, such as PERK, GCN2, and HRI, may be phosphorylating eIF2α while P58IPK is inhibiting PKR-mediated eIF2α phosphorylation. We observed that NS1 synthesis reaches steady-state faster in the absence of P58IPK. However, for both conditions, the time at which NS1 synthesis reaches steady-state lags the times at which PKR and eIF2α phosphorylation reach steady-state. By steady-state, the level of NS1 synthesis is 150% greater in the presence of P58IPK than in its absence, suggesting that P58IPK may function to promote long term viral replication in influenza virus-infected cells. Together, these extended timecourse simulations provide new data about the equilibrium states of the proteins described in the model and the window of time when the proteins become rapidly activated, a period that may be beneficial to target the proteins for potential therapeutic intervention.
TABLE 2.
Steady-State Protein Levels
| Parameter | P58IPK−/− | P58IPK+/+ | ||
|---|---|---|---|---|
| Value | Time (h) | Value | Time (h) | |
| P58a | 0 | n.a. | 9.94 | 34 |
| PKRP | 1.89 | 5 | 1.51 | 56 |
| eIF2αP | 1.72 | 20 | 1.66 | 66 |
| NS1 | 29.5 | 190 | 44.7 | 240 |
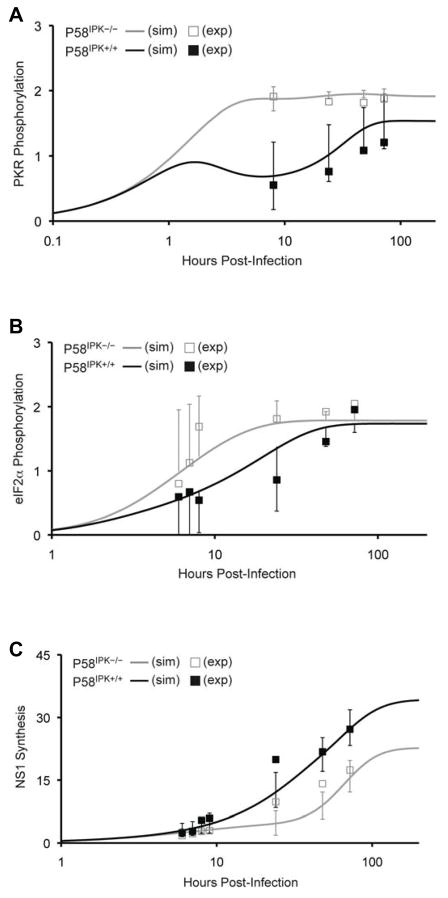
Even though there was strong correlation between our optimized parameter set and the test set of biological data, we next investigated the uniqueness of the optimized parameter set by comparing it to a parameter set generated by rigorously fitting the simulated data to all of the biological data. With a larger set of biological data, we could also generate more robust statistics associated with the fitted parameter set. These parameters are shown in Table 3, along with their covariances and confidence intervals. The correlation coefficients between all biological data and simulated data remain high (0.95 for P58IPK−/− and 0.97 for P58IPK+/+). The major difference in this parameter set as compared to the previously optimized set is with regard to P58IPK activation. With this parameter set, we observed a greater rate of P58IPK deactivation, although its covariance and confidence intervals are high. However, both parameter sets generate simulation curves that follow the same trends. Together, these results suggest that both sets of parameter estimates were non-unique and can be used for further analysis of the model. Since the second parameter set was generated by fitting the simulated data with all of the biological results, and the parameter intervals for the simulated data overlap with most biological results (Fig. 4), subsequent analysis of P58IPK activation and model sensitivity were performed using the optimized parameters in Table 3.
TABLE 3.
Parameters Fitted with All Biological Data
| Symbol | Value | Covariance (σ2) | 95% Confidence Interval [low; high] |
|---|---|---|---|
| rPKR,12,Flu | 0.1245 PFU−1·h−1 | 0.0093 | [−0.0731; 0.3221] |
| rP58,12 | 0.0417 PFU−1·h−1 | 0.0056 | [−0.1113; 0.1948] |
| rP58,21 | 0.1597 h−1 | 1.16 | [−2.0464; 2.3658] |
| reIF2α,12 | 0.0790 nM−1·h−1 | 0.0021 | [−0.0152; 0.1732] |
| reIF2α,21 | 0.0184 h−1 | 0.0001 | [0.0019; 0.0348] |
Parameters were determined by the Levenberg-Marquardt optimization algorithm described in the Methods section.
Figure 4. Prediction intervals for simulated PKR and eFI2α phosphorylation and NS1 synthesis show overlap with biological data.
200 h simulation (sim) results are shown for PKR phosphorylation (A), eIF2α phosphorylation (B), and influenza virus NS1 synthesis (C), in the presence (black line) or absence of P58IPK (grey line), using the parameter set generated from fitting simulated data with all biological data. At the timepoints where experimental data exists, prediction intervals for the simulated data are shown. Experimental (exp) data are represented with black or grey boxes. Only single direction prediction intervals are shown in panel B.
Using the parameter set derived using all of the biological data, we next examined the kinetics of P58IPK activation. In contrast with the PKR and eIF2α phosphorylation responses and NS1 synthesis, there are no published data on P58IPK activation rates during viral infection. This rate is difficult to measure in the laboratory because P58IPK becomes activated during influenza virus infection following dissociation from its two inhibitors, P52rIPK and Hsp40 (Gale et al., 1998; Melville et al., 1997). However, model predictions show that P58IPK activation is well approximated by an exponential growth equation (R2 = 0.99) until 200 h post-infection:
| (6) |
revealing an apparent activation rate of 0.168 h−1. This prediction suggests the apparent rate of P58IPK activation is directly related to the infectious dose of the virus because the rate for P58IPK activation is roughly equal to the product of rP58,12 (rate of influenza virus-mediated P58IPK activation) and Flu(0) (initial dose of influenza virus). Further evidence for this relation between P58IPK activation and infectious dose is provided in Figure 5, showing that P58IPK is activated earlier post-infection when the infectious dose is greater. Additionally, the rate for PKR activation is roughly three times greater than the P58IPK activation rate. This suggests that activation of PKR is followed by activation of the cellular inhibitor of the host defense, P58IPK, allowing the cellular environment to be better suited for viral replication.
Figure 5. P58IPK reaches maximal, steady-state activation levels faster with increasing infectious dose.
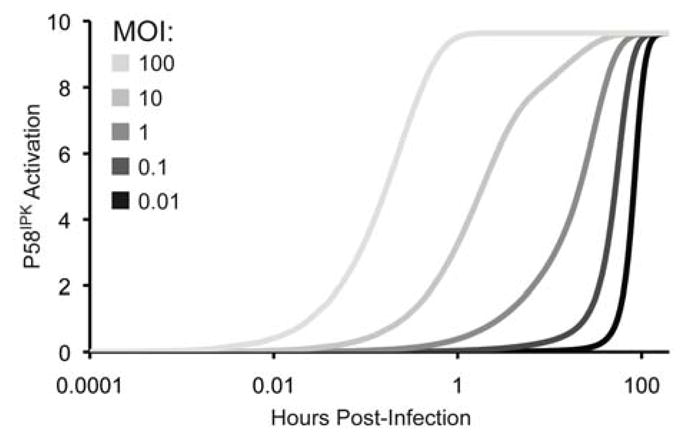
200 h simulation results are shown for P58IPK activation upon infection with 0.01, 0.1, 1, 10, or 100 PFU of virus. P58IPK activation reaches steady-state at 180, 150, 120, 80, or 2 h, respectively.
Sensitivity of viral protein synthesis to changes in model parameters
The inverse correlation between levels of PKR activation or eIF2α phosphorylation and viral protein synthesis or replication is well accepted (Goodman et al., 2007; Smith et al., 2006) and further supported by our model, but the extent to which these processes affect viral growth kinetics in the presence and absence of P58IPK remains unclear. To further understand the relationship between these cellular processes and viral growth kinetics, we performed a sensitivity analysis to determine the correlation between the cellular processes represented in our model and NS1 protein synthesis (Table 4). This analysis showed that the parameters rFlu and K were more strongly correlated with NS1 synthesis in the absence of P58IPK at 120 h, suggesting viral replication may be more sensitive to influenza virus levels within the cell when P58IPK is absent. The rate of P58IPK-mediated PKR inhibition (rPKR,21,P58) was also positively correlated with NS1 synthesis, but only at late times post-infection. Since PKR activation does not reach steady-state until ~80 h post-infection, modifying the rate of P58IPK-mediated PKR inhibition will alter the time at which PKR reaches steady-state, thus affecting levels of NS1 synthesis.
TABLE 4.
Model Parameters Significantly Correlated with NS1 Synthesis
| Parameter | Correlation Coefficient
|
|||
|---|---|---|---|---|
| 10 h post-infection | 120 h post-infection | |||
| P58IPK−/− | P58IPK+/+ | P58IPK−/− | P58IPK+/+ | |
| rPKR,12,Flu | n.s. | n.s. | n.s. | −0.52 |
| rPKR,21,P58 | n.s. | n.s. | n.s. | 0.37 |
| rPKR,21,NS1 | n.s. | n.s. | −0.59 | −0.55 |
| reIF2α,12 | −0.59 | n.s. | −0.69 | −0.69 |
| reIF2α,21 | n.s. | n.s. | 0.66 | 0.62 |
| rFlu | 0.41 | 0.44 | 0.47 | n.s. |
| rNS1 | 0.88 | 0.88 | 0.73 | 0.75 |
| K | n.s. | n.s. | 0.62 | 0.44 |
| PKR_total | −0.72 | n.s. | −0.87 | −0.87 |
| eIF2α_total | 0.88 | 0.88 | 0.73 | 0.76 |
| Flu(0) | 0.83 | 0.85 | n.s. | n.s. |
Two thousand simulation runs were performed using different sampled parameter values ranging from 25–175%. PRCC values determined to be significant (P < 10−70) are shown. n.s., not significant. Highlighted data is discussed further in the text.
Other parameters were negatively correlated with NS1 synthesis, namely reIF2α,12, PKR_total, and rPKR,12,Flu, which correspond to processes that promote eIF2α phosphorylation. At early times post-infection, the absence of P58IPK results in a negative correlation for reIF2α,12 and PKR_total because PKR has reached a level of steady-state activation. Therefore, variations in total PKR or the rate of PKR-mediated eIF2α phosphorylation will impact NS1 synthesis to a greater extent in the absence of P58IPK. However, at late times post-infection the influenza virus-mediated PKR activation rate, rPKR,12,Flu, had a negative correlation with NS1 synthesis in the presence of P58IPK. Nevertheless, these two correlations, one at early times post-infection in the absence of P58IPK and the other at late times in the presence of P58IPK, are consistent in showing that levels of PKR and eIF2α phosphorylation are negatively correlated to viral protein synthesis
Enhanced PKR expression in cells lacking P58IPK inhibits viral replication
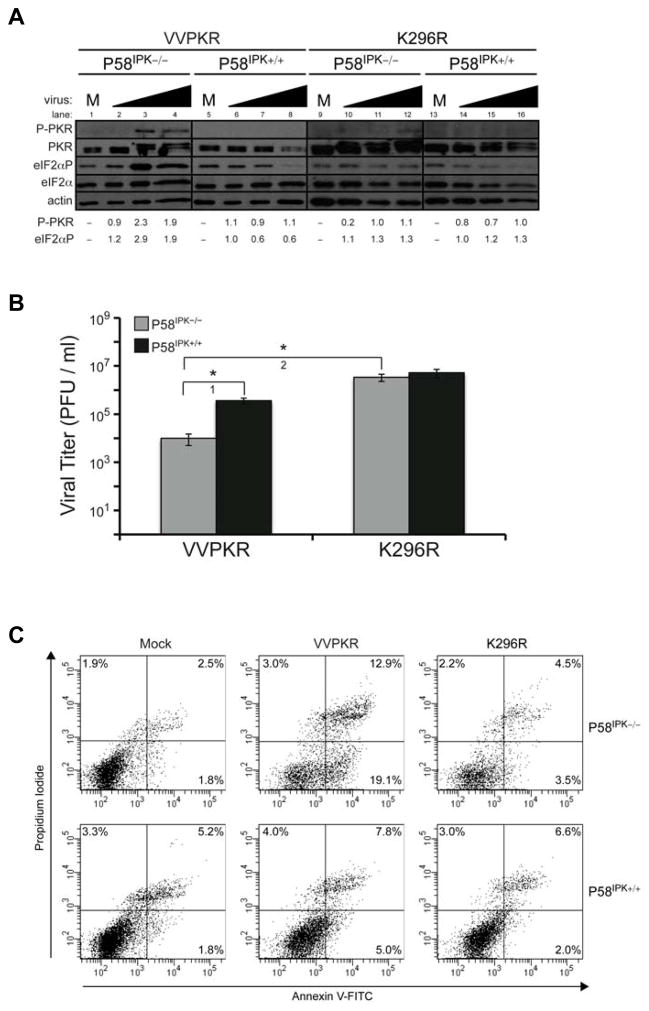
One of the major conclusions from our sensitivity analysis was that NS1 synthesis is particularly sensitive to parameters of the model pertaining to PKR activation and its downstream effects: reIF2α,12, PKR_total, and rPKR,12,Flu. To test the validity of our hypotheses, and also to determine the wider applicability of our model, we took advantage of a recombinant vaccinia virus system that expresses wild-type PKR (VVPKR), or a catalytically inactive PKR mutant (K296R) (Lee and Esteban, 1993). This K296R PKR mutant also acts as a dominant negative for eIF2α phosphorylation (Gil et al., 2001), serving as a negative control for the effects of wild-type PKR over-expression. While these experiments do not utilize influenza virus, per se, vaccinia virus represents another tool for perturbing the P58IPK pathway and studying the downstream effects of P58IPK activation. Influenza and vaccinia virus are remarkably different viruses, but they also share their similarities with respect to the host response. Similar to influenza virus, vaccinia virus activates PKR via dsRNA intermediates that are part of its viral replication cycle, and like influenza virus NS1, vaccinia virus E3L binds dsRNA, resulting in PKR inhibition. Additionally, vaccinia virus K3L inhibits PKR-mediated eIF2α phosphorylation (Davies et al., 1993; Lee et al., 1994a). Therefore, this experimental design represents a self-contained viral infection system to test the effects of PKR over-expression on virus replication in the presence and absence of P58IPK, using the same experimental conditions as previous experiments used to derive the mathematical model.
In this vaccinia virus system we tested the prediction of the model that certain cellular processes were inversely related to viral replication, particularly in the presence or absence of P58IPK. The activation state of PKR and eIF2α was determined in P58IPK−/− and P58IPK+/+ MEFs infected with the VVPKR or K296R strains of vaccinia virus, showing greatest PKR and eIF2α phosphorylation during VVPKR infection in P58IPK−/− MEFs (Fig. 6A, lanes 3 and 4 compared to 1). PKR and eIF2α phosphorylation in P58IPK+/+ MEFs or during K296R infection were similar to that of mock infection (Fig. 6A, lanes 6–8 compared to 5, 10–12 compared to 9, or 14–16 compared to 13). Increased PKR and eIF2α phosphorylation during VVPKR infection in P58IPK−/− MEFs was correlated to decreased viral replication, as compared to infection in P58IPK+/+ MEFs (Fig. 6B, t-test 1). Infection with K296R, which expresses non-phosphorylateable PKR, in P58IPK−/− MEFs resulted in increased viral replication, as compared to VVPKR infection (Fig. 6B, t-test 2). It should be noted that we also performed infections with a wild-type strain of vaccinia virus (WR); however, we observed no differences in PKR activation, eIF2α phosphorylation, or viral replication between P58IPK−/− and P58IPK+/+ MEFs (data not shown). While WR infection resulted in slightly increased levels of viral replication and decreased PKR and eIF2α phosphorylation, no differences were observed in P58IPK−/− and P58IPK+/+ MEFs, like K296R infection. Therefore, K296R infection was pursued as a control, since it over-expresses total PKR, as does VVPKR. Together, these results corroborate the sensitivities predicted by the model, showing that viral replication becomes more sensitive to increased levels of activated PKR in the absence of P58IPK.
Figure 6. Over-expression of wild-type PKR during infection in cells lacking P58IPK results in increased eIF2α phosphorylation and apoptosis and decreased viral replication.
P58IPK−/− and P58IPK+/+ MEFs were mock-infected (M) or infected with recombinant strains of vaccinia virus which express wild-type PKR (VVPKR) or a catalytically inactive mutant (K296R) at increasing MOIs of 0.1, 1, and 10 PFU/cell for 8 h. (A) The levels of phosphorylated PKR and eIF2α, total PKR and eIF2α, and actin were determined by immunoblot analysis. Data for densitometry analysis showing the relative levels of phosphorylated PKR and phosphorylated eIF2α are provided, which is represented numerically. (B) Infectious virus present in cells infected with 1 PFU/cell was measured in triplicate. Standard deviations and P-values from a two-tailed Student’s t-test assuming non-equal variance are indicated (*, P < 0.05). (C) Cells infected with 1 PFU/cell were stained with annexin V-FITC and propidium iodide and analyzed by flow cytometry. Percentages represent the fraction of the total cell population that is positive for annexin V and/or propidium iodide.
Prior studies show over-expression of wild-type PKR during vaccinia virus infection results in increased apoptosis as compared to expression of PKR containing the K296R mutation (Lee and Esteban, 1994). Furthermore, P58IPK is anti-apoptotic, due to its inhibitory effects on PKR (Tang et al., 1999). To establish whether levels of apoptosis are enhanced in the presence of PKR and absence of P58IPK, we performed flow cytometry on cells infected with VVPKR and K296R (Fig. 6C). We observed the greatest number of cells positive for apoptosis in the presence of wild-type PKR over-expression in P58IPK−/− MEFs (19.1%, as compared to 5.0% in P58IPK+/+ MEFs). Infection with K296R resulted in increased apoptosis as compared to mock infection and the greatest levels of apoptosis resulted in the least amount of viral replication. These results support the inverse correlation between PKR over-expression and viral replication in the absence of P58IPK, as predicted by the sensitivity analysis of the mathematical model, showing how the analysis of a model can lead to novel experimental designs and results.
DISCUSSION
This study integrated computational and experimental analyses to predict and elucidate kinetic interactions within the P58IPK pathway, which we had previously investigated only experimentally (Goodman et al., 2007). After establishing kinetic parameters that predicted measured biological behavior in the presence and absence of P58IPK, we used this model to probe kinetic interactions within the P58IPK pathway and identify protein interactions that confer viral replication. Strengths of this model are multi-faceted: it predicts that P58IPK is rapidly activated in response to influenza virus infection but dependent on infectious dose, it simulates long-term viral infection kinetics, and it correlates varied model parameters with viral protein synthesis. Model analyses, in combination with corroborative experimental results, identify favorable targets within the P58IPK pathway for counteracting virus infection.
Although empirical data from previous influenza virus infection experiments was useful for guiding model formulations and parameter optimization, the generation of a test set of biological data was necessary to examine the validity of the model. However, a scarcity of published data from other viral infection models interrogating the P58IPK pathway remains, highlighting a need for more viral infection experiments perturbing the P58IPK pathway. To validate the conclusions drawn from the model analyses and to instill more confidence in the model structure, we performed experiments with vaccinia virus, which, like influenza virus, is particularly sensitive to translational control, eIF2α phosphorylation, and innate immune responses (Garcia, Meurs, and Esteban, 2007). Greater similarity between influenza and vaccinia viruses exists in the host-range genes they encode to inhibit the anti-viral response. Influenza virus NS1 is necessary for replication in wild-type mice, but is dispensable for replication in mice lacking PKR (Bergmann et al., 2000). Similarly, vaccinia virus lacking E3L only produced lethal disease in mice lacking PKR and replicated to higher titers than in wild-type mice (Rice et al.), providing further evidence that E3L is a critical host range protein necessary for efficient viral replication (Beattie et al., 1996; Langland and Jacobs, 2002). Taken together, mutant influenza and vaccinia viruses are useful tools to study the PKR anti-viral pathway.
As the absence of P58IPK had no effect on the replication of vaccinia virus lacking E3L (data not shown), the experimental design we pursued in this study made use of a recombinant vaccinia virus expressing PKR, and we described that the absence of P58IPK had a profound effect on the replication of this virus due to increased levels of PKR and eIF2α phosphorylation. Model predictions showed that at early times post-infection, viral protein synthesis was particularly sensitive to levels of PKR and the rate of PKR activation when P58IPK was absent. Taking advantage of the experimental design derived from the analysis of the model, we also showed that levels of apoptosis were enhanced during infection when PKR was over-expressed in the absence of P58IPK. Future studies could take advantage of other recombinant vaccinia viruses expressing mutant eIF2α (Gomez et al., 2005) to explore the model’s sensitivities to the rate of eIF2α phosphorylation and its role in viral protein synthesis and virulence with respect to P58IPK. Additionally, the role of NS1-mediated PKR inhibition in the context of P58IPK could be further studied and modeled using influenza viruses containing mutations in NS1 that reduces the protein’s ability to bind dsRNA and inhibit PKR (Hatada, Saito, and Fukuda, 1999; Min et al., 2007).
This modeling effort facilitated identifying potential targets for intervening against viral replication by probing the correlation between NS1 synthesis and rate values or protein concentrations in the P58IPK pathway during infection. Current influenza virus therapeutics consist of anti-viral drugs that inhibit the virus’ ion channel and neuraminidase. Interferon treatment has also been proposed as an adjuvant for these drugs (Bracci et al., 2005). If a drug could be discovered that acted specifically on a cellular protein involved in the response against infection, treatment of the infection could be improved. For example, Budd, et al. have demonstrated that modulating the host cytokine response with an anti-inflammatory agent affects the outcome to influenza virus infection (Budd et al., 2007). Our analysis suggested that at early times post-infection, heightened levels of total PKR would decrease levels of NS1 synthesis, especially when P58IPK is absent and not inhibiting PKR activation. The down-regulation of P58IPK would allow for a quicker and more robust PKR-mediated response at the onset of infection to curb viral replication. To further test this hypothesis, one could transiently downregulate P58IPK via siRNA and induce PKR expression prior to virus infection. This could also be tested in animals with the use of intranasal siRNAs (Sioud and Barik, 2009). Late in infection, our analysis predicted that to reduce viral replication, it would be most prudent to heighten PKR sensitivity, particularly when P58IPK is fully activated to regulate PKR hyperactivation, for this too is detrimental to the host (Goodman et al., 2009). Experimentally, one could boost PKR activation with dsRNA as the infection continues. These methods could be used in conjunction with established anti-viral compounds to decrease the overall burden of the virus.
Understanding how cellular proteins affect viral infection is important for gaining better insight about therapeutic targets. Using mathematical modeling to test the mental picture of these cellular pathways allows one to develop and perturb the network dynamics describing a signaling pathway in silico, complementing the interpretation of biological experiments. In this study, we were able to develop a straightforward mathematical model to study how the P58IPK pathway is associated with virus infection. This model offers significant insight about the kinetics of protein interactions downstream of P58IPK, even in its absence, providing an opportunity to simulate a specific metabolic signaling pathway during viral infection in a mammalian cell culture system. Future computational studies could expand the model’s scope to include other molecules that play a role in the P58IPK pathway during viral infection. Of particular significance would be MK2 and MK3, two MAPKAPKs which form a multimeric protein complex with P58IPK to inhibit PKR (Luig et al., 2010) or proteins of the unfolded protein response which are up-regulated during coxsackievirus infection due to P58IPK inhibition (Zhang et al., 2010). Together, our work shows that the merging of qualitative laboratory data with quantitative modeling data can allow the researcher to uncover coordinated behavior between molecules or identify structures of burgeoning molecular networks. From this, new experiments can be designed to discover novel mechanisms for the designing and evaluation of therapeutics for potential future viral pandemics.
METHODS
Parameter derivation and simulation procedures
Transition rates and relative, initial concentration values were based upon our experimental measurements, all gathered under identical experimental conditions (Goodman et al., 2007), published literature values, and optimization techniques (Table 1). Prior studies reported that influenza virions are produced by 12 h post-infection (Borland and Mahy, 1968), supporting our empirical measurements (Goodman et al., 2007) and the mathematics describing logistical influenza virus growth (Eq. 4) with a growth rate (rFlu) of 0.075 h−1. NS1 is highly abundant at early times post-infection, but appears relatively dynamic (Lamb et al., 2001), leading us to scale the NS1 growth rate (rNS1) at two-thirds the value of rFlu. We derived a carrying capacity (K) of 100 PFU for influenza virus within a cell based on the observation that 105 mouse embryo fibroblasts release 107 PFU/ml at 24 h post-infection (Goodman et al., 2010). The rate constant for P58IPK-mediated PKR inhibition (rPKR,21,P58) was derived from Fig. 3B of Lee, et al. (Lee et al., 1994b), which portrayed a titration of the molar ratio between of PKR and P58IPK needed to achieve PKR inhibition in 10 minutes. Similarly, the rate constant for NS1-mediated PKR inhibition (rPKR,21,NS1) was derived from Fig. 5 of Lu, et al. (Lu et al., 1995), which described the amount of NS1 needed to inhibit PKR in 15 minutes. Because NS1 inhibits PKR phosphorylation by 24 h p.i during an infection at 2 PFU/ml (Bergmann et al., 2000) but P58IPK inhibits PKR phosphorylation by 8 h post-infection during an infection at 1 PFU/ml (Goodman et al., 2007), rPKR,21,P58 was greater than rPKR,21,NS1. While half of the parameter values (rPKR,21,P58, rPKR,21,NS1, rFlu, rNS1, and K) were derived from the literature (Borland and Mahy, 1968; Goodman et al., 2010; Lamb et al., 2001; Lee et al., 1994b; Lu et al., 1995), a weighted, non-linear least squares optimization algorithm was used to derive the remaining parameter values (rPKR,12,Flu, rP58,12, rP58,21, reIF2α,12, and reIF2α,21).
All computation was performed in Matlab (v7.1, The Mathworks, Natick, MA.), using stiff, numerical integration (ode15s.m) to solve the system of differential equations. Curve fitting of numerical data derived from the modeled P58IPK activation was performed with the Curve-Fitting Toolbox built in to Matlab, and sample correlation was performed with the corrcoef.m function. To optimize the five unknown parameters (rPKR,12,Flu, rP58,12, rP58,21, reIF2α,12, and reIF2α,21), we applied an unconstrained non-linear minimization (fminsearch.m, implementing a Nelder-Mead simplex algorithm) to minimize the sum-squared residuals for the biological data obtained in the presence or absence of P58IPK using the weighted error function:
| (7) |
| (8) |
where “data” and “sim” refer to values calculated from biological and simulated experiments respectively, and σ refers to the standard deviation of a specific biological data point. Because there was no standard deviation data published for PKR phosphorylation at 8 h post-infection, we implemented a standard error of 10% for this pair of data points. Parameters derived from the literature, namely rPKR,21,P58, rPKR,21,NS1, rFlu, rNS1, and K, were fixed for all simulations, and thus excluded from the parameter estimation. The remaining five unknown parameters were estimated using the training set of data consisting of previously published infection results from early timepoints post-infection in the presence or absence of P58IPK (Goodman et al., 2007). To fit the model to all biological data and re-derive the five unknown parameter values, we used the nlinfit.m function, which uses the Levenberg-Marquardt algorithm for nonlinear least squares to compute non-robust fits. Fitting results were passed to the nlparci.m function to calculate parameter covariances and confidence intervals and to the nlpredci.m function to calculate parameter intervals. Finally, all parameter values were identical whether simulating the P58IPK−/− or wild-type (P58IPK+/+) conditions, except for the parameter representing P58IPK concentration in the cell, which was set P58_total = 0 to simulate P58IPK−/−. The model can be found at the “JWS Online Cellular Systems Modelling” database (http://www.jjj.bio.vu.nl).
While our model describes proteins downstream from P58IPK that are involved in influenza virus infection, it was not possible to include all proteins related to virus infection and the P58IPK pathway. Besides PERK, other eIF2α kinases, namely HRI and GCN2, were also excluded from the model, as they have not been shown to be activated during influenza virus infection or inhibited by P58IPK (Berlanga et al., 2006; Lee et al., 1994b). Even though influenza virus hemagglutinin (HA) is highly glycosylated and can induce ER stress in a virus-free system (Braakman et al., 1991; Galli et al., 2011), infection with influenza virus has not been shown to induce ER stress or an unfolded protein response. Recently, Luig, et al. showed that the mitogen-activated protein kinase-activated protein kinases (MAPKAPKs) MK2 and MK3 were activated upon influenza virus infection, forming a part of the complex which inhibits PKR along with P58IPK (Luig et al., 2010). As MK2 and MK3 activation are upstream of P58IPK-mediated PKR inhibition, these molecules were excluded from our current model. However, they represent sound directions for expanding the model to include a subsequent level of signaling in the future.
Sensitivity analysis
The goal of sensitivity analysis is to correlate variances in parameter values to variances in model output and is useful when parameter values are not known with certainty. Sampling-based sensitivity analysis entails specifying a distribution for each parameter from which values are selected at random and used in model simulations (Chang, Linderman, and Kirschner, 2005; Helton and Davis, 2001). In particular, non-zero parameters were varied by assigning uniform distributions ranging from 25% to 175% of respective baseline values and sampling 2000 values from these distributions by Latin Hypercube Sampling. Runs were generated for random combinations of these parameter values, with the output chosen to be NS1 concentrations at timepoints 10 h and 120 h. The sensitivity of the output to variation in each parameter was determined by partial rank correlation coefficients (PRCC) values varying between −1 and 1, corresponding to perfect negative and positive correlations, respectively. P-values were assigned to each PRCC value following the method of Blower and Dowlatabadi (Blower and Dowlatabadi, 1994) and Bonferroni-corrected for the number of samplings.
Cells, viruses, and infections
Mouse embryo fibroblasts (MEFs) derived from wild-type C57BL/6 (P58IPK+/+) mice or mice lacking Dnajc3, the gene for P58IPK generated on the C57BL/6 background (P58IPK−/−) were grown as previously described (Goodman et al., 2007; Ladiges et al., 2005). BSC-40 monkey kidney epithelial cells were grown as monolayers in supplemented high glucose Dulbecco’s modified Eagle’s medium (hgDMEM) supplemented to contain 2 mM L-glutamine, 0.1 mM nonessential amino acids, Fungizone Amphotencin B (0.5 μg/ml), penicillin G (100 units/ml), streptomycin sulfate (100 μg/ml) and 10% newborn calf serum (NCS) (Sigma). Wild-type vaccinia virus (strain WR) and recombinant viruses expressing wild-type PKR (VVPKR) or its catalytically inactive mutant (K296R) were grown on monkey BSC-40 cells, purified by a 45% (w/v) sucrose cushion, and titrated on BSC-40 cells by plaque assay. The A/WSN/33 (WSN) strain of influenza virus was grown in Madin-Darby bovine kidney cells as previously described (Etkind and Krug, 1975).
Near-confluent monolayers of cells were mock-infected or infected with vaccinia virus diluted in supplemented hgDMEM to the indicated multiplicity of infection (MOI). After 1 h of adsorption at 37°C, virus and medium was removed. Fresh supplemented hgDMEM containing 2% NCS was added to the cells and infections were allowed to proceed at 37°C until the indicated time post-infection. Recombinant viruses express wild-type PKR or its mutant form under regulated control of an isopropyl β-D-1-thiogalactopyranoside (IPTG) inducible promoter at 1.5 mM, as previously described (Lee and Esteban, 1993). Influenza virus infections in P58IPK−/− and P58IPK+/+ MEFs were performed as previously described (Goodman et al., 2007).
Protein analyses and plaque assays
Protein and immunoblot analyses were performed as previously described (Goodman et al., 2010) using primary antibodies for influenza virus NS1 (a kind gift from Adolfo García-Sastre), total PKR, total eIF2α (Santa Cruz Biotechnology), pT451 PKR, pS52 eIF2α (Invitrogen), or actin (MP Biomedicals).
At the indicated times post-infection, infected cells and cell media supernatant were collected and assayed in triplicate for viral yield by standard plaque assay on BSC-40 cells. Viral yields were calculated according to the formula: log10 yieldt=x = [log10(PFU/ml)t=x]-[log10(PFU/ml)t=0], where t is time and x is the time post-infection.
Flow cytometry analysis
At the indicated times post-infection, cells were collected via trypsinization, resuspended in 1× annexin V Binding Buffer, stained with 10μL/106 cells of annexin V-FITC and propidium iodide according to the manufacturer’s instructions (Beckman Coulter). Flow cytometry was performed with the LSR II System (BD Biosciences) and data was analyzed with BD FACSDiva Software v. 6.1.
Acknowledgments
We thank Dr. Kalyan C. Vinnakota for advice regarding parameter optimization techniques. We also thank Ma del Carmen Moreno-Ortiz Navarro and Sara Escudero García and the Flow Cytometry Core Facility at the Centro Nacional de Biotecnología for cytometric services.
This work was supported by Ministry of Science and Education of Spain Program JAE-DOC (CSIC-FSE) (to A.G.G.), National Science Foundation Postdoctoral Fellowship in Biology DBI-0905830 (to B.C.W.T.), the Marcelino Botín Foundation (to M.E.), and federal funding from the National Institute of Allergy and Infectious Diseases, National Institutes of Health, Department of Health and Human Services under contract number HHSN272200800060C, and Public Health Service grants R01AI022646 and U54AI081680 (to M.G.K.).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Beattie E, Kauffman EB, Martinez H, Perkus ME, Jacobs BL, Paoletti E, Tartaglia J. Host-range restriction of vaccinia virus E3L-specific deletion mutants. Virus Gene. 1996;12(1):89–94. doi: 10.1007/BF00370005. [DOI] [PubMed] [Google Scholar]
- Bergmann M, García-Sastre A, Carnero E, Pehamberger H, Wolff K, Palese P, Muster T. Influenza virus NS1 protein counteracts PKR-mediated inhibition of replication. J Virol. 2000;74(13):6203–6206. doi: 10.1128/jvi.74.13.6203-6206.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berlanga JJ, Ventoso I, Harding HP, Deng J, Ron D, Sonenberg N, Carrasco L, de Haro C. Antiviral effect of the mammalian translation initiation factor 2[alpha] kinase GCN2 against RNA viruses. EMBO J. 2006;25(8):1730–1740. doi: 10.1038/sj.emboj.7601073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blower SM, Dowlatabadi H. Sensitivity and Uncertainty Analysis of Complex Models of Disease Transmission: An HIV Model, as an Example. International Statistical Review. 1994;62(2):229–243. [Google Scholar]
- Borland R, Mahy BWJ. Deoxyribonucleic Acid-dependent Ribonucleic Acid Polymerase Activity in Cells Infected with Influenza Virus. J Virol. 1968;2(1):33–39. doi: 10.1128/jvi.2.1.33-39.1968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braakman I, Hoover-Litty H, Wagner KR, Helenius A. Folding of influenza hemagglutinin in the endoplasmic reticulum. The Journal of Cell Biology. 1991;114(3):401–411. doi: 10.1083/jcb.114.3.401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bracci L, Canini I, Puzelli S, Sestili P, Venditti M, Spada M, Donatelli I, Belardelli F, Proietti E. Type I IFN is a powerful mucosal adjuvant for a selective intranasal vaccination against influenza virus in mice and affects antigen capture at mucosal level. Vaccine. 2005;23(23):2994–3004. doi: 10.1016/j.vaccine.2004.12.006. [DOI] [PubMed] [Google Scholar]
- Budd A, Alleva L, Alsharifi M, Koskinen A, Smythe V, Mullbacher A, Wood J, Clark I. Increased Survival after Gemfibrozil Treatment of Severe Mouse Influenza. Antimicrob Agents Chemother. 2007;51(8):2965–2968. doi: 10.1128/AAC.00219-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang ST, Linderman JJ, Kirschner DE. Multiple mechanisms allow Mycobacterium tuberculosis to continuously inhibit MHC class II-mediated antigen presentation by macrophages. Proc Natl Acad Sci USA. 2005;102(12):4530–4535. doi: 10.1073/pnas.0500362102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davies MV, Chang HW, Jacobs BL, Kaufman RJ. The E3L and K3L vaccinia virus gene products stimulate translation through inhibition of the double-stranded RNA dependent protein kinase by different mechanisms. J Virol. 1993;67:1688–1692. doi: 10.1128/jvi.67.3.1688-1692.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dever TE. Gene-Specific Regulation by General Translation Factors. Cell. 2002;108(4):545–556. doi: 10.1016/s0092-8674(02)00642-6. [DOI] [PubMed] [Google Scholar]
- Dey M, Cao C, Dar AC, Tamura T, Ozato K, Sicheri F, Dever TE. Mechanistic Link between PKR Dimerization, Autophosphorylation, and eIF2[alpha] Substrate Recognition. Cell. 2005;122(6):901–913. doi: 10.1016/j.cell.2005.06.041. [DOI] [PubMed] [Google Scholar]
- Etkind PR, Krug RM. Purification of influenza viral complementary RNA: its genetic content and activity in wheat germ cell-free extracts. Journal Of Virology. 1975;16:1464–1475. doi: 10.1128/jvi.16.6.1464-1475.1975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gale M, Jr, Blakely CM, Hopkins DA, Melville MW, Wambach M, Romano PR, Katze MG. Regulation of interferon-induced protein kinase PKR: modulation of P58 IPK inhibitory function by a novel protein, P52rIPK. Mol Cell Biol. 1998;18:859–871. doi: 10.1128/mcb.18.2.859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galli C, Bernasconi R, Soldà T, Calanca V, Molinari M. Malectin Participates in a Backup Glycoprotein Quality Control Pathway in the Mammalian ER. PLoS ONE. 2011;6(1):e16304. doi: 10.1371/journal.pone.0016304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garcia MA, Meurs EF, Esteban M. The dsRNA protein kinase PKR: Virus and cell control. Biochimie. 2007;89(6–7):799–811. doi: 10.1016/j.biochi.2007.03.001. [DOI] [PubMed] [Google Scholar]
- Garfinkel MS, Katze MG. Translational control by influenza virus: selective and cap-dependent translation of viral mRNAs in infected cells. J Biol Chem. 1992;267:9383–9390. [PubMed] [Google Scholar]
- Gil J, Rullas J, García MA, Alcamí J, Esteban M. The catalytic activity of dsRNA-dependent protein kinase, PKR, is required for NF-kB activation. Oncogene. 2001;20(3):385–394. doi: 10.1038/sj.onc.1204109. [DOI] [PubMed] [Google Scholar]
- Gomez CE, Vandermeeren AM, Garcia MA, Domingo-Gil E, Esteban M. Involvement of PKR and RNase L in translational control and induction of apoptosis after Hepatitis C polyprotein expression from a vaccinia virus recombinant. Virol J. 2005;2:81. doi: 10.1186/1743-422X-2-81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodman AG, Fornek JL, Medigeshi GR, Perrone LA, Peng X, Dyer MD, Proll SC, Knoblaugh SE, Carter VS, Korth MJ, Nelson JA, Tumpey TM, Katze MG. P58(IPK): A Novel “CIHD” Member of the Host Innate Defense Response against Pathogenic Virus Infection. PLoS Pathog. 2009;5 (5):e1000438. doi: 10.1371/journal.ppat.1000438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodman AG, Smith JA, Balachandran S, Perwitasari O, Proll SC, Thomas MJ, Korth MJ, Barber GN, Schiff LA, Katze MG. The cellular protein P58IPK regulates influenza virus mRNA translation and replication through a PKR-mediated mechanism. J Virol. 2007;81(5):2221–2230. doi: 10.1128/JVI.02151-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodman AG, Zeng H, Proll SC, Peng X, Cilloniz C, Carter VS, Korth MJ, Tumpey TM, Katze MG. The Alpha/Beta Interferon Receptor Provides Protection against Influenza Virus Replication but Is Dispensable for Inflammatory Response Signaling. J Virol. 2010;84(4):2027–2037. doi: 10.1128/JVI.01595-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hatada E, Saito S, Fukuda R. Mutant Influenza Viruses with a Defective NS1 Protein Cannot Block the Activation of PKR in Infected Cells. J Virol. 1999;73(3):2425–2433. doi: 10.1128/jvi.73.3.2425-2433.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Helton JC, Davis FJ. Sampling-Based Methods. In: Saltelli A, Chan K, Scott EM, editors. Sensitivity Analysis. Wiley; New York: 2001. pp. 101–153. [Google Scholar]
- Ladiges WC, Knoblaugh SE, Morton JF, Korth MJ, Sopher BL, Baskin CR, MacAuley A, Goodman AG, LeBoeuf RC, Katze MG. Pancreatic beta-cell failure and diabetes in mice with a deletion mutation of the endoplasmic reticulum molecular chaperone gene P58IPK. Diabetes. 2005;54(4):1074–1081. doi: 10.2337/diabetes.54.4.1074. [DOI] [PubMed] [Google Scholar]
- Lamb RA, Krug RM, Knipe DM, Howlet PM, Griffin DE, Martin MA, Roizman B, Straus SE. Fields virology. Lippincott Williams & Wilkins; Philadelphia, PA: 2001. Orthomyxoviridae: the viruses and their replication; pp. 1487–1532. [Google Scholar]
- Langland JO, Jacobs BL. The Role of the PKR-Inhibitory Genes, E3L and K3L, in Determining Vaccinia Virus Host Range. Virology. 2002;299(1):133–141. doi: 10.1006/viro.2002.1479. [DOI] [PubMed] [Google Scholar]
- Lee SB, Esteban M. The Interferon-Induced Double-Stranded RNA-Activated Human p68 Protein Kinase Inhibits the Replication of Vaccinia Virus. Virology. 1993;193(2):1037–1041. doi: 10.1006/viro.1993.1223. [DOI] [PubMed] [Google Scholar]
- Lee SB, Esteban M. The interferon-induced double-stranded RNA-activated protein kinase induces apoptosis. Virology. 1994;199:491–496. doi: 10.1006/viro.1994.1151. [DOI] [PubMed] [Google Scholar]
- Lee SB, Green SR, Mathews MB, Esteban M. Activation of the double-stranded RNA (dsRNA)-activated human protein kinase in vivo in the absence of its dsRNA binding domain. Proc Natl Acad Sci USA. 1994a;91:10551–10555. doi: 10.1073/pnas.91.22.10551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee TG, Tang N, Thompson S, Miller J, Katze MG. The 58,000-dalton cellular inhibitor of the interferon-induced double-stranded RNA-activated protein kinase (PKR) is a member of the tetratricopeptide repeat family of proteins. Mol Cell Biol. 1994b;14:2331–2342. doi: 10.1128/mcb.14.4.2331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee TG, Tomita J, Hovanessian AG, Katze MG. Characterization and regulation of the 58,000-dalton cellular inhibitor of the interferon-induced, dsRNA-activated protein kinase. J Biol Chem. 1992;267:14238–14243. [PubMed] [Google Scholar]
- Liu CY, Kaufman RJ. The unfolded protein response. J Cell Sci. 2003;116(Pt 10):1861–1862. doi: 10.1242/jcs.00408. [DOI] [PubMed] [Google Scholar]
- Lu Y, Wambach M, Katze MG, Krug RM. Binding of the influenza virus NS1 protein to double-stranded RNA inhibits the activation of the protein kinase that phosphorylates the eIF-2 translation initiation factor. Virology. 1995;214(1):222–228. doi: 10.1006/viro.1995.9937. [DOI] [PubMed] [Google Scholar]
- Luig C, Köther K, Dudek SE, Gaestel M, Hiscott J, Wixler V, Ludwig S. MAP kinase-activated protein kinases 2 and 3 are required for influenza A virus propagation and act via inhibition of PKR. FASEB J. 2010;24(10):4068–4077. doi: 10.1096/fj.10-158766. [DOI] [PubMed] [Google Scholar]
- Melville MW, Hansen WJ, Freeman BC, Welch WJ, Katze MG. The molecular chaperone hsp40 regulates the activity of P58 IPK, the cellular inhibitor of PKR. Proc Natl Acad Sci USA. 1997;94:97–102. doi: 10.1073/pnas.94.1.97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Min JY, Li S, Sen GC, Krug RM. A site on the influenza A virus NS1 protein mediates both inhibition of PKR activation and temporal regulation of viral RNA synthesis. Virology. 2007;363(1):236–243. doi: 10.1016/j.virol.2007.01.038. [DOI] [PubMed] [Google Scholar]
- Regoes RR, Bonhoeffer S. Emergence of Drug-Resistant Influenza Virus: Population Dynamical Considerations. Science. 2006;312(5772):389–391. doi: 10.1126/science.1122947. [DOI] [PubMed] [Google Scholar]
- Rice AD, Turner PC, Embury JE, Moldawer LL, Baker HV, Moyer RW. Roles of Vaccinia Virus Genes E3L and K3L and Host Genes PKR and RNase L during Intratracheal Infection of C57BL/6 Mice. J Virol. 2011;85(1):550–567. doi: 10.1128/JVI.00254-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sioud M, Barik S. Treating Respiratory Viral Diseases with Chemically Modified, Second Generation Intranasal siRNAs. In: Walker JM, editor. siRNA and miRNA Gene Silencing: From Bench to Bedside. Vol. 487. Humana Press; New York, NY: 2009. pp. 331–341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith JA, Schmechel SC, Raghavan A, Abelson M, Reilly C, Katze MG, Kaufman RJ, Bohjanen PR, Schiff LA. Reovirus induces and benefits from an integrated cellular stress response. J Virol. 2006;80(4):2019–2033. doi: 10.1128/JVI.80.4.2019-2033.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang NM, Korth MJ, Gale M, Jr, Wambach M, Der SD, Bandyopadhyay SK, Williams BRG, Katze MG. Inhibition of double-stranded RNA- and tumor necrosis factor alpha-mediated apoptosis by tetratricopeptide repeat protein and cochaperone, P58IPK. Mol Cell Biol. 1999;19:4757–4765. doi: 10.1128/mcb.19.7.4757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang HM, Ye X, Su Y, Yuan J, Liu Z, Stein DA, Yang D. Coxsackievirus B3 Infection Activates the Unfolded Protein Response and Induces Apoptosis through Downregulation of p58IPK and Activation of CHOP and SREBP1. J Virol. 2010;84(17):8446–8459. doi: 10.1128/JVI.01416-09. [DOI] [PMC free article] [PubMed] [Google Scholar]