Changes in frontal-parietal activation and math skills performance following adaptive number sense training: Preliminary results from a pilot study

Abstract

Number sense is believed to be critical for math development. It is putatively an implicitly learned skill and may therefore have limitations in terms of being explicitly trained, particularly in individuals with altered neurodevelopment. A case series study was conducted using an adaptive, computerized program that focused on number sense and general problem solving skills was designed to investigate training effects on performance as well as brain function in a group of children with Turner syndrome who are at risk for math difficulties and altered development of math-related brain networks. Standardized measurements of math and math-related cognitive skills as well as functional magnetic resonance imaging (fMRI) were used to assess behavioral and neurobiologic outcomes following training. Participants demonstrated significantly increased basic math skills, including number sense, and calculation as well as processing speed, cognitive flexibility and visual-spatial processing skills. With the exception of calculation, increased scores also were clinically significant (i.e. recovered) based on reliable change analysis. Participants additionally demonstrated significantly increased bilateral parietal lobe activation and decreased frontal-striatal and mesial temporal activation following the training program. These findings show proof of concept for an accessible training approach that may be potentially associated with improved number sense, math and related skills, as well as functional changes in math-related neural systems, even among individuals at risk for altered brain development.

INTRODUCTION

Several experts in the field of mathematical cognition suggest that number sense, an inherent understanding of numbers and their relationships, is essential for math skills development (Dehaene, Dehaene-Lambertz, & Cohen, 1998; Geary et al., 2009; von Aster & Shalev, 2007; Wilson, Dehaene, et al., 2006; Wilson, Revkin, Cohen, Cohen, & Dehaene, 2006; Zago et al., 2001). Number sense is defined as a nonverbal skill that involves spatial relationships between numbers along a mental number line allowing for number comparison and processing (Dehaene et al., 1998; Nieder & Dehaene, 2009; von Aster & Shalev, 2007). Many individuals who have difficulty with math skills, including those with math disability, are believed to have a core deficit in number sense (Dehaene et al., 1998; Geary et al., 2009; von Aster & Shalev, 2007; Wilson, Dehaene, et al., 2006; Wilson, Revkin, et al., 2006; Zago et al., 2001).

Number sense is assessed in children primarily via tests of numerical distance, subitizing, calculation and counting strategies, and number comparison, among others (Geary et al., 2009; Jordan, Kaplan, Locuniak, & Ramineni, 2007). Number sense development is believed to be biologically determined, relying largely on intuitive or implicit learning (Dehaene, 2009; Dehaene et al., 1998; Nieder & Dehaene, 2009). As children gain proficiency in number sense, they shift from using effortful counting methods that rely heavily on attention and working memory to more frequent use of spatial-based counting and/or fact retrieval type strategies (Geary, Hoard, Byrd-Craven, & DeSoto, 2004). Number sense has been shown to have a reproducible cerebral network common to humans and primates involving frontal and parietal regions (Davis et al., 2009; Nieder & Dehaene, 2009; Tsang, Dougherty, Deutsch, Wandell, & Ben-Shachar, 2009). Because number sense is putatively a core skill underlying math development, it may represent a more critical target of math intervention than the math skills themselves, impacting a variety of math abilities. This is based on developmental models of cognitive rehabilitation suggesting that more fundamental skills (e.g. number sense) should be trained before higher-level skills (e.g. specific math skills) (Eack et al., 2010; Laatsch, Pavel, Jobe, Lin, & Quintana, 1999). However, if number sense is an intuitive, spontaneous process subserved by a specialized neural network (Nieder & Dehaene, 2009), it may be difficult to explicitly train, particularly in individuals who have altered neurodevelopment in math systems.

For this study, a program of number sense training was designed that utilized a spatial-based, retrieval strategy known as decomposition, a commonly used strategy among typically developing children and adults (Lemaire & Callies, 2009). Metacognitive instruction and distributed, adaptive practice of computational operations utilizing the decomposition strategy were combined with practice of pattern recognition and categorical reasoning skills. This novel addition of cognitive flexibility skills training to number sense training was designed to help participants improve flexible thinking in order to better transfer training to higher-level math skills like applied problem solving, for example. Additionally, improved cognitive flexibility skills would be expected to help participants more effectively recognize and utilize efficient problem solving strategies. Cognitive flexibility skills are essential for problem solving and strategy development across cognitive domains (Rende, 2000).

The math training program was conducted with girls with Turner syndrome (TS), a genetic condition where affected girls share the same biological risk factor. TS is characterized by the complete or partial absence of one X chromosome in a phenotypic female and is associated with high risk for deficits in math skills as well as in math-related executive and visual-spatial abilities (Bruandet, Molko, Cohen, & Dehaene, 2004; Kesler, Menon, & Reiss, 2006; Mazzocco, 2006; Murphy & Mazzocco, 2008; Murphy, Mazzocco, Gerner, & Henry, 2006; Rovet, Szekely, & Hockenberry, 1994; Temple & Marriott, 1998). Girls with TS tend to show immature math strategies as well as problems with counting, subitizing, estimation and comparison (Bruandet et al., 2004; Kesler et al., 2006; Murphy & Mazzocco, 2008), consistent with disrupted number sense development.

Females with TS also demonstrate disrupted frontal-parietal function associated with arithmetic processing including decreased activation during math tasks relative to healthy control groups (Kesler et al., 2006; Molko et al., 2003). Although math impairment in TS remains highly complex and may not be specific to a core deficit of number sense (Mazzocco, 2009), TS provides a unique opportunity to examine math performance and development in a well-defined, relatively homogeneous population (Dehaene, Molko, Cohen, & Wilson, 2004; Ergur et al., 2008; Mazzocco, 2005; Molko et al., 2003) that is typically without comorbid intellectual or reading impairments (Hong, Scaletta Kent, & Kesler, 2009; Kesler, 2007). Importantly, the investigation of training and practice effects in a group such as TS contributes vital information regarding neuroplasticity in individuals with potentially altered neurodevelopment. It was hypothesized that the training program would be associated with significantly increased activation of frontal-parietal regions as well as improved scores on tests of mathematical skill and math-related cognitive skills (e.g. attention, processing speed).

METHODS

Participants

We enrolled 16 right-handed females with TS age 7–14 years (mean = 10.9 ± 2.6) in this case series study. Documentation of X monosomy on standardized karyotype was obtained from the diagnosing physician or facility with 7 participants having a non-mosaic and 9 have a mosaic genotype. Participants were enrolled if they could commit to the 6 week training program and had been exposed to at least single digit addition instruction so that there was an adequate foundation for teaching the math training strategy. Participants were excluded for neurologic or psychiatric conditions, major sensory impairments (e.g. blindness, profound deafness) or language-based learning disabilities (e.g. dyslexia). This study was approved by the Institutional Review Board at Stanford University. Informed consent for participation was obtained from the participants’ parents and informed assent was obtained from participants.

Training Program

Each participant met with the first author (S.K.) for approximately 30 minutes of metacognitive instruction regarding the use of the decomposition math strategy. This strategy involves decomposing math problems into smaller problems that are easier and/or already memorized. For example, 39+12 = 39+10+2. All strategy instruction was done by S.K. for consistency in this small sample and involved a review of the decomposition strategy, a comparison of decomposition with less efficient strategies (e.g. finger counting) and practice of decomposition strategy implementation. During the training session, participants and their parents were introduced to the computerized, online practice program. This program was developed in collaboration with Lumos Labs, Inc. (San Francisco, CA USA) and built in Flash (Adobe Systems, San Jose, CA USA) for web production. The program involved game-like exercises that allowed participants to practice quantity comparison, mental calculation (to automatize arithmetic and practice the decomposition strategy) and cognitive flexibility skills. The development of the exercises is described in detail elsewhere (Hardy & Scanlon, 2009). The authors paid Lumos Labs for use of this program and have no commercial interests in Lumos Labs, Inc., or any other conflicts of interest related to this program.

There were 3 different exercises presented during each session. “Chalkboard Challenge” was designed to practice quantity comparison and estimation. Participants viewed an illustrative (digital) chalkboard that presented them with single numbers or equations on either side of the chalkboard while asking them to indicate which side was larger (e.g. 12 vs 19; 15 vs. 12-1). Difficulty was increased by increasing the number of operands and including equations. Because the exercise was timed, participants were encouraged to use estimation to evaluate equations. “Raindrops” was designed to practice mental calculation. Participants were shown arithmetic equations inside of raindrops that fell from the sky into a body of water (e.g. 2+7). They were asked to enter the correct answer to the equation before the raindrop hit the water. Difficulty was increased by increasing the number of operands and the speed with which the raindrop fell.

“By the Rules” was based on sorting tasks such as the Wisconsin Card Sorting Test (Bujoreanu & Willis, 2008) that require cognitive flexibility - the generation of alternate solutions to ambiguous stimuli. Participants were shown a single card depicting one or more geometric figures and asked to determine if the card followed “the rule” or not. The rule had to be ascertained implicitly, initially via trial and error, and responses had to be recalled in order to establish a pattern. Participants were required to sort 140 cards during each session with no time limit. Difficulty was increased by increasing the number of possible rules in play as well as rule subtlety or complexity. For example, “blue” would be an easier rule whereas “blue triangle with a dashed card border” would be a more difficult rule. Each exercise included an online demonstration of the rules and procedure. Exercises were adaptive to the individual’s performance using algorithms that considered both intra- and inter-session performance including speed and accuracy. All exercise trials provided immediate feedback regarding response accuracy.

Each participant was provided with an anonymous user ID number and password to login to the encrypted website from their home computer. No personal information was stored. Participants and their parents were given verbal and written instructions as well as a live demonstration of how to perform each exercise. After logging in, participants were automatically directed to their “trainer page” which listed the exercises assigned that day. Participants were required to complete one session, consisting of all 3 exercises, 5 days per week for 6 weeks. Sessions were approximately 20 minutes in duration. Previous computerized training studies have ranged from 5 to 8 weeks, 1 to 7 sessions per week and 25–45 minutes per session (Bangirana et al., 2009; Klingberg et al., 2005; Klingberg, Forssberg, & Westerberg, 2002; Shalev, Tsal, & Mevorach, 2007; Thorell, Lindqvist, Bergman Nutley, Bohlin, & Klingberg, 2009). Our duration parameters were chosen in an effort to balance consistent, intensive practice with feasibility while remaining relatively consistent with previous studies. Research staff tracked participant progress and communicated with participants’ parents on a weekly basis to ensure compliance. Participants were paid $100 for completing the training program.

Math and Math-Related Cognitive Skills Assessment

All participants were administered a battery of standardized tests by trained psychometricians to assess math and certain math-related cognitive skills. The KeyMath Diagnostic Assessment 3^rd Edition provides comprehensive evaluation of math basic concepts, operations and applications (Connolly, 2007). Several measures were utilized to assess math related skills. The Wechsler Intelligence Scale for Children 4^th Edition (WISC-IV) measures general intellectual function (Full Scale IQ), which is comprised of Verbal Comprehension (VCI), Perceptual Reasoning (PRI), Working Memory (WMI) and Processing Speed (PSI) indices (Wechsler, 2003). The Sky Search subtest of the Test of Everyday Attention for Children was administered to measure attention (Heaton et al., 2001). The Animal Sorting subtest of the NEPSY-II was used to measure cognitive flexibility (Brooks, Sherman, & Strauss, 2009) and the Motor-free Visual Perception Test 3^rd Edition (MVPT) was utilized as a measure of visual-spatial processing (Colarusso & Hammill, 2003). These cognitive skills have been shown to be associated with math skills development and performance (Ayr, Yeates, & Enrile, 2005; Bull, Espy, & Wiebe, 2008; Clark, Pritchard, & Woodward, 2010).

The testing battery was administered to participants at two time points - within 1 week prior to beginning and within 1 week after completing the training program. Tests were administered by psychometricians that were not involved in the rehabilitation study. However, testing could not be blinded to intervention participation given that all participants were enrolled. All tests were given at both time points with the exception of the Verbal Comprehension and Perceptual Reasoning indices of the WISC-IV (thus, Full Scale IQ also was not measured twice). Tests were double scored by independent raters to ensure interrater reliability. Alternate test versions were administered at Time 2 when available to reduce the effects of practice (see Table 1). All tests, including alternate forms, were administered in a randomized order for each participant.

Table 1.

Demographic, cognitive and fMRI behavioral data

	Time 1 Mean (SD) N = 16	Time 2 Mean (SD) N = 14	LMM		Effect Size	RCI	Cut Score	RCI Classification
			slope	p
Age (years)	10.9 (2.6) range: 7–14
Grade	4.8 (2.5) range: 1–9
Mosaic genotype	9 (56%)
KeyMath Total*	89 (12)	94 (12)	.451	.03	.82	1.82	89	recovered
KeyMath Basic Concepts*	89 (12)	95 (13)	.584	.04	.64	1.71	89	recovered
KeyMath Operations*	88 (13)	92 (13)	.532	.02	.91	.94	89	unchanged
KeyMath Applications*	92 (13)	94 (11)	−.081	.80	.19
WISC-IV Full Scale IQ	90 (15)
WISC-IV Verbal	99 (17)
Comprehension Index (VCI)
WISC-IV Perceptual Reasoning Index (PRI)	86 (13)
WISC-IV Processing Speed Index (PSI)	86 (13)	102 (13)	2.41	.001	.40	2.14	96	recovered
WISC-IV Working Memory Index (WMI)	88 (15)	93 (11)	.585	.31	.04
NEPSY II Animal Sort	7 (2)	10 (3)	.370	.01	.44	1.33	9	recovered
Test of Everyday Attention Sky Search*	7 (4)	9 (2)	.072	.64	.42
Motor-free Visual Perception Test (MVPT)	82 (26)	104 (12)	2.54	.009	.69	2.47	93	recovered
fMRI Task Percent Accuracy Level 1*	.79 (.21)	.92 (.14)	.018	.02	.44
fMRI Task Mean Reaction Time (ms) Level 1*	2054 (600)	2084 (797)	15.7	.68	.06
fMRI Task D′ Level 1*	3.9 (2.3)	4.5 (2.2)	.061	.52	.41
fMRI Task Percent Accuracy Level 2*	.57 (.17)	.66 (.23)	.011	.16	.47
fMRI Task Mean Reaction Time (ms) Level 2*	3212 (778)	2631 (572)	−90.7	.03	.30
fMRI Task D′ Level 2*	.81 (1.2)	2.5 (2.4)	.251	.02	.47

^*Alternate test forms used; LMM: linear mixed modeling; RCI: reliable change index; RCI classification of Time 2 mean: Recovered = passed both cutoff score and RCI criteria, Improved = passed RCI criterion but not the cut score, Unchanged = passed neither criteria

Math-Related Brain Function Assessment

Brain images were acquired on a 3 Tesla GE Signa scanner (GE Medical Systems, Milwaukee, WI USA) using a custom head coil. Functional images were prescribed parallel to the anterior and posterior commissures in 30 oblique-axial slices (4mm thick, 1mm skip), covering the whole brain. Functional imaging parameters for the T2*-weighted spiral in-out pulse sequence were as follows: TR = 2000ms, TE=30ms, flip angle=80 deg, FOV=22 cm. A high-order shim protocol was run prior to functional scans to improve the magnetic field homogeneity. High-resolution structural images were acquired for each participant for anatomical spatial alignment using the following imaging parameters: T1-weighted 3D SPGR pulse sequence with 124 coronal slices, 256×256 matrix, 1.5mm thickness, Ti=300ms, FOV=22 cm. Images were reconstructed as a 256×256×174 matrix with voxel size of 0.78 × 0.78 × 1.0 mm. Participants underwent fMRI scanning within 24 hours of their cognitive assessments. Participants were excluded (N = 3) from the fMRI assessment for MRI contraindications including certain orthodontia and non-MRI safe metallic implants or biomedical devices.

During the fMRI scan, participants performed a modified version of a math task that has been previously shown by our group to reliably assess frontal-parietal activation in both typically developing children and individuals with TS (Kesler et al., 2006; Menon, Mackenzie, Rivera, & Reiss, 2002; Menon, Rivera, White, Eliez, et al., 2000; Menon, Rivera, White, Glover, & Reiss, 2000). The modified version of this task as utilized for this study included two experimental conditions representing two levels of difficulty paired with two control conditions, and two 30-second rest periods. In the easier, Level 1 experimental condition, participants were shown one-digit, two-operand math equations involving addition, subtraction, or multiplication problems (e.g. 4+3=7). The more difficult Level 2 experimental condition featured two-operand equations with at least one of the operands or the result having two-digits (e.g. 85−25=60). Participants were asked to respond to each stimulus by pressing a button if the equation was correct and withholding response if the equation was incorrect.

For the control conditions, participants were shown a string of digits, and asked to respond to a featured digit (“Press for 5”). Six digits were shown in the Level 1 control condition, and eight digits in the Level 2 control condition. There were five trials of 6-seconds each (5-second stimulus and 1-second interstimulus interval) per 30-second epoch, and three epochs of each condition, resulting in fifteen trials per condition. The order of these fifteen trials was randomized within each condition. For every condition, 60% of trials were correct, requiring a button-press response, and 40% were incorrect, requiring no button press. The entire task took 7 minutes. An alternate version of the task with different equations was used at Time 2 to reduce the effects of practice. Performance data were recorded during the fMRI math task for each participant. Percent correct, mean reaction time and d prime (d′) were calculated for each participant. D′ represented the participant’s ability to discriminate between correct and incorrect equations based on signal detection theory (Green & Swets, 1998). D′ was also included given that a participant’s percent accuracy could be inflated by non-response since incorrect equations required no button press.

fMRI Preprocessing

Functional data was processed using Statistical Parametric Mapping 5 (SPM5) software (http://www.fil.ion.ucl.ac.uk/spm/). Each functional scan was reconstructed and realigned to the third image in the series. The data were then processed to remove linear trends. Spatial smoothing was performed using a 4-mm FWHM Gaussian kernel, followed by motion correction. A mean image of each functional scan was co-registered to the individual’s grey-matter-segmented high-resolution structural image. Each structural image was normalized to the Cincinnati Children’s Hospital Medical Center template for girls’ age 5–18 years (Wilke, Holland, Altaye, & Gaser, 2008), and the transformation was then applied to the functional data. To perform group analysis, functional data was smoothed using a 7mm full width-half maximum Gaussian filter. Functional data were inspected for quality using custom software (http://cibsr.stanford.edu/tools/ArtRepair/ArtRepair.htm). One subject’s data were excluded from the analysis due to significant scanner artifact in the Time 2 scan.

Statistical Analyses

Changes in cognitive and testing data as well as fMRI task performance (percent accuracy, reaction time and d′) between pre- and post-training were estimated using linear mixed modeling in PASW 18.0 (www.spss.com). This approach was chosen to allow baseline performance to be random given that TS is associated with significant individual variation in cognitive profile (Hong et al., 2009) and mixed modeling allows inferences over a wider population than general linear modeling (Diggle, Liang, & Zeger, 1994; Laird & Ware, 1982; Raudenbush & Bryk, 2002). Age and Perceptual Reasoning Index (PRI) were used as covariates. The PRI of the WISC-IV was used to control for individual baseline variation in general cognitive ability rather than the WISC-IV Full Scale or Verbal IQ score given that individuals with TS tend to show significantly greater variation in PRI compared to Full Scale IQ or Verbal IQ (Hong et al., 2009; Kesler, 2007). All cases with available data at Time 1 were included in the analysis assuming that data were missing at random at Time 2, conditional on observed information (Little & Rubin, 2002). Effect sizes were measured for mixed models by computing the proportion of total variance accounted for by the effect of interest using the estimates of covariance parameters. This results in an R² type effect size (Bickel, 2007).

Changes in standardized test scores associated with the math training program were also examined using the Reliable Change Index (RCI) to determine if statistically different scores were also clinically significant (i.e. recovered). The RCI indicates if a test score change is reliable rather than due to test measurement error (i.e., practice effects). The RCI utilizes test-retest reliabilities and score distributions for normal and clinical samples determined during the test’s standardization (Maassen, 2004). The RCI method includes computation of a cut score that separates the normal and clinical distributions and is thus used to determine if the post-test score is “recovered”, or assumed to fall within the normal score distribution (Jacobson & Truax, 1991). Normative data for math learning disorder samples for all tests with the exception of MVPT were available from test technical manuals and utilized as the clinical sample data. MVPT standardization included a sample of individuals with general learning disorder and these data were used for the MVPT RCI. Mean RCIs and cut scores were calculated with MacRCI software (http://www.public.asu.edu/~mwwatkin/Watkins3.html) using the pre- and post- test mean for each test showing statistical significance. An RCI criterion of ≥ 1.28 was utilized (Jacobson & Truax, 1991). Mean RCIs were then classified as 1) Recovered: passed both cutoff score and RCI criteria, 2) Improved: passed RCI criterion but not the cut score, 3) Unchanged: passed neither criteria or 4) Deteriorated: passed RCI criterion but RCI is negative.

Statistical analyses of whole brain fMRI data were performed in SPM5. Individual statistical parametric maps were calculated using a general linear model for each subject and each timepoint. Data were high-pass filtered at 128 Hz and globally scaled. Paired-sample t-tests were then used to determine changes in whole brain activation associated with the training program for the following contrasts: 1) Level 1 experimental versus Level 1 control conditions, 2) Level 2 experimental versus Level 2 control conditions, and 3) Level 1 experimental versus Level 2 experimental conditions. These analyses were controlled for age and PRI. The statistics for analyses were normalized to T scores, and significant clusters of activation were determined using a voxel-wise dual threshold of p < 0.01 for both height and extent, uncorrected, in addition to a cluster-wise FWE-corrected threshold of p < 0.01. We used small volume correction to investigate regional effects within a priori regions (i.e. prefrontal and parietal cortices) using a 10mm sphere around the peak cluster when these regions were identified as significant clusters in whole-brain analyses. Activation foci were superimposed on high-resolution T1-weighted images using MRIcron software (www.mricron.com) and their locations interpreted using known neuroanatomical landmarks.

RESULTS

Intervention Compliance

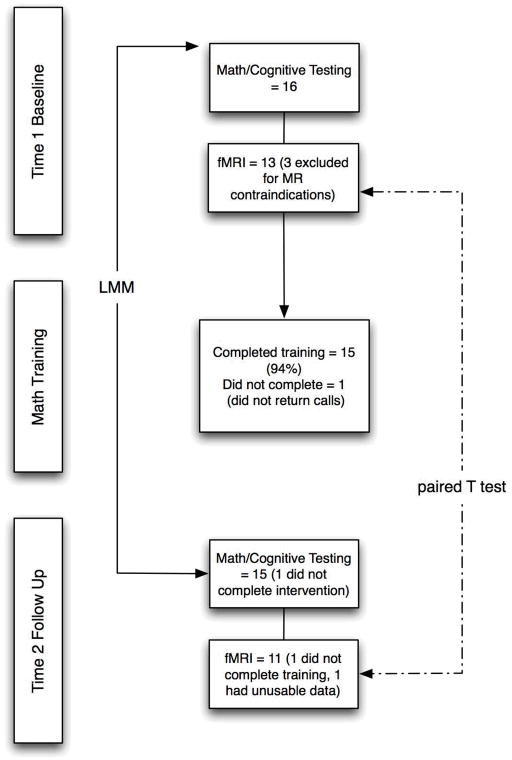
Of the 16 participants who enrolled in the study, 15 completed the training program (Figure 1). The one who did not was lost to follow-up (did not respond to efforts to contact). All 15 participants who completed the math training program finished all 30 sessions within the specified 6 week time limit. Fourteen of these 15 participants completed the Time 2 math/cognitive assessments within the specified time limit (one could not be scheduled for several months after completing the training program due to scheduling conflicts and was therefore not included). Of the 13 participants who were eligible for fMRI assessment, 11 of these had usable fMRI data at Time 2 (one was the individual who was lost to follow up and did not complete the training program and the other had unusable Time 2 data due to significant scanner-related artifact).

Figure 1.

Summary of sample sizes and analyses. Fifteen of the 16 participants completed the math training program (one was lost to follow up). The Time 2 math/cognitive assessment of one participant who completed the math training program was not included as her assessment could not be scheduled for several months. Thirteen of the 16 total participants were eligible for fMRI assessments at Time 1 and 11 usable fMRI assessments were obtained at Time 2 (one did not complete the training program and one had unusable data at Time 2). LMM = linear mixed modeling.

Changes in Math and Cognitive Test Performance

As shown in Table 1, participants demonstrated significantly increased KeyMath Total, Basic Concepts and Operations composite scores following the math training program. The KeyMath Applications composite was not significantly changed. Participants demonstrated significantly increased accuracy on Level 1 but not Level 2 of the fMRI math task following the math training program. However, they showed significantly increased discrimination (d′) as well as reduced reaction time for Level 2 (Table 1).

Participants also demonstrated significantly increased processing speed (PSI), cognitive flexibility (Animal Sort) and visual-spatial processing (MVPT) performance following the math training program (Table 1).

RCI analysis indicated that, on average, changes in KeyMath Total, KeyMath Basic Concepts, PSI, Animal Sort and MVPT test scores were clinically significant and classified as recovered. KeyMath Operations Index was classified as having no clinically significant change (Table 1).

Changes in Brain Function

There were no significant changes in brain activation associated with Level 1 of the fMRI math task. Level 2 was associated with significantly increased brain activation in the right parietal lobule extending into left parietal lobule, left inferior parietal cortex and precuneus that were significant at FWE-corrected cluster extent, p < 0.01 and voxel-level FWE (p = 0.001) following small volume correction. Compared to Level 1, Level 2 was associated with significantly decreased activation in the right anterior cerebellum (culmen) and right putamen extending into inferior frontal gyrus, superior and middle temporal gyri, hippocampus and amygdala (Figure 2).

Figure 2.

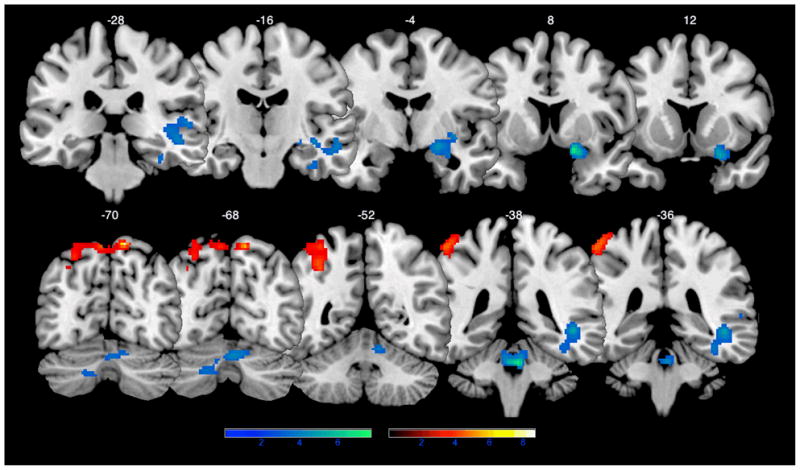
Regions of significant change in brain activation following the math training program. The more difficult Level 2 conditions of the fMRI math task (Level 2 pre- vs. post-intervention contrast) were associated with significantly increased (red-yellow) brain activation in the right parietal lobule extending into left parietal lobule, left inferior parietal cortex and precuneus (corrected cluster p = 006, 850 voxels, FWHM: 12.8×12.1×10.7, resel count: 1033.5, T score = 8.60, MNI coordinates: 12, −70, 62; FWE corrected voxel-level p < .0001 following small volume correction). Level 2 was also associated with significantly decreased activation (blue-green), compared to the easier Level 1 condition (Level 2 vs. Level 1 contrast), in the right anterior cerebellum (corrected cluster p = .001, 1025 voxels, FWHM: 11.9×11.2.10.6, resel count: 1216.9, T score = 7.66, MNI coordinates: 4, −38, −28) and the right putamen extending into inferior frontal gyrus, superior and middle temporal gyri, hippocampus and amygdala (corrected cluster p < .0001, 1346 voxels, FWHM: 11.9×11.2.10.6, resel count: 1216.9, T score = 7.48, MNI coordinates: 18, 8, −14). Color bars represent T score.

DISCUSSION

The results of this study suggest that children with TS who undergo training in effective math strategy in addition to adaptive, distributed skills practice may demonstrate improved math skills in certain areas. Performance was significantly increased on KeyMath Total, Basic Concepts and Operations. Basic Concepts includes comprehensive assessment of number sense (Connolly, 2007) and therefore results suggest that number sense may be potentially trainable, even in children genetically at risk for altered development of neural systems subserving number sense. This is consistent with research demonstrating a reciprocal interaction between behavior, neurobiologic and genetics (Kremen & Jacobson, 2010). KeyMath Operations includes measures of addition, subtraction, multiplication and division. Thus, in addition to basic number sense, participants demonstrated increased performance in specific math skills related to fact retrieval and calculation. Participants also showed significantly increased accuracy, increased ability to discriminate between correct and incorrect math equations and reduced reaction time on the fMRI math measure.

Increased performances on KeyMath Total and KeyMath Basic Concepts were not only statistically significant but were also clinically significant. RCI analysis indicated that these scores were classified as recovered at Time 2, meaning that they increased reliably irrespective of practice effects and also increased to be considered within the normal score distribution (Bauer, Lambert, & Nielsen, 2004). KeyMath Operations was classified by RCI analysis as unchanged. Although this score was statistically significant, participants did not show clinical improvement. This finding may reflect small sample size, non-optimal intervention duration and/or design and/or other unknown factors and warrants further investigation.

Assessments of applied math problem solving involving application of strategies and procedures (e.g. word problems) were not significantly changed. Applied math problems may involve different math and cognitive skills compared to number sense and fact retrieval and thus may require a different remediation approach (Fuchs et al., 2009). It was hypothesized that the addition of cognitive flexibility or general problem solving training would enhance the effectiveness of the training program for applied math problems. However, these particular skills may require problem solving training that is specific to math such as the math word problem training program described by Fuchs and colleagues (Fuchs et al., 2009).

The fMRI findings suggest that there was a decrease in frontal-striatal and mesial temporal activation and an increase in parietal lobe activation after the training program. These results are consistent with previous neuroimaging studies of math skills development, proficiency and learning in typically developing individuals (Ischebeck, Zamarian, Schocke, & Delazer, 2009; Ischebeck et al., 2006; Rivera, Reiss, Eckert, & Menon, 2005) as well as math skills training in an individual with frontal-parietal lesions (Zaunmuller et al., 2009). These findings may imply that less proficient math performers rely on attention, memory and/or verbal based strategies as these are typically subserved by frontal-striatal and temporal regions, while more proficient performers utilize more spatial/retrieval-based strategies that are associated with parietal regions (Rivera et al., 2005). The present results suggest that brain function potentially changed following training during more difficult math trials but was not altered during easier conditions. A previous study from our group indicated that individuals with TS tended to demonstrate the greatest neurofunctional deficit when math task difficulty was increased (Kesler et al., 2006). Laborious approaches such as attention/working memory based strategies may suffice for simpler tasks but neural resources are likely overwhelmed when the task becomes more challenging. These findings potentially lend further evidence to this functional specialization of the parietal lobe for math skills and suggest that training may help to improve this specialization even in individuals with high risk for abnormal frontal-parietal development and function.

These results may have potentially important implications for remediation of math deficits in children. Although the participants of our study did not have documented math disability and in fact demonstrated scores on math assessments that were within what is considered to be the “average” range (85–115) (Connolly, 2007), our findings provide promising preliminary evidence that simple instruction in an efficient math strategy and computerized, home-based skills practice may be associated with improved math skills and functional changes in frontal-parietal brain networks. Previous math remediation studies have relied on more intensive instruction involving tutoring or teaching methods (Fuchs et al., 2008; Fuchs et al., 2009; Powell, Fuchs, Fuchs, Cirino, & Fletcher, 2009) that many students may not have access to and/or are complicated and difficult to implement. The computerized program we utilized is readily available to the public for a small fee (http://www.lumosity.com/courses/lumosity-math-tutor) and thus represents a promising and practical alternative and/or complementary approach to math remediation. Computerized training has several advantages over other approaches including immediate feedback, availability for home practice, the ability to systematize delivery of the intervention and modifications to difficulty level, the ability to quantify multiple aspects of performance and progress and the provision of an entertaining and engaging interface.

Participants in the present study also showed statistically and clinically significant increases in math-related cognitive skills including processing speed, cognitive flexibility and visual-spatial processing performance following the math training program. A critical issue in cognitive training research is whether training-induced changes transfer or generalize to other relevant skills and/or real-world tasks (Green & Bavelier, 2008). In particular, it is expected that untrained tasks or skills involving a similar neural system to the trained task might also be influenced by the training (Thorell et al., 2009). Calculation skills, number sense and cognitive flexibility were directly trained during our training program. Processing speed was indirectly trained via the timed nature of the two math-related tasks. However, visual-spatial processing was not specifically trained and thus improvements in this area may potentially suggest a degree of transfer to untrained math-related skills. Visual-spatial processing skills are largely subserved by frontal-parietal regions and abnormalities in these areas have been shown to be associated with visual-spatial deficits in TS and other groups (Eckert et al., 2005; Holzapfel, Barnea-Goraly, Eckert, Kesler, & Reiss, 2006; Kesler et al., 2004). Thus, altered frontal-parietal function following the training program may have improved visual-spatial processing as well as math performance. The present findings are consistent with a previous study of visual-spatial skills training in healthy adolescent females that showed significantly increased posterior parietal activation and decreased prefrontal activation (Haier, Karama, Leyba, & Jung, 2009).

Processing speed and cognitive flexibility also involve frontal-parietal systems (Genova, Hillary, Wylie, Rypma, & Deluca, 2009; Lie, Specht, Marshall, & Fink, 2006). The present results may suggest that training-induced improvement of these skills is potentially associated with decreased frontal and increased parietal activation. Decreased activation following training is purported to reflect increased neural efficiency and has been previously associated with training of higher-level cognitive tasks (Dahlin, Backman, Neely, & Nyberg, 2009; Kelly, Foxe, & Garavan, 2006). Increased activation is believed to stem from recruitment of additional neural resources and/or heighted regional response (Poldrack, 2000), but has previously been associated only with sensorimotor training (Kelly et al., 2006). The present findings of increased rather than decreased parietal activation during a high-level cognitive task may reflect the adaptive nature of the training program. Adaptive training is designed to continuously increase learning and challenge neural systems with the goal of eventually producing more stable neurobiologic changes (Moucha & Kilgard, 2006). Thus, hierarchical skills training may be associated with increased cognitive load in certain regions and concomitantly increased, rather than decreased, activation in components of these networks. However, working memory and visual attention were not improved by our training program despite their reliance on frontal-parietal networks and their previously demonstrated improvement via training-induced changes in frontal-parietal function (Klingberg, 2010; Tomasi, Ernst, Caparelli, & Chang, 2004). These skills may require direct rather than indirect training approaches, longer training duration and/or other modifications to the training program.

There are several limitations to this pilot, case series study that should be considered. Most importantly, the lack of a no-training or alternate training comparison group increases the probability that our findings were due to practice effects or regression towards the mean. We utilized math tests that have strong test-retest reliabilities (.83–.97) and employed alternate forms for these as well as our fMRI task to reduce the effects of practice. The sample demonstrated math and cognitive test scores that were all within 1 standard deviation of the normative mean (100 ± 15), with the exception of MVPT, which was 1.2 standard deviations below the normative mean. These are not extreme scores and thus not as influenced by regression towards the mean. Advanced statistical methods and robust covariates were employed to reduce variability in baseline scores due to confounding factors and to evaluate the reliability of test score changes. Additionally, a previous study of computerized math skills training (Wilson, Revkin, et al., 2006) as well as neuroimaging studies of executive function training have successfully utilized a similar AB design (Dux et al., 2009; McNab et al., 2009). Nevertheless, a randomized trial is necessary to demonstrate the true potential of training number sense and math skills.

The sample size was relatively small and limited the ability to address the effects of demographic or other variables on training efficacy, for example. It is also not known whether changes in cognitive ability and brain activation would be stable over time. Longitudinal follow-up is required to address this limitation. The fMRI math task involved an element of response inhibition given that participants were required to respond only if the math equation was correct and thus inhibit responding to incorrect equations. We did not assess response inhibition performance and therefore do not know the impact of participants’ functioning in this cognitive domain on the math training or brain activation outcomes. The math strategies that participants used pre- or post-training were not assessed and thus some of them may have already been familiar with decomposition and/or other advanced strategies. These results may be specific to children with TS and/or to children who do not demonstrate severely impaired math or cognitive function at baseline. It is unknown how critical the strategy instruction session was to the success of the training program. Although this session was very basic and could technically be implemented by non-professional individuals, S.K. is a licensed clinical psychologist and therefore subtle, specialized clinical skills that are difficult to standardize or quantify may have played a role in the training procedure.