Assessment of linear-scale indices for perimetry in terms of progression in early glaucoma

Abstract

Currently, global indices that summarize the visual field combine sensitivities on a logarithmic (decibel) scale. Recent structure-function models for glaucoma suggest that contrast sensitivity should be converted to a linear scale before averaging across visual field locations, to better relate sensitivity with the number of surviving retinal ganglion cells (RGCs). New indices designed to represent the number of RGCs already lost are described. At least one was found to be a significantly better predictor of subsequent rate of change than traditional Mean Deviation (p=0.014) in participants with glaucomatous optic neuropathy. Issues concerning the creation of optimal global indices are discussed.

1 Introduction

Primary open-angle glaucoma is characterized by loss of retinal ganglion cells (RGCs). Therefore, when assessing the visual field in order to predict the future rate of functional progression, it would appear reasonable to assess and predict the rate of RGC loss. Both structural and functional tests for glaucoma may be regarded as surrogates for measuring the current number of functioning RGCs. These surrogate measures are imperfect, as they are affected by between-participant and within-participant variability, as well as non-pathologic neural factors. These imperfections are evidenced by the observed weakness of the cross sectional and longitudinal structure-function relations (Anderson, 2006, Bowd, Zangwill, Medeiros, Tavares, Hoffmann, Bourne, Sample & Weinreb, 2006, Caprioli, 1989, Gardiner, Johnson & Cioffi, 2005, Strouthidis, Vinciotti, Tucker, Gardiner, Crabb & Garway-Heath, 2006) Recently, work has been conducted to link more accurately results from perimetric and imaging measures to RGC counts (Drasdo, Mortlock & North, 2008, Garway-Heath, Caprioli, Fitzke & Hitchings, 2000, Harwerth, Carter-Dawson, Smith, Barnes, Holt & Crawford, 2004, Harwerth, Crawford, Frishman, Viswanathan, Smith & Carter-Dawson, 2002, Harwerth, Vilupuru, Rangaswamy & Smith, 2007, Hood, 2007, Hood, Anderson, Wall & Kardon, 2007, Hood & Kardon, 2007, Hood, Anderson, Wall, Raza & Kardon, 2009). Contrast sensitivity measured during perimetry is generally reported in decibels (dB); for the most commonly used perimetric stimuli, 1dB difference represents a change of 0.1 log₁₀ units of light attenuation, where attenuation is the reciprocal of the stimulus luminance in candelas per meter squared (cd/m²) or apostilbs (asb), where 1 cd/m² = π asb. These papers have suggested that perimetric sensitivity values should be transformed from the dB scale to a linear scale before they are averaged, as this may result in better correlations with RGC counts. It is therefore prudent to consider the use of linear-scaled global indices as summary measures of the visual field, as possible alternatives to the current decibel-based measures such as Mean Deviation (MD).

Recognizing when a patient’s vision is deteriorating rapidly is a key aspect of glaucoma follow-up, so that appropriate management strategies can be implemented to slow or halt progression. However, measuring and predicting rates of progression remains challenging. Non-perimetric indices have been found to be associated with an increased probability of future progression, and/or a more rapid rate of future progression. These include higher Intraocular Pressure (IOP) (Friedman, Wilson, Liebmann, Fechtner & Weinreb, 2004, Gordon, Beiser, Brandt, Heuer, Higginbotham, Johnson, Keltner, Miller, Parrish, Wilson, Kass & Ocular Hypertension Treatment Study Group, 2002, Leske, Heijl, Hussein, Bengtsson, Hyman, Komaroff & Group, 2003, Nouri-Mahdavi, Hoffman, Coleman, Liu, Li, Gaasterland & Caprioli, 2004), greater IOP fluctuation (Hong, Seong & Hong, 2007, Nouri-Mahdavi et al., 2004), increased age (Broman, Quigley, West, Katz, Munoz, Bandeen-Roche, Tielsch, Friedman, Crowston, Taylor, Varma, Leske, Bengtsson, Heijl, He & Foster, 2008, Friedman et al., 2004, Gordon et al., 2002, Leske et al., 2003, Nouri-Mahdavi et al., 2004) and belonging to certain racial groupings (Broman et al., 2008, Drance, Anderson & Schulzer, 2001, Gordon et al., 2002), although some of these factors have been disputed (Bengtsson, Leske, Hyman & Heijl, 2007, Drance et al., 2001, Friedman et al., 2004). Even after taking these factors into account, the current status of the patient’s visual field may also be a predictor of their functional prognosis (Gardiner, Demirel & Johnson, 2011, Leske et al., 2003), with patients exhibiting more severe functional loss being at higher risk of more rapid subsequent progression.

This study derives linear-based indices from published structure-function models that have been designed to reflect the number or loss of RGCs. They are then compared to current decibel-based indices in terms of their ability to predict subsequent rate of change in eyes with high-risk ocular hypertension and early glaucoma. Issues surrounding the design of an optimal global index are then discussed. While it is unlikely that clinical decisions concerning progression would be made on the basis of just one visual field modality without considering other factors, an index showing improved prognostic ability in isolation would be expected to improve the overall prognostic ability when additional information is added. The overall goal of this project is to develop indices that can be used for identification of participants at higher risk of rapid subsequent functional progression, so that their management can be tailored appropriately, while also learning more about the disease process.

2 Methods

2.1 Data

Data for this study were obtained from an ongoing longitudinal study of progression in participants with early and suspected glaucoma, at Devers Eye Institute in Portland, Oregon, USA. The study adheres to the tenets of the Declaration of Helsinki, complies with the United States Health Insurance Portability and Accountability Act of 1996 (HIPAA), and the protocol was approved by the Institutional Review Board at Legacy Health. Each participant provided written informed consent, after having the risks and benefits of participation explained to them.

Participants were tested annually with a variety of structural and functional tests (Gardiner et al., 2005, Spry, Johnson, Mansberger & Cioffi, 2005). In 93% of cases, testing took place within two months of the same date as the previous year (mean interval 368 days, standard deviation 62 days). At study entry, participants had either a clinical diagnosis of early glaucoma, or ocular hypertension (untreated IOP ≥ 22mmHg on more than one occasion) plus one or more possible risk factors for glaucoma as determined by their clinician (age > 70, systemic hypertension, diet controlled diabetes, peripheral vasospasm, African ancestry or self-reported family history of glaucoma) and/or previously diagnosed glaucomatous optic neuropathy (GON) or suspicious optic nerve head appearance (cup-disc ratio asymmetry >0.2, neuroretinal rim notching or narrowing, disc hemorrhage) (Gardiner et al., 2005, Spry et al., 2005). Participants who had other serious ocular diseases or who were using medications likely to affect the visual field, or who had undergone ocular surgery (except for uncomplicated cataract surgery), were excluded. In addition, glaucoma participants with visual acuity worse than 20/40 in either eye or with MD from standard automated perimetry worse than −6dB at enrollment were excluded to minimize potentially compromising factors such as cataract and higher variability associated with more advanced glaucoma.

Visual field tests were performed with a Humphrey Field Analyzer II (Carl Zeiss Meditec Inc, Dublin, CA, USA). The 24-2 testing pattern and conventional test procedures were employed (Anderson & Patella, 1999). For the current analysis only fields collected with the SITA standard algorithm (Bengtsson, Olsson, Heijl & Rootzen, 1997) were used. An optimal lens correction was placed before the tested eye, and the fellow eye was occluded with a translucent eye patch. All participants had undergone at least one visual field test prior to entering the study. In addition, stereo optic nerve head photos (3-Dx, Nidek Co. Ltd., Gamagori, Japan) taken at each participant’s initial visit were evaluated to determine whether the eyes exhibited GON. Optic nerve heads were classified as either GON or within limits of normal appearance by two masked experienced fellowship-trained glaucoma specialists, with adjudication by a third masked glaucoma specialist if consensus was not reached (Fortune, Demirel, Zhang, Hood, Patterson, Jamil, Mansberger, Cioffi & Johnson, 2007). This was recorded along with age at baseline, IOP at baseline measured by Goldmann Applanation Tonometry (Haag-Streit, Bern, Switzerland) with the participant seated at a slit lamp, and treatment status (whether the patient reported that they were taking ocular hypotensive medications prescribed by their eye care specialist).

For inclusion in this study, participants were required to have performed reliable SITA standard visual field tests (≤33% fixation losses, ≤15% false positives) at seven or more annual visits (i.e. over a six year period). All such participants were included. False negative rates were not considered for reliability because they increase with visual field loss due to higher variability of response in damaged visual field areas (Bengtsson & Heijl, 2000). If results from more than seven annual visual field tests were available, data from the seven most recent tests were used. To increase the range of rates of change in the dataset and so make the conclusions more generalizable, the fastest changing eye of each participant was chosen as detailed below. In total, 95 participants satisfied these entry criteria. These were split for analysis into two cohorts; 50 participants exhibiting GON at baseline (who are therefore assumed to have glaucoma), and 45 participants with optic disc appearance within normal limits at baseline (who are assumed to have either very early glaucoma or moderate- to high-risk ocular hypertension). The non-GON cohort can be thought of as an independent dataset to test indices that appear useful based on results from the GON cohort, although the reduced severity and range of disease may hinder the ability to draw firm conclusions. Age, MD and Pattern Standard Deviation (PSD) for these two groups at the first of the seven visits used in this study are summarized in Table 1. The study population is 95% white due to the demographics of the region in which the study was conducted. The new Visual Field Index (VFI) (Bengtsson & Heijl, 2008) had a median value of 99.6% of ‘normal vision’ in the GON cohort at the first visit, and a median of 99.9% in the participants without GON; MD was used in preference to VFI to assess progression in this cohort due to the ceiling effect that is present for VFI in early glaucoma (Artes, O’Leary, Hutchison, Heckler, Sharpe, Nicolela & Chauhan, 2011).

Table 1.

Baseline characteristics of the study population.

	Participants with GON		Participants without GON
	Mean	Standard Deviation	Mean	Standard Deviation
Age (years)	57.2	10.5	53.4	8.9
MD (dB)	−0.31	2.56	0.93	2.07
PSD (dB)	6.14	1.94	5.27	1.21

2.2 Indices

The indices described here generate an estimate of the RGC count across the central visual field. They do this by estimating the RGC count at each location, and then averaging this across locations. However, if it were assumed that each individual RGC has a constant statistical hazard over the duration of the study (i.e. the probability of the RGC dying in the next month is constant, independent of how many months have already passed, giving a constant percentage loss of remaining RGCs per unit time), then the total RGC count would decline exponentially over time. This would manifest as a linear reduction in the logarithm of the RGC count. Therefore, the indices are transformed back onto a decibel scale after the process of averaging over locations. This makes linear regression of dB scaled indices over time appropriate to measure functional change. This choice eases interpretation compared to exponential regression of linear scaled indices, and is applied to all the indices.

Sensitivity values at each location are reported by the Humphrey perimeter in two formats, as raw dB sensitivity and as a total deviation (TD), the latter representing how much higher or lower the sensitivity is compared with an age-corrected and location-specific normal database. Each of these can be expressed either in dB (as output by the perimeter), or transformed onto a linear scale by the transformations Sens_dB = 10 * log₁₀(Sens_Lin) and TD_dB = 10 * log₁₀(TD_Lin); equivalently, Sens_Lin = 10^SensdB/10 and TD_Lin = 10^TDdB/10.

Six summary measures of the visual field were used.

1. LMS: Linear Mean Sensitivity. The arithmetic mean of the linear sensitivity values Sens_Lin, transformed back onto a decibel scale (Hot, Dul & Swanson, 2008, Yang & Swanson, 2007).

2. Count_G: The RGC count according to a model published by Garway-Heath et al (Garway-Heath et al., 2000). At each location, this is given by Sens_Lin = −392 + (208 * Count)^k where k is an eccentricity-dependent coefficient of summation. This count is averaged over all 52 locations and then transformed back onto a decibel scale.

3. Count_Ha: The RGC count according to a model published by Harwerth et al (Harwerth et al., 2004, Harwerth & Quigley, 2006). At each location, the RGC count in dB is given by (Sens_dB −b)/m, where m = 0.95 + (0.054 * ε) and b = −14.8 − (1.5 *ε), with ε being the retinal eccentricity in degrees. These RGC counts are then transformed into linear units, averaged (arithmetic mean), and then converted back onto a decibel scale.

4. Loss_Ho: The loss of RGCs according to a model published by Hood et al (Hood, 2007, Hood et al., 2007, Hood & Kardon, 2007). At each location, this is given by the total deviation expressed in linear units, TD_Lin. The arithmetic mean of these values is then converted back onto a decibel scale.

5. Count_D: The RGC density according to a model published by Drasdo et al (Drasdo et al., 2008). Below 29dB, this is given by density = 0.2065 * Sens_Lin. Above 29dB, a non-linear relation applies, given by density = 191.1 − 1.088*Sens_Lin + 0.003101*Sens_Lin2 − 0.00000319*Sens_Lin3 + 0.00000001223*Sens_Lin4. As above, these values were averaged across locations, and then converted back to a decibel scale.

6. Count_DA: The RGC density according to the model published by Drasdo et al as above, but after the sensitivities have been age-corrected (Drasdo et al., 2008). The equations were based on a participant of age 60; therefore, the sensitivity Sens_dB was age-adjusted accordingly before it was converted to linear units, by addition of the normal sensitivity at that location at age 60 to the total deviation TD_dB.

For reference, results using Mean Deviation (MD) are also reported. A summary of all the indices considered is given in Table 2.

Table 2.

Summary of the indices considered in this study. Additionally, a capped version of each index (except MD) was calculated, in which all sensitivities were constrained to no more than the age-corrected normal value before the index was calculated; these are referred to as LMS(cap) etc.

Index Name	Description	Structure-function model used	Based on	RGC count adjusted for:	Formula for one location	Other parameters
MD	Mean decibel deviation from normal		TDdB	Age	TDdB
LMS	Mean linear deviation from normal		SensLin		SensLin
CountG	RGC count	Garway-Heath et al	SensLin	Eccentricity	SensLin = −392 + (208 * CountG)k	k is an eccentricity-dependent scaling factor
CountHa	RGC count	Harwerth et al	SensdB	Eccentricity	CountHa = (SensdB −b)/m	m = 0.95 + (0.054 * ε) b = −14.8 − (1.5 * ε) ε = eccentricity
LossHo	RGC loss	Hood et al	TDLin	Age	TDLin
CountD	RGC density	Drasdo et al	SensLin		Below 29dB: CountD = 0.2065* SensLin Above 29dB: CountD = 191.1 − 1.088*SensLin + 0.003101*SensLin2− 0.00000319*SensLin3 + 0.00000001223*SensLin4
CountDA	RGC density	Drasdo et al	TDLin	Age	Same as CountD	SensLin replaced by TDLin+Sens60, the normal sensitivity at age 60

Note that the published models produce RGC counts across different areas of the retina, and so the resultant indices may differ by (on the dB scale) an additive constant. This was not corrected for, to maintain equivalence with the published works. An additive constant offset will not affect any of the results for predictability or comparisons between the prognostic utility of the indices. By the same logic, it makes no difference whether values are summed or averaged across locations (giving RGC counts differing by a multiplicative constant of 52 on the linear scale, and hence by an additive constant of 17.2dB). Although we refer to indices as representing RGC count for brevity, in fact some indices represent RGC count, some RGC loss and some RGC density. However, this does not affect comparisons when converted to a decibel scale.

While these models have been derived to predict RGC counts in eyes with glaucoma, there is considerable variability among normal eyes. The relation between retinal nerve fiber layer thickness (a presumed surrogate for RGC count) and sensitivity in normal eyes is weak (Hood et al., 2007). For this reason, the model described by Hood et al was derived based on the amount of damage, without above-normal sensitivities. Also, the SITA standard algorithm is designed to minimize errors on a dB scale. Therefore as an example, a true sensitivity of 34dB being measured as 36dB due to 2dB measurement error corresponds to an error of 1470 linear (1/contrast) units; whereas a true sensitivity of 16dB being measured as 18dB corresponds to an error of only 23 units on the same linear scale. This means that apparently small measurement errors at locations with normal and above-normal sensitivity have a disproportionately large effect on the outcome measure compared with the same dB measurement error at a damaged location, when the overall index is generated by calculation of the average over all locations. Due to these factors, it may be a reasonable tradeoff to suggest that the new global indices could perform better if the sensitivities at each location were ‘capped’ at normal, to effectively provide an estimate of RGC loss due to glaucoma, rather than the existing RGC count. Hence, all seven indices were recalculated after sensitivity values were capped at each individual location, so that the capped TD_dB has a maximum of zero, and the capped Sens_dB has a maximum of the age-referenced normal value. These will be referred to as LMS(cap) etc.

2.3 Analyses

For each of the thirteen indices (the six indices enumerated above, both capped and uncapped in each case, plus traditional MD), baseline values were calculated (the value in Year 1 of the series), together with the subsequent slope, defined as the slope of a linear regression of that index over years 2–7 of the series. The aim is then to find the baseline index that best predicts subsequent slope, i.e. the rate of subsequent functional progression. An improved ability of an index to predict subsequent change of that same index illustrates that the relation between its value and its rate of change is less variable, and hence it may be useful as a prognostic indicator However, an index with a fixed value of zero would be perfectly predictable over time, yet uninformative about the status of the visual field. Therefore, it is necessary also to test the ability of the index to predict subsequent changes in an index that is already known to represent the visual field status. Subsequent slope of MD was chosen as the outcome measure for this purpose. In all analyses below, the baseline value of an index is used to predict both its own subsequent slope and the subsequent slope of MD. This subsequent slope of MD was also used to define the fastest changing eye for each participant, for use in all analyses.

Linear regression was used to predict subsequent slope of MD based on the value of each of the indices in turn, plus IOP, Treatment status and Age, measured at baseline. Of the 95 participants, three had missing IOP readings at baseline and so were excluded from these analyses. Stepwise backwards elimination was used to exclude the least significant predictor at each stage, to maximize the adjusted R² of the fit. The value of the index being considered as a predictor was not eligible for elimination from the regression during this process. Once backwards elimination had been completed, the adjusted R² of the final model was recorded, as a measure of how well the index predicts the subsequent slope of MD after other factors have been accounted for. The correlation between the actual subsequent slope and that predicted by the model for each participant was compared against the equivalent correlation for MD predicting the subsequent slope of MD, to determine whether the index demonstrated significantly better predictability, using the Z₂* test statistic (Steiger, 1980).

After this had been carried out for all predictor indices, the process was repeated when the indices were used to predict their own subsequent slopes, instead of the slope of MD. Analyses were carried out both for the 49 participants exhibiting GON at the initial visit (excluding one of the fifty GON participants with missing baseline IOP), referred to as the GON cohort, and also for the remaining 43 participants (excluding two participants with no baseline IOP), referred to as the non-GON cohort.

Use of a linear regression model such as that above to predict subsequent slope relies on implicit assumptions about the relation between the predictor and the outcome. Therefore, non-parametric analyses were also carried out, which do not require such stringent assumptions for validity. These cannot predict the actual subsequent slope, but aim instead to predict the ranking of the subsequent slope, i.e. to identify the participants likely to undergo the most rapid rate of subsequent change. Firstly, the Spearman rank correlations between the value of an index at baseline and the subsequent slopes of MD and of the same index were calculated for both cohorts. To determine whether correlations were significantly better than that predicting subsequent slope of MD from baseline MD, the same Z₂* statistic was used as before.

The participants were then divided into tertiles based on their subsequent rate of progression as measured by the subsequent slope of MD and of each other index in turn. Note that this may result in participants being placed in different tertiles for different indices. Tertiles were chosen over other possible categorizations to ensure a reasonable sample size in each (Kass, Gordon, Gao, Heuer, Higginbotham, Johnson, Keltner, Miller, Parrish, Wilson & for the Ocular Hypertension Treatment Study, 2010). Wilcoxon rank sum tests were performed to compare the baseline values of the indices between participants in the worst tertile (most rapid progression) and participants in the other two tertiles. Then, logistic regression was performed to predict the probability that a participant would be in the worst tertile, with the baseline index value, Age, IOP and Treatment status as predictors. Stepwise backwards elimination was used to minimize the Akaike Information Criterion; AIC = 2k − 2 ln(L), where k is the number of parameters in the statistical model and L is the maximized value of the likelihood function for the estimated model, to give a measure of goodness-of-fit for the model that penalizes over-fitting by inclusion of too many predictors. Nagelkerke’s pseudo-R² coefficient of determination was used to assess the strength of association in the final model (Nagelkerke, 1991). These analyses are designed to evaluate whether the baseline value of an index could be used to identify those participants most likely to undergo more rapid subsequent progression, since these are the most crucial participants to identify in a clinical situation. Again, the tests were repeated for both cohorts.

3 Results

Table 3 shows results from the parametric linear regression analysis. When the subsequent slope of the same index is predicted, the two indices based on RGC count showed significantly worse predictive power than MD in the GON cohort; Count_G (p=0.012) and Count_G(cap) (p=0.043). The best predictor was RGC loss, Loss_Ho(cap), which showed greater predictive power than MD for the GON participants (p=0.014). While other indices also produced greater adjusted R² values than MD, for both the GON and non-GON cohorts, none reached statistical significance (p>0.10 in all cases).

Table 3.

Adjusted R² of models that use the baseline value of each index to predict the subsequent rate of change. Values in bold were significantly different (better or worse) from the model that used MD to predict subsequent slope of MD (p<5%). A backwards-elimination linear regression model was used as outlined in the Methods section. Definitions of each index are given in the Methods section. The indices labeled ‘cap’ are calculated after pointwise sensitivities were capped at the age-corrected normal value.

		Participants with GON		Participants without GON
Baseline Index:	Based on model from:	Adjusted R2 predicting slope of MD	Adjusted R2 predicting slope of same index	Adjusted R2 predicting slope of MD	Adjusted R2 predicting slope of same index
MD		0.14	0.14	0.17	0.17
LMS	Linear-scaled mean	0.13	0.14	0.15	0.08
CountG	Garway-Heath	0.10	0.01	0.15	0.01
CountHa	Harwerth	0.13	0.06	0.15	0.03
LossHo	Hood	0.12	0.12	0.14	0.07
CountD	Drasdo	0.09	0.13	0.14	0.09
CountDA	Drasdo (age-corrected)	0.08	0.08	0.13	0.10
LMS(cap)	Linear-scaled mean	0.12	0.20	0.16	0.18
CountG(cap)	Garway-Heath	0.05	0.01	0.19	0.02
CountHa(cap)	Harwerth	0.10	0.05	0.18	0.08
LossHo(cap)	Hood	0.15	0.27	0.12	0.20
CountD(cap)	Drasdo	0.04	0.03	0.11	0.07
CountDA(cap)	Drasdo (age-corrected)	0.06	0.22	0.11	0.13

Table 4 presents non-parametric Spearman correlation coefficients between baseline values of each index and the subsequent slopes both of the same index and of MD. Count_G again performed significantly worse than MD in the GON cohort (p=0.029). Count_DA(cap) performed significantly better in the GON cohort (p=0.035); Loss_Ho(cap) performed better in both cohorts (p=0.031 for GON, and p=0.012 for non-GON). Note that these rank correlations can appear artificially high when tied observations occur in the dataset. In particular, for the capped indices, there are multiple fields in the dataset for which the index value is the same (since every test location was at or above the age-corrected normal sensitivity), especially in the non-GON cohort. Therefore, correlations for these capped indices should be interpreted with caution; they are reported here for completeness.

Table 4.

Spearman correlation coefficients obtained when the baseline value of each global index is used to predict the rate of change, with associated p-values in brackets. Values in bold were significantly different from the model that used MD to predict subsequent slope of MD (p<5%). The indices labeled ‘cap’ are calculated after pointwise sensitivities were capped at the age-corrected normal value.

		Participants with GON		Participants without GON
Baseline Index:	Based on model from:	Correlation with slope of MD	Correlation with slope of same index	Correlation with slope of MD	Correlation with slope of same index
MD		0.34 (p=0.02)	0.34 (p=0.02)	0.09 (p=0.55)	0.09 (p=0.55)
LMS	Linear-scaled mean	0.45 (p<0.01)	0.37 (p=0.01)	0.21 (p=0.16)	0.12 (p=0.45)
CountG	Garway-Heath	0.41 (p<0.01)	0.13 (p=0.37)	0.25 (p=0.10)	−0.00 (p=1.00)
CountHa	Harwerth	0.41 (p<0.01)	0.32 (p=0.02)	0.21 (p=0.16)	0.13 (p=0.38)
LossHo	Hood	0.35 (p=0.01)	0.25 (p=0.08)	0.09 (p=0.56)	−0.00 (p=0.98)
CountD	Drasdo	0.42 (p<0.01)	0.36 (p=0.01)	0.18 (p=0.23)	0.01 (p=0.97)
CountDA	Drasdo (age-corrected)	0.32 (p=0.02)	0.25 (p=0.08)	0.10 (p=0.52)	−0.10 (p=0.52)
LMS (cap)	Linear-scaled mean	0.40 (p<0.01)	0.39 (p=0.01)	0.24 (p=0.11)	0.39 (p=0.01)
CountG (cap)	Garway-Heath	0.32 (p=0.03)	0.14 (p=0.32)	0.27 (p=0.07)	0.21 (p=0.16)
CountHa (cap)	Harwerth	0.35 (p=0.02)	0.31 (p=0.03)	0.23 (p=0.13)	0.39 (p=0.01)
LossHo (cap)	Hood	0.43 (p<0.01)	0.57 (p<0.01)	0.05 (p=0.73)	0.48 (p<0.01)
CountD (cap)	Drasdo	0.30 (p=0.04)	0.24 (p=0.10)	0.09 (p=0.56)	−0.04 (p=0.81)
CountDA (cap)	Drasdo (age-corrected)	0.38 (p=0.01)	0.59 (p<0.01)	0.12 (p=0.44)	0.32 (p=0.03)

Table 5 presents p-values from Wilcoxon rank sum test comparisons of the baseline values of each index between the worst tertile for subsequent rate of change (as defined either by the slope of MD, or the slope of the same index) and the remaining participants. Almost all indices showed significant differences in the GON cohort whichever tertiles were used. In the non-GON cohort, only three indices showed significant differences at baseline when tertiles were based on the same index; LMS(cap), Count_Ha(cap) and Loss_Ho(cap).

Table 5.

Comparison of the baseline values of each index between those participants in the worst tertile of subsequent slope vs. the remaining participants. Values given are p-values from a Wilcoxon’s rank sum test.

		Participants with GON		Participants without GON
Baseline Index:	Based on model from:	Compare tertiles of slope of MD	Compare tertiles of slope of same index	Compare tertiles of slope of MD	Compare tertiles of slope of same index
MD		0.03	0.03	0.99	0.99
LMS	Linear-scaled mean	<0.01	0.04	0.43	0.80
CountG	Garway-Heath	<0.01	0.96	0.60	0.61
CountHa	Harwerth	<0.01	0.05	0.45	0.73
LossHo	Hood	0.02	0.03	0.26	0.36
CountD	Drasdo	<0.01	0.01	0.25	0.59
CountDA	Drasdo (age-corrected)	0.02	0.09	0.20	0.21
LMS (cap)	Linear-scaled mean	<0.01	<0.01	0.18	<0.01
CountG (cap)	Garway-Heath	<0.01	0.02	0.24	0.38
CountHa (cap)	Harwerth	<0.01	<0.01	0.35	0.01
LossHo (cap)	Hood	0.01	<0.01	0.95	0.01
CountD (cap)	Drasdo	0.01	0.18	0.77	0.08
CountDA (cap)	Drasdo (age-corrected)	0.03	<0.01	0.80	0.10

Table 6 presents Nagelkerke pseudo-R² values from the logistic regression analysis, in which baseline values of each index were used to predict whether a participant would be in the worst tertile for subsequent rate of change.

Table 6.

Nagelkerke pseudo-R² index for models that used the baseline value of each index to predict the probability of the participant being in the worst tertile of subsequent rate of change. Backwards-elimination logistic regression was used as outlined in the Methods section. The indices labeled ‘cap’ are calculated after pointwise sensitivities were capped at the age-corrected normal value.

		Participants with GON		Participants without GON
Baseline Index:	Based on model from:	R2 predicting tertile of slope of MD	R2 predicting tertile of slope of same index	R2 predicting tertile of slope of MD	R2 predicting tertile of slope of same index
MD		0.33	0.33	0.31	0.31
LMS	Linear-scaled mean	0.34	0.35	0.29	0.26
CountG	Garway-Heath	0.35	0.04	0.28	0.22
CountHa	Harwerth	0.35	0.22	0.28	0.07
LossHo	Hood	0.34	0.36	0.28	0.27
CountD	Drasdo	0.34	0.18	0.26	0.28
CountDA	Drasdo (age corrected)	0.34	0.12	0.26	0.29
LMS (cap)	Linear-scaled mean	0.31	0.18	0.31	0.50
CountG (cap)	Garway-Heath	0.29	0.09	0.30	0.10
CountHa (cap)	Harwerth	0.30	0.21	0.31	0.19
LossHo (cap)	Hood	0.34	0.34	0.34	0.65
CountD (cap)	Drasdo	0.28	0.04	0.24	0.29
CountDA (cap)	Drasdo (age-corrected)	0.28	0.33	0.31	0.29

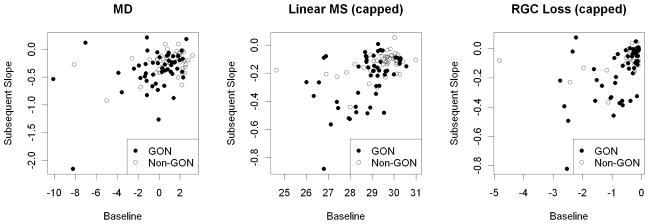
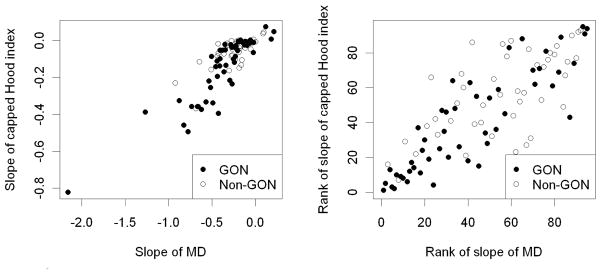
Figure 1 shows plots of baseline value against subsequent slope for MD and two of the indices, LMS(cap) and Loss_Ho(cap). Figure 2 shows plots that compare the rates of change by MD and Loss_Ho(cap), both as actual values and when the ranks of the rates are compared. Mostly the same eyes are identified by both indices as being rapid progressors.

Figure 1.

The subsequent rate of change over years 2–7 of the sequence, plotted against baseline value in Year 1, for three of the global indices considered in this study; Mean Deviation (MD), Capped Linear Mean Sensitivity (LMS(cap)), and Capped RGC Loss according to the model by Hood et al (Loss_Ho(cap)). Note that while the units for all indices are decibels, the scales on the axes differ, since the indices took values over different ranges. Shading of the data points indicates whether the participant exhibited glaucomatous optic neuropathy at their initial visit.

Figure 2.

Comparison of the rates of change in Mean Deviation (MD) and in the Capped RGC Loss according to the model by Hood et al (Loss_Ho(cap)). The left plot compares the actual rates of change (slope of linear regression over time); the right plot compares the ranks of the rates.

4 Discussion

This manuscript is part of a study designed to improve estimates of the level of functional damage in glaucoma, and to predict which patients are likely to undergo rapid progression. Here, we examine linear-based indices from visual field sensitivities in such predictive models. Specifically, in this study we assessed participants with early or suspected glaucoma, and examine the relation between baseline parameters and subsequent rate of functional change when using linear-scaled indices. Several issues arise from such a study, each worthy of further consideration.

Increased damage to the visual field was found to be predictive of a more rapid subsequent rate of progression. There are several possible explanations for this ability of the current value of an index to predict the rate of subsequent change:

• The rate of change is not truly linear over time. This may be because the rate varies substantially during the series; or may be because the scale used to measure sensitivity is sub-optimal. If damage ‘accelerates’ on a dB scale, this would cause an apparent correlation between current status and subsequent rate of change. This issue is discussed further in subsection 4.4 below.

• Participants had already undergone some damage before entering the study. For example, suppose that two patients were enrolled two years after onset of damage, having previously had identical healthy visual fields. Of these two patients, the one progressing at the fastest rate will have a worse visual field upon study entry, causing an apparent correlation between ‘baseline’ (i.e. study entry) and subsequent rate of change. However, there are many factors influencing time of entry into the study, such as the date of first diagnosis; not all patients will have entered the same amount of time after onset of damage. These factors will dilute any such effect.

• Some participants are moderate- to high-risk ocular hypertensives, but have not developed actual glaucomatous damage and possibly never will. These participants will have normal fields, and little or no subsequent change, using current testing and analysis methods. This would again cause an apparent correlation between damage and more rapid subsequent change. However, all such participants would be expected to be within the non-GON cohort, so this is unlikely to explain the relation found among participants with GON at baseline.

It may be considered likely that the relation is in fact due to a combination of these factors.

Differences were found in the abilities of indices to predict subsequent change in that same index.

• Predictability of an index will be influenced by the manner in which it changes over time. If the relation between the index value and its rate of change is close to linear in one index, this could result in the initial value of that index appearing to be more predictive. By contrast, if the index changed absolutely linearly over time, its initial value would only derive any predictive value from the possibility that a patient with worse damage upon presentation may have developed glaucoma at the same date, but undergone more rapid progression since then. It should also be noted that all indices were expressed on a logarithmic scale before the comparisons were conducted, and so there may not be much difference in linearity between indices.

• Some of the indices exaggerate variability at locations that are still within the normal range; while others reduce this pointwise variability. In particular, capping sensitivities aims to reduce this normal variability to improve the signal-to-noise ratio; this is discussed further in subsection 4.2 below.

• Models of the structure-function relation that adjust for eccentricity-related changes may improve the ability of an index to reflect the true density of remaining RGCs. However, as discussed in subsection 4.3 below, it may also have an unintended and less welcome side-effect, by increasing the effect of pointwise variability at more central locations.

• The testing algorithm (SITA standard in this study) could increase the variability in some indices more than others. As discussed below, the SITA standard algorithm is designed to reduce pointwise measurement errors on a dB scale. However, linear-based algorithms, or algorithms where the density of test locations varies with eccentricity, may improve the performance of specific indices. Appropriate global indices should be one of the factors considered when choosing testing algorithms. Again, these possibilities are not mutually exclusive, and it would seem likely that a combination of different factors affects the overall results.

4.1 Predictability

No single measurement accurately predicted the future rate of change. Clinical decisions will be made on the basis of several sources of information, rather than just one index as used in this study. The weighting that is applied to each source of clinical information will also influence management decisions. However, improving the accuracy of any important source of information should have a beneficial effect on the overall prediction of progression. Obtaining and quantifying such an improvement in isolation from other factors, as in this study, produces findings that can then be incorporated into more complete prediction models in the future.

An example of a more realistic prediction model would be one that uses the index value at visit 1, and the change in that index between visits 1 and 2, together with IOP, Age, current treatment status, and the determination of whether the participant exhibited GON. A clinician could seek to use this information to predict the rate of change of MD over visits 1–7. When a regression was carried out with this model, IOP and treatment status turned out not to be significant predictors of outcome. When MD at visits 1 and 2 is used as the predictor, this model achieves an adjusted R-squared of 26%. When Loss_Ho(cap) is used as the predictor, the adjusted R-squared of the model is 30%. When Loss_Ho(cap) is used in this way to predict the rate of change of itself, rather than MD, the adjusted R-squared of the model rises to 52%. This analysis contains statistical bias, since an increased value of an index at visit 1 will cause the rate of change over visits 1–7 to be more negative. However, it demonstrates the potential utility of these linear-based indices in a more clinically realistic situation.

We focus not on an attempt to distinguish ‘progressing’ from stable participants, as this requires an arbitrary definition of what constitutes ‘progression’. Methods such as pointwise linear regression (Fitzke, Hitchings, Poinoosawmy, McNaught & Crabb, 1996, Gardiner & Crabb, 2002, Viswanathan, Fitzke & Hitchings, 1997), and indices related to irregularities of the visual field such as PSD and the Glaucoma Hemifield Test (GHT) can evaluate the characteristic patterns of loss corresponding to retinal nerve fiber layer defects, and can be used to identify deepening of existing scotomas. However, they have a more limited ability to detect generalized loss of function. It has been reported that pattern deviation analyses, which adjust for generalized visual field loss, underestimate the occurrence and severity of progression (Artes, Chauhan, Keltner, Cello, Johnson, Anderson, Gordon & Kass, 2010, Artes, Nicolela, LeBlanc & Chauhan, 2005). By contrast, global measures of ‘overall sensitivity’ such as MD may be less useful for the initial identification of glaucomatous damage, in part because a reduction in these indices could be the result of other pathologies such as cataract and in part because the contribution of very small defects may be diluted if the majority of the visual field is still normal. However, they are also sensitive to worsening generalized damage. If susceptibility to damage is greater at all locations in glaucomatous eyes than in normal eyes, as opposed to the susceptibility being higher at some locations but the same as normal elsewhere, then these indices may also be more predictable over time. Although in this study only global measures of ‘overall sensitivity’, analogous to MD, were considered, as a next step the same techniques will be used to generate linear pattern indices analogous to PSD.

There are several possible explanations for the relatively weak correlations observed between a participant’s current status and their subsequent rate of change. The dataset consisted of participants with very early glaucoma or (in many cases) only ocular hypertension, which limits the range of individual values. It may be that participants with more severe disease would have resulted in greater predictability, without the confounding variability caused by high-risk individuals who may never develop glaucoma. Certainly, if it were the case that current status does indeed predict future rate of change, a wider range of rates of change would be expected to result in stronger correlations. A problem more specific to this particular dataset is that not all participants were following the same treatment regimen. Indeed, participants seen to be progressing more rapidly will most likely have been prescribed more aggressive treatment by their clinician, with the intent of reducing their subsequent rate of change. This would decrease any true correlation between worse initial status and worse subsequent rate of change. At Year 1, 45% of participants in the GON cohort reported that they were undergoing treatment for ocular hypertension, and 19% of the non-GON cohort (although this is based purely on self report, with no means to assess compliance). These caveats lead us to believe that we may be underestimating the true predictive ability of current status, but further studies will be needed to confirm or refute this.

4.2 Capping Sensitivities

For each new index used, we also calculated a ‘capped’ index, in which the sensitivity at each location in the field was set to equal no more than the age-corrected normal value. The aim behind these capped indices is to reduce the problematic variability observed at normal and above-normal sensitivities, without affecting the true signal from below-normal sensitivities in damaged areas of the field. There is considerable variability among normal eyes. The relation between retinal nerve fiber layer thickness (a presumed surrogate for RGC count) and sensitivity in normal eyes is weak (Hood et al., 2007). Variability in undamaged areas represents a greater problem when expressed on a linear scale, since the SITA standard algorithm (Bengtsson et al., 1997) used for determining sensitivity is designed to minimize errors on a dB scale. As pointed out in the Methods section, a 2dB measurement error when the sensitivity is 34dB corresponds to an error of 1470 linear (1/contrast) units; whereas the same measurement error when the sensitivity is 16dB corresponds to an error of only 23 units on the same linear scale. Therefore when values from different locations are summed or averaged (before converting the resultant total back to the dB scale), the variability at a location with near-normal sensitivity will have more of an influence on the index than the variability at a damaged location in the same eye.

The capping performed in this study is very simplistic. Participants whose sensitivities are initially above the age-corrected normal value could progress for some time without any change occurring in the capped indices, particularly if the progression was generalized rather than localized. An ideal capping system would be individualized, such that the maximum pointwise sensitivity would be based on that expected in that particular participant in the absence of damage. However, there is currently no way of knowing what a participant’s “healthy” sensitivity would be. An approximation could be calculated by comparing undamaged areas of their visual field with the normal hill of vision; yet there is no way of knowing that an area (or even the fellow eye) is truly undamaged, especially given the possibility of generalized sensitivity losses due to glaucoma (Artes et al., 2010, Henson, Artes & Chauhan, 1999).

Despite the simplistic nature of the process used here, there was still some evidence that capping may improve the ability to predict subsequent change. For example, Loss_Ho(cap) frequently outperformed the uncapped Loss_Ho. The question then arises as to how much of this effect is due to a genuine reduction in the variability of the index, and how much is purely a mathematical artefact caused by participants with consistently above-normal sensitivities throughout the study period (who would exhibit a baseline index value equal to the capped maximum, and zero subsequent rate of change). To address this, we repeated the analysis used to generate Table 4 to calculate the correlation between baseline index value and subsequent rate of change for three of the indices, firstly among participants (from either the GON or non-GON cohorts) with a baseline MD < 0dB, and secondly among participants with baseline MD < 1dB. In all, 32 and 52 participants satisfied these respective criteria. Results are shown in Table 7. Although differences between the indices were not significant in this case, we believe that the observed improvement in predictability using the capped version of Loss_Ho supports our assertion that at least part of the benefits of capping is genuine and not merely artefactual.

Table 7.

Spearman correlation coefficients obtained when the baseline value of each global index is used to predict the rate of change, as in Table 4, in two subsets of the dataset.

	Participants with MD < 0dB		Participants with MD < 1dB
Baseline Index:	Correlation with slope of MD	Correlation with slope of same index	Correlation with slope of MD	Correlation with slope of same index
MD	0.13	0.13	0.39	0.39
LossHo	0.17	0.09	0.32	0.20
LossHo (cap)	0.33	0.35	0.50	0.53

Any benefits of capping in reducing the variability of an index may not be present in participants with more advanced disease. Future refinement of the capping process must take into account the need to be able to utilize the procedure in eyes at different stages of the disease and/or with coexisting ocular pathologies. An alternative approach to reducing the effect of variability in near-normal regions of the visual field could be to use testing algorithms based on the linear scale instead of SITA standard, so that measurement errors in these regions (when expressed in linear units) are no longer disproportionately large when compared to those at damaged locations. It is possible that this could reduce or remove the benefits of using capped global indices. More likely, it would improve the predictability of linear-based indices by reducing their variability. Due to this issue, any benefits of using the new indices described in this paper over the established indices may be underestimated. A linear staircase testing algorithm has been described (Malik, Swanson & Garway-Heath, 2006), and further work extending this concept is warranted.

4.3 Adjusting for Eccentricity

The models of Garway-Heath et al (Garway-Heath et al., 2000) and Harwerth et al (Harwerth et al., 2004, Harwerth & Quigley, 2006) both contain a fundamental difference from that of Hood et al (Hood, 2007, Hood et al., 2007, Hood & Kardon, 2007). They both adjust for eccentricity when predicting RGC counts. This may indeed make them more accurate in terms of relating structure to function, which is the purpose for which all the models were designed, as normal sensitivities differ with eccentricity. However, when averaging across locations, this eccentricity term causes some locations to receive greater weighting than others, causing the variability of the final index to increase. This causes the variability about Count_G(cap) and Count_Ha(cap) to be increased, which would be expected to make them less predictable than indices such as Loss_Ho(cap) that weight all test locations equally. There is some evidence for this in the Results section, where Loss_Ho(cap) exhibited higher correlations than these two alternatives when used as a predictor of the subsequent change in the same index.

As an illustration, let us assume that the variability is constant across the visual field (for a given sensitivity level) (Henson, Chaudry, Artes, Faragher & Ansons, 2000) with standard deviation σ. When all 52 locations have equal weight, their average has variance σ²/52. However, an index = 1.5 * (Sens₁+…+Sens₂₆) + 0.5 * (Sens₂₇+…+Sens₅₂) with varying weights has variance (26*1.52 + 26*0.5²) * σ²/52² = 1.25 * σ²/52; in other words, 25% higher. In reality, pointwise sensitivity and variability vary across the visual field, so the true increase in index variability caused by eccentricity weighting will not be as simple to calculate as in this example.

In order to negate this effect, and reduce the variability present in eccentricity-weighted indices, it is necessary to reduce the variability in the (higher weighted) central region of the field. This could be done by increasing the proportion of stimulus presentations that are made in the central regions, so that these sensitivity estimates have a smaller measurement error (in dB) than those in the periphery. Ideally, the measurement error in the estimate of the RGC count (and hence, in the linear-scaled sensitivity) should be constant across locations. An alternative method would be to employ a testing pattern that is denser in the center than in the periphery (i.e. more testing locations per unit area). The contribution to the total RGC count from each test location would then be more equal across sensitivities. Such testing grids are available on the Octopus 900 perimeter (Haag Streit International, Koeniz, Switzerland), although they are not optimized for this particular purpose; they are not currently available on the Humphrey Field Analyzer.

It should be noted that indices containing corrections for eccentricity might be optimal for other purposes, even if higher-weighted central locations are not measured more accurately than peripheral locations. Our results should not be taken as an indication as to which model is more accurate for studying the cross-sectional structure-function relationship.

4.4 Linearity of Progression

While MD is based on a dB scale, the other indices transform sensitivities/RGC counts onto a linear scale before averaging over locations, and then transforming back to a dB scale to produce the final index value. If the proportion of RGCs lost per unit time remains constant, this would result in a straight line on a plot of the index (in dB) against time. Coefficients obtained from linear regression over time then provide the appropriate measure of the rate of change.

However, the assumption that the proportionate rate of RGC loss remains constant throughout the disease is a simplification (Caprioli, Mock, Bitrian, Afifi, Yu, Nouri-Madhavi & Coleman, 2010). It is possible that in fact the actual number of RGCs lost per unit time remains constant, in which case linear regression of indices expressed in linear units would be more appropriate; this would result in progression appearing to accelerate when expressed in dB units. The reality may well be somewhere between these two extremes, with dB-scaled progression accelerating but not by as much as would be predicted by a constant rate of reduction in the RGCs count. Additionally, it may be considered unlikely that the rate of loss (by whichever scaling is chosen) would be consistent over time for any given eye; factors such as spikes in IOP and short-term compliance with medications could affect the rate in any given time period.

In this study, we used the structure-function models as described in the original literature. These models are still being refined. Notably, it has been suggested that the structure-function relation may change depending on disease stage (Gonzalez-Hernandez, Pablo, Armas-Dominguez, Rodriguez de la Vega, Ferreras & Gonzalez de la Rosa, 2009, Poinoosawmy, Fontana, Wu, Fitzke & Hitchings, 1997). Harwerth and colleagues have suggested that the relation between retinal nerve fiber layer thickness and RGC count varies with disease stage (Harwerth, Wheat, Fredette & Anderson, 2010). The index Count_G was constructed assuming that spatial summation remains constant throughout the disease process, which may not be the case (Garway-Heath et al., 2000, Redmond, Garway-Heath, Zlatkova & Anderson, 2010). Such refinements to the models may result in more accurate measurement of RGC count, and hence progression, in the future.

4.5 Conclusions

Participants with worse baseline visual fields were more likely to undergo more rapid subsequent loss of function in most, but not all, indices, presumably caused by glaucomatous progression, even after other risk factors such as age and IOP were adjusted for. This was especially true among eyes that already exhibited GON. This is an important problem facing clinicians; namely, determining whether a high-risk glaucoma suspect is likely to progress rapidly and require more aggressive management. Use of linear-based indices might in the future improve the assessment of the current status of the field, providing the clinician with a more accurate measurement of this risk factor. However, there are many issues to be overcome before an optimal index can be derived. The choice of index will likely depend on the purpose intended. For optimal performance, testing algorithms and patterns may need to be adjusted to reduce the variability present in a specific global index.

Research Highlights.

• Visual field status is predictive of subsequent rate of progression

• Current indices of field status are based on logarithmic scaled sensitivities

• Retinal ganglion cell counts have previously been shown to be related to linearly scaled sensitivities

• Linearly scaled indices may offer benefits over current indices

• Issues caused by logarithmic-scaled testing algorithms complicate this process