Abstract
Brightness induction refers to a class of visual illusions in which the perceived intensity of a region of space is influenced by the luminance of surrounding regions. These illusions are significant because they provide insight into the neural organization of the visual system. A novel quadrature-phase motion cancelation technique was developed to measure the magnitude of the grating induction brightness illusion across a wide range of spatial frequencies, temporal frequencies and test field heights. Canceling contrast is greatest at low frequencies and declines with increasing frequency in both dimensions, and with increasing test field height. Canceling contrast scales as the product of inducing grating spatial frequency and test field height (the number of inducing grating cycles per test field height). When plotted using a spatial axis which indexes this product, the spatiotemporal induction surfaces for four test field heights can be described as four partially overlapping sections of a single larger surface. These properties of brightness induction are explained in the context of multiscale spatial filtering. The present study is the first to measure the magnitude of grating induction as a function of temporal frequency. Taken in conjunction with several other studies (Blakeslee & McCourt, 2008; Robinson & de Sa, 2008; Magnussen & Glad, 1975) the results of this study illustrate that at least one form of brightness induction is very much faster than that reported by DeValois et al. (1986) and Rossi and Paradiso (1996), and are inconsistent with the proposition that brightness induction results from a slow “filling in” process.
Keywords: Brightness induction, cancelation, filling-in, spatial frequency, temporal frequency, quadrature motion
1. Introduction
Brightness induction refers to a class of visual illusions in which the perceived intensity of a region is modulated by the luminance of its surround. The spatial characteristics of these illusions have been and continue to be extensively studied because they reveal fundamental properties of neural organization in the visual system (for review see Kingdom, 2011). The temporal properties of brightness induction, however, have received much less attention and results from the few experiments which have been conducted appear contradictory. Two early studies measured the temporal characteristics of simultaneous brightness contrast (SBC), an induction effect in which a gray patch on a dark background looks brighter than an equivalent gray patch on a bright background. Magnussen and Glad (1975), and DeValois, Webster, DeValois and Lingelbach (1986), used direct brightness matching to compare the temporal frequency characteristics of induced brightness modulations versus real luminance modulations in SBC displays with 1° test fields and 3° surrounds. Using squarewave temporal modulation Magnussen and Glad (1975) found that the shapes of the matching functions for real and induced brightness were very similar, except that the functions describing the brightness of real luminance modulations were greater in magnitude and possessed slightly higher peak and cut-off temporal frequencies. For example, at a mean luminance of 3.2 cd/m2, real (induced) luminance modulations (for 80% modulation of test patch or inducing background) showed a peak temporal frequency around 3 Hz (1.5 Hz) with a cut-off near 20 Hz (8 Hz). At the higher mean luminance of 3200 cd/m2, peak temporal frequency for real (induced) modulations increased to 6 Hz (5 Hz) with a cut-off frequency of 40 Hz (20 Hz). DeValois et al. (1986) used sinusoidal temporal modulation, a mean luminance of 37 cd/m2, and modulation depths of 60% and 15%. They found that while brightness changes in the luminance-modulated test patch were visible over the entire temporal frequency range studied from 0.5 to 8 Hz, surround-induced brightness changes decreased rapidly for frequencies above 2.5 Hz, which is much lower than the value (8 Hz) reported by Magnussen and Glad (1975) in their low luminance condition. Subsequently, Rossi and Paradiso (1996) investigated whether the size of the induced region influenced the temporal properties of induction. They temporally modulated every other bar of a square-wave grating while holding the luminance of the intervening bars (the induced regions) constant. The temporal frequency cutoff for induction decreased as bar width increased. Narrow bars (0.25°) possessed cutoff frequencies of 1.5 to 5 Hz; for wider bars (16.7°) the cutoff frequency decreased to 0.5 to 2.0 Hz. Although they didn't measure it directly, based on the fact that they expected the critical flicker-fusion frequency (CFF) for luminance-modulated stimuli under the conditions of their experiment to be much higher, and to increase (rather than decrease) with increasing bar size, Rossi and Paradiso (1996) suggested that a “fast” process accounted for luminance modulation and that a slower “filling-in” process (Gerrits & Vendrik, 1970), specifically a neural spreading of information from the edges of the induced area, was responsible for induced brightness modulations.
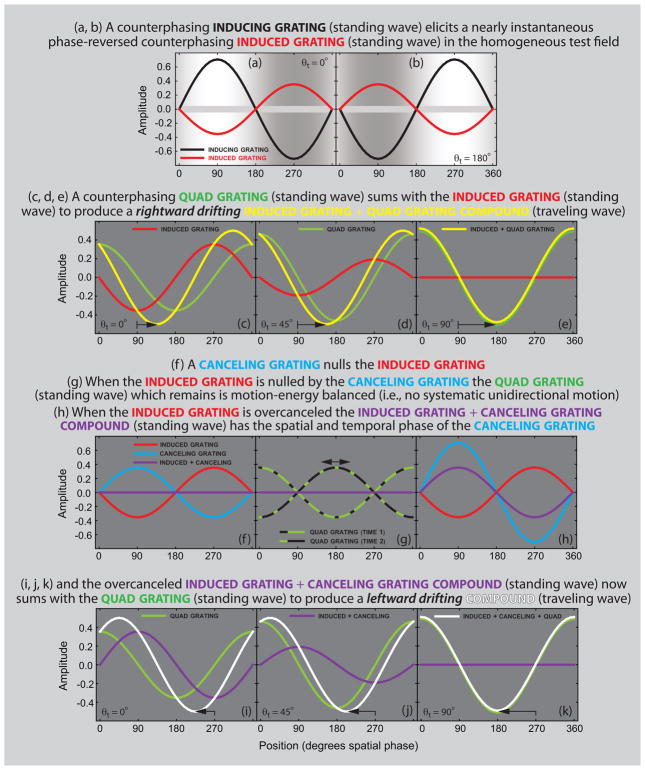
Two more recent studies, however, call into question the idea that brightness induction results from a separate slow “filling-in” process (Blakeslee & McCourt, 2008; Robinson & de Sa, 2008). Blakeslee and McCourt (2008) measured the phase (time) lag of grating induction, rather than the magnitude of induction discussed above. In grating induction a sinusoidal luminance grating induces a counterphase spatial brightness variation (a grating) in an extended homogeneous test field (Foley & McCourt, 1985; McCourt, 1982). The sinusoidal brightness profile of the induced grating allowed Blakeslee and McCourt (2008) to use a quadrature phase motion paradigm to precisely measure the phase (time) lag of induction at four temporal frequencies (2 Hz, 8 Hz, 16 Hz and 24 Hz). Note that DeValois et al. (1986) and Rossi and Paradiso (1996) attempted to measure the phase (time) lag of induction using direct phase matching, but found that these measurements were extremely difficult and yielded variable results. Sinusoidally counterphasing the inducing grating of a grating induction stimulus produces a counterphasing induced grating in the test field whose spatial phase is precisely opposite to that of the inducing grating (Blakeslee & McCourt, 1997; McCourt, 1982; 1994), and whose temporal phase lags the inducing grating by 180° plus a quantity corresponding to the time lag of brightness induction (Figure 1a, b). By adding to the test field a genuine luminance grating (a quadrature grating) of the same spatial and temporal frequency as the induced grating, but in spatial and temporal quadrature (90°) phase to it, a conspicuous traveling wave (i.e., quadrature motion) is produced, to which the visual system is extremely sensitive [Figure 1(c–e)]. Blakeslee and McCourt (2008) varied the temporal phase of the quadrature grating to measure the phase (time) lag of induction and compared the results to those obtained in a control condition using two luminance gratings. They found that the temporal response of induced brightness differed from that of luminance gratings by a small temporal phase lag (< 0.016 cycle) or by a small time lag (<1 ms), and remained constant across wide variations of temporal frequency and test field height (0.5°, 3.0°, 6.0° and 9°). The findings that the phase (time) lag of induction did not vary with test field height and that induction was present even at 24 Hz both argued strongly against a slow “fill-in” explanation for brightness induction.
Figure 1.
Explanation of the quadrature-phase motion cancelation technique. (a, b) The background illustrates the appearance of a grating induction stimulus for inducing gratings at 0° and 180° temporal phase. A counterphasing inducing grating (standing wave illustrated by black line) elicits a nearly instantaneous phase reversed counterphasing induced grating (standing wave illustrated by red line) in the homogeneous test field. (c–e) A counterphasing quadrature grating (standing wave illustrated by green line) added to the test field sums with the induced grating (red line) to produce a rightward drifting induced-plus-quadrature grating compound (traveling wave illustrated by yellow line). (f) A canceling grating (blue line) added to the test field in the same temporal phase as the induced grating (red line) but in 180° spatial phase is used to null the induced grating (purple line). (g) When the induced grating is nulled by the canceling grating the quad grating which remains is motion-energy balanced and causes no systematic unidirectional motion. (h) When the induced grating is over-canceled the induced grating plus canceling grating compound (standing wave illustrated by purple line) has the spatial and temporal phase of the canceling grating (blue line). (i–k) The over-canceled induced-plus-canceling grating compound sums with the quadrature grating to produce a leftward drifting compound (traveling wave illustrated by white line).
This conclusion is further supported by the recent work of Robinson and de Sa (2008). These investigators used brightness matching and stimuli that were spatially very similar (bar widths of 1° or 10.6°) to those of Rossi and Paradiso (1996) to investigate the time course of induction. However, instead of modulating the luminance of the inducing bars they measured induction magnitude for very brief presentations followed by a noise mask. They found that brightness induction was not only observable, but strengthened at presentation durations as short as 58 ms. In addition, bar width had little influence on induction magnitude. If anything, wider bar widths enabled brightness matches to be made at shorter presentation durations. These results are also inconsistent with the idea that brightness induction depends on a slow “filling-in” process.
The present study employs the quadrature phase motion paradigm used by Blakeslee and McCourt (2008) in combination with a canceling technique in order to measure the magnitude of induction. The canceling technique has often been used to measure grating induction magnitude in static displays (McCourt, 1982; Foley & McCourt, 1985; McCourt & Blakeslee, 1994). This new quadrature-phase motion cancelation paradigm allows us to characterize the spatiotemporal surface of brightness induction by measuring its magnitude in dynamic displays across a wide range of spatial frequencies, temporal frequencies and test field heights.
2. Materials and methods
One of the authors (BB) and three naïve observers (NP, AM and MT) participated in the experiments. All observers possessed normal or corrected-to-normal vision. Each participant provided informed consent and the experimental protocol was approved by the NDSU IRB.
Stimuli were presented on a 22” Mitsubishi DiamondPro (model 2070) CRT display at a frame refresh rate of 140 Hz. To ensure that temporal resolution exceeded 8 temporal frames per cycle, the highest temporal modulation frequency used was 16 Hz. Stimuli were generated and presented using MATLAB routines to control a Cambridge Research Systems ViSaGe system (14-bit intensity resolution per channel). Gamma linearization was accomplished via look-up tables following photometric calibration. Display format was 1024 (w) × 768 (h) pixels. Viewing distance was 57 cm resulting in a stimulus field that was 40° in width and 30° in height. Individual pixels measured 0.039° × 0.039°. Mean display luminance was 50 cd/m°.
The inducing gratings of the grating induction stimulus filled the region above and below the test field (see background in Fig. 1a, b). Inducing gratings (100% contrast) with spatial frequencies of 0.03125, 0.0625, 0.125, 0.25, 0.50, 1.0, 2.0, and 4.0 c/d were counterphased at temporal frequencies of 0.25, 0.5, 1.0, 2.0, 4.0, 8.0 and 16.0 Hz. Test field heights were 0.5°, 1.0°, 2.0° and 4.0°. The quadrature phase motion cancelation technique can be summarized as follows. A counterphasing inducing grating (standing wave) [Figure 1a, b (black line)] produces a nearly instantaneous phase-reversed counterphasing induced grating (standing wave) [Fig. 1a, b (red line) in the homogeneous test field of a grating induction display (Blakeslee & McCourt, 1997; 2008; McCourt, 1982, 1994). Blakeslee and McCourt (2008) showed that induction phase lag was nearly zero (< 0.016 cycle), so for methodological simplicity we treat it as zero. A counterphasing quadrature grating (standing wave in 90° spatial and temporal phase relative to the induced grating) [Fig. 1c–e (green line)] sums with the induced grating (standing wave) [Fig. 1c–e (red line)] to produce a rightward drifting induced-plus-quadrature grating compound (traveling wave) [Fig. 1c–e (yellow line)] to which the visual system is extremely sensitive (Blakeslee & McCourt, 2008). Blakeslee and McCourt (2008) varied the temporal phase of the quadrature grating to measure the phase (time) lag of induction. Here the temporal phase of the quadrature grating is held constant at 90° phase relative to the induced grating, and a second luminance grating is added to the test field. This second “canceling” grating [Fig. 1f, h (blue line)] possesses the same spatial and temporal frequency as the induced grating, but is 180° out of spatial phase with it. The canceling grating is added to the test field at a number of contrast levels, using the method of constant stimuli. When canceling grating contrast is less than induced grating contrast (i.e., when the induced grating is under-canceled) the compound grating possesses the spatial and temporal phase of the induced grating. It therefore combines with the quadrature grating to produce a rightward moving traveling wave just as in the case where no canceling grating is present [Fig. 1c–e (yellow line)]. When canceling grating contrast exceeds induced grating contrast (i.e., when the induced grating is over-canceled) the compound grating now possesses the spatial and temporal phase of the canceling grating [Fig. 1h (purple line)]. This compound combines with the quadrature grating to produce a leftward moving traveling wave [Fig. 1i–k (white line)]. When canceling grating contrast equals induced grating contrast the sum is zero (i.e., the induced grating is nulled) [Fig. 1f, g (purple line)]. The motion energy of the counterphasing quadrature grating which remains is left/right balanced (i.e., a standing wave) [Fig. 1g (green/black lines)] yielding a 50:50 proportion of left/right motion judgments in a forced-choice motion direction discrimination task. An annotated video demonstration and explanation of the quadrature phase motion cancelation technique is included as supplemental material.
On each trial quadrature grating contrast was ramped from 0.0 to 0.5 over the 1500 ms duration of stimulus presentation. Quadrature grating contrast was ramped because quadrature-pair standing waves sum to produce a pure traveling wave only when the contrasts of the components are equal. Optimal quadrature grating contrast therefore depends on the contrast of each induced-plus-canceling grating compound, which itself depends upon the variable level of canceling grating contrast. Rather than attempting to estimate a singular optimal quadrature grating contrast value we smoothly increased its contrast from 0.0 to 0.5 over the duration of each inspection interval, reasoning that observers would experience the optimal quadrature grating contrast (yielding a motion signal with a maximal signal-to-noise ratio) at some point during the inspection interval. In preliminary measurements we determined that the motion signals in grating compounds remained strong even for large mismatches of quadrature and induced grating contrast.
The contrast of the canceling grating, which also filled the test field, was varied from −15% to 100%, where negative contrast signifies a spatial phase reversal of the canceling grating such that it augments rather than cancels the induced grating. Canceling grating contrast was constant over the 1500 ms duration of stimulus presentation. Separate blocks of trials were run at each of the four test field heights. Within each block, trials presenting 10–15 levels of canceling contrast at each combination of inducing grating spatial and temporal frequency were randomly interleaved. Subjects completed between 10 and 20 blocks per condition, such that psychometric functions were based on an average of approximately 200 trials.
3. Results and Discussion
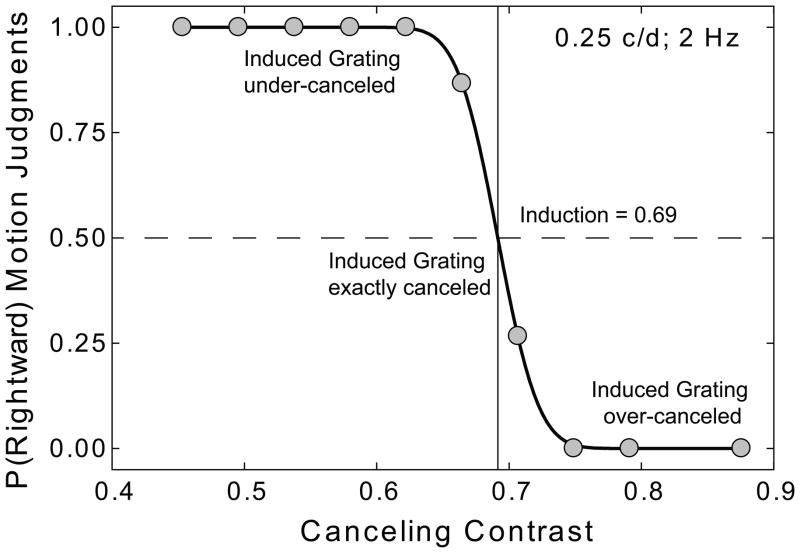
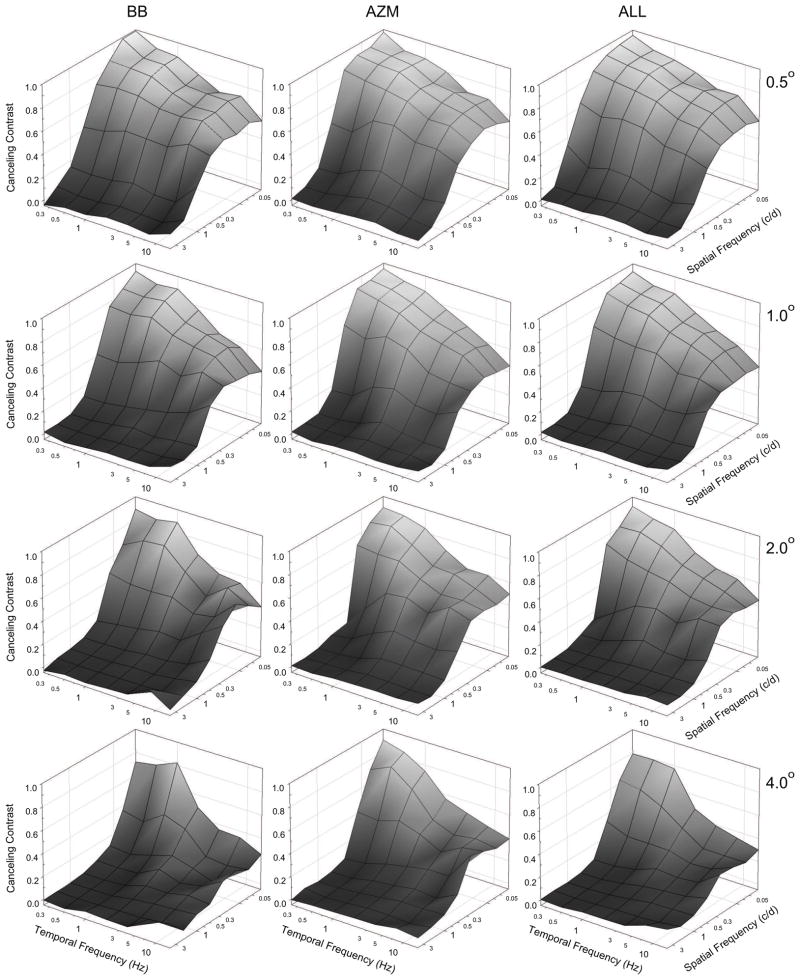
Psychometric data were fitted with a two-parameter (midpoint and slope) cumulative-normal function using a maximum-likelihood criterion. The fitted midpoint parameter corresponded to the contrast of the canceling grating yielding 50% “right” motion responses and was taken as a measure of grating induction magnitude. Figure 2 shows an example of fitted psychometric data for one observer. The mesh plots in the first two columns of Figure 3 plot separately for two observers (BB and AZM), mean canceling contrast as a function of inducing grating spatial and temporal frequency. The third column depicts the average mean canceling contrast for all four observers (ALL). The rows plot data for the four test field heights 0.5°, 1.0°, 2.0° and 4.0°, respectively. Individual datasets from all four observers were highly consistent and are well represented by the aggregated mean plots.
Figure 2.
A psychometric function from the forced-choice motion direction discrimination task. The canceling grating is added to the test field at a number of contrast levels, using the method of constant stimuli. When canceling grating contrast is less than induced grating contrast the sum is under-canceled and combines with the quadrature grating to produce rightward motion. When canceling grating contrast is more than induced contrast the sum is over-canceled and results in leftward motion. When canceling grating contrast equals induced grating contrast the sum is zero and the induced grating is nulled. At this point the motion energy of the counterphasing quadrature grating which remains is left/right balanced and yields a 50:50 proportion of left/right motion judgments.
Figure 3.
The mesh plots in the first two columns plot separately for two observers (BB and AZM), mean canceling contrast as a function of inducing grating spatial and temporal frequency. The third column depicts the average mean canceling contrast for all four observers (ALL). The rows plot data for the four test field heights 0.5°, 1.0°, 2.0° and 4.0°, respectively. At all test field heights canceling contrast is a low-pass function of spatial and temporal frequency. Induction is greatest at low frequencies and declines with increasing frequency in both dimensions.
At all test field heights canceling contrast is a low-pass function of spatial and temporal frequency. Induction is greatest at low frequencies and declines with increasing frequency in both dimensions. Induction magnitude also declines with increasing test field height. As observed in previous studies using cancelation paradigms (McCourt, 1982; Foley & McCourt, 1985), the strength of induction at some locations is remarkably robust. For example, at the narrowest test field height (0.5°), and for inducing gratings of low spatial (0.0313 c/d) and temporal (0.25 Hz) frequency, mean canceling grating contrast for the four observers was 0.95! Even at the largest test field height (4°), mean canceling contrast at this spatiotemporal locus was still 0.80. Similarly, at a temporal frequency of 16 Hz, mean canceling contrast was 0.55 for the lowest inducing grating spatial frequency (0.0313 c/d) at the narrowest test field height (0.5°), and declined slowly to 0.30 for the largest test field height (4.0°). Such large values of induction magnitude are not observed using matching paradigms (McCourt & Blakeslee, 1994; Blakeslee & McCourt, 1997; Blakeslee & McCourt, 1999). McCourt and Blakeslee (1994) showed that canceling contrast grows approximately linearly with inducing grating contrast while induction magnitude determined from contrast matching grows as a decelerating function of inducing grating contrast to a maximum value of approximately 0.30.
The present results are also consistent with previous studies of grating induction which showed that canceling contrast decreases with both increasing inducing grating spatial frequency and increasing test field height (McCourt, 1982; Foley & McCourt, 1985). In a parametric study, Foley and McCourt (1985) made the simplifying discovery that canceling contrast was inversely proportional to the product of inducing grating spatial frequency and test field height, meaning that induction magnitude scales with the number of inducing grating cycles that would “fit” within the height of the test field. This explains why grating induction magnitude remains essentially constant with changing viewing distance, since changes in inducing grating spatial frequency and test field height are reciprocal, and their product remains constant. This invariance of induction magnitude with viewing distance played a key role in giving rise to the idea that grating induction, as well as other brightness effects, might originate as the result of spatial filtering across multiple scales (Kingdom & Moulden, 1992; Blakeslee & McCourt, 1997; 1999).
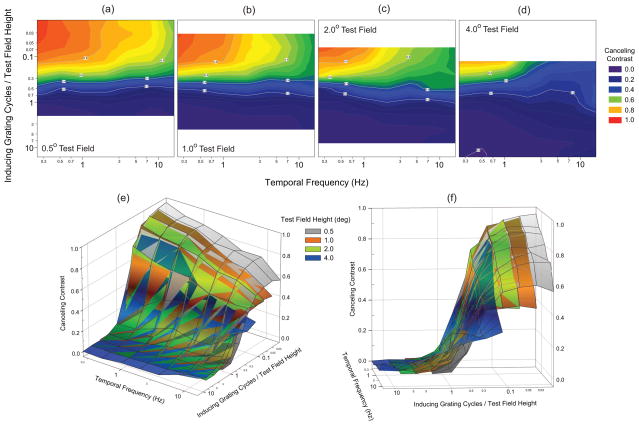
These relationships are confirmed and extended to the temporal domain by the present findings. This is illustrated in Figure 4 where the mean induction magnitude data for the 4 observers (ALL) from Fig. 3 are replotted as contour (Fig. 4a–d) and mesh plots (Fig. 4e, f) after replacing the inducing spatial frequency axis with one that indexes the product of inducing spatial frequency (c/d) and test field height (d), whose unit is the number of grating cycles (c) that would fit within the specified test field height. Note that color represents canceling contrast in the contour plots where the four test field heights are plotted separately but refers to the four different test field heights in the mesh plots. Plotting the induction magnitude data from the four test field heights in this manner illustrates that they can be described as four partially overlapping sections of a single larger surface. Each section shifts toward larger values on the inducing grating cycles/test field height axis as test field height increases.
Figure 4.
Mean induction magnitude data for the 4 observers (ALL) from Fig. 3 replotted as contour (a–d) and mesh plots (e, f) after replacing the inducing spatial frequency axis with one that indexes the product of inducing spatial frequency (c/d) and test field height (d), whose unit is the number of grating cycles (c) that would fit within the specified test field height. Color indexes canceling contrast in the contour plots where the four test field heights are plotted separately; but, distinguishes the four different test field heights in the mesh plots. Plotting the induction magnitude data at the four test field heights in this manner illustrates that they can be described as four partially overlapping sections of a single extended spatiotemporal induction surface.
While the present study is the first to characterize the magnitude of grating induction as a function of temporal frequency, the results are consistent with those of Blakeslee and McCourt (2008), who used the quadrature phase motion technique to measure the phase (time) lag of grating induction at temporal frequencies up to 24 Hz. Together these studies illustrate that at least one form of brightness induction is very much faster than reported by DeValois et al. (1986) and Rossi and Paradiso (1996). It remains unclear, however, whether the sluggish process identified by these authors and proposed to operate exclusively at temporal frequencies below 5 Hz, is truly a separate class of induction mechanism or whether it is an underestimate of the frequency response of the mechanism we identify using the quadrature phase motion technique. As discussed in detail in Blakeslee and McCourt (2008), an underestimate might reflect methodological difficulties of using direct brightness matching in conjunction with temporally varying stimuli. The studies of Magnussen and Glad (1975) and Robinson and de Sa (2008), using very similar stimuli to DeValois et. al. (1986) and Rossi and Paradiso (1996), respectively, are consistent with this explanation. In addition, we favor a one mechanism hypothesis based on a large body of evidence showing that the spatial dependencies of brightness induction in simultaneous contrast displays like those used by Magnussen and Glad (1975), DeValois et al. (1986), Rossi and Paradiso (1996), and Robinson and de Sa (2008), as well as in numerous other configurations including grating induction, can all be parsimoniously explained by the normalized output of oriented spatial filters summed across multiple spatial scales (Blakeslee & McCourt, 1997, 1999, 2001, 2004, 2005; Blakeslee, Pasieka & McCourt, 2005; Blakeslee, Reetz & McCourt, 2009; Dakin & Bex, 2003; Robinson, Hammon & de Sa, 2007). In other words, a “filling-in” mechanism, in the form of neural spreading, is not required to explain any of these effects.
Figure 5 illustrates ODOG filters at the seven spatial scales which comprise the ODOG model (Blakeslee & McCourt, 1999). Fig. 5(d) shows the ODOG filter which will produce the largest amplitude (spatial counterphase) response in the horizontal test field of the depicted grating induction stimulus. The “off” sub-regions of this filter flank the central “on” sub-region above and below and tune this filter to horizontal stimuli. Note also that this filter is relatively indifferent to the spatial frequency of the inducing grating provided that the width of the filter’s “off” sub-region remains within an inducing grating half-cycle. For inducing gratings that are low in spatial frequency relative to filter size, therefore, it is mostly test field height which determines the relative activity of the ODOG filters at different spatial scales. Induction magnitude increases with decreasing test field height because as the test field grows smaller it “fits” into the “on” sub-region of an increasing number of ODOG filters. For example, the test field illustrated in Fig. 5 is too large for ODOG filters (a), (b) and (c) to respond, because they are balanced and do not respond to a homogeneous test field. However, activity will occur in ODOG filters (d), (e), (f) and (g), each of which contributes a counterphase signal in the test field. Induction magnitude will increase with decreasing test field height until the test field becomes smaller than the “on” sub-region of the smallest ODOG filter (a), at which point induction magnitude will start to decline.
Figure 5.
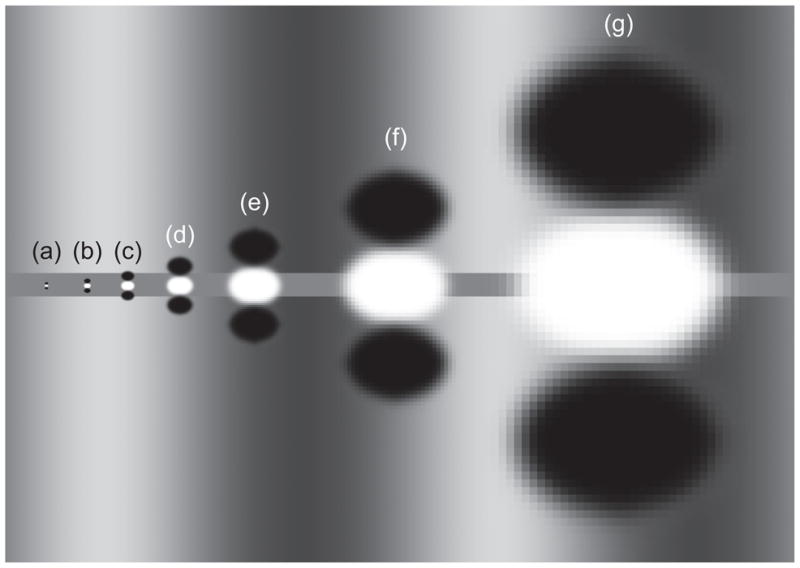
(a–g) The ODOG filters at the seven spatial scales which comprise the ODOG model. (d) The ODOG filter which will produce the largest amplitude (spatial counterphase) response in the horizontal test field of the depicted grating induction stimulus. The “off” sub-regions of this filter flank the central “on” sub-region above and below and tune this filter to horizontal stimuli.
The quadrature-phase motion cancelation technique has furthered our understanding of brightness induction in the temporal domain and provides the opportunity to extend the ODOG model to include temporal parameters and to make further critical tests of the multiscale spatial filtering approach to understanding brightness induction. For example, because the array of filters proposed to underlie induction is bounded, the inverse proportionality between canceling contrast and the product of inducing spatial frequency and test field height will break down when test field size becomes smaller than the “on” sub-region of the smallest filter. The range of parameter values used in the present study was too limited to test this prediction, but such tests of the model are planned in future studies. The multiscale spatial filtering approach also predicts that grating adaptation (or masking) at particular spatial frequencies, temporal frequencies, and orientations will selectively decrease the magnitude of induction at predictable locations on the spatiotemporal induction surface. Such experiments are made possible by the quadrature-phase motion cancelation technique.
4. Conclusions
A novel quadrature-phase motion cancelation technique allowed the spatiotemporal surface of induction to be easily and precisely measured. Over a range of test field heights from 0.5° to 4.0°, canceling contrast is a low-pass function of spatial and temporal frequency. Induction is greatest at low frequencies and declines with increasing frequency in both dimensions. Induction magnitude also declines with increasing test field height. Induction magnitude was found to scale as the product of inducing grating spatial frequency (c/d) and test field height (d), i.e., as a function of the number of inducing grating cycles per test field height. This result is consistent with and extends earlier findings (McCourt, 1982; Foley & McCourt, 1985). When canceling contrast is plotted as a function of temporal frequency and the number of inducing grating cycles per test field height, the data from the four test field heights overlap and form a single extended induction surface. These properties of the data are easily explained in the context of multiscale spatial filtering (McCourt, 1982; Foley & McCourt, 1985; Blakeslee & McCourt, 1997; 1999).
While the present study is the first to measure the magnitude of grating induction as a function of temporal frequency, the results are consistent with an earlier study which measured the phase (time) lag of grating induction (Blakeslee & McCourt, 2008). Together these studies illustrate that at least one form of brightness induction is very much faster than that reported for simultaneous brightness contrast by DeValois et al. (1986) and Rossi and Paradiso (1996). The results of Magnussen and Glad (1975) and Robinson and de Sa (2008), which were obtained with simultaneous brightness contrast stimuli similar to those of DeValois et al. (1986) and Rossi and Paradiso (1996), respectively, argue for a faster brightness induction mechanism as well. These results make it clear that a slow “filling-in” process is not sufficient to explain brightness induction in any of these stimuli and raises the question of whether such a mechanism is required at all.
Supplementary Material
Research Highlights.
Brightness induction is a low pass function of spatial and temporal frequency.
Brightness induction declines with increasing test field height.
Brightness induction is faster than previously reported.
Acknowledgments
This work was supported by grants R01 EY014015 (BB) and NIH P20 RR020151 (MEM). The National Center for Research Resources (NCRR) and the National Eye Institute (NEI) are components of the National Institutes of Health (NIH). The contents of this report are solely the responsibility of the authors and do not necessarily reflect the official views of the NIH, NCRR, or NEI. The authors thank Huanzhong (Dan) Gu for programming assistance.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Barbara Blakeslee, Email: barbara.blakeslee@ndsu.edu.
Mark E. McCourt, Email: mark.mccourt@ndsu.edu.
References
- Blakeslee B, McCourt ME. Similar mechanisms underlie simultaneous brightness contrast and grating induction. Vision Research. 1997;37:2849–2869. doi: 10.1016/s0042-6989(97)00086-2. [DOI] [PubMed] [Google Scholar]
- Blakeslee B, McCourt ME. A multiscale spatial filtering account of the White effect, simultaneous brightness contrast and grating induction. Vision Research. 1999;39:4361–4377. doi: 10.1016/s0042-6989(99)00119-4. [DOI] [PubMed] [Google Scholar]
- Blakeslee B, McCourt ME. A multiscale spatial filtering account of the Wertheimer-Benary effect and the corrugated mondrian. Vision Research. 2001;41:2487–2502. doi: 10.1016/s0042-6989(01)00138-9. [DOI] [PubMed] [Google Scholar]
- Blakeslee B, McCourt ME. A unified theory of brightness contrast and assimilation incorporating oriented multiscale spatial filtering and contrast normalization. Vision Research. 2004;44:2483–2503. doi: 10.1016/j.visres.2004.05.015. [DOI] [PubMed] [Google Scholar]
- Blakeslee B, McCourt ME. A multiscale filtering explanation of gradient and remote brightness induction effects: A reply to Logvinenko (2003) Perception. 2005;34:793–802. doi: 10.1068/p5303x. [DOI] [PubMed] [Google Scholar]
- Blakeslee B, McCourt ME. Nearly instantaneous brightness induction. Journal of Vision. 2008;8(2):15, 1–8. doi: 10.1167/8.2.15.. http://journalofvision.org/8/2/15/ [DOI] [PMC free article] [PubMed]
- Blakeslee B, Pasieka W, McCourt ME. Oriented multiscale spatial filtering and contrast normalization: a parsimonious model of brightness induction in a continuum of stimuli including White, Howe and simultaneous brightness contrast. Vision Research. 2005;45:607–615. doi: 10.1016/j.visres.2004.09.027. [DOI] [PubMed] [Google Scholar]
- Blakeslee B, Reetz D, McCourt ME. Spatial filtering versus anchoring accounts of brightness/lightness in staircase and simultaneous brightness/lightness contrast stimuli. Journal of Vision. 2009;9(3):22, 1–17. doi: 10.1167/9.3.22. http://journalofvision.org/9/3/22/ [DOI] [PMC free article] [PubMed]
- Dakin SC, Bex PJ. Natural image statistics mediate brightness ‘filling-in’. Proceedings of the Royal Society of London Series B–Biological Sciences. 2003;270:2341–2348. doi: 10.1098/rspb.2003.2528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeValois RL, Webster MA, DeValois KK, Lingelbach B. Temporal properties of brightness and color induction. Vision Research. 1986;26:887–897. doi: 10.1016/0042-6989(86)90147-1. [DOI] [PubMed] [Google Scholar]
- Foley JM, McCourt ME. Visual grating induction. Journal of the Optical Society of America A Optics and Image Science. 1985;2:1220–1230. doi: 10.1364/josaa.2.001220. [DOI] [PubMed] [Google Scholar]
- Gerrits HJM, Vendrik AJH. Simultaneous contrast, filling-in process and information processing in man's visual system. Experimental Brain Research. 1970;11:411–430. doi: 10.1007/BF00237914. [DOI] [PubMed] [Google Scholar]
- Kingdom FAA. Lightness, brightness and transparency: A quarter century of new ideas, captivating demonstrations and unrelenting controversy. Vision Research. 2011;51:652–673. doi: 10.1016/j.visres.2010.09.012. [DOI] [PubMed] [Google Scholar]
- Kingdom F, Moulden B. A multi-channel approach to brightness coding. Vision Research. 1992;32:1565–1582. doi: 10.1016/0042-6989(92)90212-2. [DOI] [PubMed] [Google Scholar]
- Magnussen S, Glad A. Temporal frequency characteristics of spatial interaction in human vision. Experimental Brain Research. 1975;23:519–528. doi: 10.1007/BF00234919. [DOI] [PubMed] [Google Scholar]
- McCourt ME. A spatial frequency dependent grating-induction effect. Vision Research. 1982;22:119–134. doi: 10.1016/0042-6989(82)90173-0. [DOI] [PubMed] [Google Scholar]
- Robinson AE, de Sa VR. Brief presentations reveal the temporal dynamics of brightness induction and White’s Illusion. Vision Research. 2008;48:2370–2381. doi: 10.1016/j.visres.2008.07.023. [DOI] [PubMed] [Google Scholar]
- Robinson AE, Hammon PS, de Sa VR. Explaining brightness illusions using spatial filtering and local response normalization. Vision Research. 2007;47:1631–644. doi: 10.1016/j.visres.2007.02.017. [DOI] [PubMed] [Google Scholar]
- Rossi AF, Paradiso MA. Temporal limits of brightness induction and mechanisms of brightness perception. Vision Research. 1996;36:1391–1398. doi: 10.1016/0042-6989(95)00206-5. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.