Analyses of a Cantilever-Beam Based Instrument for Evaluating the Development of Polymerization Stresses

Abstract

Polymerization stress (PS) remains one of the most critical properties of polymeric dental materials, yet methods that can accurately quantify PS has been limited in part due to the complexity of polymerization, and in part due to the instrumentation itself. In this study, we performed analytical and finite element analyses on a cantilever-beam based tensometer to evaluate shrinkage stresses during the polymerization of dental restorative composite. Results for these analyses were used to generate 1) guidelines for designing a tensometer that satisfies the necessary accuracy requirements, and 2) a formula for calculating PS and the instrument sensitivity. The PS generated by a commercial dental composite determined using our new tensometer agrees with the predicted trend when the beam length and/or specimen height is varied. An analytical solution is also derived for the vertical deflection of beam, which can be used for any combination of bending and shearing to properly calculate the PS. This work demonstrates the importance of beam dimension and component relative rigidity to the accuracy of PS evaluation. In addition, an easy-to-conduct calibration procedure is provided that is desirable for periodic tensometer recalibration.

Introduction

Human tooth structures (both their mineral and proteinaceous components) are adversely affected by caries, and the resulting cavities usually do not fully regenerate. Therefore, they require reconstruction utilizing adhesive and restorative and dental materials. Polymeric dental composites have been used widely in the restoration of tooth decay or cavity that occurs by primary caries or traumatic events. These materials, along with appropriate adhesive systems, are noted for their efficacy in restoring the function and appearance of tooth structure. However, failure of these dental restorations due to secondary caries is a major concern, and replacement of failed restorations creates extra pain, anxiety, and economic burdens for the patients [1]. Dental restorations fail for a variety of reasons [2]. For example, the stresses magnified (stress singularity) at or near the tooth/composite interface due to the mismatch of tooth and restorative mechanical properties are important contributors to failure. The polymerization shrinkage that occurs during the composite curing process has been implicated as a major stress source for the interfacial stress singularity [3, 4]. This shrinkage can lead to marginal microcracks and subsequent microleakage at or near the composite-tooth interface, permitting bacteria to pass beneath the restoration surface and ultimately resulting in the secondary caries.

Polymerization stresses (PS) of resin-based dental materials have been measured using a variety of methods. Those interested in methods traditionally used to quantify the PS of polymeric dental materials may refer to the existing literature [5-8]. In general, the development of PS is measured through perturbing physically constrained specimens, and the resulting PS can be deduced through a corresponding governing equation for the response of constraints to the perturbation. Our interest here is not to propose a new method or to compare the relative merits of existing methods. Instead, the aim of this study is to assess and improve a widely used cantilever-beam based instrument [7] in terms of the applicability of a formula for deducing PS from the constrained polymerization shrinkage. A necessity of this type of measurement is that the instrument be sufficiently sensitive to accurately detect shrinkage, manifested in beam deflection.

The aforementioned tensometer was designed and constructed by the American Dental Association Foundation (ADAF) located at the National Institute of Standards and Technology [7]. Using this device, composite (or resin) specimens are mechanically attached to a cantilever beam via a quartz rod adhesively in contact with the specimen, and the specimen is also adhesively attached to a fixed lower rod. Upon polymerization, the composite shrinkage stress induces a deflection in a calibrated cantilever beam, and the beam deflection is measured using a linear variable differential transformer (LVDT). The PS is calculated through a beam formula according to the measured deflection [7]. The original publication also noted that the level of tensometer compliance can be conveniently adjusted by varying the specimen position along the beam span to match that of a variety of clinically-relevant restorative configurations. In a separate work, a similar tensometer was couple to an IR spectroscopy and used to determine the conversion dependent development of shrinkage and stress [9]. In addition, the relationships between PS development and the physical/chemical evolution of network structure associated with dental polymers were examined [9].

In this study, the importance of relative rigidities between tensometer components and the testing materials on the instrument sensitivity is demonstrated. As a result, revised design criteria have been proposed for instrument fabrication to achieve more reliable measurements. Also, we have expanded the formula for extracting PS from the tensometer response through the elasticity theory when the beam shearing is important. This formula has been validated by finite element analysis. A tensometer constructed according to the new design criteria was used to quantify PS varying beam locations and heights. By comparing the analytical solution with experimental results, the new instrument gives the correct trend in the PS development as a function of beam length. The same trend is not attainable from the original instrument [7]. In addition, a very simple, straightforward, and portable calibration method is developed; this simple calibration method can avoid extra instrumental setups and unnecessary experimental procedures.

Measurement Methodology and Experiments¹

Theory

The fundamental concept governing the operation of a cantilever-beam based tensometer is that PS is related to the beam deflection [7]; Fig. 1a presents a photograph of the typical tensometer setup. The composite specimen in a cylindrical geometry is bonded to quartz rods via a silane-coupling chemistry. The top surface of the upper rod (shrinkage-transmitting rod) is mechanically attached to the cantilever beam by means of a collet, while the lower rod is affixed to the base stand by a separate collet. As light transmit through the lower rod onto the specimen, the irradiation process initiates polymerization resulting in shrinkage, which exerts force causing the beam to deflect. LVDT is used to measure the beam deflection, δ. The force, F, is derived based on the configuration shown in Fig.1b through the following equation:

$$F=\frac{6\delta EI}{a^2(3\ell -a)}$$ (1)

where ℓ and a are the distances between the clamped edge and the LVDT and sample location, respectively. E and $I(=\frac{w{h}^3}{12})$ are the Young’s modulus and the moment of inertia of the beam; h and w are the height and width of beam cross-section, respectively. The polymerization stress, σ, is simply the force divided by the cross-section area of specimen, A, as follows:

$$\sigma =\frac{F}{A}$$ (2)

Figure 1.

Photographs of a cantilever-beam based tensometer for evaluating the development of polymerization stresses (a), schematic of cantilever beam configuration for the mathematical analyses, where ℓ and a are the distances between the clamped edge and the LVDT and sample location, respectively (b).

The formula shown in eq. 1 is derived based on a linear elastic system and Euler-Bernoulli beam theory [10] in which the vertical deflection of a beam is assumed to arise from bending while deflection due to shearing is negligible. Under these stated condition, the beam length is much greater than the beam depth (large slenderness ratio, i.e., length/depth ratio (ℓ / h)). It should be emphasized that the effective beam length (span) of the tensometer configuration shown in Fig. 1b should be the length of “a”, where the sample is located and polymerization stress is exerted. Therefore, the aspect ratio of the beam in this study is defined as the ratio of effective beam length to beam height (a/h). Figure 2 shows the displacements calculated using eq. 1 and the analytical solution that includes bending and shearing at the LVDT location as a function of span/depth ratio for various values of a / ℓ. The analytical solution is derived from the elasticity theory that includes bending and shearing and will be discussed in more details later. From Fig. 2, it is apparent that the span/depth ratio should be 8 or greater for the contribution of beam shearing to the beam deflection (measured at the location of LVDT) to be negligible. Otherwise, the force deduced through eq. 1 can be artificially low due to contributions from beam shearing. Also, results shown in Fig.2 indicate the ratio of a / ℓ minimally affects the shearing contribution. In the experiment, the beam deflection at the sample position, δ_s, should be less than half of the beam’s thickness (i.e., δ_s/h < 0.5) to avoid in-plane stretching of the beam (diaphragm strain) and fulfill the requirements to satisfy linear elasticity. These requirements have been proven to be valid by our analyses using the finite element method in a previous study on the deformation of flexible membranes [11].

Figure 2.

Normalized deflection at the end of the beam as a function of ℓ / h (slenderness ratio of the beam) for different a / ℓ (sample positions). δ and δ* are the displacements at the beam end obtained from the beam solution (eq. 1) and the elasticity solution (eq. 5), respectively.

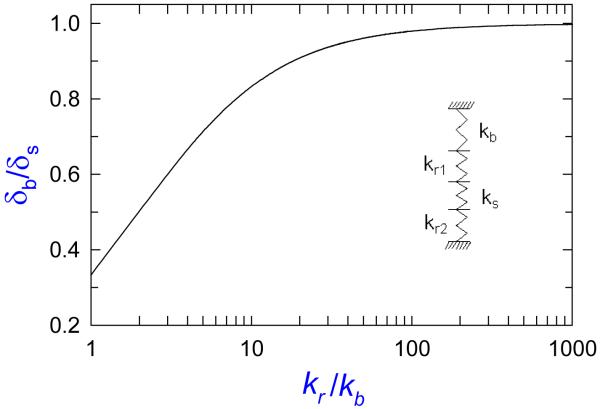
The tensometer system shown in Fig. 1 can be modeled as four springs in series (four components shown in the insert of Fig. 3: beam, upper rod, specimen, and lower rod) during the beam deflection. The beam spring constant is $k_b(=\frac{3EI}{a^3})$; the upper rod is $k_{r1}(=\frac{E_{r}A}{{\ell }_{r1}})$, the specimen is $k_s(=\frac{E_{s}A}{{\ell }_s})$, and the lower rod is $k_{r2}(=\frac{E_{r}A}{{\ell }_{r2}})$, where E and ℓ are the modulus and length of each component. Subscripts r and s represent the rod and the sample, respectively; subscripts 1 and 2 refer to the upper and lower rods, respectively. Ideally, the measured beam deflection should reflect exclusively the specimen deformation due to shrinkage, and no rod deformation contributions. A commercial finite element code, SIMULIA [12], was employed to analyze the effect of relative rigidity of component on the beam deformation. The results shown in Fig. 3 indicate that the ratio of k_r to k_b should be relatively large (i.e., > 100, assuming ℓ_r1 = ℓ_r2 ) so that the deformation of quartz rods becomes negligible. From the expression using the beam spring constant, it is clear that span/depth ratio (a/h) affects not only the applicability of eq. 1, but also the sensitivity of the beam to the presence of shrinkage.

Figure 3.

Normalized beam deformation as a function of the ratio of the rod (k_r = k_r1= k_r2) to beam spring constants. δ_s and δ_b are the sample deformation and the beam displacement at the corresponding sample location, respectively.

Instrument Calibration

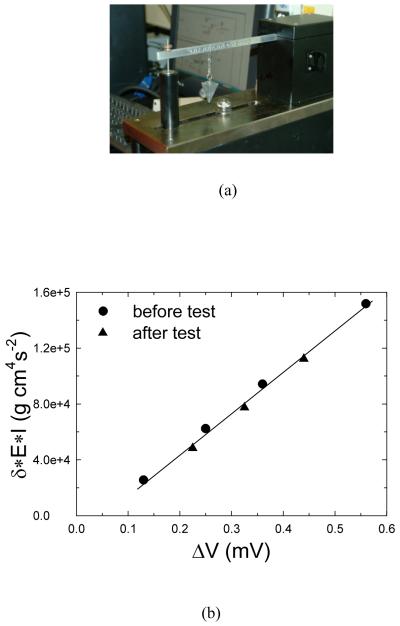
Besides fundamental requirements for instrument accuracy, a facile procedure to calibrate voltage to displacement is needed for periodic recalibration. A constant known weight (in this case a fishing sinker) is used as a load source (P) to characterize the force exerted on the beam (Fig. 4a). For each hanging location along the beam from the clamped beam edge (x), an LVDT voltage reading (ΔV) is recorded and a factorized beam displacement (δ_c = δ · E · I ) is calculated from the following equation:

$${\delta }_c=\frac{P{x}^2(3\ell -x)}{6}$$ (3)

As mentioned earlier, the ratio of x to h needs to be greater than eight (i.e., x/h ≥ 8 ) so that eq. 3 is valid. Figure 4 displays a typical δ_c vs ΔV calibration curve, which was generated by varying the sinker location along the beam; as expected a linear relationship is obtained. In a PS measurement, the force (F, used in eq. 2) corresponding to a sample position can be readily obtained through the following equation:

$$F=\frac{6S\Delta V}{a^2(3\ell -a)}$$ (4)

where S is the slope of the δ_c - ΔV relationship as shown in Fig. 4b. One can see from eqs. 3-4, the knowledge of beam geometry and material property is not required as far as the evaluation of polymerization stress is concerned.

Figure 4.

Photo image of the newly designed tensometer with deadweight for calibration (a), calibration plot of the beam displacement vs. the voltage reading from LVDT obtained before and after tests for the stress measurement (b). The solid line is a linear fit of the data. The relative uncertainty for ΔV measurement is less than 0.5%.

Experimental Validation

In this investigation, a commercial composite (TPH Micro Matrix Restorative: lot #070403, shade A1, Dentsply-Caulk, Milford, DE, USA) was used as a test material to demonstrate the validity of our newly designed tensometer in the evaluation of PS. TPH is based on a visible-light activated, urethane-modified Bis-GMA and TEGDMA (1:1 mass ratio) filled primarily with a barium boron aluminum silicate glass at 78 % mass fraction (filler volume fraction is approx. 57 %). The specimen/rod diameter was 6.0 mm. The visible-light curing pen light (Spectrum Curing Unit, Denstply-Caulk, Milford, DE) was attached to the lower quartz rod with an opaque flexible light guide. The faces of quartz rods connected to the specimen were silanized to promote adhesion between the composite sample and rods. The silanization process was conducted by applying a 1% by mass acetone solution of 3-methacryloxypropyltrimethoxysilane (MPTMS; Gelest, Morrisville, PA) activated with 0.1% by mass formic acid. The rods were then heated at 60 °C for 12 h. Specimen height was determined using a rigid spacer of known height inserted between the two rods. A flexible tygon tubing sleeve with an injection hole and a smaller air-release hole was used to encase the rods and composite specimens. The composite pastes were delivered to this sample chamber by means of a syringe fitted with a tapered tube through the larger hole in the sleeve. The composite pastes were irradiated for 60 s through the lower quartz rod to initiate photo-polymerization, and the development of PS was monitored for 60 min. The light intensity, measured by a Demetron Model 100 radiometer (Demetron Research, Danbury, CT) was (510 ± 25) mW/cm² at the upper end of the top quartz rod where the sample was bonded. We note that the polymerization stress from chemical-cure can be measured in the same tensometer.

During irradiation, chemical bonds establish between the polymeric composite and silanized quartz rod-end surfaces via a bridging of polymer macrogel networks, thus permitting transmission of dimensional change into a measured stress. Both polymerization shrinkage and heat can contribute to the dimensional change. However, the contribution from latter is of minor importance or negligible [9], especially in highly filled composites such as the one used in the current study.

Results and Discussion

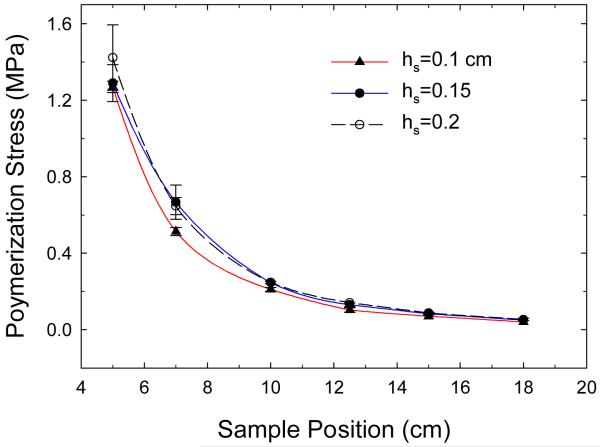
Based on our analyses, a new tensometer equipped with an aluminum beam ( ℓ = 24.5 cm , h = 1.0 cm, and w = 0.625 cm) was constructed. Figure 5 displays PS values determined as a function of effective beam length (sample positions) for different sample heights (data values are provided in Table 1). As expected, PS increased with a decrease in the effective beam length since the rigidity of tensometer system increased. Additionally, PS increased as a cubic polynomial function of decreasing sample location. This is because the system’s rigidity (beam spring constant) is a cubic function of beam length (see eq. 1). This agreement in a cubic function between the experimental results and theoretical calculation demonstrates the sensitivity of system to the presence of sample deformation and the accuracy of measurement. In contrast, a nearly linear relationship between PS and sample location (effective beam length) was found when the earlier cantilever-beam based tensometer was used [7]. The previous tensometer had a beam height of 4.0 cm; six different effective beam lengths (5.0 cm, 7.0 cm, 10.0 cm, 12.5 cm, 15.0 cm, and 18.0 cm) were used to match the different compliances related to dental restoration configurations. Under this range of aspect ratios (a/h = 1.25 to 4.5), the shear deformation contributes significantly to the beam deflection; thus, the applicability of eq. 1 is severely violated. In such case, eq. 1 would need to be modified as follows:

$${\delta }^{\ast }=F\left(\frac{a^2(3\ell -a)}{6EI}+\frac{h_2\ell (1+v)}{4EI}\right)$$ (5)

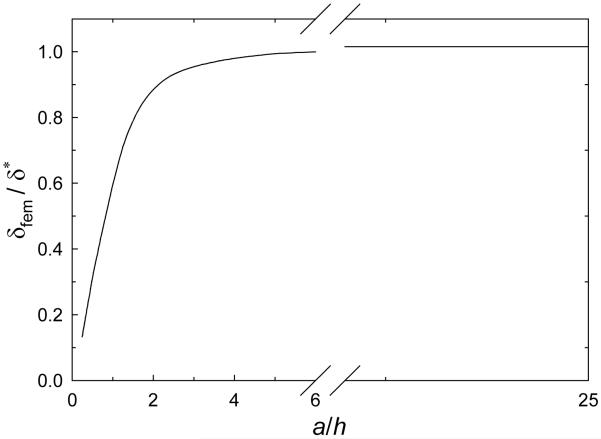
where ν is the Poisson’s ratio of the beam material. In the derivation of eq. (5), first, a cantilever beam with a narrow rectangular cross section was considered having length “a” and bent by a force “F” applied at the beam end of “a”; the displacement solution at the beam end can be obtained analytically based on the theory of elasticity [10]. Then, for the subject tensometer system, the beam displacement corresponding to the LVDT location, δ, is determined by the superposition of the displacement at “a” due to the stresses and strains as well as the displacement due to a rigid body rotation of the beam cross section at “a.” One can note that the first term on the right hand side of eq. 5 represents the bending contribution, while the second term comes from shearing and diminishes as the ratio of a/h increase. The near linear relationship between PS and beam length presented in the literature (Fig. 5 of ref. 7) is attributed to the dominance of shearing, where the shearing has a linear relationship with the beam aspect ratio as indicated in eq. 5. A finite element analysis was invoked to obtain the displacement–aspect ratio relationship of the cantilever beam depicted in Fig. 1b. Fig 6 shows good agreement between the solution of eq. 5 and our finite element analysis for a wide range of aspect ratios, except when the sample location is comparable to beam height (i.e., a/h ≤ 2). This indicates that eq. 5 can be used for any beam length (i.e., any combined situation of bending and shearing) to properly calculate the PS. The discrepancy between the analytical and finite element solutions shown in Fig. 6 is due to the edge effect. Practically, the sample location would not be that close to the beam edge.

Figure 5.

The development of polymerization stresses measured using the newly designed tensometer as a function of sample position for different sample heights (h_s). The error bars indicate the standard deviation of the measurement, which is a Type A standard uncertainty. The lines are best fit for the corresponding data. The stress was obtained at 1 hr after irradiation.

Table 1.

Mean polymerization stress (n=3 or greater, unit: MPa) induced at different effective beam length

Sample Position (effective beam length) cm	Sample Height (cm)
	1.0		1.5		2.0
	PS	SD	PS	SD	PS	SD
5	0.7388	0.0175	0.7504	0.0561	0.8280	0.0995
7	0.2986	0.0121	0.3878	0.0521	0.3762	0.0262
10	0.1222	5.8173e-3	0.1435	3.3586e-3	0.1435	3.3586e-3
12.5	0.0601	6.7173e-3	0.0756	5.8173e-3	0.0814	0.0000
15	0.0407	0.0000	0.0485	3.3586e-3	0.0504	3.3586e-3
18	0.0233	0.0000	0.0291	0.0000	0.0310	3.3586e-3

Figure 6.

Comparison of analytical solution (eq. 5) and the finite element solution on the beam deflection at tip depicted in Fig. 1b.

It is of great interest to determine the trend in the PS development as the sample height is varied. From the results presented in Fig. 5, one can see that samples with a greater height give a slightly higher PS value at the same beam length. For all the beam positions studied, the PS increased nearly 20 % when the sample height increased from 1 mm to 1.5 mm, and the development of PS has less dependency when the sample height increased from 1.5 mm to 2.0 mm. A similar trend has also been reported in the literature [6]. However, these trends were not observed when the previously designed tensometer was used [13]. Based on the beam material, dimensions, aspect ratio, and the spring constants of quartz rod used in the previous instrument [7], it is clear that the beam deflection did not completely reflect the shrinkage of testing material transmitted to the beam through the rods since $\frac{k_r}{k_b}⪡100$; therefore, the notable change in the shrinkage due to the variation of sample height has been mostly masked by the deformation of rod rather than the deflection of beam. Consequently, no difference in the development of PS was found when the sample height was varied using the original tensometer design.

Recently, the PS values of dental composites varying in filler contents were determined using the original tensometer design [14]. Essentially no difference in PS was detected while the shrinkage decreased significantly as the filler content increased from 55 % to 70 % (by mass). One reason for a lack of a clear trend is competing factor of a decrease in shrinkage and an increase in modulus, resulted in smaller changes in stress as filler content increased. Accordingly, the relationships between the leakage area at the tooth-composite interface and the composite properties have been inferred in the literature [14]. We calculated that the change in filler content by mass from 55 % to 70 % corresponds to the change by volume from 34 % to 50 %. This change also resulted in a decrease in polymer content (23 % by volume) and an increase in composite modulus by 42 % if the rule of mixture is adopted. Therefore, the lack of sensitivity of the old tensometer system likely contributed to the lack of differences in PS over the filler content studied. Future studies will focus on experiments that compare the sensitivity as well as reproducibility using systematically varied samples.

It is hoped that with improved accuracy and sensitivity, the cantilever-beam based tensometer can be extended to characterize the kinetics of polymerization shrinkage and elastic modulus development for restorative materials. These are important metrics in the modeling and simulation of stresses incurred during the polymerization of dental restorative under clinically relevant configuration, as well as in the development of new materials.

Conclusions

This work utilized analytical and finite element analyses to demonstrate the importance of tensometer system compliances on the accuracy of polymerization stress evaluation. A new tensometer constructed following the new design criteria showed the correct trend and improved sensitivities. It is expected that these improvements in instrumentation will enhance our ability to characterize PS and allow us to discern more subtle differences in PS.

An analytical solution (without a brute-force finite element analysis) is provided to determine the vertical deflection of beam at any length, which can be used to properly calculate the polymerization stress. Additionally, a simple method to calibrate the instrument is presented. When direct measurements are not possible, material properties are often determined by indirect measurements through governing equations based on physics. Those equations can sometimes be oversimplified; therefore, application and interpret of the measurements must be done with caution.