SUMMARY
In electron crystallography membrane protein structure is determined from two-dimensional crystals where the protein is embedded in a membrane. Once large and well-ordered 2D crystals are grown one of the bottlenecks in electron crystallography is the collection of image data to directly provide experimental phases to high resolution. Here we describe a new approach to bypass this bottleneck, eliminating the need for high-resolution imaging. We use the strengths of electron crystallography in rapidly obtaining accurate experimental phase information from low-resolution images and accurate high-resolution amplitude information from electron diffraction. The low-resolution experimental phases were used for the placement of α-helix fragments and extended to high resolution using phases from the fragments. Phases were further improved by density modifications followed by fragment expansion and structure refinement against the high-resolution diffraction data. Using this approach, structures of three membrane proteins were determined rapidly and accurately to atomic resolution without high-resolution image data.
Keywords: phase extension, electron crystallography, aquaporin, bacteriorhodopsin, cryo EM
INTRODUCTION
Electron crystallography is the only electron cryomicroscopy (Cryo EM) technique capable of delivering structural information for membrane proteins at atomic resolution. With recent advancements in both hardware and methodology, a number of membrane protein structures have been determined by electron crystallography to resolutions that rival those achieved by X-ray crystallography (Gonen et al., 2005; Gonen et al., 2004; Grigorieff et al., 1996; Henderson et al., 1990; Hiroaki et al., 2006; Hite et al., 2010; Holm et al., 2006; Jegerschold et al., 2008; Kimura et al., 1997; Kuhlbrandt et al., 1994; Mitsuoka et al., 1999; Murata et al., 2000; Ren et al., 2001; Subramaniam and Henderson, 2000; Tani et al., 2009; Vonck, 2000). Structure determination in electron crystallography begins with two-dimensional (2D) crystals, where the membrane protein of interest is crystallized within a lipid bilayer in which extensive lipid-protein interactions can exist and where lipids can influence the protein structure and function (Reichow and Gonen, 2009). Given 2D crystals of sufficient order, both protein and lipid structures and their interactions can be determined and studied in detail by electron crystallography (Gonen et al., 2005; Hite et al., 2010; Mitsuoka et al., 1999; Tani et al., 2009).
For data collection, the 2D crystals are frozen and both image and diffraction data are recorded under low-dose conditions to minimize damage to the crystals (Fujiyoshi, 1998). The images directly provide the phase information (reviewed by (Glaeser and Downing, 1993)) while diffraction patterns yield accurate amplitude measurement. Usually both the image and the electron diffraction data sets are combined for structure determination and the resolution limit is defined by the resolution that is obtained from images. In practice it is very challenging, time consuming and laborious to record an image data set to high resolution. This is mainly because of instabilities in the cryogenic stage (mechanical and thermal drift), instabilities of the electron beam, and charging effects, all of which “smear out” the high-resolution features in the images (Fujiyoshi, 1998). Moreover, the amplitudes in the Fourier transforms of the images are relatively inaccurate because they are modulated by the contrast transfer function (CTF). On the other hand, image data sets can be collected to low-resolution (~6Å) with relative ease given well-ordered crystals. This is especially true with recent developments in sample preparation and instrumentation. These images provide low resolution, but accurate, phase information.
In sharp contrast to imaging, electron diffraction typically yields higher resolution information because it is not affected by any of the above instabilities or charging affects and the amplitudes are accurate, as they are not modulated by the CTF. However, electron diffraction only provides amplitude information (from diffraction intensities) but not the phase information. Molecular Replacement (MR) is a useful method for phasing high-resolution electron crystallographic data. This technique is common in protein X-ray crystallography but was only recently implemented for use in electron crystallography (Gonen et al., 2005; Gonen et al., 2004; Hiroaki et al., 2006) and depends on the existence of a homologous protein structure to be used as a search model for phasing. If a suitable search model does not exist, MR cannot be used and phases have to be determined by other means.
Here we present a new approach for rapid structure determination of membrane proteins by electron crystallography based upon phase extension. The concept is similar to some of the pioneering work employed by X-ray crystallographers where low-resolution phases from heavy atom derivatives were extended to high resolution for native data sets (Hogle et al., 1985; Liddington et al., 1991; Rossmann et al., 1985) or EM images of viruses were used to provide a molecular envelope for phase extension of X-ray diffraction intensities for structure determination (Dokland et al., 1997; Dokland et al., 1998; Prasad et al., 1999). We applied our method to three previously determined electron crystallographic structures of (i) aquaporin-4 at 3.2Å resolution (Hiroaki et al., 2006), (ii) bacteriorhodopsin at 3.0Å resolution (Mitsuoka et al., 1999), and (iii) aquaporin-0 at 1.9Å resolution (Gonen et al., 2005). Our approach allowed us to solve all three structures rapidly and within ~1Å r.m.s.d. accuracy of the previously published structures. This newly developed approach can dramatically accelerate structure determination by electron crystallography because it eliminates the need for high-resolution image data collection, which is arguably one of the most time-consuming and laborious steps in electron crystallography.
RESULTS
The overall strategy for phase extension
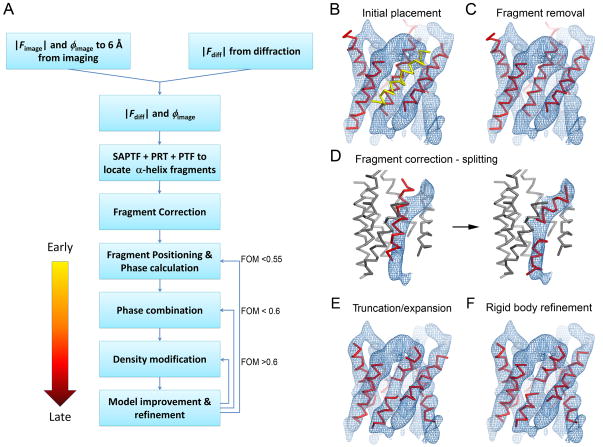
We set to develop a new approach for rapid structure determination of membrane proteins by electron crystallography in the 2–3.5 Å resolution range without relying on high-resolution imaging or the existence of a homologous structure for MR. We exploited the strengths of electron crystallography in low-resolution imaging (~6Å to obtain accurate initial low resolution phases) and high-resolution diffraction (to obtain accurate amplitudes to high resolution 3.2-1.9Å), both of which can be collected rapidly given large and well-ordered 2D crystals. The low-resolution experimental phases from images were used for initial placement of a number of idealized α-helix fragments. The fragments were then refined against the high-resolution diffraction data to obtain more accurate spatial positions (Figure 1). Phase extension was carried out by combining the low-resolution experimental phases (obtained from image data) with the high-resolution phases calculated from the positioned fragments using phase probabilities (Hendrickson and Lattman, 1970). The combined phases were further improved by the maximum likelihood density modification procedure (Terwilliger, 2000) (Figure 2). The density-modified phases were then used for fragment expansion, followed by structure refinement against the high-resolution diffraction amplitudes. These procedures were iterated until the structure model was complete (Figures 1A and 3). Our approach was developed and tested with three data sets as outlined below without the use of prior knowledge of the previously-determined structures. Detailed procedures can be found in the Supplemental Experimental Procedures while the progress in the phase extension is documented in Figures 1 – 6.
Figure 1. The fragment-based phase extension method for electron crystallography.
(A) Flowchart of the fragment-based phase extension procedures. (B–F) Fragment positioning procedures prior to phase calculation. The example shown here is for the AQP4 test case. (B) The 20-residue α-helix fragments were initially located by the SAPTF+PRF+PTF algorithm using the experimental amplitude and phase data to 6Å resolution. One helix (yellow) was incorrectly placed outside the density. (C) The fragment outside the density was manually removed. (D) During fragment correction, the fragment that was placed into the kinked density was split into two shorter fragments. (E) Fragments were further corrected by shortening fragments that were too long or elongating fragments that were too short to match the visible density. (F) The fragment positions were refined as rigid bodies against the diffraction amplitude data to correctly position the fragments in the asymmetric unit. Following rigid body refinement all fragments were well positioned and used for the initial phase calculation.
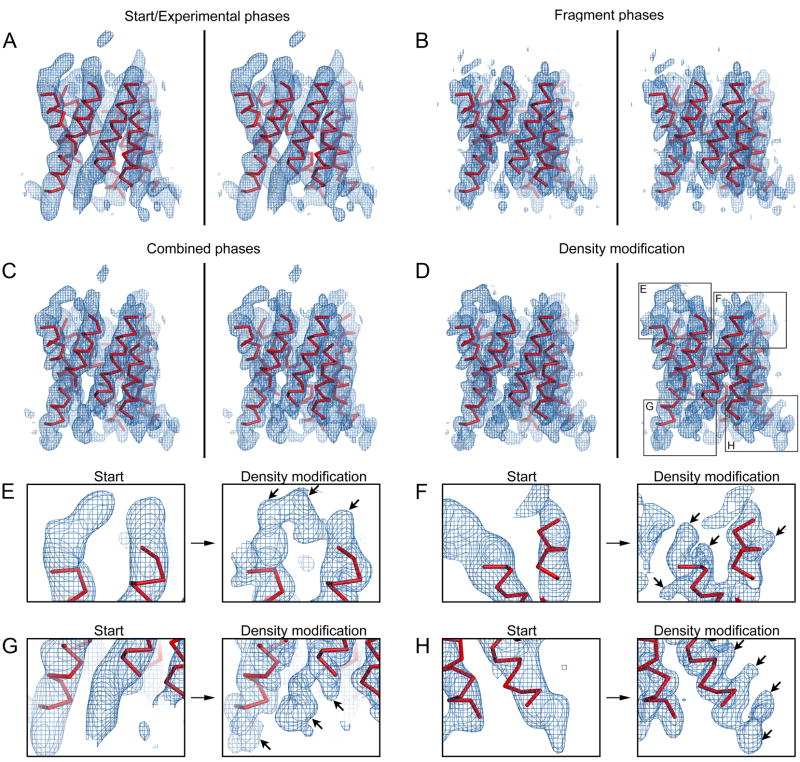
Figure 2. Initial phase extension steps in the AQP4 test case.
Stereo views are presented for panels A–D. Fragments (red) are shown with Cα atoms in all panels. Maps (blue) shown in (B–H) include amplitude information to 3.2Å resolution by electron diffraction. The density maps in all panels are shown at 1σ contour level. (A) Initial 6Å resolution experimental density map obtained from images of AQP4 2D crystals. The density for all helices can be seen but density for the loops appear fragmented. (B) Map calculated from the positioned fragments. (C). Map after phase combination (the phases from A and B were combined). (D) The map from (C) after density modifications. (E–H) Close up views of the boxed regions in (D) showing density features that were not part of the fragments. Loop regions appear more continuous and the density for several amino acid main chains and side chains become apparent (arrows).
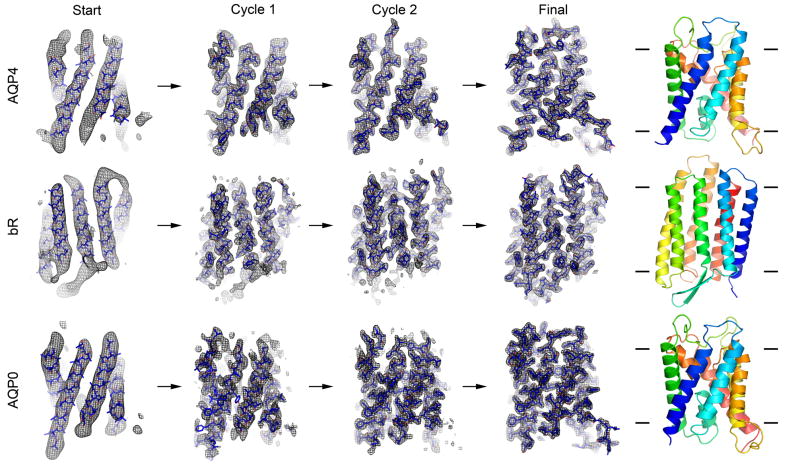
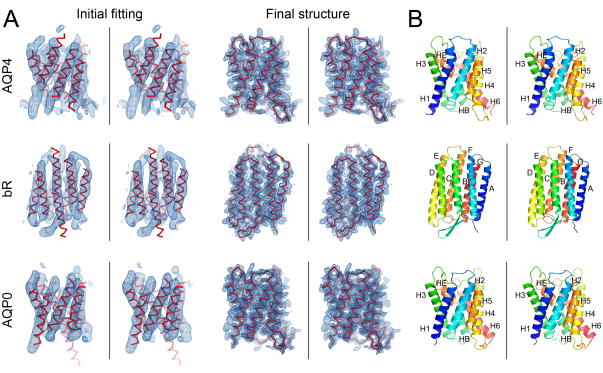
Figure 3. Fragment-based phase extension of AQP4, bR and AQP0 to 3.2Å, 3.0 and 1.9Å resolution, respectively.
(Start) Image phase data to 6Å resolution served as the starting point for fragment positioning. (Cycles 1 and 2) Close up views of the σA-weight 2Fo-Fc density maps (with the corresponding models overlaid) at the end of cycles 1 and 2 of the phase extension procedures, respectively. (Final) Close up view of the final structure of AQP4, bR and AQP0 with the density from phases extended to 3.2Å, 3.0 and 1.9Å resolution, respectively. As the phases improved, more and more densities for amino acid residues became apparent and loops connecting α-helices became visible. The ribbon diagrams represent the final structures as indicated and colored in spectrum from blue to red corresponding to the N- to C-termini, respectively.
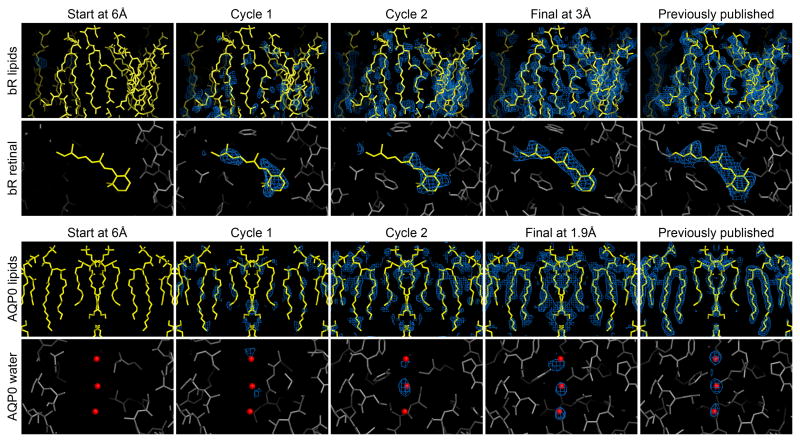
Figure 6. Progressive appearance of density for lipids, ligand, and water molecules.
(Start) The map at 6Å resolution did not reveal densities for the lipid, retinal (bR ligand), or water molecules. (Cycles 1 and 2) The density for lipid, ligand and water molecules became progressively more apparent and more well-defined as phases were extended to 3.0Å and 1.9Å for bR and AQP0, respectively. (Final) In the final map, as the phases were significantly improved, the densities for the lipid, retinal, and water molecules became more accurate and appear similar to the previously published studies (Gonen et al., 2005; Mitsuoka et al., 1999). The σA-weight 2Fo-Fc density maps (blue) from each cycle are shown overlaid with the models of lipid and retinal (yellow), or water molecules (red spheres). The protein models at each stage are displayed in gray.
To make our approach readily accessible and applicable to the wider structural biology community, our procedures rely solely on programs that are publically available to perform all of the required calculations. These programs are well-established and user-friendly, and most are available as part of the Collaborative Project Number 4 (CCP4) (Collaborative Computational Project, 1994) or the Python-based Hierarchical ENvironment for Integrated Xtallography (Phenix) (Adams et al., 2010) software for macromolecular crystallography. These programs run through shell scripts or through the CCP4i (Potterton et al., 2003) or Phenix graphic user interfaces, respectively.
Aquaporin-4 (AQP4)
The rat AQP4 structure was previously determined at 3.2 Å resolution by electron crystallography using molecular replacement as the phasing method (PDB 2D57) (Hiroaki et al., 2006). The AQP4 structure contains 224 residues forming 6 transmembrane (TM) helices (H1–H6) and 2 short non-TM helices (HB and HE) (Figure 4B). HB and HE dip into the membrane from opposite sides of the lipid bilayer and meet at the center of the membrane such that the N-terminus of HB is oriented opposite to the N terminus of HE. The orientation of HB and HE is a signature structural feature shared by all aquaporins studied to date (Gonen and Walz, 2006). The density map of AQP4 at 6Å resolution, obtained by imaging of AQP4 2D crystals, was kindly provided by Drs. Yoshinori Fujiyoshi and Kazutoshi Tani of Kyoto University, Japan. At 6Å resolution, the map contains 6 rod-like densities corresponding to 6 TM helices plus a seventh long kinked density belonging to helices HB and HE (that merge into a single density at this resolution) (Figure 1D).
Figure 4. Stereo view of the 6Å starting model and the final structure for AQP4, bR and AQP0.
(A) Initial fitting: The initial placement of idealized α-helix fragments is the starting point for the fragment-based phase extension procedures. The fragments of 20 alanine residues (red) were initially placed by the SAPTF+PRF+PTF algorithm into the 6Å experimental density (blue). Final structure: The density maps and final structures after our fragment-based phase extension procedures. The σA-weight 2Fo-Fc density maps are shown overlaid with the final structures. The density maps in all panels are shown at 1σ contour level. (B) Stereo views of the final structures shown as ribbon diagrams colored in spectrum from blue to red corresponding to the N- to C-termini, respectively. Helices are labeled as in the previously published structures (Gonen et al., 2005; Hiroaki et al., 2006; Mitsuoka et al., 1999)
Bacteriorhodopsin (bR)
The structure of Halobacterium salinarium bR was previously determined at 3.0 Å resolution (PDB 2AT9) by electron crystallography using a combination of electron diffraction and high-resolution imaging of bR 2D crystals (Mitsuoka et al., 1999). The structure contained 222 residues forming 7 transmembrane (TM) helices (named A to G) and a single 2-stranded anti-parallel β-sheet in the loop connecting helices B and C (named loop BC) (Figure 4B). In addition to the protein, the structure also contained a bound retinal molecule and several ordered lipid and water molecules. The 6Å resolution density map, obtained by imaging of bR 2D crystals, was kindly provided by Dr. Kauro Mitsouka of the Biomedical Information Research Center, Tokyo, Japan. At 6Å resolution, the density map contained 7 rod-like densities that correspond to the 7 TM helices and also a density for the beta-sheet loop BC. However, at this resolution, the density for the beta sheet appears continuous with one of the rod-like densities. The densities for the lipid, water and retinal molecules that were originally reported (Mitsuoka et al., 1999) were invisible in the 6Å resolution map.
Aquaporin-0 (AQP0)
The structure of ovine lens AQP0 was previously determined at 1.9 Å resolution (PDB 2B6O) by electron crystallography, using molecular replacement as the method for phasing (Gonen et al., 2005). The structure contains 235 residues consisting of 6 transmembrane (TM) helices (H1-H6), two short non-TM helices (HB and HE) and a C-terminal helix outside the membrane plane (Figure 4B). As in AQP4, HB and HE dip into the membrane from opposite sides of the lipid bilayer and meet at the center of the membrane such that the N-terminus of HB is oriented opposite to the N terminus of HE. In addition to the protein, the structure also contained several ordered lipid and water molecules. Since an electron microscopy image data set for AQP0 2D crystals was not available, we simulated phases to 6Å to be used in place of the experimental phases for our procedure. The 6Å phases were calculated from a polyalanine model of the AQP0 structure (PDB 2B6O) lacking protein loop regions, lipids and water molecules. This AQP0 6Å simulated map appeared similar to the experimental AQP4 6Å resolution map. It contained 7 long, rod-like densities because the density for helices HB and HE at this resolution merge into a single long density that is kinked at the center (similarly to Figure 1D). Although this map was simulated, it actually contained less information than the experimental maps for AQP4 and bR because our AQP0 simulated map did not contain density for loop regions so the connectivity between adjacent helices was not apparent.
The fragment-based phase extension approach
Initial positioning of fragments
We initially placed idealized α-helix fragments of 20 alanine residues in the asymmetric unit using the spherically averaged phased translation function (SAPTF) followed by phased rotation function (PRF) and phased translation function (PTF) algorithms in the program Molrep (Vagin and Isupov, 2001). Using only the default parameters, in all three test cases the program placed a total of 8 fragments into the density. Even though AQP4 was predicted to have only 6 TM helices plus the two short HB and HE (Hiroaki et al., 2006), the program placed 7 helical fragments into the apparent 7 rod-like densities of the map, while fragment 8 was incorrectly placed and did not occupy any density region (Figure 1B, yellow helix). For bR, the program also placed 8 helix fragments in the asymmetric unit even though the density only contained 7 rod-like densities. Each of six fragments occupied a single rod-like density while 2 fragments were placed in a head-to-tail fashion into a single elongated rod-like density. (This elongated density is the product of a helix and the beta sheet, which appeared merged at 6Å resolution). Finally, for AQP0 the program again placed 8 fragments into the density - 6 fragments were each placed into a single rod-like density while 2 helices were placed into the long, kinked density.
Fragment removal and correction
We examined the result from the Molrep program using the graphic program Coot (Emsley and Cowtan, 2004) and corrected the initial fragments (Figures 1B-E). Fragments that occupied no density were manually removed from the asymmetric unit (Figures 1B, yellow helix and 1C). At low resolution the direction of the α-helix fragments was not easily distinguishable, although we found that the SAPTF+PRF+PTF algorithm provided an advantage over manual placement because this algorithm placed the majority of the α-helix fragments in the correct direction. To detect errors in the fragment direction, we used the helix dipole principle (Hol, 1985; Hol et al., 1978) to examine all remaining helix fragments. Based on the helix dipole principle, two adjacent helices should pack against each other in an anti-parallel fashion because of the opposite partial charges at the helical termini. We were able to detect an error in the directional placement of only 2 helices for AQP4 and 3 helices for bR, and were able to correct the error by a manual 180° flip. For AQP0 we could only detect 1 fragment that was placed in the reverse direction and this fragment was also flipped manually by 180°. We then examined all of the fragments in all three test cases for good fit with the density. A close examination of the three density maps revealed that all structures contained kinked densities. When the density contained a sharp kink or a pronounced curvature, the idealized α-helix fragment could only partially fit into the density. As a rule of thumb, therefore, we split such helices into 2 shorter fragments at the kink (an example is presented in Figure 1D). We then manually extended or truncated all of the fragments to roughly match their corresponding density length (Figure 1E and Supplemental Experimental Procedures). We found that the expansion/truncation of the helices is an important step although expansion/truncation by ±5 residues gave equally good results.
Rigid body refinement and phase probability calculation
After fragment correction, we carried out rigid body refinement and phase calculation using the program Phaser (McCoy et al., 2007). Here we refined the positions of α-helix fragments against the diffraction amplitudes. We found that manual model correction prior to rigid body refinement was crucial in allowing the helices to be positioned more precisely and at the correct register (Figure 1F). Without fragment correction, large errors in helical registers were observed. Phase probability extended to the resolution limit of the diffraction data was then calculated from the position-refined fragments for each test case (Figure 2B).
Phase combination
We used probability-weighted phase combination as a basis for our phase extension approach. Phases from different sources can be combined to obtain a new phase set in order to improve the overall phase and map quality (Rossmann and Blow, 1961). This is often accomplished by using the phase probability distribution expressed as Hendrickson-Lattman (HL) coefficients (Hendrickson and Lattman, 1970). In our procedure, we calculated the HL coefficients and combined the phase probability of the positioned fragments with the phase probability originating from the image data. Phases calculated from the fragments (Figure 2B) usually contain large phase errors due to model incompleteness, imprecise placement of the fragments, and coordinate errors between the idealized and the real conformations of the helices. To minimize these errors and possible bias toward the fragments, we underweighted the phase probability from the fragments during phase combination. The resulting density map contained both low-resolution features from the image data set (including unaccounted density belonging to loop regions) and high-resolution features originating from the positioned fragments (Figure 2C).
Density modification
Density modification is a widely used method for improving phases, especially for data below atomic resolution. This is achieved by improving the real space density map. We used the program Resolve (Terwilliger, 2000) to perform maximum likelihood density modification starting with the combined phase probability. The procedure substantially improved the phase quality and the density map appeared more defined and the density for several amino acid residues began to appear (Figures 2D–H).
Fragment expansion and refinement
Following density modification, we used the automated model building feature of the Resolve program (Terwilliger, 2003) to perform 50 cycles of model building into the density-modified map. The amino acid sequence information was used during the automated model building so that the initial polyalanine fragments were rebuilt and expanded gradually to include other amino acid side chains for residues where the density permitted such modifications. This was coupled with cycles of geometry refinement. Each of the 50 cycles resulted in a possible model with its own Rfree value. The top 5–10 resulting models that were the most complete and had the lowest Rfree were inspected closely in Coot (Emsley and Cowtan, 2004) and used as a guide for cycles of manual model building and refinement in Refmac (Murshudov et al., 1997). The σA-weighted 2Fobs-Fcalc and Fobs-Fcalc maps were then used for additional cycles of manual model building and correction followed by refinement (see details in the Supplemental Experimental Procedures). The model at the end of the first cycle of our fragment-based phase extension procedures contained 179 residues with Rwork/Rfree = 0.368/0.459 for AQP4, 176 residues with Rwork/Rfree = 0.375/0.383 for bR and 143 residues with Rwork/Rfree = 0.416/0.443 for AQP0 (Figure 3, cycle 1).
Iteration and final refinement cycles
After cycle 1, we reiterated the procedures described above and in Figure 1A. The fragment positions were refined with rigid body refinement using the amplitude data to the maximum resolution for each test case. Phase probability was calculated from the fragments and combined with phase probability from the image data. This was followed by density modification, fragment expansion and refinement as described above. The model after cycle 2 contained 203 residues with Rwork/Rfree = 0.332/0.413 for AQP4, 178 residues with Rwork/Rfree = 0.317/0.349 for bR and 185 residues with Rwork/Rfree = 0.327/0.372 for AQP0 (Figure 3, cycle 2). In the final iterated cycle of our fragment-based phase extension procedures, the phase probability from the refined model of cycle 2 was directly combined with the phase probability from the image data and used in density modification followed by automatic model expansion and refinement. Cycles of manual model building and subsequent refinement were carried out until the model was complete. The final model contained 222 residues with Rwork/Rfree = 0.291/0.346 for AQP4, 222 residues with Rwork/Rfree = 0.257/0.308 for bR and 218 residues with Rwork/Rfree = 0.281/0.336 for AQP0 (Figure 3, final). A detailed description of the iteration procedure can be found in the Supplemental Experimental Procedures while the initial fitting of the idealized helices versus the final structures for all three test cases are presented in Figure 4.
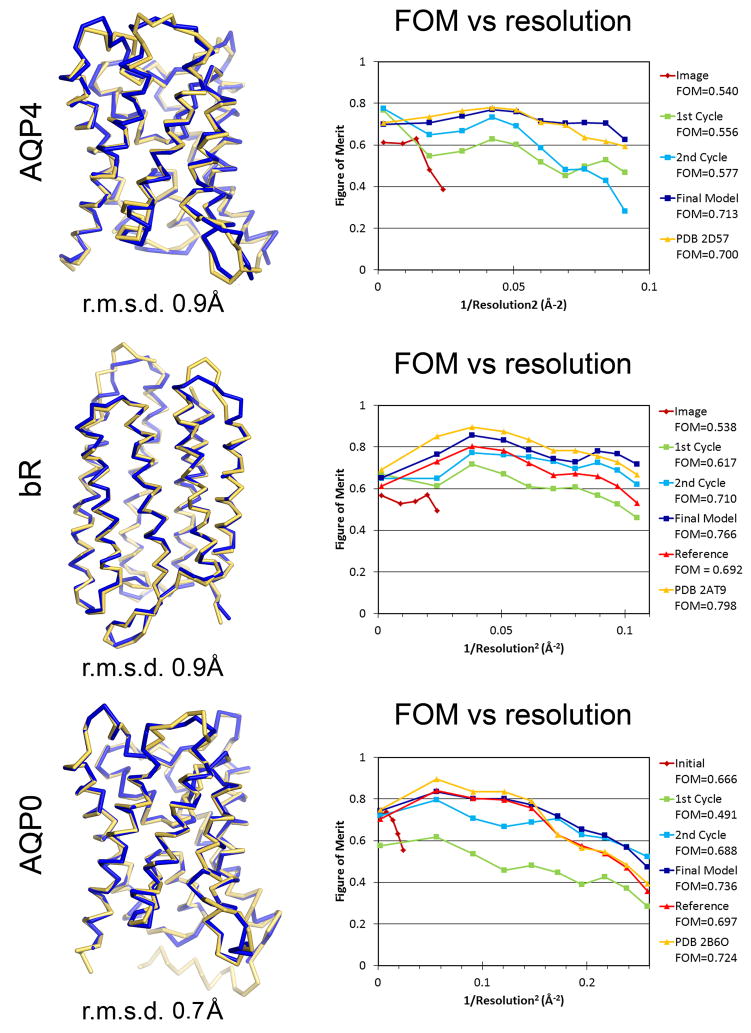
Close comparison of the structures determined by our method with the previously published structures indicates that the structures are essentially the same. In the case of AQP4 our structure is similar to the previously determined AQP4 structure (PDB 2D57, (Hiroaki et al., 2006)) with an r.m.s.d of 1.2 Å for all Cα atoms, and 0.9 Å for 219 Cα atoms using the Secondary Structure Matching (SSM) algorithm (Krissinel and Henrick, 2004) (Figure 5). The main differences between our structure and the previously published structure of AQP4 originate from the flexible loop regions where the density is poorly defined. For bR, the final structure can be superimposed with the previously determined structure (PDB 2AT9, (Mitsuoka et al., 1999)) with an r.m.s.d of 1.3 Å for all Cα atoms, and 0.9 Å using the SSM method for 210 Cα atoms (Figure 5). The main differences are in loop AB and EF regions. Moreover, the C-termini of helices A and E are helical in our structure but were previously modeled in an extended conformation. Similarly, for AQP0 the final structure can be superimposed with the previously-determined structure of AQP0 (PDB 2B6O, (Gonen et al., 2005)) with an r.m.s.d of 1.3 Å for all Cα atoms, and 0.7 Å using the SSM method for 213 Cα atoms (Figure 5). The main differences are again in the flexible loop regions where the density is not well-defined. Our refinement statistics for all three test cases are also comparable to the previously-determined structures (Table 1). The progress in structure determination and phase improvement was evaluated for all three test cases using the plot of figure of merit (FOM) versus resolution (Figure 5). Typically when the FOM was better than 0.6, additional iteration cycles did not provide significant phase improvements. The density maps at this stage were of sufficiently high quality that manual building and refinement could be carried out to improve the phases and complete the model. The final structures have a FOM of 0.713, 0.766 and 0.736 for AQP4, bR and AQP0, respectively.
Figure 5. Comparison of the structures determined by the fragment based phase extension method with the previously published structures.
(Left) The superposition between the structures determined by our method (blue) and the previously published structures (yellow). The SSM r.m.s.d. values for AQP4, bR and AQP0 are indicated. (Right) Plot of figures of merit (FOM) versus resolution. The phases and the models were improved as shown by FOM as the iterated cycles progressed. FOM for the previously published structures were calculated with protein atoms only (labeled in the plot as Reference) and with all atoms (labeled as PDB ID).
Table 1.
Refinement Statistics
| Aquaporin-4 | Bacteriorhodopsin | Aquaporin-0 | |
|---|---|---|---|
| Refinement statistics | |||
| Space group | P4212 | P3 | P422 |
| Unit cell dimensions (c assumed) (Å) | a = b = 69.0, c = 160 | a = b = 62.45, c = 100 | a = b = 65.5, c = 160 |
| Resolution range (Å) | 22.2–3.2 | 27.0–3.0 | 22.9–1.9 |
| Completeness (%) | 87.0 | 76.6 | 62.6 |
| Reflections used (working/free) | 5,654/337 | 6,349/487 | 16,007/1,748 |
| Rwork (%)a | 29.1 | 25.7 | 28.1 |
| Rfree (%)a | 34.6 | 30.8 | 33.6 |
| Average B-factors (Å2) | 43.6 | 39.2 | 29.7 |
| No. of residues | 222 | 222 | 218 |
| No. of refined atoms | 1,644 | 1,715 | 1,652 |
| R.m.s.d. from ideal geometry | |||
| Bond lengths (Å) | 0.009 | 0.009 | 0.011 |
| Bond angles (deg.) | 1.151 | 1.081 | 1.385 |
| Ramachandran statistics | |||
| Favored (%) | 79.1 | 93.2 | 82.6 |
| Allowed (%) | 20.9 | 6.8 | 17.4 |
| Disallowed (%) | 0 | 0 | 0 |
| Reported refinement statistics of previously determined structures | |||
| PDB accession code | 2D57 | 2AT9 | 2B6O |
| Rwork (%)a | 28.3 (28.5)b | 23.7 (32.0)b | 25.8 (29.9)b |
| Rfree (%)a | 33.8 (35.0)b | 33.0 (31.5)b | 29.9 (33.0)b |
| No. of refined atoms | 1,659 | 2,549 | 2,211 |
Rwork and Rfree were calculated from reflections in the working and the FreeR sets, respectively, according to: R-factor = Σ ||Fobs|−|Fcalc||/Σ |Fobs|
Number in parenthesis indicates the R-factor recalculated with only protein atoms (lipid, ligand, and water molecules were excluded) using the program Refmac
Lipid, ligand and water densities
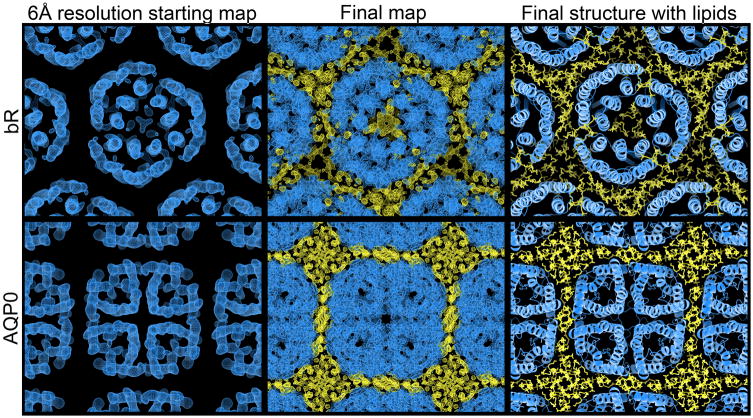
In the original electron crystallographic studies of both bR and AQP0, the density for a belt of annular lipids that mediated crystal contacts was resolved (Gonen et al., 2005; Mitsuoka et al., 1999). These lipids interacted intimately with the proteins by fitting snugly into irregularities on the protein surface. A network of charge complementation, van der Waal contacts, and hydrophobic interactions all contributed to the tight packing of the lipids with the proteins.
The starting 6Å resolution experimental density maps for bR and AQP0 used in our fragment based phase extension method did not initially resolve the density for lipid molecules (Figures 6 and 7). However, as the phase extension procedure progressed and phases became more accurate, the density map generally revealed additional features of ordered entities that contributed to the total diffraction amplitudes, including ligand, water and lipid molecules (Figures 6 and 7). For bR, the density for both lipid molecules as well as retinal appeared. With AQP0 the density for lipid molecules as well as a number of water molecules became apparent. (No lipids were observed for AQP4 likely due to the low-resolution diffraction). These observations serve as a validation that our method can produce accurate phases because the lipid molecules, retinal and water molecules were excluded from the initial fragments and were invisible in the starting low-resolution maps.
Figure 7. Lipids mediate crystal contacts in bacteriorhodopsin and aquaporin-0.
In the starting 6Å resolution experimental map, the density for lipids was not visible. However, as the phases were extended and improved, the density for lipids became increasingly apparent. In the final σA-weight 2Fo-Fc map, the lipid densities were pronounced and matched the previously published structures of the membrane surrounding both bR and AQP0. bR and AQP0 are illustrated in blue and lipids in yellow.
DISCUSSION
Once large and well-ordered 2D crystals are obtained, one of the bottlenecks in structure determination by electron crystallography is the requirement of image data collection to directly provide experimental phase information to high resolution. Using our fragment-based phase extension approach we were able to determine the high-resolution structure of each of the above three membrane proteins rapidly and accurately to atomic resolution without the use of high-resolution image data. This approach takes advantage of the strengths of electron crystallography (in rapidly obtaining accurate low resolution experimental phase information from low-resolution image data and in obtaining accurate high-resolution amplitude information from electron diffraction) and, at the same time, introduces less model bias than molecular replacement because it does not require a homologous structure for phasing.
Image acquisition at low-resolution such as ~6Å is relatively simple and routine in electron crystallography given large and well-ordered 2D crystals. Image data collection to high resolution is much more challenging. Various instabilities such as charge and mechanical and thermal drifts in the electron microscope all affect the quality of the images and therefore the phase information (Fujiyoshi, 1998; Gyobu et al., 2004). For a complete 3D density map to be obtained at 3Å resolution from image data, one must tilt the 2D crystals to at least 60° to minimize the missing cone and maximize data completeness (Fujiyoshi, 1998; Hiroaki et al., 2006; Kimura et al., 1997). Unfortunately, all of the artifacts mentioned above are more severe with high tilt angles, further limiting the information that is recorded. Even with the use of crystal unbending protocols (Kunji et al., 2000), no example exists to date where images of 2D crystals yielded a 3D density map better than 3Å resolution.
In sharp contrast, high-resolution electron diffraction data can be collected rapidly and accurately typically delivering information well beyond the 3Å resolution mark for large and well-ordered 2D crystals. Electron diffraction is independent of the CTF and the data is not affected by the stage and temperature instabilities or by the charging affects. As a result, data can be collected from highly tilted 2D crystals (60° or even 70° is feasible if the 2D crystals are large enough) resulting in a data set where the missing cone is significantly minimized and the data is more complete (Fujiyoshi, 1998; Glaeser and Downing, 1993). The downside of using electron diffraction data alone is that phases need to be determined by other methods. While molecular replacement proved itself as a useful technique for phase determination (Gonen et al., 2005; Gonen et al., 2004; Hiroaki et al., 2006) it can only be used when a homologous search model is available.
Our new approach does not require a homologous structure for phasing and therefore introduces less bias and has fewer restrictions than molecular replacement. Instead, we obtain initial experimental phase information from low-resolution image data. Image data acquisition to low-resolution is fast and relatively simple and the phases that are obtained are accurate enough that the density for helices is well defined, allowing us to place α-helix fragments in the asymmetric unit in real space. Our procedure has been developed and tested for structures containing mostly α-helices but has not been tested or optimized for β-barrel membrane proteins. The procedure works well for α-helical proteins as phases extended using the fragments are more reliable when (i) the fragments are positioned accurately with low r.m.s.d. between the fragment and the target structure – a condition more suitable to α-helices than β-sheets at ~6Å low resolution, and (ii) the fragments occupy the majority of the asymmetric unit and contribute to a large portion of the total diffraction amplitudes.
Initial phases calculated from the fragments are usually biased toward the fragments and have poor quality due to coordinate errors (deviation of idealized helices from real helices and inaccuracy in positioning) and model incompleteness. In our procedures, these problems were significantly reduced by (i) using the maximum likelihood approach for fragment phase probability calculation so that reflections with more accurate phases have higher weight, (ii) using low-resolution experimental phases from images to restrain phase accuracy by phase combination, (iii) underweighting the overall fragment phase probability during phase combination, and (iv) employing the maximum likelihood density modification to improve the combined phases. Using these procedures, the fragments with small errors showed improvement in the density (well-defined features for backbone and side chain) while fragments with large errors (such as conformational differences and large rotational and translational shifts along the helical axis) showed low correlation with the modified density map. We were able to correct the errors originating from the fragments after cycles of density modification, model building and refinement as the models were routinely checked against the σA-weighted 2Fobs-Fcalc and Fobs-Fcalc maps. Therefore, our procedures were able to minimize, identify, and correct errors and/or bias initiated from the starting fragments to ensure the fidelity of the final model.
Using our approach we were able to determine the structures of AQP4, bR and AQP0 rapidly and accurately (within ~1Å r.m.s.d. to the published structures determined by other methods) (Figure 5). The bR test case provides a valuable comparison between the use of high-resolution image phases and our approach for structure determination. Our phase extension approach produced lower refinement Rfree than the value reported previously (Table 1) even though our structural model did not include retinal, lipid and water molecules in the refinement. Our bR structure differs from the previously reported structure (PDB 2AT9) (Mitsuoka et al., 1999) in the loop AB and EF regions and the C-terminal ends of helices A and E in (Figure 5). The conformation at these loops and helical ends in our structure was not a result from the fragment bias as the fragments did not extend into these regions. The reported bR structure was previously refined against both diffraction amplitudes and high-resolution phases from images (Mitsuoka et al., 1999) while in our approach the refinement was done against diffraction amplitudes only. Therefore, we were able to refine our structure to better agree with the amplitudes and used phases obtained from the refined model to calculate density maps to further improve the structure. Interestingly, the loop and helical conformations observed in our structure are similar to the conformations in the recently reported 1.6Å-resolution bR structure (PDB 3HAP) that was determined by X-ray crystallography (Joh et al., 2009) with 0.7Å r.m.s.d. for all Cα atoms.
As the phase extension procedure progressed and phases became more accurate, the density maps for AQP0 and bR revealed bound ligand, water and lipid molecules (Figures 6 and 7). These observations serve as a validation that our method can produce accurate phases because the lipid molecules, retinal and water molecules were excluded from the initial fragments and were invisible in the starting low-resolution maps. Our fragment-based phase extension approach was therefore able to rapidly and accurately determine the structures of membrane proteins while eliminating the need for high-resolution image data collection, which is arguably one of the most significant bottlenecks in protein structure determination by electron crystallography.
EXPERIMENTAL PROCEDURES
Data files were prepared using the CCP4 programs Sfall, CAD, and SigmaA (Collaborative Computational Project, 1994) via CCP4i version 1.4.4.2 (Potterton et al., 2003). The initial placement of the idealized α-helix fragments was performed using the spherically average phased translation function (SAPTF) followed by the phased rotation function (PRT) and the phased translation function (PTF) algorithm in the program Molrep (Vagin and Isupov, 2001). The fragments were manually corrected in the graphic program Coot (Emsley and Cowtan, 2004). The rigid body refinement of the fragments and phase probability calculation were performed using the program Phaser (McCoy et al., 2007). The program Clipper hltofom in CCP4i was used for phase combination. Density modification and automated model expansion were carried out using the program Resolve (Terwilliger, 2000, 2003) followed by the geometry refinement using the program Refmac (Murshudov et al., 1997). Manual model building was done in Coot followed by the geometry and B-factor refinement against diffraction amplitudes using Refmac. Same working and FreeR reflections used in the previously published structures were used in our procedures for comparison purposes of refinement statistics. The refinement was carried out using only the reflections in the working set. The FreeR reflections (5–10% of all reflections) were excluded from the refinement and were used to calculate Rfree (Table 1) and monitor the progress of the refinement. The progress in structure and phases was analyzed using the CCP4 program SigmaA (Read, 1986). Detailed protocols are described in the accompanying Supplemental Experimental Procedures.
Supplementary Material
Highlights.
Phase extension approach was developed to solve membrane protein structure
a new approach was developed to accelerate structure analysis by electron cryst.
Acknowledgments
We thank the Murdock Charitable Trust and the Washington Research Foundation for generous support of our electron cryomicroscopy laboratory. We thank Yoshinori Fujiyoshi, Kazutoshi Tani (Kyoto University, Japan) and Kaoru Mitsuoka (Biomedical Information Research Center (BIRC) Tokyo, Japan) for kindly providing the data sets for aquaporin-4 and bacteriorhodopsin. Research in the Gonen laboratory is supported by the American Diabetes Association Career Development award 1-09-CD-05 and by the National Institutes of Health grants R01GM079233 and U54GM094598. T.G. is a Howard Hughes Medical Institute Early Career Scientist. The authors declare no conflict of interest.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Adams PD, Afonine PV, Bunkoczi G, Chen VB, Davis IW, Echols N, Headd JJ, Hung LW, Kapral GJ, Grosse-Kunstleve RW, et al. PHENIX: a comprehensive Python-based system for macromolecular structure solution. Acta Crystallogr. 2010;D66:213–221. doi: 10.1107/S0907444909052925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collaborative Computational Project, Number 4. The CCP4 suite: programs for protein crystallography. Acta Crystallogr. 1994;D50:760–763. doi: 10.1107/S0907444994003112. [DOI] [PubMed] [Google Scholar]
- Dokland T, McKenna R, Ilag LL, Bowman BR, Incardona NL, Fane BA, Rossmann MG. Structure of a viral procapsid with molecular scaffolding. Nature. 1997;389:308–313. doi: 10.1038/38537. [DOI] [PubMed] [Google Scholar]
- Dokland T, McKenna R, Sherman DM, Bowman BR, Bean WF, Rossmann MG. Structure determination of the phiX174 closed procapsid. Acta Crystallogr. 1998;D54:878–890. doi: 10.1107/s0907444998002467. [DOI] [PubMed] [Google Scholar]
- Emsley P, Cowtan K. Coot: model-building tools for molecular graphics. Acta Crystallogr. 2004;D60:2126–2132. doi: 10.1107/S0907444904019158. [DOI] [PubMed] [Google Scholar]
- Fujiyoshi Y. The structural study of membrane proteins by electron crystallography. Adv Biophys. 1998;35:25–80. doi: 10.1016/s0065-227x(98)90004-1. [DOI] [PubMed] [Google Scholar]
- Glaeser RM, Downing KH. High-resolution electron crystallography of protein molecules. Ultramicroscopy. 1993;52:478–486. doi: 10.1016/0304-3991(93)90064-5. [DOI] [PubMed] [Google Scholar]
- Gonen T, Cheng Y, Sliz P, Hiroaki Y, Fujiyoshi Y, Harrison SC, Walz T. Lipid-protein interactions in double-layered two-dimensional AQP0 crystals. Nature. 2005;438:633–638. doi: 10.1038/nature04321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gonen T, Sliz P, Kistler J, Cheng Y, Walz T. Aquaporin-0 membrane junctions reveal the structure of a closed water pore. Nature. 2004;429:193–197. doi: 10.1038/nature02503. [DOI] [PubMed] [Google Scholar]
- Gonen T, Walz T. The structure of aquaporins. Q Rev Biophys. 2006;39:361–396. doi: 10.1017/S0033583506004458. [DOI] [PubMed] [Google Scholar]
- Grigorieff N, Ceska TA, Downing KH, Baldwin JM, Henderson R. Electron-crystallographic refinement of the structure of bacteriorhodopsin. J Mol Biol. 1996;259:393–421. doi: 10.1006/jmbi.1996.0328. [DOI] [PubMed] [Google Scholar]
- Gyobu N, Tani K, Hiroaki Y, Kamegawa A, Mitsuoka K, Fujiyoshi Y. Improved specimen preparation for cryo-electron microscopy using a symmetric carbon sandwich technique. J Struct Biol. 2004;146:325–333. doi: 10.1016/j.jsb.2004.01.012. [DOI] [PubMed] [Google Scholar]
- Henderson R, Baldwin JM, Ceska TA, Zemlin F, Beckmann E, Downing KH. Model for the structure of bacteriorhodopsin based on high-resolution electron cryo-microscopy. J Mol Biol. 1990;213:899–929. doi: 10.1016/S0022-2836(05)80271-2. [DOI] [PubMed] [Google Scholar]
- Hendrickson WA, Lattman EE. Representation of phase probability distributions for simplified combination of independent phase information. Acta Crystallogr. 1970;B26:136–143. [Google Scholar]
- Hiroaki Y, Tani K, Kamegawa A, Gyobu N, Nishikawa K, Suzuki H, Walz T, Sasaki S, Mitsuoka K, Kimura K, et al. Implications of the aquaporin-4 structure on array formation and cell adhesion. J Mol Biol. 2006;355:628–639. doi: 10.1016/j.jmb.2005.10.081. [DOI] [PubMed] [Google Scholar]
- Hite RK, Li Z, Walz T. Principles of membrane protein interactions with annular lipids deduced from aquaporin-0 2D crystals. EMBO J. 2010;29:1652–1658. doi: 10.1038/emboj.2010.68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hogle JM, Chow M, Filman DJ. Three-dimensional structure of poliovirus at 2.9 A resolution. Science. 1985;229:1358–1365. doi: 10.1126/science.2994218. [DOI] [PubMed] [Google Scholar]
- Hol WG. Effects of the alpha-helix dipole upon the functioning and structure of proteins and peptides. Adv Biophys. 1985;19:133–165. doi: 10.1016/0065-227x(85)90053-x. [DOI] [PubMed] [Google Scholar]
- Hol WG, van Duijnen PT, Berendsen HJ. The alpha-helix dipole and the properties of proteins. Nature. 1978;273:443–446. doi: 10.1038/273443a0. [DOI] [PubMed] [Google Scholar]
- Holm PJ, Bhakat P, Jegerschold C, Gyobu N, Mitsuoka K, Fujiyoshi Y, Morgenstern R, Hebert H. Structural basis for detoxification and oxidative stress protection in membranes. J Mol Biol. 2006;360:934–945. doi: 10.1016/j.jmb.2006.05.056. [DOI] [PubMed] [Google Scholar]
- Jegerschold C, Pawelzik SC, Purhonen P, Bhakat P, Gheorghe KR, Gyobu N, Mitsuoka K, Morgenstern R, Jakobsson PJ, Hebert H. Structural basis for induced formation of the inflammatory mediator prostaglandin E2. Proc Natl Acad Sci USA. 2008;105:11110–11115. doi: 10.1073/pnas.0802894105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joh NH, Oberai A, Yang D, Whitelegge JP, Bowie JU. Similar Energetic Contributions of Packing in the Core of Membrane and Water-Soluble Proteins. J Am Chem Soc. 2009;131:10846–10847. doi: 10.1021/ja904711k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura Y, Vassylyev DG, Miyazawa A, Kidera A, Matsushima M, Mitsuoka K, Murata K, Hirai T, Fujiyoshi Y. Surface of bacteriorhodopsin revealed by high-resolution electron crystallography. Nature. 1997;389:206–211. doi: 10.1038/38323. [DOI] [PubMed] [Google Scholar]
- Krissinel E, Henrick K. Secondary-structure matching (SSM), a new tool for fast protein structure alignment in three dimensions. Acta Crystallogr. 2004;D60:2256–2268. doi: 10.1107/S0907444904026460. [DOI] [PubMed] [Google Scholar]
- Kuhlbrandt W, Wang DN, Fujiyoshi Y. Atomic model of plant light-harvesting complex by electron crystallography. Nature. 1994;367:614–621. doi: 10.1038/367614a0. [DOI] [PubMed] [Google Scholar]
- Kunji ER, von Gronau S, Oesterhelt D, Henderson R. The three-dimensional structure of halorhodopsin to 5 A by electron crystallography: A new unbending procedure for two-dimensional crystals by using a global reference structure. Proc Natl Acad Sci USA. 2000;97:4637–4642. doi: 10.1073/pnas.080064697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liddington RC, Yan Y, Moulai J, Sahli R, Benjamin TL, Harrison SC. Structure of simian virus 40 at 3.8-A resolution. Nature. 1991;354:278–284. doi: 10.1038/354278a0. [DOI] [PubMed] [Google Scholar]
- McCoy AJ, Grosse-Kunstleve RW, Adams PD, Winn MD, Storoni LC, Read RJ. Phaser crystallographic software. J Appl Crystallogr. 2007;40:658–674. doi: 10.1107/S0021889807021206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitsuoka K, Hirai T, Murata K, Miyazawa A, Kidera A, Kimura Y, Fujiyoshi Y. The structure of bacteriorhodopsin at 3.0 A resolution based on electron crystallography: implication of the charge distribution. J Mol Biol. 1999;286:861–882. doi: 10.1006/jmbi.1998.2529. [DOI] [PubMed] [Google Scholar]
- Murata K, Mitsuoka K, Hirai T, Walz T, Agre P, Heymann JB, Engel A, Fujiyoshi Y. Structural determinants of water permeation through aquaporin-1. Nature. 2000;407:599–605. doi: 10.1038/35036519. [DOI] [PubMed] [Google Scholar]
- Murshudov GN, Vagin AA, Dodson EJ. Refinement of macromolecular structures by the maximum-likelihood method. Acta Crystallogr. 1997;D53:240–255. doi: 10.1107/S0907444996012255. [DOI] [PubMed] [Google Scholar]
- Potterton E, Briggs P, Turkenburg M, Dodson E. A graphical user interface to the CCP4 program suite. Acta Crystallogr. 2003;D59:1131–1137. doi: 10.1107/s0907444903008126. [DOI] [PubMed] [Google Scholar]
- Prasad BV, Hardy ME, Dokland T, Bella J, Rossmann MG, Estes MK. X-ray crystallographic structure of the Norwalk virus capsid. Science. 1999;286:287–290. doi: 10.1126/science.286.5438.287. [DOI] [PubMed] [Google Scholar]
- Read RJ. Improved Fourier Coefficients for Maps Using Phases from Partial Structures with Errors. Acta Crystallogr. 1986;A42:140–149. [Google Scholar]
- Reichow SL, Gonen T. Lipid-protein interactions probed by electron crystallography. Curr Opin Struct Biol. 2009;19:560–565. doi: 10.1016/j.sbi.2009.07.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ren G, Reddy VS, Cheng A, Melnyk P, Mitra AK. Visualization of a water-selective pore by electron crystallography in vitreous ice. Proc Natl Acad Sci USA. 2001;98:1398–1403. doi: 10.1073/pnas.041489198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rossmann MG, Arnold E, Erickson JW, Frankenberger EA, Griffith JP, Hecht HJ, Johnson JE, Kamer G, Luo M, Mosser AG, et al. Structure of a human common cold virus and functional relationship to other picornaviruses. Nature. 1985;317:145–153. doi: 10.1038/317145a0. [DOI] [PubMed] [Google Scholar]
- Rossmann MG, Blow DM. Refinement of Structures Partially Determined by Isomorphous Replacement Method. Acta Crystallogr. 1961;14:641–647. [Google Scholar]
- Subramaniam S, Henderson R. Molecular mechanism of vectorial proton translocation by bacteriorhodopsin. Nature. 2000;406:653–657. doi: 10.1038/35020614. [DOI] [PubMed] [Google Scholar]
- Tani K, Mitsuma T, Hiroaki Y, Kamegawa A, Nishikawa K, Tanimura Y, Fujiyoshi Y. Mechanism of aquaporin-4’s fast and highly selective water conduction and proton exclusion. J Mol Biol. 2009;389:694–706. doi: 10.1016/j.jmb.2009.04.049. [DOI] [PubMed] [Google Scholar]
- Terwilliger TC. Maximum-likelihood density modification. Acta Crystallogr. 2000;D56:965–972. doi: 10.1107/S0907444900005072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Terwilliger TC. Improving macromolecular atomic models at moderate resolution by automated iterative model building, statistical density modification and refinement. Acta Crystallogr. 2003;D59:1174–1182. doi: 10.1107/S0907444903009922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vagin AA, Isupov MN. Spherically averaged phased translation function and its application to the search for molecules and fragments in electron-density maps. Acta Crystallogr. 2001;D57:1451–1456. doi: 10.1107/s0907444901012409. [DOI] [PubMed] [Google Scholar]
- Vonck J. Structure of the bacteriorhodopsin mutant F219L N intermediate revealed by electron crystallography. EMBO J. 2000;19:2152–2160. doi: 10.1093/emboj/19.10.2152. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.