Abstract
Dihydrofolate reductase from Mycobacterium tuberculosis catalyzes the NAD(P)H dependent reduction of dihydrofolate, yielding NAD(P)+ and tetrahydrofolate, the primary one carbon unit carrier in biology. Tetrahydrofolate needs to be recycled so that reactions involved in dTMP synthesis and purine metabolism are maintained. Previously, steady-state studies revealed that the chemical step significantly contributes to the steady state turnover number, but that a step after the chemical step was likely limiting the reaction rate. Here, we report the first pre-steady state investigation of the kinetic sequence of the MtDHFR aiming to identify kinetic intermediates, and the identity of the rate limiting steps. This kinetic analysis suggests a kinetic sequence comprising two parallel pathways with a rate determining product release. Although product release is likely occurring in a random fashion, there is a slight preference for the release of THF first, a kinetic sequence never observed for a wild type dihydrofolate reductase of any organism studied to date. Temperature studies were conducted to determine the magnitude of the energetic barrier posed by the chemical step, and the pH dependence of the chemical step was studied, demonstrating an acidic shift from the pKa observed under steady-state. The rate constants obtained here were combined with the activation energy for the chemical step to compare energy profiles for each kinetic sequence. The two parallel pathways are discussed, as well as their implications on the catalytic cycle of this enzyme.
Keywords: Folate Metabolism, DNA synthesis, Kinetics, Pre-steady-state kinetics, Kinetic Sequence, Energy profile, Tuberculosis
Dihydrofolate reductase (5,6,7,8-tetrahydrofolate:NADP+ oxidoreductase, EC 1.5.1.3, DHFR) catalyzes the NADPH-dependent reduction of dihydrofolate (DHF) to tetrahydrofolate (THF) (Scheme 1). This enzyme is required for the regeneration of THF, a crucial one carbon unit carrier essential for reactions involved in deoxythymidine monophosphate (dTMP) synthesis, as well as reactions involved in the biosynthesis of purines (1). Drugs that inhibit DHFR have been used since 1947, when aminopterin was introduced in the treatment of leukemia (2), followed by the development of pyrimethamine and trimethoprim in the 1950’s, which were found to be effective in the treatment of malaria and bacterial infections (3). In addition to its relevance as a drug target, DHFRs from several organisms have been thoroughly studied kinetically and structurally, furthering our understanding of protein folding (4), the importance of dynamics and coupled motions to catalysis (5), and the contribution of chemistry and conformational changes to catalysis (6), just to name a few. Recently, our group demonstrated by a combination of pH studies, and kinetic isotope effects under steady-state and pre-steady state conditions that the chemical step of the DHFR from Mycobacterium tuberculosis (MtDHFR) had a remarkably slow rate at neutral pH compared to DHFRs from other organisms (7). Additionally, it was demonstrated that the chemical step was contributing significantly to the turnover rate of the reaction, but that a step after the chemical step was decreasing the magnitude of the kinetic isotope effects observed under steady-state conditions. In this work, we investigate the kinetic sequence of MtDHFR by stopped-flow absorbance and fluorescence, aiming to identify which step is the rate-determining step in turnover, and whether this reaction follows a preferential pathway, as seen for other DHFRs (8–14). Our kinetic analysis allowed us to put forward a complex kinetic sequence based on a slow chemical step followed by a rate limiting random product release occurring via two possible, and likely parallel, pathways.
Scheme 1.
Reaction catalyzed by the MtDHFR
EXPERIMENTAL PROCEDURES
Materials
All chemicals were of analytical or reagent grade and were used without further purification. DHF, THF, NADPH, and NADP+ were purchased from Sigma.
Purification of MtDHFR
Competent E. coli BL21 (DE3) cells (Novagen) were transformed with the recombinant plasmid pET28a(+):dfrA, and MtDHFR was expressed and purified as described previously (15). Protein concentration was determined by using the theoretical value ε280 = 40,450 M−1cm−1, or ε340 = 6,220 M−1cm−1 due to bound NADPH (16). The NADP+ bound form of the enzyme was generated by immobilizing MtDHFR-NADPH onto a Ni-NTA resin, and 10mL of 100 mM NADP+ were passed through the column, to form the MtDHFR-NADP+ form of the enzyme. The enzyme was eluted with 500 mM imidazole, dialyzed against 2 × 2L of 100 mM HEPES with 50 mM KCl, pH 7.5, and frozen at −80 °C.
Equilibrium dissociation constants
THF binding to MtDHFR-NADPH and MtDHFR-NADP+ was measured by fluorescence titration at 25°C using a Horiba spectrofluorometer. Excitation and emission wavelengths were 280 and 340 nm, respectively. Titrations were conducted by serial additions of 1 μL aliquots of ligand to a 1 cm2 quartz cuvette that contained 2 mL of 0.5 μM of MtDHFR in 100 mM HEPES with 50 mM KCl pH 7.5. Fluorescence readings were recorded 2 min after the addition of ligand to allow temperature equilibration, and the dissociation constants were estimated by nonlinear regression. Data for THF binding to MtDHFR-NADPH were fitted to a quadratic equation (eq. 1) due to the fact that the concentration of enzyme and ligand were comparable, whereas data for THF binding to MtDHFR-NADP+ were fitted to a hyperbolic equation (eq. 2), where F is the fraction of ligand bound to the enzyme, E0 is the initial enzyme concentration, ST is the total ligand concentration, S is the substrate concentration, and Kd is the dissociation constant for enzyme-substrate complex (17).
The concentration of THF did not exceed 10 μM to avoid inner filter effects.
| (1) |
| (2) |
Stopped-Flow General Procedures
All pre-steady-state experiments were performed on an Applied Photophysics model SX20 stopped-flow spectrofluorometer equipped with a Xenon lamp, which has a dead-time of 3 ms, and a 1 cm path length for absorbance measurements and a 2mm path length for fluorescence measurements. All experiments were performed at 25 °C in 100 mM HEPES, 50 mM potassium chloride buffer pH 7.5, unless stated otherwise. Typically, each observed rate constant was obtained after averaging 5–10 shots, and fitting the average to the appropriate exponential equation. The reported concentrations are final, after volumes of 60 μL were mixed from each syringe.
Stopped-Flow Absorption Experiments
The conversion of DHF and NADPH to THF and NADP+ was monitored by observing the change in absorbance at 340 nm, using an extinction coefficient of 11,800 M−1cm−1 (18). For single turnover experiments, DHF was kept at 1 μM, and NADPH was saturating (100 μM), while the concentration of MtDHFR was varied from 5 μM to 28 μM. Traces were fitted analytically using Microsoft Origin version 7, and the first 3 ms of data were discarded when fitting the data. Inspection of residuals provided an assessment of the quality of the fits. The fitting functions had a general form (eq. 3), where y(t) is the observed signal at time t, i is the number of transients, Ai is the amplitude of the ith transient, ki is the observed rate constant for the ith transient, and C is the offset.
| (3) |
Multiple turnovers were measured by monitoring the change in absorbance at 340 nm. For these experiments, the concentration of DHF and NADPH were 100 μM each, and MtDHFR was varied from 1 to 10 μM. The curves obtained were fitted to eq. 4, which is identical to eq. 3 but includes a linear phase, whose rate is represented by v.
| (4) |
Stopped-Flow Fluorescence Experiments
Single and multiple turnovers were also monitored by using fluorescence energy transfer (FRET), emitted when the protein is excited at 280 nm, emitting fluorescence at 340 nm, which then excites the bound NADPH molecules, emitting fluorescence at 450 nm. A cut off filter of 420 nm was used to assure that only the signal coming from the transfer was being observed. The conditions were the same as described for the stopped-flow absorbance measurements. Binding and dissociation rate constants were measured by stopped-flow fluorescence quenching or enhancement, and the measurement of dissociation rates utilized NADPH, NADP+, or methotrexate as competitors. For binding experiments monitoring protein fluorescence, the concentration of THF did not exceed 10 μM to avoid inner filter effects. THF binding experiments were also conducted using FRET, which significantly decreases inner filter effects. Binding of DHF to MtDHFR-NADPH was measured by performing single turnover experiments with 2 μM DHF, 100 μM NADPH, and variable concentrations of enzyme (at least five times higher than the concentration of DHF, to maintain pseudo-first order conditions). Observed rate constants obtained after fitting the data to eq. 1 were used in replots of kobs versus concentrations of substrate, product, or competitor. Linear concentration dependencies of the observed rate constant (kobs) were fitted to eq. 5, where k1 is the association rate constant, L is the concentration of ligand, k−1 is the dissociation rate constant.
| (5) |
When binding was a two-step process, data for the first phase was fitted to a modified version of eq 5, in which the intercept is equal to k1+ k2 + k−2 (19).
Hyperbolic concentration dependencies of the observed rate constant (kobs2) were fitted to eq. 6. Hyperbolic concentration dependency refers to a two-step binding process, with kobs1 ≫ kobs2.
| (6) |
The apparent dissociation constant (Kov) for this two-step association was obtained using eq. 7.
| (7) |
When saturation of the second phase (kobs2) wasn’t observed, and the concentration of the ligand could not be increased due to inner filter effects, data were fitted to the linear equation below (eq. 8), a simplification of eq.6 for [L]≪ Ks,
| (8) |
In eq. 6, 7, and 8, k1 is the association rate constant, k−1 is the dissociation rate constant, k2 and k−2 are, respectively, the forward and reverse rate constants of the unimolecular isomerization step, and KS is the dissociation constant for the first bimolecular step. Equations for pre-steady state analysis were adapted from Hiromi (20).
Temperature and pH dependence of the chemical step
Single turnover experiments were conducted at 15–35°. The rate constants for the chemical step (kH) obtained after fitting the single turnover transients with a single exponential equation (eq. 4) were reploted as a function of temperature, and the activation energy was calculated from fitting the temperature dependence of kH to eq. 9. The temperature dependence of kcat data was also fitted to eq. 9.
| (9) |
Additionally, rate constants obtained in the forward and reverse directions were used to calculate the activation energy of each step in the forward and reverse directions respectively, according to eq. 10. For eq. 9, and 10, k represents the rate being measured (kH or kcat), ki is the rate constant of the reaction step, Ea is the experimental activation energy, T is the temperature in Kelvin degrees, R is the gas constant (1.98 cal mol−1), and A represents a pre-exponential factor that correlates collision frequency and the proper orientation of colliding molecules with the rate of the reaction (21), and κB and h are the Boltzmann and the Planck constants, respectively. It’s important to note that the activation energy and the enthalpy of activation are related by Ea = ΔH≠ + RT (22).
| (10) |
To investigate the pH-dependence of the chemical step, single turnover experiments were performed from pH 5.5 to 7.5. For the reactions at different pH values, 100 mM MES with 50 mM KCl was utilized for pH values of 5.5–6.5, and 100 mM HEPES with 50 mM KCl was used for pH values 6.5–7.5. Data for single turnovers at each pH were collected at saturating enzyme concentrations and analyzed as mentioned above, and then the kH values obtained were reploted as a function of pH, and fitted to eq. 11, where y is the kinetic parameter, C is the pH-independent value of y, H is the proton concentration, and Kb is the apparent basic dissociation constant for ionizing groups.
| (11) |
Global data fitting
Fluorescence stopped-flow data with more than one transient phase, and experiments with concentration series were fit globally by regression analysis based upon numerical integration of the rate-equations using KinTek Global Kinetic Explorer version 2.2 (KinTek Corp. Austin, TX). For different ligand concentrations, scaling factors were included in the data fitting process, and estimates for errors on parameters were derived by nonlinear regression and by FitSpace confidence contour analysis (23, 24).
Analysis of kinetic scheme using Markov chains
Continuous time Markov chains were generated (CTMC), where rates or frequencies of occurrence over time are used. In order to generate CTMCs, a vector (i.e. an array of numbers) is multiplied by a matrix, where the rates of the kinetic scheme are defined for all existent enzyme forms. The matrix representing the kinetic scheme with all possible connections between enzyme forms was generated using the software KApattern (25). Once the matrix was defined, a direct method (a linear system of equations) was used to calculate the stationary regime, e.g., the stage where the system was simulated for a sufficiently large amount of time until changes no longer occurred. The result of this computation provided the probability of permanence for each state. The computation of such results was conducted by executing an online application available for free access. In the case of this paper, since nine enzyme forms were present, the matrix had 9×9 positions, which corresponds to the solution of a linear system of eleven unknown variables (26). Concentrations of substrates and products were calculated assuming a Keq = 5.06 × 107 (7, 8).
RESULTS AND DISCUSSION
Multiple turnover studies
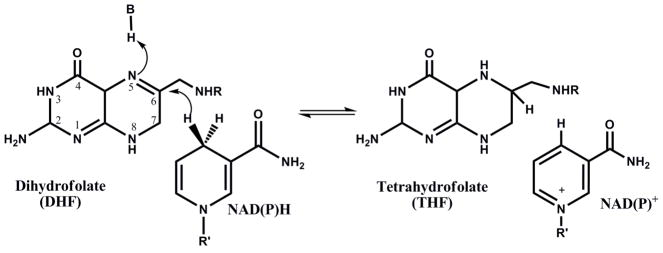
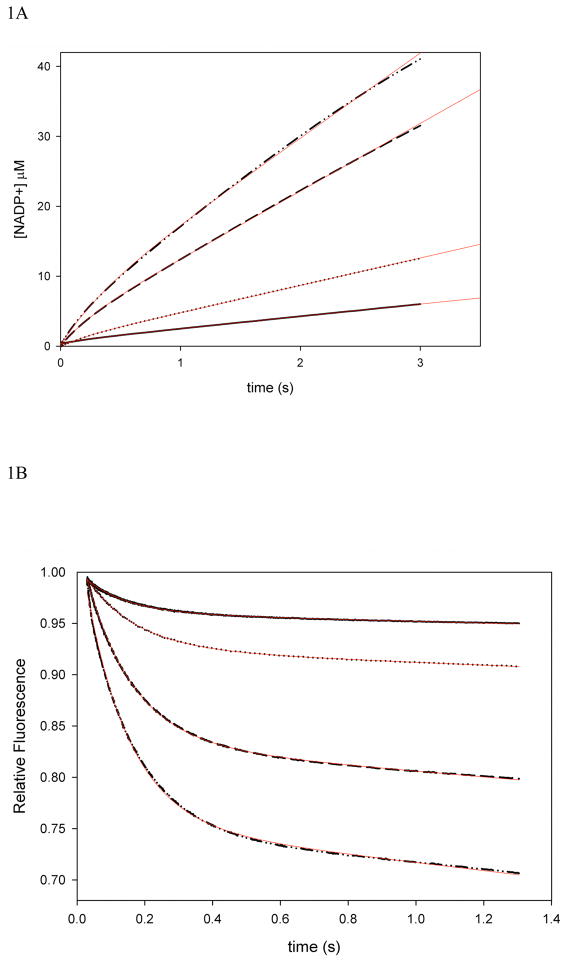
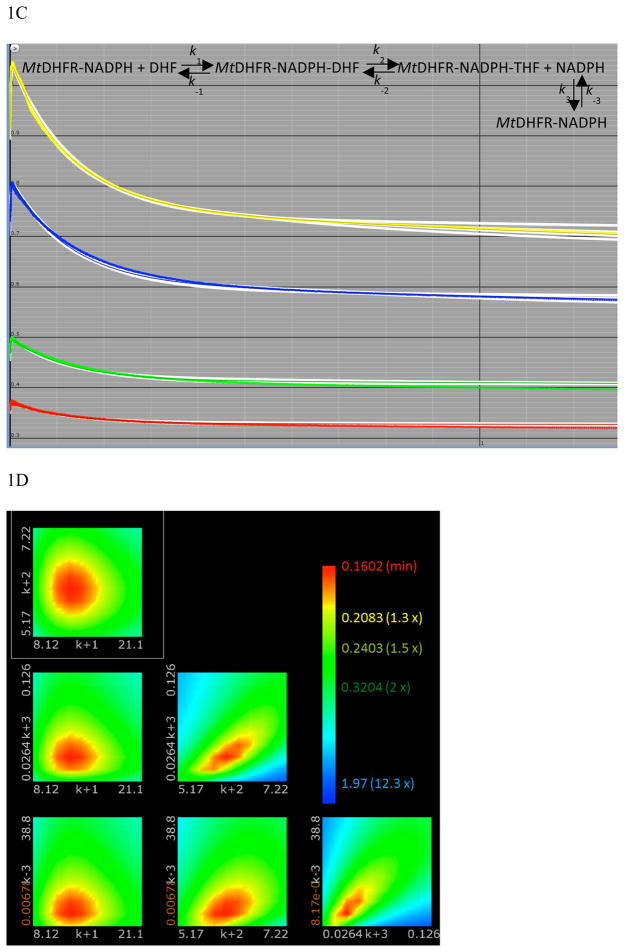
Previously, it was demonstrated by the analysis of kinetic isotope effects under steady-state and single turnover conditions that the isotope effect on the chemical step (DkH) and the D(V/KDHF) were of equal magnitude, both being larger than DV. This suggests that a step after chemistry is contributing to the rate of the reaction, decreasing the magnitude of DV. Thus, it is likely that a step involved in product release is determining the rate of the reaction, which would be observed as a burst of product formation in a multiple turnover experiment (7, 21, 27, 28). Figure 1A shows that indeed, a small burst was observed when absorbance changes during turnover were monitored. The linear phase had a rate of 2.3 ± 0.1 s−1, in good agreement with the kcat obtained under steady-state conditions (2.5 ± 0.2 s−1). The first exponential phase had small amplitude, and simulations conducted by the KinTek Global Kinetic Explorer software demonstrated that if the rates of chemistry and product release are comparable in magnitude, the distinction between the exponential phase and the linear phase becomes troublesome, and the fitting might result in an incorrect determination of both rates. Moreover, it was clear that the amplitude of the burst was smaller than the concentration of active sites, suggesting that the rates of chemistry and product release are comparable or that an internal equilibrium is decreasing the burst amplitude (29). In order to increase the signal obtained, and better estimate the rate of exponential phase, multiple turnover experiments monitoring FRET due to NADPH bound to the MtDHFR were measured (Figure 1B). These data showed a much more distinctive burst of product formation, and the rate for the exponential phase was 7.4 ± 0.3 s−1, which can be a good estimate of the rate of chemistry (kH) even though it is slightly larger than the kH value obtained in single turnover experiments (see below). This value is in agreement with the fact that the observed burst rate is greater or equal to the rate of the chemical reaction, being a function of forward and reverse rates of chemistry plus the rate of product release (29). Figure 1C demonstrates the global fitting of the FRET burst data to the most simple plausible mechanism shown in the figure using KinTek Global Explorer, and Figure 1D shows the FitSpace error contour analysis demonstrating that the rate of the burst phase is most likely between 5.17 and 7.22 s−1 (24). Unfortunately, the amplitude of the burst kinetics using FRET cannot be used to calculate active site concentration, since there is a complex and often nonlinear relationship between the FRET signal obtained and the amount of enzyme-ligand complex being formed (30).
Figure 1.
Pre-steady state burst of product formation. The reaction was conducted with 100 μM DHF, 100 μM NADPH, and 1 (—), 2 (…), 5 (---), and 7 (-..-) μM MtDHFR. A) Decrease in absorbance at 340 nm due to NADPH consumption was monitored, and the change in absorbance was converted into product formation by using the extinction coefficient of 11,800 M−1 cm−1 (18). The line is a fit to eq. 4, yielding a steady state rate constant of 2.3 ± 0.1 s−1. B) Fluorescence decrease due to NADPH consumption. The signal was obtained by excitation at 280 nm, and emission at 450 nm by fluorescence energy transfer caused by enzyme bound NADPH. The larger amplitude of the burst phase allowed a better estimation of the burst rate; the line is a fit to eq. 4, resulting in a burst rate constant of 7.4 ± 0.3 s−1. C) Global fit of the burst data shown in B with different concentrations of MtDHFR (from bottom to top: 1, 2, 5, 7 μM) to the mechanism shown in the figure. The white contour represents fits of data within the parameters boundaries, so that all of the reasonable fits to the data are superimposed with the data and the best fit. D) FitSpace confidence contours (24) for the global fit of the burst data. To avoid excessive fluctuation of kinetic parameters, the value for k−2 was fixed at 0.0004 s−1, and the values for k1 and k−1 were linked based on a Kd = 2 μM for DHF.
Single turnover experiments
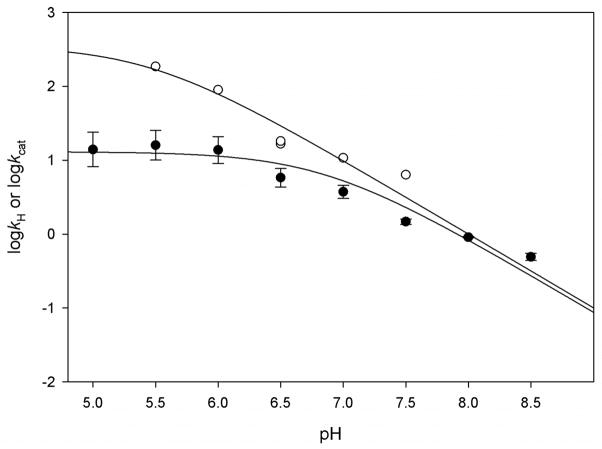
To obtain information about the rate of the hydride transfer step at different pH values and temperatures, as well as to determine the binding rate constants for DHF to the binary complex MtDHFR-NADPH, experiments under single turnover conditions were performed. In these experiments, a biphasic transient was observed, consisting of a first fast concentration dependent phase with a negative amplitude attributed to DHF binding, followed by a slower fluorescence decay caused by NADPH consumption. The enzyme concentration dependency of the observed rate constant of this second phase showed saturation behavior permitting the maximal chemistry rate constant to be estimated: 5.8 ± 0.3 s−1. This value is very similar to the chemistry rate measured in the burst experiments. In order to further investigate the hydride transfer step, single turnover experiments were measured at different pH values. Figure 2 compares the pH dependence of kH and kcat, and fitting to eq. 11 yielded pKa values of 6.8 ± 0.2 for kcat, and 5.4 ± 0.3 for kH. As expected for a reaction in which a step after the chemical step is at least partly rate-limiting, there is an outward shift on the pKa observed on the kcat profile (31). In addition, it is clear that chemistry becomes increasingly rate-limiting as the pH becomes higher than 6.0, corroborating previous studies that showed a kinetic isotope effect close to unity at acidic pH, but increasing in magnitude at more basic pH values (7). A similar pattern was observed in the EcDHFR, but higher pKa values were observed for this enzyme (pKa = 6.5 for kH, and pKa = 8.5 for kcat) (8). The contribution of the chemical step to the turnover rate was additionally assessed by measuring the dependence of kH and kcat on temperature. Activation energies of 11.7 ± 0.2 kcal mol−1, and 13.2 ± 0.3 kcal mol−1 were obtained for kcat and kH, respectively (Supplementary Figure S18). The calculation of the magnitude of the Gibbs free energetic barrier based on the rate constants measured for the forward and reverse rate of chemistry yielded a value of 15.1 kcal mol−1, very similar to the activation energy measured by temperature studies (23). The fact that the activation energies for kH and kcat are very comparable implies that the energetic barrier imposed by the chemical step is a significant contributor to the overall turnover rate. For comparison, the activation energies for the EcDHFR-catalyzed reaction are 6.7 kcal mol−1, and 11.4 kcal mol−1, for kH and kcat, respectively, under similar experimental conditions (32). These values are consistent with the much faster hydride transfer step in the E. coli enzyme, and with the fact that chemistry has a small contribution for the turnover rate at neutral pH values. Additional information about the temperature studies is available in the Supporting information.
Figure 2.
pH dependence of kcat (●) and kH (○). For pH values of 5.0 – 6.5, 100 mM MES with 50 mM KCl was utilized, and for pH 6.5–8.5, 100 mM HEPES with 50 mM KCl was used. The lines represent fits to eq. 11, to give a kH profile pKa = 5.4 ± 0.3, and a kcat profile pKa = 6.8 ± 0.2. Values for kcat and kH are in s−1.
Binding kinetics
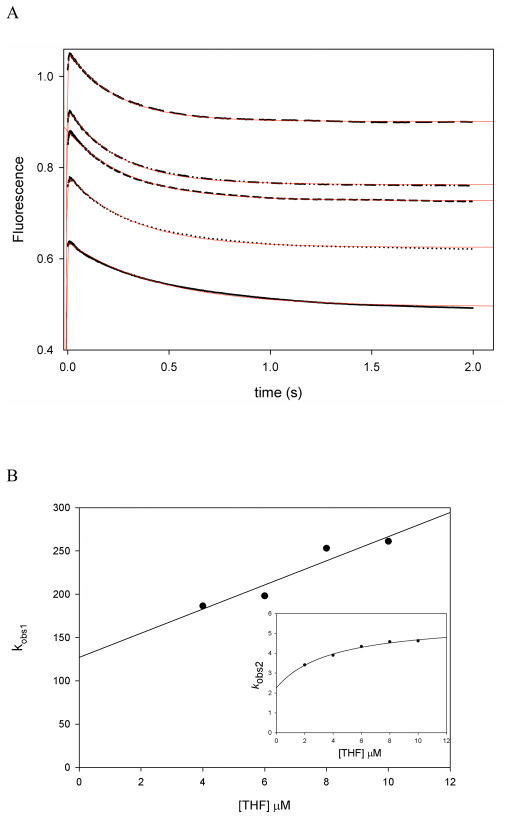
The observation of a burst of product formation argues that another step or other steps occurring after the hydride transfer contribute to the turnover rate. Therefore, binding and dissociation experiments were conducted to identify these steps. The association and dissociation rate constants for DHF and THF were measured by monitoring protein fluorescence, and FRET (Table 1). Both THF binding to MtDHFR-NADPH and to MtDHFR-NADP+ resulted in biphasic binding transients (Figure 3A) with the kobs of the fast phase linearly dependent on the concentration of THF followed by a slower phase with a kobs showing hyperbolic concentration dependence (Figure 3B). Hence, THF binds to both complexes via the two-step binding mechanism with a fast bimolecular association step followed by a slow isomerization step. Fitting of the replots of the observed rate constants allowed the determination of the four rate constants of a two-step binding mechanism for each complex (Table 2, Figures S7, and S9. See Materials and methods for the equations used for data fitting). The likelihood of the two-step binding mechanism was tested by global fitting of the data (23). Table 2 compares the rates obtained by analytical fitting and global fitting, and summarizes the experiments conducted to determine each of the rate constants.
Table 1.
Binding and dissociation rate constants.
| Binding rate constants
| |||||
|---|---|---|---|---|---|
| Enzyme species | ligand | k1 (μM−1s−1) | k−1 (s−1) | k2 (μM−1s−1) | k−2 (s−1) |
| MtDHFR-NADPH | THF | 7.3 ± 0.4 | 870 ± 2.5 | 0.19 ± 0.01 | 1.3 ± 0.1 |
| MtDHFR-NADP+ | THF | 13.9 ± 3.2 | 127.1 ± 23.5 | 3.4 ± 0.3 | 2.3 ± 0.6 |
| MtDHFR-NADP+ | DHF | 0.21 ± 0.02 | 2.7 ± 0.1 | - | - |
| MtDHFR-NADPH | DHF | 22.1 ± 4.3 | 140.2 ± 29.4 | - | - |
|
| |||||
| Dissociation rate constants: Competition method
| |||||
| Enzyme species | Ligand | Competitor | koff (s−1) | ||
| MtDHFR-NADPH | THF | MTX | 4.7 ± 0.1 | ||
| MtDHFR-NADPH | - | NADP+ | 0.13 ± 0.01 | ||
| MtDHFR-NADP+ | - | NADPH | 97.6 ± 4.1 | ||
| MtDHFR-NADP+ | DHF | NADPH | 7.8 ± 0.1 | ||
| MtDHFR-NADPH | THF | NADP+ | 1.7 ± 0.6 | ||
| MtDHFR-NADP+ | DHF | MTX | 0.47 ± 0.04 | ||
| MtDHFR-NADP+ | THF | MTX | 3.6 ± 0.3 | ||
| MtDHFR-NADP+ | THF | NADPH | 8.0 ± 0.1 | ||
Figure 3.
THF binding to MtDHFR-NADP+. A) Increasing concentrations of THF [2 (—), 4 (…), 6 (---), 8 (-..-), and 10 (— —) μM] were mixed with 0.5 MtDHFR-NADP+, monitoring change in protein fluorescence (excitation at 280 nm, emission above 320). Traces were fitted to a double exponential equation (line, eq. 3). B) The observed rate constants obtained(s−1) were plotted as a function of THF concentration, and the rate constants were obtained after fitting to eq. 5 or eq. 6 (inset). The lowest concentrations were excluded from replots to maintain pseudo-first order conditions, but were kept for the global fitting of the data, summarized on Table 2. C) Global fit of the THF binding to MtDHFR-NADP+ to the two step binding mechanism shown in the figure. The white contour represents fits of data within the parameters boundaries, so that all of the reasonable fits to the data are superimposed with the data and the best fit. D) FitSpace confidence contours (24) for the global fit of the binding data occurring in a two-step binding model.
Table 2.
Comparison between rate constants obtained by analytical fitting and global fitting. The bimolecular steps have rate constants expressed in μM−1s−1, whereas unimolecular steps have rate constants in s−1.
| Rate constant | Best-fit value – global fitting | Lower boundary | Upper boundary | Value obtained by analytical fitting | Experiment conducted to determine |
|---|---|---|---|---|---|
|
| |||||
| k 1 | 31.9 ± 0.5 | 25.6 | 45.4 | 22 ± 4. | Single turnover |
| k −1 | 64.3 ± 0.1a | - | - | 140 ± | Single turnover |
| k 2 | 4.5 ± 0.1 | 3.18 | 6.17 | 5.8 ± 0.3 | Single turnover |
| k −2 | 0.00056 ± 0.00003 | 0.00052 | 0.00068 | 0.0004 ± 0.00001 | Single turnover |
| k 3 | 7.3 ± 0.1 | 6.3 | 8.3 | 8.02 ± 0.02 | NADPH competition |
| k −3 | 109 ± 6 | 28 | 213 | ND | - |
| k 4 | 101 | - | - | ND | - |
| k −4 | 1.1 ± 0.1 | 0.29 | 4.2 | 1.7 ± 0.6 | NADP+ competition |
| k 5 | 1.1 ± 0.1 | 0.9 | 1.2 | 1.04 ± 0.02 | MTX competition |
| k −5 | 1.5 ± 0.1 | 1.2 | 1.8 | 4.1 ± 0.2 | THF binding |
| k 6 | 165.5 ± 4.6 | 106 | 632 | 147 ± 2 | THF binding |
| k −6 | 59 ± 2 | 38 | 223 | 7.4 ± 0.4 | THF binding |
| k 7 | 1.7 ± 0.1 | 0.7 | 3.39 | 3.6 ± 0.3 | MTX competition |
| k −7 | 2.3 ± 0.1 | 2.1 | 2.5 | 3.26 ± 0.3 | THF binding |
| k8 | 78 ± 2 | - | 46.8 | 100 ± 23 | THF binding |
| k−8 | 38 ± 1 | 12.8 | 39.5 | 18 ± 3 | THF binding |
| k9 | 81 ± 2 | 64.8 | 101 | 98 ± 4 | NADPH competition |
| k−9 b | 268 ± 7 | 215 | 420 | ND | - |
| k10 | 129 ± 4 | 66.1 | 252 | ND | - |
| k−10 | 0.08 ± 0.01 | 0.07 | 0.09 | 0.13 ± 0.01 | NADP+ competition |
| k11 | 0.7 ± 0.1 | 0.5 | 0.9 | 0.21 ± 0.01 0.47 ± 0.04 |
DHF binding MTX competition |
| k−11 | 1.1 ± 0.1 | 0.2 | 2.1 | 2.7 ± 0.1 | DHF binding |
| k12 | 2.1 ± 0.2 | 0.5 | 9.1 | 7.8 ± 0.1 | NADPH competition |
| k−12 | - | - | - | ND | - |
| k13 | 6.7 ± 0.3 | 4.98 | 12.1 | ND | - |
| k−13 | 0.32 ± 0.04 | 0.0005 | 0.78 | ND | - |
These data suggest that THF release from both ternary complexes (MtDHFR-NADPH-THF and MtDHFR-NADP+-THF) is a biphasic process with a slow isomerization step followed by a fast dissociation step. The slowest step in THF release from both complexes is a slow isomerization between a tightly bound and a loosely bound complex, occurring at rates of 1.3 s−1 and 1.9 s−1 from MtDHFR-NADPH-THF and MtDHFR-NADP+-THF, respectively. Both values are close to the steady-state turnover rate. The release of THF from MtDHFR-NADPH-THF is the rate limiting step in the kinetic sequences from Escherichia coli DHFR (EcDHFR), Lactobacillus casei DHFR (LcDHFR), mouse DHFR (mDHFR), and Pneumocystis carinii (PcDHFR) (8, 10–12). In contrast to the results obtained here, THF release from ternary complexes occurs as a single bimolecular step for all previously characterized DHFRs.
In the catalytic cycle of the human DHFR (HsDHFR) THF can be released first from the enzyme-products ternary complex, followed by DHF binding, NADP+ release, and subsequent binding of NADPH to reinitiate the cycle. In order to rule out this possibility in the MtDHFR kinetic sequence, DHF binding to both MtDHFR enzyme forms was investigated. The results obtained showed that the association of DHF to the MtDHFR-NADPH, to generate the catalytic productive complex, is fast and does not limit the turnover rate (Tables 1 and 2, Figure S1). Binding of DHF to the MtDHFR-NADP+ complex, on the other hand, is a single step process with a slow association rate constant of 0.7 s−1, and thus is unlikely to occur during the catalytic cycle (Figure S15). Rate constants for the formation of the dead-end complex MtDHFR-NADP+-DHF complex are shown in Scheme 2, and in Tables 1 and 2.
Scheme 2.
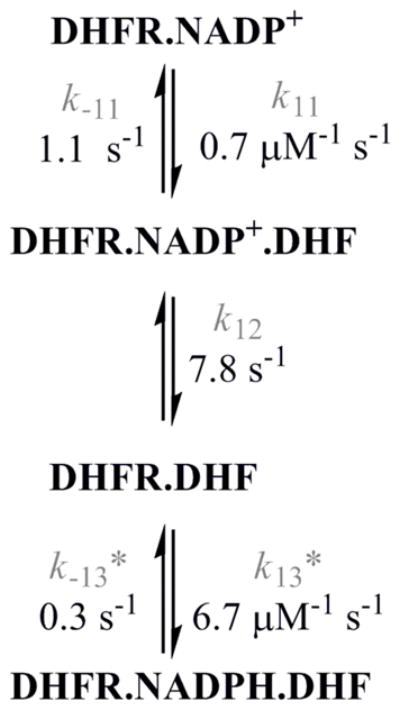
Formation of the dead-end complex MtDHFR-NADP+-DHF1. The values of the rate constants were obtained by global fitting of the data with KinTek Global Kinetic Explorer1.
Since MtDHFR is purified in a complex with NADPH, and this tightly bound NADPH could not be removed without a loss of protein stability but only replaced by NADP+, binding experiments that required free enzyme could not be performed. Given the extremely high affinity of MtDHFR for phosphorylated pyridine nucleotides, it is unlikely that free enzyme exists for a long period of time in vivo.
Dissociation kinetics – competition experiments
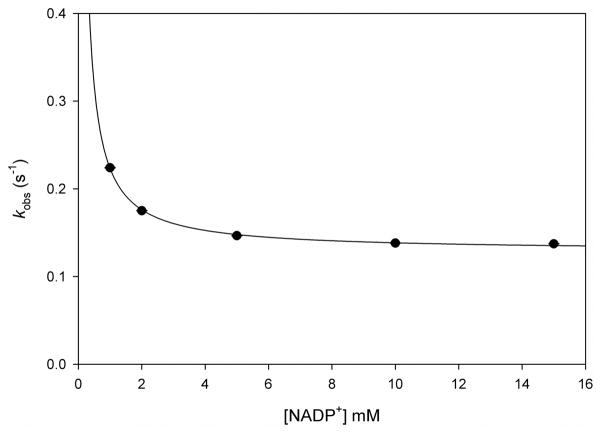
Dissociation rate constants were measured by conducting competition experiments, where there is an equilibrium for the binding of two competing ligands, as shown in Scheme 3. The dissociation rate constant for ligand 1 can be measured as long as k2[L2]≫k−1, k1[L1], and this condition is satisfied by using increasing concentrations of the competitor, ligand 2, until no change in the observed rate constant is seen (33, 34). Figure 4 shows the dependence of the dissociation rate constant for NADPH from the MtDHFR-NADPH complex on the concentration of NADP+. Two processes that would generate free enzyme were evaluated, one being the fast NADP+ dissociation (~ 98 s−1, Figure S12), and the other being the very slow NADPH dissociation (0.13 s−1, Figure S13). Interestingly, all other dissociation rate constants thought to be relevant for the main catalytic pathway were of the same magnitude, ranging from 1.3 s−1 to 8.0 s−1 (Figures S4, S5, S8, S11, S12, S13, S16, and S17). Rate constants determined by dissociation, and binding experiments, are summarized in Table 1.
Scheme 3.
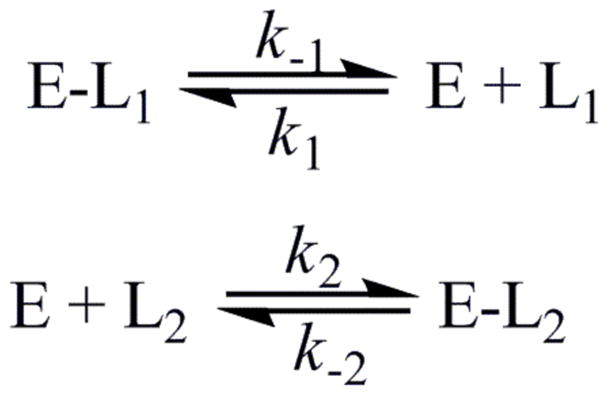
Events occurring during a competition experiment with ligand L2 used as a competitor in order to determine the dissociation rate constant of L1 from the E-L1 complex.
Figure 4.
NADP+ competition with MtDHFR-NADPH. Increased concentrations of NADP+ were mixed with the complex MtDHFR-NADPH. According to scheme 3, at infinite concentrations of the competitor (NADP+), the rate obtained is the dissociation rate constant (koff) for ligand 1 (NADPH). The line is a hyperbolic fit, yielding a koff = 0.13 ± 0.01 s−1.
Reverse reaction
The conversion of THF and NADP+ to DHF and NADPH catalyzed by MtDHFR was monitored by the increase in absorbance at 340 nm, and analyzed by steady state kinetics, single, and multiple turnover experiments. The results show that both kcat-rev and kchem-rev have the same rate of 0.0004 s−1, and consequently no burst of product formation was observed (Figure S3). This result indicates that the chemical step is virtually irreversible with an internal equilibrium constant for THF formation of approximately 1500, a value essentially equal to the one observed for the EcDHFR-catalyzed reaction (8). This result provides an explanation for the fact that kinetic isotope effects measured on kcat exhibit a lower value than the ones measured for D(V/KDHF) (7). Since D(V/KDHF) reports to steps up to and including the first irreversible step, now known to be the chemical step, any decrease in observed kinetic isotope effects caused by product release does not affect the D(V/KDHF), but decreases the magnitude of DV isotope effects.
Catalytic cycle of the MtDHFR and comparison to other DHFRs
Measurement of association and dissociation rate constants of substrates and products to most possible enzyme forms, as well as rates for the forward and reverse chemical steps allow the assignment of the pathway or pathways that the enzyme most likely follows during steady-state turnover. In this discussion, an important corollary of pre-steady state kinetics must be reinforced: a rate constant of an elementary step in the main path of the reaction cannot be smaller than the overall reaction rate constant (kcat). Thus, it is assumed that a step with a rate constant smaller than kcat is not part of the main path followed by the overall reaction (20). Considering this restriction, a mechanism that includes NADPH dissociation from any enzyme form must be discarded, since NADPH dissociation is a slow process from all complexes analyzed (ranging from 0.078 s−1 to 1.1 s−1), so that the catalytic cycle of the MtDHFR starts with MtDHFR-NADPH as a complex. Comparison with other DHFRs shows that some of them have a relatively high koff of NADPH from DHFR-THF-NADPH, so it is possible that NADPH dissociation from this complex occurs during turnover [koff values of 85 s−1 for the E.coli, (8), 480 s−1 for S. pneumoniae (14), 100 s−1 for the human (9)]. Next, DHF binds to MtDHFR-NADPH to form the productive ternary complex, whose formation is fast and unlikely to be rate limiting, unless the concentration of DHF is in the submicromolar range. After the ternary complex MtDHFR-NADPH-DHF is formed, the chemical step occurs at a relatively slow rate of ~ 5 s−1 compared to other DHFRs at pH 7.5 [e.g., kH is equal to 250 s−1 [EcDHFR, (8)], 500 s−1 [mDHFR, (10)], and 1360 s−1 [HsDHFR, (9)]. To further illustrate the diversity of kinetic schemes for DHFRs from different species, in the SpDHFR, the chemical step is preceded by a rate-determining conformational change, and the bifunctional thymidilate synthase-DHFR from Leishmania major undergoes a rate determining conformational change when free of ligands, or bound to THF (13, 14). As previously shown (7), kinetic isotope effects greater than 1 and of practically equal magnitudes were obtained for D(V/KDHF) and DkH, strongly suggesting that a conformational change prior to the chemical step is not limiting kH in the MtDHFR. Following the chemical step, which is also the first “kinetically” irreversible step in the sequence, the enzyme-products complex (MtDHFR-NADP+-THF) can decompose via two pathways of product release. In the first pathway, NADP+ is released and NADPH binds, followed by a biphasic THF release where a rate-limiting isomerization step is followed by fast THF dissociation, generating the initial complex MtDHFR-NADPH (pathway A, Scheme 4). Pathways with the same order of product release, which is known as a “nucleotide exchange pathway”, have been found for the majority of DHFRs (8, 10–12). Alternatively, the MtDHFR-NADP+-THF complex can proceed to first release THF in a biphasic process, where a rate-limiting isomerization is followed by fast NADP+ dissociation to form the apo enzyme, which then rapidly binds NADPH to yield the initial complex MtDHFR-NADPH (pathway B, Scheme 4). This pathway is rather unique, and a similar sequence was suggested to be a secondary route followed by the HsDHFR under saturating NADPH concentrations and very low concentration of DHF (9).
Scheme 4.
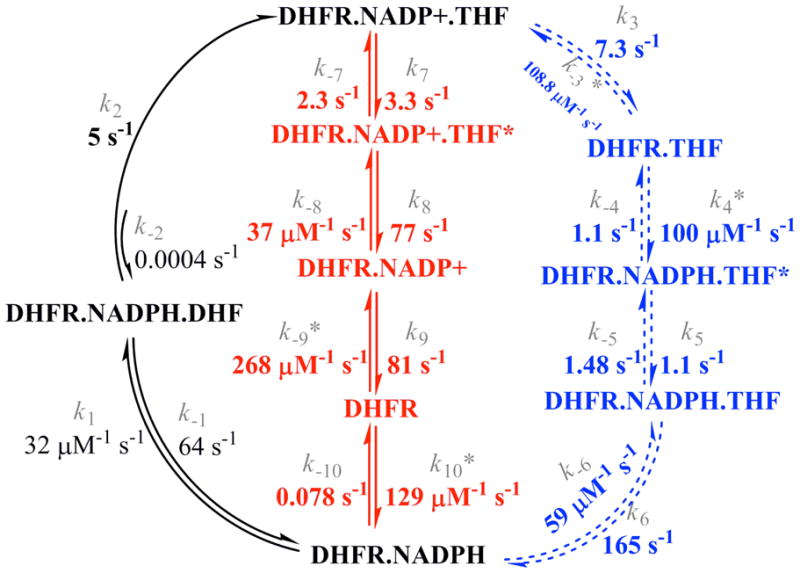
Kinetic scheme for the MtDHFR-catalyzed reaction. Pathway A is represented in the outward circular portion in dashed lines, while pathway B is shown in the center. The values of the rate constants were obtained by global fitting of the data with KinTek Global Kinetic Explorer1.
The kinetic sequence shown here (Scheme 4) includes isomerization steps preceding THF release from MtDHFR-NADPH and MtDHFR-NADP+ complexes, and the likelihood of these mechanisms was evaluated by global fitting of all binding and dissociation experiments, which showed that the model is well constrained by the data (Table 2). This is the first report of a biphasic rate-limiting product release for a DHFR. It was previously demonstrated for EcDHFR that an NMR-determined exchange rate constant for residues surrounding the folate binding pocket correlates precisely with the rate constant for THF release from MtDHFR-NADPH, the rate limiting step for this reaction (6). Although this rate determining step in the EcDHFR kinetic sequence seems to be coupled to a conformational change, binding experiments demonstrated that THF binds in a single step manner to the EcDHFR, so that the observed first order rate constant increased linearly with increasing THF concentration, showing no sign of saturation. While tempting to suggest the same conformational change is limiting THF release in the MtDHFR reaction, no information about the conformational dynamics of this protein is available.
Likelihood of parallel pathways for product release
The comparable magnitudes of rate constants obtained for both pathways of product release, together with the fact that none of the slowest steps in both pathways is equal to kcat (kcat = 2.3 s−1, THF release equal to 1.3 s−1, from MtDHFR-NADPH-THF in pathway A, and 3.3 s−1 from MtDHFR-NADP+-THF*, in pathway B) suggests a contribution from both pathways to kcat.
To better explore this hypothesis, simulations were conducted using KinTek Global Kinetic Explorer. The two potential pathways for product release were evaluated by the assumption that if the enzyme products complex followed pathway A (with NADP+ released first) an enzyme form called E-NADPHa would be formed, and when the enzyme products complex followed pathway B, an enzyme form called E-NADPHb would form. By conducting this simulation, one can imagine that after several turnovers the reaction would reach completion, and the final concentrations of E-NADPHa and E-NADPHb would be a way of quantifying how many turnovers occurred via pathways A or B. The simulation was conducted at varying initial concentrations of substrates in order to estimate how different conditions can influence the pathway followed. Figure 5A shows that, when both substrates are saturating, 31 % of the E-NADPH complex was generated by following pathway A, and 69 % of the generated E-NADPH was due to turnover following pathway B. Figure 5C shows that the only condition where pathway A was preferred was when the concentration of DHF was subsaturating, and equimolar to the concentration of enzyme.
Figure 5.
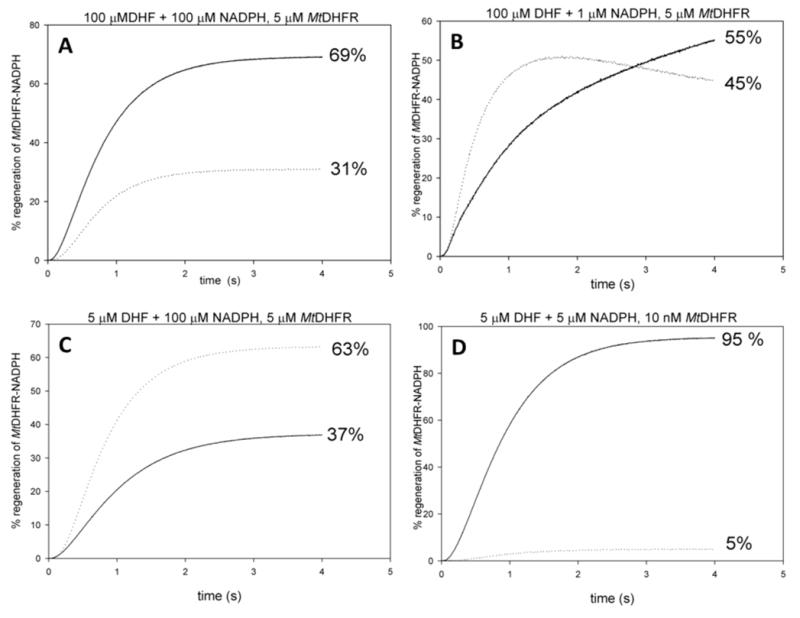
Product release through two parallel pathways. Simulations conducted using KinTek Global Kinetic Explorer, with A) saturating concentrations of both substrates (100 μM), and 5 μM MtDHFR, B) 100 μM DHF, 1 μM NADPH, 5 μM MtDHFR, C) 5 μM DHF, 100 μM NADPH, 5 μM MtDHFR, and D) simulating typical steady-state conditions with 5 μM DHF + 5 μM NADPH, and 10 nM MtDHFR. The dotted line represents that MtDHFR-NADPH is being generated by pathway A, and the solid line indicates that pathway B generated MtDHFR-NADPH.
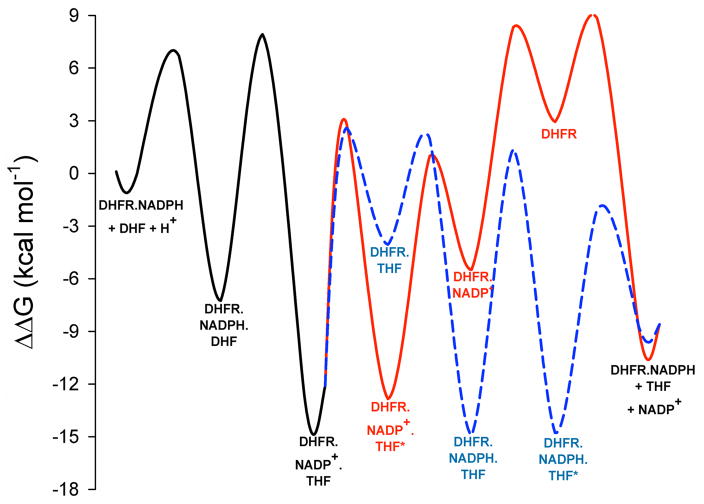
An evaluation of both pathways in terms of free energy was conducted by generating the reaction coordinate of the NADPH-dependent reduction of DHF by MtDHFR at pH 7.5 and 25°. The Gibbs free energy barrier for each reaction step was calculated using eq. 10. Substrate concentrations were taken at 1 M, and concentrations of products were calculated based on the Keq of 5.06 × 107 between substrate and product (7). The MtDHFR-NADPH state was taken as the reference state. Figure 6 shows that path A has the two most stable intermediates in the sequence, which are followed by THF dissociation (MtDHFR.NADPH.THF and MtDHFR.NADPH.THF*), whereas path B has the formation of the high energy apoenzyme (DHFR), and one relatively stable intermediate (MtDHFR.NADP+.THF*).
Figure 6.
Energy profile comparing the two pathways for product release. The energy barrier for each step was calculated using the eq. 10. (38). Substrates and products concentrations were 1 M and 1.26 M, respectively, calculated based on the equilibrium constant for the reaction (7). The profile in a dashed line represents pathway A, and the profile showed in a solid line represents pathway B.
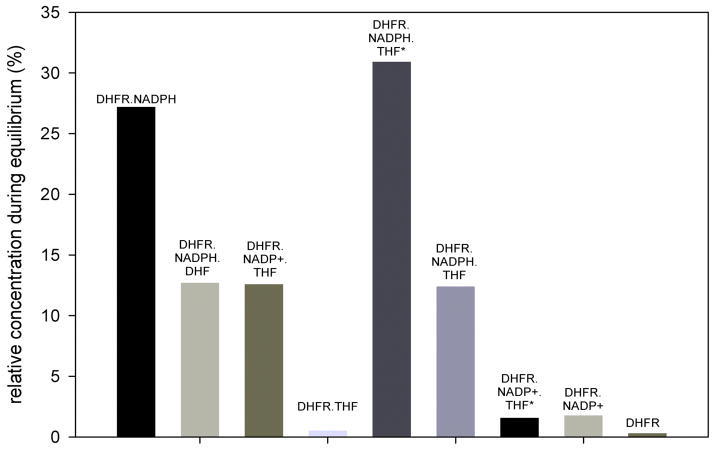
To quantify the relative stability of each intermediate in the kinetic sequence, and to substantiate the intuitive notion that based on the magnitudes of the rate constants a majority of enzyme-products complex will likely accumulate, and then partition almost equally towards MtDHFR-NADP+-THF* and MtDHFR-THF, a mathematical analysis was conducted by combining the software KApattern (25) and Markov chains. A Markov Chains (MCs) approach is a well-known mathematical formalism used in many fields with a very broad application, in which states and transitions among states according to rates that were observed in the system under study are utilized. In this work, the system consists of enzymes species (states) and rate-constants (rates). The purpose of MCs is to calculate the permanence probabilities when the system remains stable assuming that it was simulated for a large period of time, a situation analogous to when the reaction has reached equilibrium. MCs have the Markov property, which asserts that the only information needed to find the next state is present in the current state, and is the most fundamental property in MCs, stating that the states visited in the past do not influence how the future state will be chosen (26). For the kinetic scheme investigated here, Figure 7 illustrates that the enzyme-products complex accumulates to a certain extent, given that the reverse chemical rate (kchem-rev, see discussion above) is negligible, and the rates driving the dissolution of this complex are similar in magnitude (3.5 and 7.3 s−1) as the forward chemistry rate constant (5 s−1). After the MtDHFR-THF complex is formed, the rapid binding of NADPH causes the formation of the MtDHFR-NADPH-THF* complex, whose isomerization prior to THF release represents the rate-limiting step in this pathway (pathway A). The isomerization of the enzyme-products complex prior to THF dissociation, on the other hand, is the rate-limiting step of pathway B. After this isomerization occurs, all subsequent steps are in rapid-equilibrium, except for NADPH binding to the enzyme, which drives the reaction forward to restart a new cycle. The fact that none of the enzyme intermediates from pathway B are present in high amounts during equilibrium illustrates the fact that once the MtDHFR-NADP+-THF complex isomerizes, it is driven to regenerate the initial MtDHFR-NADPH complex. This is in contrast with the situation in pathway A, where the formation of two very stable intermediates traps the enzyme in non-productive forms. These results, taken together with the energy profile (Fig. 6), show that the two very stable intermediates in pathway A, together with MtDHFR-NADPH, the enzyme substrates complex, and the initial enzyme products complex are the most abundant enzyme forms in equilibrium.
Figure 7.
Accumulation of enzyme intermediates in equilibrium, analyzed by the generation of continuous time Markov chains (CTMC). A matrix representing the kinetic scheme with all possible connections between enzyme forms was generated using the software KApattern (25), and the system was simulated until equilibrium. The result is the probability of permanence in each enzyme form, when the reaction has reached equilibrium. Concentrations of substrates and products were calculated assuming a Keq = 5.06 × 107 (7, 8).
It has been hypothesized in the literature that intracellular levels of NADPH and NADP+ are responsible for the natural selection of enzymes that bind with different affinities to the reduced and oxidized forms of the pyridine cofactor. In the cytoplasm of eukaryotes, NADP+ is present at no more than 1% of the concentration of NADPH (9), whereas the concentration of these nucleotides is comparable in prokaryotes, like E. coli (35), and can explain why EcDHFR binds NADPH more tightly than NADP+ (dissociation constants are 0.17 μM and 23 μM, for NADPH and NADP+, respectively). Moreover, once the EcDHFR-NADP+ complex is formed it can rapidly bind DHF and generate a very stable dead-end complex, which wouldn’t be selectively advantageous if kcat was under selective pressure. The HsDHFR binds to both nucleotides with similar affinity, but the intracellular difference in concentration between NADPH and NADP+ makes unproductive pathways that require NADP+ binding to apo enzyme negligible. In the case of MtDHFR assuming that the concentrations of NADPH and NADP+ are comparable (36), even though NADP+ binding is in rapid equilibrium with the free enzyme, NADPH binding generates a very stable enzyme complex whose dissociation is extremely slow, so that NADPH binding is favored over NADP+ binding to the apo enzyme. The only other DHFR that possesses a kinetic sequence that passes through free enzyme is a mutant of the HsDHFR where the widely conserved phenylalanine 34 was replaced by an alanine (37). This mutant enzyme has an ordered product release, with THF being released first, followed by NADP+. It is important to point out that the MtDHFR has this phenylalanine.
Steady-state turnover
A vital check to the validity of a model is whether or not it can account for the events that occur during steady-state turnover. To better corroborate the kinetic scheme where two parallel pathways occur for MtDHFR, and that kcat represents a combination of the rates of both pathways, the software KApattern was utilized to generate rate equations for each one of the pathways, thus obtaining kcat values for each parallel pathway. In the process of obtaining the rate equations, the concentration of products were assumed to be zero. The rate equations were rearranged to the form of equation 12, describing a sequential kinetic mechanism, so that kcat could be isolated. In this equation, v is the velocity, Et is the total concentration of enzyme, kcat is the turnover rate, A and B are the substrate concentrations, Kia is the inhibition constant for substrate A, Ka is the Michaelis constant for substrate A, Kb is the Michaelis constant for substrate B.
| (12) |
For pathway A,
v/Et = k6[DHFR.NADPH.THF]/(Σ[all enzyme forms in path A]), so that
kcat = k6k5k3k2 / [k6k5(k−2 + k3 + k2) + k3k2(k6 + k5 + k−5)]
Similarly, for pathway B,
v/Et = k5[DHFR.NADP+]/(Σ[all enzyme forms in path B]), so that
kcat = k6k5k3k4k2k1 / [k1k6(k2k5(k−3 + k4) + k5(k−2k−3 + k−2k4 + k4k3) + k3k2k5k4k2]
Finally, the rate constants obtained in the global fitting (Table 2) were utilized to obtain kcat values of 0.90 s−1 for pathway A, and 2.0 s−1 for pathway B. These values are in good agreement with the values obtained under steady-state conditions, considering that for this calculation a situation analogous to the one depicted in Fig. 5D is occurring, where turnover through path B predominates. Furthermore, the kinetic sequence presented here corroborates the previously proposed kinetic mechanism for this enzyme, i.e. steady-state random, since the rate of chemistry is comparable to the rates of substrate dissociation, and product release is random.
A final test of the events that occur during steady-state turnover was accessed by calculating the equilibrium difference in Gibbs free energy (ΔG) for this reaction based on the proposed reaction coordinate starting from the MtDHFR-NADPH state using the rate constants obtained experimentally, and comparing this to the ΔG calculated from the Keq for this reaction (7). The values are −9.5 kcal mol−1 (ΔG obtained from the Keq) and −8.7, and −8.5, for ΔG calculated using the rate constants from pathways A or B, respectively. These values only differ by one kcal mol−1, additionally assuring the robustness of the sequence proposed here.
Summary
In this work, the kinetic sequence of the MtDHFR-catalyzed reaction was studied by a combination of equilibrium binding, pre-steady-state kinetics, global fitting and simulation. This reaction was shown to follow two parallel pathways, one similar to other DHFRs where NADP+ is released first, followed by NADPH binding and THF release, and an alternative pathway in which THF and NADP+ are released to transiently form free enzyme, to which NADPH binds reinitiating the cycle. The kinetic sequence with parallel pathways describes the steady-state behavior of MtDHFR, being further validated by the calculation of steady-state kcat using the rate constants obtained in the present work, and the Markov models which demonstrate that the accumulation of very stable enzyme intermediates prevents turnover via a single path. This is the first DHFR possessing two equally relevant kinetic pathways, with the unique feature that one of these pathways passes through the free enzyme.
Supplementary Material
Table 3.
Equilibrium dissociation constants (all expressed in μM)*.
| Enzyme species | ligand | Kov | Kd measured | Kov (global fit values) |
|---|---|---|---|---|
|
| ||||
| MtDHFR-NADPH | THF | 4.1 ± 0.9 | 1.4 ± 0.4 a | 1.2 ± 0.1 |
| MtDHFR-NADP+ | THF | 1.2 ± 1.5 | 1.1 ± 0.1 a | 1.2 ± 0.4 |
| MtDHFR-NADP+ | DHF | 12.1 ± 1.3c | 1.9 ± 1.3 b | 1.6 ± 0.1 |
| MtDHFR-NADPH | DHF | 6.4 ± 1.8c | ND | 5.1 ± 0.1 |
Kov: dissociation constant calculated using eq. 7 or koff/kon.
obtained from equilibrium binding experiments.
obtained from the analysis of the amplitudes of binding transients in stopped flow fluorescence measurements. See Supporting information for a description of the equation used.
calculated from koff/kon using values obtained in the binding experiments.
For additional information see Supplementary Figures S6, S9, and S14.
Acknowledgments
We thank Dr. Ricardo M. Czekster [Pontifícia Universidade Católica do Rio Grande do Sul (PUCRS)], for insightful discussions using Markov models, and Dr. Kenneth A. Johnson (University of Texas at Austin) for his help with data interpretation and analysis using KinTek Global Explorer.
This work was supported by the NIH (AI33696), the Einstein-Montefiore CFAR (NIH AI-515109), and A.V. was the recipient of a Belgian American Educational foundation fellowship.
Abbreviations
- TB
tuberculosis
- MDR-TB
multi-drug resistant tuberculosis
- XDR-TB
extensively drug resistant tuberculosis
- MtDHFR
dihydrofolate reductase from Mycobacterium tuberculosis H37Rv
- DHF
dihydrofolate
- THF
tetrahydrofolate
- NADPH
nicotinamide adenine dinucleotide phosphate (reduced form)
- NADP+
nicotinamide adenine dinucleotide phosphate (oxidized form)
- MTX
methotrexate
- dTMP
deoxythymidine monophosphate
- FRET
fluorescence resonance energy transfer
- kobs
observed rate constant
- kcat
steady state turnover number
- kcat-rev
steady state turnover number for the reverse reaction
- kH
rate constant of chemistry for the forward reaction
- kchem-rev
rate constant of chemistry for the reverse reaction
- kon
association rate constant
- koff
dissociation rate constant
- KIE
kinetic isotope effect
- DkH
kinetic isotope effect in the chemical step
- EcDHFR
DHFR from Escherichia coli
- SpDHFR
DHFR from Streptococcus pneumoniae
- MC
Markov chains
Footnotes
Rates constants not experimentally measured are indicated by an asterisk.
SUPPORTING INFORMATION AVAILABLE: A complete description of pre-steady state experiments and analytical data fitting, as well as an extended analysis of temperature studies is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Kompis IM, Islam K, Then RL. DNA and RNA synthesis: antifolates. chemical reviews. 2005;105:593–620. doi: 10.1021/cr0301144. [DOI] [PubMed] [Google Scholar]
- 2.McGuire JJ. Anticancer antifolates: current status and future directions. Curr Pharm Des. 2003;9:2593–2613. doi: 10.2174/1381612033453712. [DOI] [PubMed] [Google Scholar]
- 3.Hitchings GH., Jr Nobel lecture in physiology or medicine--1988. Selective inhibitors of dihydrofolate reductase. In Vitro Cell Dev Biol. 1989;25:303–310. doi: 10.1007/BF02624591. [DOI] [PubMed] [Google Scholar]
- 4.Ionescu RM, Smith VF, O’Neill JC, Jr, Matthews CR. Multistate equilibrium unfolding of Escherichia coli dihydrofolate reductase: thermodynamic and spectroscopic description of the native, intermediate, and unfolded ensembles. Biochemistry. 2000;39:9540–9550. doi: 10.1021/bi000511y. [DOI] [PubMed] [Google Scholar]
- 5.Hammes-Schiffer S, Benkovic SJ. Relating protein motion to catalysis. Annu Rev Biochem. 2006;75:519–541. doi: 10.1146/annurev.biochem.75.103004.142800. [DOI] [PubMed] [Google Scholar]
- 6.Boehr DD, McElheny D, Dyson HJ, Wright PE. The dynamic energy landscape of dihydrofolate reductase catalysis. Science. 2006;313:1638–1642. doi: 10.1126/science.1130258. [DOI] [PubMed] [Google Scholar]
- 7.Czekster CM, Vandemeulebroucke A, Blanchard JS. Kinetic and Chemical Mechanism of the Dihydrofolate Reductase from Mycobacterium tuberculosis. Biochemistry. 2011;50:367–375. doi: 10.1021/bi1016843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Fierke CA, Johnson KA, Benkovic SJ. Construction and evaluation of the kinetic scheme associated with dihydrofolate reductase from Escherichia coli. Biochemistry. 1987;26:4085–4092. doi: 10.1021/bi00387a052. [DOI] [PubMed] [Google Scholar]
- 9.Appleman JR, Beard WA, Delcamp TJ, Prendergast NJ, Freisheim JH, Blakley RL. Unusual transient- and steady-state kinetic behavior is predicted by the kinetic scheme operational for recombinant human dihydrofolate reductase. J Biol Chem. 1990;265:2740–2748. [PubMed] [Google Scholar]
- 10.Thillet J, Adams JA, Benkovic SJ. The kinetic mechanism of wild-type and mutant mouse dihydrofolate reductases. Biochemistry. 1990;29:5195–5202. doi: 10.1021/bi00473a028. [DOI] [PubMed] [Google Scholar]
- 11.Andrews J, Fierke CA, Birdsall B, Ostler G, Feeney J, Roberts GCK, Benkovic SJ. A kinetic study of wild-type and mutant dihydrofolate reductases from Lactobacillus casei. Biochemistry. 1989;28:5743–5750. doi: 10.1021/bi00440a007. [DOI] [PubMed] [Google Scholar]
- 12.Margosiak SA, Appleman JR, Santi DV, Blakley RL. Dihydrofolate reductase from the pathogenic fungus Pneumocystis carinii: catalytic properties and interaction with antifolates. Arch Biochem Biophys. 1993;305:499–508. doi: 10.1006/abbi.1993.1453. [DOI] [PubMed] [Google Scholar]
- 13.Liang PH, Anderson KS. Kinetic reaction scheme for the dihydrofolate reductase domain of the bifunctional thymidylate synthase-dihydrofolate reductase from Leishmania major. Biochemistry. 1998;37:12206–12212. doi: 10.1021/bi9803170. [DOI] [PubMed] [Google Scholar]
- 14.Lee J, Yennawar NH, Gam J, Benkovic SJ. Kinetic and Structural Characterization of Dihydrofolate Reductase fromStreptococcus pneumoniae. Biochemistry. 2010;49:195–206. doi: 10.1021/bi901614m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Argyrou A, Vetting MW, Aladegbami B, Blanchard JS. Mycobacterium tuberculosis dihydrofolate reductase is a target for isoniazid. Nature Structural & Molecular Biology. 2006;13:408–413. doi: 10.1038/nsmb1089. [DOI] [PubMed] [Google Scholar]
- 16.Pace CN, Vajdos F, Fee L, Grimsley G, Gray T. How to measure and predict the molar absorption coefficient of a protein. Protein Science. 1995;4:2411–2423. doi: 10.1002/pro.5560041120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Morrison JF. Kinetics of the reversible inhibition of enzyme-catalysed reactions by tight-binding inhibitors. Biochimica et Biophysica Acta. 1969;185:269–286. doi: 10.1016/0005-2744(69)90420-3. [DOI] [PubMed] [Google Scholar]
- 18.Morrison JF, Stone SR. Mechanism of the reaction catalyzed by dihydrofolate reductase from Escherichia coli: pH and deuterium isotope effects with NADPH as the variable substrate. Biochemistry. 1988;27:5499–5506. doi: 10.1021/bi00415a017. [DOI] [PubMed] [Google Scholar]
- 19.Johnson KA. Transient State kinetic analysis of enzyme reaction pathways. The Enzymes. 1992;20:1–61. [Google Scholar]
- 20.Hiromi K. Kinetics of Fast Enzyme Reactions: Theory and Practice. Halsted Press; New York, USA: 1979. [Google Scholar]
- 21.Cleland WW, Northrop DB. Energetics of substrate binding, catalysis, and product release. Method Enzymol. 1999;308:3–27. doi: 10.1016/s0076-6879(99)08003-9. [DOI] [PubMed] [Google Scholar]
- 22.Winzor DJ, Jackson CM. Interpretation of the temperature dependence of equilibrium and rate constants. Journal of Molecular Recognition. 2006;19:389–407. doi: 10.1002/jmr.799. [DOI] [PubMed] [Google Scholar]
- 23.Johnson KA, Simpson ZB, Blom T. Global Kinetic Explorer: A new computer program for dynamic simulation and fitting of kinetic data. Analytical Biochemistry. 2009;387:20–29. doi: 10.1016/j.ab.2008.12.024. [DOI] [PubMed] [Google Scholar]
- 24.Johnson KA, Simpson ZB, Blom T. FitSpace Explorer: An algorithm to evaluate multidimensional parameter space in fitting kinetic data. Analytical Biochemistry. 2009;387:30–41. doi: 10.1016/j.ab.2008.12.025. [DOI] [PubMed] [Google Scholar]
- 25.Qi F, Dash RK, Han Y, Beard DA. Generating rate equations for complex enzyme systems by a computer-assisted systematic method. BMC Bioinformatics. 2009;10:238. doi: 10.1186/1471-2105-10-238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Stewart WJ. Probability, Markov Chains, Queues, And Simulation: The Mathematical Basis Of Performance Modeling. Princeton University Press; 2009. [Google Scholar]
- 27.Northrop DB. Steady-state analysis of kinetic isotope effects in enzymic reactions. Biochemistry. 1975;14:2644–2651. doi: 10.1021/bi00683a013. [DOI] [PubMed] [Google Scholar]
- 28.Carey FA, Sundberg RJ. Part A: Structures and Mechanisms. 4. Kluwer Academic; New York: 2000. Advanced Organic Chemistry. [Google Scholar]
- 29.Johnson KA. Transient-state kinetic analysis of enzyme reaction pathways. The Enzymes. 1992;20:1–61. [Google Scholar]
- 30.Gore MG, Bottomley SP. Stopped-flow fluorescence spectroscopy. In: Gore MG, editor. Spectrophotometry and spectrofluorimetry. Oxford University Press; New York: 2000. p. 368. [Google Scholar]
- 31.Cleland WW. The use of pH studies to determine chemical mechanisms of enzyme-catalyzed reactions. Methods Enzymol. 1982;87:390–405. doi: 10.1016/s0076-6879(82)87024-9. [DOI] [PubMed] [Google Scholar]
- 32.Maglia G, Javed MH, Allemann RK. Hydride transfer during catalysis by dihydrofolate reductase from Thermotoga maritima. Biochem J. 2003;374:529–535. doi: 10.1042/BJ20030412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Chock PB, Gutfreund H. Reexamination of the kinetics of the transfer of NADH between its complexes with glycerol-3-phosphate dehydrogenase and with lactate dehydrogenase. Proc Natl Acad Sci U S A. 1988;85:8870–8874. doi: 10.1073/pnas.85.23.8870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Fersht A. Structure and Mechanism in Protein Science. W. H. Freeman and Company; New York: 1999. [Google Scholar]
- 35.Bennett BD, Kimball EH, Gao M, Osterhout R, Dien SJV, Rabinowitz JD. Absolute metabolite concentrations and implied enzyme active site occupancy in Escherichia coli. Nature Chemical Biology. 2009;5:593–599. doi: 10.1038/nchembio.186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Gopinathan KP, Sirsi M, Ramakrishnan T. Nicotin-amide-adenine nucleotides of Mycobacterium tuberculosis H37Rv. Biochem J. 1963;87:444–448. doi: 10.1042/bj0870444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Nakano T, Spencer HT, Appleman JR, Blakley RL. Critical role of phenylalanine 34 of human dihydrofolate reductase in substrate and inhibitor binding and in catalysis. Biochemistry. 1994;33:9945–9952. doi: 10.1021/bi00199a017. [DOI] [PubMed] [Google Scholar]
- 38.Cleland WW, Northrop DB. Energetics of substrate binding, catalysis, and product release. Methods Enzymol. 1999;308:3–27. doi: 10.1016/s0076-6879(99)08003-9. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.