Horizontal Information Drives the Behavioral Signatures of Face Processing

Abstract

Recent psychophysical evidence indicates that the vertical arrangement of horizontal information is particularly important for encoding facial identity. In this paper we extend this notion to examine the role that information at different (particularly cardinal) orientations might play in a number of established phenomena each a behavioral “signature” of face processing. In particular we consider (a) the face inversion effect (FIE), (b) the facial identity after-effect, (c) face-matching across viewpoint, and (d) interactive, so-called holistic, processing of face parts. We report that filtering faces to remove all but the horizontal information largely preserves these effects but conversely, retaining vertical information generally diminishes or abolishes them. We conclude that preferential processing of horizontal information is a central feature of human face processing that supports many of the behavioral signatures of this critical visual operation.

Introduction

Facial information is of paramount significance to social primates such as humans. Consequently, we have developed visual mechanisms which support the recognition of thousands of individuals based only on facial information, while resisting the sometimes drastic changes in appearance that arise from changes in distance, lighting, or viewpoint. Despite a large amount of research, the visual information supporting human face recognition remains unclear.

From the point of view of engineering, a number of automated face recognition algorithms make use of principal component analysis (or similar techniques for reducing data-dimensionality) deriving basis images from a set of sample faces, such that any face can be decomposed into a weighted-sum of eigenfaces(Sirovich and Kirby, 1987; Turk and Pentland, 1991). Such approaches enjoy varying levels of success but are limited by the fact that they operate in a space that is determined by the representation of the raw data (i.e., lists of pixel values). This makes them vulnerable to simple changes in the image that have little impact on human performance. For example it has recently been shown that the structure of many of the most significant eigenfaces (i.e., those that can capture most of the variation between individual faces) serves to capture gross image structure due to variation in lighting (Sirovich and Meytlis, 2009).

The eigenface approach relies on a multi-dimensional representation of faces, a notion that has been extended into the domain of human face recognition (Valentine, 1991). Under this view, each individual is represented as a vector within a multi-dimensional face space containing a series of measurements made along some (presently unknown) dimensions (e.g. eye separation). At the origin of this space sits the average face. Psychophysical support for this theory comes from the observation that prolonged exposure (adaptation) to a single face, elicits facial identity after-effects, shifting the perceived identity of subsequently viewed faces away from the adapting facial identity (Leopold et al., 2001) along a vector known as the identity axis (i.e., one running from the adapting face to the average). Face-space encoding requires access to attributes of a series of “common” facial features (e.g. (x,y) location of the pupil centers), i.e., features that can always be extracted from a given face. In this way one can encode two faces on a common set of feature dimensions (although the psychological validity of such dimensions remains to be established). What then are the low-level visual mechanisms that might support a visual code that is appropriate for faces?

A logical starting point for understanding what visual information is used for face coding, is to consider what information is made explicit through known mechanisms in the human primary visual cortex (V1). V1 neurons are well-characterized by Gabor filters; i.e., they primarily decompose regions of the scene falling within their receptive fields along the dimensions of spatial frequency (SF) and orientation (Hawken and Parker, 1987). The idea of decomposing faces using such a local analysis of orientation and SF has been proposed as a way to characterize facial information for automated recognition (Kruger and Sommer, 2002). Here we briefly review evidence from studies of human face recognition concerning the role of orientation and SF structure of faces.

Face perception seems to be more sensitive to manipulation of SF, than does human visual processing of other categories of objects (Biederman and Kalocsai, 1997; Collin et al., 2004 but see Williams et al., 2009). Perception of different categories of facial information is driven by different ranges of SFs (Sowden and Schyns, 2006). For example, the perception of facial identity is tuned to a narrow band of intermediate SFs (7–16 cycles per face, cpf; Costen et al., 1994, 1996; Gold et al., 1999; Näsänen, 1999; Willenbockel et al., 2010). In contrast, the coarse structure provided by low SFs contributes to both the processing of holistic facial information (interactive feature processing) and the perception of fearful expressions (Collishaw and Hole, 2000; Goffaux et al., 2003, 2005; Goffaux and Rossion, 2006; Goffaux, 2009; Vlamings et al., 2009). Interactive processing is strongly attenuated when faces are filtered to retain only high SFs, a finding that seems to support the notion that high SF channels encode only fine facial details.

With respect to the orientation structure of faces, most work has focused on the drastic impairment in recognition that occurs when faces are inverted within the picture plane. Since human recognition of objects in other visual categories is less prone to planar inversion effects (e.g., Robbins and McKone, 2007), the face inversion effect (FIE) is thought to be a signature of the particular mechanisms engaged for this visual category. Considerable evidence indicates that inversion disrupts feature interactive, so-called holistic, processing. The notion of interactive processing arises from the observation that when presented with an upright face observers find it difficult to process a given feature (e.g., top half or just the eyes) without being influenced by the surrounding features within the face (Sergent, 1984; Young et al., 1987; Rhodes et al., 1993; Tanaka and Farah, 1993; Farah et al., 1995; Freire et al., 2000). Inversion disrupts interactive processing of features, making observers better at processing features independently of each other. The fact that inversion disrupts interactive face processing suggests the latter is a core aspect of human ability to discriminate and recognize faces (though see Konar et al., 2010).

In contrast to the impairment caused by planar inversion, humans readily recognize others despite changes in viewpoint and illumination. Viewpoint generalization is presumably achieved through the combination of 2D and 3D cues in face representations (O'Toole et al., 1999; Jiang et al., 2009; Wallis et al., 2009).

Recently, it has been suggested that what is special about face processing is its dependence on a particular orientation structure. Dakin and Watt (2009) showed that recognition of familiar faces benefits most from the presence of their horizontal information, as compared to other orientation bands. Specifically, when face information is limited to a narrow band of orientations, recognition performance peaks when that band spans horizontal angles, and declines steadily as it shifts towards vertical angles. These authors also reported that it is the horizontal structure within faces that drives observers’ poor recognition of contrast–polarity–inverted faces, and their inability to detect spatially inverted features within inverted faces (Thompson, 1980). Finally they showed that, in contrast to objects and scenes, the horizontal structure of faces tends to fall into vertically co-aligned clusters of horizontal stripes, structures they termed bar codes(see also Keil, 2009). Scenes and objects fail to show such structural regularity. Dakin and Watt (2009) suggested that the presence and vertical alignment of horizontal structure is what makes faces special. This notion is also supported by Goffaux and Rossion (2007) who showed that face inversion prevents the processing of feature spatial arrangement along the vertical axis. These structural aspects may convey resistance to ecologically valid transformations of faces due to, e.g., changes in pose or lighting.

The goal of this paper is to address whether a disproportionate reliance on horizontal information is what makes face perception a special case of object processing. We investigated four key behavioral markers of face processing: the effect of inversion, identity after-effects, viewpoint invariance, and interactive feature processing. If the processing of horizontal information lies at the core of face processing specificity, and is the main carrier of facial identity, we can make and test four hypotheses. (1) The advantage for processing horizontal information should be lost with inversion as this simple manipulation disrupts face recognizability and processing specificity. (2) Identity after-effects should arise only when adapting and test faces contain horizontal information. (3) Face recognition based on horizontal structure should be more resistant to pose (here, viewpoint) variation than face recognition limited to other orientations. (4) Interactive feature processing – i.e., the inability to process the features of an upright face independently from one another – should be primarily driven by the horizontal structure within face images.

Experiment 1. Horizontal and vertical processing in faces, objects and natural scenes

A behavioral signature of face perception is its dramatic vulnerability to inversion. Inversion disrupts the interactive processing of face parts and face recognizability in general. However, what visual information is processed in upright, but not inverted, faces is the subject of current axiomatic debate driven by considerable divergence of findings within the empirical literature (e.g., Sekuler et al., 2004; Yovel and Kanwisher, 2004; Goffaux and Rossion, 2007; Rossion, 2008). Here, we investigated whether the FIE arises from the disruption of visual processing within a particular orientation band.

Materials and methods

Subjects

Eighteen Psychology students (Maastricht University, age range: 18–25) participated in face and car experiments. Thirteen additional students consented to perform the experiment with scenes. All subjects provided their written informed consent prior to participation. They were naïve to the purpose of the experiments and earned course credits for their participation. They reported either normal, or corrected-to-normal vision. The experimental protocol was approved by the faculty ethics committee.

Stimuli

Twenty grayscale 256 × 256 pixel pictures of unfamiliar faces (half males, neutral expression, full-front), cars (in front view), and natural scenes (van Hateren and van der Schaaf, 1998) were used (Figure 1). Face and car pictures were edited in Adobe Photoshop to remove background image structure. To eliminate external cues to facial identity (e.g., hair, ears, and neck), the inner features of each individual face were extracted and pasted on a generic head (one for female and one for male faces; as in Goffaux and Rossion, 2007). The mean luminance value was subtracted from every image. Filtered stimuli were generated by Fast Fourier transforming the original image using Matlab 7.0.1 and multiplying the Fourier energy with orientation filters: these allowed all SFs to pass but had a wrapped Gaussian energy profiles in the orientation domain, centered on one orientation with a particular bandwidth specified by the standard deviation parameter (cf Dakin and Watt, 2009). We used a standard deviation of 14° selected to broadly match the orientation properties of neurons in the primary visual cortex (e.g., Blakemore and Campbell, 1969; Ringach et al., 2002). Note that this filtering procedure leaves the phase structure of the image untouched, and only alters the distribution of Fourier energy across orientation. There were three filtering conditions: horizontal (H), vertical (V) and horizontal plus vertical (H + V) constructed by summing the H and V filtered images. After inverse-Fourier transformation, the luminance and root-mean square (RMS) contrast of all resulting images were adjusted to match mean luminance and contrast values of the original image set (i.e., prior to filtering). Note that this normalization was applied in all following experiments.

Figure 1.

Face, object and scene pictures (A–C) were filtered to preserve either horizontal (D–F), vertical (G–I) or both horizontal and vertical orientations (J–L).

Inverted stimuli were generated by vertically flipping each image. Stimuli were displayed on a LCD screen using E-prime 1.1 (screen resolution: 1024 × 768, refresh rate: 60 Hz), viewed at 60 cm. Stimuli subtended a visual angle of 8.9° × 8.9°.

Procedure

The procedure was identical for face, car, and scene experiments. A trial commenced with the presentation of a central fixation cross (duration range: 1250–1750 ms). The first stimulus then appeared for 700 ms, immediately followed by a 200-ms mask (256 × 256-pixel Gaussian noise mask; square size of 16 × 16 pixels). Both the first stimulus and the mask appeared at randomly selected screen locations across trials (by ± 20 pixels in x and y dimensions). After a 400-ms blank interval, where only the fixation marker was visible, the second stimulus appeared and remained visible until subjects made a response (maximum duration: 3000 ms). Subjects were instructed to respond as quickly and as accurately as possible, using the computer keyboard, whether the pair of stimuli were the same or different. On 50% of trials stimuli differed, on 50% they were identical.

In a given trial, faces were presented either both upright, or both inverted. Faces in a trial also always belonged to the same filter-orientation condition (i.e., both H, both V, or both H + V). Upright and inverted trials were clustered in 20-trial mini-blocks; the order of the other conditions (filter-orientation and similarity) was random. There was a 10-s resting pause every ten trials. Feedback (a running estimate of accuracy) was provided every 40 trials. Prior to the experiment, subjects practiced the task over 50 trials.

There were 12 conditions per experiment in a 2 × 2 × 3 within-subject design. The three conditions were: similarity (same versus different), planar-orientation (upright versus inverted), and filter-orientation (H, V or H + V). We ran 20 trials per condition, to give a total of 240 experimental trials.

Data analyses

Using hits and correct-rejections in every planar-orientation and filter-orientation condition, we computed estimates of sensitivity (d′) for each subject following the loglinear approach (Stanislaw and Todorov, 1999). Sensitivity measures were submitted to repeated-measure 2 × 2 × 3 ANOVA. ANOVAs were computed for each experiment separately. Conditions were compared two-by-two using post hoc Bonferroni tests.

Results

Faces

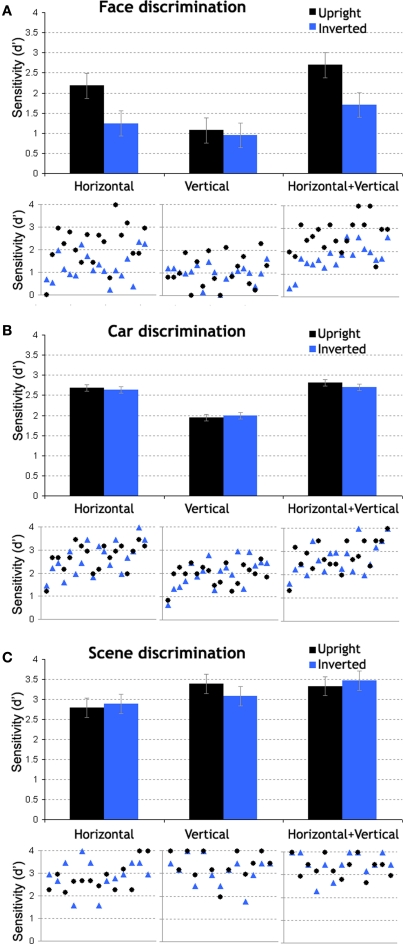
Main effects of planar-orientation and filter-orientation were significant (F(1,17) = 63.76, p < 0.0001, F(2,34) = 33, p < 0.0001). These factors interacted significantly (F(2,34) = 7.17, p < 0.003) stressing that inversion disrupted the processing of H (p < 0.0002), H + V (p < 0.0001), but not V (p = 1) face information. When faces were upright, discrimination was better for stimuli containing H or H + V information, compared to V information (H/V comparison: p < 0.0001; H + V/V comparison: p < 0.0001; Figure 2A). When faces were inverted, sensitivity level was comparably low across H and V conditions (p = 1). The only significant difference across inverted conditions was that sensitivity was higher for H + V than V filter-orientation (p < 0.005).

Figure 2.

Results from Experiment 1. Bar graphs plot mean discrimination sensitivity (d′) as a function of filter-orientation and planar-orientation (error bars indicate mean square error, MSE). Data are shown for the three classes of stimuli: (A) faces, (B) cars, and (C) scenes. The scatter plots below each bar graph show the individual data it was derived from.

Cars

In stark contrast to faces, sensitivity at discriminating cars was not affected by inversion (see Figure 2B; F(1,17) = .06, p = .8), in any of the filter-orientation conditions (planar-orientation by filter-orientation interaction: F(2,34) = .99, p = .38). Yet, the main effect of filter-orientation was significant (F(2.34) = 39.37, p < 0.0001), highlighting overall lower discrimination sensitivity based on V information than on H or H + V information (H/V comparison: p < 0.0001; H + V/V comparison: p < 0.0001).

Natural scenes

There was no inversion effect when discriminating scenes (F(1,12) = 0.001, p = 0.97; Figure 2C), in any filter-orientation (planar-orientation by filter-orientation interaction: F(2,24) = 1.45, p = 0.25). Only the main effect of filter-orientation was significant (F(2,24) = 8.3, p < 0.002). Sensitivity to scene differences was modestly worse at H orientation as compared to V and H + V orientations (ps < 0.025). There was no difference between the latter two conditions (p = 0.9) but we cannot exclude a ceiling effect.

Discussion

Similar to previous report for the naming of famous faces (Dakin and Watt, 2009), the present findings indicate that the ability to discriminate between unfamiliar faces is best supported by horizontal information. In contrast to Dakin and Watt (2009), all external face cues were removed in the present experiment and subjects had to rely on the spatial arrangement of inner facial features to discriminate faces. Our results therefore show that the horizontal advantage stems from the improved processing of inner facial cues. Critically, we report that the advantage for processing horizontal face structure is lost when faces are inverted in the picture plane, further suggesting that the horizontal advantage for upright stimuli marks the engagement of face-specific perceptual mechanisms. Furthermore, the loss of horizontal processing advantage with face inversion indicates that the better efficiency for processing horizontal information in upright faces does not merely derive from stimulus orientation structure, but arises as a consequence of the interactions between stimulus structure and observer. We also report that upright face discrimination was better when horizontal and vertical information were combined than when only horizontal information was provided to the participants. Both horizontal and vertical information are thus clearly useful for face recognition, but it is clear that, for images restricted in orientation content, recognition is easier when horizontal structure is provided.

Object discrimination was also better when images were restricted to horizontal than vertical information. Unlike faces, this advantage was observed independent of the planar-orientation of the stimuli. In agreement with previous evidence (Hansen and Essock, 2004), scene discrimination was worse at horizontal than at vertical orientation. In contrast to faces, orientation combination did not improve discrimination sensitivity for objects and scenes.

Experiment 2. Dependence of the facial identity after-effect on orientation structure

Key psychophysical support for the psychological validity of the face space model (described in section “Introduction”) comes from the observation that identity after-effects are strongest between faces that belong to the same identity axis (Leopold et al., 2001; Rhodes and Jeffery, 2006). That perception of upright faces seems to disproportionately rely on horizontal information suggests that the horizontal orientation band is largely responsible for carrying the relevant cues to facial identity. If so, identity after-effects should be preferentially driven by horizontal and not by vertical image structure. Experiment 2 addressed this issue directly by measuring identity after-effects when adapting faces contained either broadband, horizontal, or vertical information.

Materials and methods

Subjects

One of the authors (Steven C. Dakin) and two observers (DK and JAG) naïve to the purpose of the experiment (all wearing optical correction as necessary) participated in the experiment. DK and JAG provided their written informed consent prior to participation. All were experienced psychophysical observers. They familiarized themselves with the two test faces by passively viewing them for a period of at least 15 min before commencing testing. The protocol was approved by the faculty ethics committee.

Stimuli

We obtained full-front uniformly lit digital photographs of two male subjects and manually located 31 key-points (Figure 3) on these images. Faces were masked from the background and were normalized to have equal mean luminance. They were scaled and co-aligned with respect to the center of the eyes prior to morphing. We generated morphed versions of these images using custom software written in the Matlab programming environment. Specifically, for a given image and a set of original and transformed key-points, we used the original key-points to generate a mesh over the face using Delaunay triangulation (i.e., we computed the unique set of triangles linking key-points such that no triangle contains any of the key-points) and then used the same point-to-point correspondences with the transformed key-points to generate a set of transformed triangles (Figure 3). We used the original triangles as masks to cut out corresponding image regions from the face and stretched these into registration with the transformed triangles using MatLab's built-in 2D bilinear interpolation routines (interp2) to perform image stretching. The sum of all these stretched triangles is the morphed face.

Figure 3.

The location of the 31 key-points used for morphing is superimposed on an example “morphed-average” faces from our set.

To generate morphs intermediate between the identities of the two faces we first calculated a weighted average of the key-point locations of the two faces:

$$K_{morph}=w{K}_1+(1-w)K_2$$ (1)

where w is the weight given to face #1. We then morphed each face (I₁ and I₂) into registration with the new key-points (giving ${\widehat{I}}_1$and ${\widehat{I}}_2$) and generated the final image by performing a weighted average (in the image domain) of these two images:

$$I_{\text{morph}}=w{\widehat{I}}_1+(1-w){\widehat{I}}_2$$ (2)

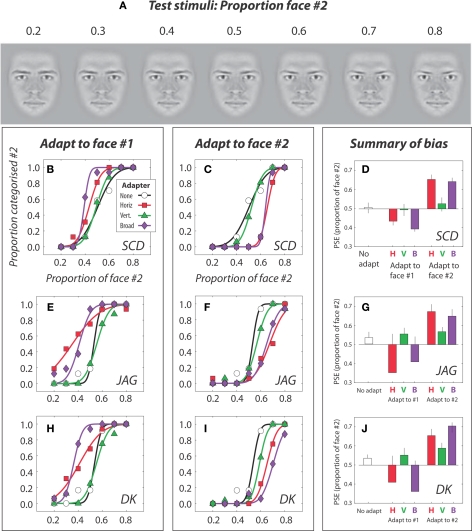
In the experiment we used test faces generated with seven values of w from 0.2 to 0.8 in steps of 0.1. Prior to presentation or filtering, we equated the RMS contrast in all SF bands of the stimulus. This ensured that all unfiltered face stimuli had identical power spectra. Examples of the unfiltered/broadband stimuli are shown in Figure 4A. Filtering methods were identical to those described above: face information was restricted to a Gaussian range of orientation energy (σ = 14°) centered on either horizontal or vertical orientation.

Figure 4.

(A) Morphed faces were used as test stimuli. Seven morphed faces were generated using w from 0.2 to 0.8 where w is the weight given to face #2. (B–J) Identity after-effects with broadband (unfiltered) and filtered faces in subjects Steven C. Dakin, JAG, and DK. Subjects were either not adapted (“none”) or adapted to a face that was either broadband (“broad”) or was restricted to horizontal (“horiz.”) or vertical (“vert.”) information. We then measured the probability that subjects classified a morphed mixture of the two faces (i.e., a test face) as more like face #1 or face #2. With no adaptation (black/white) curves were centered on the 50% identity level (i.e., a 50:50 morphed face was equally likely to be classified as face #1 or #2). The f1:f2 ratio leading to observers being equally likely to classing a stimulus as face #1 or #2 is known as the point of subjective equality (PSE). (B,E,H) After exposure to broadband face #1 (purple) curves shift leftwards so that more of face #1 needs be present for subjects to be equally likely to class the stimulus as face #1 or face #2. This is the identity after-effect. Adapting to faces that have been horizontally filtered (red curves) produced a similar substantial shift in PSE (compare red and black/white curves) whereas adapting to vertically filtered faces produced virtually no adaptation. Vertically filtered adapters produced categorization biases that closely matched biases in the un-adapted condition (compare green and black/white curves). (C,F,I) After exposure to face #2 curves shifted rightwards but only when the adapting face was broadband or horizontally filtered. Adapting to vertically filtered face produced no adaptation. (D,G,J) Summary of PSE values.

Procedure

On un-adapted trials observers were presented with a central fixation marker (200 ms) followed by a single morphed face stimulus that remained on the screen for 1000 ms. Observers then made a categorization response (using the computer keyboard) as to whether the face appeared more like face #1 or face #2. Responses were not timed but observers were encouraged to respond promptly to reduce overall testing duration. On adapted trials the initial fixation marker was followed by an adapting face stimulus that remained on the screen either for 30 s on the first trial (to build up adaptation) or for 5 s on subsequent trials. To avoid retinal adaptation observers tracked a fixation marker that moved up and down the vertical midline of the face ( ± 0.6° from the center) during the adaptation phase. The adapting face stimulus was always either 100% face #1 or face #2, and in three different blocked conditions was either (a) unfiltered, or had been restricted to (b) horizontal or (c) vertical information. Note that the test was always a broadband face.

There was a total of seven conditions (no adaptation, and the three adapting conditions with both faces #1 and #2). The order of testing was randomized on a subject by subject basis. Performance in each condition was evaluated in a run consisting of 56 trials: eight trials at each of the seven stimulus levels (w = 0.2–0.8 in steps of 0.1). At least two runs were conducted for each subject, giving a total of at least 784 trials per subject.

Experiments were run under the MATLAB programming environment incorporating elements of the PsychToolbox (Brainard, 1997). Stimuli were presented on a CRT monitor (LaCie Electron Blue 22) fitted with a Bits ++ box (Cambridge Research Systems) operating in Mono ++ mode to give true 14-bit contrast accuracy. The display was calibrated with a Minolta LS110 photometer, then linearized using a look-up table, and had a mean (background) and maximum luminance of 50 and 100 cd/m² respectively. The display was viewed at a distance of 110 cm. Face stimuli (adapters and test) were 8.5-cm wide by 11-cm tall subtending 4.4 × 5.7° of visual angle.

Data analyses

The probability that a subject categorized a given broadband test face as more like face #2, as a function of the morph level (from face #1 to face #2) was fitted with a cumulative Gaussian function to give the point of subjective-equality (PSE or bias; i.e., the morph level leading to a 50% probability that the stimulus was categorized as face #2) and the precision (the slope parameter of the best fitting cumulative Gaussian, which is equivalent to the stimulus level eliciting 82% correct performance). These parameters were bootstrapped (based on 1024 bootstraps; Efron and Tibshirani, 1993) to yield 95% percentile-based confidence intervals that were used to derive PSE error bars (Figures 4D,G,J). Specifically by assuming binomially distributed error of subjects responses (e.g. 8/10 “more like face #2”) at each morph level we could resample the data to generate a series of new response rates across morph level, which we could fit with a psychometric function to yield a new estimates of the PSE. By repeating this procedure we obtained a distribution of PSEs from which we could compute confidence intervals.

Results and discussion

Figures 4B–J shows the results from this experiment. Each data point (Figures 4B,C,E,F,H,I) is the probability that a given observer classed a stimulus at some morph level (between faces #1 and #2) as looking more like face #2. Solid lines are the fit psychometric functions used to estimate a PSE (the morph level leading that observer to be equally likely to categorize the stimulus as either face.) PSEs are plotted in the bar graphs to the right (Figures 4D,G,J). With no adaptation (black/white points, curves and bars) all curves were centered near the 50:50 morph level indicating that all subjects were equally likely to categorize an equal mix of faces #1 and #2 as face #1 or #2.

Adapting to a broadband version of face #1 (Figures 4B,E,H; purple points and curves) shifted curves leftwards and PSE's (Figures 4D,G,J; purple bars) fell below 0.5 indicating that a stimulus needed to contain < 40% of face #2 to be equally likely to be classed as face #1 or #2. When subjects adapted to a broadband version of face #2 (Figures 4C,F,I; purple points and curves) the function shifted rightwards and the PSE (Figures 4D,G,J; purple bars) were greater than 0.5 indicating that now subjects needed the morph to contain > 60% of face #2 to be equally likely to be classed as face #1 or #2. This is the standard identity after-effect; adapting to a given face pushes the subsequent discrimination function towards the adapted end of the morph continuum. The size of our effects is comparable to previous reports (Leopold et al., 2001).

Data from the horizontally and vertically filtered adapter conditions are shown as red and green data points, curves and bars, respectively. Adapting to a horizontally filtered face elicited a shift in the psychometric function for subsequent discrimination that was almost indistinguishable from the effect of adapting to the broadband face (compare purple and red bars) although we note that after adaptation to horizontally filtered face #1 the psychometric function became shallower (indicating poorer discrimination). By contrast adapting to vertically filtered faces elicited little adaptation leading to bias comparable to estimates from the ‘no-adaptation’ condition (compare green and black/white bars).

Given that we did not compare identity after-effects when adapter and test faces fell on the same or different identity vector(s), we cannot know if the measured after-effects exclusively reflect adaptation to identity. Consequently, there are three alternative reasons, which could account for the weaker identity after-effect observed with vertical compared to horizontal content: (1) the adapted mechanism may be tuned for both identity strength and the orientation of its input, (2) alternatively, it may be tuned for identity strength only (so that if vertically filtered adapter looked more similar to one another – as indicated by the results of Experiment 1 – they might induce less adaptation), or (3) it could relate to the location of the morphing key-points varying more in the horizontal than in the vertical direction.

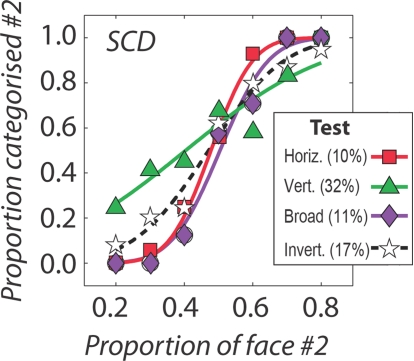
To investigate accounts (1) and (2) we measured psychometric functions for the identification of upright faces that were morphed between the two test identities. Faces were upright and either broadband or filtered to contain either horizontal or vertical information (with the same bandwidths in the adaptation phase of the main experiment). We also measured identification performance with inverted broadband faces. Results – plotted in Figure 5 – indicate that vertically filtered faces are about three times more difficult to discriminate from one another than horizontally filtered faces (% values in parentheses indicate identity change threshold – i.e., the identity increment leading to 82% correct identification). That discrimination of vertically filtered faces is so poor indicates that poor adaptation may indeed be attributable to these stimuli not eliciting a sufficiently strong sense of identity. We return to this point in the section “Discussion”.

Figure 5.

Psychometric functions are shown for the discrimination of upright/broadband faces (in purple), inverted/broadband faces (in black/white), horizontally filtered upright faces (in red) and vertically filtered/upright faces (in green). Identity thresholds - the identity levels eliciting 82% accurate discrimination - are given in parentheses.

We also looked at whether location of key-points used to morph the faces may have influenced our results. We analyzed the x and y locations of 21 key-points (corresponding to the internal facial features as shown in Figure 3) drawn from 81 male faces. The standard deviation of the y coordinates was 60% higher than of the x coordinates indicating that there was considerably more variation in the vertical than horizontal location of facial features. Because this increase in variation might arise from the elongated aspect ratio of faces (i.e., there's more room for variation in y coordinates) we also computed the ratio of Fano factors (a mean-corrected measure of dispersion) which was ~66% higher along y axis than along x axis. The notion that such a difference might contribute to our findings relies on several further assumptions, notably the validity of both the location and sampling density of key-points, the linear relationship between key-point location and discriminability of feature change, etc. Nevertheless, this analysis indicates that the robust identity after-effects observed for horizontally filtered stimuli could at least in part originate from structural properties of faces preferentially supporting the transmission of information through vertical location of features (i.e., along the y axis) (Goffaux and Rossion, 2007; Dakin and Watt, 2009).

With these caveats in mind, the present findings indicate that the visual mechanisms responsible for the representation of face identity, as indexed by identity after-effect, are tuned to horizontal bands of orientation. We proposed that the advantage for encoding face identity based on the vertical arrangement of horizontal face information would be that this information is available across viewpoint changes (Goffaux and Rossion, 2007; Dakin and Watt, 2009) a notion we explicitly test in the next experiment.

Experiment 3. Matching faces across viewpoint

So far, our experiments have used frontal-view images of faces, minimizing the need for viewpoint generalization, a core part of everyday face recognition. Because we have previously suggested that the importance of vertically arranged horizontal information to face recognition may lie in its resistance to viewpoint changes (Goffaux and Rossion, 2007; Dakin and Watt, 2009) we next sought to measure the effect of disrupting the processing of different orientation bands in faces that observers are attempting to match across viewpoint change.

Materials and methods

Subjects

Fourteen students (aged between 18 and 22) from Maastricht University provided their written informed consent to participate in the experiment. The protocol was approved by the faculty ethics committee. They earned course credits in exchange for their participation. They had not participated in the previous experiments and were naïve to the purpose of the experiment. All had normal or corrected-to-normal visual acuity.

Stimuli

Stimuli were grayscale broadband pictures of 22 unfamiliar faces (11 male, 11 female faces) – trimmed to remove background, hair, ears, and neck. The set included one front view and one three-quarter view of each model. Stimuli were 150 × 180 pixels in size, which corresponded to 5.2 × 6.6° of visual angle (viewing distance: 60 cm). Display apparatus was identical to Experiment 1.

A pilot study indicated that subjects were unable to match upright faces across viewpoint better than chance when only a narrow band of vertical facial information was presented. This is consistent with previous evidence that matching unfamiliar faces across viewpoint is perceptually challenging (Hill et al., 1997). Therefore we chose to restrict orientation content by adding oriented noise masks to the face images. Depending on the signal-to-noise ratio (SNR), masking can hinder information processing while preserving stimulus recognizability (Näsänen, 1999).

Oriented noise masks were produced by processing white noise using a filter with a wrapped Gaussian orientation profile centered on either horizontal, or vertical orientation (σ = 15°) and a box-car/band-pass amplitude profile passing two octaves of information around 10 cycles per image, since noise in this SF range is most disruptive to the recognition of facial identity (Näsänen, 1999; Tanskanen et al., 2005).

On each trial we randomly selected three noise masks and combined them with each of the full-front target faces (Figure 6A). Noise masks were drawn from independent noise samples, but were of the same orientation in a given trial. The RMS contrast (defined as image luminance standard deviation) was 0.06 for faces and 0.18 for oriented noise. This SNR was selected after pilot testing revealed that it enabled above chance matching performance when upright faces were masked using horizontal noise.

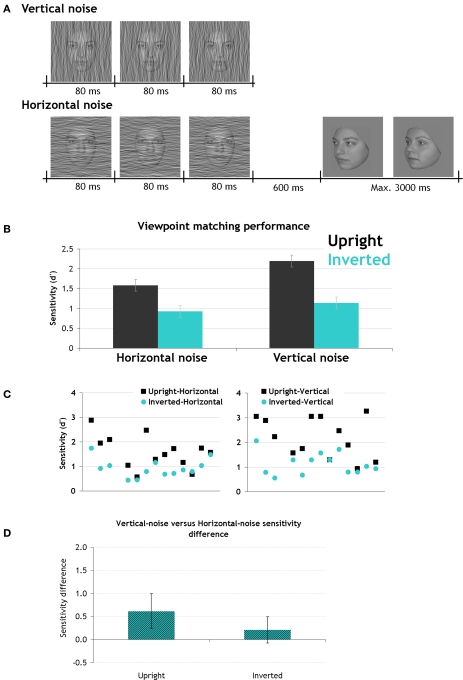
Figure 6.

(A) Stimuli and trial structure of the viewpoint matching experiment. (B) Experiment 3 results. Average discrimination sensitivity (d′) as a function of noise-orientation and planar-orientation (error bars indicate MSE). (C) Plots of individual d′ results. (D) Sensitivity difference between masking conditions is plotted at each planar orientation. Error bars represent 95% confidence intervals around the mean difference.

Procedure

A trial started with the rapid sequence of three different combinations of a given frontal view of a target face with three different noise masks. The duration of each frame was 80 ms, giving a total target-duration of 240 ms. There was no gap between the three frames. After a 600-ms blank, the target face was followed by two broadband (unfiltered) faces, i.e., the probes, simultaneously displayed in ¾ views until subjects made a response (maximum response time: 3000 ms; Figure 6A). Probes were displayed at an eccentricity of 2.85° of visual angle (i.e., distance between inner image border and screen center), in the left and right parts of the screen. Trials were separated by a 2000-ms blank interval. Subjects had to decide which of the two ¾ view faces matched the previously seen frontal-view target by pressing keys at corresponding locations (left versus right).

Noise orientation (horizontal or vertical) varied randomly across trials but was constant within a trial. Target and probe faces were presented at upright or inverted planar-orientation (in mini-blocks of 22 trials). All stimuli were matched for luminance and RMS contrast. There were four within-subject experimental conditions (planar-orientation: upright versus inverted; noise orientation: horizontal versus vertical). There were 44 trials per condition, making a total of 176 experimental trials. A self-paced resting pause occurred every 22 trials along with accuracy feedback. Prior to the experiment, subjects were briefly familiarized with full-front and ¾ views of the face stimuli.

Data analyses

One subject was excluded from the analyses because of chance level performance in one condition. We computed d′ measures for each subject following the loglinear approach (Stanislaw and Todorov, 1999). Sensitivity measures were submitted to a repeated-measure ANOVA with planar-orientation and noise-orientation as factors. Conditions were compared two-by-two using post hoc Bonferroni tests. The size of the difference between noise-orientation conditions was estimated using Cohen's d (i.e., the difference between the means divided by the pooled standard deviation; Cohen, 1988; Rosnow and Rosenthal, 1996).

Results and discussion

The main effects of planar-orientation and noise-orientation were significant (F(1,12) = 32.09, p < 0.0001 and F(1,12) = 11.81, p < 0.005, respectively). Matching across viewpoint was more sensitive when faces were displayed upright than inverted and when they were masked with vertical compared to horizontal noise (Figure 6). The interaction between these two factors was not significant (F(2,24) = 4.3, p = 0.06).

Since multiple Bonferroni comparisons control the Type I error, they could be used to compare conditions two-by-two despite the ANOVA interaction was not significant (Wilcox, 1987). Sensitivity differences between horizontal and vertical noise conditions were only significant when faces were upright (p < 0.005; Cohen's d: 0.71) and not inverted (p = 0.9; Cohen's d: 0.32), indicating that horizontal noise mostly affected the processing of upright faces. Matching inverted faces across viewpoint was poor, irrespective of the oriented noise applied to the target. As Cohen's d indicates, the difference between horizontal and vertical noise masking conditions was twice as robust at upright than inverted planar orientation. Figure 6D illustrates the mean sensitivity difference between vertical- and horizontal-noise masking conditions. The error bars reflect the 95% confidence intervals. The sensitivity difference between vertical- and horizontal-noise masking conditions ranged from 0.23 to 0.99 for upright faces and from −0.08 to 0.49 for inverted faces. For inverted faces, the confidence interval captured zero further indicating the absence of difference between horizontal- and vertical-noise masking conditions.

The fact that sensitivity differences between noise masking conditions were selectively observed at upright planar orientation indicates they are due to the face identity processing, and not to general aspects of stimulus or masking procedure.

That viewpoint generalization is worse when horizontal face information is masked supports the proposal that face identity is preferentially coded using the horizontal structure of faces due to this structure remaining more invariant under pose change.

Experiment 4. Interactive face perception

When looking at an upright face, it is difficult to perceive the constituent features independently from one another, i.e., facial features are holistically or interactively encoded. When faces are inverted, interactive processing is disrupted leading one to perceive individual feature properties more independently of one another. Interactive processing is thought to be a core aspect of face processing specificity. We used the congruency paradigm (Goffaux, 2009) in order to explore interactive face processing when only horizontal and vertical face information is preserved. We hypothesized that if the privileged processing of horizontal information is what makes faces special, markers of interactive face processing should arise only when horizontal information is available.

Materials and methods

Subjects

The same 14 students from Maastricht University who participated in Experiment 3 also took part in the main experiment. Thirteen other students took part in the follow-up control experiment. All gave written informed consent prior to and were paid 7,5/h for their participation. The protocols of the main and follow-up experiments were approved by the faculty ethical committee.

Stimuli

We used 20 grayscale pictures of faces (50% male, 50% female) posed in frontal view exhibiting neutral expression, and free of external cues (facial hair, glasses, and hairline). The inner features of each face (brows, eyes, nose, and mouth in their original spatial relations) were pasted onto a common face outline (one for each gender). Images were 256 × 256 pixels subtending 9.4 × 9.4° of visual angle. The experiment required that subjects discriminate faces based only on information within a particular targetregion while ignoring a complementary distractorregion. The target region was located over the eyes and brows and the distractor region over the nose and mouth. Feature replacement was done using Adobe Photoshop 7.0. Examples of the stimuli are shown in Figure 7.

Figure 7.

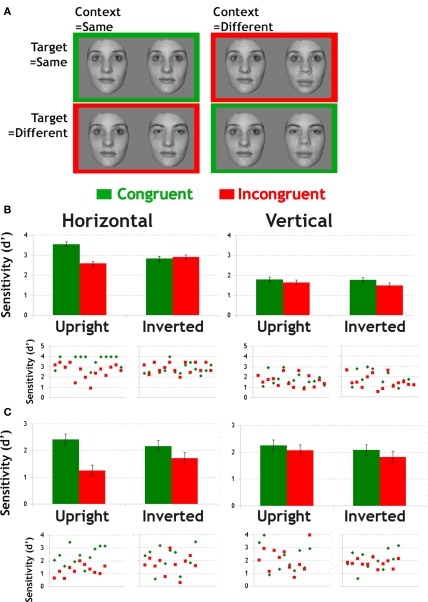
(A) Subjects matched target features (i. e., eyes and brows) of faces presented in pairs. The target features could be same or different. Orthogonally, the other (distractor) features could also be same or different, thus creating congruent or incongruent context for the matching of the target. (B)The top graphs show the mean sensitivity in the congruency paradigm when face information was restricted to horizontal (left) or vertical (right) information. Error bars represent MSE. The bottom scatter plots illustrate individual data for congruent and incongruent trials in each filter- and planar-orientation condition. (C) Results of the follow-up experiment. Horizontally filtered stimuli were combined with white noise and presented shortly in order to equate sensitivity levels in upright-congruent conditions. Top graphs show mean sensitivity and the bottom scatter plots show individual data. Error bars represent MSE.

The orientation-filtering method was identical to Experiments 1 and 2 except that filter bandwidth was set at 20° to enable above chance performance in both horizontal and vertical conditions.

In the follow-up experiment, horizontally filtered stimuli were combined with white noise. The RMS contrast (defined as image luminance standard deviation) was 0.06 for the face and 0.06 for noise, producing an SNR of 1.

Procedure

Faces were presented in pairs and subjects had to report whether target features (eyes and brows) were same or different, while ignoring distractor features (nose and mouth). We manipulated the congruency of target and distractor features (Figure 7A). In congruent conditions, both the target and distractor features should lead to an identical decision (be that same or different). In incongruent conditions, target and distractor features called for opposite responses (again, be that same or different). Thus, in a different-congruent pairing, both target and distractor regions differed across the two faces while in a same-incongruent pairing, face stimuli had identical target but different distractor features. The comparison between congruent and incongruent performance estimates the strength of face interactive processing (Goffaux, 2009).

Thus there were four crossed conditions (same-congruent, different-congruent, same-incongruent, and different-incongruent; Figure 7A) tested using upright and inverted displays under two filter-orientation conditions (horizontal and vertical), making a total of 16 experimental conditions. Planar-orientation and filter-orientation were fixed within a trial, but varied randomly across trials. There were 20 trials in each condition, resulting in a total of 320 experimental trials, divided in 40-trial blocks separated by resting pauses. During the pauses, subjects were informed about their accuracy using on-screen written feedback.

Prior to the experiment, instructions were provided on the computer monitor. Subjects were then trained to perform the task with 20 trials of upright and inverted broadband faces, followed by 20 trials of upright and inverted filtered faces. During training, subjects received feedback on their accuracy every 10 trials.

A trial began with the central presentation of a fixation cross for 300 ms, followed by a blank screen for 200 ms. Next two faces appeared side-by-side on the screen at an eccentricity of 1.1° of visual angle (i.e., the distance between the screen center and inner edge of each face image). On every trial, stimulus position was randomly jittered by 15 pixels in y direction in order to prevent subjects from scanning the faces laterally for local details. Faces remained on-screen (up to a maximum presentation of 3000 ms) until the subject made a response.

In a follow-up experiment, pairs of horizontally filtered faces appeared for 875 ms, pairs of vertically filtered faces for 1750 ms. Along with the inclusion of noise, the short duration of horizontal stimuli was intended to selectively impair performance in this filter-orientation condition, equating performance levels across orientation bands in upright-congruent conditions. All conditions were randomly ordered in the main experiment, but blocked in the follow-up experiment (randomly alternating 20 trial-blocks of each condition).

Stimulus presentation was controlled using E-prime stimulation software. Display apparatus was identical to Experiment 1.

Data analyses

In the main and follow-up experiments, we computed d′ measures for each subject following the same procedure as in Experiments 1 and 3. d′ measures were submitted to repeated-measure ANOVA with planar-orientation (upright versus inverted), congruency (congruent versus incongruent) and filter-orientation (vertical versus horizontal) as within-subject factors. Conditions were compared two-by-two using post hoc Bonferroni tests.

Results and discussion

Figure 7B clearly indicates an advantage in sensitivity for congruent conditions when faces were upright and contained horizontal information. Sensitivity in vertically filtered condition was above-chance but low overall.

Main effects of filter-orientation and congruency were significant (F(1,13) = 80.9, p < 0.0001; F(1,13) = 10.8, p < 0.006). The discrimination of faces based on eye region was more sensitive in horizontal than vertical and in congruent than incongruent conditions. The main effect of planar-orientation was not significant (F(1,13) = 2.03, p = 0.2) since it only affected performance in congruent trials (planar-orientation by congruency interaction: F(1,13) = 9.6, p < 0.008; FIE in congruent trials: p < 0.02, FIE in incongruent trials: p = 1). Most interestingly, planar-orientation, filter-orientation and congruency significantly interacted (F(1,13) = 19.5, p < 0.001). This triple interaction was explored further by running separate ANOVAs for horizontal and vertical filter-orientation conditions. When only horizontal information was available, the main effect of congruency was significant (F(1,13) = 10.06, p < 0.007), but was significantly modulated by planar-orientation (F(1,13) = 15.6, p < 0.002). Subjects matched horizontal eye information with higher sensitivity in congruent trials, but only when faces were displayed in an upright planar-orientation (congruency effect at upright planar-orientation: p < 0.001, at inverted planar-orientation: p = 1). The interaction further reveals that FIE was only significant in congruent trials (p < 0.01; FIE in incongruent condition: p = 0.7). When only vertical information was available, the ANOVA revealed no significant effect or interaction (ps > 0.5).

The above results firmly suggest that IFP as indexed by feature congruency effects are selectively driven by the horizontal structure of face stimuli. However, the absence of congruency effects for vertically filtered faces may merely be due to the overall lower sensitivity in vertical band as compared to horizontal band.

We addressed this potential confound in a follow-up experiment, in which sensitivity to horizontally filtered faces was hindered by (1) introducing noise in the stimulus and (2) shortening presentation duration. The ANOVA revealed a main effect of congruency (F(1,12) = 13, p < 0.004). In contrast to the main experiment, the main effect of filter-orientation was not significant (p = 0.185). The filter-orientation by congruency interaction was significant (F(1,12) = 9, p < 0.013) as well as the triple interaction between filter-orientation, congruency and planar-orientation (F(1,12) = 5.34, p < 0.04). When comparing conditions two-by-two using Bonferroni-corrected post hoc tests, horizontal and vertical conditions were only found to differ in upright-incongruent condition (p < 0.005; ps > 0.96 in the other congruency by planar-orientation conditions). The congruency effect was significant for upright horizontally filtered faces only (p < 0.001).

Figure 7C shows that sensitivity was equal between horizontal and vertical orientation bands in upright-congruent conditions. Interestingly, feature incongruency impaired performance for horizontally filtered faces selectively, confirming the notion that IFP is driven by horizontal, but not vertical information.

General Discussion

We have presented evidence that four specific behavioral signatures of face perception are driven by the horizontal orientation structure of faces.

Experiment 1 unequivocally demonstrates that the visual information disrupted by planar inversion, i.e., information thought to support face processing, is carried within the horizontal orientation band. This accords with previous evidence that inversion selectively disrupts the processing of the spatial arrangement of features along the vertical axis (Goffaux and Rossion, 2007), and with demonstrations in Dakin and Watt (2009) that the vertical alignment of horizontal information drives subjects ability to detect feature inversion (Thompson, 1980). When faces were displayed in an upright orientation, there was a robust discrimination advantage in horizontal bands of orientation, compared to vertical orientation bands. This supports previous evidence that face recognition benefits most from horizontal face information. Here, we further show that the horizontal advantage is eliminated by face inversion, suggesting that the horizontal tuning of face perception is not simply due to face images containing more energy in horizontal than other orientation bands (as shown by Dakin and Watt, 2009; Keil, 2009) or to a general advantage of horizontal information in visual perception (see below). To our knowledge, this is the first time that the FIE has been related to a disruption in processing of a single visual component of faces. (Gaspar et al., 2008a, 2008b; Willenbockel et al., 2010).

That planar inversion selectively impairs the processing of horizontal face information firmly indicates that preferential processing of horizontal orientation is a unique aspect of face perception. Exploring this hypothesis further using objects (i.e., cars) and natural scenes as stimuli led us to several novel findings. First, although object discrimination was (like faces) better with horizontal than vertical information, this tuning was (unlike faces) observed for upright and inverted stimuli. The role of horizontal information in object recognition may relate to observers’ disproportionate reliance on horizontal structure to signal the presence of bilateral symmetry around a vertical axis (Dakin and Watt, 1994; Dakin and Hess, 1997; Rainville and Kingdom, 2000). Inversion preserves the symmetry properties of object images, and, consequently, the advantage for horizontal processing. That said, the notion that the horizontal structure generally promotes recognition by preserving the salience of bilateral symmetry cannot fully account for the horizontal-filter advantage for face stimuli as such advantage was eliminated by inversion.

Planar inversion is known to hamper the encoding of facial identity and our finding that this effect is predominantly due to the disrupted processing of horizontal facial information provides a clear indication that horizontal information may carry the most useful cues to face identity. This is in agreement with the observation that recognition of famous faces is highest when face stimuli contain narrow bands of horizontal information and declines monotonically as one moves towards vertical bands (Dakin and Watt, 2009). In Experiment 2, we used an experimental methodology based on perceptual after-effects to probe facial identity coding (Leopold et al., 2001). We report that the identity after-effects are exclusively driven by horizontal face information. Adapting to faces filtered to contain near-vertical information (and testing with orientation broadband faces) led to little or no adaptation. Our evidence thus indicates that horizontal information underlies the measurements made from a given face to encode it in the internalized face space.

On the suggestion of one reviewer, we looked at how much variation there was in the x and y coordinates of our facial key-points used to morph the faces in order to determine how much differences in structural variation at different orientations might account for differences in adaptation. We report that there is substantially more variation in the y component of facial key-points, consistent with vertical location (i.e., along the y axis) of face features being most informative (Goffaux and Rossion, 2007).

One advantage of a neural code for facial identity based on the vertical alignment of horizontal information may be that such information is more resistant to pose variation (a property that arises from the bilateral symmetry of the frontally viewed face). We corroborated this hypothesis in Experiment 3 by showing that humans most efficiently generalize identity across differing viewpoints when horizontal information is present.

The unique vulnerability of face perception to planar inversion has been attributed to the disruption of IFP. Consequently, interactive processing is assumed to be one of the perceptual aspects differentiating the processing of faces from other visual categories (Rhodes et al., 1993; Farah et al., 1998; Rossion, 2008). From our finding that FIE relates to the disrupted processing of horizontal content of face information logically follows that interactive processing relies on this band of orientation structure. Experiment 4 indeed shows that IFP is selectively driven by horizontal facial information. When the visual system is fed with vertical face information, feature interactive processing is absent. In a follow-up experiment, we show that the absence of IFP for vertically filtered faces is not a by-product of the overall lower sensitivity in this orientation band.

Although the behavioral markers studied here are known to reflect the uniqueness of face processing, it is unclear how they relate to each other. For example, despite facial identity being presumably encoded via IFP, the SF range known to drive IFP (<8 cycles per face; e.g. Goffaux, 2009) does not coincide with SF best supporting the recognition of face identity (between 7 and 16 cpf; e.g. Gold et al., 1999; Näsänen, 1999; Willenbockel et al., 2010). Even more surprising, although face inversion profoundly disrupts low-SF-driven interactive face processing, several papers report that the magnitude of the FIE is equal across SF (Boutet et al., 2003; Gaspar et al., 2008a; Goffaux, 2008; Willenbockel et al., 2010). This divergent empirical evidence has led researchers to question the role of interactive face processing in face recognition (Konar et al., 2010). In contrast, our evidence reunifies the different aspects of face perception to a common input source and constitutes a solid basis for the building of a high-level model of face recognition.

In all experiments, RMS contrast was matched across orientation bands. RMS contrast is a measure of entropy. Two signals with equal RMS contrast can thus be said to have a similar capacity to transmit information. However, the variance of gray levels at a pixel location is, in isolation, an inadequate characterization of the information that an image conveys. To really address human ability to use the information conveyed by horizontal and vertical orientation bands one must rely on psychophysical data. Our psychophysical experiments show that humans extract face identity best based on horizontal orientation band. That this advantage is lost by simply turning the face upside–down is a good indication that results from all of our experiments are not essentially “inherited” from the changes in identity strength that arises from filtering. It rather firmly suggests that observer–dependent perceptual biases also largely contribute to the horizontal advantage. However, to systematically tackle the available stimulus information in horizontal and vertical orientation bands, we will need to compare human and ideal-observer identity discrimination thresholds in the presence of external noise (e.g., Gold et al., 1999).

While our results indicate a central role for horizontal information in face perception, we are not suggesting that other orientations do not play a significant role in processing faces. Besides identity, faces convey a wealth of fundamental social cues such as an individual's intentions (via gaze direction) and emotions (via facial expression) and it is likely that these aspects of face processing exploit other orientations more extensively. Since oriented receptive fields in the primate visual cortex were discovered more than 50 years ago, they have been characterized variously as line detectors, local Fourier analyzers, phase-analyzers, and salience detectors. In truth the structure of V1 receptive fields likely satisfies a small number of key constraints with respect to information transmission and metabolic efficiency, but the solution arrived at has the potential to support all of these operations. Our research adds another application for the output of oriented receptive fields, as a source of direct evidence to facial identity. This fits into an emerging picture that higher-level visual tasks that elicit high levels of expertise – such as face recognition and reading (Watt and Dakin, 2010) – may be coded to directly exploit the structuring of visual input that emerges from early visual analysis.

As to how or why this confers an advantage, we speculate that it relates to the encoding of spatial position. Cues to facial identity from the geometric structure of faces emerge from relatively small location offsets and local properties of internal features. It is known that observers are better at making judgments of spatial position along the horizontal and vertical meridians so it makes sense to extract critical feature cues along these dimensions. As to why this should be so, we further speculate that the individual output of oriented filters provide canonical one-dimensional reference frames that are combined to enable judgments of two-dimensional position within complex scenes. If that were the case, the requirement for such combination could be minimized by transmitting as much of face information as possible through a single orientation channel.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.