Abstract
Research in the social sciences often relies upon the motivation and goodwill of research participants (e.g., teachers, students) to do their best on low stakes assessments of the effects of interventions. Research participants who are unmotivated to perform well can engage in random responding on outcome measures, which can cause substantial mis-estimation of results, biasing results toward the null hypothesis. Data from a recent educational intervention study served as an example of this problem: participants identified as random responders showed substantially lower scores than other participants on tests during the study, and failed to show growth in scores from pre- to post-test, while those not engaging in random responding showed much higher scores and significant growth over time. Furthermore, the hypothesized differences across instructional method were masked when random responders were retained in the sample but were significant when removed. We remind researchers in the social sciences to screen their data for random responding in their outcome measures in order to improve the odds of detecting effects of their interventions.
Keywords: response set, type II error, best practices, random responding
Introduction
Random responding is a potentially significant threat to the power and validity of educational and psychological research. As much of the research in social sciences relies on the goodwill of research participants (students, teachers, participants in organizational interventions) who have incentive to expend effort in providing data to researchers, unmotivated participants may undermine detection of real effects through response sets such as random responding, increasing Type II error probabilities.
Response sets (e.g., random responding) are strategies that individuals use (consciously or otherwise) when responding to educational or psychological tests or scales. These response sets range on a continuum from unbiased retrieval (where individuals use direct, unbiased recall of information in memory to answer questions) to generative strategies (where individuals create responses not based on factual recall due to inability or unwillingness to produce relevant information from memory; see Meier, 1994, p. 43). Response sets have been discussed in the measurement and research methodology literature for over 70 years now (e.g., Lorge, 1937; Goodfellow, 1940; Cronbach, 1942), and some (e.g., Cronbach, 1950) argue that response sets are ubiquitous, found in almost every population on almost every type of test or assessment. In fact, early researchers identified response sets on assessments as diverse as the Strong Interest Inventory (Strong, 1927), tests of clerical aptitude, word meanings, temperament, and spelling, and judgments of proportion in color mixtures, seashore pitch, and pleasantness of stimuli (see Summary in Table 1 of Cronbach, 1950).
While most test administrators and researchers assume respondents most frequently use unbiased retrieval strategies when responding to questionnaires or tests, there is considerable evidence for the frequent use of the less desirable (and more problematic) generative strategies (Meier, 1994, pp. 43–51).
The goal of this paper is to demonstrate why researchers should pay more attention to response sets, particularly the detrimental effects of random responding on educational research.
Commonly discussed response sets
Examples of common response sets discussed in the literature include:
Random responding is a response set where individuals respond with little pattern or thought (Cronbach, 1950). This behavior, which completely negates the usefulness of responses, adds substantial error variance to analyses. Meier (1994) and others suggest this may be motivated by lack of preparation, reactivity to observation, lack of motivation to cooperate with the testing, disinterest, or fatigue (Berry et al., 1992; Wise, 2006). Random responding is a particular concern in this paper as it has substantial potential to mask the effects of interventions. This would bias results toward null hypotheses, smaller effect sizes, and much larger confidence intervals than would be the case in the absence of random responding.
Malingering and dissimulation. Dissimulation refers to a response set where respondents falsify answers in an attempt to be seen in a more negative or more positive light than honest answers would provide. Malingering is a response set where individuals falsify and exaggerate answers to appear weaker or more medically or psychologically symptomatic than honest answers would indicate, often motivated by a goal of receiving services they would not otherwise be entitled to (e.g., attention deficit or learning disabilities evaluation; Kane, 2008; see also Rogers, 1997) or avoiding an outcome they might otherwise receive (such as a harsher prison sentence; see e.g., Rogers, 1997; Ray, 2009). These response sets are more common on psychological scales where the goal of the question is readily apparent (e.g., “Do you have suicidal thoughts?”; see also Kuncel and Borneman, 2007).
Social desirability is related to malingering and dissimulation in that it involves altering responses in systematic ways to achieve a desired goal – in this case, to conform to social norms, or to “look good” to the examiner (see, for example, Nunnally and Bernstein, 1994). Many scales in psychological research have attempted to account for this long-discussed response set (Crowne and Marlowe, 1964), yet it remains a real and troubling aspect of research in the social sciences.
Response styles such as acquiescence and criticality, are response patterns wherein individuals are more likely to agree with (acquiescence) or disagree with (criticality) questionnaire items in general, regardless of the nature of the item (e.g., Murphy and Davidshofer, 1988; Messick, 1991). Researchers have discussed the existence of response styles for many decades, arguing for and against their existence, nature, and utility. A full review is beyond the scope of this article, but interested readers can refer to Messick (1991) for a more thorough discussion of this issue.
Response styles peculiar to educational testing are also discussed in the literature. Today, discussion of response bias remains relatively esoteric and confined to measurement journals. Rarely do research reports contain any acknowledgment that participant responses may be anything but completely valid. Nevertheless, we must assume response biases exist within educational testing and assessment. Some types of biases peculiar to tests of academic mastery (often multiple choice) include: (a) response bias for particular columns (e.g., A or D) on multiple-choice type items, (b) bias for or against guessing when uncertain of the correct answer, and (c) rapid guessing (Bovaird, 2003), which is a form of random responding. As mentioned above, random responding (rapid guessing) is undesirable as it introduces substantial error into the data, which can suppress the ability for researchers to detect real differences between groups, change over time, and the effect(s) of interventions.
Summary. We rely upon quantitative research to inform and evaluate instructional innovations, often with extremely high stakes. Some educational interventions involve tremendous financial investment (e.g., instructional technology), and many are also costly in terms of time invested. Finally, interventions are not always beneficial, and therefore can be costly to students in terms of frustration or lost learning opportunities. Thus, it is important for educational researchers to gather the best available data on interventions to evaluate their efficacy. Yet research must rely upon the good faith and motivation of participants (students, teachers, administrators, parents, etc.) to put effort into assessments for which they may find neither enjoyment nor immediate benefit. This leaves us in a quandary of relying on research to make important decisions, yet often having flawed data. This highlights the importance of all data cleaning (including examining data for response bias) in order to draw the best possible inferences.
Is random responding truly random?
An important issue is whether we can be confident that what we call “random responding” truly is random, as opposed to some other factor affecting responses. In one study attempting to address this issue, Wise (2006) reported that answers identified as random responding on a four-choice multiple-choice test (by virtue of inappropriately short response times on a computer-based tests) were only correct 25.5% of the time, which is what one would expect for truly random responses in this situation. On the same test, answers not identified as random responding (i.e., having appropriately long response times) were correct 72.0% of the time1. Further, this does not appear to be rare or isolated behavior. In Wise's (2006) sample of university sophomores, 26% of students were identified as having engaged in random responding, and Berry et al. (1992) reported the incidence of randomly responding on the MMPI-2 to be 60% in college students, 32% in the general adult population, and 53% amongst applicants to a police training program. In this case, responses identified as random were more likely to be near the end of the lengthy assessment, indicating these responses were likely random due to fatigue or lack of motivation.
Detection of random responding
There is a large and well-developed literature on how to detect many different types of response sets that goes far beyond the scope of this paper to summarize. Examples include addition of particular types of items to detect social desirability, altering instructions to respondents in particular ways, creating equally desirable items worded positively and negatively, or more methodologically sophisticated researchers, using item-response theory (IRT) to explicitly estimate a guessing (random response) parameter. Meier (1994; see also Rogers, 1997) contains a succinct summary of some of the more common issues and recommendations around response set detection and avoidance. The rest of this paper will focus on one of the most damaging common response sets, random responding.
Creation of a simple random responding scale. For researchers not familiar with IRT methodology, it is still possible to be highly effective in detecting random responding on multiple-choice educational tests (and often on psychological tests using likert-type response scales as well). In general, a simple random responding scale involves creating items in such a way that 100 or 0% of the respondent population should respond in a particular way, leaving responses that deviate from that expected response suspect. There are several ways to do this, depending on the type of scale in question. For a multiple-choice educational test, one method (most appropriate when students are using a separate answer sheet, such as a machine-scored answer sheet, used in this study, described below) is to have one or more choices be an illegitimate response2.
A variation of this is to have questions scattered throughout the test that 100% of respondents should answer in a particular way if they are reading the questions (Beach, 1989). These can be content that should not be missed (e.g., 2 + 2 = __), behavioral/attitudinal questions (e.g., I weave the fabric for all my clothes), non-sense items (e.g., there are 30 days in February), or targeted multiple-choice test items [e.g., “How do you spell ‘forensics’?” (a) fornsis, (b) forensics, (c) phorensicks, (d) forensix].
Item-response theory. One application of IRT has implications for identifying random responders using IRT to create person-fit indices (Meijer, 2003). The idea behind this approach is to quantitatively group individuals by their pattern of responding, and then use these groupings to identify individuals who deviate from an expected pattern of responding. This could lead to inference of groups using particular response sets, such as random responding. Also, it is possible to estimate a “guessing parameter” and then account for it in analyses, as mentioned above.
A thorough discussion of this approach is beyond the scope of this article, and interested readers should consult references such as Hambleton et al. (1991), Wilson (2005), orEdelen and Reeve (2007). However, IRT does have some drawbacks for many researchers, in that it generally requires large (e.g., N ≥ 500) samples, significant training and resources, and finally, while it does identify individuals who do not fit with the general response pattern, it does not necessarily identify the response set, if any. Thus, although useful in many instances, we cannot use it for our example.
Rasch measurement approaches. Rasch measurement models are another class of modern measurement tools with applications to identifying response sets.
Briefly, Rasch analyses produce two fit statistics of particular interest to this application: infit and outfit, both of which measure sum of squared standardized residuals for individuals. In particular, particularly large outfit mean squares can indicate an issue that deserves exploration, including haphazard or random responding. Again, the challenge is interpreting the cause (response set or missing knowledge, for example, in an educational test) of the substantial infit/outfit values. We will use this application of Rasch as a check on our measure of random responding below. Again, a thorough discussion of this approach is beyond the scope of this article but interested readers can explore Bond and Fox (2001) and/or Smith and Smith (2004).
Summary. No matter the method, we assert that it is imperative for educational researchers to include mechanisms for identifying random responding in their research, as random responding from research participants is a threat to the validity of educational research results. Best practices in response bias detection is worthy of more research and discussion, given the implications for the quality of the field of educational research.
The goal of this study was to test the hypothesis that student random responding will mask the effects of educational interventions, decreasing researchers’ ability to detect real effects of an educational intervention.
Specifically, we hypothesized that:
-
(1)
students who engaged in random responding performed significantly worse than students not engaged in random responding,
-
(2)
when random responders are removed from analyses, the effects of educational interventions are stronger and more likely to be detected.
Materials and Methods
Data for this paper is taken from another study (Blanchard et al., 2010) that compared the effects of two instructional methods on student learning and retention3. As the details of the intervention and instructional methods are irrelevant to this paper, we will call the instructional methods “method 1” and “method 2.”
In this study, middle school students completed a unit on forensic analysis, developed specifically to test the effects of these teaching methods, taught via one of the two methods. Prior to the unit, a pre-test was administered, and following, an identical post-test was administered to assess the effects of the instructional methods. The hypothesis was that method 1 would produce stronger growth in student test scores than method 2. In all, 560 middle school students completed both tests and were thus eligible for inclusion in this study.
Identifying random responding
We used a variation of a simple random responding scale composed of legitimate test questions with fewer than four-answer choices. With a calculated 91% chance of detecting random responding (see below), and substantial differences in performance between students identified as random responders and non-random responding status (RRSs), this method is preferable to having no method of detecting random responding. The test contained 37 multiple-choice questions assessing mastery of the unit material. Most questions had four-answer options (A–D), but several toward the end (question numbers 29, 31, 32, 35, 36, 37) had either two (true/false), or three (A–C) answer options. All answers were entered on standard machine-readable answer sheets for scoring. These answer sheets had five answer options (A–E). On a traditional test the only way to determine identify random responders (or student error) would be an answer of E where no item included E as a legitimate answer. In this data set, that was a low frequency event, occurring in only 2% of student tests.
Because 6 of the 37 items did not conform to the four-answer option question format, we had the chance to examine students who were randomly responding (or showing substantial carelessness in answering). Illegitimate answers were defined as entering a C or D on #29, 31, or 32, or a D on # 35, 36, or 37. This is a variation of what Beach (1989) discussed as a random response scale, wherein test authors embed several items within a scale or test that all respondents who read and understand the question can only answer one way (e.g., How many hours are there in a day? (a) 22 (b) 23 (c) 24 (d) 25). According to Beach, the probability of detecting a random responder through this method is:
p = 1 − (1/x)n
where p is the probability of detecting a random responder, x is the number of possible answers in each question, and n is the number of questions in the random responding subscale. In this case, as there were three items with three possible answers and three items with two possible answers (i.e., three items had one illegitimate answer (d) and three items had two illegitimate answers (c, d), with an average of 1.5 illegitimate answers across all six items). With x = 1.5, and n = 6 we had a probability of accurately detecting random responders (accuracy of classification) p = 0.91.
In this sample, 40.0% of students were identified as engaging in random responding on the pre-test, 29.5% on the post-test. Overall, of the original 560 students in the sample, 279 (49.8%) entered no illegitimate answers on either pre- or post-test, while 108 (19.3%) were identified as random responders both pre- and post-test. A dummy variable indicating Random Responding Status (RRS) was created, with random responders assigned a 1 and non-random responders assigned a 0.
General analytic framework
Because all assumptions of repeated measures ANOVA (RMANOVA) were met, and because only students with complete data on both pre- and post-test, this analysis strategy was used. The repeated pre- and post-test served as the within-subject factor (test). Instructional method (method 1 vs. method 2) was entered as a between-subjects factor.
Testing hypothesis 1: random responders perform worse than legitimate responders
To test this hypothesis, a RMANOVA was performed on pre- and post-test scores as the dependent variables, and instructional method and RRS as between-subjects factors. A significant interaction between RRS and student test score (or change in test score over time) would support this hypothesis.
Testing hypothesis 2: removing random responders improves the ability to detect the effects of an educational intervention
To test this hypothesis, two further RMANOVAs were performed. The first analysis simulated what educational researchers find with no screening for RRS. This analysis combined all 560 students in a simple RMANOVA with instructional status as the between-subjects factor. The second analysis was identical except that all students suspected of engaging in random responding were removed, theoretically leaving a more pure test of the instructional method intervention. Support for this second hypothesis would be found if the results of these two analyses are substantially different.
Results
Hypothesis #1: students who engaged in random responding performed significantly worse than students not engaged in random responding
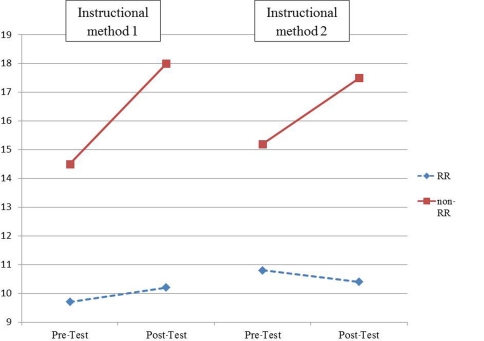
The results of the first analysis showed a striking difference between those identified as random responders and legitimate responders. Combined, all students showed a significant main effect of change in test scores over time (F(1,383) = 38.96, p < 0.0001, partial η2 = 0.09), with pre-test scores averaging 12.55 and post-test scores averaging 14.03. Random responders averaged significantly lower scores than non-random responders (F(1,383) = 177.48, p < 0.0001, partial η2 = 0.32; means = 10.27 vs. 16. 31, respectively), supporting Hypothesis #1. Finally, there was an interaction with random responding and change in test score (F(1,383) = 34.47, p < 0.0001, partial η2 = 0.08; the three-way interaction between random responding x method x time was not significant, indicating that this difference was not dependent upon instructional method). The means for this interaction are presented in Figure 1. As Figure 1 shows, random responders scored significantly lower than legitimate responders, and random responders showed no significant growth from pre- post-test, while legitimate responders showed higher mean scores and stronger growth over time. This supports Hypothesis #1, in that random responders not only scored lower, on average, than students who responded legitimately, but also that the change in test scores over time was significantly different as a function of RRS. For random responders there was no substantial change in test scores over time, as might be expected from scores with high levels of error variance. For legitimate responders, there was substantial growth in test scores over time, as might be expected of students who learned something from an instructional unit and whose test scores reflected their mastery of the topic.
Figure 1.
Differences in test score growth as a function of random responding status.
Hypothesis #2: when random responders are removed from analyses, the effects of educational interventions are stronger and more likely to be detected
With all random responders in the analysis, there was significant main effect of growth from pre-test (mean = 12.91) to post-test (mean = 15.07; F(1,558) = 127.27, p < 0.0001, partial η2 = 0.19). A statistically significant but weak main effect of instructional method indicated that students taught through method #2 generally outscored those taught through method #1 (mean = 14.53 and 13.45, respectively; F(1,558) = 7.65, p < 0.006, partial η2 = 0.01). There was no interaction between time and instructional method (F(1,558) < 0.10) indicating no difference in student growth over time as a function of instructional method. If we, as researchers, had ended our analyses here, we would have concluded no significant or substantial benefit of one instructional method over another.
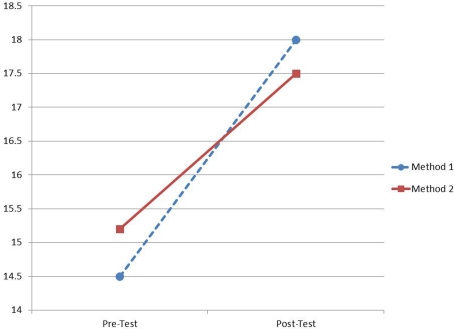
However, when random responders were removed, results indicated a significant and substantial change over time in student test scores (mean scores grew from 14.78 to 17.75; F(1,277) = 101.43, p < 0.0001, partial η2 = 0.27; note that this is a 42% increase in effect size over the previous analysis and also note that on average, these students scored higher than with the random responders in the sample). There was no significant main effect of instructional method (F(1,277) < 0.10). Finally, in contrast to the last analysis, there was a significant interaction between time and instructional method (F(1,277) = 4.38, p < 0.04, partial η2 = 0.02). As Figure 2 shows, consistent with predictions from the original study, students taught through method #1 showed significantly stronger growth than students taught through method #2.
Figure 2.
Differences in test score growth as a function of instructional method once random responders were removed from the analysis.
Validation of random responder identification via rasch measurement
Admittedly, our use of a random responding scale does not employ the powerful, modern measurement technologies available (e.g., IRT, Rasch). Our goal was to highlight a methodology that all applied social sciences researchers could employ. However, the question remains as to whether use of Rasch or IRT methodology would have afforded a similar outcome. To test this, we subjected the same data to Rasch analysis, using outfit mean square scores as an indicator of random responding (although it can also indicate other unexpected response patterns that are not random responding, and there is a question as to whether true random responding throughout the test would yield a high outfit score). The main questions are: (a) is whether those students we identified as random responders would also be identified as a student having an unexpected response pattern and (b) whether those with unexpected response patterns tend to score significantly lower than those without these patterns.
To answer the first question, we performed a binary logistic regression analysis, predicting RRS (0 = not random responding, 1 = identified as having a random response) from outfit mean square (where scores significantly above 1.0 can indicate unexpected response patterns). As expected, the odds that those with higher outfit mean squares would also be identified as a random responder were significantly and substantially higher (odds ratio = 241.73, p < 0.0001). This means that the odds of being labeled a random responder increased just over 241 times for each increase of 1.0 for outfit mean square4.
To test the second question, we examined the correlation between outfit mean square and overall test score. As expected, those with higher outfit mean squares had significantly lower test scores (r(560) = −0.53, coefficient of determination = 28.09%) than those with more expected patterns of responding.
Summary. These Rasch analyses provide convergent evidence that those students we initially identified as engaging in random responding were also identified as having unexpected response patterns by Rasch analyses. Further, these findings confirm that those students who were identified as engaging in random responding tend to score much lower on the study's knowledge test than those not engaging in random responding.
Discussion
In social sciences research, change in respondent test scores is an important method of comparing the efficacy of interventions or methods. Even under ideal conditions, students or respondents may not be motivated to demonstrate optimal performance on these tests. Students whose performance does not reflect ability or mastery of learning objectives add error to the data and reduce the validity of the test's scores (Cronbach, 1950), diminishing a researcher's ability to detect or compare effects of instructional interventions or methods.
Although there is a long tradition of research on response sets in educational and psychological research, few studies in modern times seem to attend to this issue, putting their findings at risk. In fact, classic measurement texts (e.g., Nunnally and Bernstein, 1994) rarely give the topic more than cursory attention, generally presenting random responding as nuisance or random error variance, not worth addressing actively5. However, substantial random error substantially reduces the power to detect group differences or change over time, and thus, we argue that examining data for evidence of random responding should be an integral part of initial data cleaning [readers interested in a more in-depth treatment can refer to Osborne's (2011) book on data cleaning]. The goal of this study was to demonstrate how random responding can degrade researchers’ ability to detect differences, increasing the probability of missing a real effect of an intervention.
We hypothesized that students who engaged in random responding would score significantly worse than legitimate responders, and that when random responders were removed from the data set, group differences would be easier to detect. Further, we hypothesized that a parallel analysis using modern measurement methodology (Rasch) would show convergent findings. Analyses of data from a recent instructional method intervention study showed strong support for all hypotheses. Specifically, our analyses showed that random responders had lower scores overall and substantially lower growth over time from pre-test to post-test than legitimate responders. Our results also showed that when all students were in the data the anticipated differences in instructional method was not observed (which could be considered an unfortunate Type II error). However, when random responders were removed from the data, the anticipated differences in instructional method were statistically significant. Rasch analyses of the same data showed convergent results: as fit indices increased, indicating increasingly unexpected response patterns, the odds were over 241 times higher that the individuals were identified as a random responder than not. Further, those with increasingly unexpected response patterns also tended to score much worse on the knowledge test than those with more expected response patterns.
Magnitude of the Problem
In this sample, a substantial number (up to 40.0%) of middle school students engaged in random responding (and estimates in other populations are similar in magnitude; e.g., Berry et al., 1992). While this might surprise researchers at first glance, given the low stakes of the test and no apparent motivation to succeed, it is not surprising. As can be seen from the average test scores, the test used in this research was designed to be challenging, which has been shown to increase response biases such as random responding (Cronbach, 1950; Wise and Kong, 2005; Wise, 2006)6. This reinforces the importance of including screening for response set as a routine part of data cleaning.
Although there are many studies on response sets, relatively few focus on this particularly problematic one. More exploration of this important issue would be desirable. More importantly, researchers need to be aware that not all students (or respondents in general) participating in their research are equally motivated to perform at their peak given the lack of significant incentives for compliance and consequences for failure to perform as requested. Researchers should incorporate methods to detect random responding and take this into account when performing analyses to test important hypotheses. This recommendation is particularly important where important policy or pedagogical decisions are involved, such as large scale standardized national and international tests (NAEP, TIMSS), which have substantial effects on policy and outcomes for constituencies, but for which individual students may not be significantly motivated.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Footnotes
1Wise utilized computer-based testing, allowing him to look at individual items rather than students’ total test score.
2One option, used in this particular data set included having twenty questions with four choices: A–D, with other questions scattered throughout the test, and particularly near the end, with items that contain only three (A–C) or two (A, B) legitimate answers. Students or respondents choosing illegitimate answers one or more times can be assumed to be randomly responding, as our results show.
3Note that this paper should in no way be construed as a test of these hypotheses, nor should the results be interpreted substantively to infer which teaching method is superior. Those interested in the substantive results of the study should consult Blanchard et al. (2010).
4We also examined results for the standardized outfit statistic, which is essentially a z-score of the outfit mean squares. Similar results were obtained.
5The exception to this exists in some literature around assessment of mental health and personality disorders, wherein random responding, poor effort, malingering, and exaggeration (all different types of response bias) detection can signal certain types of mental disorders or present significant ethical and health issues (e.g., Clark et al., 2003; Iverson, 2006).
6This is due to the fact that response bias on multiple-choice tests is, by definition, found in errors, not correct answers. Thus, easier tests and higher-scoring students are less likely to demonstrate response bias.
References
- Beach D. A. (1989). Identifying the random responder. J. Psychol. 123, 101 [Google Scholar]
- Berry D. T. R., Wetter M. W., Baer R. A., Larsen L., Clark C., Monroe K. (1992). MMPI-2 random responding indices: validation using self-report methodology. Psychol. Assess. 4, 340–345 10.1037/1040-3590.4.3.340 [DOI] [Google Scholar]
- Blanchard M. R., Southerland S. A., Osborne J. W., Sampson V., Annetta L. A., Granger E. M. (2010). Investigating the relative effectiveness of guided inquiry and traditional, didactic laboratory instruction: is inquiry possible in light of accountability? Sci. Educ. 94, 577–616 10.1002/sce.20390 [DOI] [Google Scholar]
- Bond T. G., Fox C. M. (2001). Applying the Rasch Model: Fundamental Measurement in the Human Sciences. Mahwah, NJ: Erlbaum [Google Scholar]
- Bovaird J. A. (2003). New Applications in Testing: Using Response time to Increase the Construct Validity of a Latent Trait Estimate. Ann Arbor, MI: ProQuest Information & Learning [Google Scholar]
- Clark M. E., Gironda R. J., Young R. W. (2003). Detection of back random responding: effectiveness of MMPI-2 and personality assessment inventory validity indices. Psychol. Assess. 15, 223. [DOI] [PubMed] [Google Scholar]
- Cronbach L. J. (1942). Studies of acquiescence as a factor in the true-false test. J. Educ. Psychol. 33, 401–415 [Google Scholar]
- Cronbach L. J. (1950). Further evidence on response sets and test design. Educ. Psychol. Meas. 10, 3–31 [Google Scholar]
- Crowne D., Marlowe D. (1964). The Approval Motive. New York: Wiley [Google Scholar]
- Edelen M. O., Reeve B. B. (2007). Applying item response theory (IRT) modeling to questionnaire development, evaluation, and refinement. Qual. Life Res. 16, 5–18 10.1007/s11136-007-9198-0 [DOI] [PubMed] [Google Scholar]
- Goodfellow L. D. (1940). The human element in probability. J. Gen. Psychol. 33, 201–205 [Google Scholar]
- Hambleton R. K., Swaminathan H., Rogers H. J. (1991). Fundamentals of Item Response Theory. Thousand Oaks, CA: Sage Publications, Inc [Google Scholar]
- Iverson G. L. (2006). Ethical issues associated with the assessment of exaggeration, poor effort, and malingering. Appl. Neuropsychol. 13, 77–90 [DOI] [PubMed] [Google Scholar]
- Kane S. T. (2008). Minimizing malingering and poor effort in the LD/ADHD evaluation process. ADHD Rep. 16, 5–9 10.1521/adhd.2008.16.5.5 [DOI] [Google Scholar]
- Kuncel N. R., Borneman M. J. (2007). Toward a new method of detecting deliberately faked personality tests: the use of idiosyncratic item responses.Int. J. Sel. Assess. 15, 220–231 [Google Scholar]
- Lorge I. (1937). Gen-like: halo or reality? Psychol. Bull. 34, 545–546 [Google Scholar]
- Meier S. T. (1994). The Chronic Crisis in Psychological Measurement and Assessment: A Historical Survey. San Diego, CA: Academic Press [Google Scholar]
- Meijer R. R. (2003). Diagnosing item score patterns on a test using item response theory-based person-fit statistics. Psychol. Methods 8, 72–87 [DOI] [PubMed] [Google Scholar]
- Messick S. (1991). “Psychology and methodology of response styles,” in Improving Inquiry in Social Science, eds Snow R. E., Wiley D. E. (Hillsdale, NJ: Erlbaum; ), 161–200 [Google Scholar]
- Murphy K. R., Davidshofer C. O. (1988). Psychological Testing. Englewood Cliffs, NJ: Prentice Hall [Google Scholar]
- Nunnally J. C., Bernstein I. (1994). Psychometric Theory, 3rd edn. New York: McGraw Hill [Google Scholar]
- Osborne J. W. (2011). Best Practices in Data Cleaning: Debunking Decades of Quantitative Mythology. Thousand Oaks, CA: Sage [Google Scholar]
- Ray C. L. (2009). The importance of using malingering screeners in forensic practice. J. Forensic Psychol. Pract. 9, 138–146 [Google Scholar]
- Rogers R. (1997). “Introduction,” in Clinical Assessment of Malingering and Deception, ed. Rogers R. (New York: Guilford; ), 1–22 [Google Scholar]
- Smith E. V., Smith R. M. (2004). Introduction to Rasch Measurement. Maple Grove, MN: JAM press [Google Scholar]
- Strong E. K. J. (1927). A vocational interest test. Educ. Rec. 8, 107–121 [Google Scholar]
- Wilson M. (2005). Constructing Measures: An Item Response Modeling Approach. Mahwah, NJ: Lawrence Erlbaum Associates Publishers [Google Scholar]
- Wise S. L. (2006). An investigation of the differential effort received by items on a Low-Stakes Computer-Based Test. Appl. Meas. Educ. 19, 95–114 [Google Scholar]
- Wise S. L., Kong X. (2005). Response time effort: a new measure of examinee motivation in computer-based tests. Appl. Meas. Educ. 18, 163–183 [Google Scholar]