Explicit Information Reduces Discounting Behavior in Monkeys

Abstract

Animals are notoriously impulsive in common laboratory experiments, preferring smaller, sooner rewards to larger, delayed rewards even when this reduces average reward rates. By contrast, the same animals often engage in natural behaviors that require extreme patience, such as food caching, stalking prey, and traveling long distances to high-quality food sites. One possible explanation for this discrepancy is that standard laboratory delay discounting tasks artificially inflate impulsivity by subverting animals’ common learning strategies. To test this idea, we examined choices made by rhesus macaques in two variants of a standard delay discounting task. In the conventional variant, post-reward delays were uncued and adjusted to render total trial length constant; in the second, all delays were cued explicitly. We found that measured discounting was significantly reduced in the cued task, with discount parameters well below those reported in studies using the standard uncued design. When monkeys had complete information, their decisions were more consistent with a strategy of reward rate maximization. These results indicate that monkeys, and perhaps other animals, are more patient than is normally assumed, and that laboratory measures of delay discounting may overstate impulsivity.

Introduction

The tradeoff between immediate and delayed gratification is a fundamental dilemma confronting both humans and animals, with important consequences for biological fitness, establishment of wealth, and psychiatric disease (Rachlin, 2000; Frederick et al., 2002). Almost 40 years of research has established that animals, when presented with a choice between smaller rewards delivered sooner (SS) and longer rewards delivered later (LL), typically prefer the smaller, sooner reward in a manner inconsistent with long-term reward rate maximization (Ainslie, 1974; Mazur, 1984, 1987; Rachlin, 2000; Shapiro et al., 2008). Such preferences are therefore costly, potentially undervaluing future incomes and leading to suboptimal foraging. This bias is observed in humans as well, and is often attributed to failures of self-control (Rachlin and Green, 1972; Ainslie, 1974).

In humans and other animals, inter-temporal preferences are generally explained by positing that the present subjective values of future rewards are discounted by the delay to receipt of reward (Mazur, 1984; Grossbard and Mazur, 1986; Shapiro et al., 2008). This pattern of discounting is generally assumed to reflect a hyperbolically diminishing utility for future rewards, although the relationship may be exponential or quasi-hyperbolic (Loewenstein and Prelec, 1992; McClure et al., 2004). According to such models, the shape and steepness of the discount curve may reflect risk-aversion (Henly et al., 2008) or uncertainty about delays (Brunner et al., 1994, 1997; Bateson and Kacelnik, 1995), and can be estimated from the pattern of revealed preferences in inter-temporal choice tasks.

However, these economically inspired models stand in stark contrast to those derived from analyses of animal foraging behavior. Foraging theorists have long argued that evolutionary processes should drive animals to act in ways that maximize long-term (undiscounted) reward rates (Stephens and Krebs, 1986), defined as the sum of total rewards divided by total foraging time. Nevertheless, rational models of foraging have been hard-pressed to explain the high discount rates observed in laboratory experiments, in which choice behavior by rats and pigeons would imply that delayed rewards may lose half their value in a matter of seconds. Though it has been argued that animals should prefer immediate rewards when energy budgets are negative or collection risk is high (Caraco et al., 1980; Mcnamara and Houston, 1992; Kacelnik and Bateson, 1996; Hayden and Platt, 2007), observed discounting rates remain difficult to explain by appeal to naturally occurring risk (Stevens and Stephens, 2010). Likewise, discount rates measured in the laboratory would appear to preclude activities like food caching and prey selection, which require valuing future rewards above immediate rewards. In fact, more recent work has questioned whether the reward rate currency calculated by animals is, in fact, long-term reward or some approximation (Bateson and Kacelnik, 1995, 1996), as well as whether decision rules that appear impulsive in the laboratory might come close to maximizing reward in the wild (Stephens and Anderson, 2001; Stephens and McLinn, 2003; Stephens et al., 2004).

These discrepancies between discount rates measured in the laboratory and the patience often observed in natural foraging behavior raises fundamental questions about the ecological validity of these common laboratory tasks (Stephens and Anderson, 2001). In typical inter-temporal choice tasks, animals are presented with a series of choices between rewards differing in both quantity and delay. In some studies, either the delay to or the amount of the larger reward is titrated until both options are equally preferred (Brunner and Gibbon, 1995; Richards et al., 1997; Cardinal et al., 2001; Green and Myerson, 2004; Green et al., 2004, 2007; Kalenscher and Pennartz, 2008). In others, a whole series of choices involving many pairs of rewards and delays is presented, and discount curves are constructed from preferences (Kim et al., 2008; Shapiro et al., 2008; Hwang et al., 2009; Louie and Glimcher, 2010). However, this latter design admits a potential loophole: if, for instance, choosing shorter delays allows an animal to collect more rewards in the allotted experimental time, preference for the smaller, sooner (SS) option may be ascribed not to irrational impulsivity or discounting, but to rational maximization of reward rates (Stephens and Krebs, 1986). To compensate, experimenters typically introduce either inter-trial intervals much longer than delays to reward or an adjusting post-reward delay that renders total trial length constant. In the former case, observed discounting behavior contradicts field experiments on prey selection, where larger rewards are strongly preferred when handling times are small in comparison with encounter rates (Stephens and Krebs, 1986). In the latter case, an animal attempting to maximize long-term gain must learn an unnatural temporal contingency – one in which long post-reward delays follow short pre-reward delays, and vice versa. Such a rule might prove tremendously difficult to learn. In fact, empirical data show that rats and pigeons are often insensitive to manipulations of post-reward delay (Logue et al., 1985; Goldshmidt et al., 1998).

In this paper, we tested the hypothesis that insensitivity to post-reward delays might account for much of the discounting behavior observed in laboratory studies using standard inter-temporal choice tasks. If the learning rules animals use to map cues to outcomes fail to make use of implicit information about post-reward delays, choice behavior may fail to maximize long-term reward rate, and discounting rates inferred from this behavior will be high. If so, then providing explicit cues to post-reward delays in a standard inter-temporal choice task should substantially reduce discounting for identical pairs of rewards and delays. We tested these predictions by comparing discount parameters of two monkeys performing identical inter-temporal choice tasks when post-reward delays were either uncued or explicitly cued. Consistent with our predictions, we found that cuing post-reward delays dramatically reduces observed temporal discounting.

Materials and Methods

Subject animals

Two adult male rhesus monkeys (Macaca mulatta) served as subjects. All procedures were approved by the Duke University Medical Center Institutional Animal Care and Use Committee and complied with Public Health Services Guide for the Care and Use of Animals. To prepare animals for electrophysiological recording in separate experiments, a small prosthesis and a stainless steel recording chamber were attached to the calvarium. Animals were habituated to training conditions and trained to perform oculomotor tasks for liquid reward. Animals received analgesics and antibiotics after all surgeries. The chamber was kept sterile with antibiotic washes and sealed with sterile caps.

Behavioral techniques

Eye position was sampled at 1000 Hz (Eyelink, SR Research). Experiments were controlled and data were recorded by a computer running Matlab (The Mathworks) with Psychtoolbox (Brainard, 1997) and Eyelink (Cornelissen et al., 2002). Visual stimuli were squares or rectangles (8° wide) on a computer monitor 50 cm in front of the monkeys’ eyes.

Monkeys’ performed three variants of a visually cued inter-temporal choice task (Figure 1). On each trial, they fixated a central cue, following which two choice targets appeared onscreen. A solenoid valve controlled juice delivery. Juice volumes were linear in solenoid open time, and we have previously shown that monkeys discriminate juice volumes as small as 20 μL (McCoy et al., 2003). Juice flavor was the same for all rewards. To motivate performance, access to fluid was controlled outside of experimental sessions; monkeys earned roughly 80% of total daily ration by performance.

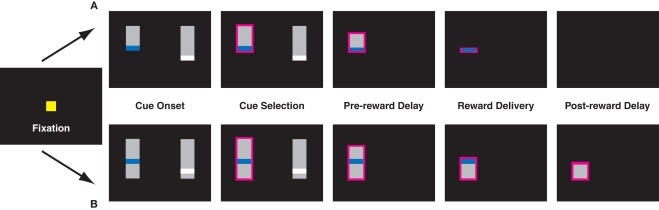
Figure 1.

Task design for the uncued (A) and cued (B) variants of the inter-temporal choice task. In the cued version of the task, pairs of targets appeared after a brief fixation period. In a third variant, monkeys had to maintain fixation to shrink the bar. Lengths of vertical bars represented delays to reward, colored stripes differing juice volumes. Monkeys were required to briefly hold fixation on the target of their choice (0.5 s), after which the unselected cue vanished and the bar corresponding to the chosen option shrank at a fixed rate. Reward was delivered when the top of the bar reached the colored stripe. In the uncued paradigm, the screen remained blank through the post-reward delay. In the cued paradigm, the remaining bar corresponded to the post-reward delay and continued to shrink through the end of the trial.

Basic task design

In all versions of the task, each choice option (target) consisted of a gray bar overlaid with a thin colored stripe, corresponding to an amount of liquid reward (Figure 1). Colors were chosen from five values, corresponding to 120 ms (red), 160 ms (yellow), 200 ms (green), 240 ms (blue), and 320 ms (white) of solenoid open time (150–400 μL). On each trial, two contiguous juice rewards were randomly selected. Likewise, in all versions, pre-reward delays varied from 0.5 to 6 s in 0.5 s intervals. In some sessions, the SS delay was restricted to be <2 s, while the LL delay was >3 s. Post-reward delays were chosen such that the sum of pre- and post-reward delays totaled either 5.25 or 6.5 s. Both this restriction, along with the stipulation of adjacent reward values, served to maximize the number of difficult decisions animals faced, thereby increasing precision in estimating the choice function.

The length of the bar from its top to the stripe indicated the delay to reward, and the length of the bar beneath the stripe indicated post-reward delay. To prevent the animals from using the absolute vertical position of the stripe as a cue, the gray bars themselves were randomly positioned along the vertical axis. After the cues appeared, the monkeys were free to look between targets, and made selections by briefly holding fixation on the target of their choice (0.5–0.75 s). After the decision was made, the unselected option immediately disappeared, and the gray bar indicating delay to reward began to shrink at a constant rate (40 pixels/s), from the top toward the bottom of the screen. When the top of the gray bar reached the colored stripe, the monkey received a liquid reward. In the cued variant (see below), the bar continued to shrink; in the standard variant, the screen went blank. After the cue disappeared, the animal waited through the post-reward delay for the next trial to begin.

Task variants

Monkeys performed three variants of the choice task. In the standard variant, delay to reward was indicated, but the post-reward delay remained uncued. The second version was identical to the first, except the post-reward delay was also cued, and the gray bar continued to shrink after reward delivery and through the post-reward delay. To test the hypothesis that effort costs might render the post-reward delay more salient, further reducing discounting, we implemented a third version of the task, in which pre- and post-reward delays were once again cued, but monkeys were required to hold fixation on the shrinking target for the duration of both the pre- and post-reward delays. Whenever the monkeys broke fixation, the bar ceased to shrink. However, trials did not end until monkeys accumulated a total fixation time equal to the indicated delay. (This did not appreciably alter the delay contingency: monkeys were able to hold unbroken fixation for total wait times of more than 6 s, and fewer than 10% of fixation holds took longer than 10% of their nominal wait time to complete.) If the effort required to hold fixation during the delay interval altered monkeys’ perception of delay intervals or reward rates, this should have resulted in altered choice behavior.

Pre-training and session structure

We began by training each animal exclusively on the uncued condition, introducing cued variants only after learning had clearly stabilized, with observed discount parameters consistent within subjects from day to day and with other published studies (see Results). Following the introduction of cued variants, monkeys performed multiple sessions (n = 5, Monkey E; n = 7, Monkey O) in which cued and uncued variants of the task were interleaved in blocks of approximately 200 trials. Following this, we collected data exclusively under the cued variants (n = 5, Monkey E; n = 9, Monkey O), followed by brief challenge sessions (n = 2, Monkey E; n = 6, Monkey O) under the uncued variant.

Controls

We began each session (n = 54) with 50 trials each of three different control tasks. In the first, pre- and post-reward delays were equated, and monkeys were required to discriminate reward color cues. In the second and third, reward cues were equated, and monkeys were required to discriminate either the pre- or post-reward delay (with the other interval held constant). Performance was better than 90% in all three control tasks. Monkeys were easily able to visually discriminate even small differences in bar length, equivalent to 0.5 s (20 pixel) differences in >10 s total wait times. This is substantially better than natural interval timing behavior, demonstrating that monkeys must have made use of the bar stimuli to inform their choices (Gibbon et al., 1984, 1988; Janssen and Shadlen, 2005).

Data analysis

We calculated reward rates as ratios of expectations

$$\text{ρ}=\frac{{{\displaystyle \mathbf{\sum }r}}_i}{{{\displaystyle \mathbf{\sum }T}}_i},$$ (1)

with T the total trial time. We fit choice preferences by assuming a standard hyperbolic discounting curve (Mazur, 1984),

$$r\prime =\frac{r}{1+kD},$$ (2)

where r′ is the present discounted value of the future reward r, D is the delay to reward, and k, which has units of time⁻¹, is the discount parameter (we exclusively use seconds as our unit of time). We further assumed that the probability of choosing the option with larger r′ was given by a logistic function of the difference in the two discounted values (Kim et al., 2008; Hwang et al., 2009; Louie and Glimcher, 2010). Behavioral parameters were fit by custom scripts written using the Matlab Optimization Toolbox (The Mathworks). Hypothesis tests for differences of discount parameters and confidence intervals were calculated by bootstrap resampling (N = 1000) of the dataset with replacement. Parameters were considered significantly different if both lay outside the 95% bootstrap confidence interval for the other. In addition, we compared and fit a number of alternative discounting hypotheses, including exponential and pure reward rate models, using an Akaike Information Criterion approach (see below).

Models and model fitting

We fit animals’ choices across all days for each task variant using a maximum log likelihood procedure. Numerical fits were performed via custom scripts utilizing the Matlab Optimization Toolbox. For each of our 13 models, we paired a value function (used to assign a number to each option) with a choice function that determined the probability of choosing each option based on these values. Models are detailed in Table 2 below. Choice functions were either Bernoulli (a fixed probability, p, of choosing the best option) or logistic, with probability of choosing the higher-valued (not necessarily larger reward) option given by

Table 2.

Model specifications for the 13 models used.

Number	Discounting	Value (v)	Decision variable	Choice function	Parameters	Half-life (γ)
1	–	r	max{r, r′}	Bernoulli	1	–
2	–	r	r − r′	Logistic	3	–
3	Hyperbolic	r/(1 + kD)	v − v′	Logistic	4	1/k
4	Hyperbolic	r/(1 + k(D + κτ))	v − v′	Logistic	5	(1 + k*κT)/(k(1 − κ))
5	Hyperbolic	r/(1 + k(D + κτ−1))	v − v′	Logistic	5	(1 + k*κT)/(k(1 − κ))*
6	Exponential	re−kD	v − v′	Logistic	4	log 2/k
7	Exponential	re−k(D + κτ)	v − v′	Logistic	5	log 2/(k(1 − κ))
8	Marginal gain	–	r − r′/(D − D)	Logistic	3	–
9	–	r	r/r′	Logistic	3	–
10	Reward rate	r/D†	v/v′	Logistic	3	2
11	Hyperbolic	r/(1 + kD)	v/v′	Logistic	4	1/k
12	Hyperbolic	r/(1 + k(D + κτ))	v/v′	Logistic	5	(1 + k*κT)/(k(1 − κ))
13	Hyperbolic	r/(D + κτ)†	v/v′	Logistic	4	κT/(1 − κ)

*Strictly speaking, this formula is only valid on average, since we have D + τ = T every trial, but D + τ ₋₁ = T only on average.

^†Because of differences in the way in which the separate decision variables (v − v′ vs v/v′) enter the logistic choice function, Models 3 and 4 also include within themselves equivalents of these two models, in which there is no constant in the denominator. In addition, Model 12 is clearly equivalent to Model 13 in the limit of large k.

Variables used: r, reward; D, delay to reward; τ, post-reward delay; τ₋₁, post-reward delay (previous trial); T, total trial length (T = D + τ). k and κ are fit to the data.

$$p(hv)=\frac{\text{α}}{1+e^{\frac{-(\text{δ}-\text{μ})}{\text{σ}}}}$$ (3)

with α, μ, and σ fit to the data and δ the relevant decision variable listed in Table 2.

We compared models using Akaike's Information Criterion (AIC), an information-theoretic goodness-of-fit measure that compensates for varying numbers of parameters. This quantity, defined as

$$AIC\equiv -2LL+2k,$$ (4)

where LL is the log likelihood of data given the best-fit (maximum likelihood) parameters and k is the number of parameters fit. Lower AIC values represent better fits to the data. For comparisons among models, we made use of the so-called “Akaike weight,” defined by

$$w_i=e^{-\frac{1}{2}{\text{Δ}}_i},$$ (5)

with Δ_i ≡ AIC_i − AIC_min the relative AIC measure. Note that, by definition,${\sum }_i{w}_i=1$, and the w's offer only a relative goodness-of-fit within the class of models considered.

Finally, for models in which the value of a given option decreased in time, we defined a cross-model measure of discounting as follows: using the fact that our total trial length, T, was a constant (T = D + τ), we defined the half-life, γ, as that value of D at which the discounted value of a given option was decreased to half its value at D = 0. Because this parameter could be defined across 9 of our 13 models, it could be calculated independently of which model gave the best fit to behavioral data. Moreover, it allowed us to appropriately average a measure of choice behavior across all models (see below).

Results

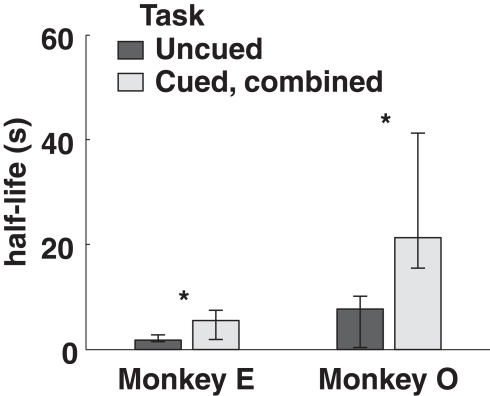
Both monkeys proved highly adept at the task. In the uncued condition, monkeys earned 89 and 92% of available reward, increasing to 96 and 93% in the fully cued condition. Since total trial times were held constant, any choice of the SS option necessarily resulted in a reduced reward rate. However, monkeys chose the LL option more frequently when post-reward delays were cued, even though delays were, on average, longer in the cued conditions (Table 1). Percentages of LL choices were uncorrelated with variations in total wait times across conditions (R = 0.18, p = 0.74, Pearson correlation; F_1,3 = 0.12, p = 0.76 main effect of total wait time, two-way ANOVA with subject and wait time as factors), suggesting that the observed effects were indeed related to the cuing paradigm and not the menus of options presented. Moreover, analysis of a subset of trials with fixed total trial time yielded the same result (Figure 3).

Table 1.

Percentage of LL choices, average trial lengths, and earned and maximum reward rates as a function of task condition.

Task	Subject	% LL choices	ERR (μL/s)	MRR (μL/s)	Avg trial length (s)	% Rwd earned
Uncued	E	0.520 ± 0.009	36.6 ± 0.1	41.3 ± 0.9	6.05 ± 0.01	0.887 ± 0.006
	O	0.500 ± 0.007	36.9 ± 0.8	41.3 ± 0.8	6.17 ± 0.01	0.894 ± 0.004
Cued	E	0.661 ± 0.009	43.0 ± 1.0	46.5 ± 0.9	5.22 ± 0.02	0.925 ± 0.005
	O	0.714 ± 0.011	40.5 ± 1.4	43.3 ± 1.2	5.85 ± 0.04	0.935 ± 0.006
Cued,	E	0.810 ± 0.006	37.9 ± 1.0	39.5 ± 0.9	6.50 ± 0.00	0.960 ± 0.003
Fixated	O	0.704 ± 0.011	39.6 ± 1.6	42.4 ± 1.4	6.20 ± 0.01	0.934 ± 0.006

Error measures are ±SEM. ERR, earned reward rate; MRR, maximum reward rate.

Figure 3.

Model-averaged half-lives for both monkeys, calculated using only trials with total length 6. 5 s. Cued, combined refers to data pooled across the two cued conditions for each subject. Error bars represent 95% confidence intervals for the means, calculated by bootstrap resampling.

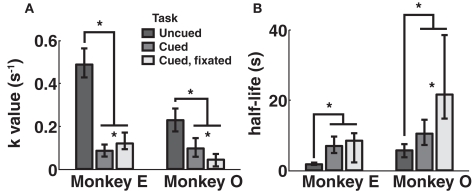
Discounting parameters for the three paradigms are shown in Figure 2. Behavior, pooled across all days, was fit to standard hyperbolic discounting models using a maximum likelihood procedure (see Materials and Methods). In the uncued task, the two monkeys’ discount parameters were k = 0.48 and 0.22 s^–1, respectively, equivalent to a reward half-life on the order of 2–5 s (Table 4). These values are comparable to those measured for rhesus monkeys in similar choice paradigms (Kim et al., 2008; Hwang et al., 2009; Louie and Glimcher, 2010), in which preferences were allowed to stabilize over many thousands of trials. Thus differences with the cued condition are unlikely to be the result of continued learning. Nevertheless, we observed significantly lower discount parameters when post-reward delays were cued (k = 0.11 and 0.04 s^–1, cued and cued fixated, respectively; p < 0.05, bootstrap randomization test; see Materials and Methods). Estimates of discounting parameter were also significantly different between the two cued variants (p < 0.05, bootstrap randomization test), though with different results in each subject. In both cases, however, cued-variant discount parameters, corresponding to reward half-lives of around 10–20 s, represent up to a full order of magnitude decrease in discounting.

Figure 2.

Discounting rates decrease with explicit information about post-reward delay. Discount parameters were estimated by a maximum likelihood analysis of a hyperbolic model (see Materials and Methods). Error bars represent 95% confidence intervals obtained by bootstrap analysis. (A) Estimated discount parameter values were significantly lower for both of the two paradigms in which post-reward delays were cued, though not significantly different from one another. (B) Model-averaged effective half-lives were significantly increased in both explicit cuing paradigms.

Table 4.

Half-lives and confidence intervals across task conditions.

Task	Monkey E		Monkey O
	Half-life (γ)	95% Confidence	Half-life (γ)	95% Confidence
Uncued	1.71	[1.53, 2.07]	5.68	[3.71, 7.46]
Cued	6.93	[4.92, 9.61]	10.44	[7.21, 14.41]
Cued, Fixated	8.45	[2.24, 10.56]	21.61	[14.75, 38.57]

Half-lives are averaged across models, weighted by Akaike weights. Confidence intervals are determined by bootstrap resampling of the data for each task condition.

In addition, to account for the possibility that hyperbolic discounting may not best capture choice behavior, we fit choices to a total of 13 separate models, a mixture of undiscounted, exponential, and hyperbolic models making use of distinct choice rules and including post-reward intervals (Table 2). For both monkeys across all conditions, we found that hyperbolic-form models produced better fits in all cases, most often by taking into account the (underweighted) post-reward delay (Table 3). Furthermore, to account for variability in model fits between monkeys and across conditions, we calculated an effective discounting half-life for 9 of the 13 models, defined as the time over which the estimated subjective value of an option was reduced by half. This allowed us to calculate a fit-weighted average of half-life across models, a model-independent measure of discounting (Table 4). As seen in Figure 2B, these calculated half-lives were again significantly different between cued and uncued conditions for both monkeys (p < 0.05, bootstrap randomization test), confirming that the observed effect was not an artifact of the particular model chosen.

Table 3.

Akaike weights for each of the 13 fitted models and task conditions.

Task	Subject	Model weight (w)
		1	2	3	4	5	6	7	8	9	10	11	12	13
Uncued	E	0	0	0.0156	0.0056	0.0049	0	0	0	0	0	0.0677	0.9058	0.0003
	O	0	0	0.5725	0.2106	0.2113	0	0	0	0	0	0.0023	0.0009	0.0023
Cued	E	0	0	0	0	0	0	0	0	0	0	0	0.2510	0.7490
	O	0	0	0.0010	0.0004	0	0	0	0	0	0	0.6117	0.2897	0.0968
Cued,	E	0	0	0.0306	0.0112	0.0111	0.0002	0	0	0	0	0.7019	0.2449	0
Fixated	O	0	0	0	0	0	0	0	0	0	0	0.0323	0.2535	0.7142

Values less than 10⁻⁴ are recorded as 0.

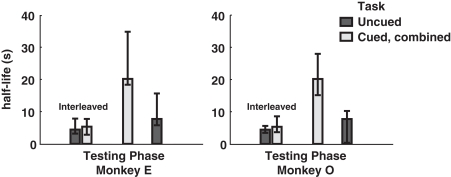
Finally, to investigate the potential effect of cue-type ordering on monkeys’ patterns of choice behavior, we calculated separate half-lives for the interleaved, cued-only, and uncued-only phases of testing. Interestingly, interleaved cuing sessions failed to produce distinct discounting behavior in either monkey, though the switch to exclusively cued sessions resulted in a dramatic drop in discounting, an effect reversed by the return to uncued-only testing (Figure 4). This implies that the observed drop in discounting cannot merely be a function of either total task experience or the presence of added information on a single trial, but rather that the larger mixture of options available during a given testing session, along with learning effects across sessions, plays a crucial role.

Figure 4.

Model-averaged half-lives for both monkeys over the course of training. In early sessions, cued and uncued conditions were interleaved in blocks of several hundred trials. Following this, both monkeys received several sessions of the cued condition only, followed by a return to the uncued condition. Cued, combined refers to data pooled across the two cued conditions for each subject. Final uncued data for Monkey O were collected after an extended hiatus from testing. Error bars represent 95% confidence intervals for the means, calculated by bootstrap resampling.

Discussion

We report that explicit cuing of post-reward delays reduced measured discounting parameters in rhesus monkeys by up to a full order of magnitude. Several factors might explain this apparent reduction in measured discounting behavior. First, the explicit post-reward cue might have rendered the post-reward delay more salient, thus enhancing animals ability to attribute post-consummatory delays to the prior choices. This would suggest that at least some portion of preference for the SS option is explained by an intrinsic difficulty with the task structure, an obstacle mitigated by explicit cuing. Again, this retrograde attribution failure may prove unimportant in typical foraging scenarios, in which delays are rarely imposed following consummatory behavior. A second possible explanation for the difference in discounting is that explicit cuing of post-reward delays alters the subjective perception of time. However, our data show no correlation between mean trial duration and discounting behavior, as would be expected if cuing had simply recalibrated monkeys rate of subjective passage of time (Gibbon et al., 1984, 1988; Staddon and Higa, 1999; Zentall, 1999; Buhusi and Meck, 2005). A third possibility is that we increased the cognitive demands of the task significantly by randomly presenting many choices between distinct reward-delay pairs rather than the same choice multiple times in succession in a blocked format. In response, the animals might have adopted a simple pick-the-best heuristic that based preferences solely on reward for all but the shortest delays (Gigerenzer and Selten, 2001). If this were the case, we would predict greater discounting when the same choices were blocked and offered repeatedly.

Yet none of these potential explanations contradicts the conclusion that observed discounting behavior does not derive primarily from intrinsic individual- and species-specific impulsivity. This idea is supported by the finding that in another common task design – the titrated choice paradigm – implemented in monkeys’ home cages, macaques showed a similar reduction in discounting (Tobin et al., 1996). Notably, the estimated discount parameters in that study were near the lowest measurable given the constraints of the experiment. Similarly, when choosing between immediate and delayed doses of cocaine, macaques were also very patient (Woolverton et al., 2007), though in this case, reward maximization may have appeared more salient, since monkeys were limited to only eight choice trials per day. In fact, after extensive training, one of the monkeys in a similar study exhibited a very low rate of discounting, with a half-life more than twice the length of the longest delay studied (Louie and Glimcher, 2010). Thus, while neither our findings nor these others suggest that all impulsivity results from informational and attributional limitations, they do suggest that such intrinsic impulsivity may be significantly less than has been assumed.

Our findings challenge many current ideas about temporal discounting. The fundamental lability of inter-temporal preferences indicates that discount parameters are highly sensitive to slight variations in task. Consistent with this notion, studies with humans typically estimate discounting rates for money on the order of weeks or months (Loewenstein and Prelec, 1992; McClure et al., 2004; Kable and Glimcher, 2007; Kalenscher and Pennartz, 2008), but tasks that involve many decisions with delays on the order of seconds often estimate much higher rates of discounting (Schweighofer et al., 2006; Luhmann et al., 2008; Carter et al., 2010). This contradiction challenges the idea that any given set of discount parameters reflects a measure of true discounted utility, rather than specific details of the task, and is consonant with the idea that impulsivity may be highly domain-specific (Stevens and Stephens, 2010), and more generally that impulsivity may not be a single unified phenomenon (Evenden, 1999).

Our results also imply that the learning algorithms employed by foraging animals may not be well-adapted to typical laboratory tasks designed to measure impulsivity. In particular, animals seem not to recognize that post-reward delays are lengthened after SS options to match the duty cycle in most tasks, even after extensive training. This could be explained by positing an updating rule acting retroactively and tied to the moment of reward delivery, resulting in “blindness” to events that occur after the reward (Kacelnik and Bateson, 1996; Shapiro et al., 2008). Indeed, such an algorithm would be expected to perform perfectly well in environments where animals make a series of sequential decisions, each ending in reward, as occurs in many types of natural foraging behavior (Stephens and Anderson, 2001). In fact, our result that interleaved blocks of the cued and uncued paradigms failed to produce decreases in discounting – decreases that followed under exclusive use of the cued version of the task – strongly suggest that the effect is related to the process of attribution during learning, not the availability of added information per se.

Our findings endorse the idea that animals are more patient than is normally thought. Of course, animals must necessarily display some limitations in patience when confronted with negative energy budgets and starvation risk. But the emerging picture is one in which, within these constraints, animals adopt decision policies adapted to their natural environments (Gigerenzer and Selten, 2001; Schweighofer et al., 2006). Our findings also suggest that inter-temporal decisions may reflect a variety of factors that are unrelated to a hypothesized neural representation of subjective utility discounted by time. By extension, our results may have important implications for neuroeconomic models of decision-making that assume discounted subject utility serves as a common neural currency mediating all decisions (Kable and Glimcher, 2007).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.