Influences of a Covariate on Growth Mixture Modeling

Abstract

This study investigated the influence of including a covariate and/or a distal outcome on growth mixture modeling (GMM). GMM was used to examine patterns of days of heroin use over 16 years among 471 heroin users and the relationship of those patterns to mortality (distal outcome). Comparisons were made among four types of models: without a covariate and a distal outcome (two-stage approach), with a distal outcome, with a covariate, and with a covariate and a distal outcome in conjunction with three different covariates. The two-stage approach and models with the inclusion of a distal outcome resulted in different conclusions when testing the impact of latent trajectory membership on the distal outcome. Differences in membership classifications between unconditional and conditional models were mainly determined by two factors: (1) the associations of the trajectories with the covariate and the distal outcome, and (2) the distribution of the covariate in the study sample.

Introduction

As evident from an increasing number of empirical papers in disciplines ranging from criminology, sociology, and psychology to public health (D’Unger, Land, McCall, & Nagin, 1998; Jung & Wickrama, 2008; Muthén, 2004; Nagin, 1999; Piquero & Buka, 2002; Sampson & Laub, 2003, 2005), growth mixture modeling (GMM) has become a popular approach to analyzing longitudinal data. Part of the increase in its popularity stems from its robust framework, which facilitates the examination of unobserved heterogeneity of growth trajectories among subjects, as well as the identification of distinct clusters (e.g., latent classes) to which such heterogeneity may be attributed. In recent studies, emphasis has often been placed on discerning distinctive trajectory groups that may provide insights into other distinctive subject or contextual characteristics or to predict consequences after the observed time period (distal outcomes). For example, we are interested in two related research questions: (1) What are distinctive patterns of heroin use across several years following heroin initiation, and (2) Do the groups of individuals with different patterns have different mortality rates when observed over a longer period of time (distal outcome)?

A conventional approach in GMM involves a two-stage process (Dekker et al., 2007; D’Unger, Land, & McCall, 2002; Feng, Shaw, & Silk, 2008; Fergusson & Horwood, 2002; McDermott & Nagin, 2001; Nagin & Land, 1993; Nagin, Farrington, & Moffitt, 1995; Sampson & Laub, 2003, 2005) in which the unconditional growth mixture model (e.g., without any covariates and/or distal outcome) is first fitted to determine the number of distinct trajectory groups. Once the clusters are identified, subject-specific background characteristics and distal outcomes are summarized and compared among trajectory groups using Chi-square, ANOVA, or multinomial logistic regression.

The GMM framework, however, allows for condensing the procedures into one step, with the inclusion of covariates as well as a distal outcome as part of a single model estimation of developmental trajectories (Muthén et al., 2002; Muthén, 2004; Nagin, 1999; Roeder, Lynch, & Nagin, 1999). By including the additional variables as part of a unifying model, rather than treating them as outcomes in post-hoc comparisons, this one-step approach allows for the simultaneous examination of the covariates’ impact on the longitudinal trajectory, their association with the distal outcome, as well as clustering patterns into latent trajectories. Muthén et al. (2002), for example, applied GMM with covariates to assess the efficacy of a preventive intervention aimed at reducing aggressive behavior among school children. The study considered the intervention as a covariate; it also considered a possible consequence, the probability of juvenile delinquency after the intervention, as a distal outcome. The analysis examined intervention effects on the slope of the developmental trajectory of aggressive behavior across latent classes as well as the impact of the trajectories on the distal outcome. See also Hix-Small, Duncan, Duncan, and Okut (2004), Rodriguez, Moss, and Audrain-McGovern (2005), and Sterba, Prinstein, and Cox (2007) for similar applications.

While applied researchers in a variety of disciplines adopt both approaches, it is unclear whether one approach is more suitable under certain circumstances than the other. Muthén (2003, 2004) recommended that regression of trajectory class membership and growth factors on covariates should be included in GMM to correctly specify the model, find the proper number of classes, and correctly estimate class membership. Lubke and Muthén (2007) investigated the effects of covariates on performance of factor mixture models in a simulation study and found that correct class membership assignment increased with increasing covariate effects.

However, a number of other issues require attention in developing a GMM with covariates and a distal outcome. First, in contrast to an unconditional growth mixture model, a conditional growth mixture model with a covariate typically involves increased complexity of model specification and the chance of occurrence of improper convergence due to a likelihood estimation problem (e.g., singularity). Furthermore, the missing-at-random assumption (MAR) that is generally applicable to an unconditional growth mixture model with partial missing data on repeated measures may no longer be appropriate when covariates are partially missing. Missing values on covariates may substantively affect the results of a conditional growth mixture model because a subject with missing values on covariates will be dropped from the estimation.

The choice of an unconditional model or conditional model seems to involve a trade-off between a gain in accuracy of latent class classification and a loss of parsimony of model specification. The magnitude and direction of this trade-off may vary according to which covariate is included. An empirical comparison among models without covariates, with various covariates, and/or a distal outcome may be helpful for developing a practical guide for growth mixture modeling.

The purpose of this paper is to provide an overview of both an unconditional two-stage process and conditional growth mixture modeling, to compare unconditional growth mixture modeling to models with inclusion of covariates and/or distal outcome, to discuss other current issues related to the inclusion of covariates and distal outcome in growth mixture modeling, and to provide a practical guide for specifying an appropriate model.

Methods

Study Sample

This study used the drug-use history data collected by the California Civil Addict Program (CAP). Originally established in 1961 by California legislation, the CAP was a compulsory drug treatment program designed to serve narcotics-dependent criminal offenders committed under court order. A total of 581 male narcotics addicts were randomly selected from the population of CAP admissions during 1964-65, and the subjects were first interviewed in 1974-75 (McGlothlin, Anglin, & Wilson, 1977), then in 1985-86 (Hser, Anglin, & Powers, 1993), and finally 1996-97 (Hser, Hoffman, Grella, & Anglin, 2001). Drug-use history data (i.e., the average number of days per month the participants used heroin during each year since their onset of heroin use) from the three interviews were combined to examine the longitudinal trajectories.

The present study sample consisted of 471 male subjects for whom natural history interview data were available for at least 16 years; the ethnic make-up of the sample was 34.4% Caucasian, 57% Hispanic, and 7.9% African American. More than 80% of the sample had been arrested before age 18, and 80% had tried marijuana. The mean age at admission in 1962 through 1964 was 24.9 years (SD = 5.3), while the mean age at the first follow-up interview in 1974 through 1975 was 36.4 years (SD = 5.5).

Measures

The heroin trajectory was calculated using self-report data on the mean number of days per month that a participant used heroin for each year across a 16-year period following onset of heroin use; a log transformation of this measure was applied in order to approximate a normal distribution for more robust estimation. Three subject characteristics were examined as possible covariates: ethnicity (White, Black, or Hispanic), early onset of heroin use (age 15 or earlier), and early onset of alcohol use (age 15 or earlier). For the 471 subjects, measures on the three covariates were completed without any missing values. The distal outcome variable, mortality, indicated a possible consequence after long-term heroin use. Mortality was measured as the cumulative number of confirmed deaths at the 33-year follow-up based on death certificates. For the 471 subjects, the mortality rate was 40.8% (n=192) by the end of 2005.

Heroin Use Trajectory Models

Growth mixture modeling was applied to identify groups with distinctive trajectory patterns of heroin use and consisted of two major components: (1) an estimated trajectory given membership in each latent group, and (2) an estimated posterior probability of membership in each latent group given a pre-specified number of latent groups. In this study, heroin-use trajectories were represented by a curve with intercept, slope and quadratic parameters (latent growth factors) and were estimated with a mixture-censored normal model. The mixture-censored normal model assumed that the target population comprised a mixture of j trajectory groups with discrete censored normal distributions on a logarithm of mean days of heroin use per month during a year. The heroin trajectories were represented as y_ijt = I_ij + S_ij*year_it + Q_ij*year_it² + ε_it, where i, j, t indicated subjects, trajectory group, and time, respectively. ε_it was a disturbance assumed to be normally distributed with zero mean and constant variance σ². y_ijt indicated the logarithm of mean days of heroin use per month for subject i in group j at time t, respectively. y_ijt was censored by the minimum of 0 and the maximum of 3.44 (= ln(31 days)). If the estimate of y_ijt was less than the minimum, it was assumed that the observed y_ijt was equal to 0. Likewise, if the estimate of y_ijt was greater than the maximum, it was assumed that the observed y_ijt was equal to 3.44. Year_it was the years of heroin use of subject i at time t. Year_it² was the quadratic term of year_it. The latent growth factors I_j , S_j and Q_j were parameters indicating the shape of the trajectory for group j. The coefficient I_j indicated the initial level of heroin use with variation among subjects. The coefficients S_j and Q_j indicated the pattern (slope and quadratic, respectively) of heroin use over time.

The probability of latent group variable (C) was estimated in a multinomial distribution, in which the probability distribution of the counts c_ij, given the j latent groups among a total of N subjects was $\mathrm{P}({\mathrm{C}}_{\mathrm{i}1}=c_{i1},{\mathrm{C}}_{\mathrm{i}2}=c_{i2},....{\mathrm{C}}_{\mathrm{ij}}=c_{ij})=\left(\begin{array}{c}\hfill N\hfill \\ \hfill ci1.....cij\hfill \end{array}\right){{\pi }_{i1}}^{ci1}....{{\pi }_{ij}}^{cij}$, where π_ij= P(C_i=j) denoted probability of the ith subject belonged to the jth group. Then, a posterior probability of membership in each group was estimated for each subject and was computed as P_j(y_i) = P_j(y_i | j) π_j / Σ_j P_j(y_i | j) π_j , where P_j(y_i | j) was the estimated probability of y_i, conditional on membership in group j and π_j was the estimated proportion of the overall sample in group j. Comparing the posterior probability in each group, a subject was assigned to the group with the largest probability.

Conditional Models with Time-invariant Covariates

The unconditional model can also be extended to a conditional model for joint estimation of the impact of a set of covariates on latent growth factors and probability of class membership. Class-varying mean coefficients, I_j , S_j and Q_j for each latent class indicate the difference of trajectory shapes. The association of a covariate X with latent growth factors, I_j , S_j and Q_j are linked by the following equations: I_ij = α_00j + α_01j * X _i + σ _0i ; S_ij = α_10j + α_11j * X _i + σ _1i ; Q_ij = α_20j + α_21j * X _i + σ _2i . The impact of covariate X on probability of class membership are expressed as P(C_i=j |X_i ) and estimated with a multinomial model.

Models with a Binary Distal Outcome

The growth mixture modeling approach also provides for the joint estimation of a conventional finite mixture growth model where different growth trajectories can be captured by class-varying means and a logistic regression of an outcome variable on the latent trajectory group. In this model, a binary distal outcome (U) is related to latent group variable C with the conditional probability, P(U_i|C_i). Let τ_i = P(U_i=1|C_i) denote the probability of occurrence of the distal outcome (U=1). The association of the binary distal outcome with latent class C and covariate X can be estimated in the logit model, logit (τ_i) = γ* C_i.

Model Evaluation

The mixture-censored normal model was estimated for a specified number of groups. A commonly used strategy is to estimate a series of models with a progressively greater number of trajectory classes and to compare fit indices to determine the optimal number of latent trajectory groups. In this study, the optimal number of trajectory groups was determined using the Bayesian Information Criterion (BIC; Schwartz, 1978) and the Lo-Mendell-Rubin likelihood ratio test (LMR-LRT; Lo, Mendell & Rubin, 2001). The BIC was computed as −2*Log(L)+(p*ln(n)), where L was the value of the model’s maximized likelihood, n was the sample size and p was number of parameters in the model. A lower BIC value indicates a better model. The LMR-LRT tests a model with j classes versus a model with j-1 classes, by assuming a latent class probability of the j classes being zero. The LMR-LRT empirically estimates its correct distribution to avoid a classic problem of likelihood ratios not following a chi-square distribution. A p-value of less than 0.05 indicates a model with j classes is better. Model estimation was conducted using Mplus 5.1 (Muthén & Muthén, 2007).

Analytic Strategies

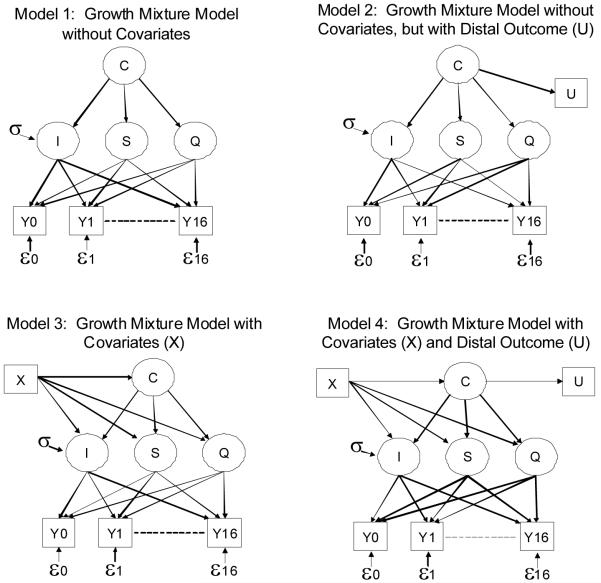
Analyses were implemented to empirically examine the influence of the inclusion of a covariate and/or a distal outcome on the growth mixture modeling. Figure 1 graphically presents the four sets of growth mixture models examined in this study. Model 1 included no covariate or distal outcome. This model is identical to the unconditional GMM used in the two-stage process previously discussed. Model 2 included no covariate (X) but did include a distal outcome (U). Model 3 included a covariate (X) but no distal outcome (U). Model 4 included both a covariate (X) and a distal outcome (U). The distal outcome in this analysis was mortality. Both latent growth factors (I, S, Q) and the latent class variable (C) can be predicted from a covariate X (e.g., early heroin use, early alcohol use, or ethnicity). In the unconditional models (Models 1 and 2), the directional arrow from the latent trajectory classes to the growth factors indicates that the means of growth factors varied across the classes of C. In the conditional models (Models 3 and 4), the directional arrow from the latent trajectory classes to the growth factors indicates that the means of growth factors after controlling for the impact of X varied across the classes of C. The directional arrow from C to U indicates that the probability of U varied across the classes C. To simplify model computation and avoid the problem of improper convergence (singularity), variances of growth factors S and Q were constrained to zero in this study. Variances of intercepts (I_j) were assumed equal across latent groups, and residual variances of ε_it were assumed equal across latent classes and years.

Figure 1.

The Four Sets of Growth Mixture Models Examined in the Study

Separate parallel analyses were conducted to examine modeling with each of three possible covariates, which were different in their association with heroin-use trajectories and mortality: early onset of heroin use (used heroin before age 15), ethnicity (White, Black, or Hispanic), and early onset of alcohol use (used alcohol before age 15). Early onset of heroin use and ethnicity were significantly correlated with heroin use over time, but the association of early onset of alcohol use with heroin use over time was negligible. Furthermore, mortality was significantly associated with early heroin use (p=0.02). Compared to a mortality rate of 38.3% for subjects with late onset of heroin use, mortality was significantly higher (51.7%) among subjects who initiated heroin use before age 15. However, ethnicity and early onset of alcohol use were not significantly related to mortality (p=0.30 and p=0.53, respectively). The mortality rates for Whites, Blacks, and Hispanics were 37.7%, 51.4%, and 41.2%, respectively. The mortality rate for subjects with early onset of alcohol use was 41.7%, in contrast to a mortality rate of 38.5% among subjects who initiated alcohol use after age 15.

Results

The Unconditional Model: First-stage of the Two-stage Process

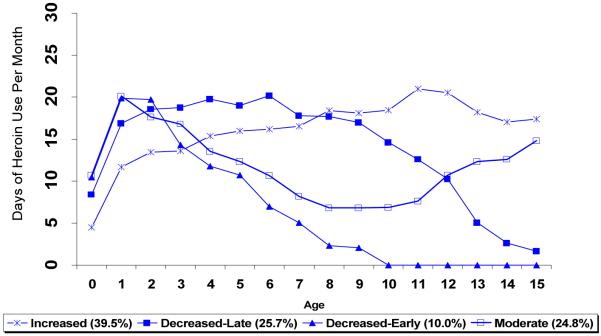
We began by fitting a GMM without covariates or the distal outcome to determine the optimal number of trajectories. The BIC value decreased from BIC=24896.3 in the two-trajectory model to BIC=24560.2 in the six-trajectory model. The LMR-LRT tests were significant for models with three (p=0.0001), four (p=0.0013), and five (p=0.02) trajectory groups but non-significant for the six-trajectory model (p=0.47), suggesting five trajectory groups from the study sample. After further examination of the four- and five-trajectory models, we found that the fifth group in the five-trajectory model comprised only a small subset of subjects (n=19) solely extracted from the fourth group in the model. Therefore, the four-trajectory model was chosen as the most parsimonious but informative description of the study data. Figure 2 shows the four estimated trajectories: 39.5% of subjects were classified into a group labeled descriptively as “Increased” whose subjects had an increased trend in level of heroin use over time; 25.7% of subjects (labeled the “Decreased-Late” group) maintained a high level of use for about 8 years, then started a significant decrease in use; about 10% of subjects were in a “Decreased-Early” group, in which subjects had a high level of heroin use during the first 3 years following initial use, followed by significantly decreased use; and 117 subjects (24.8%) belonged to a “Moderate-Use” group, in which subjects had a high level of heroin use during the first 3 years following initial use, but remained at moderate levels afterwards.

Figure 2. The Four Heroin-use Trajectories Identified by the Unconditional Model (Model 1).

Chi-square Tests and Logistic Regression Analysis in the Two-stage Process

Table 1 compares the profile of subjects’ characteristics among the four trajectory groups identified in the preceding step. While the within-trajectory group mortality was highest among subjects in the Decreased-Late group (47.1%) and lowest for the Decreased-Early groups (25.5%), the between-group difference in mortalities was not statistically significant (X²₍₃₎ = 6.66, p=0.08). The four trajectory groups significantly differed, however, in terms of ethnic composition (p<0.01), early heroin use (p=0.04) and early alcohol use (p=0.01). Among the four trajectory groups, the Decreased-Early group had the highest percentage of Whites and the lowest percentage of Hispanics. The Increased and Moderate-Use groups, relative to the other two groups, had higher percentages of subjects with early heroin use. The percentage of subjects with early alcohol use was lowest in the Decreased-Early group but was similar across the Increased, Moderate, and Decreased-Late groups.

Table 1.

Profile of Characteristics of Subjects in the Trajectory Groups from the Unconditional Four-trajectory Model

Model 1: No covariate	Increased (N=186)	Decreased Late (N=121)	Decreased Early (N=47)	Moderate (N=117)	Total (N=471)
Early heroin use (%)*	20.4	22.3	4.3	17.1	18.5
Early alcohol use (%)*	74.2	71.9	51.1	74.4	71.3
Ethnicity (%)**
White	24.7	40.5	57.5	34.2	34.4
Black	6.5	9.1	8.5	8.6	7.9
Hispanic	68.8	50.4	34.0	57.3	57.8
Mortality (%)	41.4	47.1	25.5	39.3	40.8

^*p<0.05

^**p<0.01

In addition to bivariate comparisons, three logistic regression models were applied to examine trajectory-group relationship to mortality after controlling for one of the three covariates: ethnicity, early heroin use, and early alcohol use. The logistic regression models showed that mortality was not significantly different among the four trajectory groups after controlling for each of the three covariates; however, mortality was higher for early heroin users (Odds Ratio=1.61, p=0.04) but was not significantly different by ethnicity or early alcohol use.

The Unconditional Model with a Distal Outcome

A growth mixture model including mortality as a distal outcome (see Figure 1 and Model 2 in Table 2) assessed the effects of latent trajectory classification on mortality within a multivariate context. In contrast to the preceding two-stage process, where mortality rates among trajectory groups were not significantly different, Model 2 found significant differences among trajectory groups (X²₍₃₎=34.5, p<0.01), with higher mortality in the Increased (42.1%) or Decreased-Late (48.3%) groups than those in the Moderate (25.5%) or Decreased-Early (37.2%) groups. The mortality rates in each trajectory group in Model 2 were similar to those of the corresponding trajectory group in Model 1.

Table 2.

Unconditional Growth Mixture Models with Mortality as a Distal Outcome

	Model 1: No covariate, No distal outcome				Mode 2: included mortality as a distal outcome
	Increased	Decreased Late	Decreased Early	Moderate	Increased	Decreased Late	Decreased Early	Moderate
Means
Intercept (I)	1.30**	1.79**	2.27**	2.60**	1.29**	1.80**	2.26**	2.59**
Slope (S)	0.22**	0.34**	−0.01	−0.34**	0.22**	0.34**	−0.005	−0.33**
Quadratic (Q)	−0.01*	−0.04**	−0.05**	0.02**	−0.01**	−0.04**	−0.05**	0.02**
Variance1
Intercept	0.45**	0.45**	0.45**	0.45**	0.45**	0.45**	0.45**	0.45**
Residual Variance	2.22**	2.22**	2.22**	2.22**	2.22**	2.22**	2.22**	2.22**
Logit of probability of class membership	0.42	−0.02	−0.97**	--	0.38	−0.06	−1.00**	--
Dead (vs Alive)	--	--	--	--	−0.31	0.01	−1.11**	−0.60*
Mortality %	41.4	47.1	25.5	39.3	42.1	48.3	25.5	37.2
Number of subjects (%) in each class	186 (39)	121 (26)	47 (10)	117 (25)	183 (39)	120 (25)	47 (10)	121 (26)
Goodness of fit
Bayesian (BIC)	24621.6				25274.2
LMR LRT	P=0.0013				P=0.0003

¹Variances of Slope and Quadratic were constrained to zero.

^*p <0.05

^**p <0.01

Conditional Models with a Covariate

To examine the influence of a covariate on the four trajectories and group membership, models that included early heroin use, early alcohol use, or ethnicity as a covariate were examined. The four-trajectory conditional models are summarized in Table 3. In the four-trajectory growth mixture model with early heroin use as a covariate (Model 3a), early heroin use was significantly related to the trajectory parameters for the Increased group. However, the impact of early heroin use on the trajectories for the Decreased-Late and Moderate groups was not significant. The class membership coefficients indicate the logit of the probability of each trajectory group relative to the Moderate group. Compared to the Moderate group, the coefficient of −0.96 for the Decreased-Early group indicated that subjects were 0.96 time less likely to be assigned to the Decreased-Early group. Relative to the Moderate group, the probabilities of latent class membership were significantly different by early heroin use.

Table 3.

Conditional Growth Mixture Models Including a Covariate

	Model 3a: included early heroin use				Model 3b: included early alcohol use				Model 3c: included ethnicity
	Increased	Decreased Late	Decreased Early	Moderate	Increased	Decreas ed Late	Decrease d Early	Moderate	Increased	Decreased Late	Decreased Early	Moderate
Means
Intercept (I)	1.05**	1.94**	2.27**	2.52**	−0.27	2.56**	2.49**	0.78	1.28*	1.91**	2.21*	1.69**
Slope (S)	0.28**	0.29**	−0.02	−0.29**	−0.32*	−0.40*	−0.33	0.16	0.14	0.08	−0.25	0.34
Quadratic (Q)	−0.01**	−0.03**	−0.05**	0.02**	0.04**	0.03	−0.03	−0.08	−0.01	−0.07**	0.01	−0.04
I on early use	1.06**	−0.49	−1.12	0.61	1.83**	−0.76*	0.06	1.50**	--	--	--	--
S on early use	−0.47**	0.06	0.72*	−0.60	0.41**	0.71**	−0.13	0.28	--	--	--	--
Q on early use	0.03**	0.01	−0.02	−0.01	−0.04**	−0.06**	0.05*	−0.02*	--	--	--	--
I on Hispanic	--	--	--	--	--	--	--	--	0.12	0.13	0.69	1.20
S on Hispanic	--	--	--	--	--	--	--	--	−8.22**	0.13	−1.84**	0.30
Q on Hispanic	--	--	--	--	--	--	--	--	0.06	0.20	0.03	−0.75*
I on Black	--	--	--	--	--	--	--	--	3.06**	0.10	1.09**	−0.41
S on Black	--	--	--	--	--	--	--	--	−0.004	0.04	−0.04	0.06*
Q on Black	--	--	--	--	--	--	--	--	−0.12**	0.03	−0.07**	0.04
Variance1	--	--	--	--	--	--	--	--	--	--	--	--
Intercept	0.46**	0.46**	0.46**	0.46**	0.41**	0.41**	0.41**	0.41**	0.43**	0.43**	0.43**	0.43**
Residual Variance	2.19**	2.19**	2.19**	2.19**	2.23**	2.23**	2.23**	2.23**	2.22**	2.22**	2.22**	2.22**
Logit of probability of class membership
Mean logit	0.11	−0.23	−0.96**	--	−0.80	−0.58	−0.96	--	0.12	−0.60	−0.02	--
Membership on early  Use	1.25	1.55**	1.43**	--	3.02**	2.14	1.86*	--	--	--	--	--
Membership on  Hispanic	--	--	--	--	--	--	--	--	0.07	0.77	−1.21	--
Membership on Black	--	--	--	--	--	--	--	--	−3.03	−0.16	−0.72	--
Mortality %	43.8	44.0	36.2	35.7	42.1	43.8	32.3	39.5	39.5	41.0	33.3	46.7
Number of subjects (%) in each class	162 (34)	125 (27)	58 (12)	126 (27)	209 (44)	121 (26)	65 (14)	76 (16)	185 (39)	100 (21)	66 (14)	120 (25)
Goodness of fit
Bayesian (BIC)	24655.03				24660.9				24793.89
LMR LRT	p=0.038				p=0.44				p=0.362

¹Variances of Slope and Quadratic were constrained to zero.

^*p <0.05

^**p <0.01

In contrast, early alcohol use (Model 3b) showed significant influences on the heroin-use trajectory for each of the four trajectory groups. Particularly, the estimated intercept, slope, and quadratic parameters of the trajectory were significantly different by early alcohol use for the Increased and Decreased-Late trajectory groups: that is, individuals with early onset of alcohol use had a more steeply increasing rate on heroin-use trajectories than individuals who did not start alcohol use before age 15. The probabilities of latent class membership also differed significantly by early alcohol use. Relative to the non-early alcohol users, early alcohol users were more likely to be classified into the Increased or Decreased-Early groups.

Model 3c showed ethnicity to be significantly associated with the growth factors of heroin trajectories in the Increased and Decreased-Early trajectory groups. Compared to Whites in the Increased and Decreased-Early trajectory groups, Hispanics in these two trajectory groups had a steeper decreasing pattern and Blacks had a higher level of initial use. However, the probabilities of latent class membership were not significantly different by ethnicity.

Comparing results from the two-stage process (Model 1 in Table 2) and from the conditional growth mixture modeling (Models 3a, 3b, 3c), Models 3a and 3b showed significant associations of trajectory groups (latent class membership) with early heroin use and early alcohol use, which were consistent with the findings from the two-stage process. However, no significant association between trajectory groups and ethnicity was found in Model 3c, differing from the findings of the two-stage process.

Conditional Models with a Distal Outcome

Table 4 summarizes growth mixture models that include both a covariate and a distal outcome. Mortality rates were significantly different among the four trajectory groups in the model with ethnicity as a covariate (X²₍₃₎=13.97, p<0.01), suggesting that after controlling for the impact of ethnicity on the growth factors and latent class membership, latent trajectory groups still accounted for differences in mortality. However, differences in mortality rates were not significant in the model with early heroin use (X²₍₃₎=3.50, p>0.05) or early alcohol use (X²₍₃₎=2.75, p>0.05) as a covariate.

Table 4.

Conditional Growth Mixture Models Including a Covariate and a Distal Outcome (Mortality)

	Model 4a: included early heroin use and mortality				Model 4b: included early alcohol use and mortality				Model 4c: included ethnicity and mortality
	Increased	Decreased Late	Decreased Early	Moderate	Increased	Decreased Late	Decreased Early	Moderate	Increased	Decreased Late	Decreased Early	Moderate
Means
Intercept (I)	1.00**	1.93**	2.26**	2.50**	1.82**	2.50**	2.53**	1.53**	1.93**	1.84**	1.62**	1.58**
Slope (S)	0.30**	0.30**	−0.02	−0.27**	0.42**	−0.33	−0.40**	0.28*	−0.16	0.13	0.63**	−0.02
Quadratic (Q)	−0.01**	−0.03**	−0.05**	0.02**	−0.04**	−0.03	0.03**	−0.02**	−0.07	−0.02*	−0.09**	0.004
I on early use	0.25	−0.11	0.93	−0.56*	−0.27	−0.72	−0.23	1.03	--	--	--	--
S on early use	0.35*	−0.09	−0.96**	0.21	−0.32	0.65*	0.79	−0.71*	--	--	--	--
Q on early use	−0.05**	0.01	0.12**	−0.01	0.04**	−0.01	−0.11	0.04*	--	--	--	--
I on Hispanic	--	--	--	--	--	--	--	--	−0.52	0.21	1.26**	1.32**
S on Hispanic	--	--	--	--	--	--	--	--	0.35	0.14	−1.06**	−0.20
Q on Hispanic	--	--	--	--	--	--	--	--	0.06	−0.01	0.11**	−0.03*
I on Black	--	--	--	--	--	--	--	--	−1.02	−1.26	−0.42	0.85**
S on Black	--	--	--	--	--	--	--	--	1.15**	0.31*	0.001	−0.26*
Q on Black	--	--	--	--	--	--	--	--	−0.10	−0.002	0.03*	0.01
Variance1	--	--	--	--	--	--	--	--	--	--	--	--
Intercept	0.46**	0.46**	0.46**	0.46**	0.42**	0.42**	0.42**	0.42**	0.40**	0.40**	0.40**	0.40**
Residual Variance	2.20**	2.20**	2.20**	2.20**	2.22**	2.22**	2.22**	2.22**	2.22**	2.22**	2.22**	2.22**
Logit of probability of class membership
Mean logit	−0.01	−0.32**	−1.04**	--	−0.84**	−0.93**	−0.60**	--	−1.43**	−0.14	−1.23**	--
Membership on early  Use	−0.87**	0.39	−1.26**	--	2.05	1.54	−0.32	--
Membership on  Hispanic									3.46**	−1.59**	2.41**	--
Membership on Black									0.32**	−0.06	1.14**	--
Dead (vs Alive)	−0.15	−0.12	−0.96**	0.63**	−0.31	−0.17	−1.10**	−0.38	−0.70**	0.06	−0.51	−0.41
Mortality %	48.5	44.9	28.6	35.0	42.6	45.2	22.9	40.6	32.2	51.1	40.7	39.2
Number of subjects (%) in each class	132 (28)	127 (27)	49 (10)	163 (35)	202 (43)	115 (24)	48 (10)	106 (23)	149 (32)	139 (30)	86 (18)	97 (21)
Goodness of fit
Bayesian (BIC)	25315.15				25316.7				25349.95
LMR LRT	P=0.0037				P=0.818				P=0.013

¹Variances of Slope and Quadratic were constrained to zero.

^*p <0.05

^**p <0.01

Comparison of Latent Class Membership between the Unconditional Model (No Covariate) and Conditional Models (with a Covariate and with Both a Covariate and a Distal Outcome)

Table 5a summarizes individual level of agreement on latent trajectory class membership classification between the unconditional model (Model 1) and various conditional models. Comparing the unconditional model with the model that included early heroin use as a covariate (Model 3a), agreement on membership classification was 85.7% (i.e., the summation across diagonal values in Table 5a). Differences in classification were more likely to occur among Increased-users; 7.6 % of subjects classified as Increased-users by Model 1 were classified into other latent classes by Model 3a. In comparisons stratified by early heroin use, 94.3 % of subjects without early heroin use were classified into the same latent class in Model 3a, but only 47.1 % of subjects with early heroin use remained in the same classification in Model 3a.

Table 5a.

Summary of Individual level of agreement on membership classification between unconditional model and conditional models with a covariate

		Unconditional model (model 1)
Conditional model		Increased	Decreased late	Decreased early	Moderate	Percentage of subjects in membership
Early heroin use (model 3a)	Increased	31.9%	0.0	0.0	2.6%	34.4%
	Decreased late	3.6%	22.3%	0.0	0.6%	26.5%
	Decreased early	0.0	2.6%	9.8%	0.0	12.3%
	Moderate	4.0%	0.9%	0.2%	21.7%	26.8%
Early alcohol use (model 3b)	Increased	29.1%	5.1%	0.2%	10.0%	44.4%
	Decreased late	1.5%	17.8%	0.2%	6.2%	25.7%
	Decreased early	0.0	0.6%	5.7%	7.4%	13.8%
	Moderate	8.9%	2.1%	3.8%	1.3%	16.1%
Ethnicity (model 3c)	Increased	36.1%	0.0	0.0	3.2%	39.3%
	Decreased late	0.6%	13.8%	6.2%	0.6%	21.2%
	Decreased early	1.1%	2.6%	3.4%	7.0%	14.0%
	Moderate	1.7%	9.3%	0.4%	14.0%	25.5%
	Percentage of subjects in membership	39.5%	25.7%	10.0%	24.8%	100.0%

Latent class membership changed dramatically when the model included early alcohol use as a covariate (Model 3b). The agreement rate between Model 1 and Model 3b was only 53.9%. About 21% of non-early-alcohol-use subjects and 67.3% of early-alcohol-use subjects were classified in the same latent class membership by Model 1 and Model 3b. About 23.6% of subjects in the Moderate group by Model 1 were allocated to other latent classes by Model 3b. Latent class membership also substantively changed in the model with ethnicity as a covariate (Model 3c). The agreement rate between Model 1 and Model 3c was 67.3%. In particular, 94.5% of Hispanics, 43.2 % of Blacks, and 27.1 % of Whites remained in the same membership classification in Models 1 and 3c. More subjects in the Decreased-Late and Moderate groups by Model 1 were classified differently by Model 3c (11.9% and 10.8%, respectively).

Our analyses suggest that the individual level of agreement on membership classification between the unconditional and conditional models is proportional to the distribution of the covariate in the study sample. Given the sample stratification by a covariate, a subgroup that consists of the majority of subjects in the study sample will have a higher agreement rate than the other subgroups. For example, in this study sample, the distribution of non-early-heroin users and early-heroin users was 384 (81.5%) and 87 (18.5%), respectively. The agreement rate among non-early heroin users was 94.3%, much higher than the agreement rate among early heroin users (47.1%). Similarly, early alcohol users and Hispanics had relatively higher agreement rates when respectively compared to non-early alcohol users (67% vs. 21%) and other ethnic groups (92.5% vs. 21.1% for Whites and 43.2% for Blacks) because the two subgroups comprised the majority of subjects in the study sample, relative to other stratified subgroups by early alcohol use or ethnicity.

In comparing the agreement rates among the three largest subgroups by covariates, non-early heroin users, early alcohol users, and Hispanics in the study sample, the agreement rate in the early-alcohol-use subgroup (67.3%) was much lower than that in the other two subgroups (94.3% and 92.5%). General growth curve modeling analyses, which examined differences in estimated growth factors (intercept, slope and quadratic) by each covariate, showed that the growth factors significantly varied by status of early heroin use and ethnicity. But growth factors did not vary by early-alcohol-use status. These results confirm that early heroin use and ethnicity were highly correlated with the heroin-use trajectory. The distinctive trajectory groups determined by the unconditional model were able to account for the majority of variation due to early heroin use or ethnicity. Consequently, a higher percentage of subjects remained in the same membership classification in the models that included early heroin use or ethnicity as a covariate.

Table 5b presents agreement rates between Model 1 and the three conditional models (4a, 4b and 4c) that each included a distal outcome (mortality) and one of the three covariates: early heroin use, early alcohol use, and ethnicity, respectively. The agreement rates (the summation across the diagonal values in Table 5b) between Model 1 and Models 4a, 4b, and 4c were 78.6%, 60.5%, and 56.1%, respectively. These agreement rates were different from those in the corresponding model without mortality (Models 3a, 3b and 3c), indicating that inclusion of a distal outcome would alter latent class membership classification. Comparing the agreement rate in each group in Model 4a to that in the corresponding group in Model 3a, the agreement rate substantively changed for the Increased group (24.8% vs. 31.9%) but remained similar for the other three groups. In comparisons of Models 4b and 3b, a significant difference in agreement rate occurred only in the Moderate group (9.8% vs. 1.3%). However, substantial differences on agreement rates were observed for all of the four trajectory groups between Models 4c and 3c.

Table 5b.

Summary of Individual level of agreement on membership classification between unconditional model and conditional models with a covariate and a distal outcome

		Unconditional model (model 1)
Conditional mode with a distal outcome		Increased	Decreased late	Decreased early	Moderate	Percentage of subjects in membership
Early heroin use with mortality (model 4a)	Increased	24.8%	2.8%	0.4%	0.0	28.0%
	Decreased late	3.0%	22.1%	0.0	1.9%	27.0%
	Decreased early	0.0	0.0	9.6%	0.9%	10.4%
	Moderate	11.7%	0.9%	0.0	22.1%	36.6%
Early alcohol use with mortality (model 4b)	Increased	28.7%	4.9%	0.2%	9.1%	42.9%
	Decreased late	0.6%	17.8%	4.7%	1.3%	24.4%
	Decreased early	1.3%	0.0	4.3%	4.7%	10.2%
	Moderate	8.9%	3.0%	0.9%	9.8%	22.5%
Ethnicity with mortality (model 4c)	Increased	25.5%	0.0	4.3%	1.9%	31.6%
	Decreased late	4.5%	20.8%	0.0	4.3%	29.5%
	Decreased early	0.0	4.7%	2.3%	11.3%	18.3%
	Moderate	9.6%	0.2%	3.4%	7.4%	20.6%
	Percentage of subjects in membership	39.5%	25.7%	10.0%	24.8%	100.0%

Discussion

Applications of growth mixture models have been important in longitudinal data analysis. Issues such as uncertainty about the optimal number of latent classes (Nagin & Land, 1993; Nagin & Tremblay, 2001), interpretation of the identified groups (Nagin & Tremblay, 2005), accuracy of subject classification into groups (Muthén, 2004; Nagin, 1999), and model specification with inclusion of time-invariant covariates and/or distal outcome have been discussed. This study empirically examined the issues of inclusion of covariates and a distal outcome in the growth mixture modeling and produced several interesting results. First, the unconditional model without the distal outcome (Model 1) and the unconditional model with the distal outcome (Model 2) resulted in different conclusions when testing the effect of latent trajectory groups on the distal outcome. When using a model without inclusion of the distal outcome, the association of latent trajectory groups with the distal outcome was assessed by a bivariate chi-square test. In contrast, a multivariate test was applied in assessing the association of the model with inclusion of the distal outcome. This finding is consistent with results from previous studies (Muthén, 2004; Nagin, 1999; Roeder et al., 1999). These studies suggested that a multivariate test from a model that includes an appropriate covariate and distal outcome would be more appropriate for testing the impact of latent group membership on a distal outcome. Second, group membership was relevant to how covariates related to the degree of change in the heroin-use trajectory. Our empirical analyses showed that latent class membership varied among models with different covariates, suggesting that the strengths of impact of a covariate on heroin-use trajectory and mortality varied across the covariates. The impact of the selected covariates could differ among subgroups of individuals. The covariates that predicted initial level of heroin use may differ from those predicting the pattern or continuity of heroin use.

An unconditional model differentiated trajectories by allowing for groups of individuals’ growth trajectories to vary around different means. In contrast, the conditional model that included time-invariant covariates captured some of the variation in the class-specific growth factors as well as the influence of the covariates on latent class membership and growth factors. The inclusion of a covariate provided more information to refine the membership classification and may produce a more reliable solution (Muthén, 2004). However, the inclusion of a covariate in the model also increases the complexity of model specification and difficulty in parameter estimation. Our empirical findings showed that the conditional models did not always result in a model with better model fit. The unconditional model (Model 1 in Table 2) had a better model fit than the three conditional models (Models 3a, 3b, 3c in Table 4) comparing their BIC values. These results suggest that the important issues to consider in growth mixture modeling are (1) whether to include a covariate in the modeling and (2) choosing appropriate covariates.

A general guideline for developing an appropriate growth mixture model has not been systematically addressed. Theoretically, inclusion of a covariate and/or distal outcome should be driven by the research question specified for the study. For example, in the studies of Muthén et al. (2002) and Rodriguez (2005), time-invariant covariates and distal outcomes were selected based upon the research hypotheses specified in their studies. In practice, many studies may not always involve a specific research hypothesis and may require some exploratory analyses to identify potential covariates that may correlate with trajectories. Nagin (1999) suggested that the two-stage approach could be the preliminary analyses for exploring possible covariates associated with the developmental trajectory and the distal outcome. These exploratory results would be helpful for selecting covariates and refining model specification. However, results from the two-stage process may require further validation using the conditional growth mixture modeling. As shown from our empirical analyses, the two-stage process and the conditional growth mixture modeling result in different conclusions when testing the impact of latent trajectory membership on the distal outcome.

Latent group membership varied with different model specifications. A subject belonging to one trajectory group in the unconditional model may be classified into another group in the conditional model. Our analyses showed that inclusion of early heroin use as a covariate did not substantively alter an individual’s latent group membership because early heroin use was highly related to the heroin-use trajectory, and the distribution of early heroin use in our study sample was highly unbalanced with a majority of subjects being non-early-heroin-use users. Inclusion of early heroin use affected only a small subset of subjects. In contrast, inclusion of early alcohol use as a covariate substantively changed individuals’ latent group membership. Early alcohol use had a relatively low correlation with the heroin-use trajectory and the distribution of early alcohol use in our study sample was relatively balanced with about two thirds of subjects being early alcohol users and one third non-early alcohol users.

These empirical findings suggest that the percentage of subjects with varying membership classification was mainly affected by two factors: the associations of trajectories with covariates and the distal outcome and the distribution of the included covariate in the study sample. When a specific covariate (X) is highly correlated with the trajectory of heroin use, then including the covariate will provide very little extra information for classifying subjects into distinctive trajectory groups. This would result in a small percentage of subjects with different membership classifications across models. On the other hand, when covariate X is not correlated with the trajectory of heroin use, much more extra information will be provided in the group classification process and could result in a substantial percentage of subjects classified in different latent groups by different models. In addition, the membership classification difference between unconditional and conditional models appears to be driven mainly by the distribution of the covariate in the study sample. Given the sample stratification by the covariate, subjects belonging to the subgroup with the largest sample size are less likely to have different membership classification when the covariate is included. Compared to a sample sub-stratum with a small number of subjects, a sample sub-stratum with a majority of subjects would contribute more to determining trajectory patterns and group membership in the unconditional model. When the covariate is included in the model, subjects in the main sub-stratum would be less affected by the inclusion of the covariate. Thus, preliminary consideration of potential covariates and relationships, including: (1) a correlation matrix of each potential covariate with the measure of heroin use over time, and (2) a simple frequency table by each potential covariate could be helpful to researchers in gauging possible impact.

Another important issue raised by our empirical analyses is that the number of trajectory groups emerging from an unconditional model, in general, may not closely match the trajectory groups identified in a conditional model. There is no standard approach for determining the optimal number of trajectories in growth mixture modeling. The inclusion of additional covariates related to heroin use in the model could produce different results. It is important to recognize that the trajectory groups identified from growth mixture modeling are not fixed. Sample size (D’Ugner et al., 1998; Sampson, Laub, & Eggleston, 2004), development span across assessments (Eggleston, Laub, & Sampson, 2004), set of predictors included (Lubke & Muthén, 2007; Muthén, 2004; Nagin, 1999; Roeder et al., 1999), and parameters allowed to vary across classes (Lubke & Muthén, 2007) all may influence the results of growth mixture modeling. In addition, there is little guidance for determining whether parameters vary across latent classes. This study imposed constraints on the variances of growth factors S and Q. Models freeing those constraints were also considered in our analyses. However, parameter estimation in these models became extremely difficult because of convergence and singularity problems. Further simulation studies would be helpful for evaluating the appropriateness of constraints imposed for the estimation and would provide a more comprehensive picture of the impact of the inclusion of covariates and/a distal outcome on growth mixture modeling with various model specifications.

Biographical Sketches

David Huang, Dr.P.H., is serving as senior statistician at the UCLA Integrated Substance Abuse Programs. He provides statistical support on several longitudinal studies examining risk behaviors of drug abusers. He is responsible for planning and conducting all data management and statistical analysis, especially in choosing appropriate methods for multivariate analysis.

Mary-Lynn Brecht, Ph.D., is a research statistician in the UCLA Integrated Substance Abuse Programs. Research projects have included examining patterns and correlates of methamphetamine use, treatment outcomes, HIV risk behaviors for meth users, and treatment needs assessment. She has experience in the development/adaptation, application, and integration of quantitative research methods, especially for longitudinal data.

Motoaki Hara, M.S., is an advanced doctoral student at UCLA’s Graduate School of Education and Information Studies and a Pre-doctoral Research Fellow at the UCLA Integrated Substance Abuse Programs. He is trained in statistics and advanced quantitative methods, and is particularly interested in application of Bayesian approaches to evaluation research data.

Yih-Ing Hser, Ph.D., is a Professor-in-Residence at the UCLA Integrated Substance Abuse Programs. She has been conducting research in the field of substance abuse and its treatment since 1980 and has extensive experience in research design and advanced statistical techniques applied to substance abuse data.