Low-energy Control of Electrical Turbulence in the Heart

Abstract

Controlling the complex spatio-temporal dynamics underlying life-threatening cardiac arrhythmias such as fibrillation is extremely difficult due to the nonlinear interaction of excitation waves within a heterogeneous anatomical substrate^1–4. Lacking a better strategy, strong, globally resetting electrical shocks remain the only reliable treatment for cardiac fibrillation^5–7. Here, we establish the relation between the response of the tissue to an electric field and the spatial distribution of heterogeneities of the scale-free coronary vascular structure. We show that in response to a pulsed electric field E, these heterogeneities serve as nucleation sites for the generation of intramural electrical waves with a source density ρ(E), and a characteristic time τ for tissue depolarization that obeys a power law τ∝E^α. These intramural wave sources permit targeting of electrical turbulence near the cores of the vortices of electrical activity that drive complex fibrillatory dynamics. We show in vitro that simultaneous and direct access to multiple vortex cores results in rapid synchronization of cardiac tissue and therefore efficient termination of fibrillation. Using this novel control strategy, we demonstrate, for the first time, low-energy termination of fibrillation in vivo. Our results give new insights into the mechanisms and dynamics underlying the control of spatio-temporal chaos in heterogeneous excitable media and at the same time provide new research perspectives towards alternative, life-saving low-energy defibrillation techniques.

Spatially extended non-equilibrium systems display spatio-temporal dynamics that can range from ordered to turbulent. Controlling such systems is one of the central problems in nonlinear science and has far-reaching technological consequences. Few examples of successful control with applications in physics and chemistry have been demonstrated^8,9. In biological excitable media, the systems’ complexity makes successful control challenging. This difficulty applies in particular to electrical turbulence in cardiac tissue, known as fibrillation. During fibrillation, synchronous contraction of the muscle is disrupted by fast vortex-like, rotating waves of electrical activity^1–4. At the core of the vortex is a line of phase singularities, called a filament. It is well known that vortex instabilities and interactions^10,11 lead to self-organized, turbulent electrical dynamics. In the heart electric turbulence arises within the electromechanically anisotropic and heterogeneous cardiac muscle with complex geometry¹². As we show below, this natural complexity can be used as a substrate for successful control of electrical turbulence.

The physiological mechanisms underlying the dynamics and control of electrical turbulence remain largely unknown¹³. The only clinically effective method for eliminating vortices in the heart is the delivery of a high-energy electric shock that both depolarizes and hyperpolarizes the tissue with a voltage gradient of about 5 V/cm. When applied externally this shock can be as large as 360J (1kV, 30A, 12ms)⁵. Although defibrillators employing this approach are used routinely in emergency medicine, treatments are often associated with severe side effects^6,7,14.

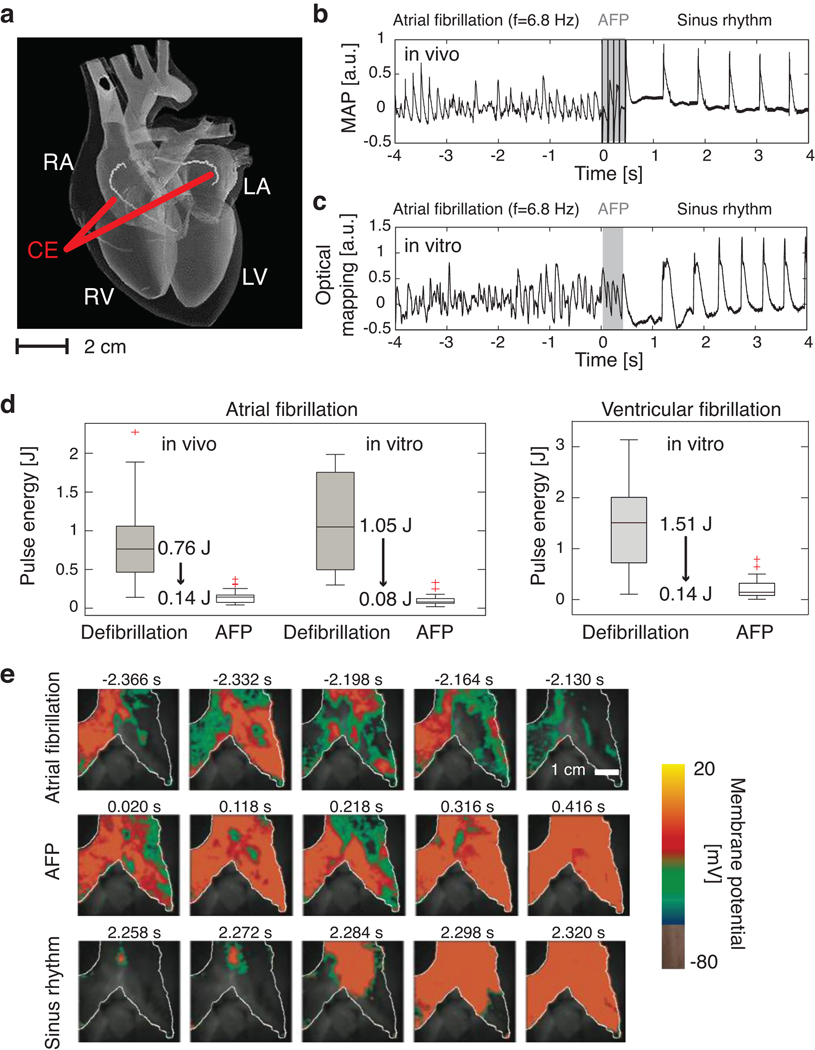
Here we provide a new understanding of the biophysical mechanisms involved in the control of cardiac fibrillation and demonstrate low-energy control and termination of cardiac fibrillation in vivo. Two internal catheters with coiled wire electrodes were inserted into the right and left atria of adult beagle dogs (Fig. 1a) and sustained atrial fibrillation (AF) was induced (see methods). We compared the energies required for defibrillation using a single, high-energy shock (standard defibrillation) and a sequence of five low-energy electric field pulses (Low-Energy Anti-fibrillation Pacing or LEAP). A representative time series for successful LEAP termination via a monophasic action potential electrode inserted into the right atrium is shown in Fig. 1b. For t<0, the signal shows irregular oscillations with a dominant frequency f_v=6.8±0.1Hz. The control interval starts at t=0 (Fig. 1b, gray shaded area). Following control, the arrhythmia is terminated and normal sinus rhythm is restored. In this example, the energy required for terminating AF was 0.074±0.012J, seven times less than needed for standard defibrillation in this preparation (0.52±0.20J). This substantial reduction in energy was reproduced in 56 episodes in seven in vivo experiments, where we found an average energy reduction of 84% (see Fig. 1d) (P<10⁻⁷).

Figure 1. Low-energy termination of cardiac electrical turbulence in vivo and in vitro.

a Schematic of the anatomy of the heart: RA=right atrium, LA=left atrium, RV=right ventricle, LV=left ventricle. A pulsed electric field was applied with standard cardioversion coiled wire electrodes (CE) inserted into the left and right atria by catheters (see SI).

b Monophasic Action Potential (MAP) recording of termination of AF using LEAP in vivo. Dominant frequency f_v=6.8±0.1Hz, n=5 pulses, pulse duration Δt=8ms, pacing cycle length T_p=99ms, pulse energy E=0.074±0.012J.

c Termination of AF in vitro measured from the atrial epicardium of the same heart as in b by optical mapping (see e). The signal from a 0.3×0.3 mm² region is shown (f_v=6.8±0.1Hz, n=5, Δt=8ms, T_p=90ms, E=0.066±0.017J).

d Pulse energy reduction of LEAP vs. standard defibrillation. In vivo AF (N=7): LEAP (56 episodes, mean energy Ē=0.14±0.08J); defibrillation (22 episodes, Ē=0.89±0.56J). In vitro AF (N=5): LEAP (46 episodes, Ē=0.10±0.07J); defibrillation (39 episodes, Ē=1.15±0.58J). In vitro ventricular fibrillation (N=7): LEAP (28 episodes, Ē=0.17±0.16J); defibrillation (12 episodes, Ē=1.34±0.89J; see SI). The box plots show the median and the 25th and 75th percentiles. The whiskers indicate the statistically significant data range and red crosses mark outliers.

e Optical mapping of the AF termination also shown in panel c. During AF complex spatio-temporal propagation of electrical excitation waves was observed (white line indicates boundary of atrium). LEAP (n=5, Δt=90 ms) progressively synchronized the tissue (movies S1, S2).

Data given as mean±standard deviation unless stated otherwise.

To identify the biophysical mechanisms underlying LEAP, we conducted in vitro experiments with isolated, perfused atria, using the same electrode configuration as the corresponding in vivo experiments. In vitro, fluorescence imaging allowed quantitative measurements of action potential propagation on the surface of the tissue with high spatial and temporal resolution (see methods). To assess differences in LEAP effectiveness between the in vivo and in vitro preparations, three of the five in vitro preparations were derived from the hearts used in the in vivo experiments. A time series of the fluorescence signal is shown in Fig. 1c (same heart as in Fig. 1b). For t<0, we observed sustained AF with a dominant frequency of f_v=6.8±0.1Hz. Following LEAP (gray shaded area), normal sinus rhythm was restored. The LEAP pulse energy was 0.066±0.017 J, compared to 1.15±0.29J for standard, single-pulse defibrillation. The overall energy reduction in the in vitro experiments (N=5 preparations, 39 defibrillation episodes, and 46 LEAP episodes) was 91% (Fig. 1d) (P<10⁻⁷). There was no significant difference in the energy required in vivo and in vitro for LEAP (P=0.49) and conventional defibrillation (P=0.63). Our findings are also in agreement with a separate set of in vitro experiments¹⁵ in canine right atrial preparations (N=8) in which LEAP terminated AF with a success rate of 93%, using only 13% of the energy per pulse required by a single shock (P<0.002). Furthermore, LEAP effectiveness was demonstrated for ventricular fibrillation in vitro (N=7 canine preparations, 12 defibrillation and 28 LEAP episodes). In these experiments (Fig. 1d), the average energy reduction of LEAP vs. a single shock was 85% (P<10⁻⁵). The spatiotemporal excitation dynamics of the right atrium in vitro before, during and after control is shown in Fig. 1d (movie S1). During fibrillation, waves of turbulent electric activation propagate across the atria. At t=0, a sequence of five electric pulses is applied at the coil electrodes followed by a transient, spatio-temporal reorganization of the activation waves. Following each pulse, the area activated increases, indicating progressive synchronization of the myocardium: fibrillation terminates and normal sinus rhythm (movie S2) can resume.

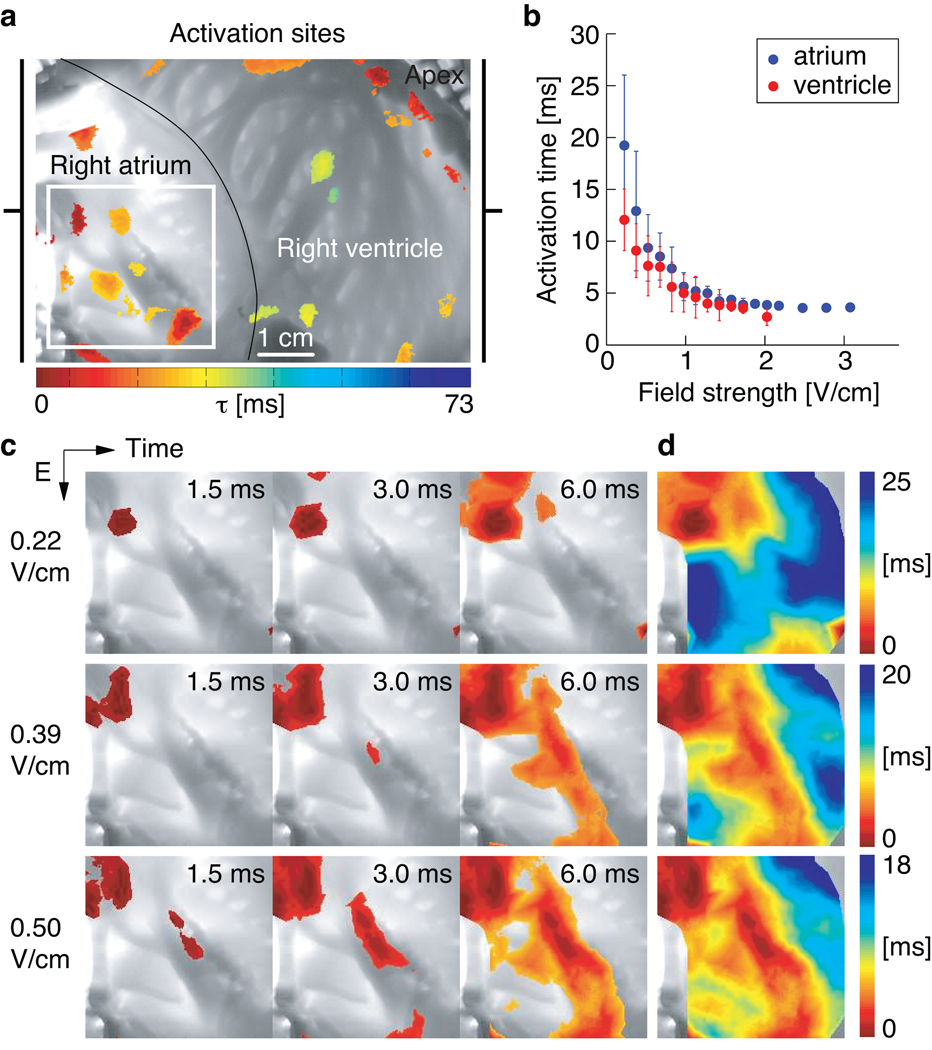
To elucidate the mechanism of defibrillation by LEAP, we studied the response of quiescent atrial and ventricular tissue to a homogeneous, pulsed electric field (Fig. 2a–b). . In Fig. 2c, images taken at 1.5, 3, and 6 ms after the pulse (0.22 V/cm) show depolarization induced by a single source. However, with increasing electric field strengths of 0.22, 0.39, and 0.50 V/cm the number of sources increases to several dozen over the entire tissue. The locations of these sources and the wave propagation patterns are summarized in the isochronal maps shown in Fig. 2d. The density of sources, shown in Fig. 2c–d, increased for both ventricle and atrium with increasing field strength thereby decreasing the activation time (Fig. 2b).

Figure 2. Sites of activation in a cardiac preparation.

a Canine wedge preparation (7.5×5.6 cm²) consisting of right atrium and right ventricle. At t=0 s an electric field pulse of strength E=0.34 V/cm was applied for 5 ms. The color indicates the time of local activation observed with fluorescence imaging on the endocardium; gray scale trans-illumination image shows its complex anatomy.

b Mean activation times τ(E) for atria (blue circles, N=3 preparations, 17 measurements of τ(E)) and ventricles (red circles, N=6 preparations, 24 measurements of τ(E)) in response to an electric field pulse of strength E and duration 5 ms. Error bars indicate the standard deviation.

c Activation of the atrium (in the region indicated by the white square in panel a) after an electric field pulse at t=0. With increasing field strength the number of activation sites increased, while the time interval for total activation decreased. The color code for each row is shown in panel d (movie S3). For E<0.2 V/cm no waves were observed.

d Isochrone maps of the activation sequences shown in panel c.

The results can be explained within the context of virtual electrodes (VE)^15–20. In the bidomain representation the voltage in cardiac tissue is the potential drop between the intracellular and extracellular medium. Theory predicts¹⁶ that in the presence of an electric field tissue conductivity discontinuities such as blood vessels, changes in fiber direction, fatty tissue, and intercellular clefts induce a redistribution of intracellular and extracellular currents that can locally hyperpolarize or depolarize the cells. At a depolarization threshold, an excitation wave is emitted^15–17,21.

The electric field necessary to produce activations as a function of conduction discontinuity sizes in quiescent tissue can be estimated by approximating the discontinuous geometries (circles in 2d, spheres in 3d) and linearizing the bidomain model equations^16,21,22 around the resting membrane potential²¹ obtaining

$${\nabla }^{2}e-\frac{e}{{\mathrm{\lambda }}^2}=0,$$ (1)

where e=Φ−Φ_rest, Φ and Φ_rest are the induced and resting membrane potentials, and λ (~0.35 mm) is the space constant. For a non-conducting tissue region of radius R, the minimum electric field E necessary to bring the voltage above the excitation threshold Φ_t at the boundary (r=R) is given by

$$E=-\frac{{\mathrm{\Phi }}_t-{\mathrm{\Phi }}_{\mathit{\text{rest}}}}{\mathrm{\lambda }}\frac{K_1^{\prime }(R/\mathrm{\lambda })}{K_1(R/\mathrm{\lambda })},$$ (2)

where K₁(R/λ) is the modified Bessel function of the second kind (see SI). Qualitatively, Eq. 2 implies that the smaller the size of the heterogeneity, the larger the electric field E required to emit waves. Equivalently, when E increases, discontinuities with a size larger than r≥R_min(E) are recruited as wave sources, where R_min(E) is obtained by solving Eq. 2; R_min(E)≈1/E when E is large (Fig. S13). The heart has heterogeneities of all sizes R, with a distribution p(R).

Assuming these heterogeneities are uniformly distributed in the tissue, the density of recruited wave sources is

$$\mathrm{\rho }(E)=\frac{N_{\mathit{\text{total}}}}{V}{\displaystyle {\int }_{R_{\text{min}}(E)}^{R_{\text{max}}}p(R)dR,}$$ (3)

where R_max is the size of the largest discontinuity in the tissue.

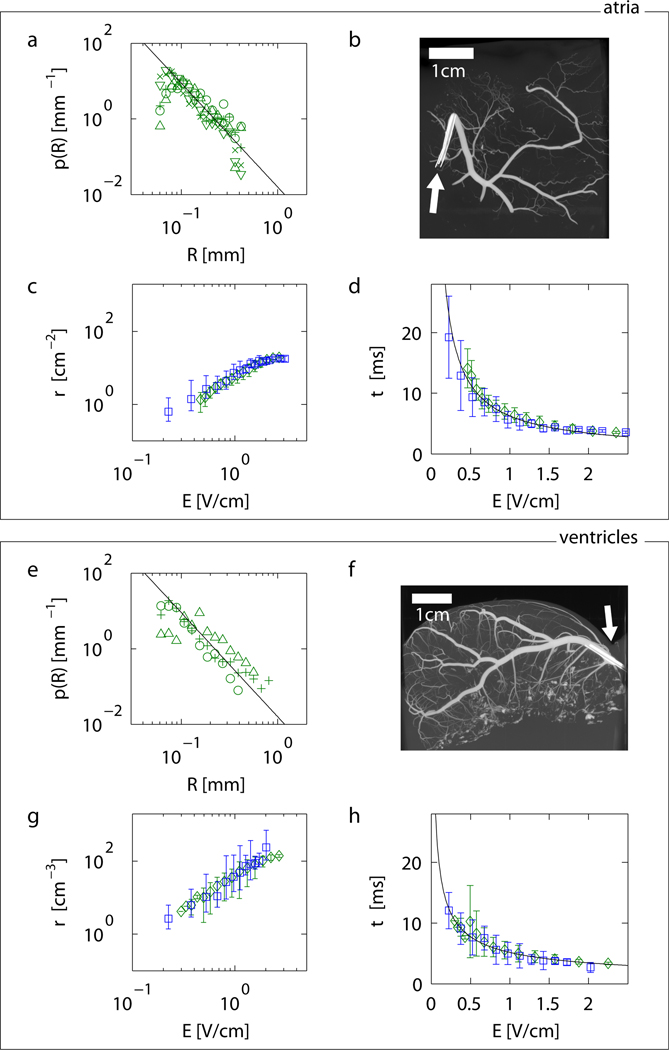
To quantify p(R) associated with blood vessels in intact cardiac tissue, the coronary arteries of eight cardiac preparations were perfused with contrast agent and scanned using micro-computed tomography (micro-CT; Fig. S1–S3, S12). As shown in Figs. 3a and 3e, the size distribution p(R) of discontinuities yielded power laws p(R)∝R^α with exponents α=−2.74±0.05 (N=5 preparations, Tab. S1, Fig. S4, S6) for atria and α=−2.75±0.30 (N=3 preparations, Tab. S2, Fig. S4, S5) for ventricles. In biological systems power law scaling reflects generic underlying physical and physiological design principles relating form and function^23,24.

Figure 3. From anatomical structure to activation dynamics in atria (a–d) and ventricles (e–h).

a Probability distribution of radii p(R) of canine coronary arteries in atrial tissue obtained from micro-CT measurements (N=5, for symbols see SI). The black line indicates the power law p∝R^{−2.74±0.05} (mean scaling exponent of all preparations).

b,f Example of (b) atrial and (f) ventricular anatomical structure of coronary arteries (movies S9–S10). White arrows indicate the position of the catheters used to inject the contrast agent (see SI).

c Density of wave sources derived from Eq. 3 and the atrial measurements shown in panel a (green diamonds) and corresponding density estimated from activation time measurements shown in panel d (blue squares). The predicted density from the structural data in a is plotted as the mean of the predictions from individual preparations.

d Atrial activation time measurements using optical mapping (blue squares) and corresponding prediction of activation dynamics (green diamonds) based on the source density obtained in c from the size distribution in a (plotted as the mean of predictions from individual preparations). The black line indicates the power law τ∝E^{−0.87±0.03} (see Tab. 1 and SI).

e Probability distribution p(R) of coronary artery radii for ventricular tissue (N=3). The black line indicates the power law p∝R^−2.75±0.3 (mean scaling exponents of all preparations).

g Density of wave sources derived from the ventricular measurements shown in panel e (green diamonds), and corresponding density estimated from activation time measurements shown in panel h (blue squares).

h Ventricular activation time measurements (blue squares) and prediction of activation times (green diamonds) based on p(R). The black line indicates the power law τ∝E^{−0.58±0.10} (Tab. 1 and SI).

Error bars indicate standard deviation in all plots.

The geometric structure of the coronary vasculature results in characteristic activation dynamics in response to a pulsed electric field, and so the activation times as a function of field strength shown in Fig. 2b can be predicted using Eq. 3 and p(R). The excitation wave emitted by a single heterogeneity and propagating radially at constant velocity v excites a volume V=4/3π(vτ)³ in a time interval τ. For N heterogeneities uniformly distributed with density ρ=N/V, the entire tissue is excited after

$$\mathrm{\tau }(\mathrm{\rho })={(3/(4\mathrm{\pi }\mathrm{\rho }))}^{1/3}/v.$$ (4)

Eqn. 2–4 relate quantitatively the structural properties (i.e., size distribution) with functional dynamics (i.e., activation times). In particular, Eqn. 2–4 imply, see SI, that the exponents of size distributions p(R)∝R^α and activation times τ∝E^β are related for large E by

$$\beta =(1+\alpha )/d,$$ (5)

where d is the geometric dimension of the tissue.. To assess the role of tissue geometry, we measured the scaling exponents α and β for the thick ventricular wall (d=3) and the thin, quasi-two-dimensional atrial wall (d=2). We used the measured size distribution exponents α to estimate the activation time exponents β_p using Eq. 5. The predicted exponents β_p are found to be in good quantitative agreement with the observed exponents β_o for atrial and ventricular tissue (Tab. 1, S3-S4; Fig. S7-S9).

From the measured size distribution p(R) shown in Fig. 3a we numerically estimate the intramural wave source density ρ(E) using Eq. 3 (green symbols in Fig. 3c) and τ(E) using Eq. 4 (green symbols in Fig. 3d, see SI). Similarly, from the measured activation time τ(E) shown in Fig. 3d (blue symbols), we numerically estimate the intramural wave source density ρ(E) (blue symbols in Fig. 3c) using the inverse of Eq. 4. Figures 3c–d and 3g–h show comparisons between measured and calculated data for atria and ventricles, respectively. Green symbols represent results based on the measured size distribution p(R), whereas results based on the measured activation time τ(E) are shown in blue. Again, excellent agreement is found (Tab. 1). Our results show that the structural properties of the coronary vasculature quantitatively describe the time scales of tissue activation.

The experimental results shown in Fig. 3 indicate that in addition to the known effect of recruiting tissue boundaries during an electric shock²⁵, the heterogeneity of the vascular structure allows the recruitment of an effective density of wave sources inside the myocardium. These distributed wave sources can be used for non-invasive intramural multi-site pacing, which is key to the novel approach of LEAP as demonstrated in Fig. 1. Previous studies aimed to control a single, isolated vortex attached to a large heterogeneity^{21, 26, 27} and it was hypothesized that in tissue with many heterogeneities of different sizes, it should be possible to control disordered regimes²⁸ by varying the electric field strength to control the number of wave sources²⁹. An experimental demonstration of this approach was provided for AF¹⁵; however, the underlying control mechanism was not explored.

As shown in Fig. 3, strengthening the electric field increases the density of wave sources. Thus, the probability of wave sources both in regions of excitable tissue and in the vicinity of filaments increases. Being excitable, these regions can be brought above the excitation threshold and fully depolarized by the applied electric field pulse. Thus they act as control sites that directly affect vortex filaments, the source of fibrillation.

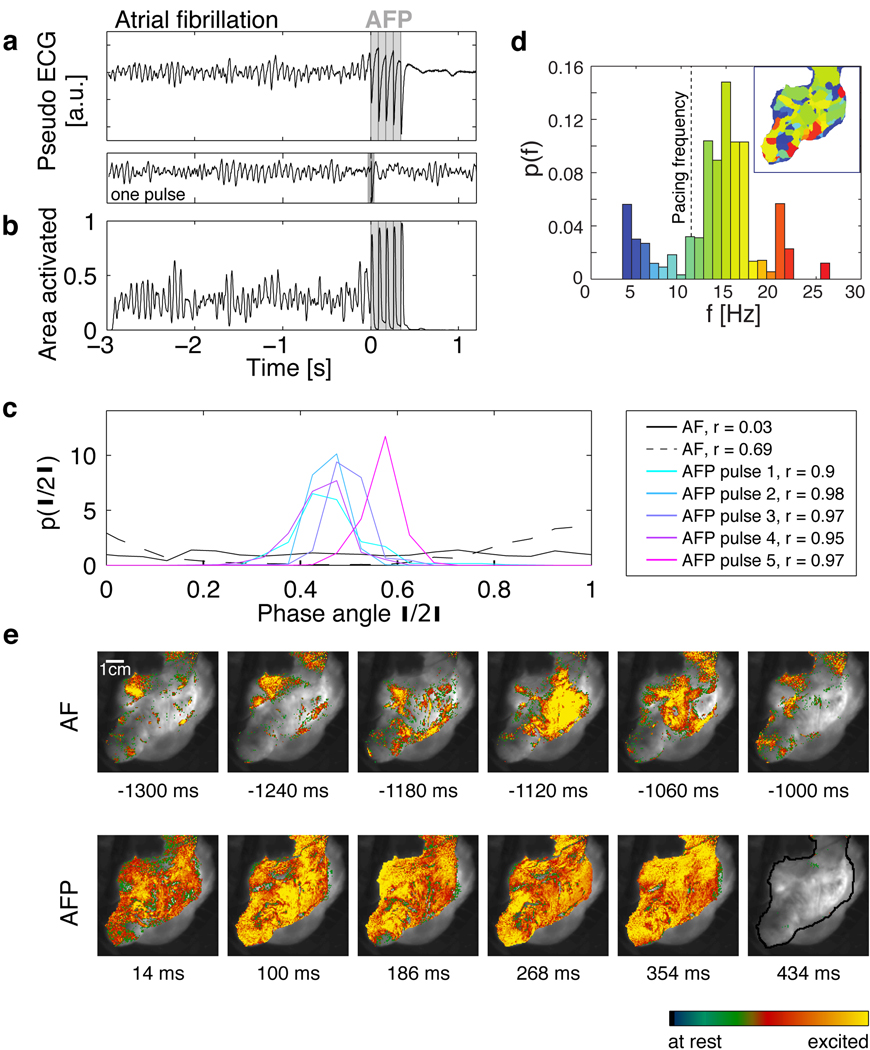
Figure 4 provides experimental evidence that LEAP interacts directly with multiple vortices simultaneously. During AF, complex spatio-temporal dynamics with multiple interacting waves is observed (Fig. 4e, movie S10), evidenced by the presence of multiple phase singularities. During the episode of AF shown in Fig. 4, we observed 9.9±4.4 (mean ± std) phase singularities, resulting in the spatial complexity of the dominant frequency map (Fig. 4d, inset) and the corresponding broad frequency probability distribution centered around 15 Hz (Fig. 4d). The observed spatio-temporal complexity can also be found in the pseudo-electrocardiogram (pseudo-ECG) and the percentage of area activated (PAA) (Fig. 4 a,b; SI). While both signals show complex amplitude fluctuations during AF, the periodic perturbations during LEAP defibrillation result in increasingly coherent dynamics of the entire tissue associated with a progressive amplitude increase of the pseudo-ECG and the PAA. During AF, the normalized PAA is 0.28±0.11 (mean±std), while during LEAP PAA increases with each pulse towards 1, i.e., simultaneous activation of the entire tissue. Following LEAP, AF is terminated and periodic normal rhythm resumes (movie S10).

Figure 4. Direct access to vortex cores.

a Termination of fibrillation with LEAP. The pseudo ECG is obtained from the optical mapping experiments (see SI). The dominant frequency during AF is f_v=15.0±0.5Hz (see inset in d). The vertical gray lines indicate the times at which 5 LEAP pulses (f_LEAP=11.8Hz, E=1.96 V/cm) were delivered. A single pulse at this field strength did not terminate fibrillation (pseudo ECG below panel A). Following LEAP normal rhythm is resumed. The termination of fibrillation with f_LEAP<f_v was observed in atria (N=3, 5 episodes) and ventricles (N=1, 3 episodes).

b Area activated indicates tissue synchronization during LEAP. Gray lines indicate timing of LEAP pulses.

c Probability distribution of phases θ_j during AF and for the times of strongest synchronization (maximum order parameter r, see legend) after each LEAP pulse (see SI). During AF, broad phase distributions indicate partial coherence (solid and dashed black lines show two representative distributions). LEAP with f_LEAP<f_v induces synchronization and thus termination of AF.

d Probability distribution of dominant frequencies during AF obtained from optical mapping. The dominant frequency map (inset) shows a complex spatial domain structure corresponding to multiple interacting waves (for color code see histogram; f_v=15.0±1.0Hz; f_LEAP=11.8±0.5Hz indicated by a vertical dashed line).

e Spatio-temporal dynamics during AF, LEAP (images taken at the times of maximum area activated after each pulse; see b), and sinus rhythm (movie S8). The grayscale image shows the atrium (see black line in the last image; 70×70 mm²). The last image shows quiescence after AF termination.

While Fig. 1 demonstrates LEAP defibrillation efficacy, Fig. 4 shows that tissue synchronization and therefore control of fibrillation is achieved by perturbing the system near the filaments, where it is most susceptible to perturbations³⁰. A periodic perturbation can reach a nearby filament only if f_LEAP>f_v, where f_LEAP is the frequency of the perturbation and f_v the frequency of the associated vortex. However, if f_v exceeds f_LEAP, a distant wave source cannot perturb the filament due to wave annihilation (Fig. S10–S11). Nevertheless, as shown in Fig. 4a–b, AF was terminated with f_v>f_LEAP. We quantified termination of multiple filaments with f_v>f_LEAP in atrial (N=4 preparations, 6 episodes) and ventricular (N=1 preparation, 3 episodes) tissue (Tab. S5). This result demonstrates simultaneous, local access to the multiple filaments. Our experiments indicate that by adjusting the number of recruited sites, this approach may successfully terminate fibrillation, regardless of whether fibrillation is caused by multiple reentrant waves or a single mother rotor^1–3. Consequently, this mechanism is applicable to multiple underlying causes for fibrillation, in both atria and ventricles. Our findings on the mechanism of defibrillation, together with the in vivo proof of defibrillation of atria with LEAP, should allow the development of new approaches toward alternative life-saving defibrillation techniques.

Methods Summary

Experiments were conducted in open-chest anesthetized dogs or in isolated arterially perfused canine atrial and ventricular preparations in vitro (see methods). Atrial fibrillation was induced in vivo using rapid pacing during stimulation of the right vagus nerve (2–4 mA at 10 Hz) and in vitro during perfusion with acetylcholine (1–3 µM). Ventricular fibrillation was induced in vitro using rapid pacing. Membrane potential was recorded in vitro by optical mapping using a voltage-sensitive dye (di-4-anepps). Standard 6.5F cardioversion catheters were used to deliver defibrillation shocks in vivo and in vitro. The shocks consisted of 1–5 symmetrical biphasic pulses of 8 ms duration at shock strengths of 20–100 V delivered via a custom-built cardioverter/defibrillator. Immediately following the optical mapping experiments, tissues were injected with 1–2 mL of Microfil contrast agent at 0.05–0.15 mL/min via the same cannula used for perfusion. The chambers were then filled with silicone to preserve tissue morphology during scans performed using a GE 120 micro-CT scanner with 25 µm x-y-z resolution to determine blood vessel sizes and distributions.

Methods

Cardiac Preparation (in vivo)

Adult beagle dogs (n = 7) were induced with Fentanyl citrate (0.05 mg/kg) and Propofol (0.025 mg/kg) given as two sequential intravenous boluses. Following administration of Atracurium (0.4 mg/kg iv), the dogs were intubated and artificially ventilated with oxygen and maintained under general anesthesia with Fentanyl continuous rate infusion (0.004 mg/kg/hr). A median sternotomy was performed and the heart suspended in a pericardial cradle. Normal body temperature was maintained with an inflatable heated body jacket and fluid losses were replaced with lactated Ringer’s solution (at 10 ml/kg/hr iv). Blood oxygen saturation and carbon dioxide levels were monitored continuously and maintained within normal limits by varying the tidal volume and/or respiratory rate.

The dogs were instrumented with 8 F introducers in both femoral veins to allow passage of catheters to provide programmed stimulation to induce AF and to suppress AF using Low-Energy Anti-fibrillation Pacing (LEAP) as well as to monitor atrial activation. The catheters were 6.5 F and 160–175 cm long, with a single coiled wire monofilament cardioversion electrode 6 cm in length situated 1 cm from the tip of the catheter (Modified Rhythm and Impact catheters, Rhythm Technologies Inc.). The catheters also carried two sensing electrodes distal to the coiled wire electrode. One catheter was placed via a femoral vein introducer and advanced until its coil electrode was positioned in the left pulmonary artery. A second catheter was placed so that its coil electrode was positioned in the right atrium. Alternatively, one of the catheters was inserted into the left atrium via a puncture wound in the left atrial appendage. The LEAP stimulus was then applied across the two catheter coils. In four of the dogs, LEAP stimulation also was delivered via patch electrodes sutured to the right and left atrial appendages. The patch electrodes consisted of 2×2 cm pieces of stainless steel wire mesh insulated with rubber membrane on the surface not in contact with the atrial tissue. Atrial sensing was performed using a monophasic action potential (MAP) catheter (7 F, EP Technologies), which was advanced via the femoral vein into the right atrium.

The following signals were recorded: lead II surface ECG, MAP from the right atrium, bipolar electrograms from the right and left atria and arterial blood pressure. The recordings were acquired at a sampling frequency of 1000 Hz and stored digitally using a data acquisition system (BioPac Systems, MP 150, software: AcqKnowledge® 3.7.3).

To permit stimulation of the vagus nerve and thereby facilitate the induction and maintenance of AF, the right cervical vagus nerve was isolated, doubly ligated and cut. Bipolar iridium wire electrodes, insulated except at the tip, were inserted into the sheath of the nerve and connected to a WPI stimulator. Immediately prior to AF induction and continuously during AF, pulses of 2 ms duration were delivered at a current strength that produced the maximum reduction in sinus rate (typically 2–4 mA) at a stimulus frequency of 10 Hz. The region surrounding the cut end of the nerve was bathed in mineral oil to prevent desiccation and preserve intact function over the 5–7 hour time course of the experiment. AF was induced using a pace-down protocol, where a train of symmetrical biphasic LEAP pulses of 8 ms duration (4 ms up/4 ms down) was delivered at an intensity of 2.0 V, initially at a cycle length of 300 ms. The cycle length subsequently was shortened progressively until AF was induced.

Following instrumentation of the dog, the experimental protocol was: 1) determine the threshold for activation of the atria using a single symmetrical biphasic LEAP stimulus pulse (4 ms up/ 4 ms down) delivered at a constant cycle length of 400 ms; 2) determine the impedances of the LEAP electrodes by delivering single 8 ms duration biphasic pulses at voltages of 10, 20, 40, 60, 80 and 100 V and measuring the resulting voltage deflection at the sensing electrode; 3) determine the intensity and frequency of vagal stimulation required to maximally reduce sinus heart rate; 4) induce AF using the pacedown protocol described above and monitor for 2 minutes; 5) attempt to cardiovert using a single 8 ms duration electric shock, starting with a shock strength of 40 V and increasing the voltage by 5–10 V increments until cardioversion occurred, up to a maximum of 100 V; 6a) if cardioversion was successful, reinitiate AF and attempt to suppress AF using 5 symmetrical biphasic LEAP pulses of 8 ms duration (4 ms up/4 ms down) delivered at a cycle length 5–10 ms shorter than the cycle length corresponding to the dominant frequency during AF, as determined using an FFT of the MAP recording, and at an initial voltage of 10 V, followed by 5–10 V increments until AF was suppressed; 6b) if cardioversion was not successful, attempt to suppress AF using LEAP stimulation; 6c) if neither cardioversion nor LEAP stimulation was successful, turn off vagal stimulation and suppress AF using a single shock or LEAP stimulation; 7) repeat steps 4–6 for an additional 3–5 trials; 8) change the LEAP electrode configuration (e.g., from catheters to patch electrodes) and repeat steps 1–7.

The experimental procedures were approved by the Institutional Animal Care and Use Committee of the Center for Animal Resources and Education at Cornell University.

Cardiac Preparation (in vitro)

Adult beagle dogs of either sex, age 1–4 years (n = 5 for the atrial and n=7 for the ventricular experiments) were anesthetized with Fatal-Plus (390 mg/mL pentobarbital sodium; Vortex Pharmaceuticals; 86 mg/kg IV) and their hearts excised rapidly. For the atrial experiments, following excision, the right and left coronary arteries were cannulated using polyethylene tubing and the right and left atria were excised and perfused with normal Tyrode solution bubbled with 95% O2, 5% CO2 at PO2 = 400–600 mm Hg, pH = 7.35 ± 0.05 and temperature = 37.0 ± 0.5°C. The flow rates of the perfusate and superfusate were 20 ml/min and 60 ml/min, respectively, at a perfusion pressure of 50–80 mm Hg. After 15 to 30 minutes of equilibration, the preparation was stained with the voltage-sensitive dye Di-4-ANEPPS (10 µmol/L bolus). Blebbistatin (10 µmol/L constant infusion over 30 to 40 minutes) was added to prevent motion artifact.

LEAP pulses were delivered from a custom-built cardioverter/defibrillator, which was capable of generating pulse sequences with a specified number of pulses, pulse duration, polarity, and shape). The computer-controlled device used a digital-to-analog converter (NI USB-6259 BNC) to generate arbitrary waveforms, which were amplified using a power amplifier (Kepco BOB 100–4M). The waveform was configured manually using a Labview program or was loaded from a database. Electrophysiological signals and various monitor signals (e.g., delivered current and voltage) were recorded using an analog-to-digital converter (NI USB-6259 BNC). The signals were analyzed in real time and used to automatically select the LEAP parameters. An automated impedance measurement was used to calibrate the pulse energy. The data obtained during the experiment were stored in a database for offline analysis.

Standard bipolar stimulating electrodes were placed on the right and left atria (in the same positions as in the corresponding in vivo experiments) and field stimulation was delivered as described above. To calculate the energy delivered, the impedance of the electrodes was determined by delivering single 8 ms duration biphasic pulses at voltages of 10, 20, 40, 60, 80 and 100 V and measuring the resulting voltage deflection at the sensing electrode. Pacing stimuli were delivered using a WPI stimulator and stimulus isolator and LEAP stimuli were delivered using a function generator and custom-built current source. Field strengths in excess of 5 V/cm could be delivered using this device at cycle lengths as short as 50 ms. The field strength between the electrodes was measured using two Teflon-coated silver wires immersed in the bath and set 5 to 10 mm apart.

To verify tissue viability, the excitation threshold for far-field stimulation in quiescent myocardium was determined by monitoring optical wave activity following application of a sequence of 5 LEAP pulses and compared to the corresponding in vivo study values. AF subsequently was initiated using rapid pacing, either with or without acetylcholine (ACh; 1–3 µM) in the perfusate, where the concentration of ACh was titrated to induce AF having a similar dominant frequency to that observed in vivo. The presence or absence of AF was documented by monitoring wave activity optically. The dominant frequency during AF was determined from the FFT of a single pixel recording that could be moved in real time to assess the range of frequencies throughout the tissue. At the end of the study, the excitation threshold was recalculated to confirm the stability of the tissue. For the ventricular experiments, the protocols were similar to those used for the atrial experiments, as described in detail previously¹⁵. However, no ACh was used and fibrillation was initiated by rapid pacing.

The experimental procedures were approved by the Institutional Animal Care and Use Committee of the Center for Animal Resources and Education at Cornell University.

Optical fluorescence imaging

Illumination was provided by LEDs (Luxeon, 5W, 530 nm). High-NA lenses (F-number 0.95, focal length 50 mm) were fitted with long wavelength-pass emission filters (580 nm). The epicardium and endocardium were imaged simultaneously using two synchronized cameras: the control site studies used two high-resolution, high-speed CMOS cameras (Vision Research Phantom V7, 600 × 800 pixels, 12 bit, 2000 frames per second), whereas arrhythmia termination experiments used two EMCCD cameras (electron multiplied charge coupled device, Photometrics Cascade 128+, 128 × 128 pixels, 16 bit, 511 frames per second). The pseudo ECG is defined as the mean of the optical fluorescence signal over the entire field of view.

Micro-computed Tomography

Immediately following optical mapping experiments, tissues were injected with 1–2 mL of Microfil contrast agent (Flow Tech Inc., USA) at 0.05–0.15 mL/min via the same cannula used for perfusing the tissue. The chambers were then filled with silicone to preserve tissue morphology during the scan. The contrast agent and silicone were allowed to set for at least 4 hours before being scanned. The scans were performed using the GE CT120 micro-CT scanner (GE Healthcare, London, Ontario, Canada). For each dataset, 1200 projections were obtained at 0.3° intervals over 360° using 80 keV, 32ma, and 25µm x-y-z resolution. Prior to each scan, 10 bright-field images were acquired with no objects in the field of view, providing a correction for detector non-uniformity. Each image dataset collected was transferred from the CT120 system to an image-processing workstation (HP xw8400 with 8 CPU cores and 16GB RAM). The projection views were used to reconstruct a CT image using a convolution back-projection approach implemented in 3D, giving a 40×40×40 mm³ volume of image data with 25 µm or 50 µm isotropic voxels in analog-to-digital units. Correction for signal non-uniformity across the field of view was determined from measurement within a water/tissue phantom (SB201), scanned with the same X-ray protocol. Ten axial slices within this water phantom were averaged, to produce a 2-D map of offset values, used to correct for non-uniformity at any point within the image. Corrected image datasets were calibrated to the conventional scale of Hounsfield units (HU), defined so that water and air have values of 0 and −1000, respectively. The maximum intensity projection (MIP) shown in Fig. 3B,F is an orthographic projection which maps voxels with maximum intensity that intersect parallel rays from the viewpoint to the plane of projection. The details of the analysis is given in S

Table 1.

Observed and predicted scaling exponents for the size distribution p(R) and the activation time τ(E) for atria and ventricles.

Tissue	d	αo	βo	βp**)	βp*)
Atrium	2	−2.74 ± 0.05	−0.81 ± 0.23	−0.88 ± 0.20	−0.87 ± 0.03
Ventricle	3	−2.75 ± 0.30	−0.75 ± 0.18	−0.74 ± 0.25	−0.58 ± 0.10

^*)β_p as obtained from the high field strength approximation Eq. 5;

^**)Average of β_p obtained from least square fits to activation times obtained from direct numerical estimation using p(R) and Eqn. 2-4 (Tab. S1-S4). Statistical analysis showed no significant difference for α_o for atria and ventricles (see SI).