Abstract
Previous studies have shown that the procedure-induced prostate edema during permanent interstitial brachytherapy (PIB) can cause significant variations in the dose delivered to the prostate gland. Because the clinical impact of edema-induced dose variations depends strongly on the magnitude of the edema, the temporal pattern of its resolution and its interplay with the decay of radioactivity and the underlying biological processes of tumor cells (such as tumor potential doubling time), we investigated the impact of edema-induced dose variations on the tumor cell survival and tumor control probability after PIB with the 131Cs, 125I and 103Pd sources used in current clinical practice. The exponential edema resolution model reported by Waterman et al. (Int. J. Radiat. Oncol. Biol. Phys. 41, 1069–1077–1998) was used to characterize the edema evolutions observed previously during clinical PIB for prostate cancer. The concept of biologically effective dose (BED), taking into account tumor cell proliferation and sublethal damage repair during dose delivery, was used to characterize the effects of prostate edema on cell survival and tumor control probability. Our calculation indicated that prostate edema, if not taken into account appropriately, can increase the cell survival and decrease the probability of local control of PIB. The edema-induced increase in cell survival increased with increasing edema severity, decreasing half-life for radioactive decay and decreasing energy of the photons energy emitted by the source. At the doses currently prescribed for PIB and for prostate cancer cells characterized by nominal radiobiology parameters recommended by AAPM TG-137, PIB using 125I sources was less affected by edema than PIB using 131Cs or 103Pd sources due to the long radioactive decay half-life of 125I. The effect of edema on PIB using 131Cs or 103Pd was similar. The effect of edema on 103Pd PIB was slightly greater, even though the decay half-life of 103Pd (17 days) is longer than that of 131Cs (9.7 days), because the advantage of the longer 103Pd decay half-life was negated by the lower effective energy of the photons it emits (~21 keV compared to ~30.4 keV for 131Cs). In addition, the impact of edema could be reduced or enhanced by differences in the tumor characteristics (e.g. potential tumor doubling time or the α/β ratio), and the effect of these factors varied for the different radioactive sources. There is a clear need to consider the effects of prostate edema during the planning and evaluation of permanent interstitial brachytherapy treatments for prostate cancer.
Keywords: prostate edema, prostate brachytherapy, cesium-131, iodine-125, palladium-103, tumor control probability
I. Introduction
Permanent interstitial brachytherapy (PIB) for early stage prostate cancer involves surgical implantation of 60 to over 100 radioactive sources into the prostate gland so that a potentially curative radiation dose can be delivered locally, to the cancer cells, with minimum radiation exposure to the normal tissues surrounding the prostate (Zelefsky and Whitmore 1997). By leaving the radiation sources permanently in the prostate gland, PIB is logistically convenient for patients compared to EBRT, which requires over six weeks of daily treatments. It also avoids the inter- and intra-fraction targeting uncertainties caused by organ motion and patient repositioning during the delivery of daily EBRT treatments.
On the other hand, the temporal pattern of PIB dose delivery is inherently more complex than that of EBRT. On-going radioactive decay causes the dose rate in PIB to decrease exponentially with time during treatment. In addition, the rate of exponential dose-rate reduction can be differ significantly among different radioactive sources. For the three sources used in current clinical practice, the decay half-lives vary over a six-fold range, from 9.7 days (131Cs) to 17 days (103Pd) and 60 days (125I). As a result, the initial dose rates and the effective treatment times differ drastically for PIB using different radionuclides. The time needed to deliver 90% of the prescribed dose varies from about one month to 2 and 6 months for PIB using 131Cs, 103Pd and 125I sources, respectively. Furthermore, the surgical procedures used to implant the sources can provoke acute swelling of the prostate gland (prostate edema) that can take days or weeks to resolve. The magnitude of the procedure-induced prostate edema and the rate of its resolution were found to vary widely from patient to patient (Moerland, Wijrdeman et al. 1997; Narayana, Roberson et al. 1997; Waterman, Yue et al. 1998). For example, the time needed to reduce the initial swelling by one-half (known as the edema resolution half-life) varied from 4 days to 25 days(Waterman, Yue et al. 1998). The combination of the implantation-induced prostate edema and the protracted radioactive decay results in a complex temporal pattern of dose delivery that is distinct for each PIB patient.
Because the cell survival after a given radiation dose can be affected profoundly by the rate at which the dose is delivered (see e.g. a review by Hall(Hall 1972)), the clinical impact of the different temporal dose delivery patterns associated with PIB should be evaluated carefully to consider the interacting effects of the choice of radionuclide and patient-specific variations in prostate edema. In our earlier work, we examined the impact of prostate edema on cell survival for PIB using 125I and 103Pd sources(Yue, Chen et al. 2002) and 131Cs in abstract form(Chen, Deng et al. 2007). The purpose of this work was to perform a comprehensive investigation tof the effects of prostate edema on PIB using 131Cs sources and to compare it with PIB using 125I and 103Pd sources. With these data, systematic assessment of the effects of procedure-induced prostate edema can be performed for all radioactive sources used currently in permanent interstitial brachytherapy for early-stage prostate cancer.
II. Methods and Materials
A. Edema model
The temporal characteristics of procedure-induced prostate edema have been studied extensively for 125I and/or 103Pd PIB using serial post-implant imaging. Waterman et al. (Waterman, Yue et al. 1998) found that the evolution of edema can be characterized quantitatively by the following function
| (1) |
where V(t) denotes the prostate volume at time t after the source implantation, V0 is the prostate volume before the implant, λE is the decay constant characterizing the rate of edema resolution, and tmax is the time of maximum edema at which prostate reaches the maximum swollen volume Vmax. The evolution of the target volume before reaching the maximum edema (typically taking about one day) was not included in Eq.(1) and its effect on dosimetry is negligible. The fractional increase in prostate volume at maximum edema is known as edema magnitude in literature and will be denoted by Δ (= (Vmax−V0)/V0) in this paper. For consistency with other publications, the edema magnitude will be expressed in percentage of the initial prostate volume, e.g. Δ = 0.3 as 30%. It has been shown that both the edema magnitude and the resolution half-life (which equals to ln2/λE) vary greatly between patients. The observed edema magnitudes have ranged from 30% to 100% of the initial prostate volume(Merrick, Butler et al. 1998; Waterman, Yue et al. 1998; Taussky, Austen et al. 2005). The observed edema half-lives ranged from 4 to 25 days (with an average around 10 days) (Merrick, Butler et al. 1998; Waterman, Yue et al. 1998; Taussky, Austen et al. 2005). Even larger variations in edema half-life, from 3 to 170 days, were reported by Leclerc et al.(Leclerc, Lavallee et al. 2006). In this work, Eq.(1) was used to describe the edema evolution for 131Cs PIB based on 1) 131Cs sources are implanted using the same guiding needle as 125I source because of their similar physical dimensions and 2) the needle pattern and number of needles needed are likely similar because the two sources emit similar photon energies.
The effect of edema on the locations of the implanted sources has been examined by several investigators. (Merrick, Butler et al. 1998; Waterman, Yue et al. 1998) Waterman et al. have shown that the variation in mean inter-seed distance also followed Eq.(1) (Waterman, Yue et al. 1998). Assuming that the edema resolution is spatially isotropic and that the implanted sources move with their surrounding tissue without relative migration, the distance between an implanted source (i) and a tumor sub-volume (P), ri(t), can be related to the distance just before the onset of edema, r0i, via Eq.(1) as
| (2) |
B. Dosimetry in the presence of edema
The instantaneous dose rate produced by a PIB at any given tumor sub-volume, Ḋ(t), was calculated following the dosimetry formalism of AAPM report TG-43 (Nath, Anderson et al. 1995), using the point source approximation,
| (3) |
where g(r) is the radial dose function, φ̄an is the average anisotropic factor, and λI is the radioactive decay constant. In absence of edema, the distances between the implanted sources and point P can be considered as stationary with ri(t)≡r0i. Equation(3) has a simple exponential dependence on time (due solely to the radioactive decay),
| (4) |
where Ḋ0 is the total initial dose rate produced at P by the static implant. In the presence of edema, ri(t) is time dependent. The total dose deposited at P can be calculated by substituting Eq.(2) into Eq.(3) with a parameterization of g(r)/r2 by r−τ such that Eq.(3) became,
| (5) |
The parameter τ was found to be 2.20 for the Model CS-1 131Cs sources (Chen, Deng et al. 2006). It is clear from examining Eq.(5) that the dose rate at a given tumor sub-volume is dependent on both the magnitude of the edema and its resolution half-life, in addition to the half-life of radioactive decay. The total dose delivered to the tumor sub-volume P can be obtained by integrating Eq.(4) or Eq.(5) over the entire time of treatment from the implant.
C. Biologically effective dose (BED) for prostate implants in the presence of edema
In the absence of prostate edema or other changes in prostate volume, the dose-rate from a permanent implant is characterized by a single exponential function, Eq.(4). For such an implant, Dale has derived an analytic form of BED that includes the effect of first-order sub-lethal damage repair and tumor cell proliferation (Dale 1985; Dale 1989). This formulation has been used by many investigators studying the radiobiological effects of PIB (see discussions in section IV on issues concerning the use of Dale model for proliferating cells in permanent brachytherapy). In presence of prostate edema, the dose rate, Eq.(5), is no longer a simple exponential function. However, Eq.(5) can be expressed as a sum of multiple exponentially decaying functions by performing a Taylor expansion of its denominator, i.e.
| (6a) |
with
| (6b) |
and
| (6c) |
Equation (6) implies that the dose rate at P in presence of edema is mathematically equivalent to an implant with multiple exponentially decaying “sources” having initial dose rates and decay time constants that are functions of the edema magnitude and half-life. Indeed, the n = 0 source represents the dose contribution by the implant in absence of edema and the rest of the “sources” (n ≥ 1) collectively give the correction due to edema. The Taylor expansion (well behaved mathematically for edemas with magnitudes <100%) was purposely done so that the BED of such an implant can now be calculated by using a formula derived by Chen and Nath for implants containing multiple sources of different half-lives as follows (Chen and Nath 2003)
| (7a) |
where
| (7b) |
and
| (7c) |
In the above equations, Teff denotes the effective treatment time at which the instantaneous tumor cell proliferation rate exceeds the rate of cell killing, D(Teff ) is the cumulative dose delivered up to Teff, α and β are the coefficients of linear-quadratic model that characterize the cell killing arising from one- and two-track radiation damages, respectively, μ is the time constant that models the first-order repair of sublethal damages during irradiation, and Tp is the potential doubling time, which is assumed to characterize the proliferation of the tumor cells during therapy. Numerical results presented in Results section were obtained with n = 300 in Eqs.(6) and (7). The convergence of series summation had been tested extensively. In general, contributions from n ≥ 200 terms were negligible (Yue et al. 2002).
It should be acknowledged that Dale et al. (Dale, Jones et al. 1994) and Antipas et al. (Antipas, Dale et al. 2001) had obtained a simpler formulation of BED when investigating the effects of tumor shrinkage during permanent implants using an isotropic and exponential volume shrinkage model, in which the tumor volume shrinks continuously from an initial volume to zero, rather than to a finite limiting volume as occurs in the case of edema resolution. For this study, we used Eq. (7) to examine the radiobiological impact of edema for the 131Cs implants.
D. Tumor control probability (TCP)
With BED, cell survival after irradiation is used as the surrogate for the potential biological responses to PIB (see the review by Fowler(Fowler 1989) for details), i.e.
| (8) |
where S denotes the surviving fraction of the irradiated cells. However, the linkage between the level of cell survival and a specific clinical response is not always linear. In this work, a TCP model based on Poisson distribution of cell survivals after irradiation was also used to assess the potential clinical impact of prostate edema. In this model, the probability of cure (i.e. the probability of having no viable tumor cells) after a given irradiation is given by
| (9) |
where <N> is the expectation value of the number of tumor cells that survived the treatment, which can be obtained directly from Eq.(8) if the initial tumor burden or the total number of tumor cells (N0) present before the start of treatment is known. Hence,
| (10) |
The dose response curve calculated by Eq.(10) usually has a steeper slope than that observed clinically. This is due in part to the averaging of individual patient’s dose response over a heterogeneous patient population (e.g., different initial tumor burden, radiosensitivity, and edema characteristics) in outcomes study. Other factors, such as variations in hypoxia or anti-tumor immune responses, that could affect the clinical response of individual patients but were not included this simple model may also contribute to the difference between the prediction of Eq.(10) and the clinically observed dose response curves. Equation (10) is used in this work to examine the potential effect of edema on individual patients. It would be inappropriate to compare the results in section III directly with a population-averaged clinical outcome. Such a comparison may be attempted only if the distribution of edema and radiobiology characteristics in a given patient population is known. Other limitations of the TCP model are discussed further in section IV.
E) Radiobiological parameters for cancer of prostate
The numerical values of α, α/β, Tp, T1/2 of sub-lethal damage repair, and N0 for prostate cancer vary significantly among the different reports in literature. In this work, a self-consistent set of nominal values for these parameters, based on the reports by Wang et al. (Wang, Guerrero et al. 2003; Wang, Li et al. 2003; Wang, Mayr et al. 2006) and recommended by AAPM report TG-137, were used. The nominal values for this set of parameters are α = 0.15 Gy−1, β = 0.05 Gy−2, α/β = 3.0 Gy, Tp = 42 days, repair half-life = 0.27 hour, and N0 = 106–107. Variations around these nominal values were used to assess the effects of prostate edema on tumors having different radiobiological and biological characteristics.
III. Results
Current clinical practice of PIB does not take into account patient-specific prostate edema during treatment planning because 1) the prostate edema that will later developing in individual patient is not known until after the source implantation and 2) the existing commercial treatment planning systems do not have tools that allow active consideration of the effects of edema in PIB planning. In this work, we used the edema model described by Eq.(1) to calculate the effects of prostate edema on BED, cell survival, and TCP for clinically relevant edema characteristics reported in literature and to examine the potential consequences of ignoring prostate edema during the pre-implant treatment planning. The prescribed doses used currently for PIB monotherapy (145 Gy for 125I, 125 Gy for 103Pd and 120 Gy for 131Cs) were used in all calculations, so that the results would be as clinically relevant as possible.
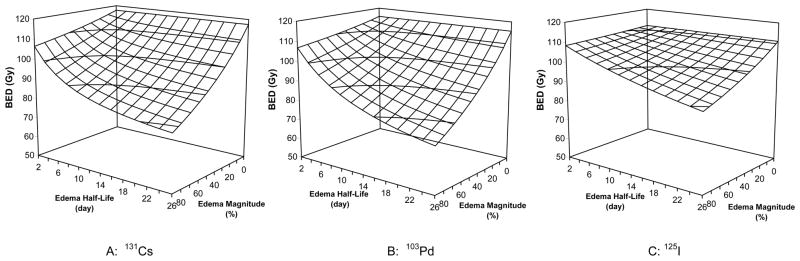
Figure 1 plots the BED as a function of edema magnitude and edema half-life for prostate PIB using 131Cs (Fig. 1A), 103Pd (Fig. 1B) and 125I (Fig. 1C) sources. The presence of prostate edema resulted in a reduction in BED comparing to PIB modeled without edema. The edema-induced reduction in BED increased with both increasing edema magnitude and increasing edema half-life. The impact of edema was modest for patients with minor edema (e.g. with a magnitude of 20% and a half-life of 5 days). The edema-induced reductions in BED were 5.2%, 4.6%, and 1.5% for PIB using 131Cs, 103Pd, and 125I sources, respectively. However, for patients with an average edema level (e.g. with a magnitude of 50% and a half-life of 10 days), the edema-induced reductions in BED were 16.5%, 15.8%, and 6.2%, for PIB using 131Cs, 103Pd, and 125I sources, respectively. For patients with severe edema (e.g. with a magnitude of 90% and a half-life of 20 days), the edema-induced BED reduction reached 31.7%, 33.6% and 16.7%, respectively, for PIB using 131Cs, 103Pd, and 125I sources.
Figure 1.
Edema-induced variations in the biologically effective dose (BED) for prostate brachytherapy using 131Cs, 125I, and 103Pd sources (α = 0.15 Gy-1, α/β = 3.0 Gy, Tp = 42 days, and repair half-time = 0.27 hour)
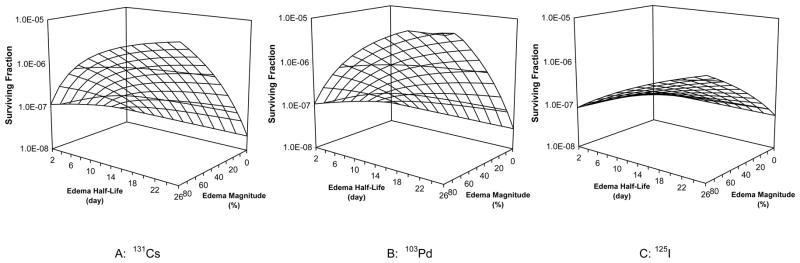
Figure 2 plots the cell survival as a function of edema magnitude and edema half-life for prostate PIB using 131Cs (Fig. 1A), 103Pd (Fig. 1B) and 125I (Fig. 1C) sources. The presence of edema increased the cell survival over that for PIB without edema. The magnitude of the edema-induced increase in cell survival increased with both increasing edema magnitude and increasing edema half-life. For patients with minor edema (e.g. with a magnitude of 20% and a half-life of 5 days), the surviving fraction increased by factors of 2.5, 2.2, and 1.3 for PIB using 131Cs, 103Pd, and 125I sources, respectively. For patients with an average level of edema (with a magnitude of 50% and a half-life of 10 days), cell survival increased by over a factor of 10 for 131Cs and 103Pd implants (approximately 18 and 15, respectively) and by a factor 2.8 for 125I implants. For patients developing severe edema (with a magnitude of 90% and a half-life of 20 days), the edema-induced increase in cell survival reached factors of 174, 333, and 16 for 131Cs, 103Pd and 125I implants, respectively.
Figure 2.
Edema-induced variations in cell survival after prostate brachytherapy using 131Cs, 125I, and 103Pd sources (α = 0.15 Gy-1, α/β = 3.0 Gy, Tp = 42 days, and repair half-time = 0.27 hour)
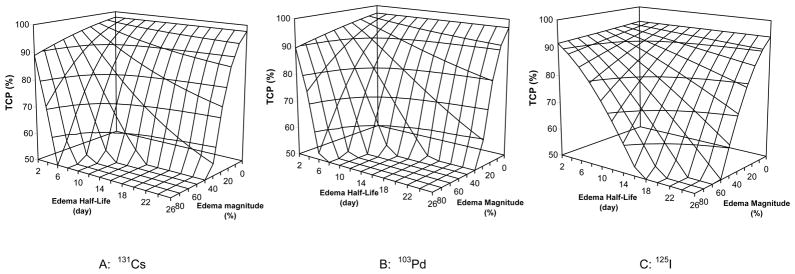
Figure 3 plots the effect of prostate edema on the tumor control probability as a function of edema magnitude and edema half-life for PIB using 131Cs (Fig. 1A), 103Pd (Fig. 1B) and 125I (Fig. 1C) sources. The edema-induced increase in cell survival led to reduced tumor control probabilities. The reduction in the TCP increased with increasing edema magnitude and increasing edema half-life. For patients with minor edema (e.g. with a magnitude of 20% and a half-life of 5 days), the reductions in TCP were small, only 3.2%, 3.5%, and 1.6% for PIB using 131Cs, 103Pd, and 125I sources, respectively. However, for patients with an average level of edema (with a magnitude of 50% and a half-life of 10 days), the TCP was reduced from 97% to 67%, from 97% to 62%, and from 94% to 85% for 131Cs, 103Pd, and 125I implants, respectively. In the extreme case of severe edema with a magnitude of 90% and a half-life of 20 days, 131Cs and 103Pd implants would fail to control the tumors while 125I implants would result in a poor TCP of about 38%.
Figure 3.
Edema-induced variations in tumor control probability for prostate brachytherapy using 131Cs, 125I, and 103Pd sources (α = 0.15 Gy-1, α/β = 3.0 Gy, Tp = 42 days, and repair half-time = 0.27 hour)
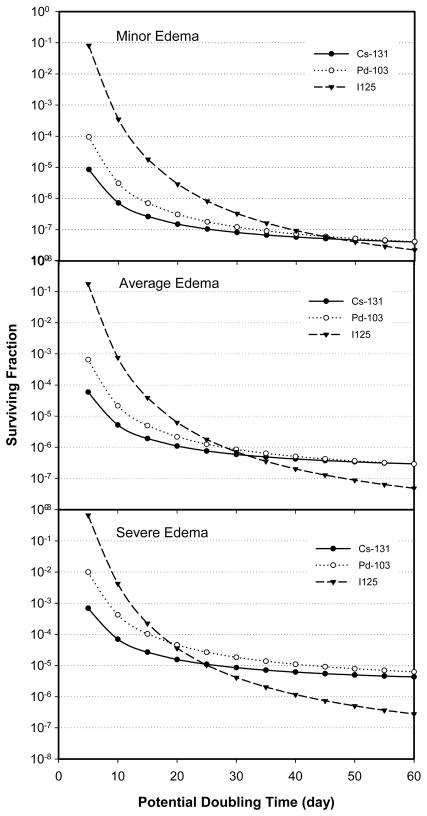
The effect of prostate edema on BED, cell survival, and TCP were also found to depend on the tumor characteristics (e.g. the potential doubling time, α/β ratio, and half-time for repair of sublethal damage). Figure 4 plots the cell survival as a function of tumor potential doubling time, while keeping the other radiobiological parameters the same ( namely, α = 0.15 Gy-1, β = 0.05 Gy-2, α/β = 3.0 Gy, and repair half-life of 0.27 hour), for PIB using 131Cs, 103Pd, and 125I sources under three edema conditions: minor edema with a magnitude of 20% and a half-life of 5 days (top panel), average edema with a magnitude of 50% and a half-life of 10 days (middle panel), and severe edema with a magnitude of 90% and a half-life of 20 days (bottom panel). Two general trends can be discerned easily from the data shown in Fig.4. First, the cell survival increased with both increasing edema magnitude and increasing edema half-life for tumors having the same potential doubling time. This finding is similar to those shown previously in Fig.2 for the Tp of 42 days. Secondly, cell survival increased with decreasing potential doubling time (i.e. for faster growing tumors). A significant difference in cell survival, by more than two orders of magnitude, was observed between a fast-growing tumor (with Tp of 5 days) and a slow-growing tumor (with Tp of 60 days) regardless of the edema condition and radioactive source used in the modeling. This implies that the actual tumor control probability for patients with fast-growing tumors could be significantly lower than expected if these patients were treated to a prescribed dose that had been established using data from patients having slow-growing tumors.
Figure 4.
Surviving fractions as a function of tumor potential doubling time for PIB using 131Cs, 103Pd, and 125I under three different edema conditions. (α = 0.15 Gy-1, α/β = 3.0 Gy, and repair half-time = 0.27 hour)
In addition to these general trends, Figure 4 also illustrates the interplay between edema, the half time for radioactive decay and tumor cell proliferation during treatment. For patients with minor edema (Fig. 4, top panel), PIB using 131Cs, 103Pd or 125I all produced similar cell survivals in slow growing tumors (tumors with Tp ≥ 40 days). As Tp decreased (i.e. moving toward faster growing tumors), PIB using 125I became increasingly ineffective, yielding cell survivals much higher than those obtained using 103Pd or 131Cs sources. PIB using 131Cs was most effective in producing low cell survivals for fast-growing tumors. At the Tp of 5 days, 131Cs produced one log10 lower cell survival than 103Pd and four log10 lower cell survival than 125Isources. For patients developing average edema (Fig. 4, middle panel), the relative differences in cell survival between 131Cs, 103Pd and 125I were similar to those in patients with minor edema for fast-growing tumors (with Tp < 30 days). However, for slow-growing tumors under this edema condition, 125I became more effective than either 131Cs or 103Pd. The advantage of 125I for treating slow-growing tumors became even more pronounced for patients developing severe edema (Fig. 4, lower panel), while the PIB using 131Cs remained consistently more effective than 103Pd and 125I for reducing cell survival in faster growing tumors.
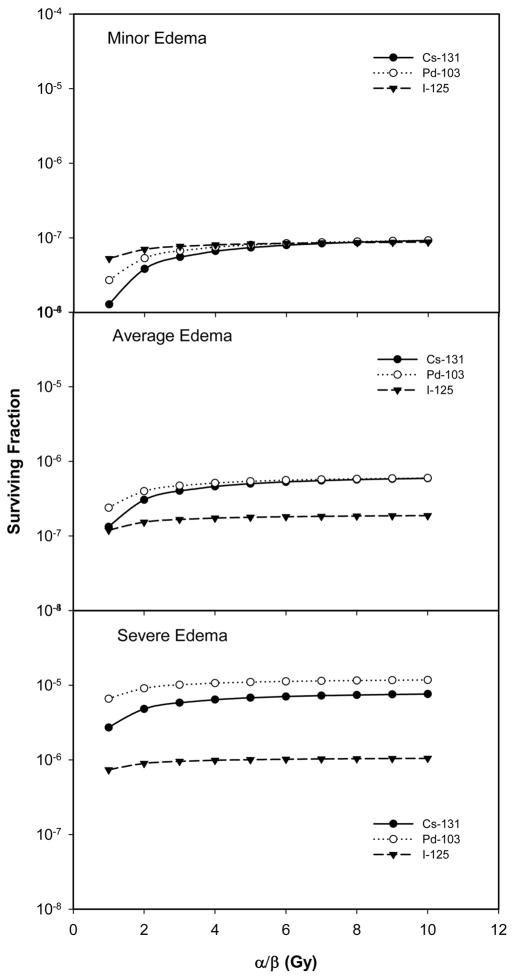
An interplay between prostate edema and the radiobiological characteristics of the tumor cells was also observed in our calculations. Figure 5 plots cell survival as a function of α/β ratio for PIB using 131Cs, 103Pd and 125I sources and for patients developing minor (top panel), average (middle panel) and severe (lower panel) edema. Other parameters were fixed, with α = 0.15 Gy−1, Tp = 42 days, and repair half-time = 0.27 hour. For patients with minor edema, the cell survivals after PIB using the three sources were similar for tumor cells having α/β ≥ 3 Gy, consistent with the fact that the prescribed doses for these sources were established to produce similar tumor control rates for PIB in the absence of prostate edema. For tumors with an α/β of 1 Gy, 131Cs was slightly more effective in decreasing cell survival than 103Pd which, in turn, was slightly better than 125I. For patients developing average edema, however, 125I became more effective in reducing cell survival while 131Cs and 103Pd remained similar because PIB using 125I is less sensitive to the effects of edema than PIB using 131Cs and 103Pd. The differences in cell survival for the three sources increased further for severe edema. For this level of edema, 125I produced 10 fold lower cell survivals than 131Cs and 103Pd over a wide range of α/β values.
Figure 5.
Surviving fraction as a function of tumor α/β ratio for PIB using 131Cs, 103Pd, and 125I under three different edema conditions. (α = 0.15 Gy-1, Tp = 42 days, and repair half-time = 0.27 hour)
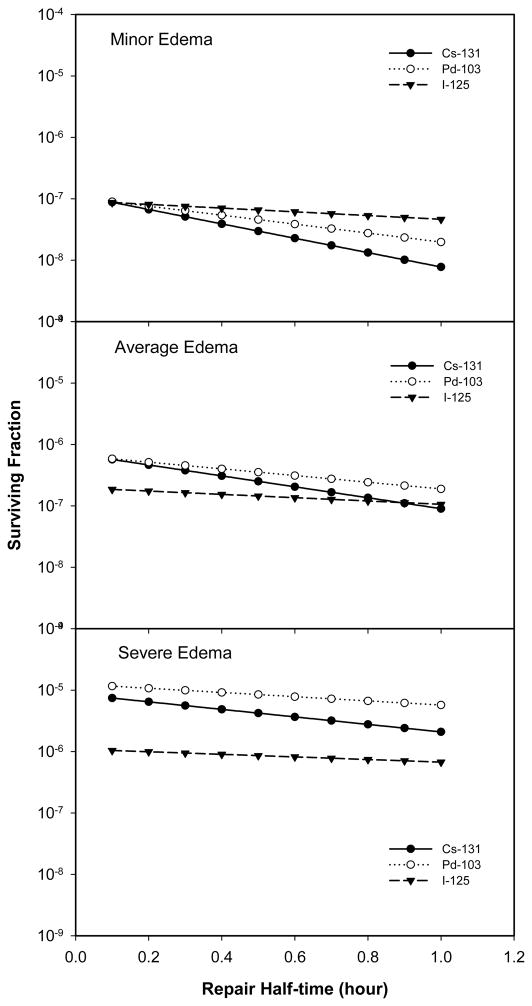
Figure 6 plots cell survival as a function of the assumed half time for sublethal damage repair for PIB using 131Cs, 103Pd and 125I sources, and for minor (top panel), average (middle panel) and severe (lower panel) edema. Other parameters were fixed, with α = 0.15 Gy−1, α/β = 3.0 Gy, and Tp = 42 days. As expected, lower cell survivals were achieved for tumors having a poor capability for sublethal damage repair (i.e. a longer repair half-time). For patients with minor edema, 131Cs was more effective (produced lower cell survivals) than 103Pd which, in turn, was better than 125I for tumors with a repair half-times greater than 0.1 hour. The difference in cell survivals between slow- and fast-repairing tumors was greatest for PIB using 131Cs sources (as seen by the steeper loop of the 131Cs curve). However, for patients with average edema, 125I became more effective than either 131Cs or 103Pd for lowering cell survival in tumors with sublethal damage repair half-time less than 0.9 hour. The differences between the three sources in their ability to decrease cell survival increased further for severe edema.
Figure 6.
Surviving fraction as a function of the half time of sublethal damage repair for PIB using 131Cs, 103Pd, and 125I under three different edema conditions. (α = 0.15 Gy-1, α/β = 3.0 Gy, and Tp = 42 days)
IV. Discussion
The results highlighted above demonstrate that prostate edema could lead to increased cell survival and hence decreased tumor control probability in PIB for prostate cancer. The negative impact of prostate edema increases with increasing severity of edema, decreasing half-life of radioactive decay and decreasing energy of the photons emitted by the sources. For the doses currently prescribed and for prostate cancer cells characterized by a set of radiobiology and biology parameters recommended in AAPM TG-137 report, PIB using 125I sources was less sensitive to the effects of edema than PIB using 131Cs and 103Pd sources, due to the long decay half-life of 125I. The sensitivities of PIB using 131Cs or 103Pd to edema were similar, with 103Pd being slightly worse even though the decay half-life of 103Pd (17 days) is longer than that of 131Cs (9.7 days). This is because the radial dose function of 103Pd falls off much faster than that of 131Cs (average photon energy emitted by 103Pd, ~21 keV, is much lower than ~30.4 keV from 131Cs), which makes 103Pd PIB more sensitive to edema-induced changes in distance. As a result, the advantage of 103Pd in decay half-life is negated by the lower effective energy of the photons it emits in presence of edema. The impact of edema can also be reduced or enhanced by the underlying radiobiological characteristics of the cancer cells and their interplay with the choice of radioactive sources. These interactions are most noticeable with the tumor potential doubling time. For example, in absence of or with minor prostate edema, PIB using 131Cs was generally more effective in reducing tumor cell survival than PIB using 103Pd and 125I, especially for fast-growing tumors. For average and severe edema, the advantage of PIB using 131Cs over PIB using 103Pd and 125I for reducing cell survival was still maintained for fast-growing tumors even though 131Cs was more sensitive to edema than 125I. In this case, the advantage of the shorter decay half-life of 131Cs for fast-growing tumor overcame the negative impact of edema. However, for slow-growing tumors, PIB using 125I became more effective in lowering cell survival than PIB using 131Cs or 103Pd.
Thus, it would be ideal if the specific edema and tumor characteristics for each patient were known when the PIB treatments were being planned, so that the negative impacts of edema could be mitigated by individualizing the treatment design. Unfortunately, data on patient-specific edema and tumor characteristics are not at present available for use in treatment planning. It is generally believed that the major causes of edema include the mechanical trauma exerted by needle insertion (Speight, Shinohara et al. 2000), intraprostatic bleeding resulting from the needle penetrations (Whittington, Broderick et al. 1999), and the general inflammatory response to the needle perforations (Whittington, Broderick et al. 1999). Except for a few reports (Badiozamani, Wallner et al. 1999; Yamada, Potters et al. 2003; Taussky, Austen et al. 2005) demonstrating a weak negative correlation between the percentage volume increase resulting from initial swelling and the pre-implant prostate volume, published studies have not found any consistent correlation of either the amount of edema or the pattern of its temporal resolution either with patient characteristics such as age (Yamada, Potters et al. 2003), pre-implant gland volume (Badiozamani, Wallner et al. 1999; Yamada, Potters et al. 2003), or use of hormones (Badiozamani, Wallner et al. 1999; Yamada, Potters et al. 2003), or with procedure details such as radionuclide type (Waterman, Yue et al. 1998), number of needles (Waterman, Yue et al. 1998; Yamada, Potters et al. 2003), number of implanted sources (Waterman, Yue et al. 1998), or total source strength (Waterman, Yue et al. 1998). On the other hand, these studies have consistently shown that the magnitude of edema and the rate of edema resolution can vary widely from one patient to another (Moerland, Wijrdeman et al. 1997; Narayana, Roberson et al. 1997; Waterman, Yue et al. 1998).
The lack of a reliable method to predict the procedure-induced prostate edema for individual patients before source implantation prompted us to use the edema model published by Waterman et al. to examine the potential effects of prostate edema systematically over the wide range of edema magnitudes and resolution half-lives reported in literature. Lee and Zaider have investigated the possibility of using an effective planning volume to compensate the effect of prostate edema (Lee and Zaider 2001) using the Waterman edema model. While the edema model was derived from real patient data, the reader should note that the expansion and resolution of the edema were assumed to be spatially isotropic. Local deviations from this assumption may occur in certain patients. Nonetheless, we believe that the results obtained from this model are still useful for physicians and treatment planners for assessing the potential impacts of prostate edema and its interplay with other dynamic processes such as the half-life for decay of radioactivity, the proliferation of the tumor cells during irradiation, and the half time of the repair of sublethal damage. We hope that future refinements to the edema model will lead to an effective method for mitigating the negative effects of prostate edema on a patient by patient basis.
It should be pointed out that our study did not include possible on-going tumor shrinkage after edema resolution is complete. Because the edema resolution model reported by Waterman et al and others were derived from post-implant serial imaging, which included both tumor shrinkage and edema resolution in the time span covered by serial imaging study, tumor shrinkage up to the last post-implant imaging study is included implicitly in the edema model, even though the overall prostate volume variation during this time period had been termed as edema resolution. Nonetheless, further tumor shrinkage beyond that time is possible and its effect was not taken into account in our study. The on-going tumor shrinkage after edema resolution, if present, could offset the negative influence of the initial edema on tumor cell kill. The degree of offset afforded by tumor shrinkage will depend on both tumor shrinkage rate and the radionuclide (the decay half-life) used. Qualitatively, post-edema tumor shrinkage would have more positive effect (in terms of tumor cell kill) on implants using radionuclides with long decay half-lives (e.g. 125I) than on implants using radionuclides with short half-lives (e.g. 103Pd and 131Cs) because the effective treatment times are much shorter for the latter radionuclides. This would further increase the difference between the sensitivities of short-lived radionuclide (e.g. 131Cs) and long-lived radionuclide (e.g. 125I) to edema.
The radiobiological modeling used in this work allowed us to investigate the interplay between the dynamics of dose delivery, the magnitude and speed of resolution of the edema, and the characteristics of the tumor cells that cannot be explored using physical dosimetry alone. While the qualitative results obtained in this study conformed to general intuition and clinical experience, it should be cautioned that the numerical values of the calculated cell survival, BED, and TCP are highly dependent on the model and on the input parameters used in the calculations. Our radiobiological modeling, based on a generalized version of Dale model, assumed that the underlying mechanism for radiation induced cell killing follows the popular linear-quadratic (LQ) model. While the advantages and limitations of the basic LQ model have been discussed extensively in the literature, a concern on the use of “effective treatment time” in Dale model for permanent implant isoeffect comparison has been raised recently in literature (Zaider and Hanin 2007). The definition of Teff is physically intuitive. However, the need to use Teff as the time point for radiobiological calculation illustrates an inherent uncertainty in the application of this model to tumors that continuously repopulate in permanent implants. The BED value calculated at other time will be different from that calculated at Teff. Even in relative comparisons of two implants, using BED calculated at Teff versus using BED calculated at other time could lead to quantitatively different results. Zaider and Hanin found that the use of Dale model for proliferating tumors underestimates the isoeffective dose (Zaider and Hanin 2007). The Poisson model for TCP is also known to underestimate the tumor cure rate when tumor cell repopulation occurs during the treatment (Tucker, Thames et al. 1990). Zaider and Minko have recently derived a more general TCP formalism capable of dealing with cell repopulation and applicable to different temporal patterns of dose delivery (Zaider and Minerbo 2000). It is desirable and valuable to re-examine the problem studied in this paper using these new models, in order to assess the robustness and validity of the generalized Dale model used in this work.
It should also be pointed out that the relative biological effectiveness (RBE) arising from different linear energy transfer (LET) among the 125I, 103Pd, and 131Cs photons was not included in this study. Relative to a high-energy photon reference source (e.g. 250 keV or 60Co photons), the LET-dependent RBE reported in literature vary from 1.0 to 1.5 for 125I sources and from 1.6 to 1.9 for 103Pd sources. Because 131Cs emits photons with similar energy as 125I, it is reasonable to assume that 131Cs has a similar LET-dependent RBE value as 125I. Hence, the three sources all have RBE >1, which could lead to decreased cell survival and better TCP values than those calculated with RBE = 1 as reported in section III. This would have a direct impact on the comparison of permanent brachytherapy with other treatment modalities such as external beam radiotherapy using high-energy photons. For the edema problem examined in this report, the influence of RBE could manifest in at least the following three aspects: 1) for any given radionuclide (e.g. 131Cs), the relative dependence of cell survival and TCP on edema would remain similar to what has been presented (although their absolute values would be different); 2) our conclusion on 131Cs being more sensitive to prostate edema than 125I would also remain because these two sources have similar RBE value (the relative comparison would remain similar); and 3) our conclusion on the sensitivities of 131Cs and 103Pd to edema being similar may become invalid because the 103Pd has a greater RBE value than 131Cs. With its greater RBE, 103Pd implants could fair better than 131Cs in presence of edema. A detailed analysis including the effects of RBE may be performed using an approach proposed by Dale and his colleagues (Dale and Jones 1999; Antipas, Dale et al. 2001; Armpilia, Dale et al. 2003). We will pursue it in a future investigation.
The radiobiological parameters for prostate cancer have also been a subject of intensive debate in the recent literature (Brenner and Hall 1999; Fowler, Chappell et al. 2001; Brenner 2003; Nahum, Movsas et al. 2003; Wang, Guerrero et al. 2003; Wang, Li et al. 2003; Bentzen and Ritter 2005) following the analysis by Brenner et al. that indicated an unusually low α/β ratio for prostate cancer (< 3 Gy) (Brenner and Hall 1999) as compared to those calculated for other solid tumors tumors (> ~8 Gy) (Thames, Bentzen et al. 1990; Brenner 2003). While an emerging consensus suggests that the α/β ratio may indeed be low for prostate cancer (Brenner 2003), the radiobiological parameters for cells of individual patients are expected to vary. We fully recognize the simplistic nature and potential pitfalls of the radiobiological model used in this study. Hence, our use of the LQ model and the self-consistent set of parameters recommended by AAPM TG-137 were aimed primarily to the study of relative effects of prostate edema for PIB using different radioactive sources and for patients with different radiobiological and biological characteristics by varying the parameters within a reasonable range. Ultimately, patient-specific assessment of the radiobiological consequences of prostate edema requires quantitative methods for reliably determining the radiobiological parameters of individual patients. Such methods are currently lacking.
V. Conclusion
Procedure-induced edema, if not taken into account appropriately during treatment planning, could cause significant reductions in BED and significant increases in cell survival after permanent interstitial brachytherapy using 131Cs, 103Pd, or 125I sources. Depending on the initial tumor burden, the edema-induced increases in cell survival could lead to significant reductions in the tumor control probability for those patients who develop average and severe edemas. In addition, the impact of edema could be either reduced or enhanced depending on the tumor characteristics (e.g. the potential doubling time or α/β ratio of the tumor cells) and the interplay of these factors with the radionuclide used to deliver the PIB. There is a clear need to actively consider the effects of prostate edema during permanent interstitial brachytherapy for prostate cancer.
Acknowledgments
Supported in part by National Institutes of Health Grant No. R01-CA134627
References
- Antipas V, Dale RG, et al. A theoretical investigation into the role of tumour radiosensitivity, clonogen repopulation, tumour shrinkage and radionuclide RBE in permanent brachytherapy implants of 125I and 103Pd. Physics in Medicine & Biology. 2001;46(10):2557–2569. doi: 10.1088/0031-9155/46/10/304. [DOI] [PubMed] [Google Scholar]
- Antipas V, Dale RG, et al. A theoretical investigation into the role of tumour radiosensitivity, clonogen repopulation, tumour shrinkage and radionuclide RBE in permanent brachytherapy implants of 125I and 103Pd. Physics in medicine and biology. 2001;46(10):2557–2569. doi: 10.1088/0031-9155/46/10/304. [DOI] [PubMed] [Google Scholar]
- Armpilia CI, Dale RG, et al. The determination of radiobiologically optimized half-lives for radionuclides used in permanent brachytherapy implants. International Journal of Radiation Oncology, Biology, Physics. 2003;55(2):378–385. doi: 10.1016/s0360-3016(02)04208-6. [DOI] [PubMed] [Google Scholar]
- Badiozamani KR, Wallner K, et al. Anticipating prostatic volume changes due to prostate brachytherapy. Radiation Oncology Investigations. 1999;7(6):360–364. doi: 10.1002/(SICI)1520-6823(1999)7:6<360::AID-ROI6>3.0.CO;2-D. [DOI] [PubMed] [Google Scholar]
- Bentzen SM, Ritter MA. The alpha/beta ratio for prostate cancer: what is it, really?[comment] Radiotherapy & Oncology. 2005;76(1):1–3. doi: 10.1016/j.radonc.2005.06.009. [DOI] [PubMed] [Google Scholar]
- Brenner DJ. Hypofractionation for prostate cancer radiotherapy--what are the issues?[comment] International Journal of Radiation Oncology, Biology, Physics. 2003;57(4):912–914. doi: 10.1016/s0360-3016(03)01456-1. [DOI] [PubMed] [Google Scholar]
- Brenner DJ, Hall EJ. Fractionation and protraction for radiotherapy of prostate carcinoma.[see comment] International Journal of Radiation Oncology, Biology, Physics. 1999;43(5):1095–1101. doi: 10.1016/s0360-3016(98)00438-6. [DOI] [PubMed] [Google Scholar]
- Chen Z, Deng J, et al. Potential impact of prostate edema on the dosimetry of permanent seed implants using the new 131Cs (model CS-1) seeds. Medical Physics. 2006;33(4):968–975. doi: 10.1118/1.2179170. [DOI] [PubMed] [Google Scholar]
- Chen Z, Deng J, et al. The Impact of Procedure-Induced Edema On Cell Survival and Tumor Control Probability in Permanent Prostate Brachytherapy Using 131Cs Radioactive Source. Medical Physics. 2007;34:2655 (Abstract). [Google Scholar]
- Chen Z, Nath R. Biologically effective dose (BED) for interstitial seed implants containing a mixture of radionuclides with different half-lives. International Journal of Radiation Oncology, Biology, Physics. 2003;55(3):825–834. doi: 10.1016/s0360-3016(02)04282-7. [DOI] [PubMed] [Google Scholar]
- Dale RG. The application of the linear-quadratic dose-effect equation to fractionated and protracted radiotherapy. British Journal of Radiology. 1985;58(690):515–528. doi: 10.1259/0007-1285-58-690-515. [DOI] [PubMed] [Google Scholar]
- Dale RG. Radiobiological assessment of permanent implants using tumour repopulation factors in the linear-quadratic model. British Journal of Radiology. 1989;62(735):241–244. doi: 10.1259/0007-1285-62-735-241. [DOI] [PubMed] [Google Scholar]
- Dale RG, Jones B. The assessment of RBE effects using the concept of biologically effective dose.[see comment] International Journal of Radiation Oncology, Biology, Physics. 1999;43(3):639–645. doi: 10.1016/s0360-3016(98)00364-2. [DOI] [PubMed] [Google Scholar]
- Dale RG, Jones B, et al. Effect of tumour shrinkage on the biological effectiveness of permanent brachytherapy implants. British Journal of Radiology. 1994;67(799):639–645. doi: 10.1259/0007-1285-67-799-639. [DOI] [PubMed] [Google Scholar]
- Fowler J, Chappell R, et al. Is alpha/beta for prostate tumors really low?[see comment] International Journal of Radiation Oncology, Biology, Physics. 2001;50(4):1021–1031. doi: 10.1016/s0360-3016(01)01607-8. [DOI] [PubMed] [Google Scholar]
- Fowler JF. The linear-quadratic formula and progress in fractionated radiotherapy. British Journal of Radiology. 1989;62(740):679–694. doi: 10.1259/0007-1285-62-740-679. [DOI] [PubMed] [Google Scholar]
- Hall EJ. Radiation dose-rate: a factor of importance in radiobiology and radiotherapy. The British journal of radiology. 1972;45(530):81–97. doi: 10.1259/0007-1285-45-530-81. [DOI] [PubMed] [Google Scholar]
- Leclerc G, Lavallee MC, et al. Prostatic edema in 125I permanent prostate implants: dynamical dosimetry taking volume changes into account. Medical Physics. 2006;33(3):574–583. doi: 10.1118/1.2168066. [DOI] [PubMed] [Google Scholar]
- Lee EK, Zaider M. On the determination of an effective planning volume for permanent prostate implants. International Journal of Radiation Oncology, Biology, Physics. 2001;49(4):1197–1206. doi: 10.1016/s0360-3016(00)01536-4. [DOI] [PubMed] [Google Scholar]
- Merrick GS, Butler WM, et al. Influence of timing on the dosimetric analysis of transperineal ultrasound-guided, prostatic conformal brachytherapy. Radiation Oncology Investigations. 1998;6(4):182–190. doi: 10.1002/(SICI)1520-6823(1998)6:4<182::AID-ROI6>3.0.CO;2-U. [DOI] [PubMed] [Google Scholar]
- Moerland MA, Wijrdeman HK, et al. Evaluation of permanent I-125 prostate implants using radiography and magnetic resonance imaging. International Journal of Radiation Oncology, Biology, Physics. 1997;37(4):927–933. doi: 10.1016/s0360-3016(96)00575-5. [DOI] [PubMed] [Google Scholar]
- Nahum AE, Movsas B, et al. Incorporating clinical measurements of hypoxia into tumor local control modeling of prostate cancer: implications for the alpha/beta ratio.[see comment] International Journal of Radiation Oncology, Biology, Physics. 2003;57(2):391–401. doi: 10.1016/s0360-3016(03)00534-0. [DOI] [PubMed] [Google Scholar]
- Narayana V, Roberson PL, et al. Impact of differences in ultrasound and computed tomography volumes on treatment planning of permanent prostate implants. International Journal of Radiation Oncology, Biology, Physics. 1997;37(5):1181–1185. doi: 10.1016/s0360-3016(96)00618-9. [DOI] [PubMed] [Google Scholar]
- Nath R, Anderson LL, et al. Dosimetry of interstitial brachytherapy sources: recommendations of the AAPM Radiation Therapy Committee Task Group No. 43. American Association of Physicists in Medicine. Med Phys. 1995;22(2):209–234. doi: 10.1118/1.597458. [DOI] [PubMed] [Google Scholar]
- Speight JL, Shinohara K, et al. Prostate volume change after radioactive seed implantation: possible benefit of improved dose volume histogram with perioperative steroid. International Journal of Radiation Oncology, Biology, Physics. 2000;48(5):1461–1467. doi: 10.1016/s0360-3016(00)00798-7. [DOI] [PubMed] [Google Scholar]
- Taussky D, Austen L, et al. Sequential evaluation of prostate edema after permanent seed prostate brachytherapy using CT-MRI fusion. International Journal of Radiation Oncology, Biology, Physics. 2005;62(4):974–980. doi: 10.1016/j.ijrobp.2004.12.012. [DOI] [PubMed] [Google Scholar]
- Thames HD, Bentzen SM, et al. Time-dose factors in radiotherapy: a review of the human data. Radiotherapy & Oncology. 1990;19(3):219–235. doi: 10.1016/0167-8140(90)90149-q. [DOI] [PubMed] [Google Scholar]
- Tucker SL, Thames HD, et al. How well is the probability of tumor cure after fractionated irradiation described by Poisson statistics?[see comment] Radiation Research. 1990;124(3):273–282. [PubMed] [Google Scholar]
- Wang JZ, Guerrero M, et al. How low is the alpha/beta ratio for prostate cancer?[see comment] International Journal of Radiation Oncology, Biology, Physics. 2003;55(1):194–203. doi: 10.1016/s0360-3016(02)03828-2. [DOI] [PubMed] [Google Scholar]
- Wang JZ, Li XA, et al. The low alpha/beta ratio for prostate cancer: what does the clinical outcome of HDR brachytherapy tell us? International Journal of Radiation Oncology, Biology, Physics. 2003;57(4):1101–1108. doi: 10.1016/s0360-3016(03)00747-8. [DOI] [PubMed] [Google Scholar]
- Wang JZ, Mayr NA, et al. Effect of edema, relative biological effectiveness, and dose heterogeneity on prostate brachytherapy. Medical Physics. 2006;33(4):1025–1032. doi: 10.1118/1.2181294. [DOI] [PubMed] [Google Scholar]
- Waterman FM, Yue N, et al. Edema associated with I-125 or Pd-103 prostate brachytherapy and its impact on post-implant dosimetry: an analysis based on serial CT acquisition. International Journal of Radiation Oncology, Biology, Physics. 1998;41(5):1069–1077. doi: 10.1016/s0360-3016(98)00152-7. [DOI] [PubMed] [Google Scholar]
- Whittington R, Broderick GA, et al. The effect of androgen deprivation on the early changes in prostate volume following transperineal ultrasound guided interstitial therapy for localized carcinoma of the prostate. International Journal of Radiation Oncology, Biology, Physics. 1999;44(5):1107–1110. doi: 10.1016/s0360-3016(99)00119-4. [DOI] [PubMed] [Google Scholar]
- Yamada Y, Potters L, et al. Impact of intraoperative edema during transperineal permanent prostate brachytherapy on computer-optimized and preimplant planning techniques. American Journal of Clinical Oncology. 2003;26(5):e130–135. doi: 10.1097/01.coc.0000091353.67232.e5. [DOI] [PubMed] [Google Scholar]
- Yue N, Chen Z, et al. Edema-induced increase in tumour cell survival for 125I and 103Pd prostate permanent seed implants--a bio-mathematical model. Physics in Medicine & Biology. 2002;47(7):1185–1204. doi: 10.1088/0031-9155/47/7/313. [DOI] [PubMed] [Google Scholar]
- Zaider M, Hanin L. Biologically-equivalent dose and long-term survival time in radiation treatments. Phys Med Biol. 2007;52(20):6355–6362. doi: 10.1088/0031-9155/52/20/017. [DOI] [PubMed] [Google Scholar]
- Zaider M, Minerbo GN. Tumour control probability: a formulation applicable to any temporal protocol of dose delivery. Phys Med Biol. 2000;45(2):279–293. doi: 10.1088/0031-9155/45/2/303. [DOI] [PubMed] [Google Scholar]
- Zelefsky MJ, Whitmore WF., Jr Long-term results of retropubic permanent 125iodine implantation of the prostate for clinically localized prostatic cancer. Journal of Urology. 1997;158(1):23–29. doi: 10.1097/00005392-199707000-00005. discussion 29–30. [DOI] [PubMed] [Google Scholar]