Quantum Mechanical Investigations of Organocatalysis: Mechanisms, Reactivities, and Selectivities

Paul Ha-Yeon Cheong; Claude Y Legault; Joann M Um; Nihan Çelebi-Ölçüm; K N Houk

doi:10.1021/cr100212h

. Author manuscript; available in PMC: 2012 Aug 10.

Published in final edited form as: Chem Rev. 2011 Jun 28;111(8):5042–5137. doi: 10.1021/cr100212h

Quantum Mechanical Investigations of Organocatalysis: Mechanisms, Reactivities, and Selectivities

Paul Ha-Yeon Cheong ^†, Claude Y Legault ^‡, Joann M Um ^§, Nihan Çelebi-Ölçüm ^§, K N Houk ^§,^*

PMCID: PMC3154597 NIHMSID: NIHMS307700 PMID: 21707120

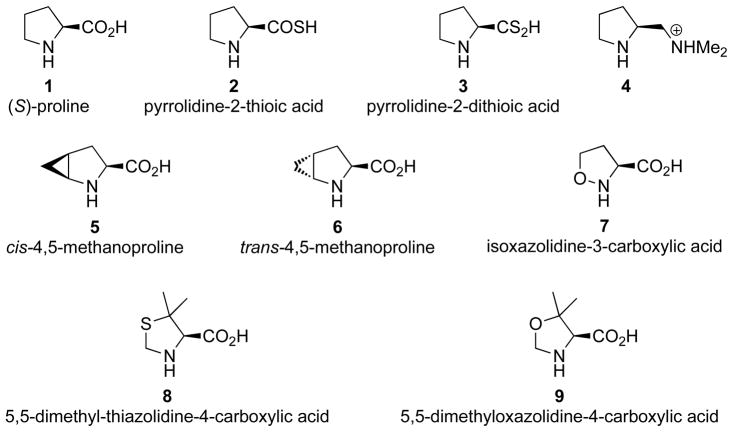
1. Introduction

Organocatalysis has captured the imagination of a significant group of synthetic chemists. Much of the mechanistic understanding of these reactions has come from computational investigations or studies involving both experimental and complementary computational explorations. As much as any other area of chemistry, organocatalysis has advanced because of both empirical discoveries and computational insights. Quantum mechanical calculations, particularly with density functional theory (DFT), can now be applied to real chemical systems that are studied by experimentalists; this review describes the quantum mechanical studies of organocatalysis.

The dramatic growth of computational investigations on organocatalysis in the last decade reflects the great attention focused on this area of chemistry since the discoveries of List, Lerner, and Barbas of the proline-catalyzed intermolecular aldol reaction, and by MacMillan in the area of catalysis by chiral amino-acid derived amines. The number of reports on the successful applications of organocatalysts and related mechanistic investigations for understanding the origins of catalysis and selectivities keep growing at a breathtaking pace. Literature coverage in this review is until October 2009, except for very recent discoveries that alter significantly the conclusions based on older literature.

1.1 Computational methods for organocatalysis

Over the last two decades, DFT has become a method of choice for the cost-effective treatment of large chemical systems with high accuracy.¹ Most of the studies reported in this review were carried out using the B3LYP functional with the 6-31G(d) basis set, which is a standard in quantum mechanical calculations. Nevertheless, DFT is experiencing continuing developments of new functionals and further improvements. The availability of many new functionals and, in particular, the rapidly evolving performance issues of B3LYP have stimulated extra efforts on benchmarking DFT methods for the prediction of key classes of organic reactions.² The well-documented deficiencies of B3LYP include the failure to adequately describe medium-range correlation and photobranching effects,^3,4 delocalization errors causing significant deviations in π→σ transformations,^2b,5 and incorrect description of non-bonding and long-range interactions,⁶ which are likely to be key factors in determining stereoselectivities. Benchmark results also show that newer functionals considerably improve some of the underlying issues.^2–7 Recent advances, especially in the treatment of dispersion effects, now offer more reliable models of the reaction profiles and stereoselectivities.

Most benchmarks focus on energetics rather than stereoselectivities. Systematic benchmarking for stereoselectivities requires more sophisticated techniques and averaging over conformations. To date, such benchmarking based upon stereoselectivity is available for only three reactions,⁸ and even there only various basis sets with B3LYP, as well as comparisons of results predicted using enthalpies and free energies. It is not possible to assign error bars for stereoselectivities for the majority of reports discussed in this review. Because stereoisomeric transition structures are very similar species, their relative energies are likely to be calculated accurately, as shown by the good agreement between calculated and experimental values.

More recently Harvey (Harvey, 2010, faraday discussions) has studied two typical organic reactions of polar species (Wittig and Morita-Baylis-Hillman reactions) at different levels of theory.²ⁱ He showed that many standard computational methods, involving B3LYP, are qualitatively useful, but the energetics may be misleading for larger reactive partners; the quantitative prediction of rate constants remains difficult. These studies suggest that although B3LYP provides valuable qualitative insight into the reaction mechanisms and selectivities, the energetics may require testing with higher accuracy methods for complex organic systems. On the other hand, Simón and Goodman found B3LYP to be “only slightly less accurate” than newer methods, and recommended its use for organic reaction mechanisms.⁹

2. Enamine/Iminium Catalysis

2.1. Proline and proline derivatives

2.1.1. Intramolecular aldol reaction

The Hajos-Parrish reaction is sometimes considered to be the first organocatalytic enantioselective transformation to be reported (1971). Two groups, Hajos and Parrish at Hoffmann La Roche¹⁰ and Eder, Sauer, and Wiechert at Schering AG,¹¹ published a series of papers and patents involving these transformations. This discovery made possible the stereoselective synthesis of enediones like the so-called Wieland-Miescher ketone, which are key structural elements of steroids, terpenoid, and taxol. It also paved the way to the growing phenomenon of organocatalysis. List has reviewed the field recently¹² and MacMillan has described his influence on creating the field of organocatalysis.¹³

2.1.1.1. Mechanism of Hajos-Parrish reaction

Four main mechanisms of the C-C bond-forming step have been proposed (Scheme 1). There were two original proposals set forth by Hajos and Parrish. The first is the nucleophilic attack by the exocyclic enol ether to a carbinolamine to displace the catalyst (Mechanism A). The second is a simultaneous proton transfer and nucleophilic attack by an enaminium, assisted by the carboxylate (Mechanism B). Based on the observation of a small non-linear effect, Agami suggested that second molecule of proline may be involved in the proton transfer process from the carboxylic acid (Mechanism C).¹⁴ Finally, a mechanism originally proposed by Jung in 1976 suggested a nucleophilic attack of the enamine terminus with simultaneous proton transfer to the developing alkoxide involving a single molecule of proline catalyst (Mechanism D).¹⁵

Houk and co-workers reported a detailed DFT investigation of the proposed mechanisms of this reaction.¹⁶ Geometry optimizations were performed at the B3LYP/6-31G(d) level of theory, while energies were computed at the B3LYP/6-31+G(d, p) level of theory with single point PCM solvation corrections for DMSO using HF/6-31+G(d, p) and the UAKS radii.¹⁷ The carbinolamine intermediate that precedes the TS corresponding to mechanism A is found to be higher in energy than the uncatalyzed reaction. Such a transition state would be even higher in energy than this intermediate. Mechanism B is disfavored by ~30 kcal/mol due to the distortion of the enamine from planarity to accommodate proton transfer. Mechanism C is disfavored due to the entropic penalties associated with the involvement of another molecule of proline. Mechanism D is favored energetically; this transition structure is ~10 kcal/mol lower in energy than the uncatalyzed process. The preference for this mechanism stems from the enhanced nucleophilicity of the planar enamine as well as the activation of the carbonyl electrophile by the carboxylic acid.

The entire transformation leading from the attack of the exocyclic ketone by the proline moiety through the aldol transition state and the subsequent hydrolysis of the product iminium has been investigated in detail.¹⁴ More recent kinetic isotope effect experiments and calculations lead to the conclusion that the rate-determining step occurs prior to C–C bond formation.¹⁸

2.1.1.2. Origins of stereoselectivity

The stereoselectivity of the Hajos-Parrish reaction has also been investigated by Houk and coworkers using B3LYP/6-31G(d) level of theory.¹⁹ Two chair Zimmerman-Traxler-like transition states are possible: the syn and the anti (Figure 1). The syn and anti refer to orientation of the enamine with respect to the carboxylic acid. The anti transition state leads to the formation of the experimentally observed product, while the syn leads to the formation of the minor product. The 3.4 kcal/mol preference for the anti TS corresponds reasonably well to the experimentally observed stereoselectivity of 95 % ee (2.2 kcal/mol). A later study involving a single point at the B3LYP/6-311+G(2df, p) level of theory was shown to reproduce the exact experimental stereoselectivity of 2.2 kcal/mol for the Hajos-Parrish reaction.²⁰

The computed *anti* and *syn* transition structures of proline-catalyzed Hajos-Parrish reaction

The enantioselectivity of the Hajos-Parrish reaction is directly related to the ability with which each of the transition states can achieve optimal enamine nucleophilicity and provide the greatest electrostatic stabilization to the developing negative charge on the carbonyl electrophile. A planar enamine allows for optimal nucleophilicity to the enamine and experiences minimal geometric distortion to form the iminium upon C–C bond formation. The proton donation from the carboxylic acid moiety and, to a lesser extent, the ^δ+NCH···O^δ− electrostatic interactions stabilize the developing alkoxide.

The enamine of the anti TS is much more planar than the syn TS. This distortion of the syn TS arises from the necessity to proton transfer to a more proximal alkoxide, which in turn, results in the distortion of the pyrrolidine ring. In contrast, such distortions are unnecessary in the anti TS in which there is ample distance between the carboxylic acid and the developing alkoxide.

The ^δ+NCH···O^δ− electrostatic interaction exists for both the syn and anti TSs. However, the distance is much shorter (2.4 Å) and therefore the interaction is stronger in the anti TS, in comparison to the syn, where this distance is much longer (3.4 Å). The absolute magnitude of the ^δ+NCH···O^δ− interaction is also greater in the anti TS than in the syn, due to the greater positive charge on the far more advanced developing iminium.

2.1.1.3. Catalysis by proline derivatives

Houk and co-workers have also reported the origins and predictions of stereoselectivities of the Hajos-Parrish reaction catalyzed by a diverse range of proline-derivatives (Scheme 2).²¹ B3LYP/6-31G(d) geometry optimizations followed by B3LYP/6-311+G(2df, p) reproduced the exact enantioselectivities of the derivatives for which the reaction has been reported. This combination of methods yielded excellent correlation between the computed and experimental stereoselectivities (mean absolute error, MAE = 0.1 kcal/mol). The Houk-List model, described later in Scheme 10, provides the basis for the experimentally observed stereoselectivities of all the catalysts in Scheme 2.

Scheme 2 — Various proline derivative catalysts for the Hajos-Parrish reaction studied by Houk

Scheme 10 — The Houk-List model for predicting the stereoselectivity of the intermolecular aldol reaction catalyzed by proline

4,5-methanoproline

The first computational investigations of proline-derivative catalyzed Hajos-Parrish reaction was reported by a joint collaboration between Houk and Hanessian groups.²⁰ At the time, the Hanessian group had reported the synthesis of cis- and trans-4,5-methanoprolines as conformationally rigid proline surrogates (5 and 6). Interestingly, the Hanessian group discovered that the cis-4,5-methanoprolines exhibited similar stereoselectivity and reactivity as proline in the Hajos-Parrish reaction, whereas the trans-4,5-methanoproline was a poorer catalyst, both in terms of selectivity and rate.

Bicyclo[3.1.0]hexanes are known to favor the boat conformation over the chair due to the torsional interactions around the fused cyclopropane ring. The computed lowest energy conformations of the cis- and trans-methanoproline enamines revealed that the trans-methanoproline enamine is the expected boat with a significantly pyramidalized amine. The cis-methanoproline was also found to be the expected boat; however, the steric repulsion of the carboxylic acid group syn to the cyclopropane ring resulted in a rather planar cis-methanoproline enamine.

The stereoselectivity of the Hajos-Parrish reactions catalyzed by these methanoprolines is dictated by the native conformational preference of the respective proline derivatives. In the cis-methanoproline case, the planar enamine allows for a facile transition to the anti, planar iminium transition structure, whereas the realization of the pyramidalized syn transition structure would require geometric distortion (Figure 2). This is in contrast to the trans-methanoproline, where the naturally pyramidalized enamine requires less geometric distortion to reach the syn, pyramidalized iminium transition structure, than the planar anti. Despite this conformational bias, trans-methanoproline is still anti-selective not only due to the stability gained by the more planar iminium of the anti transition structure but because of the accentuated interaction between the cyclopropyl methylene hydrogen and the developing alkoxide oxygen.

The computed *anti* and *syn* transition structures of 4,5-methanoproline (5, 6)-catalyzed Hajos-Parrish reactions.

The observed catalytic ability of the two derivatives can also be explained by the conformational biases. The energy required for the naturally pyramidalized trans stereoisomer to achieve the necessary planar iminium arrangement in the aldol transition state is responsible for its comparatively poorer catalytic ability.

Pyrrolidine-2-thioic and dithioic acids

The pyrrolidine-2-thioic acid (2) and the closely related pyrrolidine-2-dithioic acid (3) feature acid groups that prefer longer ideal proton transfer distances. As expected, there is a substantial penalty for the syn transition states for cases where the proton transfer occurs from the sulfur (4.8 kcal/mol), while proton transfer from the oxygen exhibited a smaller preference (2.8 kcal/mol, Figure 3).²¹

The computed *anti* and *syn* transition structures of thioic acid (2) and dithioic acid (3) catalyzed Hajos-Parrish reactions.

Protonated amine

The protonated amine case (4), which features a quaternary ammonium cation as the proton donor in lieu of a carboxylic acid moiety, was particularly unique from the other catalysts in that it exhibited a reversal in the stereoselectivity (4.7 kcal/mol preference for the syn transition structure, Figure 4).²¹ This reversal is seen to be caused by two factors: 1) the relief of geometric strain in the syn transition structure due to the change in hybridization of the proton donor; 2) and the destabilization of the anti transition structure due to the steric interactions between the ammonium ion and the substrate.

The computed *anti* and *syn* transition structures of quaternary ammonium (4) catalyzed Hajos-Parrish reactions.

Isoxazolidine-3-carboxylic acid

The isoxazolidine-3-carboxylic acid (7) is an interesting choice of catalyst, due to the possibility of increased nucleophilicity originating from an α-effect. This catalyst also lacks the ability to stabilize the developing alkoxide via ^δ+NCH···O^δ− interactions. The computed activation barrier for the C-C bond formation for this catalyst was ΔH^‡ = 10.0 kcal/mol, which was found to be similar to the analogous barrier in proline of 10.0 kcal/mol.²¹ The lack of change in reactivity is most likely due to the fact that the repulsive ^δ−NO···O^δ− interactions erode any potential reactivity gained from the α-effect. This same repulsive interaction is also responsible for the lack of any computed stereoselectivity for this catalyst (Figure 5).

5,5-dimethylthiazolidine-4-carboxylic acid (DMTC) and 5,5-dimethyloxazolidine-4-carboxylic acid (DMOC)

5,5-Dimethylthiazolidine-4-carboxylic acid (DMTC, 8) and the closely related 5,5-dimethyloxazolidine-4-carboxylic acid (DMOC, 9) were also studied.²¹ DMTC is particularly interesting because since the first reports of intermolecular aldol reactions catalyzed by proline, it has been ear-marked as a promising alternative to proline. The presence of the gem-dimethyl groups in both these catalysts create A^1,2 strain with the carboxylic acid group. The need to accommodate a proximal alkoxide in the syn TS forces the slight rotation of the carboxylate towards the gem-dimethyl groups as compared to the anti TS (Figure 6). This results in the computed greater stereoselectivity of the DMOC (3.1 kcal/mol) as compared to proline (2.1 kcal/mol). The DMTC exhibited the same stereoselectivity as proline, and this decrease in preference is seen to be from the weaker ^δ+NCH···O^δ− interaction in DMTC as compared to DMOC.

2.1.1.4. Primary amino acid catalysis

Clemente and Houk studied the stereoselectivity of Hajos-Parrish reaction catalyzed by primary amino acids (Scheme 3).²² Primary amino acids exhibit a slightly different stereoselectivity from proline. In the classic Hajos-Parrish reaction, the enantioselectivity exhibited by the primary amino acids are lower than that catalyzed by proline. However, in cases where there is an alkyl substituent on the exocyclic terminus, primary amino acids are more selective than proline.

Geometry optimizations were performed at the B3LYP/6-31G(d) level of theory, while energies were computed at the B3LYP/6-31+G(d, p) level of theory with single point PCM solvation corrections for DMSO using HF/6-31+G(d, p) and the UAKS radii.

The enamine mechanism is still operative. In the case of the Hajos-Parrish substrate, the stereoselectivity arises from the energetic discrimination between the syn and the anti enamine cyclizations. The energetic penalty of the syn TS is again explained as a consequence of the geometric distortion required to do proton transfer to a more proximal alkoxide. In the case of primary amino acids, the energetic penalty from this distortion is less than that exhibited by proline (1.7 kcal/mol less than proline), because the absence of the constraining pyrrolidine ring alleviates some of the geometric penalty of the syn TS (Figure 7).

Phenylalanine catalyzed Hajos-Parrish reaction.

In the case where the exocyclic terminus is substituted by a methyl group, the stereoselectivity is influenced by the difference in energy between the Z or E enamines. In the case of proline, the methyl group of the anti-Z-enamine experiences steric interaction with the pyrrolidine ring, while the E-enamine experiences steric interaction with the approaching cyclopentadione electrophile, leading to overall destabilization of the anti-Z transition structure. The syn transition structures are higher in energy. This is in sharp contrast to the phenylalanine anti Z-enamine structures, which exhibits little steric interaction between the methyl and the proton of the phenylalanine enamine (Figure 8).

Proline and phenylalanine catalyzed asymmetric intramolecular aldol condensation.

2.1.2. Intermolecular aldol reactions

The intermolecular aldol reaction was reported by List, Lerner, and Barbas, and is the first report of the rebirth of organocatalysis since the discovery of the Hajos-Parrish reaction (Scheme 4).²³

Scheme 4 — The intermolecular aldol reaction catalyzed by proline

2.1.2.1. Mechanism

The generally accepted mechanism of proline-catalyzed reactions involves the transformation of the starting carbonyl compound to a more nucleophilic enamine (Scheme 5, left cycle). Although the generation of enamine is critical for catalysis, the details of the process are still not well understood.

Scheme 5 — Mechanistic possibilities involving the enamine and oxazolidinone pathways

Patil and Sunoj²⁴ computed a proton-relay mechanism involving two molecules of methanol for the enamine formation between model substrates (dimethylamine and propanal) at the mPW1PW91/6-31G(d) level of theory. The PCM solvation model with UAKS radii was used to include solvent effects (THF) in the energy calculations. Significantly lower activation energies compared to the unassisted pathway (Scheme 6) suggested a facile enamine formation in the presence of protic additives. The catalytic ability of co-catalysts is explained by the improved transition state stabilization due to effective hydrogen bonding.

Scheme 6 — Activation free energies (ΔG^‡, kcal/mol) for hemiacetal, iminium and enamine formation with respect to separated reactants. mPW1PW91/6-31G(d), using PCM and UAKS radii

Clemente and Houk¹⁶ studied the pathway involving the formation of an enamine intermediate for a proline-catalyzed intramolecular aldol reaction with B3LYP/6-31+G(d, p)//B3LYP/6-31G(d). The predicted activation energies for the carbinol amine, iminium and enamine formation are 17.0, 15.3 and 26.2 kcal/mol respectively with respect to separated reactants (Scheme 7). More recently, Sunoj and co-workers²⁵ reported the gas phase free energy profile associated with the formation of the enamine intermediate in the reaction between proline and propanal at the B3LYP/6-31+G(d, p) level of theory. The activation free energies for the formation of carbinolamine, iminium and enamine intermediates are found to be 24.2, 25.1 and 26.2 kcal/mol relative to the separated starting compounds.

Scheme 7 — Activation energies (ΔE^‡, kcal/mol) for carbinolamine, iminium and enamine formation with respect to separated reactants (B3LYP-6-31+G(d, p)//B3LYP/6-31G(d))

Boyd and co-workers reported a DFT investigation of the mechanism of the proline-catalyzed intermolecular aldol reaction between acetone and acetaldehyde.²⁶ B3LYP/6-311+G(2df, p) single point energies based on B3LYP/6-31G(d) geometry optimizations along with solvation corrections using the Onsager model (DMSO, ε = 46.7) were used.

Boyd and co-workers report that the most difficult step along the reaction potential energy profile is the initial addition of proline to the donor ketone to form the carbinolamine with a barrier of ΔE_zp^‡ = 40.1 kcal/mol. This was shown to be more difficult than the enamine formation (ΔE_zp^‡ = 7.1 kcal/mol) or the C-C bond formation step (ΔE_zp^‡ = 13.7 kcal/mol) in the gas phase. Once solvation corrections have been accounted for, however, the barrier for initial addition drops to ΔE_zp^‡ = 9.7 kcal/mol, and is more facile than the enamine formation (ΔE_zp^‡ = 12.0 kcal/mol) or the C-C bond formation step (ΔE_zp^‡ = 11.1 kcal/mol). They concluded that the use of high polarity solvent is necessary to stabilize the various zwitterionic intermediates and transition state, as expected of an acid-base mechanism.

Reaction progress kinetic analysis of the proline mediated intermolecular aldol reaction by Blackmond and co-workers²⁷ provided evidence that the enamine formation cannot be rate-determining. The rate depends on the concentrations of both the donor ketone and the acceptor aldehyde. The observed isotope effects supports a role for the carboxyl group in the rate limiting step, which is suggested to be the C-C bond formation.

Only very recently, Gschwind and co-workers²⁸ detected and characterized the enamine intermediates in proline catalyzed aldol reactions for the first time experimentally, and showed the direct formation of enamine carboxylic acids from oxazolidinones in the solvent dimethylsulfoxide.

The NMR spectroscopic evidence for the formation of oxazolidinone intermediates in the reactions of proline with carbonyl compounds²⁹ has stimulated significant debate over the mechanism of catalysis. List and co-workers characterized the formation of oxazolidinones in terms of a “parasitic equilibrium”; that is, oxazolidinones are not involved in the catalytic cycle, but their formation would still allow for turnover by keeping the catalyst in solution.^29c More recently a catalytic role of oxazolidinone have been proposed that involves a key enamine carboxylate intermediate (Scheme 5, right cycle).³⁰

Sunoj and co-workers²⁵ explored the competing enamine and oxazolidinone pathways (Scheme 5) using density functional and ab-initio MP2 calculations. Scheme 8 shows the activation free energies of alternative pathways for the conversion of iminium carboxylate to various key intermediates computed with B3LYP/6-31+G(d, p). The barrier for the formation of the oxazolidinone intermediate by the intramolecular attack of carboxylate to imium is only 0.7 kcal/mol. Higher activation free energies for the formation of enamine carboxylic acid (12.8) and enamine carboxylate (18.0) suggest an equilibrium composition in favor of the oxazolidinone intermediate, in agreement with the experiments. The C-C bond formation steps for both enamine and oxazolidinone pathways were also examined (Figure 9). The C-C bond formation barriers for the oxazolidinone pathway are higher by 11.6 kcal/mol compared to the enamine pathway, and do not predict the correct stereochemistry of the major product. The resulting oxazolidinone products are also found to be significantly higher in energy than the corresponding iminium products in the enamine pathway. Although the energetics support the enamine pathway, a likely convergence between the enamine and oxazolidine pathways under the experimental conditions is proposed based on the variance of enantio- and diastereoselectivities under different conditions.

Scheme 8 — Gibbs free energies of activation (ΔG^‡, kcal/mol) for the conversion of iminium carboxylate to various key intermediates calculated with B3LYP/6-31+G(d, p) (Energies for the formation of *anti* intermediates are given along with that for *syn* intermediates in square brackets)

Gibbs free energies of activation (ΔG^‡, kcal/mol) for the C-C bond formation in the enamine and oxazolidinone pathways calculated with B3LYP/6-31+G(d, p). Free energies of iminium and oxazolidinone products (ΔG, kcal/mol) are given in parenthesis.

Blackmond and co-workers³¹ carried out experimental studies of the role of base additives in enamine catalysis of aminations and observed an unusual reversal of enantioselectivity, in line with the kinetically controlled outcome of the oxazolidinone pathway.

2.1.2.2. Origins of stereoselectivity

The Zimmerman-Traxler model

In List’s initial paper on the proline-catalyzed intermolecular aldol reaction,²³ the enantioselectivities were rationalized based on the Zimmerman-Traxler transition states (Scheme 9),³² originally described for metal enolate aldol reactions. In this model, the nitrogen of the proline enamine is aiding the proton transfer from the carboxylic acid to the forming alkoxide. The stereoselectivity arises from a switch in the axial or equatorial orientation of the electrophile substituent.

Scheme 9 — The Zimmerman-Traxler transition states proposed by List and co-workers to rationalize the stereoselectivities of proline-catalyzed intermolecular aldol reactions

The Houk-List model

Joint efforts by the Houk and List groups resulted in the Houk-List model to explain the origin of stereoselectivity of proline catalyzed intermolecular aldol reactions.^8,33 In contrast to the Hajos-Parrish reaction where the intramolecular nature of the aldol addition restricts the approach of the electrophile, the carbonyl of the electrophile in the intermolecular case can realize various dihedral angles with respect to the enamine double bond. Calculations from Bahmanyar and Houk indicate that only the transition structures that involve intramolecular proton catalysis are energetically viable. DFT (B3LYP/6-31G(d)) computations of a simple model system involving the proline enamine attack of acetaldehyde revealed that only certain rotamers with a dihedral angle of ±60° can participate in the H-bonding. In particular, transition structures with a dihedral −60° were found to be 5–10 kcal/mol higher in energy than those with +60° (Figure 10).

Rotameric *anti-re* transition structures of the intermolecular aldol reaction between acetone and acetaldehyde, catalyzed by proline.

Scheme 10 shows the Houk-List model for predicting the stereoselectivity of proline-catalyzed intermolecular aldol reactions. Transition structures involving the anti proline enamine are favored over the syn, due to: (1) the greater electrostatic stabilization arising from the ^δ+NCH···O^δ− interaction; (2) the syn transition structures suffer from distortion of the pyrrolidine ring to accommodate proton transfer to a more proximal developing alkoxide; and (3) transition structures involving the syn-enamine force the substituents at the forming C-C bond to be nearly eclipsed.

The re face attack is found to be preferred over the si face attack. This minimizes the steric interaction between the aldehyde substituent and the enamine, placing the substituent in a pseudo-equatorial conformation. The re face attack also generally features a more perfect staggering of substituents around the forming C-C bond.

The computed transition state geometries reveal that the carboxylic acid proton and enamine nitrogen (N···H distance ~2.5 Å) are not arranged to form an ideal Zimmerman-Traxler six-membered ring, as had been originally surmised by List.²³ on the other hand, the remaining five atoms are arranged in a chairlike arrangement. These findings are summarized in the Houk-List model, which can be represented as a Newman projection centered at the forming C-C bond or in the offset Newman arrangement that shows the chairlike arrangement of the five heavy atoms involved in bonding changes (Scheme 10).

The Seebach-Eschenmoser model

More recently, the Seebach-Eschenmoser model has been proposed to explain the origin of selectivity (Scheme 11).³⁰ This model involves the enamine carboxylate as a key reaction intermediate. They suggested anti-addition to the syn-enamine rotamer, which leads to the more stable, exo isomer of the product oxazolidinone, and ultimately to the experimentally observed stereoisomer of the product.

In order to gauge the accuracies of DFT in reproducing the stereoselectivities of proline-catalyzed aldol reactions, the average absolute errors in calculations for three known aldol reactions were determined.⁸ B3LYP/6-31G(d) was shown to have average absolute errors of approximately ±0.5 kcal/mol.

Predictions of stereoselectivities

Houk and Bahmanyar predicted the stereoselectivities of proline-catalyzed intermolecular aldol reactions between cyclohexanone and benzaldehyde.^8,33 The predictions were computed prior to the experiments, which were in turn performed by Benjamin List. They reported excellent agreement between the quantum mechanical prediction and the experimental results. Subsequent calculations indicated that different predictions were obtained when more extensive conformational searches were performed, and are described in a recent published interview of Houk.³⁴ List also found that the stereochemical results obtained with the proline catalyzed reaction of cyclohexanone and benzaldehyde were highly dependent on adventitious water and temperature, so that the agreement of theory and experiment was rather fortuitous.

2.1.2.3. 5-pyrrolidin-2-yltetrazole

5-Pyrrolidin-2-yltetrazole is one of the currently most interesting analogues of proline, in particular for reactions when less reactive aldehydes are employed as aldol acceptors (Scheme 12). In addition, although tetrazoles and carboxylic acids have similar pK_a values, the tetrazole group is much more lipophilic and, unlike proline, does not suffer from solvation issues in organic solvents.

Scheme 12 — The 5-pyrrolidin-2-yltetrazole catalyzed intermolecular aldol reactions

Domingo and co-workers performed a B3LYP/6-31G(d, p) study of the tetrazole-catalyzed intermolecular aldol reaction between acetone and pivaldehyde.³⁵ Solvation energies were computed for DMSO using the PCM method. The tetrazole catalyst can exist in two different tautomers (Scheme 13). The 2-tautomer is more stable than the 3-tautomer form by 2.4 kcal/mol in the gas phase. Solvation corrections increased this difference by 3.3 kcal/mol.

Scheme 13 — The two tautomeric forms of 5-pyrrolidin-2-yltetrazole catalyst. DMSO energies are in brackets

Domingo and co-workers state that the origins of stereoselectivity are similar to the reported proline case by Houk and co-workers. The transition structures involving anti enamine attack on the re face of the pivaldehyde was favored (Figure 11). However, the most interesting feature of note in this report was the discovery that the free energy of activation of the tetrazole catalyst was lower than that of the prolines. This is a consequence of the larger solvation corrections for the tetrazole transition structures (ΔG_solv = 11.1 kcal/mol) than the proline transition structures (ΔG_solv = 7.4 kcal/mol).

*Anti*-re and *anti*-si TSs of the intermolecular aldol reaction between acetone and pivaldehyde, catalyzed by proline and 5-pyrrolidin-2-yltetrazole. DMSO values in brackets.

2.1.2.4. Proline amide derivatives

Wu and co-workers have reported the development of a proline amide derivative as a catalyst for the intermolecular aldol reaction of acetone and p-nitrobenzaldehyde (Scheme 14).³⁶ These catalysts are of particular interest as a more active and stereoselective catalyst than the parent proline. They yield the same enantioselectivity as the proline aldol reactions.

Scheme 14 — Proline amide derivatives as catalysts for the intermolecular aldol reaction

HF/6-31G(d) geometries with B3LYP/6-31G(d, p) single points were used to compute the transition structures of various proline-amide derivative catalyzed aldol reactions. The computed activation barriers of simple proline amides, which lack a strongly acidic proton, are similar to those catalyzed by proline. As expected, the presence of another H-bond donor decreases the aldol barrier even further, as shown by the transition structure of (1S,2S)-diphenyl-2-aminoethanol amide derivative (Figure 12). Experimental observations also show that the doubly hydrogen bonded aminoethanol amide derivative is more reactive than proline or the parent proline amide.

*Anti*-re and *anti*-si transition structures of the intermolecular aldol reaction between acetone and benzaldehyde, catalyzed by (1S,2S)-diphenyl-2-aminoethanol amide proline derivative.

The use of (1S,2S)-diphenyl-2-aminoethanol amide derivative resulted in a substantial increase in stereoselectivity, as compared to proline. This increase in stereoselectivity is said to arise from the steric interaction between the phenyl of the benzaldehyde and the hydroxyl of the aminoethanol in the si attack of the anti enamine.

Gong and co-workers reported highly selective aldol reactions of ketones with α-keto acids using amides prepared from proline and aminopyridines (Scheme 15).³⁷ B3LYP/6-31+G(d) was used to explain the high enantioselectivity of the reaction.

Scheme 15 — Organocatalyzed aldol reaction of ketones with α-keto acids

It was proposed that the pyridine nitrogen of the catalyst could hydrogen bond with the acid, while the amide hydrogen could bind with the α-keto acid at the carbonyl of either the keto or ester group (Scheme 16). Binding at the keto group was calculated to be favored by 2.5 kcal/mol. Single hydrogen bonding of the amide hydrogen with either carbonyl group (and without interaction of the pyridine nitrogen) was calculated to be disfavored by 8.0–8.7 kcal/mol.

Scheme 16 — Possible binding modes of catalyst with α-keto acid

The Gong research group also investigated the intermolecular aldol reaction of hydroxyacetone with benzaldehyde, catalyzed by a proline amide (Scheme 17).³⁸ It was found that water influenced the regioselectivity, affording products with enantioselectivities ranging from 91 to 99% ee. Theoretical studies (B3LYP/6-31++G(d, p)//HF/6-31+G(d) with explicit solvation by water) revealed that this is due to the hydrogen bonds formed between the amide oxygen of proline amide, the hydroxy of hydroxyacetone, and water. HF generally gives poor activation energies because of the lack of correlation energy. This may also cause the position of the transition state to be in error. However, geometries with HF are reasonable, if less accurate than B3LYP geometries, so that use of HF for geometries is occasionally employed for large systems.

Scheme 17 — Intermolecular aldol reaction of hydroxyacetone with benzaldehyde, catalyzed by a proline amide

The anti enamine and anti enol enamine were predicted to differ in stability by only 0.4 kcal/mol (Scheme 18). In the absence of explicit solvation, the transition state leading to the minor 1,2-diol regioisomer (via the enol enamine) was calculated to be favored over the transition state leading to the major 1,4-diol regioisomer (via the enamine) by 4.3 kcal/mol. This regioselectivity is attributed to the short hydrogen-hydrogen distance of 2.34 Å between an amide hydrogen and hydroxy hydrogen in the disfavored transition state.

With the inclusion of an explicit water molecule, the calculated relative energies of the transition states still favor the experimental 1,2-diol (Figure 13). It was reasoned that the experimentally observed selectivity for the 1,4-diol is attributed to the stabilities of the enamine-water complexes. The 6.6 kcal/mol stability of the anti enamine compared to the anti enol enamine leads to formation of the favored 1,4-diol.

Aldol reaction of benzaldehyde and hydroxyacetone catalyzed by proline amide.

Okuyama and co-workers observed high stereoselectivities in aldol and Michael addition reactions catalyzed by 4-hydroxyprolinamide alcohols (Scheme 19).³⁹ B3LYP/6-31G(d) calculations were performed to understand the high selectivity observed in the reaction between acetone and benzaldehyde (99% ee).

Scheme 19 — Aldol reaction of acetone and cyclohexanones catalyzed by a 4-hydroxyprolineamide alcohol

The anti conformation of the enamine was assumed to be the most stable, and attack on the re- and si-faces of benzaldehyde were calculated. Only one conformation for each of these transition states was located due to steric hindrance of the two gem-diphenyl groups of the catalyst (Figure 14). The 5.3 kcal/mol difference between the transition states leading to the major (R) and minor (S) isomers is in excellent agreement with the experimental results.

*anti-re* and *anti-si* transition structures for the prolineamide-catalyzed aldol reaction.

2.1.2.5. Primary amino acids

Acyclic primary amino acids have also been discovered to be catalysts for the intermolecular aldol reactions (Scheme 20), as discussed earlier for the Hajos-Parrish reaction.⁴⁰ Simple natural and unnatural primary amino acid derivatives catalyzed the reaction between cyclohexanone and an aldehyde in high yield and enantioselectivities.

Córdova has reported the origins of stereoselectivity of this reaction using B3LYP/6-31G(d, p) geometry optimizations and B3LYP/6-31+G(2d,2p) single points.⁴¹ Four factors were seen to control the stereoselectivity of this reaction: (1) The C-N bond of the amino acid can rotate in the enamine intermediate, in contrast to the corresponding proline-derived enamine intermediates. (2) ^δ+NH···O^δ− electrostatic interactions between the amine proton and the forming alkoxide are stabilizing. Transition state (R, R), which lacks this interaction, is higher in energy by 2–5 kcal/mol (Figure 15). (3) The steric interactions between the aldehyde phenyl and the enamine cyclohexyl are destabilizing. The (S, S) transition state is thus more crowded than the corresponding (S, R) transition state, which lacks this destabilizing interaction. The same holds true for the (R, R) transition state compared to the (R, S) transition state. (4) Finally, the methyl substituent of alanine interacts unfavorably with the cyclohexyl ring, destabilizing the (R, S) transition state by 3.2 kcal/mol compared to the (S, R).

(S, R), (S, S), (*R, R*), and (R, S) TSs for the reaction between cyclohexanone enamine of alanine and benzaldehyde

The same group computed the reaction profile for formation of the major (S, R) product (Figure 16a). The overall reaction profile is analogous to various proline-catalyzed processes. It is worthy to note that the oxazolidinone is 4.6 kcal/mol more stable compared to the active catalyst enamine (Figure 16b). Córdova stated that the need for water in the reaction mixture experimentally is to drive the equilibrium towards the enamine from the oxazolidinone.

(a) Overall reaction profile for primary amino acid catalyzed aldol reaction. (b) Relative energies of oxazolidinone and enamine (kcal/mol).

Blackmond and co-workers later investigated the effect of water in proline-mediated aldol reactions using reaction progress kinetics analysis.^29e Their results showed two conflicting roles for water: 1) increasing the total catalyst concentration within the cycle due to the suppression of spectator species, such as oxazolidinones; 2) decreasing the relative concentrations of key intermediates in the cycle by shifting the equilibrium from the iminium carboxylate back toward proline.

2.1.2.6. Cyclic aminophosphonates - pyrrolidin-2-ylphosphonic acid

Dinér and Amedjkouh reported the aldol reaction of acetone and cyclohexanone derivatives with para-nitrobenzaldehyde catalyzed by pyrrolidin-2-ylphosphonic acid (Scheme 21).⁴² This catalyst is the phosphonic acid version of proline, and was studied as a candidate for the syn-aldol catalyst.

Scheme 21 — Pyrrolidin-2-ylphosphonic acid catalyzed intermolecular aldol reactions

The reaction involving acetone and para-nitrobenzaldehyde has been studied computationally using B3LYP/6-31G(d). The three most important transition structures are shown in Figure 17.

The most stable *anti*-re, *anti*-si, and *syn*-re transition structures.

The origins of stereoselectivity for this catalyst are very similar to those for the proline cases. The one notable difference between this catalyst and proline is that the syn-re transition state is only 0.9 kcal/mol disfavored compared to the most stable anti-re, whereas in proline, this difference is greater (>2 kcal/mol).

All enantioselective organocatalysts known to date yield the anti-aldol as major products. The authors hoped that the reduced preference between the anti and syn enamine preference in the aldol transition state of this catalyst would favor the formation of syn aldol in the reaction between benzaldehyde and various cyclohexanone derivatives. However, even with Lewis base additives which enhance the syn-aldol selectivity to the reaction mixture, the authors found only modest preference for the syn aldol (syn:anti ~1:1).

2.1.2.7. Nornicotine

Lovell, Noodleman, and Janda have reported the experimental and theoretical studies of nornicotine aqueous aldol reactions between acetone and substituted benzaldehydes. Notably, proline and pyrrolidine are poor catalysts for the aqueous aldol reactions. The mechanism they proposed for this reaction is shown in Scheme 22.⁴³

Scheme 22 — Nornicotine catalyzed intermolecular aldol reaction mechanism

Lovell, Noodleman, and Janda propose that the nornicotine catalyst reacts via the enamine pathway, but invoked an unusual transition state in which a molecule of water simultaneously attacks the internal carbon of the enamine olefin and donates a proton to the forming alkoxide. In addition a second molecule of water is suggested to be present in the transition structure that later participates in the hydrolysis of the catalyst. No explanations were offered to justify the necessity for the electrophile addition to the more hindered face of the enamine.

This mechanism is based on their calculations for the model reaction of acetaldehyde and acetone (Scheme 23). However, the authors did not include the 9 kcal/mol higher energy of the enol tautomer of acetone compared to acetone. Furthermore, this high energy pathway, in which the first transition structure is entropically disfavored, was not explained.

Zhang and Houk computed the same aldol reaction in water and proposed an alternative mechanism involving water ionization.⁴⁴ The reaction involves three steps: (1) water autoionization, (2) hydroxide or hydronium-catalyzed conversion of aldehyde or ketone into enol, and (3) C-C bond formation and proton transfer to give the aldol product. The overall process for the reaction of acetone and acetaldehyde using B3LYP/6-311++G(3d,3p)//B3LYP/6-31G(d) and the CPCM solvation model are shown in Scheme 24. Two alternative possible mechanisms—(1) initial proton transfer from the ketone enol to water, and (2) initial proton transfer from the ketone enol to aldehyde—were also computed, but the highest-energy species of these reactions are significantly higher in energy than that of the mechanism shown in Scheme 24. While C-C bond formation was calculated to be the rate-determining step, formation of the enol or enolate may be rate-determining for more reactive aldehydes.

Scheme 24 — Intermolecular aldol reaction mechanism computed by Janda and co-workers⁴³ (B3LYP/6-311+G(2d,2p)//B3LYP/6-311G(d, p); COSMO model for solvation energies (water))

2.1.3. Mannich reaction

The discovery of the intermolecular aldol reaction soon paved the way for the discovery that additions to various other double bonds would also be possible. The proline-catalyzed direct Mannich reaction is a natural extension of the aldol reaction, and is a highly effective carbon-carbon bond-forming reaction that is used for the preparation of enantiomerically enriched amino acids, amino alcohols, and their derivatives (Scheme 25).⁴⁵

Scheme 25 — Typical intermolecular Mannich and aldol reactions catalyzed by proline

Origin of the reverse enantioselectivity compared to the aldol reaction

The enantioselectivity of the Mannich reaction is opposite that of the aldol reaction. Computational investigations by Houk and co-workers show that the imine acceptor must be situated so as to accommodate proton transfer to nitrogen (Figure 18).⁴⁶ This situates the carbon substituent in the more crowded pseudo-axial position.

The *anti*-re and -si TSs of the Mannich reaction, and *anti-re* TS of the aldol reaction catalyzed by proline.

The enhanced rate of the Mannich reaction versus the aldol reaction

It is also of interest to note that proline-catalyzed Mannich reactions are often much faster than the corresponding aldol reaction. Hayashi and co-workers have suggested that the more basic imines are more readily activated by the carboxylic acid of proline.⁴⁷

The origin of erosion of diastereoselectivity in the pipecolic acid catalyzed Mannich reaction

Barbas’ group reported that pipecolic acid catalysis gives both syn and anti diastereomers with high enantioselectivity (Scheme 26).⁴⁸ The diastereomeric ratio of syn- versus anti-product ranged from 2:1 to 1:1. This unusual change in diastereoselectivity upon the increase in ring size from five to six was investigated computationally by Cheong and Houk.⁴⁸

The C-C bond forming steps involving both pipecolic acid and proline enamines of propionaldehyde attacking the N-PMP-protected R-imino methyl glyoxylate were calculated at the HF level of theory with the 6-31G(d) basis set.

The diastereoselectivity of this reaction is determined by whether the anti or syn enamine conformer is favored in the transition structure. In the case of proline, the transition structures involving the anti-enamine are favored over those that involve the syn-enamine. The latter involves distortions of the developing iminium from planarity to accommodate proton transfer, and the computed diastereoselectivity given by the difference in anti-si and syn-si transition structures is 1.0 kcal/mol.

This differentiation is weakened in the case of pipecolic acid – the analogous difference for pipecolic acid is only 0.2 kcal/mol (Figure 19). The piperidine ring experiences steric interactions with the anti or syn-enamines that are different than those of the pyrrolidine ring of proline. The relatively rigid piperidine ring holds the carboxylic acid more rigidly than the more flexible pyrrolidine. This alters electrostatic interactions with the ester of the iminoglyoxylate and with the protonated imine. These differences allow the imine to react via both the anti and syn-enamine, giving rise to roughly equal amounts of both syn- and anti-product experimentally and computationally. Although the calculated selectivities are in good agreement with the experiments, it should be noted that various benchmarks show that such small energy differences fall in the error margin of the most of the standard computational methods.^2–7 It is generally assumed, without proof, that these methods are able to predict small differences in the energies of stereoisomeric transition states.

The *anti-si* and *syn-si* transition structures of Mannich reaction catalyzed by pipecolic acid.

The facial re or si selectivity of the imine acceptor is governed by the necessity for intramolecular proton transfer and minimization of steric interactions between the imine and the reactive enamine. The E-imine is more stable than the Z-imine. Transition structures involving intramolecular proton transfer are favored; thus the re face attacks necessitate substantial eclipsing of the imine and enamine. Consequently, anti-re and syn-re transition structures are higher in energy by >1 kcal/mol than the anti-si or syn-si transition structure for both proline and pipecolic acid.

The Mannich reaction catalyzed by diarylprolinol silyl ethers

Hayashi and co-workers used B3LYP/6-31G(d) to investigate the role of acid additives in the Mannich reaction of imines and acetaldehyde catalyzed by diarylprolinol silyl ethers (Scheme 27).⁴⁹ The catalyst was modeled by 2-methylpyrrolidine and the imine was modeled by N-benzoyl-N-benzylidenenamine. The lowest energy conformer was calculated to have an s-cis geometry around the C=N–C=O bond (Scheme 28). The s-trans conformer converged to a transition structure for the rotation of this dihedral. The Z-isomer is approximately 30 kcal/mol higher in energy than the E. The modeled enamine was calculated to have a small 0.7 kcal/mol preference for an anti alkene with respect to the pyrrolidine methyl group. The imine was calculated to favor protonation of the nitrogen versus protonation of the carbonyl oxygen by approximately 7 kcal/mol.

Scheme 27 — Diarylprolinol silyl ether catalyzed Mannich reaction

Scheme 28 — Imine and enamine conformers

Addition of the acetaldehyde anti-enamine to the protonated imine was calculated to be highly exothermic (−31.1 kcal/mol in THF, PCM model) and barrierless. The favored transition structure was modeled by constraining the forming C–C bond at 3.0 Å and plotting the energy versus the dihedral angle around this bond. The optimal geometry was located at a dihedral angle of 140 between the reacting imine and enamine double bonds (Figure 20). Because the addition step is extremely fast, the authors conclude that enaminium formation is the rate-determining step of the reaction.

Transition state model for Mannich reaction of acetaldehyde and protonated N-benzoyl iminium.

Wong also investigated a similar Mannich reaction using the same catalyst and concluded that the reaction proceeds through an enol rather than an enamine intermediate (Scheme 29).⁵⁰ The calculated enantioselectivity is in good agreement with experimental results. Wong also proposed that the Michael-aldol condensation, Michael addition, α-amination, α-fluorination, and α-sulfenylation, and α-bromination reactions proceed by an enol intermediate with this catalyst.

Scheme 29 — Mannich reaction via an enol mechanism

The Mannich reaction catalyzed by (S)-1-(2-pyrrolidinylmethyl) pyrrolidine

Li and co-workers used BH&HLYP to explain the opposite diastereoselectivities obtained by (S)-1-(2-pyrrolidinylmethyl) pyrrolidine and proline in the direct Mannich reactions between ketimine and isovaleraldehyde reported by Jørgensen and co-workers (Scheme 30).⁵¹ Sketches and relative energies of the lowest energy transition structures for each diastereomeric product are shown in Scheme 31. The (S, S) and (R, S) transition structures are higher in energy than the (R, R) and (S, R) transition structures due to a disfavored steric interaction between the ketimine protecting group and the pyrrolidinyl moiety of the catalyst. In the (R, R) and (S, R) transition structures, the ketimine is attacked from the opposite face of the pyrrolidine group. The stability of the (R, R) transition state compared to the diastereomeric (S, R) transition structure is attributed to three factors: (1) larger degree of planarity of the developing iminium in the (R, R) transition structure, (2) electrostatic stabilization of the imine nitrogen by the catalyst in the (R, R) transition structure, and (3) better staggering around the forming C-C bond in the (R, R) transition structure.

Scheme 30 — Opposite diastereoselectivities observed in the Mannich reaction with proline and pyrrolidinylmethylpyrrolidine catalysts

Scheme 31 — Lowest energy transition structures leading to each diastereomer of the Mannich reaction (BH&HLYP/6-31G(d, p), including solvation energies—CH₂Cl₂, CPCM/UAKS model)

Catalysis of the same reaction by proline was then studied computationally and represented the first theoretical study of the Mannich reaction of ketimines. The previous studies had involved reactions of aldimines. The lowest energy transition structures for each diastereomer are shown in Scheme 32. The C-C bond forming distances are shorter than those calculated for the reactions of aldimines (2.2–2.4 Å) and the proton transfer occurs later in the ketimine reactions. In agreement with experiment, the lowest energy transition structure involves attack of the anti enamine on the si-face of the ketimine to give the (R, S) product. This transition structure has good staggering around the C–C forming bond and the iminium is stabilized by the carboxylic acid proton.

Scheme 32 — Lowest energy transition structures leading to each diastereomer of the Mannich reaction (BH& HLYP/6-31G(d, p), including solvation energies—CH₂Cl₂, CPCM/UAKS model)

The computational design of an anti-selective Mannich organocatalyst

Following on the heels of the study of pipecolic acid catalyzed Mannich reactions, Houk and Barbas reported a joint computational and experimental design of an anti-selective organocatalyst (Scheme 33).⁵² The stereoselective formation of anti-products necessitates a reversal in the facial selectivity of either the enamine or the imine, compared to the proline-catalyzed reactions. A substituent at the 5-position of the pyrrolidine was used to fix the conformation of the enamine. The acid functionality was placed at the distal 3-position of the ring, to affect control of enamine and imine facial selection in the transition state. To avoid steric interactions between the substituent at the 5-position of the new catalyst and the imine in the transition state, the substituents at 3- and 5-positions were placed in the trans configuration. On the basis of these considerations, a new catalyst, (3R,5R)-5-methyl-3-pyrrolidinecarboxylic acid, was designed. The proposed major transition state of the Mannich reaction catalyzed by the new catalyst is shown in Scheme 33.

Scheme 33 — Development of *anti-*selective Mannich reaction organocatalyst

The reaction between propionaldehyde and N-PMP-protected R-imino methyl glyoxylate was studied using HF/6-31G(d) calculations to test the design prior to synthesis. No computed structures were reported in this work. The catalyst was predicted to give 95:5 anti:syn diastereoselectivity and ~98% ee for the formation of the (2S,3R)-product.

The relative contributions of the carboxylic acid and methyl group of the catalyst in directing the stereochemical outcome of the reaction were assessed. Computational studies involving the derivative lacking the 5-methyl group, (S)-3-pyrrolidinecarboxylic acid, indicate that the methyl group contributes ~1 kcal/mol toward the anti-diastereoselectivity. That is, the stereoselectivity changes to 82:18 anti:syn dr and 92% ee when transition structures with the unmethylated catalyst are located. This unmethylated catalyst was also tested in an actual reaction, for the case where R1 = i-Pr. This derivative afforded (2R,3S)-anti-product in 95:5 anti:syn dr and 93% ee, which is a drop of 0.6 kcal/mol from the 1-catalyzed reaction with the same substrate.

2.1.4. α-Aminoxylation reaction

The proline-catalyzed aminoxylation reaction is a convenient way of oxidizing the α position of carbonyl compounds (Scheme 34).

Three different variations of the mechanism have been proposed (Scheme 35). The proposed mechanisms differed by the degree to which the carboxylic acid or the proline amine participates in the proton-transfer process. The transition state model proposed by Hayashi⁵³ is analogous to the Houk-List model; proton transfer occurs from the carboxylic acid in a “partial-Zimmerman-Traxler” chairlike transition state. Zhong proposed a Zimmerman-Traxler transition state in which the proline amine also facilitates the proton transfer,⁵⁴ while MacMillan proposed an enammonium-mediated ene-like zwitterionic transition state.⁵⁵ These pathways do not exhaust the mechanistic possibilities. Nitrosobenzene dimerizes readily, and analogous pathways involving the proline enamine attack on the nitrosobenzene dimer are also possible. Blackmond has reported the observation of an acceleration of reaction rate for the aminoxylation and the related amination reactions by the products of the reaction.^56,29f It was concluded that the autoinduction occurs in these reactions but not in the aldol reaction because of a difference in the rate-determing steps. ⁵⁷

The reaction was investigated computationally by the Cordóva,^58a Houk^58b and Wong^58c groups. Cordóva reports that the C-O bond forming step for the major R-enantiomer occurs via the anti enamine, similar to the model proposed by Hayashi (Scheme 36). Formation of the minor S-enantiomer reportedly occurs via addition of the syn enamine to the re-face of the hydrogen-bound nitrosomethane. The minor transition structure is disfavored by approximately 7 kcal/mol. Attempts to locate a transition structure according to the MacMillan model resulted in structures that are similar to the Hayashi transition structure.

Scheme 36 — B3LYP/6-311+G(2d,2p)//B3LYP/6-31G(d, p) relative gas phase transition structure energies for the aminoxylation reaction

The transition structure for the major R-enantiomer computed by the Houk group (Figure 21)^58b is similar to that of Cordóva. However, the minor transition structure (syn-O) differs in that the syn enamine attacks the si-face of the hydrogen-bound nitrosobenzene, as opposed to the re-face described by Cordóva. The transition structure for the minor enantiomer is 3.3 kcal/mol higher in energy than the most stable transition structure for the major enantiomer. This corresponds to a prediction of 99% ee of the product favored experimentally, in reasonable agreement with the experimentally reported ee of 97%.

B3LYP/6-31G(d) transition structures for the α-aminoxylation reaction. Activation energies include HF/6-31+G(d, p) DMSO, PCM model, UAKS radii solvation.

The model proposed by Zhong is found not to be a transition state, but minimizes to more stable transition state anti-O. Here the proline amine-proton distance is 2.7 Å, and there is no evidence of proline amine pyramidalization. The enammonium-mediated zwitterionic ene-like transition state proposed by MacMillan, with the carboxylate group syn to the proton-transfer face, was not found. The closest enammonium transition structure found was one in which the carboxylate group is anti to the proton transfer; it is 32.4 kcal/mol higher in energy than the most stable transition structure. The high barrier is attributed to the poor nucleophilicity of the enammonium olefin and the great energetic penalty accrued by the charge separation.^58b

The transition structures involving the nitrosobenzene dimer are disfavored due to the entropic cost of dimerization and the difficulty of a nucleophilic attack on the partially negatively charged oxygen of the nitrosobenzene dimer. The most stable transition structure involving the nitrosobenzene dimer is 24.4 kcal/mol higher than the most stable pathway involving the nitrosobenzene monomer.^58b

The transition structures for attack at nitrogen (oxyamination) were generally higher in energy than those for attack at oxygen. The attack at nitrogen to give the (R)-hydroxyamination product via transition structure anti-N is disfavored by 2.6 kcal/mol. This heteroatom selectivity is also explained by the preferential protonation of the more basic nitrogen. In the absence of Brønsted catalysis, a reversal in heteroatom selectivity is expected. The reaction between the dimethyl enamine of propionaldehyde and nitrosobenzene was computationally shown to favor the attack on the nitrogen.^58b

Wong also investigated the reaction and found that the lowest energy transition structures for each enantiomer occur from the anti enamine (Scheme 37). The calculated energy difference is large in the gas phase (5.2 kcal/mol), but decreases substantially with the inclusion of solvent effects (1.3 kcal/mol). The pathway subsequent to bond-formation was also computed with one explicit water molecule. It was found that the resulting imine favors a syn geometry with respect to the catalyst carboxylate in order to maximize hydrogen bonding. ^58c

Scheme 37 — B3LYP/6-31G(d, p) activation energies for the α-aminoxylation reaction (Solvation energy corrections (B3LYP/6-311+G(2d,2p) PCM, DMSO) are in brackets)

2.1.5. α-Fluorination

Jørgensen used DFT to explain the enantioselectivities of α-fluorination reactions catalyzed by trimethylsilyl diarylprolinol (Scheme 38).⁵⁹ Unlike proline, where the carboxylic acid directs the electrophile to the “top” face of the enamine via hydrogen bonding, the TMS diarylprolinol catalyst directs the electrophile to the “bottom” face of the catalyst due to steric shielding (Scheme 39). It was found that there is little preference for the anti or syn enamines of propanal and 3,3-dimethylbutanal (Scheme 40), so transition structures for attack of both anti and syn enamines were calculated.

Scheme 39 — Hydrogen bond and steric stereocontrol

Scheme 40 — B3LYP/6-31G(d) relative free energies of *anti* versus *syn* enamines

Transition structures for the α-fluorination of 3,3-dimethylbutanal by N-fluorobenzenesulfonamide (NFSI) were located using B3LYP/6-31G(d). The syn and anti conformations and E and Z geometries were considered. The lowest energy transition structures leading to the major (S)- and minor (R)-enantiomers are shown in Figure 22. The major (S)-enantiomer is formed by attack of the anti-E enamine from the “bottom” (si) face to NFSI. The minor (R)-enantiomer is 2.4 kcal/mol higher in energy and is formed by attack of the syn-E-enamine from the “bottom” (re) face to NFSI. This predicted selectivity (96% ee) is in excellent agreement with the enantioselectivity (97% ee) observed experimentally. The energy difference is attributed to good staggering around the forming C-F and breaking F-N bonds in the major enantiomer, but eclipsing around these bonds in the minor enantiomer. The transition structure for the major enantiomer of the α-amination of n-butanal by diethyl azodicarboxylate (DEAD) was also located, but the stereoselectivity was not discussed.

Lowest energy transition structures for the α-fluorination of 2,2-dimethylbutanal.

2.1.6. γ-Amination

The γ-amination of α,β-unsaturated aldehydes by diethyl azodicarboxylate (DEAD), catalyzed by the same TMS-protected diarylprolinol, was studied computationally by Jørgensen (Scheme 41).⁶⁰ The (R) enantiomer dominated in these reactions, which is the opposite of what was expected. Density functional theory (B3LYP/6-31G(d) with CPCM solvent corrections) was used to rationalize the stereoselectivity of the reaction. Two low-energy conformers of the enamine were located, E-s-trans-E and E-s-trans-Z (Scheme 42), which differ in energy by 1.4 kcal/mol. This is consistent with ¹H-NMR observations of a mixture of isomers; the two isomers are believed to readily interconvertible by a protonation/deprotonation mechanism.

Scheme 41 — γ-amination of α,β-unsaturated aldehydes

Scheme 42 — Mechanism for the γ-amination of 2-pentenal. B3LYP/6-31G(d) energies (with CPCM solvent corrections)

The activation energy for γ-amination of the major (R) isomer with respect to the E-s-trans-E enamine is predicted to be 17.1 kcal/mol, while that of the minor (S) enantiomer is 13.0 kcal/mol. The activation energy for α-amination of both enamine conformations is approximately 21 kcal/mol. Given the discrepancy between the calculated selectivity for the (S)-enantiomer and the experimental observation of the (R)-enantiomer, Diels-Alder cycloaddition barriers of the enamine intermediates were calculated. It was postulated that the resulting Diels-Alder cycloadducts should readily hydrolyze to the γ-aminated aldehyde, and the E-geometry of the C2-C3 double bond would be restablished via a reversible addition mechanism of a nucleophile such as water or the catalyst. The activation energy for the [4+2] cycloaddition of E-s-cis-E was calculated to be only 6.7 kcal/mol (11.6 kcal/mol with respect to the lowest energy enamine, Figure 23), while the activation energy for the [4+2] cycloaddition of E-s-cis-Z was calculated to be 12.3 kcal/mol (18.1 kcal/mol with respect to the lowest energy enamine). The Diels-Alder reactions were calculated to be exothermic, while the γ-amination reactions were calculated to be endothermic. Thus, calculations predict that the preferred mechanism for γ-amination occurs by a Diels-Alder cycloaddition of the E-s-cis-E enamine, followed by hydrolysis to give the (R) product. To support the Diels-Alder mechanism, 2-pentenal and the pyrrolidine catalyst were reacted with N-methylmaleimide instead of DEAD. The Diels-Alder cycloadduct was isolated.

Lowest energy transition structures for the [4+2] cycloaddition of enamines and DEAD.

The Seebach group computed the relative energies of the enamine formed by 2-pentenal, and the iminium formed by 3-phenyl-2-propenal, with TMS-protected diarylprolinol catalyst using B3LYP and MP2 and found that the anti-all-trans conformations are most stable (Figure 24).⁶¹ The most stable calculated iminium geometry overlays very well with the crystal structure.

DFT gas phase relative energies calculated by Seebach and co-workers (ref 47).

2.1.7. α-Alkylation

The intramolecular catalytic asymmetric α-alkylation of aldehydes was developed by List and co-workers. The synthesis of cyclic aldehydes via proline and 2-methylproline catalyzed cyclizations of acyclic halo-aldehydes are shown in Scheme 43.⁶²

Scheme 43 — The prototypical proline and 2-methylproline catalyzed alkylation reaction

Two items are of particular interest in this reaction: (1) Simple methyl substitution at the 2-position of proline enhanced the stereoselectivity of the reaction, as shown in Scheme 43. (2) Triethylamine accelerates the reaction. Thiel and List reported a computational investigation of this reaction using B3LYP with the 6-31G(d) and LANL2DZ basis sets.⁶³ CHCl₃ solvation effects were taken into account by geometry optimizations using the Onsager model and single point energies using the CPCM method with the UAKS radii. Triethylamine was modeled using trimethylamine.

The reaction proceeds via the enamine nucleophilic displacement of the halogen, analogous to the typical proline mechanisms (Figure 25). The rate and stereo-determining step was considered to be the alkylation step. It is interesting to note that the stabilization of the departing iodide by the carboxylic acid of the catalyst induces a cisoid conformation of the carboxylic acid, while in other reported reactions involving proline, the transoid conformation is preferred. Triethylamine was found to provide a salt bridge between the carboxylic acid and the departing halide.

The two lowest energy alkylation transition structures involving 2-methylproline and trimethylamine

The stereoselectivity of this reaction arises from preferred cyclization by the anti enamine. The basic origin of stereoselectivity remains the same – the cyclization of the syn enamine accrues energetic penalties due to the catalyst stabilization of a more proximal developing anion. The calculated 99% ee is in good agreement with the experimentally observed 95% ee. The enhanced enantioselectivity for the 2-methylproline catalyzed aldol reaction compared to the proline-catalyzed reaction is due to the inherently larger steric interactions between the methyl and the aldehyde substituent in the syn transition structure. Again, the calculated 66% ee for the proline-catalyzed reaction is in good agreement with the experimental 68% ee.

2.1.8. Hydrophosphination

Diaryl prolinols have been used to catalyze the asymmetric hydrophosphination of α,βunsaturated aldehydes (Scheme 44).⁶⁴ The origin of high enantioselectivity was investigated using density functional theory (B3LYP/6-311+G(2d,2p)//B3LYP/6-31G(d, p)). The lowest energy iminium intermediate is in the E geometry and is 3.5 kcal/mol lower in energy than the Z isomer (Scheme 45). In agreement with experimental observations, the lowest energy transition structure leads to the S product. The lowest energy transition structure leading to the minor R product is 1.5 kcal/mol higher in energy and also rises from the E iminium. Steric repulsion with the bulky group of the catalyst causes this transition state to be disfavored. The lowest energy transition structure that arises from the Z iminium is 4.2 kcal/mol higher in energy than the S transition state.

Scheme 45 — B3LYP/6-31G(d, p) iminium ion and transition structure energies. Solvent-corrected values (B3LYP/6-311+G(2d,2p) single point, CPCM, CHCl₃) are in parentheses

2.1.9. Michael addition

Domingo and co-workers used B3LYP/6-31G(d, p) to study the role of (S)-5-(pyrrolidin-2-yl)-1H-tetrazole in the Michael addition of (i) acetaldehyde to nitroethylene and (ii) acetone to β-nitrostyrene (Scheme 46).⁶⁵ For the former reaction, it was found that the enamine isomers formed by condensation of the catalyst with acetaldehyde differ by only 0.8 kcal/mol (Model A, Scheme 47). All possible modes of addition—of the α and β faces of both the anti and syn enamines to both faces of nitroethylene—were calculated. The lowest energy transition structure has an activation barrier of 18.7 kcal/mol and occurs by addition of nitroethylene to the β-face of the anti conformation of the enamine, with a hydrogen bond between the tetrazole hydrogen and an oxygen on the nitro group.

Scheme 46 — Michael addition of nitroalkenes to acetaldehyde and acetone

Scheme 47 — Relative energies of Michael addition

For the latter reaction, four transition structures—addition of both faces of nitrostyrene to the β-face of both the anti and syn enamines—were located (Model B). The four lowest energy transition structures for each mode of attack are shown in Scheme 48. In all four transition structures, an anti arrangement between the phenyl group of nitrostyrene and the enamine C-C double bond, and a gauche arrangement between the enamine and nitrostyrene C-C double bonds are preferred. The configuration of the lowest energy transition structure, TS-anti-re, agrees with the experimentally observed major diastereomer. The stability of this transition structure is attributed to favorable electrostatic interactions between the forming iminium and the nitro group, as well as the tetrazole hydrogen and an oxygen on the nitro group. Seebach proposed this arrangement (topological rule) for the transition states of enamine reactions with nitroalkenes.⁶⁶ The syn transition structures are approximately 2 kcal/mol higher in energy; the N=O^···H-N distances reveal weaker hydrogen bond stabilization.

Scheme 48 — Transition structures and activation energies for addition of acetaldehyde-enamine to nitrostyrene

Sunoj used mPW1PW91 and B3LYP to explore the importance of explicit solvation in computing transition structures for the proline-catalyzed Michael addition of 3-pentanone and cyclohexanone to nitrostyrene (Scheme 49).⁶⁷ Polar protic solvents had experimentally been shown to improve reaction rates and stereoselectivities,⁶⁸ and calculations without explicit solvent molecules failed to reproduce the experimentally observed stereoselectivities. The experimentally observed major diastereomer could arise from addition of the anti enamine to the re-face of nitrostyrene (TS-anti-re) to give the syn-(S, R) product. However, mPW1PW91/6–311G(d, p)//mPW1PW91/6–31G(d) gas phase calculations predict a stereochemical outcome of 6% de (syn) and 40% ee in favor of the (S, R) product for 3-pentanone, and 32% de (anti) and 97% ee in favor of the (R, R) product for cyclohexanone.

Scheme 49 — Proline-catalyzed addition of 3-pentanone and cyclohexanone to nitrostyrene

With one methanol, calculations still do not fit experiment, but the inclusion of two methanol molecules in a cooperative binding mode results in stereoselectivities that are in good agreement with experimental results. Calculations predict 80% de (syn) and 90% ee (S, R) for 3-pentanone, and 82% de (syn) and 59% ee (S, R) for cyclohexanone. The most favored transition structures for each ketone are shown in Figure 26. Both transition structures involve attack of the anti enamine to the re-face of nitrostyrene, with two methanol molecules bridging the carboxylic acid group of the catalyst and the nitro group of the alkene. The enamine and nitroalkene C-C π bonds are anti to one another.

Lowest energy transition structures for the proline catalyzed Michael addition of nitrostyrene and cyclohexanone (left) and 3-pentanone (right), with 2 explicit water molecules.

Nájera and co-workers used B3LYP/6-31G(d) to explain the stereoselectivity of the Michael addition reaction of nitroalkenes with 1,2-aminoalcohol-derived prolinamide catalysts (Scheme 50).⁶⁹

Scheme 50 — Michael addition catalyzed by prolinamide catalysts

The reaction was modeled by 3-pentanone, 1-nitropropene, and a truncated 1,2-aminoalcohol catalyst. Four possible modes of attack—attack of the nitropropene on both the Re- and Si- faces of both the anti- and syn-enamines were calculated (Scheme 51).

Scheme 51 — Possible modes of attack for the Michael addition reaction

In agreement with the experimental results, the lowest energy transition structure (Table 1, TS anti, Re, 15.0 kcal/mol), which occurs via attack of the Re-face of the anti enamine, gives the major (4S,5R)-syn product. The transition structure that gives the minor (4R,5S)-syn enantiomer occurs by attack of the nitroalkene to the Si-face of the anti enamine. The computed energy difference between these two transition structures (1.4 kcal/mol ≈ 80% ee) agrees well with the enantioselectivities obtained experimentally. The syn, re and syn, si transition structures do not have stabilizing hydrogen bond interactions and therefore have higher calculated activation energies.

Table 1.

B3LYP/6-31G(d) activation energies (kcal/mol)


TS	E_act	Forming C^···C	NH^···O1	O3H^···O1	NH^···O2	O3H^···O2
TS anti, re	15.0	2.13	2.03	1.89	2.59	2.72
TS anti, si	16.4	2.10	2.11	2.85	2.56	2.09
TS syn, re	18.2	2.01	–	–	–	–
TS syn, si	27.6	1.95	–	–	–	–

Open in a new tab

Alexakis and co-workers reported a DFT study of the pyrrolidine-type catalyzed conjugate addition of aldehydes to vinyl sulfone and vinyl phosphonate Michael acceptors (Scheme 52).⁷⁰ The reaction of 3,3-dimethylisobutyraldehyde and vinyl sulfone was computed. Because the five lowest-energy minima for the enamine formed by the pyrrolidine catalyst and 3,3-dimethylbutyraldehyde are anti, only the transition structures for si-face (“bottom”, major) and re-face (“top”, minor) attack on the anti enamine were considered (Figure 27). In agreement with experiment, si-face attack was calculated to be favored (ΔG^‡ = 6.2 kcal/mol). The stereoselectivity is attributed to favorable electrostatic interactions between the sulfone oxygens and enamine nitrogen. Compared to the reactant, the negative charge on each sulfone oxygen increases in the transition state, and these oxygens are stabilized by the developing positive charge on the enamine nitrogen. The minor (re) transition structure was calculated to be significantly higher in energy (ΔG^‡ = 13.0 kcal/mol). The sulfone oxygens in the minor transition structure are far from the enamine nitrogen (4.07 Å), and experience steric hindrance with the bulky group of the catalyst.

Scheme 52 — Michael addition reaction of vinyl sulfones

Michael addition transition structures for the addition of 3,3-dimethylisobutyraldehyde to a vinyl disulfone.

A variety of chiral amines based on the pyrrolidine skeleton are shown to catalyze the Michael addition of aldehydes to vinyl ketones.⁷¹ An interesting aspect of the reaction is that the catalyst can equally take part in the nucleophilic activation of the aldehyde by enamine formation, and/or in the electrophilic activation of the vinyl ketone by iminium ion formation. Patil and Sunoj have investigated the competing enamine and iminium pathways in the pyrollidine catalyzed Michael addition between propanal and methyl vinyl ketone (MVK)(Scheme 53).⁷² The results summarized in Table 2 suggest that the direct Michael addition of the enamine intermediate to MVK is the more likely pathway for the C-C bond formation in this reaction.

Scheme 53 — Competing pathways for pyrrolidine catalyzed Michael addition of propanal with methyl vinyl ketone (MVK)

Table 2.

Activation free energies^a (ΔG, kcal/mol) for the formation of enamine intermediate by the reaction of pyrrolidine and propanal, formation of the iminium ion by the reaction of pyrrolidine and MVK and for the C-C bond formation through various plausible pathways

Enamine Formation		Iminium Ion Formation		C-C bond formation
Addition	Dehydration	Addition	Dehydration	Pathway1	Pathway2	Pathway3	Pathway4
36.5 (17.0)^b	49.0 (24.6)^b	42.8 (24.2)^b	--- (30.9)^b	88.9	26.1	69.9	25.5

Open in a new tab

^a

With respect to the separated reactants, computed with PCM(THF)/mPW1PW91/6-311G(d, p)//6-31G(d) level of theory,

^b

Activation free energies for phenol assisted enamine and iminium ion formation are given in parenthesis.

2.1.9. Cascade Reactions

Sunoj reported a computational study of the highly stereoselective triple cascade reaction reported by Enders and co-workers (Scheme 54).⁷³ All possible conformers and faces of addition were explored using B3LYP/6-31G(d)//ONIOM2(B3LYP/6-31G(d):AM1). In excellent agreement with the reported results, the lowest energy transition structure for the first step (ΔE^‡ = 23.4 kcal/mol with respect to separated reactants) occurs via addition of the si-face of nitrostyrene to the si-face of the (E)-anti-enamine to give (2R)-methyl-4-nitro-(3S)-phenylbutanal (Figure 28). The unusual stability of this transition structure is attributed to a number of favorable electrostatic interactions, including the oxygens of the nitro group with hydrogens on the catalyst, and a short N^δ–N^δ− distance of only 2.9 Å. The other diastereomeric transition structures do not bear such stabilizing interactions. The next higher-energy transition structure is 5.0 kcal/mol higher in energy; it involves addition of the re-face of nitrostyrene to give the (2R, 3R) aldehyde.

First Michael addition transition structure in the cascade sequence of Scheme 54.

The next step, Michael addition of the anion generated from the formed nitroalkane to the iminium of 3-phenyl-2-propenal, was calculated to favor si-facial attack of the nitroalkane anion to the re-face of the iminium (Figure 29). Like the first transition structure, hydrogen bond stabilization of the nitro oxygens with the catalyst accounts for the relative stability of this transition structure compared to the higher energy conformers. There is a further stabilization arising from the carbonyl oxygen with a pyrrolidine hydrogen. Attack on the re-face of the nitroalkane was calculated to be 2.2 kcal/mol higher in energy. This transition structure is not stabilized by any C=O^···H interactions.

Second Michael addition transition structure in the cascade sequence

The final intramolecular aldol cyclization step was calculated to occur in the same geometry as the previous Michael addition step (Figure 30). The most stable transition structure adopts a chair conformation and has the same C=O^···H and N–O^···H stabilizing interactions found in the previous steps. Other transition structure conformers are at least 9.1 kcal/mol higher in energy.

Intramolecular aldol cyclization in the cascade sequence

2.1.11. Morita-Baylis-Hillman Reaction

Santos and co-workers investigated the proline-catalyzed intramolecular Morita-Baylis-Hillman reaction of hept-2-enedial reported by Hong and co-workers (Scheme 55).⁷⁴ In the presence of imidazole as co-catalyst, the enantioselectivity of the reaction improves considerably, but with an inversion of absolute configuration. Santos used DFT calculations to verify the mechanisms proposed by Hong.

Scheme 55 — Proline-catalyzed intramolecular Morita-Baylis-Hillman reaction

The results of the lowest energy proline-catalyzed reaction and proline-catalyzed reaction with imidazole as a co-catalyst are shown in Scheme 56 and Scheme 57, respectively. For the reaction without imidazole: The relative energies of the anti and syn iminiums formed between proline and hept-2-enedial are 0.0 and 2.2 kcal/mol, respectively, but the favored pathway initially involves rearrangement of the syn imine to the enamine with water assistance (TS-taut). This tautomerization is the rate-determining step. The resulting syn enamine (with C3-C4 in the Z geometry) rotates to the anti enamine, which then can cyclize via TS-MBH to give either the (S) or (R) iminium intermediate. In agreement with experiment, cyclization to the (S) product is favored. The syn enamine can also cyclize to give either the (S) or (R) product, but these barriers were calculated to be higher than those of the anti enamine.

Scheme 56 — B3LYP/6-31G(d, p) mechanism for proline-catalyzed intramolecular Morita-Baylis-Hillman reaction (Relative energies include B3LYP/6-31++G(d, p) (PCM, CH₃CN) corrections.)

Scheme 57 — B3LYP/6-31G(d, p) mechanism for proline-catalyzed intramolecular Morita-Baylis-Hillman reaction with imidazole co-catalyst (Relative energies include B3LYP/6-31++G(d, p) (PCM, CH₃CN) corrections at 0 °C)

The four possible cyclizations result in a calculated enantioselectivity of 64%. The experimental range is 5–45%, depending on the solvent.^74b,75 The most favored MBH transition structure is shown in Figure 31. Overall, the model agrees with the one proposed by Hong, which involves addition of the re-face of the anti-enamine to the re-face of the aldehyde. A significant stabilizing electrostatic interaction for the computed transition structure is seen in the 2.39 Å distance between a proline C5 methylene hydrogen and the developing alkoxide, as is found in the usual Houk-List transition structure for the aldol reaction catalyzed by proline. The corresponding distance is at least 3.10 Å in transition structures involving the syn enamine.

B3LYP/6-31G(d, p) major cyclization transition structure for the proline-catalyzed intramolecular Morita-Baylis-Hillman reaction.

The reaction in the presence of imidazole was then studied in order to explain the stereoselectivity reversal. The lowest-energy computed pathway is shown in Scheme 57. Unlike the mechanism in the absence of imidazole, the mechanism with imidazole proceeds favorably via the initially formed anti-iminium. Addition of imidazole to the iminium terminus and tautomerization to the anti-enamine proceeds with water assistance to give the (S) configuration at C3 (TS-addn, Figure 32). The transition structure for addition without water assistance is only 0.4 kcal/mol higher in energy. The transition structures for formation of the (R) stereoisomer with and without water are 5.8 and 2.4 kcal/mol higher in energy, respectively.

B3LYP/6-31G(d, p) major transition structures for the proline-catalyzed imidazole addition and intramolecular Morita-Baylis-Hillman. (im=imidazole).

The carboxylic acid of the proline catalyst activates the terminal aldehyde of the anti-enamine (C3-(S)), which cyclizes via the “top” (re) face of the enamine to the si-face of the carbonyl, giving the experimentally observed (R) product upon hydrolysis (TS-MBH-(R), Figure 32). Cyclization to the (S) product was calculated to be 2.4 kcal/mol higher in energy. This transition state proceeds via an axial orientation of the imidazole group, which is less stable than the equatorial conformation found in the (R) transition state. The overall predicted stereoselectivity of 93%ee agrees with the experimental results (80% ee with 0.1 equivalent imidazole, 93% ee with 1.0 equivalent imidazole).

The rate-determining transition structure calculated by Santos (TS-addn, Scheme 57 and Figure 32) is similar to the one proposed by Hong with respect to an explanation for the stereochemical outcome (Scheme 58). However, the two models differ with respect to the stabilizing mode of the imidazole. Hong proposed that a protonated catalyst carboxylate directs the nucleophilic imidazole nitrogen toward attack of the iminium carbon, while Santos proposed that the carboxylate interacts with the acidic C-2 hydrogen of the imidazole and directs the nucleophilic attack. Attempts by Santos to locate transition structures proposed by Hong failed.

Scheme 58 — Rate-determining transition structures proposed by Hong and Santos

2.2. Imidazolidinones

The resurgence of organocatalysis in 2000 was initiated not only by reports of the proline-catalyzed aldol reaction, but also by MacMillan’s report of an intermolecular Diels-Alder reaction catalyzed by an imidazolidinone catalyst (Scheme 59).⁷⁶ Since this discovery, imidazolidinone catalysts have catalyzed a number of reaction types in good yields and stereoselectivities.

Scheme 59 — Imidazolidinone-catalyzed Diels-Alder cycloaddition

2.2.1. Structure study

Burley and co-workers⁷⁷ and Seebach and co-workers⁷⁸ have independently reported crystallographic and DFT studies of imidazolidinone catalysts. Burley showed that the lowest energy gas phase conformations of the benzoyl groups predicted by B3LYP/6-31G(d, p) and B3LYP/6-311G(d, p) optimizations of the catalysts shown in Figure 33 are not the same as the conformers that exist in the solid state. This discrepancy can be explained by the fact that the gas phase monomeric structures are stabilized by intramolecular interactions, while the solid state structures are stabilized by intermolecular interactions.

Imidazolidinone catalysts studied by Burley and co-workers.⁷⁷

Seebach overlayed the crystal structures of the PF₆ salts formed by (E)-1-cinnamaldehyde and three imidazolidinone catalysts with DFT structures and found excellent agreement between the structures (Figure 34).

Imidazolidinones investigated by Seebach and co-workers.⁷⁸

2.2.2. Alkylation

Houk and co-workers used B3LYP/6-31G(d) calculations to rationalize varying enantioselectivities by MacMillan and co-workers in the alkylation of N-methylindole and N-methylpyrrole by (E)-crotonaldehyde, catalyzed by two imidazolidinone catalysts (Scheme 60).⁷⁹ Tomkinson and co-workers have also reported a solution phase NMR, X-ray crystallographic, and DFT study of the imidazolidinone intermediates.⁸⁰

Scheme 60 — Imidazolidinone-catalyzed indole alkylation reactions

The lowest energy transition structure for the experimental major (R) enantiomer in the reaction catalyzed by the dimethyl substituted imidazolidinone occurs via bonding of the si-face of the pyrrole to the re-face of the iminium (Figure 35). The lowest energy transition structure for the experimental minor (S) enantiomer occurs via bonding of the re-face of the pyrrole to the si-face of the iminium. A theoretical enantioselectivity of 71% ee was calculated for all low-energy conformers. This corresponds to an activation free energy difference that is 0.5 kcal/mol lower than than the experimental observation. The si-face of the iminium is shielded by the benzyl group, accounting for the observed preference for attack at the re-face. The conformation of the benzyl group is, however, different from that displayed in MacMillan’s publication.

Lowest energy transition structures and relative energies for imidazolidinone-catalyzed alkylation of N-methylpyrrole.

Like the previous catalyst, the lowest energy transition structure for the experimental major (R) enantiomer in the reaction catalyzed by the tert-butyl substituted imidazolidinone occurs via the si-face of the pyrrole bonding to the re-face of the iminium (Figure 36). The lowest energy transition structure for the experimental minor (S) enantiomer occurs via the re-face of the pyrrole to the si-face of the iminium. A theoretical enantioselectivity of 90% ee was calculated using all low-energy conformers, in excellent agreement with the experimental observation.

The enhanced enantioselectivity compared to the dimethyl substituted catalyst can be explained by the preferred conformations of the ground state iminium ions. In the dimethyl substituted catalyst, the phenyl ring lies over the face of the catalyst due to a stabilizing C-H^···π interaction between the phenyl ring and the cis-methyl group (Figure 37). Such a stabilizing interaction does not exist in the t-butyl substituted catalyst due to the steric bulk of the t-butyl group. The phenyl ring effectively rotates away from the catalyst and blocks the si-face of the iminium to a greater extent than the same group of the dimethyl substituted catalyst.

Most stable conformers of dimethyl and *tert*-butyl substitutituted iminiums.

2.2.3. Diels-Alder Cycloaddition

Since MacMillan’s first report of the imidazolidinone-catalyzed Diels-Alder cycloaddition reaction, modifications to the catalyst structure have been made in attempts to improve stereoselectivity. Table 3 lists the results of changing substituents on the catalyst. The furyl-substituted catalyst (entry 5) proved to be the most efficient in catalyzing the [4+2] cycloaddition between 4-hexene-3-one. Houk and co-workers carried out B3LYP/6-31G(d) calculations in order to explain the stereoselectivity of the reaction. ⁸¹

Table 3.

Results of imidazolidinone-catalyzed Diels-Alder cycloaddition reations


Entry	R¹	R²	R³	% yield	endo:exo	%ee (endo)
1	Me	Me	Ph	<30	7:1	0
2	tBu	H	Bn	<30	–	0
3	Ph	H	Bn	88	21:1	47
4	Ph	H	Bn	83	23:1	82
5	5-methyl-2-furyl	H	Bn	89	25:1	90

Open in a new tab

The uncatalyzed reaction was calculated to have a barrier of 20.9 kcal/mol (TS-s-cis-exo, Figure 38). A 1:4.5 endo:exo ratio was calculated in the gas phase at 0 °C (1:3.7 in water). Transition structures were also located for the Diels-Alder cycloaddition catalyzed by dimethylamine. A 3.1 kcal/mol endo:exo ratio was calculated in the gas phase at 0 °C (4.1:1 in water). The activation energy for the most favored transition structure is 9.8 kcal/mol (Figure 38), significantly lower than that of the uncatalyzed reaction.

Uncatalyzed and *N, N*-dimethylamine-catalyzed Diels-Alder cycloaddition transition structures and activation energies (B3LYP/6-31G(d)) of cyclopentadiene and 4-hexene-3-one.

Transition structures for the least and most effective imidazolidinone catalysts (dimethyl, entry 1, versus furyl, entry 5) were located. Houk and co-workers predicted an endo:exo ratio of 6:1 and >99% ee for the dimethyl substituted catalyst in the gas phase at 0 °C, and 100% endo selectivity and >99% ee in water (CPCM model, HF/6-31G(d)//B3LYP/6-31G(d), UAKS cavity model). For the furyl-substituted catalyst, an endo:exo ratio of 25:1 and 99% ee was calculated in the gas phase at 0 °C. In water the predicted endo:exo ratio increases to 35:1 and the enantioselectivity is still high (>99% ee).

The poor enantioselectivity prediction for the dimethyl substituted catalyst led the authors to propose that the iminium is slowly formed compared to the furyl substituted catalyst. The slow iminium formation would allow for the uncatalyzed background reaction to occur and erode the % ee. Gas phase calculations show that iminium formation with the dimethyl substituted catalyst is endothermic by 7.9 kcal/mol, whereas iminium formation with the furyl substituted catalyst is exothermic by 0.6 kcal/mol. The stability difference is due to strong steric hindrance between the ethyl fragment and dimethyl groups (Figure 39). The closest H–H distances are 1.93 Å and 2.05 Å; the closest H–H distance in the furyl substituted catalyst is 2.22 Å).

In conclusion, good endo:exo ratios are predicted by both catalysts, but the enantioselectivities are overestimated. The poor enantioselectivity of the dimethyl substituted catalyst can be explained by steric hindrance between the ethyl group of the ketone and the dimethyl groups of the catalyst. The catalysts decrease the activation energies compared to the uncatalyzed reaction by 11 kcal/mol.

2.2.4. α,β-unsaturated ketone reduction

Density functional theory (B3LYP/6-31G(d)) was used to investigate the stereoselectivity of the organocatalytic transfer hydrogenation of 3-phenyl-2-cyclopentenone (Scheme 61).⁸² Two low energy iminium conformers were located that could lead to the experimentally observed products (Scheme 62). Hydride attack on the “bottom” face of the E iminium would lead to the major R product, while attack on the “bottom” face of the Z iminium would lead to the minor S product. In good agreement with experimental results, attack of the E iminium was calculated to be favored by 1.1 kcal/mol (76% ee). The selectivity is due to a more favorable C-H···π interaction in the favored R transition structure.

Scheme 61 — Imidazolidinone-catalyzed transfer hydrogenation

Scheme 62 — Reduction leading to major (R) and minor (S) enantiomers (Relative B3LYP/6-31G(d) enthalpies (kcal/mol))

2.2.5. α-Arylation

Both the Nicolaou⁸³ and MacMillan⁸⁴ groups reported asymmetric intramolecular α-arylation reactions via SOMO-activation (Scheme 63).

Based on geometry, charge, spin density, and molecular orbital analyses of the uncyclized and cyclized radical enamine cation intermediates, Houk and co-workers concluded that the cyclization is best described as a radical mechanism.⁸⁵ In agreement with experiment, radical attack ortho to the methoxy group was calculated to be favored over para attack. The greater stabilization of the cyclohexadienyl radical by the methoxy group at the 1-position rather than the 3-position provides the basic origin of the selectivity (Figure 40).⁸⁶

Intramolecular α-arylation transition structures and cyclized radical cations (UB3LYP/6-31G(d) ΔG values for aqueous solution at 268 K; optimizations in CPCM water). Spin densities, followed by Mulliken charges in brackets.

An interesting reversal of selectivity occurs when an addition substituent R⁴ is introduced to the aromatic ring (Scheme 64, top). Calculations show that para, meta cyclization is favored over ortho, meta cyclization by 2.4–3.4 kcal/mol, in agreement with experiment. The ortho, meta cyclization barriers were calculated to be unachievable under the reaction conditions due to a destabilization of the ortho, meta transition states. This destabilization is due to repulsion between R³ and the iminium moiety, which results in a distortion of R³ (Scheme 64, bottom).

3. Lewis/Brønsted base catalysis

3.1. Nucleophilic carbenes

3.1.1. Benzoin condensation and Stetter reaction

The benzoin condensation is a powerful and interesting C-C bond formation, as it implies the use of an aldehyde as a carbon nucleophile.⁸⁷ It was first reported by Wöhler in a version catalyzed by cyanide ion,⁸⁸ and a thiazolium salt catalyzed variant was later reported by Ugai and co-workers.⁸⁹ The mechanism of the thiazolium salt catalyzed benzoin condensation is still a matter of debate, and various hypotheses were proposed in the past 50 years. Bofill and co-workers have even reported the possibility of a biradical mechanism based on AM1 calculations.⁹⁰ Houk and co-workers studied this reaction computationally using DFT and found evidence that the monomer-catalyzed pathway was preferred,⁹¹ which is in accord with the original mechanism proposed by Breslow (Scheme 65).⁹²

Scheme 65 — Mechanism for the benzoin condensation as proposed by Breslow

Chiral thiazolium and triazolium salts, precursors of their corresponding carbenes, were used with mixed success in order to achieve an asymmetric variant of the benzoin condensation. Houk and co-worker initially studied a small achiral system using B3LYP/6-31G(d). They found that the intramolecular proton transfer is key for controlling the stereoselectivity (Scheme 66).

Scheme 66 — Transition structure for the C-C bond formation in the benzoin condensation of formaldehyde

The C-C bond forming step for four different chiral carbene catalysts (10–13, Figure 41), as well as the reaction of a chiral aldehyde (14) with an achiral thiazolium derived catalyst (15), were studied using ONIOM(B3LYP/6-31G(d):AM1). Energies were computed at B3LYP/6-31G(d).

Chiral catalysts (10–13, 15) and aldehyde (14) studied in the benzoin condensation.

Catalyst 10, a triazolium catalyst reported by Enders and co-workers⁹³ to be highly selective, was studied. The two lowest energy transition structures leading to the enantiomeric antipodes are shown in Figure 42. In both structures, the phenyl group of the enolamine is anti to the bulky tert-butyl group. In the lower energy TS-re the aldehyde substituent is positioned anti to both the aromatic substituent of the enolamine and the N-aryl moiety of the catalyst. They proposed that the re addition structure (TS-re) is stabilized by the π-aryl-iminium ion interaction, as the distance between the aldehyde aryl group and the triazolium ring is fairly close (~3.3 Å). The stereoselectivity was predicted using a Boltzmann distribution of the most stable transition structures within 4 kcal/mol. This gave an enantioselectivity of 98% ee, which is in good agreement with experiment (90% ee).

Lowest energy transition structures for the addition with catalyst 10.

Catalyst 11 is a similar thiazolium catalyst reported by Knight and co-workers⁹⁴ that afford the (S)-benzoin product from benzaldehyde with low enantioselectivity (11% ee). The two lowest energy addition structures are shown in Figure 43. The main difference between the two transition structures is a repulsive interaction between the phenyl group of the aldehyde and the aryl of the catalyst. Moreover, there seems to be a slightly more favorable π-aryl-iminium ion interaction in the si transition structure (distance between Ph_aldehyde-thiazolium = 3.8 Å) compared to the re addition (distance 4.3 Å). These transition states are very similar in energy, and the computed enantioselectivity of 10% ee in favor of the R product is in fair agreement with the low selectivity observed experimentally (11% ee) in favor of the S product.

Lowest energy transition structures for the addition with catalyst 11.

The third catalyst (12) studied was reported by Sheehan and co-workers⁹⁵ to give modest enantioselectivity (51% ee), and the two lowest energy structures are shown in Figure 44. The main difference is the repulsive interaction between the aryl of the aldehyde and the α-methyl of the catalyst. The computed energies overestimate the enantioselectivity (91% ee) in favor of the R product.

Lowest energy TSs for the addition with catalyst 12.

Catalyst 13, reported by Enders and co-workers,⁹⁶ has many possible conformational isomers, but all located transition structures showed the same conformation of the chiral dioxirane ring. The two lowest energy transition structures leading to the R and S product are shown in Figure 45. In both structures, the chiral dioxane ring is in a chair conformation with the triazolium in an axial position and the phenyl in an equatorial position. The main difference between the re and si is the repulsive interaction between the aldehyde aryl and the phenyl ring of the catalyst in the re structure. The computed enantioselectivity is >99% ee in favor of the R product, higher than the experimentally observed 75% ee. Enders and co-workers have however reported a decrease in enantioselectivity with longer reaction times, possibly explained by the benzoin product racemization.

Lowest energy transition structures for the addition with catalyst 13.

Finally, they computed the transition structures of an intramolecular condensation of a chiral aldehyde 14 using a simple achiral thiazolium derivative (15) reported by Hachisu and co-workers.⁹⁷ The four possible transition structures are shown in Figure 46. The transition structures leading to the minor product (si attack) are clearly disfavored, as the thiazolium moiety and the ester groups are eclipsing each other. Of the two transition structures leading to the experimentally observed product (re attack), the exo transition state is slightly favored, as an unfavorable interaction between the methyl in the endo-position and the ring exists in the endo transition state. The energy difference of 6.6 kcal/mol predicts an exclusive formation of the R, S isomer, in agreement with the >20:1 selectivity observed experimentally.

Transition structures for the intramolecular crossed aldehyde-ketone benzoin condensation.

A reaction that is closely related to the benzoin condensation is the Stetter reaction, which involves the C-C coupling between aldehydes and an appropriate Michael acceptor. The suggested mechanisms of these related reactions are similar; only the second aldehyde of the benzoin condensation is replaced by a similar conjugate acceptor. Hawkes and Yates investigated a model asymmetric Stetter reaction using B3LYP/6-31G(d) on the basis of Breslow’s mechanism for benzoin condensation.⁹⁸ They located a low energy intermolecular proton transfer pathway that yields the Breslow intermediate with an overall barrier of 13.1 kcal/mol (Scheme 67), competing with the high energy intramolecular 1,2-hydrogen shift transition state (39.1 kcal/mol). The overall reaction profile is consistent with benzoin condensation: the stereo- and rate-determining step is the C-C coupling (34.4 kcal/mol). Unlike the benzoin condensation, the C-C coupling in the Stetter reaction occurs in a two step process, in which C-C bond formation precedes proton transfer. The authors suggested that the stereoselectivity is governed by the steric interactions of the enolamine N-substituents with the Michael acceptor and the exact conformation of the enolamine, which can be adjusted by tailoring the carbene substituents.

Scheme 67 — Intermolecular proton transfer pathway to the Breslow intermediate

3.1.2. Transesterification

Widely used N-heterocyclic carbenes (NHCs) have recently been shown to be excellent catalysts for transesterification reactions. Nolan and co-workers have demonstrated their use in the rapid transesterification of a vinyl acetate.⁹⁹ Hedrick and co-workers have reported similar methodologies, and have noted their potential as catalysts for the living polymerization of cyclic esters.¹⁰⁰ The actual mechanism of action of the NHC in the transesterification is still a matter of debate. Hu and co-workers computationally studied the possible pathways for the transesterification reaction,¹⁰¹ using B3LYP and the cc-pVDZ basis set. The mechanism involving a neutral tetrahedral intermediate (Scheme 68) was found to be the most favorable.

Scheme 68 — Reaction pathway for the NHC catalyzed transesterification involving a neutral tetrahedral intermediate

The pathway involving the nucleophilic attack of the NHC to the carbonyl carbon, resulting in a 2-acylimidazolium intermediate, was found to be unfavorable. They also studied different alcohols and carbenes derivatives, and found qualitative agreement between the relative energies of the tetrahedral intermediates (TD) and the experimentally observed conversions.

3.1.3. Oxidation/protonation of α,β-unsaturated aldehydes

Scheidt and co-workers gave experimental and computational evidence for the ability to divert product distributions in the esterification of α,β-unsaturated aldehydes catalyzed by N-heterocyclic carbenes. (Scheme 69).¹⁰² Prior to this report, manipulation of reaction conditions to favor the saturated product remained elusive.¹⁰³ All known reports had favored either solely the oxidized product, or mixtures of the two products.

Scheme 69 — Esterification of α,β-unsaturated aldehydes

A test of the reaction in toluene, dichloromethane, tetrahydrofuran, and methanol shows a reversal of product selectivity as the solvent polarity increases. In toluene, the saturated product dominates (approximately 2 or 3:1), while in methanol the oxidized product dominates (up to 12:1). To understand the divergent pathways, the reaction enthalpies of the competing steps—hydride loss from the tetrahedral intermediate (Scheme 70, ΔH₃) and 1,2-proton shift from the tetrahedral intermediate (ΔH₂) — were calculated in methanol and dichloromethane using density functional theory (M06-2X/6-311+G(2df, p)//M06L/MIDI!(6D)/Auto, SM8 solvation model and a single explicit methanol molecule). The results are shown in Table 4. The first step, addition of the catalyst to the aldehyde (ΔH₁), is calculated to be exothermic in both methanol and dichloromethane. In good agreement with experimental results, hydride loss from the tetrahedral intermediate to generate the cationic acyl azolium intermediate (ΔH₃ = 3.7) is more favorable than a 1,2-proton shift (ΔH₂ = 6.1) in methanol. In contrast, hydride loss in dichloromethane is significantly disfavored (ΔH₃ = 13.7), while a proton shift becomes more facile (ΔH₂ = 2.7). This difference is attributed to the sensitivity of the cationic intermediate to solvation. The oxidation pathway dominates in protic solvents, whereas the saturation pathway dominates in nonpolar solvents.

Scheme 70 — Transesterification mechanism

Table 4.

Reaction enthalpies (kcal/mol) of the competing steps in the esterification of α,βunsaturated aldehydes catalyzed by N-heterocyclic carbenes

entry	solvent	ΔH₁	ΔH₂	Δ H₃	exp. saturated:oxidized
1	MeOH	−13.2	6.1	3.7	1:12
2	CH₂Cl₂	−8.7	2.3	13.7	2:1

Open in a new tab

3.1.4. Biomimetic oxidation of aldehydes

Pyruvate ferredoxin oxireductase (PFOR), along with co-factor thiamine pyrophosphate and a [Fe₄S₄] cluster, catalyzes the oxidative decarboxylation of pyruvate.¹⁰⁴ Studer and co-workers were guided by PFOR activity in the development of a reaction system of 2,2,6,6-tetramethyl piperidine N-oxyl radical (TEMPO) and thiazolium carbene to mediate the oxidation of aldehydes (Scheme 71).¹⁰⁵ The proposed mechanism is shown in Scheme 72.

Scheme 71 — Organocatalyzed oxidation of aldehydes by TEMPO

Scheme 72 — Proposed mechanism for carbene-catalyzed oxidation of aldehydes

The structure of the intermediate radical cation (RC) was studied using several DFT methods (PBEh/TZVP, B2LYP/TZVP, and B2LYP/TZVPP). Both enol (RC-enol) and keto (RC-keto) forms were calculated (Figure 47). The enol form was calculated to be more stable than the keto form by 12.8, 9.6, and 11.4 kcal/mol using PBEh/TZVP, B2LYP/TZVP, and B2LYP/TZVPP, respectively. The electronic structures shown in Figure 47 are in agreement with the calculated spin density distributions.

Lewis structures and PBEh/TZP bond distances of enol (RC) and keto (RC′) forms of intermediate radical cation.

3.2. DMAP catalysts

3.2.1. Mechanism of the DMAP catalyzed acylation

4-(Dimethylamino)pyridine (DMAP) is an efficient catalyst for the acylation of alcohols and amines. Zipse and co-workers computationally studied the simplest acylation of alcohols with DMAP.¹⁰⁶ The currently accepted mechanism involves the facile nucleophilic addition of DMAP to acetic anhydride to form an acylpyridinium cation, followed by a rate-limiting formation of the ester from this intermediate (Scheme 73). A stoichiometric quantity of an auxiliary base, such as triethylamine, is required to regenerate the catalyst.

Scheme 73 — Accepted mechanism for the acylation of alcohols catalyzed by DMAP

The identity of the base in the rate limiting step is a matter of debate, as the acetate counterion, triethylamine or a second DMAP molecule could be involved. In order to confirm the mechanism and clarify this issue, Zipse and co-workers have done computational and kinetic studies on the simple DMAP catalyzed acetylation of alcohols. The gas phase enthalpy diagram for the accepted mechanism is shown in Scheme 74.

Scheme 74 — Gas phase enthalpy diagram of the DMAP catalyzed acylation process

As experimentally observed, the rate determining step is found to be the trans acylation of the alcohol. Single point solvation corrections were calculated for different solvents, and the results are in qualitative agreement with experimental findings that show polar solvents tend to slow down the reaction. The trans acylation step is always found to be the rate determining step, even with solvation. Other possible pathways were calculated and found to be energetically less favorable.

The identity of the base implicated in the trans acylation step was still unanswered. Some previous evidence suggests that the acetate anion plays an important role, based on the low reactivity of acylpyridinium salts containing less basic anions.¹⁰⁷ Using kinetic studies, they found strong evidence that triethylamine does not participate in the rate-limiting trans acylation reaction, in agreement with the role of the acetate anion as the actual base.

It has been shown that increasing the steric bulk of the anhydride leads to decreased reaction rates. The G3(MP2)B3 compound method was used to calculate the reaction enthalpies of acyl transfer to cyclohexanol by a variety of anhydrides (Table 5).¹⁰⁸ The reaction enthalpy is independent of the choice of anhydride, with only a 1.2 kcal/mol difference between the most reactive acetic anhydride and least reactive pivalic anhydride. Thus it was concluded that the experimental rate differences intrinsically lie in the activation barriers. The rate of the catalyzed reaction is more sensitive to the steric bulk of the anhydride than the rate of the uncatalyzed reaction. This different response has implications for the kinetic resolution of alcohols.

Table 5.

Calculated reaction enthalpy (kcal/mol) and relative rate constants for uncatalyzed and catalyzed acyl transfer reactions


R	ΔH_rxn (G3(MP2)B3)	k_rel (uncatalyzed)	k_rel (catalyzed)
CH₃	−15.1	526	8025
CH₂CH₃	−14.6	103	4543
CH(CH₃)₂	−14.2	40	2852
CH₂CH(CH₃)₂	−14.4	47	963
C(CH₃)₃	−13.9	1	1

Open in a new tab

3.2.2. Conformational analysis of chiral DMAP derivatives

Although no mechanistic studies have been reported concerning the acylation or resolution of chiral alcohols using chiral DMAP derivatives, some interesting studies have been reported concerning the properties of such chiral bases. The design of a chiral DMAP derivative requires a chiral environment around the DMAP nitrogen to effect stereoselectivity, but not enough to hinder the catalysis. Numerous groups have sought to exploit π-π interactions (Scheme 75) to achieve such a feat. Aside from providing a chiral control element, such interactions were also proposed to enhance the rate of the reactions via stabilization of the acylpyridinium intermediate. In order to better understand these proposals, Zipse and co-workers have performed a general study concerning the role of π-π interactions in DMAP derivative catalysis.¹⁰⁹

Scheme 75 — The use of π-π interactions to shield a face of DMAP derivatives

Zipse studied a number of DMAP derivatives in which π-π interactions could occur (17–19, Scheme 76). In order to account for dispersion interactions, an extensive study of different theoretical methods was performed. Zipse concluded that a conformational search at MP2/6-31G(d)//HF/3-21G level followed by SCS-MP2/6-311+G(d, p)//MP2/6-31G(d) refinements on the lowest energy conformations led to the best quality results. In an earlier publication, they found a correlation between the relative stability of the acyl pyridinium intermediates and the C_acyl-N_pyridinium bond length.¹¹⁰ With the exception of the pyridine acyl intermediate, with a C-N bond of 1.54 Å, all the other catalysts were found to have almost identical bond lengths, around 1.47–1.49 Å. Interestingly, an inspection of the different conformations of catalyst 18, all possessing very different degree of π-π interactions, showed mostly identical C-N bond lengths. They thus concluded the interaction does not seem to greatly stabilize the acyl pyridinium species.

3.2.3. Stabilities of N-acyl DMAP derivatives

Zipse showed that some correlation could be found between the relative stabilities of the acyl pyridinium species and the catalytic activity.^111,112 In order to address the relative stabilities of acyl pyridinium intermediates, they computed the isodesmic reaction shown in Scheme 77 for a number of catalysts. This strategy was also used by Han and co-workers in order to evaluate the relative efficiency of new DMAP derivative 22.¹¹³ The reaction enthalpies of select catalysts were compared with the measured half life for the equation shown in Scheme 78. The results are shown in Table 6.

Scheme 77 — Isodesmic reaction for measuring relative stabilities of acyl pyridinium intermediates

Table 6.

MP2(FC)/6-31+G(2d, p)//B98/6-31G(d) reaction enthalpies for reaction shown in Scheme 77 and half life for acyl transfer shown in Scheme 78

entry	catalyst	ΔH_rxn (calculated)	t_1/2 (min)
1	pyr	0.0	–
2	DMAP	−14.7	151
3	PPY	−16.2	67
4	24	−18.1	44
5	16	−19.7	15
6	21	−20.4	18

Open in a new tab

The nucleophilic base 4-pyrrolidinopyridine (PPY) has long been known catalyze acyl transfer reactions more efficiently than DMAP.¹¹⁴ The 3-alkyl-4-guanidinylpyridines are moderately more effective than PPY in acyl transfer reactions (23–24),^111a while 4-dialkylaminopyridines (DMAP, PPY, 16)¹⁰⁹ and 3,4-dialkylaminopyridines (21),^111b,114 are among the most effective DMAP-type catalysts. Han showed that 3,4,5-trialkylaminopyridine catalyst 22 is approximately 10% more effective than 16.

Yamada and co-workers reported their own conformational study concerning the DMAP derivative 20 (Figure 48), used as a catalyst for the resolution of chiral alcohols and amidines.¹¹⁵ In the neutral form, the chiral sidearm at the 3 position is found to be freely rotating. Upon the formation of a pyridinium salt, however, the side arm favors conformation A, thus blocking the top face. This was independently verified by NMR. They have computed the two lowest energy conformations at B3LYP/6-31G(d) of the isobutyryl acylpyridinium and showed that A is favored by 1.0 kcal/mol. B is disfavored due to repulsive interactions between the tert-butyl and the isobutyryl groups.

The computed lowest energies conformations of a chiral catalyst developed by Yamada and co-workers.

3.2.2. Structural analysis of N-acetylated DMAP salts

Schreiner and co-workers studied the salt formation between acetylated DMAP and CH₃CO₂⁻, CF₃CO₂⁻, and Cl⁻, using experimental and computational techniques (Figure 49).¹¹⁶ B3LYP/6-311+G(d, p) (PCM, dichloromethane)//B3LYP/6-31G(d) was used for the calculations. The anions can be stabilized by hydrogen bonding interactions (I and II, Figure 50), nucleophilic interactions (IV–VI), or a mixture of both (III).

Acetylated DMAP salts studied by Schreiner.

Salt formation between acetylated DMAP and various anions.

Complex I was calculated to be the preferred structure for salts 25–27, while complex II was the preferred structure for 28. IR and NMR spectra, crystal structure analyses, and experiments with deuterated DMAP support complex II as the preferred geometry for the chloride salt (28). However, experimental evidence supports the conclusion that III is the preferred geometry for 25–27, even though it is approximately 2 kcal/mol higher in energy. The authors concluded that the bidentate anions might be able to guide an alcohol to the reaction center via hydrogen bonding interactions (Figure 51).

3.3. Cinchona type catalysts

Despite their use as versatile organocatalysts,¹¹⁷ cinchona alkaloids have received little attention computationally, most probably due to their large size and flexibility. However, some mixed spectroscopic and computational studies have been reported in the literature relating the conformations of various cinchonidine derivatives (Figure 52). Baiker and co-workers reported a NMR and computational study of the conformational behavior of cinchonidine in different solvents.¹¹⁸ More recently, they also reported a mixed VCD spectroscopy and computational study of O-phenyl cinchonidine.¹¹⁹ Zaera and co-workers reported a mixed NMR and computational study of the effect of protonation of cinchonidine.¹²⁰ Lastly, Szöllösi and co-workers have reported a similar mixed study on the conformational behavior of py-hexahydrocinchonidine.¹²¹

3.3.1. Staudinger reaction

Lectka and co-workers developed an efficient cinchona alkaloid catalyzed methodology for the asymmetric synthesis of β-lactams (Scheme 79).¹²² The catalyst of choice in this case is benzoylquinine (BQ)

In order to rationally design and optimize their catalyst, they performed molecular mechanics conformational searches on the base-ketene adducts. They had some success using this method, as they obtained qualitative agreement between the enantioselectivities observed and the relative energies between the different diastereomers.¹²³

3.3.2. Decarboxylation of Naproxen

Due to the high demand of non-steroidal anti-inflammatory drugs (NSAID), such as naproxen and ibuprofen, there is a growing interest in the efficient syntheses of these compounds (Figure 53).

Two popular NSAID drugs. a) Naproxen; b) ibuprofen.

The synthesis reported by Brunner and Schmidt¹²⁴ relies on a cinchona catalyzed asymmetric decarboxylation as the critical stereodetermining step (Scheme 80) and has been the subject of a short computational study by Strassner and co-workers.¹²⁵ To explain the decarboxylation step, Brunner and Schmidt proposed a two step mechanism involving a decarboxylation/ketimine formation followed by an enantioselective protonation of the ketimine by the catalyst.

Scheme 80 — Enantioselective decarboxylation step

Strassner and co-workers computationally studied the decarboxylation step using B3LYP/6-31G(d)/AM1 level and Onsager solvation corrections. They have found that a concerted decarboxylation/protonation mechanism was energetically more favorable than the stepwise pathway. The transition structures leading to both enantiomers are shown in (Figure 54). The formation of the (S)-enantiomer is favored by 3.7 kcal/mol, in good agreement with experiment. They explain this difference by the better H-bonding arrangements in the transition state leading to the S enantiomer.

The concerted decarboxylation/protonation TSs.

3.3.3. Sulfinylation

The synthesis of chiral sulfinate esters by Ellman et. al. involves the use of cinchona alkaloids in the dynamic kinetic resolution (DKR) of racemic sulfinyl chlorides (Scheme 81).¹²⁶ In this methodology, the Ellman group used a catalytic amount of quinidine as well as an excess of proton sponge in order to neutralize the forming HCl in the reaction. A similar methodology, but using stoichiometric amounts of a cinchona alkaloid was developed earlier by Toru and co-workers.¹²⁷

Scheme 81 — Cinchona catalyzed dynamic kinetic resolution of sulfinyl chlorides

These methodologies require the fast racemization of sulfinyl chlorides under the reaction conditions, as well as an acceleration of the sulfinylation step by the base. Maseras and co-workers have studied these two issues computationally using trimethylamine as a base model. They initially studied the mechanism of racemization of different sulfinyl derivatives.¹²⁸ The calculations were done using B3LYP with the 6-31G(d) and LANL2DZ(ECP) basis sets for the first and second row elements, respectively. The inversion barriers of sulfinyl chloride and methyl sulfinate were found to be too high (63.4 kcal/mol) to occur under experimental conditions (Scheme 82).

Scheme 82 — Barriers of the base-free inversion of sulfinyl chloride and methyl sulfinate

The computed pathways for the inversion in the presence of trimethylamine were found to be substantially lower in energy and experimentally feasible. For the case of the sulfinyl chloride, the inversion barrier is lowered to 22.9 kcal/mol in the presence of the base. The analogous barrier for the methyl sulfinate is 42.7 kcal/mol, too high for racemization to occur, hence these products keep their optical activity after their formation, as observed experimentally.

A comparison of the uncatalyzed and base catalyzed inversion transition states led some insights (Figure 55). The major difference observed comes a more important elongation of the S-X bond (X = Cl, OMe) in the base catalyzed structures. These results show the importance of the base in the dynamic kinetic resolution.

Transition structures for the (a) base-free and (b) base catalyzed inversions.

More recently Maseras and co-workers also studied the effect of the base on the actual sulfinylation step.¹²⁹ They have also investigated several different mechanisms for this reaction, as shown in Scheme 83. They used the same method described for the earlier calculations, but included single point solvation corrections for toluene using CPCM.

Uncatalyzed and base-catalyzed pathways were both calculated for the neutral mechanism (Scheme 83a) and the energy diagram is illustrated in Figure 56. TS-add was considered the stereodetermining step. The intermediate between TS-add and TS-elim was not investigated.

Free energy diagram for base-free and base-assisted pathways for the neutral mechanism.

Assistance of the trimethylamine greatly stabilizes the addition step TS-add. This is due to the strong coordination of the base in the proton transfer process (Figure 57). Moreover, this results in a greater nucleophilicity of the alcohol. The close proximity of the base to the chiral sulfur center in this critical step also explains the high enantioselectivities observed by Ellman and co-workers.

Optimized addition and elimination TSs for the neutral mechanism.

The ion pair mechanism (Scheme 83b) was also studied, and the addition step was also found to be the rate determining step. The TSs involving one or two amines are shown in Figure 58.

Optimized TSs for the addition step of the ion-pair mechanism.

It is interesting to note that the chloride anion is not fully dissociated and maintains interaction with the sulfur atom, resulting in an octahedral complex. The energies show the uncatalyzed addition of the alcohol to the sulfinyl ammonium to be unfavorable (40.9 kcal/mol). However, the base assisted mechanism leads to a free energy of activation similar to what was observed for the neutral mechanism (14.4 kcal/mol). From those results, it is hard to rule out a single mechanism. However, it should be noted that the use of bulkier bases would disfavor the ion-pair mechanism.

3.3.4. α-Bromination

Recently, Lectka and co-workers also developed an asymmetric catalysis for the α-chlorination of acid halides, using cinchona alkaloid derivatives.¹³⁰ In an effort to widen the scope of the method, they extended it to α-bromination (Scheme 84).¹³¹ Unfortunately, this new methodology led to lower enantioselectivities on larger scale. They thus resorted to computational studies to assist in the optimization of their methodology.¹³²

Scheme 84 — Catalytic, asymmetric α-bromination methodology developed by Letcka and coworkers

Using molecular mechanics to guide their designs, they replaced the benzoylquinine (BQ) by a proline-quinine conjugate (ProQ). This new catalyst led to improved enantioselectivities.

Brominating agent 29a was replaced by brominating agent 29b to achieve enhanced selectivities. Computational studies of the bromination step for brominating agents 29a and 29b, using benzoyl quinine (BQ) as the catalyst, were employed with the IMOMO variation of ONIOM(HF/3-21G(d):AM1). The si and re TSs for the bromination using 29b are shown in Figure 59.

re and si TSs for the bromination step with **29b**

The strong asymmetry in the C_enolate-Br-C_29a clearly shows that these are late, product-like, transition states. The electrostatic interactions with the quinuclidine hydrogens stabilize the forming negative charge on the brominating agent. The energetic preference for the si addition originates from a repulsive van der Waals contact between the enolate α-hydrogen and the C-H hydrogen α to the benzoyl in the catalyst in the re TSs. The calculated enantioselectivity of 87% ee is in close agreement with the experimental value of 88% ee.

The transition structures for the bromination using 29a are shown in Figure 60. They share similar geometries as the one found for 29b. The preference for the si addition seems to originate from a better stabilization of the enolate oxygen through 3-point H-bond network with the quinuclidine ring. In addition, there is a destabilizing van-der-Waals contact between the ketene enolate phenyl and the quinoline methoxy in the unfavored re addition. The calculated enantioselectivity of 99% ee is an overestimation of the 78% ee experimentally observed, but the low selectivity is thought to be due to competing product racemization.

re and si TSs for the bromination step with **29a**.

Molecular dynamics on the lowest energy TSs found for the α-bromination using 29a and 29b were performed in order to monitor the time needed for the phenolate to be oriented suitably for the trans acylation. They have found that this process for 29a took 8.5 ps, more than twice as much as for 29b (3.6 ps), giving further evidence to the possible competition between epimerization and trans acylation.

3.4. Pyridine N-oxide 3.4.1. Strecker reaction

The Strecker reaction is an efficient method to rapidly access α-amino acids through the formation of the corresponding α-amino nitriles. Asymmetric versions have been developed using different catalysts. In particular, amine N-oxides have been found to be efficient catalysts for this reaction, affording the desired α-amino nitriles under mild conditions.¹³³ Hu and co-workers have computationally studied the methodology shown in Scheme 85 using small models.¹³⁴ The calculations were done using B3LYP/6-31G(d) and solvation energy corrections using PCM.

Scheme 85 — Methodology studied by Hu and co-workers; model molecules used in the study

The two mechanisms of the uncatalyzed reaction were initially studied. In pathway a, H₃SiCN first isomerizes to isocyanide, then adds to the imine, forming the α-amino nitrile (Scheme 86). Alternatively, the isomerization to the experimentally observed α-amino nitrile occurs after addition of the H₃SiCN to the imine (pathway b, Scheme 86).

Scheme 86 — Possible pathways for the uncatalyzed Strecker reaction

The two pathways are very similar energetically (Figure 61). Both addition transition states involve simultaneous silyl transfer to the nitrogen and the cyanide (or isocyanide) addition to the imine carbon.

Relative electronic energy and free energy (in parentheses) profiles for the uncatalyzed Strecker reaction. Energy units are in kcal/mol.

The reaction profiles for the pyridine N-oxide catalyzed process reveal some striking differences (Scheme 87). The catalyzed process features a stepwise formation of the initial N-oxide-H₃SiCN-imine complex, not concerted as in the uncatalyzed process. While the original mechanistic proposal involved a bis-pyridines N-oxide chelating to the silicon, only mono ligated complexes were found computationally (33 and Int1a).

The relative energy profiles are shown in Figure 62. Complexation of the N-oxide lowers slightly the isomerization process from nitrile to isonitrile, compared to the uncatalyzed process. More importantly, the complexation of the N-oxide enhances the nucleophilicities of isocyano and cyano group, resulting in a remarkable facilitation of the addition step in both cases. This is due to the strong donor ability of the N-oxide. They did not however study the stereochemical aspects of the reactions.

Relative electronic energy profiles for the uncatalyzed Strecker reaction. Energy units are in kcal/mol.

3.5. Sulfides

3.5.1. Sulfur Ylide Mediated Epoxidations

Aggarwal and co-workers have recently developed an asymmetric epoxide synthesis methodology based on the addition of sulfonium ylides to carbonyl compounds (Scheme 88).¹³⁵ Although a metal catalyst is needed in the overall reaction process, the actual epoxidation proceeds through organocatalysis.

Scheme 88 — Catalytic process for the sulfur ylide mediated epoxidation developed by Aggarwal and co-workers

The mechanism of the parent reaction is well established. Aggarwal has shown that the preference for trans-epoxides arises because the anti-betaine formation is irreversible, while the formation of the syn-betaine is reversible (Scheme 89).

Scheme 89 — Rational for the *trans* selectivity observed in the epoxidation process

Previous theoretical studies concerning the epoxidation using sulfonium ylides were either done using very small models (CH₂=SH₂ and formaldehyde)¹³⁶ or on larger models without reliable solvation corrections.¹³⁷ Aggarwal thus conducted a computational study of the transition states of this methodology, involving realistic model molecules with solvation effects.¹³⁸ They studied the reaction of a phenyl stabilized ylide (PhCH=SMe₂) with benzaldehyde at the B3LYP/6-311+G(d, p)//B3LYP/6-31G(d) level. Polarizable continuum-Poisson solvation corrections were applied during the geometry optimizations and on single points.

The lowest energy TSs for the addition of the ylide to the aldehyde all proceed through a gauche (cisoid type) conformation Scheme 90). This maximizes the stabilizing coulombic interactions between the sulfonium and the forming alkoxide in the addition step. In a smaller model system the following trans cyclization is greatly favored (Scheme 91). Hence, the rotation from the gauche staggered conformation to the anti staggered conformation must be taken into account in the overall reaction process.

Scheme 91 — Cyclization step on a small model system

The epoxidation energy profile is shown in Figure 63. It is of interest to note that the rotation is the rate determining step. In the formation of the trans stilbene oxide, the addition is found to be irreversible, whereas the formation of the cis stilbene oxide this is reversible due to the fact that the rotation is difficult.

Relative energy profiles (kcal/mol) for the epoxidation process.

The calculations are in accord with their kinetic and crossover experiments. These results are particularly interesting as experiments could not have predicted the rotational barrier following the addition to be critical in the reaction process.

More recently, they have also reported the development of an epoxidation methodology using amide stabilized ylides.¹³⁹ Although the reported methodology is stoichiometric, previous work by Seki and co-workers have reported a catalytic methodology giving moderate enantioselectivities in which the sulfur ylides are generated in situ from diazoacetamide with catalytic chiral binapthylsulfide and copper(II) acetylacetone.¹⁴⁰ In both methodologies, the reaction is found to afford exclusively the trans epoxide. In order to better understand this reactivity, they have done crossover experiments and found that in contrast to the phenyl stabilized ylides, the addition of amide stabilized ylides is reversible in both syn and anti pathways. They have then used calculations to determine if the origin of this reversibility is due to change in the barrier for rotation or cyclization. The calculations were done at the B3LYP/6-311+G(d, p)//B3LYP/6-31G(d) level including a continuum description of ethanol as the solvent. The energy profile is shown in Figure 64.

With these ylides, the elimination step, leading to the formation of the epoxides, was found to be the rate limiting step. The elimination leading to the trans epoxide is favored, as the elimination leading to the cis product exhibit repulsive interactions between the phenyl ring and amide group. These results are in accord with the crossover experiments. This difference in energetics can be attributed to the greater stabilization of the ylide afforded by the amide group, in comparison to the poorer phenyl.

Aggarwal has also reported a theoretical study discussing the importance of the leaving group ability in the reaction. Various ammonium, oxonium, phosphonium and sulfonium ylides were studied.¹⁴¹ Studies of epoxidations using ammonium show that high barriers to ring closure are due to the poor leaving group ability of the amine.¹⁴²

The theoretical work of Aggarwal focused on the understanding of the reactivity and diastereoselectivity, but studies of enantioselectivities are comparatively rare. Goodman and coworkers have recently reported a computational study¹⁴³ regarding the enantioselectivity in the epoxidation reaction catalyzed by the sulfides 35, developed by Metzner and co-workers,¹⁴⁴ and 36, by the Goodman group (Scheme 92).¹⁴⁵

Scheme 92 — Enantioselective epoxidation mediated by chiral sulfides 35 or 36

Calculations with B3LYP/6-31G(d) first explored the initial ylide conformations. While both sulfides give good enantioselectivities, there was little conformational preference. The transition states of the addition step of the ylides to the aldehyde adopt a cisoid (gauche) conformation, similar to the lowest energy addition transition states found by Aggarwal (Figure 65).

B3LYP/6-31G(d) geometries and relative energies (kcal/mol) for the addition of benzyl ylides derived from sulfide 36 to benzaldehyde.

For sulfide 36, the computed enantio- and diastereoselectivities from the relative energies of the four possible addition TSs correlate well with experiment. However, for sulfide 35, they found that the enantioselectivity is controlled by the addition step, but the diastereoselectivities are controlled by the cyclization, as shown by Aggarwal. The cyclization step for the trans diastereomer for the reaction with catalyst 35 is indeed lower in energy by 1–6 kcal/mol, confirming that the enantioselectivity is controlled by the addition step for the trans epoxide. The detailed origin of the enantioselectivities observed was not reported.

3.5.2. Cyclopropanation

In relation to the ylide based organocatalytic epoxide synthesis, a homologous variant leading to polysubstituted cyclopropanes has been developed by Tang and Dai (Scheme 93).¹⁴⁶ Of particular interest is the access of both enantiomer of the product through the use of endo or exo camphor based sulfides.

Scheme 93 — Mechanism for the sulfide catalyzed cyclopropanation

The reaction works under catalytic conditions and leads to good yields and enantioselectivities, with both endo and exo sulfides leading to the enantiomeric antipodes. Interestingly, the free hydroxyl group on the chiral sulfide is necessary for reactivity – simple dialkylsulfides or the methoxy protected variant of the chiral sulfide did not yield any desired products (Scheme 94). In order to understand this particular reactivity and explain the relative and absolute stereoselectivity of the reaction, Wu and co-workers performed computational studies.

Scheme 94 — Relative reactivities for different sulfides

The calculations were done using B3LYP with either 6-31+G(d) or 6-31G(d) basis sets for the hydrogen, carbon and oxygen and LANL2DZ(ECP) for sulfur and silicon. Single point solvation corrections were done using the IEFPCM model(THF). The model system is shown in Scheme 95. For the exo-ylide, methyl acrylate was studied (R₁ = H), and methyl cinnamate (R₁ = Ph) was used for the endo-ylide.

Scheme 95 — Model reactions studied by Wu and co-workers

The TSs of the addition step for the exo-ylide and methyl acrylate are shown in Figure 66. The addition step is found to be the rate- and stereodetermining step, as the cyclization is extremely facile. The chiral sulfide hydroxyl group directs the methyl acrylate in an s-cis conformation by H-bonding.

Computed transition structures for the addition step between the *exo*-ylide and methyl acrylate.

The two transition structures (TS8 and TS9) leading to the wrong diastereomer are both in an eclipsed conformation around the forming C-C bond. An almost staggered conformation is found in the most stable transition structures (TS6 and TS7), leading to the major products. However, in the structure leading to the minor enantiomer, a steric interaction is found between the cis hydrogen of C3 and the hydrogens of the chiral ylide. The authors also explain the greater stability of TS6 by solvation effects. TS6 has the largest surface area, and is more prone to experiencing greater solvation effects.

The calculations predict a diastereoselectivity of 99:1 in favor of the anti product in 93% ee, which is in good agreement with experiment (>99:1 anti:syn, 95% ee).

The transition structures of the addition step of endo-ylide with methyl cinnamate are shown in Figure 67; they show similarities to the addition transition structures found for the exo-ylide.

Computed transition structures for the addition step between the *endo*-ylide and methyl cinnamate.

Again, a strong H-bond with the ylide hydroxyl group orients the electrophile, in this case methyl cinnamate. A staggered conformation is found in TS10 and TS11, while an almost eclipsed conformation is found for the transition structures (TS12 and TS13), leading to the wrong diastereomer. A strong steric contact is observed in the transition structures (TS10 and TS12), leading to the minor enantiomer. The computed energies favor the anti product by 98:2 in 93 % ee, which is in good agreement with experiment (>99:1 anti:syn, 74% ee).

3.5.3. Aziridination

A related reaction to sulfur ylide mediated epoxidations and cyclopropanations is the synthesis of aziridines from the reaction of sulfur ylides with imines (Scheme 96). As in epoxidations and cyclopropanations, the reaction starts with the addition of the ylide to the imine to form both anti and syn betaines. The transoid betaine conformers then undergo a ring closure to give the trans and cis aziridines, respectively.

Scheme 96 — Aziridine formation from sulfur ylides and imines

Robiette has investigated this reaction involving semi-stabilized (R = Ph) and stabilized (R = CO₂Me) sulfur ylides using the B3LYP/6-31G(d) methodology.¹⁴⁷ The optimizations were performed in a continuum solvent with a dielectric constant of 37.5 D and a solvent probe radius of 2.179 Å to represent acetonitrile, one of the common solvents used in these reactions. Energies were obtained from single point calculations at the B3LYP/6-311+G(d, p)(CH₃CN) level. In the case of semi-stabilized ylides, the betaine formation is found to be irreversible. The steric strain induced by the N-sulfonyl group in the addition transition state determines the stereochemical outcome of the reaction. The transoid approach is favored in the case of syn betaine formation, and the cisoid mode of addition for the anti transition state (Figure 68). The observed low trans selectivity is explained by the stabilizing Coulombic interactions and stabilization by favorable C-H---O interactions in the cisoid anti addition transition state. In the case of stabilized ylides, the addition and rotation steps are reversible, and ring closure is found to be the rate- and selectivity-determining step. The computed energies of syn and anti ring-closure transition structures (16.1 and 16.5 kcal/mol relative to the separated reactants) predict a low selectivity in favor of the cis aziridine formation. Similarly, the observed low cis selectivity is accounted for by the steric strain in the elimination generated by the formation of the cis aziridine as compared to the trans aziridine.

Activation energies (kcal/mol) for the addition of Me₂SCHR (R = Ph, and R = CO₂Me given in parenthesis) to PhCH=NSO₂Me.

Sunoj and co-workers have also studied the reaction between substituted ylides and an aldimine bearing a CO₂Me group on the nitrogen atom using the B3LYP/6-31G(d) level of theory with the polarizable continuum model (SCRF-PCM).¹⁴⁸ The single-point energies were calculated using the 6-311G(d, p) basis set in acetonitrile continuum. They found that the stabilized (R = COMe) and semistabilized (R = Ph) ylides all follow a cisoid addition path leading to trans aziridines via anti betaine intermediates. Sunoj and Robiette agree on the more pronounced steric effetcs than electronic factors in favoring cisoid and transoid addition modes, and the rate- and selectivity-determining step is the addition for semistabilized ylides and elimination for stabilized ylides.

Janardanan and Sunoj later reported a density functional theory investigation of the factors controlling enantio- and diastereoselectivities in asymmetric aziridination reactions by the addition of chiral bicyclic sulfur ylides to substituted aldimines (97).¹⁴⁹ The B3LYP/6-311G(d, p)(acetonitrile)//B3LYP/6-31G(d) calculations were used to construct the energy profiles given in Figure 69. In the case of stabilized ylides, although the enantioselectivity is determined in the addition step, the energetics of the diastereoselectivity-determining elimination step affects the predicted %ee values (Figure 69). A cumulative effect of electronic and steric interactions in the diastereomeric transition states (Figure 70) controls the stereochemical outcome of the reaction.

Energy profiles (kcal/mol) for chiral sulfur ylide promoted aziridinations involving (a) SO₂Me and (b) CO₂Me protected imines.

Transition structures (*cisoid* (-c) or *transoid* (-t)) for chiral sulfur ylide promoted aziridinations involving (a) SO₂Me and (b) CO₂Me protected imines.

The nature of the N-protecting group on aldimines (CO₂Me and SO₂Me) is found to play an important role for the diastereoselectivities (Figure 69, a vs. b). The reversal of diastereoselectivity is explained by the differences in steric interactions of the N-protecting group. The orientation of SO₂Me oxygens in Y1-TSelim-RS shows an unfavorable interaction with the COMe oxygen (Figure 70a), whereas in the case of CO₂Me substituted imine (Figure 70b, Y2-TSelim-RS), this repulsion is minimized due to the planar geometry around the carbonyl carbon.

3.6. Phosphines

3.6.1. Hydroalkoxylation of methyl vinyl ketone

Phosphines are found to be efficient catalysts for the hydroalkoxylation of α-β unsaturated ketones (Scheme 98).¹⁵⁰ This allows ready access to β-hydroxy ketones, and provides a useful alternative to the typical aldol or sequential epoxidation/reduction of enones.

Interestingly, little retro-aldol or ketalization products are produced in the phosphine catalyzed hydroxylation reaction, whereas these are common side products in the analogous base (hydroxide) catalyzed systems. Li and co-workers investigated these interesting reactivity differences and studied the addition of methanol to methyl vinyl ketone catalyzed by trimethylphosphine with MP2.¹⁵¹ Geometry optimizations were done using the 6-31+G(d) basis set, and energies were computed using the 6-311+G(2df,2p) basis set. In order to account for solvation, the geometry optimizations were done using CPCM and UAHF radii.

The reaction is stepwise. The first step is the formation of the base (or nucleophile), and the second stage is the actual hydroalkoxylation step (Scheme 99).

Scheme 99 — Possible pathways for the phosphine catalyzed hydroalkoxylation reaction

In the first step, phosphine facilitates the formation of the methoxide anion by either pathway 1a or pathway 1b. In the former process, the proton transfer from MeOH to intermediate 37 is found to be the rate determining step with an activation energy of 26.6 kcal/mol. Calculations show that the direct deprotonation is disfavored by 15.7 kcal/mol.

The hydroalkoxylation can proceed through the base-catalyzed mechanism (pathway 2a) or a direct S_N2 mechanism (pathway 2b). The base catalyzed mechanism is favored over the S_N2 mechanism by 29.2 kcal/mol. The most difficult step in the reaction was the proton transfer from MeOH to 38 with a barrier of 18.1 kcal/mol. They conclude that the use of polar solvents is key in this reaction as this stabilizes the catalytically important methoxide anion.

3.6.2. Allenoate additions

Phosphine catalyzed [3 + 2] and [2 + 2 + 2] annulations of allenoates and various electrophiles have been developed recently.¹⁵² While these reactions are closely related, contrasting regioselectivities were observed depending on the nature of the electrophilic partner. The mechanisms are shown in Scheme 100.

Scheme 100 — Proposed mechanism for the annulation of allenoates with various electrophiles

Dudding and co-workers investigated the regioselectivities observed in the annulation process with methyl acrylate, N-Tosyl benzaldimine, and benzaldehyde using B3LYP/6-31G(d).¹⁵³ Trimethylphosphine was used as a model for the tri-N-butylphosphine. CPCM solvation corrections for benzene were computed.

The cycloadditions for all substrates are stepwise; concerted [3 + 2] cyclization transition structures are not found. The initial C-C bond formation is rate limiting, and these are shown in Figure 71. The computed 95:5 product ratio in favor of the α addition is in agreement with experiment.

Transition structures of the C-C bond formation with methyl acrylate.

The difference in energy between the two transition structures can be summarized by the following: First, a stronger ^δ+P···O^δ− electrostatic interaction is found in the transition state leading to the α addition (TSα). The phosphorous oxygen distance is shorter in the α addition (3.31 Å) compared to the γ (3.44 Å). Second, shorter and more symmetric hydrogen bonds are observed for the α addition. Finally, the gauche conformation around the forming C-C bond in the α addition is found to minimize more ideally the steric interactions (44º) compared to the γ addition (27º).

The transition state leading the α addition product is quite similar to the structure observed for the addition to methyl acrylate (Figure 72). A strong ^δ+P···O^δ− electrostatic interaction (3.35 Å) and two stabilizing hydrogen bonds (2.16 Å and 2.58 Å) are found. A gauche conformation around the C-C forming bond (58º), minimizing steric interactions is also observed. Moreover, an anomeric effect involving the donation of the imine lone pair to the S-O σ^* enhances the ^δ+P···O^δ− electrostatic interaction.

Transition structures of the C-C bond formation with N-Tosyl benzaldimine.

On the other hand, the transition state leading to the γ addition product exhibits a weaker ^δ+P···O^δ− electrostatic interaction (3.77 Å). The free energy difference of 1.2 kcal/mol between these structures corresponds to a α:γ ratio of 86:14, which is consistent with experiment.

Lastly, the transition structures found for the additions to benzaldehyde are shown in Figure 73. In this case, the γ addition is favored by 3.6 kcal/mol (CHCl₃), leading to a ratio of 99.8:0.2, in accord with experiment. Interestingly a stronger ^δ+P···O^δ− electrostatic interaction is observed for the α addition (2.60 Å vs. 3.11 Å) as well as relatively similar hydrogen bonds in both transition structures. However, an important difference arises in the dihedral angle around the forming bond. A staggered gauche conformation is found for the more stable α addition, whereas an almost eclipsed conformation is found for the γ addition, leading to greater steric interactions. This can also be observed by the comparison of the forming C-C bond lengths, being noticeably longer for the γ addition.

Transition structures of the C–C bond formation with benzaldehyde.

The full mechanism of the PMe₃-catalyzed [3+2] cycloaddition of 2,3-butadienoate and methyl acrylate was investigated both by the Kwon and Dudding and by the Yu groups (Scheme 101).¹⁵⁴ Kwon used B3LYP/6-31G(d) with CPCM single point corrections (benzene) to account for solvation energies, while Yu used B3LYP/6-31+G(d) with the same solvent correction method. Kwon concluded that the first C-C bond formation step (TS-CC1) is the rate-determining step, with ΔG_act = 17.9 kcal/mol, while Yu concluded that either addition of the catalyst to the allenoate (TS-add1) or TS-CC1 is the rate-determining step, depending on the phosphine. Both Kwon and Yu agree that intramolecular proton transfer from the α- to β-carbon of the allenoate is unfeasible under the reaction conditions (calculated ΔG_act = 37.6 kcal/mol and 39.6 kcal/mol, respectively). Rather, water assists the [1,2] migration by a protonation-deprotonation mechanism (TS-prot and TS-deprot). Yu and co-workers used isotopic labeling experiments in combination with DFT calculations to confirm the catalytic role of water.¹⁵⁵ The barriers for water catalyzed [1,2]-hydrogen shift were computed to be significantly lower, approximately 8 kcal/mol.

Scheme 101 — PMe₃ catalyzed [3+2] cycloaddition mechanism of allenoate and acrylate

Yu calculated the mechanism for formation of a 1,3-dipole generated by PMe₃ and alkynoate (Scheme 102). Without water assistance, the [1,3]-proton shift of the catalyst-alkynoate zwitterion intermediate has a calculated activation free energy barrier of 52.8 kcal/mol (TS-1,3). A water-assisted protonation-deprotonation mechanism occurs with a significantly lower barrier of 26.7 kcal/mol (TS-deprot; TS-prot could not be located and was presumed to be nearly barrierless).

Yu and co-workers have observed an unexpected [3+2] cycloadduct in the reaction of 2-methyl-2,3-butadienoate with dimethyl fumarate under the co-catalysis of phosphine and water (Scheme 103).¹⁵⁶ The 2-methylallenoate is thought to act as a three-carbon synthon generated through a [1,4]-proton shift process to yield the unexpected product. Geometry optimizations and single-point CPCM solvation corrections at the B3LYP/6-31+G(d) level located a highly energy-demanding intramolecular [1,4]-proton transfer transition state with an activation enthalpy of 40.8 kcal/mol. The water-catalyzed [1,4]-hydrogen shift is found to be much easier, requiring only 23.9 kcal/mol activation enthalpy (Scheme 104). These results revealed a reasonably low energy pathway for the formation of the unexpected product.

Scheme 103 — Phosphine and water co-catalyzed reaction of 2-methyl-2,3-butadienoate and dimethyl fumarate

Scheme 104 — Possible pathways for the [1,4]-proton-shift in the PMe₃-catalyzed reaction of 2-methyl-2,3-butadienoate with dimethyl fumarate (ΔH, kcal/mol)

3.6.3. Morita-Baylis-Hillman reaction

The Morita-Baylis-Hillman (MBH) reaction has been a well-known carbon-carbon bond-forming reaction for nearly 40 years,¹⁵⁷ yet computational studies of the reaction have only appeared in the literature in the last 4 years. One of the earliest computational reports, by Xu, investigated the PMe₃-catalyzed reaction of acrylonitrile and ethanal using B3LYP/6-311+G(d) using Tomasi’s IEF-PCM solvent model for CH₂Cl₂.¹⁵⁸ The calculated mechanism and relative free energies are shown in Scheme 105.

Scheme 105 — PMe₃-catalyzed MBH reaction

In agreement with experimental studies, the rate-determining step was predicted to be proton transfer from the carbon α to the cyano group of the catalyst-alkene-aldehyde adduct to the alkoxide (zwitt-II to zwitt-III via TS-H⁺). However this barrier is extremely high (63.2 kcal/mol) and involves a four-membered transition state (Figure 74).

B3LYP/6-311+G(d) rate-determining transition structure (**TS-H⁺**).

3.7. Other Amine Catalysts

3.7.1. Morita-Baylis-Hillman reaction

One year after Xu’s publication of phosphine-catalyzed MBH reactions, Aggarwal and Harvey reported a DFT study of the reaction catalyzed by tertiary amines.¹⁵⁹ Kinetic data support mechanism in which the rate-determining step involves proton transfer from the α-carbon,¹⁶⁰ addition of the aldehyde, which had been proposed earlier.¹⁶¹ Autocatalysis in the absence of protic solvents and rate acceleration in the presence of protic solvents had also been observed. The nature of the rate-determining step, the mechanism of proton transfer in protic and aprotic solvents, and the origin of rate enhancement in the presence of alcohols were the focus of Aggarwal and Harvey’s study. The B3LYP/6-311+G(d, p) (THF)//B3LYP/6-31+G(d) (THF) lowest energy pathways shown in Scheme 106.

Scheme 106 — Calculated mechanism of the MBH reaction in the absence and presence of alcohol

Both in the presence and absence of methanol, the rate-determining step is intramolecular proton transfer from the α-carbon to an alkoxide (TS-H⁺). For the non-alcohol pathway, the aldehyde adds twice to form hemiacetal intermediate hemi-I, from which proton transfer occurs via a six-membered transition state. For the alcohol catalyzed pathway, proton transfer occurs via a six-membered transition state with assistance from the alcohol. The intramolecular proton transfer via a four-membered transition state was calculated to be significantly higher in energy, 46.6 kcal/mol. All three transition structures are shown in Figure 75. These results are consistent with experimental observations and kinetic isotope effect studies.

(a) Rate-determining transition structures for proton transfer in the non-alcohol and alcohol-catalyzed MBH pathways. (b) Intramolecular proton transfer via four-membered transition state.

Similar to Aggarwal and Harvey, He and co-workers calculated the MBH reaction of acrolein and formaldehyde catalyzed by NMe₃ using B3LYP/6-311++G(d, p).¹⁶² Results of gas phase and CPCM (MeOH) calculations show that the intramolecular proton transfer is the rate-determining step, with activation energies of 45.8 and 35.1 kcal/mol, respectively, with respect to separated reactants. The calculated energies with one explicit methanol molecule is shown in Scheme 107. He found that explicit solvation with methanol significantly reduces the energies of zwitterionic intermediates and lowers the barrier for proton transfer (TS-H⁺), causing to the C-C bond forming step (TS-ald) to be rate-determining. These results appear to contradict Harvey and Aggarwal’s results, but the former authors noted that reactive aldehydes should have lower barriers for C–C bond formation (without effecting the proton transfer barrier), resulting in a change in the rate-determining step.

Scheme 107 — B3LYP/6-311++G(d, p) energies (free energies in brackets) for the MBH reaction of formaldehyde and acrolein catalyzed by NMe₃ with MeOH

In the same year that Aggarwal and Harvey’s report was published, Sunoj reported a mPW1K/6-31+G(d) study of the MBH reaction of methyl vinyl ketone and benzaldehyde catalyzed by diazabicyclo[2.2.2]octane (DABCO).¹⁶³ Single-point energy calculations using the IEF-PCM model (DMSO) were applied. In agreement with Aggarwal and Harvey, Sunoj concluded that the rate-determining step of the reaction involves proton transfer from the zwitterion intermediate generated upon C–C bond formation. While this proton transfer was proposed to occur via a four membered transition state with ΔG^‡ = 70.0 kcal/mol (Figure 76), the authors did note that calculations on a model reaction between acrolein, formaldehyde, and NMe₃ with explicit water molecules significantly reduces the barrier to 39.1 kcal/mol.

(a) mPW1K/6-31+G(d) transition structure for intramolecular proton transfer. (b) mPW1K/6-31+G(d) transition structure of water-assisted pathway.

Most recently, Sunoj showed that the inclusion of two explicit co-catalyst molecules–including water, methanol, and formic acid–significantly lowers the activation energy for the C-C bond formation and proton transfer steps.¹⁶⁴ Stabilization of the proton transfer is more effective than stabilization of the C-C bond formation. This difference is even more pronounced in the aza-MBH reaction compared to the MBH reaction.

3.7.2. 3-Alkynoate isomerization to chiral allenoates

The Brønsted base catalyzed 1,3-proton shift is a useful deprotonation-reprotonation reaction the preparation of allenes from alkynes.¹⁶⁵ Prior to a report by Huang and Tan,¹⁶⁶ only one asymmetric isomerization, catalyzed by a cinchona alkaloid derivative, had been reported.¹⁶⁷ Propyne is ~2 kcal/mol more stable than propa-1,2-diene; thus at equilibrium the isomerization yields depend on the relative stabilities of the alkyne and allene. Huang and Tan used a guanidine organocatalyst to effect the isomerization of 3-alkynoates to chiral allenoates in good yields and enantioselectivities (Scheme 108).

Scheme 108 — Guanidine-catalyzed isomerization of 3-alkynoates to chiral allenoates

The relative stabilities of four alkyne/allene pairs were calculated using B3LYP/6-31G(d, p). A comparison of the calculated and experimental results is shown in Table 7. The calculated relative stabilities qualitatively correlate with the experimental results. The thiophen-2-yl alkynoate, which gives the lowest allenoate isomerization yield (39%), shows the smallest energy difference between the two isomers (3.0 kcal/mol). The N-phthalmido alkynoate, which gives the highest isomerizatino yield (94%), shows the highest energy difference between the two isomers (6.0 kcal/mol). No discussion of the enantioselectivity was given.

Table 7.

Relative stabilities of alkyne/allene isomers at −20 °C

R	X	ΔG (allene–alkyne, kcal/mol)	experimental alkyne:allene
H	Ph	−3.7	30:70
H	6-MeO-naphth-2-yl	−4.3	20:80
H	thiophen-2-yl	−3.0	61:39
H	N-phthalimido	−6.5	6:94

Open in a new tab

3.7.3. Knoevenagel condensation

The condensation of aldehydes and activated methylenic groups, also known as the Knoevenagel condensation, was studied by Corma and co-workers (Scheme 109).¹⁶⁸ Proton affinities of seven amine catalysts were computed using B3LYP/6-31G(d, p) in order to attempt a correlation between catalyst basicity and reaction rates. The experimental turnover frequencies (TOF) and calculated proton affinities (energy difference between protonated and unprotonated species) are shown in Table 8.

Scheme 109 — Knoevenagel condensation catalyzed by amines

Table 8.

TOF and proton affinities of amine catalysts in the Knoevenagel condensation of benzaldehyde and ethyl cyanoacetoacetate

catalyst	proton affinity (kcal/mol)	TOF (min⁻¹)
44	258.8	11.2
43	258.2	1.0
41	251.5	9.6
40	250.9	26.0
39	250.1	8.1
42	241.8	0.6
45	233.3	2.2

Open in a new tab

Not surprisingly, the addition of methyl groups to parent 39 results in an increase in proton affinity (compare 39 with 40 and 41). Catalyst 43, which differs from 40 by an additional methylene bridge, has a higher proton affinity than 40. This difference is rationalized by a geometry that allows better interaction with both nitrogens and the proton in 43 (1.06 Å and 1.93 Å) compared to 40 (1.02 Å and 2.52 Å).

A reasonable correlation between proton affinity and catalyst activity could be made for catalysts 40, 39, 42, and 45. However, 41, which has a similar proton affinity as 40 (251.5 versus 250.9), has a lower TOF. Catalysts 43 and 44, which have significantly higher proton affinities compared to 40, also react with a lower TOF. The low activity of 41 might be explained by steric hindrance of proton abstraction by the four methyl groups. The low activity of 44 and 43 might also be due to steric factors, but another possible explanation is that the high proton affinities of these catalysts cause the protonation of the alkoxy intermediate to be disfavored (TS-prot, Scheme 110). The activation energies for each step in Scheme 110 for catalysts 40 and 44 were computed with HF/3-21G in order to clarify the cause of poor reactivity. The results are shown in Table 9.

Scheme 110 — Knoevenagel condensation mechanism

Table 9.

HF/3-21G activation energies (E_a) for the Knoevenagel condensation (with respect to reactants of each step)

catalyst	TS-deprot (kcal/mol)	TS-add (kcal/mol)	TS-prot (kcal/mol)
40	8.8	8.4	no barrier
44	22.4	8.4	4.1

Open in a new tab

Despite the high proton affinity of 44, the activation energy for deprotonation of ethyl cyanoacetoacetate is high (22.4 kcal/mol). This high barrier can be explained by steric hindrance by the methyl groups. While the barrier for protonation of the oxyanion intermediate by DMPMH⁺ is barrierless, the corresponding barrier with 44-H⁺ is 4.1 kcal/mol. This difference can again be explained by steric interference by the methyl groups of 44. In conclusion, both proton affinity and the steric ability to abstract protons contribute to the high reactivity of diamine catalysts.

4. Lewis/Brønsted acid/hydrogen bond catalysis

Organocatalysts may not accelerate reactions to the large extent that metal catalysts do, but they are attractive alternatives due to their environmentally benign nature, effectiveness in water, and general lack of product inhibition. Lewis (hydrogen-bonding) and Brønsted (proton-transfer) acid organocatalysts explored to date involve (thio)ureas, diols, phosphoric acids, oxazaborolidines, guanidinium/amidinium ions, and bispidine.

4.1 Urea and thiourea-based organocatalysis

The co-crystallization of N, N′-diarylureas with acetone was observed as early as 1976.¹⁶⁹ Over one decade later, Etter and co-workers co-crystallized diarylureas with substrates bearing a variety of Lewis basic functional groups, including ketones, ethers, sulfoxides, triphenylphosphine oxides, and nitroaromatics.¹⁷⁰ The ability of a single urea molecule to bind substrates by double H-bonding has led to many uses in organocatalysis.

4.1.1. Diels-Alder cycloaddition

One of the earliest theoretical studies of thioureas involves Diels-Alder cycloadditions. Schreiner used DFT to explain the experimental stereoselectivity in the N, N′-bis[3-(trifluoromethyl)phenyl]thiourea-catalyzed cycloaddition of N-acyloxazolidinone with cyclopentadiene (Scheme 111).¹⁷¹

Scheme 111 — Thiourea-catalyzed Diels-Alder cycloaddition

Model calculations (B3LYP/6-311+G(d, p)//B3LYP/cc-pVTZ on C, H, O, and N; B3LYP/6-311+G(d, p)//B3LYP/3-21G(d) on S) show that the most favored binding mode of the catalyst involves a syn relationship between the carbonyl groups, even though the anti geometry is preferred for the ground state conformation of the uncomplexed species (Figure 77). The efficiency of the catalyst was attributed to hydrogen bonding with both carbonyl oxygens of the substrate.

Binding mode of the complexed model catalyst.

A study of the catalysis of the cycloaddition between methyl vinyl ketone and cyclopentadiene by N, N′-bis[3,5-(trifluoromethyl)phenyl]thiourea and by water reveals that thioureas are effective catalysts even in the presence of water (Table 10).¹⁷² Gas phase calculations show that the thiourea reduces the activation barrier with respect to the uncatalyzed reaction by 2 kcal/mol, which correlates with the observed 9-fold rate acceleration. Catalysis by two explicit water molecules is less effective, reducing the barrier by only 0.5 kcal/mol.

Table 10.

Methyl vinyl ketone and cyclopentadiene Diels-Alder cycloaddition activation barriers ^a


catalyst	activation barrier
uncatalyzed	19.0
(H₂O)₂	18.5
thiourea catalyst	17.0

Open in a new tab

^a

Gas phase, B3LYP/6-31+G(d, p)//AM1

Fu explored the same reaction with geometry optimizations at the DFT, rather than semi-empirical, level of theory (Table 11).¹⁷³ In all cases, the endo transition state with the s-cis conformation of the dienophile is most stable. It had already been observed that the transition states of the uncatalyzed cycloaddition between methyl vinyl ketone and dienes are concerted, but asynchronous.^{174,175,176,177} This asynchronicity is enhanced in the thiourea-catalyzed transition states, and is even greater in the case of BF₃. Similarly, thiourea decreases the barrier by 3.2 kcal/mol, while BF₃ barriers are decreased by 11.2 kcal/mol. An increased charge transfer between the diene HOMO and dienophile LUMO explains both the increased asynchronicity and the decreased reaction barriers.

Table 11.

Gas phase activation enthalpies^a and bond asynchronicity (b-a)^b of the Diels-Alder between cyclopentadiene and methyl vinyl ketone


	ΔH₂₉₈^‡	b-a
uncatalyzed	17.9	0.695
thiourea-catalyzed	14.7	0.794
BF₃-catalyzed	6.7	1.007

Open in a new tab

^a

B3LYP/6-31+G(d, p) level. Activation barriers are with respect to the catalyst-ketone complex and cyclopentadiene.

^b

Bond-forming distance at vinyl carbon α to carbonyl minus bond-forming distance at terminal vinyl carbon.

Brinck used B3LYP and B2PLYP to study diene and dienophile substituent effects on the thiourea-catalyzed Diels-Alder reaction (Scheme 112).¹⁷⁸ A synergistic effect between the substituents and catalyst was found, resulting in overall reduced activation barriers of up to 6 kcal/mol. The substituent-mediated reactions display more asynchronous transition structures than the unsubstituted reactions, which led to the investigation of a stepwise Michael-type mechanism. While the Michael product is 23 kcal/mol less stable than the Diels-Alder product, the small difference between the Michael addition and concerted Diels-Alder transition structures (1.3 kcal/mol) suggests that a stepwise mechanism might compete with the concerted.

4.1.2. Claisen rearrangement

The catalysis of Claisen rearrangements of allyl vinyl ethers by water¹⁷⁹ or thiourea¹⁸⁰ has been known for over a decade, but a computational investigation of the thiourea-catalyzed reaction was only recently reported by Strassner and co-workers (Scheme 113).¹⁸¹

Scheme 113 — Thiourea-catalyzed Claisen rearrangement of allyl vinyl ether

Computational analysis of the uncatalyzed rearrangement shows that the lowest energy pathway proceeds through an s-cis geometry of the ester carbonyl (Scheme 114). The barriers for the catalyzed (3,3)-rearrangement steps with respect to the catalyst-substrate complexes are reduced by 4.0 kcal/mol for the s-trans conformation and increased by 0.2 kcal/mol s-cis conformation (Scheme 115). The doubly hydrogen-bonded s-trans transition state is more stable than singly hydrogen-bonded s-cis transition state, making the trans pathway more favorable, and offering only a 3.1 kcal/mol free energy activation barrier reduction over the uncatalyzed reaction. It is likely that substantially greater charge transfer in the transition state will be required for acceleration by hydrogen-bonding catalysts to be effective.

Scheme 114 — B3LYP/6-31++G(d, p) gas phase free energies for the uncatalyzed Claisen rearrangement

Scheme 115 — B3LYP/6-31++G(d, p) gas phase free energies for the thiourea-catalyzed Claisen rearrangement

4.1.3. Strecker reaction

The thiourea-catalyzed asymmetric hydrocyanation of imines (Strecker reaction) reported by Jacobsen is highly enantioselective and has a significant substrate scope.^{182,183,184,185} In a preliminary study Jacobsen reported that the urea functionality is responsible for catalysis and that the imine favorably binds with the urea hydrogens in the ground state (Figure 78).¹⁸⁶

Minimum energy geometry of a catalyst-imine complex 13 at the B3LYP/6-31G(d, p) level.

More recently, a detailed kinetic and computational investigation by the same group showed instead that the catalyst promotes the reaction by generating an iminium/cyanide ion pair.¹⁸⁷ The rate-determining step involves rearrangement of the catalyst-iminium-cyanide complex prior to addition of the cyanide to the iminium. The enantioselectivity is attributed to a larger stabilization of the iminium in the transition structure leading to the major (R) enantiomer (Figure 79).

Lowest energy rate-determining transition structures for the major and minor enantiomer products of the Strecker reaction.

4.1.4. Nucleophilic oxirane opening

Schreiner envisioned that diarylthioureas could mimic biological epoxide hydrolases in detoxifying living cells (Scheme 116).¹⁸⁸ The authors were pleased to find that when methyl oxirane was reacted with a range of nucleophiles and 10 mol% N, N′-bis[3,5-(trifluoromethyl)phenyl]thiourea in both CH₂Cl₂ and water, the aqueous reactions were accelerated as large as 200-fold and in excellent yields (Table 12).

Table 12.

Organocatalytic nucleophilic ring opening of methyl oxirane (+/-) at room temperature


solvent	catalyst	% yield
CH₂Cl₂	--	<0.5
CH₂Cl₂		37
water	--	29
water		94

Open in a new tab

The thiourea-catalyzed and uncatalyzed reactions of ethylene oxide and NH₃ in water, CH₂Cl₂, and in the gas phase were studied at the DFT level. Of the possible hydrogen bonding interactions between the reactants (Scheme 117), the binding of a single water molecule with thiourea (binding energy = 6.0 kcal/mol) is more favorable than its interaction with oxirane or another water molecule (binding energies = 2.8 and 1.1 kcal/mol, respectively). However, thiourea binds with oxirane (binding energy = 7.0 kcal/mol) even more strongly than it does with water.

Scheme 117 — Binding energies of possible hydrogen bond complexes

As the H-bonding ability of the solvent increases (gas phase → DCM → water, Table 13), the transition states become earlier and less asynchronous. The activation barriers decrease in the same order. These calculations show that the significant rate acceleration of nucleophilic oxirane opening is due to a strong and preferential catalyst-oxirane interaction, which is enhanced in water relative to weaker solvating systems.

Table 13.

Activation energies and bond lengths for the uncatalyzed and thiourea-catalyzed openings of oxirane by NH ₃^a


entry	solvent	catalyst	E_act	x	y
1	gas	—	36.0	2.24	1.65
2	gas	(NH₂) ₂CS	24.4	1.90	1.85
3	CH₂Cl₂	—	23.3	1.97	1.97
4	CH₂Cl₂	(NH₂) ₂CS	17.0	1.88	2.09
5	H₂O	—	21.9	1.94	2.01
6	H₂O	(NH₂) ₂CS	16.2	1.87	2.11

Open in a new tab

^a

B3LYP/6-311++G(d, p)//B3LYP/6-31G(d) level of theory (SCRF solvent inclusion).

Connon and co-workers proposed that N-tosyl-N′-aryl-(thio)ureas should be more effective hydrogen bonding catalysts than their diaryl-(thio)urea counterparts due to their higher acidities.¹⁸⁹ The calculated interaction energies of phenyl oxirane with these catalysts show that binding of the proposed catalysts is indeed more favorable than the diarylthiourea (Scheme 118).

Scheme 118 — B3LYP/6-31+G(d) interaction energies of lowest-energy catalyst phenyloxirane complexes

The favorable binding energies led to a survey of the catalyzed addition of 1,2-dimethylindole to phenyloxirane (Table 14). The designed catalyst proved to be remarkably effective, catalyzing the reaction where all tested (thio)urea catalysts failed (entries 2–4), and showing higher activity than a tosyl sulfonamide organocatalyst (entry 5).

Table 14.

Organocatalyzed addition of 1,2-dimethylindole to phenyloxirane


Entry	catalyst	% yield
1		71
2		<2
3		0
4		0
5		56

Open in a new tab

4.1.5. Tetrahydropyranilation

Schreiner presented the first acid-free organocatalytic tetrahydropyran (THP) protection of alcohols (Scheme 119).¹⁹⁰ The mechanism of this remarkably efficient reaction (turnover numbers of 100,000 at 0.001 mol% catalyst loading) was elucidated using DFT and coupled cluster computations.

The pre-organization of reactants is favored for the catalyzed reaction compared to the uncatalyzed reaction by nearly 15 kcal/mol (Figure 80). The activation for the uncatalyzed reaction is prohibitively high, in agreement with experiment. The thiourea catalyst remarkably lowers the activation barrier. The computed transition structure of the catalyzed reaction also shows that the catalyst is positioned away from the alcohol R group, explaining the ease of protecting even bulky tertiary alchohols.

B3LYP/6-31G(d, p) optimized TSs for the addition of methanol to dihydropyran; uncatalyzed (top) and catalyzed (bottom). Energies are with respect to separated reactants.

4.1.6. Pictet-Spengler-type cyclization

In 2007 Jacobsen reported the highly effective use of thiourea catalysis in the asymmetric Pictet-Spengler-type cyclization of β-indolyl ethyl hydroxylactams (Scheme 120).¹⁹¹ Possible mechanisms are shown in Scheme 121. The enhanced reactivity of alkylated lactams (R = CH₃) versus saturated lactams (R = H) led to the proposal that an S_N2-type reaction is not operative. The authors proposed that the catalyst promotes cyclization by abstracting a chloride in an S_N1-type rate-determining step. Subsequent addition of the indole to the N-acyliminium ion (S_N1-type A) or via a spiroindoline intermediate followed by alkyl migration (S_N1-type B) would afford the final product. Enantioinduction would be established by the closely associated catalyst-chloride complex.

Scheme 120 — Asymmetric cyclization of hydroxylactams catalyzed by thiourea

Scheme 121 — Proposed reaction mechanism

To gain further support of the proposed mechanism, B3LYP/6-31G(d) was used to optimize three ground state structures: (1) catalyst-ionized hydroxylactam, (2) catalyst-chlorolactam via carbonyl, and (3) catalyst-chlorolactam via chloride (Figure 81). All attempts to locate a complex in which the thiourea is bound to the carbonyl of the ionized lactam (#1) failed to converge. While the catalyst can bind to the carbonyl of the chlorinated lactam (#2), this leads to an unproductive mechanism. Finally, a complex in which the thiourea binds to the chloride of the hydroxylactam (#3) was located. In a recent work, Danishefsky was able to isolate the azaspiroindolenine intermediate of the Pictet-Spengler reaction.¹⁹²

4.2 Diols

TADDOLs have been used as metal chiral auxiliaries and stoichiometric enantiodifferentiating reagents for over a century.¹⁹³ Rawal‘s discovery of the acceleration of hetero-Diels-Alder cycloaddition reactions by TADDOLs stimulated their uses as organocatalysts in recent years.^194,195

4.2.1 TADDOL-catalyzed Diels-Alder cycloaddition

Wu and co-workers employed QM/MM methods to analyze the cycloaddition of Danishefsky‘s diene with benzaldehyde (Scheme 122).¹⁹⁶ Danishefsky‘s diene was modeled by 1,3-dimethoxy-1,3-butadiene.

Various H-bonding interactions between TADDOL and benzaldehyde were investigated (Figure 82). Of these binding modes, the trans complex was established as the mode of catalysis.

TADDOL-dienophile H-bonding interactions.

The transition structures of the uncatalyzed reaction (ΔE^‡ = 20.2, Figure 83) shows that the cycloaddition is concerted but asynchronous; the endo mode of attack is preferred; the nucleophilic terminus of the diene attacks the carbonyl carbon.

B3LYP/6-31G(d)//B3LYP/6-31G(d):PM3 transition structure of the uncatalyzed hetero-Diels-Alder cycloaddition of benzaldehyde with 1,3-dimethoxy-1,3-butadiene.

The computed transition stuctures of the catalyzed reaction with all three catalysts explain the experimentally observed enantioselectivities. The 1-naphthyl substituted catalyst, which experimentally gives the highest yield and ee, was calculated to give the lowest activation barrier of the three catalysts−6.0 and 2.5 kcal/mol lower than the lowest energy transition structures for the phenyl and 2-naphthyl substituted catalysts, respectively. The 1-naphthyl substituted catalyst was also calculated to promote the largest selectivity for the si-face attack and most effectively enhance the endo versus exo selectivity with respect to the uncatalyzed reaction. The lowest energy transition structure for the cycloaddition by the 1-naphthyl substituted catalysts is shown in Figure 84.

B3LYP/6-31G(d)//B3LYP/6-31G(d):PM3 transition structure of the TADDOL-catalyzed hetero-Diels-Alder cycloaddition.

The stabilization the Diels-Alder transition state by the catalysts is attributed to a significant charge transfer from the donor diene to the dienophile-catalyst acceptor complexes (0.47–0.49e). The transition states bear zwitterionic character, and the H-bond to the carbonyl oxygen stabilizes the developing negative charge.

The quadrant diagram shown in Figure 85 explains the energetic preference for the si-face approach. The aromatic moieties of TADDOL protrude “out” in quadrants II and IV (gray). A si-approach would place the reactants in unhindered quadrants I and III, while a re-approach would place the reactants in hindered quadrants II and IV. The 1-naphthyl moieties of the most efficient catalyst would protrude more than the phenyl or 2-naphthyl groups of the other cataylsts, causing an increased barrier for the re-approach for the 1-naphthyl catalyst, and explaining the larger observed enantioselectivity.

Quadrant diagrams of (a) *si-*face approach. (b) *re-*face approach. Adopted and modified from reference 164.

One year later Houk and co-workers reported a fully quantum mechanical study of two TADDOL-catalyzed hetero-Diels-Alder cycloaddition reactions involving Rawal-type dienes (Scheme 123).¹⁹⁷ The catalyst was initially modeled by 1,4-butanediol and was predicted to bind most favorably in a cooperative binding mode (Figure 86). Gómez-Bengoa also studied the binding modes of double hydrogen bond donors at the B3LYP and MP2/6-311++G(d, p) levels and found that the cooperative binding mode is favored for the Diels-Alder reaction.¹⁹⁸ Both reactions were found to be endo-selective. The catalyst efficiency is attributed to a charge stabilization of the zwitterionic transition state by the hydrogen bonds.

Scheme 123 — B3LYP/6-31G(d) ΔH^‡ for the uncatalyzed and alcohol-catalyzed Diels-Alder reaction with Rawal-type dienes

B3LYP/6-31G(d) transition structures for the 1,4-butanediol Diels-Alder and hetero-Diels-Alder reactions.

The Houk group then reported the use of ONIOM (B3LYP/6-31G(d):AM1) calculations to explain the origin of enantioselection in the reaction of 1-dimethylamino-3-tert-butyldimethylsiloxy butadiene and benzaldehyde.¹⁹⁹ The two lowest energy transition structures for si-face (favored) and re-face (disfavored) are given in (Figure 87). Both structures show endo selectivity and are highly asynchronous. The re-face transition structure shows that the hydrogen atoms of the naphthyl groups are within van der Waals radius of the diene moiety. The si-face attack does not suffer these repulsions, and furthermore, benefits from CH-π stabilization between the aldehyde CH and a pseudo-equatorial naphthyl ring. The calculated 1.5 kcal/mol difference between these two transition structures corresponds to an S:R product ratio of 97:3 at −40°C, which is in good agreement with the experimentally observed ratio of 99:1. To account for dispersion interactions, single point energy calculations were performed on the ONIOM geometries. MPWB1K/6-31G(d) and M06-2X/6-31+G(d) results show a 2.4 and 3.4 kcal/mol selectivity, respectively, for the si-face transition state, overestimating the selectivity substantially.

Enantiodetermining B3LYP/6-31G(d)//ONIOM(B3LYP/6-31G(d):AM1) transition structures for (R, R)-1-Np-TADDOL-catalyzed hetero-Diels-Alder reaction. R = TBDMS.

4.2.2 Biphenylene diol-catalyzed oxirane opening

Lewis acid catalysis by 1,8-biphenylene diol was first discovered by Hine and co-workers in the opening of phenyl glycidyl ether by diethylamine.²⁰⁰ Soon after, Maruoka and co-workers employed the same type of catalyst to promote carbonyl reductions, the Mukaiyama aldol reaction, Michael addition of silyl ketene acetals to α, β-unsaturated ketones, and the Claisen rearrangement.²⁰¹ Several years later Kelly furthered the scope of catalysis by applying it to the Diels-Alder cycloaddition.²⁰²

Fujimoto investigated the nucleophilic ring-opening of oxirane by ammonia, catalyzed by 1,8-biphenylene diol and various monodentate acids (Table 15).²⁰³ Calculations at both the B3LYP/6-31G(d) and MP2/6-311++G(d, p) levels confirm that the bidentate diol catalyzes the nucleophilic ring-opening more effectively than the monoacids by over 5 kcal/mol (Figure 88). A computational molecular orbital analysis showed that the H-bonded catalyst promotes charge transfer from the oxirane to the catalyst, thereby enhancing its electrophilicity and decreasing electronic repulsion with the attacking nucleophile.

Table 15.

Calculated activation barriers for the nucleophilic opening of oxirane by ammonia


entry	complex	Activation Barrier
entry	complex	B3LYP^a	MP2^b
1	uncatalyzed	38.8	38.8
2		14.0	20.1
3	PhOH	22.2	27.5
4	p-Cl-PhOH	20.8	26.7
5	p-CN-PhOH	19.4	25.8
6	p-CHO-PhOH	19.8	26.0
7	p-Me-PhOH	25.8	31.2
8	H₂O	26.2	31.9

Open in a new tab

^a

B3LYP/6-31G(d).

^b

MP2/6-311++G(d, p)//B3LYP/6-31G(d).

B3LYP/6-31G(d) optimized transition state geometry of the 1,8-biphenylenediol catalyzed nucleophilic opening of oxirane by ammonia.

4.2.3 Fluorination

Pliego envisioned the design of an organocatalyst that would accelerate S_N2 reactions more effectively than polar aprotic solvents do.²⁰⁴ A thorough research of potential catalyst structures suggested 1,4-benzenedimethanol as the most promising catalyst. The binding mode is shown in Scheme 124.

Scheme 124 — Catalysis of the S_N2 reaction by 1,4-benzenedimethanol

MP2/6-31+G(d)//HF/6-31G(d) calculations of the uncatalyzed reactions of ethyl chloride and acetate in DMSO reveal S_N2 and E2 free energy barriers of 26.1 kcal/mol and 31.9 kcal/mol, respectively, which means the E2 reaction does not compete with the S_N2 reaction. The 1,4-benzenedimethanol catalyst decreases these barriers by 4.3 kcal/mol and 3.5 kcal/mol, respectively.

It was calculated that the same catalyst could enhance the S_N2 reaction of fluoride ion with 2-chlorobutane.²⁰⁵ Experimentally these two reactants lead to 90% elimination and only 10% S_N2 product. The calculated free energy barriers of the uncatalyzed reaction in DMSO are nearly identical for all four reactions (Scheme 125). Calculations of the catalyzed reaction show that the elimination process barrier is reduced by 1.8–3.1 kcal/mol and the S_N2 by 3.7 kcal/mol. Figure 89 shows that the OH^···F distance in the S_N2 transition structure is at least 0.1 Å shorter than that of the E2 transition structures. These reduced activation barriers predict a 100 fold increase in the total reaction rate (S_N2 + E2) and a change in the S_N2:E2 product ratio from 10:90 to 40:60.

Scheme 125 — ONIOM[CCSD(T)/6-311+G(2df,2p):MP2/6-31+G(d)] free energy activation barriers for reaction of F⁻ with 3-chlorobutane. DMSO solvation by HF(PCM)/6-31+G(d)

Lowest energy transition structures for the S_N2 and E2 reactions of 2-chlorobutane and F⁻, catalyzed by 1,4-benzenedimethanol.

4.3 Phosphoric acid catalysis

Like TADDOL, the role of BINOL as a hydrogen-bond donor catalyst was not discovered until recent years when Schaus and co-workers discovered its catalytic power in the Morita-Baylis-Hillman reaction.^206,207 The phosphoric acid analog was then demonstrated by the Terada and Akiyama groups to catalyze Mannich-type reactions.²⁰⁸ These successes launched the use of dialkylphosphoric acid organocatalysts in a large array of asymmetric reactions.²⁰⁹

4.3.1 Mannich Reaction

Two nearly-simultaneous computational investigations of the BINOL-based phosphoric acid catalyzed Mannich reaction were reported in 2007.^210,211 In the first report, Terada and co-workers used DFT to explain the mechanism and stereoselectivity of the addition of acetylacetone to aldimines (Scheme 126).

Scheme 126 — Phosphoric acid catalyzed Mannich reaction²¹²

Preliminary computational analysis had shown that the catalyst-imine complex is controlled by the bulky X substituents of phosphoric acid. Four different adducts which place the imine groups away from these bulky groups two—with the trans imine and two with the cis imine–were envisioned and investigated (Figure 90).

Relative energies of possible imine-phosphoric acid catalyst adducts in the asymmetric Mannich reaction.

Attempts to locate hydrogen-bonded complex cis-2 were unsuccessful, presumably due to unfavorable interactions between the Boc group and phosphoric acid oxygens. Of the other three optimized structures, trans-1 is more stable than trans-2 and cis-1 by 0.8 and 6.9 kcal/mol, respectively. The imine carbon in complexes in trans-2 and cis-1 is completely shielded by either of the aromatic X groups. The same carbon in trans-1 is exposed to stereospecific attack. It was hypothesized that if trans-1 could freely rotate around the N-H bond, the observed enantioselectivity would presumably be destroyed. Indeed, experimental replacement of the Boc group with a benzyl and methyl ester resulted in significantly lower enantioselectivities of 26% and 6%, respectively, supporting the mechanism of the Mannich reaction via complex trans-1.

Yamanaka and co-workers reported experimental and theoretical investigation of an analogous chiral Brønsted acid catalyzed Mannich-type reaction of silyl enolates with aldimines (Table 16).

Table 16.

Addition of silyl enolate to aldimines, catalyzed by chiral phosphoric acids


entry	Ar	Y	% Yield	% ee
1	2-OH-Ph	H	57	0
2	2-OH-Ph	Ph	100	27
3	2-OH-Ph	2,4,6-Me₃C₆H₂	100	60
4	2-OH-Ph	4-MeOC₆H₄	36	32
5	2-OH-Ph	4-NO₂C₆H₄	98	89
6	4-OH-Ph	4-NO₂C₆H₄	2	20
7	4-OMe-Ph	4-NO₂C₆H₄	56	3
8	Ph	4-NO₂C₆H₄	76	39

Open in a new tab

BH and HLYP/6-31G(d) model calculations show that the reaction occurs by a dicoordination pathway (Scheme 127). The reaction was found to be a Brønsted acid-catalyzed process in which the rate-determining proton transfer from phosphate to the imine occurs prior to nucleophilic addition.

The re-face and si-face attacks were modeled to explain the origin of enantioselectivity (Figure 91). In agreement with experiment, re-face attack (TS-re) is 5.7 kcal/mol more stable than si-face attack (TS-si). TS-re possesses an aromatic stacking interaction between the catalyst and iminium N-aryl group, which fixes the iminium geometry for attack by the nucleophile. The magnitude of the aromatic stabilization depends on the substitution, which explains why the 4-nitrophenyl substituent enhances reaction rates and selectivities. TS-si is disfavored due to a steric hindrance between the 4-nitrophenyl group of the catalyst and either the trimethylsilyl group of the nucleophile or the aromatic group of the aldimine electrophile.

BHandHLYP/6-31G(d) transition structures for the *re-*face and *si-*face attack of enolate to aldimine.

4.3.2. Acid-catalyzed 1,3-Dipolar cycloadditions

Gong and co-workers synthesized spiro[pyrrolidin-3,3′-oxindole] derivatives in high enantiopurity via a 1,3-dipolar cycloaddition of methyleneindolines with azomethine ylides formed from aldehydes and amino esters in the presence of chiral phosphoric acids (Scheme 128). ²¹³

Scheme 128 — Chiral phosphoric acid catalyzed 1,3-dipolar cycloaddition

B3LYP/6-31G(d) calculations were performed to explain the high regio- and stereoselectivity. The lowest energy transition structure (Figure 92) corresponds to the experimentally obtained major regio- and stereoisomer. Both the methyleneindoline and the azomethine ylide are hydrogen-bonded to the catalyst. The transition structure that gives the minor enantiomer is 1.5 kcal/mol higher in energy and does not benefit from hydrogen bond stabilization to the same extent; the P=O^···HN distance is 4.75 Å. The stability of the major transition structure compared to the transition structure that gives the minor regioisomer is attributed to a favorable π–π interaction between the oxo-indole ring and the conjugated esters in the former transition structure. The distance between these moieties is only ~3.0 Å.

Major and minor transition structures for the chiral phosphoric acid catalyzed 1,3-dipolar cycloaddition.

4.3.3. Biginelli reactions

The same group synthesized dihydropyrimidinethiones in excellent enantioselectivities via Biginelli and Biginelli-type reactions catalyzed by phosphoric acid organocatalysts (Scheme 129). ²¹⁴ ONIOM calculations were used to explain the stereo- and regioselectivity of the reaction. First, the imine resulting from condensation of the aldehyde and thiourea was calculated to favor the E geometry by 6.2 kcal/mol, arising from steric repulsion between the sulfur atom and phenyl ring. Two activation modes were then considered (Scheme 130): (1) activation of the imine by the phosphoric acid OH to generate a zwitterionic iminium salt, and stabilization of the enol proton by the oxygen of the OH group, and (2) activation of the imine by the phosphoric acid proton to generate a zwitterionic iminium salt, and stabilization of the enol proton by the oxygen of the P=O group. All possible modes of attack for both pathways were calculated.

Scheme 129 — Chiral phosphoric acid catalyzed Biginelli reaction

Scheme 130 — Proposed activation mechanisms for organocatalyzed Biginelli reaction

The lowest energy transition structure follows mechanism B and involves attack of the Re-face of the imine by the Si-face of the enol (TS-(S)). This leads to the experimentally observed major (S) product. In contrast, the lowest energy transition structure that gives the minor (R) enantiomer ((TS(R)) was calculated to occur via mechanism A. The hydrogen bond distances between the enol and phosphoric acid in TS-(R) are shorter than those of TS-(S) and is believed to account for the 1.1 kcal/mol difference between these two enantiomeric transition structures.

4.3.4. Reductive aminations

The Goodman²¹⁵ and Himo²¹⁶ groups independently reported theoretical studies on chiral phosphoric acid-catalyzed imine reductions by Hantzsch ester. Goodman used ONIOM(B3LYP/6- 31G(d):UFF) followed by single point calculations (MPWB1K/6-31G(d, p), PCM solvation model for toluene) to investigate the mechanism and stereoselectivity of the reaction. Of the possible mechanisms, protonation of the imine by the phosphate OH and stabilization of the Hantzsch ester NH by the phosphate oxygen was calculated to be favored significantly (Scheme 131).

Scheme 131 — Chiral phosphoric acid catalyzed imine hydrogenation by Hantzsch ester

In the case of Rueping‘s catalyst (Ar² = 3,5-(CF₃)₂-Ph),²¹⁷ the transition structures favor the Z geometry of the imine, even though the ground state E conformation was calculated to be favored over the Z by 2.9 kcal. The lowest energy transition structure gives the experimentally observed R-product and is 1.1 kcal/mol lower in energy than the lowest energy transition structure that gives the S-product. This difference is attributed to a destabilizing interaction between a CF₃ group of the catalyst and the aromatic group on the imine nitrogen (Ar¹ = Ph) in the minor S-transition structure. For MacMillan‘s catalyst (Ar² = SiPh₃)²¹⁸, the lowest energy transition structure that gives the favored R-product also bears the Z conformation. Unlike Rueping‘s catalyst, the lowest energy transition structure that gives the minor S-product is in the E conformation. This minor transition structure was calculated to be 2.7 kcal/mol higher in energy than the major R-transition structure. Although no explanation for the stereoselectivity was given for the stabilization of the E transition structure, a general model that explains the stereoselectivity of the Z transition structures was given (Figure 93).

Enantioselectivity model for chiral phosphoric acid catalyzed imine hydrogenation.

Himo used B3LYP/6-311+G(2d,2p) to explain the kinetic resolution of α-branched imines (Scheme 132). For R_L = Ph and R_S = Me, the Z imine was calculated to be 3.7 kcal/mol higher in energy than the E imine. Eight transition structures—Re- and Si-face hydride attack of both the E and Z isomers of each imine diastereomer—were considered. The naphthyl groups were modeled by phenyl groups; the carboxyethyl groups of the Hantzsch ester were modeled by carboxymethyl groups; Ar² = 2,4,6-trimethylphenyl.

Unlike Goodman‘s results, the lowest energy transition structures leading to the major S-product and minor R-product arise from the E imine. This difference is not surprising, considering that different imines—conjugated aromatic and aliphatic branched—were studied by both groups. The lowest energy transition structures are shown in Figure 94. In the major (S) transition structure, R_L (R_L = Ph) points away from the phosphate, minimizing steric interactions with the mesityl group of the catalyst. The para-methoxyphenyl group on the imine nitrogen is parallel with one ester group of the Hantzsch ester (at approximately 3.5 Å) and one ortho-proton of the protecting group has a weak stabilizing interaction with a phosphate oxygen (2.27 Å). The 1.8 kcal/mol destabilization of the minor (R) transition structure is attributed to steric clashing between the para-methoxyphenyl group and a mesityl group on the catalyst (shortest H–H distance is 2.27 Å).

Lowest energy major and minor transition structures.

Goodman recently studied the Friedel-Crafts reactions of indole with N-acyl and N-tosylimines catalyzed by BINOL-phosphoric acid derivatives and discussed in detail the energy dependence of the Z/E-imine conformations in the transition state on the nitrogen substituent.²¹⁹ N-phenyl ketimines prefer a Z-conformation in the transition state, whereas, N-benzyl aldimines adopt an E-conformation. The highest preference for the E-imine is calculated for N-acylimines.

4.3.5. Hydrophosphonylation

Shi and co-workers used ONIOM(B3LYP/6-31G(d):AM1) to investigate the hydrophosphonylation reaction of imines (Scheme 133).²²⁰ A reaction screening showed that other aromatic groups on the catalyst—Ar = 4-NO₂ or 4-CF₃C₆H₄—cause both the reaction yield and enantioselectivity to drop. It was also found that changing the phosphonate from an ethyl ester to an isopropyl ester causes the enantioselectivity to increase from 43% to 52%. Finally, a benzothiazole protecting group causes an almost complete loss of stereoselectivity.

Unlike the results of the Akiyama study, the mono-coordination pathway was calculated to be higher in energy than the di-coordination pathway. The calculated mechanism shown in Scheme 134. All energies are with respect to separated reactants. The rate-determining transition structures involve addition of the phosphonate to protonated imines (R)-int and (S)-int. The 5.2 kcal/mol stability of the (R)-TS compared to the (S)-TS is overestimated, but gives a qualitative picture of the origin of enantioselectivity. The difference is mainly attributed to steric interference between a mesityl group of the catalyst and the para-methoxyphenyl group in the (S)-TS, which causes the para-methoxyphenyl group to distort from planarity (Figure 95). In agreement with experimental trends, the effect of changing the diethyl phosphite to diisopropyl phosphite resulted in a calculated 6.8 kcal/mol difference between the major and minor rate-determining transition structures.

Scheme 134 — Mechanism of chiral phosphoric acid catalyzed hydrophosphinylation mechanism

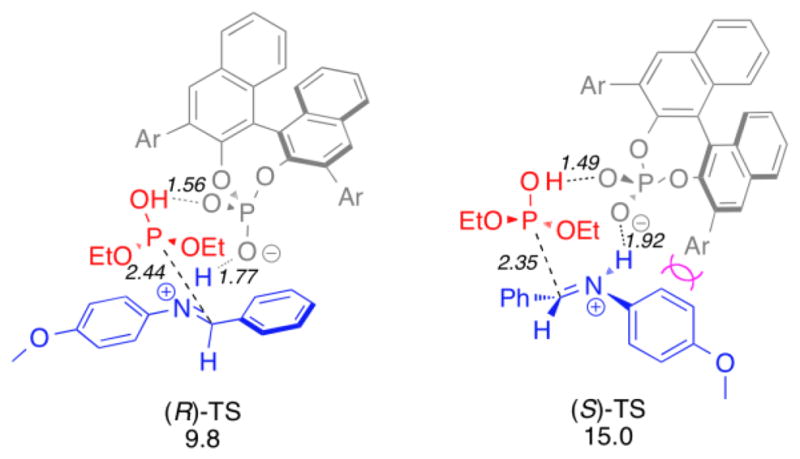
Lowest energy enantiomeric transition structures for 4-methoxyphenyl protected imine.

The rate-determining transition structures for the benzothiazole-protected imine were also calculated. In excellent agreement with the experimental results, the major R-TS was calculated to be only 0.1 kcal/mol more stable than the minor S-TS. There is no significant difference in the geometries of the enantiomeric transition structures, and the disfavored interactions between the 3,3′-substituents of the catalyst and para-methoxyphenyl group of the transition structures in Figure 95 do not exist in the benzothiozole transition structures (Figure 96).

Lowest energy enantiomeric transition structures for benzothiazole protected imine.

4.4 Oxazaborolidines

Although it could be argued that boron-containing molecules are not organocatalysts, oxazaboralidines have had significant impact on asymmetric synthesis as chiral Lewis-acid catalysts and the origins of stereoselectivities has received ample attention from computational chemists as discussed in this section. Oxazaborolidines, also known as CBS (Corey-Bakshi-Shibata) catalysts, were discovered to reduce carbonyl compounds with excellent enantioselectivities one decade ago.^221,222 Derivatives of this catalyst, including recent applications of the protonated salt, have been employed in catalytic enantioselective alkynylations,²²³ Diels-Alder reactions,^224,225,226 cyanosilylation of aldehydes,²²⁷ Michael additions,²²⁸ and vinylogous Mukaiyama aldol reactions.²²⁹

4.4.1. Carbonyl reductions

Between 1991 and 1996 Nevalainen provided a series of ab initio studies that confirmed Corey‘s mechanistic theories of oxazaborolidine-catalyzed carbonyl reductions (Scheme 135). A computational explanation was given for the experimental formation of oxazaborolidine aggregates²³⁰ and the role of Lewis basic solvents in reducing the aggregation.²³¹ The favored coordination mode of BH₃ to the catalyst²³² as well as the proper ketone-oxazaborolidine complex geometry²³³ were also elucidated.

Scheme 135 — Mechanism of oxazaborolidine-catalyzed reduction of acetophenone proposed by Corey

Li and co-workers provided a more recent series of theoretical investigations on the chiral oxazaborolidine²³⁴ and sulfur-containing chiral oxazaborolidine²³⁵ catalyzed reduction of carbonyl compounds at the HF/6-31G(d) level. The same group also used HF/6-31G(d) and B3LYP/6-31G(d) to investigate the enantioselective reduction of keto oxime ethers (3-cyclohexene-1,2-dione-1-oxime).²³⁶ Despite these successful investigations, transition structures explaining the observed enantioselectivities were not calculated. Numerous semiempirical studies have addressed this issue.²³⁷ This review focuses on high level DFT investigations which explain the general origin of enantioselectivity of these reductions.²³⁸

General Mechanism

Consistent with Corey‘s observations and earlier calculations, Alagona found that the cis oxazaborolidine-borane-THF complexation is exothermic (ΔG = −1.9 kcal/mol). The trans coordination is disfavored because of the highly strained pyrrolidine ring conformation (ΔG = +9.9 kcal/mol, Figure 97). The geometry of the cis adduct closely resembles that of the crystal structure obtained by Corey.²³⁹ Coordination of BH₃ to the catalyst shifts electron density from nitrogen to the exocyclic boron, enhancing the nucleophilicity of the hydrides, and increasing the Lewis acidity of the endocyclic boron.

*cis* and *trans* (BH₃ and C-4 hydrogen relationship) BH₃-oxazaborolidine complexes.

The ketone binds the cis catalyst-BH₃ complex from the less hindered convex face. Only two of four possible coordination geometries converged to a local minimum at the B3LYP/6-31G(d) level, each leading to opposite faces of hydride transfer (Figure 98). The si face attack is the preferred mode of hydride transfer because the transition state has a chairlike conformation, whereas the transition state of the re face attack adopts a boatlike conformation.

B3LYP/6-31G(d) transition structures for si and re face hydride transfers to phenyl methyl ketone.

The Meyer group investigated the same catalyst in the reduction of 2′,5′-dimethylphenyl isopropyl ketone.²⁴⁰ Experimental and calculated ¹³C kinetic isotope effect measurements were in excellent agreement with each other and provide strong evidence that the rate-determining step is hydride transfer to the carbonyl carbon. The computed enantiomeric transition structures show that the gem-diphenyl groups on the catalyst have little effect on the placement of the R_L and R_S groups. Rather, the phenyl groups serve to constrain the conformation of the bicyclic catalyst and dictate the coordination of the ketone.

Tang and co-workers used B3LYP/6-31G(d, p) to explain the experimental selectivities obtained by a similar diamide catalyst (Scheme 136).²⁴¹ The reaction was found to proceed via four steps, with the rate-determining step being the transfer of hydrogen from the catalyst-ketone complex to acetophenone (Figure 99). In agreement with experimental results, the activation free energy for reface attack was calculated to be favored over si-face attack by 1.2 kcal/mol. The difference is attributed to different amounts of repulsion between the ketone substituent that is closest to the catalyst and the catalyst substituents. The spatial structures of both transition structures show that the phenyl group of the re-face transition state is further away from the catalyst system than the methyl group of the si-face transition state.

B3LYP/6-31G(d, p) relative transition structure energies for the reduction of methylphenylketone.

4.4.2. Reduction of glycosyl α-ketoesters

Grison and co-workers obtained good experimental diastereoselectivities in the CBS-catalyzed reduction of glycosyl α-ketoesters (Table 17).²⁴² However, if one considers the glycosyl group as larger than the ester moiety, Corey‘s model predicts the opposite stereoselectivity than that which was obtained experimentally. Suspecting that the chiral centers of the glycosyl group may influence the asymmetric induction, Ruiz-Lopéz modeled the reaction at the B3LYP/6-31G(d) level to explain the origin of diastereoselectivity.²⁴³

Table 17.

Reduction of α-ketoesters by catecholborane


Glycosyl α-ketoester	catalyst configuration	% yield	Major product configuration	% d.e.
D-ribo	S	61	R	70
D-ribo	R	39	S	68
D-galacto	S	94	R	78
D-galacto	R	81	S	90

Open in a new tab

Model calculations with various substitution patterns at C4 and C5 show that the C4 configuration determines the product configuration, and disubstitution at C5 enhances the stereostereoselectivity. Consistent with Alagona’s calculations, the lowest energy pathway involves a cis coordination of the borane to the catalyst, binding of the carbonyl to the same face, and hydride transfer via the si face of the carbonyl carbon (Scheme 137).

Scheme 137 — B3LYP/6-31G(d) ΔG^‡ for hydride transfer

Catalysis of the glycosyl α-ketoester reduction by an achiral oxazaborolidine was calculated in order to explain the influence of the sugar moieties on the asymmetric reduction (Scheme 138). Unlike the previous calculations, the lowest energy transition structures for each enantiomeric reduction proceeds via the top face of the catalyst. The authors suggest that unlike TS-exo-anti in Scheme 137 which is favored because R_L (CO₂Me) is trans to the B-Me group, the analogous TS-exo-anti for a sugar (Me is substituted by a sugar) is disfavored because the dihedral around the adjacent carbonyls must distort from a planar conjugation to avert clashing between the ester and B- Me groups.

Scheme 138 — B3LYP/6-31G(d) ΔG^‡ for hydride transfer to chiral sugar by achiral catalyst

Further calculations of a mismatched chiral catalyst (which would favor the S product) and the α-ketoester (which favors the R product) show that induction by the catalyst dominates, yielding the S product, which is opposite to that which would have been predicted by Corey‘s model (Scheme 139).

Scheme 139 — B3LYP/6-31G(d) ΔG^‡ for hydride transfer from mismatched catalyst to α-ketoester

4.4.3. Alkynylation

Li and co-workers performed a two-part DFT investigation on the oxazaborolidine catalyzed alkynylation of aldehydes (Scheme 140).^244,245

As in the carbonyl reductions, the aldehyde can potentially bind to the catalyst-alkynylborane adduct in four possible geometries—exo-anti, exo-syn, endo-anti, or endo-syn—leading to either the R- or S-alcohol product (Scheme 141). Binding of the aldehyde to the catalyst-alkynylborane complex is exothermic for three out of four complexes, with the exo/anti geometry being the most stable adduct. Mulliken charge measurements and an NBO analysis show charge transfer from the carbonyl to alkynyl moiety upon complexation. The lowest energy adduct, exo-anti, has the largest stabilization interaction energy among the four complexes (23.1 versus 13.6, 18.9, and 21.2 kcal/mol).

Scheme 141 — Binding energies of ethanal with catalyst-borane complexes

The alkyne transfer transition state was calculated to be that of the rate-determining step of the catalytic cycle. The exo-anti transition state is the lowest energy geometry for the alkyne transfer, forming a six-membered twist chair transition state (Figure 100). An NBO analysis of these transition structures showed that the breaking B-C bond is weakest and the forming C-C interaction is strongest in the exo-anti conformation compared to the other geometries, facilitating the transfer of the alkyne moiety the most in this transition state. The calculated activation energies for the exo-syn, endo-anti, and endo-syn are 11.4, 11.7, and 11.3 kcal/mol, respectively.

B3LYP/6-31G(d) optimized transition state of lowest energy alkyne transfer (*exo-anti*).

4.4.4. Diels-Alder cycloaddition

Li investigated the cationic oxazaborolidine catalyzed Diels-Alder reaction developed by Corey‘s group (Scheme 142).²⁴⁶ B3LYP/6-31G(d) was applied to all proline ring hydrogens. B3LYP/6-31G(d, p) was applied to all other atoms. Model calculations of both the uncatalyzed and catalyzed reactions (Scheme 143) show that the exo/s-cis pathway is preferred, yielding the S product. The authors concluded that the uncatalyzed reaction is concerted, but the catalyzed reaction is stepwise, with the rate-determining step being addition of the catalyst-methylacrolein complex to cyclopentadiene to form a zwitterionic intermediate.

Scheme 143 — Uncatalyzed and catalyzed Diels-Alder cycloaddition between cyclopentadiene and 2- methylacrolein

More recently, Paddon-Row and co-workers investigated the same class of reactions in order to explain the origins of enantioselectivity proposed by Corey (Scheme 144).²⁴⁷ Key features of Corey‘s models include: (1) a preferred s-trans C=C-C=O conformation of the dienophile, (2) πstacking between the dienophile and the exo-phenyl group at C-5 of the catalyst, and (3) catalyst binding to the oxygen anti lone pair (with respect to the double bond) and formyl hydrogen in the case of aldehydes, versus catalyst binding to the syn oxygen lone pair and α-hydrogen of ketones, esters, and carboxylic acids. These different binding modes expose opposite faces of the dienophile and explain the opposite enantioselectivities observed experimentally.

Scheme 144 — Corey‘s pre-transition state models for the oxazaborolidine-catalyzed Diels-Alder cycloaddition reaction

MPW1K/6-31+G(d, p)//B3LYP/6-31G(d) calculations for seven catalyzed cycloadditions are in qualitative agreement with experimentally observed selectivities (Table 18) and agree with Corey‘s pre-transition state models. An alternative coordination mode for ester dienophiles that does not involve a CH···O bond was found, which was calculated to be significantly favored over the Corey model (Figure 101). In the new model, binding of the anti lone pair of the tethering carbonyl oxygen is predicted to be favored due to relief of repulsion interactions with the alkoxy oxygen center. Such a stabilization does not occur when the syn lone pair of the methyl ester carbonyl is bound to the catalyst.

Table 18.

Predicted^a and experimental % ee values

Entry	Calculated % ee	Experimental % ee
1	85	70
2	77	88
3	94	90
4	36	80
5	87	93^b
6	82	53
7	96	86

Open in a new tab

^a

MPW1K/6-31+G(d, p)//B3LYP/6-31G(d) + B3LYP/6-31G(d) thermal corrections and nonspecific solvent effects (dichloromethane) using the PCM model. Values were calculated at 298.15K. The modeled catalyst differs from the experimental catalyst only by substitution of the o-tolyl group with a phenyl group.

^b

The –CO₂CH₂CF₃ group was used experimentally.

Relative free energies for *s-cis* C=C-C=O versus *s-trans* C=C-C=O ester-activated Diels-Alder cycloaddition.

The same group then reinvestigated the reaction computed by Li in order to determine if the aldehyde does indeed bind to the catalyst in an s-cis conformation, which is at odds with Corey‘s model.²⁴⁸ Two major changes were made in the latter investigation, the first being that the enantiomeric ratio was determined by the activation free energies of the cycloaddition, rather than on the stabilities of the catalyst-carbonyl complexes. This modification is valid because it had been shown that complexation is rapidly reversible on the NMR timescale.²⁴⁹ Second, it was argued that the model catalyst was oversimplified because π-stacking of one of the C-5 phenyl groups plays a role in the stereochemical outcome of the reaction. Thus, the experimental catalyst was employed in the calculations, with the only change being the replacement of the o-tolyl group with a phenyl group.

The reactions of five dienophiles with 1,3-butadiene were calculated using B3LYP/6-31G(d). All possible coordination modes and conformations were considered. As shown in Table 19, the predicted enantioselectivites are in excellent agreement with experimentally observed results. The poor selectivity predicted in entry 5 is attributed to the modeling of both the bulky 2-tert-butyl-1,4-benzoquinone and 2-triisopropylsilyloxy-1,3-butadiene with simpler 2-methyl-1,4-benzoquinone and 1,3-butadiene, respectively. In four out of five cases, the computational results reinforce Corey‘s model of stereoselectivity. It was also found that the minor enantiomer is largely formed through a coordination of the dienophile to the concave (endo) face of the catalyst, and thus catalyst designs that favor this mode of binding should enhance selectivities.

Table 19.

Computed^a and experimental Diels-Alder cycloaddition selectivities

entry	Calculated er	Experimental er
1	92.4:7.6	98.5:1.5^b
2	84:16	84.5:15.5^c
3	96.8:3.2	97.5:2.5^d
4	94.7:5.3	96.5:3.5^e
5	68.6:31.4	95.5:4.5^f

Open in a new tab

^a

diene = 1,3-butadiene.

^b

experimental diene = 2-methyl-1,3-butadiene.

^c

experimental diene = cyclopentadiene.

^d

experimental dienophile = 2,2,2-trifluoroethyl acrylate.

^e

experimental dienophile = E-diethyl maleate.

^f

experimental diene = 2-triisopropylsilyloxy-1,3-butadiene, dienophile = 2-tert-butyl-1,4-benzoquinone.

4.4.5. Diels-Alder cycloaddition catalyzed by N-sulfonylated oxazaborolidines

Several groups have reported ab initio and DFT investigations^250,251 of the coordination of aldehydes to model N-sulfonylated oxazaborolidines catalysts in the asymmetric Diels-Alder cycloaddition reactions of α, β-unsaturated aldehydes with simple dienes²⁵² and in Mukaiyama aldol reactions (Figure 102).^253,254 It was consistently found that the two lowest-energy coordination modes involve a binding of the aldehyde to the “top” face of the catalyst.

Favored binding modes of aldehydes with N-sulfonylated oxazaborolidine catalysts.

Wong explored the full (S)-tryptophan-derived catalyst using DFT methods to explain the role of the tryptophan moiety of the reaction (Scheme 145).²⁵⁵

Corey had attributed the remarkable selectivities of the Diels-Alder cycloaddition to three stabilizing interactions (Scheme 146): (1) donor-acceptor interaction between the endocyclic boron of the catalyst and the carbonyl oxygen of acrolein, (2) H-bond between the formyl hydrogen of acrolein and the ring oxygen of the catalyst, and (3) π-stacking between the tryptophan and acrolein groups.

Wong proposed the same type of stabilizing interactions, but with modifications: the acrolein can adopt an s-cis or s-trans conformation, and the formyl hydrogen can bond with either the ring oxygen (as Corey had proposed) or a sulfonyl oxygen. This gives rise to four possible complexes. MP2/6-31G(d)//PW91PW91/6-31G(d)+ZPE calculations show that the most stable complex has an s-trans acrolein geometry, and the aldehyde hydrogen binds to the sulfonyl oxygen (Figure 103). The binding energy is 6.9 kcal/mol. The other complexes are at least 3.8 kcal/mol higher in energy. The acrolein and tryptophan moities are separated by 3.15 Å, indicative of a π-stacking interaction. An NBO analysis showed a strong decrease of electron population in the indole moiety by 0.13–0.16 e, indicating that the indole group acts as a π donor.

PW91PW91/6-31G(d) optimized bromoacrolein-catalyst complex.

Calculations show that the binding of s-trans bromoacrolein to a model catalyst is selective for the sulfonyl oxygen mode over the ring oxygen mode by 2.3 kcal/mol (Figure 104). A similar selectivity of 1.4 kcal/mol is predicted for s-cis-bromoacrolein. In addition, s-trans-bromoacrolein has a larger binding energy with indole than s-cis-bromoacrolein (Figure 105). Both the strong CH^···O=S interaction and trans-acrolein^···tryptophan π–π stacking interactions explain the excellent experimental enantioselectivities.

Binding energies (MP2/6-31+G(d)//PW91PW91/6-31G(d)+ZPE) of s-*trans-*2-bromoacrolein-N-sulfonylated 1,3,2-oxazaborolidine-5-one complexes.

Binding energies (MP2/6-31+G(d)//PW91PW91/6-31G(d)+ZPE) of s-*trans-* and s-*cis-*2-bromoacrolein-N-sulfonylated 1,3,2-oxazaborolidine-5-one complexes.

5. Bifunctional catalysis

5.1. Thioureas

5.1.1. Michael addition of ketones to nitroalkenes

Three groups have reported theoretical studies of thiourea-based asymmetric Michael addition reactions.²⁵⁶ The first report, by Tsogoeva and Schmatz, investigates a thiourea/cyclohexanediamine catalyst, in which the amine moiety enhances the nucleophilicity of the ketone by enamine formation, and the thiourea moiety enhances the electrophilicity of the nitro-olefin through hydrogen bonding (Scheme 147).²⁵⁷

Scheme 147 — Conjugate addition of acetone to nitro-olefins

While it had been proposed by Takemoto and accepted by most groups that both oxygens of the nitro moiety are involved in H-bonding with the thiourea (Figure 106),²⁵⁸ Tsogoeva and Schmatz found that the doubly bonded transition state is less stable than the singly bonded transition state by 1.3 kcal/mol at the B3LYP/6-31G+(d, p) level. Inclusion of zero-point and thermal corrections reverses this stability (the doubly bonded structure is 1.5 kcal/mol more stable), but it was reasoned that this structure cannot undergo Michael addition for steric reasons.

Transition state geometries and relative energies calculated by Tsogoeva and Schmatz are shown in Figure 107. DFT calculations at various basis sets show a preference for the R transition state, which leads to the formation of the major product. This is attributed to a tighter H-bonding interaction between the thiourea and nitro-olefin, as seen in the transition H-bond distances, and repulsive electrostatic interactions between the phenyl and oxygen in the minor S transition state.

Transition structures of the formation of the R and the S enantiomeric products.

5.1.2. Michael addition of 1,3-dicarbonyls to nitroalkenes

Pápai and co-workers pursued a DFT investigation of the organocatalyzed Michael addition of 1,3-dicarbonyls to nitroolefins (Scheme 148).^256b

Of the five lowest-energy catalyst conformations, only one conformation was found to favor a double H-bond coordination with either the nitro-olefin (proposed by Takemoto) or the dicarbonyl (Figure 108). The binding energies of the nitro-olefin (R²=Ph) and dicarbonyl (R¹ = Me) with the catalyst are 7.6 and 7.3 kcal/mol, respectively, implying no preference for formation of either complex. Both possible routes leading to the experimentally observed major R enantiomer were thus explored (Scheme 149).

Most stable catalyst-nitro-olefin complex and most stable catalyst-dicarbonyl complex.

Scheme 149 — Two reaction routes envisioned for the catalyzed Michael addition of acetylacetone to nitrostyrene

The conjugate addition transition structures leading to the major R enantiomer for pathways (A) and (B) are given in Figure 109. The conjugate addition activation barrier (gas phase, B3LYP/6-311++G(d, p)) with respect to separated reactants for the catalyst-dicarbonyl complex pathway (B) was calculated to be only 2.2 kcal/mol, while the barrier for the catalyst-nitro-olefin complex pathway (A) was found to be 4.9 kcal/mol. In both pathways, transition structures leading to the minor S enantiomer is less stable than those of the R enantiomer (2.6 and 2.4 kcal/mol for the former and latter pathways, respectively). The instability of the S transition structure is due to eclipsing in the C-C forming bonds, unlike the R transition sstructures, in which the forming bonds are staggered.

Michael addition transition structures for major (R) pathways A and B.

Chen and co-workers investigated similar thiourea bifunctional catalysts that contain both a chiral center and chiral axis (Scheme 150).²⁵⁹ The bis-3,5-trifluoromethylphenyl group was replaced by hydrogen. A total of four pathways—both enantiomers of each catalyst—were calculated using B3LYP/6-311++G(d, p)//B3LYP/6-31G(d). The calculations show that the stereocenter is established at the C–C bond forming step, but subsequent proton transfer is the rate-determining step. The activation energies for these steps with respect to each catalyst-substrate complex are given in Table 20.

Table 20.

B3LYP/6-311++G(d, p)//B3LYP/6-31G(d) transition state energies with respect to initial catalyst-substrate complexes^a


TS	Catalyst	product configuration	E_act (kcal/mol)
TS-CC	A	S	10.4
TS-CC	A	R	12.0
TS-CC	B	S	14.7
TS-CC	B	R	13.4
TS-PT	A	S	17.6
TS-PT	A	R	20.3
TS-PT	B	S	26.0
TS-PT	B	R	16.3

Open in a new tab

^a

Bold numbers represent favored enantiomer of each step.

All of the calculated energies agree with experimental stereoselectivities. C-C bond formation (TS-CC) and proton transfer (TS-PT) by catalyst A favor the S-enantiomer over the R-enantiomer by 1.6 kcal/mol and 2.7 kcal/mol, respectively. Likewise, C-C bond formation and proton transfer by catalyst B favor the R-enantiomer over the S-enantiomer by 1.3 kcal/mol and 9.7 kcal/mol, respectively.

The enantioselectivities were rationalized by changes in the catalyst dihedral angles in going from the ground state to the transition states (Table 21). Dihedral angle N1-C2-N3-C4 of catalyst A, which favors the S-product, changes by 7° in the S-transition state, as opposed to 15° in the minor R- transition state. The same dihedral angle of catalyst B, which favors the R-product, changes by 14° in the R-transition state, as opposed to 21° in the minor S-transition state. The authors conclude that the enantioselectivity depends on a geometrical match or mismatch of the catalyst‘s axis of chirality with the center of chirality.

Table 21.

Dihedral angle (N1-C2-N3-C4) change in TS-CC with respect to ground state


Catalyst	Product configuration	Δ(N1-C2-N3-C4)
A	S	7
A	R	15
B	S	21
B	R	14

Open in a new tab

Zhong and co-workers recently developed a highly enantioselective domino Michael-Henry reaction catalyzed by a cinchona alkaloid derived thiourea catalyst to furnish highly functionalized bicyclo[3.2.1]octanes with four stereogenic centers (Scheme 151).²⁶⁰ The B3LYP/6-31G(d) calculations revealed a new catalytic activation mode for the thiourea catalyst (Figure 110). Unlike the previously proposed “dual activation model” by Takemoto,²⁵⁸ this mode shows activation of the 1,3-dicarbonyl substrates by the thiourea group and an acidic proton in the phenyl ring, and at the same time tertiary amine activation of the nitro group, which promotes the domino reaction with excellent stereoselectivity. The lowest energy transition structure, shown in Figure 110, favors the formation of the (R, S)-enantiomer compared to the (S, R)-enantiomer by 5.7 kcal/mol.

Scheme 151 — Organocatalytic domino Michael-Henry reactons of trisubstituted carbon nucleophiles and *trans*-β-nitrosytyrene

Lowest energy Michael addition transition structure and proposed activation mode of the catalyst and the substrate.

5.1.3 Michael addition of α-aryl and α-alkyl cyanoacetates to vinyl ketones

Chen and co-workers explored the thiourea catalyzed Michael addition of α-aryl and α-alkyl cyanoacetates to vinyl ketones (Scheme 152).²⁶¹

The major S enantiomer is produced by a re-face attack of the Z-enolate of the cyanoacetate (Figure 111, top), while the undesired R enantiomer is produced by a si-face attack of the E-enolate of the cyanoacetate. (Figure 111, bottom). The R enantiomer is believed to be disfavored because of steric clashing between the vinyl ketone and cyanoacetate alkyl/aryl groups.

Possible intermediates in the Michael addition of α-2-fluorophenyl cyanoacetate to phenyl vinyl ketone. Top: *Re-*face attack, yielding the major (S)-enantiomer. Bottom: *Si-*face attack, yielding the minor (R)-enantiomer.

5.1.4. Michael addition of 1,3-dicarbonyls to azodicarboxylates (α-amination)

Liu and co-workers investigated the enantioselective α-amination of 1,3-dicarbonyl compounds to azodicarboxylates catalyzed by a bifunctional urea (Scheme 153).²⁶²

Scheme 153 — Bifunctional urea catalyzed α-amination

All possible pathways—both re-face (major) and si-face (minor) attack of the dicarbonyl via (1) binding of the dicarbonyl to the urea moiety and the azodicarboxylate to the protonated tertiary amine, and (2) binding of the azodicarboxylate to the urea moiety and the dicarbonyl to the tertiary amine—were considered. The calculated lowest energy transition structures leading to both enantiomeric products are in qualitative with experimental results (Figure 112).²⁶³ The origin of enantioselection was not discussed.

Lowest energy B3LYP/6-311++G(d, p)//B3LYLP/6-31G(d) transition state energies for the enantiomeric products of the α-amination reaction.

Liu and co-workers used B3LYP/6-311++G(d, p)//B3LYP/6-31G(d) to explain the mechanism and stereoselectivity of α-amination reactions catalyzed by a urea-based bifunctional organocatalyst (Scheme 154).²⁶⁴ The dicarbonyl was modeled by 2-acetylcyclopentanone, the aromatic ring of the catalyst was replaced by hydrogen, and the tert-butyl carboxylates were replaced with methyl carboxylates. Two activation modes of the substrates were considered (Figure 113): in mechanism A, the urea moiety activates the dicarbonyl while the tertiary amine activates the azodicarboxylate; in mechanism B, the urea moiety activates the azodicarboxylate while the tertiary amine activates the dicarbonyl. Mechanism A is favored, with a rate-determining activation barrier of 2.7 kcal/mol. This step involves nucleophilic attack of the enolate to the azodicarboxylate. The corresponding activation barrier for mechanism B is 7.8 kcal/mol. An enantiomeric excess of >99% ee was calculated, which is in reasonable agreement with the experimental results.

Scheme 154 — α-amination reaction reported by Takemoto

Activation modes for the α-amination reaction.

5.1.5. Michael addition of amines to αβ-unsaturated compounds

Aminoindanol-derived thioureas are shown to catalyze the addition of hydroxylamines to pyrazole crotonate derivatives yielding β-aminoacids with high enantioselectivities.²⁶⁵ Simón and Goodman studied the mechanism of the reaction with quantum mechanical methods in order to elucidate the role of the catalyst.²⁶⁶ Geometry optimizations were performed with the B3LYP/6-31G(d, p) in toluene using the implicit PCM solvation model and UFF cavity scheme. Energies were further refined with single point energy calculations at the MPWB1K/6-31G(d, p) level with solvent included implicitly by PCM model and UAKS cavity definition. Two possible pathways were explored using a simplified model of the catalyst (Figure 114). Mechanism A explains the stereochemical outcome of the reaction as a consequence of a H-bond between the hydroxyl group of the chiral catalyst and the oxygen in the nucleophile (Figure 114a). In mechanism B, the catalyst takes active part in proton transfer by a proton switch mechanism (Figure 114b), rather than simply stabilizing the anions via a H-bond network.

Proposed mechanisms for the conjugate addition of amines to pyrazole crotonates and corresponding transition structures calculated with a simplified model catalyst.

The calculations with the model hydroxy-thiourea catalyst showed that the transition states corresponding to mechanism B are 3–4 kcal/mol lower in energy than the transition structures located for mechanism A. Hybrid QM/MM ONIOM calculations on mechanism B with the real catalyst resulted in 1.6 kcal/mol energy difference between the enantiomeric transition states favoring the (S) enantiomer, in agreement with the experiments.

5.1.6. Enolization

Computational methods were used to design a bifunctional thiourea catalyst that accelerates enolization in non-H-bonding organic solvents such as dichloromethane.²⁶⁷ The catalyst incorporates both a basic amine for deprotonation and hydrogen donors to stabilize the forming enolate. Based on HF/6-31+G(d) transition states of the urea and methanol catalyzed enolization, 3D structural databases were searched by the computer program CAVEAT. A cyclohexenone was identified as an appropriate linker between the urea and amine moieties (Scheme 156). After further design and functionalization, a linear thiourea/amine was synthesized and accelerated the enolization five-fold. This work demonstrates the promise of using computational methods as a foundation for catalyst design.

Scheme 156 — Design of bifunctional catalyst

5.1.7. Alcoholysis of cyclic anhydrides

Chen reported highly enantioselective alcoholysis of meso-cyclic anhydrides by a bifunctional thiourea catalyst (Scheme 157).²⁶⁸ B3LYP/6-31G(d) calculations show that the transition state model leading to the major enantiomer (Figure 115) is 7.0 kcal/mol lower in energy than the complex leading to the minor isomer. The transition state is stabilized by hydrogen bonding interactions between a thiourea hydrogen and the developing alkoxide, and the amine with the adding alcohol.

Transition state model for major enantiomer in the thiourea catalyzed alcoholysis of a *meso-*anhydride.

5.1.8. Ring-opening polymerization

Zhang and co-workers investigated the ring-opening polymerization of D-lactide by a bifunctional thiourea organocatalyst (Scheme 158).²⁶⁹ Both a concerted and stepwise mechanism were calculated using B3LYP/6-311++G(d, p) (PCM, CH₂Cl₂)//B3LYP/6-31G(d) (Scheme 159). In both cases, the rate-determining step were calculated to be very high—at least 37 kcal/mol with respect to separated reactants—suggesting that the uncatalyzed reaction is energetically unfeasible.

Scheme 159 — Relative energies for the uncatalyzed reaction

The concerted and stepwise mechanisms of the catalyzed reaction were then calculated. Unlike the uncatalyzed reaction, the stepwise pathway is favored over the concerted, with transition state energies of 11.5 kcal/mol and 32.1 kcal/mol, respectively, with respect to separated reactants (25.8 kcal/mol and 46.4 kcal/mol, respectively, with respect to the catalyst-methanol-D-lactide complex). A sketch of the rate-determining transition structure for the stepwise mechanism is shown in Figure 116. The catalyst activates the lactide for ring-opening by three hydrogen bond interactions. A covalent binding mechanism involving acyl transfer to the catalyst was also calculated, but this pathway is higher in energy.

Rate-determining transition structure for the stepwise ring-opening of D-lactide catalyzed by a bifunctional thiourea.

5.2 Guanidines

Guanidinium and amidinium cation catalysts have successfully promoted highly enantioselective C-C bond forming reactions, first pioneered by Corey in the Strecker reaction.²⁷⁰ Numerous applications have followed, including in catalysis of the Diels-Alder reaction,²⁷¹ (aza)-Henry reaction,^272,273 amination of 1,3-dicarbonyl compounds,²⁷⁴ and ring-opening-metathesis polymerization.²⁷⁵

5.2.1. Strecker reaction

Han and co-workers used DFT (B3LYP/6-31G(d)) to investigate the mechanism of the bicyclic guanidine-catalyzed Strecker reaction (Scheme 160)²⁷⁶ because Corey had claimed that HCN does not react with N-benzhydrylbenzaldimine at 10°C and theoretical groups had confirmed a high energy barrier for this addition but a lower energy pathway for the HNC addition,^277,278 Han modeled and proposed two possible reaction pathways: HCN isomerizes to HNC, which adds to methanimine to yield aminonitrile (Pathway A, Scheme 161), or HCN adds to methanimine to afford aminoisoacetonitrile, which then isomerizes to aminonitrile (Pathway B).

Scheme 161 — Possible pathways for the guanidine-catalyzed Strecker reaction

The calculated free energy profile is shown in Figure 117. Pathway A (red) is lower in energy is lower in energy than pathway B (blue). Formation of aminoisoacetonitrile 51 is predicted to be unfavorable. A high energy transition structure for the isomerization of intermediate 49b to 49a was located. These calculations suggest that the Strecker reaction most likely proceeds through hydrogen isocyanide.

B3LYP/6-31G(d) free energy profile for the reaction of HCN or HNC with formylimine, catalyzed by 46, in toluene at 298.15K. Red = Pathway A. Blue = Pathway B.

5.2.2. Ring-opening polymerization

Rice and co-workers investigated two proposed mechanisms for the ring-opening polymerization of L-lactide using guanidine-based catalyst 1,5,7-triazabicyclo[4.4.0]dec-5-ene (TBD, Scheme 162). ²⁷⁹ Their mechanism was based on earlier calculations performed by Goodman on the ring-opening polymerization of lactones in the presence of TBD.²⁸⁰ The first mechanism involves both nucleophilic ring-opening of the lactide and proton donation to the opened alkoxide by the catalyst (“dual lactide activation”/”nucleophilic catalytic mechanism”), while the second mechanism involves hydrogen bond activation of both the lactide and alcohol nucleophile by the catalyst (“Lactide and alcohol H-bond activation”/”acid-base catalytic mechanism”). Geometries were optimized using MPW1K/6-31G+(d) with the CPCM model (dichloromethane). Single point calculations were carried out with MPW1K/aug-ccpVTZ.

Scheme 162 — Two proposed mechanisms for the organocatalyzed ring-opening polymerization of L-lactide

The reaction was initially modeled with guanidine as the catalyst. The first mechanism—ring-opening of the lactide prior to alcohol addition—was found to be significantly disfavored. The rate-determining step is the addition of the alcohol and the activation energy is 18.6 kcal/mol with respect to separated reactants (19.9 kcal/mol with respect to complexed starting materials). The second mechanism proceeds via a significantly lower-energy pathway. The rate-determining step is the addition of the alcohol to the lactone, with a barrier of only 6.0 kcal/mol with respect to separated reactants (13.3 kcal/mol with respect to complexed starting materials).

Having established the preferred mechanism, the rate-determining step of the hydrogen-bonded pathway was recalculated with the full experimental catalyst (TBD). This change resulted in a nearly barrierless reaction, with an activation energy of 0.3 kcal/mol with respect to separated reactants (7.9 kcal/mol with respect to complexed starting materials). This rate-determining step is shown in Figure 118.

Rate-determining transition structure for TBD-catalyzed ring-opening polymerization of L-lactide.

Similar to the results of Rice and co-workers in their earlier work on lactones, Simón and Goodman showed that the transition structures corresponding to acid-base catalytic pathway are energetically favored over the ones corresponding to the nucleophilic catalytic reaction by more than 7 kcal/mol in Gibbs free energy computed with B3LYP/6-311++G(d, p)(CH₂Cl₂)//B3LYP/6-31+G(d).²⁸⁰ However, a peculiar feature of the process is that the catalyst surprisingly failed to catalyze the ring-opening polymerization of the more reactive butyrolactone. Calculations showed that unlike the reactions of 5- and 6-ring lactones, Gibbs free energy barriers for nucleophilic addition of TBD to butyrolactone and methanol acid-base addition are within 1 kcal/mol, presumably due to the strain in the starting material favoring the former (Scheme 163). Nucleophilic addition of TBD to butyrolactone leads to the formation of a stable amide-like intermediate (1.3 kcal/mol), trapping the catalyst, as the energy barrier to form the product from this intermediate is very high (37.9 kcal/mol).

Scheme 163 — Competing reaction pathways in the ring-opening polymerization of butyrolactone catalyzed by TBD. B3LYP/6-311++G(d, p)//B3LYP/6-31+G(d) computed relative free energies are given in kcal/mol

5.2.3. Michael addition of 1,3-dicarbonyls to nitroalkenes

The Nájera group reported good enantioselectivities for the conjugate addition of 1,3-dicarbonyls to nitroalkenes catalyzed by a trans-cyclohexanediamine-benzimidazole catalyst in the presence of TFA (Scheme 164).²⁸¹ Two coordination modes of the catalyst—(1) the di-coordinated dicarbonyl nucleophile (Figure 119, top), and (2) the di-coordinated nitroalkene electrophile (Figure 119, bottom) —were calculated. The mechanism involving the coordinated nucleophile was calculated to be favored, in agreement with the activation mode reported by Pápai and co-workers for the cyclohexanediamine-thiourea-catalyzed Michael addition reaction.^256b The approximately 3 kcal/mol difference between the major R and minor S transition structures agrees well with the experimental enantioselectivities.

Scheme 164 — *Trans*-cyclohexanediamine-benzimidazole catalyzed conjugated addition reaction

B3LYP/6-311++G(d, p)//B3LYP/6-31G(d). Single-point values in a toluene model (IEF-PCM) in parentheses.

5.2.4. Acetonitrile hydrolysis

1,5,7-Triazabicyclo[4.4.0]dec-5-ene (TBD) has been shown by Sun and co-workers to be an effective catalyst for the hydrolysis of acetonitrile (Scheme 165).²⁸² The full mechanism of the uncatalyzed and catalyzed reactions were carried out with B3LYP/6-311++G(d, p) and MP2/6-311++G(d, p).²⁸³ The rate- determining step of the uncatalyzed reaction is the first step—addition of water to acetonitrile (Scheme 166). This barrier is extremely high, 58.3 kcal/mol and 64.7 kcal/mol using B3LYP and MP2, respectively, as expected for such four-center transition states.

Scheme 166 — Uncatalyzed acetonitrile hydrolysis; B3LYP/6-311++G(d, p) energies, MP2/6-311++G(d, p) values in italics; rate-determining step in bold

The catalyzed reaction was then calculated with B3LYP (Scheme 167). The activation energy for the first hydrolysis step (27.6 kcal/mol) is 30.7 kcal/mol lower in energy than that of the uncatalyzed reaction. Unlike the uncatalyzed reaction, the rate-determining step is the loss of ammonia after the second hydrolysis step (35.3 kcal/mol). This rate-limiting barrier is 23.0 kcal/mol lower in energy than the rate-limiting barrier of the catalyzed reaction. This difference would likely change if solvent effects were considered for these gas phase calculations. Nevertheless, the calculations show that TBD is effective in reducing the barrier for the hydrolysis reaction. The mechanism is similar to that of the TBD and methanol-catalyzed ring-opening polymerization (Scheme 162, bottom).

5.3. Proline Derivatives

5.3.1. Epoxidation

The asymmetric epoxidation of α, β-unsaturated ketones by tert-butyl hydroperoxide (TBHP) and β-amino alcohol catalysts have been studied by the Lattanzi and co-workers (Scheme 168).²⁸⁴ Catalyst screening and testing of reaction conditions let to the hypothesis that the catalyst plays a dual role in the reaction. The proposed mechanism is shown in Scheme 169. The catalyst deprotonates TBHP to form an ion pair, and the TBHP anion attacks the α, β-unsaturated ketone to generate an intermediate that is stabilized by the hydroxy group of the catalyst.

Scheme 168 — Diarylprolinol catalyzed asymmetric epoxidation

Scheme 169 — Mechanism for organocatalyzed epoxidation of α, β-unsaturated ketones by *tert-*butyl hydroperoxide

Two low-energy conformers were located for each cyclic catalyst—one in which the hydroxyl hydrogen is bonded to the cis hydrogen on the ammonium, and one in which the hydroxyl hydrogen is bonded to the trans hydrogen on the ammonium. In all three cases, the cis conformation is preferred, which the authors argue contributes to the experimentally observed enantioselectivities. The cis and trans conformers of the pyrrolidine catalyst are shown in Figure 120. The acyclic ammonium shows only a 0.6 kcal/mol energy difference for the two lowest energy conformers, which may explain the poor experimental selectivities.

B3LYP/6-31G(d) conformers and relative energies of protonated catalysts.

In order to better understand the structure of the ion pair and explain the experimental enantioselectivities, the protonated proline, azetidine, piperidine, and 2-methylpropylamine catalysts (Table 22) were studied using density functional theory (B3LYP/6-31G(d)).

Table 22.

Epoxidation of trans-chalcone


catalyst	% yield (exper.)	% ee (exper.)	E-trans –E-cis (calc., kcal/mol)
	93	89	0.9
	33	85	2.0
	48	75	0.3
	21	52	0.6

Open in a new tab

5.3.2. Transfer hydrogenation

Schreiner and co-workers used a proline-derived diamide catalyst to achieve moderate yields and enantioselectivities in the asymmetric transfer hydrogenation of ketimines with trichlorosilane (Scheme 170).²⁸⁵ B3PW91/cc-pVDZ was used to rationalized the mechanism and stereoselectivity. The aromatic groups of the ketimine were modeled by methyl groups, while the methyl group of the ketimine was modeled by a hydrogen. The adamantane group of the catalyst was replaced with hydrogen.

Scheme 170 — Organocatalyzed asymmetric transfer hydrogenation with trichlorosilane

The calculated activation enthalpy of the uncatalyzed reaction involving a four-center transition state is very high, 40.0 kcal/mol (Figure 121, top), while the calculated activation enthalpy of the catalyzed reaction is 19.1 kcal/mol (Figure 121, bottom). The role of the catalyst is to coordinate the trichlorosilane and serve as a proton donor to the imine. The high free energy barriers (59.7 and 47.1 kcal/mol for the uncatalyzed and catalyzed reactions, respectivitely) suggest that alternate mechanisms should be explored.

Uncatalyzed (left) and catalyzed (right) rate-determining transition structures for hydride transfer from trichlorosilane to N-methyl-methylaldimine.

5.4. Amine-amides

5.4.1. Aldol reaction

Recently Feng and co-workers introduced amino acids into the bispidine framework to catalyze the aldol and Michael addition reactions (Scheme 171).²⁸⁶ These reports represent the first effective use of bispidine as an organocatalytic core. The L-phenylalanine-derived bispidine catalyst proved to be extremely effective in catalyzing the aldol reaction between acetone and methylethylketone with α-ketophosphonates, α-ketoesters, and α, α-dialkoxyketones in up to 97% isolated yield and 97% ee. The size of the phosphonates and esters and electronic nature of the aromatic ketone has very little effect on yields and enantioselectivities.

Scheme 171 — Bispidine catalyzed aldol reaction

The transition states for the aldol addition between methyl benzoylformate and acetone were modeled theoretically. In agreement with experiment, the transition structure leading to the major R-product was calculated to be nearly 4 kcal/mol lower in energy than that of the minor product (Figure 122). The origin of enantioselectivity is attributed to a preferential conformation in both the major and minor transition states in which the phenyl group of the catalyst shields the si face of the enamine. The favored transition state shows a shorter distance between the protonated catalyst and the keto group compared to that of the disfavored transition state, indicating a stronger hydrogen bond interaction.

B3LYP/6-311G(d, p)//HF/6-31G(d) (IEFPCM, acetone) relative energies and distances for the calculated transition structures of the aldol reaction.

Feng and Hu achieved good yields and enantioselectivities in the secondary amine amide organocatalyzed asymmetric nitroaldol reaction of α-ketophosphonates (Scheme 172).²⁸⁷ The transition structures for the major (R) and minor (S) enantiomers were located using HF/3-21G(d) (Figure 123). A 3.7 kcal/mol energy difference was calculated for the two transition structures. The major transition structure benefits from stronger stabilizing hydrogen bond interactions compared to the minor transition structure. This is seen by a comparison of various hydrogen bond distances: the nitro group oxygens and piperidine hydrogen distances are 1.63 Å and 2.43 Å in the major transition state versus 1.67 Å and 2.77 Å in the minor transition state; and the carbonyl group of the ketophosphonate is separated from an amide hydrogen by 1.59 Å in the major transition state as opposed to 1.79 Å in the minor. However, the phosphonate oxygen of the minor transition state is significantly more stabilized compared to the major transition state, with O-H bond distances of 1.56 Å and 1.83 Å, respectively.

Scheme 172 — Asymmetric nitroaldol reaction of α-ketophosphonates

Major (R) and minor (S) transition structures for the nitroaldol reaction. (H-bonds were omitted from ChemDraw diagrams for clarity).

5.4.2. Michael addition of ketones to nitroalkenes

The L-4-fluorophenylglycine-derived bispidine catalyst was shown to be extremely effective for catalyzing the Michael addition of ketones to nitroolefins (Scheme 173).²⁸⁸ Electron-rich, electron- deficient, and fused aromatic rings have little effect on reactivity and selectivity.

Scheme 173 — Bispidine-catalyzed Michael addition reaction

The Michael addition of acetone to nitrostyrene catalyzed by L-phenylglycine derived bispidine was modeled computationally.²⁸⁸ For both the favored (re) and disfavored (si) faces of attack, two possible modes were considered (Figure 124). In mode A, TBBP participates in an intramolecular bond, freeing one hydroxyl group to protonate the catalyst, which activates the nitroalkene. In mode B, one hydrogen of TBBP protonates the catalyst, while the second hydrogen activates the nitroalkene. Mode A was calculated to be favored for the re and si transition structures by 4.7 and 4.3 kcal/mol, respectively.

Activation modes of the bispidine catalyzed Michael addition reaction.

The computational results show that re-face attack of the nitroolefin is favored by 2.2 kcal/mol (Figure 125). The selectivity is attributed to a stronger hydrogen bond between the protonated catalyst and nitroolefin in the favored transition structure, as indicated by the shorter distance.

B3LYP/6-311G(d, p)//HF/6-31G(d) (IEFPCM, acetone) relative energies and distances for the lowest-energy transition structures of the bispidine-catalyzed Michael addition of acetone to phenylstyrene.

5.5. Cinchona alkaloids

While cinchona alkaloids were described in Section 3.3, this current section focuses more specifically on cinchonas that appear to display a dual activating mode in organocatalysis.

5.5.1. Michael addition

The bifunctional cinchona catalyzed Michael addition of ketoesters and phenyl maleimide was studied by Cucinotta and Gervasio (Scheme 174).²⁸⁹ Molecular dynamics, ab initio methods, and quantum mechanical/molecular mechanic (QM/MM) approaches were used to investigate the mechanism. The catalytic cycle based on the calculations is shown in Scheme 175. Molecular dynamics and cluster analysis were used to locate the lowest energy binary (complex I) and ternary (complex II) complexes. Four ternary complexes were located that are within 2 kcal/mol of each other. These structures differ in the nature of the hydrogen bond interactions between the protonated quinuclidine, the catalyst hydroxyl group, and the ketoester anion. Activation energy calculations for C–C bond formation from each of these 4 complexes show that the complexation mode shown in Figure 126 is the most favored.

Scheme 175 — Catalytic cycle for Michael addition

QM/MM transition structures for C-C bond formation, with (left) and without (right) OH assistance.

The transition structures for C-C bond formation were located using QM/MM (nudged elastic band technique, NEB). The most favored transition state shown in Figure 126 (left), and gives the same major stereoisomer that was observed experimentally. The enolate is stabilized by the protonated quinuclidine, while the maleimide is stabilized by the hydroxyl group of the catalyst. A transition state that does not involve activation by the hydroxyl group was calculated to be nearly 10 kcal/mol higher in energy, which supports arguments for the bifunctional role of the catalyst. The rigid hydrogen bond network is responsible for the high diastereoselectivities.

Finally, B3LYP/6-311+G(d, p) calculations on a model system show that hydrogen bond donation to the maleimide significantly lowers the energy of the transition state for C-C bond formation (Figure 127).

B3LYP/6-311+G(d, p) activation energies for Michael addition, with and without methanol assistance.

5.5.2. Alcohol Desymmetrization

Chin and Song developed a sulfonamide-based cinchona alkaloid bifunctional catalyst to effect the desymmetrization of meso- anhydrides in excellent yields and enantioselectivities (Scheme 176).²⁹⁰ Analogs of the enantiomeric transition states for five experimental substrates were modeled using B3LYP/6-31G(d).²⁹¹ All calculations show a stabilization of the developing alkoxide by the sulfonamide hydrogen and the quinuclidine nitrogen acting as a general base in accepting the methanol hydrogen (Figure 128). While no explanation was given for the origin of stereoselectivity, the calculated relative energies of the enantiomers do agree with the experimental results.

Scheme 176 — Bifunctional catalysis of *meso-*cyclic anhydride desymmetrization

Transition state model for bifunctional cinchona alkaloid catalyzed desymmetrization of cyclic *meso*-anhydride.

5.5.3. [1,3]-rearrangements

Cinchona derivatives catalyze [1,3]-sigmatropic O- to N- rearrangements of allylic trichloroacetimidates to give the corresponding trichloroacetamides via a two-step S_N2′ mechanism (Scheme 177).^292,293 Houk and co-workers used M05-2X/6-31+G(d, p)(CPCM-toluene)//B3LYP/6-31G(d) calculations to show that the availability of H-bonding interaction between the catalyst and the substrate determines the fast reacting enantiomer and the stereochemical outcome of the reaction (Figure 129). ²⁹³

Scheme 177 — Mechanim of cinchona catalyzed [1,3]-shifts of allylic trichloroacetimidates

Enantiomeric transition structures and their activation free energies (ΔG, kcal/mol) for the addition of the catalyst to trichloroacetimidate.

5.6. Dipeptides

5.6.1. Hydrocyanation

In 1981, Inoue and co-workers reported the enantioselective hydrocyanation of aldehydes employing a cyclic dipeptide catalyst cyclo[(R)-His-(R)-Phe] or cyclo[(S)-His-(S)-Phe] (Scheme 178).²⁹⁴ This catalyst was designed to be a small molecule alternative to the enzyme hydroxynitrilase lyase (oxynitrilase) that catalyzes the identical reaction. Highest enantioselectivity is observed under heterogeneous (gel) reaction conditions. In methanol no enantioselectivity is observed. Furthermore, asymmetric autoinduction was reported.²⁹⁵

Scheme 178 — Dipeptide-catalyzed aldehyde hydrocyanation

DFT and MP2 methods, molecular mechanics, and molecular dynamics were used to elucidate the mechanism and origin of stereoselectivity and autoinduction. The active catalytic species was shown to be a dimer, with activation by the imidazole rather than the dipeptide moiety. This is consistent with experiments in which second order rate dependence with respect to the catalyst concentration was found.²⁹⁶ Dynamic studies in the gas-phase and non-polar solvent show that the dimer is stable; in contrast, simulation in MeOH showed dissociation of the dimer, consistent with loss of stereoselectivity observed experimentally. The key step involves delivery of the nucleophile and stabilization of the developing negative charge by imidazole groups in the transition state (Figure 130). DFT and MP2 results suggest that extended edge-to-face π-interaction between the catalyst dimers and substrates are critical for catalysis and selectivities.

Model transition state for enantioselective autoinduction.

5.7. Brønsted Acids

5.7.1. Additions of phenols and protected amines to olefins

In 2006, He and co-workers demonstrated that trifluoromethanesulfonicacid (TfOH) can effectively catalyze additions of phenols and amides to alkenes (Scheme 179), which complement the commonly applied methods involving transition-metal or main-group metal catalysts.²⁹⁷ Yu and co-workers used B3LYP/6-31G(d) calculations to gain insight into the mechanism of catalysis of these reactions.²⁹⁸ They found that TfOH activates the nucleophilic additions through a concerted but highly asynchronous eight-membered-ring transition state. The computed activation free energy for the addition of phenol to cyclohexene is 29.4 kcal/mol relative to the separated reactants. The methoxy substituent decreases this barrier to 27.3 kcal/mol, whereas the nitro substituent causes an increase in the activation free energy by 2.4 kcal/mol. The addition of tosylamide to cyclohexene is found to have a higher activation free energy compared to that of phenols (35.8). The authors also showed that the double-bond migration can compete with the addition reaction. The relative reactivities of the phenols towards addition determine the extent of these two competitive processes.

Scheme 179 — TfOH-catalyzed addition of phenols and amides to alkenes

6. Epoxidation by Dioxiranes

The enantioselective direct oxidation of alkenes is a highly exploited method to access enantioenriched epoxides. The in situ formation of a chiral dioxirane from a ketone and Oxone (potassium peroxymonosulfate), which can then undertake the epoxidation of alkenes, is especially effective. The epoxidation mechanism involving dioxiranes has been studied numerous times computationally. To account for experimental results, a spiro transition state has been proposed. Earlier theoretical works on the epoxidation of alkenes by dioxirane have focused on simple models and have consistently supported the preference of a spiro transition state. ²⁹⁹

graphic file with name nihms307700u1.jpg

However, there has been some debate concerning the asynchronicity of epoxidation process, as different theoretical models have given different answer relating to the synchronicity of the reaction. MP2 and CASSCF calculations have favored highly asynchronous transition states, while B3LYP and several high-level ab initio have led to a more synchronous formation of the two C-O bonds. Bach and co-workers have concluded after a thorough study of the epoxidation of ethylene with dioxirane that the potential energy surface is very flat, and that the unsymmetrical transition state is slightly favored.^299e

Of particular interest here is the study concerning the stereoselectivity aspects of the epoxidation using dioxiranes. Houk and co-workers have studied computationally the stereoelectronic effects found in the alkene epoxidation using fluorinated dioxiranes.³⁰⁰ Using initially dioxirane derived from fluoroacetaldehyde, they found that the TS of epoxidation in which the fluoro substituent is anti to the dioxirane oxygen atom that is not transferred is the most favorable (Figure 132, TS17). This conformation minimizes electrostatic repulsion between the oxygen with the greater developing negative charge. A natural bond orbital analysis confirmed the electrostatic origin of this conformational preference, as there was no significant difference between bond orders for the forming and breaking bonds and the different TSs.

TSs for the epoxidation of ethane by methyldioxirane and fluoromethyldioxirane (B3LYP/6-31G(d)).

Both equatorial and axial oxygen transfer for the axial and equatorial fluoro substituents of 2-fluorocyclohexanone dioxirane were studied (Figure 133). TS20 and TS21 show both syn and anti oxygen transfer using the axial-2-fluorocyclohexanone dioxirane. The large energy difference between TS20 and TS21 originates from a stabilization of TS20 by 5.2 kcal/mol (compared to the cyclohexanone equivalent TS), due to the optimal position of the fluoro substituent anti to the oxygen, in order to minimize electrostatic interactions. Moreover, a weak F-H interaction is found in TS20. TS22 and TS23 are found to be both disfavored due to the electrostatic F-O repulsions. The axial-anti transfer (TS21) is found to be further disfavored due to the steric interactions between the alkene and the axial hydrogens of the cyclohexanone. The experimental results expressed in Scheme 180³⁰¹ could result from epoxidation with equatorial attack syn to the fluorine.

TSs for the epoxidation of ethane by 2-fluorocyclohexanone dioxirane (B3LYP/6-31G(d)).

Scheme 180 — Epoxidation of (E)-stilbene

The methodology developed by Shi and co-workers is also of particular interest in the field of enantioselective epoxidation using chiral dioxiranes. Their systems rely on chiral ketones derived from fructose (52 and 53), which are transformed into their dioxirane homolog through reaction with Oxone. The chiral dioxiranes then proceed to stereoselectively oxidize the unsymmetrical alkene. The original catalyst 52 was found to be more effective with trans-disubstituted and tri-substituted alkenes, while the oxazolidinone 53a has been found more recently to be effective with cis- and terminal alkenes.³⁰²

graphic file with name nihms307700u2.jpg

Singleton and co-workers have studied the process of enantioselection by Shi‘s catalysts computationally.³⁰³ They also measured experimental kinetic isotope effects (KIE) to compare with computed values for the different optimized transition structures. They initially calculated the epoxidation of trans-β-methylstyrene using a model dioxirane A and the dioxirane derived from catalyst 52. Epoxidation using the unhindered reagent 54 led to what they considered the “natural” asynchronicity conformation TS (Figure 134).

TS for the epoxidation of *trans*-β-methylstyrene using dioxirane 54.

Multiple TS conformations were found for the epoxidation using the chiral dioxirane derived from 52, some selected conformations are illustrated in Figure 135. However, calculation of the KIEs of these TSs and comparison to the experimentally observed values points to TS24 as the most realistic conformation. Interestingly, this conformation is found to be the most energetically favored and shows the most “natural” asynchronicity when compared with the transition structure found for A. The structure obtained is in accord with the model proposed by Shi. In contrast, TS25 shows divergence from the optimal asynchronicity, and some steric interaction between the styrene methyl and the axial pyran hydrogen. Morever, TS26, which lead to the minor enantiomer, is found to diverge widely from the ideal conformation, as it is not even truly in a spiro TS.

TSs for the epoxidation of *trans*-β-methylstyrene using dioxirane derived from catalyst 52.

They then proceeded to study the epoxidation of styrene using the dioxirane derived from catalyst 53b. In the case of styrene, four possible TSs are illustrated in Figure 136. The two lowest TSs leading to both enantiomers (TS27 and TS29) are both found to position the phenyl of the styrene on the same side as the oxazolidinone. The asynchronicity of the reaction, favoring a longer C-O forming bond on the side of the phenyl, thus then minimizes the interaction between the phenyl and oxazolidinone in TS27 and TS29. In contrast, shorter C-O bond on the alkene terminal carbon causes repulsive interactions with the latter and the oxazolidinone in TS28 and TS30. The calculated selectivity is in accord with the experimentally observed stereoselectivity.

TSs for the epoxidation of styrene using dioxirane derived from catalyst **53b**.

They then computed the epoxidation 1-phenyl-cyclohexene. This specific substrate is interesting due to the widely different selectivities observed depending of the catalyst used, as seen in Scheme 181. The authors did not report TSs using catalyst 52, as they supposed that a conformation similar to TS24 in Figure 135 would be greatly favored, and would explain the high selectivity. However, they reported the two lowest structures leading to both enantiomeric antipodes for the epoxidation using catalyst 53b (Figure 137). The energy difference found correlates well with the low stereoselectivity observed.

Scheme 181 — Selectivity of epoxidation of 1-phenyl-cyclohexene

TSs for the epoxidation of 1-phenyl-cyclohexene using dioxirane derived from catalyst **53b**.

They explain the small difference of energy between the two enantiomeric TSs by the fact that in TS32, the asynchronicity causes steric interactions of the alkene hydrogen with the oxazolidinone. Conversely, this asynchronicity minimizes the steric clash of the phenyl group in TS31 with the same oxazolidinone. It is worth noting that the phenyl group is rotated away from conjugation in TS31 by 28°, which seems to indicate that the conjugation of the phenyl group with the alkene is not important in order to stabilize the epoxidation process.

7. Conclusions and Outlook

The experimental study of organocatalysis has accelerated enormously since the writing of this review began, and the computational investigations of these reactions have increased in number and sophistication as well. As described in the introduction, B3LYP with modest basis sets continues to be used routinely for the study of organocatalysis, but deficiencies in this functional have been discovered. This is especially true for reaction thermochemistries and in cases where dispersion effects influence weak interactions between groups.⁶ Newer, more highly parameterized functionals such as Truhlar‘s M0X series, especially M06 -2X, and now M08 for organic reactions, are being used routinely. More accurate, but also more expensive methods, like SCS-MP2 and double hybrid functionals like B2PLYP are being used with increasing frequency. The role of dispersion is likely to be important in controlling stereoselectivities of many reactions, and the addition of dispersion corrections to density functionals is now highly recommended.^7e,o

While it is important to use intrinsically accurate methods, solvation energies also have an important role for energetics and selectivities, especially due to the fact that organocatalysis is always performed in the condensed phase. CPCM, SMD, and other continuum-based models are continually being improved, but still may have appreciable errors, especially for ions.^304,2i Caution must always be exercised in using solvation models, especially for predictions.

Finally, it has been shown by Singleton that dynamic effects may alter regioselectivities; his prime example involves hydroborations.³⁰⁵ While MD may be necessary to quantify selectivities, the cases where this is true generally involve reactions with very low activation barriers.

Computational modeling will continue to complement experimental investigations to provide understanding and new vistas of organocatalysis.

Transition states and activation free energies (ΔG, kcal/mol) relative to the separated reactants for the TfOH-catalyzed addition of phenols and tosylamide to cyclohexene.

Scheme 97 — Chiral sulfur ylide promoted asymmetric aziridination

Scheme 155 — Conjugate amine additions to pyrazole crotonate derivatives

Acknowledgments

We are grateful to the National Institute of General Medical Sciences, National Institutes of Health (GM 36700, K.N.H.); Novartis/ACS (J.M.U.); and NSERC PDF fellowship (C.Y.L.) for support of this work.

Biographies

graphic file with name nihms307700b1.gif

K. N. Houk received his Ph.D. at Harvard with R. B. Woodward. He has taught at Louisiana State University, the University of Pittsburgh, and UCLA since 1986. From 1988–1990, he was Director of the Chemistry Division of the National Science Foundation. He is the Saul Winstein Chair in Organic Chemistry at UCLA.

graphic file with name nihms307700b2.gif

Paul Ha-Yeon Cheong was born in 1979 in Taegu, Korea. In 2001 he received his A.B. degree from Bowdoin College. He did his Ph.D. research with K. N. Houk at UCLA, and collaborated with Paul Wender, Timothy Jamison, Gregory Fu, Carlos Barbas, and Dean Toste during that time and a postdoc afterwards. In 2009, he joined the faculty at Oregon State University.

graphic file with name nihms307700b3.gif

Claude Y. Legault received his B.Sc. in chemistry from Université de Sherbrooke (Canada) in 1999. He did his Ph.D. research as an NSERC and FQRNT scholar with Professor André B. Charette at Université de Montréal. He then worked under Professor K. N. Houk at UCLA as an NSERC postdoctoral fellow. In 2008, he joined the Department of Chemistry at Université de Sherbrooke.

graphic file with name nihms307700b4.gif

Joann M. Um received her B.A. in biochemistry at Columbia University in 1999 and an M.S. in chemistry at University of California, Berkeley in 2001. She spent four years as a synthetic organic chemist at both Merck Research Laboratories and Genentech, Inc. before coming to UCLA to complete Ph.D. studies in computational organic chemistry under Professor K. N. Houk.

graphic file with name nihms307700b5.gif

Nihan Çelebi-Ölçüm received her B.S. degree in chemistry at Bođaziçi University in 1997, and M.S. degree in computational and theoretical chemistry at Université Henri Poincaré (Nancy, France) in 1999. She completed her Ph.D. under the direction of Viktorya Aviyente at Bođaziçi University before joining the Houk group at UCLA as a postdoc in 2009.

References

1.(a) Koch W, Holthasuen MC. A Chemist’s Guide to Density Functional Theory. Wiley-VCH; Weinheim, Germany: 2001. [Google Scholar]; (b) Curtis LA, Raghavachari K, Redfern PC, Pople JA. J Chem Phys. 1997;(106):1063. [Google Scholar]
2.(a) Wheeler SE, Moran A, Pieniazek SN, Houk KN. J Phys Chem A. 2009;113:10376. doi: 10.1021/jp9058565. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Pieniazek SN, Clemente FR, Houk KN. Angew Chem, Int Ed. 2008;47:7746. doi: 10.1002/anie.200801843. [DOI] [PubMed] [Google Scholar]; (c) Ess DH, Houk KN. J Phys Chem A. 2005;109:9542. doi: 10.1021/jp052504v. [DOI] [PubMed] [Google Scholar]; (d) Guner V, Khuong KS, Leach AG, Lee PS, Bartberger MD, Houk KN. J Phys Chem A. 2003;107:11445. [Google Scholar]; (e) Wodrich MD, Cominboeuf C, Schreiner PR, Fokin AA, Schleyer PvR. Org Lett. 2007;9:1851. doi: 10.1021/ol070354w. [DOI] [PubMed] [Google Scholar]; (f) Jones GO, Guner VA, Houk KN. J Phys Chem A. 2006;110:1216. doi: 10.1021/jp052055z. [DOI] [PubMed] [Google Scholar]; (g) Izgorodina EI, Brittain DRB, Hodgson JL, Krenske EH, Lin CY, Namazian M, Coote ML. J Phys Chem A. 2007;111:10754. doi: 10.1021/jp075837w. [DOI] [PubMed] [Google Scholar]; (h) Dkhissi A, Ducéré JM, Blossey R, Pouchan C. J Comput Chem. 2009;30:1179. doi: 10.1002/jcc.21119. [DOI] [PubMed] [Google Scholar]; (i) Harvey JN. Faraday Discuss. 2010;145:487. [Google Scholar]
3.(a) Wodrich MD, Corminboeuf C, Schleyer PvR. Org Lett. 2006;8:3631. doi: 10.1021/ol061016i. [DOI] [PubMed] [Google Scholar]; (b) Wodrich MD, Wannere CS, Mo Y, Jarowski PD, Houk KN, Schleyer PvR. Chem Eur J. 2007;13:7731. doi: 10.1002/chem.200700602. [DOI] [PubMed] [Google Scholar]; (c) Grimme S, Steinmetz M, Korth M. J Chem Thoery Comput. 2006;3:42. doi: 10.1021/ct600224b. [DOI] [PubMed] [Google Scholar]; (d) Schreiner PR, Fokin AA, Pascal RA, de Meijere A. Org Lett. 2006;8:3635. doi: 10.1021/ol0610486. [DOI] [PubMed] [Google Scholar]; (e) Stefan G. Angew Chem, Int Ed. 2006;45:4460. [Google Scholar]; (g) Schreiner PR. Angew Chem, Int Ed. 2007;46:4217. doi: 10.1002/anie.200700386. [DOI] [PubMed] [Google Scholar]
4.Paul W, Timothy C. J Comput Chem. 2004;25:725. [Google Scholar]
5.(a) Grimme S, Steinmetz M, Korth M. J Org Chem. 2007;72:2118. doi: 10.1021/jo062446p. [DOI] [PubMed] [Google Scholar]; (b) Rokob TA, Hamza A, Papai I. Org Lett. 2007;9:4279. doi: 10.1021/ol701872z. [DOI] [PubMed] [Google Scholar]
6.(a) Zhao Y, Truhlar DG. J Chem Theory Comput. 2006;3:289. doi: 10.1021/ct6002719. [DOI] [PubMed] [Google Scholar]; (b) Zhao Y, Truhlar DG. J Chem Theory Comput. 2005;1:415. doi: 10.1021/ct049851d. [DOI] [PubMed] [Google Scholar]; (c) Zhao Y, Truhlar DG. Phys Chem Chem Phys. 2005;7:2701. doi: 10.1039/b507036h. [DOI] [PubMed] [Google Scholar]
7.(a) Zhao Y, Truhlar DG. Org Lett. 2006;8:5753. doi: 10.1021/ol062318n. [DOI] [PubMed] [Google Scholar]; (b) Zhao Y, Truhlar DG. J Phys Chem A. 2006;110:10478. doi: 10.1021/jp0630626. [DOI] [PubMed] [Google Scholar]; (c) Zhao Y, Truhlar DG. J Phys Chem A. 2004;108:6908. [Google Scholar]; (d) Schwabe T, Grimme S. Phys Chem Chem Phys. 2007;9:3397. doi: 10.1039/b704725h. [DOI] [PubMed] [Google Scholar]; (e) Schwabe T, Grimme S. Acc Chem Res. 2008;41:569. doi: 10.1021/ar700208h. [DOI] [PubMed] [Google Scholar]; (f) de Jong GT, Bickelhaupt FM. J Phys Chem A. 2005;109:9685. doi: 10.1021/jp053587i. [DOI] [PubMed] [Google Scholar]; (g) Izgorodina EI, Coote ML, Radom L. J Phys Chem A. 2005;109:7558. doi: 10.1021/jp052021r. [DOI] [PubMed] [Google Scholar]; (h) Quintal MM, Karton A, Iron MA, Boese AD, Martin JML. J Phys Chem A. 2006;110:709. doi: 10.1021/jp054449w. [DOI] [PubMed] [Google Scholar]; (i) Zhao Y, Gonzalez-Garcia N, Truhlar DG. J Phys Chem A. 2005;109:2012. doi: 10.1021/jp045141s. [DOI] [PubMed] [Google Scholar]; (j) Amin EA, Truhlar DG. J Chem Theory Comput. 2007;4:75. doi: 10.1021/ct700205n. [DOI] [PubMed] [Google Scholar]; (k) White BR, Wagner CR, Truhlar DG, Amin EA. J Chem Theory Comput. 2008;4:1718. doi: 10.1021/ct8000766. [DOI] [PMC free article] [PubMed] [Google Scholar]; (l) Zhao Y, Truhlar DG. J Phys Chem A. 2008;112:1095. doi: 10.1021/jp7109127. [DOI] [PubMed] [Google Scholar]; (m) Zhao Y, Truhlar DG. Acc Chem Res. 2008;41:157. doi: 10.1021/ar700111a. [DOI] [PubMed] [Google Scholar]; (n) Zhao Y, Truhlar DG. J Chem Theory Comput. 2009;5:324. doi: 10.1021/ct800386d. [DOI] [PubMed] [Google Scholar]; (o) Korth M, Grimme S. J Chem Theory Comput. 2009;5:993. doi: 10.1021/ct800511q. [DOI] [PubMed] [Google Scholar]; (p) Zheng J, Zhao Y, Truhlar DG. J Chem Theory Comput. 2006;3:569. doi: 10.1021/ct600281g. [DOI] [PubMed] [Google Scholar]; (q) Tishchenko O, Zheng J, Truhlar DG. J Chem Theory Comput. 2008;4:1208. doi: 10.1021/ct800077r. [DOI] [PubMed] [Google Scholar]; (r) Yang K, Zheng J, Zhao Y, Truhlar DG. J Chem Phys. 2010;132:164117. doi: 10.1063/1.3382342. [DOI] [PubMed] [Google Scholar]
8.Bahmanyar S, Houk KN, Martin HJ, List B. J Am Chem Soc. 2003;125:2475. doi: 10.1021/ja028812d. [DOI] [PubMed] [Google Scholar]
9.Simón L, Goodman JM. Org Biomol Chem. 2011;9:689. doi: 10.1039/c0ob00477d. [DOI] [PubMed] [Google Scholar]
10.(a) Hajos ZG, Parrish DR. 2102623. DE. 1971 Jul 29;; (b) Hajos AG, Parrish DR. J Org Chem. 1974;39:1615. [Google Scholar]
11.(a) Eder U, Sauer G, Wiechert R. 2014757. DE. 1971 Oct 7;; (b) Eder U, Sauer G, Wiechert R. Angew Chem, Int Ed Eng. 1971;10:496. [Google Scholar]
12.List B. Angew Chem Int Ed. 2010;49:1730. doi: 10.1002/anie.200906900.For earlier reviews, see: List B. Chem Rev. 2007;107:5413. doi: 10.1021/cr0684016.List B. Chem Commun. 2006:819. doi: 10.1039/b514296m.List B, Houk KN. Acc Chem Res. 2004;37:487. doi: 10.1021/ar0300571.List B. Adv Synth Catal. 2004;346:1021.
13.MacMillan DWC. Nature. 2008;455:304. doi: 10.1038/nature07367. [DOI] [PubMed] [Google Scholar]
14.Puchot C, Samuel O, Dunach E, Zhao S, Agami C, Kagan HB. J Am Chem Soc. 1986;108:2353. doi: 10.1021/ja00269a036. [DOI] [PubMed] [Google Scholar]
15.Jung ME. Tetrahedron. 1976;3:2, 3. [Google Scholar]
16.Clemente FR, Houk KN. Angew Chem Int Ed. 2004;43:5766. doi: 10.1002/anie.200460916. [DOI] [PubMed] [Google Scholar]
17.For a study on the accuracy of DFT in predicting thermochemistries of the aldol, Mannich, and a-aminoxylation reactions, see: Wheeler SE, Moran A, Pieniazek SN, Houk KN. J Phys Chem A. 2009;113:10376. doi: 10.1021/jp9058565.
18.Zhu H, Clemente FR, Houk KN, Meyer MP. J Am Chem Soc. 2009;131:1632. doi: 10.1021/ja806672y. [DOI] [PMC free article] [PubMed] [Google Scholar]
19.Bahmanyar S, Houk KN. J Am Chem Soc. 2001;123:12911. doi: 10.1021/ja011714s. [DOI] [PubMed] [Google Scholar]
20.Cheong PH-Y, Houk KN, Warrier JS, Hanessian S. Adv Synth Catal. 2004;346:1111. [Google Scholar]
21.Cheong PH-Y, Houk KN. Synthesis. 2005;9:1533. [Google Scholar]
22.Clemente FR, Houk KN. J Am Chem Soc. 2005;127:11294. doi: 10.1021/ja0507620. [DOI] [PubMed] [Google Scholar]
23.List B, Lerner RA, Barbas CF., III J Am Chem Soc. 2000;122:2395. [Google Scholar]
24.Patil MP, Sunoj RB. J Org Chem. 2007;72:8202. doi: 10.1021/jo071004q. [DOI] [PubMed] [Google Scholar]
25.Sharma AK, Sunoj RB. Angew Chem, Int Ed. 2010;49:6373. doi: 10.1002/anie.201001588. [DOI] [PubMed] [Google Scholar]
26.Rankin KN, Gauld JW, Boyd RJ. J Phys Chem A. 2002;106:5155. [Google Scholar]
27.Zotova N, Broadbelt LJ, Armstrong A, Blackmond DG. Bioorg Med Chem Lett. 2009;19:3934. doi: 10.1016/j.bmcl.2009.03.112. [DOI] [PubMed] [Google Scholar]
28.Schmid MB, Zeitler K, Gschwind RM. Angew Chem, Int Ed. 2010;49:4997. doi: 10.1002/anie.200906629. [DOI] [PubMed] [Google Scholar]
29.(a) Pihko PM, Laurikainen KM, Usano A, Nyberg AI, Kaavi JA. Tetrahedron. 2006;62:317. [Google Scholar]; (b) Hartikka A, Arvidsson PI. Eur J Org Chem. 2005:4287. [Google Scholar]; (c) List B, Hoang L, Martin HJ. Proc Natl Acad Sci USA. 2004;101:5839. doi: 10.1073/pnas.0307979101. [DOI] [PMC free article] [PubMed] [Google Scholar]; (d) de Arriba ÁLF, Simón L, Raposo C, Alcázar V, Morán JR. Tetrahedron. 2009;65:4841. [Google Scholar]; (e) Zotova N, Franzke A, Armstrong A, Blackmond D. J Am Chem Soc. 2007;129:15100. doi: 10.1021/ja0738881. [DOI] [PubMed] [Google Scholar]; (f) Iwamuara H, Mathew SP, Blackmond DG. J Am Chem Soc. 2004;126:11770. doi: 10.1021/ja046258x. [DOI] [PubMed] [Google Scholar]
30.Seebach D, Beck AK, Badine DM, Limbach M, Eschenmoser A, Treasurywala AM, Hobi R, Prikoszovich W, Linder B. Helv Chim Acta. 2007;90:425. [Google Scholar]
31.Blackmond DG, Moran A, Hughes M, Armstrong A. J Am Chem Soc. 2010;132:7598. doi: 10.1021/ja102718x. [DOI] [PubMed] [Google Scholar]
32.Zimmerman HE, Traxler MD. J Am Chem Soc. 1957;79:1920. [Google Scholar]
33.Hoang L, Bahmanyar S, Houk KN, List B. J Am Chem Soc. 2003;125:16. doi: 10.1021/ja028634o. [DOI] [PubMed] [Google Scholar]
34.Bachrach SM. Computational Organic Chemistry. Wiley; New York: 2007. [Google Scholar]
35.Arno M, Zaragoza RJ, Domingo LR. Tetrahedron: Asymmetry. 2005;16:2764. [Google Scholar]
36.(a) Tang Z, Jiang F, Yu TL, Cui X, Gong LZ, Mi AQ, Jiang YZ, Wu YD. J Am Chem Soc. 2003;125:5262. doi: 10.1021/ja034528q. [DOI] [PubMed] [Google Scholar]; (b) Tang Z, Jiang F, Cui X, Gong LZ, Mi AQ, Jiang YZ, Wu YD. Proc Nat Acad Sci. 2004;101:5755. doi: 10.1073/pnas.0307176101. [DOI] [PMC free article] [PubMed] [Google Scholar]
37.Xu X-Y, Tang Z, Wang Y-Z, Luo S-W, Cun L-F, Gong L-Z. J Org Chem. 2007;72:9905. doi: 10.1021/jo701868t. [DOI] [PubMed] [Google Scholar]
38.Chen X-H, Luo S-W, Tang Z, Cun L-F, Mi A-Q, Jiang Y-Z, Gong L-Z. Chem Eur J. 2007;13:689. doi: 10.1002/chem.200600801. [DOI] [PubMed] [Google Scholar]
39.Okuyama Y, Nakano H, Watanabe Y, Makabe M, Takeshita M, Uwai K, Kabuto C, Kwon E. Tet Lett. 2009;50:193. [Google Scholar]
40.Córdova A, Zou W, Ibrahem I, Reyes E, Engqvist M, Liao WW. Chem Commun. 2005:3586. doi: 10.1039/b507968n.Amedjkouh M. Tetrahedron: Asymmetry. 2005;16:1411.Dziedzic P, Zou W, Háfren J, Córdova A. Org Biomol Chem. 2006;4:38. doi: 10.1039/b515880j.Córdova A, Zou W, Dziedzic P, Ibrahem I, Reyes E, Xu Y. Chem Eur J. 2006;12:5383. doi: 10.1002/chem.200501639.Correction: Córdova A, Zou W, Dziedzic P, Ibrahem I, Reyes E, Xu Y. Chem Eur J. 2006;12:5175. doi: 10.1002/chem.200501639.Klussmann M, Iwamura H, Matthew SP, Wells DH, Jr, Pandya U, Armstrong A, Blackmond DG. Nature. 2006;441:621. doi: 10.1038/nature04780.
41.Bassan A, Zou W, Reyes E, Himo F, Córdova A. Angew Chem Int Ed. 2005;44:7028. doi: 10.1002/anie.200502388. [DOI] [PubMed] [Google Scholar]
42.Diner P, Amedjkouh M. Org Biomol Chem. 2006;4:2091. doi: 10.1039/b605091c. [DOI] [PubMed] [Google Scholar]
43.Dickerson TJ, Lovell T, Meijler MM, Noodleman L, Janda KD. J Org Chem. 2004;69:6603. doi: 10.1021/jo048894j. [DOI] [PubMed] [Google Scholar]
44.Zhang X, Houk KN. J Am Chem Soc. 2005;70:9712. [Google Scholar]
45.(a) List B. J Am Chem Soc. 2000;122:9336. [Google Scholar]; (b) List B, Pojarliev P, Biller WT, Martin HJ. J Am Chem Soc. 2002;124:827. doi: 10.1021/ja0174231. [DOI] [PubMed] [Google Scholar]; (c) Pojarliev P, Biller WT, Martin HJ, List B. Synlett. 2003:1903. [Google Scholar]; (d) Yang JW, Stadler M, List B. Angew Chem Int Ed. 2007;46:609. doi: 10.1002/anie.200603188. [DOI] [PubMed] [Google Scholar]
46.Bahmanyar S, Houk KN. Org Lett. 2003;5:1249. doi: 10.1021/ol034198e. [DOI] [PubMed] [Google Scholar]
47.Hayashi Y, Urushima T, Shoji M, Uchimaru T, Shiina I. Adv Synth Catal. 2005;347:1595. [Google Scholar]
48.Cheong PH-Y, Zhang H, Thayumanavan R, Tanaka F, Houk KN, Barbas CF., III Org Lett. 2006;8:811. doi: 10.1021/ol052861o. [DOI] [PMC free article] [PubMed] [Google Scholar]
49.Hayashi Y, Okano T, Itoh T, Urushima T, Ishhikawa H, Uchimaru T. Angew Chem Int Ed. 2008;47:9053. doi: 10.1002/anie.200802073. [DOI] [PubMed] [Google Scholar]
50.Wong CT. Tetrahedron. 2009;65:7491. [Google Scholar]
51.(a) Li H, Fu A, Shi H. J Mol Catal A: Chem. 2009;303:1. [Google Scholar]; (b) Zhuang W, Saaby S, Jørgensen KA. Angew Chem Int Ed. 2004;43:4476. doi: 10.1002/anie.200460158. [DOI] [PubMed] [Google Scholar]
52.Zhang H, Mitsumori S, Utsumi N, Imai M, Garcia-Delgado N, Mifsud M, Albertshofer K, Cheong PH-Y, Houk KN, Tanaka F, Barbas CF., III J Am Chem Soc. 2008;130:875. doi: 10.1021/ja074907+. [DOI] [PubMed] [Google Scholar]
53.Hayashi Y, Yamaguchi J, Hibino K, Shoji M. Tetrahedron Lett. 2003;44:8293. [Google Scholar]
54.Zhong G. Angew Chem Int Ed. 2003;42:4247. doi: 10.1002/anie.200352097. [DOI] [PubMed] [Google Scholar]
55.Brown SP, Brochu MP, Sinz CJ, MacMillan DWC. J Am Chem Soc. 2003;125:10808. doi: 10.1021/ja037096s. [DOI] [PubMed] [Google Scholar]
56.(a) Mathew SP, Iwamuara H, Blackmond DG. Angew Chem. 2004;116:3379. doi: 10.1002/anie.200453997. [DOI] [PubMed] [Google Scholar]; (b) Iwamura H, Wells DH, Mathew SP, Klussmann M, Armstrong A, Blackmond DG. J Am Chem Soc. 2004;126:16312. doi: 10.1021/ja0444177. [DOI] [PubMed] [Google Scholar]; (c) Mathew SP, Klussmann M, Iwamura H, Wells DH, Jr, Armstrong A, Blackmond DA. Chem Commun. 2006:4291. doi: 10.1039/b609926b. [DOI] [PubMed] [Google Scholar]
57.Zotova N, Moran A, Armstrong A, Blackmond DG. Adv Synth Catal. 2009;351:2765. and references therein. [Google Scholar]
58.(a) Córdova A, Sundén H, Bøgevig A, Johansson M, Himo F. Chem Eur J. 2004;10:3673. doi: 10.1002/chem.200400137. [DOI] [PubMed] [Google Scholar]; (b) Cheong PHY, Houk KN. J Am Chem Soc. 2004;126:13912. doi: 10.1021/ja0464746. [DOI] [PubMed] [Google Scholar]; (c) Wong H, Yang C, Han K. Struc Chem. 2006;17:97. [Google Scholar]
59.Dinér P, Kjærsgaard A, Lie MA, Jørgensen KA. Chem Eur J. 2008;14:122. doi: 10.1002/chem.200701244.Four groups independently reported the organocatalyzed α-fluorination reaction of aldehydes in the same year: Beeson TD, MacMillan DWC. J Am Chem Soc. 2005;127:8826. doi: 10.1021/ja051805f.Steiner DD, Mase N, Barbas CF., III Angew Che Int Ed. 2005;44:3706. doi: 10.1002/anie.200500571.Enders D, Hüttl MRM. Synlett. 2005:991.Marigo M, Fielenbach D, Braunton A, Kjærsgaard A, Jørgensen KA. Angew Che Int Ed. 2005;44:3703. doi: 10.1002/anie.200500395.
60.Bertelson S, Marigo M, Brandes S, Dinér P, Jørgensen KA. J Am Chem Soc. 2006;128:12973. doi: 10.1021/ja064637f. [DOI] [PubMed] [Google Scholar]
61.Groselj U, Seebach D, Badine DM, Schweizer WB, Beck AK. Helv Chim Acta. 2009;92:1225. [Google Scholar]
62.Vignola N, List B. J Am Chem Soc. 2003;126:450. doi: 10.1021/ja0392566. [DOI] [PubMed] [Google Scholar]
63.Fu A, List B, Thiel W. J Org Chem. 2006;71:320. doi: 10.1021/jo052088a. [DOI] [PubMed] [Google Scholar]
64.Ibrahem I, Hammar P, Vesely J, Rios R, Eriksson L, Córdova A. Adv Synth Catal. 2008;350:1875. [Google Scholar]
65.Arnó M, Zaragozá RJ, Domingo LR. Tetrahedron: Asymmetry. 2007;18:157. [Google Scholar]
66.Seebach D, Golinski J. Helv Chim Acta. 1981;64:1413. [Google Scholar]
67.Mahendra PP, Sunoj RB. Chem Eur J. 2008;14:10472. [Google Scholar]
68.(a) List B. Tetrahedron. 2002;58:5573. [Google Scholar]; (b) Enders D, Seki A. Synlett. 2002;1:26. [Google Scholar]; (c) Betancort JM, Barbas CF., III Org Lett. 2001;3:3737. doi: 10.1021/ol0167006. [DOI] [PubMed] [Google Scholar]; (d) Mase N, Thayumanavan R, Tanaka F, Barbas CF., III Org Lett. 2004;6:2527. doi: 10.1021/ol049196o. [DOI] [PubMed] [Google Scholar]
69.Almasi D, Alonso DA, Gómez-Bengoa E, Nagel Y, Nájera C. Eur J Org Chem. 2007:2328. doi: 10.1021/jo9010552. [DOI] [PubMed] [Google Scholar]
70.Sulzer-Mossé S, Alexakis A, Mareda J, Bollot G, Bernardinelli G, Filinchuk Y. Chem Eur J. 2009;15:3204. doi: 10.1002/chem.200801892. [DOI] [PubMed] [Google Scholar]
71.Melchiorre P, Jørgensen KA. J Org Chem. 2003;68:4151. doi: 10.1021/jo026837p. [DOI] [PubMed] [Google Scholar]
72.Patil MP, Sunoj RB. Chem Asian J. 2009;4:714. doi: 10.1002/asia.200800351. [DOI] [PubMed] [Google Scholar]
73.(a) Shinisha CB, Sunoj Raghavan B. Org Biomol Chem. 2008;6:3921. doi: 10.1039/b810901j. [DOI] [PubMed] [Google Scholar]; (b) Enders D, Huttl MRM, Grandoal C, Raabe G. Nature. 2006;441:861. doi: 10.1038/nature04820. [DOI] [PubMed] [Google Scholar]
74.(a) Duarte FJS, Cabriat EJ, Frenking G, Santos AG. Chem Eur J. 2009;15:1734. doi: 10.1002/chem.200801624. [DOI] [PubMed] [Google Scholar]; (b) Chen SH, Hong BC, Su CF, Sarshar S. Tetrahedron Lett. 2005;46:8899. [Google Scholar]
75.(a) Basavaiah D, Rao AJ, Satyanarayana T. Chem Rev. 2003;103:811. doi: 10.1021/cr010043d. [DOI] [PubMed] [Google Scholar]; (b) Basavaiah D, Rao KV, Reddy RJ. Chem Soc Rev. 2007;36:1581. doi: 10.1039/b613741p. [DOI] [PubMed] [Google Scholar]
76.Ahrendt KA, Borths CJ, MacMillan DWC. J Am Chem Soc. 2000;122:4243. [Google Scholar]
77.Burley JC, Gilmour R, Prior TJ, Day GM. Acta Cryst. 2008;C64:010. doi: 10.1107/S0108270107051396. [DOI] [PubMed] [Google Scholar]
78.Groselj U, Schweizer WB, Ebert M-O, Seebach D. Helv Chim Acta. 2009;92:1. [Google Scholar]
79.(a) Gordillo R, Carter J, Houk KN. Adv Synth Catal. 2004;346:1175. [Google Scholar]; (b) Austin JF, MacMillan DWC. J Am Chem Soc. 2002;124:1172. doi: 10.1021/ja017255c. [DOI] [PubMed] [Google Scholar]
80.Brazier JB, Evans G, Gibbs TJK, Coles SJ, Hursthouse MB, Platts JA, Tomkinson NCO. Org Lett. 2009;11:133. doi: 10.1021/ol802512y. [DOI] [PubMed] [Google Scholar]
81.Gordillo R, Houk KN. J Am Chem Soc. 2006;128:3543. doi: 10.1021/ja0525859. [DOI] [PMC free article] [PubMed] [Google Scholar]
82.Gutierrez O, Iafe RG, Houk KN. Org Lett. 2009;11:4298. doi: 10.1021/ol901586t. [DOI] [PMC free article] [PubMed] [Google Scholar]
83.Nicolaou KC, Reingruber R, Sarlah D, Bräse S. J Am Chem Soc. 2009;131:2086. doi: 10.1021/ja809405c. Correction: J. Am. Chem. Soc 2009, 131, 6640. [DOI] [PubMed] [Google Scholar]
84.Conrad JC, Kong J, Laforteza BN, MacMillan DWC. J Am Chem Soc. 2009;131:11640. doi: 10.1021/ja9026902. [DOI] [PMC free article] [PubMed] [Google Scholar]
85.Um JM, Gutierrez O, Schoenebeck F, Houk KN, MacMillan DWC. J Am Chem Soc. 2010;132:6001. doi: 10.1021/ja9063074. [DOI] [PMC free article] [PubMed] [Google Scholar]
86.For ortho-selective radical additions to aromatics, see: Tiecco M, Testaferri L. In: Reactive Intermediates. Abramovitch RA, editor. Vol. 3. Plenum Press; New York: 1983. p. 61.Guadarrama-Morales O, Mendéz F, Miranda LD. Tetrahedron Lett. 2007;48:4515.Muchowski JM, Cho IS, Jaime-Figueroa S, Artis RD. J Org Chem. 1994;59:2456.For a study of the stability of cyclohexadienyl radicals, see: Birch AJ, Hinde AL, Radom L. J Am Chem Soc. 1980;102:4074.
87.For a recent review on carbene catalysts, see: Moore JL, Rovis T. In: Asymmetric Organocatalysis. List B, editor. Springer Verlag; Heidelberg: 2010. pp. 77–144.
88.Wöhler F, Liebig J. Ann Pharm. 1832;3:249. [Google Scholar]
89.Ugai T, Tanaka S, Dokawa S. J Pharm Soc Jpn. 1943;63:269. [Google Scholar]
90.(a) López Calahorra F, Castells J, Domingo L, Martí J, Bofill JM. Heterocycles. 1994;37:1579. [Google Scholar]; (b) Martí J, López Calahorra F, Bofill JM. J Mol Struct (Theochem) 1995;339:179. [Google Scholar]
91.Dudding T, Houk KN. Proc Nat Acad Sci. 2004;101:5770. doi: 10.1073/pnas.0307256101. [DOI] [PMC free article] [PubMed] [Google Scholar]
92.Breslow R. J Am Chem Soc. 1958;80:3719. [Google Scholar]
93.Enders D, Kallfass U. Angew Chem, Int Ed. 2002;41:1743. doi: 10.1002/1521-3773(20020517)41:10<1743::aid-anie1743>3.0.co;2-q. [DOI] [PubMed] [Google Scholar]
94.Knight RL, Leeper FJ. Tetrahedron Lett. 1997;38:3611. [Google Scholar]
95.Sheehan J, Hara T. J Org Chem. 1974;39:1196. [Google Scholar]
96.(a) Enders D, Breuer K, Teles JH. Helv Chim Acta. 1996;79:1217. [Google Scholar]; (b) Enders D, Breuer K. Comprehensive Asymmetric Catalysis. Vol. 3. Springer-Verlag; Heidelberg, Germany: 1999. p. 1093. [Google Scholar]; (c) Teles JH, Breuer K, Enders D, Gielen H. Synth Commun. 1999;29:1. [Google Scholar]
97.Hachisu Y, Bode JW, Suzuki K. Adv Synth Catal. 2004;346:1097. [Google Scholar]
98.Hawkes KJ, Yates BF. Eur J Org Chem. 2008:5563. [Google Scholar]
99.(a) Grasa GA, Kissling RM, Nolan SP. Org Lett. 2002;4:3583. doi: 10.1021/ol0264760. [DOI] [PubMed] [Google Scholar]; (b) Grasa GA, Guveli T, Singh R, Nolan SP. J Org Chem. 2003;68:2812. doi: 10.1021/jo0267551. [DOI] [PubMed] [Google Scholar]
100.Nyce GW, Lamboy JA, Connor EF, Waymouth RM, Hedrick JL. Org Lett. 2002;4:3587. doi: 10.1021/ol0267228.For reviews in NHC-catalyzed polymerization reactions, see: Dove AP, Pratt RC, Lohmeijer BGG, Culkin DA, Hagberg EC, Nyce GW, Waymouth RM, Hedrick JL. Polymer. 2006;47:4018.Coulembier O, Gegée P, Hedrick JL, Dubois P. Prog Polym Sci. 2006;31:723.
101.Lai C-L, Lee HM, Hu C-H. Tetrahedron Lett. 2005;46:6265. [Google Scholar]
102.Maki BE, Patterson EV, Cramer CJ, Scheidt KA. Org Lett. 2009;11:3942. doi: 10.1021/ol901545m. [DOI] [PMC free article] [PubMed] [Google Scholar]
103.See Chan A, Scheidt KA. Org Lett. 2005;7:905. doi: 10.1021/ol050100f. and references therein. [DOI] [PubMed] [Google Scholar]
104.Ragsdale SW. Chem Rev. 2003;103:2333. doi: 10.1021/cr020423e. [DOI] [PubMed] [Google Scholar]
105.Guin J, De Sarkar S, Grimme S, Studer A. Angew Chem Int Ed. 2008;47:8727. doi: 10.1002/anie.200802735. [DOI] [PubMed] [Google Scholar]
106.Xu S, Held I, Kempf B, Mayr H, Steglich W, Zipse H. Chem Eur J. 2005;11:4751. doi: 10.1002/chem.200500398. [DOI] [PubMed] [Google Scholar]
107.(a) Guibe-Jampel E, Le Corre G, Wakselman M. Tetrahedron Lett. 1979;20:1157. [Google Scholar]; (b) Kattnig E, Albert M. Org Lett. 2004;6:945. doi: 10.1021/ol0364935. [DOI] [PubMed] [Google Scholar]; (c) Lamaty G, Mary F, Roque JP. J Chim Phys Phys-Chim Biol. 1991;88:1793. [Google Scholar]
108.Fischer CB, Xu S, Zipse H. Chem Eur J. 2006;12:5779. doi: 10.1002/chem.200600280. [DOI] [PubMed] [Google Scholar]
109.Wei Y, Held I, Zipse H. Org Biomol Chem. 2006;4:4223. doi: 10.1039/b610140b. [DOI] [PubMed] [Google Scholar]
110.Held I, Villinger A, Zipse H. Synthesis. 2005;9:1425. [Google Scholar]
111.(a) Heinrich MR, Klisa HS, Mayr H, Steglich W, Zipse H. Angew Chem Int Ed. 2003;42:4826. doi: 10.1002/anie.200352289. [DOI] [PubMed] [Google Scholar]; (b) Held I, Xu S, Zipse H. Synthesis. 2007;8:1185. [Google Scholar]; (c) Held I, Larinov E, Bozle C, Wagner F, Zipse H. Synthesis. 2009;13:2267. [Google Scholar]
112.Zipse has also calculated the methyl cation affinities of commonly used nitrogen and phosphorous-based organocatalysts. See: Wei Y, Sastry N, Zipse H. J Am Chem Soc. 2008;130:3473. doi: 10.1021/ja0764409.Wei Y, Singer T, Mayr H, Sastry GN, Zipse H. J Comput Chem. 2008;29:291. doi: 10.1002/jcc.20790.The same group reported the performance of computational methods in describing zwitterionic adducts between NMe3 and PMe3 with methyl vinyl ketone. See: Wei Y, Bandaru S, Maryasin B, Sastry N, Zipse H. J Comput Chem. 2009;30:2617. doi: 10.1002/jcc.21271.
113.(a) Singh S, Das G, Singh OV, Han H. Org Lett. 2007;9:401. doi: 10.1021/ol062712l. [DOI] [PubMed] [Google Scholar]; (b) Singh S, Das G, Singh OV, Han H. Tetrahedron Lett. 2007;48:1983. doi: 10.1016/j.tetlet.2007.09.129. [DOI] [PMC free article] [PubMed] [Google Scholar]
114.(a) Steglich W, Höfle G. Tetrahedron Lett. 1970;54:4727. [Google Scholar]; (b) Hassner A, Krepski LR, Alexanian V. Tetrahedron. 1978;34:2069. [Google Scholar]
115.(a) Yamada S, Yamashita K. Tetrahedron Lett. 2008;49:32. [Google Scholar]; (b) Yamada S, Misono T, Iwai Y, Masumizu A, Akiyama Y. J Org Chem. 2006;71:6872. doi: 10.1021/jo060989t. [DOI] [PubMed] [Google Scholar]; (c) Yamada S, Misono T, Iwai Y. Tetrahedron Lett. 2005;46:2239. [Google Scholar]; (d) Yamada S, Noguchi E. Tetrahedron Lett. 2002;42:3621. [Google Scholar]
116.Lutz V, Glatthaar J, Würtele C, Serafin M, Hausmann H, Schreiner PR. Chem Eur J. 2009;15:8548. doi: 10.1002/chem.200901379. [DOI] [PubMed] [Google Scholar]
117.(a) Marcelli T, van Maarseveen JH, Hiemstra H. Angew Chem Int Ed. 2006;45:7496. doi: 10.1002/anie.200602318. [DOI] [PubMed] [Google Scholar]; (b) Tan SK, Chen Y, Hang J, Tang L, McDaid P, Deng L. Acc Chem Res. 2004;37:621. doi: 10.1021/ar030048s. [DOI] [PubMed] [Google Scholar]; (c) Hoffmann HMR, Frackenpohl J. Eur J Org Chem. 2004:4293. [Google Scholar]; (d) Kacprzak K, Gawroskik J. Synthesis. 2001;7:961. [Google Scholar]
118.Bürgi T, Baiker A. J Am Chem Soc. 1998;120:12920. [Google Scholar]
119.Vargas A, Bonalumi N, Ferri D, Baiker A. J Phys Chem A. 2006;110:1118. doi: 10.1021/jp055013j. [DOI] [PubMed] [Google Scholar]
120.Olsen RA, Borchardt D, Mink L, Agarwal A, Mueller LJ, Zaera F. J Am Chem Soc. 2006;138:15594. doi: 10.1021/ja066989s. [DOI] [PubMed] [Google Scholar]
121.Szöllösi G, Chatterjee A, Forgó P, Bartók M, Mizukami F. J Phys Chem A. 2005;109:860. doi: 10.1021/jp045882t. [DOI] [PubMed] [Google Scholar]
122.Taggi AE, Hafez AM, Wack H, Young B, Ferraris D, Lectka T. J Am Chem Soc. 2002;124:6626. doi: 10.1021/ja0258226. [DOI] [PubMed] [Google Scholar]
123.Taggi AE, Hafez AM, Dudding T, Lectka T. Tetrahedron. 2002;58:8351. [Google Scholar]
124.Brunner H, Schmidt P. Eur J Org Chem. 2000:2119. [Google Scholar]
125.Drees M, Kleiber L, Wemer M, Strassner T. Eur J Org Chem. 2002:2405. [Google Scholar]
126.Peltier HM, Evans JW, Ellman JA. Org Lett. 2005;7:1733. doi: 10.1021/ol050275p. [DOI] [PubMed] [Google Scholar]
127.Shibata N, Matsunaga M, Nakagawa M, Fukuzumi T, Nakamura S, Toru T. J Am Chem Soc. 2005;127:1374. doi: 10.1021/ja0430189. [DOI] [PubMed] [Google Scholar]
128.Balcells D, Maseras F, Khiar N. Org Lett. 2005;6:2197. doi: 10.1021/ol0493507. [DOI] [PubMed] [Google Scholar]
129.Balcells D, Ujaque G, Fernandez I, Khiar N, Maseras F. J Org Chem. 2006;71:6388. doi: 10.1021/jo060546p. [DOI] [PubMed] [Google Scholar]
130.(a) France S, Wack H, Taggi AE, Hafez AM, Wagerle TR, Shah MH, Cusich CL, Lectka T. J Am Chem Soc. 2004;126:4245. doi: 10.1021/ja039046t. [DOI] [PubMed] [Google Scholar]; (b) Wack H, Taggi AE, Hafez AM, Drury WJ, III, Lectka T. J Am Chem Soc. 2001;123:1531. doi: 10.1021/ja005791j. [DOI] [PubMed] [Google Scholar]; (c) France S, Weatherwax A, Lectka T. Eur J Org Chem. 2005;3:475. [Google Scholar]
131.Hafez AM, Taggi AE, Wack H, Esterbrook J, Lectka T. Org Lett. 2001;3:2049. doi: 10.1021/ol0160147. [DOI] [PubMed] [Google Scholar]
132.Dogo-Isonagie C, Bekele T, France S, Wolfer J, Weatherwax A, Taggi AE, Paull DH, Dudding T, Lectka T. Eur J Org Chem. 2007:1091. doi: 10.1021/jo061522l. [DOI] [PubMed] [Google Scholar]
133.(a) Liu B, Feng X, Chen F, Zhang G, Cui X, Jiang Y. Synlett. 2001;10:1551. [Google Scholar]; (b) Jiao Z, Feng X, Liu B, Chen F, Zhang GL, Jiang Y. Eur J Org Chem. 2003:3818. [Google Scholar]
134.Su Z, Hu C, Qin S, Feng X. Tetrahedron. 2006;62:4071. [Google Scholar]
135.Aggarwal VK, Alonso E, Hynd G, Lydon KM, Palmer MJ, Porcelloni M, Studley JR. Angew Chem Int Ed. 2001;40:1430. doi: 10.1002/1521-3773(20010417)40:8<1430::AID-ANIE1430>3.0.CO;2-W. [DOI] [PubMed] [Google Scholar]
136.Volatron F, Eisenstein O. J Am Chem Soc. 1987;109:1. doi: 10.1021/ja00269a009. [DOI] [PubMed] [Google Scholar]
137.(a) Lindvall MK, Koskinen AMP. J Org Chem. 1999;64:4595. doi: 10.1021/jo9818935. [DOI] [PubMed] [Google Scholar]; (b) Myllymäki VT, Lindvall MK, Koskinen AMP. Tetrahedron. 2001;57:4629. [Google Scholar]
138.Aggarwal VK, Harvey JN, Richardson J. J Am Chem Soc. 2002;124:5747. doi: 10.1021/ja025633n. [DOI] [PubMed] [Google Scholar]
139.Aggarwal VK, Charmant JPH, Fuentes D, Harvey JN, Hynd G, Ohara D, Picoul W, Robiette R, Smith C, Vasse J-L, Winn CL. J Am Chem Soc. 2006;128:2105. doi: 10.1021/ja0568345. [DOI] [PubMed] [Google Scholar]
140.Imashiro R, Yamanaka T, Seki M. Tetrahedron: Asymmetry. 1999;10:2845. [Google Scholar]
141.Aggarwal VK, Harvey JN, Robiette R. Angew Chem Int Ed. 2005;44:5468. doi: 10.1002/anie.200501526. [DOI] [PubMed] [Google Scholar]
142.Robiette R, Conza M, Aggarwal VK. Org Biomol Chem. 2006;4:621. doi: 10.1039/b516926g. [DOI] [PubMed] [Google Scholar]
143.Silva MA, Bellenie BR, Goodman JM. Org Lett. 2004;6:2559. doi: 10.1021/ol0491641. [DOI] [PubMed] [Google Scholar]
144.Zanardi J, Leriverend C, Aubert D, Julienne K, Metzner P. J Org Chem. 2001;66:5620. doi: 10.1021/jo015588m. [DOI] [PubMed] [Google Scholar]
145.(a) Winn CL, Bellenie BR, Goodman JM. Tetrahedron Lett. 2002;43:5427. [Google Scholar]; (b) Winn C, Goodman JM. Tetrahedron Lett. 2001;42:7091. [Google Scholar]
146.Deng X-M, Cai P, Ye S, Sun X-L, Liao W-W, Li K, Tang Y, Wu Y-D, Dai L-X. J Am Chem Soc. 2005;128:9730. doi: 10.1021/ja056751o. [DOI] [PubMed] [Google Scholar]
147.Robiette R. J Org Chem. 2006;71:2726. doi: 10.1021/jo052559t. [DOI] [PubMed] [Google Scholar]
148.Janardanan D, Sunoj RB. Chem Eur J. 2007;13:4805. doi: 10.1002/chem.200700303. [DOI] [PubMed] [Google Scholar]
149.Janardanan D, Sunoj RB. J Org Chem. 2008;73:8163. doi: 10.1021/jo800652c. [DOI] [PubMed] [Google Scholar]
150.Stewart IC, Bergman RG, Toste FD. J Am Chem Soc. 2003;125:8696. doi: 10.1021/ja035232n. [DOI] [PubMed] [Google Scholar]
151.Wang X, Li S, Jiang Y. J Phys Chem A. 2005;109:10770. doi: 10.1021/jp052426b. [DOI] [PubMed] [Google Scholar]
152.For examples, see: Zhang C, Lu X. J Org Chem. 1995;60:2906.Zhu G, Chen Z, Jiang Q, Xiao D, Cao P, Zhang X. J Am Chem Soc. 1997;119:3836.Wilson JE, Fu GC. Angew Chem, Int Ed. 2006;45:1426. doi: 10.1002/anie.200503312.Zhu XF, Lan J, Kwon O. J Am Chem Soc. 2003;125:4716. doi: 10.1021/ja0344009.Tran YS, Kwon O. Org Lett. 2005;7:4289. doi: 10.1021/ol051799s.Wurz RP, Fu GC. J Am Chem Soc. 2005;127:12234. doi: 10.1021/ja053277d.Evans CA, Miller SJ. J Am Chem Soc. 2003;125:12394. doi: 10.1021/ja0377798.Wang LC, Luis AL, Agapiou K, Jang HY, Krische MJ. J Am Chem Soc. 2002;124:2402. doi: 10.1021/ja0121686.Frank SA, Mergott AJ, Roush WR. J Am Chem Soc. 2002;124:2404. doi: 10.1021/ja017123j.
153.Dudding T, Kwon O, Mercier E. Org Lett. 2006;8:3643. doi: 10.1021/ol061095y. [DOI] [PubMed] [Google Scholar]
154.(a) Xia Y, Liang Y, Chen Y, Wang M, Jiao L, Huang F, Liu S, Li Y, Yu ZX. J Am Chem Soc. 2006;129:3470. doi: 10.1021/ja068215h. [DOI] [PubMed] [Google Scholar]; (b) Mercier E, Fonovic B, Henry C, Kwon O, Dudding T. Tetrahedron Lett. 2007;48:3617. [Google Scholar]; (c) Liang Y, Liu S, Xia Y, Li Y, Yu ZX. Chem Eur J. 2008;14:4361. doi: 10.1002/chem.200701725. [DOI] [PubMed] [Google Scholar]
155.Xia Y, Liang Y, Chen Y, Wang M, Jiao L, Huang F, Liu S, Li Y, Yu Z–X. J Am Chem Soc. 2007;129:3470. doi: 10.1021/ja068215h. [DOI] [PubMed] [Google Scholar]
156.Yu X–Z. Synlett. 2009;6:905. [Google Scholar]
157.(a) Baylis AB, Hillman MED. Offenlegungsschrift 2155113. 3,743,669. US Patent. 1972; Chem Abstr. 1972;77:34174q. [Google Scholar]; (b) Morita K, Suzuki Z, Hirose H. Bull Chem Soc Jpn. 1968;41:2815. [Google Scholar]
158.Xu J. THEOCHEM. 2006;767:61. [Google Scholar]
159.Robiette R, Aggarwal VK, Harvey JN. J Am Chem Soc. 2007;129:15513. doi: 10.1021/ja0717865. [DOI] [PubMed] [Google Scholar]
160.(a) Aggarwal VK, Fulford SY, Lloyd-Jones GC. Angew Chem Int Ed. 2005;44:1706. doi: 10.1002/anie.200462462. [DOI] [PubMed] [Google Scholar]; (b) Price KE, Broadwater SJ, Jung HM, McQuade DT. Org Lett. 2005;7:147. doi: 10.1021/ol047739o. [DOI] [PubMed] [Google Scholar]; (c) Price KE, Broadwater SJ, Walker BJ, McQuade DT. J Org Chem. 2005;70:3980. doi: 10.1021/jo050202j. [DOI] [PubMed] [Google Scholar]; (d) Buskens P, Klankermayer J, Leitner W. J Am Chem Soc. 2005;127:16762. doi: 10.1021/ja0550024. [DOI] [PubMed] [Google Scholar]
161.(a) Hill JS, Isaacs NS. J Phys Org Chem. 1990;3:285. [Google Scholar]; (b) Hill JS, Isaacs NS. J Chem Res. 1988:330. [Google Scholar]; (c) Hill JS, Isaacs NS. Tetrahedron Lett. 1986;27:5007. [Google Scholar]
162.Fan J-F, Yang C-H, He L-J. Int J Quantum Chem. 2009;109:1311. [Google Scholar]
163.Roy D, Sunoj RB. Org Lett. 2007;9:4873. doi: 10.1021/ol702211d. [DOI] [PubMed] [Google Scholar]
164.(a) Roy D, Patel C, Sunoj RB. J Org Chem. 2009;74:6936. doi: 10.1021/jo900622x. [DOI] [PubMed] [Google Scholar]; (b) Roy D, Sunoj RB. Chem Eur J. 2008;14:10530. doi: 10.1002/chem.200801822. [DOI] [PubMed] [Google Scholar]
165.For examples, see: Jung ME, Node M, Pfluger RW, Lyster MA, Lowe JA., III J Org Chem. 1982;47:1150.Jung ME, Lowe JA, III, Lyster MA, Node M, Pfluger RW, Brown RW. Tetrahedron. 1984;40:4751.Yasukouchi T, Kanematsu K. Tetrahedron Lett. 1989;30:6559.Ma D, Yu Y, Lu X. J Org Chem. 1989;54:1105.
166.Liu H, Leow D, Huang K-W, Tan C-H. J Am Chem Soc. 2009;131:7212. doi: 10.1021/ja901528b. [DOI] [PubMed] [Google Scholar]
167.Oku M, Arai S, Katayama K, Shioiri T. Synlett. 2000:493. [Google Scholar]
168.Climent MJ, Corma A, Domínguez I, Iborra S, Sabater MJ, Sastre G. J Catal. 2007;246:136. [Google Scholar]
169.Tel RM, Engberts JBFN. J Chem Soc Perkin Trans. 1976;2:483. [Google Scholar]
170.(a) Etter MC, Panunto TW. J Am Chem Soc. 1988;110:5896. [Google Scholar]; (b) Etter MC, Urbañczyk-Lipkowska Z, Zia-Ebrahimi M, Panunto TW. J Am Chem Soc. 1990;112:8415. [Google Scholar]; (c) Etter MC. Acc Chem Res. 1990;23:120. [Google Scholar]; (d) Etter MC. J Phys Chem. 1991;95:4601. [Google Scholar]
171.Schreiner PR, Wittkopp A. Org Lett. 2002;4:217. doi: 10.1021/ol017117s. [DOI] [PubMed] [Google Scholar]
172.Schreiner PR. Chem Soc Rev. 2003;32:289. doi: 10.1039/b107298f. [DOI] [PubMed] [Google Scholar]
173.Fu AP, Thiel W. Theochem-J Mol Struct. 2006;765:45. [Google Scholar]
174.Loncharich RJ, Brown FK, Houk KN. J Org Chem. 1989;54:1129. [Google Scholar]
175.Bernardi F, Bottoni A, Field MJ, Guest MF, Hillier IH, Robb MA, Venturini A. J Am Chem Soc. 1988;110:3050. [Google Scholar]
176.Houk KN, Lin YT, Brown FK. J Am Chem Soc. 1986;108:554. doi: 10.1021/ja00263a059. [DOI] [PubMed] [Google Scholar]
177.Sauer J, Sustmann R. Angew Chem, Int Ed Engl. 1980;19:779. [Google Scholar]
178.Linder M, Brinck T. Org Biomol Chem. 2009;7:1304. doi: 10.1039/b818655c. [DOI] [PubMed] [Google Scholar]
179.Severance DL, Jørgensen WL. J Am Chem Soc. 1992;114:10966. [Google Scholar]
180.Curran DP, Lung HK. Tetrahedron Lett. 1995;36:6647. [Google Scholar]
181.Kirsten M, Rehbein J, Hiersemann M, Strassner T. J Org Chem. 2007;72:4001. doi: 10.1021/jo062455y. [DOI] [PubMed] [Google Scholar]
182.Sigman MS, Vachal P, Jacobsen EN. Angew Chem, Int Ed. 2000;39:1279. doi: 10.1002/(sici)1521-3773(20000403)39:7<1279::aid-anie1279>3.0.co;2-u. [DOI] [PubMed] [Google Scholar]
183.Sigman MS, Jacobsen EN. J Am Chem Soc. 1998;120:4901. [Google Scholar]
184.Su JT, Vachal P, Jacobsen EN. Adv Synth Catal. 2001;343:197. [Google Scholar]
185.Vachal P, Jacobsen EN. Org Lett. 2000;2:867. doi: 10.1021/ol005636+. [DOI] [PubMed] [Google Scholar]
186.Vachal P, Jacobsen EN. J Am Chem Soc. 2002;124:10012. doi: 10.1021/ja027246j. [DOI] [PubMed] [Google Scholar]
187.Zuend SJ, Jacobsen EN. J Am Chem Soc. 2009;131:15358. doi: 10.1021/ja9058958. [DOI] [PMC free article] [PubMed] [Google Scholar]
188.Kleiner CM, Schreiner PR. Chemical Communications. 2006:4315. doi: 10.1039/b605850g. [DOI] [PubMed] [Google Scholar]
189.Fleming EM, Quigley C, Rozas I, Connon SJ. J Org Chem. 2008;73:948. doi: 10.1021/jo702154m. [DOI] [PubMed] [Google Scholar]
190.Kotke M, Schreiner PR. Synthesis. 2007;5:779. [Google Scholar]
191.Raheem IT, Thiara PS, Peterson EA, Jacobsen EN. J Am Chem Soc. 2007;129:13404. doi: 10.1021/ja076179w. [DOI] [PubMed] [Google Scholar]
192.Trzupek JD, Li C, Chan C, Crowley BM, Heimann AC, Danishefsky SJ. Pure Appl Chem. 2010;82:1735. doi: 10.1351/pac-con-09-11-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
193.Frankland PF, Twiss DF. Journal of the Chemical Society, Transactions. 1904;85:1666. [Google Scholar]
194.Huang Y, Rawal VH. J Am Chem Soc. 2002;124:9662. doi: 10.1021/ja0267627. [DOI] [PubMed] [Google Scholar]
195.Huang Y, Unni AK, Thadani AN, Rawal VH. Nature. 2003;424:146. doi: 10.1038/424146a. [DOI] [PubMed] [Google Scholar]
196.Zhang X, Du H, Wang Z, Wu Y-D, Ding K. J Org Chem. 2006;71:2862. doi: 10.1021/jo060129c. [DOI] [PubMed] [Google Scholar]
197.Gordillo RD, Anderson TCD, Houk KN. Org Lett. 2007;9:501. doi: 10.1021/ol0629925. [DOI] [PMC free article] [PubMed] [Google Scholar]
198.Gómez-Bengoa E. Eur J Org Chem. 2009:1207. It was reported that the preferred binding mode depends on the polarity of the carbonyl group. As the polarity increases, as in enamine aldol reactions, the bifurcated binding mode becomes favored. [Google Scholar]
199.Anderson CD, Dudding T, Gordillo R, Houk KN. Org Lett. 2008;10:2749. doi: 10.1021/ol800875k. [DOI] [PubMed] [Google Scholar]
200.Hine J, Linden SM, Kanagasabapathy VM. J Org Chem. 1985;50:5096. [Google Scholar]
201.Ooi T, Takahashi M, Maruoka K. J Am Chem Soc. 1996;118:11307. [Google Scholar]
202.Kelly TR, Meghani P, Ekkundi VS. Tetrahedron Lett. 1990;31:3381. [Google Scholar]
203.Omoto K, Fujimoto H. J Org Chem. 2000;65:2464. doi: 10.1021/jo9916333. [DOI] [PubMed] [Google Scholar]
204.Pliego JR. J Mol Catal A-Chem. 2005;239:228–234. [Google Scholar]
205.Pliego JR, Pilo-Veloso D. J Phys Chem B. 2007;111:1752. doi: 10.1021/jp066580p. [DOI] [PubMed] [Google Scholar]
206.McDougal NT, Schaus SE. J Am Chem Soc. 2003;125:12094. doi: 10.1021/ja037705w. [DOI] [PubMed] [Google Scholar]
207.McDougal NT, Trevellini WL, Rodgen SA, Kliman LT, Schaus SE. Adv Synth Catal. 2004;346:1231. [Google Scholar]
208.(a) Akiyama T, Itoh J, Yokota K, Fuchibe K. Angew Chem. 2004;116:1566. doi: 10.1002/anie.200353240. [DOI] [PubMed] [Google Scholar]; (b) Uraguchi D, Terada M. J Am Chem Soc. 2004;126:5356. doi: 10.1021/ja0491533. [DOI] [PubMed] [Google Scholar]
209.(a) Rowland GB, Rowland EB, Liang Y, Perman JACAJ. Org Lett. 2007;9:2609. doi: 10.1021/ol0703579. [DOI] [PubMed] [Google Scholar]; (b) Rueping M, Ieawsuwan W, Antonchick AP, Nachtsheim BJ. Angew Chem, Int Ed. 2007;46:2097. doi: 10.1002/anie.200604809. [DOI] [PubMed] [Google Scholar]; (c) Storer RI, Carrera DE, Ni Y, MacMillan DWC. J Am Chem Soc. 2006;128:84. doi: 10.1021/ja057222n. [DOI] [PubMed] [Google Scholar]; (d) Chen XH, Xu XY, Liu H, Cun LF, Gong LZ. J Am Chem Soc. 2006;128:14802. doi: 10.1021/ja065267y. [DOI] [PubMed] [Google Scholar]; (e) Terada M, Machioka K, Sorimachi K. Angew Chem, Int Ed. 2006;45:2254. doi: 10.1002/anie.200503477. [DOI] [PubMed] [Google Scholar]; (f) Uraguchi D, Sorimachi K, Terada M. J Am Chem Soc. 2005;127:9360. doi: 10.1021/ja051922a. [DOI] [PubMed] [Google Scholar]; (g) Rueping M, Sugiono E, Azap C, Theissmann T, Bolte OL. Org Lett. 2005;7:3781. doi: 10.1021/ol0515964. [DOI] [PubMed] [Google Scholar]; (h) Hoffmann S, Seayad AM, List B. Angew Chem, Int Ed. 2005;44:7424. doi: 10.1002/anie.200503062. [DOI] [PubMed] [Google Scholar]; (i) Lu M, Lu Y, Zhu D, Zeng X, Li X, Zhong G. Angew Chem Int Ed. 2010;49:8588. doi: 10.1002/anie.201002640. [DOI] [PubMed] [Google Scholar]
210.Gridnev IDK, Sorimachi MK, Terada M. Tetrahedron Lett. 2007;48:497. [Google Scholar]
211.Yamanaka M, Itoh J, Fuchibe K, Akiyama T. J Am Chem Soc. 2007;129:6756. doi: 10.1021/ja0684803. [DOI] [PubMed] [Google Scholar]
212.Uraguchi D, Terada M. J Am Chem Soc. 2004;126:5356. doi: 10.1021/ja0491533. [DOI] [PubMed] [Google Scholar]
213.Chen X-H, Wei Q, Luo S-W, Xiao H, Gong L-Z. J Am Chem Soc. 2009;131:13819. doi: 10.1021/ja905302f. [DOI] [PubMed] [Google Scholar]
214.Li N, Chen X-H, Song J, Luo S-W, Fan W, Gong L-Z. J Am Chem Soc. 2009;131:15301. doi: 10.1021/ja905320q. [DOI] [PubMed] [Google Scholar]
215.Simón L, Goodman JM. J Am Chem Soc. 2008;130:8741. doi: 10.1021/ja800793t. [DOI] [PubMed] [Google Scholar]
216.Marcelli T, Hammar P, Himo F. Adv Synth Catal. 2009;351:525. [Google Scholar]
217.Rueping M, Sugiono E, Azap C, Theissmann T, Bolte M. Org Lett. 2005;7:3781. doi: 10.1021/ol0515964. [DOI] [PubMed] [Google Scholar]
218.Storer RI, Carrera DE, Ni Y, MacMillan DWC. J Am Chem Soc. 2006;128:84. doi: 10.1021/ja057222n. [DOI] [PubMed] [Google Scholar]
219.Simón L, Goodman JM. J Org Chem. 2010;75:589. doi: 10.1021/jo902120s. [DOI] [PubMed] [Google Scholar]
220.Shi F-Q, Song B-A. Org Biomol Chem. 2009;7:1292. doi: 10.1039/b815008g. [DOI] [PubMed] [Google Scholar]
221.Corey EJ, Bakshi RK, Shibata S. J Am Chem Soc. 1987;109:5551. [Google Scholar]
222.Corey EJ, Bakshi RK, Shibata S, Chen C-P, Singh VK. J Am Chem Soc. 1987;109:7925. [Google Scholar]
223.Corey EJ, Cimprich KA. J Am Chem Soc. 1994;116:3151. [Google Scholar]
224.Corey EJ, Loh T-P. J Am Chem Soc. 1991;113:8966. [Google Scholar]
225.Payette JN, Yamamoto H. J Am Chem Soc. 2007;129:9536. doi: 10.1021/ja0735958. [DOI] [PubMed] [Google Scholar]
226.Corey EJ, Shibata T, Lee TW. J Am Chem Soc. 2002;124:3808. doi: 10.1021/ja025848x. [DOI] [PubMed] [Google Scholar]
227.Ryu DH, Corey EJ. J Am Chem Soc. 2005;127:5384. doi: 10.1021/ja050543e. [DOI] [PubMed] [Google Scholar]
228.Liu D, Hong S, Corey EJ. J Am Chem Soc. 2006;128:8160. doi: 10.1021/ja063332y. [DOI] [PubMed] [Google Scholar]
229.Boeckman RK, Pero JE, Boehmier DJ. J Am Chem Soc. 2006;128:11032. doi: 10.1021/ja063532+. [DOI] [PubMed] [Google Scholar]
230.(a) Nevalainen V. Tetrahedron: Asymmetry. 1991;2:1133. [Google Scholar]; (b) Nevalainen V. Tetrahedron: Asymmetry. 1992;3:921. [Google Scholar]; (c) Nevalainen V. Tetrahedron: Asymmetry. 1993;4:1505. [Google Scholar]; (d) Nevalainen V. Tetrahedron: Asymmetry. 1993;4:1597. [Google Scholar]; (e) Nevalainen V. Tetrahedron: Asymmetry. 1994;5:387. [Google Scholar]; (f) Nevalainen V. Tetrahedron: Asymmetry. 1994;5:395. [Google Scholar]
231.(a) Nevalainen V. Tetrahedron: Asymmetry. 1991;2:827. [Google Scholar]; (b) Nevalainen V. Tetrahedron: Asymmetry. 1992;3:933. [Google Scholar]; (c) Nevalainen V. Tetrahedron: Asymmetry. 1994;5:289. [Google Scholar]
232.Nevalainen V. Tetrahedron: Asymmetry. 1992;3:1441. [Google Scholar]
233.(a) Nevalainen V. Tetrahedron: Asymmetry. 1991;2:63. [Google Scholar]; (b) Nevalainen V. Tetrahedron: Asymmetry. 1991;2:429. [Google Scholar]; (c) Nevalainen V. Tetrahedron: Asymmetry. 1992;3:1563. [Google Scholar]
234.(a) Li M, Xie R, Hu C, Wang X, Tian A. Int J Quantum Chem. 2000;78:245. [Google Scholar]; (b) Li M, Xie R, Tian S, Tian A. Int J Quantum Chem. 2000;78:252. [Google Scholar]; (c) Li M, Xie R, Hu X, Tian A. Int J Quantum Chem. 2000;78:261. [Google Scholar]
235.(a) Li M, Tian A. THEOCHEM. 2001;544:25–35. [Google Scholar]; (b) Li M, Tian A. THEOCHEM. 2001;544:37–47. [Google Scholar]
236.(a) Li M, Zheng W, Yang F, Tian A. Int J Quantum Chem. 2001;81:291. [Google Scholar]; (b) Li M, Zheng W, He R, Tian A. Int J Quantum Chem. 2003;93:294. [Google Scholar]; (c) Li M, Zheng W, Tian A. Int J Quantum Chem. 2003;93:307. [Google Scholar]; (d) Zheng W, Li M, Tian A. THEOCHEM. 2003;634:253. [Google Scholar]; (e) Zheng W, Li M, Tian A. THEOCHEM. 2004;668:13. [Google Scholar]
237.(a) Jones DK, Liotta DC, Shinkai I, Mathre DJ. J Org Chem. 1993;58:799. [Google Scholar]; (b) Linny LP, Self CR, Williams IH. J Chem Soc, Chem Commun. 1994:1651. [Google Scholar]; (c) Linny LP, Self CR, Williams IH. Tetrahedron: Asymmetry. 1994;5:813. [Google Scholar]; (d) Bach J, Berenguer R, Farras J, Garcia J, Meseguer J, Vilarrasa J. Tetrahedron: Asymmetry. 1995;6:2683. [Google Scholar]; (e) Shen Z, Huang W, Feng J, Zhang Y. Tetrahedron: Asymmetry. 1998;9:1091. [Google Scholar]; (f) Puigjaner C, Vidal-Ferran A, Moyano A, Pericas MA, Riera A. J Org Chem. 1999;64:7902. [Google Scholar]; (g) Bringmann G, Hinrichs J, Kraus J, Wuzik A, Schulz T. J Org Chem. 2000;65:2517. doi: 10.1021/jo991729x. [DOI] [PubMed] [Google Scholar]; (h) Fan JF, Wang QX, Yun-Xiang L. THEOCHEM. 2004;674:49. [Google Scholar]; (i) Gondos GP., I Int J Quantum Chem. 2001;84:253. [Google Scholar]; (j) Tlahuextl M, Tapia-Benavides AR, Flores-Parra A, Contreras R, Tlahuext H, Cruz EM. Heteroat Chem. 2005;16:513. [Google Scholar]
238.(a) Harb W, Ruiz-Lopez MF, Coutrot F, Grison C, Coutrot P. J Am Chem Soc. 2004;126:6996. doi: 10.1021/ja031778y. [DOI] [PubMed] [Google Scholar]; (b) Alagona G, Ghio C, Tomasi S. Theor Chem Acc. 2004;111:287. [Google Scholar]; (c) Alagona GGC, Persico C, Tomasi S. J Am Chem Soc. 2003;125:10027. doi: 10.1021/ja034928d. [DOI] [PubMed] [Google Scholar]; (d) Sun L, Tang M, Wang H, Wei D, Liu L. Tetrahedron: Asymmetry. 2008;19:779. [Google Scholar]
239.Corey EJ, Azimioara M, Sarshar S. Tetrahedron Lett. 1992;33:3429. [Google Scholar]
240.Saavedra J, Stafford SE, Meyer MP. Tetrahedron Lett. 2009;50:1324. [Google Scholar]
241.Sun L, Tang M, Wang H, Wei D, Liu L. Tetrahedron: Asymmetry. 2008;19:779. [Google Scholar]
242.Grison C, Coutrot F, Coutrot P. Tetrahedron. 2002;58:2735. [Google Scholar]
243.Harb W, Ruiz-Lopéz MF, Coutrot F, Grison C, Coutrot P. J Am Chem Soc. 2004;126:6996. doi: 10.1021/ja031778y. [DOI] [PubMed] [Google Scholar]
244.Li M, He R. THEOCHEM. 2003;629:197. [Google Scholar]
245.Li M, He R. THEOCHEM. 2003;629:209. [Google Scholar]
246.Pi Z, Li S. J Phys Chem A. 2006;110:9225. doi: 10.1021/jp062320w. [DOI] [PubMed] [Google Scholar]
247.Paddon-Row MN, Kwan LCH, Willis AC, Sherburn MS. Angew Chem Int Ed. 2008;47:7013. doi: 10.1002/anie.200802002. [DOI] [PubMed] [Google Scholar]
248.Paddon-Row MN, Anderson CD, Houk KN. J Org Chem. 2009;74:861. doi: 10.1021/jo802323p. [DOI] [PMC free article] [PubMed] [Google Scholar]
249.Corey EJ, Loh T-P, Roper TD, Azimioara MD, Noe MC. J Am Chem Soc. 1992;114:8290. [Google Scholar]
250.(a) Nevalainen V. Tetrahedron: Asymmetry. 1993;4:1565. [Google Scholar]; (b) Nevalainen V. Tetrahedron: Asymmetry. 1994;5:767. [Google Scholar]; (c) Uggla R, Nevalainen V, Sundberg MR. Tetradron: Asymmetry. 1996;7:2725. [Google Scholar]
251.Salvatella L, Ruiz-Lopéz MF. J Am Chem Soc. 1999;121:10772. [Google Scholar]
252.Corey EJ, Loh T-P, Roper TD, Azimioara MD, Noe MC. J Am Chem Soc. 1992;114:8290. [Google Scholar]
253.Kiyooka S-I. Rev Heteroat Chem. 1997;17:245. [Google Scholar]
254.Corey EJ, Cywin CL, Roper TD. Tetrahedron Lett. 1992;33:6907. [Google Scholar]
255.Wong MW. J Org Chem. 2005;70:5487. doi: 10.1021/jo050474m. [DOI] [PubMed] [Google Scholar]
256.(a) Yalalov DA, Tsogoeva SB, Schmatz S. Adv Synth Catal. 2006;348:826. [Google Scholar]; (b) Hamza A, Schubert G, Soos T, Papai I. J Am Chem Soc. 2006;128:13151. doi: 10.1021/ja063201x. [DOI] [PubMed] [Google Scholar]; (c) Liu TY, Li R, Chai Q, Long J, Li BJ, Wu Y, Ding LS, Chen YC. Chem Eur J. 2006;13:319. doi: 10.1002/chem.200600796. [DOI] [PubMed] [Google Scholar]
257.Wei S, Yalalov DA, Tsogoeva SB, Schmatz S. Catal Today. 2007;121:151. [Google Scholar]
258.Okino T, Hoashi Y, Furukawa T, Xu X, Takemoto Y. J Am Chem Soc. 2005;127:119. doi: 10.1021/ja044370p. [DOI] [PubMed] [Google Scholar]
259.Chen D, Lu N, Zhang G, Mi S. Tetrahedron: Asymmetry. 2009;20:1365. [Google Scholar]
260.Tan B, Lu Y, Zeng X, Chua PJ, Zhong G. Org, Lett. 2010;12:2682. doi: 10.1021/ol1007795. [DOI] [PubMed] [Google Scholar]
261.Liu T-Y, Li R, Chai Q, Long J, Li B-J, Wu Y, Ding L-S, Chen Y-C. Chem Eur J. 2007;13:319. doi: 10.1002/chem.200600796. [DOI] [PubMed] [Google Scholar]
262.Zhu R, Zhang D, Wu J, Liu C. Tetrahedron: Asymmetry. 2007;18:1655. [Google Scholar]
263.Xu X, Yabuta T, Yuan P, Takemoto Y. Synlett. 2006;1:137–140. [Google Scholar]
264.(a) Zhu R, Zhang D, Wu J, Liu C. Tetrahedron: Asymmetry. 2007;18:1655. [Google Scholar]; (b) Xu X, Yabuta T, Yuan P, Takemoto Y. Synlett. 2006;1:137. [Google Scholar]
265.Sibi MP, Itoh K. J Am Chem Soc. 2007;129:8064. doi: 10.1021/ja071739c. [DOI] [PubMed] [Google Scholar]
266.Simón L, Goodman JM. Org Biomol Chem. 2009;7:483. doi: 10.1039/b817283h. [DOI] [PubMed] [Google Scholar]
267.Zhu Y, Drueckhammer DG. J Org Chem. 2005;70:7755. doi: 10.1021/jo0513818. [DOI] [PubMed] [Google Scholar]
268.Wang S-X, Chen F-E. Adv Synth Catal. 2009;351:547. [Google Scholar]
269.Zhu R-X, Wang R-X, Zhang D-J, Liu C-B. Aust J Chem. 2009;62:157. [Google Scholar]
270.Corey EJ, Grogan MJ. Org Lett. 1999;1:157. doi: 10.1021/ol990623l. [DOI] [PubMed] [Google Scholar]
271.Schuster T, Kurz M, Göbel MW. J Org Chem. 2000;65:1697. doi: 10.1021/jo991372x. [DOI] [PubMed] [Google Scholar]
272.Nugent BM, Yoder RA, Johnston JN. J Am Chem Soc. 2004;126:3418. doi: 10.1021/ja031906i. [DOI] [PubMed] [Google Scholar]
273.Sohtome Y, Hashimot Y, Nagasawa K. Adv Synth Catal. 2005;347:1643. [Google Scholar]
274.Terada M, Nakano M, Ube H. J Am Chem Soc. 2006;128:16044. doi: 10.1021/ja066808m. [DOI] [PubMed] [Google Scholar]
275.Lohmeijer BGG, Pratt RC, Leibfarth F, Logan JW, Long DA, Dove A, Nederberg PF, Choi J, Wade C, Waymouth RM, Hedrick JL. Macromolecules. 2006;39:8574. [Google Scholar]
276.Li J, Jiang W-Y, Han K-L, He G, Zhong, Li C. J Org Chem. 2003;68:8786. doi: 10.1021/jo034891f. [DOI] [PubMed] [Google Scholar]
277.Arnaud R, Adamo C, Cossi M, Milet A, Vallee Y, Barone V. J Am Chem Soc. 2000;122:324. [Google Scholar]
278.Walch SP, Bakes ELO. Chem Phys Lett. 2001;346:267. [Google Scholar]
279.Chuma A, Horn HW, Swope WC, Pratt RC, Zhang L, Lohmeijer BGG, Wade CG, Waymouth RM, Hedrick JL, Rice JE. J Am Chem Soc. 2008;130:6749. doi: 10.1021/ja0764411. [DOI] [PubMed] [Google Scholar]
280.Simón L, Goodman JM. J Org Chem. 2007;72:9656. doi: 10.1021/jo702088c. [DOI] [PubMed] [Google Scholar]
281.Almasi D, Alonso DA, Gómez-Bengoa E, Nájera C. J Org Chem. 2009;74:6163. doi: 10.1021/jo9010552. [DOI] [PubMed] [Google Scholar]
282.Huang SY, Ma J, Li JP, Zhao N, Wei W, Sun YH. Catal Commun. 2008;9:276. [Google Scholar]
283.Ma J, Zhao N, Xia F, Wei W, Sun YH. THEOCHEM. 2009;911:40. [Google Scholar]
284.Russo A, Lattanzi A. Eur J Org Chem. 2008:2767. [Google Scholar]
285.Zhang Z, Rooshenas P, Hausmann H, Schreiner PR. Synthesis. 2009:1531. [Google Scholar]
286.(a) Liu J, Yang Z, Wang Z, Wang F, Chen X, Liu X, Feng X, Su Z, Hu C. J Am Chem Soc. 2008;130:5654. doi: 10.1021/ja800839w. [DOI] [PubMed] [Google Scholar]; (b) Yang Z, Liu J, Liu X, Wang Z, Feng X, Hu C. Adv Synth Catal. 2008;350:2001. [Google Scholar]
287.Chen X, Wang J, Zhu Y, Shang D, Gao B, Liu X, Feng X, Su Z, Hu C. Chem Eur J. 2008;14:10896. doi: 10.1002/chem.200801958. [DOI] [PubMed] [Google Scholar]
288.Yang Z, Liu J, Liu X, Wang Z, Feng X, Su Z, Hu C. Adv Synth Catal. 2008;350:2001. [Google Scholar]
289.Cucinotta CS, Kosa M, Melchiorre P, Cavalli A, Gervasio FL. Chem Eur J. 2009;15:7913. doi: 10.1002/chem.200900406. [DOI] [PubMed] [Google Scholar]
290.Rho HS, Oh SH, Lee JW, Lee JY, Chin J, Song CE. Chem Commun. 2008:1208. doi: 10.1039/b719811f. [DOI] [PubMed] [Google Scholar]
291.Oh SH, Rho HS, Lee JW, Lee JE, Youk SH, Chin J, Song CE. Angew Chem Int Ed. 2008;47:7872. doi: 10.1002/anie.200801636. [DOI] [PubMed] [Google Scholar]
292.Kobbelgaard S, Brandes S, Jørgensen KA. Chem-Eur J. 2008;14:1464. doi: 10.1002/chem.200701729. [DOI] [PubMed] [Google Scholar]
293.Çelebi-Ölçüm N, Aviyente V, Houk KN. J Org Chem. 2009;74:6944. doi: 10.1021/jo901109s. [DOI] [PMC free article] [PubMed] [Google Scholar]
294.(a) Inoue S, Oku JI. J Chem Soc, Chem Commun. 1981:229. [Google Scholar]; (b) Tanaka K, Mori A, Inoue S. J Org Chem. 1990;55:181. [Google Scholar]
295.(a) Danda H, Nishikawa H, Otaka K. J Org Chem. 1991;56:6740. [Google Scholar]; (b) Danda H. Synlett. 1991:263. [Google Scholar]; (c) Kogut EF, Thoen JC, Lipton MA. J Org Chem. 1998;63:4604. [Google Scholar]
296.Shvo Y, Becker GM, Elgavi A. Tetrahedron: Asymmetry. 1996;7:911. [Google Scholar]
297.Li Z, Zhang J, Brouwer C, Yang C-G, Reich NW, He C. Org, Lett. 2006;8:4175. doi: 10.1021/ol0610035. [DOI] [PubMed] [Google Scholar]
298.Li X, Ye S, He C, Yu Z-X. Eur J Org Chem. 2008:4296. [Google Scholar]
299.(a) Bach RD, Glukhovtsev MN, Gonzalez C, Marquez M, Estevez CM, Baboul AG, Schlegel HB. J Phys Chem A. 1997;101:6092. [Google Scholar]; (b) Houk KN, Liu J, DeMello NC, Condroski KR. J Am Chem Soc. 1997;119:10147. [Google Scholar]; (c) Crehuet R, Anglada JM, Cremer D, Bofill JM. J Phys Chem A. 2002;106:3917. [Google Scholar]; (d) Bach RD, Dmitrenko O, Adam W, Schambony S. J Am Chem Soc. 2003;125:924. doi: 10.1021/ja026882e. [DOI] [PubMed] [Google Scholar]; (e) Dmitrenko O, Bach RD. J Phys Chem A. 2004;108:6886. [Google Scholar]
300.Armstrong A, Washington I, Houk KN. J Am Chem Soc. 2000;122:6297. [Google Scholar]
301.Armstrong A, Hayter BR. Chem Commun. 1998:621. [Google Scholar]
302.(a) Tian H, She Z, Shu L, Yu H, Shi Y. J Am Chem Soc. 2000;122:11551. [Google Scholar]; (b) Tian H, She Z, Xu J, Shi Y. Org Lett. 2001;3:1929. doi: 10.1021/ol010066e. [DOI] [PubMed] [Google Scholar]
303.Singleton DA, Wang Z. J Am Chem Soc. 2005;127:1929. doi: 10.1021/ja0435788. [DOI] [PubMed] [Google Scholar]
304.Cramer CJ, Truhlar DG. Acc Chem Res. 2008;41:760. doi: 10.1021/ar800019z. [DOI] [PubMed] [Google Scholar]
305.Oyola Y, Singleton DA. J Am Chem Soc. 2009;131:3130. doi: 10.1021/ja807666d. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R1] 1.(a) Koch W, Holthasuen MC. A Chemist’s Guide to Density Functional Theory. Wiley-VCH; Weinheim, Germany: 2001. [Google Scholar]; (b) Curtis LA, Raghavachari K, Redfern PC, Pople JA. J Chem Phys. 1997;(106):1063. [Google Scholar]

[R2] 2.(a) Wheeler SE, Moran A, Pieniazek SN, Houk KN. J Phys Chem A. 2009;113:10376. doi: 10.1021/jp9058565. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Pieniazek SN, Clemente FR, Houk KN. Angew Chem, Int Ed. 2008;47:7746. doi: 10.1002/anie.200801843. [DOI] [PubMed] [Google Scholar]; (c) Ess DH, Houk KN. J Phys Chem A. 2005;109:9542. doi: 10.1021/jp052504v. [DOI] [PubMed] [Google Scholar]; (d) Guner V, Khuong KS, Leach AG, Lee PS, Bartberger MD, Houk KN. J Phys Chem A. 2003;107:11445. [Google Scholar]; (e) Wodrich MD, Cominboeuf C, Schreiner PR, Fokin AA, Schleyer PvR. Org Lett. 2007;9:1851. doi: 10.1021/ol070354w. [DOI] [PubMed] [Google Scholar]; (f) Jones GO, Guner VA, Houk KN. J Phys Chem A. 2006;110:1216. doi: 10.1021/jp052055z. [DOI] [PubMed] [Google Scholar]; (g) Izgorodina EI, Brittain DRB, Hodgson JL, Krenske EH, Lin CY, Namazian M, Coote ML. J Phys Chem A. 2007;111:10754. doi: 10.1021/jp075837w. [DOI] [PubMed] [Google Scholar]; (h) Dkhissi A, Ducéré JM, Blossey R, Pouchan C. J Comput Chem. 2009;30:1179. doi: 10.1002/jcc.21119. [DOI] [PubMed] [Google Scholar]; (i) Harvey JN. Faraday Discuss. 2010;145:487. [Google Scholar]

[R3] 3.(a) Wodrich MD, Corminboeuf C, Schleyer PvR. Org Lett. 2006;8:3631. doi: 10.1021/ol061016i. [DOI] [PubMed] [Google Scholar]; (b) Wodrich MD, Wannere CS, Mo Y, Jarowski PD, Houk KN, Schleyer PvR. Chem Eur J. 2007;13:7731. doi: 10.1002/chem.200700602. [DOI] [PubMed] [Google Scholar]; (c) Grimme S, Steinmetz M, Korth M. J Chem Thoery Comput. 2006;3:42. doi: 10.1021/ct600224b. [DOI] [PubMed] [Google Scholar]; (d) Schreiner PR, Fokin AA, Pascal RA, de Meijere A. Org Lett. 2006;8:3635. doi: 10.1021/ol0610486. [DOI] [PubMed] [Google Scholar]; (e) Stefan G. Angew Chem, Int Ed. 2006;45:4460. [Google Scholar]; (g) Schreiner PR. Angew Chem, Int Ed. 2007;46:4217. doi: 10.1002/anie.200700386. [DOI] [PubMed] [Google Scholar]

[R4] 4.Paul W, Timothy C. J Comput Chem. 2004;25:725. [Google Scholar]

[R5] 5.(a) Grimme S, Steinmetz M, Korth M. J Org Chem. 2007;72:2118. doi: 10.1021/jo062446p. [DOI] [PubMed] [Google Scholar]; (b) Rokob TA, Hamza A, Papai I. Org Lett. 2007;9:4279. doi: 10.1021/ol701872z. [DOI] [PubMed] [Google Scholar]

[R6] 6.(a) Zhao Y, Truhlar DG. J Chem Theory Comput. 2006;3:289. doi: 10.1021/ct6002719. [DOI] [PubMed] [Google Scholar]; (b) Zhao Y, Truhlar DG. J Chem Theory Comput. 2005;1:415. doi: 10.1021/ct049851d. [DOI] [PubMed] [Google Scholar]; (c) Zhao Y, Truhlar DG. Phys Chem Chem Phys. 2005;7:2701. doi: 10.1039/b507036h. [DOI] [PubMed] [Google Scholar]

[R8] 8.Bahmanyar S, Houk KN, Martin HJ, List B. J Am Chem Soc. 2003;125:2475. doi: 10.1021/ja028812d. [DOI] [PubMed] [Google Scholar]

[R9] 9.Simón L, Goodman JM. Org Biomol Chem. 2011;9:689. doi: 10.1039/c0ob00477d. [DOI] [PubMed] [Google Scholar]

[R10] 10.(a) Hajos ZG, Parrish DR. 2102623. DE. 1971 Jul 29;; (b) Hajos AG, Parrish DR. J Org Chem. 1974;39:1615. [Google Scholar]

[R11] 11.(a) Eder U, Sauer G, Wiechert R. 2014757. DE. 1971 Oct 7;; (b) Eder U, Sauer G, Wiechert R. Angew Chem, Int Ed Eng. 1971;10:496. [Google Scholar]

[R12] 12.List B. Angew Chem Int Ed. 2010;49:1730. doi: 10.1002/anie.200906900.For earlier reviews, see: List B. Chem Rev. 2007;107:5413. doi: 10.1021/cr0684016.List B. Chem Commun. 2006:819. doi: 10.1039/b514296m.List B, Houk KN. Acc Chem Res. 2004;37:487. doi: 10.1021/ar0300571.List B. Adv Synth Catal. 2004;346:1021.

[R13] 13.MacMillan DWC. Nature. 2008;455:304. doi: 10.1038/nature07367. [DOI] [PubMed] [Google Scholar]

[R14] 14.Puchot C, Samuel O, Dunach E, Zhao S, Agami C, Kagan HB. J Am Chem Soc. 1986;108:2353. doi: 10.1021/ja00269a036. [DOI] [PubMed] [Google Scholar]

[R15] 15.Jung ME. Tetrahedron. 1976;3:2, 3. [Google Scholar]

[R16] 16.Clemente FR, Houk KN. Angew Chem Int Ed. 2004;43:5766. doi: 10.1002/anie.200460916. [DOI] [PubMed] [Google Scholar]

[R17] 17.For a study on the accuracy of DFT in predicting thermochemistries of the aldol, Mannich, and a-aminoxylation reactions, see: Wheeler SE, Moran A, Pieniazek SN, Houk KN. J Phys Chem A. 2009;113:10376. doi: 10.1021/jp9058565.

[R18] 18.Zhu H, Clemente FR, Houk KN, Meyer MP. J Am Chem Soc. 2009;131:1632. doi: 10.1021/ja806672y. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R19] 19.Bahmanyar S, Houk KN. J Am Chem Soc. 2001;123:12911. doi: 10.1021/ja011714s. [DOI] [PubMed] [Google Scholar]

[R20] 20.Cheong PH-Y, Houk KN, Warrier JS, Hanessian S. Adv Synth Catal. 2004;346:1111. [Google Scholar]

[R21] 21.Cheong PH-Y, Houk KN. Synthesis. 2005;9:1533. [Google Scholar]

[R22] 22.Clemente FR, Houk KN. J Am Chem Soc. 2005;127:11294. doi: 10.1021/ja0507620. [DOI] [PubMed] [Google Scholar]

[R23] 23.List B, Lerner RA, Barbas CF., III J Am Chem Soc. 2000;122:2395. [Google Scholar]

[R24] 24.Patil MP, Sunoj RB. J Org Chem. 2007;72:8202. doi: 10.1021/jo071004q. [DOI] [PubMed] [Google Scholar]

[R25] 25.Sharma AK, Sunoj RB. Angew Chem, Int Ed. 2010;49:6373. doi: 10.1002/anie.201001588. [DOI] [PubMed] [Google Scholar]

[R26] 26.Rankin KN, Gauld JW, Boyd RJ. J Phys Chem A. 2002;106:5155. [Google Scholar]

[R27] 27.Zotova N, Broadbelt LJ, Armstrong A, Blackmond DG. Bioorg Med Chem Lett. 2009;19:3934. doi: 10.1016/j.bmcl.2009.03.112. [DOI] [PubMed] [Google Scholar]

[R28] 28.Schmid MB, Zeitler K, Gschwind RM. Angew Chem, Int Ed. 2010;49:4997. doi: 10.1002/anie.200906629. [DOI] [PubMed] [Google Scholar]

[R29] 29.(a) Pihko PM, Laurikainen KM, Usano A, Nyberg AI, Kaavi JA. Tetrahedron. 2006;62:317. [Google Scholar]; (b) Hartikka A, Arvidsson PI. Eur J Org Chem. 2005:4287. [Google Scholar]; (c) List B, Hoang L, Martin HJ. Proc Natl Acad Sci USA. 2004;101:5839. doi: 10.1073/pnas.0307979101. [DOI] [PMC free article] [PubMed] [Google Scholar]; (d) de Arriba ÁLF, Simón L, Raposo C, Alcázar V, Morán JR. Tetrahedron. 2009;65:4841. [Google Scholar]; (e) Zotova N, Franzke A, Armstrong A, Blackmond D. J Am Chem Soc. 2007;129:15100. doi: 10.1021/ja0738881. [DOI] [PubMed] [Google Scholar]; (f) Iwamuara H, Mathew SP, Blackmond DG. J Am Chem Soc. 2004;126:11770. doi: 10.1021/ja046258x. [DOI] [PubMed] [Google Scholar]

[R30] 30.Seebach D, Beck AK, Badine DM, Limbach M, Eschenmoser A, Treasurywala AM, Hobi R, Prikoszovich W, Linder B. Helv Chim Acta. 2007;90:425. [Google Scholar]

[R31] 31.Blackmond DG, Moran A, Hughes M, Armstrong A. J Am Chem Soc. 2010;132:7598. doi: 10.1021/ja102718x. [DOI] [PubMed] [Google Scholar]

[R32] 32.Zimmerman HE, Traxler MD. J Am Chem Soc. 1957;79:1920. [Google Scholar]

[R33] 33.Hoang L, Bahmanyar S, Houk KN, List B. J Am Chem Soc. 2003;125:16. doi: 10.1021/ja028634o. [DOI] [PubMed] [Google Scholar]

[R34] 34.Bachrach SM. Computational Organic Chemistry. Wiley; New York: 2007. [Google Scholar]

[R35] 35.Arno M, Zaragoza RJ, Domingo LR. Tetrahedron: Asymmetry. 2005;16:2764. [Google Scholar]

[R36] 36.(a) Tang Z, Jiang F, Yu TL, Cui X, Gong LZ, Mi AQ, Jiang YZ, Wu YD. J Am Chem Soc. 2003;125:5262. doi: 10.1021/ja034528q. [DOI] [PubMed] [Google Scholar]; (b) Tang Z, Jiang F, Cui X, Gong LZ, Mi AQ, Jiang YZ, Wu YD. Proc Nat Acad Sci. 2004;101:5755. doi: 10.1073/pnas.0307176101. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R37] 37.Xu X-Y, Tang Z, Wang Y-Z, Luo S-W, Cun L-F, Gong L-Z. J Org Chem. 2007;72:9905. doi: 10.1021/jo701868t. [DOI] [PubMed] [Google Scholar]

[R38] 38.Chen X-H, Luo S-W, Tang Z, Cun L-F, Mi A-Q, Jiang Y-Z, Gong L-Z. Chem Eur J. 2007;13:689. doi: 10.1002/chem.200600801. [DOI] [PubMed] [Google Scholar]

[R39] 39.Okuyama Y, Nakano H, Watanabe Y, Makabe M, Takeshita M, Uwai K, Kabuto C, Kwon E. Tet Lett. 2009;50:193. [Google Scholar]

[R40] 40.Córdova A, Zou W, Ibrahem I, Reyes E, Engqvist M, Liao WW. Chem Commun. 2005:3586. doi: 10.1039/b507968n.Amedjkouh M. Tetrahedron: Asymmetry. 2005;16:1411.Dziedzic P, Zou W, Háfren J, Córdova A. Org Biomol Chem. 2006;4:38. doi: 10.1039/b515880j.Córdova A, Zou W, Dziedzic P, Ibrahem I, Reyes E, Xu Y. Chem Eur J. 2006;12:5383. doi: 10.1002/chem.200501639.Correction: Córdova A, Zou W, Dziedzic P, Ibrahem I, Reyes E, Xu Y. Chem Eur J. 2006;12:5175. doi: 10.1002/chem.200501639.Klussmann M, Iwamura H, Matthew SP, Wells DH, Jr, Pandya U, Armstrong A, Blackmond DG. Nature. 2006;441:621. doi: 10.1038/nature04780.

[R41] 41.Bassan A, Zou W, Reyes E, Himo F, Córdova A. Angew Chem Int Ed. 2005;44:7028. doi: 10.1002/anie.200502388. [DOI] [PubMed] [Google Scholar]

[R42] 42.Diner P, Amedjkouh M. Org Biomol Chem. 2006;4:2091. doi: 10.1039/b605091c. [DOI] [PubMed] [Google Scholar]

[R43] 43.Dickerson TJ, Lovell T, Meijler MM, Noodleman L, Janda KD. J Org Chem. 2004;69:6603. doi: 10.1021/jo048894j. [DOI] [PubMed] [Google Scholar]

[R44] 44.Zhang X, Houk KN. J Am Chem Soc. 2005;70:9712. [Google Scholar]

[R45] 45.(a) List B. J Am Chem Soc. 2000;122:9336. [Google Scholar]; (b) List B, Pojarliev P, Biller WT, Martin HJ. J Am Chem Soc. 2002;124:827. doi: 10.1021/ja0174231. [DOI] [PubMed] [Google Scholar]; (c) Pojarliev P, Biller WT, Martin HJ, List B. Synlett. 2003:1903. [Google Scholar]; (d) Yang JW, Stadler M, List B. Angew Chem Int Ed. 2007;46:609. doi: 10.1002/anie.200603188. [DOI] [PubMed] [Google Scholar]

[R46] 46.Bahmanyar S, Houk KN. Org Lett. 2003;5:1249. doi: 10.1021/ol034198e. [DOI] [PubMed] [Google Scholar]

[R47] 47.Hayashi Y, Urushima T, Shoji M, Uchimaru T, Shiina I. Adv Synth Catal. 2005;347:1595. [Google Scholar]

[R48] 48.Cheong PH-Y, Zhang H, Thayumanavan R, Tanaka F, Houk KN, Barbas CF., III Org Lett. 2006;8:811. doi: 10.1021/ol052861o. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R49] 49.Hayashi Y, Okano T, Itoh T, Urushima T, Ishhikawa H, Uchimaru T. Angew Chem Int Ed. 2008;47:9053. doi: 10.1002/anie.200802073. [DOI] [PubMed] [Google Scholar]

[R50] 50.Wong CT. Tetrahedron. 2009;65:7491. [Google Scholar]

[R51] 51.(a) Li H, Fu A, Shi H. J Mol Catal A: Chem. 2009;303:1. [Google Scholar]; (b) Zhuang W, Saaby S, Jørgensen KA. Angew Chem Int Ed. 2004;43:4476. doi: 10.1002/anie.200460158. [DOI] [PubMed] [Google Scholar]

[R52] 52.Zhang H, Mitsumori S, Utsumi N, Imai M, Garcia-Delgado N, Mifsud M, Albertshofer K, Cheong PH-Y, Houk KN, Tanaka F, Barbas CF., III J Am Chem Soc. 2008;130:875. doi: 10.1021/ja074907+. [DOI] [PubMed] [Google Scholar]

[R53] 53.Hayashi Y, Yamaguchi J, Hibino K, Shoji M. Tetrahedron Lett. 2003;44:8293. [Google Scholar]

[R54] 54.Zhong G. Angew Chem Int Ed. 2003;42:4247. doi: 10.1002/anie.200352097. [DOI] [PubMed] [Google Scholar]

[R55] 55.Brown SP, Brochu MP, Sinz CJ, MacMillan DWC. J Am Chem Soc. 2003;125:10808. doi: 10.1021/ja037096s. [DOI] [PubMed] [Google Scholar]

[R56] 56.(a) Mathew SP, Iwamuara H, Blackmond DG. Angew Chem. 2004;116:3379. doi: 10.1002/anie.200453997. [DOI] [PubMed] [Google Scholar]; (b) Iwamura H, Wells DH, Mathew SP, Klussmann M, Armstrong A, Blackmond DG. J Am Chem Soc. 2004;126:16312. doi: 10.1021/ja0444177. [DOI] [PubMed] [Google Scholar]; (c) Mathew SP, Klussmann M, Iwamura H, Wells DH, Jr, Armstrong A, Blackmond DA. Chem Commun. 2006:4291. doi: 10.1039/b609926b. [DOI] [PubMed] [Google Scholar]

[R57] 57.Zotova N, Moran A, Armstrong A, Blackmond DG. Adv Synth Catal. 2009;351:2765. and references therein. [Google Scholar]

[R58] 58.(a) Córdova A, Sundén H, Bøgevig A, Johansson M, Himo F. Chem Eur J. 2004;10:3673. doi: 10.1002/chem.200400137. [DOI] [PubMed] [Google Scholar]; (b) Cheong PHY, Houk KN. J Am Chem Soc. 2004;126:13912. doi: 10.1021/ja0464746. [DOI] [PubMed] [Google Scholar]; (c) Wong H, Yang C, Han K. Struc Chem. 2006;17:97. [Google Scholar]

[R59] 59.Dinér P, Kjærsgaard A, Lie MA, Jørgensen KA. Chem Eur J. 2008;14:122. doi: 10.1002/chem.200701244.Four groups independently reported the organocatalyzed α-fluorination reaction of aldehydes in the same year: Beeson TD, MacMillan DWC. J Am Chem Soc. 2005;127:8826. doi: 10.1021/ja051805f.Steiner DD, Mase N, Barbas CF., III Angew Che Int Ed. 2005;44:3706. doi: 10.1002/anie.200500571.Enders D, Hüttl MRM. Synlett. 2005:991.Marigo M, Fielenbach D, Braunton A, Kjærsgaard A, Jørgensen KA. Angew Che Int Ed. 2005;44:3703. doi: 10.1002/anie.200500395.

[R60] 60.Bertelson S, Marigo M, Brandes S, Dinér P, Jørgensen KA. J Am Chem Soc. 2006;128:12973. doi: 10.1021/ja064637f. [DOI] [PubMed] [Google Scholar]

[R61] 61.Groselj U, Seebach D, Badine DM, Schweizer WB, Beck AK. Helv Chim Acta. 2009;92:1225. [Google Scholar]

[R62] 62.Vignola N, List B. J Am Chem Soc. 2003;126:450. doi: 10.1021/ja0392566. [DOI] [PubMed] [Google Scholar]

[R63] 63.Fu A, List B, Thiel W. J Org Chem. 2006;71:320. doi: 10.1021/jo052088a. [DOI] [PubMed] [Google Scholar]

[R64] 64.Ibrahem I, Hammar P, Vesely J, Rios R, Eriksson L, Córdova A. Adv Synth Catal. 2008;350:1875. [Google Scholar]

[R65] 65.Arnó M, Zaragozá RJ, Domingo LR. Tetrahedron: Asymmetry. 2007;18:157. [Google Scholar]

[R66] 66.Seebach D, Golinski J. Helv Chim Acta. 1981;64:1413. [Google Scholar]

[R67] 67.Mahendra PP, Sunoj RB. Chem Eur J. 2008;14:10472. [Google Scholar]

[R68] 68.(a) List B. Tetrahedron. 2002;58:5573. [Google Scholar]; (b) Enders D, Seki A. Synlett. 2002;1:26. [Google Scholar]; (c) Betancort JM, Barbas CF., III Org Lett. 2001;3:3737. doi: 10.1021/ol0167006. [DOI] [PubMed] [Google Scholar]; (d) Mase N, Thayumanavan R, Tanaka F, Barbas CF., III Org Lett. 2004;6:2527. doi: 10.1021/ol049196o. [DOI] [PubMed] [Google Scholar]

[R69] 69.Almasi D, Alonso DA, Gómez-Bengoa E, Nagel Y, Nájera C. Eur J Org Chem. 2007:2328. doi: 10.1021/jo9010552. [DOI] [PubMed] [Google Scholar]

[R70] 70.Sulzer-Mossé S, Alexakis A, Mareda J, Bollot G, Bernardinelli G, Filinchuk Y. Chem Eur J. 2009;15:3204. doi: 10.1002/chem.200801892. [DOI] [PubMed] [Google Scholar]

[R71] 71.Melchiorre P, Jørgensen KA. J Org Chem. 2003;68:4151. doi: 10.1021/jo026837p. [DOI] [PubMed] [Google Scholar]

[R72] 72.Patil MP, Sunoj RB. Chem Asian J. 2009;4:714. doi: 10.1002/asia.200800351. [DOI] [PubMed] [Google Scholar]

[R73] 73.(a) Shinisha CB, Sunoj Raghavan B. Org Biomol Chem. 2008;6:3921. doi: 10.1039/b810901j. [DOI] [PubMed] [Google Scholar]; (b) Enders D, Huttl MRM, Grandoal C, Raabe G. Nature. 2006;441:861. doi: 10.1038/nature04820. [DOI] [PubMed] [Google Scholar]

[R74] 74.(a) Duarte FJS, Cabriat EJ, Frenking G, Santos AG. Chem Eur J. 2009;15:1734. doi: 10.1002/chem.200801624. [DOI] [PubMed] [Google Scholar]; (b) Chen SH, Hong BC, Su CF, Sarshar S. Tetrahedron Lett. 2005;46:8899. [Google Scholar]

[R75] 75.(a) Basavaiah D, Rao AJ, Satyanarayana T. Chem Rev. 2003;103:811. doi: 10.1021/cr010043d. [DOI] [PubMed] [Google Scholar]; (b) Basavaiah D, Rao KV, Reddy RJ. Chem Soc Rev. 2007;36:1581. doi: 10.1039/b613741p. [DOI] [PubMed] [Google Scholar]

[R76] 76.Ahrendt KA, Borths CJ, MacMillan DWC. J Am Chem Soc. 2000;122:4243. [Google Scholar]

[R77] 77.Burley JC, Gilmour R, Prior TJ, Day GM. Acta Cryst. 2008;C64:010. doi: 10.1107/S0108270107051396. [DOI] [PubMed] [Google Scholar]

[R78] 78.Groselj U, Schweizer WB, Ebert M-O, Seebach D. Helv Chim Acta. 2009;92:1. [Google Scholar]

[R79] 79.(a) Gordillo R, Carter J, Houk KN. Adv Synth Catal. 2004;346:1175. [Google Scholar]; (b) Austin JF, MacMillan DWC. J Am Chem Soc. 2002;124:1172. doi: 10.1021/ja017255c. [DOI] [PubMed] [Google Scholar]

[R80] 80.Brazier JB, Evans G, Gibbs TJK, Coles SJ, Hursthouse MB, Platts JA, Tomkinson NCO. Org Lett. 2009;11:133. doi: 10.1021/ol802512y. [DOI] [PubMed] [Google Scholar]

[R81] 81.Gordillo R, Houk KN. J Am Chem Soc. 2006;128:3543. doi: 10.1021/ja0525859. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R82] 82.Gutierrez O, Iafe RG, Houk KN. Org Lett. 2009;11:4298. doi: 10.1021/ol901586t. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R83] 83.Nicolaou KC, Reingruber R, Sarlah D, Bräse S. J Am Chem Soc. 2009;131:2086. doi: 10.1021/ja809405c. Correction: J. Am. Chem. Soc 2009, 131, 6640. [DOI] [PubMed] [Google Scholar]

[R84] 84.Conrad JC, Kong J, Laforteza BN, MacMillan DWC. J Am Chem Soc. 2009;131:11640. doi: 10.1021/ja9026902. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R85] 85.Um JM, Gutierrez O, Schoenebeck F, Houk KN, MacMillan DWC. J Am Chem Soc. 2010;132:6001. doi: 10.1021/ja9063074. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R86] 86.For ortho-selective radical additions to aromatics, see: Tiecco M, Testaferri L. In: Reactive Intermediates. Abramovitch RA, editor. Vol. 3. Plenum Press; New York: 1983. p. 61.Guadarrama-Morales O, Mendéz F, Miranda LD. Tetrahedron Lett. 2007;48:4515.Muchowski JM, Cho IS, Jaime-Figueroa S, Artis RD. J Org Chem. 1994;59:2456.For a study of the stability of cyclohexadienyl radicals, see: Birch AJ, Hinde AL, Radom L. J Am Chem Soc. 1980;102:4074.

[R87] 87.For a recent review on carbene catalysts, see: Moore JL, Rovis T. In: Asymmetric Organocatalysis. List B, editor. Springer Verlag; Heidelberg: 2010. pp. 77–144.

[R88] 88.Wöhler F, Liebig J. Ann Pharm. 1832;3:249. [Google Scholar]

[R89] 89.Ugai T, Tanaka S, Dokawa S. J Pharm Soc Jpn. 1943;63:269. [Google Scholar]

[R90] 90.(a) López Calahorra F, Castells J, Domingo L, Martí J, Bofill JM. Heterocycles. 1994;37:1579. [Google Scholar]; (b) Martí J, López Calahorra F, Bofill JM. J Mol Struct (Theochem) 1995;339:179. [Google Scholar]

[R91] 91.Dudding T, Houk KN. Proc Nat Acad Sci. 2004;101:5770. doi: 10.1073/pnas.0307256101. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R92] 92.Breslow R. J Am Chem Soc. 1958;80:3719. [Google Scholar]

[R93] 93.Enders D, Kallfass U. Angew Chem, Int Ed. 2002;41:1743. doi: 10.1002/1521-3773(20020517)41:10<1743::aid-anie1743>3.0.co;2-q. [DOI] [PubMed] [Google Scholar]

[R94] 94.Knight RL, Leeper FJ. Tetrahedron Lett. 1997;38:3611. [Google Scholar]

[R95] 95.Sheehan J, Hara T. J Org Chem. 1974;39:1196. [Google Scholar]

[R96] 96.(a) Enders D, Breuer K, Teles JH. Helv Chim Acta. 1996;79:1217. [Google Scholar]; (b) Enders D, Breuer K. Comprehensive Asymmetric Catalysis. Vol. 3. Springer-Verlag; Heidelberg, Germany: 1999. p. 1093. [Google Scholar]; (c) Teles JH, Breuer K, Enders D, Gielen H. Synth Commun. 1999;29:1. [Google Scholar]

[R97] 97.Hachisu Y, Bode JW, Suzuki K. Adv Synth Catal. 2004;346:1097. [Google Scholar]

[R98] 98.Hawkes KJ, Yates BF. Eur J Org Chem. 2008:5563. [Google Scholar]

[R99] 99.(a) Grasa GA, Kissling RM, Nolan SP. Org Lett. 2002;4:3583. doi: 10.1021/ol0264760. [DOI] [PubMed] [Google Scholar]; (b) Grasa GA, Guveli T, Singh R, Nolan SP. J Org Chem. 2003;68:2812. doi: 10.1021/jo0267551. [DOI] [PubMed] [Google Scholar]

[R100] 100.Nyce GW, Lamboy JA, Connor EF, Waymouth RM, Hedrick JL. Org Lett. 2002;4:3587. doi: 10.1021/ol0267228.For reviews in NHC-catalyzed polymerization reactions, see: Dove AP, Pratt RC, Lohmeijer BGG, Culkin DA, Hagberg EC, Nyce GW, Waymouth RM, Hedrick JL. Polymer. 2006;47:4018.Coulembier O, Gegée P, Hedrick JL, Dubois P. Prog Polym Sci. 2006;31:723.

[R101] 101.Lai C-L, Lee HM, Hu C-H. Tetrahedron Lett. 2005;46:6265. [Google Scholar]

[R102] 102.Maki BE, Patterson EV, Cramer CJ, Scheidt KA. Org Lett. 2009;11:3942. doi: 10.1021/ol901545m. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R103] 103.See Chan A, Scheidt KA. Org Lett. 2005;7:905. doi: 10.1021/ol050100f. and references therein. [DOI] [PubMed] [Google Scholar]

[R104] 104.Ragsdale SW. Chem Rev. 2003;103:2333. doi: 10.1021/cr020423e. [DOI] [PubMed] [Google Scholar]

[R105] 105.Guin J, De Sarkar S, Grimme S, Studer A. Angew Chem Int Ed. 2008;47:8727. doi: 10.1002/anie.200802735. [DOI] [PubMed] [Google Scholar]

[R106] 106.Xu S, Held I, Kempf B, Mayr H, Steglich W, Zipse H. Chem Eur J. 2005;11:4751. doi: 10.1002/chem.200500398. [DOI] [PubMed] [Google Scholar]

[R107] 107.(a) Guibe-Jampel E, Le Corre G, Wakselman M. Tetrahedron Lett. 1979;20:1157. [Google Scholar]; (b) Kattnig E, Albert M. Org Lett. 2004;6:945. doi: 10.1021/ol0364935. [DOI] [PubMed] [Google Scholar]; (c) Lamaty G, Mary F, Roque JP. J Chim Phys Phys-Chim Biol. 1991;88:1793. [Google Scholar]

[R108] 108.Fischer CB, Xu S, Zipse H. Chem Eur J. 2006;12:5779. doi: 10.1002/chem.200600280. [DOI] [PubMed] [Google Scholar]

[R109] 109.Wei Y, Held I, Zipse H. Org Biomol Chem. 2006;4:4223. doi: 10.1039/b610140b. [DOI] [PubMed] [Google Scholar]

[R110] 110.Held I, Villinger A, Zipse H. Synthesis. 2005;9:1425. [Google Scholar]

[R111] 111.(a) Heinrich MR, Klisa HS, Mayr H, Steglich W, Zipse H. Angew Chem Int Ed. 2003;42:4826. doi: 10.1002/anie.200352289. [DOI] [PubMed] [Google Scholar]; (b) Held I, Xu S, Zipse H. Synthesis. 2007;8:1185. [Google Scholar]; (c) Held I, Larinov E, Bozle C, Wagner F, Zipse H. Synthesis. 2009;13:2267. [Google Scholar]

[R112] 112.Zipse has also calculated the methyl cation affinities of commonly used nitrogen and phosphorous-based organocatalysts. See: Wei Y, Sastry N, Zipse H. J Am Chem Soc. 2008;130:3473. doi: 10.1021/ja0764409.Wei Y, Singer T, Mayr H, Sastry GN, Zipse H. J Comput Chem. 2008;29:291. doi: 10.1002/jcc.20790.The same group reported the performance of computational methods in describing zwitterionic adducts between NMe3 and PMe3 with methyl vinyl ketone. See: Wei Y, Bandaru S, Maryasin B, Sastry N, Zipse H. J Comput Chem. 2009;30:2617. doi: 10.1002/jcc.21271.

[R113] 113.(a) Singh S, Das G, Singh OV, Han H. Org Lett. 2007;9:401. doi: 10.1021/ol062712l. [DOI] [PubMed] [Google Scholar]; (b) Singh S, Das G, Singh OV, Han H. Tetrahedron Lett. 2007;48:1983. doi: 10.1016/j.tetlet.2007.09.129. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R114] 114.(a) Steglich W, Höfle G. Tetrahedron Lett. 1970;54:4727. [Google Scholar]; (b) Hassner A, Krepski LR, Alexanian V. Tetrahedron. 1978;34:2069. [Google Scholar]

[R115] 115.(a) Yamada S, Yamashita K. Tetrahedron Lett. 2008;49:32. [Google Scholar]; (b) Yamada S, Misono T, Iwai Y, Masumizu A, Akiyama Y. J Org Chem. 2006;71:6872. doi: 10.1021/jo060989t. [DOI] [PubMed] [Google Scholar]; (c) Yamada S, Misono T, Iwai Y. Tetrahedron Lett. 2005;46:2239. [Google Scholar]; (d) Yamada S, Noguchi E. Tetrahedron Lett. 2002;42:3621. [Google Scholar]

[R116] 116.Lutz V, Glatthaar J, Würtele C, Serafin M, Hausmann H, Schreiner PR. Chem Eur J. 2009;15:8548. doi: 10.1002/chem.200901379. [DOI] [PubMed] [Google Scholar]

[R117] 117.(a) Marcelli T, van Maarseveen JH, Hiemstra H. Angew Chem Int Ed. 2006;45:7496. doi: 10.1002/anie.200602318. [DOI] [PubMed] [Google Scholar]; (b) Tan SK, Chen Y, Hang J, Tang L, McDaid P, Deng L. Acc Chem Res. 2004;37:621. doi: 10.1021/ar030048s. [DOI] [PubMed] [Google Scholar]; (c) Hoffmann HMR, Frackenpohl J. Eur J Org Chem. 2004:4293. [Google Scholar]; (d) Kacprzak K, Gawroskik J. Synthesis. 2001;7:961. [Google Scholar]

[R118] 118.Bürgi T, Baiker A. J Am Chem Soc. 1998;120:12920. [Google Scholar]

[R119] 119.Vargas A, Bonalumi N, Ferri D, Baiker A. J Phys Chem A. 2006;110:1118. doi: 10.1021/jp055013j. [DOI] [PubMed] [Google Scholar]

[R120] 120.Olsen RA, Borchardt D, Mink L, Agarwal A, Mueller LJ, Zaera F. J Am Chem Soc. 2006;138:15594. doi: 10.1021/ja066989s. [DOI] [PubMed] [Google Scholar]

[R121] 121.Szöllösi G, Chatterjee A, Forgó P, Bartók M, Mizukami F. J Phys Chem A. 2005;109:860. doi: 10.1021/jp045882t. [DOI] [PubMed] [Google Scholar]

[R122] 122.Taggi AE, Hafez AM, Wack H, Young B, Ferraris D, Lectka T. J Am Chem Soc. 2002;124:6626. doi: 10.1021/ja0258226. [DOI] [PubMed] [Google Scholar]

[R123] 123.Taggi AE, Hafez AM, Dudding T, Lectka T. Tetrahedron. 2002;58:8351. [Google Scholar]

[R124] 124.Brunner H, Schmidt P. Eur J Org Chem. 2000:2119. [Google Scholar]

[R125] 125.Drees M, Kleiber L, Wemer M, Strassner T. Eur J Org Chem. 2002:2405. [Google Scholar]

[R126] 126.Peltier HM, Evans JW, Ellman JA. Org Lett. 2005;7:1733. doi: 10.1021/ol050275p. [DOI] [PubMed] [Google Scholar]

[R127] 127.Shibata N, Matsunaga M, Nakagawa M, Fukuzumi T, Nakamura S, Toru T. J Am Chem Soc. 2005;127:1374. doi: 10.1021/ja0430189. [DOI] [PubMed] [Google Scholar]

[R128] 128.Balcells D, Maseras F, Khiar N. Org Lett. 2005;6:2197. doi: 10.1021/ol0493507. [DOI] [PubMed] [Google Scholar]

[R129] 129.Balcells D, Ujaque G, Fernandez I, Khiar N, Maseras F. J Org Chem. 2006;71:6388. doi: 10.1021/jo060546p. [DOI] [PubMed] [Google Scholar]

[R130] 130.(a) France S, Wack H, Taggi AE, Hafez AM, Wagerle TR, Shah MH, Cusich CL, Lectka T. J Am Chem Soc. 2004;126:4245. doi: 10.1021/ja039046t. [DOI] [PubMed] [Google Scholar]; (b) Wack H, Taggi AE, Hafez AM, Drury WJ, III, Lectka T. J Am Chem Soc. 2001;123:1531. doi: 10.1021/ja005791j. [DOI] [PubMed] [Google Scholar]; (c) France S, Weatherwax A, Lectka T. Eur J Org Chem. 2005;3:475. [Google Scholar]

[R131] 131.Hafez AM, Taggi AE, Wack H, Esterbrook J, Lectka T. Org Lett. 2001;3:2049. doi: 10.1021/ol0160147. [DOI] [PubMed] [Google Scholar]

[R132] 132.Dogo-Isonagie C, Bekele T, France S, Wolfer J, Weatherwax A, Taggi AE, Paull DH, Dudding T, Lectka T. Eur J Org Chem. 2007:1091. doi: 10.1021/jo061522l. [DOI] [PubMed] [Google Scholar]

[R133] 133.(a) Liu B, Feng X, Chen F, Zhang G, Cui X, Jiang Y. Synlett. 2001;10:1551. [Google Scholar]; (b) Jiao Z, Feng X, Liu B, Chen F, Zhang GL, Jiang Y. Eur J Org Chem. 2003:3818. [Google Scholar]

[R134] 134.Su Z, Hu C, Qin S, Feng X. Tetrahedron. 2006;62:4071. [Google Scholar]

[R135] 135.Aggarwal VK, Alonso E, Hynd G, Lydon KM, Palmer MJ, Porcelloni M, Studley JR. Angew Chem Int Ed. 2001;40:1430. doi: 10.1002/1521-3773(20010417)40:8<1430::AID-ANIE1430>3.0.CO;2-W. [DOI] [PubMed] [Google Scholar]

[R136] 136.Volatron F, Eisenstein O. J Am Chem Soc. 1987;109:1. doi: 10.1021/ja00269a009. [DOI] [PubMed] [Google Scholar]

[R137] 137.(a) Lindvall MK, Koskinen AMP. J Org Chem. 1999;64:4595. doi: 10.1021/jo9818935. [DOI] [PubMed] [Google Scholar]; (b) Myllymäki VT, Lindvall MK, Koskinen AMP. Tetrahedron. 2001;57:4629. [Google Scholar]

[R138] 138.Aggarwal VK, Harvey JN, Richardson J. J Am Chem Soc. 2002;124:5747. doi: 10.1021/ja025633n. [DOI] [PubMed] [Google Scholar]

[R139] 139.Aggarwal VK, Charmant JPH, Fuentes D, Harvey JN, Hynd G, Ohara D, Picoul W, Robiette R, Smith C, Vasse J-L, Winn CL. J Am Chem Soc. 2006;128:2105. doi: 10.1021/ja0568345. [DOI] [PubMed] [Google Scholar]

[R140] 140.Imashiro R, Yamanaka T, Seki M. Tetrahedron: Asymmetry. 1999;10:2845. [Google Scholar]

[R141] 141.Aggarwal VK, Harvey JN, Robiette R. Angew Chem Int Ed. 2005;44:5468. doi: 10.1002/anie.200501526. [DOI] [PubMed] [Google Scholar]

[R142] 142.Robiette R, Conza M, Aggarwal VK. Org Biomol Chem. 2006;4:621. doi: 10.1039/b516926g. [DOI] [PubMed] [Google Scholar]

[R143] 143.Silva MA, Bellenie BR, Goodman JM. Org Lett. 2004;6:2559. doi: 10.1021/ol0491641. [DOI] [PubMed] [Google Scholar]

[R144] 144.Zanardi J, Leriverend C, Aubert D, Julienne K, Metzner P. J Org Chem. 2001;66:5620. doi: 10.1021/jo015588m. [DOI] [PubMed] [Google Scholar]

[R145] 145.(a) Winn CL, Bellenie BR, Goodman JM. Tetrahedron Lett. 2002;43:5427. [Google Scholar]; (b) Winn C, Goodman JM. Tetrahedron Lett. 2001;42:7091. [Google Scholar]

[R146] 146.Deng X-M, Cai P, Ye S, Sun X-L, Liao W-W, Li K, Tang Y, Wu Y-D, Dai L-X. J Am Chem Soc. 2005;128:9730. doi: 10.1021/ja056751o. [DOI] [PubMed] [Google Scholar]

[R147] 147.Robiette R. J Org Chem. 2006;71:2726. doi: 10.1021/jo052559t. [DOI] [PubMed] [Google Scholar]

[R148] 148.Janardanan D, Sunoj RB. Chem Eur J. 2007;13:4805. doi: 10.1002/chem.200700303. [DOI] [PubMed] [Google Scholar]

[R149] 149.Janardanan D, Sunoj RB. J Org Chem. 2008;73:8163. doi: 10.1021/jo800652c. [DOI] [PubMed] [Google Scholar]

[R150] 150.Stewart IC, Bergman RG, Toste FD. J Am Chem Soc. 2003;125:8696. doi: 10.1021/ja035232n. [DOI] [PubMed] [Google Scholar]

[R151] 151.Wang X, Li S, Jiang Y. J Phys Chem A. 2005;109:10770. doi: 10.1021/jp052426b. [DOI] [PubMed] [Google Scholar]

[R152] 152.For examples, see: Zhang C, Lu X. J Org Chem. 1995;60:2906.Zhu G, Chen Z, Jiang Q, Xiao D, Cao P, Zhang X. J Am Chem Soc. 1997;119:3836.Wilson JE, Fu GC. Angew Chem, Int Ed. 2006;45:1426. doi: 10.1002/anie.200503312.Zhu XF, Lan J, Kwon O. J Am Chem Soc. 2003;125:4716. doi: 10.1021/ja0344009.Tran YS, Kwon O. Org Lett. 2005;7:4289. doi: 10.1021/ol051799s.Wurz RP, Fu GC. J Am Chem Soc. 2005;127:12234. doi: 10.1021/ja053277d.Evans CA, Miller SJ. J Am Chem Soc. 2003;125:12394. doi: 10.1021/ja0377798.Wang LC, Luis AL, Agapiou K, Jang HY, Krische MJ. J Am Chem Soc. 2002;124:2402. doi: 10.1021/ja0121686.Frank SA, Mergott AJ, Roush WR. J Am Chem Soc. 2002;124:2404. doi: 10.1021/ja017123j.

[R153] 153.Dudding T, Kwon O, Mercier E. Org Lett. 2006;8:3643. doi: 10.1021/ol061095y. [DOI] [PubMed] [Google Scholar]

[R154] 154.(a) Xia Y, Liang Y, Chen Y, Wang M, Jiao L, Huang F, Liu S, Li Y, Yu ZX. J Am Chem Soc. 2006;129:3470. doi: 10.1021/ja068215h. [DOI] [PubMed] [Google Scholar]; (b) Mercier E, Fonovic B, Henry C, Kwon O, Dudding T. Tetrahedron Lett. 2007;48:3617. [Google Scholar]; (c) Liang Y, Liu S, Xia Y, Li Y, Yu ZX. Chem Eur J. 2008;14:4361. doi: 10.1002/chem.200701725. [DOI] [PubMed] [Google Scholar]

[R155] 155.Xia Y, Liang Y, Chen Y, Wang M, Jiao L, Huang F, Liu S, Li Y, Yu Z–X. J Am Chem Soc. 2007;129:3470. doi: 10.1021/ja068215h. [DOI] [PubMed] [Google Scholar]

[R156] 156.Yu X–Z. Synlett. 2009;6:905. [Google Scholar]

[R157] 157.(a) Baylis AB, Hillman MED. Offenlegungsschrift 2155113. 3,743,669. US Patent. 1972; Chem Abstr. 1972;77:34174q. [Google Scholar]; (b) Morita K, Suzuki Z, Hirose H. Bull Chem Soc Jpn. 1968;41:2815. [Google Scholar]

[R158] 158.Xu J. THEOCHEM. 2006;767:61. [Google Scholar]

[R159] 159.Robiette R, Aggarwal VK, Harvey JN. J Am Chem Soc. 2007;129:15513. doi: 10.1021/ja0717865. [DOI] [PubMed] [Google Scholar]

[R160] 160.(a) Aggarwal VK, Fulford SY, Lloyd-Jones GC. Angew Chem Int Ed. 2005;44:1706. doi: 10.1002/anie.200462462. [DOI] [PubMed] [Google Scholar]; (b) Price KE, Broadwater SJ, Jung HM, McQuade DT. Org Lett. 2005;7:147. doi: 10.1021/ol047739o. [DOI] [PubMed] [Google Scholar]; (c) Price KE, Broadwater SJ, Walker BJ, McQuade DT. J Org Chem. 2005;70:3980. doi: 10.1021/jo050202j. [DOI] [PubMed] [Google Scholar]; (d) Buskens P, Klankermayer J, Leitner W. J Am Chem Soc. 2005;127:16762. doi: 10.1021/ja0550024. [DOI] [PubMed] [Google Scholar]

[R161] 161.(a) Hill JS, Isaacs NS. J Phys Org Chem. 1990;3:285. [Google Scholar]; (b) Hill JS, Isaacs NS. J Chem Res. 1988:330. [Google Scholar]; (c) Hill JS, Isaacs NS. Tetrahedron Lett. 1986;27:5007. [Google Scholar]

[R162] 162.Fan J-F, Yang C-H, He L-J. Int J Quantum Chem. 2009;109:1311. [Google Scholar]

[R163] 163.Roy D, Sunoj RB. Org Lett. 2007;9:4873. doi: 10.1021/ol702211d. [DOI] [PubMed] [Google Scholar]

[R164] 164.(a) Roy D, Patel C, Sunoj RB. J Org Chem. 2009;74:6936. doi: 10.1021/jo900622x. [DOI] [PubMed] [Google Scholar]; (b) Roy D, Sunoj RB. Chem Eur J. 2008;14:10530. doi: 10.1002/chem.200801822. [DOI] [PubMed] [Google Scholar]

[R165] 165.For examples, see: Jung ME, Node M, Pfluger RW, Lyster MA, Lowe JA., III J Org Chem. 1982;47:1150.Jung ME, Lowe JA, III, Lyster MA, Node M, Pfluger RW, Brown RW. Tetrahedron. 1984;40:4751.Yasukouchi T, Kanematsu K. Tetrahedron Lett. 1989;30:6559.Ma D, Yu Y, Lu X. J Org Chem. 1989;54:1105.

[R166] 166.Liu H, Leow D, Huang K-W, Tan C-H. J Am Chem Soc. 2009;131:7212. doi: 10.1021/ja901528b. [DOI] [PubMed] [Google Scholar]

[R167] 167.Oku M, Arai S, Katayama K, Shioiri T. Synlett. 2000:493. [Google Scholar]

[R168] 168.Climent MJ, Corma A, Domínguez I, Iborra S, Sabater MJ, Sastre G. J Catal. 2007;246:136. [Google Scholar]

[R169] 169.Tel RM, Engberts JBFN. J Chem Soc Perkin Trans. 1976;2:483. [Google Scholar]

[R170] 170.(a) Etter MC, Panunto TW. J Am Chem Soc. 1988;110:5896. [Google Scholar]; (b) Etter MC, Urbañczyk-Lipkowska Z, Zia-Ebrahimi M, Panunto TW. J Am Chem Soc. 1990;112:8415. [Google Scholar]; (c) Etter MC. Acc Chem Res. 1990;23:120. [Google Scholar]; (d) Etter MC. J Phys Chem. 1991;95:4601. [Google Scholar]

[R171] 171.Schreiner PR, Wittkopp A. Org Lett. 2002;4:217. doi: 10.1021/ol017117s. [DOI] [PubMed] [Google Scholar]

[R172] 172.Schreiner PR. Chem Soc Rev. 2003;32:289. doi: 10.1039/b107298f. [DOI] [PubMed] [Google Scholar]

[R173] 173.Fu AP, Thiel W. Theochem-J Mol Struct. 2006;765:45. [Google Scholar]

[R174] 174.Loncharich RJ, Brown FK, Houk KN. J Org Chem. 1989;54:1129. [Google Scholar]

[R175] 175.Bernardi F, Bottoni A, Field MJ, Guest MF, Hillier IH, Robb MA, Venturini A. J Am Chem Soc. 1988;110:3050. [Google Scholar]

[R176] 176.Houk KN, Lin YT, Brown FK. J Am Chem Soc. 1986;108:554. doi: 10.1021/ja00263a059. [DOI] [PubMed] [Google Scholar]

[R177] 177.Sauer J, Sustmann R. Angew Chem, Int Ed Engl. 1980;19:779. [Google Scholar]

[R178] 178.Linder M, Brinck T. Org Biomol Chem. 2009;7:1304. doi: 10.1039/b818655c. [DOI] [PubMed] [Google Scholar]

[R179] 179.Severance DL, Jørgensen WL. J Am Chem Soc. 1992;114:10966. [Google Scholar]

[R180] 180.Curran DP, Lung HK. Tetrahedron Lett. 1995;36:6647. [Google Scholar]

[R181] 181.Kirsten M, Rehbein J, Hiersemann M, Strassner T. J Org Chem. 2007;72:4001. doi: 10.1021/jo062455y. [DOI] [PubMed] [Google Scholar]

[R182] 182.Sigman MS, Vachal P, Jacobsen EN. Angew Chem, Int Ed. 2000;39:1279. doi: 10.1002/(sici)1521-3773(20000403)39:7<1279::aid-anie1279>3.0.co;2-u. [DOI] [PubMed] [Google Scholar]

[R183] 183.Sigman MS, Jacobsen EN. J Am Chem Soc. 1998;120:4901. [Google Scholar]

[R184] 184.Su JT, Vachal P, Jacobsen EN. Adv Synth Catal. 2001;343:197. [Google Scholar]

[R185] 185.Vachal P, Jacobsen EN. Org Lett. 2000;2:867. doi: 10.1021/ol005636+. [DOI] [PubMed] [Google Scholar]

[R186] 186.Vachal P, Jacobsen EN. J Am Chem Soc. 2002;124:10012. doi: 10.1021/ja027246j. [DOI] [PubMed] [Google Scholar]

[R187] 187.Zuend SJ, Jacobsen EN. J Am Chem Soc. 2009;131:15358. doi: 10.1021/ja9058958. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R188] 188.Kleiner CM, Schreiner PR. Chemical Communications. 2006:4315. doi: 10.1039/b605850g. [DOI] [PubMed] [Google Scholar]

[R189] 189.Fleming EM, Quigley C, Rozas I, Connon SJ. J Org Chem. 2008;73:948. doi: 10.1021/jo702154m. [DOI] [PubMed] [Google Scholar]

[R190] 190.Kotke M, Schreiner PR. Synthesis. 2007;5:779. [Google Scholar]

[R191] 191.Raheem IT, Thiara PS, Peterson EA, Jacobsen EN. J Am Chem Soc. 2007;129:13404. doi: 10.1021/ja076179w. [DOI] [PubMed] [Google Scholar]

[R192] 192.Trzupek JD, Li C, Chan C, Crowley BM, Heimann AC, Danishefsky SJ. Pure Appl Chem. 2010;82:1735. doi: 10.1351/pac-con-09-11-14. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R193] 193.Frankland PF, Twiss DF. Journal of the Chemical Society, Transactions. 1904;85:1666. [Google Scholar]

[R194] 194.Huang Y, Rawal VH. J Am Chem Soc. 2002;124:9662. doi: 10.1021/ja0267627. [DOI] [PubMed] [Google Scholar]

[R195] 195.Huang Y, Unni AK, Thadani AN, Rawal VH. Nature. 2003;424:146. doi: 10.1038/424146a. [DOI] [PubMed] [Google Scholar]

[R196] 196.Zhang X, Du H, Wang Z, Wu Y-D, Ding K. J Org Chem. 2006;71:2862. doi: 10.1021/jo060129c. [DOI] [PubMed] [Google Scholar]

[R197] 197.Gordillo RD, Anderson TCD, Houk KN. Org Lett. 2007;9:501. doi: 10.1021/ol0629925. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R198] 198.Gómez-Bengoa E. Eur J Org Chem. 2009:1207. It was reported that the preferred binding mode depends on the polarity of the carbonyl group. As the polarity increases, as in enamine aldol reactions, the bifurcated binding mode becomes favored. [Google Scholar]

[R199] 199.Anderson CD, Dudding T, Gordillo R, Houk KN. Org Lett. 2008;10:2749. doi: 10.1021/ol800875k. [DOI] [PubMed] [Google Scholar]

[R200] 200.Hine J, Linden SM, Kanagasabapathy VM. J Org Chem. 1985;50:5096. [Google Scholar]

[R201] 201.Ooi T, Takahashi M, Maruoka K. J Am Chem Soc. 1996;118:11307. [Google Scholar]

[R202] 202.Kelly TR, Meghani P, Ekkundi VS. Tetrahedron Lett. 1990;31:3381. [Google Scholar]

[R203] 203.Omoto K, Fujimoto H. J Org Chem. 2000;65:2464. doi: 10.1021/jo9916333. [DOI] [PubMed] [Google Scholar]

[R204] 204.Pliego JR. J Mol Catal A-Chem. 2005;239:228–234. [Google Scholar]

[R205] 205.Pliego JR, Pilo-Veloso D. J Phys Chem B. 2007;111:1752. doi: 10.1021/jp066580p. [DOI] [PubMed] [Google Scholar]

[R206] 206.McDougal NT, Schaus SE. J Am Chem Soc. 2003;125:12094. doi: 10.1021/ja037705w. [DOI] [PubMed] [Google Scholar]

[R207] 207.McDougal NT, Trevellini WL, Rodgen SA, Kliman LT, Schaus SE. Adv Synth Catal. 2004;346:1231. [Google Scholar]

[R208] 208.(a) Akiyama T, Itoh J, Yokota K, Fuchibe K. Angew Chem. 2004;116:1566. doi: 10.1002/anie.200353240. [DOI] [PubMed] [Google Scholar]; (b) Uraguchi D, Terada M. J Am Chem Soc. 2004;126:5356. doi: 10.1021/ja0491533. [DOI] [PubMed] [Google Scholar]

[R209] 209.(a) Rowland GB, Rowland EB, Liang Y, Perman JACAJ. Org Lett. 2007;9:2609. doi: 10.1021/ol0703579. [DOI] [PubMed] [Google Scholar]; (b) Rueping M, Ieawsuwan W, Antonchick AP, Nachtsheim BJ. Angew Chem, Int Ed. 2007;46:2097. doi: 10.1002/anie.200604809. [DOI] [PubMed] [Google Scholar]; (c) Storer RI, Carrera DE, Ni Y, MacMillan DWC. J Am Chem Soc. 2006;128:84. doi: 10.1021/ja057222n. [DOI] [PubMed] [Google Scholar]; (d) Chen XH, Xu XY, Liu H, Cun LF, Gong LZ. J Am Chem Soc. 2006;128:14802. doi: 10.1021/ja065267y. [DOI] [PubMed] [Google Scholar]; (e) Terada M, Machioka K, Sorimachi K. Angew Chem, Int Ed. 2006;45:2254. doi: 10.1002/anie.200503477. [DOI] [PubMed] [Google Scholar]; (f) Uraguchi D, Sorimachi K, Terada M. J Am Chem Soc. 2005;127:9360. doi: 10.1021/ja051922a. [DOI] [PubMed] [Google Scholar]; (g) Rueping M, Sugiono E, Azap C, Theissmann T, Bolte OL. Org Lett. 2005;7:3781. doi: 10.1021/ol0515964. [DOI] [PubMed] [Google Scholar]; (h) Hoffmann S, Seayad AM, List B. Angew Chem, Int Ed. 2005;44:7424. doi: 10.1002/anie.200503062. [DOI] [PubMed] [Google Scholar]; (i) Lu M, Lu Y, Zhu D, Zeng X, Li X, Zhong G. Angew Chem Int Ed. 2010;49:8588. doi: 10.1002/anie.201002640. [DOI] [PubMed] [Google Scholar]

[R210] 210.Gridnev IDK, Sorimachi MK, Terada M. Tetrahedron Lett. 2007;48:497. [Google Scholar]

[R211] 211.Yamanaka M, Itoh J, Fuchibe K, Akiyama T. J Am Chem Soc. 2007;129:6756. doi: 10.1021/ja0684803. [DOI] [PubMed] [Google Scholar]

[R212] 212.Uraguchi D, Terada M. J Am Chem Soc. 2004;126:5356. doi: 10.1021/ja0491533. [DOI] [PubMed] [Google Scholar]

[R213] 213.Chen X-H, Wei Q, Luo S-W, Xiao H, Gong L-Z. J Am Chem Soc. 2009;131:13819. doi: 10.1021/ja905302f. [DOI] [PubMed] [Google Scholar]

[R214] 214.Li N, Chen X-H, Song J, Luo S-W, Fan W, Gong L-Z. J Am Chem Soc. 2009;131:15301. doi: 10.1021/ja905320q. [DOI] [PubMed] [Google Scholar]

[R215] 215.Simón L, Goodman JM. J Am Chem Soc. 2008;130:8741. doi: 10.1021/ja800793t. [DOI] [PubMed] [Google Scholar]

[R216] 216.Marcelli T, Hammar P, Himo F. Adv Synth Catal. 2009;351:525. [Google Scholar]

[R217] 217.Rueping M, Sugiono E, Azap C, Theissmann T, Bolte M. Org Lett. 2005;7:3781. doi: 10.1021/ol0515964. [DOI] [PubMed] [Google Scholar]

[R218] 218.Storer RI, Carrera DE, Ni Y, MacMillan DWC. J Am Chem Soc. 2006;128:84. doi: 10.1021/ja057222n. [DOI] [PubMed] [Google Scholar]

[R219] 219.Simón L, Goodman JM. J Org Chem. 2010;75:589. doi: 10.1021/jo902120s. [DOI] [PubMed] [Google Scholar]

[R220] 220.Shi F-Q, Song B-A. Org Biomol Chem. 2009;7:1292. doi: 10.1039/b815008g. [DOI] [PubMed] [Google Scholar]

[R221] 221.Corey EJ, Bakshi RK, Shibata S. J Am Chem Soc. 1987;109:5551. [Google Scholar]

[R222] 222.Corey EJ, Bakshi RK, Shibata S, Chen C-P, Singh VK. J Am Chem Soc. 1987;109:7925. [Google Scholar]

[R223] 223.Corey EJ, Cimprich KA. J Am Chem Soc. 1994;116:3151. [Google Scholar]

[R224] 224.Corey EJ, Loh T-P. J Am Chem Soc. 1991;113:8966. [Google Scholar]

[R225] 225.Payette JN, Yamamoto H. J Am Chem Soc. 2007;129:9536. doi: 10.1021/ja0735958. [DOI] [PubMed] [Google Scholar]

[R226] 226.Corey EJ, Shibata T, Lee TW. J Am Chem Soc. 2002;124:3808. doi: 10.1021/ja025848x. [DOI] [PubMed] [Google Scholar]

[R227] 227.Ryu DH, Corey EJ. J Am Chem Soc. 2005;127:5384. doi: 10.1021/ja050543e. [DOI] [PubMed] [Google Scholar]

[R228] 228.Liu D, Hong S, Corey EJ. J Am Chem Soc. 2006;128:8160. doi: 10.1021/ja063332y. [DOI] [PubMed] [Google Scholar]

[R229] 229.Boeckman RK, Pero JE, Boehmier DJ. J Am Chem Soc. 2006;128:11032. doi: 10.1021/ja063532+. [DOI] [PubMed] [Google Scholar]

[R230] 230.(a) Nevalainen V. Tetrahedron: Asymmetry. 1991;2:1133. [Google Scholar]; (b) Nevalainen V. Tetrahedron: Asymmetry. 1992;3:921. [Google Scholar]; (c) Nevalainen V. Tetrahedron: Asymmetry. 1993;4:1505. [Google Scholar]; (d) Nevalainen V. Tetrahedron: Asymmetry. 1993;4:1597. [Google Scholar]; (e) Nevalainen V. Tetrahedron: Asymmetry. 1994;5:387. [Google Scholar]; (f) Nevalainen V. Tetrahedron: Asymmetry. 1994;5:395. [Google Scholar]

[R231] 231.(a) Nevalainen V. Tetrahedron: Asymmetry. 1991;2:827. [Google Scholar]; (b) Nevalainen V. Tetrahedron: Asymmetry. 1992;3:933. [Google Scholar]; (c) Nevalainen V. Tetrahedron: Asymmetry. 1994;5:289. [Google Scholar]

[R232] 232.Nevalainen V. Tetrahedron: Asymmetry. 1992;3:1441. [Google Scholar]

[R233] 233.(a) Nevalainen V. Tetrahedron: Asymmetry. 1991;2:63. [Google Scholar]; (b) Nevalainen V. Tetrahedron: Asymmetry. 1991;2:429. [Google Scholar]; (c) Nevalainen V. Tetrahedron: Asymmetry. 1992;3:1563. [Google Scholar]

[R234] 234.(a) Li M, Xie R, Hu C, Wang X, Tian A. Int J Quantum Chem. 2000;78:245. [Google Scholar]; (b) Li M, Xie R, Tian S, Tian A. Int J Quantum Chem. 2000;78:252. [Google Scholar]; (c) Li M, Xie R, Hu X, Tian A. Int J Quantum Chem. 2000;78:261. [Google Scholar]

[R235] 235.(a) Li M, Tian A. THEOCHEM. 2001;544:25–35. [Google Scholar]; (b) Li M, Tian A. THEOCHEM. 2001;544:37–47. [Google Scholar]

[R236] 236.(a) Li M, Zheng W, Yang F, Tian A. Int J Quantum Chem. 2001;81:291. [Google Scholar]; (b) Li M, Zheng W, He R, Tian A. Int J Quantum Chem. 2003;93:294. [Google Scholar]; (c) Li M, Zheng W, Tian A. Int J Quantum Chem. 2003;93:307. [Google Scholar]; (d) Zheng W, Li M, Tian A. THEOCHEM. 2003;634:253. [Google Scholar]; (e) Zheng W, Li M, Tian A. THEOCHEM. 2004;668:13. [Google Scholar]

[R237] 237.(a) Jones DK, Liotta DC, Shinkai I, Mathre DJ. J Org Chem. 1993;58:799. [Google Scholar]; (b) Linny LP, Self CR, Williams IH. J Chem Soc, Chem Commun. 1994:1651. [Google Scholar]; (c) Linny LP, Self CR, Williams IH. Tetrahedron: Asymmetry. 1994;5:813. [Google Scholar]; (d) Bach J, Berenguer R, Farras J, Garcia J, Meseguer J, Vilarrasa J. Tetrahedron: Asymmetry. 1995;6:2683. [Google Scholar]; (e) Shen Z, Huang W, Feng J, Zhang Y. Tetrahedron: Asymmetry. 1998;9:1091. [Google Scholar]; (f) Puigjaner C, Vidal-Ferran A, Moyano A, Pericas MA, Riera A. J Org Chem. 1999;64:7902. [Google Scholar]; (g) Bringmann G, Hinrichs J, Kraus J, Wuzik A, Schulz T. J Org Chem. 2000;65:2517. doi: 10.1021/jo991729x. [DOI] [PubMed] [Google Scholar]; (h) Fan JF, Wang QX, Yun-Xiang L. THEOCHEM. 2004;674:49. [Google Scholar]; (i) Gondos GP., I Int J Quantum Chem. 2001;84:253. [Google Scholar]; (j) Tlahuextl M, Tapia-Benavides AR, Flores-Parra A, Contreras R, Tlahuext H, Cruz EM. Heteroat Chem. 2005;16:513. [Google Scholar]

[R238] 238.(a) Harb W, Ruiz-Lopez MF, Coutrot F, Grison C, Coutrot P. J Am Chem Soc. 2004;126:6996. doi: 10.1021/ja031778y. [DOI] [PubMed] [Google Scholar]; (b) Alagona G, Ghio C, Tomasi S. Theor Chem Acc. 2004;111:287. [Google Scholar]; (c) Alagona GGC, Persico C, Tomasi S. J Am Chem Soc. 2003;125:10027. doi: 10.1021/ja034928d. [DOI] [PubMed] [Google Scholar]; (d) Sun L, Tang M, Wang H, Wei D, Liu L. Tetrahedron: Asymmetry. 2008;19:779. [Google Scholar]

[R239] 239.Corey EJ, Azimioara M, Sarshar S. Tetrahedron Lett. 1992;33:3429. [Google Scholar]

[R240] 240.Saavedra J, Stafford SE, Meyer MP. Tetrahedron Lett. 2009;50:1324. [Google Scholar]

[R241] 241.Sun L, Tang M, Wang H, Wei D, Liu L. Tetrahedron: Asymmetry. 2008;19:779. [Google Scholar]

[R242] 242.Grison C, Coutrot F, Coutrot P. Tetrahedron. 2002;58:2735. [Google Scholar]

[R243] 243.Harb W, Ruiz-Lopéz MF, Coutrot F, Grison C, Coutrot P. J Am Chem Soc. 2004;126:6996. doi: 10.1021/ja031778y. [DOI] [PubMed] [Google Scholar]

[R244] 244.Li M, He R. THEOCHEM. 2003;629:197. [Google Scholar]

[R245] 245.Li M, He R. THEOCHEM. 2003;629:209. [Google Scholar]

[R246] 246.Pi Z, Li S. J Phys Chem A. 2006;110:9225. doi: 10.1021/jp062320w. [DOI] [PubMed] [Google Scholar]

[R247] 247.Paddon-Row MN, Kwan LCH, Willis AC, Sherburn MS. Angew Chem Int Ed. 2008;47:7013. doi: 10.1002/anie.200802002. [DOI] [PubMed] [Google Scholar]

[R248] 248.Paddon-Row MN, Anderson CD, Houk KN. J Org Chem. 2009;74:861. doi: 10.1021/jo802323p. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R249] 249.Corey EJ, Loh T-P, Roper TD, Azimioara MD, Noe MC. J Am Chem Soc. 1992;114:8290. [Google Scholar]

[R250] 250.(a) Nevalainen V. Tetrahedron: Asymmetry. 1993;4:1565. [Google Scholar]; (b) Nevalainen V. Tetrahedron: Asymmetry. 1994;5:767. [Google Scholar]; (c) Uggla R, Nevalainen V, Sundberg MR. Tetradron: Asymmetry. 1996;7:2725. [Google Scholar]

[R251] 251.Salvatella L, Ruiz-Lopéz MF. J Am Chem Soc. 1999;121:10772. [Google Scholar]

[R252] 252.Corey EJ, Loh T-P, Roper TD, Azimioara MD, Noe MC. J Am Chem Soc. 1992;114:8290. [Google Scholar]

[R253] 253.Kiyooka S-I. Rev Heteroat Chem. 1997;17:245. [Google Scholar]

[R254] 254.Corey EJ, Cywin CL, Roper TD. Tetrahedron Lett. 1992;33:6907. [Google Scholar]

[R255] 255.Wong MW. J Org Chem. 2005;70:5487. doi: 10.1021/jo050474m. [DOI] [PubMed] [Google Scholar]

[R256] 256.(a) Yalalov DA, Tsogoeva SB, Schmatz S. Adv Synth Catal. 2006;348:826. [Google Scholar]; (b) Hamza A, Schubert G, Soos T, Papai I. J Am Chem Soc. 2006;128:13151. doi: 10.1021/ja063201x. [DOI] [PubMed] [Google Scholar]; (c) Liu TY, Li R, Chai Q, Long J, Li BJ, Wu Y, Ding LS, Chen YC. Chem Eur J. 2006;13:319. doi: 10.1002/chem.200600796. [DOI] [PubMed] [Google Scholar]

[R257] 257.Wei S, Yalalov DA, Tsogoeva SB, Schmatz S. Catal Today. 2007;121:151. [Google Scholar]

[R258] 258.Okino T, Hoashi Y, Furukawa T, Xu X, Takemoto Y. J Am Chem Soc. 2005;127:119. doi: 10.1021/ja044370p. [DOI] [PubMed] [Google Scholar]

[R259] 259.Chen D, Lu N, Zhang G, Mi S. Tetrahedron: Asymmetry. 2009;20:1365. [Google Scholar]

[R260] 260.Tan B, Lu Y, Zeng X, Chua PJ, Zhong G. Org, Lett. 2010;12:2682. doi: 10.1021/ol1007795. [DOI] [PubMed] [Google Scholar]

[R261] 261.Liu T-Y, Li R, Chai Q, Long J, Li B-J, Wu Y, Ding L-S, Chen Y-C. Chem Eur J. 2007;13:319. doi: 10.1002/chem.200600796. [DOI] [PubMed] [Google Scholar]

[R262] 262.Zhu R, Zhang D, Wu J, Liu C. Tetrahedron: Asymmetry. 2007;18:1655. [Google Scholar]

[R263] 263.Xu X, Yabuta T, Yuan P, Takemoto Y. Synlett. 2006;1:137–140. [Google Scholar]

[R264] 264.(a) Zhu R, Zhang D, Wu J, Liu C. Tetrahedron: Asymmetry. 2007;18:1655. [Google Scholar]; (b) Xu X, Yabuta T, Yuan P, Takemoto Y. Synlett. 2006;1:137. [Google Scholar]

[R265] 265.Sibi MP, Itoh K. J Am Chem Soc. 2007;129:8064. doi: 10.1021/ja071739c. [DOI] [PubMed] [Google Scholar]

[R266] 266.Simón L, Goodman JM. Org Biomol Chem. 2009;7:483. doi: 10.1039/b817283h. [DOI] [PubMed] [Google Scholar]

[R267] 267.Zhu Y, Drueckhammer DG. J Org Chem. 2005;70:7755. doi: 10.1021/jo0513818. [DOI] [PubMed] [Google Scholar]

[R268] 268.Wang S-X, Chen F-E. Adv Synth Catal. 2009;351:547. [Google Scholar]

[R269] 269.Zhu R-X, Wang R-X, Zhang D-J, Liu C-B. Aust J Chem. 2009;62:157. [Google Scholar]

[R270] 270.Corey EJ, Grogan MJ. Org Lett. 1999;1:157. doi: 10.1021/ol990623l. [DOI] [PubMed] [Google Scholar]

[R271] 271.Schuster T, Kurz M, Göbel MW. J Org Chem. 2000;65:1697. doi: 10.1021/jo991372x. [DOI] [PubMed] [Google Scholar]

[R272] 272.Nugent BM, Yoder RA, Johnston JN. J Am Chem Soc. 2004;126:3418. doi: 10.1021/ja031906i. [DOI] [PubMed] [Google Scholar]

[R273] 273.Sohtome Y, Hashimot Y, Nagasawa K. Adv Synth Catal. 2005;347:1643. [Google Scholar]

[R274] 274.Terada M, Nakano M, Ube H. J Am Chem Soc. 2006;128:16044. doi: 10.1021/ja066808m. [DOI] [PubMed] [Google Scholar]

[R275] 275.Lohmeijer BGG, Pratt RC, Leibfarth F, Logan JW, Long DA, Dove A, Nederberg PF, Choi J, Wade C, Waymouth RM, Hedrick JL. Macromolecules. 2006;39:8574. [Google Scholar]

[R276] 276.Li J, Jiang W-Y, Han K-L, He G, Zhong, Li C. J Org Chem. 2003;68:8786. doi: 10.1021/jo034891f. [DOI] [PubMed] [Google Scholar]

[R277] 277.Arnaud R, Adamo C, Cossi M, Milet A, Vallee Y, Barone V. J Am Chem Soc. 2000;122:324. [Google Scholar]

[R278] 278.Walch SP, Bakes ELO. Chem Phys Lett. 2001;346:267. [Google Scholar]

[R279] 279.Chuma A, Horn HW, Swope WC, Pratt RC, Zhang L, Lohmeijer BGG, Wade CG, Waymouth RM, Hedrick JL, Rice JE. J Am Chem Soc. 2008;130:6749. doi: 10.1021/ja0764411. [DOI] [PubMed] [Google Scholar]

[R280] 280.Simón L, Goodman JM. J Org Chem. 2007;72:9656. doi: 10.1021/jo702088c. [DOI] [PubMed] [Google Scholar]

[R281] 281.Almasi D, Alonso DA, Gómez-Bengoa E, Nájera C. J Org Chem. 2009;74:6163. doi: 10.1021/jo9010552. [DOI] [PubMed] [Google Scholar]

[R282] 282.Huang SY, Ma J, Li JP, Zhao N, Wei W, Sun YH. Catal Commun. 2008;9:276. [Google Scholar]

[R283] 283.Ma J, Zhao N, Xia F, Wei W, Sun YH. THEOCHEM. 2009;911:40. [Google Scholar]

[R284] 284.Russo A, Lattanzi A. Eur J Org Chem. 2008:2767. [Google Scholar]

[R285] 285.Zhang Z, Rooshenas P, Hausmann H, Schreiner PR. Synthesis. 2009:1531. [Google Scholar]

[R286] 286.(a) Liu J, Yang Z, Wang Z, Wang F, Chen X, Liu X, Feng X, Su Z, Hu C. J Am Chem Soc. 2008;130:5654. doi: 10.1021/ja800839w. [DOI] [PubMed] [Google Scholar]; (b) Yang Z, Liu J, Liu X, Wang Z, Feng X, Hu C. Adv Synth Catal. 2008;350:2001. [Google Scholar]

[R287] 287.Chen X, Wang J, Zhu Y, Shang D, Gao B, Liu X, Feng X, Su Z, Hu C. Chem Eur J. 2008;14:10896. doi: 10.1002/chem.200801958. [DOI] [PubMed] [Google Scholar]

[R288] 288.Yang Z, Liu J, Liu X, Wang Z, Feng X, Su Z, Hu C. Adv Synth Catal. 2008;350:2001. [Google Scholar]

[R289] 289.Cucinotta CS, Kosa M, Melchiorre P, Cavalli A, Gervasio FL. Chem Eur J. 2009;15:7913. doi: 10.1002/chem.200900406. [DOI] [PubMed] [Google Scholar]

[R290] 290.Rho HS, Oh SH, Lee JW, Lee JY, Chin J, Song CE. Chem Commun. 2008:1208. doi: 10.1039/b719811f. [DOI] [PubMed] [Google Scholar]

[R291] 291.Oh SH, Rho HS, Lee JW, Lee JE, Youk SH, Chin J, Song CE. Angew Chem Int Ed. 2008;47:7872. doi: 10.1002/anie.200801636. [DOI] [PubMed] [Google Scholar]

[R292] 292.Kobbelgaard S, Brandes S, Jørgensen KA. Chem-Eur J. 2008;14:1464. doi: 10.1002/chem.200701729. [DOI] [PubMed] [Google Scholar]

[R293] 293.Çelebi-Ölçüm N, Aviyente V, Houk KN. J Org Chem. 2009;74:6944. doi: 10.1021/jo901109s. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R294] 294.(a) Inoue S, Oku JI. J Chem Soc, Chem Commun. 1981:229. [Google Scholar]; (b) Tanaka K, Mori A, Inoue S. J Org Chem. 1990;55:181. [Google Scholar]

[R295] 295.(a) Danda H, Nishikawa H, Otaka K. J Org Chem. 1991;56:6740. [Google Scholar]; (b) Danda H. Synlett. 1991:263. [Google Scholar]; (c) Kogut EF, Thoen JC, Lipton MA. J Org Chem. 1998;63:4604. [Google Scholar]

[R296] 296.Shvo Y, Becker GM, Elgavi A. Tetrahedron: Asymmetry. 1996;7:911. [Google Scholar]

[R297] 297.Li Z, Zhang J, Brouwer C, Yang C-G, Reich NW, He C. Org, Lett. 2006;8:4175. doi: 10.1021/ol0610035. [DOI] [PubMed] [Google Scholar]

[R298] 298.Li X, Ye S, He C, Yu Z-X. Eur J Org Chem. 2008:4296. [Google Scholar]

[R299] 299.(a) Bach RD, Glukhovtsev MN, Gonzalez C, Marquez M, Estevez CM, Baboul AG, Schlegel HB. J Phys Chem A. 1997;101:6092. [Google Scholar]; (b) Houk KN, Liu J, DeMello NC, Condroski KR. J Am Chem Soc. 1997;119:10147. [Google Scholar]; (c) Crehuet R, Anglada JM, Cremer D, Bofill JM. J Phys Chem A. 2002;106:3917. [Google Scholar]; (d) Bach RD, Dmitrenko O, Adam W, Schambony S. J Am Chem Soc. 2003;125:924. doi: 10.1021/ja026882e. [DOI] [PubMed] [Google Scholar]; (e) Dmitrenko O, Bach RD. J Phys Chem A. 2004;108:6886. [Google Scholar]

[R300] 300.Armstrong A, Washington I, Houk KN. J Am Chem Soc. 2000;122:6297. [Google Scholar]

[R301] 301.Armstrong A, Hayter BR. Chem Commun. 1998:621. [Google Scholar]

[R302] 302.(a) Tian H, She Z, Shu L, Yu H, Shi Y. J Am Chem Soc. 2000;122:11551. [Google Scholar]; (b) Tian H, She Z, Xu J, Shi Y. Org Lett. 2001;3:1929. doi: 10.1021/ol010066e. [DOI] [PubMed] [Google Scholar]

[R303] 303.Singleton DA, Wang Z. J Am Chem Soc. 2005;127:1929. doi: 10.1021/ja0435788. [DOI] [PubMed] [Google Scholar]

[R304] 304.Cramer CJ, Truhlar DG. Acc Chem Res. 2008;41:760. doi: 10.1021/ar800019z. [DOI] [PubMed] [Google Scholar]

[R305] 305.Oyola Y, Singleton DA. J Am Chem Soc. 2009;131:3130. doi: 10.1021/ja807666d. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Quantum Mechanical Investigations of Organocatalysis: Mechanisms, Reactivities, and Selectivities

Paul Ha-Yeon Cheong

Claude Y Legault

Joann M Um

Nihan Çelebi-Ölçüm

K N Houk

1. Introduction

1.1 Computational methods for organocatalysis

2. Enamine/Iminium Catalysis

2.1. Proline and proline derivatives

2.1.1. Intramolecular aldol reaction

2.1.1.1. Mechanism of Hajos-Parrish reaction

Scheme 1.

2.1.1.2. Origins of stereoselectivity

Figure 1.

2.1.1.3. Catalysis by proline derivatives

Scheme 2.

Scheme 10.

4,5-methanoproline

Figure 2.

Pyrrolidine-2-thioic and dithioic acids

Figure 3.

Protonated amine

Figure 4.

Isoxazolidine-3-carboxylic acid

Figure 5.

5,5-dimethylthiazolidine-4-carboxylic acid (DMTC) and 5,5-dimethyloxazolidine-4-carboxylic acid (DMOC)

Figure 6.

2.1.1.4. Primary amino acid catalysis

Scheme 3.

Figure 7.

Figure 8.

2.1.2. Intermolecular aldol reactions

Scheme 4.

2.1.2.1. Mechanism

Scheme 5.

Scheme 6.

Scheme 7.

Scheme 8.

Figure 9.

2.1.2.2. Origins of stereoselectivity

The Zimmerman-Traxler model

Scheme 9.

The Houk-List model

Figure 10.

The Seebach-Eschenmoser model

Scheme 11.

Predictions of stereoselectivities

2.1.2.3. 5-pyrrolidin-2-yltetrazole

Scheme 12.

Scheme 13.

Figure 11.

2.1.2.4. Proline amide derivatives

Scheme 14.

Figure 12.

Scheme 15.

Scheme 16.

Scheme 17.

Scheme 18.

Figure 13.

Scheme 19.

Figure 14.

2.1.2.5. Primary amino acids

Scheme 20.

Figure 15.

Figure 16.

2.1.2.6. Cyclic aminophosphonates - pyrrolidin-2-ylphosphonic acid

Scheme 21.

Figure 17.

2.1.2.7. Nornicotine

Scheme 22.

Scheme 23.

Scheme 24.

2.1.3. Mannich reaction

Scheme 25.

Origin of the reverse enantioselectivity compared to the aldol reaction

Figure 18.

The enhanced rate of the Mannich reaction versus the aldol reaction

The origin of erosion of diastereoselectivity in the pipecolic acid catalyzed Mannich reaction