Determining Global Population Distribution: Methods, Applications and Data

Abstract

Evaluating the total numbers of people at risk from infectious disease in the world requires not just tabular population data, but data that are spatially explicit and global in extent at a moderate resolution. This review describes the basic methods for constructing estimates of global population distribution with attention to recent advances in improving both spatial and temporal resolution. To evaluate the optimal resolution for the study of disease, the native resolution of the data inputs as well as that of the resulting outputs are discussed. Assumptions used to produce different population data sets are also described, with their implications for the study of infectious disease. Lastly, the application of these population data sets in studies to assess disease distribution and health impacts is reviewed. The data described in this review are distributed in the accompanying DVD.

1. INTRODUCTION

Deriving population at risk estimates as a basis for evaluation of disease burdens requires spatially explicit, moderate-resolution population data at the global scale. In this contribution, methods for constructing estimates of global population distribution that are suitable for geographic analysis are described. Though the basic approach has been used widely for more than a decade, particular attention is given to recent advances to increase both spatial and temporal resolution. As global data products are dependent on a diverse set of inputs, issues related to input and output data resolution have an immediate bearing on the suitability of the resulting datasets for a given task. This paper also reviews applications of these population databases in the health sector, in particular, for the study of infectious disease. Finally, the population and associated data files that accompany this volume are briefly described.

1.1. Rendering Population on a Global Grid

Global or broad-scale inquiry on the relationship between population and environmental factors such as disease vectors or habitats is intrinsically spatial. While notable exceptions exist, especially at the local scale, two key barriers have contributed to the paucity of spatially oriented analysis: (1) the methods of analysis require some knowledge of geographic data and tools for analysis; and (2) population data, at regional and global scales, have tended to be recorded in national units that do not permit cross-national, subnational, or cross-habitat analysis. These barriers have been slowly eroding. One trend that has contributed to this is that the collectors and custodians of demographic data—the national census and statistics offices—increasingly compile and distribute data for small administrative or statistical units. While data from population censuses conducted before the 1990 round of population censuses were often published only for the country and major divisions such as provinces or states, more recent census output often includes digital census databases with detailed demographic data for districts, subdistricts, or even “enumeration” areas (EAs), the smallest geographical unit in most census operations.

Great progress has been made in harmonizing subnational data released for different dates so that they are comparable across international borders. First, since census years are not synchronized across the world, this involves interpolation or extrapolation of population estimates to a common base year. Second, subnational reference units can be vastly different in size and shape across countries. For spatial analysis, it is often preferable to instead record population estimates on a set of standardized reporting units, such as regular grid cells. Grids are more commonly used to collect or compile data describing natural phenomena. In interdisciplinary work, conversion to a regular grid imposes consistency that would be more difficult to achieve with irregularly shaped census or administrative units. Methods that transform population data from native census units (which correspond to vector format) to a regular raster grid are the main focus of this paper. A third harmonization issue arises for other demographic variables where, despite efforts by the United Nations and others to promote common definitions, indicators are often not entirely comparable. This is a major reason why global, georeferenced demographic databases have so far focused on the simplest of all demographic variables: total population.

Efforts to estimate population distribution for a regular raster grid predate the computerization of geography that started in the 1980s. Early examples such as the map by Adams (1968) for West Africa served largely cartographic purposes. Census offices, most notably those of Japan and Sweden, also produced national population grids for inclusion in national atlases (e.g., Tufte, 1990, on Japan). Computerized population maps for individual countries were produced by the US Census Bureau using rectangular grid cells superimposed with circles for major urban areas (Leddy, 1994). Deichmann and Eklundh (1991) presented a continental, gridded population database for Africa used to investigate interactions between population and land degradation. Others, such as Martin and Bracken (1991), developed techniques for producing local-level population grids (see Clark & Rhind, 1992; Deichmann 1996a, for reviews).

1.2. Institutional Stewardship

While national statistical offices produce population estimates that are sometimes linked to spatial data, few agencies render their population estimates on a common grid. The first efforts to place population data on a global-scale latitude–longitude grid were completed in the mid-1990s at the National Center for Geographic Information and Analysis at the University of California, Santa Barbara (Tobler et al., 1997). This initial dataset was itself an outgrowth of prior work on regional and continental databases. The Global Demography Workshop held in 1994 at CIESIN (the Center for International Earth Science Information Network, now part of the Earth Institute at Columbia University) brought together experts in the field and helped advance methodological development and database creation for the first global grid. CIESIN is the locus of current global efforts, though it works closely with partnering institutions. Like many complex global data products, the Gridded Population of the World (GPW) database has evolved with numerous partners. Subsequent versions have included different collaborators, inputs, and outputs, but the guiding principle is to achieve the best possible suite of data products representing the distribution of human population, sometimes heuristically (i.e., without modeling) and sometimes with light modeling (Deichmann, 1996a). The fewer the assumptions and inputs that are used in the construction of the databases, the fewer the restrictions that have to be imposed on the appropriateness of use in a wide variety of applications. For example, if land cover were used to predict population densities, one could not predict expected changes in land cover from a resulting population distribution(s) that included land cover as a reallocation factor, as it would be endogenous.

Since the first version of GPW, several key advances have been made: the spatial resolution of administrative boundary data is improving; national statistical offices and spatial data providers and related institutions are adopting more open-data policies; population and spatial data providers are increasingly aware of, and increasingly collaborate with one another; and the computing capacity to manage, manipulate, and process increasingly large datasets is continually expanding (Balk and Yetman, 2005). As a result of these advances, some countries now produce and disseminate high-resolution spatially explicit population data. In local studies, nationally produced data are typically superior (i.e., of higher resolution, with more variables, and so on) to globally rendered data. Researchers asking highly place-based questions should begin with locally available data, if possible. Nevertheless, many questions are regional in scale, or at least span across more than one country, or require data that have been transformed to a common grid. For those problems, the data in this paper are highly suitable.

The basic global database to arise out of these efforts is the GPW, now in its third revision, with large gains to resolution having been made with each revision. In addition to the key advances described above, advances in ancillary data to allow for light modeling, especially valuable where input data are of suboptimal spatial resolution, have allowed for more sophisticated but still simple modeling. Thus, GPW and related population data products are the main focus of this review. The resulting datasets are also included in the accompanying DVD. Details on the variations in these databases, their methods, assumptions, and limitations follow.

2. DATA

The georeferenced population data sets that are the focus of this paper share as a critical common characteristic: the fact that they are constructed with an emphasis on the highest-resolution input data, rather than focusing on statistical or heuristic prediction of population distribution from coarse input data. That is, they attempt to measure the distribution of the population of the world, as measured at one’s usual place of residence. The basic premise is that no amount of further processing or modeling can substitute for obtaining population counts for the smallest geographic reporting units available. Censuses in many countries are far from perfect and reliable civil registration systems exist only in a small number of countries. These sources provide the only complete enumeration of a country’s population and by definition, provide the only geographically complete count of residents. By making additional assumptions about regularities in population distribution, it is possible to further disaggregate the reported district or subdistrict totals, but usually one cannot then reliably assess how accurate the resulting distributions are because there is no basis for sound validation. Population distribution modeling should therefore be considered a last resort in the absence of EA population maps, rather than as a goal in itself. When modeling is undertaken, the inputs of that model and the means for the redistribution should be made as transparent as possible.

The differences in these evolving data products are reviewed in Table 1 and are discussed in subsequent sections. Fundamental modifications include an increase in input resolution by over 20 times from the first to the current version of GPW (Balk and Yetman, 2005), and nearly a tripling again for the modeled data products of the Global Rural Urban Mapping Project (GRUMP) (Balk et al., 2005a). Increases in the input data enabled a corresponding increase in output resolution from 5 arc-minutes of GPW version 1–2.5 arc-minutes for later versions of GPW and related products. The data products from the GRUMP effort utilize higher resolution inputs, and thus outputs have been rendered at a 30 arc-second resolution.

Table 1.

Comparison of GPW versions and related databases

Data set	GPW				Accessibility model	GRUMP v1
	GPW v1	GPW v2	GPW v3	GPW 2015
Publication year	1995	2000	2004	2004	2004	2004
Years of estimation	1994	1990, 1995	1990, 1995, 2000	2015	1960–2000	1990, 1995, 2000
Number of input units	19 000	127 000	376 500	376 500	Varies by continent	c. 1 000 000
Modeled inputs	None	None	None	None	Infrastructure,  urban areas	Urban areas
Spatial extent	Global	Global	Global	Global	Africa, Asia, Latin  America	Global
Authors	Tobler et al.	CIESIN, IFPRI,  and WRI	CIESIN & CIAT	CIESIN, FAO, and  CIAT	Deichmann; WRI;  CIAT, UNEP  and CIESIN	CIESIN, IFPRI,  World Bank, and  CIAT
Gridded surface  resolutiona	5′	2.5′	2.5′	2.5′	2.5′	30″
Population density	●	●	●	●	●	●
Population counts	●	●	●	●	●	●
Land area	●	●	●	●	●	●
Population-weighted  admin. units			●	●		●
Urban extent mask						●
Settlement points (xls,  csv, shp formats)						●

Note: A dot indicates the data set is publicly available. ’ and ” represent arc-minutes and arc-seconds, respectively.

^aGridded surfaces are available in these formats: 00, bil, ascii.

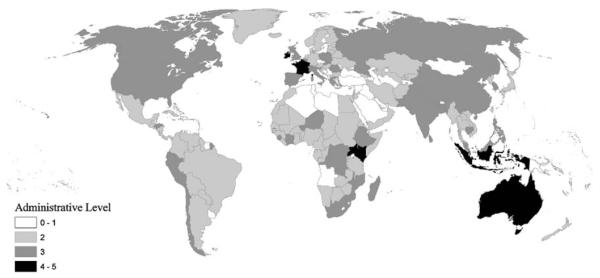
The basic method by which population counts are transformed from census units to a grid, developed for the first version of GPW (Tobler et al., 1997) and modified slightly for GPW v2 (Deichmann et al., 2001), remain the same in the third version; related databases with light modeling use additional methods, but the basic method underlies all of these databases. Population data are transformed from their native spatial units that are usually administrative division of irregular shape and resolutions (see Figure 1) to a global grid of square latitude–longitude cells at a resolution of 2.5 arc minutes (i.e., approximately 4.6 km at the equator). The main inputs consist of geographically referenced boundaries of administrative or statistical reporting units at the highest available resolution—ideally the EA, but more typically at district or subdistrict level. The methods used to distribute the reporting unit total population numbers across the raster grid cells that fall into that unit differ slightly between the different versions of GPW and closely related data. These will be discussed below. Temporal adjustments are discussed in Section 3.

Figure 1.

Administrative level used per country.

2.1. Gridded Population of the World

The GPW database uses two basic inputs: non-spatial population estimates (i.e., tables of population counts listed by administrative area names) and spatially explicit administrative boundary data. These are collected from hundreds of different data providers (often differing for the population and boundary data). The first part of the process is to match the population estimates with the administrative boundaries into what is known as polygon (or vector) format, ensure that the resulting data are geospatially consistent (e.g., that all internal boundaries match, leaving no unaccounted polygons or that island chains which might share a single population figure should they belong to the same administrative unit), and sum to the national-level population, as estimated by the data provider. These basic consistency checks mirror census principles of not leaving any resident out and not counting anyone more than once. To construct the GPW database, the administrative unit data in polygon format are converted to raster grids. In version 1, built-in geographic information systems (GIS) software functions were used to accomplish this conversion: grid cells that fall onto the boundary of two or more units were assigned to only one reporting unit based on a simple majority rule. The total unit population was then proportionally allocated over all grid cells assigned to that unit. A second product from this effort used these grids as a starting point for a re-distribution algorithm called smooth pycnophylactic (mass-preserving) interpolation (Tobler, 1979). The assumption underlying this approach is that those areas within a given administrative unit that neighbor regions with higher population densities are likely to house more people than areas that neighbor low-population density regions. The previously homogeneous population figures in grid cells within each administrative unit are thus re-distributed taking grid cells in neighboring units into account. By iteratively adjusting grid cell populations on this basis, the method results in a maximally smooth surface while preserving total population within each reporting unit.

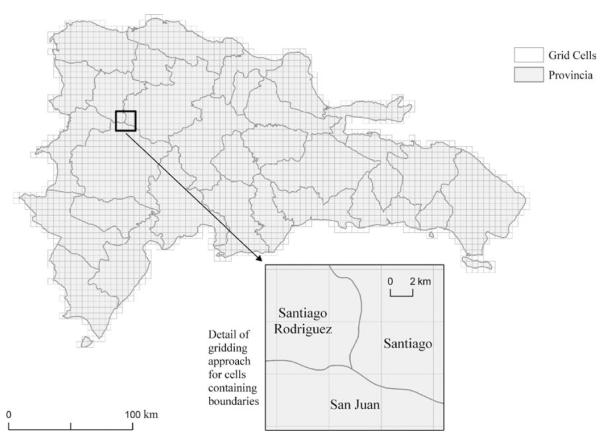
The second and third versions of GPW retained most of the characteristics of the “unsmoothed” version of GPW v1, while significantly increasing the number of reporting units that served as input to the gridding routine. While version 1 relied on about 19 000 administrative units, version 2 used 120 000, and version 3 used 375 000 units with much of the increased precision achieved in developing countries (see Table 1). The main difference in processing in these newer versions lies in the way boundary areas between administrative units are treated. While version 1 allocated grid cells to only one unit even if it was shared by two or more (i.e., majority rule), GPW v2 and v3 use a proportional allocation so grid cells are assigned population in proportion to the area of overlap of grid cell and administrative units. Figure 2 (detail) and Table 2 illustrate this for a grid cell in the Dominican Republic. Proportional allocation is often referred to as an areal weighting scheme (e.g., Goodchild et al., 1993).

Figure 2.

Grid cell size in relationship to administrative boundaries, Dominican Republic.

Table 2.

Areal weighting scheme to allocation of population whose boundaries cross grid cells

Administrative unit name	Administrative unit density (persons/sq km)	Area of overlap (sq km)	Population estimate for grid cell
Santiago Rodriguez	64.2	5.3	340
Santiago	246.5	2.2	542
San Juan	75.9	12.8	972
Total for cell	91.3	20.3	1854

2.2. Global Rural Urban Mapping Project

The allocation mechanism for the GRUMP (Balk et al., 2005a) builds on the GPW approach but explicitly considers population of urban areas. In addition to data for statistical reporting units, the project collected population estimates, point location, and the approximate footprint for urban centers in each country. The objective is to disaggregate the urban area populations from the total population of the administrative unit into which the urban area falls. This allows us to allocate urban and rural population separately, which effectively increases the number of input units and thus the effective resolution of the population grid.

In contrast to GPW, estimates of population for urban centers were needed in addition to population estimates associated with their census boundaries. Much less investment has been required from national statistical agencies to collect and publish population estimates for urban areas, unless these are entirely consistent with the census information for administrative units (which is rarely the case). Nevertheless, city population figures are published in a variety of sources. These data were collected and then matched with the urban footprint. That matching also occurs through a series of steps starting with simply a name-match of the populated places with geographic locations (i.e., latitude and longitude of the presumed center of the urban area). The geographic coordinates were found in national or international gazetteers, such as that of the US National Geospatial Intelligence Agency (see Balk et al., 2005a, for details).

A more challenging problem was to determine the footprint of major city areas. The most important source are nighttime satellite images that show areas lit by streetlights and other permanent light sources that are concentrated in urban settlements (Elvidge et al., 1999). In cases where statistical sources indicated a city that could not be detected on nighttime satellite images—a common occurrence in Africa—urban areas were delineated from other sources (e.g., Tactical Pilotage Charts) or approximated by circles whose sizes were given by population–area relationships calibrated (through a regression analysis) on existing data. It is acknowledged that a circle is not an accurate form for any city, but this assumption was the most practical one to implement and the basic shape from lights for small extents tends toward circular. Circle-generated extents in each country were cross validated with other locations of near population size to confirm that the sizes were on the same order of magnitude. Conversely, footprints that could not be matched with populated place information were not assumed to have population and were discarded from the data. The population estimates, matched with geographic point locations were summarized for each footprint, producing an urban extent data set with population estimates.

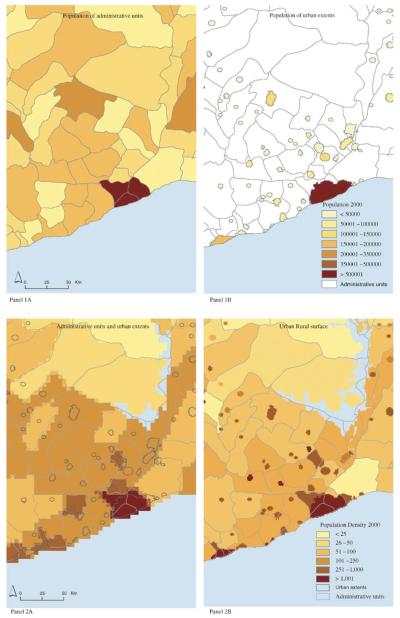
The final step was to use these many pieces of information—which are summarized as administrative regions with population estimates and urban extents with population estimates (shown as panels 1A and 1B, respectively, in Figure 3)—and generate a population grid (panel 2B, Figure 3). (Figure 3 is Plate 4.3 in the Separate Color Plate Section.).

Plate 4.3.

Process by which GRUMP population surface is constructed, illustrated for southern Ghana. Panel 1 shows inputs side by side with their population counts. Panel 1A is identical to the inputs to GPW, panel 1B shows the additional urban areas used in GRUMP. In panel 2, the inputs are merged, first illustrated as an overlay of the urban footprints over the administrative polygons in panel 2A, and the final grid, in panel 2B (with administrative and urban) boundaries overlaid (density/square km).

Because these come from different sources, it is important to make sure that the urban area population totals do not exceed those of the administrative areas in which the urban areas are located. Thus, a model is used to re-allocate population of the administrative areas given the population of the urban areas, the total population of the administrative area, and minimum and maximum criteria about each country’s urbanization trends (details are given in Balk et al., 2005a). The output resolution for this grid is 30 arc-seconds, similar to that of the nighttime lights’ data. The GRUMP population grid also uses a proportional allocation rule in gridding.

2.3. Accessibility Modeling

The final set of gridded population datasets reviewed here are based on an additional set of assumptions about population distribution: the basic premise is that people tend to live in or close to cities and tend to move toward areas that are well connected with urban centers. Even in rural areas, it is expected that densely populated areas are closer to transport links than more isolated areas, and higher densities are nearer cities than the hinterland. These stylized facts concerning the distribution of people across space are implemented using the concept of accessibility—a measure of the ease by which destinations such as markets or service centers can be reached from a given location. In practice, these measures are adapted from the well-known gravity model of spatial interaction (Haynes & Fotheringham, 1984). They represent the sum of an indicator of size or mass at destinations (such as population of surrounding cities) inversely weighted for some function of distance. The ideal measure here is an estimate of travel time using the shortest route on a geographically referenced transportation network of roads, rivers, rails, and so forth. The resulting access estimates for each grid cell are then used to proportionally distribute each administrative unit population total across the grid cells that fall into it. This approach has been implemented for continental-scale databases for Africa, Asia, and Latin America, with support from the United Nations Environment Programme, the International Center for Tropical Agriculture (CIAT), and others. Nelson and Deichmann (2004) describe the latest version for Africa and document the modeling approach in detail.

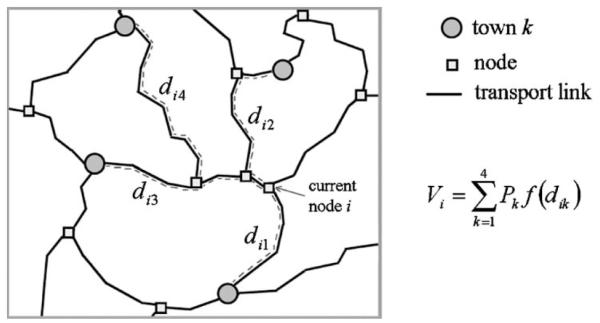
The most important input into the model is information about the transportation network consisting of roads, railroads, and navigable rivers and their associated speeds of travel (i.e. 60 km per hour for 2-lane paved roads, 30 km per hour for railroads, etc.). The second main component is information on the location and population of urban centers, which are then linked to the transport network. These inputs are used to compute a measure of accessibility (V_i) for each node (intersection) in the network, which is based on the sum of the population of towns (P_k) in the vicinity of the current node weighted by a function of travel time across the network between the node and the towns f(d_ik). Figure 4 illustrates the computation of the accessibility index for a single node based on the weighted sum of the population of four towns that are within a given travel time threshold.

Figure 4.

The computation of accessibility potential for a single node on the transport network where four towns are within the chosen travel time threshold.

The accessibility values at each node were interpolated into a raster surface to create an accessibility index for each grid cell. Raster data on inland water bodies (lakes and glaciers), protected areas, and altitude were then used heuristically to reduce the accessibility potential in areas where there is little or no population. Accessibility values in water bodies and areas of extremely high altitude were set to zero. Accessibility values in protected areas and forest reserves were reduced by 80% and 50%, respectively. Both adjustments were heuristically chosen in the absence of empirical data.

The accessibility values estimated for each grid cell serve as weights to distribute population proportionately. The grid cells in the accessibility index were summed within each administrative unit. Each value was then divided by the corresponding administrative unit sum such that the resulting weights sum to one within each administrative unit. Multiplying each cell value by the total population yields the estimated number of people residing in each grid cell. The standardization of the accessibility index implies that the absolute magnitudes of the predicted access values are unimportant—only the variation within the administrative unit determines population densities within each district (Deichmann, 1997; Nelson & Deichmann, 2004)—but that, similar to GRUMP, the sum of grid cell population values for each unit cannot exceed the value for the administrative unit in which they fall.

2.4. Highly Modeled Surfaces

Another recently developed dataset, LandScan, takes a highly modeled approach, whereby much less investment is made in using the highest possible resolution population data (ORNL, 2003). This data set is categorically different from those described above, in that it does not attempt to represent nighttime, census residence, or usual population but rather it aims to measure an “ambient” population—i.e., the average location of an individual across seasons, days of the week, and times of day. Instead, effort is spent on getting annual updates to relatively coarse-level population inputs, and to ancillary data (including roads, nighttime lights, elevation, slope, and land cover) to be fitted to a complex model (Dobson et al., 2000). The specific model parameters or their calibration are not published and, thus, it is difficult to assess the appropriateness or accuracy of this approach. LandScan receives less attention here, but is briefly discussed where it has been applied in the studies below.

3. METHODOLOGY

Though the basic method for re-distributing population from census and other units to a grid has been discussed, there are additional methodological requirements. For each reporting unit, a consistent population estimate for a baseline year is obtained. Where no census data or official estimates are available for the target year, a population figure is estimated using census year population and inter-censal growth rates.

3.1. Adjusting Population Estimates to Target Years

Key inputs in all population databases reviewed in the previous section are subnational population totals typically available for small administrative or statistical reporting units. The standard source for such data is a national population and housing census, or, in some instances, a large demographic survey. Population censuses are undertaken periodically in many countries, once a decade. Exceptions are countries in which well-functioning civil registration systems make periodic census-taking unnecessary. Many countries take their censuses on the decadal year (1980, 1990, 2000), others take them on the first year thereafter (1991, 2001). (The US Census Bureau maintains an inventory of past and future census dates for each country at www.census.gov/ipc/www/cendates/.) Some countries produce inter-censal estimates. Other countries, particularly those experiencing civil unrest, with few resources, or where census information may be deemed to be politically threatening, tend to have less regular censuses taken at intervals wider than once per decade.

Given that the population data are collected in different years, the small area population totals need to be reconciled by estimating population for the target years of interest. In GPW v3, these are 1990, 1995, and 2000 as well as a projection for 2015. GRUMP is similarly produced for 1990, 1995, and 2000. The regional Africa and Latin America data sets that are based on the accessibility model include population estimates for 1960, 1970, 1980, 1990, and 2000. For most countries, where two native population estimates were available from the national statistical offices, an average annual population growth rate was computed, as follows:

$$r=\frac{\ln \left(\frac{P_2}{P_1}\right)}{t}$$ (1)

where r is the average rate of growth, P₁ and P₂ the population totals for the first and second reference years, respectively, and t the number of years between the two census enumerations. This rate was then applied to the census figures to interpolate or extrapolate population totals to the target years. For example, the 1995 estimate is calculated (where t is now the difference between P₁ and 1995):

$$P_{1995}=P_1{\mathrm{e}}^{rt}$$ (2)

Some countries had only one population estimate. This includes newly formed states (e.g., Croatia) as well as countries that for either economic or political reasons have not conducted a census or released census results since 1990 (e.g., Angola). Others have conducted a recent census (e.g., Afghanistan) but administrative areas have changed to an extent that it cannot be matched with prior censuses. Additionally, many small islands have infrequent censuses and do not have subnational data. In these instances, national-level growth rates from the United Nations were used in lieu of intrinsically calculated growth rates (United Nations, 2001).

3.1.1. Boundary Matching Over Time

The GPW population surfaces use only population and boundary information and the other datasets use these data in combination with other sources. These pieces of information are linked. Where boundaries have changed over time, as they often do, considerable effort is made to reconcile the differences. For example, if a district in 1990 were split into two districts in 2000, the population for the two districts in 2000 would be summed so as to represent the same areal distribution as given in 1990. (It is usually impossible to adequately divide the population for the given district of 1990 in the absence of information provided by the census office to this effect.) As higher resolution data are collected, the need for reconciling boundary changes becomes greater, because lower level units such as districts are modified more frequently than provinces or states. Fitrani et al. (2005) describe how decentralization in Indonesia led to a sharp increase in the number of local governments and associated boundaries (from 292 in 1998 to 434 in 2004). In many countries, changes are less dramatic, but reconciling boundaries and reporting unit identifiers nevertheless poses one of the most challenging problems in compiling detailed, cross-national population databases. Interpolating or extrapolating population figures to a common base year often requires the use of a hybrid method, whereby growth rates are calculated at a level where boundaries have not changed (e.g., provinces), and applied to higher resolution subunits such as districts.

3.1.2. Temporal Aspects of Ancillary Data for Modeled Population Grids

Unlike the GPW databases, GRUMP and the Accessibility Model also use other datasets, which represent phenomena that change over time: changes in urbanization and infrastructure. Unfortunately, the current versions of these databases are limited to a single snapshot. The urban extents are derived primarily from a stable city-lights’ database from a 1994–1995 composite and the roads’ data are approximately as of the year 2004. Users of these databases, interested in changes over time, should be well aware of this limitation.

Future versions of this database will be able to incorporate improved temporal coverage, since the nighttime lights’ data are being processed for additional time periods. Additional research will be required to confirm that changes in nighttime satellite-derived urban extents truly reflect land-use changes surrounding major urban areas rather than changes in sensor characteristics or processing. Should time series of road networks become available, they too could be incorporated. Alternatively, historical transport networks can be approximated by altering the speed of travel over particular surfaces to represent the poorer condition of the transport network in the past and envisaged better conditions in the future.

3.2. Limitations of the Ancillary Data

GRUMP and the Accessibility Model rely on ancillary data because in all instances the best possible data are not available. For this reason, it is important to understand the strengths and weaknesses of those data sources before applying them. While some of the issues associated with the temporal shortcomings have been mentioned, there are other caveats unrelated to temporal concerns.

There have been many uses of the nighttime lights’ data as a proxy for urban areas (Elvidge et al., 1997; Sutton et al., 2001; Pozzi et al., 2003; Schneider et al., 2003) and these data are the only globally consistent and repeated sources of likely urban areas. Nevertheless, they have a few key limitations: they are known to over-represent built-up area, an effect called “blooming.” The blooming effect depends on intrinsic characteristics of the sensor and on geolocation errors in the compositing process (Elvidge et al., 2004). Studies have shown that it is not possible to find a unique threshold to reduce the blooming effect that would work globally (Small et al., 2005). In fact, a 10% threshold could reduce the blooming effect without significantly affecting many individual small settlements for the 1994/1995 dataset. But this threshold does not provide a globally consistent basis for relating lighted areas to urban extent, since the characteristics of the blooming effect are, to some extent, city and country specific. Thus, heuristic or ad hoc adjustments of this nature would make data analysis questionable. A second shortcoming of these data is that they under-represent small settlements that are either poorly or infrequently lit due to insufficient detection by the sensor. This is a particular problem in Africa or rural Asia, where population data are also often sparse.

Given the limitations with the nighttime lights’ data, GRUMP protects against overestimation of urban extents that are false positives—i.e., lights at industrial sites which may not be (or are sparsely) populated—by requiring additional information for validation (i.e., a name, location, and population estimate corresponding to the light). GRUMP also uses additional sources and indirect techniques to estimate extents for known populations that fall below the sensor’s detection threshold as discussed above (see Balk et al., 2005a).

For small-scale or even regional applications, the urban mask associated with the GRUMP data may produce areal extents that are larger than expected. In these instances, use of the urban extent mask if used with the GRUMP population grid may provide sub-urban population detail that might assist in further delineating the more- and less-densely populated areas within these enlarged—or agglomerated—urban areas and thus indicating features (density) that are associated with urban gradients. Reliance on the extent mask in and of itself may lead to overestimation of urban areas. For example, Tatem et al. (2005) found that the GRUMP urban mask overestimates urban extents for Kenya when compared with data derived from higher-resolution satellite imagery.

Future versions may be able to use improved night-lights products, both in their ability to reduce the blooming (though that work is just underway) and to make use of lights detected at more than a single time point. As mentioned, GRUMP was developed when only the 1994–1995 product was available, but subsequent to that, 1992–1993 and 2000 releases have become available. These are not fully analogous datasets, so additional work to determine their utility for urban detection would first be required.

Similarly, for use in the Accessibility Model, there are few data sources that provide consistent, geographically referenced transportation network data for large areas such as an entire continent. The combination of the Vector Map Level 0 (VMap0) spatial data (NIMA, 1997) with the improved attribute data and the transport data used for the African Accessibility Model should be viewed as currently the best available for the given constraints. The spatial data for the African transport network is derived from the Vector Map th VMap layers for roads, rivers, and railroads (NIMA, 1997). VMap0 is an updated version of the Digital Chart of the World (DCW) and is suitable for applications at a scale of 1:1 million. While this provides a consistent level of spatial detail for Africa, the transport links in the database do not contain sufficient information about their characteristics (road quality, road type), which is essential for computing the travel times in the accessibility model. For most of Africa, roads are the most important means of transport, and so the attributes of the road links were substantially improved through the use of continental-scale paper maps of Africa at a scale of 1:4 million (Michelin Travel Publications, 2004). These maps were used to identify 132 000 km of major roads and 282 000 km of secondary roads (11% and 22% of all roads in the VMap0 layer, respectively).

There are many uncertainties in the spatial and attribute data for the transportation network. There is often no easy way to determine the original data source. It is also likely that the original scale of the data varies from country to country. It is often hard to determine how current the data are and how data from different sources were reconciled at country boundaries. Indeed, it is quite possible that the final transportation network does not represent consistently the state of the road network for any one year and it needs to be used with great caution in applications that require data at scales greater than 1:1 million or that require data for the state of the transport network for Africa pre-1990 or post-2005. Future improvements in the quality of continental-scale transport networks will most likely depend on the public release of VMap Level 1 data at 1:250 000 or concerted regional efforts to publish consistent key data layers (such as SERVIR for Central America http://servir.nsstc.nasa.gov/home.html).

4. HEALTH APPLICATIONS

Since the earliest version of GPW and the Accessibility Models in the mid-1990s, health researchers have been using the data to better understand population exposure, vector-habitat, disease distribution, mortality, and related factors (from habitat change to livestock distribution to the distribution of underweight children). These data have been used effectively at the regional and global scale, and in some instance (large areas or countries), in fairly specific local areas. Gridded population data have been used to assist in sampling for a health survey in Chad (Brooker et al., 2002; Beasley et al., 2002) to estimate the geographic distribution of underweight children (Balk et al., 2005b), to determine changing habitat (for example, Reid et al., 2000), and to estimate population at risk of a specific infectious disease. Measures of population counts and density distributions have broad-scale health applications. Although the bulk of this section addresses the latter, a brief review of the former is also included, in part, because gridded population data act as a proxy for a host of other health-related data.

4.1. General Health Studies

Regional studies of mortality and malnutrition have focused largely on understanding biological and socioeconomic factors associated with those outcomes. Spatially explicit data on those outcomes is typically not available. When survey or clinic data are georeferenced, as is increasingly the case, it becomes possible to consider a range of spatially explicit factors, including population density. Density relates to disease transmission—and ultimately health status—in a variety of ways. For example, person-to-person transmission is likely to be high in densely populated urban areas, though such areas may reduce the potential for particular vector habitats. Population density estimates also provide continuous measures of the degree of urbanness (such as high-density core urban areas or less dense semi-urban areas). In the absence of explicit data on the mode of disease transmission, or the vector habitat, and with careful use, population density may be a useful proxy for an urban continuum.

In a study of West African mortality, Balk and colleagues (2004) confirm the complexities associated with measuring and interpreting population density: in urban areas, increases in population density reduced the risk of infant deaths, and the further away from an urban area, the greater the likelihood of infant death. In this study, density (GPW v3) and the GRUMP urban extent mask (alpha version) are used as proxy variables for clinic or health services density (which were not directly measured). In a study of underweight status in African children, Balk and colleagues (2005b) find that population density (GPW v3, CIESIN and CIAT, 2004)—again acting as an urban proxy—decreases the likelihood of children being underweight. Similarly, Sachs and colleagues (2001) and Gallup and Sachs (2001) use GPW v2 to explain differences in the spatial pattern of poverty and disease burden in Africa. These studies find that coastal dwellers—in large part due to their access to ports, urban areas, and infrastructure—experience less poverty and a lower economic burden associated with malaria than inland populations.

4.2. Specific Diseases

Population grids have become a key tool to understanding the populations at risk of contracting various infectious diseases. Infectious diseases have vectors or other transmission routes that are generally highly location based or geographic in nature. The means to understanding the impact of specific disease burdens depends in part on the ability to identify spatially the areas at risk as well as understanding the population in those places. Matching these spatial units—disease numerators with population denominators—is a large part of the contribution that gridded population data make toward understanding specific infectious diseases.

In many low-income countries, lack of resources and capacity in the health system prevent the development of reliable records of malaria morbidity and mortality. A large body of work has attempted to triangulate malaria risk and human population distribution to define population at risk. This work was pioneered in Africa with the development of the MARA/ARMA model of climate suitability for Plasmodium falciparum transmission (Craig et al., 1999). Combinations of this map and the African population database (Deichmann, 1996b) were used to define age-specific populations at risk in 1995. These estimates were derived using national-level age distribution data from the UN Population Division applied to subnational population totals. In combination with empirical epidemiological data from local studies, Snow and colleagues (1999a, b) produced estimates of morbidity and mortality for the total and under five-year-old populations of Africa (see also Hay et al., 2000). This work was updated and augmented (Snow et al., 2003) to the year 2000 using the African population database (Deichmann, 1996b) to determine the proportion of the population in transmission risk categories and applying these to year 2000 national population estimates from the United Nations (2001). The most accurate revision of these mortality and morbidity figures for Africa has been done by using new extractions for the year 2000 using GPWv3 (CIESIN and CIAT, 2004) and the MARA model (Hay et al., 2005a). This work is also incorporating the location of urban populations in Africa to discount morbidity and mortality estimates for the significantly lower malaria transmission rates in these urban areas.

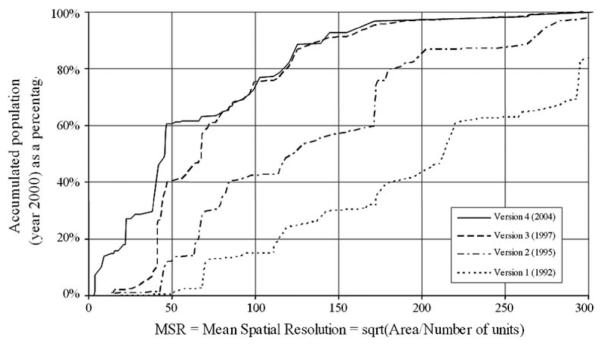
Recently, these “population at risk” assessments have been conducted using historical maps of malaria endemicity and its transmission extent to evaluate the changing population at risk between 1900 and modern times at the global scale (Hay et al., 2004). Using a similar approach to MARA/ARMA morbidity, estimates for P. falciparum have now been conducted globally (Snow et al., 2005). In addition, some (Rogers and Randolph, 2000; Van Leishout et al., 2004) have used GPWv2.0 (CIESIN et al., 2000) to estimate population at risk under coupled scenarios of population and climate change. There are many issues involved with the choice of population surfaces and their derivation and these have been evaluated with respect to population at risk of malaria in Kenya (Hay et al., 2005b). Hay and colleagues show the paramount importance of the average spatial resolution of the input census data by comparing five population surfaces including GRUMP v1, GPW v2, and v3; the Accessibility Model (version 3 not the most current); and LandScan. Figure 5 compares the error associated with each dataset at varying levels of spatial aggregation: they all estimate about the same population at the most aggregated level (the first administrative level) but two stand apart, GPW v3 and GRUMP v1, providing notably superior estimates at the highest spatial resolution. (Note that this publication was not undertaken on the most recent versions of the Accessibility Model, in which the underlying inputs have been improved, or of LandScan.) The results also highlight the issues involved and accuracy that can be obtained using simple interpolation techniques at different administrative levels, where these might be locally available. Although the interpolation methods differ, the best-fit datasets are those with inputs of the highest mean spatial resolution (MSR).

Figure 5.

Cumulative percent of the African population represented by mean spatial resolution (MSR) (i.e., for version 4, 60% of the population is represented by an MSR of 50 or better).

Given the absence of reliable data on the total number of parasitic infections in a country, estimates have often been based on prevalence data from a few limited studies and extrapolated to the country as a whole. In order to make these extrapolations more accurate, global georeferenced population datasets have been used increasingly. In particular, population totals and distribution from the Africa Population database (Deichmann, 1996b) and the first version of GPW (Tobler et al., 1995), along with district-level census data when available, have been used to estimate population at risk of parasitic diseases or to estimate the number of people infected. For example, different statistical models have been developed to estimate the number of individuals to be treated based on the prevalence of infection of a given disease and population structure and distribution (Brooker et al., 2000; Lindsay & Thomas, 2000; Noma et al., 2002). Lindsay and Thomas (2000) use climate data to predict the distribution of lymphatic filariasis and overlay the resulting risk maps with a continental population grid (Deichmann, 1994) to estimate the number of people potentially exposed to the infection in Africa.

The issue of identifying population at risk and priority areas for treatment has been addressed by combining gridded population data with remotely sensed data. For instance, a recent methodology was developed to combine ecological zones defined using satellite-derived data (land-surface temperature and photosynthetic activity averages) with population density and prevalence data to map population at risk of parasitic infections in different countries in Africa (Brooker et al., 2001a, 2002; Kabatereine et al., 2004) and Asia (Brooker et al., 2003). The results provide a targeted sampling frame of schools to guide valid epidemiological surveys and the identification of priority areas for national school initiatives and mass treatment. Noma et al. (2002) use GIS to identify bioclimatic zones of potential for onchocerciasis and to select which communities should be surveyed. The results were used to define areas of varying transmission risk to guide the implementation of control strategies. Similarly, Brooker and colleagues (2001b) used an early version of the African Population grid (Deichmann, 1996b) to determine populations at risk in particular locations resulting in observation of a significant relationship between the prevalence of Schistosoma mansoni and the distance of the schools from the lakeshore; as a matter of health policy, “distance to lakeshore” can now be used as a means to screen schools in East Africa.

A related application is one where global population data were used to study the relationship between population distribution changes and associated habitat changes. For example, Reid and colleagues (2000) predict that population distributional changes will, in effect, reduce the cattle population habitat leading to the reduction of the tsetse fly population and sleeping sickness prevalence in the human population.

Several uses of gridded population surfaces have demonstrated patterns in the distribution of human population vis-à-vis physiographic, climatic, and other environmental parameters that may be closely linked to health and disease burdens. For example, Small and Cohen (2004) use GPW v2 to show that people tend to live at low altitude (with Mexico City being an important exception) and near permanent water sources (rivers and coasts), but that population is not nearly as localized with respect to climatic variables such as precipitation or temperature. Disease vectors may be influenced by all of these factors, thus demonstrating the need for moderate-resolution population surfaces that allow for these factors to be disentangled in any given region of interest. In another study, Astrom and colleagues (2003), using GPW v2, find that populations residing above a certain altitude—due to the relationship with the physiological processing of oxygen at high altitude—experience lower tumor incidence.

In the wake of the Indian Ocean tsunami of December 26, 2004, the GRUMP population grid was used in combination with coastal buffer distances and elevation to estimate the population exposed to the great wave (Balk et al., 2005c): roughly four million persons were estimated to live within a 2 km buffer in the most-affected regions. These estimates were then used to calculate death rates in some of the affected regions. National and moderate-resolution subnational population estimates could not be used rapidly, and without considerable assumptions, to generate estimates of exposure to natural hazards. (Even if some countries had high-resolution subnational data, they would need to be gridded to make such calculations.) Further, since this tragedy occurred across many national borders, it highlighted the utility of having a global population grid that is agnostic about independent of country boundaries. A global study of natural disaster hotspots has used GPW to estimate the risk of mortality and economic loss from six major natural hazards (Dilley et al., 2005).

Lastly, an exploratory study considers the relationship of population density to the location of newly emerging or re-emerging infectious disease (Patel et al., 2006). While the evidence is preliminary and complex, it suggests that disease emergence may be causally related to population dynamics, travel and trade routes.

5. DISCUSSION

Population input data are inevitably highly variable in terms of quality, resolution, and accuracy, in ways that are not quantifiable. In part, that is the nature of demographic data, which represent social processes, but treating them as if they were an easily measurable physical variable (on a grid). Administrative units will always be larger in sparsely populated areas, and perhaps will have more detail than may be needed for some applications in high-density places. Users should bear this constraint in mind when using these data.

5.1. Ideal Spatial Resolution

The ideal resolution for the study of infectious diseases and health will vary. Localized disease outbreaks might require information on village location, boundaries, and associated population characteristics. Emergency response studies, such as the recent tsunami in the Indian Ocean (Balk et al., 2005c) require high-resolution administrative boundaries, population, and other demographic data associated with those boundaries as well as infrastructure (e.g., health clinics) at risk. Where the emergency is brought on by a geophysical phenomenon that is best estimated with physical data (such as coastal distance or elevation) gridded data are a prerequisite for establishing baseline population exposure. For broad synoptic analysis of health–environment issues, medium-resolution data would likely be sufficient.

The databases discussed herein have been constructed with enough information to incorporate uncertainty into the analysis. A simple measure for each pixel is the resolution—in this case, the size of geographic area—of the administrative unit from which the pixel population was derived or modeled. A grid of this indicator is available for version 3 of GPW. In practice, few people take the trouble to do serious uncertainty or sensitivity analyses. The responsibility of data producers is to provide all relevant information about input data, document modeling, and processing and leave it to the user to take this information into account.

In the development of the aforementioned data products, it has been useful to construct a measure of effective resolution. Measured as the country-specific average resolution, it can be thought of as the “cell size” if all units in a country were square and of equal size, which of course they are not. It is calculated as follows:

$$\text{Mean resolution}\left(\mathrm{Km}\right)=\sqrt{\left(\text{country area}\right)∕\left(\text{number of units}\right)}$$ (3)

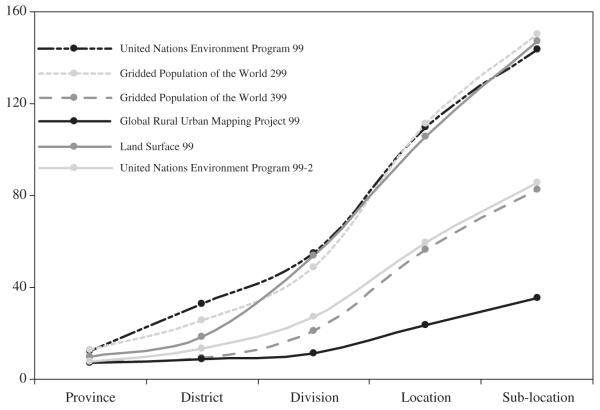
A closer look at the varying resolution (or area) of the administrative units reveals other key improvements in the database in the GPW efforts. The average resolution of all countries went from 60 to 46, with improvements of 10 times or more for particular countries. Figure 6 shows the resolution improvements in Africa, for four versions of the Accessibility Model, by cumulative population. In the current version of the accessibility model, as with GPW v3, more than 60% of Africa’s population is represented by a mean resolution of 50 km or better. This represents a significant improvement over previous models, including version 2 of the Accessibility Model and GPW v1, where 60% of the population was represented by much coarser resolution, more than three times coarser than the current resolution (about 170 km).

Figure 6.

Graph of error structure by administrative level for the five large area public-domain human population distribution surfaces (see Hay et al., 2005b). Left axis is the root mean square error expressed as a percentage of the mean population size of the administrative level.

Though GPW has always sought to be based on inputs of the best-available resolution at the time, efforts to improve version 3 of GPW included acquisition of even higher resolution data for countries with coarse-resolution inputs and islands some of which required labor inputs to compile the basic data (such as digitizing). Earlier versions of GPW had less motivation (and resources) to do this, because the output resolution of 2.5 arc-minutes rendered finer input resolution redundant. The inputs for the third version of GPW were also used as an input to the GRUMP population surface that includes reallocations toward urban areas and whose output resolution is 30 arc-seconds. Given the small footprint of many urban areas, the considerable investments in obtaining the highest available resolution population data were necessary to achieve the best-possible match between input and output resolution for each country. Often, these new inputs had to be digitized from imperfect source materials, since digital versions of these data were not available. For countries that are island chains, the improvements consisted of collecting island-level population data, and then assigning population to existing spatial inputs. GPW v2 had 41 countries with country-level (administrative level 0) data only, 31 of which were islands, which had an average resolution of 46. In version 3, fewer than half of these countries remain (with a slightly smaller share of them being islands) with an average resolution of 22.

5.2. Conclusion

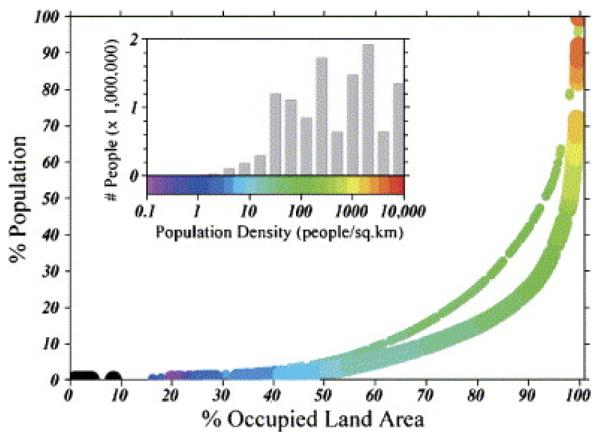
As capabilities in refining the estimates of population distribution, urban areas, and associated infrastructure networks have increased, the more evident the localized nature of the distribution of human population has become. Improved estimates show that less, not more, land area tends to be occupied by moderate and densely populated settlements, as shown in Figure 7 (Figure 7 is Plate 4.7 in the Separate Color Plate Section), for the case of Ecuador. These spatial Lorenz curves show the cumulative fraction of the population as a function of cumulative fraction of land area, where units are ordered by increasing population density. Forty percent of Ecuador’s population lives on 15% of its land area according to GPW v2. The improved resolution of GRUMP revise estimates substantially, reducing it by more than half, to only 6% of the land area in this example. People live locally, are burdened by disease locally, and receive their health services locally. Gains in the improved resolution of human population distribution will continue to lead to a better understanding of disease and health, but these gains must also be matched with improvements in information on health clinics, health catchments, and infrastructure.

Plate 4.7.

Spatial Lorenz curve for the population distribution vis-à-vis the land area of Ecuador, 2000 (with insert indicating the non-cumulative distribution of population density).

In the future, more high-resolution data should become available so that modeling will be less and less necessary for most health analyses. While there may still be a need for modeled population data—for example, to understand seasonal flows—the basic improvement would be to the baseline population distribution. Hence what is important is to ensure long-term funding for maintaining and updating these data, and to ensure open-data dissemination policies so that data are made easily available for science and policy. For health studies, priority next steps, apart from continuing to increase resolution, would be more consistent global time series (e.g., going back several decades to assess recent trends), and further demographic variables such as age distribution and other variables required to make rigorous spatial projections.

6. DATA DISSEMINATION

The following data are available in the accompanying DVD: the Gridded Population of the World version 3 (beta) at 2.5 arc-minutes: population counts, land area, and population density; version 1 (alpha) of the GRUMP 30′ population surface; and the Accessibility Model for Africa. All grids are available in GeoTIFF format. Users are strongly encouraged to visit the respective websites for updates and final versions. For GPW and GRUMP, see http://sedac.ciesin.columbia.edu/gpw, where users can also download the grids for 2015, the GRUMP settlement points (alpha), and the urban extent mask (alpha) as well as ancillary data products associated with GPW (e.g., national coastlines to match the population grid and a grid of national identifiers). The website for Accessibility Model for Africa is http://na.unep.net/globalpop/africa/Africa_index.html. An updated version of the Accessibility Model for Latin America and the Caribbean is underway and users should visit CIAT’s website http://gisweb.ciat.cgiar.org/population/ for updates. Users are strongly encouraged to supply feedback, and their publications that make use of these data, to gpw@ciesin.columbia.edu.

6.1. Data Selection

Before using the population surfaces in the companion DVD for analysis, a population model and spatial resolution must be chosen and the data evaluated to ensure that its precision meets the study requirements. Population surface and accessibility models should not be used as ‘independent’ tests of the reliability of nighttime light imagery or transportation network data (nor should they be used to modify such data in attempts to eliminate errors) when they have been derived from these original datasets in the first place. It is essential to avoid circularity in ‘improvements’ of both original and derived datasets. The choice of appropriate resolution—a 30 arc-second or 2.5 arc-minutes—depends on the scale of the study. In general, the 2.5 arc-minute data are most appropriate for continental and large-region studies; the 30 arc-second data are most appropriate for smaller regions and national studies. In some cases, subnational studies are possible with the 30 arc-second data, but it is not possible to derive meaningful results for small-area studies such as those for a single city.

For the GPW and GRUMP data, the administrative unit area grid (available from the GPW web site) may be used to determine the approximate locational precision of the population surfaces on a cell-by-cell basis. The administrative unit area grid indicates the area of the administrative unit from which the population value was derived. Where multiple units contributed to a cell, the value is the weighted mean of the input administrative unit sizes. A cutoff mean administrative unit area value can be approximated by calculating the area based on a given radius. For example, to identify the cells with a locational accuracy of approximately 10 km or greater, a cutoff value of 314 would be used, because cells with a value greater than this are derived from an administrative unit that cannot be enclosed by a circle with a radius of 10 km. In reality, a larger value should be used, as very few administrative units are circular in shape.

6.2. Methods and Issues in Analysis

Using the population data surfaces requires a software package capable of dealing with raster data, such as ArcGIS ™ (with the Spatial Analyst extension), Erdas Imagine®, Idrisi, GRASS, MatLab®, or any number of others. GeoTIFF is a well-known format supported in most packages that handle raster data. If translation is necessary, the open source Geospatial Data Abstraction Library (GDAL), available at: http://www.remotesensing.org/gdal/, can be used to convert files to a number of other formats.

The most common form of analysis is to aggregate population totals in the surfaces by some other unit of analysis (such as ecological regions or habitats, buffers around points of interest such as health clinics, and so on) using a zonal statistics function. Population density grids may be used in a similar manner to characterize the variability of population within different zones; the minimum, maximum, mean, and standard deviation of density values within a given zone are often more useful for inter-zone comparison than just for the total populations of the zones.

Regression analysis with population counts or density as an explanatory variable or as a per capita denominator for explanatory variables other than population is another tool used commonly with these data. While there are many legitimate uses of these raster population surfaces in quantitative analysis of this type, care must be taken as raster data can invalidate the assumptions in classic regression. This occurs simply as a function of the self-replicating feature of the gridded nature of the data. A raster layer comparison is useful for explanation but cannot be relied on for rejecting the null hypothesis at a given probability level (Openshaw, 1991) because these data may be biased. That is, the original administrative area data would have had a single value that was distributed across far more grid cells. While the approximate value of each grid cell would be accurate, each observed grid cell is not independent of (i.e., they are spatially dependent, being from the same original administrative area polygon; and they inflate the number of observations). Geostatistical approaches based on point observations (GPW and GRUMP make centroids of the units used in gridding available for this purpose), or using the data to first construct variables based on zonal statistics, may be better. The examples given herein have paid attention to this caveat. These approaches can be accomplished with geostatistical extensions to any other GIS software or stand-alone software packages for working with spatial data (e.g., the ArcGIS® Geostatistical Analyst extension or the free GeoDa software package).