Electromechanical models of the ventricles

Abstract

Computational modeling has traditionally played an important role in dissecting the mechanisms for cardiac dysfunction. Ventricular electromechanical models, likely the most sophisticated virtual organs to date, integrate detailed information across the spatial scales of cardiac electrophysiology and mechanics and are capable of capturing the emergent behavior and the interaction between electrical activation and mechanical contraction of the heart. The goal of this review is to provide an overview of the latest advancements in multiscale electromechanical modeling of the ventricles. We first detail the general framework of multiscale ventricular electromechanical modeling and describe the state of the art in computational techniques and experimental validation approaches. The powerful utility of ventricular electromechanical models in providing a better understanding of cardiac function is then demonstrated by reviewing the latest insights obtained by these models, focusing primarily on the mechanisms by which mechanoelectric coupling contributes to ventricular arrythmogenesis, the relationship between electrical activation and mechanical contraction in the normal heart, and the mechanisms of mechanical dyssynchrony and resynchronization in the failing heart. Computational modeling of cardiac electromechanics will continue to complement basic science research and clinical cardiology and holds promise to become an important clinical tool aiding the diagnosis and treatment of cardiac disease.

this review article is part of a collection on Electrophysiology and Excitation-Contraction Coupling. Other articles appearing in this collection, as well as a full archive of all Review collections, can be found online at http://ajpheart.physiology.org/.

The cyclic pumping of the heart arises from the synergy of its electrical and mechanical function. Understanding the individual functions, and more importantly their interaction, has been the subject of intense research in basic science and clinical cardiology. Experimental studies have provided significant insight into the electrical and mechanical activity of the heart from the molecular up to the whole body level; however, detailed information regarding the intricate processes at each level of this hierarchy cannot capture the emergent phenomena, the behavior resulting from cooperative interactions across temporal and spatial scales, as well as the behavior arising from the interactions between the electrical and mechanical components. Moreover, current experimental methodologies are limited by their inability to assess the three-dimensional (3-D) electrical and mechanical activity in the heart simultaneously and with sufficient spatiotemporal resolution. Thus a comprehensive approach that can integrate detailed information across the spatial scales of both cardiac electrophysiology and mechanics is needed to provide a better understanding of the complex relationship between electrical and mechanical activity. Computer modeling represents such an approach.

The goal of this article is to provide an overview of the latest advancements in electromechanical modeling of the 3-D ventricles. Because of space limitations, we focus our limited review predominantly on multiscale electromechanical simulations with histoanatomical models of the ventricles. The developments are firmly grounded in previous one- and two-dimensional electromechanical modeling work, which unfortunately could not be included in this article. In this review, we first detail the general framework of electromechanical modeling and describe the state of the art in computational techniques and well as experimental validation approaches. The powerful capability of ventricular electromechanical models to ascertain emergent electromechanical behavior, and thus provide insight into cardiac function in health and disease, is then demonstrated by reviewing the latest insights obtained with these models.

Overall Approach to Ventricular Electromechanical Modeling

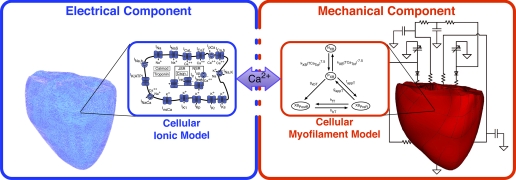
Multiscale computational models of ventricular electromechanics are primarily composed of two parts, which individually simulate the electrical and mechanical activity. A schematic diagram of the model is shown in Fig. 1. Briefly, as a depolarization wave propagates through the heart, calcium is released from the myocyte intracellular stores. Calcium then binds to troponin C, initiating cross-bridge cycling, which, in turn, results in active tension development. This ultimately leads to the deformation of the ventricles. Each of these processes is represented in an electromechanical model of the ventricles.

Fig. 1.

Electromechanical modeling of the ventricles. Overall approach to electromechanical modeling. Schematics of ionic and myofilament models, the combination of which constitutes the cell electromechanical model, are also shown.

The electrical component of the model simulates the propagation of action potential. It describes the current flow from cell to cell through low-resistance cellular gap junctions as well as the spread of current in the extracellular space. Cellular electrical activity is driven by the active ionic flow across the myocyte membrane; this is represented by the myocyte ionic model, representing current flow due to ion channels, pumps, and transporters as described by a set of ordinary differential and algebraic equations.

The mechanical component of the model simulates the active contraction and resultant deformation of the ventricles. The electrical and mechanical components are coupled by the calcium release from intracellular stores during electrical activation, caused by calcium entering the cell. The calcium transient serves as an input to the cellular myofilament model, which describes calcium binding to troponin C, cooperativity mechanisms, and cross-bridge cycling. The active tension generated by the myofilament model results in a deformation of the ventricles. Lastly, pressure and volume conditions are imposed on the ventricles by a model of the systemic and circulatory system to simulate chamber hemodynamics.

State of the Art in Ventricular Electromechanical Modeling

In the following sections, we present the latest computational techniques in ventricular electromechanical modeling, with an emphasis on the advancements in the mechanical component of the model.

Ventricular geometry.

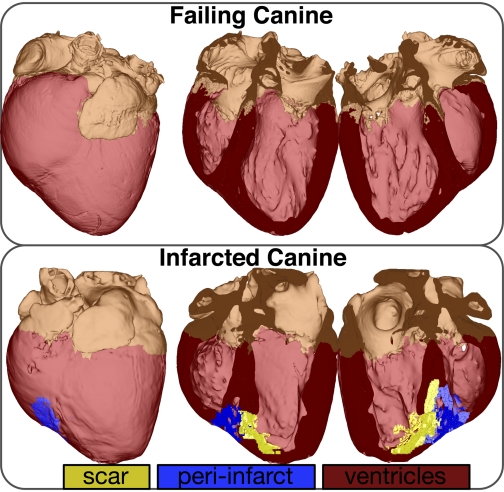
The skeleton of the electrical and mechanical parts of the model is the anatomical model of the ventricles. The initial modeling efforts in representing ventricular geometry idealized the shape of the ventricles by representing them as cylinders and ellipsoids (1, 9). Over the past decades, more sophisticated reconstructions of the first anatomical models that included realistic, albeit averaged, geometries were developed; however, this required the labor-intensive procedure of histological sectioning (18, 31, 37). Recent advancements in imaging of the heart have ushered in a new era in ventricular electromechanical modeling. High-resolution magnetic resonance (MR) and computerized tomography scans provide detailed information regarding the individual ventricular geometry. Unlike histological sectioning, MR and computerized tomography imaging of the heart takes only a few hours to complete. Novel approaches to reconstruct the ventricular geometry from MR images have recently been developed (22, 28, 35, 36). Using imaging data for reconstruction of ventricular geometry also allows for the inclusion of structural remodeling in the individual heart, such as myocardial infarction. Figure 2 illustrates image-based anatomical models of the canine ventricles.

Fig. 2.

Reconstruction of infarcted and failing canine hearts from magnetic resonance images. Modified with permission (35).

Computational meshes.

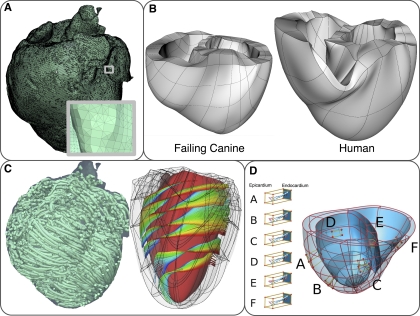
The finite element method is most commonly used to solve the electrical and mechanical problems of the model, and the spatial discretization of the ventricular geometry represents the computational mesh for the solution of the governing equations. Because the governing equations of the electrical and mechanical parts are different, each component has different requirements for the mesh element type and size. The electrical mesh requirements are based on the spatiotemporal characteristics of wave propagation; a spatial resolution of ∼250–300 μm is appropriate for electrophysiological finite elements, which typically are linear. A state-of-the-art methodology to generate the electrical mesh from directly segmented images has been recently published (24), which generates boundary-fitted conformal meshes. An electrical mesh of the normal canine ventricles is shown in Fig. 3A. Figure 3A, inset, showcases the high quality of the electrical mesh.

Fig. 3.

Computational meshes and fiber and sheet structure. A: computational mesh of the infarcted canine ventricles for the electrical component of the electromechanics model. A, inset: zoomed-in image of the mesh, showing the mesh details. B: computational meshes for the mechanics component. C: fiber and sheet orientations obtained from diffusion tensor magnetic resonance images. Fiber orientation is for the infarcted canine heart. Sheet orientation is shown on the endocardium in diastole. D: human ventricles with rule-based fiber orientation. Modified with permission (5, 22, 35). D, A–F: transmural changes in fiber angle for different regions in the ventricle.

In contrast, the mechanical mesh is constructed from larger finite elements with higher order of interpolation (Fig. 3, B and D), which are suitable for simulations of large cardiac tissue deformations. The mesh typically consists of nonlinear finite elements; Hermite-based elements are more commonly used since they are appropriate for maintaining incompressibility constraints and ensuring strain continuity across the element borders. The mechanical meshes typically have a polar (33), butterfly (38), or two-layer (5) topology, with nearly flat endocardial surfaces and rigid finite element structure. A new technique to construct the mechanical mesh from MR images has been recently developed (5). In this semiautomatic approach, two layers of elements are wrapped about the ventricles to form the left and right ventricular geometry. The least-square method is then used to better fit the mesh to the endocardial and epicardial surfaces. Figure 3B provides examples of this novel two-layer finite element mesh generation approach.

Fiber and laminar sheet geometry.

The fiber and laminar sheet organization determine the orthotropic electrical conductivities and the passive mechanical properties of the myocardium. The information regarding the fiber/sheet architecture can be obtained from histological sectioning data or diffusion tensor (DT) MR scans. It is well established the that eigenvectors of the DTs are aligned with fiber, sheet, and sheet-normal directions (6). In the electrical mesh, the fiber, sheet, and sheet-normal directions are mapped onto the centroids of the finite elements (35). To incorporate the fiber and sheet information into the mechanical mesh, the fiber and sheet angles and their derivatives are usually approximated by scalar functions (6). A more advanced approach is to use tensor metric space and operations in the tensor vector space and define a least-square approximation and interpolation of DTs on the finite elements (5), thus eliminating the discontinuity errors associated with angle interpolation. Figure 3C presents an example of the reconstructed fiber and sheet architecture from DTMR scans in the canine ventricles. Rule-based approaches to reconstruct the fiber orientation has also been used with patient-specific ventricular geometry (22) (Fig. 3D).

Electrical component.

Three-dimensional activity in the electrical component of the model is governed by the parabolic partial differential monodomain equation, which describes the flow of current from cell to cell through the low-resistance gap junctions and relates the transmembrane potential to the transmembrane current. If it is necessary to explicitly account for the extracellular current flow, the bidomain model, a coupled system of partial differential equations, is solved instead. The local tissue conductivity tensors are obtained by combining information regarding the local fiber and sheet arrangement and the myocyte-specific conductivity values; the orthotropic electrical properties of the myocardium are reflected in these conductivity tensors. Myocyte membrane kinetics is described by a set of ordinary differential and algebraic equations, myocyte ionic models that have been used in electromechanical modeling range from phenomenological models such as the two-variable Fitzhugh-Nagmo model (19) to biophysically detailed models that incorporate excitation-contraction coupling (2). The simultaneous solution of the partial differential equation(s) with the set of the ionic model equations represents the simulation of electrical wave propagation, which is significantly more computationally demanding than the simulation of cardiac contraction described in Mechanical component. A detailed review of the latest computational techniques in electrophysiological modeling can be found in Plank et al. (23) and Trayanova (32).

Mechanical component.

The governing equations for the mechanical component are the stress equilibrium equations, which are based on large deformation theory. The constitutive law for passive cardiac tissue mechanics is based on orthotropic elasticity and is expressed in a strain energy function. In addition, the myocardium is usually considered as nearly incompressible material. A variety of different constitutive laws have been developed (7). To account for the laminar sheet organization of cardiac tissue, pole-zero (31) and Holzapfel-Ogden (7) constitutive laws have been developed. Exponential strain energy functions are commonly used (3, 5, 33) because of the relative simplicity of parameter estimation and numerical stability.

Representations of myofilament dynamics, which are used to simulate active tension development, range from highly simplified models to sophisticated empirical (8, 30) and biophysical models (27), composed of ordinary differential and algebraic equations. In simplified models, the tension profile is typically a parabolic function (12). In empirical models, the average force developed by the cross bridges is represented by predefined expressions, based on experimental observations of isolated muscle contraction at different loading conditions. Finally, biophysical models of cardiac myofilament dynamics include descriptions of detachment and attachment of cross bridges and their elastic properties. When these models are incorporated into ventricular electromechanical models, the parameters are adjusted iteratively to match experimental volume and pressure curves during contraction (22, 25).

The full system of equations for the mechanical component of the model is of algebraic-differential form. The algebraic partition consists of the nonlinear equations obtained from the numerical integration of the weak form of the stress equilibrium equations. The differential part arises from the system of ordinary differential equations from the cardiac myofilament model. A major challenge in electromechanical modeling is developing an algorithm that can handle the numerical instabilities when solving this system of equations. In the explicit scheme, the algebraic system is solved with the Newton-Raphson method, and the strain tensors are used to calculate the lengths and velocities of shortening of the myofilament models at each time step. Alternatively, implicit schemes, where the integration of the cardiac myofilament model is performed at each iteration of the Newton-Raphson method, can be employed (5, 21).

Circulatory system.

Electromechanical models are typically coupled to a two- to four-element windkessel model to simulate the different phases of cardiac contraction (15). However, the incorporation of a windkessel model may lead to inaccuracies since the diastolic pressure and aortic valve opening pressure are predetermined in an open-system windkessel model. Recently, closed-loop representations of the pulmonic and systemic circulation that include a time-varying elastance model of the atria have been developed and coupled to ventricular electromechanical models (13, 29). With these types of models, the diastolic and aortic valve opening pressures are emergent properties.

To couple the ventricular and circulatory models, pressure is applied to the endocardial surfaces, simulating the interaction of the blood with the ventricles. In a new coupling method by Gurev et al. (5), the intraventricular pressures are added as additional unknown variables in the nonlinear system of equations. The ventricular volumes are expressed, using the divergence theorem, as functions of the degrees of freedom of the endocardial surface nodes. An alternative approach is to perform iterative perturbation steps of the ventricular pressures to compute the ventricular compliance matrix (13).

Coupling the electrical and mechanical components.

The two components of the electromechanical model can either be weakly or strongly coupled. In a weakly coupling scheme, the electrical activation times at different locations, as calculated from the electrical component of the model, are inputted into the mechanical model as the instances when the myofilament model is activated. This scheme is sufficient in problems when mechanoelectric feedback could be ignored. Alternatively, the ionic and cardiac myofilament models are coupled within the mechanics component, and the electrical activation times determine the instant at which this combined ionic-myofilament model is activated (5). With the employment of this more sophisticated method of weak coupling, cooperativity mechanisms, such as calcium binding to troponin C, are represented in the model. In simulations of mechanoelectric coupling where changes in tissue conductivities, membrane capacitance, or ionic currents induced by tissue deformations are considered to be important, strong coupling is necessary and can be straightforwardly implemented (20). In this case, the ionic model and the myofilament model are simply combined through the intracellular calcium transient. However, representing deformation-induced changes in tissue conductivities requires a recalculation of the stiffness matrix in the finite element method of the electrical component at each time step, which is computationally expensive.

Experimental Validation of Ventricular Electromechanics Models

Validating the model of cardiac electromechanics with experimental data is a pivotal component in model development. It constrains the model parameter space and enhances the model's physiological relevance. To validate the electrical component of the model, simulation results are often compared with electrical activation maps obtained from epicardial socks, endocardial balloons, or plunge electrodes from optical mapping (22, 34) or from ECGs and body surface potential maps (11, 14). The mechanical component is verified with gross wall motion or local strain measurements calculated from MR or ultrasound images (34) or from hemodynamical metrics such as left ventricular pressure and volume, ejection fraction, or maximal rate of pressure change (14, 22).

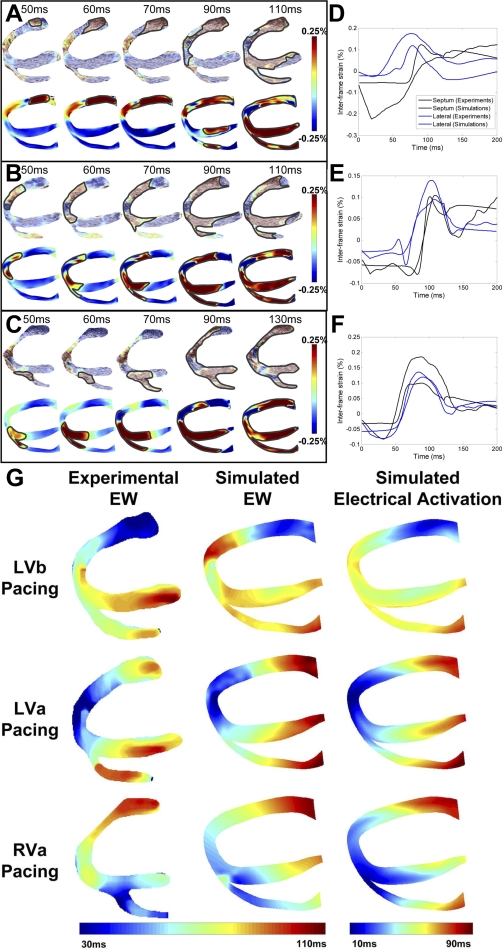
The study by Provost et al. (25) provides an interesting and novel example of electromechanical (rather than separate electrical or mechanical) heart model validation. Recently, a novel imaging technique termed electromechanical wave (EW) imaging (EWI) has been developed (26). EWI is an entirely noninvasive ultrasound-based imaging technique capable of mapping the propagation of EWs along echocardiographic planes; this is achieved by mapping the interframe axial strains. Once validated, EWI could be used in the clinic as a noninvasive surrogate for the 3-D electrical activation pattern. Provost et al. (25) conducted an in silico and in vivo reciprocity study, in which data from EWI were first used to validate the MRI-based electromechanical model of the normal canine ventricles developed by Gurev et al. (5) for different pacing protocols, and the validated electromechanical model was then used to assess the utility of EWI in mapping the electrical activation in the heart. The protocol included pacing the ventricles from the left ventricular base, left ventricular apex, and right ventricular apex in both simulation and experiment. Figure 4, A–C, presents experimental and simulated EWI maps for different pacing protocols. Figure 4, D–F, compares simulated and experimental interframe strains over time at the lateral wall and septum for different pacing protocols and demonstrates a strong agreement between simulation and experiment, indicating that the ventricular model of normal canine electromechanics reliably reproduces EW behavior.

Fig. 4.

Mapping of electromechanical wave (EW) imaging. Experimental (top) and simulated (bottom) interframe strain distribution associated with EW for left ventricular base (LVb) pacing (A), left ventricular apex (LVa) pacing (B), and right ventricular apex (RVa) pacing (C) are shown. Comparative graphs between experimental and simulated interframe strain traces at the septum (black) and lateral wall (blue) for LVb pacing (D), LVa pacing (E), and RVa pacing (F) are shown. Experimental and simulated electromechanical activation isochrones and simulated electrical activation isochrones during the 3 pacing protocols (G) are shown. Modified with permission (25).

The authors then analyzed the relation between electrical and electromechanical activation to establish the capability of EWI to map the electrical activation sequence. Figure 4G presents isochronal maps of EW propagation in experiment and simulation and of electrical activation calculated from the model, illustrating that the EW travels in the same direction as electrical activation. A linear relationship between electrical and electromechanical activation was found, with slopes ranging between 1.01 and 1.17, further demonstrating that the EW propagation correlates with the electrical activation sequence. The simulation results thus revealed a strong correlation between electrical activation sequence and EW, establishing the capability of EWI in mapping the electrical activation sequence. This example demonstrates that a thoroughly validated model can be a powerful tool in a variety of applications.

Examples of Recent Insights from Ventricular Electromechanical Modeling

Stretch-activated ventricular arrhythmias.

Experimental and clinical research has demonstrated that mechanical events can affect the electrophysiological state of the heart. Mechanoelectric coupling mechanisms, in conjunction with those associated with disease-related remodeling, are often considered as a possible cause of disturbances in heart rhythm. Stretch-activated channels (SACs) have long been implicated in contributing to the arrhythmic substrate of the heart. The nonuniform distribution of stretch during contraction under a variety of pathological conditions may produce proarrhythmic dispersion in electrophysiological properties. SACs have been shown to shorten or lengthen the action potential duration of a single myocyte, depending on the timing of the mechanical stimulus relative to the phase of the action potential (39). Because current experimental techniques cannot record the 3-D electromechanical activity of the heart with high spatiotemporal resolution, our understanding of how SACs contribute to ventricular arrythmogenesis remains incomplete. Computer simulations of stretch-activated arrhythmias provide an alternative methodology to dissect the mechanisms by which SACs contribute to the arrhythmogenic substrate.

Early computational studies of SAC-mediated arrhythmogenesis in the ventricles have provided significant insights into the mechanisms of commotio cordis, precordial thump, and defibrillation in the setting of ventricular dilatation; however, these studies employed pseudoelectromechanical ventricular models in which the mechanical activity was not explicitly represented but rather its effect on electrophysiology via SACs was. It is only recently that true electromechanical models have been used to examine the role of SACs in arrhythmogenesis in the 3-D heart and are highlighted below. The study by Keldermann et al. (11) employed an electromechanical model of the human left ventricle to study the effect of mechanoelectric feedback on reentrant wave dynamics. The authors found that a nonuniform activation of SACs can result in the degeneration of a stable spiral wave into turbulent patterns. Their simulation results revealed that regions of wave break were those undergoing stretch. At these regions, depolarization due to SAC opening blocked the propagation at the stretched region. This simulation study provided an explanation of the degeneration of ventricular tachycardia into ventricular fibrillation alternative to the restitution or mother-rotor hypotheses.

The recent study by Jie et al. (10) investigated the mechanisms of mechanically induced ventricular ectopy and those by which it degrades into reentrant arrhythmia in the regionally ischemic ventricles. A model of the beating rabbit ventricles was used that included a spatial distribution of the central ischemic zone and border zone (BZ) with realistic ischemia-induced electrophysiological and mechanical changes. Dynamic mechanoelectric feedback was represented via spatially and temporally nonuniform membrane currents through SACs. The simulation results revealed that contraction of the surrounding normal tissue resulted in stretch of the ischemic tissue, causing mechanically induced depolarizations in the ischemic region. Although the mechanically induced depolarizations in the BZ were smaller compared with those in central ischemic zone, mechanically induced ventricular premature beats originated from the endocardial BZ. Mechanically induced depolarizations also contributed to the arrythmogenic substrate by further decreasing the local excitability, causing conduction block and slow conduction in the ischemic region. The study by Jie et al. (10) provided the first direct evidence that mechanically induced membrane depolarizations and their spatial distribution within the ischemic region are possible mechanisms by which mechanical activity can contribute to spontaneous arrhythmias under the conditions of acute regional ischemia.

Electromechanical activation of the ventricles.

The mechanical effect of the altered cardiac activation sequence has been the subject of intense research since dyssynchronous electrical activation can cause abnormalities in perfusion and pump function. Ventricular simulations have played an important role in providing insight into the understanding of the relationship between the spatial pattern of electrical activation and the resultant contraction. The study by Usyk and McCulloch (34) was the first to examine the distribution of the time interval between myocyte depolarization and the onset of myofiber shortening, termed the electromechanical delay, in a ventricular canine model.

The recent study by Gurev et al. (4) aimed to determine the 3-D electromechanical delay distributions in the intact ventricles for sinus rhythm and epicardial pacing and ascertain the mechanisms that underlie the specific 3-D EMD distributions. The authors employed an electromechanical model of the rabbit ventricles that incorporated the biophysical representation of myofilament dynamics by Rice et al. (27) and assumed homogeneous excitation-contraction latency to dissect the role of the loading conditions in altering the 3-D EMD distribution. The simulation results revealed that during normal sinus rhythm, the EMD distribution was longer at the epicardium than the endocardium and at the base than the apex, consistent with experimental results. Following epicardial pacing, EMD distribution was markedly different and depended on pacing rate. For both electrical activation sequences, the late-depolarized regions were characterized with significant myofiber prestretch caused by the contraction of the early depolarized regions. This prestretch delayed the onset of myofiber shortening and thus resulted in a longer EMD, giving rise to heterogeneities in 3-D EMD distribution. This study highlighted the central role that the electrical activation sequence, and thus the loading conditions, plays in modulating the relationship between electrical activation and mechanical contraction. Understanding how this relationship is affected by electromechanical remodeling associated with cardiac disease is of paramount importance in improving pacing therapies.

Mechanisms of dyssynchrony and cardiac resynchronization therapy.

Heart failure patients often exhibit contractile dyssynchrony due to electrical intraventricular delay, which diminishes the heart systolic function. Cardiac resynchronization therapy (CRT) is a clinical treatment that recoordinates contraction by applying appropriately timed pacing stimuli to the ventricles. Although CRT reduces morbidity and mortality, 30% of patients fail to respond to the therapy. Current dyssynchrony indexes used to identify potential responders to CRT have poor predictive capability, reflecting an incomplete understanding of the electromechanical behavior in dyssychronous heart failure. Ventricular electromechanical simulations offer an opportunity to elucidate the mechanisms that underlie heart failure dyssynchrony and provide novel therapeutic strategies. Kerckhoffs et al. (14) employed a computational model of the failing canine ventricles to assess the sensitivity of current clinical indexes quantifying mechanical dyssynchrony to various abnormalities responsible for contractile dysfunction. These indexes include echocardiography-based metrics, such as width of the interval between the 10th and 90th percentiles of time to peak shortening (16), and the MR-based metrics circumferential uniformity ratio estimate (CURE) (17) and internal stretch fraction (ISF) (16), which measure regional strain magnitudes. The abnormalities examined were dilation, dyssychronous activation, decreased inotropy, and prolonged relaxation. A sensitivity analysis of these abnormalities revealed that all indexes were sensitive to dyssychronous activation; however, the synergistic effect of dyssychronous activation and dilation resulted in the greatest changes in ISF and CURE. These simulation results also demonstrated that ISF and CURE are better indexes of mechanical dyssynchrony because of their sensitivity to regional strain inhomogeneity. More importantly, these results have broad impacts in patient-specific modeling. Since dilatation and dyssynchronous activation are the dominant determinants of cardiac dysfunction, which can easily be obtained from clinical measures, patient-specific models could be constructed to predict CRT outcomes.

In fact, in a recent simulation study, Niederer et al. (22) presented such a patient-specific model of ventricular electromechanics. The model parameters were adjusted to match endocardial electrical activation maps, hemodynamical data, and cineMR images. A parameter sensitivity analysis, performed to determine the mechanisms that regulate CRT response, revealed that the degree of length dependence on tension and the minimum length of tension generation (the length at which no active tension is generated) were the significant parameters that determined CRT efficacy. At baseline (pre-CRT), attenuating length-dependent tension regulation augmented the dyssynchrony in tension development, fiber shortening, and dispersion time to the peak in tension development rate. Because synchronization of the dispersion time to the peak in tension development rate following CRT was greatest when length dependence was reduced, the change in maximal rate of change in left ventricular pressure (CRT response) was largest. Since the minimum length of tension generation is unaltered in heart failure, these results suggest that the reduced length dependence of tension is a mechanism underpinning CRT efficacy. More importantly, this simulation study demonstrates that patient-specific models are currently being developed. In the future, patient-specific simulations may be used to optimally tailor CRT to the individual.

Concluding Remarks

Recent achievements in and mechanistic insights from ventricular electromechanical modeling are highlighted in this review article and demonstrate the significant progress made in the past few years in electromechanical modeling of the ventricles. The latest advancements in computational techniques and tools have allowed for the development of anatomically detailed image-based electromechanical models of individual ventricles that integrate representations of physiologically processes across the spatial and temporal scales. The studies presented here illustrate the powerful utility of electromechanical models in providing insight into the mechanisms by which mechanoelectric coupling contributes to ventricular arrythmogenesis, the relationship between electrical activation and mechanical contraction in the normal ventricles, and the mechanisms of mechanical dyssynchrony in the failing heart. Moreover, these studies showcase the complementary role that computational modeling can play in not only basic science studies but also clinical cardiology. To make these models an integral part of electromechanics research, efforts will need to be invested in dramatically improving the parallel scalability of these biophysically detailed models, ensuring ease and speed in simulation execution. Furthermore, approaches to modularize and interface multiple model levels, as well as to preserve and curate model and data in easy-access repositories, will need to be determined.

With the future advancements of computational techniques, coupled with the development of novel experimental methodologies, it will not be long before we are able to construct biophysical, image-based electromechanical models of a patient's heart that are enriched and validated with new types of data. Currently, researchers face numerous obstacles in the development of electromechanics patient-specific heart models, among which the low resolution of the in vivo heart scans, the current impossibility of acquiring patient-specific fiber orientation, issues with segmenting out structural remodeling in the patient heart, and difficulties in model validation. The advancement of algorithms and approaches for high-speed simulations is also of critical importance for these approaches to become clinical reality. Overcoming the challenges that lie ahead, electromechanical simulations are expected to become the initial testing frameworks for new therapies and interventions and to contribute to patient-specific diagnosis and treatment for cardiac disease and dysfunction.

GRANTS

This study was supported by National Heart, Lung, and Blood Institute grants R01-HL-082729 and R01-HL-103428 (to N. A. Trayanova) and Fellowship Grant F31-HL103090 (to J. Constantino) and by National Science Foundation Grant CBET-0933029 (to N. A. Trayanova).

DISCLOSURES

N. A. Trayanova is a cofounder of Cardiosolv, LLC. CardioSolv was not involved in this research.