A quantitative description of the percentage of breast density measurement using full field digital mammography

Abstract

Rationale and Objectives

Breast density is a significant breast cancer risk factor that is measured from mammograms. However, uncertainty remains in both understanding its underlying physical properties as it relates to the breast and determining the optimal method for its measurement. A quantitative description of the information captured by the standard operator-assisted percentage of breast density (PD) measure was developed using full field digital mammography (FFDM) images that were calibrated to adjust for inter-image acquisition technique differences.

Materials and Methods

The information captured by the standard PD measure was quantified by developing a similar measure of breast density (PD_c) from calibrated mammograms automatically by applying a static threshold to each image. The specific threshold was estimated by first sampling the probability distributions for breast tissue in calibrated mammograms. A percent glandular (PG) measure of breast density was also derived from calibrated mammograms. The PD, PD_c, and PG breast density measures were compared using both linear correlation (R) and quartile odds ratio measures derived from a matched case-control study.

Results

The standard PD measure is an estimate of the number of pixel values above a fixed idealized x-ray attenuation fraction. There was significant correlation (P < 0.0001) between the PD_c-PD (R = 0.78), PD_c-PG (R = 0.87), and PD-PG (R = 0.71) measures of breast density. Risk estimates associated with the lowest to highest quartiles for the PD_c measure [odds ratios: 1.0 (ref.), 3.4, 3.6, and 5.6], and the standard PD measure [odds ratios: 1.0 (ref.), 2.9, 4.8, and 5.1] were similar and greater than that of the calibrated PG measure [odds ratios: 1.0 (ref.), 2.0, 2.4, and 2.4].

Conclusions

The information captured by the standard PD measure was quantified as it relates to calibrated mammograms and used to develop an automated method for measuring breast density. These findings represent an initial step for developing an automated measure built upon an established calibration platform. A fully developed automated measure may be useful for both research and clinical based risk applications.

1. Introduction

Breast density is a significant breast cancer risk factor that is measured from mammograms (1-4). Nevertheless, there remains uncertainty in understanding the optimal approach for its measurement. The strengths and weaknesses of various breast density measurement techniques were reviewed in detail previously (5) and are briefly discussed here to provide context for the novel calibration technique evaluated in this analysis.

In the assessment of breast density from mammograms, the breast is usually considered as a two-component model consisting of adipose and fibroglandular (abbreviated as glandular hereafter) tissue to varying degrees. A user assisted binary labeling technique is often used to estimate breast density (6-8). With this approach, image areas are labeled as radiographically dense tissue (glandular tissue) or as non-dense (adipose) tissue. Breast density is then calculated as the ratio of the radiographically dense area to the total breast area (dense + non-dense). We refer to this binary labeling technique as the standard user-assisted percentage of breast density (PD) measure (ie, the percent density measure).

The standard PD approach has repeatedly produced a measure that correlates well with breast cancer (2, 4) without considering the inter-image acquisition technique variations. This method is normally implemented by an operator at a graphical computer interface applying an interactive threshold to each raw image. Each image has its own breast density threshold because the raw image pixel value scale is not standardized and therefore inter-image pixel values are not directly comparable due to acquisition technique differences. One of the obstacles in fully automating the PD measure is estimating this image dependent threshold without user assistance. To date, the information captured by the PD measurement has not been quantified as it relates to the physical characteristics of the breast.

Another approach for estimating breast density is to calibrate for the differences in the inter-image acquisition technique (9-17). This standardization (calibration) adjusts for variations in the target/filter combination, x-ray tube voltage, radiation exposure, and compressed breast thickness. These methods produce various forms of standardized image data representations. The final measures are produced without operator interaction, although the methods can require considerable upfront data analyses and experimental imaging prior to their implementation. By hypothesis, calibration should strengthen the risk association, by reducing unwanted measurement variation and result in more accurate risk estimates. In contrast, recent work (18, 19) suggests that calibrated measures of breast density do not result in stronger associations with breast cancer than those based on the standard PD measure applied to raw mammograms.

The calibration methodology evaluated here was described in detail previously (13, 16, 20, 21) and is an extension of earlier work (10) using full field digital mammography (FFDM). The calibration process, briefly described in the Appendix, produces a normalized effective x-ray attenuation coefficient scale at the pixel level referred to as the percent glandular (PG) representation. Once establishing the supporting calibration framework, prospective mammograms are standardized automatically. The calibration results in normalized images with pixel values in this range (0,100), where increasing value represents increased x-ray attenuation.

Often calibration work relies on the same type of breast tissue equivalent phantoms. Our experience indicated that the adipose tissue equivalent phantom composition has greater x-ray attenuation than its respective adipose breast tissue counter part. The effect is most recognizable and quite severe, for example, in Rhodium/Rhodium (target/filter) breast image acquisitions that tend to have greater compressed breast thicknesses. The calibration application in these instances produces negative values in adipose image regions because the received signal is attenuated less than that anticipated by the respective calibration mapping. It is not clear if an analogous artifact exists for the glandular tissue equivalent phantom composition with image regions corresponding to increased x-ray attenuation. Image regions corresponding to near 100% adipose tissue are more recognizable by observation and also occur with greater frequency than near 100% glandular tissue. Due to the technical problems with these phantoms, it was necessary to modify our calibration methods (see the Appendix).

There are various detector technologies used in mammography (22). The calibration methodology developed on one particular mammography system may not generalize to either similarly manufactured systems (16) or to different imaging platforms without modification. Our approach is to first show that the calibration process is useful by restricting the imaging to one FFDM unit to account for unwanted measurement variation before attempting to generalize the approach. As such, we investigated the relationship between a calibrated PG breast density measurement and the information captured by the standard PD measure. This analysis resulted in another PD-type measurement, referred to as PD_c, derived from the calibrated mammograms automatically. These three measures of breast density were compared in a side-by-side case-control analysis toshow their similarities.

2. Materials and Methods

2.1 Imaging system

One General Electric (Waukesha, WI) Senographe 2000D FFDM system was used for this work. This mammography unit is used for routine breast cancer screening at this facility. This unit has a 100 μm digital spatial resolution and produces an image data matrix size of 1914 × 2294 pixels. The Senographe 2000D has a smaller detector than newer model FFDM systems, which is a limitation in accommodating large breast sizes with a single exposure (22). A more detailed description of the detector specifics can be found elsewhere (23). Craniocaudal (CC) views were used in this analysis to reduce chest muscle interference. The system produces both raw data and processed data for clinical use. Raw data was used in the analyses (not processed data for clinical viewing). The system-processed images (clinical display images) were used as raw image surrogates for display illustration purposes. The raw image data is not useful for display purposes without considerable manipulation.

2.2 Study Population and Data Collection

A quantitative description of the standard operator assisted PD measure was developed using calibrated FFDM images acquired from breast cancer cases and controls. Breast cancer cases (n=106) were selected from women undergoing mammography at the H. Lee Moffitt Cancer Center between August 2007-May 2010. For inclusion, women had to have been diagnosed with first time unilateral breast cancer. For the purpose of matching controls to cases, three groups of cases were considered based on their screening history. Group-1 was comprised of women who had screened normal within 30 months prior to their breast cancer diagnosis (n₁ = 90). Group-2 was comprised of women who had a history of normal screening that fell outside of the 30 month window, such as a woman who had a screening in 2007 (normal) but not again until 2010 at which time she was diagnosed with cancer (n₂ = 12). Group-3 was comprised of women who were just beginning screening and were diagnosed at their baseline mammogram (n₃ = 4). Cases were identified through review of retrospective records for those women with archived mammograms acquired with the study FFDM unit (n=35) or recruited, consented, and imaged for the study (n =71). These archived mammograms were used as study images. The recruited case patients are those women found to have breast cancer in screening clinics in the surrounding geographic area that were referred to the Moffitt Center for diagnostics or patients that were found to have breast cancer at the Moffitt Center that did not have mammograms archived on study FFDM unit. Recruited case participants were given a standard screening type mammogram with the study FFDM unit before their treatment commenced. In multiple-mammography unit facilities that have mixed detector sizes, x-ray technicians (as normal practice) direct women with larger breasts to units with larger detectors. Cases (as well as controls) were restricted based on breast size. Breast cancer diagnosis was histologically verified for all case patients. Sixty six case samples had non-palpable abnormalities. Height, weight, and hormone replacement therapy (HRT) usage were abstracted from patient records.

Controls (n=106) were individually matched to cases by age (±2 years), HRT usage and duration, and screening history as defined by the three screening categories above. For HRT matching, non-users were those women who never used HRT as well as those that stopped using HRT two years or more prior to the time point at which their study mammograms were acquired. For current users, controls were further matched to cases by duration of HRT usage (± 1 year). All controls were located by retrospective records review and restricted to women with archived screening mammograms acquired with the study FFDM unit over the same time period as the cases. These archived mammograms were used as study images. Height, weight, and HRT usage were abstracted from patient records.

The patient data was collected as part of a larger ongoing case-control study, designed to estimate the magnitude of association between the PG measurement of breast density and breast cancer. In this ongoing study, the PG measure estimated from the cancer-free breast of a given case will be matched with the ipsilateral control breast. To meet the objectives of this current analysis, the cancerous breast of a given case was matched with the ipsilateral breast of its control for the case-control breast density analysis to avoid over fitting and training in the ongoing PG measurement validation study. The non-cancer side / cancer side dual analysis provided two statistically similar datasets: one for explorative studies (this report) and the other for measurement validation, respectively. It is important to note that the epidemiologic considerations are not the main focus of this report but were used for internal measurement comparisons. All study procedures were approved by the institutional review board at the University of South Florida.

2.3 Calibration

The calibration approach and the methods derived from statistical estimation theory used to address the adipose phantom artifact are outlined in the Appendix. Briefly, the calibration uses previously catalogued acquisition dependent parameters derived from imaging tissue equivalent phantoms. When calibrating a given mammogram, the acquisition technique parameters are read from the image header file. These image (patient) specific acquisition technique details are used in combination with the respective catalogued calibration parameters to standardize the image at the pixel level. For this report, the PG calibration was applied at a lower resolution by averaging over 10×10 pixel regions to reduce unwanted variation. The calibration requires an accurate spatial assessment of the compressed breast thickness. Before applying the calibration, the breast area was eroded by 25% to produce the image region that was coincident with where the breast was in contact with the compression paddle (21) to eliminate the breast curvature region. This is a necessary approximation to produce the portion of the image where the compressed breast thickness is known. To determine the eroded breast area, the total breast image area was first segmented from the background automatically by setting all pixels within the breast area =1 and setting all other pixels to zero. A radial coordinate system origin was positioned at the side of the image (chest wall position) at the vertical direction (parallel to the chest wall) centroid position estimated from the segmented binary image. The breast silhouette was then eroded by 25 % of the distance measured from the radial coordinate system origin to the breast perimeter along a given radial direction The average of the calibrated pixel values within the eroded region for each image was used as the PG breast density measure of risk. Three raw image surrogates are shown in Fig. 1 (top row) with their corresponding calibrated images (second row) after applying the erosion operation.

Figure 1.

Image examples. The top row shows three display images produced by the study mammography unit used for viewing purposes. These surrogate raw images show the contrast between the glandular tissue (bright) and adipose tissue (gray) regions. The second row shows the corresponding calibrated (eroded) images in the percent glandular (PG) representation. From left to right, the average pixel values taken over the eroded breast area are 17.3, 20.2, and 30.0, respectively, in PG units. The third row shows the corresponding standard percent density (PD) labeled image examples using the Cumulus method. The PD scores from left to right are 8.6 %, 29.6%, and 42.9 %, respectively. The bottom row shows the percent density (PD_c) images derived from the calibrated images. The PD_c scores derived with the full breast area normalization from left to right are 9.5%, 26.7% and 51.4% and derived with eroded breast area normalization are 16.8%, 47.1% and 89.8%, respectively.

2.4 Percent Density

For internal comparisons, the standard PD measurements were generated with the Cumulus3 (CM) software by JJH using the batch file procedure operating on the raw (non-calibrated) FFDM images (same database described above). The images were first de-identified and randomized by KC. The CM operator was blinded to both the case-control status and original image identifiers. The case-control dataset was labeled in one session.

2.5 Calibrated Percent Density

A method was developed to generate a percentage of breast density measurement from calibrated images automatically, referred to as the PD_c measure. This method relies on applying a static (image independent) threshold to each pixel within a given image resulting in a binary labeled image, similar to that produced by the PD measurement process. To determine the threshold, the relationship between the calibrated pixel values and breast density was explored by developing inter-image sample distributions for adipose and radiographically dense tissue. To develop this measure, it was also necessary to transform both the calibrated images and samples to another data representation.

A user interactive method was developed to sample ½ cm × ½ cm regions (50 × 50 pixel regions) within each PG representation image. Five higher-intensity (bright) areas were sampled from each image ranging from high-low values (within the regions considered bright) by user discretion without spatial preference and labeled as mammographically dense tissue (DT). Five additional samples were taken from each calibrated image from areas of lower-intensity lacking tissue structure (radiolucent) in a similar manner and labeled as adipose tissue (AT). The average of the pixel values within each sample region was used in the distribution analysis. For this analysis, we used both the left and right CC views of the case-control dataset described above in addition to 26 other images acquired with the study FFDM unit not related to the case-control data (n = 450 images). The 10 × 450 sample averages were used to develop the probability distributions for each tissue type.

Both the PG representation images and the corresponding sample points were first transformed to a more favorable data representation (i.e., a representation that supports the static threshold application). We let p(x,y) = PG(x, y) /100, where PG(x,y) is the calibrated image pixel value at location (x, y). This normalization restricts p(x,y) to this range (0,1) of values. We define the normalized x-ray attenuation representation image with this transform

$$\mathrm{A}(\mathrm{x},\mathrm{y})=\mathrm{k}(1.0-\exp [-\mathrm{p}(\mathrm{x},\mathrm{y}){\mathrm{t}}_{\mathrm{s}}]),$$ Eq. (1)

where t_s is the system compressed breast thickness readout quantity expressed in cm for each image, and k =5000 is an arbitrary constant. Each calibrated image of the case-control dataset was transformed with Eq. (1) producing the A(x,y) representation (case-control) dataset. Equation (1) is a variant of Beer’s law that can be used to define an idealized attenuated x-ray beam fractional measure [i.e., A(x,y)/k]. The support for this relationship follows from the calibration methods outlined in the Appendix. This transform restricts the pixel values of A(x, y) within this range (0, k), and lends itself to a useful interpretation discussed below.

Another binary image representation, similar to PD labeled images, was generated automatically by applying a static threshold, A_c to each A(x,y) image. The DT and AT sample averages were also transformed with Eq. (1) using the respective compressed breast thicknesses. The empirical probability distributions for the transformed DT and AT samples were used to estimate the specific A_c threshold by evaluating their overlap. For a given A(x,y) image, all pixel values within the eroded breast region meeting this condition A(x,y) ≥ A_c were counted as glandular tissue regions (number of glandular pixels= d_n) and all pixel values meeting this condition A(x,y) < A_c were counted as adipose tissue regions (the number of adipose pixels = a_n). Two variations of the PD_c measure were developed differing in the normalization. For a given image, the new breast density measure was derived using the pixel counts from the eroded image area

$${\mathrm{PD}}_{\mathrm{c}}=\frac{{\mathrm{d}}_{\mathrm{n}}}{{\mathrm{d}}_{\mathrm{n}}+{\mathrm{a}}_{\mathrm{n}}}\times 100\%,$$ Eq. (2)

where PD_c indicates the PD-type measure was generated from calibrated data. The quantity d_n + a_n is the number of pixels within the eroded breast area. The other variant used the total breast area of the non-eroded image in the denominator as the normalization.

2.6 Analysis Methods

For all case-control breast density measurement comparisons, conditional logistic regression was used to assess the association between the various measures of breast density and the case-control status using the n=106 matched pair dataset. A standard quartile analysis was used for the odds ratio (OR) comparison, where the control breast density distribution for a given measure was used to determine the cutoff values. The first quartile of breast density served as the reference group for the second-fourth quartiles. The quartile analysis provided a means for comparing the inter-measure OR distributions. We adjusted for body mass index (BMI) in the analyses as a continuous variable (kg/m²). The area under the receiver operating characteristic curve (Az) was also used for predictive capability comparisons. Regression analysis was used to compare the correlation between the three breast density measures without consideration of the case-control status. For the regression analysis, m, b, and R were used to define the slope, intercept, and linear correlation coefficient, respectively.

3. Results

3.1 Breast tissue distributions

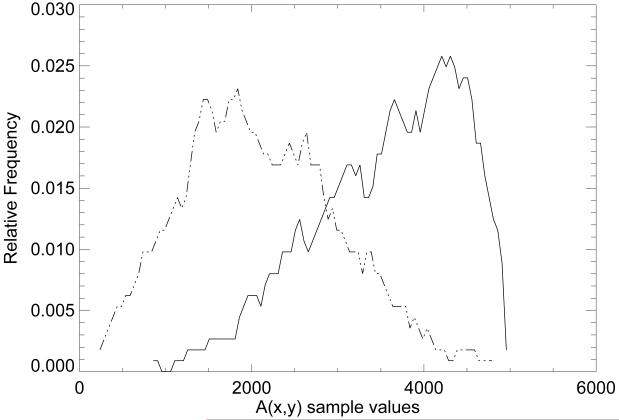
The empirical probability distributions for each tissue type were generated by processing the sample averages with Eq. (1). The distributions corresponding to the transformed AT sample averages (dashed) and transformed DT samples averages (solid) are shown in Fig. 2. As an estimate, the two distributions intersect in the vicinity of A ≈ 3200. The PG dataset was processed using A_c = 3200 as the static threshold to generate the PD_c case-control breast density scores.

Figure 2.

Tissue distribution approximations. This figure shows the adipose (AT) and radiographically dense tissue (DT) pixel value distributions in the A(x,y) representation after transforming each sample average with Eq. (1). The transformed AT distribution (left) is represented by a dashed line and the transformed DT distribution (right) by a solid line.

3.2 Breast density measurement comparisons

The three measures of breast density were compared. The patient characteristics are summarized in Table 1. The PG measure (see Fig. 1 second row) case-control quartile analysis in the non-adjusted and adjusted formats and the associated Az quantities are summarized in Table 2. Although the ORs show positive association for the PG measure with breast cancer, the confidence intervals span unity for all divisions, whereas the Az shows the measure is predictive (i.e., Az > 0.5). Figure 1 shows the corresponding (standard) PD labeled image examples (third row). The associated PD findings are also presented in Table 2. In contrast with the PG findings, these OR findings show increased magnitude of association with breast cancer and increased Az. The corresponding PD_c labeled image examples are shown in the bottom row of Fig. 1, and the corresponding measurement findings are presented in Table 3, which are similar to the standard PD measure (Table 2). In this table, PD_c was generated with both the total breast area normalization (upper portion of Table 3) and eroded breast area normalization (lower portion of Table 3) and analyzed separately as two models (similar findings).

Table 1.

Patient Characteristics. This gives the number of observations (n) in the case and control groups, hormone replacement therapy (HRT) distribution by years of usage, and the mean body mass index (BMI), mean age, and associated standard deviation (SD)

Characteristic	Case, n	Case mean (SD) or %	Control, n	Control mean (SD) or %
Age	106	58.91 (9.95)	106	58.71 (9.86)
HRT
Never	56	52.83%	61	57.55%
1-5 yrs	18	16.98%	15	14.15%
6-10 yrs	13	12.26%	14	13.21%
11-15 yrs	8	7.55%	7	6.60%
> 15 yrs	11	10.38%	9	8.49%
BMI (kg/m2)	106	26.86 (4.49)	106	25.51 (4.36)

Table 2.

Percent glandular and Percentage of breast density associations. The percent glandular (PG) and percent density (PD) findings are presented in both unadjusted and adjusted for body mass index (BMI) quantities. The odds ratios (ORs) are shown by quartile with 95% confidence intervals (CIs). The number of case/control samples for each quartile is given in the third column. The area under the receiver operating characteristic curve (Az) and its standard error (SE) are also provided

Measure: PG Quartile	OR (95% CI)	cases/controls	Az (SE)
unadjusted			0.56 (0.02)
1	1.00 (Ref.)	17/27
2	1.89 (0.81 - 4.43)	30/26
3	2.01 (0.87 - 4.63)	33/27
4	1.73 (0.69 - 4.34)	26/26
BMI adjusted			0.62 (0.02)
1	1.00 (Ref.)	17/27
2	1.96 (0.82 - 4.72)	30/26
3	2.37 (0.99 - 5.62)	33/27
4	2.43 (0.92 - 6.49)	26/26
Measure: PD
unadjusted			0.61(0.02)
1	1.00 (Ref.)	10/26
2	2.39 (0.96 - 5.97)	26/27
3	3.78 (1.51 - 9.43)	39/27
4	3.12 (1.23 - 7.95)	31/26
BMI adjusted			0.68 (0.04)
1	1.00 (Ref.)	10/26
2	2.88 (1.09 - 7.57)	26/27
3	4.81 (1.82 - 12.67)	39/27
4	5.09 (1.73 - 15.02)	31/26

Table 3.

Calibrated percent density associations. The calibrated percent density (PDc) measure was derived by applying a static threshold to the transformed percent glandular (PG) representation images. The findings are presented with the total breast area normalization (top) and eroded area normalization (bottom). All findings are presented in unadjusted and adjusted for body mass index (BMI) quantities. The odds ratios (ORs) are presented by quartile with 95% confidence intervals (CIs). The number of case/control samples for each quartile is provided in the third column. The area under the receiver operating characteristic curve (Az) and its standard error (SE) are also provided.

Measure: PDc total area Quartile	OR (95% CI)	cases/controls	Az (SE)
unadjusted			0.59 (0.02)
1	1.00 (Ref.)	11/26
2	2.94 (1.17 - 7.36)	32/27
3	3.01 (1.13 - 8.02)	29/26
4	3.83 (1.39 - 10.50)	34/27
BMI adjusted			0.65 (0.03)
1	1.00 (Ref.)	11/26
2	3.44 (1.32 - 8.99)	32/27
3	3.60 (1.29 - 10.06)	29/26
4	5.62 (1.89 - 16.76)	34/27
Measure: PDc eroded area
unadjusted			0.59 (0.02)
1	1.00 (Ref.)	11/26
2	3.11 (1.24 - 7.81)	32/27
3	3.14 (1.17 - 8.39)	28/26
4	3.74 (1.40 - 9.99)	35/27
BMI adjusted			0.65 (0.03)
1	1.00 (Ref.)	11/26
2	3.67 (1.39 - 9.63)	32/27
3	3.76 (1.34 - 10.56)	28/26
4	5.46 (1.88 - 15.80)	35/27

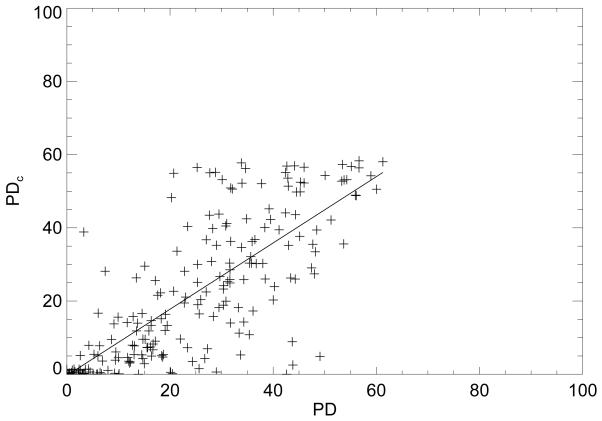
Regression analysis comparisons were also used to show the similarities between the various measures. The (PD, PD_c) regression plot is displayed in Fig. 3. For this plot, R = 0.78 (linear correlation) with m = 0.90 ± 0.05 (slope), and b = −0.33 (intercept). The (PD, PG) regression analysis gave R = 0.71, m = 0.59 ± 0.04, and b = 5.50 (not shown). The (PD_c, PG) analysis gave R=0.87, m = 0.62 ± 0.02, and b = 6.44 (not shown). For all R assessments, P < 0.0001 indicating all the measures are related. The breast density measurement distribution characteristics are summarized in Table 4 by case-control group.

Figure 3.

Percent density regression analysis. This figure shows the regression plot (crosses) of the standard percent density (PD) breast density measure and the percent density (PD_c) measure derived from calibrated images. The regression line is solid with slope = 0.90 ± 0.05 and intercept = −0.33 with R = 0.78 (linear correlation coefficient).

Table 4.

Breast density measurement distribution summary. The three breast density (BD) distribution summaries are shown: percent glandular (PG), percent density (PD) and PD generated from the calibrated data (PD_c). The mean and standard deviation (SD) for each breast density measure are provided by case and control group

	Cases	Controls
BD measure	mean (SD)	mean (SD)
PG	20.5 (18.4)	19.3 (14.1)
PD	26.5 (15.6)	22.1 (17.4)
PDc Total area	27.2 (19.1)	22.3 (19.9)
PDc Eroded area	48.2 (33.9)	39.7 (35.4)

We note that applying a static threshold to the PG images to generate a PD-like measure with without the Eq. (1) transformation was not possible. The reason for this can be explained by rearranging Eq. (1) with the threshold inequality A(x,y) ≥A_c, which gives

$$\mathrm{PG}(\mathrm{x},\mathrm{y})\ge -\frac{1}{{\mathrm{t}}_{\mathrm{s}}}\ln (1-\frac{{\mathrm{A}}_{\mathrm{c}}}{\mathrm{k}})\times 100.$$ Eq. (3)

The threshold for the PG representation images is now dependent upon t_s (i.e. image dependent) because the other terms on the right side of Eq. (3) are constants.

4. Discussion

This work produced three new findings. First, the PD_c findings show that the calibrated image data representation can be used to describe the information captured by the PD measure as it relates to a given patient’s normalized effective x-ray attenuation coefficient distribution. The PD and PG breast density measures are capturing two different properties of the same data field. The PD_c measure shows that the standard PD measurement is an approximation of the total number of pixel counts equal to or above a normalized attenuation threshold derived from an idealized model. In the scale used for this work, the critical fraction was approximated as 16/25. In contrast, the average PG breast density measure captures the central tendency of a given patient’s normalized x-ray attenuation coefficient distribution, which is not exactly a measure of degree as captured by the other measures. We would expect a positive correlation between the PG and PD measures as demonstrated, but these two measures are not equivalent or approximations for each other. Secondly, the findings show that the eroded breast area has a marginal impact on the findings (Table 3). Thirdly, the work suggests that once a calibration system is established, the PD_c breast density measurements can be automated. A comparison of the PD_c labeled images with the corresponding PD labeled images along with the odds ratio comparisons indicates the two measures are capturing similar information, which is also supported by the strong linear correlation between these measures. Both the odds ratios and the Az findings for the PD and PD_c measures found here are similar to those reported previously for the PD measure (24). The PD and PD_c measures showed stronger associations with breast cancer than the PG measure. These association comparisons agree with the findings from other calibration research (18, 19) in that the calibrated measure does not explicitly produce stronger breast cancer associations than the standard PD measure. In summary, these findings indicate that the calibration process can be used to describe the information content captured by the binary labeling and provide an explanation for the weaker association of the PG measure.

Although our findings show internal validity in the measurement comparisons, there are study limitations that will require further analysis and experimental replication. The threshold, A_c, for the PD_c generation was found by observation of the empirical distributions and not with training (not estimating the optimal A_c value with a threshold Az feedback loop for example). The degree of breast erosion was also an estimate from previous work and not found by applying optimization techniques with an objective endpoint criterion such as case-control status. The sample size is another limitation. Changing the PD_c threshold will likely alter the findings due to the limited number of patient observations used in this work. The adjustable parameters in the modified calibration approach (see Appendix B) were set as static values, rather than using optimization techniques to determine their operating points. At this time, the database size does not support applying optimization techniques to determine A_c or to make better estimates of the parameters outlined in the Appendix. We note, there is not exact correlation of PD_c with PD. The second and third case quartile distributions for PD_c and PD show some inter-measure variation whereas the first and fourth distributions are similar. There is also uncertainty in labeling the images with the CM software. On some images, multiple user selected thresholds appear to be correct simultaneously, which may be related to (a) the tissue distribution overlap, (b) pixel dynamic range issues related to the breast curvature region, and (c) operator preference. The propagation of these uncertainties is likely to induce variation between the PD and PD_c measures. One mammography unit was used for this work, which provided an important benefit while limiting the generalization of the findings. The study FFDM system has a linear pixel value response relationship with x-ray exposure that provided a significant advantage in simplifying the calibration analysis in comparison with film systems or FFDM units without this property. The work will require further evaluation with different datasets.

This work does not address the efficacy of making calibrated breast density measurements in the future. The user assisted PD approach has produced a wealth of information, which shows the human observer can essentially label the important tissue consistently with the drawback of expending considerable effort when addressing large databases. The evidence from this study suggests that PD_c can be generated automatically with a fixed threshold once a calibration system is established. Additionally, the work shows that PG measure, as well as its related variants (9, 11, 25) as described in the Appendix, and the PD measure are complementary. Future work involves determining the optimal threshold value, determining the optimal parameters for the statistical estimation techniques (26-28) used in the modified calibration approach, and investigating other distribution quantities derived from the PG representation images as possible risk factors. We hypothesize that developing a calibration system may be the price for automated breast density measurements. Similarly, a rigorously evaluated automated measure of breast density may be useful for both research and clinical based risk applications.

Appendix

A. Calibration Approach

The calibration framework developed previously (16, 21) is described to support the findings and to facilitate the description of its modifications. The development below applies to a given x-ray beam type (i.e, for a given kVp, and target-filter combination). The logarithmic response (LR) is defined as LR(x,y) = ln[r(x,y)/mAs], where, r(x,y) is the raw image data representation, (x, y) are integer valued pixel coordinates, and mAs is the system readout value. Calibration parameters were derived with linear regression analysis by measuring the LR for both adipose and glandular tissue equivalent phantoms as a function of phantom height. Two calibration points are required to standardize a given mammogram. These points correspond to the LR for each tissue equivalent phantom type for the same acquisition technique and compressed breast thickness as the respective mammogram. The two required points are generated with the calibration parameters

$${\mathrm{LR}}_{\mathrm{j}}(\mathrm{x},\mathrm{y},\mathrm{t}=\mathrm{T})=-{\mu }_{\mathrm{j}}(\mathrm{x},\mathrm{y})\mathrm{T}(\mathrm{x},\mathrm{y})+1_{\mathrm{j}}(\mathrm{x},\mathrm{y}),$$ (A1)

where μ_j (cm⁻¹) and l_j are the effective x-ray attenuation coefficient and logarithmic intercept for either the glandular (j = g) or adipose (j = f) breast tissue equivalent phantoms, respectively. In the above expression, T(x, y) is the spatially dependent compressed breast thickness assumed constant for the next development. All calibration data was acquired with the reference mAs = 160. The percent glandular (PG) calibration is given by

$$\mathrm{PG}=\mathrm{M}\times \mathrm{z}+\mathrm{B}$$ (A2)

with

$$\mathrm{M}=100\times {[({\mu }_{\mathrm{f}}-{\mu }_{\mathrm{g}})\mathrm{T}+({\mathrm{l}}_{\mathrm{g}}-{\mathrm{l}}_{\mathrm{f}})]}^{-1}$$ (A3)

and

$$\mathrm{B}=\mathrm{M}\times ({\mu }_{\mathrm{f}}\mathrm{T}-{\mathrm{l}}_{\mathrm{f}}),$$ (A4)

where z is a measured arbitrary LR at (x, y).

To show the relationship with other calibration representations, we let p(x,y) = PG(x,y)/100, where PG(x,y) is the calibrated image. The glandular height representation is given by

$${\mathrm{h}}_{\mathrm{g}}(\mathrm{x},\mathrm{y})=\mathrm{p}(\mathrm{x},\mathrm{y})\mathrm{T},$$ (A5)

which is analogous to the representation developed by these researchers (9). For a projection of a given volume that has mpixels, the average glandular-volume/pixel is given by

$$<{\mathrm{V}}_{\mathrm{d}}>=\frac{1}{\mathrm{m}}\sum _{\mathrm{x},\mathrm{y}}{\mathrm{h}}_{\mathrm{g}}(\mathrm{x},\mathrm{y}){\mathrm{d}}^2,$$ (A6)

where d is the detector element spacing (resolution) expressed in units of length. Multiplying the above equation by m gives the glandular volume. We define V_N as the glandular volume normalized by the given volume (V= mTd²) under consideration. Substituting Eq. (A5) into Eq. (A6), multiplying by m, and dividing by V gives

$${\mathrm{V}}_{\mathrm{N}}=\frac{1}{{\mathrm{mTd}}^2}\sum _{\mathrm{x},\mathrm{y}}\mathrm{p}(\mathrm{x},\mathrm{y}){\mathrm{Td}}^2=<\mathrm{p}(\mathrm{x},\mathrm{y})>.$$ (A7)

This expression is equivalent to the spatial average <PG>/100 and is analogous to normalized measures developed independently by other researchers (11, 25).

B. Calibration Modification

The calibration application was modified to overcome the adipose phantom attenuation artifact. We let p_i represent the proportion of glandular tissue and c_i represent the corresponding calibrated value for a given pixel or region if the calibration application was without error. For example when p = (1.0, 0.5, 0.0), c = (100.0, 50.0, 0.0), respectively. In this formulism, the components of p have the same interpretation as p(x,y), and the components of c are PG quantities. We let w_i assume the respective theoretical LR value (derived below) that would give c_i after applying the calibration. The corresponding components of p, c, and w are taken as known quantities. We adjust Eq. (A1) to account for the estimated uncertainty in the effective x-ray attenuation coefficient by incorporating a positive valued increment. The modified expression is given by

$$\mathrm{LR}{\left(\Delta \right)}_{\mathrm{f}}=(-{\mu }_{\mathrm{f}}+\Delta )\mathrm{T}(\mathrm{x},\mathrm{y})+{\mathrm{l}}_{\mathrm{f}}(\mathrm{x},\mathrm{y}),$$ (A8)

where Δ = 0.05 cm⁻¹ is the estimated error between the effective x-ray attenuation coefficient of the adipose phantom material and the respective coefficient for that of adipose breast tissue, which was estimated from adipose regions in mammograms. This expression [Eq.(A8)] replaces Eq. (A1) for the adipose calibration point. We generate known valuesof w_i using this relationship

$${\mathrm{w}}_{\mathrm{i}}={\mathrm{p}}_{\mathrm{i}}\times {\mathrm{LR}}_{\mathrm{g}}+(1-{\mathrm{p}}_{\mathrm{i}})\times \mathrm{LR}{\left(\Delta \right)}_{\mathrm{f}}.$$ (A9)

For this application, p, c, and w were generated with n components to calibrate an arbitrary LR = z with compressed breast thickness = T. The original calibration application [Eqs.(A2-A4)] was replaced with an approach based on non-parametric probability density estimation (26, 27) and generalized regression (28) techniques. Results are stated without the mathematical development. We define a symmetric distance metric

$$\mathrm{D}(\mathrm{z},{\mathrm{x}}_{\mathrm{i}})={\left(\frac{\mathrm{z}-{\mathrm{w}}_{\mathrm{i}}}{\sigma }\right)}^2$$ (A10)

and related kernel

$$\mathrm{k}(\mathrm{z},{\mathrm{w}}_{\mathrm{i}})=\exp [-\mathrm{D}(\mathrm{z},{\mathrm{w}}_{\mathrm{i}})],$$ (A11)

where normalization factors are suppressed, and σ is an adjustable weight. The probabilistic calibration then takes the form of a conditional expectation for PG

$$\mathrm{E}[\mathrm{PG}\mid \mathrm{z}]=\frac{\underset{\mathrm{i}=1}{\overset{\mathrm{n}}{\Sigma }}{\mathrm{c}}_{\mathrm{i}}\times \mathrm{k}(\mathrm{z},{\mathrm{w}}_{\mathrm{i}})}{\underset{\mathrm{i}=1}{\overset{\mathrm{n}}{\Sigma }}\mathrm{k}(\mathrm{z},{\mathrm{w}}_{\mathrm{i}})},$$ (A12)

where E is the expectation operator and n = 10. This expression constrains the calibration between the desired range and incorporates the parameter uncertainty. The estimated weight is given by

$$\sigma =\frac{{\mathrm{LR}}_{\mathrm{f}}\left(\Delta \right)-{\mathrm{LR}}_{\mathrm{g}}}{10}.$$ (A13)

The σ and Δ parameters were held constant for all acquisition techniques, which is not optimal. These parameters are most likely functions of the acquisition technique. There may be 13-15 different values for each parameter (upper limit).