Thermodynamics of Boroxine Formation from the Aliphatic Boronic Acid Monomers R–B(OH)₂ (R = H, H₃C, H₂N, HO, and F): A Computational Investigation

Abstract

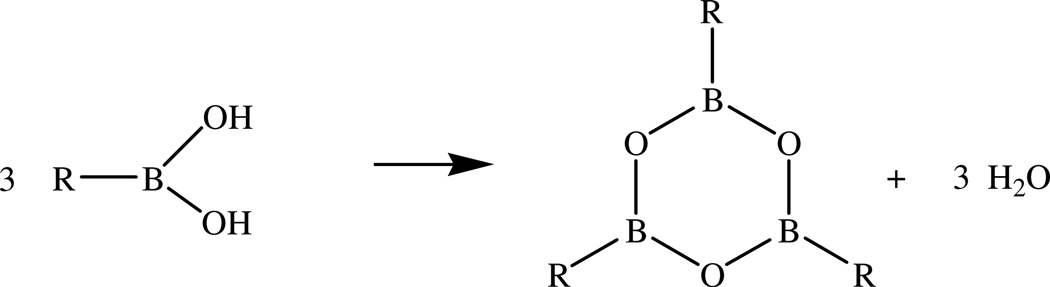
Boroxines are the 6-membered cyclotrimeric dehydration products of organoboronic acids: 3 R– B(OH)₂ → R₃B₃O₃ + 3 H₂O, and in recent years have emerged as a useful class of organoboron molecules with applications in organic synthesis both as reagents and catalysts, as structural components in boronic acid derived pharmaceutical agents, as anion acceptors and electrolyte additives for battery materials [AL Korich and PM Iovine, Dalton Trans. 39 (2010) 1423–1431]. Second-order Møller-Plesset perturbation theory, in conjunction with the Dunning-Woon correlation-consistent cc-pVDZ, aug-cc-pVDZ, cc-pVTZ, and aug-cc-pVTZ basis sets, was used to investigate the structures and relative energies of the endo-exo, anti, and syn conformers of the aliphatic boronic acids R–B(OH)₂ (R = H, H₃C, H₂N, HO, and F), as well as the thermodynamics of their boroxine formation; single-point calculations at the MP2/aug-cc-pVQZ, MP2/aug-cc-pV5Z, and CCSD(T)/aug-cc-pVTZ level using the MP2/aug-cc-pVTZ optimized geometries were also performed in selected cases. The endo-exo conformer was generally lowest in energy in vacuo, as well as in PCM and CPCM models of aqueous and carbon tetrachloride media. The values of $\mathrm{\Delta }{\mathrm{H}}_{298}^0$ for boroxine formation via dehydration from the endo-exo conformers of these aliphatic boronic acids ranged from −2.9 for (H₂N)₃B₃O₃ to +12.2 kcal/mol for H₃B₃O₃ at the MP2/aug-cc-pVTZ level in vacuo; for H₃B₃O₃ the corresponding values in PCM:UFF implicit carbon tetrachloride and aqueous media were +11.2 and +9.8 kcal/mol, respectively. Based on our calculations, we recommend that ΔH_f(298 K) for boroxine listed in the JANAF compilation needs to be revised from −290.0 kcal/mol to approximately −277.0 kcal/mol.

Introduction

Boroxines (1,3,5,2,4,6–trioxatriborinanes, R₃B₃O₃) are six-membered cyclotrimeric anhydrides of organoboronic acids R–B(OH)₂ ^1,2, as well as the most stable forms of R–BO polymers ³. Formation of boroxines is generally accomplished by the simple dehydration of boronic acids, i.e. 3 R–B(OH)₂ → R₃B₃O₃ + 3 H₂O, see Figure 1, either through thermal azeotropic removal of water or by exhaustive drying over sulfuric acid or phosphorus pentoxide. In some cases the formation of this 6-membered heterocyclic ring is known to occur by simply warming the corresponding boronic acid in an anhydrous solvent such as carbon tetrachloride or chloroform ⁴.

Figure 1.

Boroxine formation reaction 3 R–B(OH)₂ → R₃B₃O₃ + 3 H₂O.

Some boronic acid derivatives, e.g. Bortezomib (Velcade™, PS-341, [(1R)–3–methyl–1–[[(2S)– 1–oxo–3–phenyl–2–[(pyrazinyl carbonyl) amino] propyl] amino] butyl]boronic acid), a dipeptidylboronic acid which is an FDA approved ⁵ drug for the treatment of refractory multiple myeloma, when present in equilibrium with their mannitol esters, are known to exist in their cyclic anhydride forms as trimeric boroxines ⁶; additional peptidyl boronic acid-based approaches for imaging and therapy are currently in use clinically ⁷ or under development ⁸ and these may also form boroxine structures. Some water soluble substituted boroxines are active ingredients in pharmaceutical, cosmetic and dermatological formulations which are effective for the treatment and/or inhibition of both benign and malignant skin disorders ⁹. Boroxines have also found applications in a wide variety of other fields including ¹: flame retardant materials ¹⁰, battery technology ¹¹, assembly of end-functionalized telechelic polymers ^12,13, nonlinear optical materials ^14–16, molecularly imprinted polymers for biosensor applications ¹⁷, alternatives to boronic acids for carrying out Miyaura-Suzuki¹⁸ and Rhodium-catalyzed coupling reactions ¹⁹, curing agents with encapsulants for solid state devices that function as optoelectronic devices ²⁰, sources to transfer phenyl groups effectively to a variety of aldehydes ²¹, crystalline covalent organic framework (COF-1) materials ²², etc. ²³.

Despite the widespread applications of both aryl ^20,22 and aliphatic ^{10,11,17–20} boroxines, few experimental or computational studies on the thermodynamics and kinetics of their formation from monomeric boronic acids have been reported ^24–29. Recently, Kua and coworkers ^24–27 carried out a series of calculations (primarily at the B3LYP/6-311+G(d) level) to help clarify the thermodynamics and kinetics for the formation of boroxines from aryl boronic acids. Thanks to these computational results and the experimental findings of the Tokunaga group ^28,29, it is now clear that the formation of boroxines from a variety of aryl boronic acids is endothermic in vacuo and in aqueous media. However, despite their utility much less is known about the thermochemistry of aliphatic boroxines.

Our goal in this study was two-fold: 1) to establish relative energies of various conformers of the aliphatic boronic acids, R–B(OH)₂, R = H, H₃C, H₂N, HO, and F and 2) to determine reliable thermochemical parameters for their dehydration leading to the formation of the corresponding trimeric boroxines; calculations have been performed in vacuo and using implicit solvation models to approximate experimental conditions.

Computational Methods

Equilibrium geometries of the molecules involved in this article were obtained using second-order Møller-Plesset perturbation theory (MP2) ³⁰; the frozen core (FC) option, which neglects core-electron correlation, was employed in all cases. Dunning-Woon cc-pVDZ, aug-cc-pVDZ, cc-pVTZ, and aug-cc-pVTZ basis sets ^31–34 were used in the calculations. Frequency analyses were performed analytically to confirm that the optimized structures were local minima. Single-point calculations for boroxine were performed at the MP2/aug-cc-pVQZ, MP2/aug-cc-pV5Z, and CCSD(T)/aug-cc-pVTZ levels using the MP2/aug-cc-pVTZ optimized geometry ^35–39. Density functional theory (DFT) calculations were also performed using the B3LYP ^40,41 and PBE1PBE ^42,43 functionals with Pople-style split-valence basis sets ^44,45. All calculations were performed using the GAUSSIAN 03 ⁴⁶ and GAUSSIAN 09 ⁴⁷ suites of programs. Atomic charges were obtained from natural population analyses (NPA) and the bonding was analyzed with the aid of natural bond orbitals (NBOs) ^48–51.

Results from continuum solvation models were employed to assess the effects of a bulk aqueous or organic environment on the gas-phase results ⁵²; such continuum models, however, only provide a description of the effects of long-range interactions and, as a consequence, have limitations in describing protic solvents ^53,54. The IEF Polarizable Continuum Model (PCM), developed by Tomasi and coworkers ^55–59, and the conductor-like PCM model (CPCM), introduced by Barone and Cossi ^60,61 were used at the MP2/cc-pVDZ(cc-pVTZ) computational levels for the implicit solvation calculations. (The UFF radii were used for the PCM calculations, which incorporate explicit hydrogen atoms; the UAKS cavity was used for the CPCM solvent model based on the performance criteria suggested by Takano and Houk ⁶²).

Results and Discussion

A. Relative Energies of the Monomers: R–B(OH)₂ (R = H, H₃C, H₂N, HO, and F)

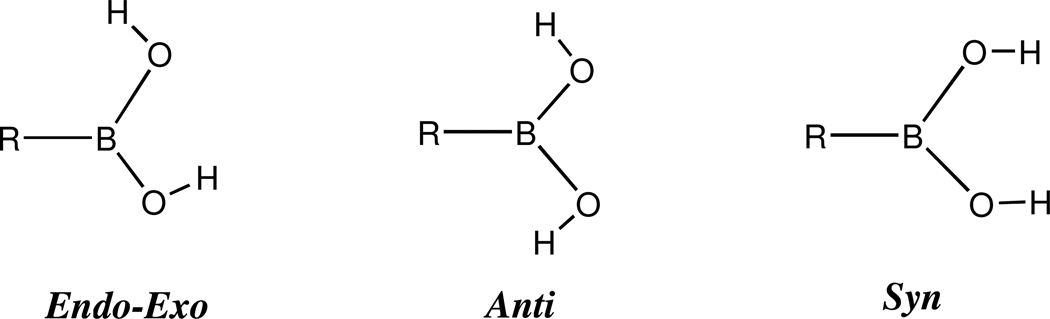
Three orientations of the hydroxyl groups in the monomeric boronic acids were studied: endo-exo, anti, and syn, see Figure 2; no symmetry was enforced during the optimizations. All three of these forms have been observed experimentally in crystal structures as a result of various inter- and intra-molecular interactions ^63–72. Unfortunately, it is difficult to obtain pure samples of aliphatic boronic acids that actually have the formula R–B(OH)₂ ⁷³; these acids frequently separate from aqueous solutions as hydrates, and the latter, on standing in a desicator over the usual drying agents, undergo dehydration to yield boron oxides RBO, although molecular weight determinations often reveal that these oxides are actually trimers R₃B₃O₃ ⁷³. This complication has led to a paucity of experimental data for aliphatic boronic acids ^{64,66–68,74–77}. Detailed computational investigations comparing the relative energies of isolated boronic acid conformers remain relatively rare, but the available studies have consistently found that all three forms of the monomers shown in Figure 2 are local minima on the potential energy surfaces and that the endo-exo form is lowest in energy ^{67,68,78–81}.

Figure 2.

Endo-Exo, Anti, and Syn Conformers of R-B(OH)₂ Monomers.

To be prudent, however, the conformers of the aliphatic boronic acids R–B(OH)₂ (R = H, H₃C, H₂N, HO and F), were all geometry optimized in the endo-exo, anti, and syn forms with no symmetry constraints. Relative energies in the gas-phase are shown in Table 1, where it can be seen that the endo-exo conformers are consistently lower in energy than the anti or syn forms at every computational level we employed. It is important to point out, however, that the anti form of F–B(OH)₂ is less than 1 kcal/mol higher in energy than the endo-exo form, consistent with the results reported by Boggs and Cordell ⁷⁸ and Duan et al. ⁷⁹ This is only to be expected as a result of two relatively strong intramolecular F^…H bonds in the anti form; the F–H distance is 1.938Å in this conformer at the MP2/aug-cc-pVTZ level, whereas in the endo-exo conformer the one F-H distance is nearly 0.5Å longer. In most cases the anti form is lower in energy than the syn form, the only exception being H₂N–B(OH₂), see Table 1C; this appears to be the result of steric overcrowding involving two relatively close B–O–H^…H–N contacts in the anti conformer. Of course the anti and syn forms of HO–B(OH)₂ are equivalent. We note in passing that ΔH^† for the conversion of the endo-exo conformers to the corresponding anti conformers for the boronic acids R–B(OH)₂ (R = H, H₃C, H₂N, HO, and F) are 9.3, 9.4, 7.0, 7.7 and 7.5 kcal/mol respectively at the MP2/aug-cc-pVTZ level.

Table 1.

Relative Energies, E (kcal/mol), (Thermally Corrected Values to 298K° in Parentheses), of the endo-exo, anti, and syn Conformers of R–B(OH)₂ in vacuo: A. R=H, B. R=H₃C, C. R=H₂N, D. R=HO, and E. R=F at the MP2(FC)/cc-pVDZ//MP2(FC)/cc-pVDZ, MP2(FC)/aug-cc-pVDZ//MP2(FC)/aug-cc-pVDZ, MP2(FC)/cc-pVTZ//MP2(FC)/cc-pVTZ, MP2(FC)/aug-cc-pVTZ//MP2(FC)/aug-cc-pVTZ, and CCSD(T)/aug-cc-pVTZ//MP2(FC)/aug-cc-pVTZ levels.

	MP2(FC)// MP2(FC)				CCSD(T)// MP2(FC)
Conformer	cc-pVDZ	aug-cc-pVDZ	cc-pVTZ	aug-cc-pVTZ	aug-cc-pVTZ
A. R=H
endo-exo	0.0 (0.0)	0.0 (0.0)	0.0 (0.0)	0.0 (0.0)	0.0
anti	+1.7 (+1.6)	+1.2 (+1.1)	+1.2 (+1.2)	+1.0 (+1.0)	+1.1
syn	+3.5 (+3.3)	+3.0 (+2.9)	+3.1 (+3.0)	+3.1 (+2.9)	+3.0
B. R=H3C
endo-exo	0.0 (0.0)	0.0 (0.0)	0.0 (0.0)	0.0 (0.0)	0.0
anti	+2.7 (+2.6)	+2.1 (+2.1)	+2.1 (+2.1)	+2.0 (+2.0)	+2.0
syn	+2.9 (+2.8)	+2.6 (+2.4)	+2.7 (+2.6)	+2.6 (+2.5)	+2.7
C. R=H2N
endo-exo	0.0 (0.0)	0.0 (0.0)	0.0 (0.0)	0.0 (0.0)	0.0
anti	+3.5 (+3.4)	+3.1 (+3.0)	+3.0 (+3.0)	+3.0 (+2.9)	+3.0
syn	+1.8 (+1.7)	+1.4 (+1.3)	+1.6 (+1.5)	+1.5 (+1.4)	+1.5
D. R=HO
endo-exo	0.0 (0.0)	0.0 (0.0)	0.0 (0.0)	0.0 (0.0)	0.0
anti	+5.1 (+4.9)	+4.2 (+4.1)	+4.4 (+4.2)	+4.2 (+4.0)	+4.2
syn	+5.1 (+4.9)	+4.2 (+4.1)	+4.4 (+4.2)	+4.2 (+4.0)	+4.2
E. R=F
endo-exo	0.0 (0.0)	0.0 (0.0)	0.0 (0.0)	0.0 (0.0)	0.0
anti	+0.7 (+0.7)	+0.5 (+0.5)	+0.8 (+0.7)	+0.7 (+0.6)	+0.7
syn	+4.2 (+4.1)	+3.5 (+3.4)	+3.4 (+3.3)	+3.3 (+3.2)	+3.3

It should be mentioned that the optimized structure of H₂N–B(OH)₂ is planar and NBO analyses using the MP2/aug-cc-pVD(T)Z densities suggests that the N–B bond is best described as a double bond composed of σ bond and a π dative bond, similar to the bonding found in H₂N–BH₂⁸². Some insights into the effects of this bonding feature in H₂N–B(OH)₂ can be obtained by examining the transition state(TS) for rotation about B–N bond. This rotation minimizes the overlap between the empty p-orbital on the boron atom and the lone-pair orbital on the nitrogen atom. The environment around the nitrogen atom is pyramidal in this TS and the B–N bond is ~0.05 Å longer than in the endo-exo form; the value of ΔH^† for the rotation is substantial, 21.3 kcal/mol.

The main effect of the PCM and CPCM implicit solvation models ^55–61 for either an aqueous medium or CCl₄ is to reduce the energy differences between the endo-exo, anti, and syn conformers, compare Tables 1, 1S and 2S. Nevertheless, the endo-exo form generally remains lowest in energy.

B. Dehydration: 3 R–B(OH)₂ → R₃B₃O₃ + 3 H₂O (R = H, H₃C, H₂N, HO, and F)

In Table 2 we list our calculated values of ΔE, $\mathrm{\Delta }{\mathrm{H}}_{298}^0$, and $\mathrm{\Delta }{\mathrm{G}}_{298}^0$ for the dehydration reactions:

$$3\mathrm{R}-\mathrm{B}{(\text{OH})}_2\to {\mathrm{R}}_3{\mathrm{B}}_3{\mathrm{O}}_3+3{\mathrm{H}}_2\mathrm{O}(\mathrm{R}=\mathrm{H},{\mathrm{H}}_3\mathrm{C},{\mathrm{H}}_2\mathrm{N},\text{HO},\text{and}\mathrm{F})$$

in vacuo, consistently using the endo-exo conformer for the monomers.

Table 2.

Thermodynamic Parameters (kcal/mol) in vacuo for the Reactions: 3 R–B(OH)₂ (endo-exo) → R₃B₃O₃ + 3 H₂O with A. R=H; B. R=H₃C; C. R=H₂N; D. R=HO; and E. R=F at the PBE1PBE/6-311++G(d, p){cc-pVDZ}//PBE1PBE/6-311++G(d,p){cc-pVDZ}, B3LYP/6-311++G(d,p){cc-pVDZ}//B3LYP/6-311++G(d,p){cc-pVDZ}, MP2(FC)/aug-cc-pVDZ//MP2(FC)/aug-cc-pVDZ, MP2(FC)/cc-pVTZ//MP2(FC)/cc-pVTZ, and MP2(FC)/aug-cc-pVTZ//MP2(FC)/aug-cc-pVTZ levels.

	DFT		MP2(FC)
	PBE1PBE	B3LYP
	6-311++G(d, p) {cc-pVDZ}		cc-pVDZ	aug- cc-pVDZ	cc-pVTZ	aug- cc-pVTZ
A. 3 H–B(OH)2 (endo-exo)→ Boroxine + 3 H2O
ΔE (kcal/mol)	+21.0 {+25.1}	+21.0 {+33.6}	+28.5	+15.2	+20.8	+15.2
$\mathrm{\Delta }{\mathrm{H}}_{298}^0$ (kcal/mol)	+17.8 {+21.6}	+17.7 {+30.0}	+25.1	+12.0	+17.6	+12.2
$\mathrm{\Delta }{\mathrm{G}}_{298}^0$ (kcal/mol)	+11.0 {+14.8}	+11.0 {+23.4}	+19.2	+5.2	+10.9	+5.4
B. 3 H3C–B(OH)2 (endo-exo)→ Trimethylboroxine + 3 H2O
ΔE (kcal/mol)	+15.9 {+26.7}	+15.7 {+28.1}	+22.9	+10.0	+15.7	+10.2
$\mathrm{\Delta }{\mathrm{H}}_{298}^0$ (kcal/mol)	+12.5 {+23.1}	+11.7 {+24.4}	+19.3	+6.5	+12.4	+6.7a
$\mathrm{\Delta }{\mathrm{G}}_{298}^0$ (kcal/mol)	+5.5 {+15.9}	+6.4 {+17.3}	+12.2	−1.1	+6.1	−0.9a
C. 3 H2N–B(OH)2 (endo-exo)→ Triaminoboroxine + 3 H2O
ΔE (kcal/mol)	+4.0 {+11.5}	+4.1 {+12.6}	+7.8	−0.8	+3.5	−0.4
$\mathrm{\Delta }{\mathrm{H}}_{298}^0$ (kcal/mol)	+1.7 {+9.1}	+1.8 {+10.8}	+5.3	−3.3	+1.3	−2.9a
$\mathrm{\Delta }{\mathrm{G}}_{298}^0$ (kcal/mol)	−4.2 {+4.2}	−4.1 {+5.8}	−0.6	−9.2	−4.6	−8.8a
D. 3 HO–B(OH)2[orthoboric acid](endo-exo)→ Trihydroxyboroxine[MBA-I] + 3 H2O
ΔE (kcal/mol)	+15.7 {+22.3}	+15.8 {+23.2}	+19.1	+9.8	+14.3	+10.1
$\mathrm{\Delta }{\mathrm{H}}_{298}^0$ (kcal/mol)	+12.8 {+19.4}	+12.8 {+20.2}	+16.0	+6.9	+11.6	+7.3
$\mathrm{\Delta }{\mathrm{G}}_{298}^0$ (kcal/mol)	+6.1 {12.6}	+6.2 {+13.5}	+9.1	+0.1	+4.8	+0.5
E. 3 F–B(OH)2 (endo-exo)→ Trifluoroboroxine +3 H2O
ΔE (kcal/mol)	+19.2 {+26.7}	+19.4 {+27.3}	+23.8	+14.3	+18.3	+13.7
$\mathrm{\Delta }{\mathrm{H}}_{298}^0$ (kcal/mol)	+16.2 {+23.5}	+16.3 {+24.1}	+20.6	+11.3	+15.4	+10.8
$\mathrm{\Delta }{\mathrm{G}}_{298}^0$ (kcal/mol)	+10.0 {+17.0}	+10.0 {+17.7}	+14.0	+4.9	+8.9	+4.3

^aThermal and entropy corrections to the reaction energy are from the MP2/aug-cc-pVDZ level.

H₃B₃O₃

Boroxine⁸³ is thermodynamically unstable at room temperature, decomposing to diborane and boron trioxide ^84,85 with a lifetime of 10 min to 4 hrs, depending upon the surface conditions of the vessel ⁸⁶. Nevertheless, as the simplest member of this family of compounds, H₃B₃O₃ has been studied by a variety of experimental techniques, including vibrational spectroscopy ^86–88, electron diffraction in the gas phase ⁸⁹, and inner shell electron energy loss spectroscopy ³.

The calculated structure of boroxine is planar at all the computational levels we considered. At the MP2(FC)/aug-cc-pVTZ level the B–O and B–H bond lengths are 1.381 Å and 1.183 Å respectively, see Table 3SA; for comparison we note that the two B–O bond lengths in the endo-exo form of boronic acid, 1.364 Å and 1.374 Å, are both shorter than the B–O bond lengths in H₃B₃O₃. The calculated B–O–B and O–B–O angles in H₃B₃O₃ are both nearly equal to 120° at this level, whereas the O–B–O angle in H–B(OH)₂, 119.1°, is slightly smaller. The values of the calculated structural parameters for boroxine are in good agreement with those reported in the gas-phase electron diffraction study of Porter and coworkers: B–O and B–H bond lengths of 1.376(2) and 1.19(2) Å respectively, and B–O–B and O–B–O bond angles of 120.0(6)° ⁸⁹. It should be noted that using less complete basis sets with MP2 methodology the B–O–B and O–B–O bond angles are predicted to be somewhat different, e.g. 119.4° and 120.6° respectively at the MP2/aug-cc-pVDZ level; the corresponding results at the B3LYP/6-311++G(d,p) are reversed, 120.7° and 119.3°, in accord with the values reported by Beckmann et al. ⁹⁰ at the B3LYP/6-311+G(d) level. This appears to be a feature of the B3LYP functional, since an optimization at the MP2/6-311++G(d,p) level yields B–O–B and O–B–O bond angles of 119.8° and 120.2° respectively

The formation of boroxine from the dehydration of boronic acid in vacuo is predicted to be endothermic at every computational level we employed, see Table 2A; the value of $\mathrm{\Delta }{\mathrm{H}}_{298}^0$ is +12.2 kcal/mol at the MP2/aug-cc-pVTZ level. As can be seen from this Table, it is important to include diffuse functions in the basis set to adequately describe the bonding changes in this reaction. Although this dehydration is entropically favored by ~7 kcal/mol, the calculated values of $\mathrm{\Delta }{\mathrm{G}}_{298}^0$ remain positive. Heats of formation at 298 K, ΔH_f(298 K), for H–B(OH)₂, H₃B₃O₃, and H₂O are available from various sources in the literature, see Table 4S ^{79,84,91–97}. Based on these values of ΔH_f(298 K), the reaction enthalpy, ΔH_r(298 K), for the dehydration can be calculated to be slightly exothermic, −0.6 kcal/mol. In this calculation, we used the most recent estimate of ΔH_f(298 K) for H–B(OH)₂ from the high-level calculations of Grant and Dixon (−154.6 kcal/mol ⁹⁶); using the value of ΔH_f(298 K) suggested 30 years earlier by Guest et al. (−153.1 kcal/mol⁹⁴) leads to a value for ΔH_r(298 K) of −5.1 kcal/mol, which is even more exothermic. These results are clearly in very poor agreement with the calculated enthalpies in Table 2A. This discrepancy led us to carry out additional higher-level single-point calculations using the MP2/aug-cc-pVTZ geometry; the calculated reaction energies, ΔE, are +15.9, +16.0, +15.2, and +15.1 kcal/mol at the MP2/aug-cc-pVQZ, MP2/aug-pV5Z, CCSD/aug-cc-pVTZ, and CCSD(T)/aug-cc-pVTZ levels respectively; based on the thermal corrections in Table 2A the corresponding values of $\mathrm{\Delta }{\mathrm{H}}_{298}^0$ would be reduced by only ~3 kcal/mol, leaving a discrepancy of at least 12–13 kcal/mol compared to the corresponding results based on the heat of formation data. It is noteworthy that the reaction energies we calculated for the formation of F₃B₃O₃ are in good agreement with accepted literature values (see below). Upon consideration of our results, it appears that the value for the heat of formation of boroxine generated by Porter and Gupta⁸⁴ and listed in the JANAF compilation ⁹² needs to be revised from −290.0 kcal/mol to approximately −277 kcal/mol.

Using PCM:UFF implicit aqueous solution at the MP2/aug-cc-pVTZ level, the value of $\mathrm{\Delta }{\mathrm{H}}_{298}^0$ for the dehydration is reduced by ~2.4 kcal/mol to +9.8 kcal/mol; the corresponding value of $\mathrm{\Delta }{\mathrm{G}}_{298}^0$, +3.5 kcal/mol, remains positive, see Table 5S. Thus, there is only a modest effect of these aqueous solvent models on the dehydration process. At this level the B–O and B–H bond lengths are 1.382 Å and 1.183 Å respectively, almost identical to the gas-phase results, and the B–O–B and O–B–O bond angles are only slightly different, 119.9° and 120.1°. Since some boroxines are formed by simply warming the corresponding boronic acid in an anhydrous solvent such as carbon tetrachloride or chloroform⁴, we also calculated thermodynamic parameters for the dehydration of H₃B₃O₃ in the PCM:UFF reaction field of CCl₄; the calculated values of $\mathrm{\Delta }{\mathrm{H}}_{298}^0$ and $\mathrm{\Delta }{\mathrm{G}}_{298}^0$ are +11.2 and +4.5 kcal/mol respectively.

(H₃C)₃B₃O₃

Trimethylboroxine is relatively stable compared to boroxine itself. As a result of this stability and questions concerning the aromaticity of boroxines in general, (H₃C)₃B₃O₃ has been the subject of a variety of experimental and computational investigations ^{26,63,85,98,99}.

At all the computational levels we employed, the 6-membered ring in trimethylboroxine remains essentially planar and there is good agreement among the values of the corresponding structural parameters, see Table 3SB. At the MP2/aug-cc-pVTZ level the B–O and B–C bond lengths, 1.387 Å and 1.563 Å, are in accord with the reported gas-phase electron diffraction values, 1.39±0.02 Å and 1.57±0.03 Å ⁶³. For comparison we note that the two B–O bond lengths in the H₃C–B(OH)₂ monomer, 1.368 Å and 1.378 Å, are both shorter than in the trimer. The differences in the B–C bond lengths for H₃C–BH₂ (1.558 Å), H₃C–B(OH)₂ (1.574 Å), and (H₃C)₃B₃O₃ (1.563 Å) at this level are not indicative of substantial electron delocalization in the boroxine core ¹⁰⁰. The calculated B–O–B and O–B–O angles in trimethylboroxine are 121.1° and 118.9° respectively, in reasonable agreement with the corresponding values reported by Yao et al. ⁸⁵; the O–B–O angle in the corresponding monomer is 2° smaller than in the trimer. The Bauer and Beach ⁶³ electron diffraction study reported a B–O–B angle of 112°, but the uncertainty was quite large, ±4°; no value was given for the O–B–O angle. Comparing the calculated structures of the boroxine rings in H₃B₃O₃ and (H₃C)₃B₃O₃ at the MP2/aug-cc-pVTZ level shows that the methyl group increases in the B–O bond length by ~0.006 Å and decreases the O–B–O bond angle by 1.1°. It should also be noted that the NPA charge on the boron atoms in (H₃C)₃B₃O₃, +1.13e, is ~0.16e more positive than in H₃B₃O₃, whereas the charge on the oxygen atoms is nearly the same.

The formation of trimethylboroxine from the dehydration of methylboronic acid in vacuo is predicted to be endothermic at every computational level we employed, see Table 2B; the value of ΔE, +10.2 kcal/mol at the MP2/aug-cc-pVTZ level, is ~5 kcal/mol less positive than for boroxine itself. Using thermal corrections from the MP2/aug-cc-pVDZ level leads to a value of +6.7 kcal/mol for $\mathrm{\Delta }{\mathrm{H}}_{298}^0$. Single-point values of ΔE for the dehydration at the CCSD/aug-cc-pVTZ and CCSD(T)/aug-cc-pVTZ levels using the MP2(FC)/aug-cc-pVTZ optimized geometry are +10.5 and +10.3 kcal/mol respectively, just slightly more positive than the value calculated at the MP2/aug-cc-pVTZ level. The dehydration is entropically favored by ~7.6 kcal/mol, and the calculated value of $\mathrm{\Delta }{\mathrm{G}}_{298}^0$ is slightly negative, −0.9 kcal/mol.

To the authors knowledge, the heat of formation of (H₃C)₃B₃O₃ is not available from the literature. However, the value of ΔE for the dehydration reaction has been reported by the Kua group (using Jaguar¹⁰¹) to be +18.0 kcal/mol in vacuo at the B3LYP/6-311+G(d) level²⁶. At the B3LYP/6-31G(d), B3LYP/6-31+G(d), B3LYP/6-311+G(d), B3LYP/6-311++G(d,p), B3LYP/6-311++G(2df,2p), and B3LYP/6-311++G(2df,2pd) levels we find ΔE (using GAUSSIAN 03⁴⁶) to be +18.8, +14.6, +17.8, +15.7, +14.1, and +14.0 kcal/mol respectively; the corresponding values of $\mathrm{\Delta }{\mathrm{H}}_{298}^0$ are +15.4, +11.5, +14.4, +11.7, +10.8, and +10.6 kcal/mol. Thus, as the basis set is improved, the calculated values of $\mathrm{\Delta }{\mathrm{H}}_{298}^0$ using the B3LYP functional are in somewhat better accord with the more rigorous MP2/aug-cc-pVTZ results, see Table 2B. Using the PCM:UFF aqueous solvation model at the PBE1PBE/6-311++G(d,p) and B3LYP/6-311++G(d,p) levels, the enthalpy change for the dehydration is reduced by ~4 kcal/mol.

(H₂N)₃B₃O₃

The authors’ could not identify any report of an experimental characterization of triaminoboroxine. Our calculations find this molecule to be planar at all the computational levels we employed and there is generally good agreement for the corresponding structural parameters at these levels, see Table 3SC. In particular at the MP2/aug-cc-pVTZ level the B–O and B–N bond lengths are 1.389 Å and 1.407 Å respectively and the B–O–B and O–B–O angles are 119.4° and 120.6°; the lengths of the two B–O bonds in the monomer are 1.379 Å and 1.387 Å, the length of the B–N bond is 1.417 Å (vs. 1.395 Å in H₂N–BH₂), and the O–B–O bond angle is 117.9°. Thus, the amine groups elongate the B–O bonds by ~0.008 Å compared to these bonds in boroxine, but only by ~0.002 Å compared to trimethylboroxine. As might be expected, the calculated O–B–O angles in (H₂N)₃B₃O₃ of 120.6° are greater than 120°, opposite to what we found for (H₃C)₃B₃O₃. It should be noted that the optimized geometry of triaminoboroxine at the B3LYP/6-311++G(d,p) level, predicts the O–B–O angles to be 119.8°, i.e. less than 120°, see Table 3SC; at the MP2/6-311++G(d,p) level this bond angle is 120.7°, in good agreement with the other MP2 calculations, suggesting the discrepancy is a result of the B3LYP functional and not the basis set. In addition, using the LDA, PBE, and TPSS functionals and the B3P86 and B3PW91 hybrid functionals with the 6-311++G(d,p) basis set, we find O–B–O angles of 120.3°, 120.5°, 120.4°, 120.0°, and 120.1° respectively, in good agreement with the MP2 results. The NPA charge on the boron atoms in (H₂N)₃B₃O₃ is only ~0.01e more positive than in (H₃C)₃B₃O₃, and the charge on the oxygen atoms remains nearly the same as in H₃B₃O₃ and (H₃C)₃B₃O₃.

Interestingly, the dehydration of H₂N–B(OH)₂ leading to (H₂N)₃B₃O₃ is calculated to be exothermic at the MP2/aug-cc-pVDZ and MP2/aug-cc-pVTZ levels where the values of $\mathrm{\Delta }{\mathrm{H}}_{298}^0$ are −3.3 and −2.9 kcal/mol respectively; MP2 calculations using correlation consistent basis sets without diffuse functions, as well as the PBE1PBE and B3LYP calculations including diffuse functions predict the dehydration to be slightly endothermic, see Table 2C. However, at all the computational levels we employed the calculated values of $\mathrm{\Delta }{\mathrm{H}}_{298}^0$ for this dehydration are lower than for any of the other boronic acids in this study. The low values of $\mathrm{\Delta }{\mathrm{H}}_{298}^0$ in this case may be partly the result of eliminating the adverse hydrogen-hydrogen steric contact in the endo-exo conformer of the monomer where the closest (N)H^…H(OB) distance is 2.525 Å (compared to the analogous (C)H^…H(OB) distance of 2.719 Å in H₃C–B(OH)₂) and there is an asymmetry in the two H–N–B angles of ~3.7° at the MP2/aug-cc-pVTZ level. In addition, this adverse interaction in the monomer is replaced by an enhanced electrostatic interaction (O_ring ^…H(N)) in the trimer; the O_ring ^…H distance is 2.655 Å. Unfortunately, it is difficult to quantify the impact of these structural differences on the dehydration enthalpy. The dehydration reaction is entropically favored by ~6 kcal/mol and the resulting values of $\mathrm{\Delta }{\mathrm{G}}_{298}^0$ are approximately −9 kcal/mol at the MP2/aug-cc-pVD(T)Z levels.

(HO)₃B₃O₃

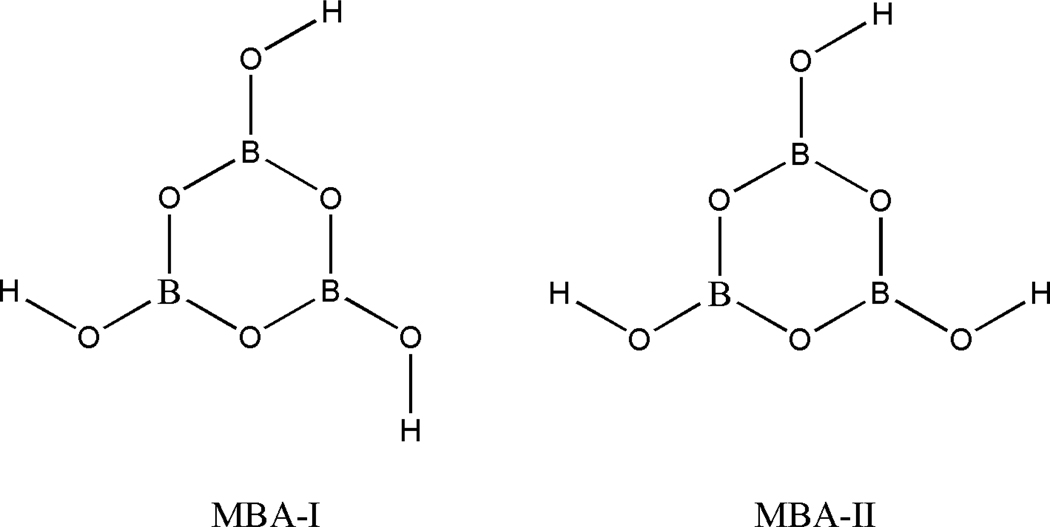
Trihydroxyboroxine, or orthorhombic metaboric acid, MBA, has two distinct conformers, i.e. MBA-I and MBA-II²³, see Figure 3.

Figure 3.

Structures of Orthorhombic metaboric Acid, MBA-I and MBA-II.

We optimized both forms of the MBA and found MBA-I to be lower in energy than MBA-II by ~0.7 kcal/mol at both the MP2/aug-cc-pVDZ and MP2/aug-cc-pVTZ levels. Consequently, we used MBA-I for the thermochemical calculations reported in Table 2D.

The calculated structures of MBA-I (and MBA-II) are planar at all the computational levels we employed and the main geometrical parameters are in reasonably good agreement at these levels, see Table 3SD. As a result of intramolecular hydrogen bonding, there are two slightly different B–O bond lengths in the ring, e.g. 1.383 Å and 1.386 Å at the MP2/aug-cc-pVTZ level; the B– O_exo bond lengths are considerably shorter, 1.360 Å, and the H^…O distances are quite long, 2.445 Å, consistent with weak intramolecular hydrogen bonds. All the B–O bond lengths in the monomeric (ortho)boric acid, 1.374 Å, are shorter than in the trimer; the B–O bond length in HO– BH₂ is 1.361 Å, nearly identical to the B–O_exo bond length in (HO)₃B₃O₃. The calculated B–O–B and O–B–O(ring) bond angles in MBA-I are 119.4° and 120.6° respectively, essentially the same as in (H₂N)₃B₃O₃ at this computational level; of course, all the O–B–O angles in the endo-exo conformer of the monomer (C_3h symmetry) are 120°. Again there is a discrepancy with respect to whether the B–O–B or O–B–O(ring) bond angles are greater in (HO)₃B₃O₃, i.e. at the B3LYP/6-311++G(d,p) level the calculated value of the O–B–O(ring) angle is 119.8°, see Table 3SD; at the MP2/6-311++G(d,p) level, the O–B–O(ring) angle is 120.7°, in reasonable agreement with the values from our other MP2 calculations. In addition, using the 6-311++G(d,p) basis set the LDA¹⁰², PBE⁴², and TPSS¹⁰³ functionals, as well as the B3P86^40,104 and B3PW91^40,105 hybrid functionals, all find O–B–O(ring) angles that are over 120°. Thus, some caution needs to be exercised in using the popular B3LYP/6-311++G(d,p) computation level for detailed structural considerations around boron atoms. The NPA charges on the boron atoms in MBA-I are 1.23e at the MP2/aug-cc-pVTZ level, ~0.1e more positive than in trimethylboroxine.

The X-ray diffraction structure of MBA-II has been determined at −130 °C ^106,107. This crystal structure is obviously quite distorted as a result of intermolecular interactions, e.g. there are B–O– H bond angles as large as 129° and one of the B–O bond lengths in the ring is actually shorter than the B–O_exo bond attached to the same boron atom, making it difficult to compare it to our gas-phase structure¹⁰⁸. Interestingly, two of the three O–B–O bond angles in the ring of the crystal structure are found to be greater than 120° whereas one is 119.3°; in the calculated gas-phase structure, all three of the O–B–O bond angles in the ring are greater than 120° at the MP2/aug-cc-pVTZ level and less than 120° at the B3LYP/6-311++G(d,p) level.

At all the computational levels we considered, the formation of trihydroxyboroxine (MBA-I) from the dehydration of boric acid in vacuo is predicted to be endothermic, see Table 2D; the values of ΔE and $\mathrm{\Delta }{\mathrm{H}}_{298}^0$ are +10.1 and +7.3 kcal/mol respectively at the MP2/aug-cc-pVTZ level. Based on the JANAF⁹² values of ΔH_f(298 K), the dehydration is found to be slightly exothermic, ΔH_r(298 K) = −4.9 kcal/mol in poor agreement with the calculated values. Part of this discrepancy appears to be the JANAF value for boric acid, ΔH_f(298 K) = −237.16 kcal/mol. Recently, in a high-level theoretical study Grant and Dixon⁹⁶ predicted a more negative value for the heat of formation, −239.8 kcal/mol. Using this revised value, the dehydration is found to be endothermic, ΔH_r(298 K) = +3.0 kcal/mol, in better agreement with our calculated values. Furthermore, based on a computer analysis of thermochemical boron data, Guest et al.⁹⁴ recommended a value for the heat of formation of trihydroxyboroxine of −542.4 kcal/mol, giving a value for ΔH_r(298 K) = +3.6 kcal/mol.

Using the PCM:UFF implicit aqueous solution model with either the B3LYP or PBE1PBE functional and the 6-311++G(d,p) basis set, the exothermicity of the dehydration reaction is approximately 7.6 kcal/mol lower than in the gas phase; at the MP2/aug-cc-pVDZ level the decrease in $\mathrm{\Delta }{\mathrm{H}}_{298}^0$ is even greater, 9.4 kcal/mol. The calculated values of $\mathrm{\Delta }{\mathrm{G}}_{298}^0$ in solution are predicted to be slightly negative.

F₃B₃O₃

Trifluoroboroxine has been known since the 1930s and has been studied by a variety of experimental and computational techniques ^{96,99,109–113}. To the authors’ knowledge there are no experimental structural parameters available for F₃B₃O₃ in the literature. At the computational levels we employed trifluoroboxoxine is planar and the structural parameters calculated at these various levels are generally in good agreement, see Table 3SE. At the MP2/aug-cc-pVTZ level the B–O and B–F bond lengths are 1.377 Å and 1.317 Å respectively; for comparison, we note that the B–O bond lengths in F–B(OH)₂, 1.361 Å and 1.369 Å, are shorter than the B–O bond lengths in the ring, consistent with what we observed for the other monomer-trimer pairs in this study. The calculated B–F bond length in the monomer, 1.338 Å, is ca. 0.02 Å longer than in the trimer; the corresponding bond length in F–BH₂ is 1.326 Å. The calculated B–O–B and O–B–O bond angles in trifluoroboroxine are 118.9° and 121.1° respectively, while the O–B–O angle in the corresponding monomer is 121.4°. These structural results for F₃B₃O₃ are similar to those reported by Ghiasi¹¹² at the B3LYP/6-31+G(d,p) level and by Türker et al.⁹⁹ at the MP2/6-31G(d,p) level. As would be expected the NPA charge on the boron atoms in F₃B₃O₃, +1.29e, is the largest value we observed for the boroxines in this study, ~0.32e more positive than in H₃B₃O₃ and the charge on the oxygen atoms is ~0.01e more negative.

The formation of trifluoroboroxine from the dehydration of fluoroboronic acid in vacuo is predicted to be endothermic, see Table 2E; the values of ΔE and $\mathrm{\Delta }{\mathrm{H}}_{298}^0$ are +13.7 and +10.8 kcal/mol respectively at the MP2/aug-cc-pVTZ level. The need for thermal data on F-B-O systems by workers in the fields of solid and liquid propellants around 1960 led to numerous determinations of the heat of formation of F₃B₃O₃⁹⁷, arguably making the value of −565.3 kcal/mol (Table 4SA) listed in the JANAF compilation ⁹² the most reliable experimentally-based heat of formation currently available for any boroxine derivative. Using the heat of formation for F–B(OH)₂ suggested by Elkaim et al. ¹¹⁴, −249.6 kcal/mol (Table 2SB), gives a value for ΔH_r(298 K) for the dehydration reaction of +10.1 kcal/mol, in quite good agreement with the MP2/aug-cc-pVTZ value; using the Sanderson value ^95,115, for the heat of formation of F–B(OH)₂ gives a slightly higher value for ΔH_r(298 K), +10.4 kcal/mol. Using MP2/aug-cc-pVTZ optimized geometries, we carried out single point calculations for F–B(OH)₂, F₃B₃O₃, and H₂O at the MP2/aug-cc-pVQZ, MP2/aug-cc-pV5Z, CCSD/aug-cc-pVTZ, and CCSD(T)/aug-cc-pVTZ levels; the resulting values of ΔE are +14.5, +14.7, +13.8, and +13.5 kcal/mol, respectively. Using the MP2/aug-cc-pVTZ thermal corrections the values for $\mathrm{\Delta }{\mathrm{H}}_{298}^0$ are +11.6, +11.8, +10.9, and +10.6 kcal/mol for these calculations, in good agreement with the value of ΔH_r(298 K). Although this reaction is favored entropically by ~6.4 kcal/mol, the calculated values of $\mathrm{\Delta }{\mathrm{G}}_{298}^0$ remain positive. Note also that the dehydration reactions for F–B(OH)₂ are a few kcal/mol less endothermic than for H–B(OH)₂ at every computational level we used. This is due in part to the F^…H hydrogen bond in the endo-exo conformer of the monomer, presumably stabilizing it to some extent.

Using the PCM:UFF implicit aqueous solution model with either the B3LYP or PBE1PBE functional and the 6-311++G(d,p) basis set, the exothermicity of the dehydration reaction is approximately 4 kcal/mol lower than in the gas phase; at the MP2/aug-cc-pVDZ level, the decrease in $\mathrm{\Delta }{\mathrm{H}}_{298}^0$ is only ~1.9 kcal/mol. The calculated values of $\mathrm{\Delta }{\mathrm{G}}_{298}^0$ remain positive at these levels.

Concluding Remarks

In this article relative energies of the endo-exo, anti, and syn conformers of the boronic acids R– B(OH)₂, R = H, H₃C, H₂N, HO, and F were calculated at a variety of computational levels and the thermochemical parameters were assessed for their dehydration leading to the formation of the corresponding boroxines R₃B₃O₃. We have shown the following:

1) The endo-exo form of the boronic acids is consistently lowest in energy in vacuo, although the anti and syn conformers are typically only a few kcal/mol higher in energy. The barriers connecting the endo-exo and anti forms of these acids are found to range from 7.0 to 9.4 kcal/mol at the MP2/aug-cc-pVTZ level. PCM:UFF implicit solvation models (H₂O and CCl₄) typically lower the energy gap between the various forms but the endo-exo conformer remains lowest in energy.

2) The structures of R₃B₃O₃ for R = H, H₂N, HO, and F are planar and the boroxine ring for R = H₃C is practically planar. The main geometrical parameters in the boroxine ring that are altered by changing the substitutent are the O–B–O bond angles, which ranges from 118.9° for R=H₃C to 121.1° for R=F at the MP2/aug-cc-pVTZ level. In all cases, the O–B–O bond angle is greater in the boroxine than in the corresponding monomer. It should be noted, however, that the suggestion put forth by Türker et al.⁹⁹. that the O–B–O angles in boroxines tend toward 120° as the electronegativity of the substituents increases is not corroborated at the MP2/aug-cc-pVTZ level.

3) In contrast to the MP2 calculations for the symmetrically trisubstituted boroxines with R = H₂N and HO, the popular B3LYP/6-311++G(d,p) computational level predicts the O–B–O angle to be less than 120°. It should be noted that other problems have surfaced concerning the capability of the B3LYP functional with split-valence basis sets for describing various aspects of boron chemistry, most notably dative bonding issues ^{68,116,–121}.

4) The reactions 3 R–B(OH)₂ → R₃B₃O₃ + 3 H₂O for R = H, H₃C, HO, and F are predicted to be endothermic with values of $\mathrm{\Delta }{\mathrm{H}}_{298}^0$ ranging from +6.7 kcal/mol for H₃C–B(OH)₂ to +12.2 kcal/mol for H–B(OH)₂ at the MP2/aug-cc-pVTZ computational level in the gas phase. In contrast, for R = H₂N the dehydration is exothermic at this level with $\mathrm{\Delta }{\mathrm{H}}_{298}^0$ = −2.9 kcal/mol. For the group of substituents with lone pairs, H₂N, HO, and F, $\mathrm{\Delta }{\mathrm{H}}_{298}^0$ increases as the σ-electron withdrawing capacity increases and the π-electron donating ability of the group decreases based on values of the Hammett σ- and π-constants¹²².

5) Interestingly, NICS calculations¹²³ at the PBE1PBE/6-31+G(d)//MP2/aug-cc-pVTZ level suggest that the boroxines R₃B₃O₃ (R = H₃C, H₂N, OH, and F) are all slightly aromatic and that the aromaticity increases as the electronegativity of the substituent increases. This progressive increase in the aromaticity of these boroxines does not correlate with the values of $\mathrm{\Delta }{\mathrm{H}}_{298}^0$ for their formation from the corresponding boronic acids.

6) The dehydration reactions are entropically favored by 6.8, 7.6, 5.9, 6.8, and 6.5 kcal/mol for R = H, H₃C, H₂N, HO, and F respectively. For H₃B₃O₃ implicit solvation models (H₂O and CCl₄) lower the values of $\mathrm{\Delta }{\mathrm{H}}_{298}^0$.

7) Diffuse functions are critical in describing the bonding changes that occur in the course of the reactions 3 R–B(OH)₂ → R₃B₃O₃ + 3 H₂O for R = H, H₃C, H₂N, HO, and F. Comparing MP2 calculations using the cc-pVTZ and aug-cc-pVTZ basis sets shows that diffuse functions can lower the values of $\mathrm{\Delta }{\mathrm{H}}_{298}^0$ by more than 5 kcal/mol and the effect is even more pronounced when comparing the cc-pVDZ and aug-cc-pVDZ basis sets. Based on this observation, it is likely that reactions involving related compounds such as boronates and aminoboranes will require diffuse functions for an accurate description of their thermochemistry.

8) Heat of formation data, ΔH_f(298 K), for boron compounds that are available from various sources in the literature should be viewed with caution. Specifically, the value for boroxine listed in the JANAF compilation, −290.0 kcal/mol, certainly needs to be revised to approximately −277.0 kcal/mol. This highlights the important work of Grant and Dixon ⁹⁶, Schlegel and Harris ¹²⁴, Duan et al. ⁷⁹, and Karton and Martin ^79,125 in using high-level calculations to improve the accuracy of heats of formation for boron compounds.