Broad Inhibition Sharpens Orientation Selectivity By Expanding Input Dynamic Range in Mouse Simple Cells

Abstract

Orientation selectivity (OS) is an emergent property in the primary visual cortex (V1). How OS arises from synaptic circuits remains unsolved. Here, in vivo whole-cell recordings in the mouse V1 revealed that simple cells received broadly tuned excitation and even more broadly tuned inhibition. Excitation and inhibition shared a similar orientation preference and temporally overlapped substantially. Neuron modeling and dynamic-clamp recording further revealed that excitatory inputs alone would result in membrane potential responses with significantly attenuated selectivity, due to a saturating input-output function of the membrane filtering. Inhibition ameliorated the attenuation of excitatory selectivity by expanding the input dynamic range, and caused additional sharpening of output responses beyond unselectively suppressing responses at all orientations. This “blur-sharpening” effect allows selectivity conveyed by excitatory inputs to be better expressed, which may be a general mechanism underlying the generation of feature-selective responses in the face of strong excitatory inputs that are weakly biased.

Introduction

The primary visual cortex (V1) is the first site along the visual pathway where neuronal responses exhibit robust sensitivity to orientation of stimuli (Hubel and Wiesel, 1962). The orientation selectivity (OS) is likely important for tasks such as edge detection and contour completion. Despite extensive studies in the past decades, how OS is created by the computation of neural circuits is still an issue under intense debate (reviewed by Sompolinsky and Shapley, 1997; Ferster and Miller, 2000; Shapley et al., 2003). In particular, how the cortical inhibitory process is involved in sculpting orientation tuning has remained controversial. In one view, cortical inhibition does not contribute significantly to the creation of OS in simple cells (Ferster et al., 1996; Anderson et al., 2000). The orientation-tuned excitatory inputs, attributable to a linear arrangement of receptive fields (RFs) of relay cells (Chapman et al., 1991; Reid and Alonso, 1995; Ferster et al., 1996), are thought to be sufficient to generate OS under a spike thresholding mechanism (Anderson et al., 2000; Priebe and Ferster, 2008). In a contrasting view, inhibition is required to sharpen OS (Sillito, 1975; Tsumoto et al., 1979; Sillito et al., 1980; Sato et al., 1996; Ringach et al., 2003). In theoretical studies, inhibition that is more broadly tuned than excitation has been employed to effectively sharpen OS (Somers et al. 1995; Ben-Yishai et al., 1995; Troyer et al., 1998; McLaughlin et al., 2000). However, except for a few cases (Wu et al., 2008; Poo and Isaacson, 2009), a match of excitatory and inhibitory tunings is widely observed in the sensory cortex (in cat visual cortex, Anderson et al., 2000; Monier et al., 2003; Mariño et al., 2005; Priebe and Ferster, 2005; in rodent auditory and somatosensory cortex, Wehr and Zador, 2003; Zhang et al., 2003; Tan et al., 2004; Okun and Lampl, 2008; Tan and Wehr, 2009).

While previous mechanistic studies were mostly carried out in cats, mouse visual cortex has recently emerged as an important experimental model for visual research. Recent recordings in the mouse V1 have shown that similarly as in the cat V1, spiking responses of simple cells can be strongly orientation-tuned (Mangini and Pearlman, 1980; Niell and Stryker, 2008; Liu et al., 2009). However, the spatial distribution of excitatory and inhibitory synaptic inputs largely differs from that proposed for cat simple cells (Liu et al., 2010), implying that the mouse circuits for OS might be different from those in cats. First, each synaptic subfield (On or Off, excitatory or inhibitory) often possesses a rather round shape with small aspect ratios, which suggests that the spatial arrangement of synaptic inputs may not sufficiently account for OS. Second, while excitation and inhibition are organized in a spatially opponent manner in cat simple cells (Ferster, 1988; Hirsch et al., 1998; Anderson et al., 2000), in mouse simple cells the excitatory and inhibitory subfields for the same contrast display a large spatial overlap, suggesting that excitation and inhibition evoked by oriented stimuli may temporally overlap significantly at whichever stimulus orientation. These properties of synaptic inputs to mouse simple cells suggest that inhibition can play a significant role in determining orientation tuning properties of their spike responses.

To investigate the synaptic mechanisms underlying OS in the mouse V1, we carried out in vivo whole-cell voltage-clamp recordings from simple cells in layer 2/3. We dissected excitatory and inhibitory synaptic inputs evoked by oriented stimuli and characterized the spatiotemporal interplay between these inputs. We found that excitatory conductances are broadly tuned with only a moderate bias for a preferred orientation. Inhibition exhibits the same preferred orientation, but the tuning is significantly broader than that of excitation. Interestingly, excitatory inputs alone would result in membrane potential responses with greatly diminished or blurred tuning selectivity compared to that of excitatory inputs themselves, due to a saturating input-output function exhibited by the membrane filtering property. Inhibition, which interacts intimately with excitation, slows down saturation and increases the input dynamic range. This leads to a sharpening of selectivity of membrane potential responses. Our results demonstrate that inhibition plays an indispensable role in the generation of sharp OS in mouse simple cells. The broad inhibition revealed in these cells suggests that different cortical circuits combine excitation and inhibition in unique ways to produce OS.

Results

Orientation selectivity of simple cells in the mouse V1

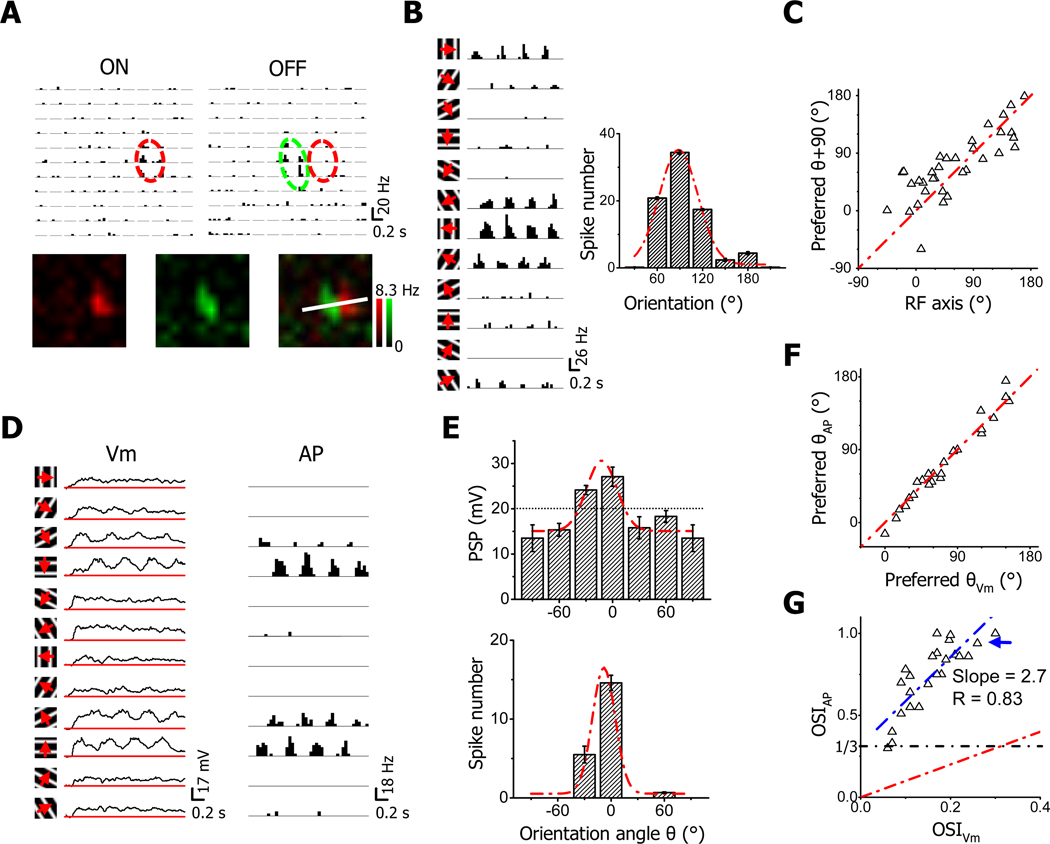
In this study, we focused on simple cells since they have been thought as the group of neurons in which OS first emerges. Different from cats, in the mouse V1, neurons exhibiting conventional simple-type receptive fields (RFs) are much more abundant in layer 2/3 than layer 4 (Liu et al., 2009). With loose-patch recordings, which detect spike signals from patched neurons without affecting their intracellular milieu, we first examined OS of simple cells in layer 2/3. The On/Off spatial RF was mapped to determine the cell type, and the relationship between the RF structure and OS was determined. As shown in Figure 1A, the example neuron displayed a typical simple-cell RF with spatially segregated On and Off subfields. When tested with drifting sinusoidal gratings, the cell responded maximally to vertically oriented gratings (Figure 1B). The cell’s preferred orientation is similar to the orientation perpendicular to the RF axis, which is defined as the line connecting the centers of On and Off subfields (see Experimental Procedures). A summary of 34 simple cells (Figure 1C) indicates a strong correlation between the preferred orientation and the RF axis, consistent with previous observations in the cat V1 (Lampl et al., 2001). According to this result, the preferred orientation of a simple cell can be predicted rather precisely from its On/Off RF structure.

Figure 1. Orientation selectivity of simple cells in layer 2/3 of the mouse V1.

(A) Spike On and Off subfields of an example simple cell as examined by loose-patch recording. Top, arrays of post-stimulus spike-time histograms (PSTHs, generated from all the trials) for spike responses to unit On or Off stimuli. PSTHs were arranged according to the corresponding stimulus locations. Each pixel represents visual space of 5°. Red and green ovals depict the two-dimensional Gaussian fits of the On and Off subfield, respectively. Bottom, color maps for spike On (red) and Off (green) responses. The brightness of color represents the average evoked firing rate. The maps were smoothed by bilinear interpolation. The white line depicts the RF axis which passes through the centers of the On and Off subfields determined by the Gaussian fits.

(B) Orientation tuning of the same cell in (A). Left, PSTHs for spike responses evoked by drifting sinusoidal gratings of various orientations. Arrow indicates the drifting direction of the grating. Right, orientation tuning curve as measured by the number of spikes evoked. The responses to gratings of opposite directions were averaged for each orientation. Red dash curve indicates the Gaussian fit, the peak of which indicates the preferred orientation angle θ. Error bar = SEM.

(C) The relationship between θ and the orientation angle of RF axis. The red dash line is the identity line. The difference between θ +90° and the angle of RF axis is significantly smaller than 35° (p < 0.05, t-test, n = 34).

(D) Subthreshold membrane potential (Vm, with spikes filtered out, left) and spike (AP, right) responses of another simple cell examined by whole-cell current-clamp recording. The red lines in the plots of Vm indicate the level of resting membrane potential.

(E) The orientation tuning curves of Vm (top) and spike (bottom) responses for the cell in (D) and the corresponding Gaussian fits (red dash curves). Vm response was measured as the peak depolarization level relative to the resting membrane potential in the cycle-averaged waveform (first 3 cycles). Error bar = SEM. The average level of spike threshold of the cell is marked by the dotted line.

(F) The plot of θ for spike responses versus that for Vm responses for the population of simple cells. The red dash line is the identity line. The difference between the two angles is significantly smaller than 15° (p < 0.001, t-test, n = 24).

(G) The plot of OSI for spike responses versus that for Vm responses. The value for the cell in (E) is marked by the blue arrow. The red dash line is the identity line and the blue dash line is the best-fit linear regression line. R indicates the correlation coefficient. The black dash line labels OSI_AP = 1/3, which is a criterion for defining orientation-selective cells.

By whole-cell current-clamp recording with a K⁺ gluconate-based intracellular solution, we next compared OS exhibited in spiking responses with that in subthreshold responses (i.e. residual membrane potentials after filtering out spikes). As shown by an example cell (Figure 1D), robust membrane depolarization responses were evoked by gratings at all testing orientations, although significant spiking responses were only observed for two orientations. Therefore, the orientation tuning of postsynaptic potential (PSP) response was much weaker compared to that of spiking response, although the two types of response exhibited the same optimal orientation (Figure 1E). In a total of 24 simple cells, similarly we found that spiking and PSP responses in the same cell exhibited essentially identical preferred orientations (Figure 1F). The orientation selectivity index (OSI, see Experimental Procedures) of spiking response was positively correlated with that of PSP response (Figure 1G). However, the selectivity of spiking response was much stronger than that of PSP response (Figure 1G), consistent with many intracellular recording results showing that spike thresholding can be a powerful mechanism for sharpening response selectivity (Carandini and Ferster, 2000; Anderson et al., 2000; Schummers et al., 2002; Van Hooser et al., 2006; Priebe and Ferster, 2008; Liu et al., 2010; Jia et al., 2010). When OSI > 1/3 was used as a criterion to define orientation-selective neurons, essentially all the simple cells were selective (Figure 1G).

Orientation tuning of excitatory and inhibitory synaptic inputs to simple cells

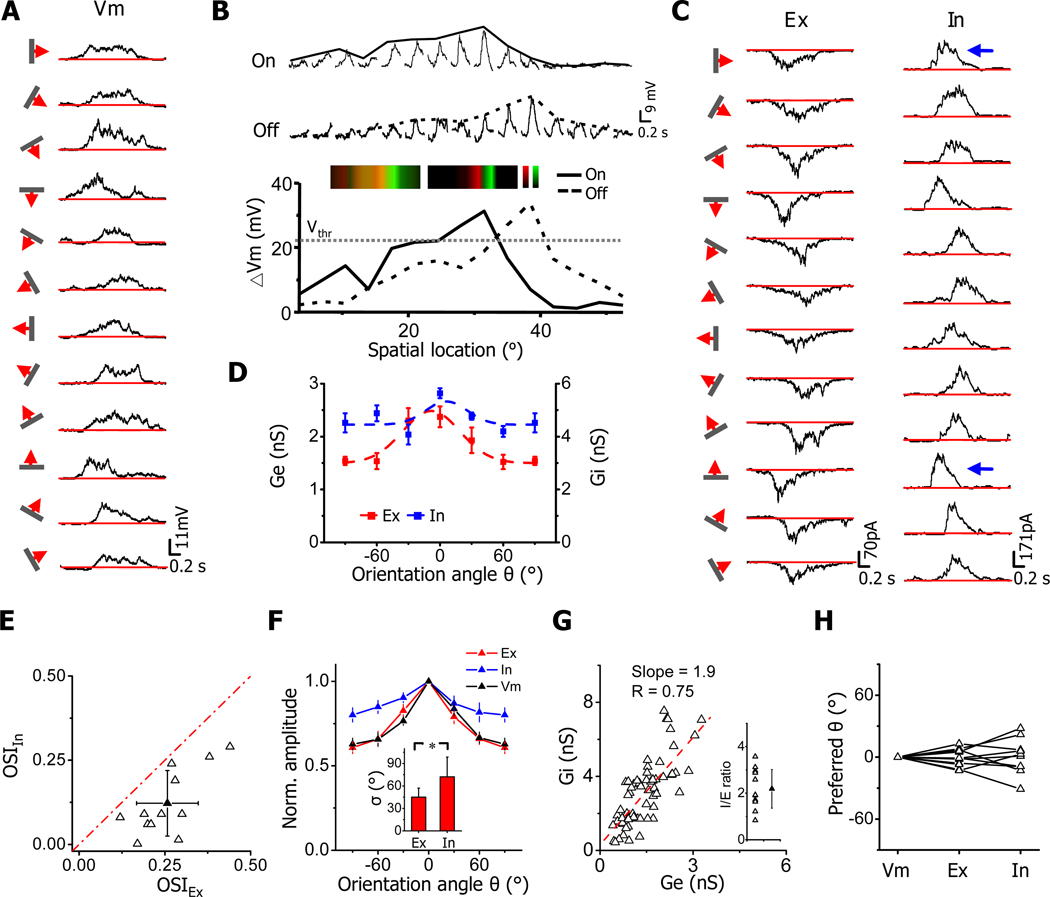
To understand how the orientation tuning of membrane potential responses arises from the integration of synaptic inputs, we applied in vivo whole-cell voltage-clamp recordings to isolate excitatory and inhibitory inputs evoked by oriented stimuli (see Experimental Procedures). We used a cesium-based intracellular solution containing QX-314, which blocked spike generation. Recordings with good voltage-clamp quality were achieved under our experimental condition, as evidenced by the linear current-voltage relationship and the proximity of the derived reversal potential of early synaptic currents to 0 mV (Figure S1A). Under current-clamp mode, we first recorded membrane potential responses to drifting bars of various orientations as to determine the preferred orientation of the cell (Figure 2A). Note that these PSP responses represented bona fide membrane potential responses which had not been disturbed by spike generation. Because of the strong correlation between the preferred orientation and the axis of On/Off segregation, we could use flashing bright/dark bars of preferred orientation to map the one-dimensional RF as to determine the simple-cell type. As shown by the example neuron, the PSP responses to bright (On) and dark (Off) bars were substantially overlapping in space (Figure 2B). However, the maximum On and Off responses were clearly segregated. Based on the average spike threshold of mouse V1 neurons (22.4 ± 6.3 mV above the resting potential, mean ± SD, n =19 cells), the recorded PSP responses would result in spatially distinct spiking On and Off subfields, indicating that the cell was most likely a simple cell (Figure 2B). The overlapping On and Off subthreshold subfields with segregated maximum On and Off responses were also observed for simple cells in our previous study of two-dimensional synaptic RFs (Liu et al., 2010).

Figure 2. Orientation tunings of excitatory and inhibitory synaptic inputs to simple cells.

(A) Vm responses to single drifting bars of various orientations. Red lines indicate the level of resting membrane potential.

(B) One-dimensional RF of Vm responses to flashing bars of preferred orientation. Middle, average Vm responses evoked by bright (On) and dark (Off) bars at different spatial locations. Bar width was 3.5°. The solid and dash curves depict the spatial tuning curves (i.e. the envelope of peak response amplitudes) for On and Off responses, respectively. Bottom, superimposed On and Off spatial tuning curves. An arbitrary spike threshold (V_thr) of 22 mV above the resting level was applied. Inset, color maps for On (red) and Off (green) Vm responses before (left) and after (right) subtracting the spike threshold. The brightness of colors represents the peak amplitude of membrane depolarization.

(C) Average excitatory (Ex) and inhibitory (In) currents evoked by bars of various orientations.

(D) Orientation tuning curves for excitatory (red) and inhibitory (blue) conductances in the cell, fitted with a Gaussian function (dash curve). Error bar = SEM.

(E) Plot of OSI of inhibitory input vs. that of excitatory input for 12 recorded simple cells. Solid symbol = mean ± SD. The red dash line is the identity line. OSI of inhibition is significantly lower than that of excitation (p < 0.001, paired t-test).

(F) Average tuning curves (normalized) for excitatory input (Ex), inhibitory input (In) and the recorded Vm response (n=12). The tuning curves were aligned according to the preferred orientation angle, which is set as 0°. Error bar = SEM. Inset, average tuning width σ for excitation and inhibition. *, p < 0.01, paired t-test.

(G) Plot of excitatory conductance vs. inhibitory conductance evoke by the same stimulus. The slope of the best-fit linear regression line is 1.9. Inset, distribution of I/E ratios. The I/E ratio was quantified as the ratio between the peak inhibitory and excitatory conductances for each orientation and then averaged for all orientations in each cell. Solid symbol = mean ± SD.

(H) The preferred orientation angles of excitatory and inhibitory inputs relative to that of the Vm response, which is set as 0°. The values for the same cell are connected with lines. The inhibitory tuning curves in two cells were too flat so that the preferred orientation could not be determined. The difference between inhibition and excitation or between excitation and Vm is smaller than 20° (p<0.01, t-test).

Under voltage-clamp mode, we next recorded the excitatory and inhibitory synaptic currents evoked by drifting bars of various orientations, with the cell’s membrane potential clamped at −70 and 0 mV, respectively. Robust excitatory and inhibitory responses were observed at all testing orientations (Figure 2C), consistent with the broad tuning of PSP response (Figure 2A). Notably, the amplitude of the excitatory responses varied in an orientation-dependent manner, while this was less obvious for the inhibitory responses. From the tuning curves plotted for the peak amplitude of synaptic conductances, it became clear that the inhibitory input exhibited weaker orientation tuning than the excitatory input (Figure 2D). We obtained similar results from a total of twelve simple cells, identified by the relative separation of maximum On and Off PSP responses (Figure S1B). As shown by the distribution of OSIs (Figure 2E) and the average tuning curve (Figure 2F), excitatory inputs were only weakly tuned, with the response at orthogonal angle larger than half of that at the preferred angle. Such weak tuning is consistent with the result of a recent Ca²⁺ imaging study in mice, which showed that layer 2/3 neurons receive individual inputs tuned for many different orientations (Jia et al., 2010). Remarkably, inhibitory inputs were even more broadly tuned, as indicated by the smaller OSI values and the much flattened population tuning curve compared with excitation (Figure 2E, 2F). The average OSI for inhibition is 0.12 ± 0.10, while that for excitation is 0.26 ± 0.09 (mean ± SD, n = 12). The tuning width, as quantified by the standard deviation (σ) of the Gaussian fit of the synaptic tuning curve, was significantly broader for inhibition than for excitation (Figure 2F, inset). It is worth noting that although inhibition and excitation differed in detailed tuning profile, on a global scale excitation and inhibition were approximately balanced, with the strength of inhibition largely co-vary with that of excitation (Figure 2G), On average, inhibition was 2.1 ± 0.8 (mean ± SD) fold as strong as excitation (Figure 2G, inset). In addition, excitation and inhibition exhibited a similar preferred orientation as that measured with PSP responses (Figure 2H).

Comparing temporal profiles of the evoked synaptic conductances, we found that the synaptic responses evoked by an optimally oriented bar had an apparently shorter time course than those evoked by the orthogonal bar (Figure S1C), suggesting that the spatial RF of synaptic inputs may be elongated. To test whether this is related to the orientation bias of synaptic inputs, we mapped the spatial distribution of synaptic inputs with flashing bars of preferred and orthogonal orientations, respectively (Figure S1D). We reasoned that potential non-linear interactions between inputs underlying drifting-bar evoked responses might be better captured by flashing bars than flashing spots. In the same cell as shown in Figure 2, we found that selectivity of flashing-bar evoked responses was more evident for excitation than inhibition (Figure S1D), similar as responses evoked by drifting bars. The envelope of peak response amplitudes was fitted with a skew-normal function (Liu et al., 2010). We noticed that the bandwidth at half-height of the excitatory spatial tuning curve was shorter for responses to optimally oriented bars than those to orthogonal bars. This difference was less evident for the inhibitory RF. We completed mapping of synaptic RFs in 11 out of 12 simple cells, and calculated the ratio between the bandwidths at half-height of the spatial tuning curves tested with orthogonally and optimally oriented bars (orth/pref) (Figure S1E).

The ratios were significantly larger than 1 (p < 0.01, t-test), but less than 2, suggesting that the synaptic subfields were slightly but significantly elongated. The excitatory RF was significantly more elongated than the inhibitory RF (Figure S1E), consistent with a stronger bias of excitation than inhibition. Thus, there is a strong correlation between the orientation bias of synaptic inputs and the geometry of their spatial RFs, i.e. a biased distribution of inputs along an axis consistent with their orientation preference. This is reminiscent of the model originally proposed by Hubel and Wiesel (Hubel and Wiesel, 1962). Nevertheless, the spatial arrangement of synaptic inputs brings about at most a weak orientation bias of synaptic inputs in mouse simple cells.

Orientation tuning of membrane potential responses with and without inhibition

Comparing response temporal profiles, we found that excitatory and inhibitory conductances overlapped considerably during the whole course of the responses at both the preferred and orthogonal angles (Figure 3A). In addition, the peak excitatory and inhibitory responses were temporally close at both angles. This finding is in contrast to previous observations in cat simple cells that excitation and inhibition evoked by optimally oriented stimuli are temporally out of phase (Ferster, 1988; Anderson et al., 2000; Priebe and Ferster, 2005). We further recorded responses to drifting sinusoidal gratings similar as in Anderson et al. (2000) study, and observed that in most of examined simple cells excitation and inhibition were temporally in phase (phase difference < 30°) (Figure S2). This observation in fact agreed with our previous results that excitatory and inhibitory subfields have a considerable spatial overlap (Liu et al., 2010).

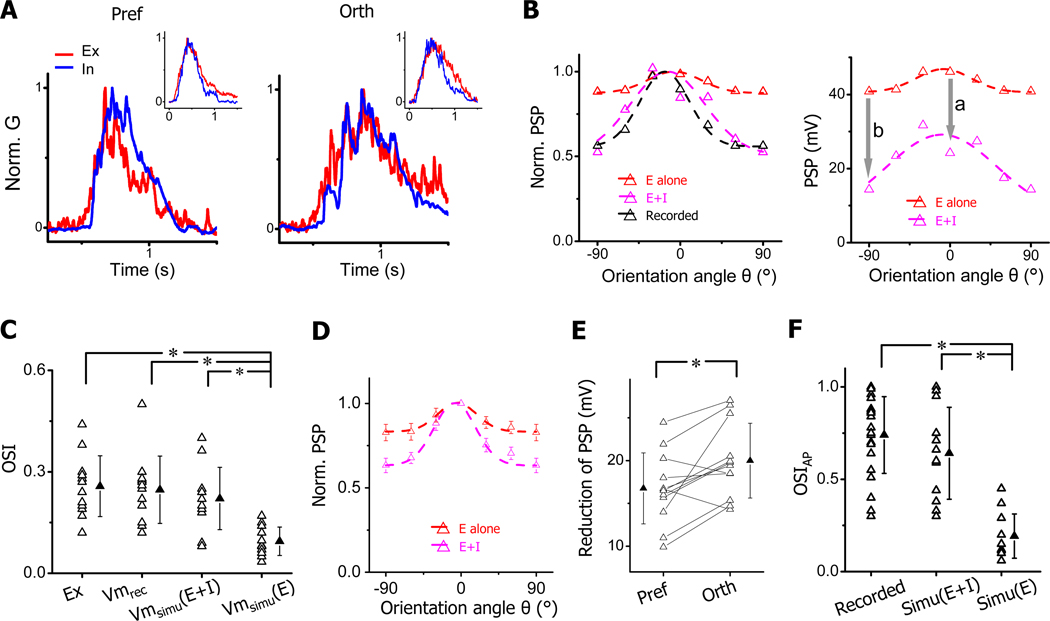
Figure 3. Orientation tunings of output responses with and without inhibition.

(A) Superimposed normalized excitatory (red) and inhibitory (blue) conductances evoked by bars of preferred and orthogonal orientations in the example cell shown in Figure 2 (marked by arrows). Inset, average conductance waveforms of all the recorded cells. Before averaging traces were aligned according to the onsets of excitatory responses.

(B) Left, normalized orientation tuning curves of the same cell’s PSP responses derived from excitatory inputs alone (red), derived by integrating excitatory and inhibitory inputs (magenta), and experimentally recorded (black). Right, actual tuning curves of derived PSP responses. “a” and “b” with arrows mark the reduction of PSP response at preferred and orthogonal orientations, respectively.

(C) OSIs of excitatory conductance (Ex), recorded Vm response (Vm), simulated Vm response with the excitatory input alone (Vm_simu(E)) and simulated Vm responses with integrating excitatory and inhibitory inputs (Vm_simu(E+I)). Solid symbol = mean ± SD. *, p < 0.01, ANOVA with post hoc test, n = 12.

(D) Average normalized PSP tuning curves. Bar = SE, n = 12.

(E) Reduction of PSP response at preferred and orthogonal orientations. Solid symbol = mean ± SD. *, p < 0.01, paired t-test.

(F) OSIs of spike response (OSI_AP) for spikes recorded, spikes simulated by integrating excitatory and inhibitory inputs (Simu(E+I)), and those simulated with the excitatory input alone (Simu(E)). Solid symbol = mean ± SD. *, p < 0.001, ANOVA with post hoc test.

The substantial temporal overlap between excitation and inhibition suggests that they would interact intimately in determining the membrane potential response. To understand the excitatory-inhibitory interplay, we derived the PSP response by feeding the experimentally obtained synaptic conductances into a single-compartment neuron model (see Experimental Procedures). We also derived the PSP response generated by the excitatory input alone by setting the inhibitory conductance as constant zero. As shown by the results for the example cell in Figure 2, when the PSP response was generated from the excitatory input alone, the original tuning selectivity existing in the excitatory input was severely attenuated (Figure 3B, left, red). Interestingly, when the PSP response was derived with the inhibitory input present, the tuning selectivity largely recovered (Figure 3B, left, magenta) and became similar to that of the experimentally recorded PSP response (Figure 3B, left, black). This suggests that it is due to the inhibition that the initial selectivity carried by the excitatory input has been able to be expressed. Comparing tuning curves of absolute PSP values with and without inhibition, we found that inhibition had globally reduced the level of PSP responses (Figure 3B, right). Notably, the reduction at the orthogonal angle was larger than that at the preferred angle, making the absolute PSP tuning curve also appear sharper after integrating inhibition (Figure 3B, right).

We summarized the inhibitory effect for all the simple cells. In our cell population, the selectivity of recorded PSP responses was similar to that of excitatory inputs (Figure 3C). Underlying this apparent “linear” transformation are two concurrent nonlinear processes: the tuning selectivity existing in excitatory inputs would become significantly weakened or blurred when the inputs were transformed into PSP responses (Figure 3C, Vm_simu(E)); inhibitory inputs restored the level of PSP tuning back to that defined by the excitatory inputs (Figure 3C, Vm_simu(E+I)). The average tuning curves showed clearly that the PSP tuning was sharpened after integrating inhibition (Figure 3D). In addition, there was a larger reduction in PSP at the orthogonal angle than at the preferred angle (20.0 ± 4.3 vs. 16.7 ± 4.1 mV, mean ± SD) (Figure 3E), indicating that inhibition had caused an additional sharpening of PSP tuning beyond unselectively lowering responses at all orientations. Based on the derived PSP responses, we next estimated OS of spiking responses by applying a spike threshold in the integrate-and-fire neuron model (22mV above the resting potential, see Experimental Procedures). Because PSP responses generated from excitatory inputs alone had a considerably flat tuning and most responses were above the spike threshold, OS would fail to be created in most of the cells (OSI_AP< 0.3, Figure 3F, Simu(E)). In the presence of inhibition, however, derived spiking responses were as sharply tuned as those observed in loose-patch recordings (Figure 3F, Simu(E+I)). These data demonstrate that inhibition is indispensable for the generation of sharp OS in mouse simple cells.

Membrane filtering and inhibitory sharpening of blurred selectivity

The above data have indicated that the intrinsic input-output transformation could lead to a blurring of tuning selectivity. To further illustrate this effect of membrane filtering, we carried out a more generalized simulation using the neuron model. For simplicity, we simulated PSP responses resulting from model excitatory inputs that vary only in amplitude but not in temporal profile (see Experimental Procedures). The filtering property of the membrane is demonstrated in the plot of membrane potential depolarization versus excitatory conductance (Figure 4A, left). Within a physiological range of excitatory conductances (0.4 – 3.3 nS, see Figure 3C), the input-output function exhibited a fast saturating curve (Figure 4A, left, black). Its first-order derivative decreased rapidly to a small value (Figure 4A, left, inset), indicating that within a large input range the increase of the PSP response was much slower than the growth of the excitatory input strength. This is vividly demonstrated by two model excitatory inputs with one twice as strong as the other (Ge₁:Ge₂ =1: 2), which generated PSP responses that had a much smaller fold difference in amplitude (ΔVm₁: ΔVm₂ = 1: 1.2) (Figure 4A, right). Both numerically (Figure 4B) and geometrically (Figure S3A), we confirmed that ΔVm₁/ΔVm₂ > Ge₁/Ge₂ (with Ge₂ >Ge₁) held true for all the model inputs. Such a “compression” effect has a great impact on stimulus selectivity of neuronal responses. Imagine that Ge₂ and Ge₁ represent the excitatory inputs evoked by the optimal and null stimuli respectively. The selectivity existing in the excitatory inputs, as reflected by the ratio of Ge₂ to Ge₁, is greatly attenuated when the inputs are transformed into PSP responses. Since Ge can represent an input evoked by any type of physical stimulus, such attenuation of tuning selectivity poses a ubiquitous problem for any feature-specific neuronal responses.

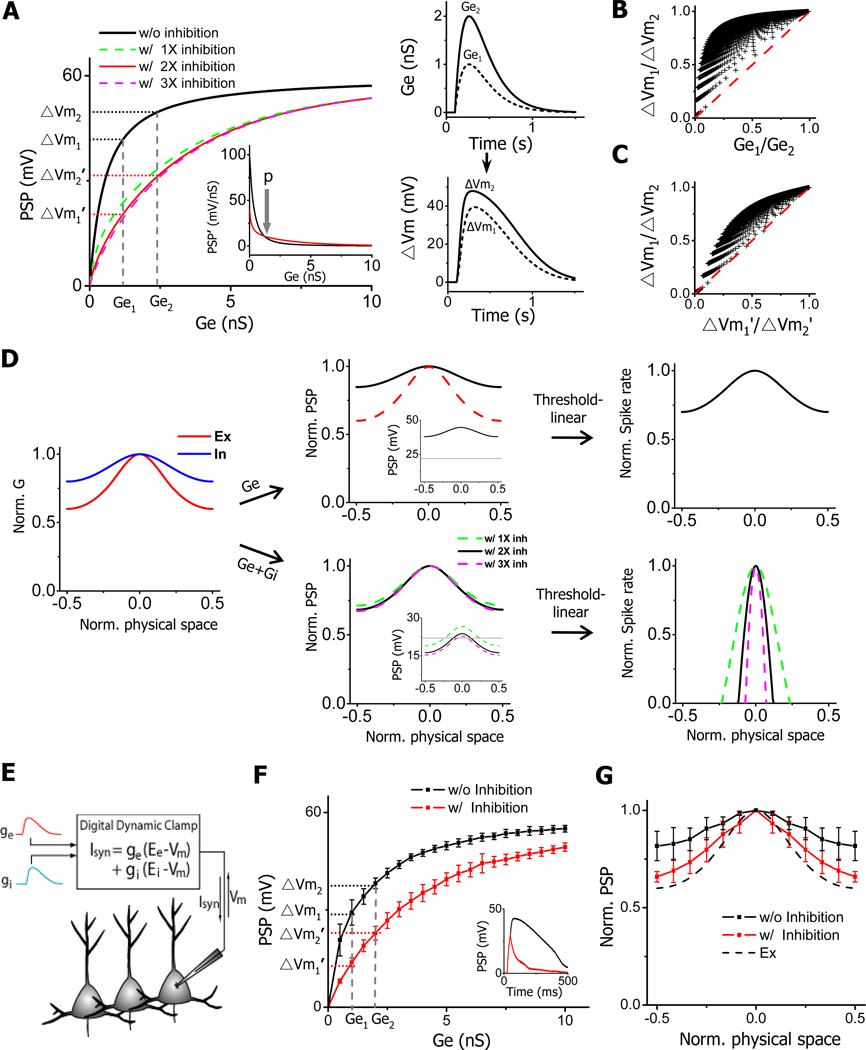
Figure 4. Membrane filtering and inhibitory sharpening of blurred selectivity.

(A) Left, plot of peak amplitude of simulated PSP response vs. that of excitatory conductance (Ge) in two scenarios: without inhibition (black) and with co-variant inhibition (1X, 2X and 3X as strong as excitation). Ge₁ and Ge₂ are the amplitudes of two example excitatory inputs. ΔVm₁ and ΔVm₂, ΔVm₁’ and ΔVm₂’ are the amplitudes of corresponding PSP responses they generated when inhibition is excluded and included respectively. Inset, the first-order derivative of PSP-Ge function with (red, 2X) and without (black) inhibition. “p” (“parallel”) point marks where the two curves intercept. Right, temporal profiles of two model excitatory inputs (1nS and 2nS peak conductance) (top) and their corresponding PSP responses without inhibition (bottom).

(B) The ratio of ΔVm₁/ΔVm₂ is consistently larger than that of Ge₁/Ge₂ (with 2X inhibition). Ge₁ and Ge₂ were sampled from 0.1nS to 10nS with an interval of 0.1nS, with Ge₂ always > Ge₁. The red dash line is the identity line.

(C) The ratio of ΔVm₁/ΔVm₂ is consistently larger than that of ΔVm₁’/ΔVm₂’ (with 2X inhibition, in the range of 0.1–10nS).

(D) Normalized tuning curves of simulated excitatory (red) and inhibitory (blue) inputs (left), of derived PSP responses without (Ge) and with (Ge+Gi) of inhibition (middle), and of derived spike responses (right). Excitation and inhibition evoked by the preferred stimulus is 1.5nS and 3nS respectively. Spike rates were derived according to a threshold-linear scheme. OSIs of the excitatory or inhibitory tunings were taken from the averaged values of our experimental results.

(E) Schematic drawing of the design of dynamic clamp. The instantaneous Vm is sampled. The current injected into the cell (I_syn) is based on Vm and synaptic conductance.

(F) The input-output curve for real cells in dynamic clamp recordings. PSP was measured as the peak amplitude of membrane depolarization in response to the injection of synaptic conductances, which were modeled the same as in (A). Inhibition was twice as strong as excitation. Data were presented as mean ± SD (n = 5 cells). Dashed lines mark injected excitatory conductances at 1nS and 2nS. Inset, example traces of recorded PSP responses in the absence (black) and presence (red) of inhibition (Ge = 2.5nS).

(G) Normalized tuning curves of PSP responses (mean ± SD, n = 6 cells) in the absence (black) and presence (red) of inhibition in dynamic clamp recordings. The tunings of excitation (labeled by dashed curve, Ex) and inhibition were the same as in (D). Excitation and inhibition for the preferred stimulus were 2ns and 4nS respectively. Red data points except for the one at preferred stimulus are all significantly different from black data points (p <0.05, paired t-test).

To test how inhibition sharpens the blurred selectivity, we incorporated in the model an inhibitory input which followed the excitatory input with a temporal delay (50ms) and whose conductance was the same as that of the excitatory input (1X inhibition), or double (2X) or triple (3X) that of the excitatory input. As shown by the colored curves in Figure 4A, the presence of the inhibitory input slows down the saturation of PSP responses, and greatly expands the input dynamic range (Figure S3B), i.e. the range of excitatory input strengths that can be faithfully represented. With this altered input-output function, the ratio between the PSP amplitudes (ΔVm’₁/ΔVm’₂) became much closer to that between the initial input strengths (Ge₁/Ge₂). We also confirmed that over the physiological range of excitatory conductances, ΔVm’₁/ΔVm’₂ was always smaller than ΔVm₁/ΔVm₂ (Figure 4C, Figure S3C), indicating that inhibition effectively ameliorated the attenuation of tuning selectivity caused by the membrane filtering.

To further illustrate the inhibitory effect on OS, we modeled excitatory and inhibitory inputs with their tuning profiles taken from experimental data, and simulated PSP responses resulting from excitatory inputs alone and from integrating excitatory and inhibitory inputs (Figure 4D). Similar as observed earlier (Figure 3D), the PSP tuning was largely flattened when only excitatory inputs were present (Figure 4D, top middle). To derive the tuning of spiking responses, we first used a threshold-linear model (Carandini and Ferster, 2000, see Experimental Procedure). Due to the blurred tuning selectivity of PSP responses which were all suprathreshold (Figure 4D, top middle, inset), the spiking response tuning exhibited only a weak bias with an OSI (=0.18) much lower than observed experimentally (Figure 4D, top right). On the other hand, the presence of inhibition led to a sharper tuning of PSP responses (Figure 4D, bottom middle). In the meantime, inhibition suppressed many responses to off-optimal stimuli below the spike threshold. Together, sharp OS (OSI =1) was created in the spiking response (Figure 4D, bottom right). Using another spike thresholding scheme, power-law, which considers membrane potential fluctuations and trial-to-trial variability (Miller and Troyer, 2002; Priebe and Ferster, 2005), we observed a similar effect of inhibition: it greatly sharpened OS of spiking response (Figure S3D). Depending on the exponent of power-law function, OSI similar to that observed experimentally (0.74 ± 0.21, mean ± SD, n = 24) could be obtained. In our data, the onset delay of inhibition relative to excitation varied (54.3 ± 57.7ms, mean ± SD). By varying this parameter, we found that the larger the temporal separation between inhibition and excitation, the less effect inhibition had on the input-output function and the orientation tuning of PSP response (Figure S3E). Therefore, a large temporal overlap between inhibition and excitation is important for the inhibitory sharpening of OS of output responses. Furthermore, inhibition may not be the only strategy neurons can exploit for sharpening membrane-blurred selectivity. Increasing membrane leakage conductance can achieve a similar effect (Figure S3F).

Excitatory-inhibitory interplay under in vivo dynamic clamp

To examine whether an inhibitory sharpening of PSP tuning could indeed occur in real cells, we carried out dynamic clamp recordings in V1 neurons (Sharp et al., 1993; see Experimental Procedures). The synaptic current injected into the cell was determined based on the instantaneous membrane potential as well as the time-dependent synaptic conductances (Figure 4E). The PSP response was recorded under the condition that spikes were blocked. As shown in Figure 4F (black), the relation between the peak amplitude of membrane depolarization and that of excitatory conductance displayed a saturating curve, similar as that in Figure 4A. Injecting inhibitory conductance lowered the level of depolarization and prevented its fast saturation (Figure 4F, red). Under such input-output function, a better selectivity (i.e. ΔVm’₁/ΔVm’₂ < ΔVm₁/ΔVm₂) would be achieved. We next injected synaptic condunctances with tuning profiles the same as in Figure 4D. As expected, a significantly sharper tuning selectivity was observed in the PSP response when inhibitory conductance was co-injected (Figure 4G). These results in real cells further support the conclusion that broadly-tuned and temporally interacting inhibition can be an effective strategy for sharpening tuning selectivity blurred by the membrane filtering.

Discussion

In this study, we have measured orientation tunings of excitation and inhibition for simple cells in the mouse visual cortex, and determined the role of inhibition in the establishment of OS. We found that excitation is broadly tuned with a mild bias for a preferred orientation. Inhibition, sharing the same preferred orientation, is even more broadly tuned than excitation. By closely interacting with excitation, inhibition ameliorates the membrane blurring of excitatory selectivity, or in another word sharpens the blurred selectivity. This “blur-sharpening” is achieved through expanding the input dynamic range and lowering the membrane potential response at orthogonal orientation more than that at preferred orientation. Such reshaping of membrane potential tuning leads to a more effective “tip of the iceberg” effect. Thus, in mouse simple cells, weakly biased excitation determines the orientation preference, while sharp OS is a result emerging from combined interactions between excitation, inhibition and intrinsic membrane properties, for which inhibition plays an indispensable role.

Species difference in synaptic circuitry mechanism underlying simple-cell OS

Although simple cells in the mouse V1 exhibit several functional properties similar to those of cat simple cells, such as spatially segregated On/Off spiking subfields and sharp orientation selectivity, at the level of synaptic inputs they have distinct differences. First, in cat simple cells, excitatory and inhibitory subfields are organized in a “push-pull” or spatially opponent manner (Ferster, 1988; Hirsch et al., 1998; Anderson et al., 2000; Priebe and Ferster, 2005). On the other hand, mouse simple cells have largely overlapped but only slightly displaced excitatory and inhibitory subfields (Liu et al., 2010). Second, the temporal relationship between excitation and inhibition observed in this study differs from that reported for cat simple cells. In cat simple cells, a drifting bar or grating of preferred orientation activates excitation and inhibition sequentially, i.e. excitation and inhibition are temporally out of phase (Ferster, 1988; Anderson et al., 2000; Priebe and Ferster, 2005), which is consistent with their spatial opponency. In contrast, in mouse simple cells we observed that bars of preferred orientation evoke temporally overlapping excitation and inhibition (Figure 3A), consistent with their large spatial overlap. Third, the synaptic tuning profiles are different. In cat simple cells, excitation and inhibition are both well tuned with zero or small conductances at orthogonal orientation, and inhibition has the same tuning width as excitation (Anderson et al., 2000). Inhibition is proposed not to have a significant impact on OS, and spike threshold alone is thought to be sufficient for generating sharp OS (Anderson et al., 2000; Carandini and Ferster, 2000). In mouse simple cells, excitation and inhibition are both broadly tuned, and inhibition is significantly more broadly tuned than excitation. The extremely broad inhibitory tuning is in fact consistent with the functional properties of inhibitory neurons in the mouse V1, which have been shown to be mostly untuned or only weakly tuned for orientation (Sohya et al., 2007; Niell and Stryker, 2008; Liu et al., 2009; Kerlin et al., 2010; Ma et al., 2010; but see Runyan et al., 2010). The close temporal interaction between excitation and inhibition at all orientations allows inhibition to significantly affect the tuning of membrane potential responses. These differences in excitatory-inhibitory interplay point to a potential species difference in circuitry mechanism underlying simple-cell OS.

The species dependence is further evidenced by differences in cortical organization between cat and mouse V1. First, in the cat V1, simple cells are found in thalamocortical recipient layers (layer 4 and 6, Hirsch and Martinez, 2006) and the spatial arrangement of feedforward thalamic inputs is important for the establishment of OS. In the mouse V1, neurons in layer 4 are mostly monocontrast and simple cells primarily appear in layer 2/3 (Liu et al., 2009). OS of simple cells we recorded likely results from integrating recurrent inputs from layer 2/3 and feedforward inputs from layer 4 (Dantzker and Callaway, 2000; Mooser et al., 2004), some of which may already be orientation tuned (Niell and Stryker, 2008; Ma et al., 2010). Second, there is a columnar organization of OS in the cat V1, whereas in the mouse V1 neurons preferring different orientations are intermingled in a “salt-and-pepper” fashion (Ohki et al., 2005). It has been shown that patterns of synaptic inputs to cat V1 neurons vary depending on the cell’s location in the orientation map (Schummers et al., 2002; Mariño et al., 2005). Within the orientation domain, the neuron receives intracortical inputs from other cells sharing the same orientation preference, whereas at pinwheel centers the intracortical inputs are from cells with a wide range of different orientation preferences. Therefore, both excitation and inhibition are much more broadly tuned at pinwheel centers than within orientation domains (Mariño et al., 2005, note that the simple or complex cell type was not explicitly identified in this study). In comparison, synaptic inputs to our recorded cells exhibited less selectivity than those to cat cells within orientation domains. This observation is consistent with a lack of orientation maps in the mouse V1 and the result that local synaptic inputs to the layer 2/3 neuron have a wide variety of orientation preferences (Jia et al., 2010). A more careful comparison indicates that excitatory inputs to mouse simple cells are more selective than those to cat cells at pinwheel centers, implying that synaptic connections to mouse simple cells might be slightly more selective than cat cells at pinwheel centers.

Expansion of input dynamic range by inhibition underlies OS

Our study demonstrates two effects that significantly impact OS. The first one is the membrane blurring of selectivity when PSP responses are generated from excitatory inputs alone. This is due to a saturation of PSP response with increasing excitatory input strength, caused by a rapid reduction in the excitatory driving force as the depolarizing potential approaches the reversal potential for excitatory currents. For relatively small excitatory conductances, the membrane blurring would be less a problem, since the initial phase of the input-output curve can be approximated by a linear function crossing the origin, i.e. f(x) = ax. The blurring effect becomes much more detrimental when excitatory conductances fall into the saturating phase of the input-output curve (Figure 4A), because the relative difference in excitatory input strength can not be reflected by that in the level of PSP response. In such a case, any mechanism that prevents the fast saturation would be helpful to preserve the original selectivity conveyed by the weakly biased excitatory inputs. The inhibitory sharpening, the second effect observed in this study, exactly serves this purpose. Our modeling and experiments demonstrate that inhibition flattens the input-output curve, likely by counteracting excitation and increasing membrane conductance. This leads to an expansion of the input dynamic range, which allows a more linear transformation of strong excitatory inputs. Our results on the inhibitory effect and the effect of increasing membrane leakage (Figure S3F) are to some degree consistent with previous proposals that inhibition and in general membrane conductance increase can reduce the gain of input-output transformation (Chance et al., 2002; Fellous et al., 2003; Mitchell and Silver, 2003; Silver, 2010; Murphy and Miller, 2003; Prescott and De Koninck, 2003; but see Holt and Koch, 1997). The expansion of dynamic coding range operated at the single-cell level is reminiscent of a recent proposal at the network level that global feedfoward inhibition can increase the dynamic range of cortical operation (Pouille et al., 2009).

Phases of input-output function and different inhibitory mechanisms

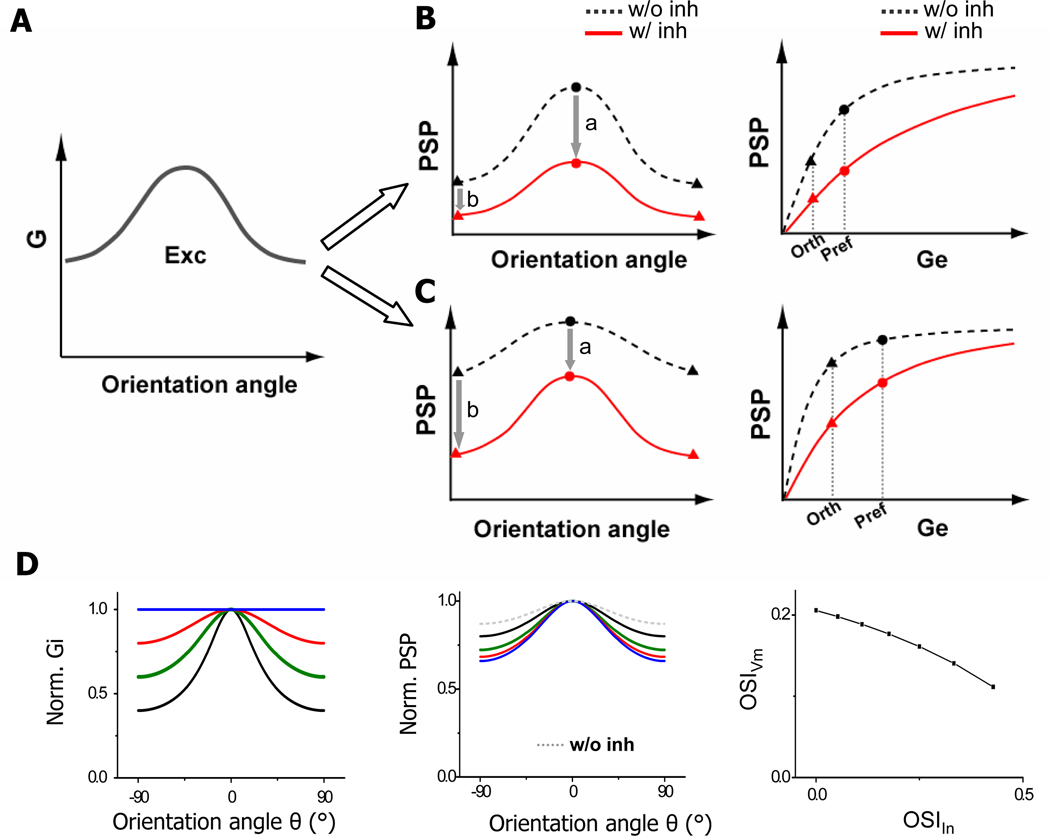
The inhibitory effect observed in this study is different from a commonly proposed normalization model, which was often used to explain the “iceberg” effect. The model is based on a matching of tuning selectivity between excitation and inhibition, which has been observed widely in sensory cortices (Monier et al., 2003; Mariño et al., 2005; Zhang et al., 2003; Wehr and Zador, 2003; Tan et al., 2004; Okun and Lampl, 2008; Tan and Wehr, 2009; but see Wu et al., 2008; Poo and Isaacson, 2009 for a more broadly tuned inhibition). It proposes that inhibition scales down the membrane potential tuning by reducing responses in a divisive manner (Carandini and Heeger, 1994; Murphy and Miller, 2003; Wehr and Zador, 2003; Katzner et al., 2011). Such operation does not alter the tuning shape or selectivity of membrane potential responses per se. Considering that OSI is expressed by (R_pref – R_orth) / (R_pref + R_orth), with R_pref and R_orth representing the responses at preferred and orthogonal orientations respectively, if R_pref and R_orth are divided by the same factor, OSI will remain the same. The normalization model does increase the sharpness of spiking responses by elevating the effective spike threshold. In this study, however, we do observe that inhibition causes a change in tuning shape and an increase in OSI. This is due to an increase of (R_pref – R_orth) and a concomitant decrease of (R_pref + R_orth), together leading to a more effective enhancement of tuning selectivity.

The normalization effect and the “blur-sharpening” effect in fact can be accounted for by excitatory conductances falling into difference phases of the input-output curve. For simplicity, here we consider the scenario that inhibition is covariant or exquisitely balanced with excitation. The input-output curve can be divided into two phases, separated by the point where the PSP’ functions with and without inhibition intercept (the “p” point, Figure 4A inset). In the first phase, the rising of PSP is faster in the absence than presence of inhibition, so that inhibition suppresses the PSP response at preferred orientation more than that at orthogonal orientation (a > b; Figure 5B). The PSP tuning would appear scaled down by inhibition, similar as in the normalization model. In the second phase, the growth of PSP is slower in the absence than presence of inhibition, so that inhibition suppresses the response at orthogonal orientation more than that at preferred orientation (a < b; Figure 5C). Such “supralinear” effect can lead to a sharper “tip of the iceberg” and a more effective thresholding effect. It is also possible that excitatory inputs occur around the “p” point, so that the suppression of PSP is about equal at preferred vs. orthogonal orientation, resulting in an apparent subtraction of the tuning curve. In this case, OSI is still improved, since (R_pref + R_orth) becomes smaller while (R_pref – R_orth) is unchanged.

Figure 5. Models of inhibitory mechanisms underlying OS.

(A) Schematic drawing of the tuning curve of excitatory conductance, with conductance at orthogonal orientation about half of that at preferred orientation.

(B) Left, the tunings of PSP response in the absence (black) and presence of inhibition (red). Circles and triangles label the PSP responses at preferred and orthogonal orientations respectively. “a” and “b” mark the suppression of the PSP response at preferred and orthogonal orientations respectively. Right, input-output function in the absence (black) and presence (red) of inhibition. Excitatory conductances at orthogonal and preferred orientations and their corresponding PSP responses are marked by dotted lines. Excitatory conductances fall into the initial phase of the input-output curve which could be approximated by a linear function f(x) = ax.

(C) Similar plot as in (B) except that excitatory conductances fall into a more saturating phase of the input-output curve.

(D) Left, the excitatory tuning (green curve) is fixed while varying the inhibitory tuning. Blue, untuned inhibition; red, broader inhibition; green, co-tuned inhibition, black, narrower inhibition. Middle, the corresponding PSP tuning curves. Dotted curve marks the PSP tuning in the absence of inhibition. Right, OSI of PSP responses vs. that of inhibitory inputs, with the excitatory tuning fixed.

Additional implications of broader inhibition

While exquisitely balanced inhibition can already achieve a sharpening of PSP tuning through increasing input dynamic range (Figure 4A, Figure 5C), inhibition being more broadly tuned than excitation is more advantageous since it can further suppress the PSP response at orthogonal orientation. We simulated orientation tuning of PSP responses with a fixed excitatory tuning while varying the tuning strength of inhibition. As shown in Figure 5D, as the tuning strength of inhibition is reduced, the sharpening effect on the PSP tuning is enhanced. This may have important implications on achieving contrast invariance of OS (Sclar and Freeman, 1982; Alitto and Usrey, 2004; Niell and Stryker, 2008). If inhibition is always exquisitely balanced with excitation, contrast invariance is difficult to be achieved. This is because as the input strength monotonically increases with the increase of contrast, the PSP response at orthogonal orientation would eventually cross the spike threshold (see Figure 4A). By reducing its tuning strength, inhibition can exert a larger suppression on the response at orthogonal orientation, keeping it below the spike threshold. Previously, theoretical models exploiting cortical inhibitory interactions more broadly tuned than excitatory interactions have successfully generated sharp OS at various contrasts in the cortical networks (Somers et al., 1995; Ben-Yishai et al., 1995). In particular, a recent model of cat simple-cell responses proposes that an untuned inhibitory component arising from complex inhibitory neurons is necessary for achieving contrast invariant OS (Lauritzen and Miller, 2003). Nonetheless, inhibition broader than excitation has not been observed in intracellular recordings in cat visual cortex (Anderson et al., 2000; Monier et al., 2003; Mariño et al., 2005). Here, having found nearly untuned inhibition, we postulate that a contrast-dependent modulation of inhibitory tuning strength is employed by mouse simple cells to achieve contrast invariance of OS. This hypothesis will be tested in future experiments.

Experimental Procedures

Animal preparation

All experimental procedures used in this study were approved by the Animal Care and Use Committee of USC. Female adult mice (12–16 weeks, C57BL/6) were anesthetized with urethane (1.2 g/kg) and sedative chlorprothixene (0.05 ml of 4 mg/ml), and surgical procedure was performed as previously described (Niell and Stryker, 2008; Liu et al., 2009; Liu et al., 2010). Throughout the surgical procedure, the lids were sutured. After surgery, right eyelid was reopened and drops of 30k silicone oil were applied to prevent eye drying. The eye movement and the RF drift of single units were negligible within the time windows of recordings (Mangini and Pearlman, 1980; Liu et al., 2010).

In vivo whole-cell current-clamp and voltage-clamp recording and loose-patch recording

Whole-cell recordings were performed with an Axopatch 200B (Molecular Devices) according to previous studies (Moore and Nelson, 1998; Zhang et al., 2003; Liu et al., 2010). The patch pipette had a tip opening of ~2 µm (4 – 6 MΩ). The Cs⁺-based intrapipette solution contained (in mM) 125 Cs-gluconate, 5 TEA-Cl, 4 MgATP, 0.3 GTP, 8 phosphocreatine, 10 HEPES, 10 EGTA, 2 CsCl, 1 QX-314, 0.75 MK-801, pH 7.25. And K⁺-based intrapipette solution contained (in mM) 130 K-gluconate, 2 KCl, 1 CaCl₂, 4 MgATP, 0.3 GTP, 8 phosphocreatine, 10 HEPES, 11 EGTA, pH 7.25. The pipette capacitance, whole-cell capacitance were compensated completely, and series resistance (25–50 MΩ) was compensated by 50%–60% (100µs lag). A 11 mV junction potential was corrected. Only neurons with relatively stable series resistance (less than 15% change during recording) were used for further analysis. Our whole-cell recording method biases sampling towards pyramidal neurons (Wu et al., 2008; Liu et al., 2010). For loose-patch recordings, glass electrodes with the same opening size containing ACSF were used. Instead of a gigaohm seal, a 100–250 MΩ seal was formed on the targeted neuron. All the neurons recorded under this condition showed regular-spike property, consistent with sampling bias towards excitatory neurons. The pipette capacitance was completely compensated. All neurons recorded in this study were located at a depth of 220–350µm below the pia according to the microdrive reading, corresponding to layer 2/3.

Visual stimulation

Softwares for data acquisition and visual stimulation were custom-developed with Lab VIEW (National Instrument) and MATLAB (Mathworks) respectively. Visual stimuli were provided by a 34.5 × 25.9 cm monitor (refresh rate 120 Hz, mean luminance ~10 cd/m²) placed 0.25 m away from the right eye (Liu et al., 2010). The center of monitor was placed at 45° Azimuth, 0° Elevation⁴⁰, and it covered ±35° horizontally and ±27° vertically of the mouse visual field. To map spatial RF, a set of bright and dark squares within an 11×11 grid (grid size 3 – 5°) or a set of bright and dark bars (3 – 3.5°) at optimal and orthogonal orientations were flashed individually (duration = 200 ms, inter-stimulus-interval = 240 ms) in a pseudo-random sequence. For 2-D mapping of spike RFs, each location was stimulated for ≥ 5 times; for 1-D mapping of membrane potential and synaptic RFs, each location was stimulated for 10 times. The same number of On and Off stimuli were applied. The On and Off subfields were derived from responses to the onset of bright and dark stimuli respectively. To measure orientation tuning, two types of oriented stimuli were used: drifting sinusoidal gratings (2Hz, 0.04cycle/°, contrast 40%) or drifting bars (4° width, 60° length, 50°/s speed, contrast 40%) of 12 directions (30° step). For drifting sinusoidal gratings, stationary grating of one orientation was first presented on the full screen for 1.8 sec before it drifted for 1.5 sec. The grating stopped drifting for 500ms before another grating pattern appeared. Drifting bars were moved across the screen with an inter-stimulus interval of 1.5 sec. The twelve patterns were presented in a random sequence, and were repeated for 5–10 times. Orientation preference tested with sinusoidal gratings was similar to that tested with single bars (Figure S2A, also see Niell and Stryker, 2008).

Data analysis

Spikes were sorted offline after loose-patch recordings. Spikes evoked by flashing stimuli were counted within a 70–270 ms time window after the onset of the stimulus. Spikes evoked by drifting gratings were counted within a 70–2000ms window after the start of drifting. The baseline firing rate was subtracted from stimulus-evoked spike rates. Responses with peak firing rates exceeding three standard deviation of the baseline activity were considered as significant. The averaged firing rates were used to plot RF maps, which were smoothed with bilinear interpolation. In current-clamp recordings with the K⁺ gluconate-based intrapipette solution, subthreshold V_m responses were analyzed after removing spikes with a 8ms median filter (Carandini and Ferster, 2000). Simple cells were identified by overlap index (OI) of spike response < 0.3 or OI of membrane potential response < 0.71 according to previous criteria (Liu et al., 2009; Liu et al., 2010).

In voltage-clamp recordings, excitatory and inhibitory synaptic conductances were derived according to the following equation (Wehr and Zador 2003; Tan et al., 2004; Liu et al., 2007; Wu et al., 2008).

$$I\mathit{(}t\mathit{)}=G_r\mathit{(}V\mathit{(}t\mathit{)}-E_r\mathit{)}+G_e\mathit{(}t\mathit{)}\mathit{(}V\mathit{(}t\mathit{)}-E_e\mathit{)}+G_i\mathit{(}t)\mathit{(}V\mathit{(}t\mathit{)}-E_i\mathit{)}.$$

I(t) is the amplitude of current at any time point; G_r and E_r are the resting leak conductance and resting membrane potential respectively; G_e and G_i are the excitatory and inhibitory synaptic conductance respectively; V(t) is the membrane voltage, and E_e (0 mV) and E_i (−70 mV) are the reversal potentials. V(t) is corrected by V(t) = V_h – R_s*I(t), where R_s was the effective series resistance and V_h is the applied holding voltage.

Membrane potential responses were derived using a single-compartment neuron model (Somers et al., 1995; Troyer et al., 1998; Liu et al., 2010):

$$V_m(t+dt)=-\frac{dt}{C}[G_e(t)*(V_m(t)-E_e)+G_i(t)*(V_m(t)-E_i)+G_r(V_m(t)-E_r)]+V_m(t)$$

where V_m(t) is the membrane potential at time t, C the whole-cell capacitance, G_r the resting leak conductance, E_r the resting membrane potential (−60mV). C was measured during experiments and G_r was calculated based on the equation G_r = C*G_m/C_m, where G_m, the specific membrane conductance is 1e–5 S/cm², and C_m, the specific membrane capacitance is 1e–6 F/cm². To estimate spiking responses, the spike threshold was set at 22mV above the resting membrane potential. After each spike, membrane potential was returned to 10mV above the resting level for a refractory period of 5ms.

To quantify the strength of orientation selectivity, the responses to drifting sinusoidal gratings or bars of two directions at each orientation were averaged to obtain the orientation tuning curve between 0–180 degrees, which was then fit with a Gaussian function R(θ)=A*exp(−0.5*( θ-φ)²/ σ²)+B. φ is the preferred orientation and σ controls the tuning width. For inhibitory responses, when the tuning curve was too flat to be fitted with a Gaussian function, σ was arbitrarily set as 100°. The orientation selectivity index (OSI) is defined as (R_pref − R_orth)/(R_pref + R_orth) = A/(A+2*B), where R_pref is the response level at the angle of υ, and R_orth is that at the angle of υ+90°.

Modelling

A simple model was built with a neuron receiving both excitatory and inhibitory synaptic inputs. Synaptic conductance was simulated as:

$$G=G_{\text{max}}*(1-\text{exp}(-(t-t_0)/{\tau }_1))*\text{exp}(-(t-t_0)/{\tau }_2,\text{for}t>t_0$$

in which t₀ is the onset time, and τ₁ = 2.8s and τ₂ = 0.17s for both excitatory and inhibitory conductances (Figure 4A). The onset of the inhibitory response was set at 50ms after that of the excitatory response. Membrane potentials were derived similarly as described above from the simulated synaptic conductances. For Figure 4A, the peak conductance of excitation varied from 0.01 to 10 nS. Inhibition was as strong as, twice as strong as, or three times as strong as excitation. For Figure 4D, the tuning curves were based on average experimental data, and the maximum excitatory conductance was 1.5nS. To derive the tuning curve for spiking responses, a threshold-and-linear transformation (Carandini and Ferster, 2000) was used to derive peak firing rate, which was proportional to the peak depolarizing potential subtracting the spike threshold (22mV). A power-law spike thresholding scheme (Miller and Troyer, 2002; Priebe and Ferster, 2008) was applied as:

$$R(V_m)=k{[V_m-V_{\mathit{\text{rest}}}]}_{+}^P$$

R is the firing rate, k is the gain factor (set as 9e5 to obtain experimentally observed firing rates), p (=2, 3, or 5) is the exponent. The “+” indicates rectification, i.e. the values below zero are set as zero.

Dynamic clamp

Dynamic clamp recordings were carried out according to (Sharp et al., 1993; Chance et al., 2002; Nagtegaal and Borst, 2010). The current injected in dynamic clamp was calculated on-line by a custom-written LabVIEW routine and controlled by National Instrument Interface:

$$\begin{array}{c}I(t)=G_e(t)*(V_m(t)-E_e),\text{without inhibition};\hfill \\ I(t)=G_e(t)*(V_m(t)-E_e)+G_i(t)*(V_m(t)-E_i),\text{with inhibition};\hfill \end{array}$$

The time-dependent G_e and G_i were generated by the computer according to the same function as shown above, and the difference in onset delay between excitation and inhibition was set as 50ms. E_e and E_i were set as 0mV and −70mV respectively. The membrane potential V_m was sampled at 5kHz. Measurements of V_m were corrected off-line for the voltage drop on the uncompensated, residual series resistance (15–20MΩ). The corrected V_m was only slightly different from the recorded V_m (data not shown).