Motor cortical prediction of EMG: evidence that a kinetic brain-machine interface may be robust across altered movement dynamics

Abstract

During typical movements, signals related to both the kinematics and kinetics of movement are mutually correlated, and each is correlated to some extent with the discharge of neurons in the primary motor cortex (M1). However, it is well known, if not always appreciated, that causality cannot be inferred from correlations. Although these mutual correlations persist, their nature changes with changing postural or dynamical conditions. Under changing conditions, only signals directly controlled by M1 can be expected to maintain a stable relationship with its discharge. If one were to rely on noncausal correlations for a brain-machine interface, its generalization across conditions would likely suffer. We examined this effect, using multielectrode recordings in M1 as input to linear decoders of both end point kinematics (position and velocity) and proximal limb myoelectric signals (EMG) during reaching. We tested these decoders across tasks that altered either the posture of the limb or the end point forces encountered during movement. Within any given task, the accuracy of the kinematic predictions tended to be somewhat better than the EMG predictions. However, when we used the decoders developed under one task condition to predict the signals recorded under different postural or dynamical conditions, only the EMG decoders consistently generalized well. Our results support the view that M1 discharge is more closely related to kinetic variables like EMG than it is to limb kinematics. These results suggest that brain-machine interface applications using M1 to control kinetic variables may prove to be more successful than the more standard kinematic approach.

reaching is a deceptively simple action. We are typically aware only of the relatively straight, smoothly accelerating movement of the hand toward a target. However, even in the absence of external perturbations, reaching requires the nervous system to execute a complex sequence of muscle activations. Movement control can be viewed from a hierarchical perspective in which the extrinsic kinematic command (the desired straight hand path) is transformed into a sequence of joint rotations, joint torques, and finally the necessary patterns of muscle activity that ultimately produce the motion (Atkeson 1989; Hollerbach 1982; Kawato 1999; Kawato et al. 1987; Shadmehr and Mussa-Ivaldi 1994). Whether this sequence actually evolves as a series of discrete operations within the brain or as a more continuous process is very much an open question (Kalaska and Crammond 1992).

The role of primary motor cortex (M1) within this transformation has been the topic of numerous experimental and theoretical studies. While correlations exist between M1 and both kinematic and kinetic signals, it is not clear which, if any, may represent the “true” signal type encoded by M1. Experimentally, numerous attempts have been made to dissociate kinematic and kinetic signals by adding loads to the limb (Evarts 1968; Fagg et al. 2009; Gandolfo et al. 2000; Gribble and Scott 2002; Kalaska et al. 1989) or by changing the posture of the limb to alter its mechanics (Caminiti et al. 1990; Kakei et al. 1999; Morrow et al. 2007; Scott and Kalaska 1997). Taken together, these studies indicate that the discharge of many, but not all, M1 neurons is influenced by posture and external load. There is anatomic evidence that the proportion of neurons with these musclelike properties may increase with proximity to the central sulcus (Johnson et al. 1996; Rathelot and Strick 2006). As such, M1 is now generally viewed as a heterogeneous structure, involved in the coding of both kinematics and kinetics, and perhaps also in the transformation of these commands (Kakei et al. 2001; Kalaska et al. 1989; Shen and Alexander 1997; Thach 1978).

In the last decade, research has moved from an interest in the basic scientific questions addressing the nature of the movement-related information within M1 to include the application of this information to the development of the brain-machine interface (BMI). Following dramatic developments in electrode and computational technology, it has become possible to use kinematic information extracted in real time from M1 in monkeys and even humans for closed-loop control of the movement of computer cursors or robotic devices (Carmena et al. 2003; Chapin et al. 1999; Ganguly and Carmena 2009; Hochberg et al. 2006; Serruya et al. 2002; Taylor et al. 2002; Velliste et al. 2008). In parallel, a small number of groups have begun to develop BMI applications based on the control of kinetic variables. One group found accuracy in joint torque predictions that was nearly comparable to kinematic predictions during planar reaching (Fagg et al. 2009). Another study achieved predictions of electromyogram (EMG) activity that were of similar or greater accuracy than those typical of kinematic studies (Pohlmeyer et al. 2007b). Similar muscle activity predictions have been used as inputs to a forward dynamical model of the limb to provide both joint torque and kinematics predictions (Kim et al. 2007). This “muscle activation method” yielded kinematic predictions that generalized better across viscous fields than did linear kinematic models.

There have also been several attempts to use these predicted kinetic signals for closed loop control. One such example was the control of both end point position and the force exerted by a gripper (Carmena et al. 2003). BMIs are also under development that could restore voluntary limb movement to a spinal cord-injured patient. Muscle activity (EMG) predictions have been used to control muscles directly via electrical stimulation to produce isometric torque about the wrist (Moritz et al. 2008; Pohlmeyer et al. 2007a, 2009). More recently, a similar approach was used to restore the ability to grasp objects (Oby et al. 2010). To implement these increasingly disparate BMI applications, a control system must be developed that can function in a variety of tasks. Understanding which output variables are causally related to M1 discharge might allow more robust generalization of BMIs across varied dynamical conditions.

In two experiments, we used either altered posture or mechanical loading to change the relationship between hand kinematics and muscle activation during planar reaching movements. We tested the ability of BMI decoders to generalize across these altered conditions. Using multielectrode techniques, we recorded a population of M1 neurons and constructed an optimal set of linear filters between M1 activity and either EMG or hand movement (position and velocity). Predictions from both types of decoders were reasonably accurate within any given task. However, the across-task performance of the EMG decoder was significantly better than that of either kinematic decoder, suggesting a stronger causal link between M1 discharge and muscle activations. These results reinforce several earlier studies demonstrating the predominance of kinetic movement representation within M1. They also have practical implications for development of BMIs designed to be robust against varied movement conditions.

METHODS

Tasks and training.

Two monkeys (A and F) were trained on a random target task. Each monkey sat in a primate chair with its upper arm and forearm supported largely in a horizontal plane, grasping the handle of a two-link planar manipulandum that moved within a 20-cm by 20-cm workspace. Handle position was displayed on a computer screen in front of the monkey as a circular cursor, ∼1 cm in diameter, together with a 2-cm-square target that could appear at any location on the screen. The monkey had either 0.85 s (workspace experiment, described below) or 1.10 s (force field experiment) to move the cursor into each target. Immediately after the monkey acquired one target, the next was presented in a random location. After successfully acquiring three targets, the monkey received a fluid reward. After a short intertrial interval of 1.75–2.00 s, the monkey was presented with the next sequence of targets. This design encouraged the monkey to move as fast as possible. There were typically no pauses in movement during the three-target sequence.

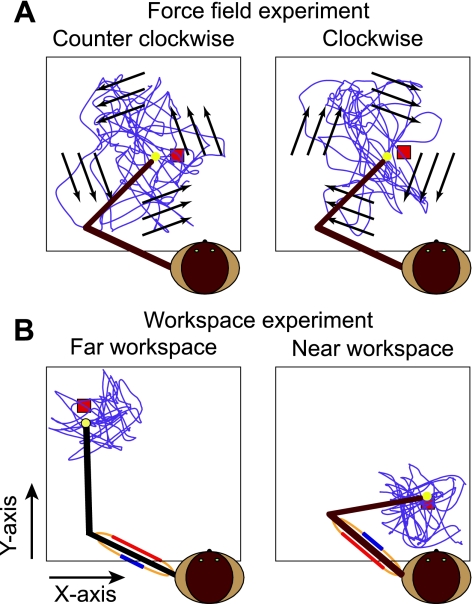
We studied the signals encoded by M1 discharge during two different experiments, one in which we added two different nonlinear viscous force fields to the handle during movements that spanned the entire workspace (Fig. 1A) and the other in which the monkey's movements were restricted to two different quadrants of the workspace (Fig. 1B). In the force field experiment, force was applied at the handle by torque motors acting at the elbow and shoulder joints of the manipulandum. The magnitude of the force was proportional to the hand speed (β = 0.07 Ns/cm), in a direction either 45° clockwise (CW) or 80° counterclockwise (CCW) to movement direction. These angles were chosen because of practical limitations of the hardware. We avoided using force fields orientated 90° from the direction of motion, as the handle tended to become unstable. The force field experiment was adapted from similar work of Li and colleagues (Li et al. 2001).

Fig. 1.

Schematic representation of the force field and workspace experiments. A: counterclockwise (CCW) and clockwise (CW) fields. Purple curve represents a typical 200-s hand path. Arrows represent the orientation of the fields. B: workspace experiment. Movements were made in the absence of any external force field but were confined to 1 of 2 smaller workspaces.

In the workspace experiment (Fig. 1B), targets were presented in two distinct workspaces, each 10 cm by 10 cm in size. The “far” workspace was distant from the monkey's body and ipsilateral to the hand used to grasp the handle. In this workspace, the triceps and posterior deltoid were relatively short, while the biceps and anterior deltoid were long. The “near” workspace was contralateral to the arm and closer to the animal's body, effectively reversing the muscle length biases.

Surgery.

Once a monkey was able to perform both experiments satisfactorily and switch readily between them, we performed surgery to implant a 100-electrode intracortical array (Blackrock Microsystems). We made a craniotomy centered above the arm area of M1, ∼15 mm from the midline and 14 mm anterior of the intra-aural line. After opening the dura we stimulated (50 Hz, 100-μs pulse width, <4 mA) within the crown of the precentral gyrus just medial to the spur of the arcuate sulcus, using a ball electrode. We selected the location that elicited proximal arm movement and inserted the array with a pneumatic inserter. A piece of artificial pericardium (Preclude ePTFE membrane, Gore and Associates) was placed over the array to prevent the array from adhering to the dura. The dura was then closed over the pericardium, and another piece of Preclude was placed over the dura. The original bone flap was replaced, and the skin was closed over the craniotomy. We implanted and recorded from both hemispheres of monkey F (designated data sets F_R and F_L), and the left hemisphere of monkey A.

In a separate surgical procedure performed 30–45 days later, we implanted epimysial electrodes on various muscles of the shoulder and arm. We identified muscles intraoperatively with reference to photographs of previous dissections and by observing the twitches produced by electrical stimulation (30 Hz, 200-μs pulse width, 2–20 V). The electrodes were sutured to the fascia of the muscle belly and the leads routed subcutaneously to a connector in the monkey's back. Across three different implants, we studied the following muscles: clavicular head of pectoralis, latissimus dorsi, anterior deltoid, medial deltoid, posterior deltoid, biceps, lateral head of triceps, long head of triceps, and brachioradialis. All surgery was performed under aseptic conditions, and all surgical and experimental procedures were approved by the Institutional Animal Care and Use Committee of Northwestern University.

Data acquisition and recording.

After recovery from the second surgical procedure, experiments began when each monkey was able to perform at least 300 of the 3-movement sequences correctly. A typical session required 40–60 min and averaged 1,500–2,000 target acquisitions. Signals from the neuronal array were examined, and spikes were saved if the signal-to-noise ratio was at least 3:1. Both single and multiunit signals were used in subsequent analyses. Kinematic and EMG signals were sampled at 2 kHz. We digitally rectified and then filtered the EMG data, using a 4-pole, 20-Hz, low-pass Butterworth filter to obtain the envelope of each signal. We filtered the kinematic data, using the same filter parameters as the EMG data, and all signals were then subsampled at 100 Hz. In each experimental session we recorded at least 10 min of data under one condition (the far workspace or CCW force field), followed by 10 min in the second condition (the near workspace or CW field). If possible, depending upon the motivation of the monkey, we ended the experimental session with a repetition of the first task.

Data analysis.

To quantify the effect of the force fields, we calculated EMG tuning curves. We parsed individual movements from the random-target task, and classified them into 45°-wide bins according to their direction. We measured the mean activity during each movement in a 200-ms window centered 50 ms before movement onset and plotted this average as a function of direction. The vector sum of the activity in the eight directions determined the muscle's preferred direction (PD). We used a bootstrapping procedure to estimate the uncertainty of these PDs. In brief, we randomly resampled the binned data 1,000 times, with replacement, and recomputed the tuning curves and PD from each sample. We calculated the 95% confidence bound on the direction of the PD vector from the resulting distribution (Davison and Hinkley 1997; Efron and Tibshirani 1997).

We constructed multiple-input, single-output decoders consisting of a set of optimal linear filters between the firing rate of the M1 neurons and each of the output variables (hand kinematics and EMG signals). We used a least squares regression method to compute a linear filter that minimized the error between the output of the decoder and the measured output (Pohlmeyer et al. 2007b). The filters were 50 points long, thereby providing a weighted average of the discharge rates in 10-ms bins up to 500 ms in the past. These decoders were tested by N-fold cross validation in which data were divided into N 1-min segments (folds). A given decoder was built with N − 1 folds and tested on the remaining fold. We determined the within-task prediction performance for any given experimental condition by computing the mean coefficient of determination (R²) between the predicted and the measured outputs across the N test folds.

To determine how well each decoder generalized across tasks, we trained decoders using all of the data from one experimental condition (task A) and used this decoder to predict the individual folds from the second condition (task B). We repeated this procedure, using the data from task B to predict task A. Finally, we computed the “percent generalization,” a ratio that related the performance across tasks to that within task by normalizing the across-task R² (R_A²) to the corresponding within-task R² (R_W²)

$$\%{\text{Gen}}_{R^2}=\frac{R_{\text{A}}^2}{R_{\text{W}}^2}$$ (1)

We eliminated from consideration the data from any fold in which either R² was >5 standard deviations from the mean. This procedure was particularly important in preventing large ratios caused by uncharacteristically small R² values in the denominator.

R² is useful because it is sensitive only to the modulation of the signals independent of their scale. This allows comparisons between the predictions of signals that are measured in different units. However, this characteristic makes R² insensitive to errors in either the gain or offset between the actual data and the prediction. To address this limitation, we also computed percent generalization based on mean squared error (MSE). While MSE itself is not unitless, the ratio is, yet it is still sensitive to gain and offset errors. In order that this metric (like the one based on R²) be an increasing function of the quality of generalization, we computed it as:

$$\%{\text{Gen}}_{\text{MSE}}=\frac{{\text{MSE}}_{\text{W}}}{{\text{MSE}}_{\text{A}}}$$ (2)

RESULTS

Effect of force fields on muscle activation and movement kinematics.

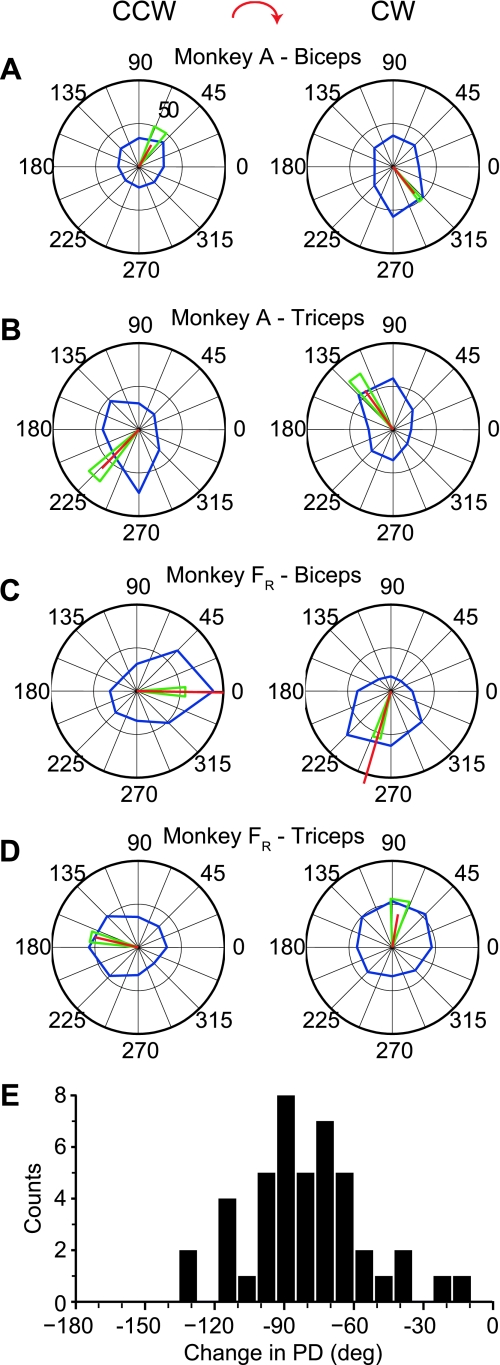
We recorded data from monkeys A and F (data set F_R) during a total of eight sessions in the force field experiment. We determined the effect of the force fields on muscle activation patterns by comparing the tuning curves of each muscle in the two different conditions (Fig. 2). The PD of biceps (Fig. 2, A and C) and triceps (Fig. 2, B and D) pointed in approximately opposite directions for both monkeys during movements in either field. However, the PDs under the CW force field were rotated clockwise from their directions in the CCW force field. Figure 2E shows the distribution of the changes between the CCW and CW fields across all recordings, which averaged −80 ± 27° (mean ± SD). Seven of the eleven muscles had significantly higher overall activation in the CCW task (ANOVA, P < 0.01). The differences for the remaining four muscles were not significant (ANOVA, P < 0.01).

Fig. 2.

Tuning characteristics of biceps and triceps in monkeys A and F [right hemisphere (F_R)] during CCW (left) and CW (right) force fields. Blue line shows the average activity as a function of the direction of hand movement in 45° bins. Red line is the vector sum of the 8 averages, the length of which reflects both the discharge rate of the cell and the extent to which the tuning curve approximated a sinusoid. Green triangle denotes the edges of the 95% confidence interval of the preferred direction (PD) estimate. A and B: biceps and triceps recorded from monkey A. C and D: biceps and triceps recorded from monkey F_R. E: distribution of PD changes across all muscles recorded from both monkeys.

We also compared the average position and root mean squared (RMS) velocity across N folds in the two different fields. Although there were no differences in the distribution of positions for either monkey, there were significant differences in the velocity for both monkeys (ANOVA, P < 0.01). Across the eight sessions from the two subjects, the RMS velocity was ∼10% higher for the CCW task. Note that this was also the field having the greater muscle activation. For half of these sessions the difference was significant. When we examined the difference between the X and Y components of velocity within a workspace, we found that in all but one case the X component of velocity (the axis parallel to the shoulders) was 20% higher than Y (ANOVA, P < 0.01). This was likely due to the lower moment of inertia for movements along this axis.

Prediction of EMG and kinematics within task: force fields.

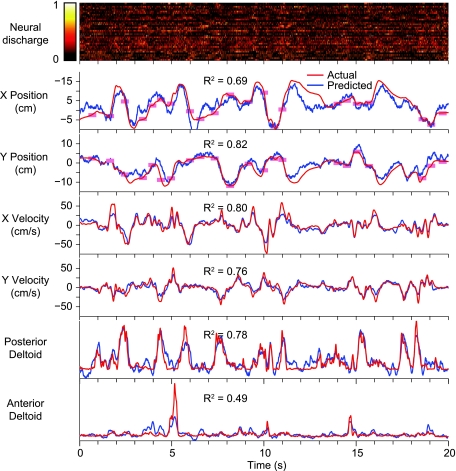
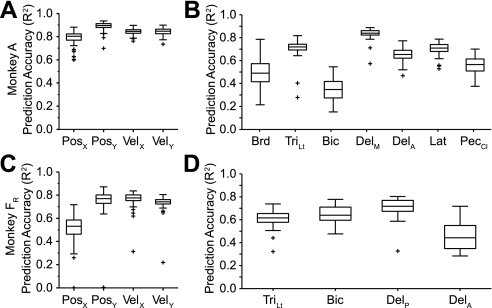
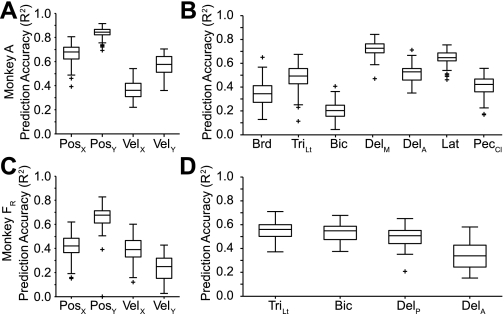
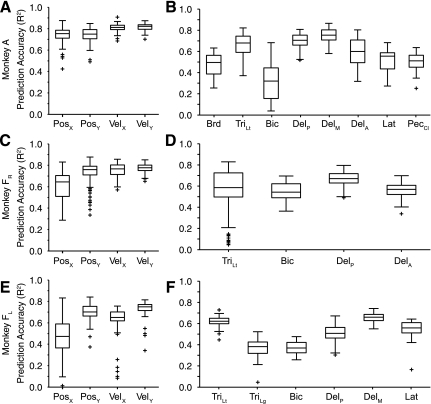
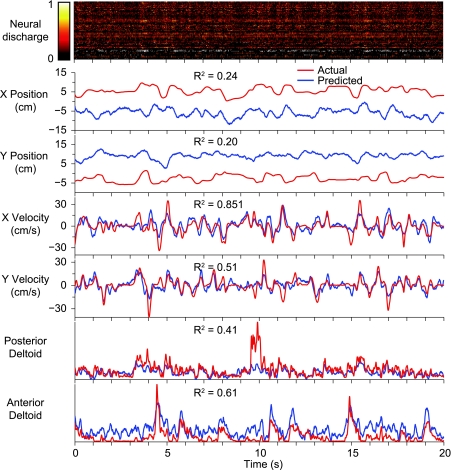
We examined the accuracy of the within-task, cross-validated predictions for both EMG and kinematic signals. A 20-s segment of the raw data from 1 fold is presented in Fig. 3. Figure 3, top, is a color scale plot of the firing rates of the 39 neural signals (18 single-unit, 21 multiunit signals) used for the predictions. Figure 3, bottom, shows the actual output signals (red traces) and the decoder predictions (blue traces). The light red rectangles plotted along the X and Y position traces represent the timing and position of the random target presentations. The performance of the decoders was quite good, capturing much of the structure of each of the output signals. Figure 4 summarizes these results across monkeys. Figure 4, A and B, are from data set A, and Fig. 4, C and D, are from data set F_R. Both components of position and velocity were predicted equally well for data set A, but for data set F_R the X component of hand position was significantly less accurate than the other kinematic signals (ANOVA, P ∼ 0). As a group, the predicted EMG signals were somewhat less accurate than the predictions of kinematic signals.

Fig. 3.

Within-task predictions of kinematics and EMG during the force field experiment. Data were recorded from monkey F_R during the random-target task in the CCW field. Normalized discharge rate for each of 39 neural signals (a combination of single and multiunit recordings) is shown by a color scale (top). Red rectangles on the position traces (bottom) indicate the size and the times of appearance and disappearance of the targets. Prediction accuracy in terms of R² is shown for just the plotted 20-s segment of each signal.

Fig. 4.

Summary quartile plots of within-task R² prediction performance for the force field experiment. A and B: data set A. C and D: data set F_R. Each box has lines at the lower quartile, median, and upper quartile. The whiskers extend 1.5 times the interquartile range within each box. Values outside this range are plotted as “+” symbols. The means across position (Pos), velocity (Vel), and EMG were 0.84/0.84/0.61 for data set A and 0.63/0.75/0.62 for data set F_R. Brd, brachioradialis; Tri_Lt, lateral head of triceps; Bic, biceps; Del_M, medial deltoid; Del_A, anterior deltoid; Del_P, posterior deltoid; Lat, latissimus dorsi; Pec_CL, clavicular head of pectoralis.

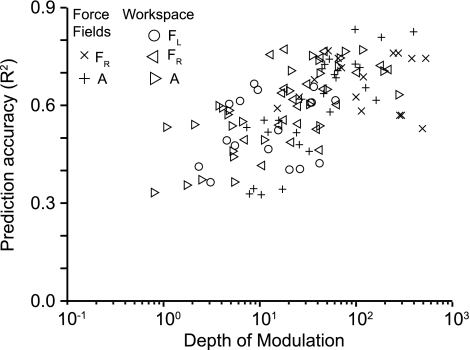
Unlike kinematics for which high-quality signals can be consistently recorded, EMG signals are more prone to contamination by sources of noise (e.g., radiated noise from various sources, movement artifacts, and electrocardiogram). Furthermore, some muscles have a higher level of task-related modulation than others. We wondered to what extent this varied signal quality might explain variation in EMG prediction quality. It seems reasonable to expect that, other things being equal, noisier EMGs or those with relatively little task-related modulation would be difficult to predict. To characterize the relationship between the quality of EMG recordings and decoder performance, we computed a measure of EMG depth of modulation (DOM). We determined the baseline activity of each EMG by computing the variance (power) during a period in which all EMGs were quiescent. We also computed the EMG variance within the same 1-min folds used for prediction. DOM was defined simply as the ratio of the active power to the quiescent power. We compared the R² performance to DOM for each data fold. These results are summarized in Fig. 5. For both experiments, decoder performance tended to increase with increasing EMG quality up to a DOM of ∼50, after which prediction accuracy appeared to saturate.

Fig. 5.

Relationship between R² prediction accuracy and EMG depth of modulation (DOM; see methods). Data from all experiments are combined, as indicated.

Prediction and generalization across tasks: force fields.

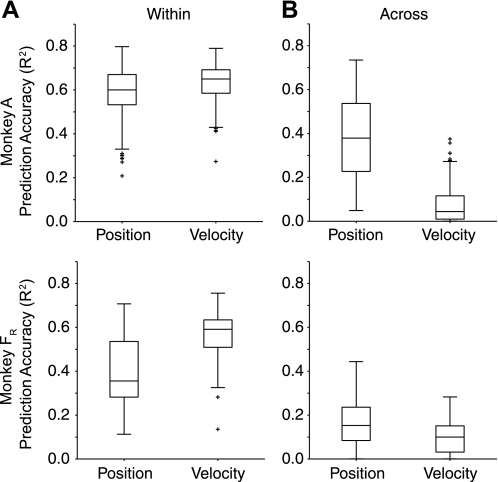
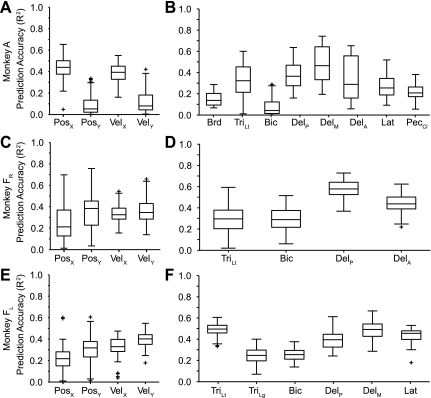
The goal of our experiments was to understand the relationship between neural discharge, kinematics, and EMG under changing dynamical conditions. A cortical neuron that actually encodes a particular output signal may also contribute strongly to the prediction of a different output, provided that the two outputs are well correlated. However, a decoder generated from these data would fail to generalize to a novel task in which the relation between the two output signals was altered. To test these effects we used decoders trained with data from the CW force field to predict data collected from the CCW field. We also used CCW data to train and CW data to test. There was no difference between these two sets of results, and they have been combined. Under these conditions, the change in accuracy of the velocity predictions was marked (Fig. 6). Prediction accuracy of both X and Y components of velocity was reduced to approximately one-half of its within-task level.

Fig. 6.

Summary quartile plots of across-task R² prediction performance for the force field experiment. A and B: data set A. C and D: data set F_R. All conventions as in Fig. 4. The means across position, velocity, and EMG were 0.75/0.47/0.47 for data set A and 0.54/0.31/0.49 for data set F_R.

However, despite the dramatically different forces on the hand and the corresponding changes in muscle activation during movement (Fig. 2), the decrease in accuracy for the across-task EMG predictions was relatively modest. The small change in prediction accuracy suggests that the changes in muscle activation patterns were accompanied (and perhaps caused) by corresponding changes in neural activation. Again, we noted that there was a substantial range of prediction quality across the muscles that was partially accounted for by the quality of the recorded signals. Interestingly, the position generalizations were largely unaffected by the viscous force fields, although the X component generalized more poorly than the Y for both monkeys.

It might be expected that the small change in the position predictions could be explained at least in part, if the velocity-dependent fields had a only a small effect on the relationship between end point position and force. We tested this possibility by using EMG instead of neural signals to predict kinematics. If the fields failed to affect the position prediction from EMG, there would be no reason to expect them to affect the neuron-to-position predictions, either. The ability to predict position from EMG for data set A dropped from an average of 0.60 (within) to 0.38 (across). For data set F_R, the effect was a bit larger, from 0.35 to 0.15. The smaller overall accuracy for data set F_R was likely the result of the smaller number of available muscles. On the other hand, the force fields dramatically disrupted the ability to predict velocity from EMG. Predictions dropped from an average of 0.65 for data set A and 0.60 for data set F_R to 0.10 and 0.04, respectively (Fig. 7). Consistent with the effects shown in Fig. 2, these results indicate a strong disruption of the relation between EMG and movement velocity. Roughly speaking, the effect of the force fields was five times greater on velocity than on position.

Fig. 7.

Prediction of movement kinematics from EMG both within and across force field conditions. A: cross-validated predictions of both position and velocity signals using the full set of EMG signals as inputs and using training and testing data collected under a single force field condition. B: kinematic predictions made across force field conditions. The velocity-dependent fields prevented generalization of velocity predictions to a much greater extent than they did position.

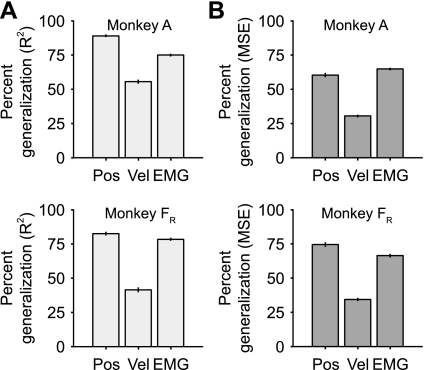
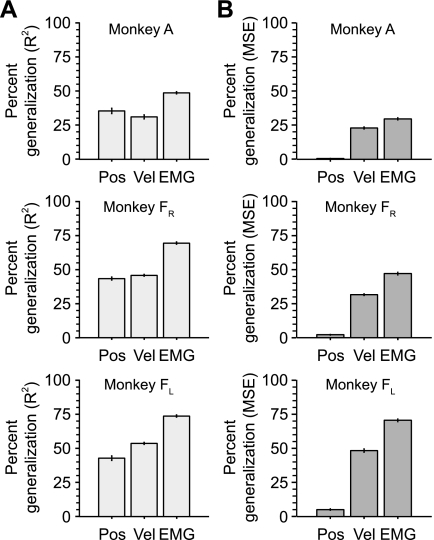
To summarize decoder generalization across tasks, we computed a new metric, “percent generalization,” which normalized decoder performance across force fields to that within fields (Eq. 1). We combined the data into three groups, position, velocity, and EMG, and noted the relative performance of each group (Fig. 8A). Despite the large changes in the EMG tuning curves caused by the different force fields, the EMG decoders generalized fairly well, essentially 75% for both monkeys. In contrast, the velocity decoders generalized less well, just over 50% for data set A and ∼40% for data set F_R. The position generalizations were relatively unaffected by the viscous force fields, at least in part, because of the more modest effects of the viscous forces on the relation between EMG and position (Fig. 6). The means from the position, velocity, and EMG percent generalizations all differed significantly (ANOVA, P < 0.01).

Fig. 8.

Percent generalization for position, velocity, and EMG in the force field experiment. Percent generalization was calculated by dividing the across-task prediction accuracy by the corresponding within-task value. A: percent generalization computed with the R² metric. B: percent generalization computed with the mean squared error (MSE) metric. Error bars indicate SE.

The large range in R² across different muscles raises a potential concern. R² is bounded at 0 and 1, but it is possible that substantial noncausal noise correlations in the data might further raise the effective lower bound. If this were the case, muscles with within-task prediction accuracy near the noise correlation floor would not decrease much, and might have an artifactually high percent generalization. We tested this by dividing the muscles into two sets based on their within-task prediction accuracy. There was no significant difference for data set F_R (ANOVA, P = 0.08), but for data set A the muscles with the better within-task prediction accuracy also generalized better (percent generalization of 0.83 and 0.72, respectively; ANOVA, P ∼ 0). The difference between the two monkeys is very likely due to the smaller range of within-task R² for data set F_R that diminished the difference between the upper and lower halves. Similar analyses for position and velocity yielded three significant differences, all with better generalization of those data sets with the better within-task accuracy. In general, those signals that predicted poorly also generalized poorly. This suggests that elevated noise correlations are not a likely explanation for our results.

Another factor that is important to consider is that R² is not sensitive to errors in the magnitude or offset of the predicted signals, a potentially serious consequence if these predicted signals are actually to be used for control. For this reason, MSE is sometimes used instead of R² to evaluate the quality of such predictions. Its chief disadvantage is that it has the (squared) units of the signal being measured, making it difficult to compare the quality of prediction of different signal types. However, by using an MSE ratio (as we have done in the computation of percent generalization, Eq. 2), this disadvantage is eliminated. Figure 8B summarizes the percent generalization using MSE. While all of the measures were slightly lower using MSE rather than R², it is worth noting that the main difference between the two measures was in the kinematic predictions for data set A, presumably because of gain and offset errors. Despite the modest effect of the force fields on position, the position generalization became slightly poorer than EMG for data set A. It was slightly better than EMG for data set F_R.

Finally, we were concerned that the relatively large number of parameters used in the decoder models might fail to generalize as well as a model with fewer parameters. To test the possibility, we repeated the basic analysis on two representative data sets using 250- and 120-ms filters (25 and 12 points, respectively). Predictions of EMG signals using the 500-ms filters generalized marginally better than with 250-ms filters (ANOVA, P = 0.046). The 120-ms filters had 25% poorer performance (ANOVA, P ∼ 0). The results for kinematics were similar. Consequently, all additional analyses were restricted to the full 500-ms filters.

Effect of workspace location on muscle activation and movement kinematics.

We recorded a total of 14 sessions in the workspace task from monkeys A (right motor cortex) and F (left and right motor cortices). Across these sessions, velocity was ∼4% higher in the far workspace. Five of the fourteen differences were significant (ANOVA, P < 0.01). We also examined differences between the X and Y components of velocity. For the 28 comparisons there were 8 instances in which X was significantly higher and 4 when X was significantly lower (ANOVA P < 0.01).

EMG activity also differed across the two workspaces. Of the 18 muscles recorded, 11 were significantly more active when short, while 3 were significantly more active when long. The increase in activity at shorter muscle lengths may partially be explained by the length tension property of muscles, which would cause greater activation to be required to produce equal force at a shorter length.

Prediction of EMG and kinematics within task: workspaces.

Overall, the kinematic predictions in the workspace experiment were similar to those of the force field experiment. The decoders predicted velocity slightly better than position (Fig. 9). As noted above for the force field experiment (Fig. 4), the prediction of the Y component of position was somewhat better than that of X for both hemispheres of monkey F. EMG prediction accuracy was lower than that of kinematics, and slightly lower than in the fields experiment. However, for both this experiment and the force field experiment, higher EMG DOM tended to yield better decoder performance. On average, DOM for this task was approximately three times smaller than during the force field experiment, probably because of the greater forces required to oppose the viscous fields. This may account for the slightly poorer overall prediction performance in the workspace experiment.

Fig. 9.

Summary quartile plots of within-task R² prediction performance for the workspace experiment. A and B: data set A. C and D: data set F_R (right hemisphere). E and F: data set F_L (left hemisphere). All conventions as in Fig. 4. Means across position, velocity, and EMG were 0.74/0.81/0.58 for data set A, 0.67/0.77/0.59 for data set F_R, and 0.58/0.67/0.53 for data set F_L. Tri_Lg, long head of triceps.

Prediction and generalization across tasks: workspaces.

When we altered the dynamical relationship between velocity and EMG in the force field experiment, the EMG decoders generalized better than the velocity decoders. However, the force field manipulation left the relationship between position and EMG relatively unaffected compared with the large change it caused between EMG and velocity. By altering the posture of the limb, we changed the relationship between EMG and both position and velocity. Consequently, we were able to test more completely the generalization of both kinematic and EMG decoders. We trained the decoders from data collected when monkey F was moving in the far workspace (where biceps was relatively long and triceps short) and tested it on data from the near workspace. Conversely, we also trained on near workspace data and tested on far. These two results were not different, and have been combined below. As in the force field experiment, the performance of both the kinematic and the EMG decoders decreased as a result of the generalization across workspaces. Position was predicted particularly poorly, often with a large offset between the actual and predicted signals (Fig. 10). It is important to note, however, that the low R² in this example does not reflect this offset between the actual and predicted signals. Predictions of the more phasic velocity and EMG signals appeared to generalize better than position, although many of the peaks were underestimated. More striking is the single example in the posterior deltoid prediction in which the decoder completely missed the peak in EMG activity at time 10 s. Figure 11 summarizes the results across all workspace experiments, confirming the slightly less accurate predictions of the X components of position and velocity for both data sets from monkey F. On the other hand, the Y components of position and velocity were predicted much more poorly for data set A.

Fig. 10.

Across-task predictions of kinematics and EMG during the workspace experiment. Monkey F was working in the far workspace, but predictions were made using decoders computed for the near workspace. In the far workspace, biceps and anterior deltoid were relatively long, while triceps and posterior deltoid were shortened.

Fig. 11.

Summary quartile plots of across-task R² prediction performance for the workspace experiment. A and B: data set A. C and D: data set F_R. E and F: data set F_L. Means across position, velocity, and EMG were 0.26/0.25/0.30 for data set A, 0.30/0.35/0.41 for data set F_R, and 0.27/0.36/0.40 for data set F_L.

For both monkeys, the R² generalization ratios for position and velocity were significantly lower than for the EMG decoders (ANOVA, P < 0.01; Fig. 12A). To account for the large offset errors in the position predictions, we also computed the MSE percent generalization (Fig. 12B). Using this metric, the generalization performance of the position decoders was much worse than with R², while the relative performance of the velocity and EMG decoders remained largely unchanged. The differences in the means of the position, velocity, and EMG percent generalization ratios were all statistically significant (ANOVA, P < 0.01).

Fig. 12.

Percent generalization for position, velocity, and EMG in the workspace experiment. A: percent generalization computed with the R² metric. B: percent generalization computed with the MSE metric. Error bars indicate SE.

DISCUSSION

Summary.

This study is the first that we are aware of using multiple-neuron decoding across varied loads and posture. This approach provides a sensitive means not only to address the question of the output signal encoded by a given population of neurons but also to determine the most robust control signal available for BMI applications. We used both single and multiple units as inputs to position, velocity, and EMG decoders, the performance of which we tested under two different end point force fields and within two regions of the workspace. Both of these manipulations altered the relation between EMG and kinematics. Overall, the EMG decoders generalized better across these conditions than the kinematic decoders. This observation indicates that the activation of M1 neurons changed in a manner similar to that of the muscles, thereby maintaining the neural/EMG dynamical relation approximately constant. Although it cannot be proven by these methods, these results suggest that M1 discharge fundamentally encodes muscle activity to a greater extent than it does movement kinematics, and that a BMI exploiting these musclelike characteristics might provide more robust control.

Determining the dynamics of the signal encoded by M1 discharge.

Many studies have tested the robustness of the signals encoded by single neurons by observing the relation between the neural discharge and movement-related variables while varying postural or loading conditions (Caminiti et al. 1990; Evarts 1968; Kakei et al. 1999; Kalaska et al. 1989; Morrow et al. 2007; Scott and Kalaska 1997; Sergio et al. 2005). Numerous BMI studies have reported kinematic decoder performance similar to ours but restricted to a single set of dynamical conditions (Brockwell et al. 2004; Carmena et al. 2003; Gupta and Ashe 2009; Kim et al. 2006; Koike et al. 2006; Serruya et al. 2002; Stark and Abeles 2007; Taylor et al. 2002; Wu et al. 2006; Yu et al. 2007). However, few BMI studies have directly addressed the role of M1 in the control of dynamical systems. Ironically, one of the earliest multielectrode studies concluded that force and its first derivative were encoded more prominently in M1 than were movement kinematics (Humphrey et al. 1970). A recent study found that torque computed for the shoulder and elbow joints during planar reaching movements was predicted only slightly less accurately than joint angular position or velocity (Fagg et al. 2009). A direct comparison of end point kinematics and grip force found the latter to be predicted dramatically better (Carmena et al. 2003), although EMG was predicted less accurately in that study. However, two other studies achieved predictions of the EMG measured from wrist muscles during isometric contractions with R² in the 0.7–0.8 range (Oby et al. 2010; Pohlmeyer et al. 2007b).

As limited as are multiple neuron studies of the encoding of dynamical signals, our present study is the only one of which we are aware that has made predictions across dynamical conditions. Just as in the single-neuron studies of the last several decades, correlations (or the ability to predict a given movement-related signal) under a single condition cannot be considered compelling evidence of a causal relation with M1 discharge. However, the relatively robust generalization of EMG for all of our experimental conditions suggests that muscle activity may be closest to the dynamics of the population M1 activity of the signals that we considered. However, the performance of all three decoders, including that of EMG, decreased significantly when tested across tasks. There is increasing evidence that the neurons of M1 are not fully homogeneous, but vary with respect to their dependence on external loads and limb posture (Kakei et al. 1999; Kalaska et al. 1989; Thach 1978). Because our decoders were computed using all of the neurons that modulated during movement, it is likely that some were relatively load and posture insensitive. If this were the case, it would cause less than complete generalization of the EMG predictions across these conditions.

One must also consider the possibility that another kinetic variable, such as muscle force, is more closely related to M1 activity than EMG is. If M1 actually specifies the desired force output of muscles, spinal circuitry would be left to compensate for the effects of muscle fiber length, the speed of contraction, or muscle fatigue. However, there is some evidence from the single neuron literature that M1 discharge reflects neither position nor force, but rather the amount of excitation necessary to produce the desired force at a given muscle length (Cheney and Fetz 1980; Fromm 1983). A separate population of M1 neurons has even been described that appears to control limb stiffness by regulating the level of antagonist cocontraction (Humphrey and Reed 1983).

Historically, many single-neuron studies have considered only neural discharge and its “relation to the task.” Consequently, if the monkey does not actually execute the desired task (e.g., fails to move directly to the intended target), inferences taken only from the neural discharge may not be correct. Instead, we adopted what have become rather standard methods in the BMI domain, to compute the statistical relation between input and the actual measured output (EMG or trajectory). By altering the dynamics of the task, we can more rigorously ask which type of output signal remains more nearly related to the neural inputs. A prudent concern in any of these studies is that proving causality under these conditions is at best difficult and at worst impossible. One of the appeals of moving this persistent question about the nature of the signals encoded in M1 from the purely theoretical domain to the (somewhat) more practical domain of the BMI is the eventual opportunity to test which approach actually provides more robust control.

We have begun using EMG predictions like those described here as control signals to a multichannel muscle stimulator designed to restore motor function to monkeys whose forearms have been temporarily paralyzed by peripheral nerve blocks. These monkeys are able to grasp and move objects despite complete paralysis of the flexor muscles distal to the wrist (Oby et al. 2010; Pohlmeyer et al. 2009). This work builds on the “Freehand” neuroprosthesis that has been implanted in several hundred spinal cord-injured patients since 1986 (Keith et al. 1989; Kilgore et al. 2009). Movement of a prosthetic or robotic limb using a kinematic control signal is typically accomplished with a PD (proportional-derivative) controller. Note that in this context, “PD” does not refer to the “preferred direction,” defined earlier. A PD controller compares both the intended position and velocity (the derivative component) to the current state of the limb and delivers commands that are proportional to the error in each state variable. It might be anticipated that BMI control of an object with mass (as opposed to a cursor) might be more natural if it made use of the dynamic information already available in M1 rather than relying solely on kinematic inputs and a PD controller.

Input optimization for a kinetic brain-machine interface.

An important consideration for an optimal EMG-based BMI control signal may be access to large numbers of neurons with direct projections to motoneurons. Recent anatomic work using retrograde virus transport has indicated that relatively few of the corticospinal neurons on the crown of the central sulcus have these direct projections (Rathelot and Strick 2009). There is also physiological evidence that, as one moves anterior from the central sulcus, the discharge of neurons may become less like that of muscles while taking on other higher-order characteristics (Johnson et al. 1996; Kakei et al. 2001). The multielectrode arrays that we used in this study preclude recording from within the bank of the central sulcus, and thereby may actually have missed many of these directly connected, musclelike neurons. It is thought that caudal M1, with its increased tactile responsiveness, represents a newer cortical system that has evolved to provide the increased dexterity of humans and more advanced primates (Nakajima et al. 2000; Strick and Preston 1978a, 1978b). Attempts to decode muscle activity related to the wrist and hand may well profit from recordings made in caudal M1 (Oby et al. 2010; Pohlmeyer et al. 2007b, 2009).

The same problem may not apply as strongly to the proximal limb, which is represented to a greater extent on the crown of the sulcus surrounding the distal limb representation (Park et al. 2001). The propriospinal system that plays a critical role in distributing descending projections in lower primates and cats may continue to be involved in the control of reaching movements (Alstermark et al. 2007). However, it is worth noting that the original paper describing preferred directions of neurons during reaching actually included more premotor cortical neurons than M1 neurons (Georgopoulos et al. 1982). The extent to which moving from rostral to caudal M1 might have further improved the generalization of EMG relative to kinematics in our experiments remains unanswered.

Choice of prediction accuracy metrics.

Many studies examining the performance of kinematic and EMG decoders have used either the correlation coefficient (R) or the coefficient of determination (R²) to compare actual and predicted values. The chief advantage of these metrics is that they are dimensionless, enabling one to compare completely different types of signals. However, these metrics are insensitive to errors in gain or offset that may result from inadequate generalization across conditions (as in our position predictions across workspaces). These types of errors may have considerable consequences for BMI control and should be considered in a performance analysis.

MSE, on the other hand, is a performance measure that is sensitive to gain and offset errors. By itself, it cannot be used directly to compare the quality of prediction across different types of signals. However, normalization of the across-task MSE to the within-task MSE provides a dimensionless measure of generalization and serves as a good measure for our study. Using the ratio of across- to within-task prediction accuracy effectively addresses a second, less obvious issue. The EMG signal, because of both its stochastic nature and relatively broad bandwidth, may be intrinsically more difficult to predict than movement kinematics. Also unlike kinematics, the difficulty in recording a high-quality signal may contribute reduced prediction performance. The percent generalization metric that we adopted served to mitigate these factors by providing a measure of the extent to which prediction accuracy was maintained across dynamical conditions.

Improving the design of future BMI applications.

The most common approach to robotic control using kinematic information from M1 is to relegate the production of torques and the control of dynamics to a PD controller. A PD controller compares the intended position and velocity to the current state of the limb and commands the necessary torques to drive these differences to zero. The parameters of the PD controller can be tuned in order to minimize feedback delays and achieve critical damping under specific conditions. One problem with this approach is that the optimal parameter settings depend on the exact system dynamics. If the mass is altered, such as when an object is grasped, the control is likely to become suboptimal. Applications that require the combined control of both end point position and force, or of limb compliance, impose even greater challenges with a PD controller.

The implications of the limitations imposed by purely kinematic approaches to BMI control may be significant. In real-world applications, a BMI user will need to make similar movements under different loading conditions, e.g., when grasping and moving different objects. Ideally, a given decoder would be trained on a robust data set that includes the full range of motor behaviors to which it will be subjected in use. In practice, this is unlikely to be feasible. Any regression system performs most poorly for extrapolations outside of the space in which it was trained. For example, the position decoders in our experiment had to extrapolate across workspace conditions, as did many muscles in both the workspace and force field experiments. Our results suggest that rather than extracting only kinematic information from the brain and dealing with the limitations of generalization within a PD controller, it may be advantageous to use the available force or muscle-related information. In so doing, the user might readily modulate limb compliance and deal with the combined control of movement and force in a more natural manner that better reflects normal motor control.

GRANTS

This work was supported in part by National Institute of Neurological Disorders and Stroke Grant NS-048845, with further support from the Chicago Community Trust through the Searle Program for Neurological Restoration.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).