Contribution of motoneuron intrinsic properties to fictive motor pattern generation

Abstract

Previously, we reported a canonical ensemble model of the heart motoneurons that underlie heartbeat in the medicinal leech. The model motoneurons contained a minimal set of electrical intrinsic properties and received a synaptic input pattern based on measurements performed in the living system. Although the model captured the synchronous and peristaltic motor patterns observed in the living system, it did not match quantitatively the motor output observed. Because the model motoneurons had minimal intrinsic electrical properties, the mismatch between model and living system suggests a role for additional intrinsic properties in generating the motor pattern. We used the dynamic clamp to test this hypothesis. We introduced the same segmental input pattern used in the model to motoneurons isolated pharmacologically from their endogenous input in the living system. We show that, although the segmental input pattern determines the segmental phasing differences observed in motoneurons, the intrinsic properties of the motoneurons play an important role in determining their phasing, particularly when receiving the synchronous input pattern. We then used trapezoidal input waveforms to show that the intrinsic properties present in the living system promote phase advances compared with our model motoneurons. Electrical coupling between heart motoneurons also plays a role in shaping motoneuron output by synchronizing the activity of the motoneurons within a segment. These experiments provide a direct assessment of how motoneuron intrinsic properties interact with their premotor pattern of synaptic drive to produce rhythmic output.

rhythmic motor behaviors, such as swimming and walking, are generated by networks of rhythmically active neurons called central pattern generators (CPGs; Marder and Calabrese 1996). A defining characteristic of these networks is their ability to generate a rhythmic pattern in in vitro preparations in which sensory feedback has been removed (i.e., the fictive pattern). The majority of CPGs provide a pattern of rhythmic synaptic activation to the motoneurons that underlie the behavior. While much work has focused on identifying and analyzing elements of these rhythmically active networks, less is known about how motoneurons themselves contribute to the generation of the motor pattern.

Some studies have shown that motoneurons possess intrinsic properties that may affect motor pattern generation. For example, motoneurons in cats (Lee and Heckman 1998) and turtles (Hounsgaard and Kiehn 1989) exhibit bistable membrane properties (i.e., a stable membrane potential at rest and at depolarized levels) that may confer upon them the ability to sustain motor output in the absence of synaptic input. Kiehn et al. (2000) characterized a hyperpolarization-activated current, I_h, present in motoneurons in the neonatal rodent spinal cord. They showed that this current advanced the transition of a motoneuron from its inhibited phase to its firing phase, suggesting that this current could confer upon a motoneuron an ability to “escape” from ongoing inhibitory synaptic input and thus influence motor output.

Electrical coupling between motoneurons can also affect motor pattern generation. For example, studies have shown that there is electrical coupling between hypoglossal motoneurons associated with breathing (Rekling et al. 2000) and tongue movements (Sharifullina et al. 2005) as well as among motoneurons in Xenopus embryos (Perrins and Roberts 1995). Furthermore, when gap junctions were blocked in Xenopus embryos, Zhang et al. (2009) noted that the burst durations of motoneurons increased, resulting in alteration of rostro-caudal delays during fictive swimming. These results indicate that electrical coupling in these preparations may contribute to the motor output observed in vitro.

Elucidating the functional significance of neuronal intrinsic properties has remained elusive, however, owing in part to a lack of detailed information about the activity patterns and synaptic connections of premotor interneuronal networks that provide the synaptic information to the motoneurons in these systems. For example, in the absence of synaptic input, the motoneurons involved in fictive scratch in turtles exhibit large-amplitude voltage fluctuations in response to current injections, indicating that they possess complex intrinsic properties (Alaburda et al. 2005). When the premotor network driving fictive scratch is activated, however, the voltage fluctuations observed are diminished because of the synaptic conductance impinging upon the motoneurons. This result implies that the intrinsic properties responsible for the voltage oscillations make a minor contribution to the motor pattern observed in vitro. These results suggest that a detailed description of the premotor pattern of synaptic drive onto these motoneurons is required in order to determine the role of motoneuron intrinsic properties in the generation of the fictive scratch.

Invertebrates, with their simple and accessible nervous systems, have long been useful for elucidating synaptic connectivity within central pattern generating networks (Nusbaum and Beenhakker 2002) and how motor patterns are modulated and selected (DeLong et al. 2009). Here we use the leech heartbeat CPG to assess how motoneuron intrinsic properties and electrical coupling contribute to rhythmic motor output.

The leech heartbeat system has been described in detail (Kristan et al. 2005; Thompson and Stent 1976a, 1976b, 1976c), so we provide a brief summary here. Blood flow in the leech circulatory system is accomplished by the rhythmic constriction of a pair of longitudinal vessels, the lateral heart tubes (referred to as “hearts”). The hearts are coordinated such that one heart constricts with a rear-to-front progression (i.e., peristaltically), while the other heart constricts nearly synchronously along its length. The asymmetry in the constriction patterns is not permanent; rather, there are regular switches in the constriction patterns roughly every 20–40 cycles. The constriction patterns of the hearts are the result of excitatory drive arising ipsilaterally from segmental heart (HE) motoneurons (Thompson and Stent 1976a). Heart motoneurons occur as electrically coupled bilateral pairs in midbody segmental ganglia 3 through 18 of the 21 midbody ganglia in the ventral nerve cord. The heart motoneurons receive rhythmic inhibitory input from ipsilateral premotor heart (HN) interneurons that are components of the heartbeat CPG. The firing pattern of the heart motoneurons (i.e., the fictive motor pattern) is also bilaterally asymmetric: motoneurons on one side fire with a rear-to-front progression of activity while the heart motoneurons on the other side fire nearly synchronously with the appropriate side-to-side coordination (Wenning et al. 2004a, 2004b). The firing pattern of the premotor heart (HN) interneurons (i.e., the temporal pattern) is bilaterally asymmetric, with heart interneurons on one side firing with a rear-to-front progression, while the interneurons on the other side fire nearly synchronously.

Previously, Norris and colleagues (2006, 2007a, 2007b) quantified the individual components of presynaptic input to the heart motoneurons as well as their output. In the first of a series of studies, they quantified the temporal patterns (peristaltic and synchronous) of the heart interneurons. They then characterized the pattern of synaptic strengths arising from each of the premotor interneurons onto their appropriate heart motoneuron targets (i.e., a heart motoneuron's synaptic strength profile). Finally, they quantified the phasing of the heart motoneurons with respect to the premotor interneurons. These studies led to the development of a first-generation model of the ensemble of heart motoneurons (Garcia et al. 2008). The model motoneurons were single-compartment, conductance-based models and were given a minimal set of voltage-gated conductances. The synaptic input pattern introduced to the model motoneurons was based on the Norris et al. (2006, 2007a, 2007b) experiments just described. Although this first-generation model exhibited general trends in activity (i.e., a peristaltic and synchronous pattern of activity) as those observed in the living system, a quantitative comparison revealed substantive differences in phase between the model and the living system (Fig. 9, Garcia et al. 2008). For example, in the peristaltic mode (pink lines, Fig. 9, Garcia et al. 2008), the model motoneurons do not capture the amount of peristaltic phase progression observed in the living system; in anterior segments (e.g., 8), the phase of the model motoneurons leads the average of that in the living system, whereas in more posterior segments (e.g., 14), the phase of the model motoneuron lags the average of that in the living system. In the synchronous mode (blue lines, Fig. 9, Garcia et al. 2008), model motoneuron activity occurs nearly synchronously, but the phase of the model motoneurons lags the average of that in the living system in midbody segments 7–15, as illustrated in Fig. 9 of Garcia et al. (2008). These results raise the possibility that the intrinsic properties of the heart motoneurons in the living system, which were not accounted for in our model motoneurons, may be critical for their appropriate phasing.

To test this hypothesis, we used the dynamic clamp technique (Prinz et al. 2004; Sharp et al. 1993) to construct hybrid networks in which heart motoneurons in the living system received the same synaptic conductance waveform introduced into our model motoneurons (Fig. 1). We show that, although the segmental input pattern determines the phasing differences observed in motoneurons in segments 8 through 14, the intrinsic properties of the motoneurons also influence their phasing in the hybrid system. Indeed, appropriate phasing can be achieved when motoneurons receive the synchronous segmental input patterns. We also explore how the heart motoneurons in the living system integrate their inputs differently from our canonical model motoneurons. Finally, we show that electrical coupling between heart motoneurons can influence their phasing. Taken together, these results show that motoneurons can be active participants in motor pattern generation.

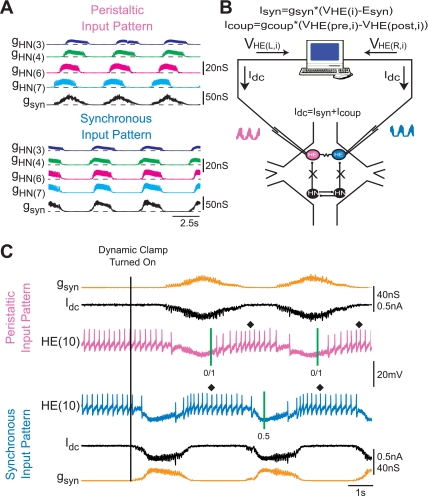
Fig. 1.

Hybrid system design and implementation. A: simultaneous computed synaptic conductances arising from each of the premotor heart interneurons [g_HN(i); color traces] as well as the sum of these synaptic conductances (g_Syn; black trace) for both the peristaltic and synchronous coordination modes. g_Syn is the time-varying conductance [g_Syn(t); see methods] introduced into the HE(10) motoneuron. The 2 g_Syn traces illustrate the difference between the peristaltic and synchronous input patterns. In the peristaltic mode g_Syn rises and declines gradually, as the firing of the premotor inputs are spread out over time, while in the synchronous mode g_Syn rises and falls rapidly, as the firing of the premotor inputs occurs at nearly the same time. B: hybrid system setup. We recorded simultaneously from a pair of heart motoneurons [V_HE(L,i) and V_HE(R,i)] from a given segment and pharmacologically isolated the motoneurons from their premotor heart interneuron inputs (“X”; see methods). The dynamic clamp computes and injects in real time the artificial equivalent of the appropriate synaptic current (I_dc) into the heart motoneurons. In some experiments, the dynamic clamp was also used to compute I_coup. C: exemplar dynamic clamp experiment and calculation of phase. Simultaneous intracellular recordings from a pair of HE(10) motoneurons are shown. At the beginning of the voltage recording, the heart motoneurons were firing tonically; g_Syn is 0 nS. Once the dynamic clamp synapse was activated (vertical line), the dynamic clamp injects a time-varying current proportional to the synaptic conductance. In some figures, the dynamic clamp current (I_dc) is omitted and only the synaptic conductance is shown. The vertical green lines on the traces show the middle spike of the peristaltic HN(4) interneuron (0/1—our phase reference) and of the synchronous HN(4) interneuron (0.5). The interval between the 2 green lines of our phase reference is the cycle period. The average phase for an individual experiment here and in subsequent figures is indicated next to a filled diamond.

METHODS

Terminology.

Heart (HE) motoneurons and heart (HN) interneurons are indexed according to midbody ganglion number [e.g., HE(8), HN(4)]. In all experiments, we used bilateral pairs of heart motoneurons. We introduced the peristaltic input pattern to one heart motoneuron and the synchronous input pattern to the other heart motoneuron. Therefore, we omitted body-side indexing and labeled heart motoneurons as receiving the peristaltic or the synchronous input pattern.

Animals and solutions.

Leeches (Hirudo sp.) were purchased from a commercial supplier (Leeches USA, Westbury, NY) and maintained in artificial pond water at 15°C. Animals were anesthetized in ice and then dissected in chilled saline. Individual ganglia from segments 8, 10, 12, and 14 were dissected and pinned out, ventral surface up, in 35-mm petri dishes lined with Sylgard (184, Dow Corning, Midland, MI). The ventral sheath of the ganglion was removed in all experiments. We superfused the preparation with leech saline containing (in mM) 115 NaCl, 4 KCl, 1.8 glucose, 10 HEPES buffer, and 1.8 CaCl₂ adjusted to a pH of 7.4 with NaOH at 1–2 ml/min in a bath volume of 0.5–1 ml. All experiments were performed at room temperature (20–25°C). In most of the experiments included in this study, 10⁻⁴ M bicuculline methiodide (Sigma-Aldrich, Allentown, PA) was added to the leech saline to block inhibitory synaptic input to heart motoneurons (Cymbalyuk et al. 2002). In other experiments, CaCl₂ was replaced with an equimolar amount of MnCl₂ (Sigma-Aldrich) to block the premotor inputs.

Intracellular recording techniques and data acquisition.

Heart motoneurons were identified based on soma location within the ganglion, by soma size, and finally by their characteristic activity of bouts of firing interrupted by barrages of inhibitory postsynaptic potentials (IPSPs). Intracellular voltage recordings from heart motoneurons were made with sharp intracellular microelectrodes (∼25–40 MΩ filled with 2 M KAc, 20 mM KCl) made from borosilicate glass (1.0-mm outer diameter, 0.75-mm inner diameter; AM Systems, Sequim, WA). Intracellular recordings and current injections were performed with an Axoclamp-2A amplifier (Molecular Devices, Sunnyvale, CA) in discontinuous current clamp (DCC) mode with a sampling rate of 2.5–3.0 kHz. To ensure electrode settling, the electrode potential was monitored with an oscilloscope. Output bandwidth of the amplifier was 0.3 kHz. Data were digitized (10-kHz sampling rate) with a digitizing board (Digi-data 1200 Series Interface, Molecular Devices) and acquired with pCLAMP software (Molecular Devices) on a personal computer (Dell, Round Rock, TX).

In all experiments, both heart motoneurons in a given ganglion were impaled and recorded simultaneously. After penetration, the input resistance of both cells was measured with −0.3-nA pulses. We did not proceed with experiments unless the input resistance of both motoneurons was >30 MΩ and the difference in input resistance between the two motoneurons was <15%. Upon termination of the experiment, the microelectrode was withdrawn from the cell and the electrode potential was recorded. Only experiments in which the electrode potential was within ±5 mV of 0 mV were accepted in this study. Therefore, membrane potentials are accurate to ±5 mV.

Standard heart motoneuron ensemble model.

We compared data from our physiological experiments with a model of the entire ensemble of heart motoneurons previously developed by Garcia et al. (2008). Briefly, the motoneurons in this model were single-compartment, conductance-based models whose membrane potential (V) is given by the following current-balance equation:

$$C\frac{\text{dV}}{\text{d}t}=-\left(I_{\text{Na}}+I_{\text{p}}+I_{\text{KA}}+I_{\text{K}1}+I_{\text{K}2}+I_{\text{leak}}+I_{\text{coup}}+I_{\text{Syn}}+I_{\text{inject}}\right)$$

where t is time, C is the total membrane capacitance, I_leak is the leak current, I_coup is the current due to electrical coupling between the motoneurons, I_Syn is the sum of the inhibitory synaptic currents arising from each of the premotor inputs, and I_inject is any injected current. The model motoneurons contained five voltage-dependent ionic currents: 1) a fast Na⁺ current (I_Na), 2) a persistent Na⁺ current (I_p), 3) a fast transient K⁺ current (I_KA), 4) an inactivating delayed rectifier K⁺ current (I_K1), and 5) a noninactivating delayed rectifier K⁺ current (I_K2). The Hodgkin-Huxley equations (Hodgkin and Huxley 1952) describing these voltage-gated currents were the same as those used in a model of an oscillator heart interneuron (Hill et al. 2001). Each motoneuron was modeled as an isopotential cylinder whose length and diameter were both 60 μm with a specific membrane resistance of 1.1 Ωm² and a specific membrane capacitance of 0.05 Fm⁻². With these parameters, the input resistance of a model motoneuron was 97 MΩ. The maximal conductances of the individual ionic currents as well as electrical coupling were set empirically so that the activity of the model motoneurons mimicked that observed during intracellular recordings of heart motoneurons in the absence of synaptic input (Garcia et al. 2008).

The model motoneurons received an inhibitory synaptic input pattern that consisted of both timing information and a pattern of synaptic strengths; both components were determined from physiological experiments of the type performed by Norris and colleagues (2006, 2007a, 2007b) as described below.

For the model motoneurons, the firing pattern of the premotor interneurons (referred to here as the temporal pattern) was taken from 60 s of simultaneous extracellular recordings of the ipsilateral HN(3), HN(4), HN(6), and HN(7) premotor interneurons in both the peristaltic and synchronous coordination modes, as in Norris et al. (2006). The peristaltic and synchronous input patterns were aligned to each other to create a bilateral input pattern—left synchronous-right peristaltic—by assigning a phase of 0.0 to the middle spike of the first peristaltic HN(4) premotor interneuron burst [therefore, the peristaltic HN(4) premotor interneuron is our absolute phase reference] and a phase of 0.506 to the middle spike of the first burst of the synchronous HN(4) premotor interneuron. These phase values match the average phase difference between the two HN(4) interneurons as measured in the living system (Norris et al. 2006). Each segmental pair of model motoneurons received the same temporal pattern (1 peristaltic, 1 synchronous) offset by an intersegmental conduction delay of 20 ms per segment. Therefore, the model heart motoneurons in segment 12 receive the same temporal pattern as the model heart motoneurons in segment 8, offset by 80 ms. The period of the input pattern was 4.3 s [the range of periods measured in the living system is 4–8.5 s; average period = 5.3 s (Norris et al. 2006)]. Because the timing information used in our temporal pattern came from a living preparation, the temporal pattern is not precisely regular, and therefore the average phases presented for the ensemble model display a variance.

The distribution of synaptic conductances elicited by each of the premotor heart interneurons in a postsynaptic heart motoneuron (referred to here as a heart motoneuron's synaptic strength profile) was also derived from experiments in the living system, described in Fig. 1B of Norris et al. (2007b). They recorded from each of the premotor heart interneurons, as described above, and then voltage clamped a series of ipsilateral heart motoneurons. They recorded spontaneous inhibitory postsynaptic currents (IPSCs) in the heart motoneurons arising from activity in the premotor interneurons. From these recordings, they generated spike-triggered averages of the IPSCs for each presynaptic heart interneuron to each heart motoneuron. They selected the peak of the spike-triggered average trace as their measure of an individual premotor heart interneuron's synaptic input. These peak IPSCs were then converted to conductances [E_Syn = −62.5 mV (Angstadt and Calabrese 1991)]. They then computed the average synaptic conductance across animals and expressed these averages as peak synaptic conductances [g_SynHN(i)]. There is no difference in the synaptic strength profile between the synchronous and peristaltic coordination modes (Norris et al. 2007b). The set of four maximal conductances [g_SynHN(i)] is unique to each segmental motoneuron pair; thus each motoneuron pair has a unique synaptic strength profile. Each model motoneuron received its segment-specific synaptic strength profile as in Fig. 3 of Garcia et al. (2008). Each presynaptic heart interneuron spike elicited a unitary conductance that followed a double exponential function scaled by the synaptic weight for that input in that motoneuron [g_SynHN(i)]. The model computes g_Syn(t) from the sum of the four individual inhibitory synaptic conductances [g_SynHN(i)] associated with a particular presynaptic input HN_i. The heart motoneuron ensemble model with standard parameters (Garcia et al. 2008) is referred to as the canonical ensemble model.

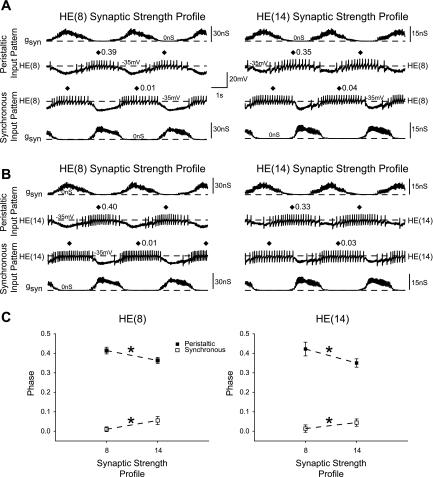
Fig. 3.

Heart motoneurons respond differently to different synaptic strength profiles. A: simultaneous intracellular recordings from a pair of HE(8) motoneurons receiving the segment 8 (left) followed by the segment 14 (right) input patterns. Both panels are from the same experiment. The synaptic strength profiles are different between the 2 segmental patterns (note the different scale bars). B: same as in A, but for the HE(14) motoneurons. Both preparations came from the same animal. C: the average phase (±SD, n = 6) of heart motoneurons in segments 8 (left) and 14 (right) each receiving the synaptic strength profiles for segments 8 and 14 are shown. Asterisks on each dashed line connecting data points indicate a significant effect of synaptic strength profile on motoneuron phase (2-way repeated-measures ANOVA, P < 0.05).

The heart motoneuron ensemble model was implemented in GENESIS (GEneral NEural Simulator System), with each model motoneuron receiving its segment-appropriate temporal pattern and synaptic strength profile. We ran the model for 60 s of model time. The model used the Euler integration method with a time step of 0.0001 s. The 13 bouts of inhibitory synaptic input sculpted 12 bursts of activity of the model motoneurons. We used these 12 bursts to assess the phase of the model fictive motor pattern (see below). We recorded and saved the computed synaptic conductance waveforms arising from each premotor HN interneuron as well as their sum (g_SynTotal; Fig. 1) in each motoneuron for subsequent use in the dynamic clamp (see below).

Hybrid system design and implementation.

We used the dynamic clamp technique (Prinz et al. 2004) to produce a virtual version of the heart interneuron-to-heart motoneuron synapse. The dynamic clamp both computes and injects, in real time (time step: 0.0001 s), a model of the synaptic current (I_Syn) based on the recorded intracellular membrane potential (V_m), a conductance [g_Syn(t)], and a reversal potential (E_Syn) according to Ohm's law. Because we are linking a model of this synapse with heart motoneurons in the living system, we refer to these preparations as hybrid systems. The virtual synapse was implemented according to the following equation:

$$I_{\text{Syn}}=\sigma g_{\text{Syn}}\left(t\right)\left(V_{\text{m}}-E_{\text{Syn}}\right)$$

where I_Syn is the synaptic current, g_Syn(t) is the time-varying synaptic conductance waveform representing the sum of all the individual synaptic inputs to a model motoneuron, σ is an integer value used to scale g_Syn(t), V_m is the membrane potential of the motoneuron, and E_Syn is the synaptic reversal potential (Angstadt and Calabrese 1991). To generate the synaptic conductance waveforms introduced in our hybrid system experiments, we extracted g_Syn(t) from canonical ensemble model simulations (see above). For simplicity, we label g_Syn(t) as g_Syn in figures and text. Figure 1A shows how g_Syn was assembled by summing the individual time-varying synaptic conductance waveforms from each input to an HE(10) motoneuron pair. Figure 1A also illustrates the difference in the total synaptic conductance trajectory (g_Syn, black trace) between the peristaltic (Fig. 1A, top) and the synchronous (Fig. 1A, bottom) modes. In the peristaltic mode, the synaptic conductance trajectory rises and falls slowly because the firing of the premotor interneurons is spread out, with the HN(7) interneuron leading the HN(3) interneuron, resulting in a gradual rise and decay of the synaptic conductance. In the synchronous mode, however, the synaptic conductance trajectory rises and falls more precipitously because the firing of the premotor interneurons occurs at nearly the same time, resulting in a much more rapid rise and decay of the synaptic conductance envelope. The synaptic conductance waveforms used in our hybrid system experiments were the same as in the ensemble model except they were scaled by σ. The scaling factor allowed us to increase the overall synaptic conductance while preserving the relative synaptic strength of the individual premotor synaptic conductances. Unless indicated otherwise, the canonical segmental input pattern was used both in the dynamic clamp and in the ensemble model.

In some experiments, we used the dynamic clamp to add to the natural electrical coupling between heart motoneurons. Electrical coupling was implemented according to:

$$I_{\text{coup}}=g_{\text{coup}}\left(V_a-V_b\right)$$

where V_a and V_b each represent the membrane potentials of one member of the pair of coupled heart motoneurons, I_coup is the coupling current from cell b to cell a (and −I_coup is the coupling current from cell a to cell b), and g_coup is the junctional conductance. Therefore, the total dynamic clamp current, I_dc, introduced to a pair of heart motoneurons (Fig. 1B) is defined as:

$$I_{\text{dc}}=I_{\text{Syn}}+I_{\text{coup}}$$

where, unless otherwise noted, I_coup = 0 nA (i.e., g_coup = 0 nS).

In another set of experiments, we varied the structure of the premotor synaptic conductance waveform in order to study how the coherence of the synaptic input pattern influences HE motoneuron phase. The temporal pattern of this synaptic input was based on the firing pattern of the HN(4) interneurons (both peristaltic and synchronous, each with their appropriate phasing) only; in this way, we could compute phase using the same phase reference as in our other experiments. The synaptic strength profile associated with this temporal pattern was the sum of the individual premotor heart interneuron synaptic conductances [i.e., g_Syn = ∑g_SynHN(i)]. The synaptic conductance waveform was trapezoidal in shape. The onset of the conductance envelope was triggered by the first spike of the HN(4) interneuron burst. The conductance envelope increased linearly from 0 nS to g_Syn during the first 500 ms of the HN(4) interneuron burst and then returned (termed “offset ramp conductance” in this study) to 0 nS 1) abruptly at the last spike of the HN(4) interneuron burst, 2) during the last 250 ms of the HN(4) interneuron burst, or 3) during the last 500 ms of the HN(4) interneuron burst. One heart motoneuron received this series of waveforms in order of increasing offset ramp conductance while its contralateral partner was receiving the same set of waveforms in order of decreasing offset ramp conductance.

In hybrid system experiments, we blocked the endogenous synaptic input with 10⁻⁴ M bicuculline methiodide unless otherwise noted. All dynamic clamp calculations were performed with a real-time dedicated processing board (DS1104; dSPACE, Detroit, MI). We activated the dynamic clamp synapses and electrical coupling only when the motoneurons were spiking tonically and had no discernible IPSPs in the voltage recording (Fig. 1C). In our hybrid system experiments, we 1) bilaterally varied the synaptic scaling factor (σ) introduced to a pair of heart motoneurons, 2) varied the origin of the segmental input pattern introduced into the same heart motoneuron pair, 3) varied the coupling conductance, g_coup, between heart motoneurons within a segment, or 4) introduced modified synaptic conductance patterns to heart motoneurons (see above). In experiments 1–3, we introduced 13 cycles of inhibitory synaptic conductance into a heart motoneuron pair, yielding 12 bursts of activity over 60 s. In experiment 4, we introduced 10 cycles of inhibitory synaptic conductance over 45 s, yielding 9 bursts of heart motoneuron activity.

Data analysis.

Electrophysiological data were analyzed off-line with a combination of pCLAMP 9.2 (Molecular Devices) and custom scripts written in Matlab (The Mathworks, Natick, MA) and Spike2 (CED Systems, Cambridge, UK). First, the raw voltage recordings were high-pass filtered (cutoff frequency ∼1 Hz). These data were then used for spike detection. Spike detection was carried out by methods reported previously (Norris et al. 2006).

After detection, spikes were grouped into bursts as follows: After an interburst interval of 500 ms, the next spike was deemed the first spike of that burst. Each subsequent spike was included in that burst until the interspike interval became > 500 ms (interburst interval). A minimum of four spikes were required in order to qualify as a burst. In some experiments, the dynamic clamp-mediated inhibitory synaptic current injected into a heart motoneuron did not inhibit it sufficiently, so that the heart motoneuron continued firing, but at a low frequency, during the inhibited phase of its oscillations (i.e., during the peak dynamic clamp injected current). In those recordings, we removed this small number (usually < 4) of spikes during the trough of the inhibited phase to create a sufficient interburst interval for burst detection.

We defined period as the interval between successive middle spikes of the peristaltic HN(4) interneuron [T_HN(4)]. We then computed the phase of the heart motoneurons with respect to the synaptic input pattern that they received. We defined phase as the difference in time for a spike of interest of a heart motoneuron and the time of the middle spike of the phase reference, the peristaltic HN(4) interneuron [Δt_{HE(i)f,m,l−HN(4)}]. This difference is then normalized to the period of the phase reference. Thus phase is given by:

$${\phi }_{\text{f},\text{m},\text{l}}=\left[\Delta t_{\text{HE}\left(i\right)\text{f},\text{m},\text{l}-\text{HN}\left(4\right)}/T_{\text{HN}\left(4\right)}\right]$$

We calculated the average first (f), middle (m), and last (f) spike phases, burst period (T), and duty cycle (D) for each heart motoneuron recorded. In the text and figures, the generic term phase and symbol ϕ are applied to the middle spike phase as defined above. In figures, we indicate the middle spike phase within each heart motoneuron burst by a filled diamond above that burst. All phase values are expressed modulo one. Duty cycle is defined as the difference between the average last spike phase and the average first spike phase:

$$D={\phi }_{\text{last}}-{\phi }_{\text{first}}$$

Because the duty cycle is the difference between two averages, standard deviation is not reported.

Statistics.

Data were compiled and analyzed with Microsoft Excel (2010, Microsoft, Redmond, WA), SigmaPlot 11 (Systat Software, San Jose, CA), Minitab (v14, Minitab, State College, PA), or Matlab (The Mathworks). We generated an average phase and duty cycle for each preparation, and the average (±SD, n = either 6 or 7 preparations) across animals was used for all statistical analyses. In the experiments in which the synaptic conductance was scaled (by varying σ; see Hybrid system design and implementation, above), the coupling conductance (g_coup) was varied, or the synaptic conductance (g_Syn) was modified, all phases and duty cycles were analyzed with a one-way repeated-measures ANOVA with follow-up Bonferroni posttests. For comparisons between the hybrid and living systems, we used a two-sample t-test to compare the appropriate phases. For comparisons between either the living or hybrid system and the model, we used a one-sample t-test. Finally, in experiments in which the segmental input pattern was varied, a two-way (Cell × Pattern) repeated-measures ANOVA was used, with Bonferroni posttests. Statistical significance was set at P < 0.05 for all statistical tests. All figures were generated with Adobe Illustrator 15.0 (Adobe Systems, San Jose, CA).

RESULTS

Scaling the synaptic input conductance by a constant factor affects hybrid system heart motoneuron duty cycles but not their phasing.

In our previous modeling efforts (Garcia et al. 2008), we hand-tuned the output of the model motoneurons by scaling the synaptic conductance waveform by a constant factor. This manipulation allowed us to match total synaptic conductance to the model neuron intrinsic properties while preserving the relative contribution of each of the premotor heart interneurons. Adjusting the scaling factor effectively tuned the duty cycle of the model motoneurons, without affecting their middle spike phasing. To determine the appropriate scaling factor for our experiments and to determine its effects on firing phase and duty cycle, we varied the scaling factor of the synaptic conductance in the hybrid system. We recorded simultaneously from the pair of heart motoneurons in segment 10 (n = 6) and played in the segmental input pattern for the HE(10) motoneurons from our canonical ensemble model. We then scaled this input by three different constant values: 3, 5, and 8 (σ; see methods) (Fig. 2, A–C). We chose these values because values < 3 resulted in bursts that were poorly defined at their beginning and ends, with duty cycles typically > 0.9, while values > 8 did not further decrease the duty cycle because at these scaling values the heart motoneurons were silenced for the duration of the input waveform each cycle. We then compared the average first spike, middle spike, and last spike phase, as well as the duty cycles observed among the three different scaling factors. Figure 2D shows summarized results for experiments performed in segments 8, 10, 12, and 14 as a bilateral phase diagram. There was a significant decrease in duty cycle with increasing scaling factor in all segments tested in the peristaltic mode and in segments 10, 12, and 14 in the synchronous mode (1-way repeated-measures ANOVA, P < 0.05). In those segments where there was a significant difference in duty cycle, there were also significant differences in the average first and last spike phase among the three scaling factors (1-way repeated-measures ANOVA, P < 0.05). As the scaling factor is increased, burst onsets (as measured by the average first spike phase) are delayed, while burst offsets (as measured by last spike phase) are advanced. The middle spike phase, therefore, is not affected because the scaling factor decreases the incidence of spikes nearly equally from both the beginning and the end of each heart motoneuron burst.

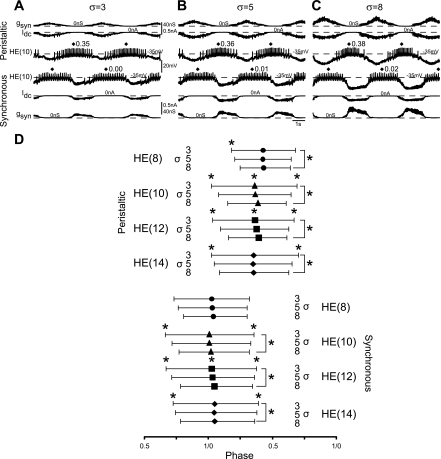
Fig. 2.

Tuning the output of heart motoneurons using the synaptic scaling factor in the hybrid system. A–C: simultaneous intracellular recordings from a pair of HE(10) motoneurons receiving the same HE(10) segmental input pattern as that used in our canonical ensemble model. A–C are from the same experiment. The synaptic conductance was scaled by a constant value (σ; see methods) of 3 (A), 5 (B), or 8 (C). D: bilateral phase diagram for HE motoneurons in segments 8, 10, 12, and 14 for each of the 3 scaling factors. Symbols show the average (n = at least 6 preparations per segment) middle spike phase for segment 8 (●), 10 (▲), 12 (■), and 14 (♦); vertical bars connected to the filled symbols show the average first (left vertical lines) and last (right vertical lines) spike phase. Lines and asterisks indicate significant differences in the appropriate phasing or duty cycle among the 3 scaling factors (1-way repeated-measures ANOVA, P < 0.05).

The middle spike phase, however, was significantly different across the three scaling factors in some of the segments tested, specifically the HE(10) motoneuron receiving the peristaltic input pattern and the HE(10) and HE(12) motoneurons receiving the synchronous input pattern. To assess which of the scaling factors were different, we conducted Bonferroni posttests. In each segment, the scaling factor of 8 was significantly different from both scaling factors 3 and 5 (P < 0.05); scaling factors 3 and 5 were not significantly different from each other. Although there are significant differences in middle spike phase among the three scaling factors in our experiments, it is important to note that each of the values observed falls within the range of middle spike phase measured in the living system (Norris et al. 2007a). In subsequent experiments, however, we focused only on segments where the scaling factor did not show this effect (i.e., segments 8 and 14).

Taken together, these results suggest that, as in our canonical ensemble model (Garcia et al. 2008), scaling the synaptic conductance waveform by a constant factor over a moderate range allowed us to tune the output of the heart motoneurons without affecting the middle spike phase. We settled on the scaling factor of 3 for comparison of hybrid system phasing to living system phasing, because the duty cycle associated with this scaling factor was the most similar to that observed in the living system (Table 1).

Table 1.

Statistical comparison of phasing observed in the living system, hybrid system, and ensemble model for heart motoneurons in segments 8, 10, 12, and 14

	Peristaltic Coordination Mode						Synchronous Coordination Mode
Segment	First spike	SD	Middle spike	SD	Last spike	SD	First spike	SD	Middle spike	SD	Last spike	SD
8
Living	0.20	0.07	0.47	0.04	0.77	0.07	0.73	0.06	0.01	0.04	0.32	0.05
Hybrid	0.18†	0.03	0.43*	0.02	0.68*	0.05	0.73	0.04	0.02†	0.04	0.32	0.04
Model	0.26‡	0.01	0.43‡	0.02	0.67‡	0.04	0.82‡	0.04	0.12‡	0.03	0.35	0.04
10
Living	0.03	0.09	0.37	0.07	0.71	0.08	0.70	0.10	0.02	0.07	0.36	0.05
Hybrid	0.02†	0.02	0.36	0.02	0.69†	0.04	0.66†	0.04	0.01†	0.03	0.36†	0.04
Model	0.16‡	0.03	0.38	0.01	0.62‡	0.01	0.83‡	0.04	0.15‡	0.03	0.39‡	0.03
12
Living	0.05	0.08	0.35	0.05	0.69	0.07	0.73	0.13	0.03	0.08	0.35	0.07
Hybrid	0.04†	0.02	0.36	0.02	0.67†	0.04	0.67†	0.04	0.03†	0.03	0.38†	0.04
Model	0.10	0.02	0.36	0.01	0.63‡	0.04	0.83‡	0.04	0.15‡	0.03	0.41‡	0.04
14
Living	0.94	0.11	0.27	0.10	0.69	0.10	0.73	0.13	0.04	0.10	0.44	0.09
Hybrid	0.02	0.03	0.35	0.02	0.70	0.04	0.72†	0.05	0.05†	0.03	0.39†	0.04
Model	0.07‡	0.02	0.36‡	0.02	0.71	0.04	0.82	0.04	0.16‡	0.03	0.43	0.04

Comparison of first, middle, and last spike phasing among the living system, hybrid system and canonical ensemble model is shown.

^*Significant differences between hybrid and living systems (2-sample t-test);

^†significant differences between hybrid system and model (1-sample t-test);

^‡significant differences between model and living system (1-sample t-test). See methods.

The segmental input pattern determines segmental phase differences in motoneuron phasing in the hybrid system.

Before assessing whether heart motoneuron intrinsic properties contribute to their appropriate segmental phasing, we asked whether the intrinsic properties of the motoneurons were similar across segments. Because the canonical ensemble model motoneurons are identical in their intrinsic properties, they naturally assume different output phasing depending on the segmental input pattern introduced into them. To test whether heart motoneurons in midbody segments 8 through 14 show any systematic variation in their intrinsic properties, we isolated segmental ganglia 8 and 14 (n = 6 each) in each experiment and synaptic strength profiles for segments 8 and 14 were introduced into the heart motoneuron in both ganglia. Figure 3A compares the response of the HE(8) motoneurons to the HE(8) and HE(14) synaptic strength profiles; Fig. 3B compares the response of the HE(14) motoneurons to the HE(8) and the HE(14) synaptic strength profiles. Figure 3C shows the average (±SD) phase of the HE(8) motoneuron (Fig. 3C, left) and the HE(14) motoneuron (Fig. 3C, right) when receiving both synaptic strength profiles. The lines connecting the phase symbols show the effect of the synaptic strength profile on phase. There was a significant effect of the synaptic strength profile on phase in both coordination modes (2-way repeated-measures ANOVA; peristaltic mode F = 410.87, df = 1, P < 0.01; synchronous mode F = 147.47, df = 1, P < 0.01). Comparison of the average phase of the HE(8) and HE(14) motoneurons when receiving the same synaptic strength profile [e.g., compare the HE(8) and the HE(14) motoneuron phase when both receive the HE(8) synaptic strength profile in Fig. 3C] indicates the effect of the segmental origin of the heart motoneuron on phase. There was no significant effect of the segmental origin of the heart motoneuron on phase in either mode (2-way repeated-measures ANOVA; peristaltic mode F = 0.04, df = 1, P = 0.85; synchronous mode F = 0.41, df = 1, P = 0.55). These results suggest that there are no systematic differences in heart motoneuron intrinsic properties between midbody segments 8 and 14 that cause them to respond differently to similar input patterns. In addition, they suggest that the segmental input pattern independently determines the phasing differences observed in motoneurons in segments 8 through 14, regardless of any role heart motoneuron intrinsic properties may play in the final phasing assumed.

Comparison of motoneuron phasing in the hybrid and living systems.

We now compared the phasing of heart motoneurons in the hybrid system to the phasing observed in the living system and the model. Figure 4, A–D, show typical recordings from heart motoneurons from segments 8 (Fig. 4A), 10 (Fig. 4B), 12 (Fig. 4C), and 14 (Fig. 4D) (n = at least 6 per segment). Each of these motoneurons received the same segment-appropriate input pattern as those in our canonical ensemble model. Figure 4E shows a bilateral phase diagram for the summarized data for each of these segments. Asterisks in Fig. 4E show comparisons of the hybrid system to the living system, and pound signs show comparisons of the canonical ensemble model to the living system; Table 1 includes all possible comparisons. We present the segment-specific results for the peristaltic mode first, followed by the synchronous mode.

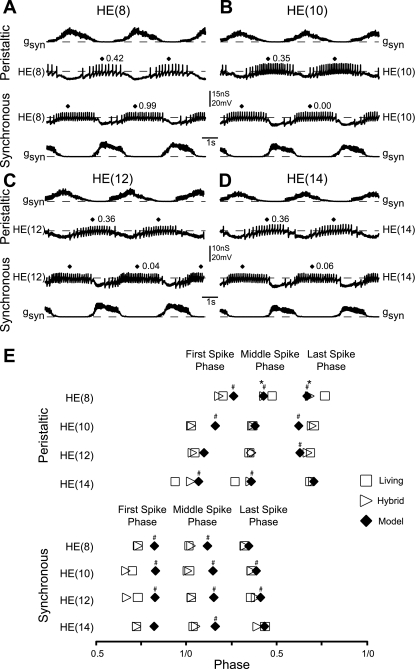
Fig. 4.

Heart motoneuron intrinsic properties contribute to their segment-appropriate phasing in the hybrid system. A–D: simultaneous intracellular recordings and synaptic input conductances from heart motoneurons in segments 8 (A), 10 (B), 12 (C), and 14 (D). E: bilateral phase diagram of the average first, middle, and last spike phases measured in the living system (n = at least 8 preparations per segment), the hybrid system (n = at least 6 preparations per segment), and the canonical ensemble model for segments 8, 10, 12, and 14. *Significant difference between the hybrid and living systems; #significant difference between the ensemble model and the living system (t-test, P < 0.05). Statistical comparisons between the hybrid system and the canonical ensemble model can be seen in Table 1.

In the hybrid system for HE(8) motoneurons receiving the peristaltic input pattern, first spike phase was similar to that observed in the living system (2-sample t-test, P = 0.41), but their middle and last spike phases were delayed (2-sample t-test, P < 0.05 for both comparisons) (Fig. 4E). Comparing canonical ensemble model phasing to the living system, model first spike phase was delayed and middle and last spike phases were advanced (1-sample t-test, P < 0.05 for all comparisons) (Fig. 4E). Compared with the canonical ensemble model, the hybrid system first spike phase was advanced (1-sample t-test, P < 0.05), but middle and last spike phases were similar (1-sample t-test, middle spike P = 0.50; last spike P = 0.27) (Table 1). Considering middle spike phase only, HE(8) bursts in both the model and the hybrid system are phase advanced compared with the living system.

In the hybrid system for HE(10) motoneurons receiving the peristaltic input pattern, first, middle, and last spike phases were similar to those observed in the living system (2-sample t-test, first P = 0.86, middle P = 0.69, last P = 0.66) (Fig. 4E). Comparing canonical ensemble model phasing to the living system, model first spike phase was delayed (1-sample t-test, P < 0.05), middle spike phase was similar (1-sample t-test, P = 0.67), and last spike phase was advanced (1-sample t-test, P < 0.05) (Fig. 4E). Compared with the canonical ensemble model, the hybrid system first spike phase was advanced (1-sample t-test, P < 0.05), middle spike phase was similar (1-sample t-test, P = 0.11), and last spike phase was delayed (1-sample t-test, P < 0.05) (Table 1). Considering middle spike phase only, HE(10) bursts in both the model and the hybrid system are phased similarly to the living system.

In the hybrid system for HE(12) motoneurons receiving the peristaltic input pattern, first, middle, and last spike phases were similar to those observed in the living system (2-sample t-test, first P = 0.61, middle P = 0.54, last P = 0.55) (Fig. 4E). Comparing canonical ensemble model phasing to the living system, model first and middle spike phases were similar (1-sample t-test, first spike P = 0.06, middle spike P = 0.67) and last spike phase was advanced (1-sample t-test, P < 0.05) (Fig. 4E). Compared with the canonical ensemble model, the hybrid system first spike phase was advanced (1-sample t-test, P < 0.05), middle spike phase was similar (1-sample t-test, P = 0.57), and last spike phase was delayed (1-sample t-test, P < 0.05) (Table 1). Considering middle spike phase only, HE(12) bursts both the in the model and in the hybrid system are phased similarly to the living system.

In the hybrid system for HE(14) motoneurons receiving the peristaltic input pattern, first and middle spike phases tend to be delayed compared with those observed in the living system, although this delay is not statistically significant (2-sample t-test, first spike P = 0.11, middle spike P = 0.06, last spike P = 0.67) (Fig. 4E). Comparing canonical ensemble model phasing to the living system, model first and middle spike phases were delayed (1-sample t-test, P < 0.05 for both comparisons), whereas last spike phase was similar (1-sample t-test, P = 0.97) (Fig. 4E). Compared with the canonical ensemble model, the hybrid system first, middle, and last spike phases were similar (1-sample t-test, first spike P = 0.12, middle spike P = 0.99, last spike P = 0.77) (Table 1). Considering middle spike phase only, HE(14) bursts in the hybrid system are phased similarly, but in the model they are delayed compared with the living system.

In the hybrid system for HE(8), HE(10), HE(12), and HE(14) motoneurons receiving the synchronous input pattern, the results were similar, so we treat them together. In each of these motoneurons, the hybrid system first, middle, and last spike phases were similar to the living system (2-sample t-test, P > > 0.05 for all comparisons) (Fig. 4E). Comparing canonical ensemble model phasing to the living system, in the HE(8) motoneuron first and middle spike phases were delayed (1-sample t-test, P < 0.05 for both comparisons) and last spike phase was similar (1-sample t-test, P = 0.14) (Fig. 4E). In the HE(10) and HE(12) motoneurons first, middle, and last spike phases were delayed (1-sample t-test, P < 0.05 for all comparisons) (Fig. 4E). In the HE(14) motoneuron only the middle spike phase was delayed (1-sample t-test, P < 0.05); the first and last spike phases were similar (1-sample t-test, first spike P = 0.06, last spike P = 0.95) (Fig. 4E). Compared with the canonical ensemble model, the hybrid system first, middle, and last spike phases were all advanced (1-sample t-test, P > 0.05 for all comparisons) (Table 1). Considering middle spike phase only for all these motoneurons, bursts in the hybrid system are phased similarly but bursts in the model are delayed compared with the living system.

Because the motoneurons in the hybrid system received the same segmental input pattern as the model motoneurons, we infer that any differences in phasing (first, middle, or last spike phase) between the hybrid system and the canonical ensemble model indicate that the motoneurons in the living system possess additional intrinsic properties, not present in the model motoneurons. Similarity in the phasing of the motoneurons in the hybrid and living systems further corroborates this inference and further suggests that these additional intrinsic properties contribute to appropriate motoneuron phasing in the living system. Heart motoneurons in the hybrid system receiving the synchronous segmental input pattern showed phasing similar to that observed in the living system and different from the model. We conclude that living motoneurons possess intrinsic properties that contribute to proper phasing when receiving the synchronous input. When receiving peristaltic input in the hybrid system, in those cases [i.e., HE(10) and HE(12) motoneurons] where ensemble model phasing is similar to the living system, the hybrid system also showed phasing similar to the living system. However, the HE(8) motoneurons in the hybrid system, like their model counterparts, are phase advanced compared with the living system, and the HE(14) motoneurons in the hybrid system show a tendency to be phase delayed compared with the living system, although this delay is not statistically significant, as this delay is in their model counterparts.

To assess whether the discrepancies observed between the hybrid system and the living system phasing (in the peristaltic mode) were due to nonspecific effects of the bicuculline methiodide block of the premotor inputs, we performed experiments in which we blocked the premotor inputs with a modified leech saline in which the Ca²⁺ was replaced with an equimolar amount of Mn²⁺. In these experiments, the HE(8) motoneurons received the HE(8) segmental input pattern during exposure to this modified saline. We then compared the phasing observed with the modified saline to that observed in bicuculline methiodide. Although the average (n = 6) middle spike phase was delayed in both the peristaltic (0.01) and synchronous (0.02) modes compared with the bicuculline methiodide block, there was not a significant difference in middle spike phase between the two forms of presynaptic block (2-sample t-test; data not shown). Furthermore, the delay in phase did not change the correspondence between the hybrid system and the living system in either mode. This result indicates that bicuculline methiodide did not strongly affect the phasing observed in the hybrid system.

Heart motoneurons in the hybrid system receiving the synchronous segmental input pattern, however, show phasing consistent with that observed in the living system.

Contribution of heart motoneuron intrinsic properties to phasing observed in the hybrid system.

Next, we explored how the intrinsic properties of the heart motoneurons in the living system may allow them to integrate a segmental input pattern differently from the model motoneurons in the canonical ensemble model. In the canonical ensemble model, the current primarily responsible for depolarization and burst formation is a persistent Na⁺ current, which was characterized by Opdyke and Calabrese (1994) in heart interneurons and termed I_p. The I_p in the model was hand-tuned so the model motoneurons fired tonically at an appropriate spike frequency in the absence of synaptic input (Schmidt and Calabrese 1992). The model motoneurons did not include currents such as I_h, which could produce postinhibitory rebound in response to the synaptic input pattern they received. The synchronous premotor synaptic conductance declines precipitously because of near synchrony in the termination of the premotor inputs. Therefore, model motoneurons receiving the synchronous input pattern are only able to initiate their bursts once the synaptic conductance has nearly ended. When a model motoneuron initiates its firing, its spike frequency increases throughout a burst. Heart motoneuron pairs share inhibitory synaptic current via their electrical coupling. As inhibition in the opposite motoneuron wanes, spike frequency in uninhibited motoneurons increases because of less shared inhibitory current. This sharing of inhibitory current delays the depolarization of a model motoneuron during its burst (cf. Fig. 5, Garcia et al. 2008). Therefore, the lack of postinhibitory rebound, combined with the delaying effect of the electrical coupling, contributes to a delay in model phase compared with the living system in the synchronous mode. In the hybrid system, heart motoneurons receiving the synchronous input pattern show modest rebound spiking and, on average, initiate their firing at an earlier phase than model motoneurons (Fig. 4). Although there were some significant differences in last spike phase between the model and the hybrid system in the synchronous mode (Table 1), these differences were not as substantial as those observed in the first and middle spike phases, so we focused on the role of intrinsic properties in the initiation of firing rather than on the termination of firing. We hypothesized that heart motoneurons, owing to their intrinsic properties, are able to initiate their bursts earlier in the hybrid system than the motoneurons in the canonical ensemble model. Therefore, motoneurons in the hybrid system are able to match the phasing observed in the living system, unlike the model motoneurons.

Fig. 5.

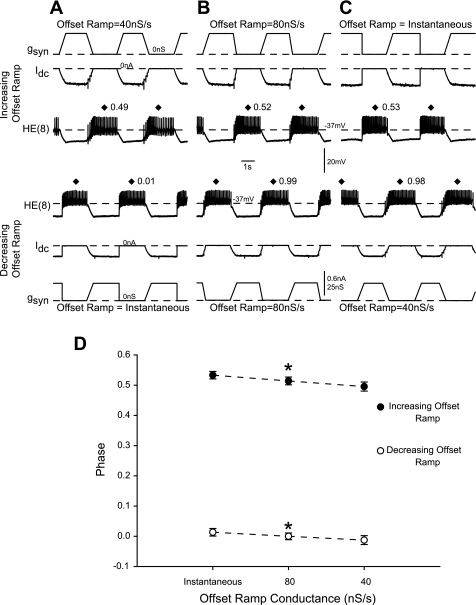
Replacing the standard synaptic conductance waveform with a modified conductance waveform affects heart motoneuron phase. Simultaneous intracellular recordings from the HE(8) motoneurons (top) receiving a trapezoidal conductance waveform in which the offset rate increased from 40 nS/s (A) to 80 nS/s (B) to instantaneous (C) while the other heart motoneuron (bottom) received a trapezoidal conductance waveform in which the offset rate decreased from instantaneous (A) to 80 nS/s (B) to 40 nS/s (C) are shown. Because we played in the series of waveforms to the 2 heart motoneurons in opposite directions, A and C correspond. All panels are from the same experiment. D: summary phasing of the HE(8) motoneurons receiving the series of modified waveforms described in A–C. Asterisks on each line indicate significant differences in phase among the 3 waveforms (1-way repeated-measures ANOVA, P < 0.05).

Opdyke and Calabrese (1995) characterized multiple outward currents in the heart motoneurons. The inward currents they found were small when measured at the level of the heart motoneuron soma and hence not analyzed. Therefore, it was not feasible to test, via pharmacological blockade, which inward currents might account for the difference in synaptic input integration between the model and living heart motoneurons. As a compromise, we tested our hypothesis that heart motoneurons initiate their firing earlier by replacing the g_Syn extracted from the canonical ensemble model simulations with modified inhibitory synaptic conductance waveforms (Fig. 5). These modified waveforms were designed to engage the complement of intrinsic properties present in the heart motoneurons in different ways. The waveforms were timed to the inputs from the HN(4) premotor interneuron (to preserve our absolute phase reference) and were trapezoidal in shape. The modified conductance waveforms had the same onset kinetics (a ramp conductance rising from 0 nS to g_Syn over 500 ms) but varied in their offset kinetics (i.e., the offset ramp conductance returning from g_Syn to 0 nS) 1) instantaneously (offset ramp conductance = instantaneous), 2) over the last 250 ms of the HN(4) interneuron burst (offset ramp conductance = 80 nS/s) or 3) over the last 500 ms of the HN(4) interneuron burst (offset ramp conductance = 40 nS/s). To determine how these waveforms were integrated by the heart motoneurons, we performed bilateral recordings of heart motoneurons in segment 8. One of the HE(8) motoneurons received three waveforms in which the offset ramp conductance increased from 40 nS/s to the instantaneous offset (increasing offset ramp; Fig. 5, top), while the other HE(8) motoneuron received the reverse sequence (decreasing offset ramp; Fig. 5, bottom). We then compared the average (n = 7) first, middle, and last spike phases among the three waveforms. There was a significant difference in the first and middle spike phases among the three inhibitory synaptic conductance waveforms (Fig. 5D; 1-way repeated-measures ANOVA, P < 0.05), with heart motoneurons receiving the instantaneous offset ramp conductance waveform firing later in phase than the 40 nS/s ramp offset waveforms. As expected, there was not a significant difference in last spike phase, as the conductance waveform onset ramp was the same for each of the trapezoidal waveforms used (1-way repeated-measures ANOVA, P > 0.05). The waveform with the instantaneous offset should most closely replicate the situation observed in the canonical ensemble model; by leaving g_Syn at its maximal value until the end of the HN(4) interneuron burst, this waveform overrides the expression of those heart motoneuron intrinsic properties that would initiate firing at an earlier phase. In contrast, the waveform with the slowest offset ramp allows the heart motoneurons to initiate their firing earlier in phase owing to their intrinsic properties. Interestingly, the phasing observed in Fig. 5A, top, would be well matched to the peristaltic mode phasing while that in Fig. 5A, bottom, would be well matched to the synchronous mode phasing observed in the living system (Norris et al. 2007b), suggesting that these two waveforms correspond roughly to our “peristaltic” and “synchronous” coordination mode segmental input patterns. That the hybrid system phasing with the “peristaltic” waveform results in a better match to the living system than the biologically derived peristaltic input waveform could be due to the fact that this waveform provides a greater amount of overall inhibition to the heart motoneurons and thus forces the heart motoneurons to assume a nearly antiphase (i.e., 0.5) output compared with the HN(4) interneuron. Alternatively, these waveforms may access heart motoneuron intrinsic properties in a manner not replicated completely by the dynamics of the biological segmental input pattern. Taken together, these results suggest that heart motoneuron intrinsic properties contribute to their appropriate phasing, particularly when receiving the synchronous input pattern, by promoting phase advances.

Adding and subtracting electrical coupling alters the middle spike phasing of the heart motoneurons in the hybrid system.

In addition to their intrinsic properties, another potential contribution to the phasing of heart motoneurons observed in the living system is the electrical coupling between segmental pairs (Peterson 1983). Our canonical ensemble model (Garcia et al. 2008) suggested that this coupling may be important in establishing motoneuron phasing. We wanted to explore, then, the extent to which electrical coupling could modify the phasing of motoneurons observed in the hybrid system and whether or not this influenced the difference in phase between the hybrid system and the living system in the peristaltic mode. We explored the effect of electrical coupling in the hybrid system by adding virtual electrical coupling between the pair of heart motoneurons in segment 8.

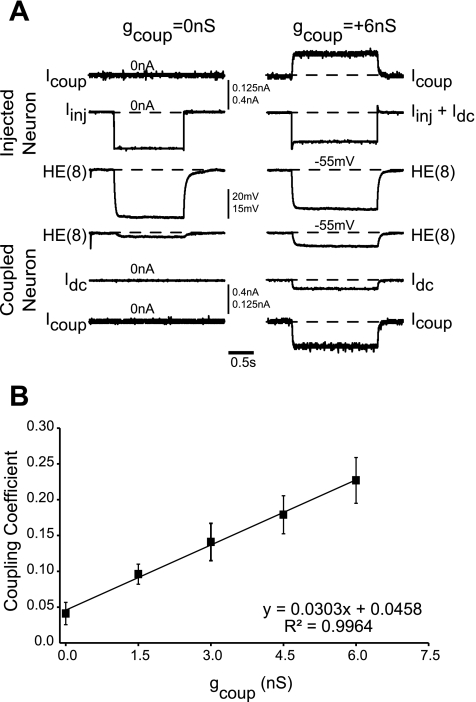
First, we assessed the efficacy of virtual electrical coupling achieved with the dynamic clamp. We measured the endogenous level of soma-to-soma coupling present in pairs of HE(8) motoneurons with hyperpolarizing current pulses (Fig. 6A) and then computed the coupling coefficient (Fig. 6B) as the ratio of the postsynaptic voltage response to the presynaptic voltage response (n = 7). We then turned on the virtual electrical coupling with the synaptic conductance (g_Syn) set to 0 nS and varied the virtual coupling conductance (g_coup) from 1.5 nS to 6 nS in 1.5-nS increments (Fig. 6A), computing the coupling coefficient for each value of g_coup. As can be seen in the average data of Fig. 6B, there was a linear increase in the coupling coefficient as the virtual coupling conductance was increased. Greater than 99% of the variance in coupling coefficient is explained by its regression on the artificial coupling conductance applied (R² = 0.996, F = 385.90, df = 1, P < 0.05). This control protocol indicates that our virtual electrical coupling was effective and did not negatively affect the performance of the dynamic clamp.

Fig. 6.

Augmentation of endogenous gap coupling. A: simultaneous intracellular recordings from a pair of HE(8) motoneurons. The dynamic clamp was running, but the dynamic clamp inhibitory synaptic input had been turned off (g_Syn = 0 nS). A −0.5-nA step of current (I_inj) was injected into 1 heart motoneuron (injected cell, top traces), and the voltage deflection in both neurons was recorded; the dynamic-clamp coupling conductance (g_coup) was set to 0 nS (left) or +6 nS (right). With no dynamic-clamp conductance, the contralateral heart motoneuron shows a voltage deflection (coupled neuron, bottom traces) indicative of the endogenous coupling present between the 2 heart motoneurons. With the dynamic-clamp coupling conductance set to +6 nS, the same current injection now produces a much larger voltage deflection in the coupled cell. We then computed the coupling coefficient as the ratio of the contralateral cell's voltage deflection to the injected cell's voltage deflection for a range of dynamic-clamp coupling conductances. B: effect of artificial coupling on coupling coefficient. In 7 experiments of the type described in A, we computed the coupling coefficient across a range of artificial coupling conductances in the dynamic clamp. The average (±SD) coupling coefficient is plotted vs. the artificial coupling conductance used in the dynamic clamp.

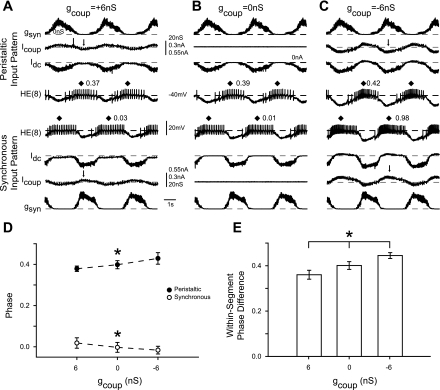
After performing the above control protocol, we then turned on the dynamic clamp synapse (in the same preparation) and played in the segment-appropriate peristaltic and synchronous inhibitory synaptic conductance waveforms along with the virtual coupling conductance set to 6 nS (Fig. 7A), 0 nS (Fig. 7B), or −6 nS (Fig. 7C). When the virtual coupling conductance in this preparation was set to 6 nS, the phasing of the peristaltic heart motoneuron was shifted to an earlier phase (0.37 from 0.39) while the phasing of the synchronous motoneuron was shifted to a later phase (0.03 from 0.01) compared with g_coup = 0 nS. In the average (n = 6) data, we saw significant differences in both coordination modes for phase (Fig. 7D; 1-way repeated-measures ANOVA, P < 0.05).

Fig. 7.

Effect of artificial coupling on HE(8) motoneuron phase: simultaneous intracellular recordings from the HE(8) motoneurons with the artificial coupling conductance g_coup set to −6 nS (A), 0 nS (B), and +6 nS (C). Each panel is from the same experiment. D: summary phase (average ± SD, n = 6) for the HE(8) motoneurons receiving the coupling conductances as described in A–C. Asterisks on each line indicate a significant difference in phase among the 3 artificial coupling values (1-way repeated-measures ANOVA, P < 0.05). E: summary (average ± SD, n = 6) within-segment phase difference between the 2 HE(8) motoneurons. Asterisks indicate a significant difference in the within-segment phase difference across the 3 artificial coupling values (1-way repeated-measures ANOVA, P < 0.05).

In the hybrid system experiments described above, we tested the removal of electrical coupling by setting the virtual coupling conductance to −6 nS. In the preparation illustrated in Fig. 7C, the phase of the peristaltic heart motoneuron is shifted to a later phase (0.42 from 0.39) while the phasing of the synchronous motoneuron is shifted to an earlier phase (0.98 from 0.01) compared with g_coup = 0 nS. There is a significant difference in the average (n = 7) phase in both coordination modes (1-way repeated-measures ANOVA, P < 0.05).

Increasing electrical coupling in the ensemble model (Garcia et al. 2008) produces a synchronizing effect on the activity of the heart motoneurons (i.e., the side-to-side phase difference within a segment decreased). Here we explored the physiological significance of the electrical coupling between the heart motoneurons in the hybrid system. In the case of adding to the endogenous coupling between heart motoneurons, when one heart motoneuron is hyperpolarized because of the inhibitory input pattern, that motoneuron passes hyperpolarizing current to its contralateral homolog (arrow on top I_coup trace, Fig. 7A); at the same time, the contralateral motoneuron, which is spiking, passes depolarizing current back to the hyperpolarized cell (arrow on bottom I_coup trace, Fig. 7A). The net effect of enhancing endogenous electrical coupling is twofold: The first effect is to decrease the impact of a given heart motoneuron's I_Syn because some portion of that motoneuron's synaptic current is passed to its contralateral homolog via the electrical coupling. Second, hyperpolarizing current passing from an inhibited motoneuron to its contralateral homolog during its spiking phase attenuates spiking activity during its burst. In the peristaltic mode, these two effects combine to promote a phase advance, as passage of hyperpolarizing current to the peristaltic motoneuron from its inhibited contralateral homolog slows its burst, shifting a greater incidence of spikes to the beginning of the burst. In the synchronous mode, these two effects promote a phase delay, as passage of hyperpolarizing current attenuates the onset of the burst. These two effects result in a significantly smaller within-segment phase difference compared with g_coup = 0 nS (Fig. 7E; 1-way repeated-measures ANOVA, P < 0.05), suggesting that electrical coupling synchronizes (i.e., brings their phasing closer together) activity between heart motoneurons within a segment. In our ensemble model, Garcia et al. (2008) suggested that this synchronizing effect was not uniform across segments because of the side-to-side differences in the phasing of the input among segments; therefore, in addition to affecting segmental phasing, electrical coupling could also influence intersegmental coordination. Alternatively, in setting the coupling conductance to a negative value, we reverse the sign of the coupling current (i.e., I_coup), thus effectively canceling part or all of the endogenous coupling, potentially even adding net negative coupling. By removing endogenous coupling, we enhance the net effect of a given motoneuron's own I_Syn and functionally uncouple the two motoneurons. Note that −g_coup enhances the inhibition of one motoneuron during its inhibited phase (top arrow on I_coup, Fig. 7C) as well as enhancing the depolarization of the contralateral motoneuron (bottom arrow on I_coup, Fig. 7C). The net effect is a phase delay of the peristaltic motoneuron and a phase advance of the synchronous motoneuron, thus promoting a significant increase in side-to-side phase difference (Fig. 7E, 1-way repeated-measures ANOVA, P < 0.05).

Taken together, these results affirmed our modeling prediction that the electrical coupling between the heart motoneurons serves to synchronize their ongoing bursting activity. Although these results show that electrical coupling affected the phase of the heart motoneurons in the hybrid system, the synchronizing effect did not improve the correspondence between the hybrid and living systems in the peristaltic mode, nor did it change the good correspondence between the hybrid and living systems in the synchronous mode.

DISCUSSION

The goal of the present investigation was to assess how motoneuron intrinsic properties contribute to rhythmic motor output. We used the leech heartbeat CPG, a system in which the pattern of premotor synaptic drive has been quantitatively defined, to address this question. Previously, we introduced a biologically derived input pattern into a canonical model of the ensemble of heart motoneurons in which their intrinsic electrical properties were kept to a minimum (Garcia et al. 2008). While the model motoneurons captured the bilateral asymmetry observed in the living system, model output phasing was significantly different from that observed in the living system (Fig. 4, Table 1), suggesting a role for heart motoneuron intrinsic properties in producing their appropriate output phasing. Here we constructed hybrid systems using segmental input patterns which were derived from the living system and which were used in the canonical ensemble model. We show directly in living motoneurons that receive these segmentally appropriate input patterns that motoneuron intrinsic properties do contribute to appropriate motor output phasing.

The segmental input pattern determines the segmental phase differences in heart motoneuron phasing.

The same heart motoneuron [HE(8) and HE(14) motoneurons] responds differently to different synaptic strength profiles (i.e., the segment 8 and 14 synaptic strength profiles), while different motoneurons (segments 8 and 14) respond similarly to the same input pattern (segment 8 input pattern, Fig. 3). This result implies that the segmental input pattern determines the phasing differences observed in motoneurons in segments 8 through 14 and that the intrinsic properties present in the heart motoneurons in these segments show no systematic segmental variation. In previous work with the heart motoneurons, Opdyke and Calabrese (1995) showed that passive properties (input resistance and capacitance) were not significantly different, particularly among heart motoneurons between segments 7 and 12. It was also shown that there were no significant differences in the maximal current measured for two of the outward currents, which are termed I_K1 and I_K2, between these segments. Although measuring heart motoneuron inward currents at the level of the soma has proved difficult, these results suggest we should not expect to find significant differences among the inward currents in these segments.

The finding that the input pattern determines the segmental phasing differences observed in motoneurons is perhaps not surprising. In the absence of premotor synaptic input, the heart motoneurons fire tonically and do not show intrinsic bursting oscillations (Schmidt and Calabrese 1992). Furthermore, heart motoneurons do not appear to exhibit voltage sags indicative of the hyperpolarization-activated I_h (A. Wenning and R. L. Calabrese, personal communication), a current that has been shown in neonatal rodent motoneurons to promote the transition from their inhibited phase to their firing phase (Kiehn et al. 2000). Therefore, in the absence of intrinsic oscillations and rebound-promoting currents, the output of the motoneurons should be largely determined by the input pattern they receive. Although heart motoneurons receiving the synchronous pattern of input show modest rebound spiking, this rebound spiking does not cause them to assume a phasing inconsistent with the segmental input pattern they receive.

If the segmental input pattern determines the segmental phasing differences observed in motoneurons, we might expect to find correlations between the premotor synaptic conductance and the output phasing observed in the living system. In the pyloric network of the stomatogastric system, for example, the onset of the LP motoneuron is correlated to the synaptic conductance of each of its inputs from the pacemaker kernel, the AB/PD complex (Goaillard et al. 2009). We do not see such correlations between single inputs and output phase in our system (Norris et al. 2011), suggesting that there may be a more complex interaction between elements of the premotor synaptic conductance pattern and the heart motoneuron intrinsic properties.

In our experiments, within a coordination mode, the only difference between the segmental input patterns introduced into the heart motoneurons was the synaptic strength profile. The temporal pattern was identical; therefore, we cannot determine, on the basis of these results, what the relative contributions of the temporal pattern and the synaptic strength profile of a segmental input pattern are to motoneuron output phase or to intersegmental coordination. Hybrid experiments in which several temporal patterns and synaptic strength profiles are mixed and matched could help to address this question.

Heart motoneuron intrinsic properties are important for appropriate phasing.

Despite the importance of the input pattern, we show that the intrinsic properties of heart motoneurons play a substantive role in determining their output. While it is well established that motoneuron intrinsic properties contribute to motor pattern generation in the pyloric (Marder and Bucher 2007) and gastric mill (Nusbaum and Beenhakker 2002) networks of the crustacean stomatogastric system, almost all of the neurons within those CPGs are themselves motoneurons, and the stomatogastric system is not segmentally distributed like the leech heartbeat system. Because we used the identical segmental input patterns used in our canonical ensemble model, any differences between the hybrid system and model phasing should be attributable to the additional intrinsic properties of the living heart motoneurons not present in the model motoneurons. Specifically, for motoneurons receiving the synchronous pattern of synaptic input, regardless of the segmental strength profile, the intrinsic properties of the motoneurons promote a phase advance (compared with the canonical ensemble model) sufficient to match the phasing observed in the living system. In many cases, this phase advance is substantial: In each of the segments tested, the average phase advance per segment (compared with the ensemble model) is at least 0.09. While we are unable to determine what set of intrinsic properties are present in the heart motoneurons, a likely candidate could be a low-threshold Ca²⁺ current. In the experiments where endogenous inputs were blocked with 0 Ca²⁺- high Mn²⁺ instead of bicuculline methiodide, hybrid system synchronous phasing was delayed (although not significantly so) by ∼0.02 compared with bicuculline methiodide block. This shift in phase may serve as an estimate of the contribution of such a current to the output phasing of these motoneurons. Addition of a low-threshold Ca²⁺ current to the model motoneurons, therefore, could provide a phase advance compared with the canonical ensemble model.

Our inability to replicate, in the hybrid system, a similar correspondence between the hybrid system and the living system in the peristaltic mode is surprising. Across segments, heart motoneurons receiving the peristaltic pattern of synaptic input show phasing similar to the ensemble model. We do not attribute these discrepancies to experimental or procedural errors; furthermore, all of the appropriate inputs are accounted for in the segmental input patterns that were used in our model and dynamic clamp experiments (Norris et al. 2011). A modulatory extrinsic input, acting on a cycle-by-cycle basis, may contribute to peristaltic phasing, but as of yet no such inputs have been identified in the leech. One final possibility is that, because we are using the identical inputs in every experiment in the presence of the normal intrinsic properties of the heart motoneurons, we are not accounting for natural animal-to-animal variability in both the temporal pattern and synaptic strength profiles. We are currently exploring how natural variability of both the temporal pattern and synaptic strength profiles affect output phasing.

Heart motoneurons escape rhythmic inhibition, while model motoneurons are released from inhibition.

We used trapezoidal waveforms designed to control when a motoneuron initiated its firing (Fig. 5). By constraining the onset of heart motoneuron firing until at or very near the offset of the premotor synaptic conductance, we were able to delay middle spike phase in a manner similar to that observed in the model motoneurons. Alternatively, waveforms that allowed for an earlier onset of motoneuron firing during the premotor synaptic conductance show phasing consistent with that measured in our hybrid system experiments with natural synaptic input patterns. This result suggests a fundamental difference between how motoneurons in the living system and the ensemble model may integrate their inputs: Heart motoneurons in the living system seem able to escape inhibition by beginning to fire at a point where the synaptic conductance is still ongoing (note the difference in first spike phase between the hybrid system and model, Fig. 4E). Model motoneurons, on the other hand, initiate firing only when the synaptic conductance has fallen to a lower conductance value; i.e., model motoneurons fire when they are nearly fully released from inhibition (Sharp et al. 1996). These results also suggest potential improvements to the model motoneurons; we are currently revising our canonical model to account for the spatial extent of the motoneurons in the living system as well as implementing inward currents that may affect their response to segment-specific patterns of synaptic input (Lamb et al. 2010).

Electrical coupling synchronizes ongoing heart motoneuron activity within a segment.

Adding artificial electrical coupling via dynamic clamp promotes synchronization of phase between heart motoneurons in the same segment. This observation is consistent with our previous modeling efforts (Garcia et al. 2008), as well as observations in Xenopus embryos (Zhang et al. 2009). This result suggests that electrical coupling also contributes to the output phasing observed in the living system. The synchronizing effect of the artificial coupling did not improve the correspondence in peristaltic phase between the hybrid system and the living system. Because the artificial coupling was added at the soma, distant from the potential endogenous coupling sites on fine neurites (Tolbert and Calabrese 1985), the synchronizing effect shown here may represent the lower physiological limit of the synchronizing effect observed in the living system.

Electrical coupling may also influence intersegmental coordination. When similar (although using different values of g_coup) hybrid experiments were done in segment 14 receiving the segment 14 input pattern, the reduction in side-to-side phase difference in segment 14 was smaller than that measured in segment 8. At present, we cannot distinguish whether this segment-specific effect is due to side-to-side phasing in the input pattern, as suggested in out ensemble model (Garcia et al. 2008), or possibly due to segmental variation in the coupling between heart motoneurons. A systematic survey of the coupling coefficients between heart motoneurons in the midbody segments could address this question.

Larger implications.

The results presented here show that motoneuron intrinsic properties can make a functional contribution to motor output in the context of an ongoing rhythmic input. Work in the cat spinal cord (Lee and Heckman 1998), neonatal rodent spinal cord (Kiehn et al. 2000), hypoglossal motoneurons (Purvis and Butera 2005), and turtle fictive scratch (Hounsgaard and Kiehn 1989) have all shown that motoneurons in these preparations possess intrinsic properties (and electrical coupling) that appear ideally suited to influence the phase and intensity of motor output. Our work suggests that a prerequisite for assessing how motoneuron intrinsic properties in these preparations contribute to motor output will be a quantitative description of the premotor pattern of synaptic input. For example, recent studies in which the patterns of premotor synaptic drive to motoneurons in the neonatal rodent spinal cord (Endo and Kiehn 2008) and turtle fictive scratch (Berg et al. 2007) were decomposed into their inhibitory and excitatory components were used to make inferences about the composition of the premotor interneuronal networks that drive these motor patterns. The neurons that make up these networks and their connections are still being identified. The strength of the present study is that we have identified the constitutive premotor elements and their relative contributions to the inhibitory synaptic drive impinging upon the motoneurons in this system. By focusing on those segments in which the premotor inputs have been clearly defined, we have provided the relevant context to ascertain how motoneuron intrinsic properties may contribute to motor output.

GRANTS

This work was supported by a Ruth L. Kirschstein National Research Service Award, funded by National Institute of Neurological Disorders and Stroke (NINDS) Grant NS-8472431, a National Science Foundation IGERT Program Grant (DGE-0333411), and American Psychological Association/Diversity Program in Neuroscience Predoctoral Fellowship 5 T06 MH-1882, funded by the National Institute of Mental Health, to T. M. Wright, Jr. and by NINDS Grant NS-24072 to R. L. Calabrese.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).