Trial type probability modulates the cost of antisaccades

Abstract

The antisaccade task, where eye movements are made away from a target, has been used to investigate the flexibility of cognitive control of behavior. Antisaccades usually have longer saccade latencies than prosaccades, the so-called antisaccade cost. Recent studies have shown that this antisaccade cost can be modulated by event probability. This may mean that the antisaccade cost can be reduced, or even reversed, if the probability of surrounding events favors the execution of antisaccades. The probabilities of prosaccades and antisaccades were systematically manipulated by changing the proportion of a certain type of trial in an interleaved pro/antisaccades task. We aimed to disentangle the intertwined relationship between trial type probabilities and the antisaccade cost with the ultimate goal of elucidating how probabilities of trial types modulate human flexible behaviors, as well as the characteristics of such modulation effects. To this end, we examined whether implicit trial type probability can influence saccade latencies and also manipulated the difficulty of cue discriminability to see how effects of trial type probability would change when the demand on visual perceptual analysis was high or low. A mixed-effects model was applied to the analysis to dissect the factors contributing to the modulation effects of trial type probabilities. Our results suggest that the trial type probability is one robust determinant of antisaccade cost. These findings highlight the importance of implicit probability in the flexibility of cognitive control of behavior.

in the ever-changing world, probabilistic information relating to the surrounding environment is actively utilized by individuals to adapt their behaviors flexibly to achieve their goals. The saccadic eye movement system is an excellent model for studying the flexibility of human behavior because it is conducive to measurement in the laboratory and has been well characterized on a neurophysiological basis (Hutton 2008; Munoz and Everling 2004). The effects of prior probabilistic information on saccadic performance have been well documented. For example, gaze is directed to specific locations faster when they represent higher likelihoods of target presence based on past experience (e.g., Carpenter and Williams 1995; Gmeindl et al. 2005; Liu et al. 2010; Miller 1988; Milstein and Dorris 2007; for recent reviews see Angelaki et al. 2009; Summerfield and Egner 2009). Most importantly, this utilization of probabilistic information is not constrained at the simple stimulus-and-response level, because it can also be observed when the task requires visual analysis and response selection. Recently, Liu et al. (2010) used a central cue to indicate to participants whether they should saccade to (prosaccade) or away from (antisaccade) an oddball stimulus. Of the four possible saccade locations, one location enjoyed higher probability of being selected than the other three locations, but only for prosaccades. Thus there was an equal chance for antisaccades to land on this highly probable prosaccade location. If the effect of probability was purely determined by simple location information, antisaccades made to the high-probability location should also benefit in their saccadic reaction times in a similar manner to prosaccades (compared with the other 3 locations). This was not the case. They found facilitation only in prosaccades to the high-probability location and no effect of probability on antisaccades. Their results suggest that the visual system's sensitivity to probability is not a simple location-and-response coupling, but a process that incorporates task (e.g., saccade type) and location information and other possible events that together provide specific probabilistic contexts (Liu et al. 2010). In the present study, we tested whether the visual system can also be sensitive to “events” (e.g., trial type probability in current study) that are intangible but predictive. Specifically, we manipulated the ratio between pro- and antisaccades within each block to investigate whether the visual system would learn these intangible cues that are not purely spatial or stimulus bound but become predictive only when the system learns the complex contingencies among events.

To study probabilistic learning beyond the level of simple stimulus and response, in the present study we employed an antisaccade task that requires an indirect sensory-response transformation (Hallett 1978; for review see Munoz and Everling 2004). To be specific, the antisaccade task requires one to suppress the natural tendency to look toward (i.e., prosaccade) a salient stimulus and exert control to make a rather arbitrary sensory-response transformation: to look in the opposite direction (i.e., make an antisaccade). Because of this arbitrary transformation that separates the location of the stimulus and saccade direction, it has been consistently reported that antisaccades have longer saccade latencies and are more prone to errors than prosaccades (Hallett and Adams 1980). This difference in latency is called the antisaccade cost. The antisaccade cost has been observed in various paradigms (Barton et al. 2006b; Evdokimidis et al. 1996; Fischer and Weber 1997; Godijn and Kramer 2007, 2008; Olk and Kingstone 2003) and cannot be eliminated with mere practice (Dyckman and McDowell 2005).

Recent studies have shown that the antisaccade cost can be modulated under some circumstances (Kristjánsson et al. 2001; Juan et al. 2008). Kristjánsson et al. (2001) found that shifting attention to a secondary task before saccade target onset can interfere with the reflexive prosaccade and consequently allow faster antisaccades. Liu et al. (2010) found that spatial probability of saccade locations can also effectively modulate the antisaccade cost. Most important, Olk and Kingstone (2003) found that antisaccade cost can also be altered by changing the way pro- and antisaccade trials are organized. Their interesting study gave rise to other studies that reported an elimination of antisaccade cost in a pro/antisaccade task when pro- and antisaccade trials were interleaved (Juan et al. 2004, 2008; Liu et al. 2010). The key factor in these studies is that the antisaccade cost was only observed when pro- and antisaccades were presented in separate blocks but decreased when trials were interleaved. Although this may seem like an indirect variable to modulate antisaccade cost, these results can be reinterpreted from the perspective of probability. That is, the equal likelihood of pro- and antisaccade appearance within an interleaved design could be interpreted as a reduced predictability of the forthcoming saccade type from 100% to 50%. In traditional block designs, saccade types (i.e., pro- vs. antisaccade) do not vary on a trial-by-trial basis, thus the expectancy for the next saccade type is always 100% valid, or the information indicating the trial type and response to be made precedes the stimulus to which the response must be generated. By merely mixing pro- and antisaccades in one block and not offering the response instruction until the stimulus is presented, the probability of the next saccade being of a particular type suddenly drops to 50%, thereby forcing the participants to withhold reflexive prosaccades and actively program a pro- or antisaccade once the instruction is given. As seen from these studies, when the two events (pro- and antisaccades) were equiprobable, it was strong enough to eliminate the latency difference between pro- and antisaccades. This new interpretation of these designs and findings emphasize the critical role of trial type probability in the interaction between our bottom-up (i.e., reflexive prosaccades) and top-down (i.e., suppression of reflexive prosaccades) visual processes.

In light of these findings, it is reasonable to hypothesize that the antisaccade cost can be effectively modulated by trial type probability. The antisaccade cost can perhaps be reduced, or even reversed, if the probability of surrounding events favors the execution of antisaccades, and vice versa. To our knowledge, no study has investigated the interaction of antisaccade cost with probability information. Thus, in experiment 1, we asked whether the trial type probability (e.g., the probability of pro- and antisaccade trials) can also influence saccade latencies and, more specifically, modulate antisaccade cost. Furthermore, some studies have demonstrated that saccadic performance can be influenced by what occurred in the previous trial, such as effects of location repetition priming and task switching between the trials (Emeric et al. 2007; Fecteau and Munoz 2003; Manoach et al. 2007). To dissect the contributing factors to the modulation effects originated from the manipulation of event probabilities and the possible carryover effects from the previous trial, such as repetition priming (Geyer et al. 2007; Maljkovic and Nakayama 1996; for review see Kristjánsson 2008), task switching (Barton et al. 2006a, 2006b; Hodgson et al. 2004), and post-error slowing (Rabbitt 1966a, 1966b; Talter and Hutton 2007), we also applied a new trial-by-trial analysis consisting of a mixed effects model in a post hoc manner. The results of the mixed-effects model provide insights to the mechanisms of these effects.

To extend our understandings of the probability effect, we further investigated whether the demand on visual perceptual analysis in the task would interact with the manipulation of trial type probability and thus suggest dependence between the two processes. In experiment 2, we manipulated different levels of cue discriminability to see how the effects of probability are changed at different difficulty levels.

MATERIALS AND METHODS

Participants

The experiments were approved by Institutional Review Board of the Chang-Gung Memorial Hospital, Taoyuan, Taiwan. Twenty undergraduate and graduate students from the National Central University (10 female; mean age 21.7 years) participated in these experiments. Ten subjects participated in experiment 1, and 10 additional subjects participated in experiment 2. All participants had normal or correct-to-normal vision. Each participant received monetary payment for their participation on completion of the experiment. They were naive to both the purpose of this study and the experiment design of relative probabilities of pro- and antisaccade trials across blocks.

Apparatus

Stimuli were presented on a 19-in. color cathode ray tube monitor (ViewSonic Professional Series P95f+), positioned 86 cm in front of the subjects. The monitor had a spatial resolution of 1,024 × 768 pixels and a refresh rate of 100 Hz. The computer was equipped with a Radeon 9600 series display card manufactured by ATI Technologies. The brightness of stimuli and background were measured by a ColorCAL colorimeter (Cambridge Research Systems). Eye movements were recorded from the left eye with an EyeLink II tracker (SR Research, Mississauga, ON, Canada). The sampling rate was set at 500 Hz, which provided one data point every 2 ms.

Throughout the experiment, subjects sat in a dimly lit room with their head in an adjustable chin rest. The chin rest was also used to maintain a fixed distance from the monitor while restricting head movements to ensure subjects' eye height matched the center of the display screen.

Stimuli, Design, and General Procedure

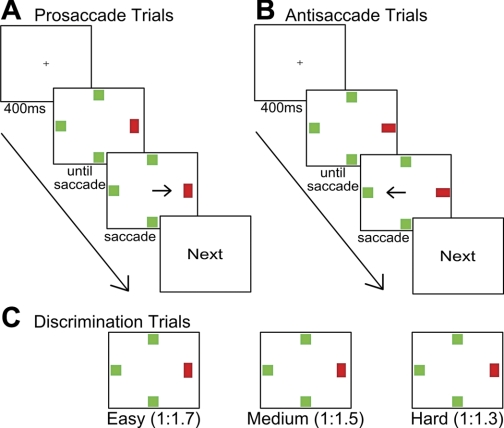
Both experiments used a pro/antisaccade task. Figure 1, A and B, illustrates the trial procedure and stimuli arrangement for both experiments. The trial began with a white fixation cross (0.5° × 0.5°, CIE x = 0.286, y = 0.309, z = 96.4 cd/m²) in the center against a black background (CIE X = 0.278, Y = 0.352, Z = 0.13 cd/m²) for 400 ms, followed by the search array. The search array was composed of three green squares (1° × 1°, CIE X = 0.289, Y = 0.601, Z = 26.7 cd/m²) and one red rectangle (1.23° × 0.82°, CIE X = 0.575, Y = 0.373, Z = 26.7 cd/m²). The red rectangle (target) appeared randomly either to the left or right or above or below the fixation position with equal probabilities. The green squares filled the three remaining positions. Eccentricity of all stimuli was 8°. The red rectangle could be either horizontal or vertical. Participants were instructed to make a saccade toward the target (prosaccade) when the target was vertical or away from the target (antisaccade) when the target was horizontal. The search array disappeared 400 ms after saccade execution, followed by the word “Next” at the center of the screen. Subjects could then initiate the next trial any time by pressing the space bar.

Fig. 1.

Schematic of the saccade tasks. A and B denote typical pro- and antisaccade trials, respectively. All experiments shared the same trial procedure. Pro- and antisaccade trials were interleaved in all blocks. The trial began with a central cross for 400 ms, and then an array of 4 isoeccentric stimuli was presented. Prosaccade (A) and antisaccade trials (B) were cued by orientation of the red singleton. The arrows indicate the correct saccade directions and were not displayed on the screen during experiments. Subjects were required to shift their gaze to the correct location within 1,000 ms of array onset and maintain fixation of that saccade target for at least 400 ms. The trial ended with a “Next” display, which stayed on the screen until the space bar was pressed by the participant. C: in experiment 2, the size ratios of the singleton were manipulated to vary the difficulties of cue discriminability. Three kinds of target width-length ratios were used: 1:1.3 (0.88° × 1.14°), 1:1.5 (0.82° × 1.23°), and 1:1.7 (0.78° × 1.32°). These ratios were selected to maintain the same overall area (1°) of the target across the different ratios.

Before the experiment, the eyetracker was calibrated while participants performed a nine-point calibration and validation procedure. The formal experiment began when the validation error was less than 1° of visual angle. Participants were instructed to press the space bar when they were ready for the next trial. Drift correction was performed in the beginning of every trial. After drift correction, participants had to maintain fixation during the fixation and search array display until they identified the orientation of the target and performed the correspondent responses. Participants had the option of taking a break without time limit between every trial.

Scoring of Eye Movement Data

Eye positions were recorded by the EyeLink II tracker every 2 ms (500 Hz). Saccades were automatically identified by the EyeLink system according to acceleration and amplitude criteria (minimum speed 30°/s, minimum acceleration 8,000°/s², minimum amplitude 1°) so that eye drift or small eye movements were not erroneously categorized as saccades. Only the first saccade made by the subjects was analyzed. Correct responses were defined as saccades with amplitude greater than 1° and a distance between target and the landing point of less than 4°. Only correct responses were used for analysis. Saccade latency was defined as the time interval between target onset and the initiation of a saccadic eye movement. Trials with saccade latency <100 ms were excluded (0% in this study) because these trials were probably generated not as responses to the visual target (Fischer et al. 1993). Trials (0.01%) with saccade latency >1,000 ms were also excluded in experiment 1. These thresholds served to exclude outliers. The error trials were excluded from all statistical analysis. Overall, 85.4% of total trials (93∼76.5% between subjects) in experiment 1 were included for analysis.

In experiment 2, the data inclusion criterion for saccade and correct responses were the same as in experiment 1 except for the criterion of response time. The new outlier criterion was set to exclude trials with saccade latency <100 ms or >2,000 ms (because of the increase in task difficulty). However, it was not necessary to exclude any trials on this basis. Ninety percent of total trials (99∼76% between subjects) in experiment 2 were included for analysis.

Statistical Analysis

Accuracy and latency were analyzed with a repeated-measures ANOVA, with saccade type (antisaccades, prosaccades) and block (A20P80, A50P50, A80P20) as variables. The target aspect ratio (1.3, 1.5, 1.7) was added as a third variable in experiment 2. Accuracy was defined as the percentage of correct responses made. Greenhouse-Geisser adjustments were used if the assumption of homogeneity of variance was violated. The α level for all tests was 0.05, and the Bonferroni correction was used in multiple comparisons.

Experiment 1

In experiment 1, we systematically manipulated the relative probabilities of pro- and antisaccade trials across blocks. We hypothesized that antisaccade cost would be absent when a block contained equal probabilities between pro- and antisaccade trials and increase when antisaccade probability was relatively low. Most importantly, we expected “negative” antisaccade cost when its probability was relatively higher than that of prosaccade trials. That is, antisaccade latencies should be faster than prosaccade latencies. This is a logical yet novel prediction and has never been reported in the literature.

Experimental design and procedure.

Each subject completed 480 trials in 2 sessions on 2 separate days. Each session began with 32 practice trials, followed by 240 trials of the formal experiment. The 240 trials were divided into 3 blocks of 80 trials. Each block was assigned a different pairing of pro- and antisaccade probabilities, namely, 20% antisaccade vs. 80% prosaccade, 50% antisaccade vs. 50% prosaccade, and 80% antisaccade vs. 20% prosaccade (for simplicity, we will refer to the probability assignments as A20P80, A50P50, and A80P20, respectively). The first block for each subject in the two sessions was always A50P50, and the order of the two remaining blocks was counterbalanced within and between subjects. Subjects were not informed about the variation in probability assignments across blocks. Note that the three blocks were not labeled with any display on screen and were not separated by a break or pause. Thus it is more accurate to say that the trials were presented in three “invisible” blocks, and from the participants' point of view, the blocks appeared as one continuous 240-trial experiment.

Analysis of consequences of the previous trial.

Eye movement data containing repetition priming and task switching effects were analyzed as two consecutive trials in a time series. This type of analysis requires that each trial is treated as an individual data point, rather than using participant means; thus the assumption of independence in ANOVA and linear regression is seriously violated. The mixed-effects model, also known as a hierarchical linear model, was chosen because this approach provides unbiased analysis of balanced and unbalanced repeated-measures data, detection of within-subject effects (fixed effects), and individual subject effects (random effects), thereby making the best use of all available data (Laird and Ware 1982; Rochon and Helms 1989).

The linear mixed-effects model (MEM) used in experiment 1 was

$$Y_{jt}={\beta }_0+{\displaystyle \sum {\beta }_i{X}_i}+b_j+{\epsilon }_{jt}$$

$$b_j\sim N\left(0,{\tau }_{00}\right)$$ (1)

where Y_jt is the saccade latency for the jth individual (j = 1,..., 10) at the tth trial (t = 1,..., 480), β_o is the fixed intercept, β_i is the effect for variable X_i, X_i is the ith explanatory variable and its interaction with other ith variables, b_j is the random intercept, and ε_jt is the error in predicting the latency of jth individual at the tth trial. Note that b_j is free to vary between participants to model the random effects associated with the jth individual and is assumed to follow the Gaussian distribution with mean zero and variance τ₀₀.

The procedure for the linear mixed-effects model analysis in experiment 1 was started with adjustments of variance-covariance structure (ε_jt) for the random effects by use of a restricted maximum likelihood method. An appropriate covariance structure of the MEM is essential to obtain valid inferences for the parameters in the fixed structure, which are usually of primary interest (Verbeke and Molenberghs 2000). Fixed effects were then specified by a backward elimination variable selection procedure with maximum likelihood estimation: first, all potential contributors to saccade latency and their interactions were composed of the full model (M_F) to assess their effects on saccade latency concurrently. If the effect of one variable was significant at P < 0.05, that variable was retained. However, variables that contained a significant interaction should be retained in the model even if they were not statistically significant (Morrell et al. 1997). After this selection step, variables retained were considered as influential and formed a reduced model (M_R).

The fixed effects, β_o + Σβ_iX_i, are assumed to be constant across participants. These X_i variables included the planned variables (saccade types and trial type probability) in experiment 1 and unplanned but potentially influential factors that were chosen by reference to the literature. These unplanned categorical factors included whether the trial followed an error, saccadic location repetition, singleton location repetition, and task switches. Saccadic location repetition was defined as two consecutive trials sharing the same saccade location, regardless of whether it was a pro- or antisaccade. The same logic applied to singleton location repetition, which specified a repetition of target location in two consecutive trials regardless of pro- or antisaccade. Task repetition was defined as the repetition of saccade type for two consecutive trials (2 consecutive prosaccade trials, PP; or 2 consecutive antisaccade trials, AA). The absence of repetition was coded as a task switch (prosaccade then antisaccade, PA; antisaccade then prosaccade, AP). All four possible combinations of task repetition and switch (i.e., AA, PP, AP, and PA) were recorded for analysis. Also, the session factor was added to control for practice effects, and the trial sequence was a covariate.

All variables except the trial sequence were categorical. A number of binary dummy variables were created to code each level of the categorical variable. For example, in the case of trial type probability, we created a dummy variable with the value 1 if probability was 20% and 0 if not, another dummy variable with the value 1 if probability was 50% and 0 if not, and a third level with a probability of 80% represented by a 0 for both of these variables. After one less than the number of all possible levels of the categorical variables were converted into dummy variables, in addition to the interaction term, there were 26 parameters to be estimated in the fixed parts of the M_F. It is worth noting that during the aforementioned process of backward elimination, the contribution of a categorical factor to saccade latency was assess across all levels of this factor, rather than for each dummy variable.

Also, a model (M_P) containing only the planned experimental variables was built as

$$\begin{array}{c}{Y}_{jt}={\beta }_0+{\beta }_1\left(\text{antisaccade}\right)+{\beta }_2\left({\text{probability}}_{20}\right)+{\beta }_3\left({\text{probability}}_{50}\right)+b_j+{\epsilon }_{jt}\\ b_j\sim N\left(0,{\tau }_{00}\right)\\ \begin{array}{cc}{\epsilon }_{jt}=\rho {\epsilon }_{j,t-1}+\varphi a_{j,t-1}+a_{jt}& a_{jt}\sim N\left(0,{\sigma }^2\right)\end{array}\end{array}$$ (2)

We compared the deviance (−2 log likelihoods) of the three nested models M_F, M_R, and M_P with a likelihood ratio test to select the best-fitting model. The likelihood ratio test follows a χ² distribution, with q degrees of freedom, where q is the difference in the number of parameters between the two models (Morrell et al. 1997). Last, relationships between the current trial type probability and previous trial consequences were analyzed by estimation of the best-fitting model and are discussed in results.

Experiment 2

This experiment was designed to investigate the possible process whereby trial type probability has an impact on saccade latency. Specifically, we aimed to probe whether the effect of trial type probability happens at the stage of visual selection or at the stage of saccade decision. The paradigm used in the current study was adopted from the studies by Schall and colleagues (Juan et al. 2004; Sato and Schall 2003) because the neural mechanisms underlying the task are more well understood than many other tasks. Neurophysiological studies on monkeys have demonstrated that at least two types of frontal eye field (FEF) neurons are involved in the task, one of which (type I neurons) encodes visual selection processes (including the singleton location encoding and then the shape identification), whereas the other (type II neurons) is highly correlated with saccade selection (Sato and Schall 2003). In type I neurons, when a prosaccade is performed, the target singleton continues to be selected until the time of saccade execution. In contrast, in antisaccade trials the singleton is initially selected, but a dramatic transition occurs so that the end point of the antisaccade is ultimately selected. Interestingly, the time it takes for type I neurons to select a target singleton and identify its shape is not affected by subsequent response types (i.e., pro- or antisaccade) or final saccade latency. This marks a sharp contrast to the activity of type II neurons, where the time to select saccade end point varies systematically with the final saccade latency, and thus can be used to account for most of the trial type effect on saccade latency (i.e., latency differences between pro- and antisaccade). On the basis of these contrasting characteristics between type I and II neurons, Sato and Schall (2003) concluded that visual selection and saccade selection are two dissociable processes. Indeed, intracortical microstimulation of FEF in monkeys has suggested that visual selection in the peripheral vision can be operated without the involvement of a saccade preparation (Juan et al. 2004). Similar findings have also been demonstrated in studies using transcranial magnetic stimulation (TMS) over human FEF (Juan et al. 2008). Together, these findings suggest that the neural correlate of visual selection in the task is segregated from that of saccade selection in the FEF.

In the above-mentioned study by Sato and Schall (2003), the pro- and antisaccade trials were randomly interleaved and thus are akin to the A50P50 block of experiment 1 in the present study. On the basis of the findings from Sato and Schall (2003), we speculate that the modulation of trial type probability on antisaccade cost is likely to occur at the saccade selection stage. Thus the effects of visual selection processes should be independent from the effects of saccade selection due to the dissociation of these two stages. To this end, in experiment 2 we systematically varied levels of cue discriminability by manipulating the size ratios of the singleton to incur effects on the visual selection processes. If our results from experiment 1 emerged from the differing degrees of cue discriminability (i.e., visual selection), then an interaction should be observed between the effects of trial type probability and cue discriminability. Alternatively, such interaction should not be present if the effect of trial type probability was solely due to the modulation of saccade selection processes.

Experimental design and procedure.

The general procedure and stimuli were the same as in experiment 1 except for the added manipulation of target width-length ratio (Fig. 1C) and an increased number of trials. Three kinds of target width-length ratios were used: 1:1.3 (0.88° × 1.14°), 1:1.5 (0.82° × 1.23°), and 1:1.7 (0.78° × 1.32°). These ratios were selected to maintain the same overall area (1°) of the target across the different ratios. All other properties of the stimuli were the same as in experiment 1.

The assignments of probability across three blocks were also the same as in experiment 1 (i.e., A20P80, A50P50, and A80P20). Thus, with the added variations in different target aspect ratios, there were nine conditions (3 × 3) for each subject: three levels of target aspect ratios plus the original three levels of probability between task types. As a result, the total number of trials for each participant increased to 1,080 in the second experiment. We separated the whole experiment into three sessions for each participant. Each session consisted of 360 trials, which consisted of 3 probability blocks of 120 trials without intermission. For each trial type probability block, the three kinds of target aspect ratios were randomly assigned with equal probabilities.

Participants were instructed to look toward the red singleton when the red singleton was a vertical rectangle and to look toward the opposite location when the singleton was horizontal. They were informed that the visual discrimination of target orientation would be difficult in some trials, and they had to make judgments about the orientation quickly and accurately before making any eye movement. Trials were self-paced by the subjects, allowing for a break between trials.

RESULTS

Experiment 1

Influence of trial type probability on antisaccade cost.

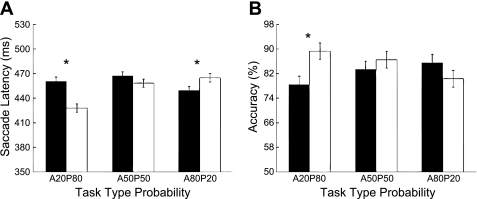
The influence of trial type probability on antisaccade cost was first checked by examining the latency difference between pro- and antisaccades. Figure 2A shows saccade latencies as a function of trial type probabilities for pro- and antisaccades. The two-way repeated-measures ANOVA showed that there were no main effects in either condition for saccade types [F_(1,9) = 1.23, P = 0.3] or for relative probability design of blocks [F_(2,18) = 1.28, P = 0.3]. The result of interest was the significant interaction between saccade types and their relative probabilities [F_(2,18) = 28.28, P < 0.001] (Fig. 2A). Antisaccades were slower than prosaccades when antisaccade probability was lower [A20P80: t(9) = 7.256, P < 0.05] and faster when its probability was higher [A80P20: t(9) = 3.379, P < 0.05]. In the even probability condition (i.e., A50P50), the difference between the two saccade types was eliminated [t(9) = 1.941, not significant (NS)].

Fig. 2.

Results of experiment 1: saccade latency (A) and accuracy (B) as a function of the 3 blocks of probabilities. Open bars denote prosaccade trials and filled bars denote antisaccade trials. A20P80 indicates a block for which the probability was 20% and 80% for antisaccades and prosaccades, respectively. Likewise, A50P50 indicates 50% for antisaccades and 50% for prosaccades, and A80P20 indicates 80% for antisaccades and 20% for prosaccades. Error bars represent the 95% within-subjects confidence intervals. *P < 0.05.

The influence of trial type probability on antisaccadic cost was also indexed by the accuracy difference between pro- and antisaccades. Figure 2B shows the accuracy as a function of the three probabilities for both saccade types. Analyses of accuracy data revealed no significant main effects of relative probability design of blocks or saccade types in accuracy [F_(2,18) = 0.654, P = 0.532; F_(1,9) = 2.599, P = 0.141] but did indicate a significant interaction between the two [F_(2,18) = 10.815, P < 0.001]. Pairwise comparisons revealed that the interaction was driven by the fact that antisaccade errors were greater than prosaccade errors only when antisaccade probability was lower [A20P80: t(9) = 4.437, P < 0.05] (Fig. 2B). When antisaccade probability was equal to [A50P50: t(9) = 1.277, NS] or higher than [A80P20: t(9) = 2.139, NS] prosaccade probability, antisaccades were no longer prone to more errors.

Relationships between trial type probability and consequences of the previous trial.

The relative contributions of trial type probability and other trial history factors on saccade latencies were explored with a linear mixed-effects model. First, an appropriate covariance structure was specified to account for the random variation observed in the data. The form that most parsimoniously accounted for the pattern of autocorrelated residuals was a first-order autoregressive moving average structure [ARMA(1,1)] with homogenous variances [χ²(1) = 617.884, P < 0.001]:

$$\begin{array}{c}{\epsilon }_{jt}=\rho {\epsilon }_{j,t-1}+\varphi a_{j,t-1}+a_{jt}\\ a_{jt}\sim N\left(0,{\sigma }^2\right)\end{array}$$ (3)

where ρ is an autoregressive parameter, φ is a moving average parameter, and a_jt is assumed to follow the Gaussian distribution with a mean of zero and variance of σ². Equation 3 was used as the structure of residuals whenever fixed effects were estimated. The fixed effects of the MEM were specified by selecting significant variables of the M_F, and the results of the selection process are listed in Table 1. Fixed intercept, saccadic type, session, saccadic location repetition, interaction between saccadic type and task switch, and interaction between probability and saccadic location repetition were kept in the analysis as a result of the F statistic results (all P < 0.05). Factors of probability and task switch did not reach statistical significance but were also kept in the analysis due to their significant interactions with other factors. These retained factors composed the M_R. When the deviance of M_R (52,165.53) was compared with that of M_F (52,149.34), although the value of M_F was small, this difference of 16.19 was not small enough [χ²(12) = 16.19, P = 0.18], indicating that adding the 12 parameters in M_F did not improve the explanatory power of fixed effects of our model. Thus M_R is preferred due to the advantage of parsimony. When the deviance of M_R was compared with that of M_P (52,551.04), the small enough value of M_R [χ²(6) = 385.51, P < 0.001] indicated that the M_R, with six more parameters, significantly improved the model fit to the data. The parameter estimates, standard errors, and goodness of fit statistics for M_R and M_P are listed in detail in Tables 2 and 3.

Table 1.

M_F and backward elimination procedure

Variables	F Statistics	Selection
Fixed effects
Intercept (β0)	F(1,13) = 222, P < 0.001	Enter
Saccadic type	F(1,4321) = 8.80, P < 0.01	Enter
Probability	F(2,1827) = 1.38, P = 0.25	Enter
Session	F(1,50) = 65.56, P < 0.001	Enter
Trial sequences (covariate)	F(1,340) = 0.03, P = 0.872	Remove
Posterror	F(1,4244) = 1.23, P = 0.267	Remove
Saccadic location repetition	F(1,4228) = 6, P < 0.05	Enter
Singleton location repetition	F(1,4206) = 0.07, P = 0.790	Remove
Task switch	F(1,4221) = 2.18, P = 0.140	Enter
Saccadic type × posterror	F(1,4253) = 2.09, P = 0.148	Remove
Saccadic type × singleton location repetition	F(1,4327) = 0.684, P = 0.44	Remove
Saccadic type × saccadic location repetition	F(1,4285) = 0.43, P = 0.510	Remove
Saccadic type × task switch	F(1,4256) = 34.56, P < 0.001	Enter
Probability × posterror	F(2,4244) = 0.69, P = 0.691	Remove
Probability × singleton location repetition	F(2,4235) = 0.47, P = 0.592	Remove
Probability × saccadic location repetition	F(2,4214) = 10.06, P < 0.001	Enter
Probability × task switch	F(2,4196) = 2.54, P = 0.079	Remove
Random effects
τ00	8,026.95 (3762.59)
σ2	8,205.16 (276.26)
ρ	0.95 (0.01)
ϕ	0.25 (0.02)
Fit statistics
Deviance (−2LL)	52,149.34
No. of parameters	26

In the full model (M_F), the criterion for variable selection in the backward elimination procedure is set at α = 0.05 in F statistics. Some factors did not reach statistical significance but were also kept in the analysis due to their significant interactions with other factors. −2LL, −2 log likelihood; see text for other definitions.

Table 2.

Model fitting results of the M_R

Variables	Parameter Estimates	t or Wald Z Statistics
Fixed effects
Intercept (β0)	414.2 (29.13)	t(10.79) = 14.218, P < 0.001
Saccadic type (= Anti)	−5.97 (3.42)	t(59.96) = 8.159, P = 0.081
Probability (= 20%)	21.84 (4.82)	t(3,078.62) = 4.533, P < 0.001
Probability (= 50%)	17.04 (6.82)	t(228.56) = 2.499, P < 0.05
Session (= first)	62.89 (7.71)	t(59.96) = 8.159, P < 0.001
Saccadic location repetition (= repetition)	39.64 (8.46)	t(4,187.45) = 4.684, P < 0.001
Task switch (= nonswitch)	−19.19 (4.12)	t(4,228.88) = −4.659, P < 0.001
Saccadic type (= Anti) × task switch (= nonswitch)	35.03 (5.51)	t(4,167.76) = 6.354, P < 0.001
Probability (= 20%) × saccadic location repetition(= repetition)	−57.79 (11.52)	t(4,247.9) = −5.017, P < 0.001
Probability (= 50%) × saccadic location repetition(= repetition)	−27.66 (9.57)	t(4,151.4) = −2.891, P < 0.01
Random effects
τ00	7,984.17 (3,653.85)	Z = 29.723, P < 0.001
σ2	8,233.46 (277)	Z = 2.185, P < 0.05
ρ	0.95 (0.01)	Z = 92.518, P < 0.001
ϕ	0.25 (0.02)	Z = 10.295, P < 0.001
Fit statistics
Deviance (−2LL)	52,165.53
No. of parameters	14
Model comparison
χPR2(6) = 385.51, P < 0.001; χRF2(12) = 16.19, P = 0.18

In the reduced model (M_R), the likelihood ratio test for fixed effects was used under maximum likelihood estimation. The subscripts of the χ² test denote the two models compared: P, planned model, R, reduced model, F, full model.

Table 3.

Model fitting results of the M_P

Variables	Parameter Estimates	t or Wald Z Statistics
Fixed effects
Intercept (β0)	446.23 (28.83)	t(10.23) = 15.48, P < 0.001
Saccadic type (= Anti)	8.16 (2.75)	t(4,218.19) = 2.972, P < 0.01
Probability (= 20%)	16.36 (3.79)	t(3,848.33) = 4.321, P < 0.001
Probability (= 50%)	1.03 (7.51)	t(360.98) = 0.137, P = 0.891
Random effects
τ00	7,486.76 (3,684.75)	Z = 2.032, P < 0.05
σ2	10,235.73 (740.31)	Z = 13.826, P < 0.001
ρ	0.98 (0,01)	Z = 185.252, P < 0.001
ϕ	0.36 (0,05)	Z = 8.105, P < 0.001
Fit statistics
Deviance (−2LL)	52,551.04
number of parameters	8

The planned model (M_P) only contains the variables in experiment 1.

Thus the effects on saccade latency can be dissected from M_R:

$$\begin{array}{c}{Y}_{jt}=414.2-5.97\left(\text{antisaccade}\right)+21.84\left({\text{probability}}_{20}\right)+17.04\left({\text{probability}}_{50}\right)+62.89\left({\text{session}}_{1\text{st}}\right)+39.64\left(\text{sacc}\text{.loc}\text{.rep}\right)-19.19\left(\text{task}\text{.rep}\right)+35.03\left(\text{antisaccade}\right)\times \left(\text{task}\text{.rep}\right)-57.79\left({\text{probability}}_{20}\right)\times \left(\text{loc}\text{.rep}\right)-27.66\left({\text{probability}}_{50}\right)\times \left(\text{loc}\text{.rep}\right)+b_j+{\epsilon }_{jt}\\ b_j\sim N\left(0,7,984.17\right)\\ \begin{array}{cc}{\epsilon }_{jt}=0.95{\epsilon }_{j,t-1}+0.25a_{j,t-1}+a_{jt}& a_{jt}\sim N\left(0,8,233.46\right)\end{array}\end{array}$$ (4)

According to M_R (Eq. 4), prosaccade trials from the second session with high probability (80%), task switching (AP), and target location switching yielded a mean saccade latency of 414 ms, which was the fixed intercept β_o (t = 14.22, P < 0.001). Overall, participants were faster in the second session by ∼63 ms, indicating a practice effect (t = 8.1, P < 0.001).

When investigating the effects of probability, it is important to tease apart the confounding effects of repetition priming. That is, trials of higher probability are more likely to have more consecutive identical trials, thereby improving performance (Walthew and Gilchrist 2006). Therefore, we further explored the possibility of repetition priming at the stimulus level, response level, and task-set level. First, at the stimulus level, MEM analysis showed that repetition of target location had no effect on saccade latencies in our task (Table 1). This suggests that the observed effect of probability was not due to repetition priming at the stimulus level.

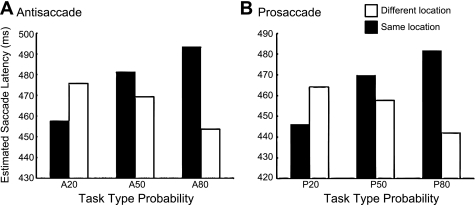
At the response level, saccade location repetition priming had inconsistent effects on saccade latency when compared under different probability conditions. Figure 3 illustrates saccade location repetition priming effects from M_R. The estimation showed that for both antisaccades (Fig. 3A) and prosaccades (Fig. 3B), saccadic location repetition led to a positive priming effect under a probability of 20% but produced a reversed priming effect under probabilities of 50% and 80%. The estimated saccade latency from trials with saccade location repetition was 11.98 ms slower (i.e., 39.64 − 27.66 ms) (t = −2.891, P < 0.01) than those without repetition in the 50% condition and 18.15 ms faster (i.e., 39.64 − 57.79 ms) (t = −5.017, P < 0.001) in the 20% condition. Under the 80% probability condition, however, saccade location repetition led to a negative priming effect such that saccade latency increased by 39.64 ms (t = 4.684, P < 0.001) when the saccade end points between two consecutive trials were the same. To our surprise, MEM analysis showed that repetition of saccade direction reduced saccade latency in the low-probability condition but elevated latency in the high-probability condition. Thus it is hard to say that the speeded saccade latency from the high-probability condition was due to an advantage of location priming from the previous trial. This provides evidence suggesting that the observed effects of probability on saccade latency of both pro- and antisaccades are not due to repetition priming at the response level.

Fig. 3.

Influence of saccadic location repetition on saccade latency for antisaccades (A) and prosaccades (B). The estimated mean saccade latencies are plotted as a function of trial type probabilities. The x-axis denotes the current trial type probability. Open bars indicate trials with incongruent saccade locations from the previous trial. Filled bars indicate trials with congruent saccade locations from the previous trial.

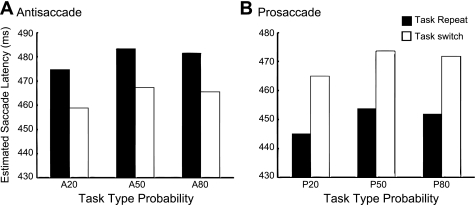
Finally, at the task level, our MEM analysis is illustrated in Fig. 4, which shows the reverse task switch effects between pro- and antisaccades obtained by model estimation. For a prosaccade (Fig. 4B), if it was preceded also by a prosaccade, saccade latency was 19.19 ms faster than if it was preceded by an antisaccade (t = −4.659, P < 0.001). For antisaccades (Fig. 4A), saccade latency slowed down by 16 ms (35.03 − 19.19 ms) (t = 6.354, P < 0.001) when preceded by an antisaccade compared with when preceded by a prosaccade. Thus we did not observe simple task repetition facilitation in saccade latency at the task level. Task repetition only speeded saccade latency when it was a prosaccade-prosaccade pairing and caused a prolonged latency when it was an antisaccade-antisaccade coupling. We further address this point in the discussion.

Fig. 4.

Influence of task switch on saccade latency for antisaccade (A) and prosaccade (B). Bar graphs show estimated latency for the current trial divided by that of the previous trial type under 3 probabilities. Open bars denote trials whose previous trial was different from the current trial; filled bars represent trials whose current trial type was the same as the previous trial.

Experiment 2

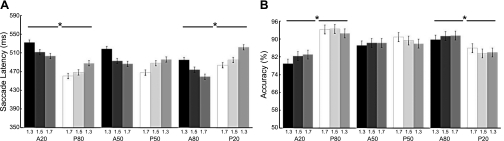
Figure 5A plots saccade latencies as a function of the three blocks of probabilities and saccade types for each target aspect ratio. There was a main effect of target aspect ratio [F_(2,18) = 16.277, P < 0.001], indicating that saccade latencies were longest (508 ms) for the target with the smallest aspect ratio (1.3), fastest (477 ms) with the largest aspect ratio (1.7), and in between (488 ms) with the medium aspect ratio (1.5). As predicted, neither saccade type [F_(1,9) = 1.299, P = 0.284] nor relative probability [F_(2,18) = 0.090, P = 0.914] had an impact on saccade latencies. The significant interaction between saccade type and their relative probabilities [F_(2,18) = 11.833, P < 0.001] demonstrated similar probability effects to experiment 1: antisaccades were slower than prosaccades when antisaccadic probability was lower [A20P80: t(9) = 5.856, P < 0.05] and faster when its probability was higher [A80P20: t(9) = 3.224, P < 0.05]. In the even probability condition (i.e., A50P50), the difference between two saccade types was eliminated [t(9) = 2.072, NS]. There was no significant interaction between target aspect ratio and saccade types or interaction between target aspect ratio and relative probabilities. Specifically, the three-way interaction between target aspect ratio, saccade types, and relative probabilities was not significant (all F < 1, NS), demonstrating an independent effect of trial type probability and task difficulty on saccade latencies.

Fig. 5.

Results of experiment 2: saccade latencies (A) and accuracy (B) for 3 levels of discrimination are plotted for pro- and antisaccades separately. On the x-axis, 1.3 indicates a hard discrimination and 1.7 indicates the easiest one. Dark-shaded bars are antisaccades and light-shaded bars are prosaccades. *P < 0.05.

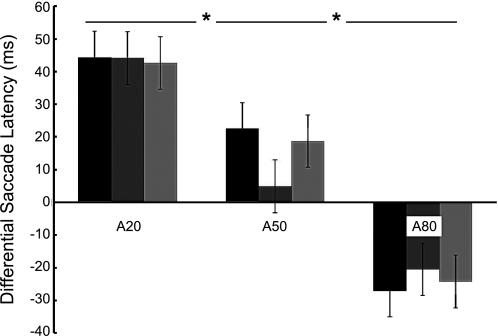
Figure 6 plots the differential saccade latency (antisaccades minus prosaccades) to further depict the effects of trial probability and cue discriminability on antisaccade cost. The antisaccade cost was mainly influenced by the antisaccade trial probability [F_(2,18) = 11.895, P < 0.01] and not the cue discriminability [F_(2,18) = 0.125, P = 0.883]. Also, the effects of trial probability and cue discriminability on antisaccade cost were not dependent on each other, since there was no interaction between the effects of antisaccade probability and cue discriminability [F_(4,36) = 0.760, P = 0.558].

Fig. 6.

Antisaccade costs (antisaccade minus prosaccade latency) are plotted as a function of probability. The gradient shading indicates difficulty of discrimination; darker shading indicates a hard discrimination, and the lightest shading indicates the easiest discrimination. Error bars represent the 95% within-subjects confidence intervals. *P < 0.05.

The average accuracy across participants was 88% (79∼95%). Figure 5B plots accuracy as a function of the three blocks of probabilities and saccade types with target aspect ratios. There was no effect of block (F < 1, P = 0.779), task type [F_(1,9) = 1.408, P = 0.266], or aspect ratio [F_(2,18) = 3.317, P = 0.059] on accuracy. There was a significant interaction between saccade type and their relative probabilities [F_{(1.283,11.551)} = 14.956, P < 0.01 with Greenhouse-Geisser correction], which was driven by the lowered antisaccade accuracy in its lower probability block [A20P80: t(9) = 5.062, P < 0.05] and the lowered prosaccade accuracy in its lower probability block [A80P20: t(9) = 2.613, P < 0.05]. There was no difference in accuracy between pro- and antisaccades when the probability of the two was held equal (A50P50).

DISCUSSION

In the present study, we interleaved pro- and antisaccade trials by the manipulation of peripheral cue discrimination and systematically adjusted their relative probabilities across blocks. By design, we contrasted pro- with antisaccades within each block and observed an antisaccade cost only when antisaccade trials were of low likelihood (A20P80 condition). In addition, when antisaccade trial probability was equivalent to prosaccade trial probability (A50P50), the antisaccade cost was eliminated, replicating the findings from Juan et al. (2008). Most important, when antisaccade trial probability increased (A80P20), antisaccades were generated faster than prosaccades (Fig. 2A), a novel finding that has not been reported before. Our findings demonstrate that the visual system is sensitive not only to probabilistic information associated with the stimulus properties but also to arbitrary events when circumstances favor one saccade type over another. As such, even action that requires effortful inhibition of one's response that has a potent tendency (prosaccade), such as an antisaccade, can be efficiently executed when favored by trial type probability.

Trial Type Probability Is Not Repetition Priming

It has been suggested that task switching between trials requires control over cognitive operations, thereby incurring a cost to the system (Hodgson et al. 2004). On the other hand, benefit of trial repetition in saccade performance may be a result of early accumulation of baseline activity for a particular saccadic type program (Dorris et al. 2000; Tatler and Hutton 2007). In experiment 1, we tested whether our findings from the A80P20 block could have been driven by a combination of task-repetition priming and task-switching cost, which should facilitate high-probability antisaccades and impede low-probability prosaccades, respectively. Results from our MEM analysis did not support this possibility. The switching cost was only found in prosaccades (AP sequence), whereas repeating a task set in antisaccades (AA sequence) actually led to an increase in latency, suggesting that trial type probability cannot be explained by simple trial-to-trial repetition. Since this slowing effect occurred to both pro- and antisaccades (as long as they were preceded by an antisaccade), it is best explained as a leftover inhibitory effect from the preceding antisaccade trial (Mueller et al. 2009). Although this is difficult to test with the present data, it would not be inconsistent with previous findings (Barton et al. 2006a, 2006b; Manoach et al. 2007). Manoach et al. (2007) compared brain activity between trials preceded by either an antisaccade or prosaccade and found that a preceding antisaccade would prolong saccadic latency and reduced blood oxygen level-dependent activity in the frontal (FEF), supplementary (SEF), and parietal eye fields (PEF) during preparation for antisaccade repeat trial.

Trial Type Probability Effect Is Independent From Difficulties of Visual Discrimination

Previous findings have suggested that visual selection and saccade selection are dissociable processes (Juan et al. 2004, 2008; Muggleton et al. 2003; Schall 2004, 2009; Sato and Schall 2003; Thompson et al. 1997). Thus in experiment 2 we added varying levels of target aspect ratio to the task of experiment 1 to manipulate difficulty in cue discriminability and thereby selectively interfere with the visual selection process but not the saccade selection process. This was done to test whether trial type probability operates on the visual selection or the saccade selection stage. We found that the effect of visual discrimination on saccade latency was independent of trial type probability. When the orientation of color singleton (used to cue subjects which saccade type to perform) became hard to identify, overall saccade latency was increased in both pro- and antisaccades (Fig. 5). The antisaccade cost, however, still changed as a function of trial type probability rather than discrimination difficulties (Fig. 6). Our findings from experiment 2 suggest that the effect of trial type probability on antisaccade cost is likely to have originated from the saccade preparation process, and not visual discrimination. Such a hypothesis requires careful consideration, because our explanation of multiple cognitive component processes is based on the saccade latency, which is an end product of that multiple processes.

Possible Neural Mechanisms

The present behavioral data also shed light on the possible neural mechanisms behind trial type probability. As mentioned, the present findings suggest the saccade preparation stage benefit from trial type probabilities. This is similar to probability priming, where the end points of the probable saccade type enjoy a lower threshold or earlier neural activity buildup (Connolly et al. 2005; Dorris and Munoz 1998; Dorris et al. 2000; Everling and Munoz 2000), which speeds up the process of saccade preparation and thus decreases saccade latency. In contrast, the less probable saccade type not only misses out on such facilitation but also has to inhibit and override those preestablished neural responses that favor the likely saccade type and reselect a new end point. Again, converging evidence has pointed to FEF for this kind of probabilistic responses (Liu et al. 2011; Sato and Schall 2003). However, the FEF neurons prefer a specific retinotopic end point for saccades, yet our paradigm does not rely on spatial probabilities. Instead, probability of trial type relies on the symbolic meaning of an abstract instruction rather than on spatial locations. Neurophysiologically, FEF also shows decreased activity during antisaccades (Everling and Munoz 2000), making it an unlikely candidate to be solely responsible for the effect of abstract trial type probability.

Thus a novel insight of the present study is that additional high-level neural regions are necessary to mediate the effect of trial type probability. One likely region that processes such probabilistic information is SEF, a region that projects directly to FEF and superior colliculus (SC) and modulate their activity (Schall et al. 1993; Shook et al. 1990). Although SEF is not the primary center for making saccades, its activity can modulate saccade performance due to its direct output connection to the saccade centers such as FEF and SC. For example, Schlag-Rey and colleagues (Amador et al. 2004; Schlag-Rey et al. 1997) have found that SEF neurons consistently fire more rapidly before antisaccades compared with prosaccades. Cortical potential studies conducted by Everling et al. (1997) also observed larger negativity in SEF before antisaccades. Everling et al. (1998) later demonstrated a shift in negativity from the contralateral to the ipsilateral hemisphere during the performance of antisaccades. Furthermore, functional magnetic resonance imaging (fMRI) studies showed that SEF showed larger activation during the preparatory period (e.g., Curtis and D'Esposito 2003; Brown et al. 2007) on antisaccade trials than on prosaccade trials. Thus both neurophysiology and human studies suggest that the SEF is directly involved in generating the motor signals necessary for antisaccades.

In addition, the SEF is also a good candidate for the mediation of the effect of trial type probabilities due to its supervisory role in oculomotor control. Stuphorn et al. (2010) recently investigated the role of SEF with a stop signal paradigm in which subjects were instructed to respond as fast as possible to a stimulus unless a stop signal was presented after a variable delay. In this study, although SEF neurons did not exhibit activity that could directly trigger saccade initiation or contribute to canceling a saccade, neural activity in SEF before the stop signal or target presentation was effective in predicting whether monkeys could successfully inhibit a saccade in a stop signal trial or not. Stuphorn et al. (2010) proposed that SEF may regulate saccade production by biasing the balance between gaze holding and gaze shifting, depending on prior performance and anticipated task requirements, thereby serving as a proactive control area. Indeed, several studies concerning the functional roles of SEF have observed high SEF activity when rule learning occurs in both a spatial and nonspatial manner and suggested that the SEF plays a critical role in acquiring rules about the environment (e.g., Chen and Wise 1995; Olson et al. 2000; Olson and Gettner 2002). Together, these characteristics of SEF make it a likely region to be critically involved in mediating the effect of trial type probability that we report presently.

Since the present paradigm required strong top-down control over both location and saccade type, it is possible that the effects of probability first take place within SEF, which then send their outputs to eye movement control areas like FEF and SC. The probabilistic representations in SEF may directly benefit the selection processes of FEF by increasing the motor preparation level near threshold, which would decrease saccade latency as a result (Connolly et al. 2002, 2005; Hanes and Schall 1996; Koval et al. 2004; Monoach et al. 2007). Future studies should use tools of high spatial and temporal resolution, such as fMRI, TMS, or magnetoencephalography (MEG) to clarify the precise neural populations that mediate trial type probability.

Limitations of This Study

The paradigm used in the present study is not identical to the conventional antisaccade task, which is usually carried out in a block design (e.g., Everling and Fischer 1998; Munoz and Everling 2004). To incorporate both prosaccade and antisaccade trials in a block of trials in an interleaved design, discrimination of a visual cue is essential for participants to distinguish which type of saccades they should make for the trial. However, the time when this discrimination is executed could be critical to the relative difficulty for prosaccades compared with antisaccades. Prosaccade following a peripheral visual discrimination, as in the present paradigm, may be harder than when participants follow a central cue, which is easier to discriminate before the appearance of the visual display with the saccade target. The concurrent peripheral visual discrimination may occupy visual attention that is typically thought to be captured by the pop-out saccadic target in the central cue condition and thus lessen the reflexive tendency of prosaccades (Kristjánsson et al. 2001). Nonetheless, this is not to say the difficulties of prosaccades are equal to those of antisaccades in the present study. Prosaccades in the present paradigm still have an advantage over antisaccades in that the cue location is the same as the saccade location. In other words, there should be still a cost, although it may be small, for the antisaccade in the present paradigm due to the need to reallocate attention irrespective of the manipulation of trial type probability (Liu et al. 2010; Olk and Kingstone 2003). However, further variability in the antisaccade cost is not uncommon and is often reported in studies that interleave pro- and antisaccade trials with the saccade type indicated by a central cue before the visual display of the saccade target (Amador et al. 1998; Gottlieb and Goldberg 1999; Liu et al. 2010). For example, in Gottlieb and Goldberg's study (1999), monkeys were required to make a prosaccade when the central cue was a filled square and an antisaccade when it was an open square. Even though the discrimination task was easier than in the current study and finished before the target display, Gottlieb and Goldberg also failed to observe an antisaccade cost in their experiments (monkey 1: prosaccade, 293 ± 33 ms vs. antisaccade, 278 ± 43 ms; monkey 2: prosaccade, 265 ± 26 ms vs. antisaccade, 265 ± 33 ms). Together with our current findings, it seems that the discrimination task and the singleton task may need to coexist to eliminate the antisaccade cost that is usually observed in a block design. However, trial type probability is an independent and influential factor that affects the antisaccade cost. Whether the antisaccade cost would be reinstated regardless of the probability distribution in a conventional antisaccade paradigm needs to be tested.

Conclusions

Our results suggest that the antisaccade cost is modulated, in large part, by trial type probability. The effects of trial type probability on antisaccade cost are likely originated from the saccade preparation process. Therefore, prior probabilistic information is an important factor not only for simple decision making but also for flexibility of voluntary control. Further studies are needed to determine how trial type probability is represented at the neuronal level to modulate antisaccade cost.

GRANTS

This work was sponsored by National Science Council, Taiwan Grants 99-2410-H-008-022-MY3, 97-2511-S-008-005-MY3, 98-2410-H-008-010-MY3, 98-2517-S-004-001-MY3, and 97-2511-S-008-008-MY5. N. G. Muggleton was supported by the UK Medical Research Council. C.-H. Juan was supported by National Science Council, Taiwan Grant 98-2918-I-008-011 and the Fulbright Scholarship, Taiwan and USA.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).