Measuring sparseness in the brain: Comment on

Abstract

Bowers (2009) challenged the common view in favor of distributed representations in psychological modeling and the main arguments given against localist and grandmother cell coding schemes. He revisited the results of several single-cell studies arguing that they do not support distributed representations. We praise the contribution of Bowers for joining evidence from psychological modeling and neurophysiological recordings, but disagree with several of his claims. In this comment we argue that distinctions between distributed, localist and grandmother cell coding can be troublesome with real data. Moreover, these distinctions seem to be lying within the same continuum, and we argue that it may be sensible to characterize coding schemes using a sparseness measure. We further argue that there may not be a unique coding scheme implemented in all brain areas and for all possible functions. In particular, current evidence suggests that the brain may use distributed codes in primary sensory areas and sparser and invariant representations in higher areas.

Understanding the principles of how our brains are capable of different functions arguably constitutes one of the greatest scientific challenges of our times. Such an enterprise requires a combined effort across diverse disciplines, such as neuroscience, biology, computer science, psychology, philosophy and physics, to name only a few. Along these lines, the recent contribution of Bowers (2009) should be praised for its significant attempt to put together knowledge derived from neurophysiological recordings, computational models and psychology. In this comment we discuss a few ideas to clarify some of the neurophysiological concepts addressed in Bowers’ review. In particular, we emphasize the technical difficulties in addressing questions about the coding of information by neurons based on single-cell recordings and discuss how these experimental constraints affect claims of distributed, sparse and grandmother-cell representations.

One of the most striking facts in visual perception is how, in a fraction of a second, our brains can make sense of very rich sensory inputs and use this information to create complex behaviours. It is perhaps the easiness with which we perform such functions that may make us typically unaware of the exquisite machinery in the brain required for such computations. We may be amazed at realizing that we can solve “Rubik’s cube” or at beating a master in a chess game, but we are hardly surprised when we perform something as complex as recognizing a familiar face in a crowd. A key question to understand how the brain processes information is to determine how many neurons, in a given area, are involved in the representation of a visual percept (or a memory, a motor command, etc) and what information each of these neurons encodes about the percept. On the one hand, the representation of a given percept could be given by the activity of a large population of neurons. In this case the percept emerges from the ensemble response and cannot be understood by inspecting the responses of individual neurons without considering the whole population. On the other hand, the percept might be represented by very few and more abstract cells, and each of these cells gives explicit information about the stimulus. In neuroscience, the first scenario is usually referred to as distributed population coding and the second one as sparse coding, its extreme case -of having one neuron coding for one percept- usually referred to as “grandmother cell representation” (but note that the term “grandmother cell” can also be taken as meaning many neurons encoding for one percept, or just meaning an abstract representation). We anticipate that these definitions may be imprecise (as noted by Bowers) and that the same terms may be used with different meanings by different communities of researchers. For example, we already mentioned different uses of the term grandmother cell. Moreover, for Bowers sparse codes are a form of distributed codes and in neuroscience these two types of coding are taken as the opposite. To avoid confusion, in the following we will refer to distributed and localist codes, following Bowers notation. It is indeed the vagueness and different meaning of these definitions that give rise to some of the discussions in the field.

A central theme in the discussion by Bowers concerns the biological plausibility of localist models. To address this question, Bower refers to evidence from single-cell recordings, the gold standard to elucidate the function of neural circuits. Such parallels between neurophysiology and psychological models could have a major impact in both fields. It is in this spirit that we aim to contribute to this discussion by adding to and commenting on Bowers’ claims from the perspective of neurophysiologists trying to extract this type of information from single-cell recordings.

Defining distributed and local (or sparse) coding

Bowers defined distributed codes as a representation in which each unit is involved in coding more than one familiar “thing”, and consequently, the identity of a stimulus cannot be determined from the activation of a single unit (Bowers, 2009) (our emphasis on “thing”). Moreover, he distinguishes between dense distributed representations, i.e. distributed coding schemes where each neuron is involved in coding many different things, as commonly associated with Parallel Distributed Processing (PDP) theories in psychological modeling (McClelland, Rumelhart, & Group, 1986; Rumelhart, McClelland, & Group, 1986) -for related ideas in Theoretical Neuroscience, see (Hopfield, 1982, 2007)-, and coarse coding schemes, i.e. distributed codes where single neurons have broad tuning curves, such that a single neuron codes for a range of similar “things”. Although a broadly-tuned neuron may respond most strongly to a preferred stimulus, noise would preclude identifying the stimulus precisely from the single-cell activity (Bowers, 2009). In contrast to distributed codes, according to Bowers, a localist representation is characterized by neurons coding for one thing, where it is possible to infer a stimulus from the activation of a single unit. In between localist and coarse coding schemes, Bowers introduced one more term, sparse distributed coding, but it seems that these definitions lay within the same continuum and the distinction between a localist and a sparse distributed code is just given by the number of objects encoded by a neuron.

The above definitions seem at first plausible but the distinction among them becomes fuzzy when considering neurophysiological recordings. We should first mention that the distinction between distributed representation and coarse coding appears to be in how “similar” the neuronal preferences are. Defining “similarity” in a rigorous way is already quite a complex challenge in itself. For example, we can loosely imagine that a front view of a face is similar to a profile view of the same face, and very different from a front view of a different face. However, such a statement is quite arbitrary: at the pixel level, the similarity between front views of two different faces is much larger than between a front and profile views of the same face. This is far from a trivial consideration: achieving a good definition of what humans consider similar things constitutes a central challenge in computer vision, neuroscience and psychology. A second problem with these definitions, and perhaps a more fundamental one, is given by the ambiguity of what is meant by “thing”. A “thing” could be a face, a car, an animal but also a pixel, an oriented bar or an abstract concept. How “thing” is defined may radically alter our conclusions regarding how distributed or local a neural coding is. For example, a neuron in V1 may have a local representation for oriented bars in their receptive fields but at the same time a distributed representation for faces. To address this problem, Bowers argues that we cannot think of a distributed representation of a complex familiar thing (e.g. a face) at a low level of the system (e.g. the retina or V1). Indeed, the retina does not “know” that there is a face. This dichotomy is usually referred to as implicit versus explicit representation. The retina encodes information about the face in an implicit manner (it seems far-fetched to argue that the retina does not encode the visual information at all!). In contrast, the representation of the face at the level of the temporal lobe becomes explicit, in the sense that single-cells can give us reliable information about the presence or absence of a face. To be more precise, an explicit representation can be defined by requiring that the information can be decoded by a single layer network (Koch, 2004).

Given the activity of a single V1 neuron, we can discriminate the presence or absence of an oriented bar within the receptive field well above chance but we cannot tell whether a particular face is present or not because this information is not explicit at the level of V1. But even when considering only oriented bars, should an oriented bar at 49 degrees constitute a different “thing” compared to an oriented bar at 50 degrees? How many degrees of separation do we require before an oriented bar becomes a new “thing”? The continuum nature of orientation makes this distinction difficult. In higher visual cortex it is also possible that there exists a similar continuum of features to which neurons respond, only that it is in general difficult to assess what those features are (Connor, Brincat, & Pasupathy, 2007; Tanaka, 1996). This distinction is even harder for areas such as the hippocampus, where a neuron could fire preferentially to the different views of the tower of Pisa and the Eiffel Tower and another one to different pictures of Jennifer Aniston and Lisa Kudrow (both actresses of the TV series “Friends”), see Figures S6 and S7 in (Quian Quiroga, Reddy, Kreiman, Koch, & Fried, 2005). Clearly, these responses are related at some high level of abstraction, which seems plausible given the role of hippocampus, among other areas, in coding associations (Miyashita, 1988; Wirth et al., 2003). However, it is unclear how different these concepts are or whether they should be considered as the same “thing” (landmarks of Europe in the first case, and the two actresses of Friends in the second one).

Another problem with these definitions is that, in real life, identifying the stimulus encoded by the neural activity involves setting a responsiveness criterion for defining what is a significant response and what is not, which of course depends on the particular criterion chosen. Alternatively, it is also possible to use decoding algorithms or the information theory formalism to extract information about the stimulus from the neural responses (Abbott, 1994; Quian Quiroga & Panzeri, 2009; Rieke, Warland, de Ruyter van Steveninck, & Bialek, 1997). But this can be also problematic for the above definitions because, due to trial-to-trial variability, noise, lack of enough number of trials, etc, decoders or information theory do not provide yes/no answers, but estimations of performance or amount of information.

To avoid defining what is a “thing” and whether two stimuli are similar or not, it seems to us preferable to simplify the nomenclature by describing a continuum with dense distributed representations at one end and localist representations at the other. Central to this discussion is to determine where neuronal representations reside within this continuum, something that can be quantified with a sparseness measure, as the one to be discussed in the following sections. Then, a high degree of sparseness will imply a local coding and, conversely, a low degree of sparseness will be evidence for a distributed representation.

Neural responses and neural codes

Bowers discusses the interactive activation (IA) model of visual word recognition (McClelland & Rumelhart, 1981; Rumelhart & McClelland, 1982) to distinguish between what a neuron “responds to” and what a neuron “codes for”. In his example (see Figure 4 in (Bowers, 2009)), a unit at the top level of the IA model responds to both “blur” and “blue” due to the similarity between these two stimuli: they share the first 3 letters and differ only in the last one. However, he argues that a particular unit only codes for blur by construction. According to Bowers, in this case the neuron shows a localist code because, although it responded to two “things”, the neuron encoded the meaning of only one of them. He therefore claims that responses to multiple objects do not provide evidence of a distributed representation. But this argument has some problems. For example, suppose that the same network is used with a new set of words, containing “blue” but not “blur”.

The neuron will consistently fire to “blue” and, in fact, from the firing of this neuron we may accurately predict the presence of this word. Will we then say that in spite of such an explicit representation the neuron does not code for “blue”, given that it was trained to code for a similar word in the first place? These distinctions become even more problematic with real neuronal activity, because we do not have direct access to what a neuron “codes for”, but rather to what it “responds to”. In other words, if a neuron responds to more than one thing, how could we know which response is “meaningful” and which one is not? Moreover, if we extrapolate Bower’s argument based on the IA model, we could easily conclude that every single neuron in the brain is only coding for one “thing”: when the neuron responds to many “things” we could simply state that it surely prefers only one “thing” and it merely responds to the other “things” due to similarity. What would then constitute evidence for a distributed representation (but a neuron responding to multiple “things”)? In other words, how can we falsify a localist coding scheme if we do not accept the evidence from neurons responding to multiple “things”? In fact, it seems implausible to argue that we do not have evidence for distributed coding because we do not know if we should ignore most of the responses. For any definition of localist and distributed coding, it is important to specify what type of evidence would support or falsify each type of code. Below, we propose to characterize neuronal responses quantitatively by a single “degree of sparseness”. While many of our caveats described above remain even under this approach, this quantitative definition allows us to provide support for or falsify both distributed and localist representations.

Measuring sparseness

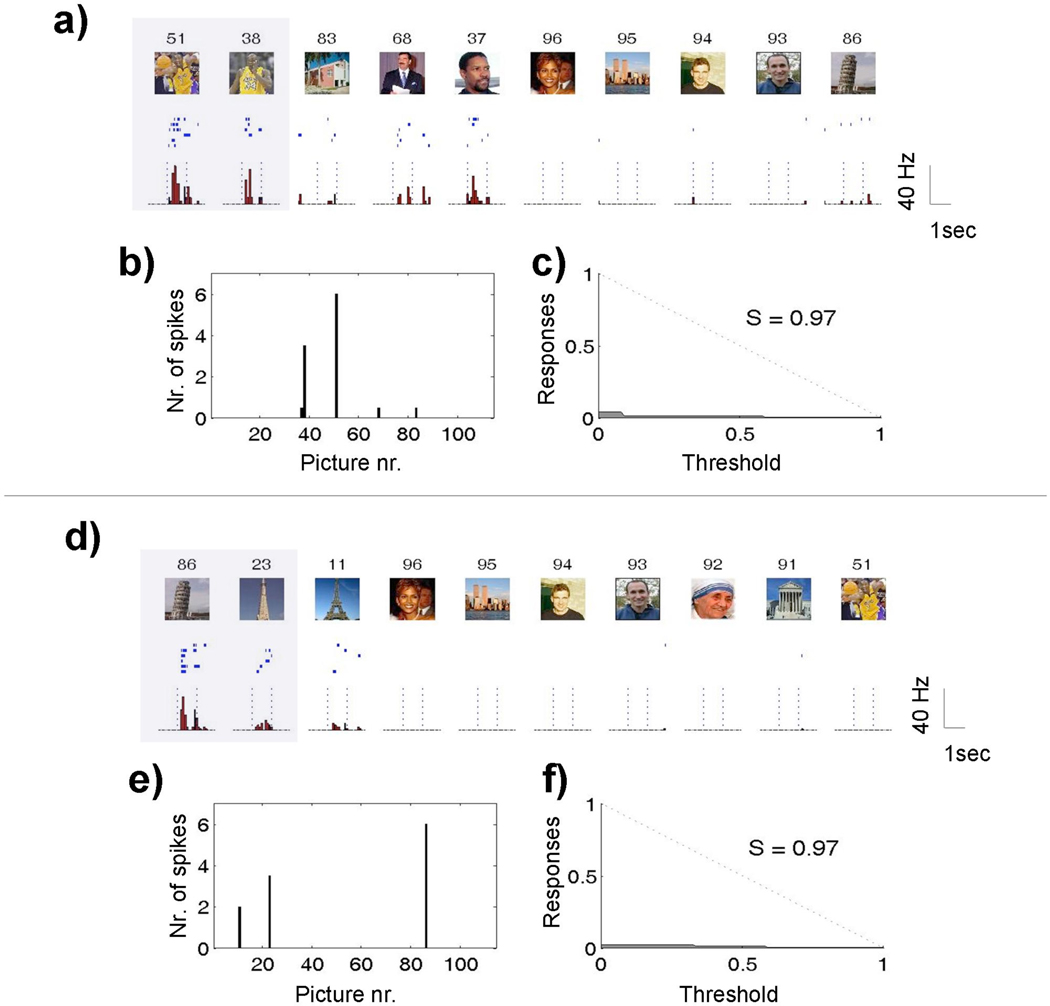
Given the problems highlighted in the previous sections, it seems preferable to refer to distributed and local (or sparse) responses, with the understanding that neuronal responses constitute a proxy for neuronal codes. In order to quantify the distinction between localist and distributed responses, we need to be able to measure the degree of sparseness of single-cell activations in a reliable way. Figures 1A and 1D show the responses of 2 single units simultaneously recorded from the same micro-wire, whose activity could be separated after spike sorting (Quian Quiroga, 2007; Quian Quiroga, Nadasdy, & Ben-Shaul, 2004). Both units are nearly silent during baseline (average < 0.01 spikes/sec) and fired with up to 40 spikes/sec to only a few of the 114 pictures shown in this recording session. The first unit responded to two basketball players and the second one to two landmark buildings. Due to space constraints, only 10 responses are shown. There were no responses to the other pictures not shown.

Figure 1.

a–d) Ten largest responses of two simultaneously recorded single units in the right posterior hippocampus. There were no responses to the other 104 pictures shown to the patient. For each picture (upper subplots) the corresponding raster plots (middle subplots; first trial on top) and post-stimulus time histograms with 100 ms bin intervals (lower subplots) are given. Highlighted boxes mark significant responses. The vertical dashed lines indicate the times of image onset and offset, 1 second apart. Note the marked increase in firing rate of these units roughly 300 ms after presentation of the responsive pictures. b–e) median number of responses (across trials) for all the pictures presented in the session. c–f) relative number of responses as a function of the variable threshold (see text). Note the high selectivity values for both units (S=0.97), thus implying a sparse representation. Data reprinted from (Quian Quiroga et al., 2007).

From Figures 1A and 1D the high degree of selectivity of these neurons is clear, but how can we measure sparseness? There are two notions of sparseness (or local coding, according to Bowers notation) in the literature: 1) ‘population sparseness’ refers to the activation of a small fraction of neurons of a population in a given time window; and 2) ‘lifetime sparseness’ refers to the sporadic activity of a single neuron over time, going from near silence to a burst of spikes in response to only a small subset of stimuli (Olshausen & Field, 2004; Quian Quiroga, Reddy, Koch, & Fried, 2007; Willmore & Tolhurst, 2001). These two notions are related, since one expects that if a cell fires to few stimuli, then each stimulus will be encoded by a relatively small population of cells. However, it is in principle possible that most cells in a given population respond to one (or a few) stimuli, or that a small subset of neurons is very promiscuous, responding exuberantly to many stimuli. Most studies usually assess lifetime sparseness, assuming that it will be similar to population sparseness. In this context, lifetime sparseness, also termed selectivity or specificity, means that a given cell responds only to a small subset of the presented stimuli. On the contrary, if a neuron responds to many stimuli it is said to be broadly tuned, pointing towards a distributed representation.

The notion of sparseness –and any measure to quantify it- depends on the stimulus set. In particular, the units of Figure 1A and 1D have sparse responses because they were activated only by very few of the more than 100 pictures presented. However, it is conceivable that a lower degree of sparseness would have been obtained for the unit in Figure 1D if more views of landmarks (and in particular of the tower of Pisa) had been used. To give a more clear (and extreme) example, if one neuron responds to many different faces, as in monkey IT (C.G. Gross, 2008; C. G. Gross, Rocha-Miranda, & Bender, 1972; Hung, Kreiman, Poggio, & DiCarlo, 2005), it would appear to respond in a highly sparse manner if the stimulus set contains only one face and a large number of other stimuli. This seemingly trivial point makes it difficult to compare the degree of sparseness in different areas because different stimulus sets are typically used.

The simplest measure of sparseness would be to report the relative number of stimuli eliciting significant responses in a neuron. However, this number depends on the criterion used for defining what is a significant response and what it is not. In particular, if a very strict threshold is used, then only the few largest responses will cross this threshold and, consequently, this neuron will appear to be sparse. To overcome this dependence, a novel sparseness index (S) was introduced (Quian Quiroga et al., 2007) by plotting the normalized number of ‘responses’ as a function of a threshold (Figures 1C, 1F). One hundred threshold values between the minimum and the maximum response were taken, and for each threshold value the fraction of responses above the threshold was computed. The area under this curve (A) is close to zero for a sparse neuron and is close to 0.5 for a uniform distribution of responses (dotted line in Figures 1C and 1F). The sparseness index (S) was defined as S=1 – 2A. S is 0 for a uniform distribution (a dense representation) and approaches 1 the sparser the neuron is (for a localist representation). The sparseness index values in Figures 1C and 1F (0.97 in both cases) confirm that the sparseness of these neurons is not just the consequence of the arbitrary choice of a very strict threshold.

Related to the discussion of how localist (sparse) or distributed is the representation of neurons in a given area, it should be noted that highly selective neurons, as the ones presented in Figures 1A and 1D, are hard to be detected without optimal data processing and recording conditions. This basically relies on: 1) the recording of broad band continuous data allowing off-line analysis; 2) the use of an optimal spike detection and sorting algorithm and 3) the use of semi-chronic multiple electrodes in contrast to traditional single electrode recordings. In fact, single electrode recordings are usually carried out with movable probes that tend to miss sparsely firing cells - that are quiet when the electrode passes by their vicinity unless the right stimulus is shown - and are more likely to record the activity of neurons with high spontaneous rates and broadly-tuned responses. This introduces a bias towards distributed representations, which is likely to be prevalent in multiple descriptions of apparently distributed representations in the literature. This issue is becoming quite relevant given recent evidence of highly sparse neurons in different systems (for a review see (Olshausen & Field, 2004)). For example, Perez-Orive and coworkers (Perez-Orive et al., 2002) using multi-electrode recordings found cells in the mushroom body of the locust with a baseline activity of about 0.025 spikes per second, which fired about 2 spikes to very few odors. Hahnloser and coworkers (Hahnloser, Kozhevnikov, & Fee, 2002) using antidromic stimulation found ultra-sparse firing neurons in the songbird. These neurons had less than 0.001 spikes per second baseline activity and elicited bursts of about 4 spikes when the bird sang one particular motive. As shown in Figure 1, neurons in the human medial temporal lobe can have a baseline firing of less than 0.01 Hz and respond with up to 50Hz to very few stimuli.

Evidence for local and distributed codes in the brain

In his overview, Bowers revisits neurophysiology evidence of sparse and distributed representations and reinterprets these works as evidence for localist and even grandmother cell codes. He particularly refers to the recordings in macaque monkeys by Young and Yamane (Young & Yamane, 1992) saying that these authors claimed to have provided evidence for a distributed code. It seems that Bowers’ criticism of this paper is due to the different meanings given to some terms by different communities of researchers. In fact, Young and Yamane argued for a sparse representation (in the sense of being opposite to distributed, as generally taken in neuroscience) already in the title of their well known Science paper “Sparse population coding of faces in the inferior temporal cortex” (Young & Yamane, 1992). What may be confusing is the fact that they also referred to population coding, but this is just reflecting the fact that even with sparse responses a population of neurons –in contrast to a single-cell- is needed to encode a percept.

Hung and coworkers showed that neurons in monkey IT respond to multiple images ((Hung et al., 2005), see also (Kreiman et al., 2006)). They used a statistical classifier to decode the activity of an ensemble of hundreds of neurons. Bowers argues that the classifier units coded for only one object and concludes that the data do not support distributed coding arguments. Here it is important to distinguish between the experimental data (the recordings of neurons in inferior temporal cortex) and the classifier units. The units in IT cortex responded to multiple objects and it was not possible to decode the presence of individual objects with high accuracy from only one neuron. In contrast to the case of IT neurons (the physiological data), the classifier units that operated on the output of hundreds of IT neurons, showed sparser responses. But this does not provide any direct evidence that such a code exists in the brain, as the classifier is a theoretical construct. Further support to the claim of distributed coding by these neurons is given by the fact that decoding performance increased nonlinearly with the number of neurons. For a pure localist code, each neuron contributes to identify one or a few objects and therefore, the decoding performance or alternatively the capacity -i.e.: the number of objects that can be identified at a fixed performance level- grows linearly with the number of neurons, as it is the case for recordings in the human MTL (Quian Quiroga et al., 2007). On the contrary, for a distributed code each neuron contributes to the representation of many objects and both decoding performance and capacity have a nonlinear grow with the number of neurons, as observed in IT recordings in monkeys ((Hung et al., 2005); see Point 15 in http://klab.tch.harvard.edu/resources/ultrafast/index.html). In fact, it is in principle possible to encode 2^N objects with a fully distributed network of N binary neurons, but it has to be noted that the exact nonlinear functional dependence with the number of neurons depends on several factors, such as noise levels, trial-to-trial variability and saturation of decoding performance due to limited sampling of stimuli (Abbott, Rolls, & Tovee, 1996). In this respect, Bowers claims that the exponential increase of decoding performance with the number of neurons found by Hung and colleagues (and also by Rolls and colleagues, as described in the next paragraph) does not constitute evidence of distributed representations. This argument brings us back to the previous discussion of how to experimentally establish what a neuron codes for, given what it responds to. In our view, the fact that neurons fire to multiple stimuli (therefore having an exponential increase of performance with the number of neurons) gives strong evidence for distributed coding. Again, the claim that these neurons may encode only one “thing” and fire to the other ones by mere “similarity” (as in Bowers’ argument with the IA model) is of limited relevance since it cannot be verified or falsified with the existing data and recording tools.

Further evidence for distributed representations in visual processing areas comes from the recordings of Rolls and coworkers (Rolls, Treves, & Tovee, 1997), showing also an exponential increase of decoding performance with the number of neurons (see also (Abbott et al., 1996)). Bowers criticizes these results because: i) the study was carried out on a set of face cells that were not highly selective, and ii) the same analysis carried out on our MTL neurons would likely lead to a different conclusion. If Rolls and colleagues had recorded data from different areas, results may have been different because different areas may represent information in a different way. However, we do not see this as a problem with the experiment or the approach taken by these authors, as claimed by Bowers. Rolls and colleagues report observations based on the area they recorded from and do not generalize their claims to other areas. In fact, they explicitly mention that this encoding may be different in other parts of cortex and for other category of visual stimuli (Rolls et al., 1997). Interestingly, a similar decoding analysis was indeed carried out with our selective responses in the human MTL (Quian Quiroga et al., 2007). In contrast to the findings of Rolls et al (Rolls et al., 1997) and Hung et al (Hung et al., 2005), in this case the decoding performance increased linearly rather than exponentially, in agreement with a very sparse or localist coding scheme.

An extreme example of sparse coding is given by the single-cell responses to picture presentations in the human medial temporal lobe, as showed in the examples depicted in Figure 1. In spite of the striking degree of sparseness of these neurons, we argue that they cannot be taken as conclusive evidence of the existence of grandmother cells -understood in the sense that one neuron encodes only one object (Quian Quiroga, Kreiman, Koch, & Fried, 2008; Quian Quiroga et al., 2005)-. In particular, given the number of responsive units in a recording session, the number of stimuli presented and the total number of recorded neurons, using probabilistic arguments we estimated that from a total population of about 10⁹ neurons in MTL, less than 2×10⁶ neurons (not 50–150 as incorrectly reported by Bowers) are involved in the representation of a given percept (Waydo, Kraskov, Quian Quiroga, Fried, & Koch, 2006). Bowers argues that this estimation is flawed because: (i) multiple neurons can respond to the same image and (ii) these calculations assume that a grandmother cell should only respond to one face or object. Briefly, the fact that multiple neurons can respond to the same image – a possibility that we consider very likely - is not a problem for the above calculations. In fact, it seems highly unlikely that we happened to find the one and only neuron that responds to a particular face. This argument was explicit in (Quian Quiroga et al., 2005) and further quantified in (Waydo et al., 2006). With regards to the second point, we did not assume that grandmother cells should respond to only one object, as claimed by Bowers, but rather estimated an upper bound for the number of objects that a neuron may respond to. In fact, in our calculations we did not consider any properties of how grandmother cells should or should not respond at all. It should be also stressed that, as discussed in Waydo et al (Waydo et al., 2006), the estimated number of neurons responding to one concept could be much lower because: 1) images known to the subjects are more likely to elicit responses than unfamiliar stimuli, and 2) neurons with a higher degree of sparseness are very difficult to detect in our recording sessions lasting, on average, about 30 minutes.

Evidence from single-cell recordings shows that the brain may go from distributed representations in lower sensory areas to sparse representations in higher areas. We already mentioned the very sparse responses to odors by Kenyon cells (KC) in the locust (Perez-Orive et al., 2002). KC neurons receive direct inputs from projection neurons in the antennal lobe, which have a largely distributed representation for odors (compare the responses of Figure 1A and Figure 1B in (Perez-Orive et al., 2002)). Similarly, the ultra-sparse responses of RA (robust nucleus of the archistriatum) neurons in the zebra-finch are driven by HVC (high vocal centre) neurons with distributed responses (see Figure 2b in (Hahnloser et al., 2002)). Further evidence in other species is still scarce since, as mentioned in the previous section, to compare selectivity across different areas one should use the same stimulus set. Barnes and coworkers showed that neurons in the hippocampus in rats responded more selectively than neurons in entorhinal cortex to the rat spatial location (Barnes, McNaughton, Mizumori, Leonard, & Lin, 1990). These results seem to support the hypothesis of complementary learning systems, with higher level of sparseness in the hippocampus than in cortex (Norman & O'Reilly, 2003), an appealing idea that would explain fast learning of new episodic memories and associations in the hippocampus by using sparse coding on the one hand, and generalization in cortex by using a distributed representation on the other. Bowers criticizes the study of Barnes et al and its support to the complementary systems hypothesis by claiming that entorhinal cortex is not part of neocortex and that a proper comparison of sparseness should be made between hippocampus and neocortex. However, the entorhinal cortex is the main gateway to the hippocampus –i.e.: most of the information from neocortex is conveyed to the hippocampus through the entorhinal cortex. To us this gives valuable evidence of how the representation gets sparser when reaching the hippocampus. Moreover, a more recent study with single-cell recordings in the human medial temporal lobe showed that the selectivity of the single-cell responses was significantly lower in the parahippocampal cortex (one of the main inputs to entorhinal cortex) compared to the one in the entorhinal cortex, amygdala and hippocampus (Mormann et al., 2008).

It seems also plausible to argue that a distributed representation in IT is transformed to the sparser representation shown in the medial temporal lobe (compare responses of Hung et al (Hung et al., 2005) in IT with those of Quian Quiroga et al (Quian Quiroga et al., 2007; Quian Quiroga et al., 2005) in MTL), given the close anatomical connections between these areas. However, we emphasize that this is still a conjecture due to the different recording techniques, species and stimuli used in these studies. In this respect, it has been argued that more distributed representations in IT (compared to MTL) may be necessary to identify the different views of the same person or object with a population code (DiCarlo & Cox, 2007), in contrast to the sparse and invariant responses in the human MTL, where neurons fire to the concept in an abstract manner and the particular view or details of the pictures are irrelevant. It is also possible that very sparse neurons are also present in IT but are hard to be found, partially due to the technical difficulties described in the previous sections.

Conclusions

In summary, Bowers made a commendable effort to link psychological theories and computational models to the firing of individual neurons in the brain. This effort should be praised and hopefully extended through further interactions across these fields. In this commentary, we tried to emphasize the difficulties inherent to neurophysiology and the challenges involved in distinguishing between distributed and local codes. We also attempt to provide a quantitative framework to describe neuronal representations, residing in a continuum that ranges from distributed to local representations. Given how poor our understanding of visual cortex currently is, we hope that this quantitative formulation will avoid semantic discussions and will pave the way to comparisons across areas, laboratories, experimental conditions and between physiology and computational models. Unraveling the codes used by circuits of neurons to represent information is arguably one of the most fascinating and challenging adventures at the intersection of psychology, computer science and neuroscience.