A Two-Step Chemical Mechanism for Ribosome-Catalyzed Peptide Bond Formation

Abstract

The chemical step of protein synthesis, peptide bond formation, is catalyzed by the large subunit of the ribosome. Crystal structures have demonstrated that the active site for peptide bond formation is composed entirely of RNA¹. Recent work has focused on how an RNA active site is able to catalyze this fundamental biological reaction at a suitable rate for protein synthesis. Based on the absence of important ribosomal functional groups², lack of a dependence on pH³, and the dominant contribution of entropy to catalysis⁴, it has been suggested that the role of the ribosome is limited to bringing the substrates into close proximity. Alternatively, the importance of the 2′-hydroxyl of the peptidyl-tRNA⁵ and a Bronsted coefficient near zero⁶ were taken as evidence that the ribosome coordinates a proton-transfer network. Here we report the transition state of peptide bond formation based upon kinetic isotope effect analysis at five positions at the reaction center of a peptidyl-tRNA mimic. Our results indicate that in contrast to the uncatalyzed reaction, formation of the tetrahedral intermediate and proton-transfer from the nucleophilic nitrogen both occur in the rate-limiting step. Unlike previous proposals, the reaction is not fully concerted, instead breakdown of the tetrahedral intermediate occurs in a separate fast step. This suggests that in addition to substrate positioning, the ribosome is contributing to chemical catalysis by changing the rate-limiting transition state.

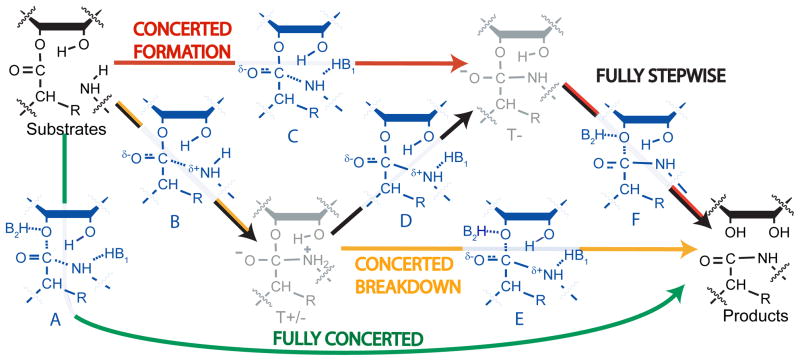
Several reaction mechanisms have been proposed for peptide bond formation (Figure 1). The peptidyl transferase reaction occurs through nucleophilic attack of the α-amino group of aminoacyl-tRNA on the carbonyl carbon of the peptidyl-tRNA. A peptide bond forms and the ester bond linking the peptide to the 3′-oxygen of peptidyl-tRNA breaks, leaving a deacylated tRNA and a peptide lengthened by one amino acid. If substrate positioning is the sole contribution to catalysis, the mechanism on the ribosome is expected to be equivalent to the well-studied uncatalyzed reactions where a pathway involving two tetrahedral intermediates is followed (T± and T-, Figure 1, black pathway, see figure legend for explanation of mechanisms and intermediates). At high pH, the rate-limiting transition state for the uncatalyzed reaction was predicted to occur during deprotonation of the zwitterionic T± intermediate based on the pH-rate dependence of the reaction and a Bronsted coefficient near 1 (transition state D)⁷. At low pH, breakdown of the negatively charged T- is rate-limiting (transition state F).

Figure 1.

Proposed reaction mechanisms. Ground states are shown in black, intermediates in grey, and transition states in blue. The ribosomal reaction may involve two intermediates like the uncatalyzed reaction (black pathway). Nucleophilic attack leads to an intermediate with a positively charged nitrogen and negatively charged carbonyl oxygen (T+/−). Deprotonation leads to a negatively charged intermediate (T-), which breaks down to products. Alternatively, one or both of these steps may be concerted, with only one intermediate (red and orange pathways), or no intermediates (green). The identities of B1 and B2 are uncertain; the 2′-hydroxyl may be one, both, or neither.

It has also been suggested that the peptidyl-tRNA 2′-hydroxyl acts as a “proton shuttle” that abstracts a proton from the nucleophilic amine and simultaneously donates another proton either directly or indirectly to the leaving group oxygen^8,9. This could happen in a stepwise fashion (Figure 1, red and orange pathways) involving a tetrahedral intermediate. Alternatively, the reaction has been proposed to be fully concerted, with the amide bond to the nucleophile formed at the same time that the ester bond to the leaving group is broken (green pathway). Recently, computational methods were used to evaluate concerted proton shuttle mechanisms with and without an additional water molecule, and favored a fully concerted eight-member proton shuttle(similar to transition state A)¹⁰. Alternatively, other computational studies have indicated a stepwise proton shuttle would be favorable^11,12. All of these possibilities have been proposed^4,8–13.

Each mechanism predicts a different transition state and hence a different role for the ribosome in catalysis. Therefore we sought to obtain experimental constraints for modeling the transition state of ribosome-catalyzed peptide bond formation using kinetic isotope effect (KIE) analysis (reviewed in 14). Generally, if the rate effect of isotopic substitution (defined as k_light/k_heavy ) is greater than one (termed “normal”), it indicates bonding to that isotope is weaker in the transition state. Reaction coordinate motion of a substituted atom will also contribute to a normal isotope effect. Alternatively, if the isotope effect is less than one (termed “inverse”) it indicates stronger bonding. The magnitude of the effect is correlated with the change in bond order. To make this analysis possible, we previously synthesized a complete series of molecules that differ by a single isotopic substitution at each atom within the reaction center^15,16. These molecules are substrates for the ribosomal 50S fragment reaction^17,18. Previous studies indicate chemistry is rate-limiting for this assay and that unlike the 70S reaction, which has a complete commitment to catalysis, this reaction is amenable to KIE analysis¹⁸. The Bronsted coefficient of the nucleophile and the structure of the active site are within experimental error for 50S and 70S ribosomes, indicating the mechanism of catalysis is similar^6,19.

To achieve the necessary precision, KIEs were measured by a competitive assay. The light and heavy substrates were incubated in the same reaction, and the change in their ratio as the reaction proceeded was used to determine their relative reaction rates. We used two remote radiolabels, ³²P and ³³P, attached to the 5′-ends of the P-site substrate and performed scintillation counting to define the relative abundance of the two substrates as previously described for the uncatalyzed reaction^20,21.

Given the small magnitude of the expected effects (typically in the range of 0.95 to 1.05) and the complexity of the experimental system (a 1.5 MDa complex altered by 1–2 Da), we performed several controls to determine the extent of random and systematic error. First, we demonstrated that the effect from the remote label alone [1.001 ± 0.002 (standard error)] is much smaller than the effects we expect for atoms at the reaction center. This value and the effect of deuterium substitution at the amino acid α-carbon were determined thirty-three and forty times, respectively. Repeated measurements in both cases yielded normally distributed data, with a significant difference between the mean of the control and the mean of the α-deuterium substitution (Figure 2). Furthermore, two sets of measurements were made for each substitution, one pairing ³²P with the light isotope at the reaction center and ³³P with the heavy isotope, and a second with the opposite pairings – ³²P with the heavy isotope and ³³P with the light isotope. These determinations gave the same values within experimental error.

Figure 2.

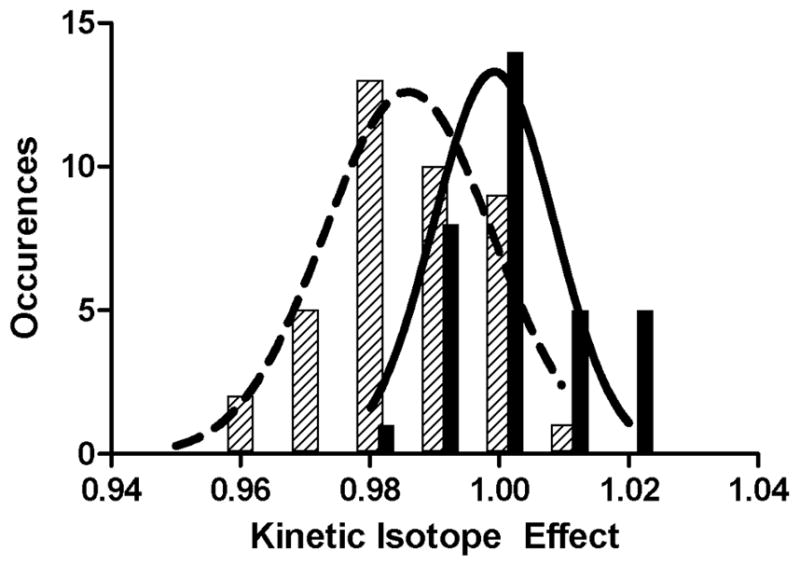
Histograms of measured isotope effects. Controls (solid bars) and α-deuterium substitution (hatched bars) both fit to normal distributions.

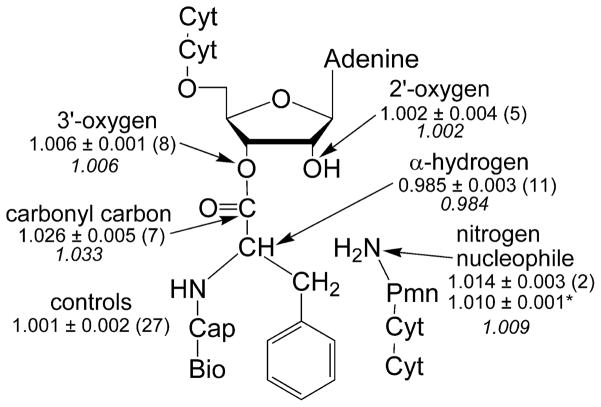
We measured isotope effects for five positions at the reaction center: the 3′-oxygen leaving group, the carbonyl carbon, the nucleophilic nitrogen, the hydrogen attached to the α-carbon, and the vicinal 2′-hydroxyl (Figure 3). The simplest effect to interpret is that of ¹⁸O substitution on the leaving group, which measures the extent of C-O bond dissociation in the transition state. Effects in the range of 1.02 to 1.06 have been observed when cleavage of the C-O bond is rate-limiting^22,23. Conversely, if formation of the amide bond or deprotation of the T± intermediate is the rate-limiting step, then a maximum effect of only 1.01 is expected²². We observed a small effect (1.006) upon 3′-¹⁸O substitution, which indicates there is not significant C-O bond-breaking in the rate-limiting step. This is inconsistent with transition state A, the mechanism in which bond formation to the nucleophile is concerted with breaking the bond to the leaving group, and limits the possible transition states to B, C, and D (Figure 1). Notably, the leaving group oxygen effect previously predicted for fully concerted proton-shuttle mechanisms varied from 1.023 to 1.038¹⁰ (transition state A), which is inconsistent with the value of 1.006 measured here.

Figure 3.

Kinetic isotope effects. Values are reported as means ± standard errors with the number of independent trials in parentheses. The second value for the nitrogen nucleophile (asterisked) was previously determined using mass spectrometry instead of scintillation counting as the readout. Calculated values for the transition state in figure 4 are shown in italics. Full substrates are shown; cyt=cytidine, cap=caproic acid, bio=biotin, pmn=puromycin.

The primary carbonyl-¹³C isotope effect is derived from a combination of bond breaking to the leaving group oxygen, bond formation to the nitrogen, and the accompanying change in hybridization. Given that the bond to the leaving group is intact, the latter two factors should dominate. The observed effect for the carbonyl carbon is large and normal, 1.026. For hydrazinolysis of methyl formate, a similar effect has been interpreted as resulting from rate-limiting C-N bond formation²⁴. However, it was also shown computationally that an effect of approximately 1.02 could be derived from rate-limiting deprotonation of the zwitterionic intermediate (transition state D)²⁵. The remaining isotope effects made it possible to differentiate between these possibilities.

The deuterium effect on the amino acid α-carbon is primarily derived from the loss of hyperconjugation between the carbonyl π bond and the antibonding orbital of the C-H bond, which increases the strength of the C-H bond. The magnitude of this effect is largest when the ground state has a large geometric overlap between the π bond and the antibonding orbital and the transition state is very tetrahedral. Calculations and previous reactions indicate a lower limit of this isotope effect to be approximately 0.96^21,26. The measured isotope effect, 0.985, indicates a significant decrease in overlap in the transition state. This is consistent with the decreased π bond character in a partially tetrahedral transition state.

The KIE of the nucleophilic nitrogen was previously measured to be 1.010, suggestive of an early transition state with partial C-N bond order¹⁸. We remeasured this value using the remote radiolabel-based assay, and again obtained a normal isotope effect, 1.014. Formation of the C-N bond is expected to produce an inverse isotope effect on the nitrogen. The normal isotope effect observed can be derived from two factors: reaction coordinate motion and deprotonation of the nitrogen. Calculations here and elsewhere indicate either of these factors alone is insufficient to result in a normal isotope effect (Supplementary Tables S1 and S2)¹⁰. This suggests that the nitrogen is being deprotonated in the rate-limiting step, simultaneous with C-N bond formation (transition state C). Such a mechanism is consistent with the near-zero Bronsted coefficient⁶ which indicates there is no buildup of positive charge on the nucleophile in the transition state.

The 2′-hydroxyl contributes 100- to 2000-fold to ribosome-catalyzed peptide bond formation⁵ and has been postulated to be involved in proton transfer^8–13. The isotope effect for this position is close to unity (1.002). Changes in bond order between the 2′-oxygen and protons can be compensated by opposite changes in bond strength to the 2′-carbon; therefore this effect is relatively insensitive to the protonation state of the 2′-oxygen ²⁷. The measured effect indicates the oxygen does not bear a large positive or negative charge, consistent with previous studies¹³.

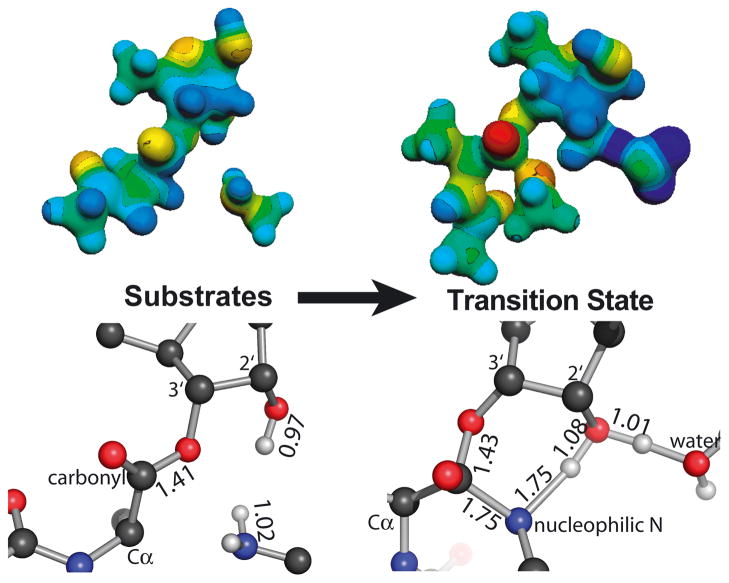
To supplement the qualitative descriptions above, we calculated isotope effects for several potential transition state structures (Supplementary Tables S1–S3). Though we cannot exclude the possibility that multiple steps contribute to the isotope effects, a single transition state did yield calculated values in reasonable agreement with the experimental measurements (Figure 4). As expected for a transition state, there is a single large imaginary frequency corresponding to reaction coordinate motion (carbon-nitrogen bond formation and nitrogen deprotonation). The error inherent in these calculations and our measurements produces an uncertainty in the precise structure of the transition state; however, a single rate-limiting step is consistent with the measured isotope effects. Formation of the tetrahedral intermediate is simultaneous with deprotonation (transition state C). This step is followed by fast breakdown of the tetrahedral intermediate into products (red pathway). The data are not consistent with a fully concerted reaction mechanism.

Figure 4.

Electrostatic (top) and geometric (bottom) structures of the substrates and transition states for peptide bond formation shown in similar orientations. Bond lengths are shown in angstroms. Protons on the nucleophilic nitrogen, 2′-hydroxyl, and water are displayed; for clarity, all others are omitted.

This mechanism is markedly different from what has been observed for similar uncatalyzed reactions^7,21. For uncatalyzed reactions at low pH, stepwise formation of T- is rate-limiting. At high pH, or with the strong nucleophile hydroxylamine, breakdown of the T-intermediate is rate-limiting. Our results indicate that the ribosome not only alters the relative rates of formation and breakdown of tetrahedral intermediates, but also substantially alters the energy landscape such that nucleophilic attack and deprotonation are coordinated.

Concerted attack and deprotonation has also been proposed for aminolysis of the acyl-enzyme intermediate by chymotrypsin^28,29. This conclusion was supported in part by a low Bronsted coefficient, similar to that observed for peptide bond formation. This indicates that the pK_a of the intermediate in the context of these active sites is lower than that of a catalytic group, so that T+/− does not have a finite lifetime and instead T- is the only stable intermediate⁷. Although the pK_a of the amine is initially high, it decreases dramatically as the C-N bond is formed. For chymotrypsin, a catalytic histidine is responsible for deprotonating the nucleophile. For the ribosome, the lack of a pH dependence of the reaction argues against general-acid or -base catalysis³. The 2′-hydroxyl is important for the ribosome reaction, but the pK_a of a hydroxyl dictates that if it abstracts the amino proton it must donate its proton elsewhere. This mechanism, termed the “proton shuttle” has been proposed in a variety of forms for the ribosome^8–12. Alternatively, the 2′-hydroxyl may provide an important transition state hydrogen bond, with another group or a water molecule deprotonating the nucleophile. Either possibility would be consistent with measured solvent isotope effects, which indicate more than one proton is in motion at the transition state (S. Kuhlenkoetter and M. Rodnina, personal communication).

The destination of the proton originating from the nucleophile is uncertain. Two computational studies favor the carbonyl oxygen, which would otherwise develop a negative charge^11,12. This would result in an uncharged tetrahedral intermediate, which would be consistent with the lack of pH dependence of the reaction. Alternatively, a water molecule observed in crystal structures is correctly positioned to accept a proton from the 2′-hydroxyl and later donate it to the 3′-oxygen leaving group. Finally, the 3′-oxygen could receive the proton from the 2′-hydroxyl. Our data cannot distinguish these possibilities; for simplicity, we have modeled a water molecule as the proton acceptor.

The ribosome increases the rate of peptide bond formation by an estimated ten-million-fold through an altered chemical mechanism. The rate of nucleophilic attack is likely increased through positioning effects – first, the increased likelihood of the two substrates being in proximity and second, precise orientation of the nucleophile (possibly by the 2′-hydroxyl of A2451²). The ribosome also plays a significant catalytic role, beyond substrate positioning, to coordinate nucleophilic attack and deprotonation in a single rate-limiting step. Catalysis by the ancient, conserved, RNA active site of the ribosome fundamentally alters the reaction pathway for peptide bond formation relative to the uncatalyzed reaction.

Methods Summary

A general strategy for measuring isotope effects with these substrates using a competitive assay has been described²¹. The P-site substrate cytidylyl-(3′5′)-cytidylyl-(3′5′)-3′ (2′)-O-(N-(6-D-(+)-biotinoylaminohexanoyl)-L-phenylalanyl)adenosine (CCApcb) was synthesized as described. For each measurement, two substrates differing by a single isotopic substitution at the reaction center were mixed. Each substrate was labeled with either ³²P or ³³P to allow differentiation by scintillation counting.

Reactions contained 7 mM MgCl₂, 140 mM NH₄Cl, 25 mM HEPES pH 8.5, trace P-site substrate, 250–500 mM A-site substrate, and 6–10 μM 50S ribosomes. At these concentrations the isotope effect is on k_cat/K_M for the P-site substrate. Timepoints were quenched at 15–30% reacted and near the reaction endpoint. Substrate and product were separated on an acrylamide gel and the fraction reacted determined by phosphorimaging. Each band was eluted and scintillation counted to determine the ratio of ³²P to ³³P in each sample.

To account for substrate that hydrolyzed before the reaction was started, the amount of ³²P- and ³³P-labeled product at zero time was subtracted from all determinations of the product isotope ratio. Additionally, some substrate was unreactive even at long timepoints. The amounts of ³²P- and ³³P-labeled unreactive substrate were similarly subtracted from all determinations of the substrate isotope ratio.

Isotope effects were calculated as previously described²¹, using hybrid density functional methods implemented in Gaussian03. Transition state structures were optimized and frequencies computed on the optimized structures using the three-parameter Becke exchange functional, the LYP correlation functional and the standard 6-31G (d,p) basis set. Isotope effects were calculated from the computed frequencies using ISOEFF 98³⁰. Methylamine was used to model the nucleophile. Calculated isotope effects for tetrahedral intermediate formation were repeated with a set of nucleophiles of increasing size and complexity; these effects varied by less than 0.003.

Methods

Reaction Assay

A general strategy for measuring isotope effects with these substrates using a competitive assay has been described²¹. The P-site substrate cytidylyl-(3′5′)-cytidylyl-(3′5′)-3′ (2′)-O-(N-(6-D-(+)-biotinoylaminohexanoyl)-L-phenylalanyl)adenosine (CCApcb) was synthesized as previously described^15,16. Substrates were prepared that differed only by a single isotopic substitution at the reaction center. Each substrate was 5′-end labeled with either γ³²P- or γ³³P-ATP by polynucleotide kinase and purified on a pH 6 denaturing 15% polyacrylamide gel. ³²P- and ³³P-CCApcb were mixed at an approximately 1:4 ratio and purified on a pH 6 non-denaturing 12% polyacrylamide gel. Purified mixes were used as soon as possible to minimize hydrolysis in the starting material.

The isotopic enrichment of each sample was determined by high-resolution Fourier-transform – ion cyclotron resonance mass spectrometry. Each molecule had 95% or greater isotopic purity.

Ribosome reactions contained 7 mM MgCl₂, 140 mM NH₄Cl, 25 mM HEPES pH 8.5, trace P-site substrate, 250–500 mM A-site substrate, and 6–10 μM 50S ribosomes. At these concentrations the A-site substrate is saturating but the ribosome concentration is not; therefore the isotope effect is on k_cat/K_M for the P-site substrate. All reactions were performed at room temperature. Reaction aliquots at 15–30% reacted (approximately 1 minute) and near the reaction endpoint (greater than 30 minutes) were quenched with three volumes of formamide loading buffer. Each timepoint was run on a pH 6 denaturing 15% polyacrylamide gel to separate substrate from product.

Substrate and product bands were visualized using a Storm 840 PhosphorImager with a two-ply sheet of duck tape between the gel and screen to block ³³P emission. The fraction of ³²P-labeled substrate reacted could then be determined. The ratio of ³²P to ³³P was determined by scintillation counting. Each product band was excised from the gel and eluted into 1 mL of 50mM NaCl overnight. This elution was then added to 13 mL of Optima Gold scintillation fluid and counted for thirty minutes along with ³²P and ³³P standards.

Data Analysis

Counts per minute were divided into two channels, 0–400 keV and 400–2000 keV. Approximately 70% of the ³²P standard was detected in the high energy channel, and greater than 99% of the ³³P sample was detected in the low energy channel. The ratio of ³²P to ³³P in each sample could be determined using equation 1:

$${}^{33}\text{P}/{}^{32}\text{P}=(\text{A}-{\text{B}}^{\ast }\text{r})/[{\text{B}}^{\ast }(1+\text{r})]$$ (1)

where A is the counts per minute in the low energy channel, B is the counts per minute in the high energy channel, and r is the fraction of total emission of a ³²P standard detected in the low energy channel. To account for substrate that hydrolyzed before the reaction was started, the amount of ³²P- and ³³P-labeled product at zero time was determined. These were subtracted from all other determinations of the product isotope ratio. Additionally, some substrate was unreactive even at long timepoints. The amounts of ³²P- and ³³P-labeled unreactive substrate were similarly subtracted from all other determinations of the substrate isotope ratio. The observed isotope effect was then determined from the ratio in the midpoint and endpoint samples and the fraction reacted using equation 2:

$$\text{KIE}=log(1-\text{f})/log(1-{\text{f}}^{\ast }{\text{R}}_{\text{p}}/{\text{R}}_0)$$ (2)

where f is the fraction reacted, R_p is the isotope ratio in the product at that fraction reacted, and R₀ is the isotope ratio in the product at the reaction endpoint. For high fraction reacted samples (greater than 50%) the isotope effect was also determined from substrate and endpoint samples using equation 3:

$$\text{KIE}=log(1-\text{f})/log[{(1-\text{f})}^{\ast }{\text{R}}_{\text{s}}/{\text{R}}_0]$$ (3)

where R_s is the isotope ratio in the remaining substrate at f fraction reacted, and R₀ is as above. This value was corrected for incomplete isotopic incorporation as determined by mass spectrometry with equation 4:

$${\text{KIE}}_{\text{corrected}}=1+({\text{KIE}}_{\text{observed}}-1)/[1-{{\text{KIE}}_{\text{observed}}}^{\ast }(1-\text{e})]$$ (4)

where e is the isotopic enrichment of the heavy sample. This equation assumes a negligible amount of heavy isotope in the light sample^14,21.

For the control and α-deuterium isotope effects, enough trials were performed to plot a histogram of the data (Figure 2). Both datasets were fit to a normal distribution, equation 5:

$$\text{c}={\text{A}}^{\ast }{\text{e}}^{\wedge }(-{0.5}^{\ast }{((\text{x}-\mu )/\sigma )}^{\wedge }2)$$ (5)

where c is the number of counts in a given bin, A is the amplitude, μ is the mean and σ is the standard deviation. For some substitutions, the standard errors for trials performed on the same day were smaller than those from different days, indicating each trial may not be independent. Therefore, for all substitutions each set of experiments from a single day were averaged. The mean and standard error of multiple datasets are reported.

Computation of Transition States

Transition state structures that reproduced the experimental KIEs were determined in vacuo using hybrid density functional methods implemented in Gaussian03. Tetrahydro-4,5-dihydroxy-2-(methoxymethyl)furan-3-yl 2-acetamidopropanoate was used to model the P-site substrate and methylamine was used to model the A-site nucleophile. Calculated isotope effects for tetrahedral intermediate formation were repeated with a set of nucleophiles of increasing size and complexity; the calculated isotope effects varied by less than 0.003.

Structures of the transition states were optimized and the frequencies were computed on the optimized structures using the three-parameter Becke (B3) exchange functional, the LYP correlation functional and the standard 6-31G (d,p) basis set. The 5′-methoxy group and the reaction center were constrained during the optimization and many of these constraints were modified to match the experimental KIEs.

Kinetic and equilibrium isotope effects (KIEs and EIEs, respectively) were calculated from the computed frequencies using ISOEFF 98³⁰. KIEs and EIEs were calculated at the temperature of 298 K and the frequencies were scaled using a factor of 0.964, corresponding to B3LYP/6-31G(d, p). KIEs were calculated whenever the magnitude of the imaginary frequency was greater than 50i cm⁻¹, otherwise EIEs were computed. All vibrational modes were used to calculate isotope effects.

Geometric and the electrostatic models were generated by iteratively optimizing the transition states by modifying the applied constraints until the computed isotope effects closely match the experimental KIEs.

The natural bond orbital (NBO) calculations were performed on optimized structures by including the pop = nbo keyword in the route section of input files. The molecular electrostatic potential (MEP) surfaces were calculated by the CUBE subprogram of Gaussian03. The formatted checkpoint files used in the CUBE subprogram were generated by constrained geometry optimization at the B3LYP level of theory with the 6-31G** basis set. MEP surfaces of the substrate and the transition states were visualized using Molekel4.0 at a density of 0.008 electrons/bohr³. Geometric figures were created using PyMol.