Volumetric lean percentage measurement using dual energy mammography

Abstract

Purpose: Currently, there is no accepted standard for measuring breast density. Dual energy mammography, which has demonstrated accurate measurement in phantoms, has been proposed as one possible method. To examine the use of chemical analysis as a possible means to validate breast density measurements from dual energy mammography, a bovine tissue model was investigated. Known quantities of lean and adipose tissue were compared with composition values measured from dual energy images and chemical analysis.

Methods: Theoretical simulations were performed to assess the impact variations in breast composition would have on measurement of breast density from a single calibration. Fourteen ex-vivo tissue samples composed of varying amounts of pure lean tissue and pure adipose tissue (lean percentage) from 0 to 100%, in increments of 10%, were imaged using dual energy mammography. This was followed by chemical analysis based on desiccation, trituration, and fat extraction with petroleum ether to determine water, lipid, and protein content. The volumetric lean percentage (VLP) as measured from images (VLP_I) and as derived from chemical analysis data (VLP_CA) were compared with the VLP calculated from measurements of sample mass with a scale (VLP_M). Finally, data from the bovine tissue model in this study were compared to compositional data from a previous report of human tissue composition.

Results: The results from simulation suggest a substantial impact on measuring breast density is likely due to changes in anatomical breast composition. VLP_I was related to the VLP_M by VLP_I = 1.53 VLP_M + 10.0 (r²>0.99). VLP_CA was related to VLP_M by VLP_CA = 0.76 VLP_M + 22.8 (r²>0.99). VLP_I was related to VLP_CA by VLP_I = 2.00 VLP_CA − 35.6 (r²>0.99). Bovine adipose tissue was shown to be very similar to human adipose tissue in terms of water, lipid, and protein content with RMS differences of 1.2%. Bovine lean tissue was shown to be very similar to human skeletal muscle tissue and somewhat similar to human mammary gland tissue with RMS differences of 0.4 and 22.2%, respectively.

Conclusions: The results of this study show strong linear relationships between volumetric lean percentage measurements using dual energy mammography, chemical analysis and the actual mass. Determining the existence of a relationship between VLP_I and VLP_CA was necessary before comparing density results from the dual energy technique to composition data from chemical analysis for samples of unknown composition.

INTRODUCTION

Mammographic density is an important, strong indicator of breast cancer risk in women.^{1, 2, 3, 4} Four and six category classifications schemes have been proposed for characterizing mammographic (i.e., breast) density; since it is believed that a relationship exists between the accuracy of breast density measurements and the ability to assess future risk.⁴ Several other volumetric quantitative methods of measuring breast density have also been proposed. However, these other methods pose one major limitation: they have not been able to validate in-vivo measurements of breast density against any accepted gold standard. Sample calibration can be found utilizing destructive chemical analysis for ex-vivo samples. The quantities yielded by chemical analysis are composite measures of water, lipid, lean (i.e., protein) and mineral content for the whole sample as opposed to compartmentalized measures of distinct tissue types (e.g., glandular tissue and adipose tissue). Still, validation could be possible if the relationship between chemical analysis and a proposed technique can be established. One group suggested using the “fibroglandular ratio” to relate data from chemical analysis to compartmental measures, such as breast density.⁵ The fibroglandular ratio was defined as (t_w +t_p)/(t_w + t_p + t_l), with t_w equal to the thickness of water in a sample, t_p the thickness of protein and t_l the thickness of lipid. This ratio can be calculated for a whole breast sample by averaging the measurement thicknesses of water, lipid, and protein over the entire breast. The assumption is that the water and protein recovered from the sample come from only the glandular tissue. This is not universally true because all tissues contain some amount of water and protein; however, it does provide a starting point for further investigation.

We have previously reported a dual energy mammography technique to measure breast density.^{6, 7} The system was calibrated with plastic resin phantoms designed to match the attenuation characteristics of glandular and adipose tissues (model 014a, Computed Image Reference Systems (CIRS), Norfolk, Virginia). Their compositions are shown in Table TABLE I. alongside the average compositions of adipose and glandular tissues as reported by Hammerstein et al.⁸ As shown, the compositions of the plastic resins are almost alike, and based on primarily carbon, oxygen, and hydrogen with small added amounts of calcium and chlorine to balance the final attenuation. Since this tissue analog material was intended for calibrating automatic exposure control with single energy mammography applications, it was unclear how well these phantoms would serve as calibration materials in dual energy imaging. Previous reports have studied the impact of calibration phantom errors when the material being measured differed significantly from the calibration phantom in mammography; however, their results were limited to theoretical predictions.⁹ It is necessary to know the magnitude and nature of these errors from experiment, before the clinical implementation of the dual energy mammography technique. Also, another potential difficulty is the reported variation in breast and adipose tissue composition. As only a single pair of materials may be used for tissue calibration, this presents an additional challenge when choosing a reference composition for dual energy calibration. All the reports of breast tissue composition considered in this study^{8, 10, 11} detail three measurements: a mean tissue composition along with either a minimum and maximum observed composition or a mean tissue composition with an observed composition and one standard deviation from the mean. The effect and impact of these variations, in terms of both the mean observed value and the range of observed values, on system calibration are considered in this study.

Table 1.

Density and elemental compositions of adipose tissue, glandular tissue as reported by Hammerstein and their phantom equivalents.

	Phantom and natural breast tissue composition
Tissue	H (%)	C (%)	N	O (%)	Cl	Ca	Density (g/cc)	Ash (S,P,K,Ca)
Glandular equivalent (CIRS)	9.41	69.13	1.84%	17.66%	0.14%	1.75%	1.05	—
Adipose equivalent (CIRS)	9.78	71.41	2.01%	16.34%	0.25%	0.13%	0.94	—
Glandular tissue	10.2	18.4	3.2%	67.7%	—	—	1.04	0.5%
Adipose tissue	11.2	61.9	—	25.1%	—	—	0.93	0.1%

Additionally, to assess the ability of dual energy imaging to measure breast density, experimental comparisons must be made between: breast density as measured by dual energy images, the known percentages of glandular (lean) tissue and adipose tissue present in a sample, and the net composition of water, lipid and protein for a sample as determined by chemical analysis. Specifically, the aims of this report are: (1) to study the impact of anatomical differences in breast composition on breast density measurements, (2) to study the relationship between the lean content of samples of known tissue type and composition using a bovine tissue model with lean (“breast”) density values measured from a dual energy mammography system calibrated with commercially available “tissue equivalent” phantoms, (3) to determine if relationships exists between tissue samples of known lean and adipose content, the lean density of these samples measured from dual energy images and the compositional results of chemical analysis.

All experiments in this study utilized lean bovine muscle tissue as a representation for breast glandular tissue, while fat tissue (suet) served as an analog for breast adipose tissue. The choice of bovine tissue here was not intended to exactly represent human breast tissue but served as a starting point to address the challenges associated with measuring breast density with dual energy mammography. Determining the existence of a relationship between the data from chemical analysis and lean density values measured from the images should help determine the feasibility of dual energy mammography for breast density measurement.

MATERIALS AND METHODS

Theoretical model of breast composition

As mentioned in the introduction, only a single pair of reference materials may be used for dual energy calibration. Here we would like to consider the effect on breast density measurement when the tissue composition differs from the reference materials used for calibration. In the Hammerstein report, a range in the observed tissue composition was reported.⁸ Similarly, a range of tissue compositions was also reported in the data of Woodard and White¹⁰ as was a range in the measured attenuation in the data of Johns and Yaffe.¹¹ These differences can likely be explained as normal anatomical variation; however, it will be useful to know the impact these variations have on breast density measurement from a single calibration. The approach used here is to model the expected measured thicknesses based on the solution to a dual energy system of two materials ¹²:

$$\left(\frac{t_A}{t_G}\right)=\left(\frac{1}{{\mu }_A^L{\mu }_G^H-{\mu }_G^L{\mu }_A^H}\right)\left(\begin{array}{cc}{\mu }_G^H& -{\mu }_G^L\\ -{\mu }_A^H& {\mu }_A^L\end{array}\right)\left(\begin{array}{c}-U^L\\ -U^H\end{array}\right)$$ (1)

where t_G and t_A are the thicknesses of glandular and adipose tissue, respectively. ${\mu }_G^L$, ${\mu }_G^H$, ${\mu }_A^L$, and ${\mu }_A^H$ represents the attenuation of the plastic resin phantoms used as reference materials for calibration with the subscript representing either glandular or adipose tissue and the superscript representing either low or high energy. These values were calculated by weighting the linear attenuation of individual elements by the composition provided by the manufacturer with simulated polyenergetic beam spectra at energies of 28 and 49 kVp, designed to approximate the experimental spectra used in this study and also at monoenergetic energies of 20 and 40 keV for use with the data of Johns and Yaffe where reported measurements of x-ray attenuation were provided at these discrete monoenergetic energies. U^L and U^H are the low and high energy attenuation measurements, respectively. For each input material (e.g., pure glandular tissue), the apparent thicknesses of adipose and glandular tissue were used to calculate the apparent breast density using Eq. 1. The error between the known breast density and the apparent breast density was calculated. By definition, the breast density of pure glandular tissue is 100% and the breast density of adipose tissue is 0%. Pure adipose and pure glandular tissues from the three sets of data were used as inputs: the compositions of Hammerstein, the compositions of Woodard and White and the attenuation measurements of Johns and Yaffe. For all three sets, both the data of the mean and the two endpoints, which represented either the extreme values observed or the values one standard deviation from the mean were used. The tissue compositions investigated here are shown in Table TABLE II..

Table 2.

Density and elemental compositions of adipose tissue and glandular tissue used in theoretical investigations.

Tissue	H (%)	C (%)	N (%)	O (%)	Cl	Ca	Density (g/cc)	Ash (S,P,K,Ca)
Glandular tissue (Hammerstein8)	10.2	10.8	3.2	75.9	—	—	1.04	0.5%
		18.4	3.2	67.7	—	—
	30.5	3.2	55.2	—	—
Adipose tissue (Hammerstein8)	11.2	49.1	1.7	35.7	—	—	0.93	0.1%
		61.9	1.7	25.1	—	—
	69.1	1.7	18.9	—	—
Glandular tissue (Woodard and White10)	10.2	15.8	3.7	69.8	—	—	1.06	—
	10.6	33.2	3.0	52.7	—	—	1.02	—
	10.9	50.6	2.3	35.8	—	—	0.99	—
Adipose tissue (Woodard and White10)	11.2	51.7	1.3	35.5	—	—	0.97	—
	11.4	59.8	0.7	27.8	—	—	0.95	—
	11.6	68.1	0.2	19.8	—	—	0.93	—

Sample preparation

Twelve unique samples from the 14 total samples of bovine tissue were prepared from cuts of pure lean muscle tissue and pure fatty tissue (suet) purchased from a local USDA compliant butcher. Both lean and adipose tissues were cut into cubes approximately 1 cm³ in volume. Sample tissue was designated as pure lean if no fat was visible in the sample. Likewise, a tissue was designated as pure adipose if no trace of lean meat was visible. Cartilage and bone were excluded from both samples. The fourteen samples were proportioned, according to their lean percentage (LP), which is the proportion of lean tissue mass, M_LEAN, to the sum of lean tissue mass and adipose tissue mass, M_LEAN + M_FAT:

$${\mathrm{LP}}_{\mathrm{M}}=100\times \left(\frac{M_{\mathrm{LEAN}}}{M_{\mathrm{LEAN}}+M_{\mathrm{FAT}}}\right)$$ (2)

The subscript “M” was added to signify this measure was determined from measurements of scale mass. The range of LPs varied from 0 to 100%, in increments of 10%, for a total of 12 measurement points. Two additional samples were prepared for use at each one of the LP_M end points (0 and 100%) to test each endpoint value twice as all other lean percentages can be seen as linear combinations of these two basis points. The mass of all samples were fixed at 500 grams. Since the main quantity of interest is a volumetric measure, a related quantity for comparison was derived from the LP_M by normalizing the mass values by nominal tissue densities of adipose and soft tissue¹³ to obtain the volumetric lean percentage (VLP_M), as follows:

$${\mathrm{VLP}}_{\mathrm{M}}=100\times \left(\frac{M_{\mathrm{LEAN}}∕M_{\mathrm{LEAN}}1.061.06}{M_{\mathrm{LEAN}}∕M_{\mathrm{LEAN}}1.061.06+M_{\mathrm{FAT}}∕M_{\mathrm{FAT}}0.950.95}\right)$$ (3)

The samples were prepared according to their mass and subsequent LP, but were compared with other data according to their VLP_M.

Image acquisition and processing

A dual energy image was acquired for each sample in the study using a full field digital mammography system (Selenia, Hologic, Inc., Bedford, MA). The acquisition parameters and steps in image processing were the same as described in a previous report about the dual energy calibration.⁸ Low energy images were acquired at 28 kVp with a 50 μm rhodium filter at 60 mAs. High energy images were acquired at 49 kVp with a 300 μm copper filter at 30 mAs.

All images were acquired with the use of a grid [cellular (cross-hatch) 4:1 grid ratio, 15 lines/cm] and then further corrected for x-ray scatter using a convolution-based technique modified for dual energy imaging.¹⁴ For manual offline gain calibration, a dark field image and an open field image at each energy level was acquired to remove any nonuniformities in the image field. The time between each exposure was set to 4 min to minimize the effect of detector ghosting.¹⁵ All image processing was performed using ImageJ.¹⁶

Image based lean percentage measurement

Dual energy decomposition of the low and high energy images yielded individual pixel measurements of glandular and adipose equivalent material thickness. The decomposition was based on a previous calibration⁷ with glandular and adipose equivalent phantoms. The calibration accounted for beam hardening and image magnification differences due to a diverging beam. As in the previous report, a region of interest (ROI) was drawn to encompass the sample and the mean glandular (T_G) and adipose thicknesses (T_A) were measured for the whole sample. These values were used to calculate the VLP_Iaccording to:

$${\mathrm{VLP}}_{\mathrm{I}}=100\times \left(\frac{T_G}{T_G+T_A}\right)$$ (4)

The subscript “I” here designates that this measure of VLP was determined from image measurements. The term VLP_I is also known as the breast density. However, VLP_I was preferred in this study as no actual breast tissue was used. As this value was calculated from a ratio of thicknesses and not masses, no further normalization by density was necessary to convert this quantity to a volume measure.

Chemical analysis

The chemical analysis method was based on a standardized procedure devised by the United States Department of Agriculture to measure the content of water, lipid, lean and mineral in a sample.¹⁷ Here, separating the mineral ash content from the lean component was not performed, since the mass of such content was assumed to be negligible.¹⁸

Each 500 g sample was placed into a vacuum oven maintained at approximately 95 °C for 48 h to evaporate the water content. The time and temperature parameters were empirically determined in preliminary studies to be suitable for this sample size. The sample was then removed and reweighed. The lost mass was assumed to be purely water. The dried sample was then mixed with petroleum ether, grounded into a slurry, and agitated at 30 °C for approximately 1 h to extract the lipid content of the fatty tissue into the ether solvent. The sample was then cooled at room temperature at approximately 20 °C for 24 h. Next, the sample mixed in solution was vacuum filtered through a Buchner funnel of known weight. An additional 1 l of pure petroleum ether was passed over the sample to wash away any residual lipid content. The sample was reweighed and what remained of the dry sample was assumed to be purely protein mass. The difference in mass was assumed to be purely lipid. Therefore, the petroleum ether solution was assumed to contain all the lipid content. This lipid content was then isolated from the solution by driving off the petroleum ether with heat under vacuum distillation. The mass of the lean and isolated lipid content were each weighed, yielding the lipid and protein masses with the balance assumed to be water. A VLP similar to the fibroglandular ratio mentioned in the introduction was then calculated by normalizing the measured masses by their nominal densities⁵ according to:

$${\mathrm{VLP}}_{\mathrm{CA}}=100\times \left(\frac{M_W∕M_{W}1.01.0+M_P∕M_{P}1.351.35}{M_W∕M_{W}1.01.0+M_L∕M_{L}0.920.92+M_P∕M_{P}1.351.35}\right)$$ (5)

where the subscript CA indicates these results were derived from chemical analysis and M_W, M_L, and M_P represent the masses of water, lipid and protein, respectively.

Quantities compared

The purpose of the experimental portion of this study was to examine the relationships between the VLP quantities calculated according to scale mass, images, and chemical analysis.

First, the relationship between VLP_I and VLP_M is presented. This is followed by the relationship between VLP_CA and VLP_M and then the relationship between VLP_I and VLP_CA. Last, the water, lipid and protein contents of bovine adipose and lean tissues were compared to the compositional data of human adipose, skeletal muscle and mammary gland tissues from the data of Woodard and White.¹⁰

RESULTS

The results from the theoretical simulations are shown in Table TABLE III..

Table 3.

Summary of the apparent densities of breast tissue as compared to the composition determined from chemical analysis.

Composition study author	Tissuetype	Known density	Range in apparent density	Average apparent density	RMS error
Hammerstein8	Adipose	0	[ − 11.3–22.6]	4.1	14.6
	Glandular	100	[84.6–136.5]	112.3	24.6
Woodard and White10	Adipose	0	[ − 7.6–26.4]	9.0	16.5
	Glandular	100	[34.2–121]	74.6	43.8
Johns and Yaffe11	Adipose	0	[ − 31.8– − 18.5]	−25.7	26.2
	Glandular	100	[109.6–115.8]	113.5	13.8

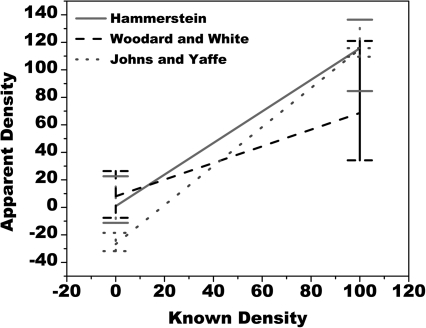
These values were used to generate a graphical representation of how linear fits of measured versus known densities for a range of data might deviate from an ideal slope of one. Shown in Fig. 1 is a graph with the apparent density from Table TABLE III. plotted against the known density. The bands shown on the end points span the range of observed values found from this analytical model. The maximum single error in apparent breast density when compared to the plastic resin phantom calibration used in this study was as great as −65.8% for glandular tissue in the data of Woodard and White and −31.8% for adipose tissue in the data of Johns and Yaffe. These results and the data seen in Fig. 1 indicate that differences in composition arising from variations in anatomy can have a substantial impact on breast density measurement.

Figure 1.

Comparison of apparent breast density to known density for published values of breast composition vs a single calibration with the plastic resin phantoms. Note the lines at the endpoints are not measurement error bars but illustrate the range of values observed for all values of breast composition used in this analytical model.

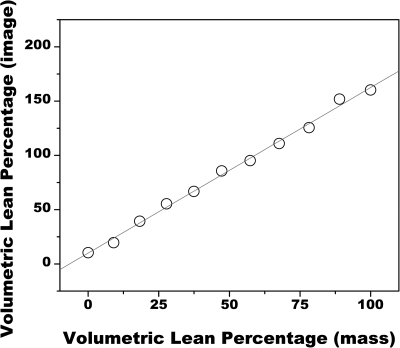
The relationship between VLP_I and VLP_M is presented in Fig. 2. VLP_I values ranged from 10 (at a VLP_M of 0) to 160 (at a VLP_M of 1.0). The data were linearly related by VLP_I = 1.53 VLP_M + 10.0 (r²>0.99).

Figure 2.

Comparison of VLP as measured from dual energy images to VLP as determined by scale mass. The data were related by VLP_I = 1.53 VLP_M + 10.0 (r²>0.99).

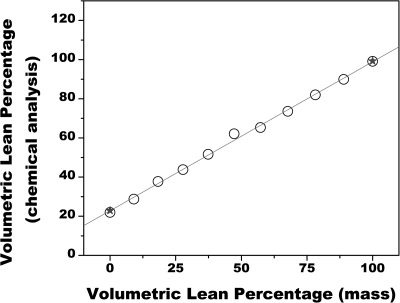
Figure 3 shows the relationship between VLP_CA and VLP_M. Here, values of VLP_CA ranged from 24%, at a VLP_M of 0%, to 100%, at a VLP_M of 100%. The data were linearly related by VLP_CA = 0.76 VLP_M + 22.8 (r²>0.99). Data from the repeated tests on the endpoints of 0 and 100% agreed within 1% of the first test.

Figure 3.

Comparison of VLP as measured from chemical analysis to VLP as determined by scale mass. The data from the repeat tests of the endpoints of 0 and 100%, as signified by the star symbol, agreed within 1% of the first test. The data were related by VLP_CA = 0.76 VLP_M + 22.8 (r²>0.99).

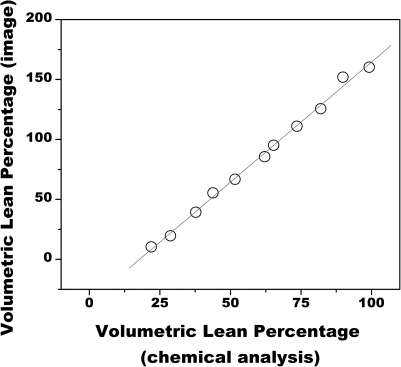
Figure 4 shows the relationship between VLP_I and VLP_CA. The data were linearly related by VLP_I = 2.00 VLP_CA − 35.6 (r²>0.99).

Figure 4.

Comparison of breast density as measured from dual energy images to glandular volume percentage as measured from chemical analysis. The data were related by VLP_I = 2.00 VLP_CA – 35.6 (r²>0.99).

A summary of the results from this study are presented in Table TABLE IV..

Table 4.

Summary data of the lean percentage, VLP_M, VLP_I, and VLP_CA for all points in the study. The repeat measurements of the two endpoints from chemical analysis are shown sequentially and separated by a comma.

Lean percentage	Volumetric ean percentage (mass)	Volumetric lean percentage (image)	Volumetric lean percentage (chemical analysis)
0	0.0	10.4	22.0,21.0
10	9.1	19.6	28.8
20	18.3	39.3	37.7
30	27.8	55.4	43.8
40	37.4	66.7	51.6
50	47.3	85.6	62.1
60	57.3	95.2	65.3
70	67.7	111.0	73.6
80	78.2	125.6	82.0
90	89.0	151.9	89.9
100	100.0	160.3	99.2, 100.0

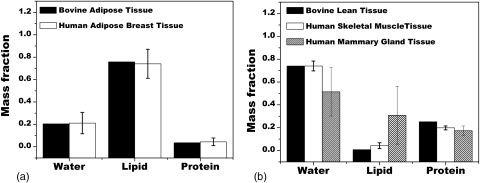
Shown in Fig. 5 is the comparison of water, lipid and protein content from the measured adipose and lean tissue data in this study compared to the data of Woodard and White.¹⁰ Bovine adipose tissue was shown to be nearly identical to human adipose tissue with an RMS difference of 1.2%. Bovine lean tissue was shown to be very similar to human skeletal muscle tissue and somewhat similar to human mammary gland tissue with RMS differences of 0.4 and 22.2%, respectively.

Figure 5.

The data of Woodard and White is shown alongside the bovine tissue data in this study. Note for the data in this study, the error bars were too small to be seen. The RMS difference for the two adipose tissues was 1.2%. The RMS difference for lean and skeletal muscle tissue were 0.4 and 22.2% for lean and mammary gland tissues.

DISCUSSION

All the data showed strong linear relationships. While it was initially expected that the volumetric lean percentage from scale mass measurements would correspond to the volumetric lean percentage from images, Fig. 2 showed there was not an exact agreement between VLP_M and VLP_I. Nevertheless, a strong linear relationship was still observed. As was explored in Sec. 2, it was expected that the data could exhibit a slope that differs from 1.0 if the materials used for calibration and for measurement were different in composition. This suggests that the materials used for dual energy calibration were not optimal for measuring the thickness of pure lean and pure fat bovine tissue. Furthermore, this effect was also seen in a prior clinical study, which utilized single energy absorptiometry methods, which studied a population of women and also reported a similar offset, indicating this effect was not limited to bovine tissue alone but was also seen with human breast tissue.¹⁹ The exact nature of this discrepancy is specific to the material equivalent phantoms used in this study for calibration and the bovine tissues being imaged. However, this would be expected for any material where the composition of the materials used for calibration deviated from the measured tissue. In addition, the attenuations of the calibration phantoms were designed to match the mean compositions of adipose and glandular tissues given in the Hammerstein report. However, as mentioned in Sec. 2, a range of compositions for each tissue was presented. This indicates that adipose and glandular tissues contain significant anatomical variation in composition within the population and standardizing on a single mean value can be difficult. This explanation of anatomical variation is best illustrated by the data of Woodard and White¹⁰ who reported a range of lipid percentages in glandular breast tissue ranging from 5.6 to 56.2%. Adipose tissue tended to be more consistent, however, with lipid percentages ranging from 61.4 to 87.3%.

The data in Fig. 2 were related by a slope of 1.53. This value is just outside the largest predicted difference between apparent breast density and known breast density seen from the data in Table TABLE III. and Fig. 1. This seems reasonable given the very low lipid content of the lean tissue. The issue of intracompositional differences in a single tissue due to anatomical variation within the population is likely the biggest impediment in establishing clear relationships from any gold standard method based when measuring breast density with a dual energy mammography system calibrated with a single pair of reference materials.

A bovine tissue model was utilized as a surrogate for human breast tissue due to the ease of procuring samples for testing. One immediate limitation, as mentioned above, is the wide anatomical variations seen in human breast tissues as compared to the bovine tissues tested here.^{8, 10, 20} Repeated measurements taken here with bovine tissue from different origins showed very little differences in the measured content of water, lipid, and protein. As seen from Fig. 5, the composition of bovine adipose tissue was shown to be very similar to human adipose. The data for mammary gland tissue showed a higher level of lipid content than bovine muscle tissue which contained almost no lipid. As a whole, trends were shown to be similar indicating that the compositions of the bovine tissues were not too different from human tissues.

Results from Fig. 3 also showed a linear relationship between the VLP_CA and VLP_M. An offset and nonunity slope in the linear relationship between VLP as measured from chemical analysis and VLP as measured from scale mass was attributed to two factors: (1) a significant amount of water was present in pure adipose tissue and (2) a small amount of lean and mineral was present in adipose tissue. The VLP_CA lumps together the water content with the protein content in an attempt to recover the amount of lean tissue. Therefore, the amounts of water and protein recovered in pure adipose tissue were effectively considered to be lean tissue. This effect appears to be a fundamental limitation in comparing data from chemical analysis to other measurements that consider the tissues to be distinctly separated. Nevertheless, this does not seem to pose a problem, since it was still possible to determine a linear relationship between VLP_CA and VLP_M. Likewise, there was strong linear relationship between measurements of VLP_I and VLP_CA in Fig. 4. This relationship may prove to be valuable as it illustrates how the data obtained from the images might be compared to the data from chemical analysis for samples of known composition. This can ultimately help determine of the usefulness of dual energy mammography in measuring breast density for samples of unknown composition when a two compartment model of glandular and adipose tissue is assumed.

Thus, in spite of the clear relationships seen from the data in this study, a level of uncertainty is expected when working with human breast tissue. While there is no known way to account for this uncertainty, further research is necessary to study the ultimate impact of this variation on measuring breast density. Approaches like the one suggested by Laidevant,⁵ which seeks to better characterize breast composition, may offer opportunities for improving risk assessment.