Complete set of material properties of single domain 0.24Pb(In_1∕2Nb_1∕2)O₃-0.49Pb(Mg_1∕3Nb_2∕3)O₃-0.27PbTiO₃ single crystal and the orientation effects

Abstract

Multidomain relaxor-based single crystals have intrigued the enthusiasm of many researchers due to their superior electromechanical properties. In order to understand the physical origin of multidomain properties, one must know the complete set of material coefficients in single domain state. Previous published single domain data were all measured under bias because single domain state is unstable. Here, we report a set of single domain data without bias for rhombohedral 0.24Pb(In_1∕2Nb_1∕2)O₃-0.49Pb(Mg_1∕3Nb_2∕3)O₃-0.27PbTiO₃ single crystal. Comparing rotated coefficients from single domain data with measured multidomain material coefficients, we concluded that the orientation effects account for more than 90% of the observed multidomain properties.

Multidomain relaxor-based ferroelectric single crystals, (1-x)Pb(Mg_1∕3Nb_2∕3)O₃-xPbTiO₃ (PMN-xPT) and (1-x)Pb(Zn_1∕3Nb_2∕3)O₃-xPbTiO₃ (PZN-xPT) with compositions near the morphotropic phase boundary (MPB) exhibit giant piezoelectric properties (d₃₃ > 2000 pC∕N) and very high electromechanical coupling factor (>90%). They were already used in high end medical imaging transducers, and may lead to revolutionary changes in next generation sensors, actuators, and other electromechanical devices.^{1, 2, 3, 4} In order to understand the origin of such large electromechanical properties in multidomain states, it is necessary to know the complete set of single domain properties. Such data will also allow theoretical explorations on the optimum orientation cut.^{5, 6, 7} However, it was found that all binary PMN-PT and PZN-PT single crystals cannot maintain the single domain state without bias. Up to date, there is only one set of single domain data for binary systems in the literature, i.e., [111]_c poled single-domain PMN-0.33PT single crystal, which was obtained under a dc bias in all samples in order to maintain their single-domain state.⁸

Recently, Liu et al. reported another complete set of material properties of single-domain 0.26Pb(In_1∕2Nb_1∕2)O₃-0.46Pb(Mg_1∕3Nb_2∕3)O₃-0.28PbTiO₃ (0.26PIN-0.46PMN-0.28PT) ternary single crystal under dc bias.⁹ They have also estimated the external field influence and found that the application of the dc bias will cause about 5% and 10% changes in the elastic compliance $s_{11}^E$ and elastic constant $c_{33}^D$, respectively.⁹ This means that the corresponding calculations based on the biased data will not give accurate account for the orientation contribution in the multidomain crystals. The relaxor-based ferroelectric ternary xPb(In_1∕2Nb_1∕2)O₃-(1-x-y)Pb(Mg_1∕3Nb_2∕3)O₃-yPbTiO₃ (PIN-PMN-PT) single crystal system shows much higher coercive fields (E_C ∼ 5–6 kV∕cm) than that of PMN-PT single crystals (E_C ∼ 2–3 kV∕cm).^{10, 11} Through proper poling procedure, we were able to stabilize the single domain state in 0.24Pb(In_1∕2Nb_1∕2)O₃-0.49Pb(Mg_1∕3Nb_2∕3)O₃-0.27PbTiO₃ (0.24PIN-0.49PMN-0.27PT) single crystal, which allows us to obtain a complete set of single domain data in a relaxor-based single crystal in natural conditions.

The 0.24PIN-0.49PMN-0.27PT single crystal used in this work was grown by the modified Bridgman method and all samples used were properly oriented by the Laue machine with an accuracy of ±0.5°. Samples of desired geometries were cut from the same slice of a crystal boule with uniform composition. Each sample was polished into parallelepiped shape with the three pairs of surfaces along [$1\stackrel{-}{1}0$]_c, [$11\stackrel{-}{2}$]_c, and [111]_c (the crystal axes were adopted according to Ref. 12). In addition, a k₃₃ bar with three pairs of parallel surfaces along [100]_c, [010]_c, and [001]_c was also prepared for the [001]_c poled multi-domain state measurements. The samples were sputtered with gold electrodes on the opposite [111]_c or [001]_c surfaces, and poled at 10 kV∕cm in silicone oil at room temperature. The single-domain state of [111]_c poled sample was confirmed by polarizing microscope. For the rhombohedral 3m symmetry, there are total 12 independent material constants to be determined: 6 elastic, 4 piezoelectric, and 2 dielectric constants. We used combined resonance and ultrasonic methods together with capacitance measurements to get 17 independent combinations, which allowed us to determine uniquely these coefficients with high degree of self-consistency. Self-consistency is of vital importance in the complete set of material properties. Lack of self-consistency will lead to wrong simulated designs and create conceptual confusions as discussed recently in Refs. ^{13, 14}.

In resonance measurements, the dimensions and geometries of vibrators were specified by the IEEE standards on piezoelectricity.¹⁵ The resonance and anti-resonance frequencies were obtained by an HP 4194A impedance-phase gain analyzer, which were used to calculate the electromechanical coupling factors k₃₁, k₃₃, k_t, piezoelectric strain constants d₃₁, d₃₃, elastic compliance constants $s_{11}^E$, $s_{11}^D$, $s_{33}^E$, $s_{33}^D$, and elastic stiffness constants $c_{33}^E$, $c_{33}^D$, respectively. The free and clamped dielectric constants ${\varepsilon }_{11}^T$, ${\varepsilon }_{33}^T$, ${\varepsilon }_{11}^S$, ${\varepsilon }_{33}^S$ were determined from the low (1 kHz) and high frequency (2f_a) capacitance measurements.

In ultrasonic measurements, a 0.5 cm cube sample with the orientations of [$1\stackrel{-}{1}0$]_c × [$11\stackrel{-}{2}$]_c × [111]_c was used. A 15 MHz longitudinal wave transducer (Ultran Laboratories, Inc.) and a 20 MHz shear wave transducer (Panametrics Com.) were used for the ultrasonic pulse-echo measurements. The transducers were excited by a 200 MHz pulser∕receiver (Panametrics Com.) and the time of flight between echoes was measured using a Tektronix 460A digital oscilloscope. The phase velocities of the longitudinal and shear waves were measured along [$1\stackrel{-}{1}0$]_c, [$11\stackrel{-}{2}$]_c, and [111]_c, respectively. From them, seven elastic stiffness constants $c_{11}^E$, $c_{14}^D$, $c_{33}^D$, $c_{44}^E$ (=$c_{55}^E$), $c_{44}^D$ (=$c_{55}^D$), $c_{66}^E$, and $c_{66}^D$ can be deduced based on the Christoffel wave equations.

A computational algorithm was developed utilizing those excess number of measurements to guarantee self-consistency of the final full set material constants. The measured and derived elastic, piezoelectric, and dielectric constants of the 0.24PIN-0.49PMN-0.27PT single-domain single crystal poled along [111]_c are given in Table TABLE I..

Table 1.

Measured and derived material constants of [111]_c poled 0.24PIN-0.49PMN-0.27PT single-domain single crystal. [Directly measured constants are indicated by star (*).]

Elastic stiffness constants: $c_{\mathit{ij}}^E$ and $c_{\mathit{ij}}^D$ (1010 N∕m2)
$c_{11}^{E*}$	$c_{12}^E$	$c_{13}^E$	$c_{14}^E$	$c_{33}^E$	$c_{44}^{E*}$	$c_{66}^{E*}$
20.26	9.02	5.32	−2.67	18.47	2.34	5.62
$c_{11}^D$	$c_{12}^D$	$c_{13}^D$	$c_{14}^{D*}$	$c_{33}^{D*}$	$c_{44}^{D*}$	$c_{66}^D$
20.38	9.10	4.80	−2.33	21.29	7.90	5.64
Elastic compliance constants: $s_{\mathit{ij}}^E$ and $s_{\mathit{ij}}^D$ (10−12 m2∕N)
$s_{11}^{E*}$	$s_{12}^E$	$s_{13}^E$	$s_{14}^E$	$s_{33}^E$	$s_{44}^E$	$s_{66}^E$
11.62	−7.81	−1.10	22.17	6.05	93.33	38.86
$s_{11}^D$	$s_{12}^D$	$s_{13}^D$	$s_{14}^D$	$s_{33}^{D*}$	$s_{44}^D$	$s_{66}^D$
6.87	−3.21	−0.83	2.93	5.07	14.23	20.15
Piezoelectric coefficients: eiλ(C∕m2), diλ (10−12 C∕N), giλ (10−3 Vm∕N), and hiλ (108 V∕m)
e15	e22	e31	e33	d15	d22	$d_{31}^{*}$	$d_{33}^{*}$
20.99	−1.28	−2.16	11.62	2015	−490	−21	75
g15	g22	g31	g33	h15	h22	h31	h33
39.26	−9.55	−3.65	13.04	26.92	−1.64	−4.51	24.25
Dielectric constants: ɛij(ɛ0) and β(10−4∕ɛ0)
${\varepsilon }_{11}^{S*}$	${\varepsilon }_{33}^{S*}$	${\varepsilon }_{11}^{T*}$	${\varepsilon }_{33}^{T*}$	${\beta }_{11}^S$	${\beta }_{33}^S$	${\beta }_{11}^T$	${\beta }_{33}^T$
881	541	5800	650	11.35	18.47	1.72	15.39
Electromechanical coupling factors kij and density (kg∕m3)
k15	$k_{31}^{*}$	$k_{33}^{*}$	$k_t^{*}$	density
0.84	0.08	0.40	0.36	8095

It was found that the piezoelectric constant d₃₃ and electromechanical coupling factor k₃₃ are only 75 pC∕N and 40%, respectively, in the single domain state, which are much lower than that of [001]_c or [011]_c poled PIN-PMN-PT multi-domain single crystals. However, the shear piezoelectric constant d₁₅ of single domain 0.24PIN-0.49PMN-0.27PT is 2015 pC∕N, much higher than its other piezoelectric constants, viz., d₃₁, d₂₂, and d₃₃. In fact, it was recognized that the origin of the large piezoelectric properties d₃₃ in [001]_c poled multi-domain single crystal is mainly from the contribution of large shear property d₁₅ of the single-domain state.⁵

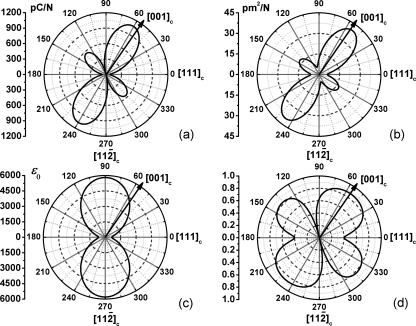
As shown in Fig. 1, the orientation dependence of material constants has been calculated for [111]_c poled 0.24PIN-0.49PMN-0.27PT single-domain single crystal based on the measured full matrix single-domain data. The property transformation is performed based on the standard matrix transformation for piezoelectric materials.¹⁶ It can be seen that the maximum values of material constants, d₃₃ = 1076 × 10⁻¹² C∕N, $s_{33}^E$ = 40.17 × 10⁻¹² m²∕N, ${\varepsilon }_{33}^T$ = 5800, and k₃₃ = 0.87, occur in the directions of 60.3°, 52.6°, 90°, and 53.3° from the spontaneous polarization direction [111]_c, respectively. The [001]_c direction is 54.7° from the poling direction [111]_c, we can calculate the rotated longitudinal material constants along [001]_c in the [111]_c-[$11\stackrel{-}{2}$]_c plane from the single domain data. These calculated values are: d₃₃ = 1048 × 10⁻¹² C∕N, $s_{33}^E$ = 40.03 × 10⁻¹² m²∕N, ${\varepsilon }_{33}^T$ = 4080, and k₃₃ = 0.87, respectively. In addition, the elastic compliance constant $s_{33}^D$ and piezoelectric charge constant g₃₃ can be calculated, $s_{33}^D=s_{33}^E(1-k_{33}^2)$ = 9.60 × 10⁻¹² m²∕N and $g_{33}=d_{33}∕{\varepsilon }_{33}^T$= 29.03 × 10⁻³ Vm∕N along [001]_c, respectively. As shown in Table TABLE II., the rotated material constants along [001]_c are very close to the measured constants for [001]_c poled multidomain single crystal. In fact, the electromechanical coupling factor k₃₃ is exactly the same. This shows that the orientation effect plays a major role in the multidomain material properties of this relaxor-based ferroelectric single crystal, particularly for longitudinal properties.

Figure 1.

(Color online) Orientation dependence of (a) piezoelectric strain constant d₃₃, (b) elastic compliance constant $s_{33}^E$, (c) dielectric constant ${\varepsilon }_{33}^T$, and (d) electromechanical coupling factor k₃₃ of [111]_c poled single domain 0.24PIN-0.49PMN-0.27PT single crystal in the [111]_c-[$11\stackrel{-}{2}$]_c plane.

Table 2.

Comparison between rotated single-domain properties along [001]_c and the directly measured [001]_c poled multi-domain crystal properties for 0.24PIN-0.49PMN-0.27PT single crystal.

	Rotated single-domain properties along [001]c	Measured constants for [001]c poled multi-domain crystal	Ratio of rotated constant to measured constant
d33	1048	1109	95%
$s_{33}^E$	40.03	43.48	92%
${\varepsilon }_{33}^T$	4080	4222	97%
k33	0.87	0.87	100%
$s_{33}^D$	9.60	10.53	91%
g33	29.03	29.68	98%

In summary, we have measured a complete set of elastic, dielectric, and piezoelectric constants of single-domain 0.24PIN-0.49PMN-0.27PT ternary single crystal poled along [111]_c in natural conditions by using combined resonance and ultrasonic methods.

Up to date, no other complete sets of material constants for relaxor-based ferroelectric single crystals, including both binary and ternary systems, have been reported in the literature. The unbiased completed set of single domain data allowed us to get more accurate account of the contributions from orientation effects in the mutidomain properties through matrix transformation. In the longitudinal coefficients, the orientation effects play the dominant role, particularly for the giant piezoelectric d₃₃ coefficient and the very large electromechanical coupling factor k₃₃.