On the mechanisms involved in the recovery of envelope information from temporal fine structure

Abstract

Three experiments were designed to provide psychophysical evidence for the existence of envelope information in the temporal fine structure (TFS) of stimuli that were originally amplitude modulated (AM). The original stimuli typically consisted of the sum of a sinusoidally AM tone and two unmodulated tones so that the envelope and TFS could be determined a priori. Experiment 1 showed that normal-hearing listeners not only perceive AM when presented with the Hilbert fine structure alone but AM detection thresholds are lower than those observed when presenting the original stimuli. Based on our analysis, envelope recovery resulted from the failure of the decomposition process to remove the spectral components related to the original envelope from the TFS and the introduction of spectral components related to the original envelope, suggesting that frequency- to amplitude-modulation conversion is not necessary to recover envelope information from TFS. Experiment 2 suggested that these spectral components interact in such a way that envelope fluctuations are minimized in the broadband TFS. Experiment 3 demonstrated that the modulation depth at the original carrier frequency is only slightly reduced compared to the depth of the original modulator. It also indicated that envelope recovery is not specific to the Hilbert decomposition.

INTRODUCTION

The challenge inherent in evaluating the individual contribution of frequency-specific (place) and temporally coded (temporal) cues to auditory perception typically arises from difficulty in decomposing an auditory signal (such as speech) into a modulator (or envelope) and a carrier so that either can be “independently” altered, reduced or replaced. Several methods have been proposed for decomposing a signal into a form that would allow independent evaluation. One such method involves decomposition of the signal by means of the Hilbert transform. This method will be referred to as the Hilbert approach. Although it has several variants, it can generally be described as follows. A priori, it is assumed that a broadband signal, S(t), can be described as the sum of N modulated bands, S_n(t), such as

$$S\left(t\right)=\sum _{n=1}^N{S}_n\left(t\right)=\sum _{n=1}^N{m}_n\left(t\right)c_n\left(t\right),$$ (1)

where m_n(t) and c_n(t) are, respectively, the modulator and the carrier in the nth band. In order to reduce possible confusion, the original modulator and carrier will always be referred to as m(t) and c(t), respectively. The computed envelope and phase (or temporal fine structure; TFS), defined later on, will always be referred to as a(t) and cosφ(t). From Eq. 1, it is clear that the modulator and the carrier could easily be manipulated separately. However, for an observed signal such as speech, m_n(t) and c_n(t) are unknown, and therefore must be determined. By introducing Z_n(t), the analytic signal defined by

$$Z_n\left(t\right)=S_n\left(t\right)+\mathit{iH}\left[S_n\left(t\right)\right],$$ (2)

where $i=\sqrt{-1}$ and H[…] is the Hilbert transform, one can determine the Hilbert instantaneous amplitude, a_n(t), and the Hilbert instantaneous phase, φ_n(t), respectively given by

$$a_n\left(t\right)=\left|Z_n\left(t\right)\right|,$$ (3)

$${\phi }_n\left(t\right)=\mathit{arg}\left[Z_n\left(t\right)\right]$$ (4)

so that the original signal can be rewritten as

$$S\left(t\right)=\sum _{n=1}^N{a}_n\left(t\right)\mathit{cos}{\phi }_n\left(t\right).$$ (5)

It is commonly assumed that m_n(t) ≈ a_n(t) and c_n(t) ≈ cos φ_n(t), and thus one can manipulate the envelope and∕or the fine structure independently and synthesize a modified version of the original signal. This approach has been widely used in past studies to investigate, among other things, the range of modulation frequencies most relevant for speech (e.g., Drullman et al., 1994et al.,) and the dichotomy in auditory perception between temporal envelope and temporal fine structure cues (e.g., Smith et al., 2002).

Several recent studies, however, suggest that the Hilbert approach may be inappropriate to decompose complex signals such as speech. It should be noted that this restriction is limited to those situations where the envelope and∕or the fine structure are manipulated (e.g., filtered) prior to be added back together to synthesize a new signal.

Ghitza (2001) first suggested that part of the original envelope information can be recovered from the Hilbert fine structure at the output of the auditory filters. According to Ghitza, two theorems provide analytic support for the recovery of amplitude modulation (AM). First, the Hilbert instantaneous amplitude and the Hilbert instantaneous phase are related (Voelcker, 1966). Second, if the Hilbert fine structure, cos φ_n(t), is the input to a band-pass filter, then the filter’s output has an envelope, a_n’(t), that is related to φ_n(t) (Rice, 1973). One consequence of these two theorems is that when a listener is presented only with the fine structure of speech [cos φ_n(t)] part of the original temporal envelope may be recovered from the phase information [φ_n(t)] [see, Fig. 2d in Ghitza, 2001]. In this case the cochlear filters play the role of the band-pass filter.

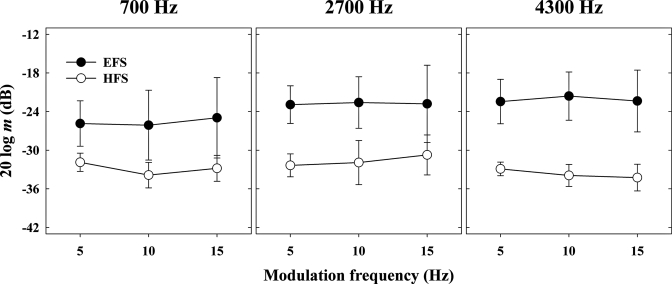
Figure 2.

Averaged modulation detection thresholds as a function of the modulation frequency. Each panel corresponds to results when a given carrier frequency was the modulated carrier. The circles and squares correspond to the EFS and the HFS condition, respectively. Errors bars indicate ± one standard deviation.

More recently, Atlas et al. (2004) offered a more general demonstration of the limits of the Hilbert approach. The authors pointed out that an implicit assumption of the Hilbert approach is that the original modulator is necessarily real and non-negative. This postulation is apparent in Eq. 3. However, for most complex signals such as speech and music there is no indication that this assumption is met. In other words, although the “true” envelope may be complex and not strictly non-negative, the Hilbert envelope is systematically real and non-negative. It follows that envelope∕phase decomposition by means of the Hilbert approach may lead to an inaccurate estimation of the original envelope for a large variety of signals, including speech. Since the Hilbert envelope and the Hilbert instantaneous phase are related [see Eq. 5], the fine structure cannot be accurately estimated either. A corollary of the incorrect estimation of the original modulators and carriers is that the Hilbert envelope and the Hilbert fine structure are contaminated with fine structure and envelope information, respectively. Since envelope information is present in the fine structure, it is therefore possible to recover part of this information as described in Ghitza (2001).

Several behavioral (Zeng et al., 2004; Gilbert and Lorenzi, 2006) and neurophysiological (Heinz and Swaminathan, 2009) studies have since confirmed that envelopes derived from the TFS can produce good speech intelligibility. In the behavioral studies, normal-hearing (NH) listeners were presented with the TFS of speech stimuli or with a series of noise or tone carriers amplitude-modulated by the recovered envelopes. In the latter case, a technique similar to vocoder processing (Shannon et al., 1995et al.,) was used and the recovered envelopes corresponded to the outputs of a bank of gammachirp auditory filters (Irino and Patterson, 1997) in response to the original speech fine structure. Zeng et al. (2004) found up to 40% correct performance for sentences and Gilbert and Lorenzi (2006) found up to 60% correct performance for consonants. Gilbert and Lorenzi (2006) also showed that performance decreases with increasing number of analysis bands. The authors attributed the effect of the number of bands to the ratio between the bandwidth of the analysis filters and that of the auditory filters. They also concluded that consonant identification is essentially abolished when the bandwidth of the analysis filters is less than or equal to four times the bandwidth of normal auditory filters.

The initial goal of the present study was to provide supporting evidence of a relationship between non-negativity and envelope recovery using a psychophysical approach. In contrast to previous behavioral studies, speech material was not used because it was not possible to determine the “true” envelope of such complex stimuli. Instead, various stimuli were artificially created so that the envelope would be known a priori. The first experiment sought to verify experimentally that only the stimuli whose original envelope is not strictly non-negative produce envelope recovery and that the nature of the carrier has no influence on this outcome. Two conditions were compared. In one condition (complex carrier), we assessed envelope recovery with various complex carriers modulated by a sinusoidal modulator. In this case, no envelope recovery was expected (strictly positive modulator). In the other condition (complex modulator), we assessed envelope recovery with a relatively simple carrier modulated by a partially negative modulator. In this case, envelope recovery was expected.

EXPERIMENT 1

Method

Subjects

Data were collected from four normal-hearing listeners (one female, three males), ranging in age from 26 to 38 yr. Three of the listeners were authors REM, CAB, and FA. The fourth listener was paid an hourly wage for his services. Normal hearing was defined as having pure-tone air-conduction thresholds 20 dB hearing level (HL) or above (ANSI, S3.6-2004) at octave frequencies from 250 to 8000 Hz in both ears. Listeners received no training before data collection began but three of them had extensive prior experience with modulation detection experiments.

Stimuli and procedure

Stimuli were computer generated and produced at a sampling rate of 44.1 kHz via custom software routines using MATLAB and a 16-bit D∕A converter and delivered diotically to Sennheiser HD 250 headphones. The overall level of the stimuli was fixed at 65 dBA SPL. Subjects were tested individually in a double-walled sound-attenuating booth. As mentioned previously, two conditions were tested in this first experiment, and the stimuli and procedure used in each are described separately.

Experiment 1a: Complex carrier.

Three complex carriers were tested. The first was a Gaussian noise. The second was an equal-amplitude harmonic complex. The fundamental frequency was 200 Hz, with components from 200 to 5000 Hz; the phase of each component was randomly selected from a rectangular distribution. The third, a positive Schroeder-phase complex, was derived from the harmonic complex (Kohlrausch and Sander, 1995). These complex carriers were sinusoidally amplitude-modulated so that the envelope was always strictly non-negative. Three modulation frequencies (f_m = 5, 10, and 15 Hz) were tested, covering the range of prominent modulations in speech (Houtgast and Steeneken, 1985; Drullman et al., 1994et al.,, Apoux and Bacon, 2008). Modulation depth, d_m, expressed in terms of 20 log d_m, was set to −0.45 dB (d_m = 0.95) to ensure that the modulation depth of the recovered envelope would not be a limiting factor to detection. All carriers had an overall duration of 1000 ms, including 20-ms cosine-squared rise∕fall ramps. Because evidence of the existence of AM recovery comes from studies in which listeners were presented with “pre-recovered” envelopes using simulated auditory filters (Zeng et al., 2004et al.,; Gilbert and Lorenzi, 2006), a comparable condition was added to the present experiment. A sinusoidally amplitude-modulated Gaussian noise was decomposed into a temporal envelope and a fine structure using the Hilbert approach. Then, the fine structure was band-pass filtered into 16 frequency bands (100–5000 Hz) using gammachirp filters (Irino and Patterson, 2001) and the envelope at the output of each filter was used to modulate bands of noise having the same characteristics as the original gammachirp filters. The resulting modulated noises were finally summed to produce the broadband stimuli.

Percent correct discrimination was measured using a two-interval, two-alternative forced-choice procedure. On each trial, a standard and a target stimulus were successively presented in random order. The target consisted of the Hilbert fine structure of the modulated carrier and the standard consisted of the Hilbert fine structure of the same realization of the target carrier left unmodulated. The two intervals were always preceded by the unprocessed version of the target stimulus (i.e., envelope + TFS), so that listeners knew what rate of modulation to expect. The modulation depth in the cue interval was set to −20 dB. The listener’s task was to discriminate between the fine structure of unmodulated and modulated carriers by choosing the interval that contained the stimulus that was originally modulated. Visual feedback indicating the correct interval was provided after each trial. Each listener completed 150 trials in every condition, resulting in a total of 600 trials.

Experiment 1b: Complex modulator.

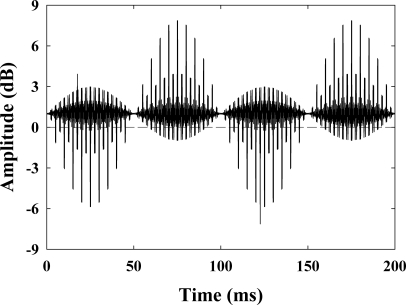
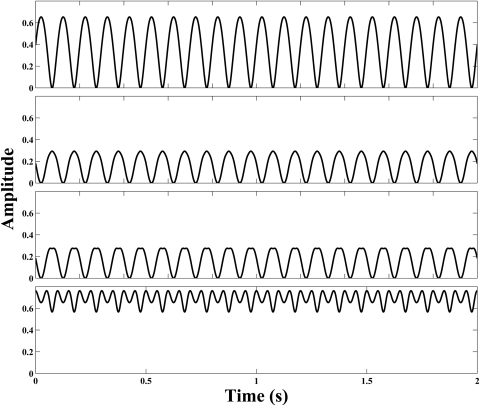
In experiment 1b, the carriers were created by adding together three sinusoids with frequencies f_c1 = 700 Hz, f_c2 = 2700 Hz, and f_c3 = 4300 Hz and random starting phases. Each sinusoid had a duration of 500 ms, including 10-ms cosine-squared rise∕fall ramps. On each trial, three new sinusoids were generated; however, the same realization was used in each interval. In one interval, chosen at random, one sinusoid was sinusoidally amplitude-modulated, before summation, throughout its entire duration and the other sinusoids were left unmodulated. It was determined a priori that the original envelope1 of these stimuli would violate the non-negativity assumption and therefore, their fine structure should elicit envelope recovery. Figure 1 shows an example of the original envelope of the resulting stimuli. Two conditions were compared. In one condition (EFS), listeners were presented with the originally modulated and unmodulated stimuli containing both intact envelope and TFS. In the other condition (HFS), the listeners were only presented with the Hilbert fine structure2 or TFS extracted from the modulated and unmodulated stimuli. In this condition, the fine structure alone was presented in both intervals.

Figure 1.

Example of the “true” envelope of the stimuli used in experiment 1b. The original stimulus was created by adding together three sinusoids with frequencies 700, 2700, and 4300 Hz. The 2700-Hz sinusoid was sinusoidally amplitude modulated at 10 Hz with d_m = 0.9 before adding the other sinusoids. The envelope was obtained by dividing the signal by itself with the modulation depth, d_m, set to 0.

Modulation detection thresholds were measured using a two-interval, two-alternative forced-choice (2IFC) procedure. The subjects were asked to determine which of the two intervals contained a modulated signal. The modulation depth (20 log d_m) of the original stimulus was increased (before decomposition) after one incorrect response and decreased after two successive correct responses. This procedure tracks the modulation depth required for 70.7% correct detection (Levitt, 1971). Each run consisted of a block of 10 reversals. The initial step size of 4 dB was reduced to 2 dB after the first two reversals. The first two reversal points were discarded, and the values of 20 log d_m (before decomposition) at the remaining reversals points were averaged to obtain a threshold estimate for a given block. On the rare occasions when the stepping rule called for a modulation depth greater than 1 or when the standard deviation of the given threshold estimate was greater than 5 dB, the run was discarded. Thresholds presented here are based upon the average of three estimates for each listener. If the standard deviation of that average was greater than 3 dB, an additional estimate was obtained and all four estimates were averaged. Visual feedback indicating the correct interval was provided after each trial.

Results and discussion

Results from experiment 1a (not presented) were largely consistent with the initial hypothesis in that performance remained essentially at chance, despite the large modulation depth used to create the original stimuli. In other words, listeners could not discriminate between the fine structure of unmodulated and modulated stimuli when the original envelope was strictly non-negative, irrespective of the nature of the carrier. The same outcome was observed with pre-recovered envelopes, indicating that the present findings cannot be attributed to the fact that previous studies used pre-recovered envelopes. Figure 2 shows the data obtained in experiment 1b. Each panel in Fig. 2 shows the averaged AM detection thresholds as a function of the frequency of the modulated sinusoid. The parameter is the processing condition (EFS or HFS). Results from experiment 1b were consistent with the assumption that the TFS of stimuli whose original envelope is not strictly non-negative should elicit envelope recovery in that listeners were able to discriminate between the two intervals when presented with the fine structure only (HFS condition). More surprisingly, the present data indicated that listeners are better at detecting modulation when presented with the Hilbert fine structure only. The difference in thresholds between the HFS and EFS conditions ranged from 7 to 12 dB, depending upon the carrier frequency. A repeated-measures analysis of variance with factors processing (EFS or HFS), modulated sinusoid (700, 2700, or 4300 Hz) and modulation frequency (5, 10, or 15 Hz) was performed. The results of this analysis confirmed a significant effect of processing [F(1,3) = 26.5, p < 0.05]. They also indicated a significant effect of modulating a given sinusoid [F(2,6) = 10.7, p < 0.05] but no effect of modulation frequency (p = 0.92). None of the interactions were significant (p > 0.2).

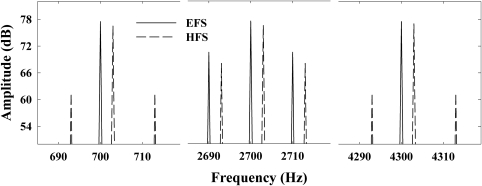
According to Ghitza (2001), the original envelope may be faithfully restored at the output of the auditory filters, as illustrated in his Fig. 2d. Therefore, presenting only the fine structure should have, at the very best, resulted in comparable performance in both the EFS and the HFS conditions. It is unclear then why modulation detection thresholds were lower in the HFS condition than in the EFS condition. To better understand what factor may have been responsible for these lower thresholds, the HFS stimuli were closely examined. The results revealed the presence of sidebands at ±f_m in the TFS at the original carrier frequency after Hilbert decomposition. Even more surprisingly, sidebands at ±f_m were also present at the other carrier frequencies, indicating that listeners were in fact presented with at least three modulated carriers when listening to the fine structure only. Figure 3 shows three selected regions of the spectra of stimuli from the EFS and HFS conditions corresponding to the three carriers (see the upper panel of Fig. 8 below for a formal representation). In Fig. 3, the 2700-Hz carrier was modulated at 10 Hz with d_m = 0.9. For clarity, the spectrum of the HFS stimulus has been shifted toward higher frequencies by 3 Hz. It can be seen that sidebands at ±10 Hz are still present in the fine structure at the original carrier frequency as well as at the other carrier frequencies. The sidebands at the original carrier and the sidebands at ±f_m around the “unmodulated” carriers will be referred to as the original and generated sidebands, respectively.

Figure 3.

Partial representation of the amplitude spectra of the stimuli used in experiment 1b. The original stimulus consisted of the sum of three sinusoids with the middle component modulated at 10 Hz with d_m = 0.9 prior to adding. The two components at 700 and 4300 Hz were unmodulated. For clarity, the spectrum of the HFS stimulus has been shifted toward higher frequencies by 3 Hz.

Figure 8.

Example of amplitude spectra of TFS stimuli used in experiment 3. The original stimulus consisted of the sum of three sinusoids with the 800-Hz component modulated at 10 Hz with d_m = 0.9 prior to adding. The two components at 600 and 1000 Hz were unmodulated. The TFS was obtained using the Hilbert (upper panel) or the RLP (lower panel) technique.

The presence of the generated sidebands may account, at least partly, for the difference between thresholds in the EFS and the HFS conditions. Indeed, several studies have reported that detection of complex signals composed of equally detectable components that excite independent auditory filters should improve with the number of components (e.g., Green, 1958; van den Brink and Houtgast, 1990a,b; Higgins and Turner, 1990). More specifically, performance should improve as a function of the square root of the number of components, provided that detectability, d’, is proportional to signal energy in each filter (Green and Swets, 1966; Buus et al., 1986et al.,). Assuming that for AM detection d’ is proportional to the square of d_m (Moore and Sek, 1992; Edward and Viemeister, 1994), the modulation depth at threshold should be 20 × log($\sqrt{\mathrm{n}}$) lower, where n is the number of modulated components. In other words, thresholds for three modulated carriers should be about 4.8 dB lower than for either one presented in isolation. Accordingly, most of the difference in thresholds between EFS and HFS may be attributed to the presence of envelope information at all three carrier frequencies in the latter condition.

EXPERIMENT 2

Rationale

The results from experiment 1 suggest that when the non-negativity assumption is violated, not all the spectral components related to the original envelope (i.e., the sidebands) are removed from the TFS. Instead, it looks like, at least in the specific conditions tested here, new spectral components are generated by the Hilbert decomposition and that these newly generated components interact with those already present in the original stimulus in a way that minimizes fluctuations in the new stimulus. In other words, the seemingly constant amplitude of the broadband fine structure may be due to a particular phase and amplitude relationship between the original and the generated sidebands. Figure 4 shows the phase—and to some extent the amplitude—relationship between three envelopes extracted from the output of three 128-Hz wide band-pass filter each centered at a carrier frequency and the sum of output of these three filters.3 The HFS stimulus shown in Fig. 3 was used here (i.e., only the 2700-Hz carrier was modulated at 10 Hz with d_m = 0.9 and the TFS was estimated from the broadband signal). The top panel of Fig. 4 shows the narrowband envelope of the carrier that was originally modulated. The two middle panels show the narrowband envelopes of the other carriers. As can be seen, the envelope in the top panel and the envelopes in the middle panels are in opposite phase and the modulation depth of the envelope in the top panel is about twice as large as the depth of the ones in the middle panels. These observations are consistent with the suggestion that original and newly generated sidebands interact in such way that envelope fluctuations are minimized in the wideband fine structure. To further illustrate this idea, the sum of the three narrowband envelopes is shown in the lower panel of Fig. 4.4 As expected, the depth of the resulting envelope is very low. One question that emerges at this point is how thresholds might be affected when the three modulated carriers excite the same auditory filter. Although it is not expected that perfect “cancellation” should be achieved,5 detectability may be reduced in those conditions. Such cancellation would account for the effect of analysis filter bandwidth reported by Gilbert and Lorenzi (2006). This possibility was tested in experiment 2 by using a narrowband stimulus designed so that the three carriers were spaced in frequency such that nominally they would all fall within one auditory filter. For comparison, a second condition was tested in which the three carriers were presented in the low-frequency region such that nominally they would each primarily fall within distinct auditory filters. While the partial envelope cancellation shown in the lower panel of Fig. 4 was systematically observed after many replications, it seemed necessary to confirm this finding experimentally. Accordingly, listeners were also presented with stimuli whose envelope was created by summing the three narrowband envelopes (as in the lower panel of Fig. 4).

Figure 4.

Example narrow-band envelopes of a stimulus from the Hilbert fine structure condition. The original stimulus is the same as in Fig. 3. Successively lower panels show envelopes extracted from the output of a 128-Hz band-pass filter centered at 2700, 700, and 4300 Hz, respectively. The lowest panel shows sum of the three envelopes.

Method

Subjects

Data were collected from three normal-hearing listeners (two females). Two of the listeners were authors REM and FA. The third listener was paid an hourly wage for her services. All participants had pure-tone air-conduction thresholds of 20 dB HL or better at octave frequencies from 250 to 8000 Hz (ANSI, S3.6-2004). They all had extensive prior experience in modulation detection experiments.

Stimuli and procedure

Stimuli were similar to those used in Experiment 1b and consisted of three sinusoids whose starting phase was randomly selected in each trial. The frequency of these three sinusoids, however, differed from those used in experiment 1b. In one case, the sinusoids were located in the low-frequency region (LO; 600, 800, and 1000 Hz) and it was assumed that the components could be resolved individually by the auditory system. In another case, the sinusoids were located in the high-frequency region (HI; 4200, 4400, and 4600 Hz). In this case, the components comprising the stimuli were assumed to be unresolved. Only one modulation frequency (10 Hz) was tested and the modulator was only imposed on the center component.

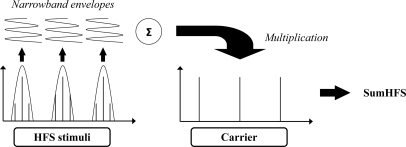
In addition, three processing conditions were tested. The first two corresponded to the EFS and HFS conditions described in experiment 1b. The last condition, SumHFS, evaluated the sensitivity to the sum of “recovered” envelopes as seen in the lower panel in Fig. 4. The SumHFS stimuli were created as follows (see Fig. 5): First, three narrowband signals were obtained from the stimuli used in the corresponding HFS condition using three 128-Hz wide band-pass filters, each centered at a carrier frequency. In each band, an envelope was extracted by half-wave rectification and low-pass filtering (6th-order Butterworth filter, 64-Hz cutoff frequency). The three envelopes were then added together and the sum was used to modulate the three original sinusoids. A total of 6 conditions were tested resulting from all possible combinations of frequency region (LO and HI) and processing (EFS, HFS, and SumHFS). Again, the subjects were asked to discriminate between the originally modulated stimulus and an unmodulated stimulus. Other methodological and procedural details were identical to those used in experiment 1b.

Figure 5.

Schematic of the processing used to create the SumHFS stimuli.

Results and discussion

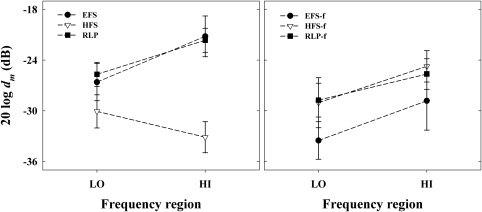
In the EFS and HFS conditions (see left panel of Fig. 6), thresholds were relatively similar when the carriers were presented in the low-frequency region (−27 and −30 dB, respectively). One interpretation is that channel independence was reduced in experiment 2 compared to experiment 1b in that the overlap between the auditory filters stimulated by the three carriers was larger in the LO condition of experiment 2. It is not surprising then that the difference between EFS and HFS thresholds was greatly reduced. This interpretation is consistent with the earlier assumption that spectral integration presumably accounts for most of the difference between EFS and HFS performance in experiment 1b. In the unresolved condition (HI), thresholds were about −21 dB in the EFS condition and about −33 dB in the HFS condition. This 12 dB difference resulted from both an increase in threshold in the EFS condition and a decrease in the HFS condition.

Figure 6.

Averaged modulation detection thresholds as a function of the frequency region of the carriers. Left panel shows the thresholds for unfiltered stimuli. Right panel shows the thresholds for the same stimuli filtered using a 128-Hz band-pass filter centered at the original modulated carrier.

It is interesting to note that performance in the EFS condition was almost identical to that in the corresponding condition of experiment 1b (i.e., similar target carrier frequency) in that thresholds in the LO and HI conditions were similar to that obtained in the 700 and 4300 Hz conditions. This apparent lack of effect suggests that AM detection is primarily affected by the carrier frequency of the target and that the spectral location of the nontarget carriers has little influence on performance. For the HFS stimuli, thresholds measured in the LO condition were about 3 dB higher than in the 700 Hz condition (experiment 1b). This difference may be interpreted as evidence that spectral integration was slightly better in the latter condition, further illustrating that adjacent auditory filters are less independent than widely separated ones. In contrast, thresholds measured in the HI condition were identical to that measured in the 4300 Hz condition (experiment 1b). This lack of difference suggests that no cancellation occurred when the three modulated carriers excited the same auditory filter. It also suggests that the decrease in potential spectral integration produced by having the three modulated carriers exciting the same auditory filter was somehow compensated for. The results obtained in the SumHFS condition (not displayed) confirmed that narrowband envelopes in the Hilbert fine structure interact in such a way that fluctuations are minimized in the wideband stimuli. In this condition, the mean thresholds for the low- and high-frequency location were indeed −6.5 and −4.5 dB, respectively. Therefore, one may reasonably assume that the envelope relationship illustrated in Fig. 4 was preserved in the HFS condition. One factor that may have prevented perfect cancellation is the differential effect of band-pass filtering on the spectral components of a sound. For instance, when a sinusoidally AM tone is passed through a band-pass filter, the amplitude of the sidebands may be differentially affected by the filtering process if the filter is not perfectly centered at the carrier frequency (see also Atlas et al., 2004et al.,).

To illustrate this idea, three new narrowband envelopes were obtained using the same stimulus and processing as for Fig. 4. However, only one of the three 128-Hz wide band-pass filter was centered at a carrier frequency. The other two filters, those originally centered at 700 and 4300 Hz, were now centered at 646 and 4346 Hz, respectively. Figure 7 shows the sum of the three narrowband envelopes obtained this way. As can be seen, the modulation depth of the resulting envelope is much larger than that of the envelope in the lower panel of Fig. 4. In the present experiment, the auditory filters played the role of the band-pass filter. Accordingly, the possibility exists that the relationship between the amplitude and∕or phase of the narrowband envelopes was not preserved in the auditory system, resulting in limited cancellation.

Figure 7.

Sum of three narrow-band envelopes extracted from the output of a 128-Hz band-pass filter centered at 646, 2700, and 4346 Hz, respectively. The original stimulus is the same as in Fig. 4.

EXPERIMENT 3

Rationale

In experiments 1 and 2, the recovery of envelope information from fine structure was investigated using the Hilbert approach. However, Atlas et al. (2004) indicated that the possibility to recover envelope information from the TFS may not be specific to the Hilbert approach. Experiment 3 therefore used a different envelope∕phase decomposition approach not only to explore this possibility but also because it is widely employed (e.g., in both real and simulated cochlear implant processing) and is thought to be physiologically relevant. It can be summarized as follows: The first stage consists of extracting the envelope by rectification and low-pass filtering. The second stage, the fine structure derivation, consists of dividing the original signal by the envelope obtained from stage one. The assumption of a non-negative envelope is also evident here and, consequently, AM recovery is expected when using this technique as well. Experiment 3 was conducted to evaluate whether the limitations observed with the Hilbert approach could be generalized to this rectification∕low-pass filtering technique. In addition, modulation detection thresholds were measured when the subjects were only presented with the original modulated carrier. In that additional condition, the generated sidebands (as well as the “unmodulated” carriers) were simply removed from the stimuli. The purpose of this manipulation was to provide an estimate of the modulation depth at the original modulated carrier without the interference produced by the generated sidebands.

Method

Subjects

Data were collected from the three normal-hearing listeners who participated in experiment 2.

Stimuli and procedure

The first condition, RLP (rectification∕low-pass filtering), corresponded to the new decomposition approach described previously. Briefly, the broadband envelope was extracted by half-wave rectification and low-pass filtering with a cut-off frequency of 64 Hz (6th-order Butterworth) and the fine structure was computed by dividing the original stimulus by its own envelope at each corresponding point in time. Again, only the fine structure was presented in both intervals in this condition. In a second set of conditions, the stimuli used in EFS and HFS (experiment 2) and RLP were filtered using a 128-Hz band-pass filter centered at the original modulated carrier (EFS-f, HFS-f and RLP-f, respectively). As a result, listeners were presented with the middle carrier only and the original sidebands only. Other methodological and procedural details were identical to those used in experiment 1b.

Results and discussion

The average results across listeners are summarized in Fig. 6. The left panel shows the results for the RLP condition. For comparison, the data for the EFS and HFS conditions from experiment 2 are also shown. The right panel shows the results for the EFS-f, HFS-f and RLP-f conditions. In both panels, thresholds for the frequency regions LO and HI are displayed. As can be seen in the left panel, the thresholds obtained for the RLP condition were identical to the thresholds obtained for the EFS condition and therefore differed from that in the HFS condition. A possible explanation for the difference in results between the two decomposition techniques involves the presence of distortion in the fine structure obtained using the Hilbert approach. Indeed, the RLP technique produces less distortion consisting of spectral components modulated at f_m as illustrated in Fig. 8. It is therefore not surprising that modulation detection thresholds were generally lower in the HFS condition relative to the RLP condition.

For filtered stimuli (right panel), thresholds in the LO condition (resolved) were 3 to 5 dB lower than the thresholds obtained in the HI condition (unresolved). Thresholds for the HFS-f and RLP-f conditions were similar to one another while thresholds for the EFS-f condition were about 4 dB lower. The difference in thresholds between the EFS-f condition and the HFS-f condition is in line with the difference in amplitude between the sidebands of the carrier that was originally modulated in the EFS and HFS conditions of experiment 1b (see Fig. 3). The similarity between the HFS-f condition and the RLP-f condition supports the assumption that the 12-dB difference observed in the left panel was due to additional distortion in the Hilbert fine structure as most distortion components were removed in these filtered conditions. More importantly, the fact that most distortion was removed confirms what can be seen in Fig. 3: modulation depth at the original carrier frequency is only slightly reduced after decomposition. Finally, the results obtained in the filtered condition suggest that thresholds measured previously in the TFS only conditions cannot be attributed to the perception of distortion. In other words, the results from experiments 1 and 2 are not just an artifact due to the introduction of distortion but they may be attributed, for the most part, to the presence of the original sidebands in the TFS.

CONCLUDING REMARKS

The main finding of the present study is that—at least in the situations tested here—envelope information is not properly removed from the TFS and NH listeners may recover this information at the output of the auditory filters, as described in Ghitza (2001) and Heinz and Swaminathan (2009). It should be noted that envelope recovery, as observed here, did not imply frequency-modulation-to-amplitude-modulation conversion mechanisms as suggested in previous studies (e.g., Gilbert and Lorenzi, 2006). In fact, the present results could be accounted for entirely by the failure of the decomposition process to remove the spectral components related to the envelope from the TFS and additionally by the introduction of new spectral components related to the original envelope. Both theoretical analyses and behavioral data suggest a causal relationship between violation of the non-negativity assumption and the possibility of recovering envelope information from the TFS. Finally, the present study suggests that envelope recovery is not specific to the Hilbert approach and may be observed with other decomposition approaches, provided that the non-negativity of the original envelope is also assumed.

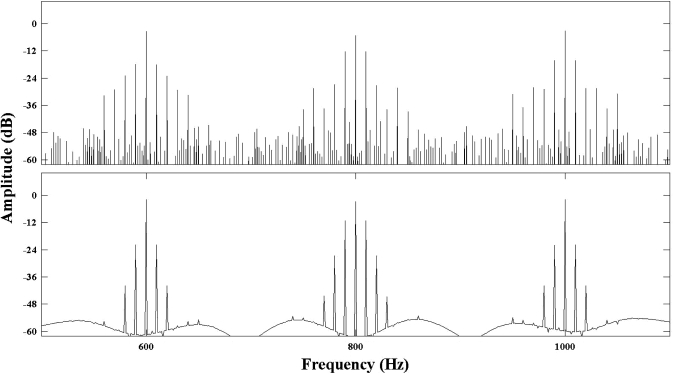
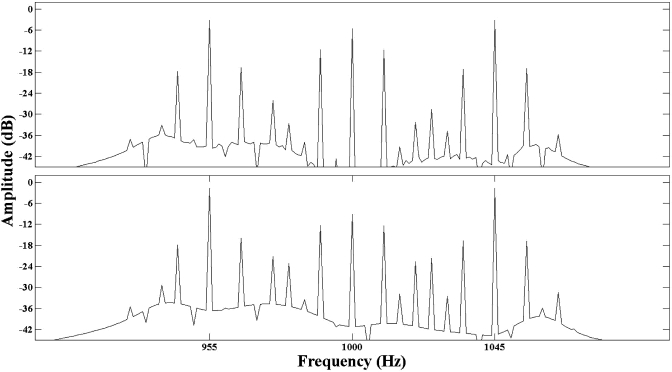
One may reasonably argue at this point that our results were a consequence of the broadband approach used in all the experiments. Indeed, Hilbert decomposition is usually carried out on narrowband signals. Our decision to use a broadband approach was primarily motivated by the results of Gilbert and Lorenzi (2006) showing that speech recognition is better when the TFS is estimated at the output of broad analysis filters. It seems, however, that the use of narrow analysis filters has little, if any, influence on the presence of envelope information in the TFS of our stimuli. To illustrate this, we computed the TFS at the output of a one equivalent rectangular bandwidth (ERB; Glasberg and Moore, 1990) band-pass filter centered at 1000 Hz. After computation, the TFS was filtered again using the same 1-ERB filter. In order for all three sinusoids to be included within this 1-ERB-wide frequency band, their frequencies were set to 955, 1000, and 1045 Hz. The modulator was identical to that used in Fig. 3 and was imposed on the 1000-Hz sinusoid before adding. Figure 9 shows the spectrum of the TFS after Hilbert decomposition (upper panel) and after RLP decomposition (lower panel). As can be seen, the narrowband analysis filter had no visible effect on the presence of envelope information in the TFS. In both panels, sidebands at ±f_m in the fine structure at the original carrier frequency and at the other carrier frequencies are still present after decomposition (i.e., in the TFS). Therefore, it may be assumed that the present findings were not the consequence of our broadband approach.

Figure 9.

Amplitude spectra of a TFS stimulus. The original stimulus consisted of the sum of three sinusoids with the 1000-Hz component modulated at 10 Hz with d_m = 0.9 prior to adding. The two components at 955 and 1045 Hz were unmodulated. The upper panel corresponds to a TFS obtained using the Hilbert approach. The lower panel corresponds to a TFS obtained using the RLP approach. Both approaches to TFS estimation were computed at the output of a 132-Hz (i.e., 1-ERB_N) band-pass filter centered at 1000 Hz.

The finding that original envelope information is well preserved in the fine structure seems to contradict previous studies showing that the intelligibility of envelope-processed speech is somewhat poor (Zeng et al., 2004et al.,; Gilbert and Lorenzi, 2006). It should be noted, however, that the current study also revealed the presence of major distortion (i.e., the generated sidebands) in the TFS. Although this distortion is related to the original envelope information and those sidebands may significantly improve detection performance (experiment 1b), the possible influence on speech intelligibility is difficult to predict, at best. First, the temporal envelope of speech in different spectral regions is not generally the same (Houtgast and Steeneken, 1985; Apoux and Bacon, 2004, 2008). Second, the results from previous studies suggest that speech recognition can be adversely affected by altered spectral distribution of envelope cues whether or not this information is otherwise relevant (e.g., Shannon et al., 1998et al.,). While additional work is clearly needed before the present findings can be extended to speech stimuli, results from studies in which the envelope and∕or TFS have been manipulated should be interpreted with caution. Indeed, the possibility exists that envelope information (i) was not properly removed from the fine structure and (ii) it was introduced at inappropriate spectral locations.

A more general concern raised by our analysis of the envelope∕phase decomposition techniques is the meaning and definition of “temporal fine structure.” It seems clear that an operational definition such as the Hilbert fine structure may not be appropriate for studying auditory temporal processing.