Abstract
There are three standard methods for generating two channels of partially correlated noise: the two-generator method, the three-generator method, and the symmetric-generator method. These methods allow an experimenter to specify a target cross correlation between the two channels, but actual generated noises show statistical variability around the target value. Numerical experiments were done to compare the variability for those methods as a function of the number of degrees of freedom. The results of the experiments quantify the stimulus uncertainty in diverse binaural psychoacoustical experiments: incoherence detection, perceived auditory source width, envelopment, noise localization∕lateralization, and the masking level difference. The numerical experiments found that when the elemental generators have unequal powers, the different methods all have similar variability. When the powers are constrained to be equal, the symmetric-generator method has much smaller variability than the other two.
INTRODUCTION
The study of binaural hearing frequently requires noise stimuli with a controllable amount of interaural correlation. Two channels of partially correlated noise can be presented directly to the two ears as in the early binaural incoherence studies by Pollack and Trittipoe (1959a,b) or the masking level difference studies by Jeffress et al. (1962) and Robinson and Jeffress (1963). Alternatively, two channels of partially correlated noise may be reproduced by loudspeakers in a simple or complicated environment (e.g., Schneider et al., 1988; Blauert, 1996).
In 1948, Licklider and Dzendolet described two ways of making two channels of noise with a tunable value of cross correlation. These were the asymmetric two-generator method and the asymmetric three-generator method. Experimentally, the methods were implemented with analog noise generators, but the mathematical foundations of the methods are still used today when noises are created by digital means. Both methods can be used to make noise with a targeted value of cross correlation from −1.0 to +1.0, and both methods have been used repeatedly in hearing research as will become apparent below. A third method, the symmetric generator, was introduced by Plenge (1972).
The noises that are generated by these methods have values of cross correlation that approximately agree with the targeted value on the average. Therefore over an ensemble of a very large number of noises—all stochastically identical and generated with the same targeted value of cross correlation—the ensemble average value of the cross correlation will be close to the targeted value. However, any particular noise will show a deviation from the targeted value. The purpose of this report is to study the statistical properties of such deviations. The value of the study is that by knowing the uncertainty in cross correlation, one can more effectively evaluate the historical literature that uses partially correlated noise.
A second value is that one can detect potential biases for the different generators wherein the actual cross correlation differs systematically from targeted values. A third value is that one can decide whether some noise generators are better than others in the sense that they produce noise pairs with cross correlation that more often resembles the target value.
DEFINITIONS
There are several definitions of cross correlation (often shortened to “correlation” in this article) in common use. They all describe comparisons between time-dependent signals, yL(t) in a left channel and yR(t) in a right channel. It will be assumed that the time-averaged value of each signal is zero, i.e., the signals have no dc component.
The finite-lag cross correlation function is an answer to the question, “How similar is one of the signals to the other signal given that one of the signals has been delayed by a certain time (the lag).” It is defined as ρ(τ),
| (1) |
The overbar notation in the preceding text refers to an integral of the signals over a duration, TD, evaluated at a lag of τ, for example,
| (2) |
Power PL is the time-average power in the left channel, and it has an overbar representation independent of τ,
| (3) |
An equivalent formula gives the time-average power in the right channel, .
The zero-lag cross correlation function is an answer to the question, “How similar is one signal to a second signal?” It is the τ = 0 limit of ρ(τ). Often, treatments of correlation are entirely limited to the zero-lag function, as in the article by Licklider and Dzendolet (1948).
Also, there are perceptual models of the masking level difference that are based on ρ(0), as reviewed by Bernstein and Trahiotis (1996). Calculations for the zero-lag function are more straightforward than calculations for the finite-lag function.
THREE GENERATORS
All the noise generators discussed in this article operate by adding together the outputs of independent, elemental generators. We consider them in turn.
Asymmetric two-generator method
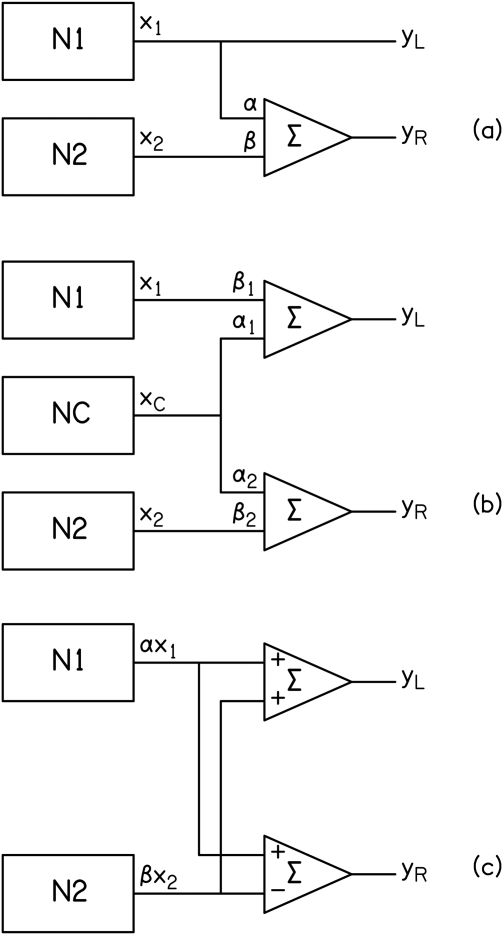
The asymmetric two-generator method from Licklider and Dzendolet, depicted in Fig. 1a, was used by Gabriel and Colburn (1981) in their study of the minimum detectable decorrelation from perfect binaural correlation. The mothod was recently used by Hall et al. (2006) with cross-correlation very close to 1.0. The method was applied in loudspeaker experiments by Schneider et al. (1988) and in physiological studies of the ascending binaural system by Coffey et al. (2006). The asymmetric two-generator method adds two independent, statistically identical noises from separate elemental generators. The two noises are here called x1(t) and x2(t), and they have time-averaged powers P1 and P2, respectively. These noises have the same spectral envelope and the same duration. They have the same expected time-average power (i.e., they have the same expected energy). This feature will be called the “weak equal-power assumption” because it applies only statistically and not to every noise pair.
Figure 1.
Block diagrams of generators with symbols from text equations. Signals move from left to right. (a) The asymmetric two-generator method. (b) The asymmetric three-generator method. (c) The symmetric (two) generator method.
The signal sent to the left channel, namely, yL(t), is simply the noise directly from one of the generators,
| (4) |
The signal sent to the right channel is the weighted sum from the two elemental generators,
| (5) |
where the expected value of the power in the right channel is caused to be the same as the power in the left channel by insisting that the weighting factors obey the rule α2 + β2 = 1. Therefore β is set equal to
The normalizing denominator for the correlation function, is obtained by squaring Eq. 4 (PL = P1) and Eq. 5 (PR) so that the finite-lag correlation function is
| (6) |
and for the zero-lag correlation,
| (7) |
Because noises x1 and x2 are independent, the expected value of is zero. Also the expected values of P2 and P1 are the same. Then from Eq. 7, one expects ρ(0) = α. Thus an experimenter can adjust the summing weights α and to target a particular value of correlation.
Asymmetric three-generator method
The asymmetric three-generator method from Licklider and Dzendolet is depicted in Fig. 1b. The elemental noise generators 1 and 2 and the common noise generator, c, are all independent and all have the same ensemble average time-average power. The three-generator method was used in incoherence detection studies by Pollack and Trittipoe (1959a,b).1 It was used in lateralization centering studies by Jeffress, Blodgett, and Deatherage (1962), and in masking studies by Robinson and Jeffress (1963). Blauert and Lindemann (1986) used this method in their study of auditory spaciousness. Albeck and Konishi (1995) used it to study interaural time difference sensitivity in barn owl, and Akeroyd and Summerfield (1999) used it in their binaural gap experiment.
The left and right channel signals are given by
| (8) |
and
| (9) |
To target a particular correlation, the experimenter is free to choose two parameters, α1 and α2. The values of β1 and β2 are constrained by the rules, and . Our research on the three-generator method was confined to the homogeneous case, α1 = α2, as considered by Licklider and Dzendolet. Then there is only one parameter, called α, and β2 is equal to 1 − α2. The expression for the finite-lag correlation is straightforward but long. The expression for the zero-lag correlation is a little shorter,
| (10) |
Then because the expected values are , and all the powers are expected to be the same, the expected value of correlation is α2.
Symmetric-generator method
The symmetric two-generator method introduced by Plenge (1972) is shown in Fig. 1c. It was also used by van der Heijden and Trahiotis (1998) and by Bernstein and Trahiotis (2008), inspired by a decomposition of the general noise in a theory article by van der Heijden and Trahiotis (1997). The corresponding equations are
| (11) |
and
| (12) |
This method uses only two generators, but it has some advantages over the asymmetrical generator methods of Figs. 1a, 1b. Using analog noise sources and (±)-unity-gain mixers, one can keep α constant and vary the correlation by changing β without changing the expected interchannel level difference, though the overall level will change. However, the following calculations will assume that α2 + β2 = 1, as usual. The zero-lag correlation is then
| (13) |
and its expected value is α2 − β2, or 2α2 − 1.
Expected values
The expected values noted above for the correlations, ρ(0), for the three generators depend on two facts. First, one expects that all the overlap integrals (e.g., ) are zero. Second, according to the weak equal-power assumption, all the elemental generators are expected to have the same power (e.g., P1 = P2 = Pc). Actually insisting that all the generators have equal power will be called the “strong equal-power assumption,” treated in Sec. 5.
If the signals are generated digitally, it is possible to orthogonalize all the overlap integrals using the Gram–Schmidt method to ensure that they are exactly zero for every individual noise (e.g. Culling et al., 2001; Shackleton et al., 2005; Goupell and Hartmann, 2006). Then given the strong equal-power assumption, the correlation of every two-channel noise will be exactly given by its expected value. However, if the outputs of the elemental noise generators are not deliberately orthogonalized, or the powers from those generators are not identical (and these both occur whenever analog noise generators are used), the values of correlation for individual noise pairs will deviate from the expected values. The statistical nature of the deviations, specifically the standard deviation, is the topic of this report.
NUMERICAL EXPERIMENTS
Numerical experiments for all three generators were conducted using only the weak equal-power assumption. Experiments studied only the zero-lag correlation ρ(0) because it is the simplest. The experiments used noise pairs of the Fourier series form,
| (14) |
and
| (15) |
when there are two elemental generators, supplemented with
| (16) |
for the three-generator method.
Here all the spectral component frequencies, fn, are harmonics of fo, and fo is the inverse of the duration, fo = 1∕TD. These harmonics do not need to be consecutive, nor do they need to start with the first. For instance, they might be harmonics numbered 500, 501, 502,… of a fundamental fo = 1 Hz. The components have amplitudes such as An and phases such as φn. The number of spectral components in the noise, N, is an important variable because the number of degrees of freedom is 2N. This number depends jointly on the bandwidth, W, and the duration, TD; i.e., N = W∕fo = W TD.
Over a rectangular integration window with duration TD = 1∕fo, the cosine terms of different frequencies are orthogonal, and the correlation integrals can be done analytically and exactly (e.g.):
| (17) |
| (18) |
These analytic results considerably simplify the calculations of correlation. They also show that in the zero-lag limit, τ = 0, the correlation is independent of stimulus frequencies, although it depends on bandwidth. The effects of violating the 1∕TD relationship between the duration and the frequency spacing are discussed in the Caveats section.
In the numerical experiments, the phases were independently chosen and uniformly distributed from 0 to 360°. The amplitudes were independently chosen and Rayleigh distributed consistent with the weak equal-power assumption, namely, that only the ensemble-average powers of the generators are the same. These are the correct distributions to represent white, Gaussian noise from independent, stochastically similar generators.
The numerical experiments targeted different values of correlation. The targeted values were the expected values, as defined for each generator in the sections in the preceding text.
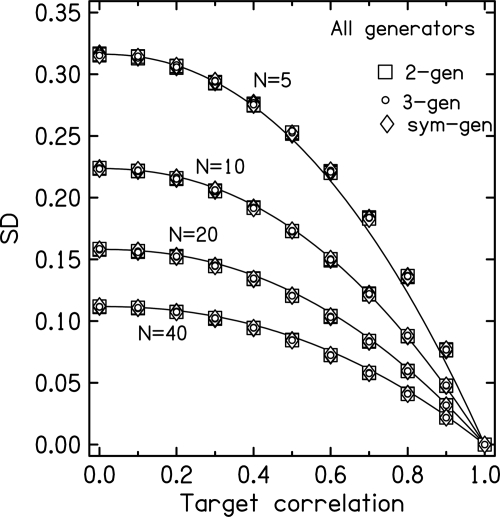
The results of the experiments are very simple to describe. All generators led to the same standard deviations (SD), as shown in Fig. 2, for number of components N equal to 5, 10, 20, and 40. Each point in Fig. 2 was actually plotted 12 times. For each value of N, each generator was run four times with different random starts. Then, as noted, all three generators produced the same standard deviations. The 12 symbols overlap almost entirely.
Figure 2.
The standard deviation, SD, of the correlation from numerical models for all three generators as a function of the target correlation. Parameter N is the number of spectral components in the noise, equal to the product of the bandwidth and the duration. Symbols show the mean SD for 100000 trials using Rayleigh-distributed amplitudes with the weak equal-power assumption. Each symbol is actually plotted four times because the numerical experiments were performed four times with different random starts. However, the individual symbols cannot be distinguished because they overlap. The solid lines show the fit to the formula in Eq. 19.
The variability in correlation, measured by the standard deviation, is greatest when the target correlation α is zero. It can be shown that in this limit the SD is given by . The variability decreases monotonically as α increases until there is no variability at all when α = 1 and the left and right channels are the same.
The SDs for N = 40 exhibit the large-N limit. Those SDs are almost exactly a factor of less than the SDs for N = 20. The large-N limit is incorporated into a one-parameter fit to the standard deviations from the numerical experiments,
| (19) |
shown by the solid lines in Fig. 2. We expect the formula to hold good for all generators when N is 10 or greater. There is no theoretical basis for the functional dependence on α, including the single parameter, 2.2, nor do we understand in any fundamental way why all three generators lead to the same standard deviation plots.
Figure 2, and the fitting formula, allow the reader to find the variability in correlation whenever analog generators are used. Knowing the variability in the stimulus correlation allows an experimenter to estimate how much of the variability observed in psychoacoustical or physiological experiments can be attributed to the stimulus itself.
STRONG EQUAL-POWER ASSUMPTION
The standard deviations computed for Fig. 2 arise from two causes: finite overlaps between non-orthogonal elemental noises such as , and unequal elemental-generator powers. The latter cause reflects the weak equal-power assumption in which only the ensemble-average powers are the same. Studying the generator mathematics, we discovered interesting and useful simplifications that arise if one assumes that all the elemental generators have identical power. That assumption is the strong equal-power assumption. It says that for every noise pair generated, the two (or three) elemental noise generators have the same power, e.g., P1 = P2. Beyond the mathematical simplification, the strong equal-power assumption is also required when making noises using Gram–Schmidt orthogonalization. The remainder of this article investigates the results of making that assumption. The treatment begins with the zero-lag correlation ρ(0) because of its simplicity.
Two-generator method
If P1 = P2 then Eq. 7, becomes
| (20) |
and the overlap, , can be computed from Eq. 18 with τ = 0,
| (21) |
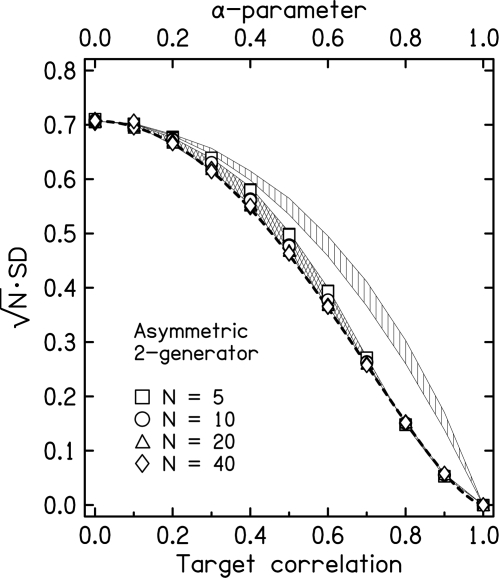
Numerical experiments were done to compute the standard deviation of the correlation. Correlation ρ(0) was computed 100 000 times from Eqs. 20, 21, using uniformly distributed phases and Rayleigh-distributed amplitudes, to find an average correlation and a mean squared deviation (sample variance) from the average correlation. The square root of the mean squared deviation is the standard deviation of ρ(0). The amplitudes were scaled to be consistent with the strong equal-power assumption. Values of the standard deviation can be read from the symbols in Fig. 3 for each of 4 values of N and 11 values of the target correlation, α. Because the standard deviations (SD) decrease as the square root of 1∕N, Fig. 3 plots SD.2 The vertically hatched region shows the data from Fig. 2 replotted in this way. A comparison with the symbols shows that the standard deviation is always reduced by making the strong equal-power assumption.
Figure 3.
The standard deviation, SD, from the asymmetric two-generator method, plotted as SD. Parameter N is the number of spectral components in the noise. Symbols show the results for 100 000 trials using Rayleigh-distributed amplitudes with the strong equal-power assumption. The symbols for N = 20 and N = 40 overlap; N = 20 is asymptotically large; no change would be expected for N > 40. Each symbol is actually plotted four times because the numerical experiments were performed four times with different random starts, but the individual symbols cannot be distinguished. The cross-hatched region shows the result of setting all the amplitudes equal to 1.0. It is bounded by the standard deviations for N = 5 on the top and N = 40 on the bottom. The heavy dashed line shows the large-N prediction from the model based on the normal distribution, Eqs. 23, 24. For α = 0, its limit is 1∕. The vertically hatched region shows the results for the weak equal-power case, replotted from Fig. 2. The vertical extent of the region again indicates the range for N = 5 to N = 40. The vertically hatched region is characteristic of all the generators discussed in this article.
The numerical experiments found that the standard deviations were insensitive to the distribution of the amplitudes. When the Rayleigh-distributed amplitudes were replaced by equal amplitudes (An = Bn = 1), the standard deviations of the correlations changed negligibly, as shown by comparing the symbols and the cross-hatched region in Fig. 3.
Because of this amplitude insensitivity, it is possible to replace x1 and x2 by functions in which all the amplitudes are 1.0 to obtain an expression entirely in terms of the phases. With that replacement,
| (22) |
In words, the power-normalized overlap between independent noises is the average, computed over the N spectral components, of the cosine of the difference between two random phases.
For large N, this statistic is normally distributed with zero mean and with a variance given by σ2 = 1∕(2N). Knowing this fact makes it possible to compute statistical properties of the distribution of ρ(0) from moments.3 Letting Q represent the power-normalized overlap, the kth moment is given by
| (23) |
where the normalized distribution of the cosine of the angle difference is
| (24) |
For example, the variance of ρ(0) is μ2 − . The square root of the variance calculated from Eq. 23 with density P(Q) from Eq. 24 is an excellent large-N limit for the computed standard deviation. It is shown by the heavy dashed line in Fig. 3. When N ≥ 10, the discrepancy between symbols and the dashed line is less than 0.02 for any value of target correlation α. When N = 40, there is no observable discrepancy; the symbols fall right on the dashed line. The limit at α = 0 is rigorously .
The heavy dashed line from Eqs. 23, 24 can be used to compute expected standard deviations to two significant figures. For instance, for a noise targeting a correlation of 0.4, the dashed line gives SD = 0.54. Therefore if the noise is made with 1000 components, the expected standard deviation is .
The analytic simplifications for the asymmetric two-generator model were possible because the correlation involved only a single stochastic function, ∕P1. Therefore statistical properties of the correlation could be determined from a single integral over the density of this function.
Three-generator method
With the strong equal-power assumption, i.e., Pc = P1 = P2 for every noise in the ensemble, the correlation for the three-generator model becomes
| (25) |
It is evident that the correlation for the three-generator method involves three stochastic functions, and they are not independent. Consequently analytic simplifications such as those used for the two-generator method are not available for the three-generator.
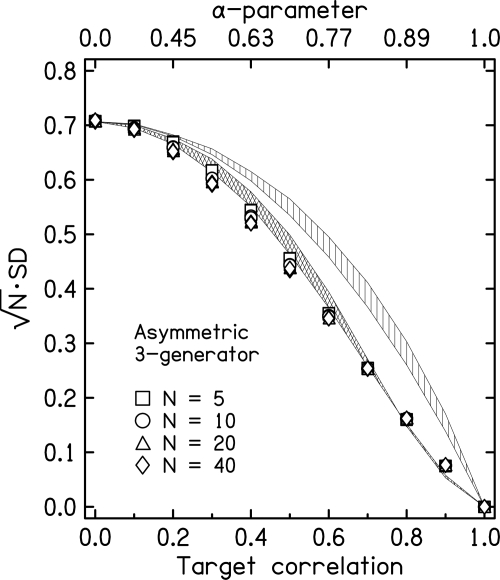
We performed a numerical experiment, computing ρ(0) for 100 000 trials using the same procedures as for the two-generator method. The values of ρ(0) computed as a function of target α2 for different values of N (N as small as 5) had a mean value that closely tracked the target when the target correlation was greater than 0.4. For smaller target correlations, the computed correlation was smaller than the target by a few percent.
The standard deviation can be read from the symbols in Fig. 4 for four values of N, N = 5, 10, 20, 40. Again the plot shows SD. The figure shows that the standard deviations are close to those from the two-generator method shown in Fig. 3. The cross-hatched region in Fig. 4 repeats the two-generator standard-deviation data shown by symbols in Fig. 3. That region is bounded by the data for N = 5 on the top and N = 40 on the bottom. Only for 0.3 ≤ α ≤ 0.6 is there a difference between the standard deviations for the two methods that is greater than 0.02; the three-generator method gives a slightly smaller standard deviation. It is not surprising that the two methods give similar results. In the limit of totally uncorrelated noise (Nu), where α = 0, recently used by Edmonds and Culling (2009) and by Huang et al. (2009), the methods become identical, as can be seen from Eqs. 4, 5 compared to Eqs. 8, 9.
Figure 4.
Standard deviation for the three-generator method with the strong equal-power assumption plotted as SD. The cross-hatched region shows the results for the two-generator method from Fig. 3 for comparison. The top of the cross-hatched region corresponds to N = 5, and the bottom of the region corresponds to N = 40. Both the target-correlation and α-parameter axes apply to the three-generator data. Only the target-correlation axis applies to the two-generator data. The vertically hatched region shows the results for the weak equal-power case, replotted from Fig. 2. The vertical extent of the region again indicates the range for N = 5 to N = 40.
The three-generator experiments were run a second time with the amplitudes all replaced by 1.0. The standard deviations did not change from those shown in Fig. 4. Once again, the standard deviations could be accurately computed from only the phases for the strong equal-power case, Pc = P1 = P2.
The vertically hatched region in Fig. 4 replots the data from Fig. 2, computed with only the weak equal-power assumption. Because the three-generator variance is slightly smaller than the two-generator variance, when the strong equal-power assumption is made, that assumption makes a slightly larger difference for the three-generator method than for the two-generator method.
Symmetric-generator method
Figures 34 for the asymmetrical generators show that the strong equal-power assumption led to rather minor effects on the final standard deviations. For the symmetric generator, however, the strong equal-power assumption leads to qualitatively different results as will be seen below.
From squaring Eqs. 11, 12, the power in the left channel is (1+ε)P1, and the power in the right channel is (1-ε)P1, where ε is the error that occurs because x1 from generator N1 and x2 from generator N2 are not orthogonal,
| (26) |
and is given by Eq. 21.
The correlation for zero lag can be computed by substituting Eqs. 11, 12 into Eq. 1,
| (27) |
The important difference between the symmetric generator and the asymmetrical generators is that the error ε cancels in computing the numerator of Eq. 27 for the symmetric generator. Also, as for the asymmetric two-generator, the correlation involves only a single stochastic function, ε, and our analytic approach in terms of an integral over a density would again be legitimate.
As for the other generator methods, one can calculate an expected value of ρ(0) assuming that the overlap is zero, i.e., ε = 0. That expected value can be taken as a initial target value, defined as tg = 2α2 − 1. An improved target value will emerge below. Then because Eq. 27 can be written in terms of the initial target value. The correlation for zero lag is
| (28) |
The initial target correlation can be any value − 1 ≤ tg ≤ 1, but the sign of tg is a trivial factor in Eq. 28, and it is enough to consider only positive values.
The variance is smaller for the symmetric generator than for the asymmetric generator because an expansion of Eq. 28 is quadratic in the small quantity ∕P1, but an equivalent expansion for the asymmetric generator described by Eq. 20 is linear. Computer experiments were done to calculate moments of ρ(0). The experiments showed that the standard deviation of ρ(0) is dramatically smaller than for the asymmetrical generators given the strong equal-power assumption.
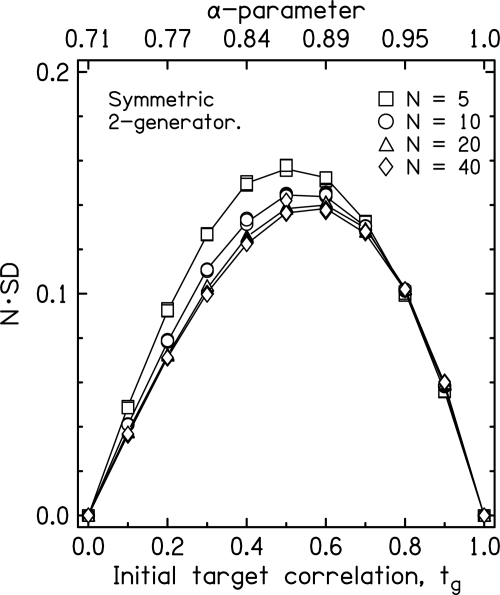
Because appears as the square in Eq. 28, the standard deviation of ρ(0) decreases as 1∕N for the symmetric generator. Therefore the standard deviation over 100 000 trials shown in Fig. 5 is plotted as N · SD. By contrast, the standard deviation decreased only as for the asymmetrical generators and for generators without the strong equal-power assumption. As shown in Fig. 5, the SD vanishes for both limits of targeted correlation.
Figure 5.
Symbols show the standard deviations, SD, computed for the symmetric generator, plotted as N · SD, as a function of the initial target value tg. Each symbol actually appears four times, representing four different random starts of the numerical experiment. The very small values of SD are a result of the strong equal-power assumption.
Equation 28 shows that in the symmetric generator method, the computed value of ρ(0) is guaranteed to be greater than the initial target value. No such guaranteed bias occurs for the asymmetrical generators. Because ρ(0) computed for the symmetric generator is greater than tg, it is possible to correct the value of tg to target a desired correlation more successfully. Analytically, we know that the function ∕P1 is normally distributed with variance 1∕(2N), so that 1∕(2N) is the expected value of the square of this function, as it appears in Eq. 28. Therefore the experimenter will be able to target a desired correlation, ρo, more successfully by adjusting tg so that it satisfies the equation
| (29) |
i.e.,
| (30) |
In practical terms, that means choosing α such that
| (31) |
where ρo is the desired correlation, and β2 = 1 − α2 as usual.
FINITE-LAG CROSS-CORRELATION
The finite-lag correlation function ρ(τ) is more general than the zero-lag function. It is of particular value in models of sound localization where the peak of the correlation occurs at a value of lag τ that represents the interaural time difference (ITD). [See, for example, Rakerd and Hartmann (2010).]
The maximum value of ρ(τ) over all allowed values of τ is defined as the coherence, γ. Typically, τ is allowed to range from −1 to 1 ms (Hartmann, Rakerd, and Koller, 2005) because this range approximately corresponds to the range of interaural delays that a listener experiences in free field. That range is a standard in architectural acoustics (Beranek, 2004). Wider ranges, including very wide ranges, e.g., −9 to 9 ms, have been explored psychophysically (Blodgett et al., 1958; Langford and Jeffress, 1964; Mossop and Culling, 1998). The practical value of the coherence measure is that if the coherence is high, a listener receives strong ITD localization cues even if the zero-lag correlation is small.
Because of the ±1 ms range, calculations of the finite-lag correlation are necessarily somewhat specific. They depend on details of the noise. In the calculations that follow, noise bands were centered on 500 Hz, the duration of the noise was 1 s, and the spacing of the N frequency components was 1 Hz. In principle, calculations are also sensitive to computational resolution. In the calculations below, the time increments were 10 μs, and the coherence was taken to be the largest value found on 10-μs intervals of τ without further optimization.
Asymmetric two-generator method
With the strong equal-power assumption, the finite-lag correlation function in Eq. 6, becomes
| (32) |
Expectations
Because noises x1 and x2 are independent, the expected value of is zero for any τ. Then from Eq. 32, ρ(τ) is given by the autocorrelation function, ρ(τ) = α ∕P1. The coherence is the maximum of ρ(τ), but the maximum value of occurs for τ = 0, i.e., it is . Then because = P1, the expected coherence is γ = α, the same answer as for the zero-lag function. However, if is not zero, the actual coherence will be greater than α, especially if α is close to zero because there are many opportunities to maximize over the range of τ.
Experiments
Numerical experiments for ρ(τ) were done by substituting Eqs. 14, 15 with random amplitudes and phases into Eq. 32. The target coherence values were limited to 0 ≤ α < 1. Calculations for α < 0 would make little sense in our context where the coherence is defined as a maximum value. In the experiments, a coherence was computed for each two-channel noise in a large ensemble, and the squared deviation about the average value of coherence was used to find the standard deviation. The experiments showed that the results were insensitive to the distribution of the amplitudes. When the Rayleigh-distributed amplitudes were replaced by equal amplitudes (An = Bn = 1), the means and standard deviations of the computed coherences changed somewhat, but the change was no bigger than the change caused by using different sets of random phases and Rayleigh-distributed amplitudes.
Because the coherence computed from the noise pairs is a maximum value, it is inevitable that the computed coherence will be greater than the target coherence—much greater when the target coherence is near zero. The larger the number of components and the larger the value of α, the smaller is the discrepancy between the target coherence and the ensemble mean of the computed coherence, γ, averaged over many noise pairs. When N ≥ 21 and α ≥ 0.6, the discrepancy is about 1% or less. The standard deviation of the distribution of γ is not a monotonic function of α. It is maximum for α in the range 0.2 to 0.4. The standard deviation for α greater than or equal to 0.6 can be computed using the zero-lag limit, as noted in Sec. 6A4 below.
Target correlation of zero
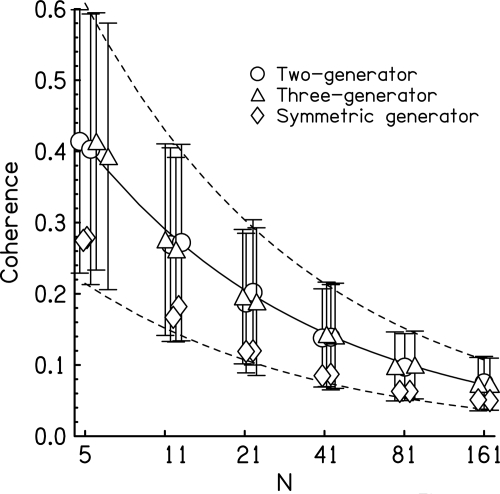
The coherence from numerical experiments on the finite-lag correlation in the important case of α = 0 (completely independent left and right noises) is plotted in Fig. 6. The figure shows that the ensemble-average coherence is well approximated by the formula 〈γ over the range 5 ≤ N ≤ 161. This formula is likely to continue to hold good for N > 161, and it is likely to fail for N < 5. For N = 5, the ensemble average coherence is about 0.4, as indicated by the formula, but for individual noise pairs the coherence can be larger than 0.9. Such large values of coherence from waveforms that are constructed to be entirely incoherent arise as a consequence of the maximizing computation, required by the definition of finite-lag coherence. When lag τ can be varied, there are many opportunities to obtain a large value of the correlation function, and the coherence is the largest of these.
Figure 6.
Computed coherence for finite-lag correlation as a function of the number of spectral components when the target coherence is zero. Five hundred waveforms were computed for the three different generators. Symbols show the average, and error bars are two standard deviations in overall length. Symbols are in pairs illustrating two different random starts. They are slightly jogged horizontally for clarity. The solid line is the function 0.92∕, and the dashed lines are the same function plus and minus 0.44∕.
The large variability for α = 0 can be expected to have experimental consequences. Akeroyd and Summerfield (1999) devised a binaural analog to gap detection using noise that targeted α = 0. Such noise is normally called “completely uncorrelated” in the literature and is given the designation “Nu.” Because the bands were narrow, the effective value of N was small, and one expects that large values of coherence can occur by chance in individual noises. Similar effects would be expected in the narrow-bandwidth Nu experiments by Pollack and Trittipoe (1959a,b) and Gabriel and Colburn (1981). For larger bandwidth (e.g., Schubert and Wernick, 1969; Perrott and Buell, 1982) equivalent to larger values of N, γ is more narrowly distributed about the mean. The numerical experiments show that the standard deviation of the distribution of γ for α = 0 is approximately 0.44∕, as shown in Fig. 6.
Approaching the zero-lag limit
When α is large, the numerator of Eq. 32 for ρ(τ) is dominated by α , and this term is largest when τ = 0. Therefore the coherence is given by ρ(0). Numerical experiments with the general ρ(τ) showed that the coherence is accurately given by ρ(0) for α greater than or equal to 0.6. This useful simplifying result appears to hold good for all values of N tested, namely N ≥ 5.
Three-generator method
Everything that was written in the preceding text about coherence for the two-generator method holds good for the three-generator method as well. Figure 6 compares calculations for the two methods for the special case that the target correlation is zero (α = 0). Each symbol appears twice, corresponding to two different random starts of the computation.
Symmetric-generator method
The coherence values for the symmetric generator are also shown in Fig. 6, plotted as diamonds. They are considerably closer to the target value of zero than the values for the asymmetrical generators, but the standard deviations (not shown) are the same as for the asymmetrical generators as shown by the error bars.
CAVEATS
The equations for the overlap integrals in terms of component amplitudes and phases [e.g., Eq. 18 for are valid if the signal duration and the component frequencies are matched (Hartmann and Wolf, 2009). For instance, a duration of 1 s is matched by component frequencies that are integer numbers of hertz, i.e., components can be separated by 1 Hz, or by 2 Hz, etc. A duration of half a second can be matched only if the frequencies are all integer multiples of 2, and so on. Matching means that the sines and cosines of the component frequencies are all orthogonal on a rectangular time interval equal to the duration. The equations that depend on matched components, like Eq. 18, greatly simplified the computations of this article and made it easy to average over 100 000 trials. The results of these simplified computations were tested by long computations, computing waveforms as functions of time using integer frequencies, and then calculating their correlations over a duration of 1 s. These long computations and the simplified computations agreed perfectly, validating the simplified calculations. However, the simplified calculations were valid only for matched conditions.
If the component frequencies are not matched to the duration, the relationship between the targeted correlation and the actual correlation becomes much more variable. This effect was studied by repeating the long calculations for ρ(0) in the asymmetric two-generator method using time-dependent waveforms and successive-integer frequencies as before, but reducing the duration of the signals to TD = 500 ms, 250 ms,… 32 ms. The plots of SD × had the same shape as shown in Fig. 3, but instead of a limit of 1∕ for α = 0, the limit increased monotonically with decreasing duration up to a value near 2.7 for TD = 32 ms.
For the results of this article to apply to digitally generated noises, the frequencies in the noises must match the duration. Matching is all that is required for the standard deviation to be well approximated by the generally useful function shown by the dashed line in Fig. 3. For instance, if the duration is 250 ms and the frequencies are all integer multiples of 4 Hz, the standard deviation agrees with the heavy dashed line in Fig. 3 when the number of components is 20 or greater.
SUMMARY
Partially correlated noise has been used in the study of binaural hearing to control the cross correlation. It is generated by adding the outputs of independent elemental noise generators. With digital methods, Gram–Schmidt orthogonalization can be used together with the strong equal-power assumption to control the cross correlation precisely. However, for experiments using analog generators, or for those experiments using digital techniques without orthogonalization, the cross correlation is not precisely controlled. To design new experiments or to evaluate old experiments from the literature, it is helpful to know the variability in cross correlation that can be expected when the experiment targets a particular correlation.
In this article, the variability was computed for the three noise generation methods that have been used in psychoacoustical and physiological research: the asymmetric two-generator, the asymmetric three-generator, and the symmetric generator. Computations were done using two different assumptions about the power of the elemental generators. With the weak equal-power assumption, the elemental generators have equal power only on the ensemble average. Numerical experiments discovered that all three generation methods lead to the same standard deviation in the correlation, varying as 1∕ in the limit of large N, where N is the number of spectral components. That standard deviation is shown as a function of the target coherence in Fig. 2 and by the vertically hatched regions in Figs. 34.
With the strong equal-power assumption, the elemental generators have equal power in every experimental trial. That assumption led to considerable mathematical simplification, and analytic results could be obtained leading to insight into the numerical results. The numerical experiments found that the standard deviation of the correlation was the same when the amplitudes of the spectral components were Rayleigh distributed and when they were all made equal. Figure 3 is an example. The experiments found that the standard deviation of the correlation was approximately the same for both of the two asymmetrical generators, as shown in Fig. 4.
With the strong equal-power assumption, the symmetric generator led to uniquely small standard deviations, varying as 1∕N. The difference between the symmetric generator and the asymmetric generator is striking. Example for the asymmetric two-generator: If the target correlation is 0.2 and the number of components is N = 9, then from Fig. 3, SD = 0.68, so that the standard deviation is 0.23. Example for the symmetric generator: If the target correlation is again 0.2 and the number of components is again N = 9, then from Fig. 5 9SD = 0.075, so that the standard deviation is 0.0083, smaller by a factor of 28.
This article briefly considered the finite-lag cross correlation function, particularly the coherence, which is the maximum cross correlation across all allowed values of the lag. The coherence can differ hugely from targeted values when the targeted value of coherence is small. When the targeted value is greater than 0.6, the statistical variability of the coherence becomes the same as for zero lag. This leads to the useful result that the standard deviation of the coherence becomes the same as the standard deviation for cross correlation.
As noted in Sec. 7, all the calculations presented in this article depend on matched conditions. The spacing between the frequency components in the noise waveform must be an integer multiple of the inverse of the noise duration.
ACKNOWLEDGMENTS
We thank Shujie Ma from the Michigan State CSTAT for an interesting discussion about the β distribution. Dr. Les Bernstein and Dr. Tino Trahiotis commented usefully on an early draft of this article. We are grateful to two anonymous reviewers for helping to make the presentation more readable. This work was supported by the NIDCD Grant No. DC-00181 and by the Air Force Office of Scientific Research Grant No. 11NL002.
Footnotes
Axis labels in the articles by Pollack and Trittipoe (1959a,b) are given as the square of the coherence. As noted by Jeffress and Robinson (1962), these labels should actually be the coherence itself. Consequently, in viewing the plots in those two articles, the reader should simply ignore the exponent 2 in the axis labels.
The calculations in Fig. 3 agree with Fig. 1 in Shackleton et al. (2005) in the low-coherence limit. As expected, this agreement is obtained when our value of N is equal to their value of WT, e.g. N = WT = 20. As the targeted value of coherence increases, the standard deviation computed by Shackleton et al. drops somewhat less rapidly than shown in our Fig. 3, a difference that might be caused by different forms of the equal-power assumption. The discrepancy in correlation is always less than 0.04.
Moments are defined in Hartmann (1997).
References
- Akeroyd, M. A., and Summerfield, A. Q. (1999). “A binaural analog of gap detection,” J. Acoust. Soc. Am. 105, 2807–2820. 10.1121/1.426897 [DOI] [PubMed] [Google Scholar]
- Albeck, Y., and Konishi, M. (1995). “Responses of neurons in the auditory pathway of the barn owl to partially correlated binaural signals,” J. Neurophysiol. 74, 1689–1700. [DOI] [PubMed] [Google Scholar]
- Beranek, L. L. (2004) Concert Halls and Opera Houses–Music, Acoustics, and Architecture (Springer, New York: ), pp. 615. [Google Scholar]
- Bernstein, L. R. (1990). “Measurement and specification of the envelope correlation between two narrow bands of noise,” J. Acoust. Soc. Am. 88, S145–S146. 10.1121/1.400108 [DOI] [PubMed] [Google Scholar]
- Bernstein, L. R., and Trahiotis, C. (1996). “On the use of the normalized correlation as an index of interaural envelope correlation,” J. Acoust. Soc. Am. 100, 1754–1763. 10.1121/1.416072 [DOI] [PubMed] [Google Scholar]
- Bernstein, L. R., and Trahiotis, C. (2008). “Binaural signal detection, overall masking level and masking interaural correlation: Revisiting the internal noise hypothesis,” J. Acoust. Soc. Am. 124, 3850–3860. 10.1121/1.2996340 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blodgett, H. G., Jeffress, L. A., and Taylor, R.W. (1958). “Relation of masked thresholds to signal duration for various interaural phase combinations,” Am. J. Psychol. 71, 283–290. 10.2307/1419217 [DOI] [PubMed] [Google Scholar]
- Blauert, J. (1996) Spatial Hearing; The Psychophysics of Human Sound Localization, revised ed. (MIT Press, Cambridge, MA: ), pp. 239. [Google Scholar]
- Blauert, J., and Lindemann, W. (1986). “Spatial mapping of intracranial auditory events for various degrees of interaural coherence,” J. Acoust. Soc. Am. 79, 806–813. 10.1121/1.393471 [DOI] [PubMed] [Google Scholar]
- Coffey, C. S., Ebert, C. S., Marshall, A. F., Skaggs, J. D., Falk, S. E., Crocker, W. D., Pearson, J. M., and Fitzpatrick, D. C. (2006). “Detection of interaural correlation by neurons in the superior olivary complex, inferior colliculus, and auditory cortex of the unanesthetized rabbit,” Hear. Res. 221, 1–16. 10.1016/j.heares.2006.06.005 [DOI] [PubMed] [Google Scholar]
- Culling, J. F., Colburn, H. S., and Spurchise, M. (2001). “Interaural correlation sensitivity,” J. Acoust. Soc. Am. 110, 1020–1029. 10.1121/1.1383296 [DOI] [PubMed] [Google Scholar]
- Edmonds, B. A., and Culling, J. F. (2009). “Interaural correlation and the binaural summation of loudness,” J. Acoust. Soc. Am. 125, 3865–3870. 10.1121/1.3120412 [DOI] [PubMed] [Google Scholar]
- Gabriel, K. J., and Colburn, H. S. (1981). “Interaural correlation discrimination I. Bandwidth and level dependence,” J. Acoust. Soc. Am. 69, 1394–1401. 10.1121/1.385821 [DOI] [PubMed] [Google Scholar]
- Goupell, M. J., and Hartmann, W. M. (2006). “Interaural fluctuations and the detection of interaural incoherence: Bandwidth effects.” J. Acoust. Soc. Am. 119, 3971–3986. 10.1121/1.2200147 [DOI] [PubMed] [Google Scholar]
- Hall, J. W., Buss, E., and Grose, J. H. (2006). “Binaural comodulation masking release: Effects of masker interaural correlation,” J. Acoust. Soc. Am. 120, 3878–3888. 10.1121/1.2357989 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartmann, W. M. (1997) Signals, Sound, and Sensation (Springer, New York: ), pp. 386. [Google Scholar]
- Hartmann, W. M., Rakerd, B., and Koller, A. (2005). “Binaural coherence in rooms.” Acta Acustica 91, 451–462. [Google Scholar]
- Hartmann, W. M., and Wolf, E. M. (2009). “Matching the waveform and the temporal window in the creation of experimental signals,” J. Acoust. Soc. Am. 126, 2580–2588. 10.1121/1.3212928 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang, Y., Wu, X., and Li, L. (2009). “Detection of the break in interaural correlation is affected by interaural delay, aging, and center frequency,” J. Acoust. Soc. Am. 126, 300–309. 10.1121/1.3147504 [DOI] [PubMed] [Google Scholar]
- Jeffress, L. A., Blodgett, H. C., and Deatherage, B. H. (1962). “Effect of interaural correlation on the precision of centering a noise,” J. Acoust. Soc. Am. 34, 1122–1123. 10.1121/1.1918257 [DOI] [Google Scholar]
- Jeffress, L. A., and Robinson, D. R. (1962). “Formulas for the coefficient of interaural correlation for noise,” J. Acoust. Soc. Am. 34, 1658–1659. 10.1121/1.1909077 [DOI] [Google Scholar]
- Langford, T. L., and Jeffress, L. A. (1964). “Effect of noise cross–correlation on binaural signal detection,” J. Acoust. Soc. Am. 36, 1455–1458. 10.1121/1.1919224 [DOI] [Google Scholar]
- Licklider, J. C. R., and Dzendolet, E. (1948). “Oscillographic scatter plots illustrating various degrees of correlation,” Science 107, 121–124. 10.1126/science.107.2770.121-a [DOI] [PubMed] [Google Scholar]
- Mossop, J. E., and Culling, J. F. (1998). “Lateralization of large interaural delays,” J. Acoust. Soc. Am. 104, 1574–1579. 10.1121/1.424369 [DOI] [PubMed] [Google Scholar]
- Perrott, D. R., and Buell, T. N. (1982). “Judgements of sound volume: Effects of signal duration, level and interaural characteristics on the perceived extensity of broadband noise,” J. Acoust. Soc. Am. 72, 1413–1417. 10.1121/1.388447 [DOI] [PubMed] [Google Scholar]
- Plenge, G. (1972). “On the problem of inside-the-head locatedness,” Acustica 26, 241–252. [Google Scholar]
- Pollack, I., and Trittipoe, W. J. (1959a). “Binaural listening and interaural noise cross-correlation,” J. Acoust. Soc. Am. 31, 1250–1252. 10.1121/1.1907852 [DOI] [Google Scholar]
- Pollack, I., and Trittipoe, W. J. (1959b). “Interaural noise correlations: examination of variables,” J. Acoust. Soc. Am. 31, 1616–1618. 10.1121/1.1907669 [DOI] [Google Scholar]
- Rakerd, B., and Hartmann, W. M., (2010). “Localization of sound in rooms. V. Binaural coherence and human sensitivity to interaural time differences in noise,” J. Acoust. Soc. Am. 128, 3052–3063. 10.1121/1.3493447 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson, D. E., and Jeffress, L. A. (1963). “Effect of varying the interaural noise correlation on the detectability of tonal signals,” J. Acoust. Soc. Am. 35, 1947–1952. 10.1121/1.1918864 [DOI] [Google Scholar]
- Schneider, B. A., Bull, D., and Trehub, S. E. (1988). “Binaural unmasking in infants,” J. Acoust. Soc. Am. 83, 1124–1132. 10.1121/1.396057 [DOI] [PubMed] [Google Scholar]
- Schubert, E. D., and Wernick, J. (1969). “Envelope versus microstructure in the fusion of dichotic signals,” J. Acoust. Soc. Am. 45, 1525–1531. 10.1121/1.1911633 [DOI] [PubMed] [Google Scholar]
- Shackleton, T. M., Arnott, R. H., and Palmer, A. R. (2005). “Sensitivity to interaural correlation of single neurons in the inferior colliculus of guinea pigs,” J. Assn. Res. Otolaryngol. 6, 244–259. 10.1007/s10162-005-0005-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Heijden, M., and Trahiotis, C. (1997). “A new way to account for binaural detection as a function of interaural noise correlation,” J. Acoust. Soc. Am. 101, 1019–1022. 10.1121/1.418026 [DOI] [PubMed] [Google Scholar]
- van der Heijden, M., and Trahiotis, C. (1998). “Binaural detection as a function of interaural correlation and bandwidth of masking noise: Implications for estimates of spectral resolution,” J. Acoust. Soc. Am. 103, 1609–1614. 10.1121/1.421295 [DOI] [PubMed] [Google Scholar]