Single-Trial Neural Correlates of Arm Movement Preparation

Summary

The process by which neural circuitry in the brain plans and executes arm movements is not well understood. Prevailing data (single-neuron and field potential recordings) do not reveal how individual neurons’ activities are coordinated within the population, and thus inferences about how the neural circuit forms a motor plan have been indirect. Here we frame and test a new ‘initial condition hypothesis’ in which the reaction time (RT) of upcoming movements may be predicted on each trial using neurons’ moment-by-moment firing rates and rates of change of those rates. Using microelectrode array recordings from premotor cortex of monkeys performing delayed-reach movements, we compare such single-trial RT predictions to those of other theories. The initial condition hypothesis model can explain approximately four-fold more RT variance than the best alternative method. Thus, the initial condition hypothesis elucidates a new view of the relationship between single-trial preparatory neural population dynamics and single-trial behavior.

In 1991, Leroy Burrell set a world record for the 100 m dash with a spectacular time of 9.90s, stunning the pre-race favorite Carl Lewis, who finished second with a time of 9.93s. It was later noted, however, that Burrell was not the faster runner. Rather, his reaction time to the gun that marked the start of the race was much shorter than Lewis’s: a hair-trigger 117ms against a relatively lethargic 166ms. Without this difference, Lewis would have won handily. Why was Carl Lewis so much slower than Leroy Burrell to start the race that day?

Of course, non-athletes also often prepare movements in anticipation of events: while preparing to swat a fly, to press a car accelerator when a traffic light turns green, or to select the appropriate button while playing a video game. Sometimes we are slow in reacting and sometimes we move before we are fully ready. This inability to precisely time the onset of a movement can often be extremely frustrating.

What is the cause of this imprecision? Presumably, it is related to the operation of planning and executing movements. Voluntary movements are believed to be “prepared” before they are executed (e.g., Wise, 1985). Important evidence for this belief comes from behavioral tasks in which a delay period separates a stimulus instructing the goal of a reaching movement from a subsequent ‘go’ cue. Reaction time (RT) is the time elapsed from the go cue until movement onset in these delayed-reach tasks, and RT is shorter when delays are longer (e.g., Rosenbaum, 1980; Riehle & Requin, 1989). This suggests that a time-consuming preparatory process is given a head start by the delay period. How is this process reflected in neural activity, and why should the preparation take time? One view, drawn by analogy to the oculomotor system (Hanes & Schall, 1996), would be that neural activity in a subpopulation of cells might be increased in order to reside near a threshold level, and that the initiation of movement would follow from the subsequent crossing of this threshold. Thus, if the distance of preparatory neural activity from this threshold were measured experimentally, it should correlate inversely with RT (Erlhagen & Schoner, 2002).

Neurons in a number of brain areas, including dorsal premotor cortex (PMd), exhibit delay-period activity changes according to the direction, distance, and speed of the upcoming movement (Messier & Kalaska, 2000; Churchland et al., 2006b). Electrical disruption of this activity in PMd largely erases the RT savings earned during the delay (Churchland & Shenoy, 2007b). PMd is thus broadly implicated in arm movement preparation. In support of the “rise-to-threshold” hypothesis, higher firing rates in PMd are often associated with shorter RTs (Riehle & Requin, 1993; Bastian et al., 2003), although Crammond & Kalaska (2000) found that peak firing rates after the go cue, when the movement is presumably triggered, were on average lower after an instructed delay.

We recently proposed an alternative hypothesis (Churchland et al., 2006c), illustrated in Fig. 1. The “optimal subspace hypothesis” assumes that the movement produced is a function of the state of preparatory activity (p_go) at the time the movement is externally triggered. For each possible movement there would be an “optimal subspace”: a subset of possible population firing rates that are appropriate to generate a sufficiently accurate movement. Motor preparation might therefore be an optimization in which firing rates are brought from their initial state to a state within the subregion of adequately planned movements (gray region with green outline in Fig.1A). Each point in this optimal subregion corresponds to movements that are planned equally well for the purpose of completing the behavioral task and receiving reward. Thus, firing rates would remain within this optimal region while awaiting the cue to initiate movement, so as to preserve the appropriately-prepared state. This contrasts with the rise-to-threshold model, where the crossing of an appropriate threshold actually triggers the movement. The most obvious predictions of this optimal subspace hypothesis are well-established: delay-period firing rates are concentrated in a subregion of the accessible space, and this subregion is different for each instructed movement. However, if evidence could be found to show that the brain actively attempted to contain firing rates within that subregion, and that a penalty was paid for failing to do so, then the optimal subspace hypothesis could prove to be a valuable framework for further investigation of arm movement preparation.

Figure 1.

Illustrations of the optimal subspace hypothesis (A), the elaborated optimal subspace hypothesis (B), and the initial condition hypothesis discussed in this work (C). (A) The configuration of firing rates is represented in a state space, with the firing rate of each neuron contributing an axis, only three of which are drawn here. Under this hypothesis the goal of motor preparation is to optimize the configuration of firing rates so that it lies within the optimal subregion for the desired movement (small gray region with green outline). The formation of a motor plan for a given trial is represented by an individual gray trace. Adapted from Churchland et al. (2006c). (B) The hypothesis extended to include the entire trial. The across-trial variance, represented in this illustration by the area of the colored ellipses, reduces from target onset (red) to go cue (green) to movement onset (blue). Bold dots represent individual trials at target onset, go cue, and movement onset. P_go marks the neural state of a particular trial at the time of the go cue. Adapted from Yu et al. (2009) and Churchland et al. (2010). (C) In this work, we hypothesize that if the neural state on a given trial was far along the mean neural trajectory across all trials to that target, then that trial would have a short reaction time. This is possible due to the neural activity being closer to a movement threshold (dashed line). This corresponds to a given trial’s RT correlating with α (length of bold line segment), which is the projection of P_go along p⁻ _go+Δt. Vector P_go connects the mean neural activity at the go cue across all trials to a given target (green asterisk) to the neural activity measured at the go cue on a given trial. Vector P⁻ _go+Δt connects the mean neural activity at the go cue across all trials to a given target (green asterisk) to the mean neural activity at some offset after the go cue (Δt=100ms; see Fig. S1B). Bold line is the mean neural trajectory. Colored asterisks are the mean neural state across all trials at target onset, go cue, and movement onset.

Three recent experiments have probed the process of motor preparation further, yielding averaged measurements consistent with the optimal subspace hypothesis, and motivating the present study of single-trial neural correlates of behavior. First, we found that movement speed is predicted by the state of preparatory activity at the time of presentation of the go cue (Churchland et al., 2006a,b). Second, we found that the across-trial FanoFactor (FF; the variance in firing rate normalized by the mean rate) in neural activity decreases following target onset and results in low across-trial FF at the time of the go cue (Churchland et al., 2010). In Fig.1B, this is closely related to the reduction of across-trial scatter from the time the target appears (red dots) to the time that the go cue appears (green dots). Consistent with the idea that the brain actively attempts to bring firing rates to a focal subregion during the planning period, the variance between trials with RTs shorter than the median value was smaller at the go cue (lower FF) than that between trials with RTs in the upper half of the distribution (Churchland et al., 2006c). Finally, when the exact state of the preparatory activity is perturbed with electrical microstimulation, which most likely moves p_go in Fig. 1B to outside of the optimal subregion, we found that the RT savings created by the delay period (i.e., presumed motor preparation) is largely erased (Churchland & Shenoy, 2007a).

These initial experiments studied the process of preparation by averaging measures across multiple trials. Their consistency with the optimal subspace hypothesis motivated us to now ask how individual movements are prepared on individual trials, and how the initiation of the movement is related to transition of activity from preparatory to movement states. More specifically, we asked how the preparatory activity at the time of the go cue is related to the reaction time on each individual trial.

Our earlier work (Yu et al., 2009; Churchland et al., 2010b) revealed that neural activity across different trials to the same reach target becomes progressively more stereotyped during the planning and movement periods (Fig.1B). We wondered if we could exploit this the mean. To see how this might be possible, consider the average neural activity across all trials to the given target, shown by the bold trace in Fig. 1C. This can be viewed as a low-dimensional representation of the mean neural activity that creates the motor plan for, and generates the arm movement to, a given target. We hypothesized that if the point corresponding to the neural population activity were farther along this mean path on a given trial at the time of the go cue, but still within the optimal subspace, then that trial would have a correspondingly fast RT (compare points labeled ‘shortRT’ versus ‘longRT’ in Fig.1C). This view is consistent with the hypothesis that there exists a boundary along the mean neural trajectory (dotted line in the figure), which is crossed at the initiation of a movement. Importantly, as discussed below, this is a different “threshold” than that of the rise-to-threshold models. This view augments the optimal subspace hypothesis, which does not suggest that different neural states within the optimal subregion would correspond to different RTs. We call this augmented view the ‘initial condition hypothesis’, as it is consistent with the idea that differences in RT reflect the different times taken for the motor network to evolve from each state of the optimal subregion to the states associated with motor initiation.

To test this hypothesis we conducted experiments with rhesus monkeys performing a delayed-reach task, while recording from tens to hundreds of neurons simultaneously (Churchland et al., 2007). Our subjects performed multiple reaches to different targets throughout the workspace (see Methods for details). The task design is shown in Fig. 2. Simultaneous measurement of multiple neurons is essential to gather enough information about the population preparatory state on a millisecond timescale to make it feasible to account for individual trial RTs. We found that visualizing these neural data in a lower dimensional space helped reveal a stereotyped “neural trajectory” (Yu et al., 2009; Churchland et al., 2010b) and helped lead to a new neural measure(based on our initial condition hypothesis) that predicts roughly four times more RT variance than previously-published methods.

Figure 2.

Task design and neural data. (A) Monkeys performed a delayed-reach task, similar to that described previously Santhanam et al. (2006) and Churchland et al. (2006c) while simultaneous neural data were recorded via a 96-channel microelectrode array (Blackrock Microsystems, Salt Lake City, Utah). (B) One of 53 trials to a given target (G20040123, target 5, which is at a distance of 60mm and angle 225°). Gray corresponds to the baseline period (before a target is presented), red to the delay period (after target presentation but before go cue), green to the reaction time period (after go cue but before movement onset), and blue to movement period (after recorded movement onset). A spike raster is shown, which is organized with one neuron per row and with each tick corresponding to a spike time for a given neuron. Neurons are organized by preferred direction as determined by plan period activity. Hand and eye traces are also shown.

Results

Neural Activity Predicts Trial-by-Trial RT

A low dimensional representation of neural data from our experiments is shown in Fig. 3. Panel A shows neural data from three reaches to a given target, while panel B shows all of the 49 reaches. Dimensionality reduction was performed using Gaussian-process factor analysis(GPFA); see Experimental Procedures for details (also Yu et al. (2009); Churchland et al. (2010b)). Note that qualitatively similar results are obtained when using principal components analysis (PCA), but in general PCA can be erroneously dominated by just a few high firing-rate neurons (Yu et al., 2009). As in the illustrations in Fig.1, the neural activity seems to behave in a stereotyped way during motor planning and execution. Notably, the three trials shown are in approximately the same location in the GPFA state-space at the time of target onset (red points in Fig. 1A). The neural states during all three trials then move together along the second latent dimension during the plan period (red traces) before changing direction after the go cue is given (green and blue traces are along a different direction than red traces). This stereotypy is also evident even when looking at all trials to a given reach target (Fig.3B). Furthermore, the drift speed in neural space (calculated by measuring the distance traveled per time step along the mean neural trajectory) also has a stereotyped shape and decreases markedly after about 200ms, which is the approximate presumed length of time required for motor preparation (Fig.3C).

Figure 3.

Low-D representations of recorded neural data and correlations of single-trial RT predictions with RT. GPFA reductions of neural data recorded for three randomly selected (A) and for all 49 (B) preparations and movement initiations to the same target (G20040123, target 13, which is at a distance of 100mm and angle 45°). Same color code is used here as in the previous figure. The neural state at the time of target onset are bold red dots; at the time of the go cue are bold green dots; at the time of measured movement onset are bold blue dots. Lighter dots are separated by 20ms. (C) Normalized path neural speed in GPFA space as a function of time relative to target onset. Same color code used here as in previous figures. Dark black trace is the mean speed across all trials. Note that this speed increases after target onset and decreases to near zero until the go cue (green portion of traces). (D) Histograms of correlations coefficients of neural metric described in Fig. 1C with Δt = 100ms across all reach targets performed by two monkeys (G and H). The medians of both distributions (marked with arrows) are not 0 with p<0.01 (Wilcoxon sign-rank test). Colored bars represent those correlations that are statistically significant (p<0.05).

As described above, we reasoned that the degree to which the neural state had advanced by the time of the go cue along the mean neural path across similar trials would be predictive of RT (Fig. 1C). To test this, we calculated the projection of an individual trial’s neural activities along the mean neural path (the ‘mean neural trajectory’) for the appropriate target. This is shown in Fig. 1C as α, which is the length of the bold line segment. This segment is the projection of the vector p_go along the vector p⁻_go+Δ_{_t}; p_go links the target’s mean neural activities at the go cue to the activity on a single trial at the go cue, while p⁻_go+Δ_{_t} links the target’s mean neural activities at the go cue to the mean neural activities at a time Δt later for this target.

This projection was correlated with the reaction time for all trials to the same target on a trial-by-trial basis. The offset Δt was chosen to maximize the average RT variance explained across all datasets (100 ms for our data; see Fig. S1B). The exact Δt used does not appear to be critical, as any from of a range of values yields similar results (Fig. S1B). This analysis and all subsequent analyses were performed without dimensionality reduction so as to preserve complete information about firing rates from all neurons recorded.

Histograms of correlation coefficients across all reach targets for both monkeys are shown in Fig.3D. For both monkeys, the histograms are shifted significantly to the negative values, with medians less than zero (p<0.01; Wilcoxon signed-rank test). This is consistent with the hypothesis that trials with neural activities that are farther along the mean neural trajectory at the time of the go cue have shorter RTs, which predicts that correlation coefficients should be negative. Thus, these data are consistent with the hypothesis as depicted in Fig. 1C.

We performed several controls, as described in the Supplementary Materials (Fig. S1), to rule out some alternative hypotheses, as well as potential artifacts in the experimental design or analysis. Specifically, we found that a model based on the distance between the neural state and an arbitrary reference point performed more poorly (panels A,B); our results did not depend on the inclusion of multi-neuron units(panel C and qualititive observations that spike sorting was of good quality); subjects remained motivated during the planning period (panels D, E); the smoothing used to create continuous firing rates from spike times did not introduce an artifact (panelF); the results could not be explained by a systematic change of neural position with delay period (panelG); the results could not be explained by small anticipatory arm movements during the delay period (panels H, I, J); nor by small muscle contractions as measured by EMG (panels J, K, L).

The results of the previous section show that the degree to which the neural activity has progressed along the average neural trajectory by the time of the go cue (the ‘neural position’) is predictive of RT trial-by-trial. We further hypothesized that the direction and rate of change of neural activity at the time of the go cue (the ‘neural velocity’) also relates to that trial’s RT.

We investigated this possibility using a similar analysis to that above, now correlating the neural velocity at the time of the go cue (v_go) projected onto the mean neural trajectory with RT (Fig.4A). In order to isolate the effects of neural velocity from position, we grouped trials together that had similar neural positions, which was done by further segregating our data by delay period into100 ms bins (justified by results in Fig. S1G). As shown in Fig.4B, for both monkeys the histograms have medians significantly less than zero (p<0.01; Wilcoxon signed-rank test). This is consistent with the hypothesis that the greater the rate of change of neural activity in the direction of the mean neural trajectory at the time of the go cue, the shorter the RT.

Figure 4.

Illustration depicting neural velocity correlate (A) and resulting histogram of cor- relation coefficients when using neural velocity to predict RT for all targets by two monkeys (B). (A) Neural velocity at time t, labeled vt, was defined as (the neural position at t+10ms − position at t − 10ms). The component of the vgo along the mean neural trajectory across trials was correlated with that trial’s RT. (B) Histogram of correlation coefficients from all comparisons of projections of neural velocity with trial-by-trial RT for monkeys G and H when segregating by delay period in 100ms bins. Medians are denoted by arrows and gray bars represent significant correlations (p<0.05). The medians of both distributions (marked with arrows) are not 0 with p<0.01 (Wilcoxon sign-rank test).

We again performed control analyses to rule out alternative hypotheses, as described in the Supplementary Materials (Fig. S2). Specifically, we found that the overall neural speed (i.e., magnitude of velocity) did not provide a stronger correlate with RT; and that the observed correlations did not derive solely from the correlation of neural position and neural velocity to each other (panels A, B).

Comparison with Other Published RT Predictors

We combined both neural position and velocity along the mean neural trajectory at the time of the go cue to construct a multivariate predictor of trial-by-trial RT.

Since the mean neural trajectory changes direction around the time of the go cue (see neural trajectory at times both before and after the go cue. The vector representing the mean trajectory prior to the go cue, p⁻ _go−Δt′, was based on an offset of Δt′ chosen to maximize the average correlation as before (see Fig. S1B). The four resulting covariates (each of neural position and velocity projected onto each of the pre-and post-’go’ directions) were used as inputs to a multivariate linear regression for RT.

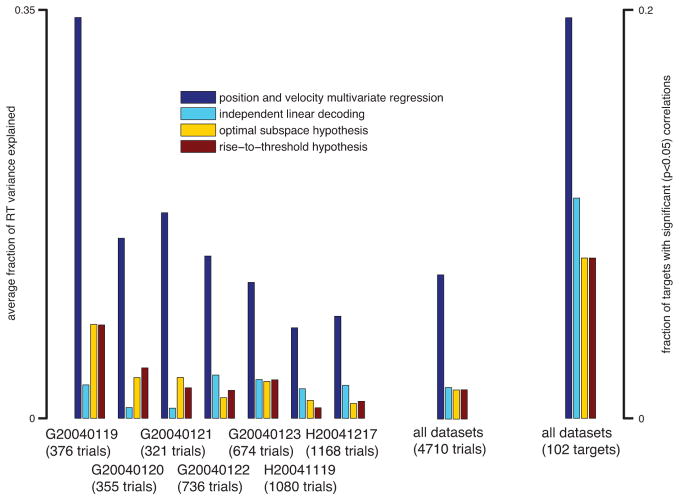
This model was compared with other RT predictors in the literature: the rise-to-threshold hypothesis (the best performing of three different definitions of the rise-to-threshold process is shown); the optimal subspace hypothesis; and an independent linear decoding method (see Experimental Procedures). The percentage of total data variance explained is shown in the bar graph in Fig. 5. This method explained more variance for each dataset, had the most targets with significant correlations, and explained approximately four-fold more variance than the next best model overall.

Figure 5.

Bar graph comparing full multivariate model of RT with other models by dataset and overall. On right is a bar graph of the fraction of targets that had a significant correlation (p<0.05) between the given neural metrics and RT.

In order to ensure that this effect was not simply due to the use of more predictor variables (four in our model versus one in others), we performed the following controls. First, we computed the Bayesian Information Criterion (BIC) for all the models tested (McQuarrie & Tsai, 1998). The BIC is a method for comparing models that use different numbers of parameters, and a lower score corresponds to a better model. Our model had a lower score for every dataset and overall. Second, the full four-parameter model predicts significantly more RT variance than models that use a subset of the parameters by F-test and BIC comparisons (Fig. S3A). Note that since this four-parameter model greatly out performs the one-parameter models mentioned previously, the percent of RT variance explained in the bar graph is much greater than those that would be expected by the histograms of correlation coefficients in Figs. 3 and4. Finally, using just a simple one-parameter model (neural position projected onto the mean neural trajectory after the go cue) also significantly outperforms the other models (Fig. S3B). Therefore, we conclude that our model’s superior RT predictability is not due solely to its use of more parameters.

In sum, the combination of neural state position and velocity provides the best known predictor of single-trial RT, suggesting that the initial condition of the neural state at the time of the go cue is predictive of RT.

Discussion

The precise function and mechanism of the time-consuming process of motor preparation are currently unknown. Evidence has been collected to support at least two different accounts for the neural activity that is observed during such preparation: the rise-to-threshold hypothesis (Riehle & Requin, 1993; Bastian et al., 2003) and, more recently, the optimal subspace hypothesis (Churchland et al., 2006c, 2010a). Our results are consistent with a hybrid view, combining elements of both of these preceding theories. We suggest that during motor preparation the network firing activity in the motor system is brought to a suitable initial condition from which the sequence of neural commands that underlies a movement may efficiently be generated (see also Churchland et al., 2010a). We call this the ‘initial condition hypothesis’.

Our specific findings built on the observation that neural activity consistently follows a movement-dependent trajectory during preparation, at least in tasks as strongly stereotyped as ours. We showed here that the degree to which the neural activity has advanced, and the speed with which it has been advancing, along this trajectory at the time of the go cue contributes substantially to determining RT. Indeed, to our knowledge, the initial condition hypothesis leads to the best known trial-by-trial predictor of fluctuations in RT.

This observation is consistent with the presence of a movement-dependent boundary in firing-rate space, which separates firing-rate states corresponding to preparation from those corresponding to movement, and which is crossed at a fixed time relative to the initiation of the arm movement (Fig. 1C). However, the function of the pre-movement preparatory activity seems not to be simply to rise to a point close to this boundary, as the rise-to-threshold hypothesis would suggest. Instead we note that the firing rates of some neurons fall (rather than rise) after the go cue, and – crucially -- do so even if the firing of those same neurons had increased during the preparatory phase. Thus, the path by which the system approaches this crossing point may be indirect. This observation was reflected in our RT predictions in two ways. First, the directions of the mean neural trajectory before and after the go cue (p⁻ _go−Δt ′ and p⁻ _go+Δt′) differed, so that taking both into account improved RT predictions. Second, three alternative schemes (see Methods) that used the extent of rise or change in firing rates from their baseline values at the time of the go cue to predict RT did not perform as well; results from the best performing of the three are shown in Fig.5. Thus, we conclude that neural activity during movement preparation does not simply rise to, or directly approach, a movement-initiation threshold.

The optimal subspace hypothesis suggests that for each possible desired movement goal there is a set of consistent preparatory network states which all lead to movements that achieve that goal. The role of preparation is then to find one such state, and the possibly involved computation necessary to do so is reflected in the dynamical evolution of the network state from its relatively uncontrolled pre-task value to a point in the optimal subregion. Our results augment this view of preparation. There are many possible mechanisms by which the preparatory activity may determine the activity associated with the execution of the movement, and thus the parameters of the movement itself. Our results suggest that the mechanism is, in fact, embodied in the dynamics of the network. It seems that the network activity evolves smoothly away from the optimal preparatory states when the movement is triggered. Thus, the optimality of the subregion may simply reflect the fact that all states within it form suitable initial conditions from which the dynamics of the network may evolve to generate the appropriate muscular control signals to generate the corresponding movement. All such points may lead to movements that achieve the task goals adequately well. However, those states that happen to fall farther in the direction along which neural activity needs to evolve to generate the movement, and which reflect continued movement in that direction, allow the movement to begin sooner.

Previous results that have provided evidence for the optimal subspace hypothesis remain consistent with this view. Preparatory activity must still reach the subregion of adequate initial conditions, leading to a fall in neural variance across trials during motor preparation (Churchland et al., 2006c). Electrical disruption of a formed plan is very likely to move the state outside the set of suitable initial conditions, requiring further computation to regain a state of preparation and thus increasing RT (Churchland & Shenoy, 2007b). Furthermore, random fluctuations away from the center of the region of optimal initial conditions are, in a high dimensional space, unlikely to be directed towards the movement initiation states, and may indeed bring the state outside the optimal region. Both effects would lead to a tendency towards longer RTs for greater deviations from the center as reported previously (Churchland et al., 2006c) and also seen in single-trial correlations here (Fig. S1B; point at ‘Go Cue’). We see here, however, that when they happen to fall along the direction associated with movement initiation, some displacements away from the center can benefit RT.

The subjects in our (and similar preceding) experiments had extensive training, and so their neural circuitry is likely to have become skilled at performing the optimizations required in planning, resulting in the observed stereotypy of neural trajectories (Fig. 3A,B). We took advantage of this stereotypy to identify the region of suitable initial conditions, and the direction of network state evolution associated with movement initiation. We believe that the initial condition hypothesis should continue to apply under even less stereotyped conditions. However, it remains to be seen whether the relevant network states and directions could be found in tasks where shorter delay periods, varying reach requirements, or lack of training might disrupt the stereotypy of planning and movement. If they cannot be found then the gains in RT prediction may fail to generalize, even if the process of movement initiation is the same.

Furthermore, although our method’s predictive power was significantly greater than that of previously published methods by approximately four-fold, the majority of RT variance remains unexplained (Fig.5). This may be because variance in RT is predicted by factors other than pre-go cortical activiy in highly-trained subjects.

We focused on RT in this study in order to provide a thorough treatment and perform all necessary controls. However, we have performed unreported analyses, including correlations with peak movement speeds, endpoint accuracies, and muscle activities and found similar results (not shown here). Indeed, investigating the relationship between the neural trajectory and other such parameters may reveal correlations important for deeper scientific understanding and of value to brain-machine interface design (Gilja et al. 2011).

As described above, our results are consistent with a boundary separating preparatory states of the network from movement states. It is difficult to tell from our data alone whether an inadvertent crossing of this boundary by the state of the network being monitored might itself cause an initiation of the movement; or whether the trigger for movement lies elsewhere in the brain, with a change in input to the monitored network releasing it from the preparatory phase and consequently allowing the state to evolve across the boundary. This question of causality must be deferred to future work. We note, however, that Carl Lewis had committed a false-start immediately before his losing to Leroy Burrell in 1991. One possible interpretation is that Lewis altered his perceptual threshold of the gun shot to be certain that he would not start prematurely twice in a row. However, it is a tantalizing conjecture that both his false-start and subsequent loss may have been related to an inability to precisely control his neural state while waiting for the cue to run.

Behavioral task

We trained two rhesus monkeys (Macaca mulatta)(G and H) to perform instructed-delay center-out reaches. Animal protocols were approved by the Stanford University Institutional Animal Care and Use Committee. Hand and eye position were tracked optically (Polaris, Northern Digital; Iscan). Stimuli were back-projected onto a frontoparallel screen 30cm from the monkey. Trials (Fig.2A) began when the monkey touched a central yellow square and fixated on a magenta cross. After a touch hold time (200–400ms), a visual reach target appeared on the screen. After a randomized (30–1000ms) delay period, a go cue (fixation and central touch cues were extinguished and reach target was slightly enlarged) indicated that a reach should be made to the target. Fixation was enforced throughout the delay period to control for eye-position-modulated activity in PMd (Cisek & Kalaska, 2004). Subsequent to a brief reaction time, the reach was executed, the target was held (~200ms), and a juice reward was delivered along with an auditory tone. An inter-trial interval (~250ms) was inserted before starting the next trial.

Datasets

We collected and analyzed a number of ‘datasets’. Each dataset consisted of the recording from a single day and included 30–60 single-unit and multiunit recordings. We collected five datasets with monkey G using a 200–1000 ms delay (labeled G20040119–G20040123). For monkey H, two datasets were collected using discrete delays of 750 and 1000 ms with catch trials of 200–500 ms (labeled H20041119) or 200–400ms (H20041217). For all analyses, only non-catch trials were included to ensure that planning had completed (>400ms for monkey G and >700ms for monkey H).

These datasets come from experiments that were designed to address a number of issues, only some of which are considered in the current study. For this reason, the different datasets differ modestly in the task details. For datasets G20040120–G20040123, targets were presented in seven directions (e.g., 45, 90, 135, 180, 225, and 315°) and two distances (e.g., 60 and 100 mm). For dataset G20040119, targets were located in a grid 20 cm by 20 cm at 5 cm increments. Three targets that were covered by the outstretched arm (located on the bottom half of the vertical column in the middle of the grid) were removed, thereby making 22 total possible targets. For monkey H, targets were located at eight possible directions (e.g., 0, 45, 70, 110, 150, 190, 230, 310, and 350°) and two possible distances (e.g., 70 and 120 mm) for H20041119 or one distance (100mm) for H20041217. These variations in design across datasets serve, if anything, to strengthen the result of this study because similar effects were found regardless of the details of the task. Note that some of these datasets are precisely the same ones used in previous studies (Churchland et al. 2006c, Santhanam et al., 2006).

For all datasets, trials that had outlier RTs (>500ms and <150ms) were not analyzed. This comprised a small percentage (<5%) of all trials. We did not have enough statistical power to fully study those trials here and defer those interesting investigations to future work.

Neural recordings

Signals from the implanted array were amplified and manually sorted using the Cerebus system (Blackrock Microsystems) for monkey G or sorted by computer for monkey H using an algorithm described previously (see Supp Mats in Santhanam et al., 2006). Arrays were implanted at the border of PMd and M1 as determined by anatomical landmarks (please see Supp Mats in Santhanam et al., 2006). Units were included in our analysis if (1) they possessed tuned (p<0.05; ANOVA) delay period activity with reasonable modulation [more than ten spikes per second (spikes/s)], and (2) the mean delay-period firing rate was at least one-third the mean rate during the movement. For this comparison, delay-period rate was averaged over the delay period, excluding the first150ms (to exclude the initial, possibly “visual” transient response), whereas movement activity was considered from 100ms before to 200ms after movement onset. The goal of these criteria was to select, from the 100–200 isolations (single unit and multiunit), only those that were responsive and selective during the delay period. We also wanted to exclude neurons whose activity was dominated almost entirely by movement-related responses.

Ocular fixation

Ocular fixation was tracked and enforced for both monkeys. A small purple cross appeared near the initial central spot (1.5cm lateral and 1.5cm above its center). The trial began only once the central spot was touched and the purple cross was fixated. Fixation requirements were quite forgiving (±3cm), but actual fixation was much more more accurate (~6 and 9mm standard deviation (SD) of horizontal and vertical eye position). For monkey G, after the onset of the target, the purple cross was moved near the target, and fixation was enforced there for the duration of the delay (thus, a saccade was made during the delay). However, for experiments with monkey H, fixation was enforced near the central spot throughout the delay. This was done so as to ensure that changes in neural activity/RT were not indirectly the result of saccadic behavior.

Data preprocessing

Spike trains were preprocessed to produce a continuous firing rate as a function of time by smoothing with a modified Gaussian kernel with 30ms SD. Only 50ms (less than the time required for PMd to process the go cue) of the a causal portion of the filter was used. This means that the estimated continuous firing rates at the time of the go cue did not take into account spikes that occurred more than 50ms after the go cue. Since it is highly unlikely that movement activity exists in the PMd as little as 50ms after a go cue, this method ensured that the predictions of trial-by-trial RT were not influenced by peri-movement activity. After smoothing, the data was down-sampled by a factor of ten, meaning that only every tenth sample was kept. This was done to reduce computational time. The resulting vector is a neural activity every millisecond. These data were then used to calculate a trial-by-trial estimation of RT based on the hypothesis tested.

Dimensionality reduction

Dimensionality reduction was done only for the purposes of visualization in this work. All quantitative analysis relied on data of full dimensionality.

GPFA (Yu et al., 2009) was performed on the neural data from 200ms before target onset to 100 ms after movement onset of all trials to a single target. Briefly, this method works by performing smoothing of spike trains and dimensionality reduction simultaneously within a common probabilistic framework. It assumes that the observed activity of each neuron is a linear function (plus noise) of a low-dimensional neural state, whose evolution in time is well-described by a Gaussian process. This common probabilistic framework allows for better resolution of subtle neural dynamics than other methods (Yu et al., 2009).

The data were reduced to twelve dimensions (consistent with the results of Yu et al. (2009)) to produce the trajectories in Figure 3 so that the axes would best describe the neural dynamics of both motor planning and execution. The two latent dimensions that resulted in a good separation of the data points are used to produced the figure. These dimensions explain the second and third most covariance overall.

Neural speed calculation

For calculation of neural projected speed (used in Fig. 3C), the neural velocity in GPFA space was first calculated by taking the difference between neural states at two consecutive timepoints. This neural velocity was then projected onto the neural velocity of the mean neural trajectory (across all trials) time point by time point. This is can be viewed as the speed along the path. Note that a very similar plot is produced if this projection is not done. The normalized projected speed at a given time is reported as the magnitude of Normalization is done so that the speed computed from datasets with different numbers of neurons are comparable.

RT Correlations

When correlating our single-trial neural metrics with RT, we did not include that trial’s neural data in the computation of the mean neural trajectory used for that prediction. The predicted RTs and measured RTs were then correlated against each other. This leave-one-out technique was done to ensure that we did not use the current trial’s neural data in the creation of the prediction model.

To report an average RT variance explained across multiple datasets, a weighted average was computed in which each dataset’s r² was weighted by the number of trials in the dataset.

Optimal Subspace Method

The optimal subspace method was implemented by correlating trial-by-trial RT with the unsigned difference between the firing rate at the go cue and the average firing rate across similar trials, averaged across all recorded neurons. This reflects the optimal subspace hypothesis, which states that trials in which firing rates are close to the mean rates observed for similar trials have shorter RTs. Note that this is identical to how it was implemented in Churchland et al. (2006c).

One might implement this hypothesis directly without averaging across neurons by correlating single-trial RT with the Euclidean distance between the high-dimensional vector of firing rates of all neurons at the time of the go cue and the vector of mean firing rates across trials at the go cue. This was implicitly performed in the Fig. S1B of the Supplementary Materials, in which it is called the distance method with an offset of 0ms. Note that this implementation of the optimal subspace hypothesis performs quite poorly, with average r² much less than the methods used here in the main text.

The rise-to-threshold method asserts that neural activity during the delay period changes so as to approach a threshold which is then crossed to initiate the upcoming movement (Erlhagen & Schoner, 2002). There are many different ways to relate such a hypothesis to a mathematical prediction, and we tried three in this paper, correlating trial-by-trialRT with: the signed difference between the firing rate at the go cue and that at target onset (i.e., the baseline firing rate), averaged across all neurons; the same metric, but only including neurons for their preferred directions; the same metric, but not subtracting the baseline firing rate. These all can be viewed to reflect the rise-to-threshold hypothesis, which states that trials in which neurons are firing more quickly have a shorter RT. We only report the method that yielded the best results, which used the signed difference between the firing rate at the go cue and that at target onset.

Independent Linear Decoding

We also compared the performance of our model to that obtained by a standard neural decoding method derived from an independent linear encoding assumption. This method assumes that the firing rate of each neuron linearly and independently encodes a single behavioral metric (RT in this work). Observed firing rates on each trial are then combined to find the corresponding maximum likelihood estimate of the behavioral metric on each trial.

Note that this method might also be viewed as a type of threshold model, with the added possibility of a neuron “falling” to threshold (i.e., it may decrease its neural activities towards a threshold during the delay) instead of only rising to it.

The relationship between the single-trial firing rate of the i^th neuron, F_i, and the RT on the same trial was modelled by F_i = α_iRT + β_i + ζ, where α_i and β_i are constants of regression, and ζ~N(0,σ_Q^2_i) is a noise random variable with variance σ_Q^2_i. This expression treats RT as the independent variable, a viewpoint often favored in decoding methods as covariates (here RT) tend to be much more stable than firing rate. In fact, taking the alternative direct decoding viewpoint, in which RT is treated as the dependent variable, did not change the results reported here.

The RT on each trial was decoded as follows. First, the firing rates and RTs measured on all other trials were used to find the regression parameters α_i, β_i and σ_Q^2_i for each neuron. Then, the maximum-likelihood value of RT was found, given these parameters and the firing rates observed on the current trial. As the encoding noise was assumed to be Gaussian, the maximum-likelihood value is that which minimizes (*** PLEASE SEE .PDF FOR THE EQUATION, WHICH I CANNOT PROPERLY FORMAT HERE IN MS WORD ***): that is, the noise-scaled sum of squared regression residuals for each of the N neurons. This maximum-likelihood value is given by:

(*** PLEASE SEE .PDF FOR THE EQUATION, WHICH I CANNOT PROPERLY FORMAT HERE IN MS WORD ***)

The assumption of Gaussian variability is sometimes supported by working with the square-roots of spike counts, which renders Poisson-distributed counts more Gaussian and stabilized their variance. Indeed, such a transform did slightly improve the performance of this method (as it does our method), but our multivariate method still outperformed linear decoding for nearly all datasets (not shown).

Bayesian Information Criterion

This criterion for model selection is well known (McQuarrie & Tsai, 1998). It is related to the log-likelihood of the data given the model and is given by

$$\text{BIC}=-2\text{logL}+\text{k}\text{logN},$$

where L is the posterior likelihood of the data given the best-fit model, k is the number of parameters in the model, and N is the number of datapoints used. A smaller BIC is associated with a better explanatory model.

Highlights.

• Single-trial neural population activity predicts single-trial reaction time (RT)

• Rate of change of neural activity predicts single-trial RT similarly

• A combination of the two is the best known neural predictor of RT