Abstract
This paper discusses the potential of graphics processing units (GPUs) in high-dimensional optimization problems. A single GPU card with hundreds of arithmetic cores can be inserted in a personal computer and dramatically accelerates many statistical algorithms. To exploit these devices fully, optimization algorithms should reduce to multiple parallel tasks, each accessing a limited amount of data. These criteria favor EM and MM algorithms that separate parameters and data. To a lesser extent block relaxation and coordinate descent and ascent also qualify. We demonstrate the utility of GPUs in nonnegative matrix factorization, PET image reconstruction, and multidimensional scaling. Speedups of 100 fold can easily be attained. Over the next decade, GPUs will fundamentally alter the landscape of computational statistics. It is time for more statisticians to get on-board.
Key words and phrases: Block relaxation, EM and MM algorithms, multidimensional scaling, nonnegative matrix factorization, parallel computing, PET scanning
1. INTRODUCTION
Statisticians, like all scientists, are acutely aware that the clock speeds on their desktops and laptops have stalled. Does this mean that statistical computing has hit a wall? The answer fortunately is no, but the hardware advances that we routinely expect have taken an interesting detour. Most computers now sold have two to eight processing cores. Think of these as separate CPUs on the same chip. Naive programmers rely on sequential algorithms and often fail to take advantage of more than a single core. Sophisticated programmers eagerly exploit parallel programming. However, multicore CPUs do not represent the only road to the success of statistical computing.
Graphics processing units (GPUs) have caught the scientific community by surprise. These devices are designed for graphics rendering in computer animation and games. Propelled by these nonscientific markets, the old technology of numerical (array) coprocessors has advanced rapidly. Highly parallel GPUs are now making computational inroads against traditional CPUs in image processing, protein folding, stock options pricing, robotics, oil exploration, data mining, and many other areas (28). We are starting to see orders of magnitude improvement on some hard computational problems. Three companies, Intel, NVIDIA, and AMD/ATI, dominate the market. Intel is struggling to keep up with its more nimble competitors.
Modern GPUs support more vector and matrix operations, stream data faster, and possess more local memory per core than their predecessors. They are also readily available as commodity items that can be inserted as video cards on modern PCs. GPUs have been criticized for their hostile programming environment and lack of double precision arithmetic and error correction, but these faults are being rectified. The CUDA programming environment (27) for NVIDIA chips is now easing some of the programming chores. We could say more about near-term improvements, but most pronouncements would be obsolete within months.
Oddly, statisticians have been slow to embrace the new technology. Silberstein et al (31) first demonstrated the potential for GPUs in fitting simple Bayesian networks. Recently Suchard and Rambaut (33) have seen greater than 100-fold speed-ups in MCMC simulations in molecular phylogeny. Lee et al (18) and Tib-bits, et al (36) are following suit with Bayesian model fitting via particle filtering and slice sampling. Finally, work is under-way to port common data mining techniques such as hierarchical clustering and multi-factor dimensionality reduction onto GPUs (32). These efforts constitute the first wave of an eventual flood of statistical and data mining applications. The porting of GPU tools into the R environment will undoubtedly accelerate the trend (3).
Not all problems in computational statistics can benefit from GPUs. Sequential algorithms are resistant unless they can be broken into parallel pieces. For example, least squares and singular value decomposition–two tasks frequently performed in statistics–cannot benefit from GPUs unless they are extremely large scale or many such small problems need to be solved simultaneously. Even parallel algorithms can be problematic if the entire range of data must be accessed by each GPU. A case in point is the alternating least squares strategy for the nonnegative matrix factorization problem featured in Section 3.1. Because they have limited memory, GPUs are designed to operate on short streams of data. The greatest speedups occur when all of the GPUs on a card perform the same arithmetic operation simultaneously. Effective applications of GPUs in optimization involves both separation of data and separation of parameters.
In the current paper, we illustrate how GPUs can work hand in glove with the MM algorithm, a generalization of the EM algorithm. In many optimization problems, the MM algorithm explicitly separates parameters by replacing the objective function by a sum of surrogate functions, each of which involves a single parameter. Optimization of the one-dimensional surrogates can be accomplished by assigning each subproblem to a different core. Provided the different cores each access just a slice of the data, the parallel subproblems execute quickly. By construction the new point in parameter space improves the value of the objective function. In other words, MM algorithms are iterative ascent or descent algorithms. If they are well designed, then they separate parameters in high-dimensional problems. This is where GPUs enter. They offer most of the benefits of distributed computer clusters at a fraction of the cost. For this reason alone, computational statisticians need to pay attention to GPUs.
Before formally defining the MM algorithm, it may help the reader to walk through a simple numerical example stripped of statistical content. Consider the Rosenbrock test function
| (1.1) |
familiar from the minimization literature. As we iterate toward the minimum at x = 1 = (1, 1), we construct a surrogate function that separates parameters. This is done by exploiting the obvious majorization
where equality holds when x and the current iterate xn coincide. It follows that f(x) itself is majorized by the sum of the two surrogates
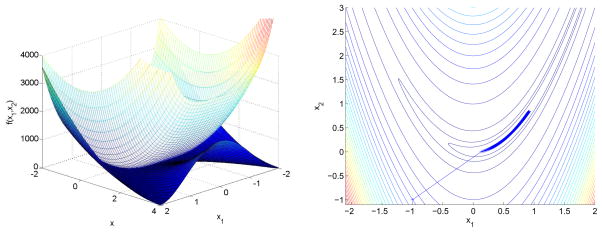
The left panel of Figure 1 depicts the Rosenbrock function and its majorization g1(x1 | xn) + g2(x2 | xn) at the point −1.
Fig 1.
Left: The Rosenbrock (banana) function (the lower surface) and a majorization function at point (−1, −1) (the upper surface). Right: MM iterates.
According to the MM recipe, at each iteration one must minimize the quartic polynomial g1(x1 | xn) and the quadratic polynomial g2(x2 | xn). The quartic possesses either a single global minimum or two local minima separated by a local maximum These minima are the roots of the cubic function and can be explicitly computed. We update x1 by the root corresponding to the global minimum and x2 via . The right panel of Figure 1 displays the iterates starting from x0 = −1. These immediately jump into the Rosenbrock valley and then slowly descend to 1.
Separation of parameters in this example makes it easy to decrease the objective function. This almost trivial advantage is amplified when we optimize functions depending on tens of thousands to millions of parameters. In these settings, Newton’s method and variants such as Fisher’s scoring are fatally handicapped by the need to store, compute, and invert huge Hessian or information matrices. On the negative side of the balance sheet, MM algorithms are often slow to converge. This disadvantage is usually outweighed by the speed of their updates even in sequential mode. If one can harness the power of parallel processing GPUs, then MM algorithms become the method of choice for many high-dimensional problems.
We conclude this introduction by sketching a roadmap to the rest of the paper. Section 2 reviews the MM algorithm. Section 3 discusses three high-dimensional MM examples. Although the algorithm in each case is known, we present brief derivations to illustrate how simple inequalities drive separation of parameters. We then implement each algorithm on a realistic problem and compare running times in sequential and parallel modes. We purposefully omit programming syntax since many tutorials already exist for this purpose, and material of this sort is bound to be ephemeral. The two tutorials (34; 35) are a good place to start for statisticians. Section 4 concludes with a brief discussion of other statistical applications of GPUs and other methods of accelerating optimization algorithms.
2. MM ALGORITHMS
The MM algorithm like the EM algorithm is a principle for creating optimization algorithms. In minimization the acronym MM stands for majorization-minimization; in maximization it stands for minorization-maximization. Both versions are convenient in statistics. For the moment we will concentrate on maximization.
Let f(θ) be the objective function whose maximum we seek. Its argument θ can be high-dimensional and vary over a constrained subset Θ of Euclidean space. An MM algorithm involves minorizing f(θ) by a surrogate function g(θ | θn) anchored at the current iterate θn of the search. The subscript n indicates iteration number throughout this article. If θn+1 denotes the maximum of g(θ | θn) with respect to its left argument, then the MM principle declares that θn+1 increases f(θ) as well. Thus, MM algorithms revolve around a basic ascent property.
Minorization is defined by the two properties
| (2.1) |
| (2.2) |
In other words, the surface θ ↦ g(θ | θn) lies below the surface θ ↦ f (θ) and is tangent to it at the point θ = θn. Construction of the minorizing function g(θ | θn) constitutes the first M of the MM algorithm. In our examples g(θ | θn) is chosen to separate parameters.
In the second M of the MM algorithm, one maximizes the surrogate g(θ | θn) rather than f(θ) directly. It is straightforward to show that the maximum point θn+1 satisfies the ascent property f (θn+1) ≥ f (θn). The proof
reflects definitions (2.1) and (2.2) and the choice of θn+1. The ascent property is the source of the MM algorithm’s numerical stability and remains valid if we merely increase g(θ | θn) rather than maximize it. In many problems MM updates are delightfully simple to code, intuitively compelling, and automatically consistent with parameter constraints. In minimization we seek a majorizing function g(θ | θn) lying above the surface θ ↦ f (θ) and tangent to it at the point θ = θn. Minimizing g(θ | θn) drives f(θ) downhill.
The celebrated Expectation-Maximization (EM) algorithm (8; 22) is a special case of the MM algorithm. The Q-function produced in the E step of the EM algorithm constitutes a minorizing function of the loglikelihood. Thus, both EM and MM share the same advantages: simplicity, stability, graceful adaptation to constraints, and the tendency to avoid large matrix inversion. The more general MM perspective frees algorithm derivation from the missing data straitjacket and invites wider applications. For example, our multi-dimensional scaling (MDS) and non-negative matrix factorization (NNFM) examples involve no likelihood functions. Wu and Lange (40) briefly summarize the history of the MM algorithm and its relationship to the EM algorithm.
The convergence properties of MM algorithms are well-known (16). In particular, five properties of the objective function f(θ) and the MM algorithm map θ ↦ M(θ) guarantee convergence to a stationary point of f(θ): (a) f(θ) is coercive on its open domain; (b) f(θ) has only isolated stationary points; (c) M(θ) is continuous; (d) θ* is a fixed point of M(θ) if and only if θ* is a stationary point of f(θ); and (e) f[M(θ*)] ≥ f(θ*), with equality if and only if θ* is a fixed point of M(θ). These conditions are easy to verify in many applications. The local rate of convergence of an MM algorithm is intimately tied to how well the surrogate function g(θ | θ*) approximates the objective function f(θ) near the optimal point θ*.
3. NUMERICAL EXAMPLES
In this section, we compare the performances of the CPU and GPU implementations of three classical MM algorithms coded in C++: (a) non-negative matrix factorization (NNMF), (b) positron emission tomography (PET), and (c) multidimensional scaling (MDS). In each case we briefly derive the algorithm from the MM perspective. For the CPU version, we iterate until the relative change
of the objective function f(θ) between successive iterations falls below a pre-set threshold ε or the number of iterations reaches a pre-set number nmax, whichever comes first. In these examples, we take ε = 10−9 and nmax = 100, 000. For ease of comparison, we iterate the GPU version for the same number of steps as the CPU version. Overall, we see anywhere from a 22-fold to 112-fold decrease in total run time. The source code is freely available from the first author.
Table 1 shows how our desktop system is configured. Although the CPU is a high-end processor with four cores, we use just one of these for ease of comparison. In practice, it takes considerable effort to load balance the various algorithms across multiple CPU cores. With 240 GPU cores, the GTX 280 GPU card delivers a peak performance of about 933 GFlops in single precision. This card is already obsolete. Newer cards possess twice as many cores, and up to four cards can fit inside a single desktop computer. It is relatively straightforward to program multiple GPUs. Because previous generation GPU hardware is largely limited to single precision, this is a worry in scientific computing. To assess the extent of roundoff error, we display the converged values of the objective functions to ten significant digits. Only rarely is the GPU value far off the CPU mark. The extra effort in programming the GPU version is relatively light. Exploiting the standard CUDA library (27), it takes 77, 176, and 163 extra lines of GPU code to implement the NNMF, PET, and MDS examples, respectively. Finally, for the PET and MDS examples, we also list run times of a CPU implementation with quasi-Newton acceleration method (42). This generic acceleration significantly reduces the number of MM iterations until convergence.
Table 1.
Configuration of the desktop system
| CPU | GPU | |
|---|---|---|
| Model | Intel Core 2 | NVIDIA GeForce |
| Extreme X9440 | GTX 280 | |
| # Cores | 4 | 240 |
| Clock | 3.2G | 1.3G |
| Memory | 16G | 1G |
3.1 Non-Negative Matrix Factorizations
Non-negative matrix factorization (NNMF) is an alternative to principle component analysis useful in modeling, compressing, and interpreting nonnegative data such as observational counts and images. The articles (19; 20; 2) discuss in detail algorithm development and statistical applications of NNMF. The basic problem is to approximate a data matrix X with nonnegative entries xij by a product VW of two low rank matrices V and W with nonnegative entries vik and wkj. Here X, V, and W are p × q, p × r, and r ×q, respectively, with r much smaller than min{p, q}. One version of NNMF minimizes the objective function
| (3.1) |
where || · ||F denotes the Frobenius-norm. To get an idea of the scale of NNFM imaging problems, p (number of images) can range 101–104, q (number of pixels per image) can surpass 102–104, and one seeks a rank r approximation of about 50. Notably, part of the winning solution of the Netflix challenge relies on variations of NNMF (13). For the Netflix data matrix, p = 480, 000 (raters), q = 18, 000 (movies), and r ranged from 20 to 100.
Exploiting the convexity of the function x ↦ (xij − x)2, one can derive the inequality
where anikj = vnikwnkj and bnij = Σk anikj. This leads to the surrogate function
| (3.2) |
majorizing the objective function . Although the majorization (3.2) does not achieve a complete separation of parameters, it does if we fix V and update W or vice versa. This strategy is called block relaxation (7).
If we elect to minimize g(V, W | Vn, Wn) holding W fixed at Wn, then the stationarity condition for V reads
Its solution furnishes the simple multiplicative update
| (3.3) |
Likewise the stationary condition
gives the multiplicative update
| (3.4) |
where cnij = Σk vn+1,ikwnkj. Close inspection of the multiplicative updates (3.3) and (3.4) shows that their numerators depend on the matrix products and and their denominators depend on the matrix products and . Large matrix multiplications are very fast on GPUs because CUDA implements in parallel the BLAS (basic linear algebra subprograms) library widely applied in numerical analysis (26). Once the relevant matrix products are available, each elementwise update of vik or wkj involves just a single multiplication and division. These scalar operations are performed in parallel through hand-written GPU code. Algorithm 1 summarizes the steps in performing NNMF.
Algorithm 1.
(NNMF) Given , find and minimizing .
| Initialize: Draw v0ik and w0kj uniform on (0,1) for all 1 ≤ i ≤ p, 1 ≤ k ≤ r, 1 ≤ j ≤ q |
| repeat |
| Compute and |
| for all 1 ≤ i ≤ p, 1 ≤ k ≤ r |
| Compute and |
| for all 1 ≤ k ≤ r, 1 ≤ j ≤ q |
| until convergence occurs |
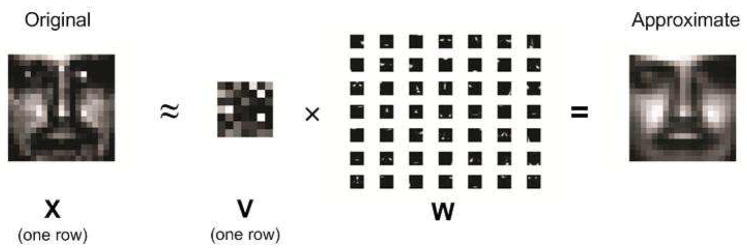
We now compare CPU and GPU versions of the multiplicative NNMF algorithm on a training set of face images. Database #1 from the MIT Center for Biological and Computational Learning (CBCL) (25) reduces to a matrix X containing p = 2, 429 gray scale face images with q = 19 × 19 = 361 pixels per face. Each image (row) is scaled to have mean and standard deviation 0.25. Figure 2 shows the recovery of the first face in the database using a rank r = 49 decomposition. The 49 basis images (rows of W) represent different aspects of a face. The rows of V contain the coefficients of these parts estimated for the various faces. Some of these facial features are immediately obvious in the reconstruction. Table 2 compares the run times of Algorithm 1 implemented on our CPU and GPU respectively. We observe a 22 to 112-fold speed-up in the GPU implementation. Run times for the GPU version depend primarily on the number of iterations to convergence and very little on the rank r of the approximation. Run times of the CPU version scale linearly in both the number of iterations and r.
Fig 2.
Approximation of a face image by rank-49 NNMF: coefficients × basis images = approximate image.
Table 2.
Run-time (in seconds) comparisons for NNMF on the MIT CBCL face image data. The dataset contains p = 2, 429 faces with q = 19 × 19 = 361 pixels per face. The columns labeled Function refer to the converged value of the objective function.
| Rank r | Iters | CPU
|
GPU
|
Speedup | ||
|---|---|---|---|---|---|---|
| Time | Function | Time | Function | |||
| 10 | 25459 | 1203 | 106.2653503 | 55 | 106.2653504 | 22 |
| 20 | 87801 | 7564 | 89.56601262 | 163 | 89.56601287 | 46 |
| 30 | 55783 | 7013 | 78.42143486 | 103 | 78.42143507 | 68 |
| 40 | 47775 | 7880 | 70.05415929 | 119 | 70.05415950 | 66 |
| 50 | 53523 | 11108 | 63.51429261 | 121 | 63.51429219 | 92 |
| 60 | 77321 | 19407 | 58.24854375 | 174 | 58.24854336 | 112 |
It is worth stressing a few points. First, the objective function (3.1) is convex in V for W fixed, and vice versa but not jointly convex. Thus, even though the MM algorithm enjoys the descent property, it is not guaranteed to find the global minimum (2). There are two good alternatives to the multiplicative algorithm. First, pure block relaxation can be conducted by alternating least squares (ALS). In updating V with W fixed, ALS omits majorization and solves the p separated nonnegative least square problems
where V(i, :) and X(i, :) denote the i-th row of the corresponding matrices. Similarly, in updating W with V fixed, ALS solves q separated nonnegative least square problems. Separation naturally suggests parallel implementations; but parallelization by GPUs hits a snag because each nonnegative least square subproblem needs to operate on the whole W matrix. Another possibility is to change the objective function to
according to a Poisson model for the counts xij (19). This works even when some entries xij fail to be integers, but the Poisson loglikelihood interpretation is lost. A pure MM algorithm for maximizing L(V, W) is
Derivation of these variants of Lee and Seung’s (19) Poisson updates is left to the reader.
3.2 Positron Emission Tomography
The field of computed tomography has exploited EM algorithms for many years. In positron emission tomography (PET), the reconstruction problem consists of estimating the Poisson emission intensities λ = (λ1, …, λp) of p pixels arranged in a 2-dimensional grid surrounded by an array of photon detectors. The observed data are coincidence counts (y1, … yd) along d lines of flight connecting pairs of photon detectors. The loglikelihood under the PET model is
where the eij are constants derived from the geometry of the grid and the detectors. Without loss of generality, one can assume Σi eij = 1 for each j. It is straightforward to derive the traditional EM algorithm (14; 39) from the MM perspective using the concavity of the function ln s. Indeed, application of Jensen’s inequality produces the minorization
where wnij = eijλnj/(Σk eikλnk). This maneuver again separates parameters. The stationarity conditions for the surrogate Q(λ | λ n) supply the parallel updates
| (3.5) |
The convergence of the PET algorithm (3.5) is frustratingly slow, even under systematic acceleration (30; 42). Furthermore, the reconstructed images are of poor quality with a grainy appearance. The early remedy of premature halting of the algorithm cuts computational cost but is entirely ad hoc, and the final image depends on initial conditions. A better option is add a roughness penalty to the loglikelihood. This device not only produces better images but also accelerates convergence. Thus, we maximize the penalized loglikelihood
| (3.6) |
where μ is the roughness penalty constant, and
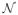 is the neighborhood system that pairs spatially adjacent pixels. An absolute value penalty is less likely to deter the formation of edges than a square penalty, but it is easier to deal with a square penalty analytically, and we adopt it for the sake of simplicity. In practice, visual inspection of the recovered images guides the selection of the roughness penalty constant μ.
is the neighborhood system that pairs spatially adjacent pixels. An absolute value penalty is less likely to deter the formation of edges than a square penalty, but it is easier to deal with a square penalty analytically, and we adopt it for the sake of simplicity. In practice, visual inspection of the recovered images guides the selection of the roughness penalty constant μ.
To maximize f(λ) by an MM algorithm, we must minorize the penalty in a manner consistent with the separation of parameters. In view of the evenness and convexity of the function s2, we have
Equality holds if λj + λk = λnj + λnk, which is true when λ = λn. Combining our two minorizations furnishes the surrogate function
To maximize g(λ | λn), we define
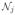 = {k : {j, k} ∈
= {k : {j, k} ∈
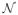 } and set the partial derivative
} and set the partial derivative
| (3.7) |
equal to 0 and solve for λn+1,j. Multiplying equation (3.7) by λj produces a quadratic with roots of opposite signs. We take the positive root
where
Algorithm 2 summarizes the complete MM scheme. Obviously, complete parameter separation is crucial. The quantities aj can be computed once and stored. The quantities bnj and cnj are computed for each j in parallel. To improve GPU performance in computing the sums over i, we exploit the widely available parallel sum-reduction techniques (31). Given these results, a specialized but simple GPU code computes the updates λn+1,j for each j in parallel.
Algorithm 2.
(PET Image Recovering) Given the coefficient matrix , coincident counts , and roughness parameter μ > 0, find the intensity vector that maximizes the objective function (3.6).
| Scale E to have unit l1 column norms. |
Compute |
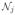 | = Σk:{j,k}∈ | = Σk:{j,k}∈
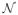 1 and aj − 2μ| 1 and aj − 2μ|
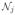 | for all 1 ≤ j ≤ p. | for all 1 ≤ j ≤ p. |
| Initialize: λ0j ← 1, j = 1, …, p. |
| repeat |
| znij ← (yieijλnj)/(Σkeikλnk) for all 1 ≤ i ≤ d, 1 ≤ j ≤ p |
| for j = 1 to p do |
bnj ← μ(|
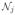 | λnj + Σk∈ | λnj + Σk∈
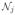 λnk) − 1 λnk) − 1 |
| cnj ← Σi znij |
| end for |
| until convergence occurs |
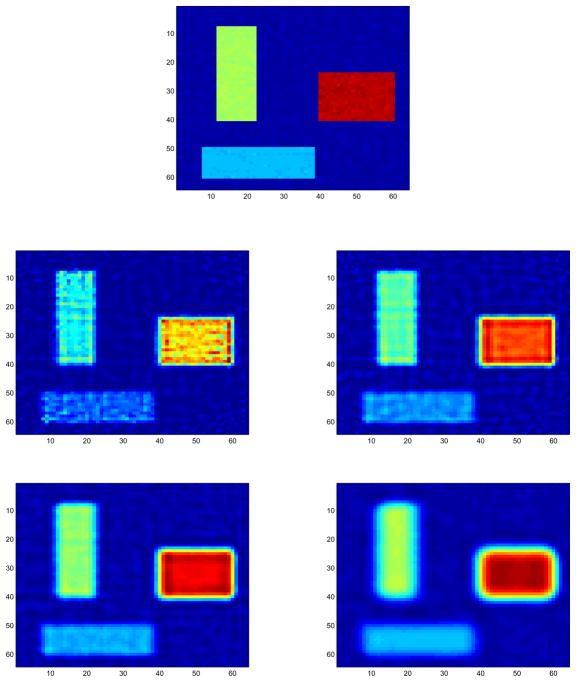
Table 3 compares the run times of the CPU and GPU implementations for a simulated PET image (30). The image as depicted in the top of Figure 3 has p = 64 × 64 = 4, 096 pixels and is interrogated by d = 2, 016 detectors. Overall we see a 43- to 53-fold reduction in run times with the GPU implementation. Figure 3 displays the true image and the estimated images under penalties of μ = 0, 10−5, 10−6, and 10−7. Without penalty (μ = 0), the algorithm fails to converge in 100,000 iterations.
Table 3.
Comparison of run times (in seconds) for a PET imaging problem on the simulated data in (30). The image has p = 64 × 64 = 4, 096 pixels and is interrogated by d = 2, 016 detectors. The columns labeled Function refer to the converged value of the objective function. The results under the heading QN(10) on CPU invoke quasi-Newton acceleration (42) with 10 secant conditions.
| Penalty μ | CPU
|
GPU
|
QN(10) on CPU
|
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Iters | Time | Function | Iters | Time | Function | Speedup | Iters | Time | Function | Speedup | |
| 0 | 100000 | 14790 | −7337.152765 | 100000 | 282 | −7337.153387 | 52 | 6549 | 2094 | −7320.100952 | n/a |
| 10−7 | 24457 | 3682 | −8500.083033 | 24457 | 70 | −8508.112249 | 53 | 251 | 83 | −8500.077057 | 44 |
| 10−6 | 6294 | 919 | −15432.45496 | 6294 | 18 | −15432.45586 | 51 | 80 | 29 | −15432.45366 | 32 |
| 10−5 | 589 | 86 | −55767.32966 | 589 | 2 | −55767.32970 | 43 | 19 | 9 | −55767.32731 | 10 |
Fig 3.
The true PET image (top) and the recovered images with penalties μ = 0, 10−7, 10−6, and 10−5.
3.3 Multidimensional Scaling
Multidimensional scaling (MDS) was the first statistical application of the MM principle (6; 5). MDS represents q objects as faithfully as possible in p-dimensional space given a nonnegative weight wij and a nonnegative dissimilarity measure yij for each pair of objects i and j. If θi ∈ ℝp is the position of object i, then the p × q parameter matrix θ = (θ1, …, θq) is estimated by minimizing the stress function
| (3.8) |
where ||θi − θj|| is the Euclidean distance between θi and θj. The stress function (3.8) is invariant under translations, rotations, and reflections of ℝp. To avoid translational and rotational ambiguities, we take θ1 to be the origin and the first p − 1 coordinates of θ2 to be 0. Switching the sign of leaves the stress function invariant. Hence, convergence to one member of a pair of reflected minima immediately determines the other member.
Given these preliminaries, we now review the derivation of the MM algorithm presented in (17). Because we want to minimize the stress, we majorize it. The middle term in the stress (3.8) is majorized by the Cauchy-Schwartz inequality
To separate the parameters in the summands of the third term of the stress, we invoke the convexity of the Euclidean norm || · || and the square function s2. These maneuvers yield
Assuming that wij = wji and yij = yji, the surrogate function therefore becomes
up to an irrelevant constant. Setting the gradient of the surrogate equal to the 0 vector produces the parallel updates
for all movable parameters .
Algorithm 3 summarizes the parallel organization of the steps. Again the matrix multiplications and Θn(W − Zn) can be taken care of by the CUBLAS library (26). The remaining steps of the algorithm are conducted by easily written parallel code.
Algorithm 3.
(MDS) Given weights W and distances Y ∈ ℝq×q, find the matrix Θ = [θ1, …, θq] ∈ ℝp×q which minimizes the stress (3.8).
| Precompute: xij ← wij yij for all 1 ≤ i, j ≤ q |
| Precompute: wi· ← Σj wij for all 1 ≤ i ≤ q |
| Initialize: Draw uniformly on [−1,1] for all 1 ≤ i ≤ q, 1 ≤ k ≤ p |
| repeat |
| Compute |
| for all 1 ≤ i, j ≤ q |
| znij ← xij/dnij for all 1 ≤ i ≠ j ≤ q |
| zni· ← Σj znij for all 1 ≤ i ≤ q |
| Compute Θ;n(W − Zn) |
| for all 1 ≤ i ≤ p, 1 ≤ k ≤ q |
| until convergence occurs |
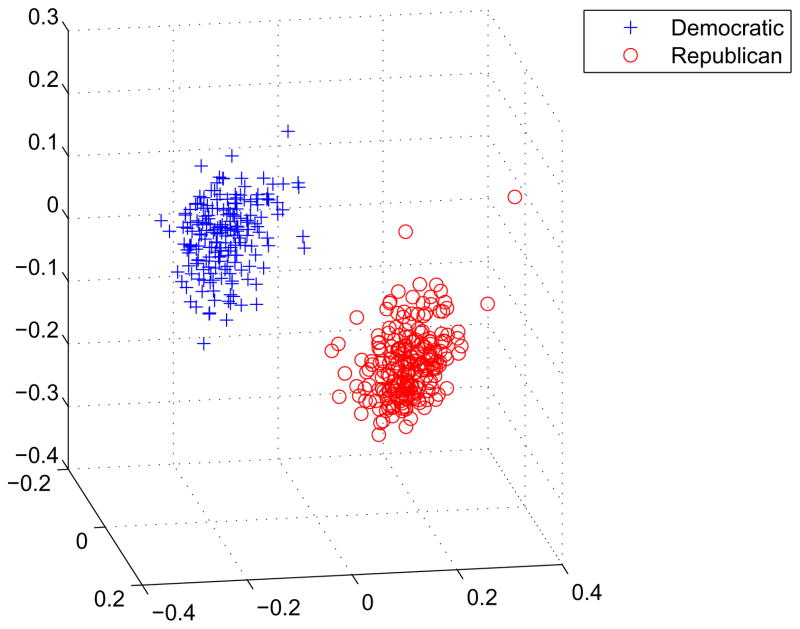
Table 4 compares the run times in seconds for MDS on the 2005 United States House of Representatives roll call votes. The original data consist of the 671 roll calls made by 401 representatives. We refer readers to the reference (9) for a careful description of the data and how the MDS input 401×401 distance matrix is derived. The weights wij are taken to be 1. In our notation, the number of objects (House Representatives) is q = 401. Even for this relatively small dataset, we see a 27–48 fold reduction in total run times, depending on the projection dimension p. Figure 4 displays the results in p = 3 dimensional space. The Democratic and Republican members are clearly separated. For p = 30, the algorithm fails to converge within 100,000 iterations.
Table 4.
Comparison of run times (in seconds) for MDS on the 2005 House of Representatives roll call data. The number of points (representatives) is q = 401. The results under the heading QN(20) on CPU invoke the quasi-Newton acceleration (42) with 20 secant conditions.
| Dim-p | CPU
|
GPU
|
QN(20) on CPU
|
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Iters | Time | Stress | Iters | Time | Stress | Speedup | Iters | Time | Stress | Speedup | |
| 2 | 3452 | 43 | 198.5109307 | 3452 | 1 | 198.5109309 | 43 | 530 | 16 | 198.5815072 | 3 |
| 3 | 15912 | 189 | 95.55987770 | 15912 | 6 | 95.55987813 | 32 | 1124 | 38 | 92.82984196 | 5 |
| 4 | 15965 | 189 | 56.83482075 | 15965 | 7 | 56.83482083 | 27 | 596 | 18 | 56.83478026 | 11 |
| 5 | 24604 | 328 | 39.41268434 | 24604 | 10 | 39.41268444 | 33 | 546 | 17 | 39.41493536 | 19 |
| 10 | 29643 | 441 | 14.16083986 | 29643 | 13 | 14.16083992 | 34 | 848 | 35 | 14.16077368 | 13 |
| 20 | 67130 | 1288 | 6.464623901 | 67130 | 32 | 6.464624064 | 40 | 810 | 43 | 6.464526731 | 30 |
| 30 | 100000 | 2456 | 4.839570118 | 100000 | 51 | 4.839570322 | 48 | 844 | 54 | 4.839140671 | n/a |
Fig 4.
Display of the MDS results with p = 3 coordinates on the 2005 House of Representatives roll call data.
Although the projection of points into p > 3 dimensional spaces may sound artificial, there are situations where this is standard practice. First, MDS is foremost a dimension reduction tool, and it is desirable to keep p > 3 to maximize explanatory power. Second, the stress function tends to have multiple local minima in low dimensions (10). A standard optimization algorithm like MM is only guaranteed to converge to a local minima of the stress function. As the number of dimensions increases, most of the inferior modes disappear. One can formally demonstrate that the stress has a unique minimum when p = q − 1 (4; 10). In practice, uniqueness can set in well before p reaches q − 1. In the recent work (41), we propose a “dimension crunching” technique that increases the chance of the MM algorithm converging to the global minimum of the stress function. In dimension crunching, we start optimizing the stress in a Euclidean space ℝm with m > p. The last m − p components of each column θi are gradually subjected to stiffer and stiffer penalties. In the limit as the penalty tuning parameter tends to ∞, we recover the global minimum of the stress in ℝp. This strategy inevitably incurs a computational burden when m is large, but the MM+GPU combination comes to the rescue.
4. DISCUSSION
The rapid and sustained increases in computing power over the last half century have transformed statistics. Every advance has encouraged statisticians to attack harder and more sophisticated problems. We tend to take the steady march of computational efficiency for granted, but there are limits to a chip’s clock speed, power consumption, and logical complexity. Parallel processing via GPUs is the technological innovation that will power ambitious statistical computing in the coming decade. Once the limits of parallel processing are reached, we may see quantum computers take off. In the meantime statisticians should learn how to harness GPUs productively.
We have argued by example that high-dimensional optimization is driven by parameter and data separation. It takes both to exploit the parallel capabilities of GPUs. Block relaxation and the MM algorithm often generate ideal parallel algorithms. In our opinion the MM algorithm is the more versatile of the two generic strategies. Unfortunately, block relaxation does not accommodate constraints well and may generate sequential rather than parallel updates. Even when its updates are parallel, they may not be data separated. The EM algorithm is one of the most versatile tools in the statistician’s toolbox. The MM principle generalizes the EM algorithm and shares its positive features. Scoring and Newton’s methods become impractical in high dimensions. Despite these arguments in favor of MM algorithms, one should always keep in mind hybrid algorithms such as the one we implemented for NNMF.
Although none of our data sets is really large by today’s standards, they do demonstrate that a good GPU implementation can easily achieve one to two orders of magnitude improvement over a single CPU core. Admittedly, modern CPUs come with 2 to 8 cores, and distributed computing over CPU-based clusters remains an option. But this alternative also carries a hefty price tag. The NVIDIA GTX280 GPU on which our examples were run drives 240 cores at a cost of several hundred dollars. High-end computers with 8 or more CPU nodes cost thousands of dollars. It would take 30 CPUs with 8 cores each to equal a single GPU at the same clock rate. Hence, GPU cards strike an effective and cost efficient balance.
In the three test examples, we implemented and reported performance results on the GTX 280 card in single precision because this particular card is not optimized for double precision computation. As the numerical results show, speedups are gained at loss of accuracy after a certain number of significant digits and in rare cases the single precision calculation on GPU may lead to an inferior mode (e.g., the μ = 10−7 case in Table 3). In some preliminary experimentation on the same PET imaging algorithm, we found that the performance of a double precision implementation on GTX 280 is about one third of the single precision implementation. In other words, it takes three times longer to perform the same number of iterations. However this lack of double precision support is soon lessened by the rapid advancement in GPU technology. The newer GTX 480 video card has twice as many cores as the GTX 280 and much improved double precision support. On the same desktop system as in Table 1, GTX 480 now delivers 89 fold speedup in single precision and 43 fold speedup in double precision over the CPU code which is in double precision. Not to mention the Tesla C2050 video card, which is already available on market and possesses a peak double precision floating point performance (515 Gflops) that is three times that of GTX 480 (168 Gflops). The challenge for the statistics community is to tackle more and more complicated statistical models on bigger and bigger datasets. Computational statisticians should decide for themselves the speed vs precision trade-off for their problem at hand.
The simplicity of MM algorithms often comes at a price of slow (at best linear) convergence. Our MDS, NNMF, and PET (without penalty) examples are cases in point. Slow convergence is a concern as statisticians head into an era dominated by large data sets and high-dimensional models. Think about the scale of the Netflix data matrix. The speed of any iterative algorithm is determined by both the computational cost per iteration and the number of iterations until convergence. GPU implementation reduces the first cost. Computational statisticians also have a bag of software tricks to decrease the number of iterations (23; 11; 21; 15; 12; 24; 38). For instance, the recent paper (42) proposes a quasi-Newton acceleration scheme particularly suitable for high-dimensional problems. The scheme is off-the-shelf and broadly applies to any search algorithm defined by a smooth algorithm map. The acceleration requires only modest increments in storage and computation per iteration. Tables 3 and 4 also list the results of this quasi-Newton acceleration of the CPU implementation for the MDS and PET examples. As the tables make evident, quasi-Newton acceleration significantly reduces the number of iterations until convergence. The accelerated algorithm always locates a better mode while cutting run times compared to the unaccelerated algorithm. We have tried the quasi-Newton acceleration on our GPU hardware with mixed results. We suspect that the lack of full double precision on the GPU is the culprit. When full double precision becomes widely available, the combination of GPU hardware acceleration and algorithmic software acceleration will be extremely potent.
Successful acceleration methods will also facilitate attacking another nagging problem in computational statistics, namely multimodality. No one knows how often statistical inference is fatally flawed because a standard optimization algorithm converges to an inferior mode. The current remedy of choice is to start a search algorithm from multiple random points. Algorithm acceleration is welcome because the number of starting points can be enlarged without an increase in computing time. As an alternative to multiple starting points, our recent paper (41) suggests modifications of several standard MM algorithms that increase the chance of locating better modes. These simple modifications all involve variations on deterministic annealing (37).
Our treatment of simple classical examples should not hide the wide applicability of the powerful MM+GPU combination. A few other candidate applications include penalized estimation of haplotype frequencies in genetics (1), construction of biological and social networks under a random multigraph model (29), and data mining with a variety of models related to the multinomial distribution (43). Many mixture models will benefit as well from parallelization, particularly in assigning group memberships. Finally, parallelization is hardly limited to optimization. We can expect to see many more GPU applications in MCMC sampling. Given the computationally intensive nature of MCMC, the ultimate payoff may even be higher in the Bayesian setting than in the frequentist setting. For example, in a recent study (35), GPU implementations deliver up to a 140 fold speedup in Bayesian fitting of massive mixture models. Of course realistically, these future triumphs will require a great deal of thought, effort, and education. There is usually a desert to wander and a river to cross before one reaches the promised land.
Acknowledgments
The authors thank the editor and two reviewers for their valuable suggestions for improving the manuscript. M.S. acknowledges support from NIH grant R01 GM086887. K.L. was supported by United States Public Health Service grants GM53275 and MH59490.
Contributor Information
Hua Zhou, Email: huazhou@ucla.edu, Department of Statistics, North Carolina State University, Raleigh, NC 27695-8203.
Kenneth Lange, Email: klange@ucla.edu, Departments of Biomathematics, Human Genetics, and Statistics, 5357A Gonda Building, UCLA, Los Angeles, CA 90095-1766.
Marc A. Suchard, Email: msuchard@ucla.edu, Departments of Biomathematics, Biostatistics, and Human Genetics, 6558 Gonda Building, UCLA, Los Angeles, CA 90095-1766.
References
- 1.Ayers KL, Lange KL. Penalized estimation of haplotype frequencies. Bioinformatics. 2008;24:1596–1602. doi: 10.1093/bioinformatics/btn236. [DOI] [PubMed] [Google Scholar]
- 2.Berry MW, Browne M, Langville AN, Pauca VP, Plemmons RJ. Algorithms and applications for approximate nonnegative matrix factorization. Comput Statist Data Anal. 2007;52:155–173. [Google Scholar]
- 3.Buckner J, Wilson J, Seligman M, Athey B, Watson S, Meng F. The gputools package enables GPU computing in R. Bioinformatics. 2009;22:btp608. doi: 10.1093/bioinformatics/btp608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.de Leeuw J. unpublished manuscript. Fitting distances by least squares. [Google Scholar]
- 5.de Leeuw J, Heiser WJ. Geometric Representations of Relational Data. Mathesis Press; Ann Arbor, MI: 1977. Convergence of correction matrix algorithms for multidimensional scaling; pp. 133–145. [Google Scholar]
- 6.de Leeuw J. Recent developments in statistics (Proc European Meeting Statisticians, Grenoble, 1976) North-Holland; Amsterdam: 1977. Applications of convex analysis to multidimensional scaling; pp. 133–145. [Google Scholar]
- 7.de Leeuw J. Information Systems and Data Analysis. Springer-Verlag; Berlin: 1994. Block relaxation algorithms in statistics. [Google Scholar]
- 8.Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. (with discussion) J Roy Statist Soc Ser B. 1977;39:1–38. [Google Scholar]
- 9.Diaconis P, Goel S, Holmes S. Horseshoes in multidimensional scaling and local kernel methods. Annals of Applied Statistics. 2008;2:777–807. [Google Scholar]
- 10.Groenen PJF, Heiser WJ. The tunneling method for global optimization in multidimensional scaling. Pshychometrika. 1996;61:529–550. [Google Scholar]
- 11.Jamshidian M, Jennrich RI. Conjugate gradient acceleration of the EM algorithm. J Amer Statist Assoc. 1993;88:221–228. [Google Scholar]
- 12.Jamshidian M, Jennrich RI. Acceleration of the EM algorithm by using quasi-Newton methods. J Roy Statist Soc Ser B. 1997;59:569–587. [Google Scholar]
- 13.Koren Y, Bell R, Volinsky C. Matrix factorization techniques for recommender systems. Computer. 2009;42:30–37. [Google Scholar]
- 14.Lange KL, Carson R. EM reconstruction algorithms for emission and transmission tomography. J Comput Assist Tomogr. 1984;8:306–316. [PubMed] [Google Scholar]
- 15.Lange KL. A quasi-Newton acceleration of the EM algorithm. Statist Sinica. 1995;5:1–18. [Google Scholar]
- 16.Lange KL. Optimization. Springer-Verlag; New York: 2004. [Google Scholar]
- 17.Lange KL, Hunter DR, Yang I. Optimization transfer using surrogate objective functions. (with discussion) J Comput Graph Statist. 2000;9:1–59. [Google Scholar]
- 18.Lee A, Yan C, Giles MB, Doucet A, Holmes CC. Technical report. Department of Statistics, Oxford University; 2009. On the utility of graphics cards to perform massively parallel simulation of advanced Monte Carlo methods. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lee DD, Seung HS. Learning the parts of objects by non-negative matrix factorization. Nature. 1999;401:788–791. doi: 10.1038/44565. [DOI] [PubMed] [Google Scholar]
- 20.Lee DD, Seung HS. NIPS. MIT Press; 2001. Algorithms for non-negative matrix factorization; pp. 556–562. [Google Scholar]
- 21.Liu C, Rubin DB. The ECME algorithm: a simple extension of EM and ECM with faster monotone convergence. Biometrika. 1994;81:633–648. [Google Scholar]
- 22.McLachlan GJ, Krishnan T. The EM algorithm and extensions. 2 Wiley-Interscience [John Wiley & Sons]; Hoboken, NJ: 2008. [Google Scholar]
- 23.Meng XL, Rubin DB. Maximum likelihood estimation via the ECM algorithm: a general framework. Biometrika. 1993;80:267–278. [Google Scholar]
- 24.Meng XL, van Dyk D. The EM algorithm—an old folk-song sung to a fast new tune (with discussion) J Roy Statist Soc Ser B. 1997;59(3):511–567. [Google Scholar]
- 25.MIT center for biological and computational learning. CBCL Face Database #1. http://www.ai.mit.edu/projects/cbcd.
- 26.NVIDIA. NVIDIA CUBLAS Library. 2008. [Google Scholar]
- 27.NVIDIA. NVIDIA CUDA Compute Unified Device Architecture: Programming Guide Version 2.0. 2008. [Google Scholar]
- 28.Owens JD, Luebke D, Govindaraju N, Harris M, Krüger J, Lefohn AE, Purcell TJ. A survey of general-purpose computation on graphics hardware. Computer Graphics Forum. 2007;26:80–113. [Google Scholar]
- 29.Ranola JM, Ahn S, Sehl ME, Smith DJ, Lange KL. A Poisson model for random multigraphs. Bioinformatics. 2010 doi: 10.1093/bioinformatics/btq309. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Roland C, Varadhan R, Frangakis CE. Squared polynomial extrapolation methods with cycling: an application to the positron emission tomography problem. Numer Algorithms. 2007;44:159–172. [Google Scholar]
- 31.Silberstein M, Schuster A, Geiger D, Patney A, Owens JD. Efficient computation of sum-products on GPUs through software-managed cache. Proceedings of the 22nd Annual International Conference on Supercomputing; ACM; 2008. pp. 309–318. [Google Scholar]
- 32.Sinnott-Armstrong NA, Greene CS, Cancare F, Moore JH. Accelerating epistasis analysis in human genetics with consumer graphics hardware. BMC Research Notes. 2009;2:149. doi: 10.1186/1756-0500-2-149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Suchard MA, Rambaut A. Many-core algorithms for statistical phylogenetics. Bioinformatics. 2009;25:1370–1376. doi: 10.1093/bioinformatics/btp244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Suchard MA, Holmes C, West M. Some of the what?, why?, how?, who and where? of graphics processing unit computing for Bayesian analysis. ISBA Bulletin. 2010;17:12–16. [Google Scholar]
- 35.Suchard MA, Wang Q, Chan C, Frelinger A, West M. Understanding GPU programming for statistical computation: studies in massively parallel massive mixtures. J Comput Graphical Stat. 2010;19:418–438. doi: 10.1198/jcgs.2010.10016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Tibbits MM, Haran M, Liechty JC. Parallel multivariate slice sampling. Statistics and Computing. 2009 to appear. [Google Scholar]
- 37.Ueda N, Nakano R. Deterministic annealing EM algorithm. Neural Networks. 1998;11:271–282. doi: 10.1016/s0893-6080(97)00133-0. [DOI] [PubMed] [Google Scholar]
- 38.Varadhan R, Roland C. Simple and globally convergent methods for accelerating the convergence of any EM algorithm. Scand J Statist. 2008;35:335–353. [Google Scholar]
- 39.Vardi Y, Shepp LA, Kaufman L. A statistical model for positron emission tomography. (with discussion) J Amer Statist Assoc. 1985;80:8–37. [Google Scholar]
- 40.Wu TT, Lange KL. The MM alternative to EM. Stat Sci. 2009 in press. [Google Scholar]
- 41.Zhou H, Lange KL. On the bumpy road to the dominant mode. Scand J Statist. 2009 doi: 10.1111/j.1467-9469.2009.00681.x. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Zhou H, Alexander D, Lange KL. A quasi-newton acceleration for high-dimensional optimization algorithms. Statistics and Computing. 2009 doi: 10.1007/s11222-009-9166-3. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Zhou H, Lange KL. MM algorithms for some discrete multivariate distributions. J Comput Graphical Stat. 2009 doi: 10.1198/jcgs.2010.09014. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]