Abstract
Five levels of disease expression were scored in a cross-inoculation study of 120 host and 60 pathogen lines of wild flax Linum marginale and its rust fungus Melampsora lini sampled from six natural populations. Patterns of partial resistance showed clear evidence of gene-for-gene interactions, with particular levels of partial resistance occurring in specific host–pathogen combinations. Sympatric and putatively more highly coevolved host–pathogen combinations had a lower frequency of partial resistance types relative to allopatric combinations. Sympatric host–pathogen combinations also showed a lower diversity of resistance responses, but there was a trend toward a greater fraction of this variance being determined by pathogen-genotype × host-genotype interactions. In this system, there was no evidence that partial resistances slow host–pathogen coevolution. The analyses show that if variation is generated by among population host or pathogen dispersal, then coevolution occurs largely by pathogens overcoming the partial resistances that are generated.
Keywords: Gene-for-gene, infectivity, parasite, plant disease
Studies of variation in resistance of hosts to their pathogens have revealed a broad sweep of genetic mechanisms underlying such resistance. Depending on the particular host–pathogen association, resistance in the host may or may not be specific to a particular genotype of the pathogen. Genotype specificity is evidenced by strong host–genotype × pathogen–genotype interaction (GH × GP) in response to pathogen challenge. Understanding the genetic basis of host–pathogen interactions is important from both applied and theoretical standpoints. Systems with strong GH × GP should promote active host–pathogen coevolution, and correspondingly the evolution of sex and recombination, whereas less genetically specific interactions should have the reverse effect. The idea that the evolution of sexual reproduction and increased recombination is the result of the coevolutionary interactions between hosts and their pathogens has been termed the Red Queen Hypothesis (Van Valen 1973; Bell 1982; Lively 2010) and has been the focal point for many more recent studies of host–pathogen coevolution (Hamilton 1980; May and Anderson 1983; Lively and Dybdahl 2000; Carius et al. 2001; Decaestecker et al. 2007).
A commonly identified pattern of host–pathogen specificity is the classic gene-for-gene system in plants characterized by clear-cut interactions among specific host and pathogen gene products (Flor 1955; Burdon and Jarosz 1991; Thompson and Burdon 1992). Similar specificities have been shown in insects (Hatchett and Gallun 1970; Bangham et al. 2007) and in coevolutionary experiments in microbial systems (Buckling and Rainey 2002; Forde et al. 2004). In other plant–fungal pathogen systems however, strong GH × GP appear to be absent (Alexander et al. 1993; Granberg 2007). Weak patterns of GH × GP may be the result of including only a limited sample of host and pathogen lines, and sampling over a broader geographical range may reveal substantial evidence of GH × GP (Burdon et al. 1999). However, there may also be evolutionary processes that move a system between the gene-for-gene pattern and one that is more additive with fewer clear cut GH × GP interactions or fewer polymorphic loci. A potential example of this is seen in the interaction between Populus and Melampsora in populations to the east and west of the northern Rocky Mountains. In the dry interior of western Canada, GH × GP interactions are the norm, whereas on the coast only nonspecific resistance is known (Hsiang and Chastagner 1993). Host and pathogen genotype specificities can themselves evolve, and may result in limited polymorphism in only one interactant (Best et al. 2009) or extensive polymorphism in both (Best et al. 2010) depending on the details of the interactions.
At the population level, genetic specificities in host–pathogen interactions can result in rapid cycling of the alleles determining virulence and resistance, and if there is recurrent mutation, there can be continuing longer-term coevolutionary cycles (Seger 1988). In an explicit multilocus model of the classical gene-for-gene systems in plants, Sasaki (2000) showed that the frequency of such cycles was dependent on the costs associated with resistance or virulence alleles, as well as the level of partial resistance. Partial resistance resulted in less-genetic variation being maintained at the resistance and virulence loci and less coevolutionary cycling, thus slowing the evolutionary arms race between host and pathogen. In his model, partial resistance was assumed to be nonspecific, and similar in all host–pathogen genotype combinations, in that there was an equal amount of disease expression in all “incompatible” (i.e., otherwise resistant) host–pathogen genotype combinations.
An opportunity to test the consequences of different degrees of expression of GH × GP interactions arose in the natural flax-rust (Linum marginale – Melampsora lini) system. In this system, host–pathogen interactions are governed by a gene-for-gene system but resistance may also show partial expression (Burdon 1994; see also methods, below). Here, we report on the analysis of partial resistance seen in a cross-inoculation study of 60 pathogen lines on 120 host lines sampled from six long-standing natural populations. The host–pathogen interactions were tested in both sympatric and allopatric combinations. Details of the source populations and methods have been reported previously (Thrall et al. 2002; Thrall and Burdon 2003). In this analysis, we use the results of this experiment to ask (1) whether partial resistance types are characteristic of gene-for-gene systems in nature, (2) if they themselves show GH × GP patterns, (3) if they are less common in coevolved than noncoevolved systems, and (4) if partial resistances reduce levels of host or pathogen diversity and therefore “slow the Red Queen” (as predicted by Sasaki 2000).
Throughout, we use the term virulence in the plant pathology sense of ability to cause disease rather than in the sense of damage done to the host, as in animal systems.
Methods
The model L. marginale – M. lini host–pathogen system involves an interaction between a herbaceous perennial host and its obligate rust pathogen (Burdon and Jarosz 1991). In the study area (the subalpine region of New South Wales), this system is prone to annual pathogen epidemics in the summer followed by marked population crashes with the onset of winter. Host plants typically develop one or more floral shoots in summer and then die back to a few green shoots during winter.
POPULATION SAMPLING
The data analyzed here was collected as part of an investigation of local adaptation in the L. marginale – M. lini host–pathogen system in which a total of six host populations were sampled in three groups of two populations each, distributed across the Kiandra and adjacent Wild Horse Plains in the northern end of the Kosciuzko National Park, NSW, Australia (G1, G3 = northern Kiandra Plain; S1, S2 = southern Kiandra Plain; W1, W2 = Wild Horse Plain). In each host population, seeds from 25 plants were individually collected haphazardly and irrespective of whether individuals showed signs of rust resistance. At the same time, approximately 25 rust samples were collected from each population and returned to the laboratory where each was increased individually on a universally susceptible line of L. usitatissimum after reduction to a single pustule to ensure each isolate consisted of a single pathogen genotype. Further details on the field sites and sampling procedure are in Thrall et al. (2002).
INOCULATION AND SCORING OF RESISTANCE
Twenty host lines from each of the six populations were randomly selected from the 25 collected in the field, grown up, and then challenged with a random subset of 10 of the pathogen isolates from each population (10 isolates × 6 host populations, in all possible pairwise combinations). Resistance reactions were determined using a standard inoculation procedure that uses detached shoots gathered from vigorously growing plants (Burdon and Jarosz 1991; Thrall et al. 2002). Following inoculation, plants were grown in a naturally lit glasshouse and resistance reaction types were scored 12–14 days later. Resistance was scored on a scale of 1–5 using a scale adapted from Lawrence and Burdon 1989 (Thrall et al. 2002), viz:
Fully susceptible [S]: Large full-sized sporulating pustules (uredia) on all leaves.
Partial resistance [P2]: Large full-sized sporulating pustules on the younger leaves, grading down to no pustules on the oldest leaves.
Partial resistance [P3]: Large full-sized pustules only on one or two of the youngest leaves.
Partial resistance [P4]: No sporulation, but with necrotic flecks on older leaves.
Fully resistant [R]: No macroscopic evidence of damage or sporulation.
Categories 1–4 therefore show varying levels of damage to host plants, whereas category 5 represents complete resistance with no evidence of damage. In Category 4, there appears to be recognition of the pathogen with some ensuing damage (perhaps due to a hypersensitive response), but there is complete suppression of sporulation. Suppression of sporulation, even with local damage, would prevent intraplant transmission of this pathogen that has multiple sporulation cycles per growing season.
Because the goal of the original experiment (Thrall et al. 2002) was to compare populations, rather than individual lines, inoculations were not replicated at the level of individual pathogen/host-line combinations. However, previous experimental comparisons have shown that the resistance scores are highly repeatable (Lawrence and Burdon 1989; Burdon and Jarosz 1991).
DATA ANALYSIS
Occurrence of partial resistance categories
To assess the number and types of resistance/virulence reactions, we carried out cluster analysis on host and pathogen lines based on similarity of their resistance scores. Clustering was done independently for host lines and pathogen lines. We used the R packages “Cluster,” and the SAS procedure CLUSTER (SAS Institute, 2003) for confirmatory analysis because some inconsistencies were noted between the results from the programs in the R packages. We used Euclidean distances and Ward’s method for clustering; this protocol creates clusters by minimizing the within-cluster variance over all possible partitions and is thus suitable for identifying similar phenotypes, with less regard to the precise degree of difference between them (Kaufman and Rousseeuw 1990).
These hierarchical clustering techniques are descriptive. There exist no statistical methods to identify either the best clustering algorithm, or the significance of any cut-off points used to determine the number of clusters. Recent interest in identifying similarities among genes in expression arrays has led to attempts to identify clusters more objectively (Pollard and van der Laan 2005). We applied these methods to our data, but the various partitioning algorithms (e.g., using “silhouette” plots) failed, in that they did not identify an optimal number of clusters. The R package “Hopach,” that uses a mixture of partitioning and hierarchical methods, indicated 35 host and 12 pathogen clusters. However, visual inspection of the data suggested these were extreme over-and underestimates of the number of clusters, respectively. To take into account the difficulties of objectively identifying clusters, we based our visual analysis on two levels of cut-off, namely 15 and 30 clusters, thus bracketing the extremes identified by “Hopach.” The two cut off levels for the clusters are indicated by bold and thin lines in Figure S1, but in the text we only discuss groups at the 15-cluster level.
To examine if the scoring scheme for partial resistance types was appropriately ranked, a cluster analysis was carried out giving the P2, P3, and P4 classes the same score. It was evident (Fig. 1, Supporting information) that the score of P4 was more often associated with full resistance, and P2 was associated more often with full susceptibility (no resistance). The original ranking scores were therefore retained for the analyses reported here.
GH × GP patterns in partial resistance categories
Because the clustering had been done independently on the hosts and on the pathogens, a significant host cluster by pathogen cluster interaction effect on resistance score indicates significant GH × GP interaction. To test for GH × GP interaction of partial scores, we used a Mantel–Haentszel test based on partial resistance scores only by setting fully resistant and fully susceptible scores to missing values (SAS PROC FREQ, with CMH option; Stokes et al. 2000, SAS Institute 2003).
Partial resistances in coevolved and noncoevolved host–pathogen combinations
The host and pathogen lines were grouped by their six populations of origin, with each of two populations coming from three regions. We compared the outcomes of three different types of cross-inoculations that tested host–pathogen interactions across a gradient of decreasing levels of sympatry: (1) among regions, (2) among populations within regions, and (3) within populations. These categories can be hypothesized to represent a gradient of increased time opportunity for coevolution of the host and the pathogen.
To test whether the proportion of partial resistance responses varied among the three cross-inoculation types, the data were transformed to a binary format of partial resistance scores (P2–P4) and complete resistance scores (S and R). Explanatory fixed variables were region from which host and pathogen populations originated, host and pathogen population (nested under region), and the level of sympatry of the inoculation (within populations, among populations of the same regions, and among regions). Plant lines and pathogen isolates, hierarchically nested under their respective population and region, were defined as random effects in the model. The Akaike information criterion was used to select the best model. We used the GLIMMIX procedure implemented in SAS (Littell et al. 2006).
We also used chi-square tests to assess if the number of partials within each population was less than the number expected based on the marginal frequencies observed for that population, either when the host was tested against sympatric and allopatric pathogen lines or when the pathogen was tested on sympatric or allopatric host lineages.
Host and pathogen diversity in coevolved and noncoevolved populations
To estimate if diversity differed between cross-inoculations done among regions, within regions, and within populations, we used the Shannon–Weaver index (−Σpi ln pi, where pi = frequency of the ith resistance score) to measure diversity in resistance scores among host and pathogen lines.
To estimate if the level of host-specificity differed between cross-inoculations done among regions, within regions, or within populations, we measured the variance among host lines, among pathogen lines, and their interaction (GH × GP), based on variance components from two-way analyses of variance (SAS PROC GLM Type III Sums of Squares) with pathogen line and host line as fixed effects.
Results
OCCURRENCE OF PARTIAL RESISTANCE CATEGORIES
The number of partial resistance type scores in categories 2, 3, and 4 (P2, P3, P4) were 747, 319, and 347, respectively (out of 7200 plant–pathogen combinations tested). Variation among pathogen and host lines in the number of partial scores was similar (coefficient of variation of number of P2, P3, P4 in pathogen lines = 0.78, 1.53, and 1.18, and in host lines = 0.78, 0.98, 1.29 respectively).
The resistance/virulence reactions showed clear clustering of host and pathogen genotypes, and strong host-genotype × pathogen-genotype (GH × GP) interactions (see Fig. S1, Supporting information, for the full cross-inoculation matrix ordered by cluster). No such obvious groupings emerged from an identical cluster analysis of the same set of cross-inoculation scores that had been randomized across host and pathogen genotypes; instead this produced small clusters scattered over the whole array of cross-inoculations (results not shown).
There were pathogen and host lines that gave a large number of partial resistance types (P2 + P3 + P4). For example, one pathogen cluster including seven fungal isolates (S1–19…W2–7; Fig. S1) gave an average of 52.1 partials (range 46–61) out of 120, whereas another cluster with 10 fungal isolates (S1–9…W2–20; Fig. S1) gave an average of 10.1 partials (range 2–25).
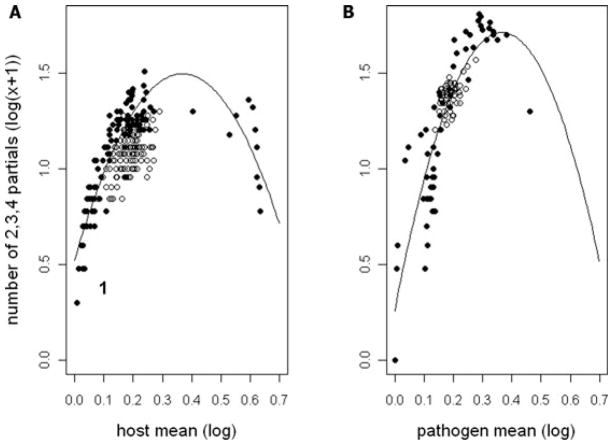
At the level of the whole cross-inoculation experiment (120 hosts × 60 pathogens), the number of partial resistance types was greatest when the virulence/resistance reaction of the individual families or pathogen lines was intermediate (Fig. 1). We used a randomization method to investigate if this pattern was due to chance because, for example in extremis, a genotype that was completely resistant/virulent to all other genotypes would be expected to have no intermediate resistances, and similarly for a completely susceptible/avirulent genotype. Randomizing the resistance classes (but keeping their overall frequency equal to that observed) showed a much tighter clustering of points over repeated runs (open circles, Fig. 1). The observed pattern cannot therefore be attributed to chance sampling.
Figure 1.
(A) Relationship between the number of partial resistances within a host line (tested against all pathogen lines) and the mean resistance of the host line. (B) Relationship between the number of partial resistances expressed when a pathogen line is tested against all host lines and the mean resistance expressed in inoculations using that pathogen line. Sum of number of partial resistances for each line is log10 (x + 1) transformed; mean resistance scores for each line are log10 (x) transformed. Filled circles are the observed data, and open circles represent one typical instantiation of a simulation that generates random expectations based on overall frequencies (see text for further explanation).
GH × GP PATTERNS IN PARTIAL RESISTANCE CATEGORIES
There was a highly significant interaction effect between host and pathogen cluster for the partial resistance scores P2, P3, and P4 considered together (general association: df = 28, Chi square = 372.00, P < 0.0001). Interactions were also significant at P < 0.0001 when the number of each of the partial resistance scores was tested individually.
Visual inspection of the cross-inoculation matrix (Fig. S1) confirmed clear GH × GP interactions for not only the occurrence of partials, but also for the exact level of these partial resistance types. Thus one group defined by a cluster of seven pathogen lineages (S-19 to W2–7) and two adjacent clusters of 22 host lineages (W1–19 to W1–2) had mostly P2 and P3 partials, whereas the same seven pathogen lineages when used to inoculate three different but adjacent clusters of 28 host lineages (S2–12…G3–6) gave mostly P3 and P4 partials.
PARTIAL RESISTANCES IN COEVOLVED AND NONCOEVOLVED HOST–PATHOGEN COMBINATIONS
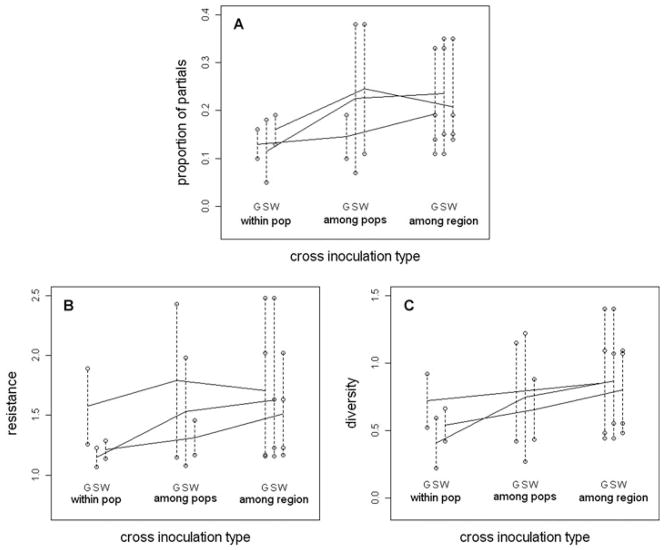
Cross-inoculations among sympatric host and pathogen lineages within populations showed less resistance (or higher virulence of the pathogen), fewer partial resistance types (P2 + P3 + P4), and a lower overall diversity of resistance scores than cross-inoculations among allopatric lineages from greater distances (Fig. 2).
Figure 2.
(A) Proportion of partial resistances, (B) average resistance scores, and (C) diversity of resistance scores (Shannon–Weaver index, see text) for cross-inoculations using lines from within populations (two per region), from among populations (two different populations within each region), and among regions (lines from each region are tested against those from two other regions, in reciprocal combinations of the host and pathogen, giving four sets of cross-inoculations for each region). S, G, and W identify the regions (northern Kiandra Plain, southern Kiandra Plain, and Wild Horse Plain, respectively). Open circles are means for each set of cross-inoculations, and the dotted lines joining them identify the same region.
The proportion of partial resistance scores was significantly lower for the sympatric, and putatively more coevolved, host–pathogen combinations than it was for host–pathogen combinations from different populations of the same region (P = 0.0015) or among different regions (P < 0.0001) (Overall effect of the level of sympatry P < 0.0001; Table 1, Fig. 2A). Also, there were highly significant differences among host and pathogen regions in the proportion of partial responses, as well as significant differences among host and pathogen populations within regions in the proportion of partial resistance scores (Table 1).
Table 1.
Results of a generalized linear mixed model with binomial link, analyzing the proportion of partial resistance scores. Wald’s Z-statistic is given for random effects and the F-statistic is given for fixed effects.
| Random effects | Estimate (±SE) | Z | P |
|---|---|---|---|
| Host (Host population, Host region) | 0.45±0.08 | 5.41 | <0.0001**** |
| Pathogen (Host population, Host region) | 1.16±0.25 | 4.66 | <0.0001**** |
| Residual | 0.99±0.02 | 59.17 | <0.0001**** |
| Fixed effects | df, error df | F | P |
| Level of sympatry | 2, 7019 | 10.33 | <0.0001**** |
| Host population (Host region) | 3, 114 | 17.12 | <0.0001**** |
| Pathogen population (Host region) | 3, 54 | 3.12 | 0.0335* |
| Host region | 2, 114 | 9.97 | <0.0001**** |
| Pathogen region | 2, 54 | 6.56 | 0.0028** |
Note, in all tables: ns=P>0.10;
P<0.10;
P<0.05;
P<0.01;
P<0.001;
P<0.0001.
When populations were considered separately, the number of partial scores within each population was less than the number expected based on the marginal frequencies observed for that population when it was tested against either allopatric host lines or allopatric pathogen lines (Table 2). Pathogens from sympatric populations generated fewer partial resistance scores when tested on their local host populations in four of the six cases, but it was the reverse in the case of population W2. Hosts from sympatric populations also tended to have fewer partials when inoculated with pathogen lines from their local populations in three of six cases, and significantly so in S1. Analyses on numbers of P2, P3, and P4 individually all showed the same trends (data not shown).
Table 2.
Observed number of partial resistance scores by host lineage (n=200) for sympatric within population cross-inoculations, in relation to the expected number of partials (n=1000) based on marginal frequencies for the same lineages in allopatric populations. The section of rows labeled “Pathogen” represents pathogen lineages from the six populations tested on sympatric and allopatric hosts, and correspondingly “Host” represents host families tested using sympatric and allopatric pathogens. Chi-square is for a 2×2 contingency test with 1 degree of freedom.
| Population | Sympatric vs. allopatric | Chi-square |
|---|---|---|
| Pathogen | ||
| G1 | 20<51.2 | 22.90**** |
| G3 | 31<43.6 | 4.02* |
| S1 | 9<18.2 | 4.62* |
| S2 | 35=39.8 | 0.61 ns |
| W1 | 26<72.8 | 41.60**** |
| W2 | 38<25.2 | 5.64* |
| Host | ||
| G1 | 20<29.6 | 3.19 (*) |
| G3 | 31<21.4 | 3.77 (*) |
| S1 | 9<88.4 | 111.98**** |
| S2 | 35=38.2 | 0.28 ns |
| W1 | 26=22.8 | 0.41 ns |
| W2 | 38<50.4 | 3.50 (*) |
With regard to average resistance scores (Table 3; Fig. 2B), pathogens from sympatric populations were more virulent on their sympatric host populations than they were on allopatric host populations. Hosts from sympatric populations were significantly more susceptible to their pathogen lines than were hosts from allopatric populations, except in G3 where they were more resistant.
Table 3.
Observed mean resistance scores (n=200) for sympatric within population cross-inoculations, in relation to resistance for the same lineages in allopatric populations (n=1000). Higher values indicate greater resistance. The section of rows labeled “Pathogen” represents pathogen lineages from the six populations tested on sympatric and allopatric hosts, and correspondingly “Host” represents host families tested using sympatric and allopatric pathogens. F values are from analyses of variance testing for differences between sympatric and allopatric populations (Procedure GLM, Type III Sums of Squares; SAS Institute 2003) with levels of sympatry and lineage as main effects; interaction effects were also included but were generally small relative to main effects.
| Population | Sympatric vs. allopatric | F1,1180 |
|---|---|---|
| Pathogen | ||
| G1 | 1.26<1.65 | 31.16**** |
| G3 | 1.89<2.67 | 72.41**** |
| S1 | 1.07<1.14 | 3.21 (*) |
| S2 | 1.23<1.38 | 6.19* |
| W1 | 1.14<1.54 | 44.05**** |
| W2 | 1.29=1.23 | 1.57 ns |
| Host | ||
| G1 | 1.26<1.44 | 2.39* |
| G3 | 1.89>1.14 | 209.11**** |
| S1 | 1.07<2.34 | 163.88**** |
| S2 | 1.23<1.56 | 17.07**** |
| W1 | 1.14<1.47 | 16.93**** |
| W2 | 1.29<1.66 | 19.08**** |
HOST–PATHOGEN DIVERSITY IN COEVOLVED AND NONCOEVOLVED POPULATIONS
Although most of the comparisons were not statistically significant (Table 4; Fig. 2C), in general, sympatric host–pathogen combinations tended to have less total diversity (10 of 12 comparisons in this direction). However, the GH × GP interaction variance component tended to be a greater proportion of this total (again, 10 of 12 comparisons in this direction; Table 4).
Table 4.
Variance component analysis of resistance scores for sympatric within population cross-inoculations in relation to the variance components for allopatric populations (average of five allopatric populations). For the total variance, the section of rows labeled “Pathogen” represents interactions generated by using the same pathogen lineages inoculated on hosts from sympatric or allopatric populations. Correspondingly “Host” represents interactions generated by using the same host families inoculated by pathogens from sympatric or allopatric populations. The percent variation explained by the interaction is similarly presented. Statistical significance is based on a two tailed t-test using among allopatric population variation (n=5) to estimate standard error.
| Population | Total variance Sympatric vs. allopatric | % Interaction variance component Sympatric vs. allopatric |
|---|---|---|
| Pathogen | ||
| G1 | 0.678=1.028 | 19.6=33.1 |
| G3 | 2.350<3.290*** | 71.2>29.8*** |
| S1 | 0.137=0.242 | 90.9>74.3** |
| S2 | 0.314=0.660 | 82.1=60.9 |
| W1 | 0.143<0.524(*) | 78.0>62.8* |
| W2 | 0.475=0.442 | 73.6=67.8 |
| Host | ||
| G1 | 0.678=0.877 | 19.6<57.4** |
| G3 | 2.350>0.216*** | 23.5> 2.2*** |
| S1 | 0.137<0.188* | 90.9>31.1*** |
| S2 | 0.314=1.070 | 82.1=61.0 |
| W1 | 0.143=0.991 | 78.0=54.0 |
| W2 | 0.475=1.151 | 73.6>52.0 (*) |
Many of the genotypes distinguishable in the overall 120 × 60 cross-inoculation matrix were not distinguished in the intrapopulation cross-inoculations (Fig. 3, where the horizontal and vertical lines delimit genotypic clusters identifiable in the overall cross-inoculations at the 15-cluster level in Fig. S1). Only a subset of these genotypes (clusters indicated by the double lines, drawn visually) is clearly distinguishable based on the within population cross-inoculations. Some of these host–pathogen genotype combinations were characterized by partial resistance (e.g., Fig. 3: left-hand column in G1 are predominantly P2 types and top left-hand corner of W2 are predominantly P3 and P4 types).
Figure 3.
Data for sympatric cross-inoculations for each of the six populations; cross-inoculations only involve hosts and pathogens from the same population. Shading and numbers are the same as in Figure S1. The single and double lines both identify clusters at the 15 level of clustering (see Fig. S1), based on the overall cross-inoculation matrix. The double lines highlight clusters that are visually identifiable only within populations (assessed qualitatively—cluster analysis did not identify a specific cut off point that provided a reasonable fit to the data from every population). The numbers on the top and left of each population are lineage IDs for the pathogens and hosts in that population in Figure S1 (e.g., under G1, 11 identifies pathogen lineage G1–11).
On the basis of within-population inoculations, the pattern seen in populations S1 and W1 might be interpreted as showing complete susceptibility with some “quantitative variation,” whereas the pattern seen in G1, S2, and W2 might be interpreted as showing partial resistance and “single locus variation”(in both host and pathogen); only G3 clearly shows a “canonical” gene-for-gene pattern.
Discussion
Our results show that the Linum – Melampsora gene-for-gene system commonly has partial resistance phenotypes, and that these partial types also show GH × GP interactions. Partial resistance types have been commonly found in other host–pathogen systems. For example, in the interactions occurring between bread wheat and each of its rust pathogens (Puccinia graminis f.sp. tritici, P. recondita, P. striiformis) many resistances that show host-genotype × pathogen-genotype interactions also often have intermediate resistance phenotypes typified by different degrees of chlorosis, necrosis, and sporulation (McIntosh et al. 1995).
In gene-for-gene systems, such partial resistance types could be generated by the action of single genes acting alone, or by the action of modifiers that may, or may not, be cued by environmental factors. Genetically determined partial resistance types may also be generated by incomplete dominance in the heterozygous state of a resistance gene that confers full resistance when in a homozygous state, or may be caused by the presence of resistance genes that only confer partial resistance even in a homozygous state. Both of these types of partial resistance occur in the Linum – Melampsora system (Burdon 1994). In other instances, the expression of one or more resistance genes may be affected by modifer genes that influence their expression (Nelson et al. 1997).
In the present study, individual inoculations were not replicated, and therefore it is possible that some of the partial resistance types observed may represent scoring errors or environmentally induced variation in disease expression. However, several lines of evidence suggest that the observed patterns represent, at least to a large degree, genetic expressions of resistance phenotypes. First, scoring errors in previous studies have been low in related studies using identical methods (<5% in all resistance scores, J.J. Burdon unpubl. data). Second, Burdon (1994) showed clear evidence of single-locus determination of partial resistance in one interpopulation cross in the same system. As noted above, the occurrence of partial resistance types has also been recorded in other wild plants (e.g., Glycine spp.–Phakopsora pachyrhizi, Burdon 1987; Senecio vulgaris–Erysiphe fischeri, Bevan et al. 1993) and in gene-for-gene systems of crop plants (e.g., Phaseolus spp.–Uromyces sp., Ochoa et al. 2007) including the closely related cultivated flax–rust system (L. usitatissimum – M. lini) (Flor 1955). Third, we simulated random variation in disease expression and this did not result in distinct clusters of intermediate phenotypes, as observed in the data from the experimental inoculations. It is therefore likely that the clusters represent genetic differences in disease expression associated with particular host or pathogen lineages.
In the region from where the populations were sampled for this study, the host is highly inbred and the pathogen asexual (Burdon and Roberts 1995; Burdon et al. 1999); hence lineages carrying a major gene could be in complete linkage disequilibrium with modifier genes affecting the level of resistance. It is therefore impossible from the data to assess whether one or more genes are involved in the resistance/virulence of any host/pathogen lineage. Functionally, the partial resistance phenotypes P2 and P3 (which have pustules on younger leaves, rather than on all leaves as in a fully susceptible reaction) may represent a higher resistance of developmentally older leaves, and would be consistent with quantitative control of resistance. Where lesions are present but no sporulating pustule is formed (partial resistance type P4) a quite different resistance mechanism may be involved in which the initial resistance is successful, but a stronger than normal hypersensitive reaction leads to greater necrosis and chlorosis than occurs in a fully resistant reaction; such sequential resistance components have been characterized in gene-for-gene systems at the molecular level (Jones and Dangl 2006). Limiting pathogen transmission would be advantageous for the host as it prevents secondary transmission of this polycyclic pathogen among leaves within the same plant (or to other related individuals). Although P4 partials are found more often in host–pathogen combinations showing complete resistance, it is impossible to say if this is the result of a functional relationship or linkage disequilibrium.
The occurrence of partial resistance types in specific host–pathogen interactions raises the question of how their presence influences the process of host–pathogen coevolution.
Populations composed of fully expressed resistant and susceptible phenotypes are likely to show coevolutionary scenarios that are different from those seen in populations containing large proportions of partial resistance phenotypes. In the former situation, pathogen survival is restricted to those lineages whose virulence matches the resistances present in the host population. On the other hand, in populations dominated by partial resistance phenotypes, most if not all lineages survive (although their relative frequency may change) and selection for the appearance of pathogens fully virulent on the partials may be lower, depending on the costs and strength of selection against unnecessary virulence genes (Leonard 1977; Marshall and Weir 1985).
These scenarios are supported by the model of coevolution in a gene-for-gene system developed by Sasaki (2000). In this model, increasing levels of partial resistance had the effect of decreasing the likelihood that there would be selection for specific host and pathogen phenotypes. Greater levels of partial resistance/virulence resulted in lower variation in both host and pathogen. Importantly, this also had the consequence of reducing the probability of coevolutionary cycles and effectively slowing the evolutionary arms race between host and pathogen. In contrast to this, Agrawal and Lively (2002) showed that partial resistances can sometimes accelerate coevolutionary cycles, but the partial resistances in this study were imposed in a specific way to mimic a continuum between matching allele and gene for gene. Although the accelerated cycles were interpreted as the result of the matching allele properties (rather than the result of the partial resistance per se), the greatest variance in allele frequency occurred if the partial resistances were intermediate. Clearly the role of partial resistance in coevolutionary responses deserves further investigation both theoretically and empirically.
Sasaki’s (2000) model was of an asexual host and pathogen population, and hence it reflected features characteristic of the Linum – Melampsora populations in this study, where the host is self-fertilizing and the pathogen is asexual. It also assumed the presence of costs for both resistance and virulence, and such costs have been shown to be present in this system for pathogen virulence (Thrall and Burdon 2003); there have been no studies carried out testing directly for resistance costs. Although Sasaki’s model assumed that partial resistance was a feature of all of the specific gene-for-gene interactions, our results show that these interactions themselves can be restricted to particular host–pathogen combinations. If we assume (in the absence of phylogeographic evidence) that the results from our sympatric inoculations reflect “more coevolved” interactions than those from inoculations between allopatric isolates, the present study shows that the majority of putatively coevolved populations have decreased proportions of partial resistances relative to noncoevolved populations, and that pathogen virulence has increased. Increased pathogen virulence was also observed in previous and independent analyses of the same dataset (Thrall et al. 2002). This evolution of increased virulence in the pathogen is accompanied by a reduced number of partial resistance responses, perhaps because such partial resistances are readily overcome by evolution in the pathogen.
Our results also showed that the diversity of virulence and resistance phenotypes is reduced in sympatric cross-inoculations, but that there was a trend toward the overall GH × GP interaction component t becoming greater within populations, even while total variance was lost. There is therefore no evidence from our data that allopatric populations with many partial resistance types evolve toward decreased levels of GH × GP (i.e., toward quantitative or horizontal resistance, in plant pathology terminology: Van der Plank 1963). Partial resistance types therefore appear to be very much a part of the coevolutionary race but there is no evidence that they are capable of “slowing the Red Queen.” Rather the Red Queen appears to be enlivened by regional processes of dispersal and colonization that generate novel, although often partially expressed, GH × GP combinations. Testing how coevolutionary host–pathogen cycles are slowed or accelerated (and whether the Red Queen stops and starts, as she did with Alice) remains an empirical challenge for future studies of gene-for-gene systems.
The results also strongly argue that host–pathogen genetic systems, such as gene-for-gene, are evolved characteristics and only partly predetermined by mutational processes impinging on a particular mechanism at the molecular/physiological level. In the plant breeding literature, there has also been substantial controversy about whether gene-for-gene systems are an artifact of the plant breeding process, rather than properties of the wild host–pathogen systems that are so often the source of genes for crop improvement. In our study, there is substantial evidence that the phenotype of partial resistance and virulence evolves to become a phenotype with more all-or-nothing characteristics. Unfortunately, because we do not know the genetic or molecular bases for partial and complete resistance, we do not know if this is by virtue of selection for more specificity of elicitor/receptor alleles or whether initially nonspecific mechanisms are changed by indirect selection on modifier alleles.
Supplementary Material
Overall results from the cross-inoculations.
Acknowledgments
We are grateful to J. Taylor (CSIRO Bioinformatics Team) for advice on cluster analysis. This work was partially supported by NIH grant 5RO1 GM074265-01A2 and NSF grant DEB 0640777.
LITERATURE CITED
- Alexander HM, Antonovics J, Kelly A. Genotypic variation in plant disease resistance: physiological resistance in relation to field disease transmission. J Ecol. 1993;81:325–333. [Google Scholar]
- Agrawal A, Lively CM. Infection genetics: gene-for-gene versus matching—alleles models and all points in between. Evol Ecol Res. 2002;4:79–90. [Google Scholar]
- Bell G. The masterpiece of nature: the evolution and genetics of sexuality. Univ. of California Press; Berkeley, CA: 1982. [Google Scholar]
- Best A, White A, Boots M. The implications of coevolutionary dynamics to host-parasite interactions. Am Nat. 2009;173:779–791. doi: 10.1086/598494. [DOI] [PubMed] [Google Scholar]
- Best A, White A, Kisdi E, Antonovics J, Brockhurst MA, Boots M. The coevolution of host-parasite range. Am Nat. 2010;176:63–71. doi: 10.1086/653002. [DOI] [PubMed] [Google Scholar]
- Bangham J, Obbard DJ, Kim KW, Haddrill PR, Jiggins FM. The age and evolution of an antiviral resistant mutation in Drosophila melanogaster. Proc R Soc Lond B. 2007;274:2027–2034. doi: 10.1098/rspb.2007.0611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bevan JR, I, Crute R, Clarke DD. Diversity and variation in expression of resistance to Erysiphe fischeri in Senecio vulgaris. Plant Pathol. 1993;42:647–653. [Google Scholar]
- Buckling A, Rainey PB. Antagonistic coevolution between a bacterium and a bacteriophage. Proc R Soc Lond B. 2002;269:931–936. doi: 10.1098/rspb.2001.1945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burdon JJ. The distribution and origin of genes for race specific resistance to Melampsora lini in Linum marginale. Evolution. 1994;48:1564–1575. doi: 10.1111/j.1558-5646.1994.tb02196.x. [DOI] [PubMed] [Google Scholar]
- Burdon JJ. Phenotypic and genetic patterns of resistance to the pathogen Phakopsora pachyrhizi in populations of Glycine canescens. Oecologia. 1987;73:257–267. doi: 10.1007/BF00377516. [DOI] [PubMed] [Google Scholar]
- Burdon JJ, Jarosz AM. Host-pathogen interactions in natural populations of Linum marginale and Melampsora lini: I. Patterns of resistance and racial variation in a large host population. Evolution. 1991;45:205–217. doi: 10.1111/j.1558-5646.1991.tb05278.x. [DOI] [PubMed] [Google Scholar]
- Burdon JJ, Roberts JK. The population genetic structure of the rust fungus Melampsora lini as revealed by pathogenicity, isozyme and RFLP markers. Plant Pathol. 1995;44:270–278. [Google Scholar]
- Burdon JJ, Thrall PH, Brown AHD. Resistance and virulence structure in two Linum marginale-Melampsora lini host-pathogen metapopulations with different mating systems. Evolution. 1999;53:704–716. doi: 10.1111/j.1558-5646.1999.tb05365.x. [DOI] [PubMed] [Google Scholar]
- Carius HJ, Little TJ, Ebert D. Genetic variation in a host-parasite association: potential for coevolution and frequency dependent selection. Evolution. 2001;55:1136–1145. doi: 10.1111/j.0014-3820.2001.tb00633.x. [DOI] [PubMed] [Google Scholar]
- Decaestecker E, Gaba S, Raeymaekers JAM, Stoks R, Van Kerckhoven L, Ebert D, De Meester L. Host-parasite ‘Red Queen’ dynamics archived in pond sediment. Nature. 2007;450:870–873. doi: 10.1038/nature06291. [DOI] [PubMed] [Google Scholar]
- Flor HH. Host-parasite interaction in flax rust: its genetics and other implications. Phytopathology. 1955;45:297–301. [Google Scholar]
- Forde SE, Thompson JN, Bohannan BJM. Adaptation varies through space and time in a coevolving host-parasitoid interaction. Nature. 2004;431:841–844. doi: 10.1038/nature02906. [DOI] [PubMed] [Google Scholar]
- Granberg A. Doctoral Dissertation. Umea University; Sweden: 2007. Microbotryum violaceum on Silene dioica – understanding traits that influence plant-pathogen interactions. [Google Scholar]
- Hamilton WD. Sex versus non-sex versus parasite. Oikos. 1980;35:282–290. [Google Scholar]
- Hatchett JH, Gallun RL. Genetics of the ability of the Hessian fly, Mayetiola destructor, to survive and on wheat having different genes for resistance. Ann Entomol Soc Am. 1970;63:1400–1407. [Google Scholar]
- Hsiang T, Chastagner GA. Variation in Melampsora occidentalis rust on poplars in the Pacific northwest. Can J Plant Pathol. 1993;15:175–181. [Google Scholar]
- Jones JDG, Dangl JL. The plant immune system. Nature. 2006;444:323–329. doi: 10.1038/nature05286. [DOI] [PubMed] [Google Scholar]
- Kaufman L, Rousseeuw PJ. Finding groups in data: an introduction to cluster analysis. Wiley; NY: 1990. [Google Scholar]
- Lawrence GJ, Burdon JJ. Flax rust from Linum marginale: variation in a natrual host-pathogen interaction. Can J Bot. 1989;67:3192–3198. [Google Scholar]
- Lively CM. A review of Red Queen models for the persistence of obligate sexual reproduction. J Heredity. 2010;101:S13–S20. doi: 10.1093/jhered/esq010. [DOI] [PubMed] [Google Scholar]
- Lively CM, Dybdahl MF. Parasite adaptation to locally common host genotypes. Nature. 2000;405:679–681. doi: 10.1038/35015069. [DOI] [PubMed] [Google Scholar]
- Littell RC, Milliken GA, Stroup WW, Wolfinger RD, Schabenberger O. SAS for Mixed Models. 2. SAS Institute; Cary, NC: 2006. [Google Scholar]
- Leonard KJ. Selection pressures and plant pathogens. Ann NY Acad Sci. 1977;287:207–222. [Google Scholar]
- Marshall DR, Weir BS. Multiline varieties and disease control. 5. The “dirty crop” approach with complex mixtures of genotypes based on overlapping gene sets. Theor Appl Genet. 1985;69:463–474. doi: 10.1007/BF00251086. [DOI] [PubMed] [Google Scholar]
- May RM, Anderson RM. Epidemiology and genetics in the coevolution of parasites and hosts. Proc R Soc Lond B. 1983;219:281–313. doi: 10.1098/rspb.1983.0075. [DOI] [PubMed] [Google Scholar]
- McIntosh RA, Wellings CR, Park RF. Wheat rusts: an atlas of resistance genes. CSIRO Publishing; Australia: 1995. [Google Scholar]
- Ochoa J, Criz E, Murillo A, Danial DL. Variation in virulence and resistance in the bean-bean rust pathosystem in Ecuador. Euphytica. 2007;153:313–319. [Google Scholar]
- Nelson JC, Singh RP, Autrique JE, Sorrells ME. Mapping genes conferring and suppressing leaf rust resistance in wheat. Crop Sci. 1997;37:1928–1935. [Google Scholar]
- Thompson JN, Burdon JJ. Gene-for-gene coevolution between plants and parasites. Nature. 1992;360:121–125. [Google Scholar]
- Pollard KS, Van Der Laan MJ. UC Berkeley Division of Biostatistics Working paper Series Paper 167. University of California; Berkeley, CA: 2005. Cluster analysis of genomic data with applications in R; pp. 1–25. [Google Scholar]
- SAS Institute. Statistical analysis system 9.1.3. SAS Institute; Cary, N.C.: 2003. [Google Scholar]
- Seger J. Dynamics of some simple host-parasite models with more than two genotypes in each species. Philos Trans R Soc Lond B. 1988;319:541–555. doi: 10.1098/rstb.1988.0064. [DOI] [PubMed] [Google Scholar]
- Sasaki A. Host-parasite coevolution in a multilocus gene-for-gene system. Proc R Soc Lond B. 2000;267:2183–2188. doi: 10.1098/rspb.2000.1267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stokes ME, Davis CS, Koch GG. Categorical data analysis using the SAS system. SAS Institute; Cary, NC: 2000. [Google Scholar]
- Thrall PH, Burdon JJ. Evolution of virulence in a plant host-pathogen metapopulation. Science. 2003;299:1735–1737. doi: 10.1126/science.1080070. [DOI] [PubMed] [Google Scholar]
- Thrall PH, Burdon JJ, Bever JD. Local adaptation in the Linum marginale-Melampsora lini host-pathogen interaction. Evolution. 2002;56:1340–1351. doi: 10.1111/j.0014-3820.2002.tb01448.x. [DOI] [PubMed] [Google Scholar]
- Van Der Plank JE. Plant diseases: epidemics and control. Academic Press; London: 1963. [Google Scholar]
- Van Valen L. A new evolutionary law. Evol Theory. 1973;1:1–30. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Overall results from the cross-inoculations.