Microwave tomography of extremities: 2) Functional fused imaging of flow reduction and simulated compartment syndrome

Abstract

Medical imaging has recently expanded into the dual- or multi-modality fusion of anatomical and functional imaging modalities. This significantly improves the diagnostic power while simultaneously increasing the cost of an already expensive medical devices or investigations and decreasing their mobility. We are introducing a novel imaging concept of four-dimensional (4D) Microwave Tomographic (MWT) functional imaging: three-dimensional (3D) in spatial domain plus one-dimension (1D) in the time, functional dynamic domain. Instead of a fusion of images obtained by different imaging modalities, 4D MWT fuses absolute anatomical images with dynamic, differential images of the same imaging technology.

The approach was successively validated in animal experiments with short term arterial flow reduction and a simulated compartment syndrome in an initial simplified experimental setting using dedicated microwave tomographic system. The presented fused images are not perfect as MWT is a novel imaging modality at its early stage of the development and ways of reading of reconstructed MWT images need to be further studied and understood. However, the reconstructed fused images present clear evidence that microwave tomography is an emerging imaging modality with great potentials for functional imaging.

1. Introduction

Medical imaging plays a significant role in the advances of modern non-invasive diagnostics, treatment planning and post-treatment follow-up studies. Recently medical imaging has expanded into dual- or multi-modality fusion of morphological/anatomical (for example: CT and MRI) and functional (for example: FDG-PET and DCE-MRI) imaging modalities. This significantly improves the diagnostic power while simultaneously increasing the cost of already expensive medical devices/investigations.

We are introducing the novel imaging concept of four-dimensional (4D) Microwave Tomographic (MWT) functional imaging - three-dimensional (3D) in spatial domain plus one-dimension (1D) in the time, functional dynamic domain. Instead of a fusion of images obtained by different imaging modalities, 4D MWT fuses absolute anatomical images with dynamic, differential images of the same imaging technology. The areas of applications include but not limited to cardiovascular and brain imaging, detection of malignancies in breast, lung, liver and kidney, and musculoskeletal applications.

As well as the increased costs, an additional downside of multi-modalities imaging system is their large size decreasing their mobility. Given recent progress in mobile and telecommunications (the technologies that are directly applicable to MWT), we envision that future MWT systems will be applicable for “bed-side functional imaging” or placed in an emergency vehicle or helicopter. The goal of this project is to test a novel 4D MWT functional imaging concept using an initial simplified 3D setting: 2D spatial domain plus 1D time dimension, functional domain.

This is the second of two companion papers focused on an application of microwave tomography for extremity soft tissue imaging using a dedicated microwave tomographic (MWT) system. The system’s technical performance and test results were presented in the first companion paper. The imaging results are presented and discussed in this paper. The paper is organized as follows: 1. The developed and used image reconstruction algorithms are presented in Section 2. 2. Obtained imaging results are summarized and discussed in Section 3.

2. Materials and Methods

In this study we used iterative approaches based on 2D Newton (2DN) and 2D Born (2DB) methods. Both methods were used for reconstruction of both absolute and differential (functional) images. The particulars of each method are summarized in two following sub-sections 2.1 and 2.2.

2.1 2D Newton (2DN) approach

In order to obtain an absolute image of an object we used a Newton-based iterative method. The use of Newton-based methods for imaging 2D high contrast object in diffraction tomography was developed in (Burov et al 1986, Chew et al 1990, Souvorov et al 1998, Joachimowicz et al 1998). Our microwave tomographic system has a cylindrical imaging chamber. A plurality of transmitting and receiving antennas are located along the perimeter of the inner surface of the cylinder with a diameter of 21.5 cm at its central cross-section. The total number of antennas is 24 and each of the antennas can perform as a transmitter or receiver. We suppose that each antenna generates a linearly polarized electromagnetic field (E component in parallel to the axis of the cylindrical imaging chamber) when it works as a transmitter and each receiver measures the same E component of scattered field only when it works as a receiver. At this point we have not considered any depolarization effect of EM field, which may occur within biological objects.

The geometrical sketch of the problem is presented in Figure 1. The imaging domain defined here is the inner area of the circled measurement domain. The imaging domain includes an object domain with an unknown distribution of dielectric properties ε(r⃗) immersed into a homogeneous media with known dielectric properties ε₀. Suppose that i^th (i varies from 1 to 24) transmitter generates EM field E_i. According to the perturbation theory, the change in the electrical fields registered by the receiver number j (j varies from 1 to 23) due to a small change δε in the complex dielectric properties of an object illuminated by the i^th transmitter is equal to:

$$\delta E_{ij}=\frac{k_0^2}{{\epsilon }_0}\int E_i(\overrightarrow{r})G_j(\overrightarrow{r})\delta \epsilon (\overrightarrow{r})d\overrightarrow{r}=\widehat{D}\delta \epsilon$$ (1)

where $k_0=2\pi f\sqrt{{\epsilon }_0}/\text{c}$ and ε₀ are the wave number and dielectric properties of the background media, f - is a frequency, and c – is a speed of light in vacuum. The direct propagating wave E_i and the Green’s function G_j can be found from the Helmholtz’s Equations:

$$\begin{array}{l}({\nabla }^2+k^2)E_i=-\delta (\overrightarrow{r}-{\overrightarrow{r}}_i)\\ ({\nabla }^2+k^2)G_j=-\delta (\overrightarrow{r}-{\overrightarrow{r}}_j)\end{array}$$ (2)

where $\text{k}=2\pi \sqrt{\epsilon }/c$ and ε(r⃗) are the wave number and dielectric properties at r⃗, r⃗_i and r⃗_j are the coordinates of the transmitter and the receiver. If operator D̂ is calculated, the step of the Newton’s iterative procedure is:

$$\begin{array}{l}{\epsilon }^{n+1}={\epsilon }^n+\delta {\epsilon }^n\\ ({\widehat{D}}^{+}\widehat{D}+\alpha \mathrm{\Omega })\delta {\epsilon }^{n+1}=\beta {\widehat{D}}^{+}(f^{exp}-f^n)\end{array}$$ (3)

Figure 1.

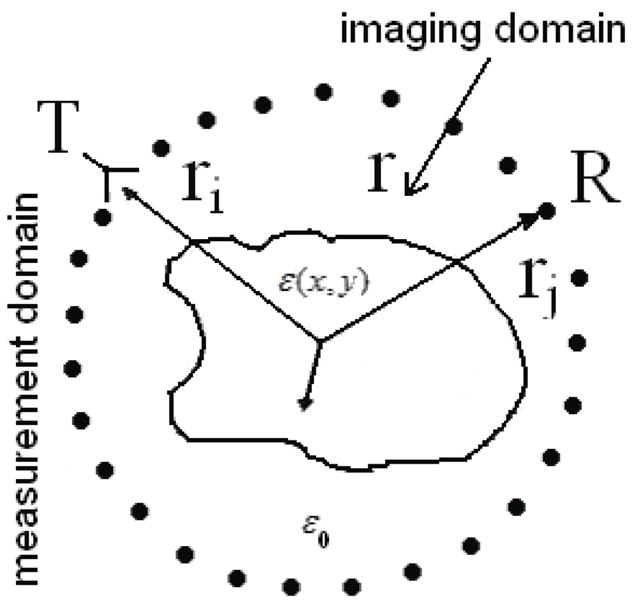
Geometrical sketch of MWT imaging problem.

The vectors f^exp and fⁿ are the measured and calculated EM fields and symbol ⁺ denotes conjugate transpose. We used a Tichonov regularization described in details in (Tichonov and Arsenin 1977). The regularization parameter α and the relaxation parameter β were chosen by trial methods. Excellent review of different regularization approaches can be found in Mojabi and LoVetri (2009).

In our new tomographic system each scanning antenna may perform as a transmitter (Tx) or a receiver (Rx) at certain time points. The previously implemented approach (Souvorov et al 1998) was modified to take into account the geometrical independence of an antenna’s location relative its Tx or Rx function. A magnetic dipole model was used here to simulate the antenna’s field pattern (Semenov et al 1999).

There are various potential schemes for obtaining differential images. In this imaging approach we calculated differential images as simple differences between two reconstructed absolute images, for example for two different time frames. Absolute images were obtained starting from homogeneous background with known dielectric properties ε₀. Another approach is when reconstructed absolute image at one given frame is used as a background for the reconstruction of all other frames. The performance assessment of various schemes for obtaining differential images is the subject of separated ongoing study.

2.2 2D Born (2DB) approach

To supplement the 2DN approach and to explore a potential of using a simplified imaging approach, we used the Born iterative method (BIM), previously developed for imaging breast tissues (Bindu et al 2007, 2006). As BIM was not very successful in imaging high contrast objects, we have adopted the distorted Born iterative method (Taflove 1998, Chew et al 1990) to reconstruct high contrast, absolute images using measured scattered field E_ij(t_k). The BIM was used for reconstruction of low contrast differential images using the differential scattered field computed as E_ij(t_k)-E_ij(t_m) where t_k, t_m represents the time of acquisition of frames k and m. The source is simulated as (Taflove 1998, Chew et al 1990):

$$E_i(\overline{r})=\frac{j}{4}{H}_0^{(1)}(k(\overline{r}-{\overline{r}}_i))$$ (4)

The volume integral equation given in Eq 1 is linearized using the Born Approximation and discretized to take the form.

$$E_{ij}=\overline{M}.\delta \overline{\epsilon }$$ (5)

The cost functional is then minimized using an optimization technique as

$$I={\left|\right|E_{ij}-\overline{M}\delta \overline{\epsilon }\left|\right|}_{\overline{C}}^2+{\delta }_t{\left|\right|\delta \overline{\epsilon }\left|\right|}_{\overline{D}}^2$$ (6)

The optimal choices of the Tichonov regularization parameter δ_t for both absolute and differential imaging were chosen by trial method.

3. Results and Discussion

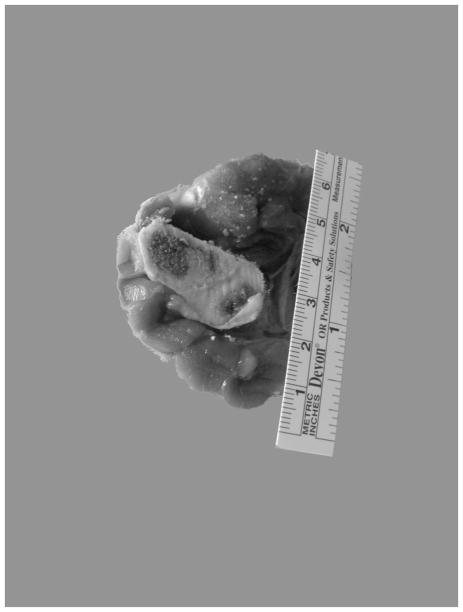
The anatomical cross-section of swine medial fore leg is presented in Figure 2. Imaging results are presented below as fused images. The background images in the gray palette are the absolute images of a 2D cross-section of the upper portion of swine’s foreleg. On the top of the background images are time-differential images presented in color. These images reflect physiological activity or interventions during the study. The degree of such changes obtained from reconstructed images is represented in the color bar as a percentile of changes:

Figure 2.

Anatomical cross-section of swine medial foreleg.

• i)For circulatory changes (systolic vs diastolic) they are (ε_systolic-ε_diastolic)/ε_diastolic [%];
• ii)For reperfusion vs occlusion they are (ε_reperfusion-ε_occlusion)/ε_occlusion [%];
• ii)For a simulated compartment syndrome they are: (ε_+xmin of comp injury-ε_baseline)/ε_baseline [%].

3.1. Circulatory related changes: systolic vs diastolic and reperfusion vs occlusion

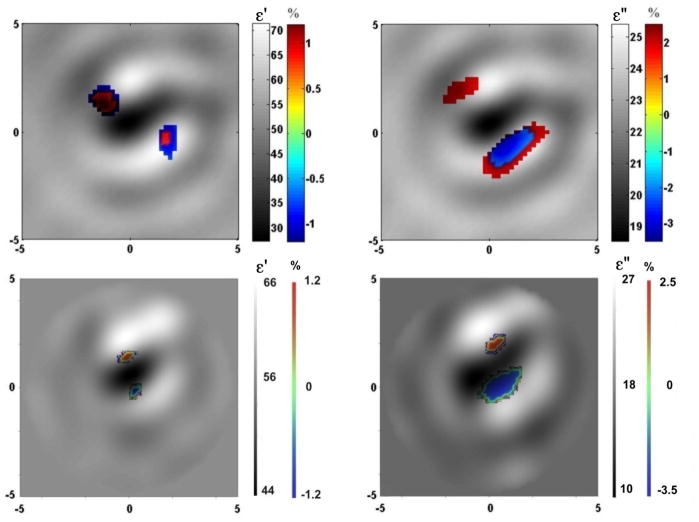
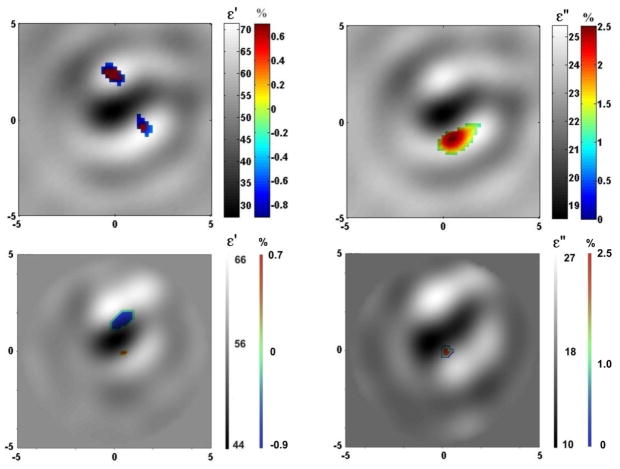
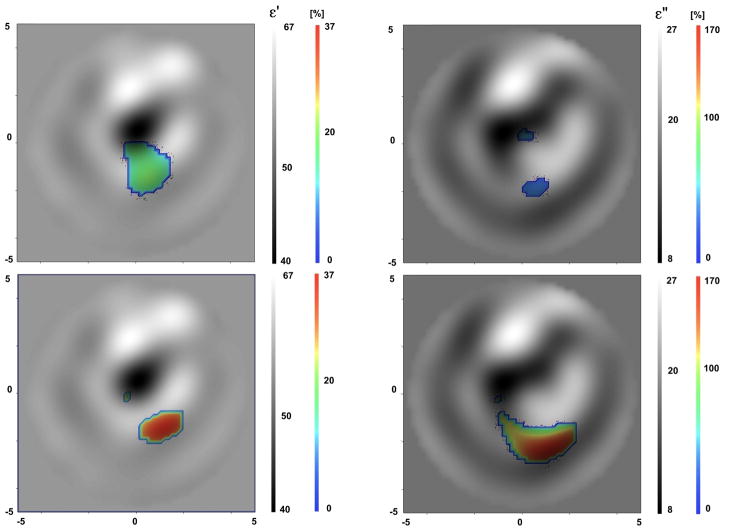
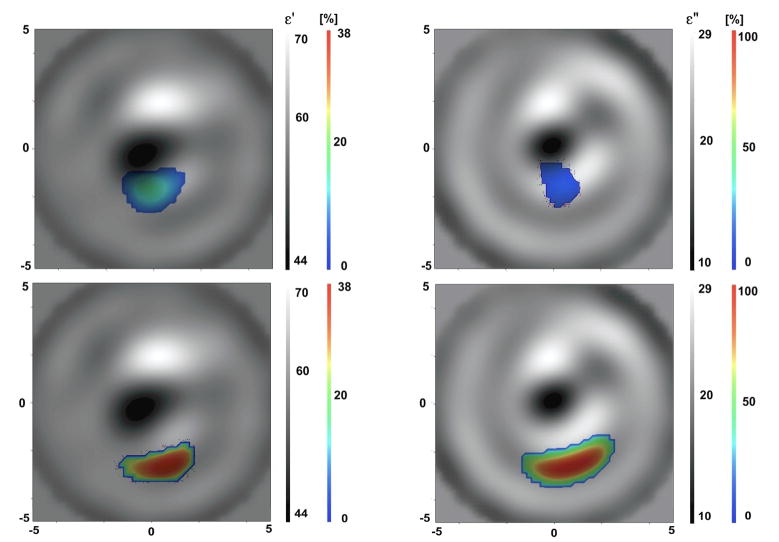
Fused images of circulatory related changes are presented in Figure 3 and 4 for the systolic vs diastolic case and reperfusion vs occlusion case correspondingly. In both groups of images the left column represents fused images (absolute and time-differential) of ε′ and the right column represents corresponding fused images of ε″. The reconstructed absolute images correlate well with anatomy (presented in Figure 2) and clearly reveal the boney area with low dielectric properties (dark colored) and the soft tissue component with higher dielectric properties (bright colored). The reconstructed values of dielectric properties are not within a range of expected/tabulated properties of the tissues. For example, at a frequency of 1GHz, the expected values for the dielectric properties are ε ~ 12 +j4 for bone and ε ~ 56 +j18 – for skeletal muscle (Gabriel et al 1996, FCC). In our previous study using a computer simulated model of the extremity (Semenov et al, 2007 ) we were able to more precisely reconstruct the absolute values of the dielectric properties even with a 5–10% noise figure. However, as pointed out in the companion paper, the distribution of the EM field within a small imaging chamber is much more complex as compared with the “un-reflecting” model in our previous study. An accounting for a casing together with an optimization of the number of Tx/Rx may improve the reconstruction of absolute images.

Figure 3.

Fused reconstructed images of circulatory related changes (systolic vs diastolic) in cross section of swine extremity. Top: 2DB imaging approach (left of ε′ and right for ε″). Bottom: 2DN imaging approach (left of ε′ and right for ε″). Frequency 1.5 GHz.

Figure 4.

Fused reconstructed images of reperfusion vs occlusion in cross section of swine extremity. Top: 2DB imaging approach (left of ε′ and right for ε″). Bottom: 2DN imaging approach (left of ε′ and right for ε″). Frequency 1.5 GHz

Prior to executing our time-differential and fused imaging strategy, we studied the ability of the system to detect signals associated with physiological changes resulting from interventions to soft tissue–we called them “physiological signatures”. As pointed out earlier, this is a critical issue since if there are no changes in experimentally measured EM fields associated with physiological changes or interventions, it would be impossible to image them no matter how perfect the image reconstruction algorithm is. The results are presented in Figures 6 and 7 in the companion paper. In summary, there were differences in measured EM fields up to 10–20% in amplitude and 4–6 degrees in phase, detected only on 2–3 receivers of the maximum 13 receivers within the system (for particular configuration of Tx/Rx). This confirmed that more receivers per measurement domain would be preferable.

Figure 6.

Fused reconstructed images of a simulated compartment syndrome in cross section of swine extremity. Top: +5 min of compartment syndrome (left for ε′ and right for ε″). Bottom: +16 min of compartment syndrome (left of ε′ and right for ε″). Frequency 1.05 GHz. 2DB imaging approach.

Figure 7.

Fused reconstructed images of a simulated compartment syndrome in cross section of swine extremity. Top: +5 min of compartment syndrome (left for ε′ and right for ε″). Bottom: +16 min of compartment syndrome (left for ε′ and right for ε″). Frequency 1.5 GHz. 2DN imaging approach.

Time-differential images fused with anatomical ones in Figures 3 and 4 indicate circulatory related changes while they are consistent with the anatomical location of blood vessels. The percentile of changes was small, within the range of 1% in ε′ and 2–3% in ε″. It has to be noted that within microwave tomography the averaged dielectric properties over a certain volume are reconstructed. In this case, it includes blood vessels together with a portion of skeletal muscle. In our early non-imaging experiments and computer simulations we suggested that in spite of the fact that MWT technology is in its early development stage, it is estimated, that this technology is able to reconstruct about 3–5% change in overall cross-sectional blood flow (Semenov et al, 2007 ). A further in-depth study is under way in order to ascertain the relationship in between changes in extremity blood flow and the values of reconstructed differential images. This will allow for direct applications of this novel imaging modality in clinical settings. It can be noted from the images that the performance of 2DN imaging approach shows better spatially resolute time-differential images.

3.2. Simulated Compartment Syndrome

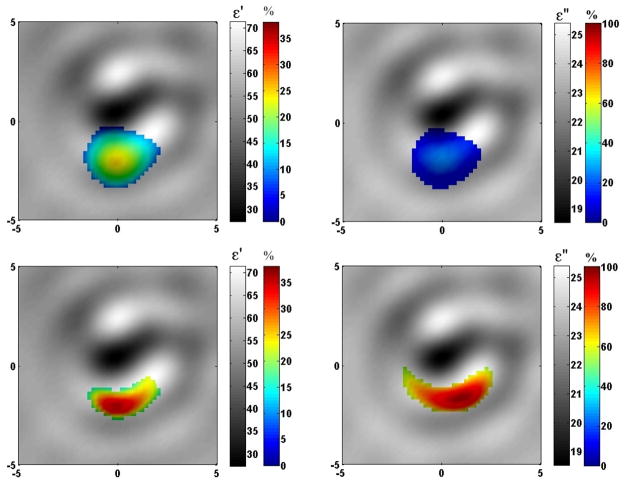
Fused images in the development of a simulated compartment syndrome in the swine extremity are presented in Figures 5–8. Images in Figures 5 and 6 were obtained when the MWT system operates at a frequency of 1.05 GHz. Images in Figures 7 and 8 were obtained in another swine experiment when the MWT system operated at 1.5 GHz. At each Figure there are four fused images representing ε′ – left column and ε″ – right column. Two fused images on the top correspond to + 5 min in the development of a simulated compartment syndrome and two images on the bottom correspond to +16 min in the development of a simulated compartment syndrome. The 2DN imaging approach was used for the reconstruction of the images presented in Figures 5 and 7, while results of an application of a 2DB imaging approach are presented in Figures 6 and 8.

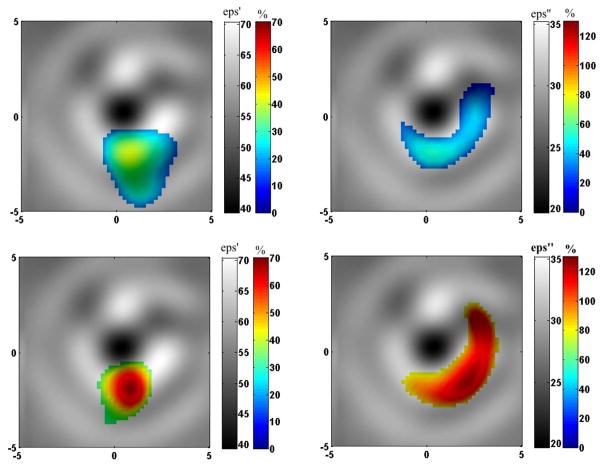
Figure 5.

Fused reconstructed images of simulated compartment syndrome in cross section of swine extremity. Top: +5 min of compartment syndrome. Bottom: +16 min of compartment syndrome.

Frequency 1.05 GHz. 2DN imaging approach.

Figure 8.

Fused reconstructed images of a simulated compartment syndrome in cross section of swine extremity. Top: +5 min of compartment syndrome (left for ε′ and right for ε″). Bottom: +16 min of compartment syndrome (left for ε′ and right for ε″). Frequency 1.5 GHz. 2DB imaging approach.

Similar to previous cases presented in Figures 3–4, the reconstructed absolute images clearly reveal the boney area with low dielectric properties (dark colored) and the soft tissue component with higher dielectric properties (bright colored). As earlier, prior to execution of our time-differential and fused imaging strategy, we studied the ability of the system for detecting signals associated with the development of a simulated compartment syndrome’s – “physiological signatures”. The results are presented in Figure 8 of companion paper. Overall, the differences associated with the development of a simulated compartment syndrome in an animal extremity are much more significant: up to 6 times in amplitude and up to 150 degrees in phase at +16 min of the development of the syndrome. This suggests confident image reconstruction revealing the location and degree of an injury within the extremity soft tissue.

Time-differential images fused with anatomical ones in Figures 5–8 indicate changes in the extremity associated with the development of a simulated compartment syndrome and are consistent with the anatomical location of intervention. At this stage methodologically it was not possible for simultaneous performance of MWT experiment and monitoring of the compartmental pressure as an independent marker of an injury. However, a visual inspection reveals clear evidence of swelling. Additionally, after immediate infusion of a lactate ringer solution into the muscular compartment a decrease of arterial blood flow (down 20%) was observed indicating an elevation the compartmental pressure.

The images in Figures 5–8 show that there was an anticipated accumulation of extra fluid suggested by the pronounced blue-to-red areas on the differential image. It has to be emphasized that MWT is a novel imaging modality and ways of reading reconstructed MWT images have to be further studied and understood.

The percentile of changes was significant. For example, in the case of a simulated compartment syndrome, presented in Figures 4 and 5, the maximal changes at +5 min in the development of injury (top two images in both Figures) are about 20% for both ε′ and ε″ (blue color), while at +16 min in the development of injury (bottom two images in both Figures) the maximal changes are much larger: about +38% for ε′ and about +100% for ε″ (red color). In this case the frequency was 1.05 GHz. Overall, the changes are more localized and more pronounced especially on ε″ at higher frequency (1.5 GHz) – Figures 6 and 7.

In our early non-imaging experiments and computer simulations we suggested that in spite of the fact that MWT technology is in its early development stage, it is estimated, that the technology is able to reconstruct approximately 12–25% of the elevated compartment pressure (Semenov et al, 2007 ). A further in-depth study is planned in order to find a relationship in between changes in compartmental pressure and the values of reconstructed differential images. This will allow for direct applications of this novel imaging modality in the clinical setting.

The need for further improvement of reconstructed images is applicable to both absolute and time-differential portions of fused images. An appropriate accounting for an imaging domain casing, an optimization of the number of transmitting and receiving antennas and the use of a 3D MWT system and 3D image reconstruction method are just a few improvements required to obtain better absolute images. In our early experiments we’ve studied the applicability of 2D vs. 3D approaches for microwave tomographic imaging of biological objects (Semenov et al 2000). It was concluded that qualitative imaging requires a use of 3D system and 3D imaging approach. The limitations of the use of 2D approach in this study are well understood. However, it allows for clear demonstration that microwave tomography is feasible for fast functional imaging of soft tissues. This was achieved by the use of biological object which is most similar to 2D representation – the upper (cross section) portion of an animal extremity. This was achieved also by the development of as favorable as possible physical conditions for 2D imaging within the imaging domain. We used a matching solution with as much loss as possible to enhance total attenuation while not compromising the favorable SNR. We assume that this might be one of a reason why a simplified approach based on Born iterations works here, but fails in previous cases when using MWT computer simulations of extremity imaging (Semenov et al, 2007). Overall, the ways of reading the reconstructed MWT images have to be further studied and understood.

4. Conclusions

We present a novel approach for functional fused imaging using microwave tomography. The approach was successively validated in animal experiments with short term flow reduction and a simulated compartment syndrome using a dedicated MWT system. The presented fused images, while not perfect, as MWT is an emerging imaging modality, do indicate the great potential for this technology in functional imaging.