The social network (of protein conformations)

Proteins possess thousands of degrees of freedom, and yet, they can rapidly and reliably find their way into well-defined folded configurations (1). In the cell, these folded proteins carry out highly specific motions critical to cargo transport and force transduction, energy generation, and catalysis. However, how is this possible given their incongruously large conformation spaces? Is their behavior intrinsically complex, where the nuanced details of all of the interatomic interactions are critical to their behavior, or can this motion be understood in terms of simpler collective behavior? In PNAS, Ceriotti et al. (2) examine this question by formulating an algorithm that attempts to uncover simple collective behavior in the conformation spaces of biomolecules in an automated fashion.

Over the last few decades, a number of sophisticated computer simulation techniques have been developed that allow these conformation spaces to be explored, generating compendia of thousands or millions of conformational snapshots in a typical computer experiment. However, as computer hardware and clever software have advanced, making sense of these datasets has become harder and not easier. When it might have sufficed for a skilled structural biologist with a graphics terminal to extract insight into molecular mechanism from picoseconds to nanoseconds of molecular dynamics, it is no longer possible when these trajectories are microseconds to milliseconds in length or if the sampled ensembles represent a substantial fraction of the thermodynamically accessible conformation space. To make sense of these large datasets and learn something useful about the molecular motions that they represent, some form of data reduction is necessary.

In one form or another, dimensionality reduction methods have been a workhorse of data visualization and analysis for centuries. By transforming a high-dimensional representation into a representation in only a few dimensions—generally two or three to facilitate human comprehension—these approaches can often provide useful insight about how the data are organized and structured, or useful guidance for further exploration. The challenge here is that, because any such projection from high to low dimension must result in a loss of information, a decision must be made about what information is to be retained and what information is irrelevant.

A familiar example is the Mercator projection of the globe, in which the dimensionality of a dataset (the location of large land masses on the Earth) is reduced from three (their location in 3D space) to two (coordinates on a flat, rectangular sheet of paper). In constructing his projection in 1569, Gerardus Mercator made particular choices of what information was most critical to preserve:

In this mapping of the world we have [desired] to spread out the surface of the globe into a plane that the places shall everywhere be properly located, not only with respect to their true direction and distance, one from another, but also in accordance with their due longitude and latitude; and further, that the shape of the lands, as they appear on the globe, shall be preserved as far as possible (3).

In more modern terms, Mercator chose to make his mapping conformal—preserving the equality of stretching North–South and East–West directions at every point—and ensure that all lines of constant bearing become straight lines, features that made his map particularly suited to maritime navigation (4). Although the choices of properties to be preserved in mapping conformation spaces of proteins will differ from Mercator's choices, the fundamental challenges remain the same.

The simplest dimensionality reduction methods applied to biomolecular simulations are linear transformations that project the data onto a few orthogonal principal axes aligned with the directions of largest variation in molecular geometry. Although still a common technique, these methods often reveal little about complex large-scale motions, failing to provide more insight because of the highly nonlinear structure of the populated regions of protein conformation spaces (5). Other methods, such as multidimensional scaling (6), attempt to preserve the distances between pairs of conformations when embedded in a low-dimensional space. Unfortunately, these methods are challenged when the low-dimensional object of interest is embedded in the high-dimensional space in a complex way, such as the classic example of a jelly roll—a 2D dataset rolled into a 3D structure, much like the popular snack cake.

More recently, dimensional reduction techniques such as locally linear embedding (7) were developed to overcome these limitations, preserving local spatial relationships to nearest neighbors in constructing the embedding, and allowing the scheme to unroll the jelly roll. Unfortunately, the structure of biomolecular spaces is such that these methods seem to be of limited use for biomolecules (2, 8). Das et al. (9) instead explored schemes that combine the best ideas from these earlier methods by trying to preserve distances between conformations but measuring distances along either geodesics (shortest distances within the low-dimensional manifold of populated conformational space) or typical diffusion times between conformations (10). These methods show great promise but can be time-consuming to construct.

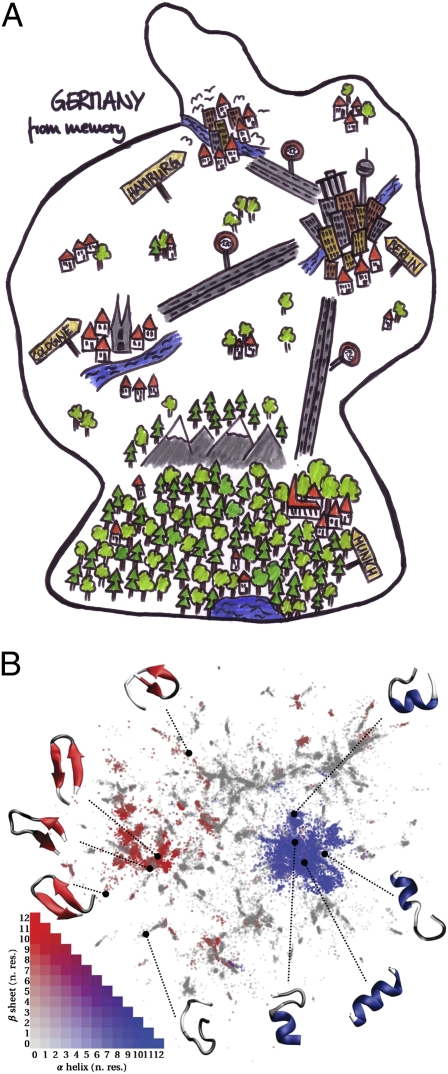
Ceriotti et al. (2), in their article in PNAS, take a different approach to embedding biomolecular conformations in low-dimensional spaces. They suggest that, although it may not be possible to build the analog of a Mercator projection map of conformations, it might, instead, be possible to build a Facebook (2). They examine the distribution of distances between thermally accessible conformations, finding that most of the information about the local connectivity of basins—much like directly connected friends on the popular Web site—can be found in an intermediate range of conformational distances (2). By using a multidimensional scaling-like embedding that focuses on these intermediate distances between friends, they show that a projection that preserves the local connectivity relationship between conformational basins can be constructed (2). The resulting projection constitutes a rough map of conformational space that is locally accurate but globally distorted. Applied to a small alanine repeat peptide, they show that this scheme—which they call a sketch map because of its similarity to roughly sketching a map from memory in a way that preserves local relationships—produces more informative projections than previous attempts at dimensional reduction, neatly segregating helical and β-turn conformational states (Fig. 1).

Fig. 1.

(A) Map of Germany sketched from memory (image courtesy of Nomsa Buchholz) preserves connections between important neighbors while distorting global layout, much like the (B) sketch map scheme of Ceriotti et al. (2) in mapping the conformation space of peptides (reprinted from ref. 2).

The sheer difficulty of identifying a set of nonlinear low-dimensional reaction coordinates to project onto has led some researchers to take a different direction altogether, focusing instead on summarizing the kinetic connectivity of closely related basins in a graph theoretic manner rather than trying to project them into a continuous space of low dimension. These approaches include disconnectivity graphs, which arrange minima into trees based on the transition state barrier heights connecting them (11), conformation space networks, which assume that conformational similarity is identical to kinetic connectivity (12), and Markov state models, which cluster conformations using both kinetic and conformational similarity from simulations of dynamics (13, 14). In addition to providing more direct means to connecting with biophysical spectroscopic experiments, these approaches offer alternative ways to extract insight from the resulting models (15, 16).

With this growing fracturing of approaches (continuous projections vs. network models), it is timely to review the benefits and limitations of each approach. Projection to a few degrees of freedom is a natural extension of the analysis of simple chemical reactions, where free energy landscapes in the appropriate reaction coordinates can provide human visual understanding along with quantitative predictive power. However, this scheme relies on the ease of selecting appropriate reaction coordinates as collective variables—degrees of freedom that are kinetically relevant to the motions of interest, like folding or force generation. Although on the surface, this approach may seem straightforward, much work has pointed to numerous challenges in discovering these coordinates, even when the endpoints are known (17, 18). Moreover, overestimating the kinetic relevance of a given degree of freedom could lead to qualitative and quantitative misinterpretation.

A network approach seeks to resolve this problem by never requiring a reaction coordinate. Instead, one deals with a potentially high-dimensional representation directly. This method does not completely remove the challenge of requiring that the kinetically relevant coordinates be identified, but in a sense, it deals with it constructively, rather than with a priori assumptions, by using algorithmic schemes for producing kinetically relevant state decompositions (13, 14). However, the challenge of ensuring that these decompositions are kinetically relevant and can be systematically constructed for a wide variety of systems without extensive human intervention remains, although these challenges are universal.

Still, a continuous representation of conformation space offers potential advantages over network-centric pictures. One way in which this advantage could be realized is to use the low-dimensional representation to bias simulations to ensure coverage of important, but poorly sampled, regions of conformation space. Recent adaptive biasing techniques such as metadynamics (19)—essentially, a continuous version of the Wang–Landau algorithm (20) that has been wildly successful in statistical physics—or equation-free approaches (21) could well prove a powerful combination combined with approaches like sketch map to identify appropriate collective variables, especially if the maps could be built up on the fly. Adaptive sampling schemes also show the potential for large efficiency gains in constructing network-based representations of conformation space (22).

Exciting combinations of the two perspectives—continuous embeddings and network representations—could offer more advantages than either perspective alone, but this territory remains largely uncharted. Because biological simulation tackles larger and more complex systems—a feat relatively recently possible because of the availability of structural data for large-scale biomolecular assemblies such as the ribosome and nuclear pore complex—additional development of automated approaches to driving simulations and extracting useful insight will only become more important.